{ "cells": [ { "cell_type": "markdown", "metadata": {}, "source": [ "# A simple economic model with an analytical solution\n", "\n", "In this notebook, we use `TensorFlow 1.13.1` to showcase the general workflow of setting up and solving dynamic general equilibrium models with _deep equilibrium nets_. Use `pip install tensorflow==1.13.1` to install the correct version.\n", "\n", "The notebook accompanies the working paper by [Azinovic, Gaegauf, & Scheidegger (2021)](https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3393482) and corresponds to the model solved in appendix H with a slighly different model calibration.\n", "\n", "Note that this is a minimal working example for illustration purposes only. A more extensive implementation will be published on Github. \n", "\n", "The economic model we are solving in this example is one for which we know an exact solution. We chose to solve a model from [Krueger and Kubler (2004)](https://www.sciencedirect.com/science/article/pii/S0165188903001118), which is based on [Huffman (1987)](https://www.journals.uchicago.edu/doi/10.1086/261445), because, in addition to being analytically solvable, it is closely related to the models solved in the paper. Therefore, the approach presented in this notebook translates directly to the models in working paper.\n", "\n", "## The model \n", "\n", "We outline the model briefly. \n", "\n", "### tldr\n", "The model has $A$ agents that only work in the first period of their lives. They optimize lifetime log utility by saving in risky capital. Agents consume everything in the last period. There is a representative firm that produces with labor and capital and is affected by TFP and depreciation shocks. The firm pays market prices for labor and capital.\n", "\n", "***\n", "\n", "### Households\n", "Agents live for $A$ (here we consider $A = 6$) periods and have log utility. Agents only work in the first period of their life: $l^h_t=1$ for $h=0$ and $l^h_t=0$ otherwise. Therefore, the aggregate labor supply is constant and equal to one: $L_t=1$. Agents receive a competitive wage and can save in risky capital. Households cannot die with debt. Otherwise, there are no constraints or adjustment costs.\n", "The household's problem is\n", "\n", "$$ \\max_{\\{c_{t+i}^{i}, a_{t+i}^{i}\\}_{i=0}^{A-1}}\\mathbb{E}_{t}{\\sum_{i=0}^{A-1}\\log(c_{t+i}^{i})} $$\n", "subject to:\n", "$$c_{t}^{h} + a_t^{h} = r_t k_t^h + w_t l^h_t$$\n", "$$k^{h+1}_{t+1} = a_t^h $$\n", "$$a^{A-1}_t \\geq 0$$\n", "\n", "where $c_t^h$ denotes the consumption of age-group $h$ at time $t$, $a^h_t$ denotes the saving, $k_t^h$ denotes the available capital in the beginning of the period, $r_t$ denotes the price of capital, $l_t^h$ denotes the exogenously supplied labor endowment, and $w_t$ denotes the wage.\n", "\n", "### Firms\n", "\n", "There is a single representative firm with Cobb-Douglas production function.\n", "The production function is given by\n", "$$f(K_t,L_t,z_t) = \\eta_t K^{\\alpha}_t L^{1-\\alpha}_t + K_t(1-\\delta_t),$$\n", "where $K_t$ denotes aggregate capital, where\n", "$$K_t = \\sum_{h=0}^{A-1} k^h_t,$$\n", "$L_t$ denotes the aggregate labor supply, where\n", "$$L_t = \\sum_{h=0}^{A-1} l^h_t,$$\n", "$\\alpha$ denotes the capital share in production, $\\eta_t$ denotes the stochastic TFP, and $\\delta_t$ denotes the stochastic depreciation. The firm's optimization problem implies that the return on capital and the wage are given by\n", "$$r_t = \\alpha \\eta_t K_t^{\\alpha - 1} L_t^{1 - \\alpha} + (1 - \\delta_t),$$\n", "$$w_t = (1 - \\alpha) \\eta_t K_t^{\\alpha} L_t^{-\\alpha}.$$\n", "\n", "## Equilibrium\n", "\n", "A competitive equilibrium, given initial conditions $z_0, \\{ k_0^s \\}_{s=0}^{A-1}$, is a collection of choices for households $ \\{ (c_t^s, a_t^s)_{s = 0}^{A-1} \\}_{t=0}^\\infty$ and for the representative firm $(K_t, L_t)_{t=0}^\\infty$ as well as prices $(r_t, w_t)_{t=0}^\\infty$, such that\n", "\n", "1. given prices, households optimize,\n", "2. given prices, the firm maximizes profits,\n", "3. markets clear.\n", "\n", "\n", "## Table of contents\n", "\n", "0. [Set up workspace](#workspace)\n", "1. [Model calibration](#modelcal)\n", "2. [_Deep equilibrium net_ hyper-parameters](#deqnparam)\n", " 1. [Neural network](#nn)\n", "3. [Economic model](#econmodel)\n", " 1. [Current period (t)](#currentperiod)\n", " 2. [Next period (t+1)](#nextperiod)\n", " 3. [Cost/Euler function](#cost)\n", "4. [Training](#training)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## 0. Set up workspace \n", "\n", "First, we need to set up the workspace. All of the packages are standard python packages. This version of the _deep equilibrium net_ notebook will be computed with `TensorFlow 1.13.1`. Make sure you are working in an environment with TF1 installed. Use `pip install tensorflow==1.13.1` to install the correct version.\n", "\n", "The only special module is `utils` from which we import a mini-batch function `random_mini_batches` and a function that initializes the neural network weights `initialize_nn_weight`.\n", "\n", "### Saving and continuing training\n", "\n", "You can save and resume training by saving and loading the tensorflow session and data starting point.\n", "* The saved session stores the neural network weights and the optimizer's state. If you have saved a session that you would like to reload, set `sess_path` to the session checkpoint path. For example, to load the 100th episode's session set `sess_path = './output/sess_100.ckpt'`. Otherwise, set `sess_path` to `None` to train from scratch. Currently, this script saves the session at the end of each [episode](#deqnparam).\n", "* The saved data starting point stores the an exogeneous shock and a capital distribution, which can be used to simulate states into the future from. If you have saved a starting point that you would like to reload, set `data_path` to the numpy data path. For example, to load the 100th episode's starting point set `data_path = './output/data_100.npy'`. Otherwise, set `data_path` to `None` to train from scratch." ] }, { "cell_type": "code", "execution_count": 5, "metadata": { "scrolled": true }, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "tf version: 1.13.1\n" ] } ], "source": [ "%matplotlib notebook\n", "\n", "# Import modules\n", "import os\n", "import re\n", "from datetime import datetime\n", "\n", "import tensorflow as tf\n", "import numpy as np\n", "from utils import initialize_nn_weight, random_mini_batches\n", "\n", "import matplotlib.pyplot as plt\n", "plt.rcParams.update({'font.size': 12})\n", "plt.rc('xtick', labelsize='small')\n", "plt.rc('ytick', labelsize='small')\n", "std_figsize = (4, 4)\n", "\n", "# Make sure that we are working with tensorflow 1\n", "print('tf version:', tf.__version__)\n", "assert tf.__version__[0] == '1'\n", "\n", "# Set the seed for replicable results\n", "seed = 0\n", "np.random.seed(seed)\n", "tf.set_random_seed(seed)\n", "\n", "# Helper variables\n", "eps = 0.00001 # Small epsilon value\n", "\n", "# Make output directory to save network weights and starting point\n", "if not os.path.exists('./output'):\n", " os.mkdir('./output')\n", "\n", "# Path to saved tensorflow session\n", "sess_path = None\n", "# Path to saved data starting point\n", "data_path = None" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## 1. Model calibration \n", "\n", "### tldr\n", "\n", "We solve a model with 6 agents. There are 4 exogenous shock which are the product of 2 depreciation ($\\delta \\in \\{0.5, 0.9\\}$) and 2 TFP shocks ($\\eta \\in \\{0.95, 1.05\\}$). Each shock-state has an equal probably of 0.25 of realizing in the next period. Agents only work in the first period. The economic parameters are calibrated to: $\\alpha = 0.3$, $\\beta=0.7$, and $\\gamma = 1.0$.\n", "\n", "***\n", "\n", "We solve the model for $A = 6$ agents and base our parameterization on [Krueger and Kubler (2004)](https://www.sciencedirect.com/science/article/pii/S0165188903001118). \n", "\n", "### Shocks\n", "The depreciation $\\delta$ takes one of two values, $\\delta \\in \\{0.5, 0.9\\}$. The TFP $\\eta$ also takes one of two values, $\\eta \\in \\{0.95, 1.05\\}$.\n", "Both the TFP and depreciation shocks are i.i.d. with a transition matrix:\n", "\\begin{equation}\n", "\\Pi^{\\eta} = \\Pi^{\\delta}=\n", "\\begin{bmatrix}\n", "0.5 & 0.5 \\\\\n", "0.5 & 0.5\n", "\\end{bmatrix}.\n", "\\end{equation}\n", "and evolve independently of each other. In total, there are four possible combinations of depreciation shock and TFP shock that are labeled by $z \\in \\mathcal{Z}=\\{1,2,3,4\\}$ and correspond to $\\delta=[0.5, 0.5, 0.9, 0.9]^T$ and $\\eta=[0.95, 1.05, 0.95, 1.05]^T$. The overall transition matrix is given by\n", "\\begin{equation}\n", "\\Pi= \\Pi^{\\delta} \\otimes \\Pi^{\\eta} = \\begin{bmatrix}\n", "0.25 & 0.25 & 0.25 & 0.25 \\\\\n", "0.25 & 0.25 & 0.25 & 0.25 \\\\\n", "0.25 & 0.25 & 0.25 & 0.25 \\\\\n", "0.25 & 0.25 & 0.25 & 0.25\n", "\\end{bmatrix},\n", "\\end{equation} where $\\Pi_{i, j}$ denotes the probability of a transition from the exogenous shock $i$ to exogenous shock $j$, where $i,j \\in \\mathcal{Z}$. \n", "\n", "### Labor\n", "Agents in this economy are alive for 6 periods. Agents work in the first period of their lives before retiring for the remaining 4. That is, their labor endowment during their working age is 1 (and 0 otherwise).\n", "\n", "### Production and household parameters\n", "The output elasticity of the Cobb-Douglas production function is $\\alpha = 0.3$, the discount factor of agents' utility is $\\beta=0.7$, and the coeffient of risk aversion (in CRRA utility) is $\\gamma = 1.0$.\n" ] }, { "cell_type": "code", "execution_count": 8, "metadata": {}, "outputs": [], "source": [ "# Number of agents and exogenous shocks\n", "num_agents = A = 6\n", "num_exogenous_shocks = 4\n", "\n", "# Exogenous shock values\n", "delta = tf.constant([[0.5], [0.5], [0.9], [0.9]], dtype=tf.float32) # Capital depreciation (dependent on shock)\n", "eta = tf.constant([[0.95], [1.05], [0.95], [1.05]], dtype=tf.float32) # TFP shock (dependent on shock)\n", "\n", "# Transition matrix\n", "# In this example we hardcoded the transition matrix. Changes cannot be made without also changing\n", "# the corresponding code below.\n", "p_transition = 0.25 # All transition probabilities are 0.25\n", "pi_np = p_transition * np.ones((4, 4)) # Transition probabilities\n", "pi = tf.constant(pi_np, dtype=tf.float32) # Transition probabilities\n", "\n", "# Labor endowment\n", "labor_endow_np = np.zeros((1, A))\n", "labor_endow_np[:, 0] = 1.0 # Agents only work in their first period\n", "labor_endow = tf.constant(labor_endow_np, dtype=tf.float32)\n", "\n", "# Production and household parameters\n", "alpha = tf.constant(0.3) # Capital share in production\n", "beta_np = 0.7\n", "beta = tf.constant(beta_np, dtype=tf.float32) # Discount factor (patience)\n", "gamma = tf.constant(1.0, dtype=tf.float32) # CRRA coefficient" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## 2. _Deep equilibrium net_ hyper-parameters \n", "\n", "Here, we will briefly outline the _deep equilibrium net_ architecture and choice of hyper-parameters. By hyper-parameters, we refer too all of the parameters that can be chosen freely by the modeller. 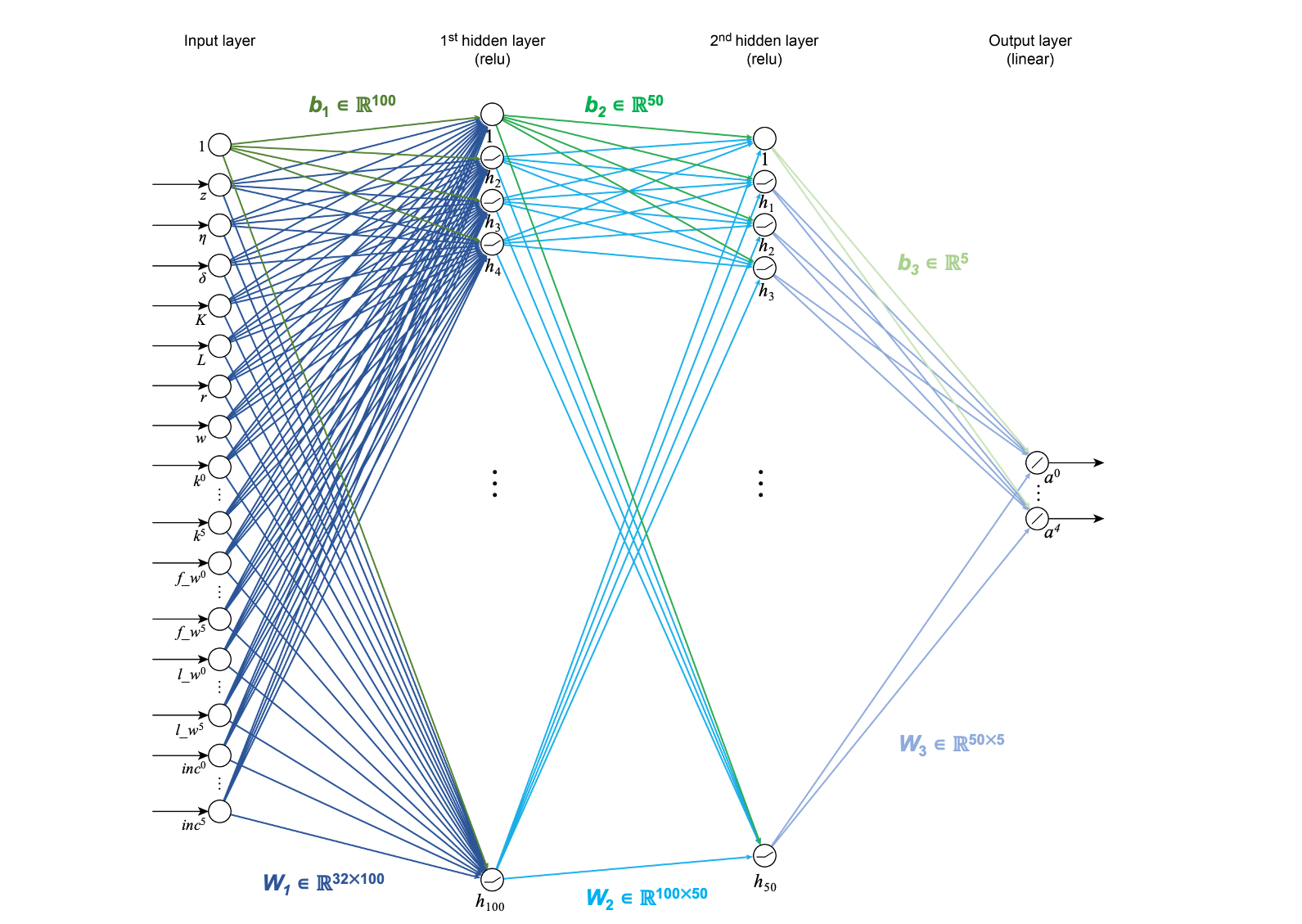This is in contrast to \"parameters\", which refers to the neural network weights that are learned during training.\n", "We found it helpful to augment the state we pass to the neural network with redundant information, such as aggregate variables and the distribution of financial wealth.\n", "In this notebook, we do the same.\n", "\n", " * Neural network architecture (see NN diagram below):\n", " * The neural network takes an extended state that is 32-dimensional:\n", " * Natural state:\n", " * 1 dimension for the shock index,\n", " * 6 dimensions for the distribution of capital across age groups\n", " * Redundant extension:\n", " * 1 dimension for the current TFP,\n", " * 1 dimension for the current depreciation,\n", " * 1 dimension for aggregate capital,\n", " * 1 dimension for aggregate labor supply, \n", " * 1 dimension for the return on capital,\n", " * 1 dimension for the wage,\n", " * 1 dimension for the aggregate production,\n", " * 6 dimensions for the distribution of financial wealth,\n", " * 6 dimensions for the distribution of labor income, \n", " * 6 dimensions for the distribution of total income.\n", " * The first and second hidden layers have 100 and 50 nodes, respectively.\n", " * The output layer is 5-dimensional.\n", " * Training hyper-parameters:\n", " * We simulate 5'000 episodes.*\n", " * Per episode, we compute 20 epochs.\n", " * We use a minibatch size of 512.\n", " * Each episode is 10'240 periods long.\n", " * The learning rate is set to 0.00001.\n", "\n", "\\* In the _deep equilibrium net_ framework we iterate between a simulation and training phase (see [training](#training)). We first simulate a training dataset based on the current state of the neural network. That is, we simulate a random sequence of exogenous shocks for which we compute the capital holdings of the agents. We call the set of simulated periods an _episode_. 5'000 episodes means that we re-simulate the training data 5'000 times.\n", "\n", "Note that this calibration is not optimal for the economic model being solved. This script is intended to provide a simple introduction to _deep equilibrium nets_ and not an indepth discussion on optimizing the performance.\n", "\n", "" ] }, { "cell_type": "code", "execution_count": 9, "metadata": {}, "outputs": [], "source": [ "num_episodes = 5000 \n", "len_episodes = 10240\n", "epochs_per_episode = 20\n", "minibatch_size = 512\n", "num_minibatches = int(len_episodes / minibatch_size)\n", "lr = 0.00001\n", "\n", "# Neural network architecture parameters\n", "num_input_nodes = 8 + 4 * A # Dimension of extended state space (8 aggregate quantities and 4 distributions)\n", "num_hidden_nodes = [100, 50] # Dimension of hidden layers\n", "num_output_nodes = (A - 1) # Output dimension (capital holding for each agent. Agent 1 is born without capital (k^1=0))" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### 2.A. Neural network \n", "\n", "Since we are using a neural network with 2 hidden layers, the network maps:\n", "$$X \\rightarrow \\mathcal{N}(X) = \\sigma(\\sigma(XW_1 + b_1)W_2 + b_2)W_3 + b_3$$\n", "where $\\sigma$ is the rectified linear unit (ReLU) activation function and the output layer is activated with the linear function (which is the identity function and hence omitted from the equation). Therefore, we need 3 weight matrices $\\{W_1, W_2, W_3\\}$ and 3 bias vectors $\\{b_1, b_2, b_3\\}$ (compare with the neural network diagram above). In total, we train 5'954 parameters:\n", "\n", "| $W_1$ | $32 \\times 100$ | $= 3200$ |\n", "| --- | --- | --- |\n", "| $W_2$ | $100 \\times 50$ | $= 5000$ |\n", "| $W_3$ | $50 \\times 5$ | $= 250$ |\n", "| $b_1 + b_2 + b_3$ | $100 + 50 + 5$ | $= 155$|\n", "\n", "\n", "We initialize the neural network parameters with the `initialize_nn_weight` helper function from `utils`.\n", "\n", "Then, we compute the neural network prediction using the parameters in `nn_predict`. " ] }, { "cell_type": "code", "execution_count": 14, "metadata": {}, "outputs": [], "source": [ "# We create a placeholder for X, the input data for the neural network, which corresponds\n", "# to the state.\n", "X = tf.placeholder(tf.float32, shape=(None, num_input_nodes))\n", "# Get number samples\n", "m = tf.shape(X)[0]\n", "\n", "# We create all of the neural network weights and biases. The weights are matrices that\n", "# connect the layers of the neural network. For example, W1 connects the input layer to\n", "# the first hidden layer\n", "W1 = initialize_nn_weight([num_input_nodes, num_hidden_nodes[0]])\n", "W2 = initialize_nn_weight([num_hidden_nodes[0], num_hidden_nodes[1]])\n", "W3 = initialize_nn_weight([num_hidden_nodes[1], num_output_nodes])\n", "\n", "# The biases are extra (shift) terms that are added to each node in the neural network.\n", "b1 = initialize_nn_weight([num_hidden_nodes[0]])\n", "b2 = initialize_nn_weight([num_hidden_nodes[1]])\n", "b3 = initialize_nn_weight([num_output_nodes])\n", "\n", "# Then, we create a function, to which we pass X, that generates a prediction based on\n", "# the current neural network weights. Note that the hidden layers are ReLU activated.\n", "# The output layer is not activated (i.e., it is activated with the linear function).\n", "def nn_predict(X):\n", " hidden_layer1 = tf.nn.relu(tf.add(tf.matmul(X, W1), b1))\n", " hidden_layer2 = tf.nn.relu(tf.add(tf.matmul(hidden_layer1, W2), b2))\n", " output_layer = tf.add(tf.matmul(hidden_layer2, W3), b3)\n", " return output_layer\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## 3. Economic model \n", "\n", "In this section, we implement the economics outlined in [the model](#model).\n", "\n", "Each period, based on the current distribution of capital and the exogenous state, agents decide whether and how much to save in risky capital and to consume. Their savings together with the labor supplied implies the rest of the economic state (e.g., capital return, wages, incomes, ...). We use the neural network to generate the savings based on the agents' capital holdings at the beginning of the period. The remaining economic state is computed using the equations outlined [above](#model). The economic mechanisms are encoded in helper functions. We create one for the `firm`, the `shocks`, and `wealth` (see cell below).\n", "\n", "Then, in the face of future uncertainty, the agents again decide whether and how much to save in risky capital for the next period. We use the neural network to generate new savings for each of the future states (one for each shock). The input state for these network predictions is the next period's capital holding which are current periods savings.\n", "\n", "First, we define the helper functions for the `firm`, the `shocks`, and `wealth`.\n" ] }, { "cell_type": "code", "execution_count": 5, "metadata": {}, "outputs": [], "source": [ "def firm(K, eta, alpha, delta):\n", " \"\"\"Calculate return, wage and aggregate production.\n", " \n", " r = eta * K^(alpha-1) * L^(1-alpha) + (1-delta)\n", " w = eta * K^(alpha) * L^(-alpha)\n", " Y = eta * K^(alpha) * L^(1-alpha) + (1-delta) * K \n", "\n", " Args:\n", " K: aggregate capital,\n", " eta: TFP value,\n", " alpha: output elasticity,\n", " delta: depreciation value.\n", "\n", " Returns:\n", " return: return (marginal product of capital), \n", " wage: wage (marginal product of labor).\n", " Y: aggregate production.\n", " \"\"\"\n", " L = tf.ones_like(K)\n", "\n", " r = alpha * eta * K**(alpha - 1) * L**(1 - alpha) + (1 - delta)\n", " w = (1 - alpha) * eta * K**alpha * L**(-alpha)\n", " Y = eta * K**alpha * L**(1 - alpha) + (1 - delta) * K\n", "\n", " return r, w, Y\n", "\n", "def shocks(z, eta, delta):\n", " \"\"\"Calculates tfp and depreciation based on current exogenous shock.\n", "\n", " Args:\n", " z: current exogenous shock (in {1, 2, 3, 4}),\n", " eta: tensor of TFP values to sample from,\n", " delta: tensor of depreciation values to sample from.\n", "\n", " Returns:\n", " tfp: TFP value of exogenous shock, \n", " depreciation: depreciation values of exogenous shock.\n", " \"\"\"\n", " tfp = tf.gather(eta, tf.cast(z, tf.int32))\n", " depreciation = tf.gather(delta, tf.cast(z, tf.int32))\n", " return tfp, depreciation\n", " \n", "def wealth(k, R, l, W):\n", " \"\"\"Calculates the wealth of the agents.\n", "\n", " Args:\n", " k: capital distribution,\n", " R: matrix of return,\n", " l: labor distribution,\n", " W: matrix of wages.\n", "\n", " Returns:\n", " fin_wealth: financial wealth distribution,\n", " lab_wealth: labor income distribution,\n", " tot_income: total income distribution.\n", " \"\"\"\n", " fin_wealth = k * R\n", " lab_wealth = l * W\n", " tot_income = tf.add(fin_wealth, lab_wealth)\n", " return fin_wealth, lab_wealth, tot_income\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### 3.A. Current period (t) \n", "Using the current state `X` we can calculate the economy. The state is composed of today's shock ($z_t$) and today's capital ($k_t^h$). Note that this constitutes the minimal state. Often, including redundant variables is a simple way to increase the speed of convergence (see the [working paper](https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3393482) for more information on this). However, this notebook attempts to present the most basic example for simplicity.\n", "\n", "Using the current state `X`, we predict how much the agents save ($a_t^h$) based on their current capital holdings ($k_t^h$). We do this by passing the state `X` to the neural network.\n", "\n", "Then we can calculate the agents' consumptions. To do this, we need to calculate the aggregate capital ($K_t$), the return on capital payed by the firm ($r_t$), and the wages payed by the firm ($w_t$). \n", "$$K_t = \\sum_{h=0}^{A-1} k_t^h,$$\n", "$$r_t = \\alpha \\eta_t K_t^{\\alpha - 1} L_t^{1 - \\alpha} + (1 - \\delta_t),$$\n", "$$w_t = (1 - \\alpha) \\eta_t K_t^{\\alpha} L_t^{-\\alpha}.$$\n", "\n", "Aggregate labor $L_t$ is always 1 by construction. Then, we can calculate each agent's total income. Finally, we calculate the resulting consumption ($c_t^h$):\n", "$$c_{t}^{h} = r_t k_t^h + w_t l^h_t - a_t^{h}.$$" ] }, { "cell_type": "code", "execution_count": 6, "metadata": { "scrolled": false }, "outputs": [], "source": [ "# Today's extended state: \n", "z = X[:, 0] # exogenous shock\n", "tfp = X[:, 1] # total factor productivity\n", "depr = X[:, 2] # depreciation\n", "K = X[:, 3] # aggregate capital\n", "L = X[:, 4] # aggregate labor\n", "r = X[:, 5] # return on capital\n", "w = X[:, 6] # wage\n", "Y = X[:, 7] # aggregate production\n", "k = X[:, 8 : 8 + A] # distribution of capital\n", "fw = X[:, 8 + A : 8 + 2 * A] # distribution of financial wealth\n", "linc = X[:, 8 + 2 * A : 8 + 3 * A] # distribution of labor income\n", "inc = X[:, 8 + 3 * A : 8 + 4 * A] # distribution of total income\n", "\n", "# Today's assets: How much the agents save\n", "# Get today's assets by executing the neural network\n", "a = nn_predict(X)\n", "# The last agent consumes everything they own\n", "a_all = tf.concat([a, tf.zeros([m, 1])], axis=1)\n", "\n", "# c_orig: the original consumption predicted by the neural network However, the\n", "# network can predict negative values before it learns not to. We ensure that\n", "# the network learns itself out of a bad region by penalizing negative\n", "# consumption. We ensure that consumption is not negative by including a penalty\n", "# term on c_orig_prime_1\n", "# c: is the corrected version c_all_orig_prime_1, in which all negative consumption\n", "# values are set to ~0. If none of the consumption values are negative then\n", "# c_orig_prime_1 == c_prime_1.\n", "c_orig = inc - a_all\n", "c = tf.maximum(c_orig, tf.ones_like(c_orig) * eps)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### 3.B. Next period (t+1) \n", "\n", "Now that we have calculated the current economic variables, we simulate one period forward. Since we have 4 possible futures---1 for each of the possible shocks that can realize---we simulate forward for each of the 4 states. Hence, we repeat each calculation 4 times. Below, we first calculate the aggregate variables for the beginning of the period. Then, we calculate the economy for shock $z=1$. The calculations for shock 2, 3, and 4 are analogous and will not be commented on.\n", "\n", "From the current period's savings $a_t$ we can calculate the next period's capital holdings $k_{t+1}^h$ and, consequently, aggregate capital $K_{t+1}$. Again, aggregate labor $L_{t+1}$ is 1 by construction.\n", "\n", "Then, like above, we calculate economic variables for each shock $z_{t+1} \\in \\{1, 2, 3, 4\\}$. That is, the new state `X'`$=[z_{t+1}, k_{t+1}^h]$ (together with the redundant extensions) is passed to the neural network to generate the agents' savings $a_{t+1}^h$. Then, we use `firm`, the `shocks`, and `wealth` to calculate the return on capital ($r_{t+1}$), the wages ($w_{t+1}$), and the agents' total income. Finally, consumption $c_{t+1}^h$ is calculated." ] }, { "cell_type": "code", "execution_count": 7, "metadata": {}, "outputs": [], "source": [ "# Today's savings become tomorrow's capital holding, but the first agent\n", "# is born without a capital endowment.\n", "k_prime = tf.concat([tf.zeros([m, 1]), a], axis=1)\n", "\n", "# Tomorrow's aggregate capital\n", "K_prime_orig = tf.reduce_sum(k_prime, axis=1, keepdims=True)\n", "K_prime = tf.maximum(K_prime_orig, tf.ones_like(K_prime_orig) * eps)\n", "\n", "# Tomorrow's labor\n", "l_prime = tf.tile(labor_endow, [m, 1])\n", "L_prime = tf.ones_like(K_prime)\n", "\n", "# Shock 1 ---------------------------------------------------------------------\n", "# 1) Get remaining parts of tomorrow's extended state\n", "# Exogenous shock\n", "z_prime_1 = 0 * tf.ones_like(z)\n", "\n", "# TFP and depreciation\n", "tfp_prime_1, depr_prime_1 = shocks(z_prime_1, eta, delta)\n", "\n", "# Return on capital, wage and aggregate production\n", "r_prime_1, w_prime_1, Y_prime_1 = firm(K_prime, tfp_prime_1, alpha, depr_prime_1)\n", "R_prime_1 = r_prime_1 * tf.ones([1, A])\n", "W_prime_1 = w_prime_1 * tf.ones([1, A])\n", "\n", "# Distribution of financial wealth, labor income, and total income\n", "fw_prime_1, linc_prime_1, inc_prime_1 = wealth(k_prime, R_prime_1, l_prime, W_prime_1)\n", "\n", "# Tomorrow's state: Concatenate the parts together\n", "x_prime_1 = tf.concat([tf.expand_dims(z_prime_1, -1),\n", " tfp_prime_1,\n", " depr_prime_1,\n", " K_prime,\n", " L_prime,\n", " r_prime_1,\n", " w_prime_1,\n", " Y_prime_1,\n", " k_prime,\n", " fw_prime_1,\n", " linc_prime_1,\n", " inc_prime_1], axis=1)\n", "\n", "# 2) Get tomorrow's policy\n", "# Tomorrow's capital: capital holding at beginning of period and how much they save\n", "a_prime_1 = nn_predict(x_prime_1)\n", "a_prime_all_1 = tf.concat([a_prime_1, tf.zeros([m, 1])], axis=1)\n", "\n", "# 3) Tomorrow's consumption\n", "c_orig_prime_1 = inc_prime_1 - a_prime_all_1\n", "c_prime_1 = tf.maximum(c_orig_prime_1, tf.ones_like(c_orig_prime_1) * eps)" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "#### Repeat for the remaining shocks\n", "Then, we do the same for the remaining shocks ($z = 2,3,4$). Nothing changes in terms of the math for the remaining shocks." ] }, { "cell_type": "code", "execution_count": 8, "metadata": {}, "outputs": [], "source": [ "# Shock 2 ---------------------------------------------------------------------\n", "# 1) Get remaining parts of tomorrow's extended state\n", "# Exogenous shock\n", "z_prime_2 = 1 * tf.ones_like(z)\n", "\n", "# TFP and depreciation\n", "tfp_prime_2, depr_prime_2 = shocks(z_prime_2, eta, delta)\n", "\n", "# return on capital, wage and aggregate production\n", "r_prime_2, w_prime_2, Y_prime_2 = firm(K_prime, tfp_prime_2, alpha, depr_prime_2)\n", "R_prime_2 = r_prime_2 * tf.ones([1, A])\n", "W_prime_2 = w_prime_2 * tf.ones([1, A])\n", "\n", "# distribution of financial wealth, labor income, and total income\n", "fw_prime_2, linc_prime_2, inc_prime_2 = wealth(k_prime, R_prime_2, l_prime, W_prime_2)\n", "\n", "# Tomorrow's state: Concatenate the parts together\n", "x_prime_2 = tf.concat([tf.expand_dims(z_prime_2, -1),\n", " tfp_prime_2,\n", " depr_prime_2,\n", " K_prime,\n", " L_prime,\n", " r_prime_2,\n", " w_prime_2,\n", " Y_prime_2,\n", " k_prime,\n", " fw_prime_2,\n", " linc_prime_2,\n", " inc_prime_2], axis=1)\n", "\n", "# 2) Get tomorrow's policy\n", "a_prime_2 = nn_predict(x_prime_2)\n", "a_prime_all_2 = tf.concat([a_prime_2, tf.zeros([m, 1])], axis=1)\n", "\n", "# 3) Tomorrow's consumption\n", "c_orig_prime_2 = inc_prime_2 - a_prime_all_2\n", "c_prime_2= tf.maximum(c_orig_prime_2, tf.ones_like(c_orig_prime_2) * eps)\n", "\n", "# Shock 3 ---------------------------------------------------------------------\n", "# 1) Get remaining parts of tomorrow's extended state\n", "# Exogenous shock\n", "z_prime_3 = 2 * tf.ones_like(z)\n", "\n", "# TFP and depreciation\n", "tfp_prime_3, depr_prime_3 = shocks(z_prime_3, eta, delta)\n", "\n", "# return on capital, wage and aggregate production\n", "r_prime_3, w_prime_3, Y_prime_3 = firm(K_prime, tfp_prime_3, alpha, depr_prime_3)\n", "R_prime_3 = r_prime_3 * tf.ones([1, A])\n", "W_prime_3 = w_prime_3 * tf.ones([1, A])\n", "\n", "# distribution of financial wealth, labor income, and total income\n", "fw_prime_3, linc_prime_3, inc_prime_3 = wealth(k_prime, R_prime_3, l_prime, W_prime_3)\n", "\n", "# Tomorrow's state: Concatenate the parts together\n", "x_prime_3 = tf.concat([tf.expand_dims(z_prime_3, -1),\n", " tfp_prime_3,\n", " depr_prime_3,\n", " K_prime,\n", " L_prime,\n", " r_prime_3,\n", " w_prime_3,\n", " Y_prime_3,\n", " k_prime,\n", " fw_prime_3,\n", " linc_prime_3,\n", " inc_prime_3], axis=1)\n", "\n", "# 2) Get tomorrow's policy\n", "# Tomorrow's capital: capital holding at beginning of period and how much they save\n", "a_prime_3 = nn_predict(x_prime_3)\n", "a_prime_all_3 = tf.concat([a_prime_3, tf.zeros([m, 1])], axis=1)\n", "\n", "# 3) Tomorrow's consumption\n", "c_orig_prime_3 = inc_prime_3 - a_prime_all_3\n", "c_prime_3 = tf.maximum(c_orig_prime_3, tf.ones_like(c_orig_prime_3) * eps)\n", "\n", "# Shock 4 ---------------------------------------------------------------------\n", "# 1) Get remaining parts of tomorrow's extended state\n", "# Exogenous shock\n", "z_prime_4 = 3 * tf.ones_like(z)\n", "\n", "# TFP and depreciation\n", "tfp_prime_4, depr_prime_4 = shocks(z_prime_4, eta, delta)\n", "\n", "# return on capital, wage and aggregate production\n", "r_prime_4, w_prime_4, Y_prime_4 = firm(K_prime, tfp_prime_4, alpha, depr_prime_4)\n", "R_prime_4 = r_prime_4 * tf.ones([1, A])\n", "W_prime_4 = w_prime_4 * tf.ones([1, A])\n", "\n", "# distribution of financial wealth, labor income, and total income\n", "fw_prime_4, linc_prime_4, inc_prime_4 = wealth(k_prime, R_prime_4, l_prime, W_prime_4)\n", "\n", "# Tomorrow's state: Concatenate the parts together\n", "x_prime_4 = tf.concat([tf.expand_dims(z_prime_4, -1),\n", " tfp_prime_4,\n", " depr_prime_4,\n", " K_prime,\n", " L_prime,\n", " r_prime_4,\n", " w_prime_4,\n", " Y_prime_4,\n", " k_prime,\n", " fw_prime_4,\n", " linc_prime_4,\n", " inc_prime_4], axis=1)\n", "\n", "# 2) Get tomorrow's policy\n", "# Tomorrow's capital: capital holding at beginning of period and how much they save\n", "a_prime_4 = nn_predict(x_prime_4)\n", "a_prime_all_4 = tf.concat([a_prime_4, tf.zeros([m, 1])], axis=1)\n", "\n", "# 3) Tomorrow's consumption\n", "c_orig_prime_4 = inc_prime_4 - a_prime_all_4\n", "c_prime_4 = tf.maximum(c_orig_prime_4, tf.ones_like(c_orig_prime_4) * eps)\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### 3.C. Cost / Euler function \n", "\n", "#### tldr\n", "\n", "We train the neural network in an unsupervised fashion by approximating the equilibrium functions. The cost function is composed of the Euler equation, and the punishments for negative consumption and negative aggregate capital.\n", "\n", "***\n", "\n", "The final key ingredient is the cost function, which encodes the equilibrium functions.\n", "\n", "A loss function is needed to train a neural network. In supervised learning, the neural network's prediction is compared to the true value. The weights are updated in the direction that decreases the discripancy between the prediction and the truth. In _deep equilibrium nets_, we approximate all equilibrium functions directly. That is, we update the weights in the direction that minimizes these equilibrium functions. Since the equilibrium functions are approximately 0 in equilibrium, we do not require labeled data and can train in an unsupervised fashion.\n", "\n", "Our loss function has 3 components:\n", "\n", " * the Euler equation,\n", " * the punishments for negative consumption, and\n", " * the punishments for negative aggregate capital.\n", "\n", "The relative errors in the Euler equation is given by:\n", "$$e_{\\text{REE}}^i(\\mathbf{x}_j) := \\frac{u^{\\prime -1}\\left(\\beta \\mathbf{E}_{z_j}{r(\\hat{\\mathbf{x}}_{j,+})u^{\\prime}(\\hat{c}^{i+1}(\\hat{\\mathbf{x}}_{j,+}))}\\right)}{\\hat{c}^i(\\mathbf{x}_j)}-1$$" ] }, { "cell_type": "code", "execution_count": 9, "metadata": {}, "outputs": [], "source": [ "# Prepare transitions to the next periods states. In this setting, there is a 25% chance\n", "# of ending up in any of the 4 states in Z. This has been hardcoded and need to be changed\n", "# to accomodate a different transition matrix.\n", "pi_trans_to1 = p_transition * tf.ones((m, A-1))\n", "pi_trans_to2 = p_transition * tf.ones((m, A-1))\n", "pi_trans_to3 = p_transition * tf.ones((m, A-1))\n", "pi_trans_to4 = p_transition * tf.ones((m, A-1))\n", "\n", "# Euler equation\n", "opt_euler = - 1 + (\n", " (\n", " (\n", " beta * (\n", " pi_trans_to1 * R_prime_1[:, 0:A-1] * c_prime_1[:, 1:A]**(-gamma) \n", " + pi_trans_to2 * R_prime_2[:, 0:A-1] * c_prime_2[:, 1:A]**(-gamma) \n", " + pi_trans_to3 * R_prime_3[:, 0:A-1] * c_prime_3[:, 1:A]**(-gamma) \n", " + pi_trans_to4 * R_prime_4[:, 0:A-1] * c_prime_4[:, 1:A]**(-gamma)\n", " )\n", " ) ** (-1. / gamma)\n", " ) / c[:, 0:A-1]\n", ")\n", "\n", "# Punishment for negative consumption (c)\n", "orig_cons = tf.concat([c_orig, c_orig_prime_1, c_orig_prime_2, c_orig_prime_3, c_orig_prime_4], axis=1)\n", "opt_punish_cons = (1./eps) * tf.maximum(-1 * orig_cons, tf.zeros_like(orig_cons))\n", "\n", "# Punishment for negative aggregate capital (K)\n", "opt_punish_ktot_prime = (1./eps) * tf.maximum(-K_prime_orig, tf.zeros_like(K_prime_orig))\n", "\n", "# Concatenate the 3 equilibrium functions\n", "combined_opt = [opt_euler, opt_punish_cons, opt_punish_ktot_prime]\n", "opt_predict = tf.concat(combined_opt, axis=1)\n", "\n", "# Define the \"correct\" outputs. For all equilibrium functions, the correct outputs is zero.\n", "opt_correct = tf.zeros_like(opt_predict)\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "#### Optimizer\n", "\n", "Next, we chose an optimizer; i.e., the algorithm we use to perform gradient descent. We use [Adam](https://arxiv.org/abs/1412.6980), a favorite in deep learning research. Adam uses a parameter specific learning rate and momentum, which encourages gradient descent steps that occur in a consistent direction." ] }, { "cell_type": "code", "execution_count": 10, "metadata": {}, "outputs": [ { "name": "stdout", "output_type": "stream", "text": [ "WARNING:tensorflow:From /home/lpupp/anaconda3/envs/tf1_cpu/lib/python3.7/site-packages/tensorflow/python/ops/losses/losses_impl.py:667: to_float (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.\n", "Instructions for updating:\n", "Use tf.cast instead.\n", "WARNING:tensorflow:From /home/lpupp/anaconda3/envs/tf1_cpu/lib/python3.7/site-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.\n", "Instructions for updating:\n", "Use tf.cast instead.\n" ] } ], "source": [ "# Define the cost function\n", "cost = tf.losses.mean_squared_error(opt_correct, opt_predict)\n", "\n", "# Adam optimizer\n", "optimizer = tf.train.AdamOptimizer(learning_rate=lr)\n", "\n", "# Clip the gradients to limit the extent of exploding gradients\n", "gvs = optimizer.compute_gradients(cost)\n", "capped_gvs = [(tf.clip_by_value(grad, -1., 1.), var) for grad, var in gvs]\n", "\n", "# Define a training step\n", "train_step = optimizer.apply_gradients(capped_gvs)\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## 4. Training \n", "\n", "### tldr\n", "\n", "We iterate between simulating a dataset using the current neural network and training on this dataset.\n", "\n", "***\n", "\n", "In the final stage, we put everything together and train the neural network. \n", "\n", "In this section, we iterate between a simulation phase and a training phase. That is, we first simulate a dataset. We simulate a sequence of states ($[z, k]$) based on a random sequence of shocks. The states are computed using the current state of the neural network. We created the `simulate_episodes` helper function to do this. Then, in the training phase, we use the dataset to update our network parameters through multiple epochs. After completion of the training phase, we resimulate a dataset using the new network parameters and repeat.\n", "\n", "By computing the error directly after simulating a new dataset, we are able to evaluate our algorithms out-of-sample performance.\n", "\n", "First, we define the helper function `simulate_episodes` that simulates the training data used in an episode." ] }, { "cell_type": "code", "execution_count": 11, "metadata": {}, "outputs": [], "source": [ "def simulate_episodes(sess, x_start, episode_length, print_flag=True):\n", " \"\"\"Simulate an episode for a given starting point using the current\n", " neural network state.\n", "\n", " Args:\n", " sess: Current tensorflow session,\n", " x_start: Starting state to simulate forward from,\n", " episode_length: Number of steps to simulate forward,\n", " print_flag: Boolean that determines whether to print simulation stats.\n", "\n", " Returns:\n", " X_episodes: Tensor of states [z, k] to train on (training set).\n", " \"\"\"\n", " time_start = datetime.now()\n", " if print_flag:\n", " print('Start simulating {} periods.'.format(episode_length))\n", " dim_state = np.shape(x_start)[1]\n", "\n", " X_episodes = np.zeros([episode_length, dim_state])\n", " X_episodes[0, :] = x_start\n", " X_old = x_start\n", "\n", " # Generate a sequence of random shocks\n", " rand_num = np.random.rand(episode_length, 1)\n", "\n", " for t in range(1, episode_length):\n", " z = int(X_old[0, 0]) # Current period's shock\n", "\n", " # Determine which state we will be in in the next period based on\n", " # the shock and generate the corresponding state (x_prime)\n", " if rand_num[t - 1] <= pi_np[z, 0]:\n", " X_new = sess.run(x_prime_1, feed_dict={X: X_old})\n", " elif rand_num[t - 1] <= pi_np[z, 0] + pi_np[z, 1]:\n", " X_new = sess.run(x_prime_2, feed_dict={X: X_old})\n", " elif rand_num[t - 1] <= pi_np[z, 0] + pi_np[z, 1] + pi_np[z, 2]:\n", " X_new = sess.run(x_prime_3, feed_dict={X: X_old})\n", " else:\n", " X_new = sess.run(x_prime_4, feed_dict={X: X_old})\n", " \n", " # Append it to the dataset\n", " X_episodes[t, :] = X_new\n", " X_old = X_new\n", "\n", " time_end = datetime.now()\n", " time_diff = time_end - time_start\n", " if print_flag:\n", " print('Finished simulation. Time for simulation: {}.'.format(time_diff))\n", "\n", " return X_episodes" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### The true analytic solution\n", "This model can be solved analytically.\n", "Therefore, additionally to the relative errors in the Euler equations, we can compare the solution learned by the neural network directly to the true solution.\n", "The true policy is given by\n", "\\begin{align}\n", "\\mathbf{a}^{\\text{analytic}}_t=\n", "\\beta\n", "\\begin{bmatrix}\n", "\\frac{1-\\beta^{A-1}}{1-\\beta^{A}} w_t \\\\\n", "\\frac{1-\\beta^{A-2}}{1-\\beta^{A-1}} r_t k^{1}_t \\\\\n", "\\frac{1-\\beta^{A-3}}{1-\\beta^{A-2}} r_t k^{2}_t \\\\\n", "\\dots \\\\\n", "\\frac{1-\\beta^{1}}{1-\\beta^2} r_t k^{A-2}_t \\\\\n", "\\end{bmatrix}.\n", "\\end{align}" ] }, { "cell_type": "code", "execution_count": 12, "metadata": {}, "outputs": [], "source": [ "beta_vec = beta_np * (1 - beta_np ** (A - 1 - np.arange(A-1))) / (1 - beta_np ** (A - np.arange(A-1)))\n", "beta_vec = tf.constant(np.expand_dims(beta_vec, 0), dtype=tf.float32)\n", "a_analytic = inc[:, : -1] * beta_vec" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Training the _deep equilibrium net_\n", "\n", "Now we can begin training." ] }, { "cell_type": "code", "execution_count": null, "metadata": { "scrolled": false }, "outputs": [ { "data": { "application/javascript": "/* Put everything inside the global mpl namespace */\nwindow.mpl = {};\n\n\nmpl.get_websocket_type = function() {\n if (typeof(WebSocket) !== 'undefined') {\n return WebSocket;\n } else if (typeof(MozWebSocket) !== 'undefined') {\n return MozWebSocket;\n } else {\n alert('Your browser does not have WebSocket support. ' +\n 'Please try Chrome, Safari or Firefox ≥ 6. ' +\n 'Firefox 4 and 5 are also supported but you ' +\n 'have to enable WebSockets in about:config.');\n };\n}\n\nmpl.figure = function(figure_id, websocket, ondownload, parent_element) {\n this.id = figure_id;\n\n this.ws = websocket;\n\n this.supports_binary = (this.ws.binaryType != undefined);\n\n if (!this.supports_binary) {\n var warnings = document.getElementById(\"mpl-warnings\");\n if (warnings) {\n warnings.style.display = 'block';\n warnings.textContent = (\n \"This browser does not support binary websocket messages. \" +\n \"Performance may be slow.\");\n }\n }\n\n this.imageObj = new Image();\n\n this.context = undefined;\n this.message = undefined;\n this.canvas = undefined;\n this.rubberband_canvas = undefined;\n this.rubberband_context = undefined;\n this.format_dropdown = undefined;\n\n this.image_mode = 'full';\n\n this.root = $('
');\n this._root_extra_style(this.root)\n this.root.attr('style', 'display: inline-block');\n\n $(parent_element).append(this.root);\n\n this._init_header(this);\n this._init_canvas(this);\n this._init_toolbar(this);\n\n var fig = this;\n\n this.waiting = false;\n\n this.ws.onopen = function () {\n fig.send_message(\"supports_binary\", {value: fig.supports_binary});\n fig.send_message(\"send_image_mode\", {});\n if (mpl.ratio != 1) {\n fig.send_message(\"set_dpi_ratio\", {'dpi_ratio': mpl.ratio});\n }\n fig.send_message(\"refresh\", {});\n }\n\n this.imageObj.onload = function() {\n if (fig.image_mode == 'full') {\n // Full images could contain transparency (where diff images\n // almost always do), so we need to clear the canvas so that\n // there is no ghosting.\n fig.context.clearRect(0, 0, fig.canvas.width, fig.canvas.height);\n }\n fig.context.drawImage(fig.imageObj, 0, 0);\n };\n\n this.imageObj.onunload = function() {\n fig.ws.close();\n }\n\n this.ws.onmessage = this._make_on_message_function(this);\n\n this.ondownload = ondownload;\n}\n\nmpl.figure.prototype._init_header = function() {\n var titlebar = $(\n '
');\n var titletext = $(\n '
');\n titlebar.append(titletext)\n this.root.append(titlebar);\n this.header = titletext[0];\n}\n\n\n\nmpl.figure.prototype._canvas_extra_style = function(canvas_div) {\n\n}\n\n\nmpl.figure.prototype._root_extra_style = function(canvas_div) {\n\n}\n\nmpl.figure.prototype._init_canvas = function() {\n var fig = this;\n\n var canvas_div = $('
');\n\n canvas_div.attr('style', 'position: relative; clear: both; outline: 0');\n\n function canvas_keyboard_event(event) {\n return fig.key_event(event, event['data']);\n }\n\n canvas_div.keydown('key_press', canvas_keyboard_event);\n canvas_div.keyup('key_release', canvas_keyboard_event);\n this.canvas_div = canvas_div\n this._canvas_extra_style(canvas_div)\n this.root.append(canvas_div);\n\n var canvas = $('');\n canvas.addClass('mpl-canvas');\n canvas.attr('style', \"left: 0; top: 0; z-index: 0; outline: 0\")\n\n this.canvas = canvas[0];\n this.context = canvas[0].getContext(\"2d\");\n\n var backingStore = this.context.backingStorePixelRatio ||\n\tthis.context.webkitBackingStorePixelRatio ||\n\tthis.context.mozBackingStorePixelRatio ||\n\tthis.context.msBackingStorePixelRatio ||\n\tthis.context.oBackingStorePixelRatio ||\n\tthis.context.backingStorePixelRatio || 1;\n\n mpl.ratio = (window.devicePixelRatio || 1) / backingStore;\n\n var rubberband = $('');\n rubberband.attr('style', \"position: absolute; left: 0; top: 0; z-index: 1;\")\n\n var pass_mouse_events = true;\n\n canvas_div.resizable({\n start: function(event, ui) {\n pass_mouse_events = false;\n },\n resize: function(event, ui) {\n fig.request_resize(ui.size.width, ui.size.height);\n },\n stop: function(event, ui) {\n pass_mouse_events = true;\n fig.request_resize(ui.size.width, ui.size.height);\n },\n });\n\n function mouse_event_fn(event) {\n if (pass_mouse_events)\n return fig.mouse_event(event, event['data']);\n }\n\n rubberband.mousedown('button_press', mouse_event_fn);\n rubberband.mouseup('button_release', mouse_event_fn);\n // Throttle sequential mouse events to 1 every 20ms.\n rubberband.mousemove('motion_notify', mouse_event_fn);\n\n rubberband.mouseenter('figure_enter', mouse_event_fn);\n rubberband.mouseleave('figure_leave', mouse_event_fn);\n\n canvas_div.on(\"wheel\", function (event) {\n event = event.originalEvent;\n event['data'] = 'scroll'\n if (event.deltaY < 0) {\n event.step = 1;\n } else {\n event.step = -1;\n }\n mouse_event_fn(event);\n });\n\n canvas_div.append(canvas);\n canvas_div.append(rubberband);\n\n this.rubberband = rubberband;\n this.rubberband_canvas = rubberband[0];\n this.rubberband_context = rubberband[0].getContext(\"2d\");\n this.rubberband_context.strokeStyle = \"#000000\";\n\n this._resize_canvas = function(width, height) {\n // Keep the size of the canvas, canvas container, and rubber band\n // canvas in synch.\n canvas_div.css('width', width)\n canvas_div.css('height', height)\n\n canvas.attr('width', width * mpl.ratio);\n canvas.attr('height', height * mpl.ratio);\n canvas.attr('style', 'width: ' + width + 'px; height: ' + height + 'px;');\n\n rubberband.attr('width', width);\n rubberband.attr('height', height);\n }\n\n // Set the figure to an initial 600x600px, this will subsequently be updated\n // upon first draw.\n this._resize_canvas(600, 600);\n\n // Disable right mouse context menu.\n $(this.rubberband_canvas).bind(\"contextmenu\",function(e){\n return false;\n });\n\n function set_focus () {\n canvas.focus();\n canvas_div.focus();\n }\n\n window.setTimeout(set_focus, 100);\n}\n\nmpl.figure.prototype._init_toolbar = function() {\n var fig = this;\n\n var nav_element = $('
');\n nav_element.attr('style', 'width: 100%');\n this.root.append(nav_element);\n\n // Define a callback function for later on.\n function toolbar_event(event) {\n return fig.toolbar_button_onclick(event['data']);\n }\n function toolbar_mouse_event(event) {\n return fig.toolbar_button_onmouseover(event['data']);\n }\n\n for(var toolbar_ind in mpl.toolbar_items) {\n var name = mpl.toolbar_items[toolbar_ind][0];\n var tooltip = mpl.toolbar_items[toolbar_ind][1];\n var image = mpl.toolbar_items[toolbar_ind][2];\n var method_name = mpl.toolbar_items[toolbar_ind][3];\n\n if (!name) {\n // put a spacer in here.\n continue;\n }\n var button = $('