{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"# Quantization of Signals\n",
"\n",
"*This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Oversampling\n",
"\n",
"[Oversampling](https://en.wikipedia.org/wiki/Oversampling) is a technique which is applied in [analog-to-digital converters](https://en.wikipedia.org/wiki/Analog-to-digital_converter) to lower the average power of the quantization error. It requires a joint consideration of sampling and quantization."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Ideal Analog-to-Digital Conversion\n",
"\n",
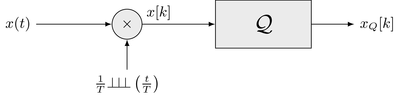
"Let's consider the ideal sampling of a signal followed by its quantization, as given by the following block diagram\n",
"\n",
"\n",
"\n",
"Ideal sampling is modeled by multiplying the continuous signal $x(t)$ with a series of equidistant Dirac impulse, resulting in the discrete signal $x[k] = x(k T)$ where $T$ denotes the sampling interval. The discrete signal $x[k]$ is then quantized. The output of the ideal analog-to-digital converter is the quantized discrete signal $x_\\text{Q}[k]$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Nyquist Sampling\n",
"\n",
"Sampling of the continuous signal $x(t)$ leads to repetitions of the spectrum $X(j \\omega) = \\mathcal{F} \\{ x(t) \\}$ at multiples of $\\omega_\\text{S} = \\frac{2 \\pi}{T}$. We limit ourselves to a continuous real-valued $x(t) \\in \\mathbb{R}$, band-limited signal $| X(j \\omega) | = 0$ for $|\\omega| > \\omega_\\text{C}$ where $\\omega_\\text{C}$ denotes its cut-off frequency. The spectral repetitions due to sampling do not overlap if the [sampling theorem](https://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem) $\\omega_\\text{S} \\geq 2 \\cdot \\omega_\\text{C}$ is fulfilled. In the case of Nyquist (critical) sampling, the sampling frequency is chosen as $\\omega_\\text{S} = 2 \\cdot \\omega_\\text{C}$."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Oversampling\n",
"\n",
"The basic idea of oversampling is to sample the input signal at frequencies which are significantly higher than the Nyquist criterion dictates. After quantization, the signal is low-pass filtered by a discrete filter $H_\\text{LP}(\\mathrm{e}^{\\,\\mathrm{j}\\,\\Omega})$ and resampled back to the Nyquist rate. In order to avoid aliasing due to the resampling this filter has to be chosen as an ideal low-pass\n",
"\n",
"\\begin{equation}\n",
"H_\\text{LP}(\\mathrm{e}^{\\,\\mathrm{j}\\,\\Omega}) = \\text{rect} \\left( \\frac{\\Omega}{2 \\, \\Omega_\\text{C}} \\right)\n",
"\\end{equation}\n",
"\n",
"where $\\Omega_\\text{C} = \\omega_\\text{C} \\cdot T$. For an oversampling of factor $L \\in \\mathbb{N}$ we have $\\omega_\\text{S} = L \\cdot 2 \\omega_\\text{C}$. For this case, the resampling can be realized by keeping only every $L$-th sample which is known as decimation. The following block diagram illustrates the building blocks of oversampled digital-to-analog conversion, $\\downarrow L$ denotes decimation by a factor of $L$\n",
"\n",
"\n",
"\n",
"In order the conclude on the benefits of oversampling we have to derive the average power of the overall quantization error. According to our [model of the quantization error](linear_uniform_quantization_error.ipynb#Model-for-the-Quantization-Error), the quantization error $e[k]$ can be modeled as uniformly distributed white noise. Its power spectral density (PSD) is given as\n",
"\n",
"\\begin{equation}\n",
"\\Phi_{ee}(\\mathrm{e}^{\\,\\mathrm{j}\\,\\Omega}) = \\frac{Q^2}{12}\n",
"\\end{equation}\n",
"\n",
"where $Q$ denotes the quantization step. Before the discrete low-pass filter $H_\\text{LP}(\\mathrm{e}^{\\,\\mathrm{j}\\,\\Omega})$, the power of the quantization error is uniformly distributed over the entire frequency range $-\\pi < \\Omega \\leq \\pi$. However, after the ideal low-pass filter its frequency range is limited to $- \\frac{\\pi}{L} < \\Omega \\leq \\frac{\\pi}{L}$. The average power of the quantization error is then given as\n",
"\n",
"\\begin{equation}\n",
"\\sigma_{e, \\text{LP}}^2 = \\frac{1}{2 \\pi} \\int\\limits_{- \\frac{\\pi}{L}}^{\\frac{\\pi}{L}} \\Phi_{ee}(\\mathrm{e}^{\\,\\mathrm{j}\\,\\Omega}) \\; \\mathrm{d}\\Omega = \\frac{1}{L} \\cdot \\frac{Q^2}{12}\n",
"\\end{equation}\n",
"\n",
"The average power $\\sigma_x^2$ of the sampled signal $x[k]$ is not affected, since the cutoff frequency of the low-pass filter has been chosen as the upper frequency limit $\\omega_\\text{C}$ of the input signal $x(t)$. \n",
"\n",
"In order to calculate the SNR of the oversampled analog-to-digital converter we assume that the input signal is drawn from a wide-sense stationary (WSS) uniformly distributed zero-mean random process with $x_\\text{min} \\leq x[k] < x_\\text{max}$. With the results from our discussion of [linear uniform quantization](linear_uniform_quantization_error.ipynb#Uniformly-Distributed-Signal) and $\\sigma_{e, \\text{LP}}^2$ from above we get\n",
"\n",
"\\begin{equation}\n",
"SNR = 10 \\cdot \\log_{10} \\left( 2^{2 w} \\right) + 10 \\cdot \\log_{10} \\left( L \\right) \\approx 6.02 \\, w + 10 \\cdot \\log_{10} \\left( L \\right) \\quad \\text{in dB}\n",
"\\end{equation}\n",
"\n",
"where $w$ denotes the number of bits used for a binary representation of the quantization index. Hence, oversampling by a factor of $L$ brings a plus of $10 \\cdot \\log_{10} \\left( L \\right)$ dB in terms of SNR. For instance, an oversampling by a factor of $L = 4$ results in a SNR which is approximately 6 dB higher. For equal SNR the quantization step $Q$ can be chosen larger. In terms of the wordlength of a quantizer this accounts to a reduction by one bit. Consequently, there is a trade-off between accuracy of the quantizer and its sampling frequency."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Example\n",
"\n",
"The following numerical simulation illustrates the benefit in terms of SNR for an oversampled linear uniform quantizer with $w = 16$ for the quantization of the harmonic signal $x[k] = \\cos[\\Omega_0 k]$."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDYxMi4xNSAyNjkuMTYgXSAvUGFyZW50IDIgMCBSIC9SZXNvdXJjZXMgOCAwIFIgL1R5cGUgL1BhZ2UKPj4KZW5kb2JqCjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMSAwIFIgPj4Kc3RyZWFtCnictVhNTxw5EL33r/Axe4jHLrv8cQTtBmm1WgmCtOdoAgQ0AwEi+Pv7bHe3q/mYZFY7SIO6X5er6z2Xy+W26maw6koZdYPfs7LqBL+rweBuOwRL2jIuN9MlhaxtwL3pl9+G4XJYHWHYI0xPBh90ZuWNpuLC+PluM91RsDqXoc10vq2e7pVwwJwUkdUxqIcL9Y+6VasjKi8i9ScCRdA6IWyjQzY2BxOTRwSr3y+ertcXZyfHav04kM2avc8pTEEJZH738Hk4VfeTewNNhHuoAmS3Jxd0LH6OIejzcI//Rn008ELWjDbGhqiINcVkidV6OxyfF6m1Cd4EIOdfh9Unq6xR55fDB/ubOr8ZgnaBnPEhxTIVMPlgxgeekzHNl9OJ6sXoIgoPf5wPp5Xc/yysd0bbxJ7iJIdA9hJ2p6d3hfWIv9oEjikr8q+FzTHwIYSlLiwkQliRtLMuuDkzOuBSzf0Sv8naG+Y40xSIMHOsI1HsaghEmHHQeJD6YhOIMEMkyfoQ0mzWEWGWkBwW8ebZrCPCLGPVO5ts99aRbkbglU0IZjYTiDBLhIz0pgsikG7mCEvEY/nMZgIRZr5MqbOdqUCEWUBCxeD6XAlEmCWHPGDbKQhEmOWomUMys24C6WYe9COmkGczgQgzKrUiGt/NOiLMstOcPXdBBNLNGIsopIBsnswEIsw4amOcmCyBCLMYtUcFi7NuAhFm2WuTmTsFgYhEelEkoym1yZYRffm+VRXvxjVqkXJj2WyL96k+YORszGJNX0z2TM67GX6osIcb69oCb/jj6AX5irKX+4Avkx+KmeQLtvUBJtNblHox4vtUZvxYhRq8qTBh8hPS2PVXX7/34HZy5FDnBOOrt1+gKuy0jSkuArocHzAZHsvbT7itRzWwey0K5Y/RUyaTchKyvjs77+n9XrCrTzTN+F+H3cWquwAumbFB956lQ7+4ib1y5Eu9WPppiX98rnpGY4GDetE2YM/LqMyWfLBVHWvqlqQK+UNRR/2O1pLxnXqH9qEuHTXqCz87qeeybr2j7ACM1Png1Mu+ihbDZde5C2wf8gtXjf3S00762EB1cAblmyk1+vbwM28jGiiPhsEK+h3bi750NdJfeNpNP0QUsRANB3Qbjf7hZ59M0InRIuZOX2D70F+4avSXnnbSR7HHEYASkh+7TuNPh59+8qQ5cuYo+HdsL/7S1ch/4Wk3f7QFMWaTLOrkxH+e/8Wg0it8LF2D9TrW3cJS2xhrj76tJ9fi4PPfZ+r6Vn09/q8yWs1VRmzqaOYCRUarj6a5/UU8QbqmRI4pq7MTtVRY9P84JwfQrIVBNPJo2IyPjsq2IHpoC2IexxIqfRIFaIhGEaKUkQZ7MBhv0P5yXXSc0FjZZMoKcylrxzCFVBFtFpLKFx+e0VEEuCbkGS6TC7bUY7bYpdGARgcdIl6PyxILRxxpEwL3OKpanVJPhP3ls6WJQ+/gMlSMENCgC6xpmXZqxnhHWurVoIVWEyRkmqBRofm2izNBQpcJEpLMUFdjgparovDtK+KtZTZ16MtvHfAiv41sX30bgcGOLynz09H+zfGrI9cWbpmSsnifa6jtEw/OAtUex+ZgS59WzmiYgNa0dRjyojwFbGN1yicYm3q3RbucCH33Eg2j6XqQMPsW3wILGjs//pR8F1BYyqAasp5Cb7eYJCpvCvXjSoWQt3nhdgL8OL7dzhFuZmRmInzOnF8qti5frI6HnxYO9YuFY0DOMLd6mnQKbVbiC6RObZlTM83pWIoXhTK1WD3jADweompNfL7+8U3dPV08PH7Zft9c315N9bGG/8aiVbsX7RivQ2ef6zlgDrhDe0VcTqht2Bzy6u7NiE+HfwF3lkM6CmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMTM5NwplbmRvYmoKMTYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA2NSA+PgpzdHJlYW0KeJwzNTVXMFAwAhEmluYK5kaWCimGXIZmFmBmLpeRGUQwh8vQxEjBwgjIAKmDMCwMgdpyuMC6c+CacrjSAMekEKkKZW5kc3RyZWFtCmVuZG9iagoxNCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMtT2JsaXF1ZSAvQ2hhclByb2NzIDE1IDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgNzYgL0wgXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL0wgMTYgMCBSID4+CmVuZG9iagoyMSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI1OSA+PgpzdHJlYW0KeJw9UklywzAMu/sVfAJ3Se9Jpyfn/9cC9NSXEGOKAAimd4vK2fhpK1l+5McuO0sit3wHbZP7iqoHpG6CzCXHJVeIWcrnSpBYtJSZWJ+pDsrPNahV+MJPzExMhyQRS8hJPYqwfl4H96B+vaTzW2T8o2OD0luSTAWdGu6Vo5TYsFSfGuQeNN2UVp+ZdmUHLI03ZKUmdfr10+MHSzClLxLRQYjEn+RyhywLKQfxdq7eQHhXuyDVUysPO0Saj5HeUgWrOTMBS0bTDiNgbdaYIFUCvEVrCLQW4vKFTisiPjk3dDBNVZ6FyLBS4Vh7z2gNF7qGvNJwepJx//kfvCve1+8f2vNmZAplbmRzdHJlYW0KZW5kb2JqCjIyIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNzUgPj4Kc3RyZWFtCnicNY2xEcAwCAN7pmAEywET9smlwvu3CfhopBccyOTmwZ6ydLBN5wf056RN80JRkKow0HRmfXFo5A5WDhdeaEqviujPQe8HmeoXmgplbmRzdHJlYW0KZW5kb2JqCjIzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjI3ID4+CnN0cmVhbQp4nEWQS44DIRBD95zCR6D+cJ6OsurcfzsuOtFssCUo1zO5AxN78chMlG68ZLg7zBWf4Rkwc/hKmGzETOhOXCOUrhThVJ8IjsvevOmgiXtEzqOeBVnVzg1qAWeS5oLtgi7njBU3zsmtRuXN9KPXEL5pdx/XeYf2SOPew1S+zjnVzruKCGkLWdW0vpBsFMkOaz8qTdvOyxCx4GwaVugc3gi7V3cnSxh+v/IwJRM/D936UXxdN6PrFGcnVyZrz3noSelf9cqjD8VxKegXse3MJPdfp1OSqVN7Z+9p/ae4x/sPkG5WOQplbmRzdHJlYW0KZW5kb2JqCjI0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzM4ID4+CnN0cmVhbQp4nDVSS5JbQQjbv1PoAq5q/s15nJrV5P7bCOysoIEWEpAWOMjESwxRjXLFH3mC8TqBv+vlafw+3oXUgqci/cC1aRvvx5o1UbA0YinMPvb9KCHHU+PfEOi5SBNmZDJyIBmI+7U+f9abTDn8BqRpc/ooSXoQLdjdGnZ8WZBB0pMaluzkh3UtsLoITZgbayIZObUyNc/HnuEynhgjQdUsIEmfuE8VjEgzHjtnLXmQ4XiqFy9+vY3XMo+pl1UFMrYJ5mA7mQmnKCIQv6AkuYm7aOoojmbGmtuFhpIi9909nJz0ur+cRAVeCeEs1hKOGXrKMic7DUqgauUEmGG99oVxmjZKuFPT7V2xr99nJmHc5rCzUjINznFwL5vMESR73TFhEx6HmPfuEYzEvPldbBFcucy5JtOP/SjaSB8U1+dcTZmtKOEfquSJFdf4//zez88/kDd9sQplbmRzdHJlYW0KZW5kb2JqCjI1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzA0ID4+CnN0cmVhbQp4nD2SO5LDMAxDe52CF8iM+JPk82Qnlff+7T4yyVaASYkAKC91mbKmPCBpJgn/0eHhYjvld9iezczAtUQvE8spz6ErxNxF+bKZjbqyOsWqwzCdW/SonIuGTZOa5ypLGbcLnsO1ieeWfcQPNzSoB3WNS8IN3dVoWQrNcHX/O71H2Xc1PBebVOrUF48XURXm+SFPoofpSuJ8PCghXHswRhYS5FPRQI6zXK3yXkL2DrcassJBaknnsyc82HV6Ty5uF80QD2S5VPhOUezt0DO+7EoJPRK24VjufTuasekamzjsfu9G1sqMrmghfshXJ+slYNxTJkUSZE62WG6L1Z7uoSimc4ZzGSDq2YqGUuZiV6t/DDtvLC/ZLMiUzAsyRqdNnjh4yH6NmvR5led4/QFs83M7CmVuZHN0cmVhbQplbmRvYmoKMjYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMzAgPj4Kc3RyZWFtCnicNVFJbsMwDLzrFfOBAOIuv8dBT+3/rx3SCWBgaEuczREbGxF4icHPQeTGW9aMmvibyV3xuzwVHgm3gidRBF6Ge9kJLm8Yl/04zHzwXlo5kxpPMiAX2fTwRMhgl0DowOwa1GGbaSf6hoTPjkg1G1lOX0vQS6sQKE/ZfqcLSrSt6s/tsy607WtPONntqSeVTyCeW7ICl41XTBZjGfRE5S7F9EGqs4WehPKifA6y+aghEl2inIEnBgejQDuw57afiVeFoHV1n7aNoRopHU//NjQ1SSLkEyWc2dK4W/j+nnv9/AOmVFOfCmVuZHN0cmVhbQplbmRvYmoKMjcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMjcgPj4Kc3RyZWFtCnicNU87sgMhDOs5hS6QGYxtYM+zmVQv92+fZLINEv5I8vRERyZe5sgIrNnxthYZiBn4FlPxrz3tw4TqPbiHCOXiQphhJJw167ibp+PFv13lM9bBuw2+YpYXBLYwk/WVxZnLdsFYGidxTrIbY9dEbGNd6+kU1hFMKAMhne0wJcgcFSl9sqOMOTpO5InnYqrFLr/vYX3BpjGiwhxXBU/QZFCWPe8moB0X9N/Vjd9JNIteAjKRYGGdJObOWU741WtHx1GLIjEnpBnkMhHSnK5iCqEJxTo7CioVBZfqc8rdPv9oXVtNCmVuZHN0cmVhbQplbmRvYmoKMjggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDUgPj4Kc3RyZWFtCnicRVC7jUMxDOs9BRcIYP0se553SJXbvz1KRnCFIVo/kloSmIjASwyxlG/iR0ZBPQu/F4XiM8TPF4VBzoSkQJz1GRCZeIbaRm7odnDOvMMzjDkCF8VacKbTmfZc2OScBycQzm2U8YxCuklUFXFUn3FM8aqyz43XgaW1bLPTkewhjYRLSSUml35TKv+0KVsq6NpFE7BI5IGTTTThLD9DkmLMoJRR9zC1jvRxspFHddDJ2Zw5LZnZ7qftTHwPWCaZUeUpnecyPiep81xOfe6zHdHkoqVV+5z93pGW8iK126HV6VclUZmN1aeQuDz/jJ/x/gOOoFk+CmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMzMgPj4Kc3RyZWFtCnicTY9BEsMwCAPvfoWegLEB8550ekr+fy2QNu4F7YyAkYYwCDxiDOswJbx6++FVpEtwNo75JRlFPAhqC9wXVAVHY4qd+Njdoeyl4ukUTYvrEXPTtKR0N1Eqbb2dyPjAfZ/eH1W2JJ2CHlvqhC7RJPJFAnPYVDDP6sZLS4+n7dneH2Y+M9cKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0NyA+PgpzdHJlYW0KeJxNUbttRDEM698UXOAA62t5ngtSXfZvQ8kIkMIgoS8ppyUW9sZLDOEHWw++5JFVQ38ePzHsMyw9yeTUP+a5yVQUvhWqm5hQF2Lh/WgEvBZ0LyIrygffj2UMc8734KMQl2AmNGCsb0kmF9W8M2TCiaGOw0GbVBh3TRQsrhXNM8jtVjeyOrMgbHglE+LGAEQE2ReQzWCjjLGVkMVyHqgKkgVaYNfpG1GLgiuU1gl0otbEuszgq+f2djdDL/LgqLp4fQzrS7DC6KV7LHyuQh/M9Ew7d0kjvfCmExFmDwVSmZ2RlTo9Yn23QP+fZSv4+8nP8/0LFShcKgplbmRzdHJlYW0KZW5kb2JqCjMxIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzM4ID4+CnN0cmVhbQp4nEVSS3LFMAjb5xRcIDPmZ+PzvE5X6f23lXA63Tz0DAgJMj1lSKbcNpZkhOQc8qVXZIjVkJ9GjkTEEN8pocCu8rm8lsRcyG6JSvGhHT+XpTcyza7QqrdHpzaLRjUrI+cgQ4R6VujM7lHbZMPrdiHpOlMWh3As/0MFspR1yimUBG1B39gj6G8WPBHcBrPmcrO5TG71v+5bC57XOluxbQdACZZz3mAGAMTDCdoAxNza3hYpKB9VuopJwq3yXCc7ULbQqnS8N4AZBxg5YMOSrQ7XaG8Awz4P9KJGxfYVoKgsIP7O2WbB3jHJSLAn5gZOPXE6xZFwSTjGAkCKreIUuvEd2OIvF66ImvAJdTplTbzCntrix0KTCO9ScQLwIhtuXR1FtWxP5wm0PyqSM2KkHsTRCZHUks4RFJcG9dAa+7iJGa+NxOaevt0/wjmf6/sXFriD4AplbmRzdHJlYW0KZW5kb2JqCjMyIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTYzID4+CnN0cmVhbQp4nEWQuXUEMQxDc1WBEniAOuoZP0ez/acLabzeQPp4hHiIPQnDcl3FhdENP962zDS8jjLcjfVlxviosUBO0AcYIhNXo0n17YozVOnh1WKuo6JcLzoiEsyS46tAI3w6ssdDW9uZfjqvf+wh7xP/KirnbmEBLqruQPlSH/HUj9lR6pqhjyorax5q2r8IuyKUtn1cTmWcunsHtMJnK1f7fQOo5zqACmVuZHN0cmVhbQplbmRvYmoKMzMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA2OCA+PgpzdHJlYW0KeJwzMrdQMFCwNAEShhYmCuZmBgophlxAvqmJuUIuF0gMxMoBswyAtCWcgohbQjRBlIJYEKVmJmYQSTgDIpcGAMm0FeUKZW5kc3RyZWFtCmVuZG9iagozNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDQ1ID4+CnN0cmVhbQp4nDMyt1AwULA0ARKGFiYK5mYGCimGXJYQVi4XTCwHzALRlnAKIp4GAJ99DLUKZW5kc3RyZWFtCmVuZG9iagozNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI1NSA+PgpzdHJlYW0KeJxFkUuSAyAIRPeegiOA/OQ8mZpVcv/tNJhMNnaXqP2ESiOmEiznFHkw/cjyzWS26bUcq52NAooiFMzkKvRYgdWdKeLMtUS19bEyctzpHYPiDeeunFSyuFHGOqo6FTim58r6qu78uCzKviOHMgVs1jkONnDltmGME6PNVneH+0SQp5Opo+J2kGz4g5PGvsrVFbhONvvqJRgHgn6hCUzyTaB1hkDj5il6cgn28XG780Cwt7wJpGwI5MgQjA5Bu06uf3Hr/N7/OsOd59oMV4538TtMa7vjLzHJirmARe4U1PM9F63rDB3vyZljctN9Q+dcsMvdQabP/B/r9w9QimaICmVuZHN0cmVhbQplbmRvYmoKMzYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNjEgPj4Kc3RyZWFtCnicRZBLEsMgDEP3nEJH8EcGfJ50ukrvv60hTbOAp7FABncnBKm1BRPRBS9tS7oLPlsJzsZ46DZuNRLkBHWAVqTjaJRSfbnFaZV08Wg2cysLrRMdZg56lKMZoBA6Fd7touRypu7O+Udw9V/1R7HunM3EwGTlDoRm9SnufJsdUV3dZH/SY27Wa38V9qqwtKyl5YTbzl0zoATuqRzt/QWpczqECmVuZHN0cmVhbQplbmRvYmoKMzcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMTQgPj4Kc3RyZWFtCnicPVC7EUMxCOs9BQvkznztN8/Lpcv+bSScpEI2QhKUmkzJlIc6ypKsKU8dPktih7yH5W5kNiUqRS+TsCX30ArxfYnmFPfd1ZazQzSXaDl+CzMqqhsd00s2mnAqE7qg3MMz+g1tdANWhx6xWyDQpGDXtiByxw8YDMGZE4siDEpNBv+tcvdS3O89HG+iiJR08K755fTLzy28Tj2ORLq9+YprcaY6CkRwRmryinRhxbLIQ6TVBDU9A2u1AK7eevk3aEd0GYDsE4njNKUcQ//WuMfrA4eKUvQKZW5kc3RyZWFtCmVuZG9iagozOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDgwID4+CnN0cmVhbQp4nEWMuw3AMAhEe6ZgBH4mZp8olbN/GyBK3HBPunu4OhIyU95hhocEngwshlPxBpmjYDW4RlKNneyjsG5fdYHmelOr9fcHKk92dnE9zcsZ9AplbmRzdHJlYW0KZW5kb2JqCjM5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjM2ID4+CnN0cmVhbQp4nE1QS25EIQzbc4pc4EkkIQHOQ9VV5/7bscNU7SqGGH9ID+myVR7rU2J1iezypU2XyjJ5FajlT9v/UQwCbv/QyEG0t4ydYuYS1sXCJDzlNCMbJ9csH487TxtmhcbEjeOdLhlgnxYBNVuVzYE5bTo3QLqQGreqs95kUAwi6kLNB5MunKfRl4g5nqhgSncmtZAbXD7VoQNxWr0KuWOLk2/EHFmhwGHQTHHWXwHWqMmyWcggSYYhzn2je5QKjajKeSsVwg+ToRH1htWgBpW5haKp5ZL8HdoCMAW2jHXpDEqBqgDB3yqnfb8BJI1dUwplbmRzdHJlYW0KZW5kb2JqCjQwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTU3ID4+CnN0cmVhbQp4nEWQuRFDMQhEc1VBCRKwCOqxx9F3/6kX+Uq0bwAth68lU6ofJyKm3Ndo9DB5Dp9NJVYs2Ca2kxpyGxZBSjGYeE4xq6O3oZmH1Ou4qKq4dWaV02nLysV/82hXM5M9wjXqJ/BN6PifPLSp6FugrwuUfUC1OJ1JUDF9r2KBo5x2fyKcGOA+GUeZKSNxYm4K7PcZAGa+V7jG4wXdATd5CmVuZHN0cmVhbQplbmRvYmoKNDEgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzMzIgPj4Kc3RyZWFtCnicLVI5jiQxDMv9Cn5gAOvy8Z4eTNT7/3RJVQUFqmzLPORyw0QlfiyQ21Fr4tdGZqDC8K+rzIXvSNvIOohryEVcyZbCZ0Qs5DHEPMSC79v4GR75rMzJswfGL9n3GVbsqQnLQsaLM7TDKo7DKsixYOsiqnt4U6TDqSTY44v/PsVzF4IWviNowC/556sjeL6kRdo9Ztu0Ww+WaUeVFJaD7WnOy+RL6yxXx+P5INneFTtCaleAojB3xnkujjJtZURrYWeDpMbF9ubYj6UEXejGZaQ4AvmZKsIDSprMbKIg/sjpIacyEKau6Uont1EVd+rJXLO5vJ1JMlv3RYrNFM7rwpn1d5gyq807eZYTpU5F+Bl7tgQNnePq2WuZhUa3OcErJXw2dnpy8r2aWQ/JqUhIFdO6Ck6jyBRL2Jb4moqa0tTL8N+X9xl//wEz4nwBCmVuZHN0cmVhbQplbmRvYmoKNDIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA1MiA+PgpzdHJlYW0KeJwzNjZXMABCXUsjBWMg29zIUiHFkMvI1ATMzOWCCeZwWRiDVeVwGUBpmKIcrjQA36oNrQplbmRzdHJlYW0KZW5kb2JqCjQzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTcgPj4Kc3RyZWFtCnicMza0UDCAwxRDLgAalALsCmVuZHN0cmVhbQplbmRvYmoKNDQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMzEgPj4Kc3RyZWFtCnicRY/LDQQhDEPvVOES8hk+qYfVntj+r+swmkFC+EEiO/EwCKzz8jbQxfDRosM3/jbVq2OVLB+6elJWD+mQh7zyFVBpMFHEhVlMHUNhzpjKyJYytxvhtk2DrGyVVK2DdjwGD7anZasIfqltYeos8QzCVV64xw0/kEutd71Vvn9CUzCXCmVuZHN0cmVhbQplbmRvYmoKNDUgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDggPj4Kc3RyZWFtCnicLVE5kgNBCMvnFXpCc9PvscuR9//pCsoBg4ZDIDotcVDGTxCWK97yyFW04e+ZGMF3waHfynUbFjkQFUjSGFRNqF28Hr0HdhxmAvOkNSyDGesDP2MKN3pxeEzG2e11GTUEe9drT2ZQMisXccnEBVN12MiZw0+mjAvtXM8NyLkR1mUYpJuVxoyEI00hUkih6iapM0GQBKOrUaONHMV+6csjnWFVI2oM+1xL29dzE84aNDsWqzw5pUdXnMvJxQsrB/28zcBFVBqrPBAScL/bQ/2c7OQ33tK5s8X0+F5zsrwwFVjx5rUbkE21+Dcv4vg94+v5/AOopVsWCmVuZHN0cmVhbQplbmRvYmoKNDYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA3MiA+PgpzdHJlYW0KeJw1jLERwDAIA3um0Ag2WGDvk0tF9m9DfE4DLx0Pl6LBWg26giNwdan80SNduSlFl2POguFxql9IMUY9qCPj3sdPuV9wFhJ9CmVuZHN0cmVhbQplbmRvYmoKNDcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4OCA+PgpzdHJlYW0KeJw1jLsRwDAIQ3tPwQgGi4/3yaVK9m+D7dCApHf3goM6QfK4GymcLm7ZV3obj5OeJgCx9ExD7d9gRdWLWhQtX25j0GIqvj/6JCCWdfJeOPSQEt4fxRcdewplbmRzdHJlYW0KZW5kb2JqCjQ4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoxOSAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMCAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDMyIC9zcGFjZSA0NyAvc2xhc2ggL3plcm8gL29uZSAvdHdvIDUzIC9maXZlIDY2IC9CIDc4IC9OIDgyIC9SIC9TIDk3IC9hCjk5IC9jIC9kIC9lIC9mIC9nIC9oIC9pIDEwOCAvbCAvbSAvbiAvbyAvcCAxMTQgL3IgL3MgL3QgMTE4IC92IC93IF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAxOCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxNyAwIFIgPj4KZW5kb2JqCjE4IDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTcgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjAgMCBvYmoKPDwgL0IgMjEgMCBSIC9OIDIyIDAgUiAvUiAyMyAwIFIgL1MgMjQgMCBSIC9hIDI1IDAgUiAvYyAyNiAwIFIgL2QgMjcgMCBSCi9lIDI4IDAgUiAvZiAyOSAwIFIgL2ZpdmUgMzAgMCBSIC9nIDMxIDAgUiAvaCAzMiAwIFIgL2kgMzMgMCBSIC9sIDM0IDAgUgovbSAzNSAwIFIgL24gMzYgMCBSIC9vIDM3IDAgUiAvb25lIDM4IDAgUiAvcCAzOSAwIFIgL3IgNDAgMCBSIC9zIDQxIDAgUgovc2xhc2ggNDIgMCBSIC9zcGFjZSA0MyAwIFIgL3QgNDQgMCBSIC90d28gNDUgMCBSIC92IDQ2IDAgUiAvdyA0NyAwIFIKL3plcm8gNDggMCBSID4+CmVuZG9iagozIDAgb2JqCjw8IC9GMSAxOSAwIFIgL0YyIDE0IDAgUiA+PgplbmRvYmoKNCAwIG9iago8PCAvQTEgPDwgL0NBIDAgL1R5cGUgL0V4dEdTdGF0ZSAvY2EgMSA+PgovQTIgPDwgL0NBIDEgL1R5cGUgL0V4dEdTdGF0ZSAvY2EgMSA+PgovQTMgPDwgL0NBIDAuOCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAwLjggPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjQ5IDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAyMTAxMTgxMjI3NDgrMDInMDAnKQovQ3JlYXRvciAoTWF0cGxvdGxpYiB2My4zLjIsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcpCi9Qcm9kdWNlciAoTWF0cGxvdGxpYiBwZGYgYmFja2VuZCB2My4zLjIpID4+CmVuZG9iagp4cmVmCjAgNTAKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMTMwNjkgMDAwMDAgbiAKMDAwMDAxMjgyMSAwMDAwMCBuIAowMDAwMDEyODY0IDAwMDAwIG4gCjAwMDAwMTMwMDYgMDAwMDAgbiAKMDAwMDAxMzAyNyAwMDAwMCBuIAowMDAwMDEzMDQ4IDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDM5MSAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMDE4NjMgMDAwMDAgbiAKMDAwMDAwMjU0NCAwMDAwMCBuIAowMDAwMDAyMzM2IDAwMDAwIG4gCjAwMDAwMDIwMjEgMDAwMDAgbiAKMDAwMDAwMzU5NyAwMDAwMCBuIAowMDAwMDAxODg0IDAwMDAwIG4gCjAwMDAwMTE0NDggMDAwMDAgbiAKMDAwMDAxMTI0OCAwMDAwMCBuIAowMDAwMDEwODE3IDAwMDAwIG4gCjAwMDAwMTI1MDEgMDAwMDAgbiAKMDAwMDAwMzYyOSAwMDAwMCBuIAowMDAwMDAzOTYxIDAwMDAwIG4gCjAwMDAwMDQxMDggMDAwMDAgbiAKMDAwMDAwNDQwOCAwMDAwMCBuIAowMDAwMDA0ODE5IDAwMDAwIG4gCjAwMDAwMDUxOTYgMDAwMDAgbiAKMDAwMDAwNTQ5OSAwMDAwMCBuIAowMDAwMDA1Nzk5IDAwMDAwIG4gCjAwMDAwMDYxMTcgMDAwMDAgbiAKMDAwMDAwNjMyMyAwMDAwMCBuIAowMDAwMDA2NjQzIDAwMDAwIG4gCjAwMDAwMDcwNTQgMDAwMDAgbiAKMDAwMDAwNzI5MCAwMDAwMCBuIAowMDAwMDA3NDMwIDAwMDAwIG4gCjAwMDAwMDc1NDcgMDAwMDAgbiAKMDAwMDAwNzg3NSAwMDAwMCBuIAowMDAwMDA4MTA5IDAwMDAwIG4gCjAwMDAwMDgzOTYgMDAwMDAgbiAKMDAwMDAwODU0OCAwMDAwMCBuIAowMDAwMDA4ODU3IDAwMDAwIG4gCjAwMDAwMDkwODcgMDAwMDAgbiAKMDAwMDAwOTQ5MiAwMDAwMCBuIAowMDAwMDA5NjE2IDAwMDAwIG4gCjAwMDAwMDk3MDUgMDAwMDAgbiAKMDAwMDAwOTkwOSAwMDAwMCBuIAowMDAwMDEwMjMwIDAwMDAwIG4gCjAwMDAwMTAzNzQgMDAwMDAgbiAKMDAwMDAxMDUzNCAwMDAwMCBuIAowMDAwMDEzMTI5IDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gNDkgMCBSIC9Sb290IDEgMCBSIC9TaXplIDUwID4+CnN0YXJ0eHJlZgoxMzI4NgolJUVPRgo=\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import scipy.signal as sig\n",
"\n",
"w = 16 # wordlength of the quantized signal\n",
"L = 2 ** np.arange(1, 10) # oversampling factors\n",
"\n",
"N = 8192 # length of signal\n",
"Om0 = 100 * 2 * np.pi / N # frequency of harmonic signal\n",
"Q = 1 / (2 ** (w - 1)) # quantization step\n",
"\n",
"\n",
"def uniform_midtread_quantizer(x, Q):\n",
" \"\"\"Uniform mid-tread qantizer with limiter.\"\"\"\n",
" # limiter\n",
" x = np.copy(x)\n",
" idx = np.where(x <= -1)\n",
" x[idx] = -1\n",
" idx = np.where(x > 1 - Q)\n",
" x[idx] = 1 - Q\n",
" # linear uniform quantization\n",
" xQ = Q * np.floor(x / Q + 1 / 2)\n",
"\n",
" return xQ\n",
"\n",
"\n",
"def SNR_oversampled_ADC(L):\n",
" \"\"\"Estimate SNR of oversampled analog-to-digital converter.\"\"\"\n",
" x = (1 - Q) * np.cos(Om0 * np.arange(N))\n",
" xu = (1 - Q) * np.cos(Om0 * np.arange(N * L) / L)\n",
" # quantize signal\n",
" xQu = uniform_midtread_quantizer(xu, Q)\n",
" # low-pass filtering and decimation\n",
" xQ = sig.resample(xQu, N)\n",
" # estimate SNR\n",
" e = xQ - x\n",
"\n",
" return 10 * np.log10((np.var(x) / np.var(e)))\n",
"\n",
"\n",
"# compute SNR for oversampled ADC\n",
"SNR = [SNR_oversampled_ADC(l) for l in L]\n",
"\n",
"# plot result\n",
"plt.figure(figsize=(10, 4))\n",
"plt.semilogx(L, SNR, label=\"SNR with oversampling\")\n",
"plt.plot(L, (6.02 * w + 1.76) * np.ones(L.shape), label=\"SNR w/o oversampling\")\n",
"plt.xlabel(r\"oversampling factor $L$\")\n",
"plt.ylabel(r\"SNR in dB\")\n",
"plt.legend(loc=\"upper left\")\n",
"plt.grid()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* What SNR can be achieved for an oversampling factor of $L=16$?\n",
"* By how many bits could the word length $w$ be reduced in order to gain the same SNR as without oversampling?\n",
"\n",
"Solution: The SNR for the quantization of a uniformly distributed input signal without oversampling is $\\text{SNR} \\approx 6.02 w \\approx 96$ dB and with 16 times oversampling $\\text{SNR}_{L} \\approx 6.02 w + 10 \\cdot \\log_{10} (16) \\approx 96 + 12$ dB. Since the [quantization of a harmonic signal](linear_uniform_quantization_error.ipynb#Harmonic-Signal) is considered an offset of $1.76$ dB has to added to both. The wordlength could be reduced by 2 bits according to these numbers."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Anti-Aliasing Filter\n",
"\n",
"Besides an increased SNR, oversampling has also another benefit. In order to ensure that the input signal $x(t)$ is band-limited before sampling, a low-pass filter $H_\\text{LP}(\\mathrm{j}\\,\\omega)$ is applied in typical analog-to-digital converters. This is illustrated in the following\n",
"\n",
"\n",
"\n",
"The filter $H_\\text{LP}(\\mathrm{j}\\,\\omega)$ is also known as [anti-aliasing filter](https://en.wikipedia.org/wiki/Anti-aliasing_filter). The ideal low-pass filter is given as $H_\\text{LP}(\\mathrm{j}\\,\\omega) = \\text{rect}\\left( \\frac{\\omega}{\\omega_\\text{S}} \\right)$. The ideal $H_\\text{LP}(\\mathrm{j}\\,\\omega)$ can only be approximated in the analog domain. Since the sampling rate is higher than the Nyquist rate, there is no need for a steep slope of the filter in order to avoid aliasing. However, the pass-band of the filter within $|\\omega| < |\\omega_\\text{C}|$ has to be flat. \n",
"\n",
"Before decimation, the discrete filter $H_\\text{LP}(\\mathrm{e}^{\\,\\mathrm{j}\\,\\Omega})$ has to remove the spectral contributions that may lead to aliasing. However, a discrete filter $H_\\text{LP}(\\mathrm{e}^{\\,\\mathrm{j}\\,\\Omega})$ with steep slope can be realized much easier than in the analog domain."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"**Copyright**\n",
"\n",
"This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Digital Signal Processing - Lecture notes featuring computational examples*."
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.9"
}
},
"nbformat": 4,
"nbformat_minor": 1
}