{ "cells": [ { "cell_type": "markdown", "metadata": { "nbsphinx": "hidden" }, "source": [ "# The Discrete-Time Fourier Transform\n", "\n", "*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Comunications Engineering, Universität Rostock. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "## Theorems\n", "\n", "The theorems of the discrete-time Fourier transform (DTFT) relate basic operations applied to discrete signals to their equivalents in the DTFT domain. They are of use to transform signals composed from modified [standard signals](../discrete_signals/standard_signals.ipynb), for the computation of the response of a linear time-invariant (LTI) system and to predict the consequences of modifying a signal or system by certain operations." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Convolution Theorem\n", "\n", "The [convolution theorem](https://en.wikipedia.org/wiki/Convolution_theorem) states that the DTFT of the linear convolution of two discrete signals $x[k]$ and $y[k]$ is equal to the scalar multiplication of their DTFTs $X(e^{j \\Omega}) = \\mathcal{F}_* \\{ x[k] \\}$ and $Y(e^{j \\Omega}) = \\mathcal{F}_* \\{ y[k] \\}$\n", "\n", "\\begin{equation}\n", "\\mathcal{F}_* \\{ x[k] * y[k] \\} = X(e^{j \\Omega}) \\cdot Y(e^{j \\Omega})\n", "\\end{equation}\n", "\n", "The theorem can be proven by introducing the [definition of the linear convolution](../discrete_systems/linear_convolution.ipynb) into the [definition of the DTFT](definition.ipynb) and changing the order of summation\n", "\n", "\\begin{align}\n", "\\mathcal{F} \\{ x[k] * y[k] \\} &= \\sum_{k = -\\infty}^{\\infty} \\left( \\sum_{\\kappa = -\\infty}^{\\infty} x[\\kappa] \\cdot y[k - \\kappa] \\right) e^{-j \\Omega k} \\\\\n", "&= \\sum_{\\kappa = -\\infty}^{\\infty} \\left( \\sum_{k = -\\infty}^{\\infty} y[k - \\kappa] \\, e^{-j \\Omega k} \\right) x[\\kappa] \\\\\n", "&= Y(e^{j \\Omega}) \\cdot \\sum_{\\kappa = -\\infty}^{\\infty} x[\\kappa] \\, e^{-j \\Omega \\kappa} \\\\\n", "&= Y(e^{j \\Omega}) \\cdot X(e^{j \\Omega})\n", "\\end{align}\n", "\n", "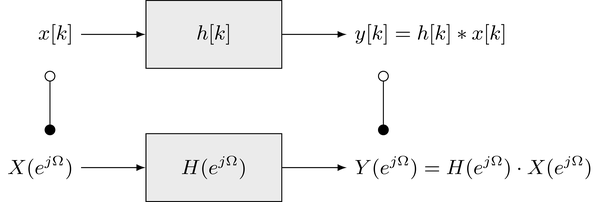The convolution theorem is very useful in the context of LTI systems. The output signal $y[k]$ of an LTI system is given as the convolution of the input signal $x[k]$ with its impulse response $h[k]$. Hence, the signals and the system can be represented equivalently in the time and frequency domain\n", "\n", "![Representation of an LTI system in the time- and spectral-domain](LTI_system.png)\n", "\n", "Calculation of the system response by transforming the problem into the DTFT domain can be beneficial since this replaces the computation of the linear convolution by a scalar multiplication. The (inverse) DTFT is known for many signals or can be derived by applying the properties and theorems to standard signals and their transforms. In many cases this procedure simplifies the calculation of the system response significantly.\n", "\n", "The convolution theorem can also be useful to derive the DTFT of a signal. The key is here to express the signal as convolution of two other signals for which the transforms are known. This is illustrated in the following example." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "#### Transformation of the trapezoidal and triangular signal\n", "\n", "The linear convolution of two [rectangular signals](../discrete_signals/standard_signals.ipynb#Rectangular-Signal) of lengths $N$ and $M$ defines a [signal of trapezoidal shape](../discrete_systems/linear_convolution.ipynb#Finite-Length-Signals)\n", "\n", "\\begin{equation}\n", "x[k] = \\text{rect}_N[k] * \\text{rect}_M[k]\n", "\\end{equation}\n", "\n", "Application of the convolution theorem together with the [DTFT of the rectangular signal](definition.ipynb#Transformation-of-the-Rectangular-Signal) yields its DTFT as\n", "\n", "\\begin{equation}\n", "X(e^{j \\Omega}) = \\mathcal{F}_* \\{ \\text{rect}_N[k] \\} \\cdot \\mathcal{F}_* \\{ \\text{rect}_M[k] \\} =\n", "e^{-j \\Omega \\frac{N+M-2}{2}} \\cdot \\frac{\\sin(\\frac{N \\Omega}{2}) \\sin(\\frac{M \\Omega}{2})}{\\sin^2 ( \\frac{\\Omega}{2} )}\n", "\\end{equation}\n", "\n", "The transform of the triangular signal can be derived from this result. The convolution of two rectangular signals of equal length $N=M$ yields the triangular signal $\\Lambda[k]$ of length $2N - 1$\n", "\n", "\\begin{equation}\n", "\\Lambda_{2N - 1}[k] = \\begin{cases} k + 1 & \\text{for } 0 \\leq k < N \\\\\n", "2N - 1 - k & \\text{for } N \\leq k < 2N - 1 \\\\\n", "0 & \\text{otherwise}\n", "\\end{cases}\n", "\\end{equation}\n", "\n", "From above result the DTFT of the triangular signal is derived by substitution of $N$ by $M$\n", "\n", "\\begin{equation}\n", "\\mathcal{F}_* \\{ \\Lambda_{2N - 1}[k] \\} =\n", "e^{-j \\Omega (N-1)} \\cdot \\frac{\\sin^2(\\frac{N \\Omega}{2}) }{\\sin^2 ( \\frac{\\Omega}{2} )}\n", "\\end{equation}\n", "\n", "Both the triangular signal and the magnitude of its DTFT are plotted for illustration" ] }, { "cell_type": "code", "execution_count": 1, "metadata": {}, "outputs": [ { "data": { "application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDQwMi4zNzkzNzUgMzE0LjM1NTc1IF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nN1YTU8bMRC9+1f4SA9MPOPvYxElUqUeoJF6qDgFSEtJK0Aq/fkdJ2E93mQXKlWJBKuI7MvsvGfPjMde1LcK9UIbfcufJ/1VX/L/K416yp+FMny3VM4Q2Jht9Hx7J28tOrDe87c7tpV335S6UZP37OSRH5oqZR14v34ognfly1LZjBBii941qLEQNi6FB4FuiGhNtGDZPBRIYjBMX35R3kDMhIakAgE6MBsB6oRn5UmdzPTkDDUaPbtRLkJAcuhipKiJIHs9u1JH5p2e3eoPM7UiVWgcZIOYrWSR6DgNGoRI6I0PCZPgoR6Pz2BYdnINj0Bf4PEekjU+B59NFjyu5SG0UHS3cZPoOA+ZDNnmkNiikoQeSYhALDqEhkSgL5CE8nuKMTmTUfCklscSgmU3PjZJKNBxnpLgOXJcykWCB3tZwC7AsXCXGiKBvkAUOI6JE61cVhJ1aXDPTxl9bDjhOX2fo5GBWB95PV+yx1K/4Eyg1cOTM9q4P/pRvCj2cv4suKstlyHYvNaLYHrgwPwjkHacUI5KnHeURfWfHGDu++/AEf+pDKXzj0P+ERNE3yeo6AgDlvCGjoIGKbwFi1sUHTpGwTPpqaOwgxQpQopbFB06RsGTaVJH4YYoiLPKbUW6oiMUxLMZaqz9IIUPkLeCXdExCp5NquEOgxTcK/xWuCs6RsGzGWu4Y62sUlTHpbzQA/Jgy9QHA34leryy/qwqy0PGuF70zNrgmfno68rAlnZgQ0Rh0qtOz42Ju4EvHH0nl7V+7/WOzmp9ZOGaQuCFgfTDtf6if7JiHgz3lUCFFHglWv9FntVofEpkPWX9sBi21I3lxbSxVMOWD4vNglWmtuu5ZXWrtT9f6skno09/dYYUOaBuc63GGd641fEbNDtX5/ofspT0R83Vyxu4V+YWZ+Hk9Pr39/n1xfREzx/Fnk40swrKZvN539oir+DrLYDQVsGmT+1dnNimCnUCbXrc/uXxAp95m2ZzI6+iTX/cv7y6+ZbyKtr01v3LSwEM51gb2w5suvLexYkDhVAn0Kaj71+e4yc5w5oVpYIHnrt6TpLqKnrYvKPsgPioidjIq+hhq1ac/uTRp6KHXfOsS2C3mplAD9sxxJFWyqvof2q2qYy26LOsDlmKQ4yh7E03qp3HV24EdknuxBVOs/UGqR+SXW+ydr6cYq+7XnEth15xFfvXvydrrTs3Y97P1V91UhoMCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKOTEzCmVuZG9iagoxNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDg3ID4+CnN0cmVhbQp4nDWNwQ3AMAgD/5nCI8QQINmn6qvd/1tI1I99soyxWOhQS3EKwjsuNk7d+DaJQ09mAWUkjWWwUVQnh8QnZFqSsRazxb6dERCvDsV2osf+J0+7P7hOGcQKZW5kc3RyZWFtCmVuZG9iagoxOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkyID4+CnN0cmVhbQp4nD2MsQ3AMAgEe6b4BSJhjG3YJ0rl7N/mLSdp4PQP19KgOKxxdlU0HziLfHhL9YSNxJSmlUdTnN3aFg4rgxS72BYWXmERpPJqmPF5U9XAklKU5c36f3c9x6sbugplbmRzdHJlYW0KZW5kb2JqCjE1IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTYgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyAxMDcgL2sgMTIwIC94IF0gL1R5cGUgL0VuY29kaW5nID4+IC9GaXJzdENoYXIgMAovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250RGVzY3JpcHRvciAxNCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDEzIDAgUiA+PgplbmRvYmoKMTQgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDk2Ci9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL0l0YWxpY0FuZ2xlIDAgL01heFdpZHRoIDEzNTAgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjEzIDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNTAgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyOCA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTcgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxNyA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA4CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5OTUgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjE2IDAgb2JqCjw8IC9rIDE3IDAgUiAveCAxOCAwIFIgPj4KZW5kb2JqCjIzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNzEgPj4Kc3RyZWFtCnicM7Y0UDBQsDBT0DU0NlQwsjRWMDczUEgx5AIKgVi5XDCxHDDLzBLEMjQ3Q2LpmhlCZZFYIONyuGAG58DMy+FKAwDxtBYjCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA2NyA+PgpzdHJlYW0KeJwztjRQMFCwNFfQNTQ2VDA2MFEwNzNQSDHkgjFzwSywbA4XTB2EZQZiGBmaILHMgMaBJeEMkBk5cNNyuNIAzoMV0wplbmRzdHJlYW0KZW5kb2JqCjI1IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzkyID4+CnN0cmVhbQp4nD1SS24FMQjbzym4QKXwTXKeqd7u3X9bm8xUqgovA7YxlJcMqSU/6pKIM0x+9XJd4lHyvWxqZ+Yh7i42pvhYcl+6hthy0ZpisU8cyS/ItFRYoVbdo0PxhSgTDwAt4IEF4b4c//EXqMHXsIVyw3tkAmBK1G5AxkPRGUhZQRFh+5EV6KRQr2zh7yggV9SshaF0YogNlgApvqsNiZio2aCHhJWSqh3S8Yyk8FvBXYlhUFtb2wR4ZtAQ2d6RjREz7dEZcVkRaz896aNRMrVRGQ9NZ3zx3TJS89EV6KTSyN3KQ2fPQidgJOZJmOdwI+Ge20ELMfRxr5ZPbPeYKVaR8AU7ygEDvf3eko3Pe+AsjFzb7Ewn8NFppxwTrb4eYv2DP2xLm1zHK4dFFKi8KAh+10ETcXxYxfdko0R3tAHWIxPVaCUQDBLCzu0w8njGedneFbTm9ERoo0Qe1I4RPSiyxeWcFbCn/KzNsRyeDyZ7b7SPlMzMqIQV1HZ6qLbPYx3Ud577+vwBLgChGQplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ3ID4+CnN0cmVhbQp4nE1Ru21EMQzr3xRc4ADra3meC1Jd9m9DyQiQwiChLymnJRb2xksM4QdbD77kkVVDfx4/MewzLD3J5NQ/5rnJVBS+FaqbmFAXYuH9aAS8FnQvIivKB9+PZQxzzvfgoxCXYCY0YKxvSSYX1bwzZMKJoY7DQZtUGHdNFCyuFc0zyO1WN7I6syBseCUT4sYARATZF5DNYKOMsZWQxXIeqAqSBVpg1+kbUYuCK5TWCXSi1sS6zOCr5/Z2N0Mv8uCounh9DOtLsMLopXssfK5CH8z0TDt3SSO98KYTEWYPBVKZnZGVOj1ifbdA/59lK/j7yc/z/QsVKFwqCmVuZHN0cmVhbQplbmRvYmoKMjcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA5MCA+PgpzdHJlYW0KeJxNjUESwCAIA++8Ik9QRND/dHrS/1+r1A69wE4CiRZFgvQ1aksw7rgyFWtQKZiUl8BVMFwL2u6iyv4ySUydhtN7twODsvFxg9JJ+/ZxegCr/XoG3Q/SHCJYCmVuZHN0cmVhbQplbmRvYmoKMjggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4MCA+PgpzdHJlYW0KeJxFjLsNwDAIRHumYAR+JmafKJWzfxsgStxwT7p7uDoSMlPeYYaHBJ4MLIZT8QaZo2A1uEZSjZ3so7BuX3WB5npTq/X3BypPdnZxPc3LGfQKZW5kc3RyZWFtCmVuZG9iagoyOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDY4ID4+CnN0cmVhbQp4nDMzNlMwULAwAhKmpoYK5kaWCimGXEA+iJXLBRPLAbPMLMyBLCMLkJYcLkMLYzBtYmykYGZiBmRZIDEgutIAcvgSkQplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzE3ID4+CnN0cmVhbQp4nDVSS3JDMQjbv1Nwgc6Yv32edLJq7r+thCcrsC1AQi4vWdJLftQl26XD5Fcf9yWxQj6P7ZrMUsX3FrMUzy2vR88Rty0KBFETPfgyJxUi1M/U6Dp4YZc+A68QTikWeAeTAAav4V94lE6DwDsbMt4Rk5EaECTBmkuLTUiUPUn8K+X1pJU0dH4mK3P5e3KpFGqjyQgVIFi52AekKykeJBM9iUiycr03VojekFeSx2clJhkQ3SaxTbTA49yVtISZmEIF5liA1XSzuvocTFjjsITxKmEW1YNNnjWphGa0jmNkw3j3wkyJhYbDElCbfZUJqpeP09wJI6ZHTXbtwrJbNu8hRKP5MyyUwccoJAGHTmMkCtKwgBGBOb2wir3mCzkWwIhlnZosDG1oJbt6joXA0JyzpWHG157X8/4HRVt7owplbmRzdHJlYW0KZW5kb2JqCjMxIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzM4ID4+CnN0cmVhbQp4nDVSOa7dQAzrfQpdIIB2zZznBal+7t+GlF8KQ7RWipqOFpVp+WUhVS2TLr/tSW2JG/L3yQqJE5JXJdqlDJFQ+TyFVL9ny7y+1pwRIEuVCpOTksclC/4Ml94uHOdjaz+PI3c9emBVjIQSAcsUE6NrWTq7w5qN/DymAT/iEXKuWLccYxVIDbpx2hXvQ/N5yBogZpiWigpdVokWfkHxoEetffdYVFgg0e0cSXCMjVCRgHaB2kgMObMWu6gv+lmUmAl07Ysi7qLAEknMnGJdOvoPPnQsqL8248uvjkr6SCtrTNp3o0lpzCKTrpdFbzdvfT24QPMuyn9ezSBBU9YoaXzQqp1jKJoZZYV3HJoMNMcch8wTPIczEpT0fSh+X0smuiiRPw4NoX9fHqOMnAZvAXPRn7aKAxfx2WGvHGCF0sWa5H1AKhN6YPr/1/h5/vwDHLaAVAplbmRzdHJlYW0KZW5kb2JqCjMyIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjMzIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMSAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMiAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQ4IC96ZXJvIC9vbmUgL3R3byAvdGhyZWUgL2ZvdXIgL2ZpdmUgL3NpeCAvc2V2ZW4gL2VpZ2h0IDkxIC9icmFja2V0bGVmdAo5MyAvYnJhY2tldHJpZ2h0IF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAyMCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOSAwIFIgPj4KZW5kb2JqCjIwIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTkgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjIgMCBvYmoKPDwgL2JyYWNrZXRsZWZ0IDIzIDAgUiAvYnJhY2tldHJpZ2h0IDI0IDAgUiAvZWlnaHQgMjUgMCBSIC9maXZlIDI2IDAgUgovZm91ciAyNyAwIFIgL29uZSAyOCAwIFIgL3NldmVuIDI5IDAgUiAvc2l4IDMwIDAgUiAvdGhyZWUgMzEgMCBSCi90d28gMzIgMCBSIC96ZXJvIDMzIDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjEgMCBSIC9GMiAxNSAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL00wIDEyIDAgUiA+PgplbmRvYmoKMTIgMCBvYmoKPDwgL0JCb3ggWyAtMy41IC0zLjUgMy41IDMuNSBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTMxCi9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nG2QQQ6EIAxF9z1FL/BJS0Vl69JruJlM4v23A3FATN000L48flH+kvBOpcD4JAlLTrPketOQ0rpMjBjm1bIox6BRLdbOdTioz9BwY3SLsRSm1NboeKOb6Tbekz/6sFkhRj8cDq+EexZDJlwpMQaH3wsv28P/EZ5e1MAfoo1+Y1pD/QplbmRzdHJlYW0KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjM0IDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA2MjYxNTQzMjkrMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgMzUKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMDg1NzUgMDAwMDAgbiAKMDAwMDAwODA5NyAwMDAwMCBuIAowMDAwMDA4MTQwIDAwMDAwIG4gCjAwMDAwMDgyMzkgMDAwMDAgbiAKMDAwMDAwODI2MCAwMDAwMCBuIAowMDAwMDA4MjgxIDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDM5OCAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMDEzODYgMDAwMDAgbiAKMDAwMDAwODMxMyAwMDAwMCBuIAowMDAwMDAyMjYwIDAwMDAwIG4gCjAwMDAwMDIwNTIgMDAwMDAgbiAKMDAwMDAwMTcyOSAwMDAwMCBuIAowMDAwMDAzMzEzIDAwMDAwIG4gCjAwMDAwMDE0MDYgMDAwMDAgbiAKMDAwMDAwMTU2NSAwMDAwMCBuIAowMDAwMDA2ODY0IDAwMDAwIG4gCjAwMDAwMDY2NjQgMDAwMDAgbiAKMDAwMDAwNjI4MSAwMDAwMCBuIAowMDAwMDA3OTE3IDAwMDAwIG4gCjAwMDAwMDMzNTUgMDAwMDAgbiAKMDAwMDAwMzQ5OCAwMDAwMCBuIAowMDAwMDAzNjM3IDAwMDAwIG4gCjAwMDAwMDQxMDIgMDAwMDAgbiAKMDAwMDAwNDQyMiAwMDAwMCBuIAowMDAwMDA0NTg0IDAwMDAwIG4gCjAwMDAwMDQ3MzYgMDAwMDAgbiAKMDAwMDAwNDg3NiAwMDAwMCBuIAowMDAwMDA1MjY2IDAwMDAwIG4gCjAwMDAwMDU2NzcgMDAwMDAgbiAKMDAwMDAwNTk5OCAwMDAwMCBuIAowMDAwMDA4NjM1IDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gMzQgMCBSIC9Sb290IDEgMCBSIC9TaXplIDM1ID4+CnN0YXJ0eHJlZgo4Nzg5CiUlRU9GCg==\n", "image/svg+xml": [ "\n", "\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "\n" ], "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" }, { "data": { "application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM3OS4wMiAzMTYuNzU5NzU3MDUxNCBdIC9QYXJlbnQgMiAwIFIgL1Jlc291cmNlcyA4IDAgUgovVHlwZSAvUGFnZSA+PgplbmRvYmoKOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDExIDAgUiA+PgpzdHJlYW0KeJylfUuvLrtx3Xz/ij20B9ri+zG0oFhAJoEeSAI4HhjytSJBR4Ei2Jrkx2etqiLZp1mSEOQK196Xa63ur7v5qCKLxfj5u4/4+ZvP8Pk7/Pvnz3/6/Gf8/3/9jJ8/w7+/+Qj4r28fuc+vkPDn79efObavXmevHWXh+//8nx8f//bx43+A/E+Q/OzjI4av/pnqVymdDFyv9a+RHkW/30UzftV1IdU9S+zSSS/9G/xE/Oyv8fjhuCGRj9K+SsTv7F+15F5x01VSvoKU/P7j4yd49j9//BH/N3z+KOBqGQ9Xyoipfqb0Nevnr799/ORXnz/+x/gZw+ev/u1jfOU+Zmgg4L//9ePvyt9//up3H//pV7hK+Aq8EP63/oD6xz/94Xf/8l///Zf/8oc//ejbb//w73/6/On/+vg5/ic/+yNGPHZuz9+5i/7aD414N6WN/5dfmv4/f+mYX+n7H2ol1+/87nfE0b7CCPn8Uv6YwB/ziR+jF08tfLVRnlffRX/98qlCAsL3l0/fXz7n9BXDeF5+F/31y+c0vmYar8uXdfln1WmZFRivpMtXke8hr/vzet1fTQnPV/5fvv3wm3/526+8fvVHyV945b1+zSCfPuevjnrS3bdu18cHmrHG2c4NTtFfuEOb+AV8zJG/Yhw5xVh7lptE/y4xt680Wivp3OZR9rfuE/G9ypi99RxL04/8F26Ea7c6whiPG52yv3mjEb9Giynm0uOQG2X/RilXdIWz5seXeZT9rRulHL9STq3Ohj5O69VfuNEoXyWEOeLjRqfsb95ooMKFEkPtoxW5UQ2nBrPy/ojVMra0FD1bnxtqLFaVWW9HZaXCFc59/u7/SL+Sv3KbsZz+5sf/mBbjvwujQR3qqJMVN7wu8j/+zq4yAyoFXny/L/ODXabFVurI+OeTTU5amzG7EH8nRLQRVBbDf/Q989z37//Cfe2xVvsNfTVg/IWOoI2Ue8shxc/CborP9Nca9B8/vx8E5b1m9F0YkVJraEPp83//8PnfPv/wieEO41kAEmsbLfEXoa+3fzqqBtQD969pfv7iZ5+453/89tc//OJnP/n89Z90zKz44K1kaQD4bzBz0cKO3okV5pcuoHT8vKLX6CGlduhvQOgDrb9baRqjb/oFKL22GLWwjFYP+1Wu5NHnmFqKijUP+w0IfcbZi5X2PM9PuQClo5Umuyer06G/AaWj97HHmXj8w36VcwRHH9DKWKV5rF/uAEpH1bOyEuohf18sVPS2MdmzjFHOlS9A6XitbT360N7ily4g9BQSDCB7sTWfq1+A0kuKra/PlvKhvwGlj5JqsipR5zj0NyD0nNJYTxRiP/QLUHqPsVStzq3l8xovQOglolZkLc021P3SBZRea0OLYmmdoR/2q1zJ6Aqjvq1aczk/5QKEjsEc/bOUlll23XIApY+eit4SjfzxkS5A6K1NdCVSihdXNvtdLmQ0j1abFCaMLueXX4DQB95P1h+IynreyrtcyBisYpWHh61Q8nnMCwAd5llteKVSio62rs/vAEJHQ21THqegubS26Rcg9DZX68r4EvXQLwD0jHab5pTSFEvZlcsBhJ4xnlQpheWbd3VxANALn4PNpWC4h7W537oDgI7xP4XRPstgu+lxvce7HFY0PlzLM+ES+OCpxW49gAeADqMitdkGPSHUCXQSRncA0CsHQn66PIjXYa/RA2jSo+ViEKksjTHn/WMcQOgD3S8eGvbumGO/Rg8AHYNpKaFraay7j/YAoZeK0szSnkOLY9MvQOiNXyyyFNWpjbzpFyD0XgJqm5Sy1zlXvwCho+lGdNosLRHD+6ZfgNDnRO8hT9QIz02/ANDxUkPD4C2loaD/NroDCD1FtEP1nlFf+2a/y4WMLxGa+m4dZkfZ7AsQeqGlpb5YD2UNjR6gdFgmRS/Sdp/hlAu5lh7kVVV0hW1zX8VCbTTw1ZWqZY90HqD0Doujaymc7/NKLkDoHfVZ74jRPpyLv8uFPEIt9uCl7Y7OA5Q+ohaVei78XaHQZqk92b3yaId6AaBPGLbnXrnv2u0ASq806uyWcXWfHiD0GDKMfysduzE4gNJHC/ZS1Xvd9Dcg9NTosWnpnPX89gsQOqpwzvrFYIKf3/IuF3Jhx5RX5Znn2hcg9Br6sJmGVtpulw6g9IkfqFU+nUp4lwu5dbwqffgRwjjv/AKEPgK7d2mr6M/OY77LhTzxzFqFGnrIet74BXz7yHBOAmwk7cNYJ+yteIDQU6Whpl1e5fi36Bcg9IpaIdfosYflJDjlQh4xzynfGPY3rrHZFwA6jMEKMQsnmmu2zsopF/KcBfaIjEpDjIjFvgDQaTqg948y5o1tIzrlIBeMSRgIZMoRNltaX9MDOGFKvxFW/WehbQfTfb1CBwAd0jDgV36WhFccR7F+0wO+fUBaMG51KR05lfWBPAB02OsJgy5KM7zUHFcf7gFCh73GBoLSlNP2tDxA6BN9O6xelGbUz3yufgGg4zk6mqLcE05HX1XXA4TeQoj40izFt0hz0y9A6APGoPxCNIPyYL/LQaYxmGuWS1TYVMtK9ACh08HXx68jrhbqlAsZrwftlYUtpLJfogMIvSSYGXJHVIq53HgPEHoNg/NqUgoT4tAvQOgw7gO+rvyFFr/Z73Ih03VAzy6FGC37Zl+A0FE/Q5ev3AqGkvOgFyD0iVtWvUihB77pFwB6+YKRwX6GpRV22KI7gNJnrEkvUnNcNqIHCD2ic536tmB05EO/AKFzrtheAI2N82MuQOgYKmENWmla7pYHCJ0vCV2T3rPEc/ULEDrne6N+u5rqruoOIHTUnpC12pXZ+nnUCxA6TLretNrB/mh50y9A6LAcs76uEvI4F3+XK5kLIXpHmbnZ5Fe5kGfnfA3L0qihbfK7HOT6FdBBDX2xKaZmw4UHCD3izRa9If7Mh34BQseNpn62ipFqzeV4gNALeuw8tVt4st/lQq4cDLTDgQeTNvldLmROME2pboBzPpe+AKHDTkta9yvnhc7FL0CW3WJFuXRnME7T/vQOoKt0MFCTlALcxrMHgN7xJVLQlpVyOK/FAYSOXp5zuOyTYYjtRuEAoMPjgeuAH8YOP+a6zD8PAH2yPQUZLWPvZVfbu/zbR014HrjdTUZudA+ri/YA0Fn1O8cQjOE541tY5fIA0NsXCsXNhNOR8KFtLPIA0Duep+Qo/jqsjrlGUQ8QOoyCSq9gfKEZ0vtd9AsAndJiLjJ65bpmFTxA6DDaWxBLjx96bPa7XMiwflIW061jkG99sy8AdBpAeKdmRaa6RiMPEDqtWDXF24hjDXUeIPSa0ROLmQ+/uh32u1zIbQ6uIIixvDs5p1zIA15xTmqI5z7PpS/g20cLX+hVk/kbk/dWugcIPcKcmer14mn6oV+A0OFYFfPyOiybtukXIHT8pd5MQ+G59qtYqAX2bFTvFF3lcv08QOgYjvpy2trjZ7/LhUzz2FaZga+x3wOUPiJnc6Q0xHYe8gKEDicMZps6m7Bq46ZfgNBHLubilTrqufi7XMgzwiS19XG8h7nZFwB6hM8OXzMvFz+sn+IASkevHdbq+za4PUDokUuDc91zvxcHEDraYF4/sbaZNv0ChJ7ZxO0FYIg9V78AoWNgzWXY/Eta/ZYHCB3jErxvLa0cqxb9AoTeAi6j96yc29v0CxA6fFn1OCs6/DVYOOVCxuuHW2BOfmnnI12A0CesdmsusGrCeY0XAHrivHSP2m7nmSD0AKHjiat+Os5/LffSA4Re6N7ptCGGnF42/QKEjnE+JZvyDHvKxQOEDv8Xdo92rXXXgLsc5Mx5dAyq0m3n1ndtdAChZ3gaceiswExrrsgDhI6Xa4PCRG1dk5seADos6wKjo8vox3a5PpIDgA4rcsCJTCyFt7RdVw8AnTO6M9lAD4N2LRN4wLePrhWDHg2aTskh2KN6AOiM42iFyweormOO9U09QOiwDNlg6JZPdJl10y8AdDhAteYk9hJuHtbanwcIHRUz0L5O9Jz23LwHCB1u8iwyqVFGWKaRUw4yjHHYKJGFOcLSt5bhlAsZdkZIcgn0JrvD8AChY8jjIhBLuaTeN/0ChI6WGK10omtIm34BQkdvj66PpQXO+Fpv9QDQGVVQc5WLoPferrEHCD3FxjkYlsJF3e/cAYQOe23qlyicYO+bfgFCh50nLhBKWwxrdt4DlD4bHklL6xrwnHIhwyBodgm0m8e1L0Do+HNUfR6MzeNc/AKEPmIvPWop+4ZNvwChz6i+O0vnqOfqFwA63BQ8f9IHwti8vCMPEHos6G6qlba1nOsBQk81sKfUe+Y1IeEBQqdRO6wUHva5+gUIvaAnW0/EGLBNvwCho4PHsKnf7syle4DQe4QJZ6XxkF/FQh0NXvvUKnfWWz1A6LNm9IBaoVGl06ZfAOjosssMdsfc0vIwPEDoKfakPUOJMjQv+gUIPeORh1Y6+HprYs8DhI6vNpO8WjjbdXkNHiD0hr5Gu0B4K2lZ6h4g9MF1JnkivOPHk77LQZ5wZkPXQs5XLRvWA4ReS+tTfmAKsIjjpl+A0DEIV6n+MYY9g+2Uf/sYgSveTS/B9fW1huYBQscQVaKMUSMyeHTTLwB0GIezDE4laojFmmHyANA521sqXy3tbdR/6wE8APSBusMbZX7Bmdc7d8pBxrvCp9K1BE4krWbhAd8+ZuAUSy26rIGnt+d0yoXcBsxNsZjwR1/DqAcIffY2gi6wNIwQh34BoMPcnzXp4jHN4fWJPEDolX6yWpL1zC96gNAxGk/9iQxrWLPGHiD0kYNZtSntRWinXMgTnYgu9cEDaau2eADojCvGLdWVmGgri+4AQkdHyYg3W71bLdQDhJ653m2r6mENjE65kDEuJVsvRf+0OgsPEHqdEoelXnMK5+IXIPRON9hcrDN0eYDSp8xTigMHi6ke+hsQOrrumtZaby7nx1yA0DGIlbU0XMODfgGgZwZy4jrmq8Zl13mA0uFBlOU4b7vOA4ROO2KHbo8VAOYBQqeXnZYXv6dTPEDp7LnTcpzjYb/KhQx/INunw4AWzy+/AKFLp2ML8ieMygOEXmMz9xBe845y8QChY8C2KTm04jjO1S9A6WgmNducT1v2rgcIvXOa32JCWnw86gUIHe5vXy2m7yBNDwC9cD7TImswuNLJVboDCD1OawINXX047He5kNF12+PDcktr3tADhI7mYnE4sG7LsjA8QOiwI3rU+cQeWjlXvwDQ4XwG+DbyPD3VvgxYDxB6Lvhe5jhz3mfTL0DovQz7iWPmumYDPQD0xjBoucScPa6R9C4W6uCMmUxU5xZq2dx3Oci0xcKaBZ+MfDK2AzD6lw784EhGs4PTjzv+10EoqF/ou+Ee6AJBmju6+AZIV9djyPID6mdac94uQkFn9H+LsoiXU0I1XQIHUQGq9AxSXIDncQQXQgGtW1lOYjFawY6o9BAV5BqjrrhwFnUe/htQegsMude1qLGXM11EBX12BvHIsliGwX0EF6KCCeNffydafV7Ldy5CAaOXUFdsFTDEzb8BpcOKSrbcjb63PvgXooKEwTbYireYDltwISrA39y0oWveObcjuBAVwM2BUaLFra9IDhdRQc0YNWwxOOwx30VUQJ96LZRz5fEILsQEk5aXLTefQF4PUQHMx5ZtNTuez3wDSh9ZbBlbLD+bChxEBTNxynRdJzxucCEMXOauDwal2mL/nDuG2kFUECMGbiuO6UTpO4gJaDLru4bZOZ6CN6ICGuTNitue3HMRFWBgmmFFT9T6EFyICeB86rehHRof/BegdLrLzUI/Sk4P/oWoADbc1CiXxqihxyNfiApaHMXiP1JYc/EeoHT4Y80qFzq5vZHFQ1Qw4NpaLzW5weQILkQFk2axLncPsTG34EIoiPDMUKmkzdKJKfsnOYgKcpwpr45zrxK5iApqSowwZc88czx7AxxEBb1yN5UUF8YoHsGFUJA4z6SRKTSp2n7mG1A6OjUrTnHONg//QiiQcKbRxL9H2Y7QcxEKOMeL2itTU/nhnbkIBQw7mDNK4HvtOZzW7CAUoJtKfRSJyINZvfsvB+DOAnyaUYPO9dfIsdj4HkKBOHpib9J1L5zdNIGDqKD1CTNS7J9RwpqRdBEKaDnkqsuygzObq/F7iAo4zaqBmb2gOqYjuBAVtDZHNie+x/q4w4WogCEu5jtzm9tDcCEUcJ9um1oK6/Dwb0DpcEHHsIWr1nYn7yEqSGrKiGWOMb4ewYWoIPfcoi28wZ7oR3AhKigD398Wx3vc5oKHqIB2kK1hNi6QHcGFmACmpa2Rpx1R4gFKZ6BDsFXMUcrj+hdighnactPy3gPhIioYPeF5zGts/XGHC1HB1Gls9Ur3Uo6LUMDttrWsNeoy9w1uwOi9MczP3Pttx3uICrig2fYa+GnNDmIC9ARrWTtvq9YBlJ5iolGjtw31wb8QE9S+XOWCFvh44gtRQeZClc05cD7mCC7EBFx5WPsO2uktHMQEo4+18D9iewreiArgmra2Pv4s5QguxASw8Ff1Sqk83tKFqKBixLaYeJY/ftKFmGCsnhM1/gy1HqKCNmIu1qb23tS7XMkYJ1qyiP4Tje8iKuB0sj3WwJt7CC5EBZMzLhbXL3PYW3AhFDROWzSNeGBcxba/PEQFnFuwiCf0IeejOYgKMpyAFfSU9yy7i6iAPYcGSjBk/vRfDqKCzsgrW+OfO2rNRVQwU7IQArg2ew+Fi1DQv2hcWYAabLRdjW5A6Q1fZ8jsQeCuunn4F0IBdz2VpPFyMAj6GUQchALml5g5yNaDibZ7xn4H4VZELsfijcEKwnedM+wNoB5CASPb0qDZNGkcnC3dHsLdi3RRsqyc06FLcdt4HqICtL8SZHsw/ut8Zw+hgLE/lduEuCkz9L07yUVUIJtsZM9nCGdgcwClw96AGaR7RMMOlnQRFcwSg/7OyrjBw38DpHOpCmOFblmF07RNTg9RAXdyRtmEzIWa7cZ7iAloM+meaIyNu6J6iAqyrulUcZ92YKOLqADOQLR90TmG+RBciAoYHDd0gzEH1MdPuhATwGad+ku5SzM9BG9EBdzx0rJtp257dsRDTDDj0N26TXZtPgRvRAW9pBlWRoUd1OciJkB3PnSfNFfNnoI3ooKRepq2sz6eXe4eYgKZB9DiXMLjDheiAob72MuDTxcer/VCTFC52qSpAWJ7VNY3YHRYZmPlSyjh8VIvhAJGZrW8MknM46R6iAlQC+vKhLDdZgdQOjrD1CydwNzLtS5igs5/1u+MjxtciApSlF3H+ibStjo9xATc52Y3xij/eOQLUQEuEsJc3/L0MA5iAmmFq7bsLeceYgLUR91Gj/pY4lPwRlQA04w+gdb4va7pIiYY4hVrboT2eKtvQOmVG3YsOUIZe8rcQ0zQ4V2t9Ag5PH7QhagA1km2XqFwUD2CC1FBjxx4JenBnPnxi96A0kfAk+lt4UqMxw+6EBXAaRo6elXYKONRUy+EAvi6He63Di/o1rbZ6SEqgJOFRijFgckHjuBCVFBg2Qepjxgey+lTHUQFDR2hXocpcfaMkIdQQEdrZk3fgReRTp/qICqoafA6sCIIPwUXQgGjldDtFGZCKLHmM/I4CAXM+pYrpygbx7IdD+AiENQi31+tObh0O3bfRSioTCbBkBhGdDL6bgschAJJmlbUZUcTPJXbQ1SQmLRALd5W+rZ5PEQFJWULqG7c8FiO4EJUULl71UIp6rYLHUDp6ACbmuDMNZMfT3AhKug9VJ3JqTPs2AYXUcGItdcV+owWdgQXYgJuBVRXCK7y85EvRAUTRquFbLA2xyO4EBOgN7ft8vW7j/AGSO8Y8GRnipSGuccFD1FBDPHsgD92noeYAF7unhQ4a2AeooKEMeKRLO/xky7EBJCnuK/TH4I3YoIpsTU67dDG8w5vRAUZntAKbGAOsiO4EBNMJgmzSYGWnoI3ogKYoWvyp8riwxZciAnQ29qif6v1dAAOooJaS9Rp0NrPJIwDKJ1bUlYF5o7Ew78QE7QcbJaC24ce/BegdDgzc9ic5jxTix5iAkmLpW2cI8FD8EZUMMZIGgXGdD398ZUvRAXy3szH73trpotQML4iN0pZgAE85v3MDqICGjYaBzIZPf4QXAgFcHMzN27LhD0GpCNwEAi4SwkOExdNuOuHE98m8BAKON+FfiF+NslyWo7AQSDokZGmzLDA5Qp0KHvztQ9R0vlwMG8+mU6w1sc6uAtBMgo3rHMpN3GjG7fbLIkLfZMsnwM+XWPywIJ3mHeKJA+hgO98cqUrMbx0POqgC6kE4wbtrtSnJI7cs6supBJU5oBWy3I83onccCGVzDmYsYjlTAa2OygX+iZpGjHEwKHQcliEe6BwIZNMPGPUcvSOe9LBhVQC84DmuJSjQWyb3YVUktCaYTpLOdz53Z27kEl6YMi2ludeH3e5IZVk3BDvQsvxTh93uSGTMLta2T+4PRRvRAXMJjPsnWA4efyqCzEBLJdc14vfWz19SCVMiDj6+rzH93UhkwzZICmVaKQWHw9yQyrhrnutEHTN0qOuXIgKJtdWtaLCKY7lUVVuCBIJ8GVXIA2Iky3r2T2EgopeKXEDVuLknuaqMYUHfftIgcHSgYvWkZGw6KJX5IUPUdK4houR/VOWpEbbq/I+xPxl3OeT8Fo+Gxcc615BdhEK8BI5jcZwL+6h2vSrHOQUuOmo6kY+OBJpJ5jyEBWgNQYLUwvl5HbyEBUwn4wu43TNSLMFF6IC1P6m4bBc2sv9CC5EBZ3LABYkuMO2PcDoc5pB0DA2hscPuhAVDBgmtiYz+w4FcREVcMwttkRBy+8ILsQEsL3Hsr7b86VeCAXMo9nXemYZO4eTAxi952w7MNF9t/zgvxEVxJTq2hGctyfvIiYYKa+dtWi47SF4Iypgd2JmIoz1/hBciAlQfVdmLbb0h+CNqADtKa+0YHnUh+BCTNDZ0s1c3xtXXEQF3GPbzPp+tH8PMcGoqxhOzegPwRtRAWxj7iWTYljTjztciAlma9FCffFlHzXjQlRAj9iW39BjPWrGG1A6bLL1Jkao+fFSL8QEBU7Dzpm38915iAoGt8CosRuY9fEILkQFMxd7ExiSw/MrXAgF6StwLlaLB660BQ6igpxSVrcM5t7Jw+ghKuh0rXSxi2la5hFcCAWcNu3Mp8RJEFT5nXLQQyjAaNFn041dYTDT/RI4CARZ8lcx8KEwKjCtdK8eQLrmDNJp2cSdo+sHeQgFnH9jz6CzY33HZLuIChK8rCaz6RXm8W7PHqICfpqkaVLZptoRXIgKKm6rk9eM1t69noeogOHRYeikY569H8GFmACtNus8KIbLnXHTQ1TAbYSWize1uYJsXEQFA5XelihKLOVxhwtRAUPvpi5ScGfT47VeCAWVq91p2MLP3jfiAUbvzG2sxbmk+OC/ERVEuoo2Oc4U40dwISaoEsQvxbM/bvAGjD5GXdmQYXrVB/+NqAAtdq+aSE6NLbgQE6Cer2zb9XyCG1A6E5LpCiVzJD2vfyEmGLHsHNoxPm5wISooZaVF5rJPPvw3oPSqUVt62z3oOIDRmfLQSnuLT/4bUUFjPLyt4Iz8+PlvwOi1c0TUBZwdR+EiKuiBgUxSGp70V7mRucupr0rVHy/nQlTAlLiWe73FWh+f60JMIMvC2o7aDI8KfSEqQHcZrd5WiR/aggsxwRyWm7yENB6/6A2Q3rivbtp6FXyUtB/ZQUwwOGWrqzFh22oOoPSEZmRL7rCPzwd2EBXAM05Je9e4d1F7gNIr2o6mnOYe3njob0DpPUnUVpWE1iE9Ln8hFHSMtMzYL+swI7awn9dBVJBx46lDXJZNOVtwIRRgLO+9lCFjKPf+b4GDqACNWeKdmdj6YYJ4CNNSZ/gBedb0yYUuvJQ9+HkIBUy1y0hqSaMJd2xN3bkIM1nLklPQhZvcMMit1+ohKsBfsiMOD5niTsfhIhQwVmUyzzYdxM443SVwEBXA4Bnq/DCR3fYEPUQFfVSLhe3sCh93uBAKEvPYFfXH2APuwclDVIDxIRbbfcsoriO4EBXI3h91Qetuyne5kpk5RNM2MYtge9AvRAWVqbottq1993MuRAWwFeowK73uLIcuogJ4O6Gv6fm9D91FVEDn3xyHNnZuXBcxATOyWnqgtNdPXEQFsPBGtKWhtmc0XYSCzFQSs1pOa1TI/dAOYoJRo+2ArI9Uwx6igoiWsQJDR9hzCh5igiHJ/Gy1apvLHqIC7mlva2kolcdPuhAT9L5zXZV9qoKLqIC75VboaZ67X/UQE/S5lujKmSd1ERXgafIOMQ7l8dAXogK6wis9NoaAh+BCTDAxAltEL8b7x5e+EBW0nFZwq2wC3Pw3YHTWYUt9FndMl4uogCdSdFtvy2Vn/vYQE/Q+LM9blZpzBG9EBSPPYnUeI1h9fLYLMcFMXPPQOaJWHhXjQlQwR4821cC1/YfgQigodDzHiv9Pde6f5CAqwPuyXRh1Pu/gICpIDNC3Rbqan4ILUQFjC5udC5D2YoOLqIA7pacWo8XvhPAeogJONtq5BgPdYTuCC1HBFP9HhqQU9nEwLkJB5cETTfueDpfy1CUHUQGzkOqgMZhIOR3Bhahg5BosqHekmA//DZAOc45pfDQN+GQ/t/gO8k2OqguMoJVYj8Io5v0EDkLBhMEbmXkpyLTjnoVwANBb4XK4JQGCwX4sTw+hQBYZuYLHUDpubF39hYdQwNjwybh/Bq7VscOPXUQFTBuum5Hz6HtwcwClt8wzzRgjFh+f2AFIx2uLEgEju9rqTrXiIiqItAt0pzDa+p5Q9BAV5IhuRLPrlrl3c7mICtCYgt64dmaHOIILUUEdPdhWvtHG4xe9AaX3ROdTdi+GvFe9XUQFrOGW8BsGRTn8N6B0WEt5pTauZ4rGQyjgbvCYNHE6xoywp5k8RAUxTc7X6A7SMOsRXIgKZOlNN4QyJ0c7ggtRQeaJY7bXmVlgj+BCVFDC4N4c25a7FxQ8xASTyaVt4+/xqTxEBVzOsx3k9UQSu4gKGvfX7Rzg7fGWLkQF3De6t0eftn8DSh9lxrVzuT8/whtQOlMQVcsCLqtQm38hFExZiclxvelz1o+DqCAG2Y4jxTWcr+wgJuARhZbhHQ1rPARvRAXwKKXXZPXKbQ+CHqKCkltc2/jTTnHkIirAYDUs5XjoMTwe+kJU0AsnJnRrcTg+oYeoYDLpnKVG2AnpPQD0Hri+1atepZQzWeMhKkhR9i1oNxi3UeshKshcVtF9wrPk9rjDhaigcg1J3gTTvp6jjhxEBX1kvW+BFXcOXroB0iOPoInazXK68TyBg6gAdWRqA2Tisj0f5CEUJIZFS41n6qJxjrPxEApYqeTMBSZ/pAex+DdAOlogmhEdFOZgKPlc30EgGDACcuwajYTOLe9R2UMo4ITDmLq5KLM67tOBHEQFM8iboEHDWZZ+BBdCAVPcjabbNWGq7JAFF1EBam/T1fAx5/7KDkA6PdfebONyOtP8DqB0Zt3UGZbORA358C9EBXj0akm4uf+vHcGFqIDHnwab/+g7aMhFKKAvEMbKTFbi2I/gICqAWRbsbK+If/IRXIgKMJZqljf4DuEciHUDSueiv3qIsMd2Q3YAo/NYnXVgV6/pwX8jKuDWZlt2bjWec8UcRAWjSkC0OnBpe6ceooKZ08rGxVOZHne4EAoqrERJfaXzH2FPK3qICtB/TFtF5k6Eh+BCTDCZg3RNZ/Sn4I2ogEcC28vDYLftLw9RQWb0y5qdeDy0g6iA+/Z3HO/Y46aHqIBrf2vu4OwtdREVcB/YzkQ2WjmCC1FBD8zoYrMTrT2e4UJMMOpKB88dYfkheCMqgAXdbVtuzY8D3xxEBbAIdpb3Eerjw10IBeIAdSuGBXFOfXMQFcQk/aUU9zkfggtRQYoS8CvtqpwPfQNGn2txvvL4mfTgvxEV8NRIi1GffTz4b0DpXIW0iYD0mCX0EBUMRi1pR/g4BMZFKOgMhJw2NwFf5TRPB1EBNyLrvEGsp4O5ypXcuWdER4oQy+nAHIQCDHBZ0kzJSLSTGXiA0pl/RDOP4RWcz3sDpE/unWgr0mHOtRnIRSCYlYfDcDaF6USZ2HAJPISCxuymfWi6Uk3SbQIHoYBTSFkmAeLXkHBn498A6fTGOqMENNlqX/sxXEQFjRlXNJdrO4s6DkA6s3DNpnmCU5x7ps8BlJ4HD/2W0lHrtpU9RAVVk2LnWHdmm7tYqfAvem2W/vt4Bh6iglmiHF0kpt45KdVDeK4dj9LrUTPXovdIK37eRVSA99Qt6TJXMvIRXIgKSu5Rz7Bhcsd6+G9A6czSnDTdNcNsHz/oQlTA870sm3LtOT1+0IWogOkIx0ruXZeP7CIUMNoPrdUycKfHHRxEBVw7KtUyfO/0li6iggRrpGgCaXR8IR7BhagAvzauG88RH3e4EBUUxo2Ulef70F/lRmaagl2YHj/nQlSA1yvbDqR4B2O4iAo4uRss0/fY8eIuooLO0BV7Dy2tKGsXUQG30c2VHLw+BReiAtiolnya6eTT45VeiAngezW9MUMjHtXiQihgpFiMlhAfA3Tbr9VBVMCgtKBvm2d69CO4EBXA+rQeDabb3nnmIirIjV9U21T6TnAhKiiVWa600eLvegQXooIWZO+kOGQ72MsDlI5ReX3NcAZXF1HBDImHe0pGAQYLHMGFUADPjV9EvWEY9X1/NgdRQUpM2K5ZyWs778hBVFDQTpNlBDthvS6iAtSqoj1hKiPXcQQXogImEItSXyIzHD2e4UIoYLDf5JKtDHV5bwF2ERWMwaM45XyNutcoPIB0mgKRCROYyoKhl7taOAgFnJfPDOIpPNueCbiWwEF4SKqcWCR7LTmszn2KiYtQwPmmFIukKk9y8OMSOAgFPBI10beQ3Clzh5O6iAp0A1CW07N3BL0HkM7MTGPaceJBTts2voOogPP4uouwo0WtpSsXUUFnk9LwBW6HyEdwISoYqL9m3zaednMEF0IBfAy4kFVj9/ESd6/qISpIaEnrZN99yJoHKL2gA7eVyzlSqYd/ISpgLJuluh5MY3cEF6IC1MKRV8T1PoDGRVSAca7UlQRt5/B2ERMMMWekOO6gAxehQBaR4gqPKG3f4AaM3tc53OgF99DpAEqPjNFYybFmS4d/ISpIKa5NyjLeHcGFmABvd+wjth7078uVzHFlndxd4iG/ypVc8j51ikeDPegXogIYbWXPLIzHT38DSm/oytZcR9kbo11EBT23GdYpa6E8HvZCVDBSX9nVZh+Pb/sGlD5TO+EKfR957SEUDDnswUrHHjjuciXz2FybIJCTgjf7DRh9rHmddpYMPUDpOcu0o7r7+xRLF1FBZWDgOiR8zMevvxAVwJqvOqMIz22H17uICkaZWsHRz7fHA7zKlTynfZFWOY4c9hsgnXshmZ9C5wbyPFd3EBVI5n7dxZDrTkvvIirg8TY6n4BB53RtN8BzwQN6CzEdOYo0VK5V+T1EBWgIxU4Xg+EcHoILUQFP0tN4g8DQ4XkEF0IBT/4qMU3dDvcYgz2EgsTES0UDFEasO8uPi1CQOW3PPQZZtgnvhMMuQoEm2Ghy7Olo5/wpF6FA9n2GYG5nzPt4dg+BgAfI40894mvGvWfEA0inhyd5b7n6U09uXBdRAfd7ypogzez9mR2AdKby4unqsn6VuCd88R1EBYVn1GpMA1yr7dd4iApaKJoJvoYTZOcBSu9zFgtQyHOHLrqICibzqGvMRJvH//YQCriMVvta1Ex7u7uLqCA1W4BjVq61RuIBSs/dlt4ZdNMO+1WuZE6i29nm6cyPuogKaokrp3vbnfRdrmRuMsuahzsfd8wBlM6k1HUdbT3j48dciAoGrPdmxXXnuHARE8wwhq2iz7CnMjxEBZy0tozxNe5RwwFIZ/g1k9ivwIHdB3mICqJumNXAh2PweYgKmICkrriHbRM7gNEHDwex4h096SIqgKtoIUzciD0fN7gQFRSeK2gZ73PanaKHmGBUO8OasRLh8cgXogIGU6ZpnybPx0u9EBXwAIey0vyP1I/gQlTAFPkW4ILqldsRXIgKhqajlPrbSn889IWYoMmJhxoGtJeCXUQF6GGiBenwGKbHW7oQCrj21mVKRDO6xy1wEBUwGXpZGd13diUXUUEu63jwygF4HsGFqIAbJbQRYoTbkbUuooKOkcGK00nS4SIqmOi59dEK5x/bEVwIBQ1d7FjFMIm32eghKsioJtov5HlmoB1A6Y2eqfzOzCPJH/wLoaCLRSJthIlIT724AaXDEmMKJUlc2B79hYNQMDmVY5PAiYu++ys7CAQlSCIrTupwe3E/FoWHUJC/Ah6MhyHQkpOjmkzgIBRwxxDP2aFxxZOu9g1ugPTOaWxzBLmis11cD1EB2oRtexiVmciO4EJUIAfZanp2jOz9IbgQChijly3XF3Mp7ie+AaXDu1v7SGrdB5K4iApKYuehLkA7XquHqIAhcGHNV/Td0jxEBbCQgkVIhx2S7gFK74yR0CVrOGzhwb8QFUzGq+lsRX7+/lc5yQyGK6v06Qp5iApiHOt46Np3FIiLmKDbgjuTCcwH/ftyJSceCLz2d8xthHuICpgDfTnXj5d5A0bHl1g7Ixhf9OC/ERVg5Alpu/v98fsvxARoz2sqpJwVGw9RQeXs8p6wiA/BhZigSuJdLd7r5C6iAqbRXnMcJZaH4EJMwBWoVbz3A7iICvA7xwo+qTu8yUVMQJdkRauc6T8PUQFTfeQ1h3X6Ug9RwYTn1VeChh3S4SIQ1CAB5PZ5UN/3IO4hJsDYs/dT7UA/F1FBZCi4HeyWd8pTF1FBEr9B2nfa5/J5gNIzrBmbTWE+ynr4F6KCktLQ39mCpOXZggtRAU8lXtvgzgjoAErnXKblcssnV5iLqAAvt1kGmPqoqR6iAibEX3EYZ7ebi1AQZV+hTaiEfr7ZDSgdnU63jR15n3TiAUqv6DL1PTOZy4P+BpSOYc3OV0FPsrdiuwgF8IM797kzEIPHSu5ffwOkw4LOg/myYHB0+LTbA/EQChpjgxnIxyUW5urdr9NBIGhMIsKU+58YrlM+ewFdhIIieTq6ZrvIOwTHA0ivcgCbJjVI6HhWSIeLUNB4fibDH6QKh7ntCQ9RAVd8NCczE6XtRuYhKig5W+4KmDT7GziA0hk9rZvSmcC1Pa5/ISpAj1FsF3vIu804gNIxdvJsFWlT81RRD1HB4D5I3eWf43je4EJUMKPMo2umi7wNHA8xAfMyDEt/PPLjFV0IBV3iZ4KlxhhngthDVIAKmCxfMuct5xFciAkqD/aw5ANz91weogJmZkhtZTfoh/8GjF551Fm11OfpQX8BRucJFys1QzqVzkFUgE6bB8Jrrou5fRUPMUFHt7oyh+f0+EUXogI5xW8lr9jH3rmICRho0Ha2i/EQvBEVVFhkqazrzMdHuxATwMleCSxGSU/BG1EBT7a0rC9dchVtwYWYoPVuOVl62ZulXEQFnSfUWXF8foY3YHT0ONlSpvRHb+QgKrCHatuU/fnnHz/T53/+DJ+/+8Sg9vnnz3/6/Gf8179+/vinP/zHb3/9wy9+9pPPX/9J0yOuk337ytiIEom3DmEH9P34H+Lnb/6EK/wZ//5s3ZQn2ZRu454VyWHX0wbJP0CYRCg/glIeZfe8oel2iXc70Tyu/Bfv9vOP/wuUixykCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMTE3MzMKZW5kb2JqCjE2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggOTMgPj4Kc3RyZWFtCnicPY07DsAwCEN3TsEFKoVPArlP1Sm9/1qXfhb0ZGN7ZOfGmytuNOPQybuQWBSepC8tsqHsY4B65qt9kUUOspRyHWVQqho5S7YW97eW8Kwt0gljKkj+keMC4l0b9wplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzI3ID4+CnN0cmVhbQp4nD2SS47EMAhE9zkFF2jJ/Pw5T0az6rn/th92ehZRoQBFUbhrSpPo8lKXHCrZm/zoFVPFzeTviYbENHE30MEp97WjCP4EuA5m7gzRSolBvXWJyvKRsfPX19OXB+/L22GwUXqWmFefkrEGC/J0dPEB5tza7n+V7yuTjiy9Sk9F70u9WJaoDzH7YvUp3MbmG9t6MJ5M8Ws2UauZU9baIroM1EVKN7HVC1DtUYHjXEdvFW0DEIE7QQeVCbVqbMFISLRF1i/MaUL3xP/tAbpf2sR17IPYtI1nfEUaQ9DduEdZw8wx6nxqc8Pa09km65TiTC7XsjhWCTRKy1hqS/Csel0UY4MZaKUQzdFqbGVodujrZXg/yAxvO4qxqKVKz543p+BcfezXFHrwPIsdwZuc2C3o55CsQgYtNmHqLF2v8Dnnff1+ACo9fUYKZW5kc3RyZWFtCmVuZG9iagoxOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE1MiA+PgpzdHJlYW0KeJw9T8sRQyEIvFvFNsCMIILW8zI5mf6vAU08sbK4H/GBCmIWkFSHuMOt4sWFtaOr41OkHbQKi4PmBpa/ErGCvIHr1ukYPWabeIrnxhg6Y4awcMyRDFnaxTPuti9Fjg2Cu2FWoekplj7kemEbB1J6s7RdoaZwLqYiY4Zx22mfWyXSjtMvSv2ariK9w9SStYvGn31/Abz3NmcKZW5kc3RyZWFtCmVuZG9iagoxNCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMtT2JsaXF1ZSAvQ2hhclByb2NzIDE1IDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgODggL1ggMTAxIC9lIDEwNiAvaiBdIC9UeXBlIC9FbmNvZGluZyA+PgovRmlyc3RDaGFyIDAgL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udERlc2NyaXB0b3IgMTMgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxMiAwIFIgPj4KZW5kb2JqCjEzIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250TmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9JdGFsaWNBbmdsZSAwIC9NYXhXaWR0aCAxMzUwIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxMiAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzUwIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjggNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjE3IDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTcgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwOAo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTk1IDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoxNSAwIG9iago8PCAvWCAxNiAwIFIgL2UgMTcgMCBSIC9qIDE4IDAgUiA+PgplbmRvYmoKMjMgMCBvYmoKPDwgL0JCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjM3Ci9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nD1Ru3HFMAzrPQVG4Ef8aJ53lyrZvw0oOSl4gCkRBOSnLNGFn2eI4PtZ7v/IA5KtUG2EJzQVkQ3TwOdJEVhupCbcXtznhGyVI/biXCDCEO08CWmkCxY7GQveFz+Pqx5mrLlh/L4zmn1UdNVRHbx7DuNmTT9OlN3rzayOW5v7dO+uE4drSCaf9x+clEqnlyyDOku4sDaaGtbjvCjGWMw4/ieqsE2ytqMKwdIlSCrQgBhKEsaAxS3+IidaDgvamxtp653JTqo0ioYXowzeoPVGOIp0kXyYayuDsamYNr755CU36Ptnv5+vXwNrWusKZW5kc3RyZWFtCmVuZG9iagoyNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDU0ID4+CnN0cmVhbQp4nDM2NlcwUDA0MlfQNTI2VTAyNFAwNzNRSDHkgjFzwSywbA4XXCGECZLPgavM4UoDAEyQDxUKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0NyA+PgpzdHJlYW0KeJxNUbttRDEM698UXOAA62t5ngtSXfZvQ8kIkMIgoS8ppyUW9sZLDOEHWw++5JFVQ38ePzHsMyw9yeTUP+a5yVQUvhWqm5hQF2Lh/WgEvBZ0LyIrygffj2UMc8734KMQl2AmNGCsb0kmF9W8M2TCiaGOw0GbVBh3TRQsrhXNM8jtVjeyOrMgbHglE+LGAEQE2ReQzWCjjLGVkMVyHqgKkgVaYNfpG1GLgiuU1gl0otbEuszgq+f2djdDL/LgqLp4fQzrS7DC6KV7LHyuQh/M9Ew7d0kjvfCmExFmDwVSmZ2RlTo9Yn23QP+fZSv4+8nP8/0LFShcKgplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggOTAgPj4Kc3RyZWFtCnicTY1BEsAgCAPvvCJPUETQ/3R60v9fq9QOvcBOAokWRYL0NWpLMO64MhVrUCmYlJfAVTBcC9ruosr+MklMnYbTe7cDg7LxcYPSSfv2cXoAq/16Bt0P0hwiWAplbmRzdHJlYW0KZW5kb2JqCjI3IDAgb2JqCjw8IC9CQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM3Ci9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nOMyNDBTMDY1VcjlMjc2ArNywCwjcyMgCySLYEFk0wABXwoKCmVuZHN0cmVhbQplbmRvYmoKMjggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4MCA+PgpzdHJlYW0KeJxFjLsNwDAIRHumYAR+JmafKJWzfxsgStxwT7p7uDoSMlPeYYaHBJ4MLIZT8QaZo2A1uEZSjZ3so7BuX3WB5npTq/X3BypPdnZxPc3LGfQKZW5kc3RyZWFtCmVuZG9iagoyOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0NyA+PgpzdHJlYW0KeJw9T7kNAzEM6z0FFzjAeixb81yQ6rJ/G8pGUggiQPGRZUfHClxiApOOORIvaT/4aRqBWAY1R/SEimFY4G6SAg+DLEpXni1eDJHaQl1I+NYQ3q1MZKI8rxE7cCcXowc+VBtZHnpAO0QVWa5Jw1jVVl1qnbACHLLOwnU9zKoE5dEnaykfUFRCvXT/n3va+wsAby/rCmVuZHN0cmVhbQplbmRvYmoKMzAgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDkgPj4Kc3RyZWFtCnicNY9LDgMhDEP3OYUvMFJ+hHAeqq6m9982YVoJCQvbL8EWg5GMS0xg7Jhj4SVUT60+JCOPukk5EKlQNwRPaEwMM2zSJfDKdN8ynlu8nFbqgk5I5OmsNhqijGZew9FTzgqb/svcJGplRpkDMutUtxOysmAF5gW1PPcz7qhc6ISHncqw6E4xotxmRhp+/9v0/gJ7MjBjCmVuZHN0cmVhbQplbmRvYmoKMzEgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzMzggPj4Kc3RyZWFtCnicNVI5rt1ADOt9Cl0ggHbNnOcFqX7u34aUXwpDtFaKmo4WlWn5ZSFVLZMuv+1JbYkb8vfJCokTklcl2qUMkVD5PIVUv2fLvL7WnBEgS5UKk5OSxyUL/gyX3i4c52NrP48jdz16YFWMhBIByxQTo2tZOrvDmo38PKYBP+IRcq5YtxxjFUgNunHaFe9D83nIGiBmmJaKCl1WiRZ+QfGgR61991hUWCDR7RxJcIyNUJGAdoHaSAw5sxa7qC/6WZSYCXTtiyLuosASScycYl06+g8+dCyovzbjy6+OSvpIK2tM2nejSWnMIpOul0VvN299PbhA8y7Kf17NIEFT1ihpfNCqnWMomhllhXccmgw0xxyHzBM8hzMSlPR9KH5fSya6KJE/Dg2hf18eo4ycBm8Bc9GftooDF/HZYa8cYIXSxZrkfUAqE3pg+v/X+Hn+/AMctoBUCmVuZHN0cmVhbQplbmRvYmoKMzIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyNDggPj4Kc3RyZWFtCnicLVE5kgNBCMvnFXpCc9PvscuR9//pCsoBg4ZDIDotcVDGTxCWK97yyFW04e+ZGMF3waHfynUbFjkQFUjSGFRNqF28Hr0HdhxmAvOkNSyDGesDP2MKN3pxeEzG2e11GTUEe9drT2ZQMisXccnEBVN12MiZw0+mjAvtXM8NyLkR1mUYpJuVxoyEI00hUkih6iapM0GQBKOrUaONHMV+6csjnWFVI2oM+1xL29dzE84aNDsWqzw5pUdXnMvJxQsrB/28zcBFVBqrPBAScL/bQ/2c7OQ33tK5s8X0+F5zsrwwFVjx5rUbkE21+Dcv4vg94+v5/AOopVsWCmVuZHN0cmVhbQplbmRvYmoKMzMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAyMTAgPj4Kc3RyZWFtCnicNVDLDUMxCLtnChaoFAKBZJ5WvXX/a23QO2ER/0JYyJQIeanJzinpSz46TA+2Lr+xIgutdSXsypognivvoZmysdHY4mBwGiZegBY3YOhpjRo1dOGCpi6VQoHFJfCZfHV76L5PGXhqGXJ2BBFDyWAJaroWTVi0PJ+QTgHi/37D7i3koZLzyp4b+Ruc7fA7s27hJ2p2ItFyFTLUszTHGAgTRR48eUWmcOKz1nfVNBLUZgtOlgGuTj+MDgBgIl5ZgOyuRDlL0o6ln2+8x/cPQABTtAplbmRzdHJlYW0KZW5kb2JqCjIxIDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2FucyAvQ2hhclByb2NzIDIyIDAgUgovRW5jb2RpbmcgPDwKL0RpZmZlcmVuY2VzIFsgNDAgL3BhcmVubGVmdCAvcGFyZW5yaWdodCA0OCAvemVybyAvb25lIC90d28gL3RocmVlIC9mb3VyIC9maXZlIDEyNCAvYmFyCl0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAyMCAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOSAwIFIgPj4KZW5kb2JqCjIwIDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTkgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjIgMCBvYmoKPDwgL2JhciAyNCAwIFIgL2ZpdmUgMjUgMCBSIC9mb3VyIDI2IDAgUiAvb25lIDI4IDAgUiAvcGFyZW5sZWZ0IDI5IDAgUgovcGFyZW5yaWdodCAzMCAwIFIgL3RocmVlIDMxIDAgUiAvdHdvIDMyIDAgUiAvemVybyAzMyAwIFIgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDIxIDAgUiAvRjIgMTQgMCBSID4+CmVuZG9iago0IDAgb2JqCjw8IC9BMSA8PCAvQ0EgMCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+Ci9BMiA8PCAvQ0EgMSAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+ID4+CmVuZG9iago1IDAgb2JqCjw8ID4+CmVuZG9iago2IDAgb2JqCjw8ID4+CmVuZG9iago3IDAgb2JqCjw8IC9EZWphVnVTYW5zLU9tZWdhIDIzIDAgUiAvRGVqYVZ1U2Fucy1taW51cyAyNyAwIFIgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjM0IDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA2MjYxNTQzMjkrMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgMzUKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMTk0NDEgMDAwMDAgbiAKMDAwMDAxOTE4NiAwMDAwMCBuIAowMDAwMDE5MjI5IDAwMDAwIG4gCjAwMDAwMTkzMjggMDAwMDAgbiAKMDAwMDAxOTM0OSAwMDAwMCBuIAowMDAwMDE5MzcwIDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDM5OSAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMTIyMDcgMDAwMDAgbiAKMDAwMDAxMzU1NiAwMDAwMCBuIAowMDAwMDEzMzQ4IDAwMDAwIG4gCjAwMDAwMTMwMTkgMDAwMDAgbiAKMDAwMDAxNDYwOSAwMDAwMCBuIAowMDAwMDEyMjI5IDAwMDAwIG4gCjAwMDAwMTIzOTQgMDAwMDAgbiAKMDAwMDAxMjc5NCAwMDAwMCBuIAowMDAwMDE3OTg1IDAwMDAwIG4gCjAwMDAwMTc3ODUgMDAwMDAgbiAKMDAwMDAxNzQxOSAwMDAwMCBuIAowMDAwMDE5MDM4IDAwMDAwIG4gCjAwMDAwMTQ2NjEgMDAwMDAgbiAKMDAwMDAxNTAzMiAwMDAwMCBuIAowMDAwMDE1MTU4IDAwMDAwIG4gCjAwMDAwMTU0NzggMDAwMDAgbiAKMDAwMDAxNTY0MCAwMDAwMCBuIAowMDAwMDE1ODEwIDAwMDAwIG4gCjAwMDAwMTU5NjIgMDAwMDAgbiAKMDAwMDAxNjE4MiAwMDAwMCBuIAowMDAwMDE2NDA0IDAwMDAwIG4gCjAwMDAwMTY4MTUgMDAwMDAgbiAKMDAwMDAxNzEzNiAwMDAwMCBuIAowMDAwMDE5NTAxIDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gMzQgMCBSIC9Sb290IDEgMCBSIC9TaXplIDM1ID4+CnN0YXJ0eHJlZgoxOTY1NQolJUVPRgo=\n", "image/svg+xml": [ "\n", "\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "\n" ], "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" }, { "data": { "text/plain": [ "" ] }, "execution_count": 1, "metadata": {}, "output_type": "execute_result" } ], "source": [ "import sympy as sym\n", "import numpy as np\n", "import matplotlib.pyplot as plt\n", "%matplotlib inline\n", "\n", "N = 7\n", "\n", "x = np.convolve(np.ones(N), np.ones(N), mode='full')\n", "plt.stem(x)\n", "plt.xlabel('$k$')\n", "plt.ylabel('$x[k]$')\n", "\n", "W = sym.symbols('Omega')\n", "X = sym.exp(-sym.I*W * (N-1)) * sym.sin(N*W/2)**2 / sym.sin(W/2)**2\n", "sym.plot(sym.Abs(X), (W, -5, 5), xlabel='$\\Omega$',\n", " ylabel='$|X(e^{j \\Omega})|$')" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "**Exercise**\n", "\n", "* Change the length of the triangular signal in above example. How does its DTFT change?\n", "* The triangular signal introduced above is of odd length $2N - 1$\n", " * Define a triangular signal of even length by convolving two rectangular signals\n", " * Derive its DTFT\n", " * Compare the DTFTs of a triangular signal of odd/even length" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Shift Theorem\n", "\n", "The [shift of a signal](../discrete_signals/operations.ipynb#Shift) $x[k]$ can be expressed by a convolution with a shifted Dirac impulse\n", "\n", "\\begin{equation}\n", "x[k - \\kappa] = x[k] * \\delta[k - \\kappa]\n", "\\end{equation}\n", "\n", "for $\\kappa \\in \\mathbb{Z}$. This follows from the sifting property of the Dirac impulse. Applying the DTFT to the left- and right-hand side and exploiting the convolution theorem yields\n", "\n", "\\begin{equation}\n", "\\mathcal{F}_* \\{ x[k - \\kappa] \\} = X(e^{j \\Omega}) \\cdot e^{- j \\Omega \\kappa}\n", "\\end{equation}\n", "\n", "where $X(e^{j \\Omega}) = \\mathcal{F}_* \\{ x[k] \\}$. Note that $\\mathcal{F}_* \\{ \\delta(k - \\kappa) \\} = e^{- j \\Omega \\kappa}$ can be derived from the definition of the DTFT together with the sifting property of the Dirac impulse. Above relation is known as shift theorem of the DTFT.\n", "\n", "Expressing the DTFT $X(e^{j \\Omega}) = |X(e^{j \\Omega})| \\cdot e^{j \\varphi(e^{j \\Omega})}$ by its absolute value $|X(e^{j \\Omega})|$ and phase $\\varphi(e^{j \\Omega})$ results in\n", "\n", "\\begin{equation}\n", "\\mathcal{F}_* \\{ x[k - \\kappa] \\} = | X(e^{j \\Omega}) | \\cdot e^{j (\\varphi(e^{j \\Omega}) - \\Omega \\kappa)}\n", "\\end{equation}\n", "\n", "Shifting of a signal does not change the absolute value of its spectrum but it subtracts the linear contribution $\\Omega \\kappa$ from its phase." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Multiplication Theorem\n", "\n", "The transform of a multiplication of two signals $x[k] \\cdot y[k]$ is derived by introducing the signals into the definition of the DTFT, expressing the signal $x[k]$ by its spectrum $X(e^{j \\Omega}) = \\mathcal{F}_* \\{ x[k] \\}$ and rearranging terms\n", "\n", "\\begin{align}\n", "\\mathcal{F}_* \\{ x[k] \\cdot y[k] \\} &= \\sum_{k=-\\infty}^{\\infty} x[k] \\cdot y[k] \\, e^{-j \\Omega k} \\\\\n", "&= \\sum_{k=-\\infty}^{\\infty} \\left( \\frac{1}{2 \\pi} \\int_{-\\pi}^{\\pi} X(e^{j \\nu}) \\, e^{j \\nu k} \\; d \\nu \\right) y[k] \\, e^{-j \\Omega k} \\\\\n", "&= \\frac{1}{2 \\pi} \\int_{-\\pi}^{\\pi} X(e^{j \\nu}) \\sum_{k=-\\infty}^{\\infty} y[k] \\, e^{-j (\\Omega - \\nu) k} \\; d\\nu \\\\\n", "&= \\frac{1}{2 \\pi} \\int_{-\\pi}^{\\pi} X(e^{j \\nu}) \\cdot Y(e^{j (\\Omega - \\nu)}) d\\nu\n", "\\end{align}\n", "\n", "where $Y(e^{j \\Omega}) = \\mathcal{F}_* \\{ y[k] \\}$.\n", "\n", "The [periodic (cyclic/circular) convolution](https://en.wikipedia.org/wiki/Circular_convolution) of two aperiodic signals $h(t)$ and $g(t)$ is defined as\n", "\n", "\\begin{equation}\n", "h(t) \\circledast_{T} g(t) = \\int_{-\\infty}^{\\infty} h(\\tau) \\cdot g_\\text{p}(t - \\tau) \\; d\\tau \n", "\\end{equation}\n", "\n", "where $T$ denotes the period of the convolution, $g_\\text{p}(t) = \\sum_{n=-\\infty}^{\\infty} g(t + n T)$ the periodic summation of $g(t)$ and $\\tau \\in \\mathbb{R}$ an arbitrary constant. The periodic convolution is commonly abbreviated by $\\circledast_{T}$. With $h_\\text{p}(t)$ denoting the periodic summation of $h(t)$ the periodic convolution can be rewritten as\n", "\n", "\\begin{equation}\n", "h(t) \\circledast_{T} g(t) = \\int_{\\tau_0}^{\\tau_0 + T} h_\\text{p}(\\tau) \\cdot g_\\text{p}(t - \\tau) \\; d\\tau \n", "\\end{equation}\n", "\n", "where $\\tau_0 \\in \\mathbb{R}$ denotes an arbitrary constant. The latter definition holds also for two [periodic signals](../periodic_signals/spectrum.ipynb) $h(t)$ and $g(t)$ with period $T$.\n", "\n", "Comparison of the DTFT of two multiplied signals with the definition of the periodic convolution reveals that the preliminary result above can be expressed as\n", "\n", "\\begin{equation}\n", "\\mathcal{F}_* \\{ x[k] \\cdot y[k] \\} = \\frac{1}{2\\pi} \\, X(e^{j \\Omega}) \\circledast_{2 \\pi} Y(e^{j \\Omega}) \n", "\\end{equation}\n", "\n", "The DTFT of a multiplication of two signals $x[k] \\cdot y[k]$ is given by the periodic convolution of their transforms $X(e^{j \\Omega})$ and $Y(e^{j \\Omega})$ weighted with $\\frac{1}{2 \\pi}$. The periodic convolution has a period of $T = 2 \\pi$. Note, the convolution is performed with respect to the normalized angular frequency $\\Omega$.\n", "\n", "Applications of the multiplication theorem include the modulation and windowing of signals. The former leads to the modulation theorem introduced later, the latter is illustrated by the following example." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "**Example**\n", "\n", "Windowing of signals is used to derive signals of finite duration from signals of infinite duration or to truncate signals to a shorter length. The signal $x[k]$ is multiplied by a weighting function $w[k]$ in order to derive the finite length signal\n", "\n", "\\begin{equation}\n", "y[k] = w[k] \\cdot x[k]\n", "\\end{equation}\n", "\n", "Application of the multiplication theorem yields the spectrum $Y(e^{j \\Omega}) = \\mathcal{F}_* \\{ y[k] \\}$ of the windowed signal as\n", "\n", "\\begin{equation}\n", "Y(e^{j \\Omega}) = \\frac{1}{2 \\pi} W(e^{j \\Omega}) \\circledast X(e^{j \\Omega})\n", "\\end{equation}\n", "\n", "where $W(e^{j \\Omega}) = \\mathcal{F}_* \\{ w[k] \\}$ and $X(e^{j \\Omega}) = \\mathcal{F}_* \\{ x[k] \\}$. In order to illustrate the consequence of windowing, a cosine signal $x[k] = \\cos(\\Omega_0 k)$ is truncated to a finite length using a rectangular signal\n", "\n", "\\begin{equation}\n", "y[k] = \\text{rect}_N[k] \\cdot \\cos(\\Omega_0 k)\n", "\\end{equation}\n", "\n", "where $N$ denotes the length of the truncated signal and $\\Omega_0$ its normalized angular frequency. Using the DTFT of the [rectangular signal](definition.ipynb#Transformation-of-the-Rectangular-Signal) and the [cosine signal](properties.ipynb#Transformation-of-the-cosine-and-sine-signal) yields\n", "\n", "\\begin{align}\n", "Y(e^{j \\Omega}) &= \\frac{1}{2 \\pi} e^{-j \\Omega \\frac{N-1}{2}} \\cdot \\frac{\\sin \\left(\\frac{N \\Omega}{2} \\right)}{\\sin \\left( \\frac{\\Omega}{2} \\right)} \\circledast \\frac{1}{2} \\left[ {\\bot \\!\\! \\bot \\!\\! \\bot} \\left( \\frac{\\Omega + \\Omega_0}{2 \\pi} \\right) + {\\bot \\!\\! \\bot \\!\\! \\bot} \\left( \\frac{\\Omega - \\Omega_0}{2 \\pi} \\right) \\right] \\\\\n", "&= \\frac{1}{2} \\left[ e^{-j (\\Omega+\\Omega_0) \\frac{N-1}{2}} \\cdot \\frac{\\sin \\left(\\frac{N (\\Omega+\\Omega_0)}{2} \\right)}{\\sin \\left( \\frac{\\Omega+\\Omega_0}{2} \\right)} + e^{-j (\\Omega-\\Omega_0) \\frac{N-1}{2}} \\cdot \\frac{\\sin \\left(\\frac{N (\\Omega-\\Omega_0)}{2} \\right)}{\\sin \\left( \\frac{\\Omega-\\Omega_0}{2} \\right)} \\right]\n", "\\end{align}\n", "\n", "The latter identity results from the sifting property of the Dirac impulse and the periodicity of both spectra. The signal $y[k]$ and its magnitude spectrum $|Y(e^{j \\Omega})|$ are plotted for specific values of $N$ and $\\Omega_0$." ] }, { "cell_type": "code", "execution_count": 2, "metadata": {}, "outputs": [ { "data": { "text/plain": [ "Text(0, 0.5, '$y[k]$')" ] }, "execution_count": 2, "metadata": {}, "output_type": "execute_result" }, { "data": { "application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDQyNy42NjA2MjUgMzE0LjM1NTc1IF0gL1BhcmVudCAyIDAgUiAvUmVzb3VyY2VzIDggMCBSCi9UeXBlIC9QYWdlID4+CmVuZG9iago5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTEgMCBSID4+CnN0cmVhbQp4nO1ZTW8bNxC976/g0T2Y5szw81gjiYECPSQx2kOQQ+A4apzYhW2kQf99H6X17lCrT8DwXmpDkPSWO+9xvkhqydx0ZBbGmRu8fpoP5iPePxsyF3gtOodvt53nZGN0kQO+ftdfhbyVEFIA7Jpvf3Xdl+7sVxh5xE0XXReKzX51U7LBC0bBMkVbYot+b1AnNvYmlQWF9kS8IlpANqZis5oM6OuVLkXrkkhgrUCB3rpeQHcOr/zszi/N2Rsy5Mzlly5mS+yYU/03zLYEc/m5O3HW/WIub8zry25J2xFlmwq5EDWPRncTEcGOpCKYKisitmGNKJINLqdQGiKF7iEKYkMIUaQkEsUU1qfEzlvm6GPjOo3uYSrRMrwsSdhFxZTW58QeofdIgMZ5Gt3NxBJsJpIgFEtRTDSJE+eCNKYcG/dpdA9VyjZwQUQDFdJUk0iJsEVEQ2r8p9HdVMJk4QPENMfsNdUkVDBiXUGKNg7U6B6qKKg97yM4k85zUrG6x33OnDoUW3W4d8uqLIhxJny4uoXN2jvsqlxx+9kb7glOvlUrHay87SWPde3heyRjVRyilTVwEKzp2bLxiLlnpPyKWc0mw8G59J1rOQvr3BP/PfhdtVSV9h9g4OzV9c2nP368/3T3eHr79e7Ho3n1N7RO1SZ8SutqB3Cr2tpx8mFqnU3hudTWtkK0LndEt+olh9F8qODwbO4l77CaTAQP6HbBEm2Ihwrm5/NwwvTLRPCAbik4XMZF9Dab3VJ0v6qsFfbIw64uEOs8I7qbpyTUv+LhsJVHUC2TBB/RnTxYKC1nxRO2zwcrlkwyc0R38wT0JVY8aft8ClbGSUKN6G6enGyKAw+p+CBvkHqnNWHQj5F/8Sniuxvhv8vEC7ZQKrEadqsBT8wnH5YD0I8dUjqRGrLWTMNya0FhyGtl5OPYbu/Nhk2YwIGEfQbyj/D+cG3+NHdQTAx7OXIltT72fwleTS7kjL7PxTwsto80zch3F83IbvvIh0Vf0dWrw/ZstesaYnV1a85+d7USn0ZifcKux2Wq2xlzymLhEcFSF53fPxwh83n/sOSRX0kKcSr8bFaP03rc6MMkHDevw2weGYH/A/ZyAcPqZY5oBmx+Myg8HKkOLGEUO1bNf75eXb+7ODdXj+qUpRfJEW2a8PuXVlcQIIRGfKNuRBlnPx8yNsWzyKt7NPYpULvFUDC7ZEuaTyDWehEfSmwFKlgER0Wcfv08Ar23nimm3Aoc4cQ2+fn0jWf2Rt8I60PQy8urJ92CAmjVDejMzivBxsyF2+ai4Xmzjwn+Sc45aQQqeOb6ZQZXwGrRBljBM3dA9ftPI3CE511AOHrrhNCNW30jPLcDM8FgFm4boILnTsGSLaNAqdU3ovOWsNSDXWFfWn0KnrcHqp8SG30jPOsCImCvg0PbYBQ8s/tgMARJ0u6wNDxz/mWx0WM73zZABc9cv97hOqdc2gaj4GfrgFnKSqJAIEGNJ0qx/vbQC/eBDj2BbJQ9yKusbvI4qbW78bHW5idVsLrpedfttuddGH/EQ7N29GBml/W33X9KeMsECmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMTE2OAplbmRvYmoKMTcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4NyA+PgpzdHJlYW0KeJw1jcENwDAIA/+ZwiPEECDZp+qr3f9bSNSPfbKMsVjoUEtxCsI7LjZO3fg2iUNPZgFlJI1lsFFUJ4fEJ2RakrEWs8W+nREQrw7FdqLH/idPuz+4ThnECmVuZHN0cmVhbQplbmRvYmoKMTggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMzkgPj4Kc3RyZWFtCnicPY+xDcUwCER7prgFkAAbG8+T6Ff++7fBcZIC8XSgO/BhELDVLOloUuC141SyGmAX/MmkgdUE2i2hFWhdSigOWjrrCETbFvXpB32uk3jkUrGkai+1viliuTv0jtFtWsCjZ072rtDm4HJPRkEmTspT1qGTNH02mQfUIsllPNr70Pz+mfS7ALu8LdsKZW5kc3RyZWFtCmVuZG9iagoxNSAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMtT2JsaXF1ZSAvQ2hhclByb2NzIDE2IDAgUgovRW5jb2RpbmcgPDwgL0RpZmZlcmVuY2VzIFsgMTA3IC9rIDEyMSAveSBdIC9UeXBlIC9FbmNvZGluZyA+PiAvRmlyc3RDaGFyIDAKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udERlc2NyaXB0b3IgMTQgMCBSCi9Gb250TWF0cml4IFsgMC4wMDEgMCAwIDAuMDAxIDAgMCBdIC9MYXN0Q2hhciAyNTUgL05hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxMyAwIFIgPj4KZW5kb2JqCjE0IDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyA5NgovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250TmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9JdGFsaWNBbmdsZSAwIC9NYXhXaWR0aCAxMzUwIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxMyAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzUwIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjggNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjE3IDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTcgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwOAo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTk1IDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoxNiAwIG9iago8PCAvayAxNyAwIFIgL3kgMTggMCBSID4+CmVuZG9iagoyMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDcxID4+CnN0cmVhbQp4nDO2NFAwULAwU9A1NDZUMLI0VjA3M1BIMeQCCoFYuVwwsRwwy8wSxDI0N0Ni6ZoZQmWRWCDjcrhgBufAzMvhSgMA8bQWIwplbmRzdHJlYW0KZW5kb2JqCjI0IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggNjcgPj4Kc3RyZWFtCnicM7Y0UDBQsDRX0DU0NlQwNjBRMDczUEgx5IIxc8EssGwOF0wdhGUGYhgZmiCxzIDGgSXhDJAZOXDTcrjSAM6DFdMKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0NyA+PgpzdHJlYW0KeJxNUbttRDEM698UXOAA62t5ngtSXfZvQ8kIkMIgoS8ppyUW9sZLDOEHWw++5JFVQ38ePzHsMyw9yeTUP+a5yVQUvhWqm5hQF2Lh/WgEvBZ0LyIrygffj2UMc8734KMQl2AmNGCsb0kmF9W8M2TCiaGOw0GbVBh3TRQsrhXNM8jtVjeyOrMgbHglE+LGAEQE2ReQzWCjjLGVkMVyHqgKkgVaYNfpG1GLgiuU1gl0otbEuszgq+f2djdDL/LgqLp4fQzrS7DC6KV7LHyuQh/M9Ew7d0kjvfCmExFmDwVSmZ2RlTo9Yn23QP+fZSv4+8nP8/0LFShcKgplbmRzdHJlYW0KZW5kb2JqCjI2IDAgb2JqCjw8IC9CQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDM3Ci9TdWJ0eXBlIC9Gb3JtIC9UeXBlIC9YT2JqZWN0ID4+CnN0cmVhbQp4nOMyNDBTMDY1VcjlMjc2ArNywCwjcyMgCySLYEFk0wABXwoKCmVuZHN0cmVhbQplbmRvYmoKMjcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4MCA+PgpzdHJlYW0KeJxFjLsNwDAIRHumYAR+JmafKJWzfxsgStxwT7p7uDoSMlPeYYaHBJ4MLIZT8QaZo2A1uEZSjZ3so7BuX3WB5npTq/X3BypPdnZxPc3LGfQKZW5kc3RyZWFtCmVuZG9iagoyOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDQ5ID4+CnN0cmVhbQp4nDM2tFAwUDA0MAeSRoZAlpGJQoohF0gAxMzlggnmgFkGQBqiOAeuJocrDQDG6A0mCmVuZHN0cmVhbQplbmRvYmoKMjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA2OCA+PgpzdHJlYW0KeJwzMzZTMFCwMAISpqaGCuZGlgophlxAPoiVywUTywGzzCzMgSwjC5CWHC5DC2MwbWJspGBmYgZkWSAxILrSAHL4EpEKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0OCA+PgpzdHJlYW0KeJwtUTmSA0EIy+cVekJz0++xy5H3/+kKygGDhkMgOi1xUMZPEJYr3vLIVbTh75kYwXfBod/KdRsWORAVSNIYVE2oXbwevQd2HGYC86Q1LIMZ6wM/Ywo3enF4TMbZ7XUZNQR712tPZlAyKxdxycQFU3XYyJnDT6aMC+1czw3IuRHWZRikm5XGjIQjTSFSSKHqJqkzQZAEo6tRo40cxX7pyyOdYVUjagz7XEvb13MTzho0OxarPDmlR1ecy8nFCysH/bzNwEVUGqs8EBJwv9tD/Zzs5Dfe0rmzxfT4XnOyvDAVWPHmtRuQTbX4Ny/i+D3j6/n8A6ilWxYKZW5kc3RyZWFtCmVuZG9iagozMSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMCA+PgpzdHJlYW0KeJw1UMsNQzEIu2cKFqgUAoFknla9df9rbdA7YRH/QljIlAh5qcnOKelLPjpMD7Yuv7EiC611JezKmiCeK++hmbKx0djiYHAaJl6AFjdg6GmNGjV04YKmLpVCgcUl8Jl8dXvovk8ZeGoZcnYEEUPJYAlquhZNWLQ8n5BOAeL/fsPuLeShkvPKnhv5G5zt8DuzbuEnanYi0XIVMtSzNMcYCBNFHjx5RaZw4rPWd9U0EtRmC06WAa5OP4wOAGAiXlmA7K5EOUvSjqWfb7zH9w9AAFO0CmVuZHN0cmVhbQplbmRvYmoKMjEgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zIC9DaGFyUHJvY3MgMjIgMCBSCi9FbmNvZGluZyA8PAovRGlmZmVyZW5jZXMgWyA0NiAvcGVyaW9kIDQ4IC96ZXJvIC9vbmUgL3R3byA1MyAvZml2ZSA1NSAvc2V2ZW4gOTEgL2JyYWNrZXRsZWZ0IDkzCi9icmFja2V0cmlnaHQgXQovVHlwZSAvRW5jb2RpbmcgPj4KL0ZpcnN0Q2hhciAwIC9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnREZXNjcmlwdG9yIDIwIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDE5IDAgUiA+PgplbmRvYmoKMjAgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDMyCi9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zIC9JdGFsaWNBbmdsZSAwCi9NYXhXaWR0aCAxMzQyIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxOSAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzQyIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjMgNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjEyIDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTIgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwNQo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTgyIDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoyMiAwIG9iago8PCAvYnJhY2tldGxlZnQgMjMgMCBSIC9icmFja2V0cmlnaHQgMjQgMCBSIC9maXZlIDI1IDAgUiAvb25lIDI3IDAgUgovcGVyaW9kIDI4IDAgUiAvc2V2ZW4gMjkgMCBSIC90d28gMzAgMCBSIC96ZXJvIDMxIDAgUiA+PgplbmRvYmoKMyAwIG9iago8PCAvRjEgMjEgMCBSIC9GMiAxNSAwIFIgPj4KZW5kb2JqCjQgMCBvYmoKPDwgL0ExIDw8IC9DQSAwIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4KL0EyIDw8IC9DQSAxIC9UeXBlIC9FeHRHU3RhdGUgL2NhIDEgPj4gPj4KZW5kb2JqCjUgMCBvYmoKPDwgPj4KZW5kb2JqCjYgMCBvYmoKPDwgPj4KZW5kb2JqCjcgMCBvYmoKPDwgL0RlamFWdVNhbnMtbWludXMgMjYgMCBSIC9NMCAxMiAwIFIgPj4KZW5kb2JqCjEyIDAgb2JqCjw8IC9CQm94IFsgLTMuNSAtMy41IDMuNSAzLjUgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDEzMQovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJxtkEEOhCAMRfc9RS/wSUtFZevSa7iZTOL9twNxQEzdNNC+PH5R/pLwTqXA+CQJS06z5HrTkNK6TIwY5tWyKMegUS3WznU4qM/QcGN0i7EUptTW6Hijm+k23pM/+rBZIUY/HA6vhHsWQyZcKTEGh98LL9vD/xGeXtTAH6KNfmNaQ/0KZW5kc3RyZWFtCmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iagozMiAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMTkwNjI2MTU0MzMwKzAyJzAwJykKL0NyZWF0b3IgKG1hdHBsb3RsaWIgMy4wLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZykKL1Byb2R1Y2VyIChtYXRwbG90bGliIHBkZiBiYWNrZW5kIDMuMC4zKSA+PgplbmRvYmoKeHJlZgowIDMzCjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDA3NzIxIDAwMDAwIG4gCjAwMDAwMDcyMTggMDAwMDAgbiAKMDAwMDAwNzI2MSAwMDAwMCBuIAowMDAwMDA3MzYwIDAwMDAwIG4gCjAwMDAwMDczODEgMDAwMDAgbiAKMDAwMDAwNzQwMiAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDAzOTggMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDAxNjQxIDAwMDAwIG4gCjAwMDAwMDc0NTkgMDAwMDAgbiAKMDAwMDAwMjU2NCAwMDAwMCBuIAowMDAwMDAyMzU2IDAwMDAwIG4gCjAwMDAwMDIwMzMgMDAwMDAgbiAKMDAwMDAwMzYxNyAwMDAwMCBuIAowMDAwMDAxNjYyIDAwMDAwIG4gCjAwMDAwMDE4MjEgMDAwMDAgbiAKMDAwMDAwNjAyMyAwMDAwMCBuIAowMDAwMDA1ODIzIDAwMDAwIG4gCjAwMDAwMDU0NDggMDAwMDAgbiAKMDAwMDAwNzA3NiAwMDAwMCBuIAowMDAwMDAzNjU5IDAwMDAwIG4gCjAwMDAwMDM4MDIgMDAwMDAgbiAKMDAwMDAwMzk0MSAwMDAwMCBuIAowMDAwMDA0MjYxIDAwMDAwIG4gCjAwMDAwMDQ0MzEgMDAwMDAgbiAKMDAwMDAwNDU4MyAwMDAwMCBuIAowMDAwMDA0NzA0IDAwMDAwIG4gCjAwMDAwMDQ4NDQgMDAwMDAgbiAKMDAwMDAwNTE2NSAwMDAwMCBuIAowMDAwMDA3NzgxIDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gMzIgMCBSIC9Sb290IDEgMCBSIC9TaXplIDMzID4+CnN0YXJ0eHJlZgo3OTM1CiUlRU9GCg==\n", "image/svg+xml": [ "\n", "\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "\n" ], "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" } ], "source": [ "N = 20\n", "W0 = 2*np.pi/10\n", "\n", "k = np.arange(N)\n", "x = np.cos(W0 * k)\n", "\n", "plt.stem(k, x)\n", "plt.xlabel('$k$')\n", "plt.ylabel('$y[k]$')" ] }, { "cell_type": "code", "execution_count": 3, "metadata": {}, "outputs": [ { "data": { "application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDM3OS4wMiAzMTYuMjU5NzUgXSAvUGFyZW50IDIgMCBSIC9SZXNvdXJjZXMgOCAwIFIKL1R5cGUgL1BhZ2UgPj4KZW5kb2JqCjkgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxMSAwIFIgPj4Kc3RyZWFtCnicpX1Nzy67cdz+/IpnaS/0it8fSwuOBWQT2BYSBI4XhiwrFnwUOIKtTX58qrp7SJ5hSzJgXVzpVVfVMzMcDtkkm834+c23+Pn1J3x+g39///m7z9/jf//xEz8/x7+//hY+Pwmf799yn18h8e9/ef7OsX2lOnuFKfzw//73t2//9O2nfwH57/BbP/8Ww1f/pPpVSgeOH2v9a6Rt+ZdlmfGr2o+o6DDYryb91V/j7nDHX+O4Z1yLyLc4vjp+uH1y/6olyzW3rXwFsf3Lt28/w6P//tu/4r/lMeMnxq88Qu2ptRk/KX3N+vnl928/+8Xnp38FNHx+8U/fxlfuY4aWKlS/+Mdvf5b//POL33z7L7/AD4WvwN/CP88fUP/0L3/1m3/47//2t//w29/95Ps///bffvf5y//z7a/xj9z9t16/6qix5/N2D+Mfu982vlLsc9RZ2n/0dtN/7nZjTl8lpTr6D8V7WP9oAeOlh1rznCnl/+gdx//kHY/5lV6VQS3Xnf5wH3G0rzBCxj3bnfJmAm/mg5vRH08FpNlL/OH1ndY/fpFU8Mux91R778dl4o+XyQFILiP9UOqn9U9cZs6vXmvMM9RyXCa9LlNB6ymVH66yjX/8Irm2rzpTrSnnMI+r5OcqR03ILfOTx4vogyUstUBe8ud6yV9NCeeL/m/ff/Xrf/jTL7p+ne3AH3jR+NpmkAqXM5qJNrr7ru338Zt1NjRN+wLb9CevMOJXn7PEWltN3juwq0TcSitj5OMyh+1PXiem+YUWZNYWc8hyoeJfiHcUYu7puNC2/ekL9Y4/S5loM6uWW3MvlBLrYJ7xuNBh+5MXQvOCCtUD7qqFLhca/oVwRyO0UvNxoW37AxdqE5VEvvWOah5wpT7Qo+nXGHYNZuX9CatlbOlUSDeltZhVdlTeM8T7En/2/6Qhy18ZvUvZDdxP/yo9jP8pjPYVw8hzSJ0Nrx/5X39mvzLxglqPo98/8yv7mRbxxCPjPx9+bfKhGbML8TdCxOfRejb8Jz8y93X//A9c1x7r+XTxauzbxV8pfs0S4hgjpPgpX02f6Y99y//6+dFfyLV/oXqgS/6K+N//+6vP//j89gO/AD1/ABJrGy3xZr5Ks/90VIge6hgp1zQ/f/PzDy737//8y1/9zc9/9vnl79S5ONuJ+jVQsVr5sAnLcaD5QjX5WxcAvaEQUoUTVMfXmKj9zegOAHpH34gWNH7QkvK9xufXHUBcFdRxdJGfhpZvlqR19m9dQOhoQkONtM46UXUW/QKEXqFssMavFFLIadEvQOh416UMWnNAe1IW/QKEPuCR5ElrQd8ZF/ttV/LscF7EWEaI+1YuQOgo0TSaWGfrc9MvAHR4qbxDucGa0S1VozuA0GNFd1/E2hr6ykW/AKGj5sE/o3HMNPePv+1K7vgO5SfQdtU5N/sNCD0XNNpqTWjwN/0ClN5brGrNKOa+6W9A6CWMmaNaB76SRb8ApbfKMqIVX+TBftmFXGPqLYmx5pbiYl+A0vOIXW+wogD2g16A0tHJzKHWwTe+6G9A6bPxmxLrnHHf+gUIveWAi4m1BTAW/QKU3opVutZiPOlvQOkTbWy3H0HLs+lvQOg9pxytANCU7JK5AKXjgUa18irHzVyA0mfpKdvbmEe5X4DQ0RNWrRcVHuCu62+7kqv9QGlndXmZlYrOaep7KPC30ya/AaHPgtZAfwRNTtz0C4APzh4o8m9aY+vWcDl2JePNDvsQQdjkl13IEd1R1o+8D7y0xb4AoadQkhRTLahsfbHfdiV3PLtaY5v7Rt52IcONHkXeboHj+tRwDxA6SqlqS4aOp6T94xcg9JrDiHJJNCSl7RK8AKG3lHEtscL9TPtmLkDofeYsnyy61Rb2j7/tQp4dhS83iK4JHf1iXwDokOJl8YuFI5bSKvHbLuSaQqyDxozeuG/2BYCevqCraNfRZ0cM3/pzKw4AekZtg9OKLh7uxoS/8TynA4BeUVYY0bdPQSOVZrMP07GDPL56ZK+e0dMH+APPjd92jOKiuJ3omfALcaJO2+vxANAzBwCx0++ZCV6k/bZjB7ngA0R1G+LHoOl72hMP4IDyiz1HSPrS+njaQg8QOp43aV1G1Vw3fts5t4TvhL07rWhm8tMxe4DQC4asckG0IePp9B27kFstteAnEob3Na07cQCh94yPr9MKd6M/rpMHCH2kSQcT1gTn9XmdHqB09FxyyVRyfNw4xy5k/IDeX0LFT22R33bO9aHNGwV/wwqXF2/N2A4gdLqBWW4vF3ZJi34BSh8F3ohY8TCPi+gBQse4b7IlS6ynfb0hB1A6+tyqVnwvq8wdQOhwRdEfiRW+T6+LfgFKL4XOCK0T/ePY9Deg9I7RyaC1hIAi2PQ3IHSOJtkh0AoHaBfkBSgdHmAwKyrrQX8DSodHrZfEqCnul/q2CxmDHU4VibXE2Rb7ApTeMdIyYz/u5G0XsjhF0awh7Tu5AKXTb+lqjcuj8AClT3gO9vAYvB2//gaEjrtiuyrW0jf7bVdyg1Dr0JyrLfcAoY8wqlU5NpabfgFKL40PLVUOXc+u6Reg9DF61o8RTcjxoBcg9JlLaFpDG5qfXYwXoPSRMfLVbxeezH6lFwD6YHMds94ifu4ZEHuA0NE99arXDGyXF/0ChJ5iLlGeiA7nM/DzAKHn0IsWANrL/LhnHiD0gjLVxjji41rkl1moGIr0JnUIzmDft/22CxnfYCji2I+cxtxlcgFCn62Zo4kBRN7P+LaDzFHmnDrMzD3V8jSiDiD0MkNI4oEFDGVWx+UA378VdWNHYq/NyjHtOT0AdFwJng9ukTM1dO7t1j0AdE7o4Q7rJ3O0UVdr4QGgo99GE8JZXLw+tNzP6MMDhJ7HiDoNjLF6fLoXDxA6BtQdlZhWeBxPi+4BSu9oiiOtI4Z0sF92IdeaOCnMat3LrG2xLwB09K58c+ODYm7o0Z6uywNAR90fs8b6QbmNmVbT5QHfv1WOCCrfQC24Zs5PPfcA0BMq2+SwEQ52QDHbvTh2kDNbgqh9SOI0g92KBwgdvnTQzxBuTX8Gqx4AOm4r54SK3PBzEW/CqpcHCB2PX/jBZLwUvLe86Bcg9FJrYfOX8Z5BmIt+AUKvXG2jsWMU/vSijl3IHeMAjno5p1pj2r99AULHeEe6Ylh7foZbjl3JEw2D/MSE81sP9hsQOt3YLjfIEUEZi34BSp8YdcvD01fK+9cvAPTKdSFxUGDFA43nFTmA0jE2pesG60R7ctDfgNBjwiAC15SJ+WeQ69iV3DBqU2Oc8yC/7EJOAfWyiTGH8Ay3PEDpuXL2rehEbNnsl13JcEnwGdKKh1ofhQMIHb46+zta655O8gClVzyQWeEdbPbLrmTUhKZX5HzXvpULEHpJnAkWKwqtLvbbruSGPlsfHu5D2+SXXcn4Ams3Yz/K5AKEXjM66WzWNT/sAUpHvdc33LhGsdkvu5InWsmkj87pps1+A0JHpa/0TWmtayznAUpHZ9rMGkPdv34BSkcnkPSaGAPN/aAXIPTO3kNs6GviIr/MSsWoJ6oVDtiu4G+7kuE5Bn3BcNvSroMXIPSRh7iC/KTgme4buQClY5SG/lo+bnTvuwgvQOjo0dG8W9ORx76ZC1B6nyFGa5i4uLrobwD0htLPs2lLg17kcc48QOgxB/pebIIn+oWx6BcgdHR2URtV+O4zb/oFCB2VsnX5kc7ljn0zFyB0ui9VfgT+QH1cHA8Qem/sTKXfC6nsH3/bhTzhsHUprVg7P5uHfQGgczhYR7ExOyuJ0R0A9MEJpqEzxmwcVgvqAEKHj5G7zB6hFvUcF/0Cvn+DSxIyXtmHr5xtoLEdO8jlqxWMdsXZZJvd7Av1ANDhV6eB4QuvWHp4viPH/v1bt9U5fQ9jrFLxANDjFwofzTouja51fXWOXcgzccbg07gaXtbcpgeATr8LTh0aVtSlVNaqlgcIHW7J4HiAdamnvOkXIPQ6IycMG2fA2sht0S9A6A3uCL1H1L20Fgcdu5Dho3W1jT6OO3nbhTwGvsJMK9qeeNzIBQh9oinl+gKsdKn3j1+A0rl6GsWKAfg46G8A9EyXYXLag8vBGF1ZLfcApfciTTGsscx50N+A0OH19Kw/wq5nsd92JfcUpbAmnNJnMtSxCzkljKKLWDFAaXGxL0DpA06D3l7D+G7/+AUInSs6Oau1c5HpoV+A0vmN6+N0tMlp09+A0As+1TnUGtcH6gFKx3Chd70mhrL7US9A6LhMa3rN1kLcj3oBSh+xBC1e+GC5b/obEDpqWtBKB88jjv2oF6D0OThfTys8w7BrwAUIHT0HvUapFxKv8tAvQOgjlGhVtK1homNXMoZGtWn9L2td2wOEPjliq/Z1lbDpF6B0uGtDrjlKXNMtHgA6fQ1UDP12Y4tPi+4BQo/0vuVHOrzZURf9AoSOv9jlsEWb+XFFHbuQ0eSgQxNjKKPt374AoZdMD5ltK4f6c7HfdiHTbWjydaUSxrNU6QESSBoxfOBkMHzJPtKqug4gdEaTPq5bzOsrdQDQG2cybZ2RI7dnuOUBoA/2aIwLqsQ5N2R0B/j+bXARqMEH/5TM2JTyfEceAHqCE5FQnzlHyUG1FYxjB5nNSGZwTEG5BXhZVi4eADp81NArPGB4Nglwt3LxANAH+r8eOTWBa/bOcZDSHQB0hq1NedOMNehr6OIBQkc7mdAddM7CzDX16wHfv00uHXfOfHdOyOFrsfrlAUIvpSS1VryTZ+ziAUKHbxJxY13CHcIzP+cBQu8YVMlvdDYjY7HfdiEzFA1eL6wo5tIX+W0X8mSVm2Ksqcz9mBegdM6PFrGOnJ4v2gNAR5VDRxnkkjPChX9KxQGU3jk7Jm4Z2uK22S+7kFE6aLnFioHt81l4gNIzv0CxcuWjbvobUDqDVqJacYtz09+A0FETUpTSmlWGtg/9ApQOzwDeI60NL2M/6QUIndP6U3+kl5B3MV6A0gvXbMXYSz3YL7uSGTOpxrFi+By7kDm9F8wKz33/9AUIvcZas75lXDnvx7wApXPKQV8c/ci06W9A6DIvUbVoMRjbN3MBSsffTW+xYKjdN/0NKB0Oc9fSyvt1/mgVIqNAtT5gmLqr1cus1Dmmvl3GjB1V9gKEju+PfQatfc2bO3YlTwwZ9XstaIH3i7wAoU+GW0mtH4lxuIt+AaAndF99oO9gS4OK9rhPHiB0+Bect6QVX+P6kh1A6ImTtWKtLa8QNQ8QOt4So4o6wyJjX5+yAwi9YlCllS2FmZ+AKQ8AHQMIhi5EdgcVHeYz/+wBQq94DIZRobOJe7jtAaDDl6HPltiV0d14bv22g9zZvEscLesdl5qM7QCgo9+jc4QOXhZUl8PtAUKfTVZ0ZQ15tsed94Dv32IIEvBc+6fI5xueqQIXoQBDGgx88GFVhhrGZ8LaA0hvXxHNE/vhIuPmJ3rGRSjoXG1idBc8IQaQPU66i1AwvjB+HOxIptTyFZPnISpADWV00sAjosFc4a0eooLK+YRBcy9HjLOHqACDNwaRwQx/qz5TRy6igsEYtcw9EejE23FHb0DpXM7AVznYz6GVSZt/ISaYietDNDPw/HiCC6FgYnyeGBky+BWNkJfAQUzAhZwu5jTTChv3EBVEDnTkyVCR+zgEF2ICdBho6GhuPcZ6CN6IClLIQMTMmPKxBRdigirRM4NdcGjpeOgLUQHcXI6PaI5rcdgDjM4PpKt1tHbc0IWoAG0v+3+a0x4luogJCrtJNdfj63QQEwyZlhBzWaMWF1FB5QqPXTjWo4jegNFbpr8rD9Z+KNILUQHa4GQlAZdsBQd7iAky3GX9HS5nHY98ISZgfZQaDxd+luOtXYgKUKVy0RrfZ1px/x5igiKxr1If6zzf84WYAK5t1PpYuePlELwRFaAXz1PNOfV8PPSFmKDiZ6RCMlAkxEPwRkwwB9oqbRdmrkfVuxAVwKPkS5GWp5XzTV8IBDGgXeicQGPTVucapLqICnCblW0h2s4R62roPUQFCa4IbKOLK7jYP5qVmgcnx6Qhz3imttkXogJ6PFka8thiWU2wh1AA56UNhlp07i6Bc7Xu3kEokFUxbgeD8xCO6EAXoYBhnbWitYT/EPAzqznyEAo6Y3USt0zSmcGdL4GDqKA3fCAaTosXu0LxPUQF6IsYpcW4MIyvQtqCCzGBDCLESxl1zRa4iApmKtyqw9CXMnuLW3AhFDAQuHM4UFBXChyi9R4cRAU9YIDaGERC1zKULbgQCBJXhTK/j8IAiLxaMAcgncumlZ8HXDQMsVb4gotQ0Fh/GW4QAzvIUtc2JxdSCRpCOsUoZ3xcY4UO+ZBKBhq0lMQOd3TN8/gQJaiNmVOtNLP5zOtJHEQFiRHrtKNs0FqtbSwuZJIhhSgOZ2LnekguSCW5YnTZ1M5w0LElN6SSkivX0mlngHI8rnJDJsEArqq5z7UjwwGUXhPGSlHMhfH6eQtuyCSc+NLnw2V/ePQbMsksLejzFUbjnJILUkljQLMWfOGuwL4lN2SS1uEJqr2yrz0kF6QSDHG5mUTt3JO3JTdkktxq0IKEJ8zgmC25IJM0+MD2jG0HkvqQSvAZt5TMDp/peJYbMgkj+p6f2sNuHzIJGr9ir7iW0o/HvyGVTDYZdnX0GOdVbsgkuN/nGTFsTafkgkzCXd9W+HBJ61FiN0QJR1k5P/a4YyR9yCR4X0mfMXN/YzkkF2SSnnKzr6j35Y94iAqijk7ELhv+t+KGTFLY0qg9hxVH7kMqwRgoacVLeNGrg/MQE/QEx1rt8Ht3s+pBKoFXlqo1hZwMOS5yQyopeL+laINb4m7uHUQFTQLeaO2JK89bcCEUTEZ7hDykp6ldVhVM4UHMixHY2NILmY2xtmP1vB6iiTQmV4jSp9evwLmxJXAQCrhpZnKQzGBr9IOrbD2EgiERMfg+Jxf+xpprcADQ0c0HuhFwkxmzUFf1cADupOY0Drd4od6g6QhrnddFVDBgjh12bpw69vW5ECWMsqZXRHMqvS4310NMUNNgkhTaJ9zTeSguyCRTZgZozxg4x3JILkglsRYODcTe24qD9CGVcDqh6A1z++04rnJDJkEPhkuKPeeyNja7kEq4dT0MtcON7sdVbsgkgzE2am8prwbOhVTCJ+RefbHnuLo3F1IJOjDuNNerc5ZhS27IJBxN2dUzV6QOyQWppGFsnpqVZD/L+EJMMMrzfiW9wCF4IyroNcArUnvkZuStuCGVYPjDhDlS7zhkPy5yQyrhLlErkog+Jh3164YoYcjJ4PCNH91Ea9PWjXmQSnIoDDenveSZ1hjVhVRSWSpd0my02fvoW3JDlFR8a53dPBpKBjekNQnjQpRwl0VG751yllWfNT3nIRA0hnBnDrKibP2Ie8zgQpD0wLXigp6icqoylFVcHkIB900UbvgrXAZIu7A8RAWsokOWozuzObQtuBAVDBRazJzyjgz/nltwIRTQqU+y7SJzO3ddc4YeQkFjNJBEJNNJyKs1dQClN76UzuWAzPjOg38hFHRGVGCYwuUGjmbXEMlDVIBrcROjrk/U1rbgQlTAjq7KggYGTXX15B6igh4470Xz4KpS2oILUQHnpFFLuLQ+457J8BAVcPVrypJMYEz25r8Bo4/GSk8rfOFx0F8A6YOh49w3AGuM3OT78B1EBShpbkjvMh+V1lyYh5igzqQrlZHzKPUQvBEVJF5ZzW22svlvwOhwQqs8VxwpHw/wBpTOfYdZVgrxIc6cN/9CTIB7G0XNR1oUD1EBc/LkrmtoOa+5PA8xQUUVN/PaUecBSq9ocNL6lSeaxUVM0HJ57lOiabbgjaighcKZRjEfn9kNGB3F1vRXRtl5HTzEBMxRo2+ml71s5iEq6Lhs0LrYuId1Cy7EBEMGQjTDfUtHmV6ICtCg0X2Rysu8fVtwISYY6Xn5+DqOR3gDSsfH2nRhNfAGjkpxISbgNrOkX3ffswIeQgFnuWS/Ac3wpVev5iEqQHcv9Z1pfXKYZQsuRAWpxKhN4Bgt7ltyEBVgPC0fONMopR9u6UJUwHQqSZrxwk3nfQsuBAJOEldZi2pTNuMvf8FDVNAKY47YEw2G2aQtuBAKmLwh56mBvz3tqRYPoYCzTqM1zSTRR1rdrId8l+yAsDXUw6K+0LMA7iIUDG47q5xoZUTc+jpv+3fJZIYKwnm9zI897MkCD1FB5AJXkcFeyHXNCXuIClJ8NkT2FPbkgoeYAAP1KZsc0fzsGR8PUQETaDCHF9oHPNg8bulCIGCEWZD5A67uw6VbLrGHUMCko0Myv3CT3Iw7TY6DUMA8owy7R2XpGFAt58sBSEdfNOEYi0PTGFq3svY4iAp6whiE1T2HNNdkpQMonXFUjKkKDA2uq1f2EAr4LmUfiLgzaU+keIgKEuPe5QMcE9/JIbgQFRR8Q0XahMnthm0LLsQEcFCaNOWMbx+n4I2ooBbmuxFzK3tN20NUgKZpmMc04fKmLbgQEzS6btKWMyqzHII3ogKGOFlngTuoRyldiAqYnqpbh5fmrqkOYoIZStIedYadF+kGlD5rYMCB9vDxfAsXwgQ5zGpEz9h8iPg4hC5iAji6LT5OyrOlyUVUwC5Io6+4k3IcggsxAaqV9l9xcn/sIXgjKkDbWrqVBdN+bcGFqIAzCVnLGqPxZ+OUi5iACa6qvc01NHIRFRRuj1Y/JfW2cyA5iAoqw6Or1shRw3GFCzEBHsc+ksbF1kPwRlTQ8C2p6xRSXWvOLmICtGzTvttWzytciAoGPWprGfCqjoe+EBVwY1WU1q3PuppVF6GAQbNFgg8Dk56taCQXUUFsndt+2BzGWPYtOYgKMr6mLM1h1ARrS3AhKkBfOoI06NxV2I8rXAgFTAzCQDtGcpcdEOwBpMvYO+nOT66t76/BQSiQJDG1yMosU/Os378BZrGSJGJ8l+j66FE/oUUuQgHDuAb3InACl4kin5gQH2Lqq8LMMpzZTtwPkOEyPm2AC1HCvdGZKZ1kymiE9szu+pBK4BEwAFsmirmVKG/JDamkwfEdNv3FNK9zS25IJUykN22qGGOF8yo3ZBJ4aFHnSjPc4Ge20odUAreCrr5OGMLTOR7/hkzCWXg1zzbPi1yICjgaLzaFm3J5Zqp9yCS9mbWktbPGA0hv3COcn+nb2uZqaF3IJJ0phJ9J4r5y07mQSvD5lmf6tq1kTC5igjpytenutoLJXcQEkyl7nznlel7hjagg0duMq0DScYkbMknn8roVuQQ+bckFqSRH2Zqos9C15aN4b8gkqDHZ6hs/0XlILkglJdZu89CoPuFQXIgJ4Nnae2KY6/IpXEglFaO3aTPX3EZ1PPwNqYS5I4c+YegMX9mSG1KJBKTrNDSnMVfmOxeihDlUWpeFoQEPYhxfuwepBEPpIYsp3DeGMeYhuSHm+uOMW+SeqlSYZCavDU4+RAlTZA24cR8u181ZyuPc+hBzy6O/YD1I3KHE5FFPeTkA6XCqe6nDYl12igYXUQFnlGQxPn3hJa+Mez7ErIWSU7NUi3UJdY0+fUglURwoXcUNXNDckhtSCToMZuWQteKQ1jq9D6kEjTG8drXPvHJH+ZBKCvzf8SyUc/5rS27IJCUydF2X4/MK6fEhk2A4W+qz5L/SvfiQSipqttkLu7K6JTdkkpZ2vEua6ZRckEoYBWfmIk+7FBdigsJxiMVutBGPIr4hk+CrsTinwiSs50UuSCUd5vbY0W0c5XVDJikcET7BLmedvBATwLmb5Ymo+aGy3JBKuHMyPaE+3NO/JTdkEjS20W63xhmOWnxDJpkxRIt0KmlNxvuQStDzs5PV17sH/j5kEqZInE/gSm/H498QJVzjwg1bTWWdeBQOYgLm7NIfykwHXw/FBZkEo6XHzlHaeZELUkkcsmCscShritRFVJDq5MyptDissnMrbkglTPFaprZr3GCWt+SGVFJnixpBiGHBypTpIipgCE3VBpqbL0fcihuihOEMjckfGIfSey/LY3EhSgrGfpNpiAbz0bcViO0iFMwvvE6Wg2Qy62ENlTwEAubPZfaQxhELHbPnuR1A6XXIrjAm4WM4R9n8C1EB/E4GNHH+kbG+fQsuRAWD8bo6/8itkpv/BkhnVDlKLnH2scy8Fv9chILEgRz3eTK5TUwrl5uLUMDcPSNyCiXLROFqEzyEgs5qKbN3cI24lXQ9goOooLFBibIvqIr/vQQXQgFTNw7OO3Jf0Bgr75aLqCAyq5oEjQ9u1ChbcCEqYIKdLGHpuHBe0wYeogJ8WMypzxj5wvnRLbgQFVQ4T1E2yUS0X/UQXIgJZrMNHRGu5PoWPEQF6GxTHrozKJfVMnuICdBG62YItBJnqb4BpaOrqtn2QtQWjjK6EBUMNOhRdx717YE6gNFrtY1Nc8XSOHYl82PqusMHrUE4fvxCTDB42Inujwn1uPk3QPrkgjj3fuv2m9X9OoDSGdKYHuseBniICeBPpPrsOFpNtoeoAJ5kt98J/Ey24EJUwGxkQ3dljd3CO4DR6wi26wvlsbwHD1EBvDvuehwa6r6G+h5igj6eWhhzOIroDSgd47KoW28i84McD3AhKmhw0G1jDAbE8SjSCzFB4wZF+VLnmtj2AKUzuhVDf7YETDl5PPCFqGCgKx3SOKGKtXxUoguBoAderVdpa1oO61gRF1EBKiD39rG9HDOsoaSHUIAakgczz2gwR17fpIdQkLg/l7MRnfniykoJ5SIUMAZForEK9xnX+iSQcBFmjs/i0BVJFtJDWetILkJB4Wps1fWuAP98Nb0eQkHVJJu6x5g54JbAQVQwmXjlWRSoa27RQyjg8Wwj6dIJV2hXr+8hKkhMoCuLPxj27vbFQ1TAJLCaZ6CnsrYruIgK8N3lonvIx/HzP5qNOkuwNBM5pOVxeogKWmf+wmevfDkEF6KCHhioI+aB8fTYggsxQVm5DELOq6/xEBOgmEOy1AC5H098ISoYKXHnTJekA6Ecr+xCTMDTVDRfQlk7+DxA6Wg4LBZo1rbS9LiICWruWrXQIuxZSg8xweRASKwcmx/8F0B6Z77EoutQktZiPYCDmICxOvpcva1kLS5iggn/SO+TARPlELwRFTBTscZ7ST6MugUXYoIW45PiAv7bcUsXYgKUXbX0HHXuiucgKuBW+GaPlvaHcwNGb0/wEA/yySf/jZhgSspIMacV9eMiKkAdz3bdihbheOQLMUGT43KkOva9MOIhJpiWbGLmkdcsiwMoXeKZtfpyQ8Lxli/EBK0MK2n4NmtA4SEq4Fzr1N/hEW9HtbgQE3A7QrNGZJ5v4UJU0EJOGgCFl1rr8QwXYgI4PlE+EWZZiqfgjaigo/nT/CediUT7FlyICujl6oUbKkI7KsaFqGCi8dO2mZEu47jChVAwuHQxdV25YAS6XGYPUUGGQ6A9S+JKxCG4EBUUnj4gi75xrBQiHqD0zqN+svW+vRz8C6EAjh9cH6ZZZv8expo/9hAIZuURMUMDn7n7ac1AeAgFXBcpzLkq+2jbCghxERXkIivukm59bRL2AKPjy8t6EChuefmcHqICbndE8ycnO4S4ZoA9RAWNh0tKiFVHq3s+wYWogE/PeYMA/yHuQ6E8hAKOiAtbwsItvmmPMz2ER8PiHXKVrTMxGWdx1qEJHqJnyfKQsyGnUjA37TpTwENUMDLGQJIVuPGYybkFF0JBZrVNTCPMVNJhhXW7iAoaq6EknmQ+jXWAioeoYIwSmqTMy3BxnuG7i1BQeMQvw1Ulx15ZKT9cRAWJjcHUzKYhr9NLPEQFWTeGiT/NjHJbcCEqKJqvTvIP7v0tLqKCGmSIrvkNn9AIDzA6HJWqyRZra/GgvwClNxn2SbTkPirOA4ze69Acp5wZasfdXIgKeLbwkxR11HUEj4eYoNWSLNFpWpHjLmKCyagYSYuJ8dw4+C9A6ZL6oFty1HHe0IWYoM+siRcnXnw4LnAhKph67KeYxz6kyENMgLZGs+/CF13zKC5iAjs1RPKSjn4K3ggFlQluuPdL856WXUsdxAQMNmqWhrWvA2I8RAUxMNfOk4h1HczlISaAX58tWSrv+hC8EROMylGWJpJdOb1dRAWoX92St+aVj9gDjA5t1Puse/+Ri6ggR1kpkvoy0zpbxkNMwISTxTK4hnqU0YWooESeHfjkcF0nqXmICSpGflqF8fXG47VdiAoqz8Ar+tXWHo5nuBATcG2ta7vQ81kxLkQFLaSoaY5H3TlLXMQEnL4Z2qzFUY5buhAVoLXUt4Nx0zgr0htQ+oBfluXBmOu+ps2/EBWwtSlibtt98QDSeTb8rNNyaddQV71zEBUwql+zDGdu6e1bcCEq4LKehrjHxtO5t+BCVMBVZmbUZZFgtJ624EIo6NzzwCzgjUdl5JUnw0VUwH0DTeKxI48FiltwIRQwYDqLWdJVrTy3LsLzDSXGuDOTHNfQ4uPXegDpmakVefQRT9WhW/oUqoeoYBYJa8uT6We3M+IhFBRux+C6NOPuuXv+eQIPUQHPyUxDs9WV7YF5iAm42pY0PcxYJy+5iAp43lQQ8+R+xuMKF0JB1c0GkR47nqytQr0B0hkUNSSbDNu1nsf6fQehYHyNJtlTeUQU89E/rYWHUCCTuIwNaQHdRlvfsgOAzpNN2dxLXSkxrE22LkJBlEML9cgiVIMVFu0iKig88bkzpz8DrVfP6SEqwAA3qTkx9Pu4woWoAIM+bg+DufJc5ENwIRTIlnY5fyMzudealnMRFWBUNrMeX9TzmnRyERWgtoyhx160FJ/pCxcxwZQz4OWcjLnOwnIRFaBOMdpNz+FY53i5iAoqxnKj2TkfYb84BzHByIwkl3NEeGraIXgjKmhcfx12OtEKgnQRE7SU7GCgsLcUuYgJ5mCUmyTZHiv3rouoAHWYeUDkYBb+5hZciAlamVkP2tk7cjzA6CixqmfnoKfsR6FeiApGqlxH0wNrWjgucCEmwKAgPscbtX68hQsxAcP5zVxTPW7pQlTApclg5j77cUsXYgKGkujZOC2k4wJvwOitM+xcj0WK5w1dCAVsDUJ+zjpaZ4h5gNEz98E+ZyOtw/s8xAQ8szqu3zn4L8Dok4HYdpcpnffzRlQQJTGkFUNYQzwPMUGd/Oy0nFeKcBcxATzRogVX85o1dxEVJIyLrSTKCPkoowsxQeU5ymrOK0+Oi5gA/cvQ+p5b/kHwRlTAhN1t2ge4QkBcxASdC8n6ibd6vocLUUEJkmFbGpG2O1sPMUGpHDpIM5VXKL6LmEBPqaGZ8/vtELwRFcDfY7iTnCaXV2ZNF1FBgzOQtOVEJzyPW7oQFcDxZqY9PQxvnJXvQkwwmI5LzCj3ehTrhaiAKRLzsC7vfIQ3QDrfISNBpUvl7orHE/YQFcQag567xAim/T07iAryZPJoPecwpt2dO4gKuCW2DHU8ZovHFS5EBZPJGuRUX1bg3S04CAWVAaDc783DtFGF1xyVh1AgUwE8frnS45VZHRM4CAXcXxkZLl7pqcy237ODQJAD0zBwLZlh0HCNVuX2EAqS5PQtOlc80poIdxEKmP0k8sTzkmQc+CxHuAgFXLdOXBOsEpNcwrolB6FgfEmQnZwmhZ5jvWgHUPrkZtsix9lzZ8vY/AuhgAloIrcO83TYgR9aF3AQFbQ5Q5Vz0HlyzRr9e4gKmJAky15pdH57MtJDICiy2ZAZdeSc3dU333YlR3p+MhEd+z7G3AGUnkq3081RsdaX7ABKZ+XQs4oThrBr5sJDVMDDu5seb8rjLfsWXIgJetajk1NfSc0du5IrBhx6ejY37rTjaS/EBBw+6OHJtaxgJRdRAY+3iUNPigZ+FNCFmIBnI+jvMHvr8cAXYoIxeeCOmMc6f9BFVMAzDO3waib7T1twISZosq4vB3XHdtaJC1EBRhul2Mnebbs7HmICxu2befZ61NELMUHnGfB2pPqecPYQFfAQ8GQnmZd1comLmKDx0C61rjA2DyCdsdhJ5q1p5vt8+A5iAgZ5233GPazwEBPwjL9ph6vXg/6jXckxpWkHtwcuXm/6hZigclSlr36EeQreiAmYoHXaAet99WceogJ6t9VqIwdCW3AhJkAHbdUXI4dyCt6ICRi5XNQc9hyeh6iAiWaKfbNzN70eYgK0fDo/gRtYef1cRAVoQxiS2CQJXD0f+kJUAGvXVpC5D8rmvwGlo5Hn0UhyOns82C+7krkoX+UeOb7drZ2DqABjdE7CSAdRVuI8F1EB/kpa17mwV44CvRAKqGZT3yQNYVtTFg6g9MxTDqRHbMxgOzf/QlTAw12nHL6OYVPLfQsuhAKOAxrjfNGrpxBWtggXoaB8dW65HpxDw8BvBeK4CAU8zlRmVJiDjruq15fmIBTwqAamt9O8HG1Pl3kIBZLigU0gXQ7mYF0P7SAqmIWBWHoQ+4+CC4GA+7oqA/cz05jU3SE4AOlM5lh5SgwPcS/MvfrwHYSCwpEM98DzTOmAonjKyEMokG27XB+Fh1ti3T2Oh1DABWeMhad4e3Ht2fIApTPSNMuh7AmENRnnIRRwh0CQMTG3R/Rd8TxEBdzyRIcjcMqtPHuvXEQFPMS52XmuaexCdRAVwNsQD4U1vqyYERdRAdOi6TgjwyNeX5uHUIDRxYg8OYbzvXDZVwPjISqIkrtAzFPS4C3BhaiAkfJ6iC3Patrv2UFUAM+n6BR0ZajOIbgQFZQcOGijecYVl+IiJkDLk+UYvhbqSmfoIiqoSbbG0YxyP0vpQkzQ5Bgkmrkakw7BG1FB45ZOKQuGVYa8BRdiAn59ai451eOWLsQETNcw1bw3OruICpi/Z8rQpNWzUF92I+u6mRglzfemvxEVwC9pWV5N4yGHRz26EBOgIKI+FpNyHVe4EBVM9Fqh2e/UdAguxATo00t/7rSegjdCweRswbR3CZ96V20HMUGVCDUp6d6W0+whKsCDcbHQ+si1eO8hJqjRioKBd/PgvwCjc5FOL5vC2kfjIirgcbrPBzLPB3gDRu9ygD2/vz2XcNuVnKtOPPPzzjEcP34hKmDYWV8NyHn3F2KCORk5TnPcvo4DKL32xKN02aL1sh0FD1FBZyCf1PU8wwrBcxEV8MvTgkCJxHSU0IVAwFO7K2c9paNgx/I8soeoAJdjStcmm8zmWojzEBU0xoFHmpnjvR6CC6GAY4HKMA/rfp8q5wCkJ56U3aceasqQjeeRPYQC5iCTSMSycl/89edfP+nzXz/h85sPbv7z+8/fff4e/+8fPz/9y1/9+z//8ld/8/OffX75O83B1rb4+2N55dL46V/Ez69/hx/4Pf79+XNNnbXrx10knlRYp8p+C1kSmdwBhTzw5byae/Ovi4lm//AfutZff/v/V9iqxgplbmRzdHJlYW0KZW5kb2JqCjExIDAgb2JqCjExNDcyCmVuZG9iagoxNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDc4ID4+CnN0cmVhbQp4nDWMuxHAMAhDe6ZgBPMP++RSOfu3wRxp0JN0yIlwocs54RiceBOUP/QCeTZtkGWoTeY22f9RrRqKRhHHVVsbKLKV1aeZ0Q3PByZrFrUKZW5kc3RyZWFtCmVuZG9iagoxNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMyNyA+PgpzdHJlYW0KeJw9kkuOxDAIRPc5BRdoyfz8OU9Gs+q5/7YfdnoWUaEARVG4a0qT6PJSlxwq2Zv86BVTxc3k74mGxDRxN9DBKfe1owj+BLgOZu4M0UqJQb11icrykbHz19fTlwfvy9thsFF6lphXn5KxBgvydHTxAebc2u5/le8rk44svUpPRe9LvViWqA8x+2L1KdzG5hvbejCeTPFrNlGrmVPW2iK6DNRFSjex1QtQ7VGB41xHbxVtAxCBO0EHlQm1amzBSEi0RdYvzGlC98T/7QG6X9rEdeyD2LSNZ3xFGkPQ3bhHWcPMMep8anPD2tPZJuuU4kwu17I4Vgk0SstYakvwrHpdFGODGWilEM3RamxlaHbo62V4P8gMbzuKsailSs+eN6fgXH3s1xR68DyLHcGbnNgt6OeQrEIGLTZh6ixdr/A55339fgAqPX1GCmVuZHN0cmVhbQplbmRvYmoKMTggMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNTIgPj4Kc3RyZWFtCnicPU/LEUMhCLxbxTbAjCCC1vMyOZn+rwFNPLGyuB/xgQpiFpBUh7jDreLFhbWjq+NTpB20CouD5gaWvxKxgryB69bpGD1mm3iK58YYOmOGsHDMkQxZ2sUz7rYvRY4NgrthVqHpKZY+5HphGwdSerO0XaGmcC6mImOGcdtpn1sl0o7TL0r9mq4ivcPUkrWLxp99fwG89zZnCmVuZHN0cmVhbQplbmRvYmoKMTQgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zLU9ibGlxdWUgL0NoYXJQcm9jcyAxNSAwIFIKL0VuY29kaW5nIDw8IC9EaWZmZXJlbmNlcyBbIDg5IC9ZIDEwMSAvZSAxMDYgL2ogXSAvVHlwZSAvRW5jb2RpbmcgPj4KL0ZpcnN0Q2hhciAwIC9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL1kgMTYgMCBSIC9lIDE3IDAgUiAvaiAxOCAwIFIgPj4KZW5kb2JqCjIzIDAgb2JqCjw8IC9CQm94IFsgLTEwMjEgLTQ2MyAxNzk0IDEyMzMgXSAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIzNwovU3VidHlwZSAvRm9ybSAvVHlwZSAvWE9iamVjdCA+PgpzdHJlYW0KeJw9UbtxxTAM6z0FRuBH/Gied5cq2b8NKDkpeIApEQTkpyzRhZ9niOD7We7/yAOSrVBthCc0FZEN08DnSRFYbqQm3F7c54RslSP24lwgwhDtPAlppAsWOxkL3hc/j6seZqy5Yfy+M5p9VHTVUR28ew7jZk0/TpTd682sjlub+3TvrhOHa0gmn/cfnJRKp5csgzpLuLA2mhrW47woxljMOP4nqrBNsrajCsHSJUgq0IAYShLGgMUt/iInWg4L2psbaeudyU6qNIqGF6MM3qD1RjiKdJF8mGsrg7GpmDa++eQlN+j7Z7+fr18Da1rrCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA1NCA+PgpzdHJlYW0KeJwzNjZXMFAwNDJX0DUyNlUwMjRQMDczUUgx5IIxc8EssGwOF1whhAmSz4GrzOFKAwBMkA8VCmVuZHN0cmVhbQplbmRvYmoKMjUgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzOTIgPj4Kc3RyZWFtCnicPVJLbgUxCNvPKbhApfBNcp6p3u7df1ubzFSqCi8DtjGUlwypJT/qkogzTH71cl3iUfK9bGpn5iHuLjam+FhyX7qG2HLRmmKxTxzJL8i0VFihVt2jQ/GFKBMPAC3ggQXhvhz/8ReowdewhXLDe2QCYErUbkDGQ9EZSFlBEWH7kRXopFCvbOHvKCBX1KyFoXRiiA2WACm+qw2JmKjZoIeElZKqHdLxjKTwW8FdiWFQW1vbBHhm0BDZ3pGNETPt0RlxWRFrPz3po1EytVEZD01nfPHdMlLz0RXopNLI3cpDZ89CJ2Ak5kmY53Aj4Z7bQQsx9HGvlk9s95gpVpHwBTvKAQO9/d6Sjc974CyMXNvsTCfw0WmnHBOtvh5i/YM/bEubXMcrh0UUqLwoCH7XQRNxfFjF92SjRHe0AdYjE9VoJRAMEsLO7TDyeMZ52d4VtOb0RGijRB7UjhE9KLLF5ZwVsKf8rM2xHJ4PJntvtI+UzMyohBXUdnqots9jHdR3nvv6/AEuAKEZCmVuZHN0cmVhbQplbmRvYmoKMjYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA5MCA+PgpzdHJlYW0KeJxNjUESwCAIA++8Ik9QRND/dHrS/1+r1A69wE4CiRZFgvQ1aksw7rgyFWtQKZiUl8BVMFwL2u6iyv4ySUydhtN7twODsvFxg9JJ+/ZxegCr/XoG3Q/SHCJYCmVuZHN0cmVhbQplbmRvYmoKMjcgMCBvYmoKPDwgL0JCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzcKL1N1YnR5cGUgL0Zvcm0gL1R5cGUgL1hPYmplY3QgPj4Kc3RyZWFtCnic4zI0MFMwNjVVyOUyNzYCs3LALCNzIyALJItgQWTTAAFfCgoKZW5kc3RyZWFtCmVuZG9iagoyOCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDgwID4+CnN0cmVhbQp4nEWMuw3AMAhEe6ZgBH4mZp8olbN/GyBK3HBPunu4OhIyU95hhocEngwshlPxBpmjYDW4RlKNneyjsG5fdYHmelOr9fcHKk92dnE9zcsZ9AplbmRzdHJlYW0KZW5kb2JqCjI5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTQ3ID4+CnN0cmVhbQp4nD1PuQ0DMQzrPQUXOMB6LFvzXJDqsn8bykZSCCJA8ZFlR8cKXGICk445Ei9pP/hpGoFYBjVH9ISKYVjgbpICD4MsSleeLV4MkdpCXUj41hDerUxkojyvETtwJxejBz5UG1keekA7RBVZrknDWNVWXWqdsAIcss7CdT3MqgTl0SdrKR9QVEK9dP+fe9r7CwBvL+sKZW5kc3RyZWFtCmVuZG9iagozMCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0OSA+PgpzdHJlYW0KeJw1j0sOAyEMQ/c5hS8wUn6EcB6qrqb33zZhWgkJC9svwRaDkYxLTGDsmGPhJVRPrT4kI4+6STkQqVA3BE9oTAwzbNIl8Mp03zKeW7ycVuqCTkjk6aw2GqKMZl7D0VPOCpv+y9wkamVGmQMy61S3E7KyYAXmBbU89zPuqFzohIedyrDoTjGi3GZGGn7/2/T+AnsyMGMKZW5kc3RyZWFtCmVuZG9iagozMSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMxNyA+PgpzdHJlYW0KeJw1UktyQzEI279TcIHOmL99nnSyau6/rYQnK7AtQEIuL1nSS37UJdulw+RXH/clsUI+j+2azFLF9xazFM8tr0fPEbctCgRREz34MicVItTP1Og6eGGXPgOvEE4pFngHkwAGr+FfeJROg8A7GzLeEZORGhAkwZpLi01IlD1J/Cvl9aSVNHR+Jitz+XtyqRRqo8kIFSBYudgHpCspHiQTPYlIsnK9N1aI3pBXksdnJSYZEN0msU20wOPclbSEmZhCBeZYgNV0s7r6HExY47CE8SphFtWDTZ41qYRmtI5jZMN498JMiYWGwxJQm32VCaqXj9PcCSOmR0127cKyWzbvIUSj+TMslMHHKCQBh05jJArSsIARgTm9sIq95gs5FsCIZZ2aLAxtaCW7eo6FwNCcs6Vhxtee1/P+B0Vbe6MKZW5kc3RyZWFtCmVuZG9iagozMiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDMzOCA+PgpzdHJlYW0KeJw1Ujmu3UAM630KXSCAds2c5wWpfu7fhpRfCkO0VoqajhaVafllIVUtky6/7UltiRvy98kKiROSVyXapQyRUPk8hVS/Z8u8vtacESBLlQqTk5LHJQv+DJfeLhznY2s/jyN3PXpgVYyEEgHLFBOja1k6u8Oajfw8pgE/4hFyrli3HGMVSA26cdoV70PzecgaIGaYlooKXVaJFn5B8aBHrX33WFRYINHtHElwjI1QkYB2gdpIDDmzFruoL/pZlJgJdO2LIu6iwBJJzJxiXTr6Dz50LKi/NuPLr45K+kgra0zad6NJacwik66XRW83b309uEDzLsp/Xs0gQVPWKGl80KqdYyiaGWWFdxyaDDTHHIfMEzyHMxKU9H0ofl9LJrookT8ODaF/Xx6jjJwGbwFz0Z+2igMX8dlhrxxghdLFmuR9QCoTemD6/9f4ef78Axy2gFQKZW5kc3RyZWFtCmVuZG9iagozMyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDI0OCA+PgpzdHJlYW0KeJwtUTmSA0EIy+cVekJz0++xy5H3/+kKygGDhkMgOi1xUMZPEJYr3vLIVbTh75kYwXfBod/KdRsWORAVSNIYVE2oXbwevQd2HGYC86Q1LIMZ6wM/Ywo3enF4TMbZ7XUZNQR712tPZlAyKxdxycQFU3XYyJnDT6aMC+1czw3IuRHWZRikm5XGjIQjTSFSSKHqJqkzQZAEo6tRo40cxX7pyyOdYVUjagz7XEvb13MTzho0OxarPDmlR1ecy8nFCysH/bzNwEVUGqs8EBJwv9tD/Zzs5Dfe0rmzxfT4XnOyvDAVWPHmtRuQTbX4Ny/i+D3j6/n8A6ilWxYKZW5kc3RyZWFtCmVuZG9iagozNCAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDIxMCA+PgpzdHJlYW0KeJw1UMsNQzEIu2cKFqgUAoFknla9df9rbdA7YRH/QljIlAh5qcnOKelLPjpMD7Yuv7EiC611JezKmiCeK++hmbKx0djiYHAaJl6AFjdg6GmNGjV04YKmLpVCgcUl8Jl8dXvovk8ZeGoZcnYEEUPJYAlquhZNWLQ8n5BOAeL/fsPuLeShkvPKnhv5G5zt8DuzbuEnanYi0XIVMtSzNMcYCBNFHjx5RaZw4rPWd9U0EtRmC06WAa5OP4wOAGAiXlmA7K5EOUvSjqWfb7zH9w9AAFO0CmVuZHN0cmVhbQplbmRvYmoKMjEgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zIC9DaGFyUHJvY3MgMjIgMCBSCi9FbmNvZGluZyA8PAovRGlmZmVyZW5jZXMgWyA0MCAvcGFyZW5sZWZ0IC9wYXJlbnJpZ2h0IDQ4IC96ZXJvIC9vbmUgL3R3byAvdGhyZWUgL2ZvdXIgNTQgL3NpeCA1NgovZWlnaHQgMTI0IC9iYXIgXQovVHlwZSAvRW5jb2RpbmcgPj4KL0ZpcnN0Q2hhciAwIC9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnREZXNjcmlwdG9yIDIwIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDE5IDAgUiA+PgplbmRvYmoKMjAgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDMyCi9Gb250QkJveCBbIC0xMDIxIC00NjMgMTc5NCAxMjMzIF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zIC9JdGFsaWNBbmdsZSAwCi9NYXhXaWR0aCAxMzQyIC9TdGVtViAwIC9UeXBlIC9Gb250RGVzY3JpcHRvciAvWEhlaWdodCAwID4+CmVuZG9iagoxOSAwIG9iagpbIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwCjYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgMzE4IDQwMSA0NjAgODM4IDYzNgo5NTAgNzgwIDI3NSAzOTAgMzkwIDUwMCA4MzggMzE4IDM2MSAzMTggMzM3IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYKNjM2IDYzNiAzMzcgMzM3IDgzOCA4MzggODM4IDUzMSAxMDAwIDY4NCA2ODYgNjk4IDc3MCA2MzIgNTc1IDc3NSA3NTIgMjk1CjI5NSA2NTYgNTU3IDg2MyA3NDggNzg3IDYwMyA3ODcgNjk1IDYzNSA2MTEgNzMyIDY4NCA5ODkgNjg1IDYxMSA2ODUgMzkwIDMzNwozOTAgODM4IDUwMCA1MDAgNjEzIDYzNSA1NTAgNjM1IDYxNSAzNTIgNjM1IDYzNCAyNzggMjc4IDU3OSAyNzggOTc0IDYzNCA2MTIKNjM1IDYzNSA0MTEgNTIxIDM5MiA2MzQgNTkyIDgxOCA1OTIgNTkyIDUyNSA2MzYgMzM3IDYzNiA4MzggNjAwIDYzNiA2MDAgMzE4CjM1MiA1MTggMTAwMCA1MDAgNTAwIDUwMCAxMzQyIDYzNSA0MDAgMTA3MCA2MDAgNjg1IDYwMCA2MDAgMzE4IDMxOCA1MTggNTE4CjU5MCA1MDAgMTAwMCA1MDAgMTAwMCA1MjEgNDAwIDEwMjMgNjAwIDUyNSA2MTEgMzE4IDQwMSA2MzYgNjM2IDYzNiA2MzYgMzM3CjUwMCA1MDAgMTAwMCA0NzEgNjEyIDgzOCAzNjEgMTAwMCA1MDAgNTAwIDgzOCA0MDEgNDAxIDUwMCA2MzYgNjM2IDMxOCA1MDAKNDAxIDQ3MSA2MTIgOTY5IDk2OSA5NjkgNTMxIDY4NCA2ODQgNjg0IDY4NCA2ODQgNjg0IDk3NCA2OTggNjMyIDYzMiA2MzIgNjMyCjI5NSAyOTUgMjk1IDI5NSA3NzUgNzQ4IDc4NyA3ODcgNzg3IDc4NyA3ODcgODM4IDc4NyA3MzIgNzMyIDczMiA3MzIgNjExIDYwNQo2MzAgNjEzIDYxMyA2MTMgNjEzIDYxMyA2MTMgOTgyIDU1MCA2MTUgNjE1IDYxNSA2MTUgMjc4IDI3OCAyNzggMjc4IDYxMiA2MzQKNjEyIDYxMiA2MTIgNjEyIDYxMiA4MzggNjEyIDYzNCA2MzQgNjM0IDYzNCA1OTIgNjM1IDU5MiBdCmVuZG9iagoyMiAwIG9iago8PCAvYmFyIDI0IDAgUiAvZWlnaHQgMjUgMCBSIC9mb3VyIDI2IDAgUiAvb25lIDI4IDAgUiAvcGFyZW5sZWZ0IDI5IDAgUgovcGFyZW5yaWdodCAzMCAwIFIgL3NpeCAzMSAwIFIgL3RocmVlIDMyIDAgUiAvdHdvIDMzIDAgUiAvemVybyAzNCAwIFIgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDIxIDAgUiAvRjIgMTQgMCBSID4+CmVuZG9iago0IDAgb2JqCjw8IC9BMSA8PCAvQ0EgMCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+Ci9BMiA8PCAvQ0EgMSAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+ID4+CmVuZG9iago1IDAgb2JqCjw8ID4+CmVuZG9iago2IDAgb2JqCjw8ID4+CmVuZG9iago3IDAgb2JqCjw8IC9EZWphVnVTYW5zLU9tZWdhIDIzIDAgUiAvRGVqYVZ1U2Fucy1taW51cyAyNyAwIFIgPj4KZW5kb2JqCjIgMCBvYmoKPDwgL0NvdW50IDEgL0tpZHMgWyAxMCAwIFIgXSAvVHlwZSAvUGFnZXMgPj4KZW5kb2JqCjM1IDAgb2JqCjw8IC9DcmVhdGlvbkRhdGUgKEQ6MjAxOTA2MjYxNTQzMzArMDInMDAnKQovQ3JlYXRvciAobWF0cGxvdGxpYiAzLjAuMywgaHR0cDovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKG1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgMy4wLjMpID4+CmVuZG9iagp4cmVmCjAgMzYKMDAwMDAwMDAwMCA2NTUzNSBmIAowMDAwMDAwMDE2IDAwMDAwIG4gCjAwMDAwMTk3MjAgMDAwMDAgbiAKMDAwMDAxOTQ2NSAwMDAwMCBuIAowMDAwMDE5NTA4IDAwMDAwIG4gCjAwMDAwMTk2MDcgMDAwMDAgbiAKMDAwMDAxOTYyOCAwMDAwMCBuIAowMDAwMDE5NjQ5IDAwMDAwIG4gCjAwMDAwMDAwNjUgMDAwMDAgbiAKMDAwMDAwMDM5NCAwMDAwMCBuIAowMDAwMDAwMjA4IDAwMDAwIG4gCjAwMDAwMTE5NDEgMDAwMDAgbiAKMDAwMDAxMzI3NSAwMDAwMCBuIAowMDAwMDEzMDY3IDAwMDAwIG4gCjAwMDAwMTI3MzggMDAwMDAgbiAKMDAwMDAxNDMyOCAwMDAwMCBuIAowMDAwMDExOTYzIDAwMDAwIG4gCjAwMDAwMTIxMTMgMDAwMDAgbiAKMDAwMDAxMjUxMyAwMDAwMCBuIAowMDAwMDE4MjUxIDAwMDAwIG4gCjAwMDAwMTgwNTEgMDAwMDAgbiAKMDAwMDAxNzY3MyAwMDAwMCBuIAowMDAwMDE5MzA0IDAwMDAwIG4gCjAwMDAwMTQzODAgMDAwMDAgbiAKMDAwMDAxNDc1MSAwMDAwMCBuIAowMDAwMDE0ODc3IDAwMDAwIG4gCjAwMDAwMTUzNDIgMDAwMDAgbiAKMDAwMDAxNTUwNCAwMDAwMCBuIAowMDAwMDE1Njc0IDAwMDAwIG4gCjAwMDAwMTU4MjYgMDAwMDAgbiAKMDAwMDAxNjA0NiAwMDAwMCBuIAowMDAwMDE2MjY4IDAwMDAwIG4gCjAwMDAwMTY2NTggMDAwMDAgbiAKMDAwMDAxNzA2OSAwMDAwMCBuIAowMDAwMDE3MzkwIDAwMDAwIG4gCjAwMDAwMTk3ODAgMDAwMDAgbiAKdHJhaWxlcgo8PCAvSW5mbyAzNSAwIFIgL1Jvb3QgMSAwIFIgL1NpemUgMzYgPj4Kc3RhcnR4cmVmCjE5OTM0CiUlRU9GCg==\n", "image/svg+xml": [ "\n", "\n", "\n", "\n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", " \n", "\n" ], "text/plain": [ "
" ] }, "metadata": {}, "output_type": "display_data" }, { "data": { "text/plain": [ "" ] }, "execution_count": 3, "metadata": {}, "output_type": "execute_result" } ], "source": [ "W = sym.symbols('Omega')\n", "\n", "Y = 1/2 * ((sym.exp(-sym.I*(W+W0)*(N-1)/2) * sym.sin(N*(W+W0)/2) / sym.sin((W+W0)/2)) +\n", " (sym.exp(-sym.I*(W-W0)*(N-1)/2) * sym.sin(N*(W-W0)/2) / sym.sin((W-W0)/2)))\n", "\n", "sym.plot(sym.Abs(Y), (W, -sym.pi, sym.pi),\n", " xlabel='$\\Omega$', ylabel='$|Y(e^{j \\Omega})|$')" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "**Exercise**\n", "\n", "* Change the length $N$ of the signal by modifying the example. How does the spectrum change if you decrease or increase the length?\n", "\n", "* What happens if you change the normalized angular frequency $\\Omega_0$ of the signal?\n", "\n", "* Assume a signal that is composed from a superposition of two finite length cosine signals with different frequencies. What qualitative condition has to hold that you can derive these frequencies from inspection of the spectrum?" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Modulation Theorem\n", "\n", "The complex modulation of a signal $x[k]$ is defined as $e^{j \\Omega_0 k} \\cdot x[k]$ with $\\Omega_0 \\in \\mathbb{R}$. The DTFT of the modulated signal is derived by applying the multiplication theorem\n", "\n", "\\begin{equation}\n", "\\mathcal{F}_* \\left\\{ e^{j \\Omega_0 k} \\cdot x[k] \\right\\} = \\frac{1}{2 \\pi} \\cdot {\\bot \\!\\! \\bot \\!\\! \\bot}\\left( \\frac{\\Omega - \\Omega_0}{2 \\pi} \\right) \\circledast X(e^{j \\Omega}) \n", "= X \\big( e^{j \\, (\\Omega - \\Omega_0)} \\big)\n", "\\end{equation}\n", "\n", "where $X(e^{j \\Omega}) = \\mathcal{F}_* \\{ x[k] \\}$. Above result states that the complex modulation of a signal leads to a shift of its spectrum. This result is known as modulation theorem." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "**Example**\n", "\n", "An example for the application of the modulation theorem is the \n", "[downsampling/decimation](https://en.wikipedia.org/wiki/Decimation_(signal_processing)) of a discrete signal $x[k]$. Downsampling refers to lowering the sampling rate of a signal. The example focuses on the special case of removing every second sample, hence halving the sampling rate. The downsampling is modeled by defining a signal $x_\\frac{1}{2}[k]$ where every second sample is set to zero\n", "\n", "\\begin{equation}\n", "x_\\frac{1}{2}[k] = \\begin{cases} \n", "x[k] & \\text{for even } k \\\\\n", "0 & \\text{for odd } k\n", "\\end{cases}\n", "\\end{equation}\n", "\n", "In order to derive the spectrum $X_\\frac{1}{2}(e^{j \\Omega}) = \\mathcal{F}_* \\{ x_\\frac{1}{2}[k] \\}$, the signal $u[k]$ is introduced where every second sample is zero\n", "\n", "\\begin{equation}\n", "u[k] = \\frac{1}{2} ( 1 + e^{j \\pi k} ) = \\begin{cases} 1 & \\text{for even } k \\\\\n", "0 & \\text{for odd } k \\end{cases}\n", "\\end{equation}\n", "\n", "Using $u[k]$, the process of setting every second sample of $x[k]$ to zero can be expressed as\n", "\n", "\\begin{equation}\n", "x_\\frac{1}{2}[k] = u[k] \\cdot x[k]\n", "\\end{equation}\n", "\n", "Now the spectrum $X_\\frac{1}{2}(e^{j \\Omega})$ is derived by applying the multiplication theorem and introducing the [DTFT of the exponential signal](definition.ipynb#Transformation-of-the-Exponential-Signal). This results in\n", "\n", "\\begin{equation}\n", "X_\\frac{1}{2}(e^{j \\Omega}) = \\frac{1}{4 \\pi} \\left( {\\bot \\!\\! \\bot \\!\\! \\bot}\\left( \\frac{\\Omega}{2 \\pi} \\right) + \n", "{\\bot \\!\\! \\bot \\!\\! \\bot}\\left( \\frac{\\Omega - \\pi}{2 \\pi} \\right) \\right) \\circledast X(e^{j \\Omega}) =\n", "\\frac{1}{2} X(e^{j \\Omega}) + \\frac{1}{2} X(e^{j (\\Omega- \\pi)})\n", "\\end{equation}\n", "\n", "where $X(e^{j \\Omega}) = \\mathcal{F}_* \\{ x[k] \\}$. The spectrum $X_\\frac{1}{2}(e^{j \\Omega})$ consists of the spectrum of the original signal $X(e^{j \\Omega})$ superimposed by the shifted spectrum $X(e^{j (\\Omega- \\pi)})$ of the original signal. This may lead to overlaps that constitute aliasing. In order to avoid aliasing, the spectrum of the signal $x[k]$ has to be band-limited to $-\\frac{\\pi}{2} < \\Omega < \\frac{\\pi}{2}$ before downsampling." ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "### Parseval's Theorem\n", "\n", "[Parseval's theorem](https://en.wikipedia.org/wiki/Parseval's_theorem) relates the energy of a discrete signal to its spectrum. The squared absolute value of a signal $x[k]$ represents its instantaneous power. It can be expressed as\n", "\n", "\\begin{equation}\n", "| x[k] |^2 = x[k] \\cdot x^*[k]\n", "\\end{equation}\n", "\n", "where $x^*[k]$ denotes the complex conjugate of $x[k]$. Transformation of the right-hand side and application of the multiplication theorem results in\n", "\n", "\\begin{equation}\n", "\\mathcal{F}_* \\{ x[k] \\cdot x^*[k] \\} = \\frac{1}{2 \\pi} \\cdot X(e^{j \\Omega}) \\circledast_{2 \\pi} X^*(e^{-j \\Omega})\n", "\\end{equation}\n", "\n", "Introducing the definition of the DTFT and the periodic convolution\n", "\n", "\\begin{equation}\n", "\\sum_{k = -\\infty}^{\\infty} x[k] \\cdot x^*[k] \\, e^{-j \\Omega k} =\n", "\\frac{1}{2 \\pi} \\int_{-\\pi}^{\\pi} X(e^{j \\nu}) \\cdot X^*(e^{j (\\Omega - \\nu)}) \\; d\\nu\n", "\\end{equation}\n", "\n", "Setting $\\Omega = 0$ followed by the substitution $\\nu = \\Omega$ yields Parseval's theorem\n", "\n", "\\begin{equation}\n", "\\sum_{k = -\\infty}^{\\infty} | x[k] |^2 = \\frac{1}{2 \\pi} \\int_{-\\pi}^{\\pi} | X(e^{j \\Omega}) |^2 \\; d\\Omega\n", "\\end{equation}\n", "\n", "The sum over the samples of the squared absolute signal is equal to the integral over its squared absolute spectrum divided by $2 \\pi$. Since the left-hand side represents the energy $E$ of the signal $x[k]$, Parseval's theorem states that the energy can be computed alternatively in the spectral domain by integrating over the squared absolute value of the spectrum." ] }, { "cell_type": "markdown", "metadata": { "nbsphinx": "hidden" }, "source": [ "**Copyright**\n", "\n", "This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Continuous- and Discrete-Time Signals and Systems - Theory and Computational Examples*." ] } ], "metadata": { "kernelspec": { "display_name": "Python 3", "language": "python", "name": "python3" }, "language_info": { "codemirror_mode": { "name": "ipython", "version": 3 }, "file_extension": ".py", "mimetype": "text/x-python", "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", "version": "3.7.3" } }, "nbformat": 4, "nbformat_minor": 1 }