{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"# The Laplace Transform\n",
"\n",
"*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to [Sascha.Spors@uni-rostock.de](mailto:Sascha.Spors@uni-rostock.de).*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Inverse Transform\n",
"\n",
"So far only the [(forward) Laplace transform](definition.ipynb) has been introduced. The Laplace transform features also an [inverse transform](https://en.wikipedia.org/wiki/Inverse_Laplace_transform). The inverse Laplace transform maps a complex-valued Laplace transform $X(s) \\in \\mathbb{C}$ with complex-valued independent variable $s \\in \\mathbb{C}$ into the complex-valued signal $x(t) \\in \\mathbb{C}$ with real-valued independent variable $t \\in \\mathbb{R}$. It can be shown that the inverse Laplace transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ is uniquely determined for most practically relevant signals. This section discusses two different techniques for the computation of the inverse Laplace transform."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Integral Formula\n",
"\n",
"Using results from complex analysis, the inverse Laplace transform is given by the following complex line integral\n",
"\n",
"\\begin{equation}\n",
"x(t) = \\frac{1}{2 \\pi j} \\int_{\\sigma - j \\infty}^{\\sigma + j \\infty} X(s) \\, e^{s t} \\; ds\n",
"\\end{equation}\n",
"\n",
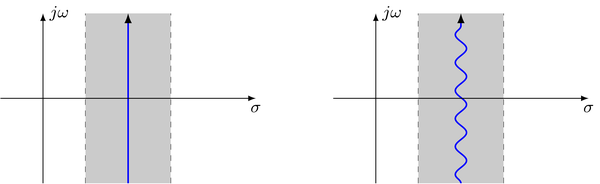
"where $X(s) = \\mathcal{L} \\{ x(t) \\}$ is assumed to be analytic in its simply connected region of convergence (ROC). The notation $\\sigma \\mp j \\infty$ for the lower/upper integration limit denotes an arbitrary integration path which lies in the ROC and ranges from $\\Im \\{s\\} = - \\infty$ to $\\Im \\{s\\} = + \\infty$. The integration path can be chosen parallel to the imaginary axis but also all other paths in the ROC are possible. This results from [Cauchy's integral theorem](https://en.wikipedia.org/wiki/Cauchy's_integral_theorem). Two equivalent paths are shown in the following illustration\n",
"\n",
"\n",
"\n",
"where the blue line indicates the integration path and the gray area the ROC."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Rational Laplace Transforms\n",
"\n",
"Computing the inverse Laplace transform by above integral formula can be challenging. The [Cauchy residue theorem](https://en.wikipedia.org/wiki/Residue_theorem) provides a practically tractable solution for Laplace transforms $X(s) = \\mathcal{L} \\{ x(t) \\}$ which are given as rational functions. It states that the value of a line integral of an holomorphic function over a closed contour is given by summing up its [residues](https://en.wikipedia.org/wiki/Residue_theorem). The residue is the value of the line integral for a path enclosing a singularity. Consequently, the inverse Laplace transform of a rational Laplace transform can be computed by summing up the individual contributions from its poles. This procedure is detailed in the following."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Basic Procedure\n",
"\n",
"A rational Laplace transform $X(s)$ can be written in terms of its numerator and denominator polynomial\n",
"\n",
"\\begin{equation}\n",
"X(s) = \\frac{\\sum_{m=0}^{M} \\beta_m s^m}{\\sum_{n=0}^{N} \\alpha_n s^n}\n",
"\\end{equation}\n",
"\n",
"where $M$, $N$ denote the order of the numerator and denominator polynomial and $\\beta_m$, $\\alpha_n$ their coefficients, respectively. It is assumed that $\\alpha_N \\neq 0$ and that $M \\leq N$. If $M > N$, $X(s)$ can be decomposed by [polynomial division](https://en.wikipedia.org/wiki/Polynomial_long_division) into a sum of powers of $s$ and a rational function fulfilling $M \\leq N$. \n",
"\n",
"Now a [partial fraction decomposition](https://en.wikipedia.org/wiki/Partial_fraction_decomposition) of $X(s)$ is performed resulting in\n",
"\n",
"\\begin{equation}\n",
"X(s) = A_0 + \\sum_{\\mu = 1}^{L} \\sum_{\\nu = 1}^{R_\\mu} \\frac{A_{\\mu \\nu}}{(s - s_{\\infty \\mu})^\\nu}\n",
"\\end{equation}\n",
"\n",
"where $s_{\\infty \\mu}$ denotes the $\\mu$-th unique pole of $X(s)$, $R_\\mu$ its degree and $L$ the total number of different poles $\\mu = 1 \\dots L$. Using the known Laplace transforms (cf. [example for the modulation theorem](theorems.ipynb#Modulation-Theorem) or [table of selected transforms](table_theorems_transforms.ipynb#Selected-Transforms))\n",
"\n",
"\\begin{equation}\n",
"\\mathcal{L} \\{ t^n e^{-s_0 t} \\epsilon(t) \\} = \\frac{n!}{(s + s_0)^{n+1}} \\qquad \\text{for } \\Re \\{ s \\} > \\Re \\{ - s_0 \\}\n",
"\\end{equation}\n",
"\n",
"and $\\mathcal{L} \\{ \\delta(t) \\} = 1$, together with the linearity of the Laplace transform yields a generic result for the inverse Laplace transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ of a right-sided signal\n",
"\n",
"\\begin{equation}\n",
"x(t) = A_0 \\cdot \\delta(t) + \\epsilon(t) \\sum_{\\mu = 1}^{L} e^{s_{\\infty \\mu} t} \\sum_{\\nu = 1}^{R_\\mu} \\frac{A_{\\mu \\nu} \\, t^{\\mu - 1}}{(\\nu -1)!}\n",
"\\end{equation}\n",
"\n",
"It remains to compute the coefficients $A_0$ and $A_{\\mu \\nu}$ of the partial fraction decomposition. The constant coefficient $A_0$ is given as\n",
"\n",
"\\begin{equation}\n",
"A_0 = \\lim_{s \\to \\infty} X(s)\n",
"\\end{equation}\n",
"\n",
"For a pole $s_{\\infty \\mu}$ with degree $R_\\mu = 1$, the coefficient $A_{\\mu 1}$ reads\n",
"\n",
"\\begin{equation}\n",
"A_{\\mu 1} = \\lim_{s \\to s_{\\infty \\mu}} \\left( X(s) \\cdot (s - s_{\\infty \\mu}) \\right)\n",
"\\end{equation}\n",
"\n",
"For a pole $s_{\\infty \\mu}$ of degree $R_\\mu > 1$, the coefficients $A_{\\mu \\nu}$ are given as\n",
"\n",
"\\begin{equation}\n",
"A_{\\mu \\nu} = \\frac{1}{(R_\\mu - \\nu)!} \\lim_{s \\to s_{\\infty \\mu}} \\frac{d^{R_\\mu - \\nu}}{d s^{R_\\mu - \\nu}} \\left( X(s) \\cdot (s - s_{\\infty \\mu})^{R_\\mu} \\right)\n",
"\\end{equation}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Example - Inverse transform of a rational Laplace transform\n",
"\n",
"The inverse transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ of \n",
"\n",
"\\begin{equation}\n",
"X(s) = \\frac{1}{(s+1) (s+2)^2} \\qquad \\text{for } \\Re \\{s \\} > -1\n",
"\\end{equation}\n",
"\n",
"is computed using the procedure outline above. First the function $X(s)$ is defined in `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAIkAAAAzCAYAAACjdSvaAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAFl0lEQVR4Ae2c0XHUMBCG7zIUAKGDo4MEKgA6CHQQ6CAZnpJX6IBQQQY6CHQA6SDpACYdhP9zLLNyZFvncBfntJrRSVqtpd1fq5Vk+zy/vr6eebhB4Pj4eEe5r4q7yl85LjcIPCodCBnDY2HwRfGP4nPFhaIHg4AbyY3HeAMmMpgDJXgTDwaBLZP3rCOQRMCNJAmLEy0CbiQWDc8nEXAjScLiRIuAG4lFw/NJBNxIkrA40SLgRmLR8HwSATeSJCxOtAi4kVg0PJ9EwI0khuVpXdyOyWWX5v6Ar7odz0M9witFnuWcK14qnulW/YnSooMbSdHDn6e8Lzd5OBXN5UZS9PDnKe9GkodT0VxuJEUPf57ybiR5OBXN5UZS9PDnKe9GkodT0VxuJEUPf57y86OjI/9PRR5WxXL5Hddihz5f8eL/UpEP1WZy1v87+lBrt6jTfdGbP6e5kWzm2C+j1UcZxPtwgfKflf+l+CzQfOMakCg3fSfD4Ol3CB+VWYjW/EnNjSRAU26KF/nZp75vXPvQKbBOHgRPsqd0eLkRU9jEPFio/ocO/6ON+wRwGfnFyxKzp7hrZU4uN2LelD9Os7aiy6iwIThkYSBdcQp4kVuf3bi13IgZS3qh9HAUsmu+SHJi/Z3fFFE9RnKldKnXEMU/eRwkIwMbxonPZvD5jEPRef2yCSr3YhDaUVqdcuryTCmvcM4iIxGR9zt/KI3cTdPbRDK1nPabIhjKE9Gbs70VVXSOdC+76i0vefFNHgfJiIF8Vvo6yK88ngCDeK3890AnVTmJgehVO2IJxgY7xoKxVXhuQTGBTjgnrzxIgFeK78Z0hPCKbxRR5jSjDXRCt9ywFhwk/2gMpAgyVjM/KKX2GGgGNrzYHapIuzDAeDgCk4bIsbiZcG0jeavKpdyyGh4bmK3ElYdaJ3TL7W9dONwFAwb2IqETHuSx6AsLbBcGouOB5+1or22MREyswdUaZBk2KI9ub4f0eUA4YAyXkveqQ6fUhMjCoN2evS3P2hatY23mUJZguLrfdZnzdLN+BZ4JpuiGjkOeMguH+8ZA/Vef8ErgXN0pVX20ea35cjGImm08iajsji+i2kRBnZ+JfKr0E1F51r9l1vtEq2shoVvkgjt6HcRhqhhILgwEHe0m1KqZi4G9ZmaNBPfEEaozSAgEYLNlrRSB2PBMPaAb8g+FXhwmjgET9ptkZPKmQi4G0bV2udlWTdf6Fl0kIfAmCPRd+eYIFjHVBdWzq2aT1Q70N1N9tEOvmc5F73Kn7XZyy6zHqXW6fX0WDpJvUhhIHnBmj9KHWy4GESbWSKKKVEECIARWylm8GnjKil3ubaa6lBFAZ6PM3cAuq0+JcBda1uAPdSB5J4eBZOJWwrbS3gkLj2KWI7A42OUGVzQ40yQIm9S5eMMG70Dlwetsp/eUR0Z0HAqDOEwJA8nCZHumtPEgyjP5UktrLgYRRtZIcEWphqsL1CkvpzQbW+UHl5qop/svMIvQcSh04jA1DCTPjpRJPULBcFITIheDCCO73JzTYVQbF1heWPeaICER5kTpVUNcf8Z+U6RPDh41oONQ6MNhMhgIcyZ02BdG4yI6h4vUMp6LQYSRNZLTutOIwRT2lQ+3kXFbBG6PJ/ccN9Wr+1W/AERg4AhfRcMLdH1TBL4cWftwmBIGbJwxlNSjja7JkIuBmjWBj9iEqL9XXCjuhPIqU/Wzp3iwyj5C2+pnoXgRykMpvIorx0F9TBYDi9GWsRey3BTLmW2ty0YVWRr6lodRjXZcxOlrmRt+68Jhyhj8g9JaDHlZ95niok1/qGV0Qadl5d8kHMZiEDBrexKsh6NUeyP0z6oeXg5dxnjHTcJhLAbVaEcvHYXx1waQDREvw6Z2yIFt8qnk56Yft6lzjr639NkEHO6KAaD8BUb2DSEj+hraAAAAAElFTkSuQmCC\n",
"text/latex": [
"$\\displaystyle \\frac{1}{\\left(s + 1\\right) \\left(s + 2\\right)^{2}}$"
],
"text/plain": [
" 1 \n",
"────────────────\n",
" 2\n",
"(s + 1)⋅(s + 2) "
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"import sympy as sym\n",
"sym.init_printing()\n",
"\n",
"s = sym.symbols('s', complex=True)\n",
"t = sym.symbols('t', real=True)\n",
"\n",
"X = 1/((s+1)*(s+2)**2)\n",
"X"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Since $X(s)$ has two real-values poles, $x_{\\infty 1} = -1$ with degree $R_1 = 1$ and $x_{\\infty 2} = -2$ with degree $R_2 = 2$, the following partial fraction decomposition is chosen as ansatz in accordance with above given formula"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAARMAAAA0CAYAAACpd9yCAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAKW0lEQVR4Ae2d6dHUOBCGhykC4MgAMuCIYCEDIAM+MoDiH/8oyAA2AhYygBAWMoAMWL4M2PfRSMaXfI08I9utKo9OS92v5FarZXmu/P79e2euisCrV69uKeWj/LvVHIu1IWB4taGSLm0p+O7Tsbyqmj6Kmzur4mheZgwvw3dnwqQ2CDQLPFKSCZIaLrGo4RVDJk36kvA1YdLs84dK+kSyOpLljrluBAyvbnyOzV0MviZMSl0t4fFGUa4fPvlaKduCNQQMrxogiaNLw9eEiR8AXgv5KR9B8tMnm2YSeUAMrwgwiZKXiO/VRLyvoZoX6sBnnpGgmdxYA2Mz8WB4zQSsr3Zx+Jpmop6TEHkg73NpbARhcruUZkGPgOE171BYKr6mmRzGxWN1YNBKSLn0w6V1maOy2FKe6HqmcONdlL58X/eSvcF4eSxeemYDnk+VHjDebQCvsX2dDN8h+I8lLlZ+88JEYD8XOLfkvyuBFJY3DQOsyrFtjCaDG51/uG25v2PxEqdvdE8hqD3OX5XutL4+PJeL1DTKU+Pbh/80Ktvv2rQwUcc5YSCf7beKUxqvBoeZtMhT+jdFvsnnfZSG68tv3LCgBPE2Gi+xd6H7eJv4i2eV3TLS7ugCx048FwTP0aQKi+T4eqyj+B9NdKmCTQsT4VCZNUu4EMRuEjSUWtZmo1PwQiv5d7OIjWN8DnxPhv9mhYlmAZYqqNsxd6mMhmYSK7z29Kl46b73NWwY3D+UjkZiziMwF76nxH+/xd4UwAgJVL/6QC/D8R8RX7acvrlwKrxUD/YmlocNo/XmQC0xfCp858Z/sGZSYnixA0E8sCblUBpayU5xNJO/5KOFOKcwg53Z05WR79abSn/hCmzoRzwnw0t1IcCxl9xVuMB7Q3A2WD0lvqfAf7AwERKLPxnqB3HD2FruZZXhXI47m1NO32I4FV5+IPMSlsPex3fyw/s8W4QX/hGqR49H1YOgjuLbl58K/EHCRMTYSdpUiG+sHj+Q2XZnsLPMwaH5bU7Tc5wn/unDty8/JTlXhnwcSQQxGNjZQKjcVny2GUV1s7zgvY8ue4aKnMeJLmaBsAzi4XirizM9+Lu+fMqkdGovd7x+iV+WSxUnuq+QYHhVYBkdEX59+Hbmj26w44ZezUTEhpO0PEC4xsA4JCf7pf6525hMrPBAkEZn1b78yQ3Hb8wdr+tx0p0w6cSz696JeVnjNZYnjbc+fDvzx7bXVX7flSlCmYXtJG0XSJZnCBgCDoE+zWRxJxetXw0BQ+A8CEQ1E2klrMXtJO15+sVaNQQWh0CXZjL45CJcS/hgW8HxYaGbikftCq6U/RgChsCqEGjdzZEg4CQt+9/lXZuwm/NF+ZW9ccUvVPaa/LCjgVZT7Hsr3HAqyw4R5eqOdnDuDdRDsPjlYNjjIhYJqMwi/79DdLsdjja2DK8mKufAa6ljq4le+pSGMBFYWLsv5DvBUG7SA8m5ispHgxRn+4k3SYvzFr7s6G1k3cf2M1vDjfbLtFj4gIDhNW4kGF7j8BpTus1mwsnF2IOMphI0B9eOyrLjgwAqazHkXeriPQxzhoAhsAEEKjYTCQaWHWNP0iJI2hzLlIrgaStkaYaAIbAMBCQfeNZfempRInDFV/MKYeI1DA61db3kUpykVbm6JnKo+s8vgiQmaP6UspAhYAgsBYHK91YkA7B7onw4s8deCRhO2QL+rovwV9IULpzij3yZYDBF6ITdm8uiYDVAHX0Cp3qHxQwBQyBnBLClBhkAncgA7JvOnHFVAYRBZXeGUmWnMtGTtMrDIEsdqD2FAdbfX4+Xq91kWFgBPCew7Sh+xwgQToyn8HrBPYXRitkhtDHVgdvMWRypiX41r1jmHEnEa92PxHIdrQ4n/En+FM0EwcS1GiccromZv3XxQPBghPWmgke7NeIFPu+EWzHJKcwsiNb8UFf4nuwU8FaH1xQQptwj3OuHbxEuxVfzGlvDUxrhHjUUlj28tMYaillkNUJBvCAgjz7NrHp4hwesrq8JH/FTccfgpXvR3Bg/lclIcV5B2MnvsutV6DhVRDQxNir0nqrtVO2M4UFlGxp2Ks1kp8qDSpqKt9zqQbvgMjcMgWPwQnB/15iqC1w0Eux3WT24oocJAkGyaGEi+sEVfGOvhqiIE+ZojkyIlaV6MmFCI+YMgUQIIDT4K4yYZpuNUOfhE60cH+l8ABPhMrka0ddrg1IZ3m4H9wtd9SWNa1vprh75bgnq4zv5PzYhTMQoUpTlF251S7ADW+l+z42X2o8dmXC7BsrPwggrOhBqL+Vn/V1k0TfYBqWyb3Vhm/pHV0WYK+7qEc8sQV1fKIzdxK1K9gqs2olptr0/yAckZg/W48G+s2repzCXK16ii8HrZsUpfM10D+OIdy1md+L/gS7OwE1x0MlDXzjVhQBAWPA81B08tT0jvFPCEhQ/XGgxTuisWjMRkww+OqE8kwFiG4BK3rbLHC/6jB3CnJYTT0RP5SGdcQShBXFNcQiAwTYo8fRe1y9dlU0UxTsN36sWJgF1gYB2wmBsnHgOZYKvskhlwK+7GyQov23wDDrNXK8w13huePk+YQsytvw5OZSiBVvJUgyuU2xQ8PZEV6vtpA3wVQsTdTgDkJkMa7sTEMR1RXeelNcmLHZKZ/Bg7c5pZmzr08lp4i07vEQTqv0N+cU7J5MZTHsj9PS+7yK6WS6c1V4nGmJCuMsGBW/wOFiY7FV41U5AoqrxnZDQ+c8Vn6ourhormMsJL9GCAOczFsXDoDACneXrud09EcARlKgTndna60Rbnw0K3kbhvFphIrA4lFR0tsK9S5zoqNhARm54iR4G+335dS0SAcObxOd2TEhROkQ3D2KbvQ7DZQ6uzwYFb6OEyZqXOSxrKpZ2dTADEePS5Rl786ZvGxvMOemoQ5ANXv5BDDauSh+KaB7QHJaag/pPtA6219EhKj+7zc630WeDwmYySoNfszB56gee+6QkHSV3KSBbbSKH7Pl+1S4PB46HFsfJazrss/zB61J35zw/OeHFA8is2LYVWt6ZmweJBLXSt7pG2etoVve0jk+lMxEebbNTPUNtUIOEZRmq1QoTgcagy2bgiZ5i3V/ugFzCOeElWiqfBc0FoxodLAM6Z27xwRINmx0TCGHsda91nUUjVbsIpIYNSmk75dV3puANHge7/eCSVpABcJZBsFDo144XD1+rTUEPZnb2OtE01gaFZlIXMJ1DcbWaSSfXEzLVGb3bgBOqXe0tG8ALrfd+pAPRRCq2HuFxNnud2kbojbVBcURglGZvwiQyGizZEOhB4IPygx2sXjQn+xO0TbFBIRBb7Td1ZkM82fdMQoXmGwJbQUAzPq8e8Gd1o2bwKfh4zeZoA+yQtr0mw8bAKNuV2UyGoGtlDIF2BBoH6NqLJUk9pQ0KY3HbQb9ORkwz6YTHMg2BbgQ0e7OEeCZ/lLGyu9bz5XqtpPLJzKHUmGYyFCkrZwi0I8CWf8XY2l5sManwMspWEjgzzSQgYb4hMBEBP5v3fu5wYvUnu018cCB26ofgd/8DQsnj18K+vy4AAAAASUVORK5CYII=\n",
"text/latex": [
"$\\displaystyle A_{0} + \\frac{A_{11}}{s + 1} + \\frac{A_{21}}{s + 2} + \\frac{A_{22}}{\\left(s + 2\\right)^{2}}$"
],
"text/plain": [
" A_{11} A_{21} A_{22} \n",
"A₀ + ────── + ────── + ────────\n",
" s + 1 s + 2 2\n",
" (s + 2) "
]
},
"execution_count": 2,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A0, A11, A21, A22 = sym.symbols('A_0 A_{11} A_{21} A_{22}', real=True)\n",
"Xp = A0 + A11/(s+1) + A21/(s+2) + A22/(s+2)**2\n",
"Xp"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The four real-valued constants $A_0$, $A_{11}$, $A_{21}$ and $A_{22}$ of the partial fraction decomposition will be determined later. First a look is taken at the inverse Laplace transforms of the individual summands composed from the constant and the individual poles. For the constant we get"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAADsAAAAVCAYAAAD4g5b1AAAACXBIWXMAAA7EAAAOxAGVKw4bAAADpklEQVRYCdWX7VEbMRCGD8YFeJIOnA4cUgG4g0AqSNyB+Wn+ZUgHkAoy0AGkAggd4A4gdOC8j6K96M4r6TzOj2RndPp6d7WfurtmvV43/1NbLpeTIfp6uFEzkM7OziaCXql/O5AlC4uyTgU4UEPuvdpc6yv1WdL+QptgirgoYCL8e7UvJnDfBgP6K2GmA3BDIBhGw3HHai9qzyVGFNf+a/XXJZztCXfLWP0nW9sjJWokBg7CWJj3avjavmQg66N6jKyScGOBvqt3syru/xBmpnEn6pqzfqj+ZWhkZ2IIHhUTabcr3UnA1y2EnAt7UcAfaQ+9vOyAD/6maqyMA0gzj+HlXelSAqgnMmYInQgLT44IxkqYjUyJfPCPi8YKgLee1GPoUzyJtZ1I8lCKmuLCKzpP+zjEHJ07l8iWahn+k9ptfKrD5vEEO/BV7sQh61H5D8KSXihJ/RKZHLEXLpsUIDnwohvOIgBTrSHrTn17A2sOwT/LGhuF3QTo74cZ+yZZ22oomdyMdgs3mhMN0nmstpGCUfiB+o16FR4DbtUT+SP1JYc9gskaq81jCbCoatqYMm4aCxsuAeFId14RvEdb0hw+lE6d9U1zlGXvQc0jIuddPIbFyByvYeCfuMZKMV7evJRTj1r6cniHhCNi1HZIH/V4+kYt9TbOIBKWIchIx8w94lxztLdPOpfqFR7OGW8YK2WCMT1FYWi0xkvZiyyGHIKBhMMojMVhZhARTDMlYCO+FpkWmw4kG13RJy23FGLj4LB9myX9uYT0C9y2UdwiHNYwSAMONaPCuh5EY8okKsXwnkdC1GPNUFIwBCDhsyFRRX57gSVnGYYe/ueOsQLCzBdHjjCgf3B/brwoGRwjufB5RKQ/exvJGk7EoR516lXnWP33seixao0VEIG890ovbwxoIpZhiTggdQTZEiIBk2SgGB8CtXoj8u/gcSgYwbrkcBZlA75PfGY+jCKI95OlRPstaRzCWL2ZsjiFuuTGzUWNw9vUBqtGiXD5QdzY/ATUiBsb/Tzi/AvJCR/76nPlh97zv/Ivq3/Hn2rT9D9T87XaoH/PlM8bS86jWke+h/PW0AF+9to09ty2xRp1Z1Fv5GHG1+rbyG4hy4Ny27s3uQfurRF9+JtBv3g9Zncqw4JAbfJRwYcDaZtLcVdGaVGyeL1Uf/BTGeLhHiLNw/t+lG7uMpbAzhfTLrIyvNR37Tu6z8pH0Z+M8PL8X12L9bcYop+wC/Ap9hfN6TcYhEeTawAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle A_{0} \\delta\\left(t\\right)$"
],
"text/plain": [
"A₀⋅δ(t)"
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x0 = sym.inverse_laplace_transform(Xp.args[0], s, t)\n",
"x0"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For the first pole $s_{\\infty 1}$ with degree zero we get"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAGIAAAAYCAYAAAABHCipAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAErklEQVRoBe2Z0VEbMRCGDUMBTujAdOAkFQQ6AFJB4g5geIK3TNIBdMBAB5AKGOgAOoC4A/J/svbmTifpZOObmBDNyHu32l2tdle7Onnt+fl58FbaycnJrda6J/iwamteeyuOkPGHMv5vwbVVcwL6rK+iUj3ptC25dz3JfrHYf94R2gEj9R+yFH3As/r4xZaLCJDcUQTdQkXpSE0l/fj4eKR+W0K7ijTorr7bl26SfVAqX3Tb0Nd1mWdHXMi1vURSK2T6QaD7dZdoReuBOrumeOeIdldyNwUvu+QzLjqnh+A3oy8q1mJgIhyBkL9a7DQ/BnVpBn0ybSJadzoSpD5cCL7L0A80fuXpzvRMcb8V3Orgge6X6D7E6EyOxnb03Dit6Z1T3GfB6UaMOYLbEQ5v74qJnNsQGKHvDaW5KbjoM0+rdoP4MRxraBRuvVsNOUOw3qfq0I3VG7TBxPCdBrj6K0FA7XiqI/0zfPBPOlOTlICQbsZnIa+tEdU3XukjQVuLQ2FsPRyos86wdRXgffE754WM/p2geRDNNBz3fPAPs44QAUo8CqL4oxfUpVg43yq8E3lbWgc5+VwwNIpzjvBVDdGzBdz71AJEQ8puODVCy47I1Q7497tS06Emm3jhNmFSsYgSc6O8ATCMOZ5oRo/QeMWyxUtqsXU0+Px8GPSwMTAYfPTvtu5g2L0S7ZXzjEAyMT7z4UwCl/RGjb0R/ClYb/DvJB3hhVG8rJlC2eJlxItAPyfRyzWEy8uCpA0cExpqkSliPHZyCQ3KvDRb9+yt+Yuz0LfRpDOyrgVx8LZgrqbdQ5N0hAYxRj2KLCKjqUm0eH9fndNK6wRRMI5cHA9/vTgSXfWA0OtS2xcv7Ujz1gVjRAp2zhGsOVaETQ4OqK/F8HUI/yjqCE1O4eLEUPe2pSQmbzTRET0YjDb3+Iytiqyhnx/0pvqV3sNo9SxLAehO9O6ZND2zBhzx3XAJiE2miTHQ2CRXH6DB0cOWI7wSA8HWdhKOq9rWjhAer98JonyrdY17Bqe0aMMc2pK3LITmsqAJdxw7m5Y7Dc0oEr9etu3yBJVDO2euRyj4okwZA+/B2FezI2Zf8lNyw/RBPeKjLhftyCKtmDN5rzeXISSj2s3eOXUanuF/ajhChDDztZdqKJaaOMVTisfJpKJWk17RndYinBMhuayn0fxcBFvJ4QCdWxnCC2zUBy83RstcD5UjRAgR1wC57UgEDDwtj8tsfEy5KDKhmod6QZ0KI9ZIlgHJ4S64mE/P6OGuHQqEo9enBJ0zMGNebutr3vNxsLnb8ESccW0rVfcfnhBBRCQnKDMUDqPAlUSNiclCyXL3O4IYgiMdDUfUT24z7HJ/v0oc6ZhA5GjeuhPKTHeuMWwXa9jmVHLd8Vgwle6x6aToCrx+XZt75hpY/T5F0zWe4ltlPOtVHy+io/j4a8HZq0pNMZf+xxVZgB286K5l18A/KLoGhzDX/La21DUWLduQOyq3HbvGc7Jfw5jWZx+iFO+i5m1C6nKfCRtFXB1EEoYCyXrRNd4h/jUM8zFIrWh9e2WU5xBS7aSl7IjMZG9myEc4/9ekinJlC9Fwc3HpA9Th/wA/XdWRrDU6FwAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle A_{11} e^{- t} \\theta\\left(t\\right)$"
],
"text/plain": [
" -t \n",
"A_{11}⋅ℯ ⋅θ(t)"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x1 = sym.inverse_laplace_transform(Xp.args[1], s, t)\n",
"x1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For the second pole $s_{\\infty 2}$ with degree two we get two contributions"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAGoAAAAYCAYAAAASy2hdAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAFZUlEQVRoBe2Z7XETMRCGL0wKCNCB6cBABZAOQqggdgcw+ZX8Y6CDpINM0kGgAiAdJB0A7iC8j9g9dLqTfL5xHOOwM+eVVrvSar+kO2/d3t5Wmw7Hx8c72uOh7XNk+ED0Wbx39b+r/0b4JqavQ3t7HZRYgQ4fZfypr6P2ido45VlEw5njdXQSOj5yRTccT+SA19EeP6o9Em0c0Ri/ivpr1XwojiKbvnVZXs7CYTiOp6KtJ3Zgl9ggmub1sluU7+LrXfpM+Fz4eXGVNRyUzqeJWjjuRnTPoPdqk1EfhC8S3qV0Ne871rRn3pwEz56eT864SEadS+hOIs2VWQXW5tnDnp404KB/nqcDBtdD1vXOPPGy3lPhXkEgvqCH8MT12epz67OFcFSl9pYL3wfW+hg0lKk560/F27i9qU/p4SLBza6+8alNNlEtHpfm1Pil8Z2qzeXju3B9IemSNb4vwmlgBHafR51dtVN9ufC8En3Wt/TtSoBoIB1Jy8aEoq8MtDblCn0WAvSWACUuyFq/EmYvdTapjwPYo5fFsI76foaFMqr+TA983BQbvEHg7w9yBEcOCBJ0+9nBgBzy07mlT0rAyOPOYSP/FGBQKcymT8ywOOa9HjcOWfFVD3Cox/caCMiowRmDHVJg7hLsSz49I2N+Aofzss5wHzQ55HeKjhIDSvwQRvEfNsE8xXyddcKUECIX7M9E+3Lj4MRn6nMmnEV0dQME54len2Fqe8A+caYUi4ezqeH0lEd99CqdXcjvzyt9lAp/UfQFs4p1KLEwyQyAYTwwiHb0cKMOmXPe2UPp8n025jd9MDgZGMML67hd4jFvky21c52oOXEO6+FsAp/yyR3gq3B901MfQH436yibjMPTwRUqHp7OPATbmkQ3h32o+8KUHRyXGmrIEkNk/OaVGhy9ALfLn17zF2eynwZoT8z1WZgAeC1cOnOv4ck6SoMYK44yj+hW6RMfkYExAR9vfEsznn2Ncxtr3YBEQ47AYDw4SW2A6IsDJhBX+PPW1jqUXvGyGJkLRclR2MXPwVjW2zgo3qvTY4z8qNNRWpyDkxtNHA1e8lg8Bd4paqeaHGdByD71iT4MDnTJQ/e1dsTP+sBTPZfqp9EcBlf0g+5E/xtfT232gKM+OC2DsdksMwYZm5TOJ3gIhJ2Wo0yJSriVjqLxqd0zhkkcJhrjPcQNyu0IWri6ChM1V8JsLgdBafGkNTrHf+d06eJBlWY0lQEo3eb+cGR+bW6vIhmuQA7OftTBQXbkjIV3EUyBbPqWEgf0/Yo8QPRORdLyxHnJS28pW1CIsuXOph9DqDCaw4O7UruLF9rPhqPEiDAlKwco1ppMcqnSOC7+lpabL6YTBJS6Fmj+Uia2+JdF0LrstwGmC8Ha53LDnroqEHM2ziebt4uXtW5qR4kRJspXKZ2JkMp4abZAY2MRMWzrwtBibhIolyHKnKy5OK84u9KIdpZVYM6QEJzoozZ6hs86PRZH75cZvuAAxmze1tcQk8OOV9vGxB3eU5GMaigiHgxPlrghw3kkeiOq1MfZbOS52q1oFD0L4g/fz4SR50oK4CjWvU840OIcB+yNy1Hrm1xBuTONYdsuwHZ8KQnXf+HccYPNpxUfZZfxHB0djfSc+FzWH3kfLNqenuuYtult9qtnPGSfksOmwV7bXa5elGbRRoniCwKlDyATGhkXqA/vhwqBLYZUBuyHfNXrbw4YSyDn/NJ4qOMxn+jhLxFzJIqSxjiSNOcbYi7dNbw5oH36izyXi15gNqM0htekZWXUvG9pKPiQs4uXZc6q1rtpwWtUqDoLl5JRhcX+D5kFLEMaf6/njCNevsxcCNcZ+BsSmiwTx14u7wAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle A_{21} e^{- 2 t} \\theta\\left(t\\right)$"
],
"text/plain": [
" -2⋅t \n",
"A_{21}⋅ℯ ⋅θ(t)"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x2 = sym.inverse_laplace_transform(Xp.args[2], s, t)\n",
"x2"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAHIAAAAYCAYAAAAmsqlBAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAFkUlEQVRoBe2a63EUORDHx5QD8B0ZLBkYLoKzMwBfBLfOAMqf7G8UZGBncAUZABHwyMDOANdmYP4/rVrVo5mRZny764VFVbIe/VCrX+od2Lu7u2t2uV1cXBzo/mdRB7M4/qv9hdeL1l+1fqHxxu9vy3x/WwR5QDneyDindr7ml5pjtCduD2MfbqsRkfORCbvD41wGOnL3f6P5THuHbg/4N7feuulvQzYN0filzzIyJgbFsPSGubo3cB/ZvffE21J7kUcf3ujUGonfaXxaPOUnA+o+V5nIGPZG+xaBrzQnIl9rfJ/hrmwp3i85N/YaXxzsufpbQ5wSke9EtDZvNIEecpRiuN9z9dxZ2f84RjYMok7kjo5e4XLmY42jHEV4QRaNc5Npb0zVGg/CkI3me0a8jlH8KSwoNo41n1QhCh+FhzRYke005601aY1Ch8o0VayaE41koj8qPBvhfIi4V5qHe2hMRVMffcT7pDF3noBufLTo6EMw9PS3xsXY1HosAryFcCasJylYdFMaikOpt1OIwJVcpENkndS4kwhIoYE2rhuN3DNFo9YYh/tb2k3naM/e0ZCqtV6og0u128FPhEvHw4GGWkkf0HHuaTW1SggQ6WY8LrPOhjJ5o1JUrPMwnWOReKk5Ssdwr9TNkYioz1GGM42mh7gVHAga3rhgzARYTuBfaic6M3+nPf6gPiId9AdFQwoBIb5rRPjvkXtNMC/EfeZ44Ki34j7Me2hIT5zJaH2uO5sj4fVPtOY9+s/ta5laMLBg6R3V3Bz+z4SVTYTD29hxjAytpg/oT/YzonxJurEfy3bgoGA58di1zkBYzuHyOAqRwZv8WWOqzDQHjtLMqYgWZDSlazmtibb49glOWjQddJhHmTAIUezbs7gwvXmYzYm2ZHzbFM9R+oj40B8PGjIy4/G2ZgIVH29DnjLqLIT5qBGFHGkMb5XnEeUhOihGwpujkZSGYXMletJ1z61yzA2CbDTT23LV/ouxuVOr6V5VfTiCa82PBg0pIArznmhe30mtwrNIgb/B0/fKGhyi2DBgpzAQPTxxKqpND8dzvbNpufH2TzzxTLL5w3FKCp6SIdHbrSfK5r36yHCgn/UaUofzcFNxeW+xlMrheeM3UzJ6pOO9seitwY0fhul7H02Ogygb+I/VP2idRwKwTTYij2zywg7VHB1hyNe2NzCi08UAjO0hfXgSHOWgY8goRKOxL73xTyUWcZ7ZXPj81jKlUr2xZ6V3Dd4Il8tb5HnezMOFhJPeyxzhIdZRZo7Os8JJlKdUjRZFrujD0wZneOR34pzoGVIY1rfI9KRE4xe/kc1rcNAxVqOzzRmY++i3nwCgbVvz6R7ZeLP5KFCKNvBIi/6O7Fmr6cPwoL9tGVIHQ0xKHGoI1jlYdLnQGC59r6zB42Gt90A0pCaLfhyIVNppEa+zv4kNnY0+Wi3Kg7OPKcC4l92xxUeLkj48LmfdJENKABiSHkvpIDzMEdczS3PBDrXACEOfnIbgQSAYiQfO4r+gkKqDhwKngaPO25lHQ4Bv8A9venDuKDeyhs9mI2RA9r8G8Er68CTo+dve+fk5QvCbzRQF85YgEhDDEGUehwe+5XVa4wwot/W9UuvQSnAHQ5ZG65ZDaU0BRlRSbtMw5NATsMTYwF/JgP4wHnJR3PE0EWnVJjycmuCxojDRaM902asPQxQe5542fDRfRZdDzNQvjVdcz7L1INzwdm2Unq7VD+9z76jja2j3zbL/Z3Tew1cWvIxGBIeIrcED9u7+IZrRFX1qQ7/Qr+y/elAgkXYZrc9lwIXWtBp8ibWDf6UjnhDqAVLp6BbxoQtP0Koisva9sggfLf2vi8jHBN7Czm/3wpWpRVIUj/qH5QKz36AVaSBGWOu/bwyxFi6F33uNqaj6AVs7itc/ZKpsAAAAAElFTkSuQmCC\n",
"text/latex": [
"$\\displaystyle A_{22} t e^{- 2 t} \\theta\\left(t\\right)$"
],
"text/plain": [
" -2⋅t \n",
"A_{22}⋅t⋅ℯ ⋅θ(t)"
]
},
"execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x3 = sym.inverse_laplace_transform(Xp.args[3], s, t)\n",
"x3"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The inverse Laplace transform of $X(s)$ is now composed from the superposition of the four individual parts"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAc0AAAAYCAYAAACYwaY1AAAACXBIWXMAAA7EAAAOxAGVKw4bAAALUElEQVR4Ae2d7ZEcNRCG164LwOAMTAbGRADOwJgIMBmY8i/7nwsyMETgsjMAIgA7A8jA5jIw76NTDxrdSJoPzc7srVQ1K43UarW632l9jHb31qdPnw4tNA3U0MCLFy/eic+3iv+pwa/x2K8GZOM7ku6Zl/Cej79X/mUodcNEqI2Wvgm4uWhmbBqooQH/MNxX3AbMGgrdP4+fZOsfTEylXynNpOmLII+BtWHCFNJiNHDyuLnd7Ng0UEkD34jP+0q8Gpv9a+CJBkpsbuEnJe4p775lKG6YCJTRkk4DJ4+bkxs09VDaVlAWg2PpskxaYVED6FkXDpPrQFpX6DiLPMYQiGez+xhFHY+GVeZfQ81hK3CgslUxQdsNF0MW2HXeyeNm9PasB+cbxV8uNYnn9aP4PNCFM+Th+0H52a09lT8VHTRZOpUTeHAf6fr56na/n5IRHVTR7bF7KdmxxY+KWVW8VPy2tgzi2exeW6kL+ckmv0QscIb/KN92G1bFBG03XEQWOIHbm4Cb2xP0/Ea0tVYQDJBcDMDf6uLwwEddySDaRyq8q3iUUxbd7zBT/CTJdD8FNXW7Va/AhtN5SgDZ4qkuVqKjV6OibXZPKXQn+bIRtsdO8YS6iAnrgnhMwkbDhWnudOOluJmKGTRVAze3xpye9Q3h2Gn0FvGSIB7wunbSLsVT9Bwo+ENx/FC6Kr6cQwgPle6tQnVP/teKe6f6XMUdfEgunE013S7tkuTB0blttQKvbmdAdVhlslL+LFVHZb95ml+Uxp7vFHeHRobqebpm9yHlVMyTnifb3JpXXXZJOATEqenuGVO6iImAxyRsiHfzB6a8hbHX5aDvLLFW3c1wo7YnYYa++L4u9idjt2cfqk1WeGx3su3ZG5gQaGL4U/S/6mKVOSbgxHkwU4EHlId3aLVKPep3J/2UnhzUZ9eG4nhbajKvqEJt3Ubsp92qf2yvIdOU0K0oVB+HBkZsm+6gtL3bcrrT/aUuaDhZ2dENNLip3SXbWjanq7uxu7fBVJsfVI9njm1YV9ffk49/yGICBRBEOwcbm+LCy70WNo6Ni5zvdDZKfch2c3wFNl+Em5mYoRtVcHM7pRDL9wLSmA2UOMWlAefJAMwqa0x4LNrcYAXQeJ/SzXSNqa9H/aVyU38pDxPLxZIJvdbWba+NI92wYmQiRHimy7ByUB9xnryTpJ9x4OHJha3tXt3mdPYm2F19wHZMSF9hYy6lOafwURchiYmrYqeHudjYGhd0oTo2NsJF0neanWrGS3HjcbapP8kOmr6DHxTjBD945ZUcXVHH4ncpIt5/saWXHYhUzsDaOeEEc2ZLuXed1H+cqLtJtvqFHqvrdpPOXDnPL9Qn3h+/Vox9LbhBVHnd+06lzeafG1Eci6bZPVbKvu7Z0uO5I7brSWB7BtQUJlTkwmRsNFyY6qrFJd9ZrSHPaCluJmOGdmvi5qKgEbZebFvTBq6koyvwcsVe+O90w0OFwXif57Z3FA8FyjqHawTiQ11kwwEzADHbhdefiuMTs9SHT261quKjhuq6HSO9dIO+AN4HT8+KAFnCgc4XjYtUl20aw0lXybfF4McKJAwP/I1hKiyzdLO7aWJhvJLNk++vETeFCevKAmw0XJgSZ8bS/Sjf6W1U21fMxs0CzKCparhJDppesbxstWAOLnt4w4iHYvFkJWKnZg+6t/ekd5ROOW0cLANsL4iegfB3xTjlbxSjlFT4WwUAZRdBsiJLVd2O6ZhvF11yaMO9S1TMFhkPRjywjWFZorGTy/GkhzYJhqmru/5ns3tfH7PuNrD5WDnnYqPhYqyGE3TCRNF37hQ3czGDJqrhJjloqhEca7h6sEFtcHtWtPbOihUMXw3pOWHdUw+HHQ66r3XPoEeZc+KK48DKyN6TxGXcM1im6ho99QflNoIjx1N1iw7YXu4mHKG80m22HFqvfwZqeIT6igfwkPXSNDsKhGdq0yX8BzbnMFBu0Dxru0s39J/JDMGw2ztx7mlyuKDesW3uBB7xMRcbDRcZXIzBTWCbQd8pHnvFzVzM0OVquBkcNKU0XrRyupFBzoJty9J4L4iOGQDv59y2qGJWfr/pCld/DKqsDENHGaZ7PIMb2r0M7uMkTj/3PhN62rkmNwVxkHz0GZ5xcP1XeTiRMJr3yh91Elh0U3XLqszkudYH8cuWm4CKzZas6pGBcFcXdopXgq6wwgeyYfNON0rTBwbNlwX+6PsodpdMq9qcfqqNSXZXFb7L2mHNy8j7IDfp1P0Yu29hc7o7JszFxtFwQSe83u35C/uFHJR3NgoKV/MHaiOLixHlgZjOrwz5zr3iZi5m6HM13FyEGiQtEDjHrDgc8ByZ8vhLFJv1ujz/wYD4tWWIDkeJMw6/noKjHALYQXThysfYFGPVQ1abFeXoSwrr6opnSka3IlZ5/L60q1tKeHkPikfrVrTohoeQ9q+FUnlQgQf/rehnyx/wKibVjsORCMNtaOo99pVnv1/2vKvZXfxWszl9NV0oHm13VXsieg7K2YSGZ4w89zUdxVlc0K7CUW1+1WT5U7Kvgg3Ptxou6Il4roYN04PiariQyFncmHV82yld7Q43pivJv7k/uW1KDGJmMinHyorNzbCMXrQonocgXjVeKo+ZwSHo8F/cB+GB0qUB86No7CELqrokxoW/OZawrZCW+vDZOkzS7QrC2tdCVmCdZBnbl217fuAAfOTCudsdZx0/Lzl9pcq2sHlKljh/DjYaLvK4GIubku/cK27mYAbcVcNNb9CUI0ORbAGlAo4uHsDie6uLkG6AzThIDPzSKiRiBmMG5qHADK1Totpxq8EBQuSIB/UBsvWyZuq2pkD0n+3Ya8Hr7Vr+kowhm/t2sAUDZymctd2lq3hiwbMS/rZrSX+UH9XmYwSCZiE2Gi76E84eLibgJuc7d4ebhZgBdtVw0w2aEoqBie2g3LYZA+HB05LMBZxjOKCyenWzGyqJBwMcTmBoTx0SCwyKX9lNFHeDofjQVu+XaAJafn6vG1yD/KMkJVtt3c6Rm+29Tv8wQGe6eH+xlm6wrcMAbSnttvGVvlS6FJrdvYakr/tK8rwM/oxkRpFb2DwjTq9oLjYaLrwaS7golOd8515xMxczaKwabi6kWJwZ32+05Torzd5vtYqGB5YZjTld965F+awYUg4QvozuLkCri+3J7hCK0t0BEaMbiF8rD/mGAu3ziyTuKLLi1LYyciP/UYPkWarbavJKFvebr4p5IPgKDoFBc029fK82sDmTBg6wXPttYOWlQrO7NON1h82+VDr1rA3qUPRb2HxQloHMudhouJAyS7golYtF0nfuGDdzMQP86uGGH2xfej1//vxfXfdDPrr/pOtemDc3LT5/6+rxH8sLGag/lj5FJx6PdD1Nla+d79tP9qNUvrZ8a/BXnza1u9fpljYHu69Mt0pz33umvIxJXFjdmxSrz5viAl16vW+CDTCgK4mLUvlNwsKUvkgvVXBzwRBcIbwUD1ZzbptPMxXSnNTsVpoL22CmzYpozqqIGRX1lwZm+ZNm+ksbbPWd3ba0+2Y29ysFts7ZoWF7loAuwPO5h7P1ByVclMrPHDhVcDPqr8HGKFrGsoGJHzdgK27RT7PFbYq/fUl79EBsAFLMS++TDL4POEsmIjhPtqDD78Sy9ZksV9lJhzO2+78y3J3YeNKH+2u+Ei7iejftvuGib9EAF1nc9Gud310N3NRaaR4kzNozYN5/8m5zygDITJ0B5WSD9MokIanbUvnJdvx/wc/V7qXf6Mzi4n/13dhUw8WAaeUPsrgZqHJuWYtxU22leQzNCxCsqvhLsdSBn04M0XDgqOYWcce7JY6rgWb34+r7VFpruDgVS+1LzqW4+Q8N3H/+vGydDQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle A_{0} \\delta\\left(t\\right) + A_{11} e^{- t} \\theta\\left(t\\right) + A_{21} e^{- 2 t} \\theta\\left(t\\right) + A_{22} t e^{- 2 t} \\theta\\left(t\\right)$"
],
"text/plain": [
" -t -2⋅t -2⋅t \n",
"A₀⋅δ(t) + A_{11}⋅ℯ ⋅θ(t) + A_{21}⋅ℯ ⋅θ(t) + A_{22}⋅t⋅ℯ ⋅θ(t)"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = x0 + x1 + x2 + x3\n",
"x"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"For the final solution the four coefficients are determined using the given limit formulas for the coefficients of a partial fraction decomposition"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAU4AAAAVCAYAAAApbQfpAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAHKElEQVR4Ae2c7XEUORCGDeUAzJGBLwNzRABkYMgAkwHU/bL/uSADIAIKZ4AvgjNkYDKwcQZ776ObHrSaXUkzq/nY9XSVrK+WuvuVpiWNZv1gsVjshXR2dnagsr8oV/oyrJ/zMwIzAjMCu4yA/N6h7DtS+KH0z9DWh2GBmN6q7J+q/Cqsj+URpvA9xnPf6mZM2o/4jFl7zDZtMWO+jKDwwFkS3iv9TYHNZE37dUoJVR4req/wSOk7vy4z/VV8eOlJkGzAFuhG4U8FQGisHjD0SJPCJMdOYcQYoveTjvMgR0yMZ+swixmTqpsA3qh4rzDH4BTuqv8htpeKvyn+TFrB0ZLjVMlThZ9ibO001QanOyWnyc73XHpdKN5TzIrxXfELhUGcp+RMChNwWEcVPkyOWwVe03BUGZy2CbNNwJkK3thwXzCvbMUPtJ3nOFCe5ZoaR/W6pn3ihZqYkxrloTOVNRFOlD5Q7PShXGkWA/IfyQ9Ek8EkZS/4KLC6vhHvlxR/j/Vbg9kmGEwIb8y4F5hjaCncizhOKcORmGA7Obz6mMSWmlUipH9V8Fz69q7fBDEJsZhcfsZs+CGZMe+G+caOU8Czu7xRjNPkXSJE2Zj0XMI5coZkjp363miimPRmb4mOZ8xKoNiujxnzdnj53Bs7TnX2TgPwoerUHNMfvpASacm4Vkges8WTs5ssrl9g4yCYBDIb2VzMGg3HKZgxGx73GfOOmIeOE6dzl9uXHkx2btw4GZnj5Aa7GFXOkF0slxYpMqcYsyPHuabkrKwfCpOVwr3Clph5LYdPzpjNmAuBnGd7eKD+l8hJ2vyKK6lv1TV5cUyvFN65mrw/dplg3Oas6KtBkuF/HvRY+SxZ4uPiousnUg09VPB4VWGhsraY4MTB/Y1sfBLqoLJofchv+R4ws677iLMxq/D4u1LC5tlr7DXF7glmZm7XuBjmOWOyTknGTaHks71O1CblXCrzKeOxgrtw3leCyYdDIwbMrF8KiY8P5fng3T8+m1fmYV8i8XHTzbtQd6xXzCUNH5Zyo5ck8dUPRoJ51btNa2L62btYKy8SS8e2mBxJsL1vXYVZtD6ldAvMUl31Vt8WMynCBObm35HSzD8+PXOnHOUHwUxyGC9+KNIYN5WtI56vVZeW6/h7KZcOreaplIhinlEftUP65D7be+IdHHfJ5BPNRzLis2IW7XMcJ4XnyjAZeedxpRA1RPVusihuOD2V8RtO2wkoWRPO+ZnlxHepgOPE+doR36o7x+qLFYz2TsegIysrJs/6l8zWmKgNDxE/6Vr6RszrM1pvfNsad8FMtp6o3VcFW+CZV5QdKYDlIJhJzp3kNk4IUx8L6d16nqYwz6gvBsuIuOMw8Wv4yMuHWKQEE85WcT4OTRErkF0Ihbw4JdvZuTrxIpABCx0Wk48dQmnioVrlvE0ve+hKym2FSUnBW9xXF8yYp1dbbPPYqveB+U6PifwXGxt26c+Udr7DOU5vJFmto45MDTlacjRaRzhDt6p5DGHeqm6VMGdmZSVifj626mUzOwQWCXR0pPQ63YwlGXfEJNnvVBnGxEyyPynU4yeMeGg5NTF3d5JK4A0w6qfLs0u7KOap+h0YFH5RyUm2nneh44zaqIbs4jgmfYow4gz3Kt4Im6vCaSYdl/o6UFgoxBx2LUt86HeruD4CK42cVwqvjbEq+6U4q19r58dqWxoTv/vOaWxTyMYsEGSXZ41FjX7FOwnMpAuLPGNc5Mi8IWYBhK2yveKNJrKtyDxNYZ6qD1ER/ybzNOyubX4t7is6cn7NyrMcZ2Ucnx1dK2Aov/lecnjKc+MEj1124GDtFv3OBAYxfYTH94DFDTrt4WtzRONh4nfpHE3YZvMKgq12vTNR2vrFJnTJJvgVNsEkW1YXRs+2bMzUhjFjt85FHuTyKrP8ntKTwEx64AiYX8X+EYlnWzZmgNSVJK9XvNFLMorNU/UVxTxVvwontbH5NAjmFSZJ3FfpulTG/+O0cHp6+l7h2vIlY/X7S+HI71P5hcKhXzZGWjocKxyMIRuZlfy1uKfqx9B7TMwk+1Dho9ld5ZfmUaXfWkyt7bbElT1jztEo5tUYRMdkW7AO9ZRtDb+4v+RF+82cq3t2o27Hp5WG9IXi5I6zX7Vc70+lx8UAcnZJxCiYaZzY9fAJErebHNUh3nNmfRPsuLfzzyh4A1UK81T9dsId1zp0nDdib7zXineRVytwPyhwbOZ4hRy+u6vfN+b1Up5L+nBER5/BSbJxAjz0LCJ8luWwUWzfukbrB1e4EjgmZlKB99GMGXFN0gkc9xRPErNa0Q6JkfFG4yjmGfUdrJ5UE+YbrxR+k78trbbbC8XHfvkup2Xr2122rw/bZsx+v97qA9+wzxnvYfH28Rf2Bwq8Zjzxyx+Q8alasTn2sPP8ovx8hPUBmtMzAjMCO4+Ad3LhBNPwg/8B5C44AwlFvAIAAAAASUVORK5CYII=\n",
"text/latex": [
"$\\displaystyle \\left\\{ A_{0} : 0, \\ A_{11} : 1, \\ A_{21} : -1, \\ A_{22} : -1\\right\\}$"
],
"text/plain": [
"{A₀: 0, A_{11}: 1, A_{21}: -1, A_{22}: -1}"
]
},
"execution_count": 8,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"coeffs = {A0: sym.limit(X, s, sym.oo)}\n",
"coeffs.update({A11: sym.limit(X*(s+1), s, -1)})\n",
"coeffs.update({A21: sym.limit(sym.diff(X*(s+2)**2, s), s, -2)})\n",
"coeffs.update({A22: sym.limit(X*(s+2)**2, s, -2)})\n",
"coeffs"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Substitution into the inverse Laplace transform yields the final solution $x(t) = \\mathcal{L}^{-1}\\{ X(s) \\}$"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAASEAAAAYCAYAAAC1H0vKAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGqUlEQVR4Ae2c7ZHVNhSGLztbAAkdQAckqSDQAZAKWDoIs//2H0M6gA4Y6ACogIQOQgdhtoPN++hKHl3ZlmVbtuxFmtHq6xx9vEc6Pjr23Ts3NzeHPYarq6u7mvelnft9mz5X/bW/HpX/Ufmp0m9+fc0vi0DFfVl8Xe/Ceffn4NwtZofpawnghZu38m+UR+E88OoQ0EO1VQXkQFkhtQej4r4C1hpi9+fgbB2cFhnlQpv9kdfza+Xvq+6hV0f7V69cs+sgUHFfB2dG2f052LMSwgr6u0vWUkQoI5QS8UBe0VdOXWyT69S3uw5G+0ili3ay4UbWp7g47qk4ptJtGNKUqW3iHKRi3UW32+uYFvM2kBDC+KZ6Z/m8VJ4n8iulHwLabEX1/Sfj2jjUL4f0ieJfQ4R7bNe6wGFR3CvepztDeBQ/B3NlsmdLqJGGQMDKeaL4S1N5zFD/KajrLAKkIhZTstUkWsa8pzRJyYnOzEXpReckbk9lEu7CYRTmoq94R/aI8Fn9HOSQyZ1cb8c0GZzAOIYfKz/KEWzBM1enCMY0vQj7VpmrEE5p3oA1b8aUxwp6r/QnpdEgmo8igPatolmH0sbB3cVs6T4rDRWfIXf9qNDCQ23g9LvSZr5dY5Su0/zY1KPkIp4k3EU3CnPRI5eK93FTbOIc5JJJzusYmw+F8P2IU/pfLYYr1ON0jiOl+BgP89/w2vJBKUqweRqrzAbmKuSuascO9Fd1zm9kzFqVrxWh5e1Oi75hPB5OlF9fiOEBH+M2b/f6Oumr19xM/0pDc7yPZXS9Xf9YuQzirn6nYA5PMbxHgzeBYSLeB/GVOgdZZHI2Aas+FjYrPplVnu4WeDblG+VRGGz+l4pOCWLJfFEkXCq2rDPLg0/HHAoIvYBgY+GZ+GMKoBcPywc/ynFqgHcO/9Rxh/iiuM/AvDTeQ+su0i482aelzkEWmeRUQjyZk3wjmaTFlYYxSV28kFCcEkQwD1TG//LOq1exCUY5qa3xGynvDvbPDVWQEQ2+iZZSC8iG8ID/WcBzG4pDuI/GvOId3RZFzkFOmZxHlzfQqIlw0LhScHDRyFgk75V+Udq8AVKedjbff4oEnpZco5zCMJVj/og36utRO1ep3uuOnRPKBOvJD7/aQkzJYOU0issxq88kPCw9/PQTs6Zc14ukFoPccunFfQbmFe+eHSBMS52DbDKZq4Q4SJ8EBIf5kVImdhJUx8Hk6Yjj2PhYlHJ1YvOHCkBVqwX3hipUJsyNEFNCKCrWdBK0rkE8PIZ/lQebIqGQXKZiXvFebpcUl8ksJeThgvIxCsarO2ijYx3xFgRvvt/O4aO+ZPjDDn6pufnzQKHinI4pISy77z5TkO/EI6CBH3xWDwXlMhXzivdyu6S4TM61IRHwZ0XS1NBYNZYBpdLlD3LWwl2NgwOYcE/xo8qhBWIaV/yDxYMV99SNabFACb1ydT0p/qLrnjaq+/DwWVByg5hrTmBIf2FgDge1d105v6q+WVfIqHIpuUzFfDW8LaY5zoQPeym8/Tn05YvLBCXEYer81qVv1n69+BGYs3j8JvLmMIqm8Q+FBCXKds4MHVpjzlE82U8zgIe/3KGDZWjVX5eSOageZcmnBFOwXV0umqdTuFkxt/327b/ReMOgPmedCX9Qm18d7445tKq2IpOz1szGV5intBbUWDbe4ujNvSYf3/PyHP4VkdHwUfHBIpswFrhKuUMV0g3h4ejhj13pHN1SaSm5TMG84r3ULjj2W1QmOZTQif9DB9g8oS1mXDm4frWCpWvVr1HRpWTsfLBOUERDgXXx9O0KMTx8esaK+Z182tz51eUyE/OKd+4doP62IpPzDGtrDpMWxdOdK4LzD/ER4Ml1wtJQ3/WBYIbpJHfBHI01480p9acUPDl+6xkphofPwhU4fAL57UvmS8llKuYV7+V2Q3GZ5FBCWA58tWxe9SltfBTKm99iKWXT80qagJP6RDEdq1f/+1wj8mNVLBq+W2r9xisyo3dq43uortCLR0DMta0IDgXlMhXzineweTIWi8sk2w9YM4Kyi650kFGq4VvCpLlbxccbQpTfpCDeOY7pSWOWZCqNd8m1b3XsXDLJ4RPaKkZLz6t1pRkxINYS/HPCtZiJP0oojfePgvOYdWaRSbWExkAe0OpJ4D7ETHYwi4frH9dXHNg1jECg4j0CrJVIc8ikWkLzhMUHge5DtNSeoC/iC0qd4IbpKt7bE85smVRLaKZQrWWT9C9bRctX4x+UJltOM6d369gr3tsT6VyZ/A+ZCWtlZdqGzQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle - t e^{- 2 t} \\theta\\left(t\\right) + e^{- t} \\theta\\left(t\\right) - e^{- 2 t} \\theta\\left(t\\right)$"
],
"text/plain": [
" -2⋅t -t -2⋅t \n",
"- t⋅ℯ ⋅θ(t) + ℯ ⋅θ(t) - ℯ ⋅θ(t)"
]
},
"execution_count": 9,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = x.subs(coeffs)\n",
"x"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The solution is plotted for illustration"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDQ1NS4xODU5Mzc1IDM0My42NTkyNSBdIC9QYXJlbnQgMiAwIFIgL1Jlc291cmNlcyA4IDAgUgovVHlwZSAvUGFnZSA+PgplbmRvYmoKOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDExIDAgUiA+PgpzdHJlYW0KeJyNmMtuHDcQRff9FVzKi1AssvhaxkgsIDs7ArLJzrGdGB4Djo04n59TPc2ZnhGlSIBsdd26LD7qRYr7uIj74IL7yO93J+6O3w9L4OuwaM5eWu6p8vlp/5k0+ZJ7zIjDxdefy/J+uf2RQb5Culuqjy4mX1MDZkgtPvDXSfTpJEqxet1GMdb+exs1Hkf9wByZr2/MGBsmWUryKkmgVZ81VTN2lqkPq+zTsrxkwd+Xl/fu9pU4Ce7+/VKCj4lF2D/Vxeh7dvd/LDfhhbv/6H6+X1ZTi6TsuxapbW9kL33ajKToaynag7SyMxMvzcTQvNYeU9mb2UufNhND9rH3rC2kGnd29MpOEx8kxp4u7Oyk/2OnVt9SLCG31nRnp1zaSTkxek5Z9nb20qftpBx8KrmUVFPfH0+7tKMRP6pNQ9/b2UuftqPSfZUeErpon+3IyQ8u9ZXxioaCh3Yfa5N41P92Oa+ZZ+bu+6XskbWrF63atZlnJoJGS6ubd/oQHrHUxffUatlbOsmeY6k1vqS1HHocxuIjxoT4TSnVurd2Fj7HnGj0OZXWs7TUh0F9xGAMwdfYCLidwbPwWQZ7YTc47BxrPhksjxm0xBdT7RcGT8LnGIxZPLHShWUyx81ge8xTQvdsxcUCT7JneQo5oEYheZJBh7mzH38haYv7QcicsbHunko/8qRtOfftgfGtDvijhzPE7au4Gbv510ZaSHxS++qQ4agwZnPz+82qkTzJjhXLTuc0yLehQm7rbY2CB8O8WHWY8uvli7uoJZqat/9TSLZU9/c795v77MRnqwocjeTSSrRBvZbtp7LT1RJWTDl29+bO3f707p+/3r57c/fSvf1KTmMXKWWXqQrnjDnY9uyi9deZHOVG8m1YulZ+KLdqSN1sOV3pPhTjB8Fbsuz9SnciR7l4ZUvD9SQm8rVKVpW6VpuSU1U9Kk/kKFefQoxJHYZLLFXjpj0BDku12fVIGarZk4qJ8aP6DEC9+Jxx2+SsqlIoUxj6M+SwNOXsc4TMcftCfehH/RlwWMiBtVGxkmOClFNif9uZKQKhEzXBylsiv0SJGrfdmSJ0AwSeklRoBoRq35n0UX8GoC74q/YmJk7rNm8TmiJGKNZtVDvvwJbXPnZoikAgYFohDbjYI6efa9lWMEWsn+FoWqscfKwJpy0SxhqmkFGqDwSNdTWZoBDVMakZAgEPj3Qn1cp586XzM9Y9haBki2lyFCdEJiR++dooU8gouDuuiM+0bi2R5jIYEwSCJeCUGnOU0shLuchGmCFGMHNsAhWFfkYjPdHY3SkEpSp9RWQoPLmbp4UwZjWFoDQaoKqBYBESFBmnp7H0KWQUcjOpN2dnfpEwH+qgzCAohACtYyDMJdipBQrBRplCRrHWdw1FwkEzxevEmCDWxAo70Uta25FcW5Btg6eIEYh75kcUMO3AOUkfhAkCgeBKuUlytRE/8ZSfZoCpU1MIy5AdDl3Zw6H9QI5yFN+kWkrkcEuTrEN9hhihU/SjFW38p9fQhndMEQjJuqZsa89W7bvdtY6EGQLBetBE2CdHO8ItpPXNM6YIBHyRQUJqjo6kaKW4b4QZYgQSHdVZnXYrHl3HAUwA1AuHgdFGga7UD/Lcpj4BUK+RLqgL/Y3iMRzP8OwpYoRuDQmtjmOBjMefgzBB7D4DO2vguLmlsoX1tIAZAgH/a+QR3EktLYZRsmaAqVt1zOYhSg3Jqn1s6AyhQaBf6djSVUwFKSMhTxEIYj0Y3sJOk38FjW1GU8QIhYJUKe8m5vJjGWUjTBBrcDjw1ovS9nSrmzriYIoYofgSCNdiYiUfyKknmiAQ7OpCHxtXsXDBGrllikBQy+mkWVoV+jxaUt0yxRQxAgHSrYiZuOTQhmNPEbuARksbYktr1lGwkxthhhih2fU9ErOIE3vZxy7NEAiFPk4yfBNHociMc5ghEKp4aVTjdaaEYslj0TPECMXTqpSyzjRwG8ljSjPEulNutWxYWm+ehGwIw8IMMQLzU+vekZJC6skzJgDqnRLG+a9CNj4PT30op/u1KxuHEdb3FJwgx+3IpogRWAru3tdxuAqP0JwBqItSSYoce+7KLWoc2BQ5HF8AaNGP/XHpZJM0CBPkcPXkAC5li4PX7ouL7pfjw9r6UHV50TjfLc9vY+fr3+7li7FOr2nra9fDJ7TD9Alt+Xx6MBsPZcdntf31Y6NdXBKuzF0+xT1q6/XyH/OuAQ4KZW5kc3RyZWFtCmVuZG9iagoxMSAwIG9iagoxNjY3CmVuZG9iagoxNiAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE3OCA+PgpzdHJlYW0KeJw9kEsSAyEIRPeeoo8gP9HzJJXV5P7bNM6YhfYTKGywpegYzsvVkF3xllYYnvg27wueiaup9YckFTL7pg4Zi2fyFCckFK8mY0DcsdXWo3Eywgy7LCZmYK6Kr0QuqFAC6lHyamaj4Gqmgr59xFaZ9RYXCEUCJixnK/6fA9PrFh0MFpjtN8uzPPYK03QszHuGeQ9FI34G5VpuYGWtg5+GHZr3tmgo/+QnexZ4tc8P3qtCoQplbmRzdHJlYW0KZW5kb2JqCjE3IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggOTIgPj4Kc3RyZWFtCnicPYyxDcAwCAR7pvgFImGMbdgnSuXs3+YtJ2ng9A/X0qA4rHF2VTQfOIt8eEv1hI3ElKaVR1Oc3doWDiuDFLvYFhZeYRGk8mqY8XlT1cCSUpTlzfp/dz3Hqxu6CmVuZHN0cmVhbQplbmRvYmoKMTQgMCBvYmoKPDwgL0Jhc2VGb250IC9EZWphVnVTYW5zLU9ibGlxdWUgL0NoYXJQcm9jcyAxNSAwIFIKL0VuY29kaW5nIDw8IC9EaWZmZXJlbmNlcyBbIDExNiAvdCAxMjAgL3ggXSAvVHlwZSAvRW5jb2RpbmcgPj4gL0ZpcnN0Q2hhciAwCi9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnREZXNjcmlwdG9yIDEzIDAgUgovRm9udE1hdHJpeCBbIDAuMDAxIDAgMCAwLjAwMSAwIDAgXSAvTGFzdENoYXIgMjU1IC9OYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL1N1YnR5cGUgL1R5cGUzIC9UeXBlIC9Gb250IC9XaWR0aHMgMTIgMCBSID4+CmVuZG9iagoxMyAwIG9iago8PCAvQXNjZW50IDkyOSAvQ2FwSGVpZ2h0IDAgL0Rlc2NlbnQgLTIzNiAvRmxhZ3MgOTYKL0ZvbnRCQm94IFsgLTEwMTYgLTM1MSAxNjYwIDEwNjggXSAvRm9udE5hbWUgL0RlamFWdVNhbnMtT2JsaXF1ZQovSXRhbGljQW5nbGUgMCAvTWF4V2lkdGggMTM1MCAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTIgMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM1MCA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDI4IDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxNyA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjE3IDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDgKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk5NSA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMTUgMCBvYmoKPDwgL3QgMTYgMCBSIC94IDE3IDAgUiA+PgplbmRvYmoKMjIgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAzOTIgPj4Kc3RyZWFtCnicPVJLbgUxCNvPKbhApfBNcp6p3u7df1ubzFSqCi8DtjGUlwypJT/qkogzTH71cl3iUfK9bGpn5iHuLjam+FhyX7qG2HLRmmKxTxzJL8i0VFihVt2jQ/GFKBMPAC3ggQXhvhz/8ReowdewhXLDe2QCYErUbkDGQ9EZSFlBEWH7kRXopFCvbOHvKCBX1KyFoXRiiA2WACm+qw2JmKjZoIeElZKqHdLxjKTwW8FdiWFQW1vbBHhm0BDZ3pGNETPt0RlxWRFrPz3po1EytVEZD01nfPHdMlLz0RXopNLI3cpDZ89CJ2Ak5kmY53Aj4Z7bQQsx9HGvlk9s95gpVpHwBTvKAQO9/d6Sjc974CyMXNvsTCfw0WmnHBOtvh5i/YM/bEubXMcrh0UUqLwoCH7XQRNxfFjF92SjRHe0AdYjE9VoJRAMEsLO7TDyeMZ52d4VtOb0RGijRB7UjhE9KLLF5ZwVsKf8rM2xHJ4PJntvtI+UzMyohBXUdnqots9jHdR3nvv6/AEuAKEZCmVuZHN0cmVhbQplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA5MCA+PgpzdHJlYW0KeJxNjUESwCAIA++8Ik9QRND/dHrS/1+r1A69wE4CiRZFgvQ1aksw7rgyFWtQKZiUl8BVMFwL2u6iyv4ySUydhtN7twODsvFxg9JJ+/ZxegCr/XoG3Q/SHCJYCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4MCA+PgpzdHJlYW0KeJxFjLsNwDAIRHumYAR+JmafKJWzfxsgStxwT7p7uDoSMlPeYYaHBJ4MLIZT8QaZo2A1uEZSjZ3so7BuX3WB5npTq/X3BypPdnZxPc3LGfQKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0NyA+PgpzdHJlYW0KeJw9T7kNAzEM6z0FFzjAeixb81yQ6rJ/G8pGUggiQPGRZUfHClxiApOOORIvaT/4aRqBWAY1R/SEimFY4G6SAg+DLEpXni1eDJHaQl1I+NYQ3q1MZKI8rxE7cCcXowc+VBtZHnpAO0QVWa5Jw1jVVl1qnbACHLLOwnU9zKoE5dEnaykfUFRCvXT/n3va+wsAby/rCmVuZHN0cmVhbQplbmRvYmoKMjYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDkgPj4Kc3RyZWFtCnicNY9LDgMhDEP3OYUvMFJ+hHAeqq6m9982YVoJCQvbL8EWg5GMS0xg7Jhj4SVUT60+JCOPukk5EKlQNwRPaEwMM2zSJfDKdN8ynlu8nFbqgk5I5OmsNhqijGZew9FTzgqb/svcJGplRpkDMutUtxOysmAF5gW1PPcz7qhc6ISHncqw6E4xotxmRhp+/9v0/gJ7MjBjCmVuZHN0cmVhbQplbmRvYmoKMjcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA0OSA+PgpzdHJlYW0KeJwzNrRQMFAwNDAHkkaGQJaRiUKKIRdIAMTM5YIJ5oBZBkAaojgHriaHKw0AxugNJgplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzE3ID4+CnN0cmVhbQp4nDVSS3JDMQjbv1Nwgc6Yv32edLJq7r+thCcrsC1AQi4vWdJLftQl26XD5Fcf9yWxQj6P7ZrMUsX3FrMUzy2vR88Rty0KBFETPfgyJxUi1M/U6Dp4YZc+A68QTikWeAeTAAav4V94lE6DwDsbMt4Rk5EaECTBmkuLTUiUPUn8K+X1pJU0dH4mK3P5e3KpFGqjyQgVIFi52AekKykeJBM9iUiycr03VojekFeSx2clJhkQ3SaxTbTA49yVtISZmEIF5liA1XSzuvocTFjjsITxKmEW1YNNnjWphGa0jmNkw3j3wkyJhYbDElCbfZUJqpeP09wJI6ZHTXbtwrJbNu8hRKP5MyyUwccoJAGHTmMkCtKwgBGBOb2wir3mCzkWwIhlnZosDG1oJbt6joXA0JyzpWHG157X8/4HRVt7owplbmRzdHJlYW0KZW5kb2JqCjI5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMTMxID4+CnN0cmVhbQp4nEWPyw0EIQxD71ThEvIZPqmH1Z7Y/q/rMJpBQvhBIjvxMAis8/I20MXw0aLDN/421atjlSwfunpSVg/pkIe88hVQaTBRxIVZTB1DYc6YysiWMrcb4bZNg6xslVStg3Y8Bg+2p2WrCH6pbWHqLPEMwlVeuMcNP5BLrXe9Vb5/QlMwlwplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjMxIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMSAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gNTIgL2ZvdXIgNTQgL3NpeAo1NiAvZWlnaHQgMTE2IC90IF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAxOSAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOCAwIFIgPj4KZW5kb2JqCjE5IDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTggMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjEgMCBvYmoKPDwgL2VpZ2h0IDIyIDAgUiAvZm91ciAyMyAwIFIgL29uZSAyNCAwIFIgL3BhcmVubGVmdCAyNSAwIFIKL3BhcmVucmlnaHQgMjYgMCBSIC9wZXJpb2QgMjcgMCBSIC9zaXggMjggMCBSIC90IDI5IDAgUiAvdHdvIDMwIDAgUgovemVybyAzMSAwIFIgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDIwIDAgUiAvRjIgMTQgMCBSID4+CmVuZG9iago0IDAgb2JqCjw8IC9BMSA8PCAvQ0EgMCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+Ci9BMiA8PCAvQ0EgMSAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+ID4+CmVuZG9iago1IDAgb2JqCjw8ID4+CmVuZG9iago2IDAgb2JqCjw8ID4+CmVuZG9iago3IDAgb2JqCjw8ID4+CmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iagozMiAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMjEwNDI3MTYzMzIyKzAyJzAwJykKL0NyZWF0b3IgKE1hdHBsb3RsaWIgdjMuMy40LCBodHRwczovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKE1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgdjMuMy40KSA+PgplbmRvYmoKeHJlZgowIDMzCjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDA4NzQ0IDAwMDAwIG4gCjAwMDAwMDg1MzkgMDAwMDAgbiAKMDAwMDAwODU4MiAwMDAwMCBuIAowMDAwMDA4NjgxIDAwMDAwIG4gCjAwMDAwMDg3MDIgMDAwMDAgbiAKMDAwMDAwODcyMyAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDAzOTkgMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDAyMTQxIDAwMDAwIG4gCjAwMDAwMDMxMDggMDAwMDAgbiAKMDAwMDAwMjkwMCAwMDAwMCBuIAowMDAwMDAyNTc3IDAwMDAwIG4gCjAwMDAwMDQxNjEgMDAwMDAgbiAKMDAwMDAwMjE2MiAwMDAwMCBuIAowMDAwMDAyNDEzIDAwMDAwIG4gCjAwMDAwMDczMjYgMDAwMDAgbiAKMDAwMDAwNzEyNiAwMDAwMCBuIAowMDAwMDA2NzQzIDAwMDAwIG4gCjAwMDAwMDgzNzkgMDAwMDAgbiAKMDAwMDAwNDIwMyAwMDAwMCBuIAowMDAwMDA0NjY4IDAwMDAwIG4gCjAwMDAwMDQ4MzAgMDAwMDAgbiAKMDAwMDAwNDk4MiAwMDAwMCBuIAowMDAwMDA1MjAyIDAwMDAwIG4gCjAwMDAwMDU0MjQgMDAwMDAgbiAKMDAwMDAwNTU0NSAwMDAwMCBuIAowMDAwMDA1OTM1IDAwMDAwIG4gCjAwMDAwMDYxMzkgMDAwMDAgbiAKMDAwMDAwNjQ2MCAwMDAwMCBuIAowMDAwMDA4ODA0IDAwMDAwIG4gCnRyYWlsZXIKPDwgL0luZm8gMzIgMCBSIC9Sb290IDEgMCBSIC9TaXplIDMzID4+CnN0YXJ0eHJlZgo4OTYxCiUlRU9GCg==\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sym.plot(x, (t, -1, 10), ylabel=r'$x(t)$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* Derive the inverse Laplace transform of $X(s)$ by manual calculation."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Classification of Poles\n",
"\n",
"Above procedure allows to compute the inverse Laplace transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ of a rational Laplace transform $X(s)$ in a systematic way. It is well suited for an algorithmic realization. However, for manual calculus it may be more efficient to classify the poles with respect to their location in the $s$-plane and their symmetries. The classification can then be used to formulate a modified partial fraction decomposition which limits the need for later algebraic simplification of the inverse Laplace transform. Three classes of poles are typically considered\n",
"\n",
"| Type | Pole-Zero Diagramm | $X(s)$ | $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\} \\qquad \\qquad$ |\n",
"|---|:---:|:---:|:---:|\n",
"| Single complex pole | 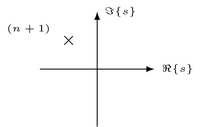 | $\\frac{n!}{(s + s_0)^{n+1}}$ | $t^n e^{-s_0 t} \\epsilon(t)$ |\n",
"| Conjugated imaginary poles | 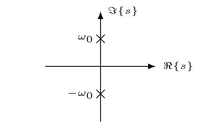 | $\\frac{A s + B}{s^2 + \\omega_0^2}$ | $\\begin{cases} \\sin(\\omega_0 t) \\epsilon(t) \\\\ \\cos(\\omega_0 t) \\epsilon(t) \\end{cases}$ |\n",
"| Conjugated complex poles | 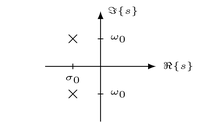 | $\\frac{A s + B}{(s + \\sigma_0)^2 + \\omega_0^2}$ | $\\begin{cases} e^{-\\sigma_0 t} \\sin(\\omega_0 t) \\epsilon(t) \\\\ e^{-\\sigma_0 t} \\cos(\\omega_0 t) \\epsilon(t) \\end{cases}$ |\n",
"\n",
"where $s_0 \\in \\mathbb{C}$ and $\\omega_0, \\sigma_0 \\in \\mathbb{R}$. The expansion coefficients $A, B \\in \\mathbb{R}$ can be derived by comparison of coefficients. Whether $x(t)$ contains a sine or cosine depends on the coefficient $A$. If $A \\neq 0$ then $x(t)$ contains a cosine (cf. [table of selected transforms](table_theorems_transforms.ipynb#Selected-Transforms))."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Example - Inverse transform of a rational Laplace transform with symmetric poles\n",
"\n",
"The inverse transform $x(t) = \\mathcal{L}^{-1} \\{ X(s) \\}$ of \n",
"\n",
"\\begin{equation}\n",
"X(s) = \\frac{2 s^2 + 14 s + 124}{s^3 + 8 s^2 + 46 s + 68} \\qquad \\text{for } \\Re \\{s \\} > -2\n",
"\\end{equation}\n",
"\n",
"is computed. First the function $X(s)$ is defined in `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAALAAAAAwCAYAAACxB/CGAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAJc0lEQVR4Ae2c7XXUOBSGJzlbAJutYEMHECog2wFsKkjogD35lfzjQAdABSx0AFtBFjqArYCQDrLvo0hGtmVL8seMPeN7jkayvvzeD11de2zv3d7erqZKl5eX94Tt3OI7tPmp6m+minnBtV4J/LLe02Wf7aWM9ZkbpfJrlT8r3Xd1S77bEtifOPtnMtpjD+NLlQ9V98CrW4o7LIGpGzDe998d1s/CekQCe0PHwPKOxKp/2fMeKb/mWPVfbF3nTHPggZ8o31gIoXPj/d8rPVQ5Govb/s+UF6FQZwGsYWCMP7V30u9Ychg0BrbMvVb+h5O1yhjdZ+qUPrn63FxjMZwnSg9zx/btr3NzMflWicXIokSJqYSx9168qSfr0i+VP/WD7676HUUO+10YbhmDsZY8jZjGG+OpYKATWcExd5LXazqJ5jlWOmtqb6rXmBulp0rw9q6pX7Ve/Z9X68Y61rk68QYejU3lr5N+x5TD0AbMBddXAcZj+YTnvaf6Q78ypWzHEILgwRE0F3HZ89hzgauKLQVGdh9hZMdg4ZLWQevgLVu/Y8thaAPGUL8JdJPSEHIyWUPl1hnb1gMrDDw6W/nU6UR430wdZCa+LvodVQ5Dx8BPGwRibntJobVYUHVsS9/tOC7O8LZuAXDPF6MnL0jtpTClaJhIQfgIHVh4UYrwHx2/zg7CmqXfHDl05WNQAw6BEBMYL1u+uzNRdFPbR+qVG8NWzhZVxFk6/rXoPJOCMMMroc63GGT1aeU/Nn4K7eIhqN8cOfThY+gQIoSFi7cPYuiV32gZ5MLD98oYecnb+mNmUuaWWTR02CL+g/qVrpLk0Feno3pgKYltlJi4aetZqQ0vhBA+qVzcfuvDmObhvHjzKh1QofZQCPJF9Y04qxOFjjWeOxxJoYMbrzFZ/Kv/RnhzeP3cYqnpt4sc/HlzyqMZsGXiQHnQKFUP43hl4kVjbBwr1UKNHIboqzlCBko995G5i1HaDXLnD/XXnIQO3GmJhg6Mp59SNv8as3beGvhlsdb0K3xZcgjNnVM3igGLCQzlvvLCo1nGVsoLBauMsRIDY8CUn6v8QsldxKlqNoTiHgl79X63iRFtPUZbLFBbnh3/wt2oX8kgWw59NDy4AYs5FIYiC0VZgDBtYkO1caFW/CWsY27PEEJM99lOy0RT5niotqv+h+XNX8yz5V/8tOpX7Tgo9FmikBxKHToeDGrAAsnqc/FsNRbkgs1t3XjcUrvajIErn7r3/c3Kmng6BSu3AUk+TZn/Rv4y9Ovz6sohObi2zvmgBiwUXJBgxKG/a/27Dafqg0HTzymXW0/B+E59Nk7C5kIDjA96rzq8zUfltbsOqmOBIgsIXhl/pZxFPDn+LT6DlR9RiL9U/d7NoF/N2yaHol/XwuBPo3UFso5xEiZefpSLuHXgbzvHNvPWxvd+W+MWtt2IJ9I20jbz1qivnfLAjVJYGmYrgV3zwLNV1AI8LIHFgMNyWWpnIoHFgGeiqAVmWAKLAYflstTORAKLAc9EUQvMsAT2Li4uZvv3bZilpXaXJLDcRtslbW8hr0sIsYVK3SWWFgPeJW1vIa9ZD/Po//ZDyYCHWa6VKD9S4vld/0EdVc2PxAMPFZ1b5PAGLV/CvJPDZH+zDFhc8BwrD2W753p5m+Ifpdm9fCnMVVq+hFmVyAyOcw34RYUnnh3FG2+EKl4TDHhRHgOsPVCdAPBM4/yxLFbq+B7FxncYcAgPL0oGHzlVPXh9ejcF3D6gUDmGW+3+zsgUJR1nGXBAIDyeWBVcCOdYdSWvyUmEESPk3bQPmSfFMKb8JUyeJ64tJPFJuEMbryaZhaucY9LGPoKoc7dSBu5WHWcZsEOkkxM6nCjxxZzaw9yuXyzX2GP14fnc7Dk0hofhQ6/g87A4YU2WAQcwYNCESzWjUX2UNK4zb9XJNRfybiIMFW/r7zp4qeLdw6aBfeoH4C+KW+eI6rirAfP2MEaHt1spuVeFcmWCoEldCO+C98k2/tjJxA/bNbtLny9h9uGtgGix3KiCVCK1gRGsj/0G1QffBPf7DFDuzF8G7qiO97syIhAIlBc3cfEIcd10pRPyYiiv9CBMR4Q0pfftXENKrrlYFMzR60uYKedK7HMiTE2LlF2CV7Fqxp0496a6peKO6rjmgSUMlPfdcsYKILZCSBjJf0qPVXbbqhPckepdnYrjkzDwtR/CBLzQD5VZTODFoIPhg+qDvGmMIbVjvPBrPJg9XikfdTu2p69lOi+hQ9tiRO6EOTgQQjr0hgz8i1Ed/iT1bZXBz56jlpJwC2tUxyUPrAG8tEc8RYhAWECcAsMrHWOs10q+MonzqP9bae0kTLyq7rwTOMETXEjq28gbwNWO8WIsk/gSpsWD4/DlDVSfcCrQkfqx8NAb3g0DZmGXSHWtMih1HvcgGbcwt+q4MGB1RIHHyn0DwKv5F0pMdq4+fIAE74Cn2thWKwwoiQWE1+EiBh74PnFJeTpO4Q0+WQDkLp1pLPNvglq/LSZczgi4zecWscOJQ3nr9VmpnCIDN3603MOUirtVx6EQglWK5619q0wnx7h9A09iVOPwbBhHlQ6oUDteo0qt3yrTGK5QWTxuLB/Ahlmwozzwl4xPx228dfozRnOOxVtb6ODLKuShWYDI50jJvzuxapOBP6krj8GfnTuKW+eO6rgwYHUmliJswLMaY+NYCS/cizSHM7LSPKrH4Lq+5k7I8Ls/oeYjZsIbf1WCBxMLq242vAkrnpL72CEFq+mO1E54wUFpkd61Fr/MZYj5lLL1qzGD6k7z5eCO6njfMUiuyYmj9lQkNGDlEiq4rUqH0yCLCSXXlKc6FI/hGu/uEKt+FrwJL0ZnvrEmzMSyJqmOCzVCPI7NdYmO0VGbfkqLQOOmIoMobmGFr6iOjQe2ApnNt8qEl1VMwnuXlCSmIZg3W6faUfaceAO3wa68IPFR+8aaGgkzCJmqxP1r5DNVGaTijurYeWC221LMJebZ3t8or3m5qrQ2dMwFJd6o5IF0TNzErTRn2HPkLSRS45H8BvHITkOs7zzySmX6/al06vWdlAwycEd1bN7I0IRmexLDGKszCKy/enXryaR/UfP3iYFXFve5kFx7aDDqwoPZPihwVrw5foQfx0JYAQ8QRnuleuJZQypjwE5vhE6lR1zHkIHm7KU7gMdw2z7YZqOON/pK0RBCgMkp0jbzhrynwp8LITZlA3hF0jbSNvOGvibB3/+FmCP0tkfbJAAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle \\frac{2 s^{2} + 14 s + 124}{s^{3} + 8 s^{2} + 46 s + 68}$"
],
"text/plain": [
" 2 \n",
" 2⋅s + 14⋅s + 124 \n",
"─────────────────────\n",
" 3 2 \n",
"s + 8⋅s + 46⋅s + 68"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"X = (2*s**2 + 14*s + 124)/(s**3 + 8 * s**2 + 46*s + 68)\n",
"X"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The poles of $X(s)$ are derived by computing the roots of the denominator polynomial"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAASsAAAAVCAYAAAAeo8jdAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAGQUlEQVR4Ae2c7XEUORCGjcsBGMgAMgAcwXEZcBeCyeCu/M//XFwGQAQcZICJ4AwZQAbHOQPf84wl1czs7M5+aHZndtVVsjSSptV6u9X6GK0f3N3dHbXp8vLylLwX5pO+bpeX54JAQaAgkBsBfM0TeD4jfCP9o83/uJ1BpT/I+xLyb9rl5fkwEMAONJoGkXdK0KAKTQCBqekQeXVQhjekPxNcNCU6SSkSFL4iekN4SPq2XpYjDU8N/c/Ay5XbT5/J/xbyBong78D7SHg+RL9yCB2weR14qSSxUmm7Wtl+oW3liLqJhvM8yNiIqOsk95Q49qFRvukDfIsOVwdxVDpU/D49Uq69/Ub8mfi9aUJFDWdFzhnhBxWHclRv4f3rfdOV4DrGr+YRsg5K+Dm47KwOUcc42hVBkFWnnQY6aScOZxcV94n0tkncJJ2Es50yXCHLPNtQ9qxy0lbRIaBuQDvXobKvqUedlmMgUdtZpYIBEjqmNBjlTyccoOckXfU8NC8XwddBVXll0s76M9uaXG1l4CMG58ipc4oDPjrvC8piXoamlmbhuUGa1freou7TvjqrlsPzoHVI/1+C2RPid6tiF+rvXIfKkUuPx2uCsM5rAv8dwZ0t6+SgPPSzEGcRB6ahoqDg+Fji8SMwhA4dK+3xMn4kBpJwmysrndKzBYPwYJUCJmLTWFmSF5fAbwfSfWGbEYGiw4xgzmG1NWeFMudtKartGeXOTL1Eve9UuiZubCl7X5xQBfrmKrTaNpNedwuwcY9p2+2pk8hjgmd+nlklPZG2zDpuAT17XEpW6hUdAtg2CKz3RoftbaDGd7sNEG0DIHVUDoL4hdDsuUR95bO+B+Z7R+JB8HxNR6xTuNlhJ8X6b+T5i6B+DDokHWmkC8t58MxR59pL1C867EUpW4Up6/BfUHhURyI5K4xIJ/A7YZvbDo38UzD4ulydaerdUuC1is7P550vTSiTfnkgqnNwFfqBoHOI28Gt9oR2/UIr3hWR9oug29XKPnh2ovmnKrz/kGF5LwWeRYe9SG1eAaynrEM/KnmWnez/hAedlLOisZ/JNcgZIl8v7WVR42VJfmnbUH+JfI3eaxLztof16ilN/TSAUuaOE8iUFRu7A0+duH39SDz33htl2dteAKcO6SVtaivqLurWSe5qwXuNIt4rOqwhAh6OhfqKNZZWKwvKu448VvrSFxkST0KH9Fn78hz3PfEF8ZXOykwNTUC8SnBDmDGmkJdlRQMv99GPiNOdK54nS5tiw/uuUo6I4+CPWLgN1IgNndcXNm07NlSP4emFPPUzT9/OeNVKitiZT4e51HlVvZ0xpemHNj+vv72i8v4mOuxyRkcBW68uuNVeiXhnH3Sok3Ji1C9dH4sACb10BMyLlIMR7Wjc3nROKyrSKkShDpW+0nG3fA76MdALhOiSJc70daeqQVWrwBHJvwsMiw4zoo4t6Sc8v/2FdLXbq5xVrQ2NsJohannZkjQq7zPi9oG6gv3M1tCKjJCna2CuyGWj6s7qcdtXZ6TTkDq35vdFg/x9ByZdlzxd4SVZAm7q1G2MpOPaCRUdzsA+OR22enDG8y16dWxUdBITQ8c06srJA3WvHUTjjs16DtK71KWOTuU/givBVZbsj0NDrgxS582LPIlX5RlYZonazlu5dOD29zXphsxZWlzMxJ9FGeJq+4i0s5yUVsSkq9UwZerUtFcSFhL1ig4XIpStcIw6tHNzx2JHzxsLmAf1fxGDIXnQ/oq4a1bt4LV8Fjw15Mq4O95a2lEEPkvds6KuzlFyReAgceXoWYs/a0lnLIEn2bv7oTMyKGPbEezsh8zIo66iE9XJazieHTQcJ89i7PnIEemEqc/ziHpL37MK/GV1cDqk705Ya51ZCRjvj0KHQZalxqJ1JWSf8UVbc1b3Ioz3L+BoGDrBxmAcr8RFsjYC+6bD0J+1nVUbnyk90/cZZ3U8pQ4MLKtnacVRDQzywOz3TYfaY7HJYDTtM6uZW6MDG9co2OOkThHEvheaKAL7qEP6lD5mTFQtm4jtmGw46vbKaubW6CatTejdcwyj94B/Qv05RFGLDvdE62Himfk1TePMyr5SMR7Keaj6gefOy4h7gkvpRkGgIDASBILv8Qu0PmjG9/wPsPpFYRjrXrIAAAAASUVORK5CYII=\n",
"text/latex": [
"$\\displaystyle \\left\\{ -2 : 1, \\ -3 - 5 i : 1, \\ -3 + 5 i : 1\\right\\}$"
],
"text/plain": [
"{-2: 1, -3 - 5⋅ⅈ: 1, -3 + 5⋅ⅈ: 1}"
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"poles = sym.roots(sym.denom(X))\n",
"poles"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The result is a real-valued pole and a conjugate complex pair of poles. According to above introduced classification of poles, the following ansatz is chosen for the partial fraction decomposition of the Laplace transform\n",
"\n",
"\\begin{equation}\n",
"X_p(s) = \\frac{A}{s + 2} + \\frac{B s + C}{s^2 + 6s + 34}\n",
"\\end{equation}\n",
"\n",
"The coefficients $A, B, C \\in \\mathbb{R}$ are derived by equating coefficients with $X(s)$"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAANYAAAAVCAYAAAA6nxA0AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAHJklEQVR4Ae2b63EUORCAweUAgBCODABHAGQA5wiADI7in/+5uAyACO4gA7gIDsgAMsCQge/7ZiWhmdHMaGYftrntKlnaVqu71epuPXZ9/fz8/FoXTk5OboC7J572h27//vPeAv93CxAXv2GDO5TPtL927XHQRUD0B7h/Av5jt3/ss8Ion8Zo9n17C/wKFgjBZEC9pP2e4maU4DC1aND5iOol5SbtH3lfZfstdEbxzgA9lfeM+tm2hML7KbwfUx4EGe86ssxeZ5Tn0H7u9F34R3RSv+dBEU8iO9MV2Tqc9ntIyX1KZ3wddHP9on6QXQ5AJ2Mhh7/ApfUN7cfU7yF6Q9FHGmgFFpgjylcIcwOsKCf+Msag3GlQBZUM5jTZCTUXdTO31wzUCb5Tf6ROBowMwanHJ+q7lK3qE2XW1OhiUL2i1rEboK3DqOtDytaO+vD29POCckrRAZNf0X5EeQXeZNV1YFAXB+ilzVxPE2VjH2o/W25TuuB66/8JDlJr/YYL12TyoNj6HCc4IMeF2wmEOZl9zU4l0EmEre2cK/az/+q0LZ2Yi7uDTq6jbBzgf4OinZR7n/aflBRUCuRz3PV14q0Ft7IWgHZxd8r1cu17d6kh3hsJLBRw8SxRsEpsFZDp7uhitRZsi0LjMTA3di5OBxG+rKpL81e9v2Cv7po4DwMg6r1Jhb2je+Sc2r114B/oEP1mkzos4oUu8eTlKSUBeHf3tOunjoHG2oGFMBfmG7XG+RbkbGOxulM4RmZr8l2CDX9ujIrMoWOe2dkgj5l4w+IXszOAxo733YBbLMiB2McEa9J7Qnsq6Z1B9zflMkGzjhW6j+rcvWONEg90eg6NR42YeW4N0BbRjDfLf8j4FOkiEjqPgPHoFdHbrs38vd0KXXRML67WHnuiDfhYBmhmzbfMpQ6LrN59MIxs7sP0DyWKOgEZFbxMqK6NgVyTYLRV1TrCb1c2c6dVf+1zTHGz8F71Flxv/cEXoRtYOsdUlkmMEKSz5XeO6FSlC14alzfgoUwXxAlNAvTS7vT4gEyNrJ7XaOf3Oh971MfHgSEHdlgC6GbNNw3cYAMdnI96b/olLibY2mDR1yYDe8c2a9YZve4hN9mH9neKu3ApYRh8tygJDmKLARr6d0qVUcI4X3pyQRpKkFcVMN4xPu/frRqwelrf5RFQtUwggs/CXsRjMZhOKX6X4ZPyJEA3d76TPBcQeLd55zwWjB0b4v1EyH1ihVnj765shpwYVHdod33MI+ubjCafkfP1vhrnf+2QDwaB52JrA6Vqu4POzO0XwnkgxqiNCkIyDfDQ2SYBOp03lzc5ZkME3q+KuyQ66aDuXO5aPsXXZOCq+ao7/LSljwFzbOo6FvUAr/086lTtsNDOgWb94R1PLqNjodMZq2wxg24T9irp7w8f9D9PVq0Ycb6Um+ANvBfUpwaWSLOu27j3JZ1jdLL0N4tM3XslAedvpKp3LGirAL7ydCFKk67isQaRO9ZYFvb8L0hXdOimd8Ef5uta1O7moxLgpWPcou6t2+jA+s4zSBvfmBqCDmZ31/LS2EtbU1R9zP+HfNuAsq/57utQLjBzch5zvC95EZ/KZh59DMQSaKy4c5X6l+JU+gi53e9e7oB35xRvkkjn4qWC8nHwk7+Q3yVXmJ9/o6Nu1El+sl+/xTx05NvUaW1pN05CvalkZSZ/Kt8Knq7lWLJaf9LLODiHoeCRY89WzEPbeoJLv1hqAkvqADqGRIMAE7Oy2+IQGO1jig2NG8Uj1wm3tmAHgPfXEL4oJocJ+OpjhvQj4HyFnmyRyDXwtJk/xizSSHeREHTUkbtJR73TXYL+dW3mlcJdUb6D9zfkSOcp6TKCR+Vu8lZPTw3uaKU1Pgp9aac7cEQtwNSA8dkxLUZh7Jm4QFvobqOgczHPKWPB2h7U/uTRw5JAnnzwFWcpz8SLxjFFg5YylUHn/ceEdJ8yCepGWWe+kzJyAmQ1awZOud4DUwHnKaVxBuq1bQYPbWSCKz7m0P+A0gQVdSMX2kmAdmc2Q5a7qIlaPRtQPg0f9p6sMMW/jd/Hnuv5v40EZv6Gq/VcHhgbxTF7N44EPhmHtlnK42FOo4LdLBllpxqa2d9RMMbMotNEeRrkX/BNpgw8leG3/0lPETXAGOerQXP++VBla0wdddaRJuhW/b1dLnRuO8hS1xK4y6b7W6CVbpHNogD4aDcdU7nR9tpq1ndB0CcIuu3EZgpFnvo7D8GrzSk4/b4HgbYVN1WB1eN0RRBM2GB3MeLiXhHNL07Nvc3m274UWAfz2VypEd4r9kE1b8n2NptnryJ1N7C+QeW2d+WBgHIbdz57qLTA3maVhuqT6WutBN4NLO8KXhQ9Ql11eMo8Bl+mrvrktqT/3mYzDRuSUe8XS607ljwh9MLpg4M7l/+TMutizpg97C3wy1sgxImPdcZLL07+A39B5VnZTpsrAAAAAElFTkSuQmCC\n",
"text/latex": [
"$\\displaystyle \\left\\{ A : 4, \\ B : -2, \\ C : -6\\right\\}$"
],
"text/plain": [
"{A: 4, B: -2, C: -6}"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"A, B, C = sym.symbols('A B C', real=True)\n",
"\n",
"Xp = A / (s+2) + (B*s + C)/(s**2 + 6*s + 34)\n",
"coeffs = sym.solve(sym.Eq(X, Xp), (A, B, C))\n",
"coeffs"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Introducing the coefficients into $X_p(s)$ yields"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAALsAAAAtCAYAAAD2rxo0AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAIWUlEQVR4Ae2d/3UUNxDH134uwFCC6QBMBXE6gLgCoAPy8pf9Xx50AKmAQAeQCgjuADoIuAPn+5ElIe3t7u3tSbe6teY9WdrRr5nRaDTa1ckHNzc3TYlweXl5Irp+t7SdKv7Os/BXFldsJBpftYh7tw90t2ie7VGyeqjOXyh+kZKIo5SNpWpLTKLobxT/6tpUGgX6Ak7hk8OXFIsu6H6vwKQ0NCrmmfBAocI4CSCv5EbtcFzfOy+FYkezWkqDlb9WQBClArRhxcPJeCzct1IJLo0uye5lLppKVfYzMfxVjKMoIaBEx8JjQYsC0fREBLH8vg0JE56VyK9QYV5NxxKQnJAfBo2QHEpVdpT6m5jvY7o9CZILZkKDrETXAzRPaPLOVTmX/CJjkVICpfrsT3uYZOY3EsiKPyccrs9/th7+MX5z32SxxZJGbKKZoNB4rgAt0PFeuNCtEapCWwKSEe7LmzY+5XORyt7FoFUi3Bf3hsYXU95H8IrNJFCMG7Ti9/sKeRJutTlV/55GpX8oPFP4kKfb/W9VsmFcWRWz7m1KdWO6RpDN3wcJ5HWYaQV1pji09ijbl7BczrT6dor+UOn2Mvy3+v4rKJOTlH1tm9eMbbkl5yWLZbcD+4+odUowhvCnqhcqrK8jPMsbLkKfe9MoD+vOhPik9NoNocpAWzIa1RbQZZmYdM8VcHOqOyMhhKBxQDZZ3RfXXy5lv1YHj1wn28RWGPf7FFh4JgHWHp8P96XhWcG7EuDaoPyUNLIE0wVt9gFLdYVAApIZMuHtWpeRCEqmSWZR9jSkGaXldd4DCcNbdCugJhSQ0ig2PjvKTvql0n8qDCmfiiUFrPaQQu9kQJNylL8x5PVY49T+dsIm/8TiMWaDhmssmcUquxiEYQTRZpQJYPw75bEJfaLYfJ1UjMLhxsxxBoKluD1oQpkVDstfXRikEYAbrwBlksL/UIJx9EauXWbKc5HKLiaZ8c7/bvtzbEbdJhVLHuUrz0wGxbu06o36Y/PMAL1SMBNU8bHo+03hmUKF8RJAboSkcFDiQTApyVdx2ecSXCnf7AcUY/1ReBTbCQcrmn1nr/46QX2z2jha7iuNO9W58e5s4A4jJScMF+POmAK8rv0svDNuBjn1T5HKPpWZWq9KYEgCh0OZNa9KYEkSqMq+pNEcyYvcAvY9vN++U1CV/U4Nt2eWPYXbV3jk0hNV2Zc+wpU/L4Gq7F4UNbF0CVRlX/oIV/68BKqye1HUxNIlUN+zL3iE7Uca94Em5JSPXcD32yj6y0e7pJ/po9ZnfDi4uLiY4xzJjCwvp2sp5cEUblSPIxUctJr0ZVL19lJnjqYKbIqQa51lSGBfdab67MvQv8rFCAlUZR8hpFpkGRI42oQNLV98dfvD1jmxMT8mvt6knVq2SmAOCWyk7CKQs9r+pi6lOZLJbyzr1W5zjF7tcyMJbKrsz6Xg4T0onN0Gx6/qZzuzrb6hI4RiLxIVrayIzmCwUvKMERn8JZPyObuf6rJPVuLFrcZWtu6XbafikVer/oqVTZWdQfpXoQiwzPGLJhgyyqKYZ0Jxq41oQ7mh1Sl7ozSvAT8q5naFobtl4CmJQVE/gxNL/ewdiCeMxuBluIebcKUG3yqEFoFB4wexkwZB9bY9aooCYMXDwUOhsv64eQu6OVbLSoiCO3C0u72Qw/tY5bNd9uk7KSCxhVyhntXdGxEQag8rj76iJ81Gyk4FB2qIZZVB2+bKDBSTsDGof/qGhugneMLv4iLRqXRjFBA+wYDo9WmHC2Mr56hOmL+w9LH4IUyBM1UavAx3UzfGEKEBYMlgJj1aN1imQp4/zGJ+bzqoLHm6ntaqaMWK3wtrC+esPJv9LjhXmcj16SpUcQ2yZe/Ypw/HK8quwigxl3IC+L0I2jegNIoOzty6ZZ8bxVldB4hpwamecaGw7ucK0Ay94QZajz9BZQd5+1lyNynRgzUyy6/S0QoFBcJlv+wzBaeic3a5ioa+8zzoB7K8ipRdiMELQpWPomOBUHbTiNJYWLcDVnJn4Ja7UReJruNtZ1SrIys7FP2xAq7NyqZfZZA1K9eujYi6HQ+ib1BnxreUvqSVszHOtH7ourDCPVMcbjZRYt6jOyDNIBG7wIbLW35XMGes/pyij7pIdCRvOUmO2kbGClzRhzV6p8C/z3HujCu7k8s+XWdTYtGMIq3TmSlNp6rDxtRfhhtZdnoQA70XhCov8jfHUqR6rAZMkjbcB6H8aBdtC405atpl9ZiEnReJqp9e3myfUZSRbt+P+mAwMBa4X/dIK+zssk9PyBYJ0VuiXNE53Fzv3kTn2ZWB7xW+5lp7QegWMmrUH9Zs0lFT1eWYqb8wydEhvFOUyDIKn4y3qXSrnvcfHb3EwqMsGAMGhpWVK/2i47d6ZhJHg6fn2UF0zS7XthBEEzrAWzmv6JTxbgwPysQX54w0m092t1wQ6lwGPRYF0DdEW2T1C+HNuH5rZIprYC77VDmsvQnCMVHO7DMKVgSInqJ0RvRgQFcuwxX+xLgxSiC8Ui4IHTuILFPmY0GrAu/9cQWYDE1hvOGucB8kcQi8WQJcnqH9FnX7V3WyXPYZ9rFJujC5GtJFEwah9zJc57OzhKI8HlSRGdL+Yurz506IvrEXiZbE28pbKytnVijcrvYkCMVMGUIpUJJcG8mOFRHjh8GIdFk4VsTXTtm5ZRYEvo4TKNaxa+OoImWA6MMv4xCVY44N7y96Dt8oFcOb6MJ4IGdHL4JkkOBjxZqTactSBqAuA/pZceTTm9zd/ilGrpZt9j3ICR1ug9GHaIPaLpH7WQM2eYOam7ah9veV7iGeSsjLLdfDmZlk2SbsG+wr3aXLOatc/wf51qKcg/MaTwAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle \\frac{- 2 s - 6}{s^{2} + 6 s + 34} + \\frac{4}{s + 2}$"
],
"text/plain": [
" -2⋅s - 6 4 \n",
"───────────── + ─────\n",
" 2 s + 2\n",
"s + 6⋅s + 34 "
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"Xp = Xp.subs(coeffs)\n",
"Xp"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The first fraction belongs to the complex conjugate poles. Applying [completion of the square](https://en.wikipedia.org/wiki/Completing_the_square) to the denominator, its inverse can be identified in the [table of Laplace transforms](table_theorems_transforms.ipynb#Transforms) as exponentially decaying cosine signal. Performing the inverse Laplace transform with `SymPy` yields"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAKcAAAAYCAYAAACfiu1MAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAHbElEQVRoBe2Z7XEUORCGxy4HYHwZQAZgRwBkcEAEBxlA+Z//uSADyICPDIAIXDgDuAjObAa+95HVQtJoNB876x2o7SqtvluvWt2t1uze9fV187vT2dnZXe3hkdKVEuUTpXO1XyoPpPo3VZ4o/xEad4XFSuBgscjGAXut4T+kdO+Ypvylsq9Kd6hDajtUdl/5TjGdRJb/86co53km6r9Ux4vGhGdNPGncuSsvTwL7y4M0HpG84SUpmvm3ynjTRu13lShb/bXq9+n7HQj8c+PcBM8ujEPXKo37I5TTBKMNvlQirnyr3K54rvtXalspEYe+UooV2aYvLhdOwpOWIam91Hao9qGKjMHCe6PUhb9j0RamvTkeRF4oKAB0rMSVuhUlEBZiy49Kn1V+o9yRyrz87ihHSRdPwon3P1Fucg2Y1fZTFfZpRkYZejB0fxqHcq6UOyN2szt+/FhCJei96rbuTUvhV2M68ReGuya/TsC0tnKKIdaKp3psi6rMFcrmH6v8xdqH5BqPV3BXcM/4FxpbfNx4HnhQDosrn3jzo/LwQOrhvdVu4UTZvip/UAKi9u9qP1JiHDL4pMStsFKekOeFLDiLRF6q0/6wNM+YqO+zysjunRLrfVN+z/pLuR9Xw+/4aG4V0xwPIhTpRQxS4PCaz9WGBxulEJqHVQZFj/mWyl4Q/6oPIZtF2yHhxWlD4Z2R+PFcITZWXYsjZPq2ggqDe1Lpj7swTBzIVdzoy6zROj8bpzWck1BuIRJeDdnx1aMmvz78gzDNEXOy0HeBxRpiQhnGxEHx3MFlrYsiIvjYK4CJ9g9KEJZ+4UpNc6o8HuubF5U91b56r9uBiDF04m4z2DDNr8Fa+dk1asOguf2cgoZJN4W+2LYP/yBMB9miU6ooIZbU2rxn1tr4lEV65uBFToXhPz+Oj/Bx/IWHIAzAmxMzdWH107eXCRux2pzGg6Fy7XcRaz1Vyo3BGbHwhLBMZTtLQooiDcQ/CNPayikwXdcLlteoP3H/qrNBNm6KhFcjDJisMH6NZB3xDOT7k9AjdBYKHiMeI8Z0ofZwyNEY4j+IfRCbxYeJDDgI+LBv6JnGFGPJm24X0gQevq2ViQeGBk8eKngyYk4nA+WsyX7ppw/nQYjFHsIjUXWItfBkQTk1hnkYSf4YI0yCasYDrxb+KZjWVk4HNfsREA4FoSSb8wDxYvyFaIJkLMqajFV9KyRc4Oah8I/KThk9bhSP65F4D8wcdhLQq50vBCjCGyUOmG+qHFYg1fuMBAVARjWC9wfxWjFIOZgJrcDzhaQ6OQr2iHblXYRxocwxofhQrmTsG6opZxH/FEwbUU6B5+A+CVCwUpURIC8/rtfYyyEY2pdCYEcJg5dUHWWAnDIot/3lh4SB8ZrlUI+UjlUm7rZ5ahqkeFcM7CLxS5RNdfCyJkodv6QZF8u6xJK1OJuYnvkKoVLcjrLzKMr3HY9BVjX8gzEdaCGY8T80+VAKni+fIH4ICGHl1715Aw6LQBviSsLb5BbqOm/7RziQAd4hGBUY1I6imheln8O8UEpI4/CqtHF1E6pwSD+Vsz8MMDFY1UuEUq9KHT1tKAxekte0KQ+GHxtZiQVj87Nnj3jecIYqMwblPFeqUR/+wZhQTgRRi4FqQJI+8eI6OFKeWLYf5ECpLzn4hMH2K+ZBLB4uIbIxNQXicCHkeqrEoRLDcs3zvbDvatfQMmkuSo6Mu87MKZr6ycHadyslyuTnsXg+j0cTFGLTm+rw37GY9oezro/UwhzAPeWxtWHFdpgwaHmbOtdb7zWPE1+NOQgb45Qg7/R1bg63b+V4UOSypz6U8rnKpryl6XjbGu/jjn6UrBHvS3IRzoB6uJVULvGlrXQNGx/YQIQsGNbK1bp/avhHYZpFOQUYYZf+akNhbeMcKtd4izSfcVsnL3gOBQVoETiV6OeAWreD+pzw1UdMikzsYaGiUxS8DtdskT9jRMgpNmjXGP2gICXjYe2giConsR3Y1Vbii1KbwTUa11I+P5dxQx6tNfyjMK2tnALOhjkMYkn+xgxJbTx+bLNca3Z4KrrDcnNU5MCXQnh+PH6uWOA3nA9V5kMzChgTY3ipm5LwoDiMB6hM3fqzLldljZNSh29z8o37tYbF8OHWUn9QOo+BPRn+eDrhQd6OATncfi77qv7NGTGs4R+FaY7/1vkUUbJI8PJACLGRyggR72nfBlHOxcWg0YGwB8PKYyb2MOwZT2LGRx3FcYqnHEPEU8TxK3uvPgA1D4Xns1XJO6rLGbWtTZUDv1IifDAsjcoOj9pxHNSLsaLa2R9OJBiMyigmCkkfOIiVw95V7ySN68SvvlGY1lbOTpS7jskS0CGiFJ1fRCYzziZ6ZcFYOg0hmzKoug7+GNP+oNV2g25bAnityS/6EWDx/Kw1N62DP2DaKefcxzIDP3kPruD8S8cMnH+x8B6KNYrX/a+R40tT8eeYdso5Xva3NYPHjf1xsYk14b1J7zwFf4JpF3Nu4thn4uk9CZ+vZn00ih8P0+SBNxPkhM0Y/CVM/wNCu0WqAY+31AAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle - 2 e^{- 3 t} \\cos{\\left(5 t \\right)} \\theta\\left(t\\right)$"
],
"text/plain": [
" -3⋅t \n",
"-2⋅ℯ ⋅cos(5⋅t)⋅θ(t)"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x1 = sym.inverse_laplace_transform(Xp.args[1], s, t)\n",
"x1"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The second fraction belongs to a real-valued pole of first degree. Its inverse Laplace transform can be looked-up directly in the [table of Laplace transforms](table_theorems_transforms.ipynb#Transforms) as exponentially decaying signal. Performing the inverse Laplace transform again with `SymPy` yields"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAFMAAAAYCAYAAACGLcGvAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAEZUlEQVRYCe2Z7VEcMQyGD4YCLqED6ABCBYEO+KggXAcw/OMfAx1ABwQ6gA4IdBA6CLkOyPs4ltHau747ho+dBM8Yy7Jky68l2XvMPT4+DvpQDg8Ph7LjINqyFNtv4o+9ferfqr+l9t7z+0Av9MGIaMOxABqZPaJPRQPcsuMB+EofgcTGeTO0B+2uQFp3dhyLXhJvxfEYv3P9XpF9AhOv/NGGjgAFVMClDqBVPchtas/iaV5LMVX9NrnehLmMO8usB9x78c0T90XjmUdqLzPZF+lq3j3WjHXSnBzwpuqJCXZ6poTITeStNy+srUU3VVezxeFfZ7zWrubYU8WDp/JiybHeotqpDkpywQ61u2ZAzTMvJGReYfJTtVqATYeQnKAwkmzjVlafMEN3VXS6yUXjlWPP65pbMlcau1B7osql1bjIcr0oc6A2P7wg6ubYEJ3sFc38t6rfVcetYGoAd392kT6HsDHrBNIDSMI56Mb+QC0bSF6pPgARZsVhi2d5NaQN9TmAcJG1yUcb0alFIQeJbQ9R3jfooT8qwlwLYjQekbxC9KsXNqxFMOwUG6Id++rbBngi3ahSDlSThwSO/kQdHCEAavzYMn9X2ZZunrO9LIdL/i4wiXroDwswpbQzYWK/yEvShCIeQGt1120AoJfVJ0edO766qQSQNZbyqmi8mPL5b9P8q3FyZXEwTalgVy2Xor/dCHNNzKlidLVEAzH8VxTEawjP4uSqE7lB6X5y3YLUOCGdHvW5QLQJYPBmX77EThdgeF0C3xQ1HwfLehwGXk20cI/cqE03uPoU9DcSmBJAgfzStShKA42zCIDzSRdyllpSA+DmGxHrzYrdqjkw2Ebp2hdgFw6kPTHPtVoOaF1t7Q74iUwCUx1u1ioYGgdwbkpkA5CiKQAM/z3LTlycW9nbARg1J8HzLC97PaMB0e/V+L5FfymAqcU51eJ0vHSkTWYoHbvxFzV2pX7uES3qr8rCA/GkLVtFNEAB5pHxWlpyaS094Si1fMmUeP1wQQvibYDTFQYIWwkTSzbPGTb+Lm0EjbXz6NiOBtVu6k6b47wWjZ1yGggHgmcivCZFkqsvnDTvM/g8CywF2PPEy/aFzsMRm89ke83zCFE8uK3gPAPpp6gTjePl86H/gGeGRJvPJP5v8Rphoz7eS1gXRfJ8p04Kh0LvJRhal5zYmAp7xMBjzAka467DnnCottLIl3FO5PNDY517PLOrgHZ+YuGl7xW0ADLw2x7KXvS1aQ4y2Ots+ip6PGFhgFnrkAkgMRbnJFLbHIbP0Lu5/Jd2CXPJcFLBxdWinN5WGufiwTt5DlBw+3fPobLBDhW7ePfyA8fEe0AypDO+49OP0OqHIh44gEdIgeq35l7xWXNUgBlm+c/+RDDSu3mW7UfAec0sz8+i+A/LFulrhr2Sk0OK+wBTSMirCF/yIWE9dYny6IXw/wDzCToe+/ZR8sStU8in3ws+cqYDK3pa418RbrhBSpaL+FJtuuT+AFsts0PncHK8AAAAAElFTkSuQmCC\n",
"text/latex": [
"$\\displaystyle 4 e^{- 2 t} \\theta\\left(t\\right)$"
],
"text/plain": [
" -2⋅t \n",
"4⋅ℯ ⋅θ(t)"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x2 = sym.inverse_laplace_transform(Xp.args[0], s, t)\n",
"x2"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The inverse Laplace transform of $X(s)$ is given by summing up these two parts"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAQgAAAAYCAYAAAAGV2PQAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAJ4ElEQVR4Ae2c63XVOBDHLzkpIIQOoAMIFQAd8KhgoQM4+cY3DnQAHfDoAKiAhQ5gK9iQDrL/n65GyLJsy697naznHEeyHqPRzF+jkXzh2sXFxWYJ9PLlyyPJcepluenTv1R+Hsun9+96f6T0V1y+5venAdkCe93Xc6aH/F09r1T+Q2mg1XZBFZcmc7ggSV8LQM9MHuXfKo8zuBWV4URuq251DqaUZaSvJcYv2eUd4ih9ruSrnuu8QypbbbdVxaX6e7AgaZ8KROxCRoDupspuW4FS6iu7UlS3ZvengVca+n00/A3liSZiWm0Xa+OS5JfkIIge/s7pTU4CR4HD4NmQ1xM7jly3QWXiS4jcSaXtOhldgQbSxQ+eaCoPlTdb7cx20fiTZqe29dT82ibbZ6xc28UcMSScC0+jyeIwCFsNeC+UZxfibPspajdZVnwJjTm+lBxhAP5DPW8mE+CSM/L6e6JpvFXejhvocnbbzaU6P6cKJlTGMddw6YbWO0eoY6WLwY5k6YNn5lHD9LWmS0oxZ4d+pjTcC8BhF+TH/qix7igfLimV50b1elzWJI/aoBxCXei93isG3Rb/+at6dr27Sl/8KW3P+THOlabOrb3jxLUan6jH5D5R/ox3lbfOeWIxHDuNyULBdp+VD85T+WLbzSHXEJ6SOYsJlf8WP+Zp+iUPVfC6Lcr/FQ/wWYwd335WPCNpKlebg/ip9oSOj+jYh9QH5+JCzI5+OKCKx9U7YOeCki8VsXMgeviosnDx1cRbbT77tu+Ux3jflYbLzrSfb/NV6Z20jndfz4XpA+VTeSm/p/IgK312RRrX6UvpAxtTeXQPAJH3i5WXpGo/2HbG3/NALywYMFRsO+Ox71Qyg5ssJlTH2jjWQxvwQERLZFvDgOczCjviMSmeJeumVK7sEUOdAddgUn88awBsKSP1czuhUtfXv2+UYgSA68CudwxDOGQePAyhMjv7WoiLl6ZtLSwMnbbODKfURAAc2c4yDejHmDuPtLwstbE1V6KHp6pnJ+90qJ6PS9Svl+3UHlv8owcnafawhUI0Q1mR7dRuSYRemzDRZ+MchR3pdA48o+ciuQ5Si0ggjImBzchpk1neNa7bCcWc8yuLGTkIm21REgF80wOd6qns5BT6Pjg3p1TKIoJ/Ez1W37ZjAg6L+5CaTnw/+h81MZ+5HEP/zIyPMz1Sedu8R4sm/ugEG8X2QCbKP+iBOm23bbaov12YKBV2MHakW9bAHHhG9iK5ag5CHZ9IsLbFAvM5iDAMYJHa89QDkPHw5rf0zs7InUJtsarcOQ7VhbBaeVu4x6qvkeo5Z8bgrrVRAXK1XYzS/3Gu4w7KmGvWefmxbf5zisIx9FS6fM6jPOCLz+MltptTvl68CzFRynMMdubCM7IXyXUYz9IbF2O2ktoBOoT/1zdkhyCszS1a36Q9Ud/WUFj1hKqNYbyXicVul3U2IGEu1OQEAHNwKK6l/ogfCmQ85souTFRDyP5Nabh80ztEf/js3LFKlqY7InafjerRWyC9z2E7xqiMEwZUxsvQaLu4LXkvI1FgjCf0Hpx01Ib7AAgMckcVbKk8OsCO8GHeEBtg9q5pW+3+ZjER1W/Eg40Knlwcgg/uIJwOlI7GjnjAezI8i9dmiFzBQagzk+S83rSQGMMGwYlwiWgKwRA4jHRxqmhnhMGgAJDt68YtFOWb5oUDqTlFzQ0+X5RipPtKAU0TAVJAsQiSrMwZe1bsoXJkXKLtgt4kI3ITQfIze+cQvNwsfvfZWynzw1lXLo1VzpcTHPkbPSwwfi9TsZveSxxVFhPiZwTvD+J1ToFSZOaY5y6FlU6BnUnx7OXsLVdwEGLAF4UKoGAak1cEN6q0jXcMgEf5PumJH5xQN5aDBd7m+DD2WdwhyQOweK5JtXulPyBZCrF4PkkPIdJZuO1ivSE7jiBEC3rHRpBbkEptfqnTB798sWIhHOs5UZ57GOunovpmQGFCrZgQv9TpIC9j4nyJZIzGYGcuPCNbsVzOQWhyeKvaLmqzjFJrg9I5a0KEWHhuFLRPYldhxw8ht/IYGgfxqkUwgBQDKG2K84vBmtbzDlAZq5O8TF/VsKi9Zxiita4BxB8bAdigB99nybZzInrdYMfg2KhQOfq3aIJ6nPE3PRVSO74uUMYxgiMvjvu3UrDJBlZxmnpvoi5M5PqBASJNvpiZ4xqDHeY5B56RvViuQyakDix4mxQMmsgxVtuKAZsa76pc8thiS6MYuzgcdDfg+aKflG86tWJAiSfOqOsMnPIvehdvHP2x0soO5zsv0nbJxNA1ZHdb27fqX2uDHpuIxQWh51M9bBLcaXDk4LcxJccMNa+T+oIFdNxkQ4dF1ZMOwo7vy+Ap7kbhGYZ95TpUHybBLwgJ22JCyXhDC/ns+FHz3HGnPefTowAyA4g2MLHLOKNmZGdRbdQ/REfKpyErTegPn72R5GIR8JUnRA7Ku8Wk1Jz/km2H7kzOOExPdWptmmzm+Pi5nykFAw67yrtIWSmf0lOsxOO0YeJEDXO2ZpPYRHynwE4q41g8I2IvuQ40IRfGKCWMDY8YsaiszilY7xiHI0WN1BeA7oU0NrJWyMuD0Uz2Sn30wpxsV4qKXbZyVvM8c20Zx4Cb8pj9XXLhzHHy6VyxiYF5kbaLlSP5sSOLgkVYI/Svh3ra1aIk1Tnwq45NDZ3YRZ+ybvESSXJUyfKnjac2TLDh5BwYY4eNRPnB2BH/ufDM9HrJdUCPBjpSOU9MhGlmBFeuybCjcr5NvV3cbxd5DO/kRSblkbXkJ9DIfVdPjsLC9zyJqHLzJNzMled4TlomeXBYLAhnB72zO7pHZVwmn/sBl2w7L6JLiIDQc7q4kd90fE95fsiEE4iJNnzBsIXKhXWKYd6tPu4b59swYboN7TWG3ceF6E2VY7EzB56RuZdctX+Locmy2AGdOQIEDd/+vTKIIuz7M8Dc+52EZDCngFx4eM6bnbu62gAyPqHVdgWVoQf0wQLc6D17l6FyxmQxdgEPNpOSHxs5c8SlXTgrKw+QF2e7VHDJabakynDGBWOwp/LMmYjpnEYiZyuVOxsoBb/slvF9BnPvvFBX30ZMqP9G9TY2ryy4Mz2V3wH5NoOxo/6mg8nwjLB95ao5CJj830hKwwgcr2yHKlaBVzigqzmYYiZrw8VpYAwmSiczF3bGyh7LdVA6mSvejtB06M02uxj9V7paGhiDiVJNzIWdsbIHuVYHIVPKY3J04NxL6FhMvj39skePYkZrw8VpYCgmSicyJ3bGyJ7KtTqIPxblgokzYx+i/dDIo884a9v9aGAIJkolnRs7Q2WvyLXeQUTm9N6z6L+RU1su/CoXZxGrNXtFNNAHE6VT3hV2+sqek+s/rnILIGAV6k0AAAAASUVORK5CYII=\n",
"text/latex": [
"$\\displaystyle 4 e^{- 2 t} \\theta\\left(t\\right) - 2 e^{- 3 t} \\cos{\\left(5 t \\right)} \\theta\\left(t\\right)$"
],
"text/plain": [
" -2⋅t -3⋅t \n",
"4⋅ℯ ⋅θ(t) - 2⋅ℯ ⋅cos(5⋅t)⋅θ(t)"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"x = x1 + x2\n",
"x"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The resulting signal is plotted for illustration"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"application/pdf": "JVBERi0xLjQKJazcIKu6CjEgMCBvYmoKPDwgL1BhZ2VzIDIgMCBSIC9UeXBlIC9DYXRhbG9nID4+CmVuZG9iago4IDAgb2JqCjw8IC9FeHRHU3RhdGUgNCAwIFIgL0ZvbnQgMyAwIFIgL1BhdHRlcm4gNSAwIFIKL1Byb2NTZXQgWyAvUERGIC9UZXh0IC9JbWFnZUIgL0ltYWdlQyAvSW1hZ2VJIF0gL1NoYWRpbmcgNiAwIFIKL1hPYmplY3QgNyAwIFIgPj4KZW5kb2JqCjEwIDAgb2JqCjw8IC9Bbm5vdHMgWyBdIC9Db250ZW50cyA5IDAgUgovR3JvdXAgPDwgL0NTIC9EZXZpY2VSR0IgL1MgL1RyYW5zcGFyZW5jeSAvVHlwZSAvR3JvdXAgPj4KL01lZGlhQm94IFsgMCAwIDQ0OC42NjgyMTA2NjUxIDM0My42NTkyNSBdIC9QYXJlbnQgMiAwIFIgL1Jlc291cmNlcyA4IDAgUgovVHlwZSAvUGFnZSA+PgplbmRvYmoKOSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDExIDAgUiA+PgpzdHJlYW0KeJyFmcuuHLcRhvf9FL2UF6ZYvHMZIbGA7OQIyCY7RXZiaAwoDuI8fr5iNzkzp0snBxCgqZ8/q0nWlZT9l032n3e//8K/33fZ3/Pv583z67al1FwpLYjw88vjz5iiK7mHjNg//frHtv20vf0Dk/wG6f22SXYp9Nz2EF2NjUFMHLtLx0xL+uVRGkN16ZxxTfAoPNWEQ83PfDQLcI0loFQlfK0TXxgcq8sp1qF3yZLzQ/Zl296xA79v7z7ub3+QXfz+8acteddDyToyBNfz/vHv2xv/3f7xl/1PH7ehZ5PYnIQm0h81PEpf1yHgPbUUpRV51CPPekIMTlLv7UnPo/R1PSE016uPXkKID2rCs5oYipMqTff5ruZR+rqaqDP3INXnlh6XE5/1pOCd9FhDfTqYB+n/ORqpzkvysfdUHtSkqebrptb6vcckmOYwKF9Klr27UJtwpp9uzKk27nobqpjg7Q/h1PDm3zrVxlQf5jdbpuRdeZZ9Y/vFhT1i5HxIPQ3JvTClNb/44HyvUsujhgfpKzp6c9FzzL6Lr6ee/C09peCwvvjwpOcufUWPlOBa5qh0Y+Nhsd9cUIhQfPKhPSp6kL6iKKi7+yo51BhOPd9aEPHB1VxTTk967tLX9HRxvfhcW0nh2LlwX9DXTS3pe7UpApEE0VPEZ89IdDelNFQ+W9J/hyVl16X2cfz+GDD1v/nbmzEiuu4llioPY16YI0OCb6e9Xqb57m6yX/czYFYGp3oPsCngWbGV6Bubv0cPEGT/1+f9r/uvO3urwVNXmEsroWb2OJXzr4KoZ7cQc+j7j+/3t3/8/J9/fvr84/t3+6ffNpy2cqAlvnARLyWy+48+8hdLrhHAZQ5AwsvBV7nmD9ckp/py7EU8Qr5vmdjycuxVfuQHwh27Mkwn1JLW6AtwDM9ZTksrQU3gPv6CDAIRUth9Fadcoy+LcEUGAbNouQwxk9Qui3BFBqGLJtvO6ebm8/2DXsoZnF323RddFdtcUopzvRYyCJU4FIdUfI5S1vgLwPDifCghtuFjpfcc4zneQgYh1JokDXGMeZ2WAYzhmQOvusvE8hSK72v8FRmEimOMXSZI9CI+LMIVgUCySc0TFlScYml+7pCFDEKM0tuQSiOv5TX+Aozh2fMXh5h9I1yt8VdkEEqRmhC3zsJI6mURrsgg9JAKKUHFtaXe4iJcEQiN2Ix9pCEuGX+ae2QhgxCJn3ioisn+KfVFuCKDkIsG9kMca1mbZCGDQKSK9VCcfZTlNhYyCK0SYo6lcUzLjw2A4R1rTITgQ1pqaPODLGQQpFe13iGNeZ2aAYzhpFWM9tSa+9ohCxkESsi5DYnCt63xF+C2ZQykdx/LcTCBxHwemYkMQkytxeNgasjE/EW4IoPAOZZy7LMe5IOGKzIIXRI2cphvwFHiIlwRCOLUeGs4HYS/88xMZBD4uBQOB0kJX8mLcEUGgXApvQ9xpS6+K7gADA8uUDGXPEIOVZHMWGoig0AU9v2oKBLpMuVFuCIQIkGtl5hG1Aye4nTukYVASK4Q+5KMMN5bjXkSLOS2Fe1jvA8kT09GisPyB8FEIASXegmdFOoJoeSAchqGiUBAW6SV0Xlw3jgdx5AzmCQUaiCmRY9xFSq7+TkWAiG7xhyqVPwo5dKZ/kwEAhVsDAmbjYIVhEDRcxIsBAJhNtfATkdhpysznq5mIhCIaUSQNqTEjzAP2QLG8ErYrzpLdGx4Smv4BWA48YN+kMNTKX2Xbskx3kIGIftMvhriGHHdsghXZBAacbX0IU6pdF8X4YrctqqdWU3+UMxJrgRiIoOgO13qENPbzlBhAWN4x9RrO6QEnyxr/BWBgAtRuoXjO0teJZ0FjOGNRbV0aq3rxEwEAqdNpKRgG8siLdb5QRYyCBrC87GulCmv+iJckUGgVU4xnUdD6XbXcEUg8H/apXMe6axtEixkEEohGx5bRz8dwxp/ARhOCFB3ysN4aZj8OmMLGYSaKFcPa2eJEu+EKwKBopYoo/097sc2lHw6golAoEIstY5mSxNAzWVqsJBBYKN7PiJC0r6wLsIVgYCDd4wqjJgTU6S/OQkWAoH6pxMG4ohpeNTKaSYyCJ3TSbigp/wLFHSyCFfktjVadlJj7CMqk7hSOM/NRCBQbZeMHSLGW3DBcq7BRCDQK7ATIYxEQb9b/SRYyG0jI8bAoZBZ2EeaZJkh2EQgFN2LiFcF0ljUyvuMSCZy24RGVCh99HKKBq6WEE4NJgKBUyTXtdZ3IT2W0nSZB8OElIINUBPkMG45KOikLooFQQkaZgmDdNl6v5lynFWeDenln3fEcWohim/as1Rn6WwiSiCM0DgQRgR3ZKVxHocNKaUyU9Pjp8/S2msVhzYEhYa7Jdyk6yUR3X2dlZKJKCE5bRGpcPRuhMieFsFAlIADkGCw50Zf5KNW5CfBQCBozSU0mIgJK8OJT4KFKIEKgQ8k4VcKZYxiHbmFKKGSzry20Vhni2TvuU0WAoGSqNJwUBYQw1KPK6+YiBLUTTDjsGucD6VMQzcRJTTSAQkq7kWL/dJm+WYiEEb0zUIgwjJJT3FmIhOBQJigFK+571qA1RLndYGJKIGyqKZG7Vu0D6fDnhZrIRDUq+izSPqZAoM2eVaUJnLbKDIpYAsHtGe8iwppRigTUQJ2Qj6gEeJkkSZZBAOBoIlP85LsFNokhjDLaBNRAt+H42JiNCOtEohkEgwEQsgkBI3XuzZ4HE8/TcNE9HYeNhtAxU+X3Whp+1yDhSiBCEoRTnzTq4uUJU4NFgIhUezkplf6elfDADk9zkSUUAi5lWi3J20W6qwTLYDhuGHHtWg1k14gsrA53kKUoF5FPuh7ooiRLmEu2UIgYIdEZ11O0h7nXhGYiBK6U67OI1quyWw2TAQC7h2EAq+pmOS22noTgdBEd7jzfQTGypfOBG8iSmBpuWO5KqYBazI1WAgE7c74XOn7uAWlJj/dx0RumybvRFbDb6P240T0c5dMRAnZVQrCJirG+PP0NxOBoFUXZ6S1SCdW5zKDjIkooWLpvePeiIW2ts9PspDbeBqiau5aEzaN1TKvGU1ECTRHjYI/q7hW5pmfZCEQYqJM01tKFZfEh0yChUBgj4WiUNvBpi6fZoYzESWQKoifx5dG7Hl2KSYCgRJnPPmML+Vg2+xETUQJ9F+aWauKCfCS5ydZCATtgSkRCFGIMeJ1W2oiEGiotIOMY2mE5zojq4koQR9cm17mUlp0vZ6ei7YQCI38mEQtUcXi1XYOgoVA0CJSRN0kajis1AsnwUKUQI1T5uMBUS73RTAQfYTQ56oc07jop5+63ylbiBKwEzXioZhE6dflnoVAEH3I1bvHIY50/vO2zkJuL55A9TpyGt+H/ese9j8fz/HjNfv5meXhXe3+lr4eJx+ex5lrvcGPJ3Hzyf32rSf37df1tj7f1B+e4R/fYe70p9eVF8qNJ/zXdH/Y/gfDZGIHCmVuZHN0cmVhbQplbmRvYmoKMTEgMCBvYmoKMjU5OAplbmRvYmoKMTYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNzggPj4Kc3RyZWFtCnicPZBLEgMhCET3nqKPID/R8ySV1eT+2zTOmIX2EyhssKXoGM7L1ZBd8ZZWGJ74Nu8LnomrqfWHJBUy+6YOGYtn8hQnJBSvJmNA3LHV1qNxMsIMuywmZmCuiq9ELqhQAupR8mpmo+BqpoK+fcRWmfUWFwhFAiYsZyv+nwPT6xYdDBaY7TfLszz2CtN0LMx7hnkPRSN+BuVabmBlrYOfhh2a97ZoKP/kJ3sWeLXPD96rQqEKZW5kc3RyZWFtCmVuZG9iagoxNyAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDkyID4+CnN0cmVhbQp4nD2MsQ3AMAgEe6b4BSJhjG3YJ0rl7N/mLSdp4PQP19KgOKxxdlU0HziLfHhL9YSNxJSmlUdTnN3aFg4rgxS72BYWXmERpPJqmPF5U9XAklKU5c36f3c9x6sbugplbmRzdHJlYW0KZW5kb2JqCjE0IDAgb2JqCjw8IC9CYXNlRm9udCAvRGVqYVZ1U2Fucy1PYmxpcXVlIC9DaGFyUHJvY3MgMTUgMCBSCi9FbmNvZGluZyA8PCAvRGlmZmVyZW5jZXMgWyAxMTYgL3QgMTIwIC94IF0gL1R5cGUgL0VuY29kaW5nID4+IC9GaXJzdENoYXIgMAovRm9udEJCb3ggWyAtMTAxNiAtMzUxIDE2NjAgMTA2OCBdIC9Gb250RGVzY3JpcHRvciAxMyAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2Fucy1PYmxpcXVlCi9TdWJ0eXBlIC9UeXBlMyAvVHlwZSAvRm9udCAvV2lkdGhzIDEyIDAgUiA+PgplbmRvYmoKMTMgMCBvYmoKPDwgL0FzY2VudCA5MjkgL0NhcEhlaWdodCAwIC9EZXNjZW50IC0yMzYgL0ZsYWdzIDk2Ci9Gb250QkJveCBbIC0xMDE2IC0zNTEgMTY2MCAxMDY4IF0gL0ZvbnROYW1lIC9EZWphVnVTYW5zLU9ibGlxdWUKL0l0YWxpY0FuZ2xlIDAgL01heFdpZHRoIDEzNTAgL1N0ZW1WIDAgL1R5cGUgL0ZvbnREZXNjcmlwdG9yIC9YSGVpZ2h0IDAgPj4KZW5kb2JqCjEyIDAgb2JqClsgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAKNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCAzMTggNDAxIDQ2MCA4MzggNjM2Cjk1MCA3ODAgMjc1IDM5MCAzOTAgNTAwIDgzOCAzMTggMzYxIDMxOCAzMzcgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNgo2MzYgNjM2IDMzNyAzMzcgODM4IDgzOCA4MzggNTMxIDEwMDAgNjg0IDY4NiA2OTggNzcwIDYzMiA1NzUgNzc1IDc1MiAyOTUKMjk1IDY1NiA1NTcgODYzIDc0OCA3ODcgNjAzIDc4NyA2OTUgNjM1IDYxMSA3MzIgNjg0IDk4OSA2ODUgNjExIDY4NSAzOTAgMzM3CjM5MCA4MzggNTAwIDUwMCA2MTMgNjM1IDU1MCA2MzUgNjE1IDM1MiA2MzUgNjM0IDI3OCAyNzggNTc5IDI3OCA5NzQgNjM0IDYxMgo2MzUgNjM1IDQxMSA1MjEgMzkyIDYzNCA1OTIgODE4IDU5MiA1OTIgNTI1IDYzNiAzMzcgNjM2IDgzOCA2MDAgNjM2IDYwMCAzMTgKMzUyIDUxOCAxMDAwIDUwMCA1MDAgNTAwIDEzNTAgNjM1IDQwMCAxMDcwIDYwMCA2ODUgNjAwIDYwMCAzMTggMzE4IDUxOCA1MTgKNTkwIDUwMCAxMDAwIDUwMCAxMDAwIDUyMSA0MDAgMTAyOCA2MDAgNTI1IDYxMSAzMTggNDAxIDYzNiA2MzYgNjM2IDYzNiAzMzcKNTAwIDUwMCAxMDAwIDQ3MSA2MTcgODM4IDM2MSAxMDAwIDUwMCA1MDAgODM4IDQwMSA0MDEgNTAwIDYzNiA2MzYgMzE4IDUwMAo0MDEgNDcxIDYxNyA5NjkgOTY5IDk2OSA1MzEgNjg0IDY4NCA2ODQgNjg0IDY4NCA2ODQgOTc0IDY5OCA2MzIgNjMyIDYzMiA2MzIKMjk1IDI5NSAyOTUgMjk1IDc3NSA3NDggNzg3IDc4NyA3ODcgNzg3IDc4NyA4MzggNzg3IDczMiA3MzIgNzMyIDczMiA2MTEgNjA4CjYzMCA2MTMgNjEzIDYxMyA2MTMgNjEzIDYxMyA5OTUgNTUwIDYxNSA2MTUgNjE1IDYxNSAyNzggMjc4IDI3OCAyNzggNjEyIDYzNAo2MTIgNjEyIDYxMiA2MTIgNjEyIDgzOCA2MTIgNjM0IDYzNCA2MzQgNjM0IDU5MiA2MzUgNTkyIF0KZW5kb2JqCjE1IDAgb2JqCjw8IC90IDE2IDAgUiAveCAxNyAwIFIgPj4KZW5kb2JqCjIyIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ3ID4+CnN0cmVhbQp4nE1Ru21EMQzr3xRc4ADra3meC1Jd9m9DyQiQwiChLymnJRb2xksM4QdbD77kkVVDfx4/MewzLD3J5NQ/5rnJVBS+FaqbmFAXYuH9aAS8FnQvIivKB9+PZQxzzvfgoxCXYCY0YKxvSSYX1bwzZMKJoY7DQZtUGHdNFCyuFc0zyO1WN7I6syBseCUT4sYARATZF5DNYKOMsZWQxXIeqAqSBVpg1+kbUYuCK5TWCXSi1sS6zOCr5/Z2N0Mv8uCounh9DOtLsMLopXssfK5CH8z0TDt3SSO98KYTEWYPBVKZnZGVOj1ifbdA/59lK/j7yc/z/QsVKFwqCmVuZHN0cmVhbQplbmRvYmoKMjMgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA5MCA+PgpzdHJlYW0KeJxNjUESwCAIA++8Ik9QRND/dHrS/1+r1A69wE4CiRZFgvQ1aksw7rgyFWtQKZiUl8BVMFwL2u6iyv4ySUydhtN7twODsvFxg9JJ+/ZxegCr/XoG3Q/SHCJYCmVuZHN0cmVhbQplbmRvYmoKMjQgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA4MCA+PgpzdHJlYW0KeJxFjLsNwDAIRHumYAR+JmafKJWzfxsgStxwT7p7uDoSMlPeYYaHBJ4MLIZT8QaZo2A1uEZSjZ3so7BuX3WB5npTq/X3BypPdnZxPc3LGfQKZW5kc3RyZWFtCmVuZG9iagoyNSAwIG9iago8PCAvRmlsdGVyIC9GbGF0ZURlY29kZSAvTGVuZ3RoIDE0NyA+PgpzdHJlYW0KeJw9T7kNAzEM6z0FFzjAeixb81yQ6rJ/G8pGUggiQPGRZUfHClxiApOOORIvaT/4aRqBWAY1R/SEimFY4G6SAg+DLEpXni1eDJHaQl1I+NYQ3q1MZKI8rxE7cCcXowc+VBtZHnpAO0QVWa5Jw1jVVl1qnbACHLLOwnU9zKoE5dEnaykfUFRCvXT/n3va+wsAby/rCmVuZHN0cmVhbQplbmRvYmoKMjYgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCAxNDkgPj4Kc3RyZWFtCnicNY9LDgMhDEP3OYUvMFJ+hHAeqq6m9982YVoJCQvbL8EWg5GMS0xg7Jhj4SVUT60+JCOPukk5EKlQNwRPaEwMM2zSJfDKdN8ynlu8nFbqgk5I5OmsNhqijGZew9FTzgqb/svcJGplRpkDMutUtxOysmAF5gW1PPcz7qhc6ISHncqw6E4xotxmRhp+/9v0/gJ7MjBjCmVuZHN0cmVhbQplbmRvYmoKMjcgMCBvYmoKPDwgL0ZpbHRlciAvRmxhdGVEZWNvZGUgL0xlbmd0aCA0OSA+PgpzdHJlYW0KeJwzNrRQMFAwNDAHkkaGQJaRiUKKIRdIAMTM5YIJ5oBZBkAaojgHriaHKw0AxugNJgplbmRzdHJlYW0KZW5kb2JqCjI4IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMzM4ID4+CnN0cmVhbQp4nDVSOa7dQAzrfQpdIIB2zZznBal+7t+GlF8KQ7RWipqOFpVp+WUhVS2TLr/tSW2JG/L3yQqJE5JXJdqlDJFQ+TyFVL9ny7y+1pwRIEuVCpOTksclC/4Ml94uHOdjaz+PI3c9emBVjIQSAcsUE6NrWTq7w5qN/DymAT/iEXKuWLccYxVIDbpx2hXvQ/N5yBogZpiWigpdVokWfkHxoEetffdYVFgg0e0cSXCMjVCRgHaB2kgMObMWu6gv+lmUmAl07Ysi7qLAEknMnGJdOvoPPnQsqL8248uvjkr6SCtrTNp3o0lpzCKTrpdFbzdvfT24QPMuyn9ezSBBU9YoaXzQqp1jKJoZZYV3HJoMNMcch8wTPIczEpT0fSh+X0smuiiRPw4NoX9fHqOMnAZvAXPRn7aKAxfx2WGvHGCF0sWa5H1AKhN6YPr/1/h5/vwDHLaAVAplbmRzdHJlYW0KZW5kb2JqCjI5IDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjQ4ID4+CnN0cmVhbQp4nC1ROZIDQQjL5xV6QnPT77HLkff/6QrKAYOGQyA6LXFQxk8Qlive8shVtOHvmRjBd8Gh38p1GxY5EBVI0hhUTahdvB69B3YcZgLzpDUsgxnrAz9jCjd6cXhMxtntdRk1BHvXa09mUDIrF3HJxAVTddjImcNPpowL7VzPDci5EdZlGKSblcaMhCNNIVJIoeomqTNBkASjq1GjjRzFfunLI51hVSNqDPtcS9vXcxPOGjQ7Fqs8OaVHV5zLycULKwf9vM3ARVQaqzwQEnC/20P9nOzkN97SubPF9Phec7K8MBVY8ea1G5BNtfg3L+L4PePr+fwDqKVbFgplbmRzdHJlYW0KZW5kb2JqCjMwIDAgb2JqCjw8IC9GaWx0ZXIgL0ZsYXRlRGVjb2RlIC9MZW5ndGggMjEwID4+CnN0cmVhbQp4nDVQyw1DMQi7ZwoWqBQCgWSeVr11/2tt0DthEf9CWMiUCHmpyc4p6Us+OkwPti6/sSILrXUl7MqaIJ4r76GZsrHR2OJgcBomXoAWN2DoaY0aNXThgqYulUKBxSXwmXx1e+i+Txl4ahlydgQRQ8lgCWq6Fk1YtDyfkE4B4v9+w+4t5KGS88qeG/kbnO3wO7Nu4SdqdiLRchUy1LM0xxgIE0UePHlFpnDis9Z31TQS1GYLTpYBrk4/jA4AYCJeWYDsrkQ5S9KOpZ9vvMf3D0AAU7QKZW5kc3RyZWFtCmVuZG9iagoyMCAwIG9iago8PCAvQmFzZUZvbnQgL0RlamFWdVNhbnMgL0NoYXJQcm9jcyAyMSAwIFIKL0VuY29kaW5nIDw8Ci9EaWZmZXJlbmNlcyBbIDQwIC9wYXJlbmxlZnQgL3BhcmVucmlnaHQgNDYgL3BlcmlvZCA0OCAvemVybyAvb25lIC90d28gL3RocmVlIC9mb3VyCi9maXZlIF0KL1R5cGUgL0VuY29kaW5nID4+Ci9GaXJzdENoYXIgMCAvRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250RGVzY3JpcHRvciAxOSAwIFIKL0ZvbnRNYXRyaXggWyAwLjAwMSAwIDAgMC4wMDEgMCAwIF0gL0xhc3RDaGFyIDI1NSAvTmFtZSAvRGVqYVZ1U2FucwovU3VidHlwZSAvVHlwZTMgL1R5cGUgL0ZvbnQgL1dpZHRocyAxOCAwIFIgPj4KZW5kb2JqCjE5IDAgb2JqCjw8IC9Bc2NlbnQgOTI5IC9DYXBIZWlnaHQgMCAvRGVzY2VudCAtMjM2IC9GbGFncyAzMgovRm9udEJCb3ggWyAtMTAyMSAtNDYzIDE3OTQgMTIzMyBdIC9Gb250TmFtZSAvRGVqYVZ1U2FucyAvSXRhbGljQW5nbGUgMAovTWF4V2lkdGggMTM0MiAvU3RlbVYgMCAvVHlwZSAvRm9udERlc2NyaXB0b3IgL1hIZWlnaHQgMCA+PgplbmRvYmoKMTggMCBvYmoKWyA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMAo2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDYwMCA2MDAgNjAwIDMxOCA0MDEgNDYwIDgzOCA2MzYKOTUwIDc4MCAyNzUgMzkwIDM5MCA1MDAgODM4IDMxOCAzNjEgMzE4IDMzNyA2MzYgNjM2IDYzNiA2MzYgNjM2IDYzNiA2MzYgNjM2CjYzNiA2MzYgMzM3IDMzNyA4MzggODM4IDgzOCA1MzEgMTAwMCA2ODQgNjg2IDY5OCA3NzAgNjMyIDU3NSA3NzUgNzUyIDI5NQoyOTUgNjU2IDU1NyA4NjMgNzQ4IDc4NyA2MDMgNzg3IDY5NSA2MzUgNjExIDczMiA2ODQgOTg5IDY4NSA2MTEgNjg1IDM5MCAzMzcKMzkwIDgzOCA1MDAgNTAwIDYxMyA2MzUgNTUwIDYzNSA2MTUgMzUyIDYzNSA2MzQgMjc4IDI3OCA1NzkgMjc4IDk3NCA2MzQgNjEyCjYzNSA2MzUgNDExIDUyMSAzOTIgNjM0IDU5MiA4MTggNTkyIDU5MiA1MjUgNjM2IDMzNyA2MzYgODM4IDYwMCA2MzYgNjAwIDMxOAozNTIgNTE4IDEwMDAgNTAwIDUwMCA1MDAgMTM0MiA2MzUgNDAwIDEwNzAgNjAwIDY4NSA2MDAgNjAwIDMxOCAzMTggNTE4IDUxOAo1OTAgNTAwIDEwMDAgNTAwIDEwMDAgNTIxIDQwMCAxMDIzIDYwMCA1MjUgNjExIDMxOCA0MDEgNjM2IDYzNiA2MzYgNjM2IDMzNwo1MDAgNTAwIDEwMDAgNDcxIDYxMiA4MzggMzYxIDEwMDAgNTAwIDUwMCA4MzggNDAxIDQwMSA1MDAgNjM2IDYzNiAzMTggNTAwCjQwMSA0NzEgNjEyIDk2OSA5NjkgOTY5IDUzMSA2ODQgNjg0IDY4NCA2ODQgNjg0IDY4NCA5NzQgNjk4IDYzMiA2MzIgNjMyIDYzMgoyOTUgMjk1IDI5NSAyOTUgNzc1IDc0OCA3ODcgNzg3IDc4NyA3ODcgNzg3IDgzOCA3ODcgNzMyIDczMiA3MzIgNzMyIDYxMSA2MDUKNjMwIDYxMyA2MTMgNjEzIDYxMyA2MTMgNjEzIDk4MiA1NTAgNjE1IDYxNSA2MTUgNjE1IDI3OCAyNzggMjc4IDI3OCA2MTIgNjM0CjYxMiA2MTIgNjEyIDYxMiA2MTIgODM4IDYxMiA2MzQgNjM0IDYzNCA2MzQgNTkyIDYzNSA1OTIgXQplbmRvYmoKMjEgMCBvYmoKPDwgL2ZpdmUgMjIgMCBSIC9mb3VyIDIzIDAgUiAvb25lIDI0IDAgUiAvcGFyZW5sZWZ0IDI1IDAgUgovcGFyZW5yaWdodCAyNiAwIFIgL3BlcmlvZCAyNyAwIFIgL3RocmVlIDI4IDAgUiAvdHdvIDI5IDAgUiAvemVybyAzMCAwIFIgPj4KZW5kb2JqCjMgMCBvYmoKPDwgL0YxIDIwIDAgUiAvRjIgMTQgMCBSID4+CmVuZG9iago0IDAgb2JqCjw8IC9BMSA8PCAvQ0EgMCAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+Ci9BMiA8PCAvQ0EgMSAvVHlwZSAvRXh0R1N0YXRlIC9jYSAxID4+ID4+CmVuZG9iago1IDAgb2JqCjw8ID4+CmVuZG9iago2IDAgb2JqCjw8ID4+CmVuZG9iago3IDAgb2JqCjw8ID4+CmVuZG9iagoyIDAgb2JqCjw8IC9Db3VudCAxIC9LaWRzIFsgMTAgMCBSIF0gL1R5cGUgL1BhZ2VzID4+CmVuZG9iagozMSAwIG9iago8PCAvQ3JlYXRpb25EYXRlIChEOjIwMjEwNDI3MTYzMzMwKzAyJzAwJykKL0NyZWF0b3IgKE1hdHBsb3RsaWIgdjMuMy40LCBodHRwczovL21hdHBsb3RsaWIub3JnKQovUHJvZHVjZXIgKE1hdHBsb3RsaWIgcGRmIGJhY2tlbmQgdjMuMy40KSA+PgplbmRvYmoKeHJlZgowIDMyCjAwMDAwMDAwMDAgNjU1MzUgZiAKMDAwMDAwMDAxNiAwMDAwMCBuIAowMDAwMDA5MzI2IDAwMDAwIG4gCjAwMDAwMDkxMjEgMDAwMDAgbiAKMDAwMDAwOTE2NCAwMDAwMCBuIAowMDAwMDA5MjYzIDAwMDAwIG4gCjAwMDAwMDkyODQgMDAwMDAgbiAKMDAwMDAwOTMwNSAwMDAwMCBuIAowMDAwMDAwMDY1IDAwMDAwIG4gCjAwMDAwMDA0MDIgMDAwMDAgbiAKMDAwMDAwMDIwOCAwMDAwMCBuIAowMDAwMDAzMDc1IDAwMDAwIG4gCjAwMDAwMDQwNDIgMDAwMDAgbiAKMDAwMDAwMzgzNCAwMDAwMCBuIAowMDAwMDAzNTExIDAwMDAwIG4gCjAwMDAwMDUwOTUgMDAwMDAgbiAKMDAwMDAwMzA5NiAwMDAwMCBuIAowMDAwMDAzMzQ3IDAwMDAwIG4gCjAwMDAwMDc5MTcgMDAwMDAgbiAKMDAwMDAwNzcxNyAwMDAwMCBuIAowMDAwMDA3MzQ5IDAwMDAwIG4gCjAwMDAwMDg5NzAgMDAwMDAgbiAKMDAwMDAwNTEzNyAwMDAwMCBuIAowMDAwMDA1NDU3IDAwMDAwIG4gCjAwMDAwMDU2MTkgMDAwMDAgbiAKMDAwMDAwNTc3MSAwMDAwMCBuIAowMDAwMDA1OTkxIDAwMDAwIG4gCjAwMDAwMDYyMTMgMDAwMDAgbiAKMDAwMDAwNjMzNCAwMDAwMCBuIAowMDAwMDA2NzQ1IDAwMDAwIG4gCjAwMDAwMDcwNjYgMDAwMDAgbiAKMDAwMDAwOTM4NiAwMDAwMCBuIAp0cmFpbGVyCjw8IC9JbmZvIDMxIDAgUiAvUm9vdCAxIDAgUiAvU2l6ZSAzMiA+PgpzdGFydHhyZWYKOTU0MwolJUVPRgo=\n",
"image/svg+xml": [
"\n",
"\n",
"\n",
"\n"
],
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"sym.plot(x, (t, -0.1, 4), xlabel='$t$', ylabel='$x(t)$');"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The same result can be derived directly from $X(s)$ by using the inverse Laplace transform of `SymPy`"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAOIAAAAaCAYAAACq0YCjAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAJmklEQVR4Ae2b63EUORDH1y4HYHwRABkAjgDI4IAIgAyO8if4RkEGkAGPDIAIOMiAuwjOOAPu/xNqlWZGr/Vql2F3u0qWRmq1Wv1Sj3Z88OPHj8XvBs+ePfsinu+p/ud3433Pb38JyA6uieodlXMV2qcqz9X/VXWAOdvNYeCyU0ObfaSCUNYCon0swjdU751wLRKuE5XsX9WxNorxQqtdF1/vVV6q/VnlU8yB+mdtN10dUZv9U5u/qfpjLITObZx8EOk609+Tq0vghXT8oY62MYznWulNtNofanM6xjBruznolZr6iPNJ9c14973aokvK8VgFZ79QwdnfqH+nnRK5qHTLDlrpCe+R5H+smhNoViCevokhgsVrlY3ZDWupVHWRwut5Ir7T5teWsrBBlSdaAyck/3+isutO+JdkcUMlgGQyeGZAfTgMBtkCGBN0iyCc10J4DO0i4gYH4VuF+4NXnr+F6o3YjdaZ6KKw9YmM3YkoIigJIwduqXCsNxu6n/9F9RUIxLAq7ZgWbdHjdumKahxyZ0H7JzM4VW16c7LQ83c1cA4LUuYovDI0yUx4GNWFapwtCx4PHu5lkTY8IF7YL4fCB7XDaa12s90Il/2T3gLVrEv4SV38nJ7+69cIMj54+vQpTkgEuWtT1OblF2buql193xMOJyFEx0axMm3jiVr0yfPfqZ44fIy37W3tH2NLvgZojLTsRAUc0qT3KmQQEyf0dDhB0PMgpdIz/bdT89TvwM/H8bsFRtHkRMf+asBpPODZJnga8E/w+arSbDfC5d0XGyOtRYYcMNeN9rj2OEldgGs01CzK+EgIbJp3rwCazGnIOwCRpcXowQ2OHAj1oR2Rc2mYCwx+gxzxFvljvG1vo7PcawCG13pCYaAESzKgMUB/YhsxktYh+CL/+yrF0zOeV2p7eilbSk4TPs7yrwpBw2zBgg7ZHX04d9VuNN8FANVuL6rZHzbGLb3RFqkBlHQBYpOMDz3iNy3EhmKA8WMYiTvHbZj0fX+Px/QME5emnaBHZOJqGjhTSUZEN7rdf+5L7j0MH4PnHcoMN0jN02edsV0EHN9A762OP5678rPn/VyEYlvA7tjTW79A1W5EBzsmC3TO6OdZVfKBmi6aZHyklXA4PH6iDM9FTRFsOqnMDrQ9C6EiSpOScAKTu+d4DhO2raE98z4SG90qW0R3pK45YJ3aaUcqDM6vBALBmWTzn2fiVHX8TtxiNy6wi4Y7OaGjttn+iac7qDTeoosmGR+JWC6auZNO47kj2Zhi00mHWJa28Nk4AjGBEslIkx19z8sgjdb4xsHzSeSM9/1Z/cGoIxwMFWAvvHvEikbGKAo67B14IJzST0BE2EDDzRj90Xz304K6uXAgmvOO6PSomvWQIesxRhDmFQT+w+WGngHWYb3S6QtdMidKLA91TwE89WZ1PJ1R7xFNeMjaqR/P2o3nCaca3HHomdQWyAW+pC5Eb2kZH/1cZ/hXhDAQlDRmbIj48wnBnqcGUn052p55IhefrjmhelyU1sJHarnufeIJuXAR8FBt53iqETxORmbAOxryw7gHL+jq5yYPw3+pgtz4rQtlBtBz1mA8EsaBnHIA3beicwGCavjl9QBePlL0TI3h3aFfdQ4IIuytBKZ71sk6AwS0FrTmqGMCFzAOcO4wUn/OEZO60D6XlnHSEbUwRmSfC6lZhBON5hhNTZzQFuMokdsq0s5YmShuTl9wsB/4x+HC6adnjB9wxq/a9jiWCwGFWzgUhdxuqT0+SUpOpiluLTN+ngcgegPH0jO8sh50OZUNwItlbf1xzTropgS2Z/aTBfEwZx0/8IyT3sZ7IFhdIMO4M2qj96wuNNYs44kjalEUhvJyKWvEh2vWmAn4BdpmfBglL8wAaRUnyDhKucGWP5oLb59UqFshnMjjCZ4eUXKQwqkfp7TTkXGM7rPKAITHaUkf6ScpN0r8rpo9EnBagh8Gf6GyDGBInH7cAJpREeTiYJKiB25NdiVDjGmuRcfxAiu00RlZQrB5tdk3jvi8QLemi2YZDxxRi3NEn6geRNUCIwxhFDBUhAptx7BwBgZeJNgwKHrwVnrfaqAyQLHTwd5hB4P+wXBYOwcoHoC3MxUUzjunfZZVS0+FOgXtF2dGf7k9Y1wLjVPDZy3bqBka5Ez3NYdci45hYBXwsoDEWBZ2AVV6P84uvayMD42SJmIMfMEeRwUiqBmWoS5dN9KenCBLL7T+CXaaxCneeFXDcUY/HvTPZBxOrqo5GZH7gcZwwEdqm6OmpmPwOdq3MmPOWUT3qyeIUyz0HLINtVM06as5mM278LRL1Zx1bLIx/nmN4Ef90r5KulhKxs4RtRiKn3wupT6cs6aIYvrSSBsapKIT0Hx4mAV4paAwDH4C8KrCOMqbZBUac8rRGO+QyNwuCdR0jkH0JV1M0gdHgKxywRHDSQUJ1g1Op/bg3QW+MzRxYAssaibBOblGWuxkdjrW3ieO5uXBvmqXhCVdLCXjIy2KUjEMcmTL4/Xo4I76aukiUY70agJL0CYtG6RjmnusPpeuTQj/2g4yBi5cOLlC2qI2vJr8bqvNZ098OohjGoDDjandWnI5MI667Dt2GptrNfRO7WFUsx4lyFJte+cOmY7mBAfTOOuR+aTeF0lxY/5Hy7lH7IcLjYlBj5DnrGP2jhwWXh7wWvy8D1xBSRdLyfhIxMiNEeYgOusZqCnBcLhkoYyV0URb89x3faoRgP3uBr1gUCw0BxBPpJVXxQvvczie8YsDuNNDNZcyGDFpp8kEGfNsTkY/joxDq3LAiQHd0in0RjgEzgkwT8X4YhxjOFe5qn7jg34iPfw6navOBVtO0poO2KftSc00aI056/ihuEZu6IiMYvCzU3pHrjerC40uJeMu/4+oDfDhL7eNVYUUNrUfapSA5IzzZ293G8kU0bxRcmudSnXDXI3zmypOHbKDMLgDDe370rrQXBzfyfiwk6zeis7knagT7T2ZqQTIHGon1XTWcj1EdNbJggzpWIM3VND/rsIquggy7uWIpGip1HZXlbPWffvTp8uNdopRH6mhXzvluOLnt8847U2R3Nq+y+piLOMujiiivEvaBcTWCn1mG+PyxS6HerMG3ZYTl4hO2XW4jC4GMu7iiF4LvPCe7bpGNrV/fwrxSaDdinZZ2tODbunCaKFxMqBwQdVl8d+UiGRBRtCsC+Gjs4GMu1zWmPy0AL9HpX6PNJR9vQUSkJ6vaRs44f5eoJM+e56ICymG32P40p9r7z1srwRIR+PfJbd3pxva2f92R3lFf+4olQAAAABJRU5ErkJggg==\n",
"text/latex": [
"$\\displaystyle 2 \\left(2 e^{t} - \\cos{\\left(5 t \\right)}\\right) e^{- 3 t} \\theta\\left(t\\right)$"
],
"text/plain": [
" ⎛ t ⎞ -3⋅t \n",
"2⋅⎝2⋅ℯ - cos(5⋅t)⎠⋅ℯ ⋅θ(t)"
]
},
"execution_count": 19,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"sym.inverse_laplace_transform(X, s, t).simplify()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"**Exercise**\n",
"\n",
"* Derive the inverse Laplace transform of $X(s)$ by manual calculation."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbsphinx": "hidden"
},
"source": [
"**Copyright**\n",
"\n",
"This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Continuous- and Discrete-Time Signals and Systems - Theory and Computational Examples*."
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.10"
}
},
"nbformat": 4,
"nbformat_minor": 1
}