scipy.signal.istft

scipy.signal.istft(Zxx, fs=1.0, window='hann', nperseg=None, noverlap=None, nfft=None, input_onesided=True, boundary=True, time_axis=-1, freq_axis=-2)

Perform the inverse Short Time Fourier transform (iSTFT).

Parameters:

Zxx : array_like

STFT of the signal to be reconstructed. If a purely real array is passed, it will be cast to a complex data type.

fs : float, optional

Sampling frequency of the time series. Defaults to 1.0.

window : str or tuple or array_like, optional

Desired window to use. If window is a string or tuple, it is passed to get_window to generate the window values, which are DFT-even by default. See get_window for a list of windows and required parameters. If window is array_like it will be used directly as the window and its length must be nperseg. Defaults to a Hann window. Must match the window used to generate the STFT for faithful inversion.

nperseg : int, optional

Number of data points corresponding to each STFT segment. This parameter must be specified if the number of data points per segment is odd, or if the STFT was padded via nfft > nperseg. If None, the value depends on the shape of Zxx and input_onesided. If input_onesided is True, nperseg=2*(Zxx.shape[freq_axis] - 1). Otherwise, nperseg=Zxx.shape[freq_axis]. Defaults to None.

noverlap : int, optional

Number of points to overlap between segments. If None, half of the segment length. Defaults to None. When specified, the COLA constraint must be met (see Notes below), and should match the parameter used to generate the STFT. Defaults to None.

nfft : int, optional

Number of FFT points corresponding to each STFT segment. This parameter must be specified if the STFT was padded via nfft > nperseg. If None, the default values are the same as for nperseg, detailed above, with one exception: if input_onesided is True and nperseg==2*Zxx.shape[freq_axis] - 1, nfft also takes on that value. This case allows the proper inversion of an odd-length unpadded STFT using nfft=None. Defaults to None.

input_onesided : bool, optional

If True, interpret the input array as one-sided FFTs, such as is returned by stft with return_onesided=True and numpy.fft.rfft. If False, interpret the input as a a two-sided FFT. Defaults to True.

boundary : bool, optional

Specifies whether the input signal was extended at its boundaries by supplying a non-None boundary argument to stft. Defaults to True.

time_axis : int, optional

Where the time segments of the STFT is located; the default is the last axis (i.e. axis=-1).

freq_axis : int, optional

Where the frequency axis of the STFT is located; the default is the penultimate axis (i.e. axis=-2).

Returns:

t : ndarray

Array of output data times.

x : ndarray

iSTFT of Zxx.

See also

stft

Short Time Fourier Transform

check_COLA

Check whether the Constant OverLap Add (COLA) constraint is met

Notes

In order to enable inversion of an STFT via the inverse STFT with istft, the signal windowing must obey the constraint of “Constant OverLap Add” (COLA). This ensures that every point in the input data is equally weighted, thereby avoiding aliasing and allowing full reconstruction. Whether a choice of window, nperseg, and noverlap satisfy this constraint can be tested with check_COLA, by using nperseg = Zxx.shape[freq_axis].

An STFT which has been modified (via masking or otherwise) is not guaranteed to correspond to a exactly realizible signal. This function implements the iSTFT via the least-squares esimation algorithm detailed in [R275], which produces a signal that minimizes the mean squared error between the STFT of the returned signal and the modified STFT.

New in version 0.19.0.

References

[R274]

Oppenheim, Alan V., Ronald W. Schafer, John R. Buck “Discrete-Time Signal Processing”, Prentice Hall, 1999.

[R275]

(1, 2) Daniel W. Griffin, Jae S. Limdt “Signal Estimation from Modified Short Fourier Transform”, IEEE 1984, 10.1109/TASSP.1984.1164317

Examples

>>> from scipy import signal
>>> import matplotlib.pyplot as plt

Generate a test signal, a 2 Vrms sine wave at 50Hz corrupted by 0.001 V**2/Hz of white noise sampled at 1024 Hz.

>>> fs = 1024
>>> N = 10*fs
>>> nperseg = 512
>>> amp = 2 * np.sqrt(2)
>>> noise_power = 0.001 * fs / 2
>>> time = np.arange(N) / float(fs)
>>> carrier = amp * np.sin(2*np.pi*50*time)
>>> noise = np.random.normal(scale=np.sqrt(noise_power),
...                          size=time.shape)
>>> x = carrier + noise

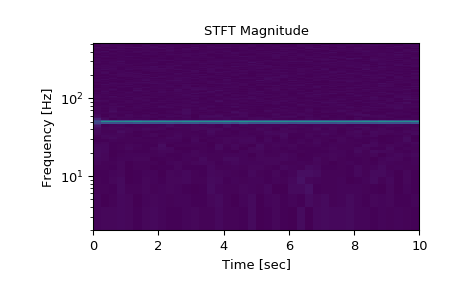
Compute the STFT, and plot its magnitude

>>> f, t, Zxx = signal.stft(x, fs=fs, nperseg=nperseg)
>>> plt.figure()
>>> plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp)
>>> plt.ylim([f[1], f[-1]])
>>> plt.title('STFT Magnitude')
>>> plt.ylabel('Frequency [Hz]')
>>> plt.xlabel('Time [sec]')
>>> plt.yscale('log')
>>> plt.show()

Zero the components that are 10% or less of the carrier magnitude, then convert back to a time series via inverse STFT

>>> Zxx = np.where(np.abs(Zxx) >= amp/10, Zxx, 0)
>>> _, xrec = signal.istft(Zxx, fs)

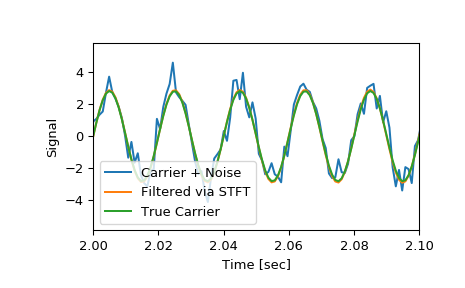
Compare the cleaned signal with the original and true carrier signals.

>>> plt.figure()
>>> plt.plot(time, x, time, xrec, time, carrier)
>>> plt.xlim([2, 2.1])
>>> plt.xlabel('Time [sec]')
>>> plt.ylabel('Signal')
>>> plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
>>> plt.show()

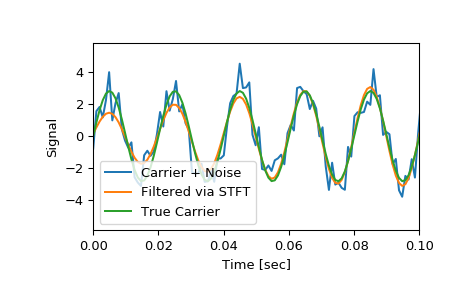
Note that the cleaned signal does not start as abruptly as the original, since some of the coefficients of the transient were also removed:

>>> plt.figure()
>>> plt.plot(time, x, time, xrec, time, carrier)
>>> plt.xlim([0, 0.1])
>>> plt.xlabel('Time [sec]')
>>> plt.ylabel('Signal')
>>> plt.legend(['Carrier + Noise', 'Filtered via STFT', 'True Carrier'])
>>> plt.show()