人工智能知识点总结
人工智能知识点总结题型第1章 绪论复习要点: 人工智能的定义、图灵测试、三大流派及其主要思想、AI学科诞生等第2章 知识表示及确定性推理复习要点:命题符号化、命题公式的计算及分类、命题公式的关系,谓词逻辑,传统推理的理论基础、三大组成部分、推理树第3章 不确定性推理复习要点:可信度及其取值含义、不确定性的传递算法及合成、带加权因子的可信度推理第4章 模糊推理复习要点:模糊集合的表示及其各种运算,贴近度,简单模糊推理的计算第5章 非单调推理复习要点:缺省理论及其分类、表示形式,TMS系统原理第6章 主观Bayes推理复习要点:LS和LN的讨论、证据确定时的推理计算、证据不确定时的推理计算第7章 机器学习复习要点:机器学习模型、决策树学习的计算(熵、最佳属性、决策树画图)、ID3算法,概念学习的相关计算(实例空间和假设空间的计算、偏序关系、FIND-S算法、树的绘制)第8章 遗传算法复习要点:遗传算法及其涉及的基本概念,了解算法步骤第9章 神经网络复习要点: 人工神经网络定义及分类、生物神经元组成部分、多层神经网络、二输入的感知器设计、三输入的感知器判断、BP网络及其学习算法、Hopfield网络分类、卷积神经网络、深度学习的模型分类、GAN对抗训练机制及其问题等
题型
填空
选择
计算
综合(设计画图)
第1章 绪论
复习要点: 人工智能的定义、图灵测试、三大流派及其主要思想、AI学科诞生等
人工智能的定义:
用人工的方法在机器(计算机)上实现的智能;或者说是人们使机器具有类似于人的智能。
强人工智能:机器真正具有人的感知、思维和意识
弱人工智能:机器只能部分模仿和实现人的智能
图灵测试:
1950年图灵发表的《计算机与智能》中设计了一个测试,用以说明人工智能的概念。
采用“问”与“答”模式,即观察者通过控制打字机向两个测试对象通话
其中一个是人,另一个是机器。要求观察者不断提出各种问题,从而辨别观察者是人还是机器
三大流派及其主要思想:
符号主义(逻辑主义,心理学派,计算机学派):
功能模拟、符号推演
人类认知的基本元素是符号,认知的过程就是符号处理的过程。
是人工智能研究中最早使用也是现在还在使用的主要方法。这种方法一般是利用显式的知识和逻辑推理来解决问题的。
连接主义(仿生学派,生理学派):
结构模拟、神经计算
结构模拟就是模拟人脑的生理结构和工作机理,实现计算机的智能。
人脑是一个动态的、开放的、高度复杂的庞大信息系统。一时还不能对它做到真正和完全模拟,只是对它的局部或近似模拟。
结构模拟法是基于人脑的生理模型,采用数值计算的方法,从微观上模拟人脑,实现机器智能
使用人工神经网络作为信息和知识的载体
用神经计算的方法实现学习、联想、识别和推理等功能
从而来模拟人脑的智能行为,使计算机表现出某种智能
行为主义(进化主义):
行为模拟、控制进化
行为模拟法基于感知-行为模型,模拟人在控制过程中的智能活动和行为特性,如自寻优、自适应、自学习、自组织等来研究和实现人工智能。
行为主义强调智能系统与环境的交互,认为智能取决于感知和行动,人的智能、机器智能可以逐步进化,但只能在现实世界中与周围环境的交互中体现出来。
智能只能放在环境中才是真正的智能,智能的高低主要表现在对环境的适应性上。
人工智能的历史回顾
神经元网络时代
通用方法时代
知识工程时代
神经网络时代
数据与网络时代
第2章 知识表示及确定性推理
复习要点:命题符号化、命题公式的计算及分类、命题公式的关系,谓词逻辑,传统推理的理论基础、三大组成部分、推理树
命题符号化: 将(复合)命题用命题标识符和联结词等符号表示
命题公式的计算及分类:
命题公式:由有限个命题常量,命题变量,联结词,括号等组成的字符串。精确定义如下:
如果
重言式、矛盾式、可满足式:
重言式(永真式):命题公式
矛盾式(永假式):命题公式
可满足式:命题公式
命题公式的关系:
等价
蕴含
谓词逻辑: 谓词逻辑表示法
e.g.
优点:
自然性
准确性
严密性
容易实现
缺点
不能表示不确定的知识
组合爆炸
效率低
应用
自动问答系统
机器人行动规划系统
机器博弈系统
问题求解系统
传统推理的理论基础:
推理是从已知事实(证据)出发,运用相关知识(或规则),逐步推导出结论的思维过程。
基于传统逻辑的推理:
原始证据是确定的
推理规则是确定的
所以结论也是确定的,又称确定性推理
人类简单推理的过程是基于传统的命题逻辑和谓词逻辑
假言推理:
假言三段论:
推理链式规则:
三大组成部分:
(传统推理技术三大组成部分)
知识库:包含一系列的规则
综合数据库:包含已知的命题
推理机:采用链式规则推理
推理树:
任何一个推理过程都可用一棵推理树表示
树节点分为:与节点、或节点
与节点:
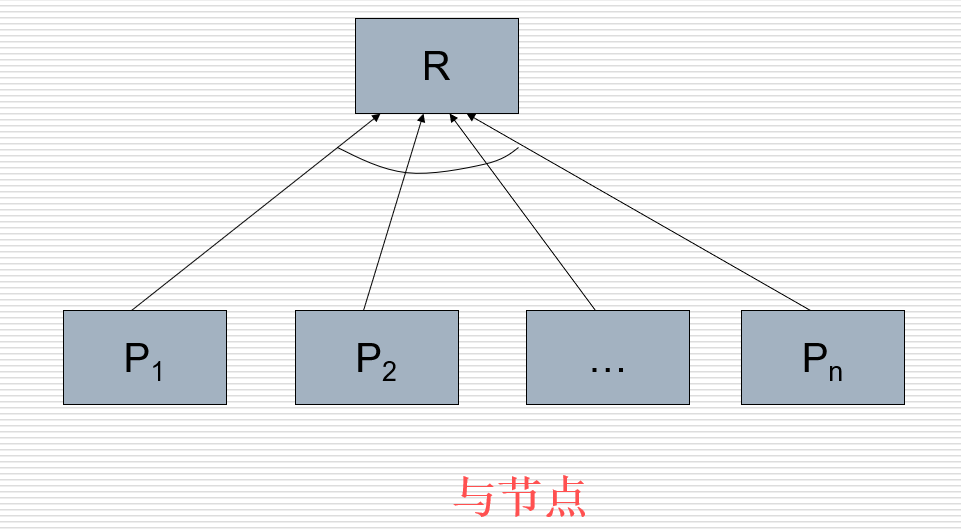
或节点:
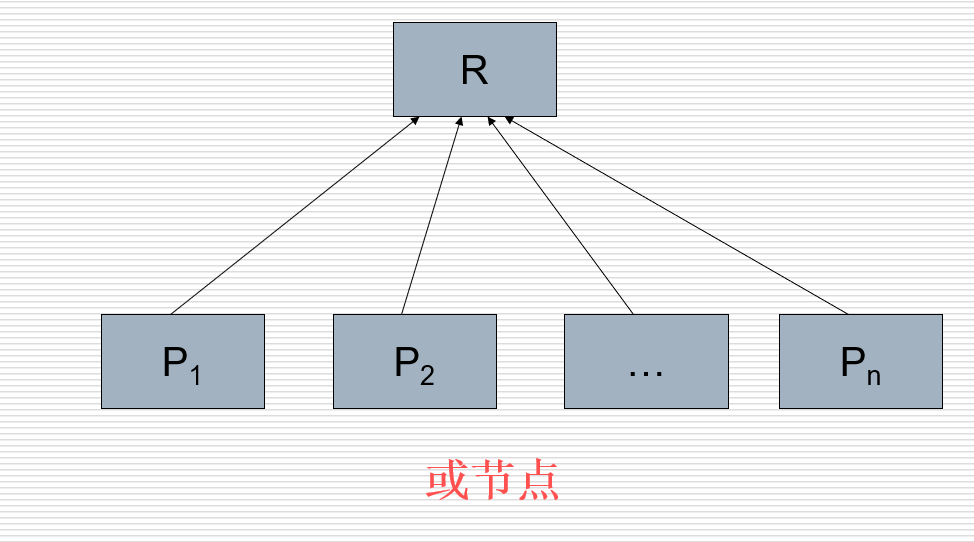
综合数据库
原始证据
对应于推理树的叶节点
只能由用户提供
不能推理得到
中间结论
对应于推理树的中间节点
最后结论
对应于推理树的根节点
以下复习要点没有,但感觉还是可以粗浅看一下
产生式表示法
确定性规则:
, 不确定性规则:
,
框架表示法
一种结构化的知识表示方法
x1框架名: <教师>2姓名: (姓、名)3年龄:4性别: range(男, 女)5缺省(男)6职称: range(教授,副教授,讲师,助教)7缺省(讲师)8部门: (系, 教研室)9住址: <住址框架>10工资: <工资框架>11开始工作时间: 单位(年、月)12
第3章 不确定性推理
复习要点:可信度及其取值含义、不确定性的传递算法及合成、带加权因子的可信度推理
可信度及其取值含义
信任增长度
不信任增长度
结论:当证据e存在时,不可能同时提高结论h的可信度增加量和不可信度增加量
可信度定义:
不确定性的传递算法及合成
可信度因子
表示证据的不确定程度
取值范围
当
当
不确定性的传递算法
结论不确定性的合成算法
利用每一条规则,分别计算
Note
此处不同于
则两条规则下的结论可信度合成公式
带加权因子的可信度推理
当
第一条公式在已经归一化的条件的条件下成立
第4章 模糊推理
复习要点:模糊集合的表示及其各种运算,贴近度,简单模糊推理的计算
模糊集合的表示及其各种运算
当映射
模糊集合的表示:
形式一
形式二
一个有限论域上可以对应无限个模糊子集,而经典子集是有限的
一个模糊子集的隶属函数的确定方法是主观的
模糊集合运算:
相等:设有两个模糊集合
包含:
并
交
补集
积
其中

答案

模糊关系
设
当论域
模糊关系矩阵的乘法(合成)
设
则
若
贴近度
令
Caution
注意:
例: 设论域
求贴近度
解:
得
模糊推理及模糊决策的计算
简单模糊推理
规则的前提
结论
知识表示形式
推理方法及步骤
首先计算
通过
如果已知证据是
计算R
极大极小原则计算
算数原则计算
设
即
即
其中
对于模糊假言推理,已知证据为
设
模糊规则为
证据为
且有
解答




模糊决策
最大隶属度法
加权平均判决法
中位数法
第5章 非单调推理
复习要点:缺省理论及其分类、表示形式,TMS系统原理
缺省理论及其分类、表示形式
规范缺省
默认条件与结论相同,由先决条件可以直接推理出结论
形式:
半规范缺省
默认条件:
规则形式:
含义:除D(x)外,由先决条件A(x)的成立,可以推导出结论C(x)的成立
不规范缺省
正确性维持系统(Truth Maintenance System,TMS)的原理
TMS在程序所产生的各个命题中,保持命题间的相容性
一旦发现命题出现不相容(矛盾),TMS就调用推理机制,回溯找到不相容的根源
修正由这一根源以前推理得到的所有命题,从而消除不相容,维持系统的正确性
在TMS中,每个命题或规则称为节点
节点的状态包括:
每个节点可以带有一个证实表(也可没有),证实表包括两种形式
支持表
只有当“
条件证明
只有当“
当推理程序得到了新证据,而且这个新证据与某个节点发生矛盾时,程序就会自动产生一个矛盾节点:矛盾
第6章 主观Bayes推理
复习要点:LS和LN的讨论、证据确定时的推理计算、证据不确定时的推理计算
产生式规则
其中
LS:充分性量度
LN:必要性量度
假设S是对E的观察

解答
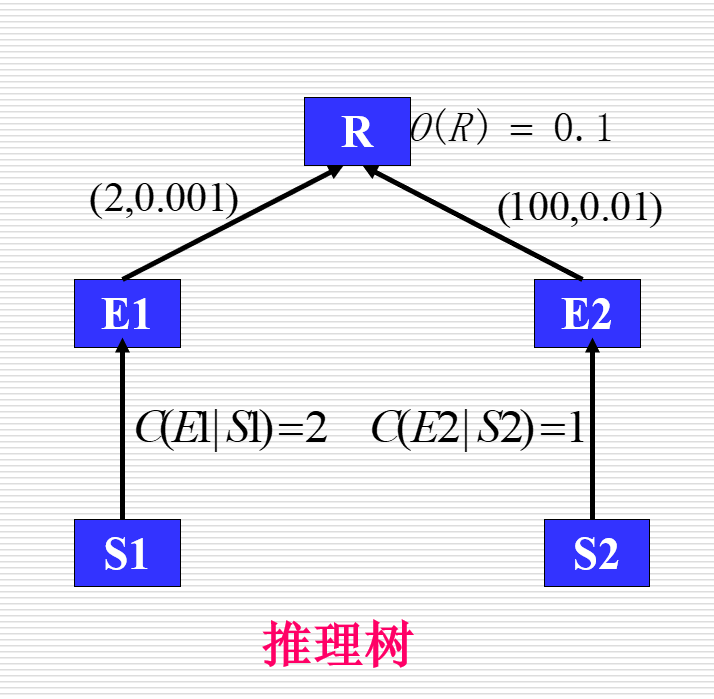



基本算法
证据
肯定存在,即
肯定不存在,即
不确定,
第7章 机器学习
复习要点:机器学习模型、决策树学习的计算(熵、最佳属性、决策树画图)、ID3算法,概念学习的相关计算(实例空间和假设空间的计算、偏序关系、FIND-S算法、树的绘制)
决策树绘画:
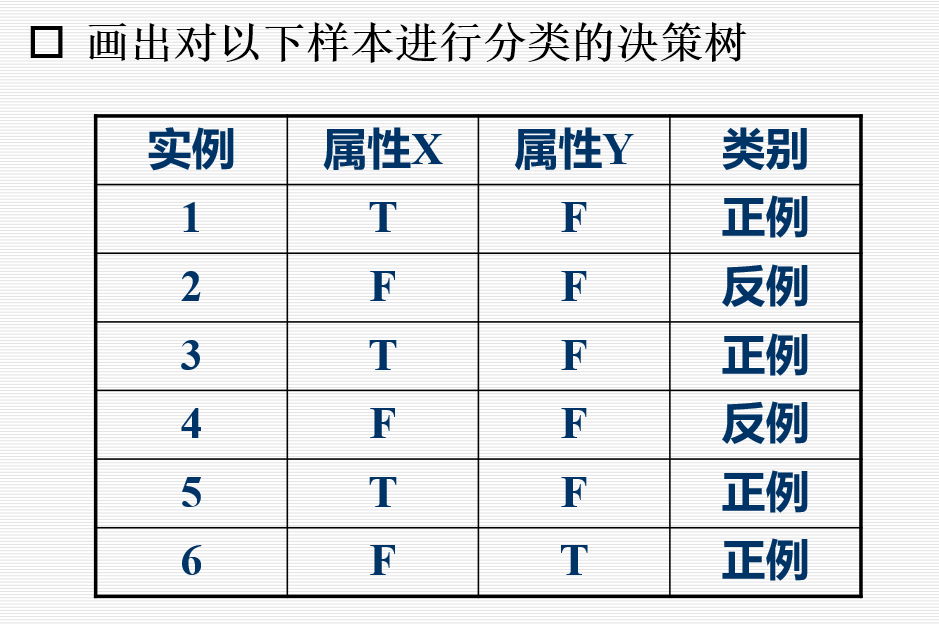
解答
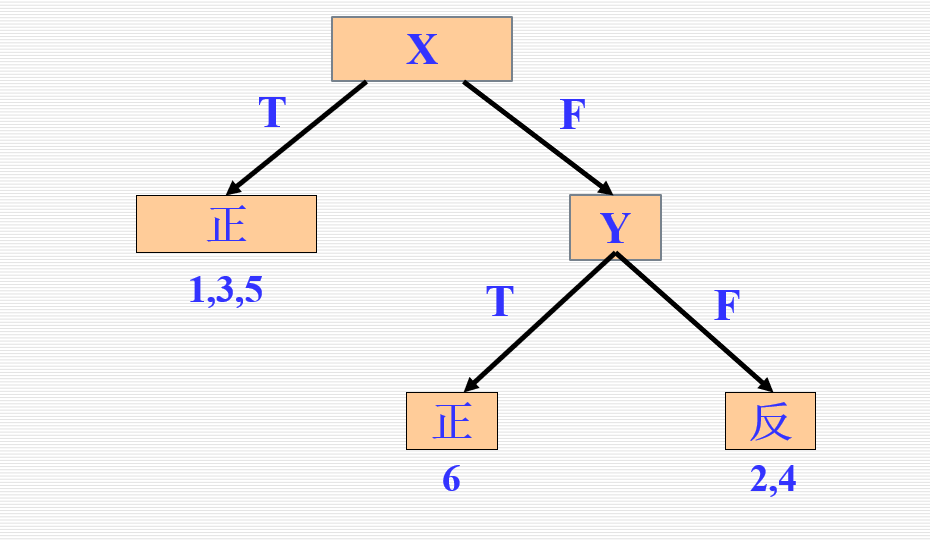
ID3算法通过自顶向下构造决策树进行学习
熵的计算:
题目跟决策树一样

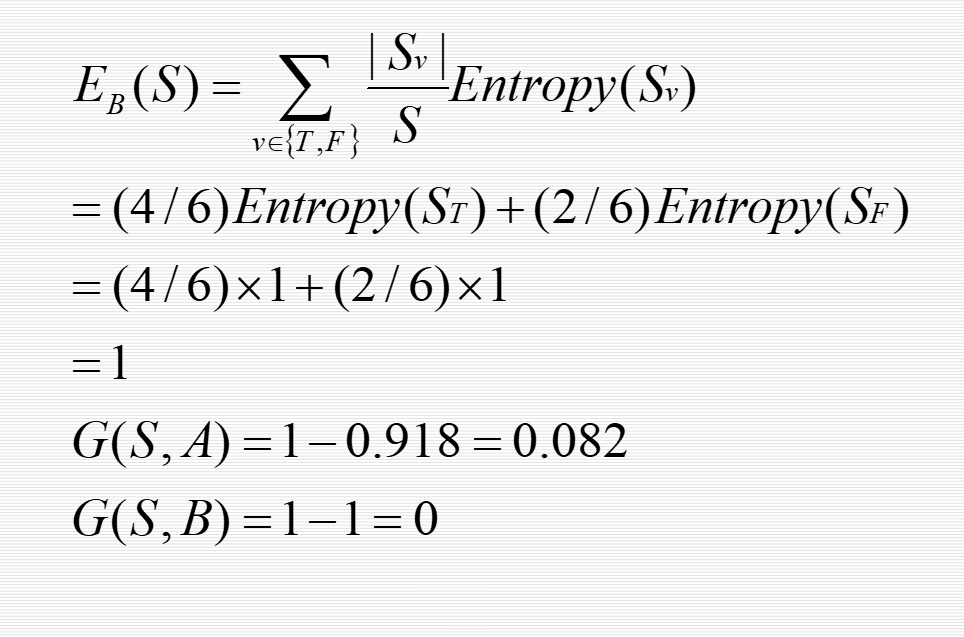
FIND-S算法:

搜索空间:
实例空间:
假设空间:
第8章 遗传算法
复习要点:遗传算法及其涉及的基本概念,了解算法步骤
第9章 神经网络
复习要点: 人工神经网络定义及分类、生物神经元组成部分、多层神经网络、二输入的感知器设计、三输入的感知器判断、BP网络及其学习算法、Hopfield网络分类、卷积神经网络、深度学习的模型分类、GAN对抗训练机制及其问题等