--- title: Rank and Nullity subtitle: Biostat 216 author: Dr. Hua Zhou @ UCLA date: today format: html: theme: cosmo embed-resources: true number-sections: true toc: true toc-depth: 4 toc-location: left code-fold: false jupyter: jupytext: formats: 'ipynb,qmd' text_representation: extension: .qmd format_name: quarto format_version: '1.0' jupytext_version: 1.15.2 kernelspec: display_name: Julia 1.9.3 language: julia name: julia-1.9 --- **Highlights**: In this lecture we will show some most important results about the rank of a matrix: 1. column rank = row rank = rank. 2. For any $\mathbf{A} \in \mathbb{R}^{m \times n}$, $\text{rank}(\mathbf{A}) \le \min \{m, n\}$. 3. Matrix multiplication can only decrease the rank: $\text{rank}(\mathbf{A} \mathbf{B}) \le \text{rank}(\mathbf{A})$ $\text{rank}(\mathbf{A} \mathbf{B}) \le \text{rank}(\mathbf{B})$. Some special cases: (1) $\text{rank}(\mathbf{A} \mathbf{B}) = \text{rank}(\mathbf{A})$ if $\mathbf{B}$ has full row rank. (2) $\text{rank}(\mathbf{A} \mathbf{B}) = \text{rank}(\mathbf{B})$ if $\mathbf{A}$ has full column rank. (3). $\text{rank}(\mathbf{A}' \mathbf{A}) = \text{rank}(\mathbf{A})$ for any $\mathbf{A}$. 4. $\text{rank}(\mathbf{A} + \mathbf{B}) \le \text{rank}(\mathbf{B}) + \text{rank}(\mathbf{B})$. 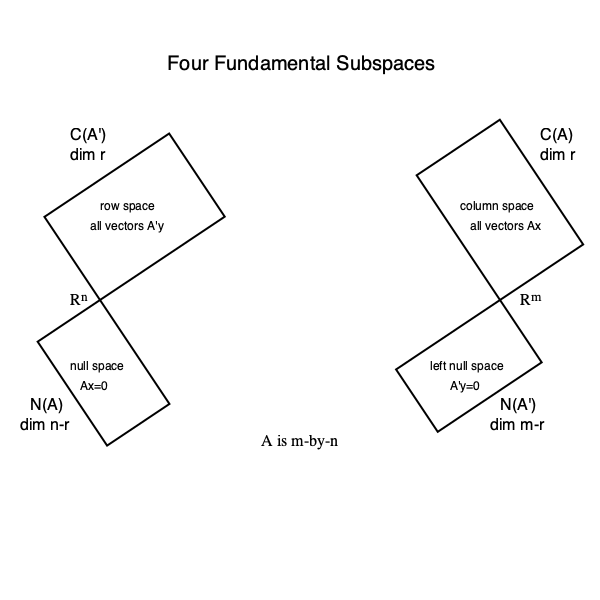5. Rank-nullity theorem: For any $\mathbf{A} \in \mathbb{R}^{m \times n}$, $\text{rank}(\mathbf{A}) + \text{nullity}(\mathbf{A}) = n$. 6. Fundamental theorem of ranks: $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}') = \text{rank}(\mathbf{A}'\mathbf{A}) = \text{rank}(\mathbf{A}\mathbf{A}')$.

```{julia} using Pkg Pkg.activate(pwd()) Pkg.instantiate() Pkg.status() ``` ```{julia} using LinearAlgebra, RDatasets, StatsModels ``` ```{julia} # the famous Fisher's Iris data # iris = dataset("datasets", "iris") ``` ```{julia} # use full dummy coding (one-hot coding) for categorical variable Species X = ModelMatrix(ModelFrame( @formula(1 ~ 1 + SepalLength + SepalWidth + PetalLength + PetalWidth + Species), iris, contrasts = Dict(:Species => StatsModels.FullDummyCoding()))).m ``` ```{julia} @show size(X) @show rank(X) @show rank(X') @show rank(X' * X) @show rank(X * X'); ``` ```{julia} # only one basis vector in N(X) nullspace(X) ``` ## Rank Let $\mathbf{A}$ be an $m \times n$ matrix \begin{eqnarray*} \mathbf{A} = \begin{pmatrix} \mid & & \mid \\ \mathbf{a}_1 & \ldots & \mathbf{a}_n \\ \mid & & \mid \end{pmatrix}. \end{eqnarray*} - The **column rank** of $\mathbf{A}$ is the maximum number of linearly independent columns of $\mathbf{A}$. In other words, column rank of $\mathbf{A}$ is $\text{dim}(\mathcal{C}(\mathbf{A}))$. - The **row rank** of $\mathbf{A}$ is the maximum number of linearly independent rows of $\mathbf{A}$. In other words, row rank of $\mathbf{A}$ is $\text{dim}(\mathcal{R}(\mathbf{A})) = \text{dim}(\mathcal{C}(\mathbf{A}'))$. - For any $m \times n$ matrix $\mathbf{A}$, its column rank is equal to the row rank, which we shall call the **rank** of $\mathbf{A}$. We will give a simple proof using rank factorization below. - For any $\mathbf{A} \in \mathbb{R}^{m \times n}$, $\text{rank}(\mathbf{A}) \le \min \{m, n\}$. ```{julia} A = [1 -2 -2; 3 -6 -6] ``` ```{julia} # column rank rank(A) ``` ```{julia} # row rank rank(A') ``` ```{julia} # another matrix @show size(X) @show rank(X) ``` - For $\mathbf{A} \in \mathbb{R}^{m \times n}$, we say $\mathbf{A}$ is **full rank** if $\text{rank}(\mathbf{A}) = \min \{m, n\}$. It is **full row rank** if $\text{rank}(\mathbf{A}) = m$. It is **full column rank** if $\text{rank}(\mathbf{A}) = n$. - A square matrix $\mathbf{A} \in \mathbb{R}^{n \times n}$ is **singular** if $\text{rank}(\mathbf{A}) < n$ and **non-singular** (or **invertible**) if $\text{rank}(\mathbf{A}) = n$. - Example: The identity matrix $$ \mathbf{I} = \begin{pmatrix} 1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 1 \end{pmatrix} $$ is full rank. ## Effects of matrix multiplication on rank - $\text{rank}(\mathbf{A}\mathbf{B}) \le \text{rank}(\mathbf{A})$ and $\text{rank}(\mathbf{A}\mathbf{B}) \le \text{rank}(\mathbf{B})$. In words, **matrix multiplication can only decrease the rank**. Proof: Because $\mathcal{C}(\mathbf{A}\mathbf{B}) \subseteq \mathcal{C}(\mathbf{A})$ (why?), we have $\text{rank}(\mathbf{A}\mathbf{B}) \le \text{rank}(\mathbf{A})$ by monotonicity of dimension. Similary, because the row space of $\mathbf{A}\mathbf{B}$ is a subset of the row space of $\mathbf{B}$, we have $\text{rank}(\mathbf{A}\mathbf{B}) \le \text{rank}(\mathbf{B})$. - $\text{rank}(\mathbf{A}\mathbf{B}) = \text{rank}(\mathbf{A})$ if $\mathbf{B}$ is square and of full rank. More general, **left-multiplying by a matrix with full column rank or right-multiplying by a matrix of full row rank does not change rank**. Proof (optional): We show the more general statement. Assume $\mathbf{B} \in \mathbb{R}^{m \times n}$ has full row rank, we want to show $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}\mathbf{B})$. Since $\mathbf{B} \in \mathbb{R}^{m \times n}$ has full row rank, there exists a permutation matrix $\mathbf{P} \in \{0,1\}^{n \times n}$ such that $$ \mathbf{B} \mathbf{P} = \begin{pmatrix} \mathbf{B}_1 : \mathbf{B}_2 \end{pmatrix}, $$ where $\mathbf{B}_1 \in \mathbb{R}^{m \times m}$ is non-singular and $\mathbf{B}_2 \in \mathbb{R}^{m \times (n-m)}$. Then $$ \text{rank}(\mathbf{A}) \ge \text{rank}(\mathbf{A}\mathbf{B}) = \text{rank}(\mathbf{A} \begin{pmatrix} \mathbf{B}_1 : \mathbf{B}_2 \end{pmatrix} \mathbf{P}') \ge \text{rank} \left( \mathbf{A} \begin{pmatrix} \mathbf{B}_1 : \mathbf{B}_2 \end{pmatrix} \mathbf{P}' \mathbf{P} \begin{pmatrix} \mathbf{B}_1^{-1} \\ \mathbf{O} \end{pmatrix} \right) = \text{rank} (\mathbf{A} \mathbf{I}_m) = \text{rank} (\mathbf{A}). $$ Thus $\text{rank}(\mathbf{A}) = \text{rank} (\mathbf{A} \mathbf{B})$. Proof for the other half of the statement follows the same argument. - Example: 2019 qual. exam Q1. ```{julia} A = [1 -2 -2; 3 -6 -6] ``` ```{julia} rank(A) ``` ```{julia} # this B does not have full row rank B = [2 2; 1 0; 0 1] ``` ```{julia} rank(A * B) ``` ```{julia} # B has full row rank B = [2 2 0; 1 0 0; 0 1 1] ``` ```{julia} # A * B preserves rank of A rank(A * B) ``` ## Rank-nullity theorem - The **nullity** of a matrix $\mathbf{A}$ is the dimension of its null space $$ \text{nullity}(\mathbf{A}) = \text{dim}(\mathcal{N}(\mathbf{A})). $$ - Let $\mathbf{A} \in \mathbb{R}^{m \times n}$, then $$ \text{rank}(\mathbf{A}) + \text{nullity}(\mathbf{A}) = n. $$ Proof (optional): Denote $\nu = \text{nullity}(\mathbf{A}) = \text{dim}(\mathcal{N}(\mathbf{A}))$. Let $\mathbf{X} \in \mathbb{R}^{n \times n}$ be $$ \mathbf{X} = \begin{pmatrix} \mathbf{X}_1 : \mathbf{X}_2 \end{pmatrix}, $$ where columns of $\mathbf{X}_1 \in \mathbb{R}^{n \times \nu}$ form a basis of $\mathcal{N}(\mathbf{A})$ and columns of $\mathbf{X}_2 \in \mathbb{R}^{n \times (n - \nu)}$ extend those in $\mathbf{X}_1$ to be a basis of $\mathbb{R}^n$. We show columns of $\mathbf{A} \mathbf{X}_2$ form a basis of $\mathcal{C}(\mathbf{A})$. Thus $\text{rank}(\mathbf{A}) = \text{dim}(\mathcal{C}(\mathbf{A})) = n - \nu$. (1) To show that columns of $\mathbf{A} \mathbf{X}_2$ are linearly independent. Assume $\mathbf{A} \mathbf{X}_2 \mathbf{v} = \mathbf{0}$. Then $\mathbf{X}_2 \mathbf{v} \in \mathcal{N}(\mathbf{A}) = \mathcal{C}(\mathbf{X}_1)$. Thus $\mathbf{X}_2 \mathbf{v} = \mathbf{X}_1 \mathbf{u}$ for some $\mathbf{u}$, or equivalently, $$ \begin{pmatrix} \mathbf{X}_1 : \mathbf{X}_2 \end{pmatrix} \begin{pmatrix} -\mathbf{u} \\ \mathbf{v} \end{pmatrix} = \mathbf{0}_n. $$ Since the matrix $\begin{pmatrix} \mathbf{X}_1 : \mathbf{X}_2 \end{pmatrix}$ is non-singular, we must have $\mathbf{u}=\mathbf{0}$ and $\mathbf{v}=\mathbf{0}$. This shows that $\mathbf{v}=\mathbf{0}$ whenever $\mathbf{A} \mathbf{X}_2 \mathbf{v} = \mathbf{0}$. So the columns of $\mathbf{A} \mathbf{X}_2$ are linearly independent. (2) Next we show the columns of $\mathbf{A} \mathbf{X}_2$ span $\mathcal{C}(\mathbf{A})$ by showing $\mathcal{C}(\mathbf{A} \mathbf{X}_2) \subseteq \mathcal{C}(\mathbf{A})$ and $\mathcal{C}(\mathbf{A} \mathbf{X}_2) \supseteq \mathcal{C}(\mathbf{A})$. One direction $\mathcal{C}(\mathbf{A} \mathbf{X}_2) \subseteq \mathcal{C}(\mathbf{A})$ is easy. To show the other direction $\mathcal{C}(\mathbf{A}) \subseteq \mathcal{C}(\mathbf{A} \mathbf{X}_2)$, let $\mathbf{w} \in \mathcal{C}(\mathbf{A})$. Then $\mathbf{w} = \mathbf{A} \mathbf{y}$ for some vector $\mathbf{y}$. Because $\mathbf{y} \in \mathbb{R}^n$, which is spanned by columns of $\mathbf{X}$, we can write $\mathbf{y} = \mathbf{X}_1 \mathbf{z}_1 + \mathbf{X}_2 \mathbf{z}_2$ for some vectors $\mathbf{z}_1$ and $\mathbf{z}_2$. Thus $\mathbf{w} = \mathbf{A} \mathbf{X}_1 \mathbf{z}_1 + \mathbf{A} \mathbf{X}_2 \mathbf{z}_2 = \mathbf{A} \mathbf{X}_2 \mathbf{z}_2 \in \mathcal{C}(\mathbf{A} \mathbf{X}_2)$. This proves $\mathcal{C}(\mathbf{A}) \subseteq \mathcal{C}(\mathbf{A} \mathbf{X}_2)$. ```{julia} A = [1 -2 -2; 3 -6 -6] ``` ```{julia} rank(A) ``` ```{julia} nullity = size(nullspace(A), 2) ``` ## Fundamental theorem of ranks (important) - $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}') = \text{rank}(\mathbf{A}'\mathbf{A}) = \text{rank}(\mathbf{A}\mathbf{A}')$. Proof: $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}')$ by definition of rank (row rank = column rank = rank). Early on we showed $\mathcal{N}(\mathbf{A}'\mathbf{A}) = \mathcal{N}(\mathbf{A})$. Thus $\text{nullity}(\mathbf{A}'\mathbf{A}) = \text{nullity}(\mathbf{A})$. Then by the rank-nullity theorem, $\text{rank}(\mathbf{A}'\mathbf{A}) = \text{rank}(\mathbf{A})$. - Matrices of form $\mathbf{A}'\mathbf{A}$ or $\mathbf{A}\mathbf{A}'$ are called the **Gram matrix** or **Gramian matrix**. ```{julia} A = [1 -2 -2; 3 -6 -6] ``` ```{julia} rank(A) ``` ```{julia} A'A ``` ```{julia} rank(A'A) ``` ```{julia} A * A' ``` ```{julia} rank(A * A') ``` ## Rank factorization (important) - Let $\mathbf{A} \in \mathbb{R}^{m \times n}$ with (column) rank $r \ge 1$. The product $\mathbf{A} = \mathbf{C} \mathbf{R}$, where $\mathbf{C} \in \mathbb{R}^{m \times r}$ and $\mathbf{R} \in \mathbb{R}^{r \times n}$ is called a **rank decomposition** or **rank factorization** of $\mathbf{A}$. - Visualize (TODO): $$ \mathbf{A} = \begin{pmatrix} | & & | \\ \mathbf{c}_1 & \cdots & \mathbf{c}_r \\ | & & | \end{pmatrix} \begin{pmatrix} - & \mathbf{r}_1' & - \\ & \vdots & \\ - & \mathbf{r}_r' & - \end{pmatrix}. $$ - **Existence of rank factorization.** Any non-null matrix has a rank decomposition. To construct one, let columns of \begin{eqnarray*} \mathbf{C} = \begin{pmatrix} \mid & & \mid \\ \mathbf{c}_1 & \cdots & \mathbf{c}_r \\ \mid & & \mid \end{pmatrix} \end{eqnarray*} be a basis of $\mathcal{C}(\mathbf{A})$. Then $\mathcal{C}(\mathbf{A}) \subseteq \mathcal{C}(\mathbf{C})$. Thus there exists $\mathbf{R}$ such that $\mathbf{A} = \mathbf{C} \mathbf{R}$. - Is rank factorization unique? No. $\mathbf{A} = \mathbf{C} \mathbf{R} = (\mathbf{C} \mathbf{M}) (\mathbf{M}^{-1} \mathbf{R})$ for any non-singular matrix $\mathbf{M}^{r \times r}$. - Suppose $\mathbf{A}$ has column rank $r > 0$ and rank factorization $\mathbf{A} = \mathbf{C} \mathbf{R}$. Then \begin{eqnarray*} & & \text{row rank of } \mathbf{A} \\ &=& \text{column rank of } \mathbf{A}' \\ &=& \text{column rank of } \mathbf{R}' \mathbf{C}' \\ &\le& \text{column rank of } \mathbf{R}' \quad \quad (\text{right matrix multiplication shrinks column space}) \\ &\le& r \\ &=& \text{column rank of } \mathbf{A}. \end{eqnarray*} Now applying the above conclusion to matrix $\mathbf{A}'$, we have $$ \text{row rank of } \mathbf{A}' \le \text{column rank of } \mathbf{A}', $$ i.e., $$ \text{column rank of } \mathbf{A} \le \text{row rank of } \mathbf{A}. $$ Thus we have a proof of the famous result $\text{rank}(\mathbf{A}) = \text{rank}(\mathbf{A}')$. - Let $\text{rank}(\mathbf{A}) = r$ and $\mathbf{A} = \mathbf{C} \mathbf{R}$ be a rank factorization. Then 1. $\text{rank}(\mathbf{C}) = \text{rank}(\mathbf{R}) = r$, 2. $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{C})$, $\mathcal{C}(\mathbf{A}') = \mathcal{C}(\mathbf{R}')$ and $\mathcal{N}(\mathbf{A}) = \mathcal{N}(\mathbf{R})$. Proof of 1: $r = \text{rank}(\mathbf{A}) = \text{rank}(\mathbf{C}\mathbf{R}) \le \text{rank}(\mathbf{C}) \le r$. Thus $\text{rank}(\mathbf{C}) = r$. Similarly $\text{rank}(\mathbf{R}) = r$. Proof of 2 (optional): $\mathcal{C}(\mathbf{A}) \subseteq \mathcal{C}(\mathbf{C})$ is trivial. Suppose $\mathcal{C}(\mathbf{C})$ is strictly larger than $\mathcal{C}(\mathbf{A})$. Then there exists vector $\mathbf{v} \in \mathcal{C}(\mathbf{C})$ that is not a linear combination of columns of $\mathbf{A}$. Let $\mathbf{u}_1, \ldots, \mathbf{u}_r$ be a basis of $\mathcal{C}(\mathbf{A})$. Then the $r+1$ vectors $\mathbf{u}_1, \ldots, \mathbf{u}_r, \mathbf{v}$ is an independent set in $\mathcal{C}(\mathbf{C})$, contadicting the fact $\text{rank}(\mathbf{C}) = r$. Therefore we must have $\mathcal{C}(\mathbf{A}) = \mathcal{C}(\mathbf{C})$. Similar argument shows $\mathcal{C}(\mathbf{A}') = \mathcal{C}(\mathbf{R}')$. To show $\mathcal{N}(\mathbf{A}) = \mathcal{N}(\mathbf{R})$, one direction $\mathcal{N}(\mathbf{A}) \supseteq \mathcal{N}(\mathbf{R})$ is trivial (why?). To show the other direction, \begin{eqnarray*} & & \mathbf{x} \in \mathcal{N}(\mathbf{A}) \\ &\Rightarrow& \mathbf{A} \mathbf{x} = \mathbf{0} \\ &\Rightarrow& \mathbf{C} \mathbf{R} \mathbf{x} = \mathbf{0} \\ &\Rightarrow& \mathbf{R} \mathbf{x} \in \mathcal{N}(\mathbf{C}). \end{eqnarray*} But by the rank-nullity theorem, $\text{nullity}(\mathbf{C}) = r - \text{rank}(\mathbf{C}) = 0$. Thus $\mathbf{R} \mathbf{x} = \mathbf{0}$, that is $\mathbf{x} \in \mathcal{N}(\mathbf{R})$. We have shown $\mathcal{N}(\mathbf{A}) \subseteq \mathcal{N}(\mathbf{R})$. ```{julia} A = [1 -2 -2; 3 -6 -6] ``` ```{julia} C = [1; 3] ``` ```{julia} R = [1 -2 -2] ``` ```{julia} C * R ```