---
title: Determinant (BR Chapter 10)
subtitle: Biostat 216
author: Dr. Hua Zhou @ UCLA
date: today
format:
html:
theme: cosmo
embed-resources: true
number-sections: true
toc: true
toc-depth: 4
toc-location: left
code-fold: false
jupyter:
jupytext:
formats: 'ipynb,qmd'
text_representation:
extension: .qmd
format_name: quarto
format_version: '1.0'
jupytext_version: 1.15.2
kernelspec:
display_name: Julia 1.9.3
language: julia
name: julia-1.9
---
```{julia}
using Pkg
Pkg.activate(pwd())
Pkg.instantiate()
Pkg.status()
```
```{julia}
using LinearAlgebra, Plots, Symbolics
```
We review some basic facts about matrix determinant.
## Definition of determinant
- The **determinant** of a square matrix $\mathbf{A} \in \mathbb{R}^{n \times n}$ is
$$
\det (\mathbf{A}) = \sum (-1)^{\phi(j_1,\ldots,j_n)} \prod_{i=1}^n a_{ij_i},
$$
where the summation is over all permutation $(j_1, \ldots, j_n)$ of the set of integers $(1,\ldots,n)$ and $\phi(j_1,\ldots,j_n)$ is the number of transpositions to change $(1,\ldots,n)$ to $(j_1,\ldots,j_n)$. $(-1)^{\phi(j_1,\ldots,j_n)}$ is also called the **sign of permutation**.
- Examples: $n = 2$ and 3.
$$
\det \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = (-1)^{\phi(1,2)} a_{11} a_{22} + (-1)^{\phi(2,1)} a_{12} a_{21} = a_{11} a_{22} - a_{12} a_{21}.
$$
```{julia}
# n = 2
@variables A[1:2, 1:2]
```
```{julia}
det(A) |> Symbolics.scalarize
```
```{julia}
# n = 3
@variables A[1:3, 1:3]
```
```{julia}
det(A) |> Symbolics.scalarize |> expand
```
```{julia}
# n = 4
@variables A[1:4, 1:4]
```
```{julia}
det(A) |> Symbolics.scalarize |> expand
```
## Some interpretations of determinant
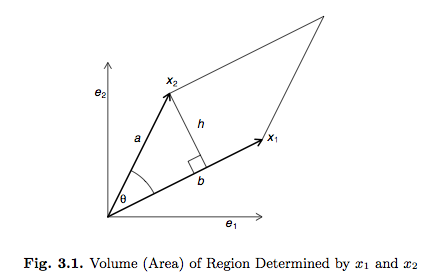 - Interpretation of the (absolute value of) determinant as the **volume of the parallelotope** defined by the columns of the matrix. For example, if $\mathbf{X} \in \mathbb{R}^2$ has two columns $\mathbf{x}_1$ and $\mathbf{x}_2$, then
\begin{eqnarray*}
\text{area} &=& bh = \|\mathbf{x}_1\|\|\mathbf{x}_2\| \sin(\theta) \\
&=& \|\mathbf{x}_1\| \|\mathbf{x}_2\| \sqrt{1 - \left( \frac{\langle \mathbf{x}_1, \mathbf{x}_2 \rangle}{\|\mathbf{x}_1\| \|\mathbf{x}_2\|} \right)^2} \\
&=& \sqrt{\|\mathbf{x}_1\|^2 \|\mathbf{x}\|^2 - (\langle \mathbf{x}_1, \mathbf{x}_2\rangle)^2} \\
&=& \sqrt{(x_{11}^2 + x_{12}^2)(x_{21}^2+x_{22}^2) - (x_{11}x_{21} + x_{12}x_{22})^2} \\
&=& |x_{11} x_{22} - x_{12} x_{21}| \\
&=& |\det(\mathbf{X})|.
\end{eqnarray*}
- Interpretation of the (absolute value of) determinant as the **volume of the parallelotope** defined by the columns of the matrix. For example, if $\mathbf{X} \in \mathbb{R}^2$ has two columns $\mathbf{x}_1$ and $\mathbf{x}_2$, then
\begin{eqnarray*}
\text{area} &=& bh = \|\mathbf{x}_1\|\|\mathbf{x}_2\| \sin(\theta) \\
&=& \|\mathbf{x}_1\| \|\mathbf{x}_2\| \sqrt{1 - \left( \frac{\langle \mathbf{x}_1, \mathbf{x}_2 \rangle}{\|\mathbf{x}_1\| \|\mathbf{x}_2\|} \right)^2} \\
&=& \sqrt{\|\mathbf{x}_1\|^2 \|\mathbf{x}\|^2 - (\langle \mathbf{x}_1, \mathbf{x}_2\rangle)^2} \\
&=& \sqrt{(x_{11}^2 + x_{12}^2)(x_{21}^2+x_{22}^2) - (x_{11}x_{21} + x_{12}x_{22})^2} \\
&=& |x_{11} x_{22} - x_{12} x_{21}| \\
&=& |\det(\mathbf{X})|.
\end{eqnarray*}
 - Another interpretation of the determinant is the volume changing factor when operating on a set in $\mathbb{R}^n$. $\text{vol}(f(S)) = |\det(\mathbf{A})| \text{vol}(S)$ where $f: \mathbb{R}^n \mapsto \mathbb{R}^n$ is the linear mapping defined by $\mathbf{A}$.
- Recall that for differentiable function $f: \mathbb{R}^n \mapsto \mathbb{R}^n$, the **Jacobian matrix** $\operatorname{D} f(\mathbf{x}) \in \mathbb{R}^{n \times n}$ is
$$
\operatorname{D} f(\mathbf{x}) = \begin{pmatrix}
\frac{\partial f_1}{\partial x_1} (\mathbf{x}) & \frac{\partial f_1}{\partial x_2} (\mathbf{x}) & \cdots & \frac{\partial f_1}{\partial x_n} (\mathbf{x}) \\
\frac{\partial f_2}{\partial x_1} (\mathbf{x}) & \frac{\partial f_2}{\partial x_2} (\mathbf{x}) & \cdots & \frac{\partial f_2}{\partial x_n} (\mathbf{x}) \\
\vdots & \vdots & & \vdots \\
\frac{\partial f_n}{\partial x_1} (\mathbf{x}) & \frac{\partial f_n}{\partial x_2} (\mathbf{x}) & \cdots & \frac{\partial f_n}{\partial x_n} (\mathbf{x})
\end{pmatrix} = \begin{pmatrix}
\nabla f_1(\mathbf{x})' \\
\nabla f_2(\mathbf{x})' \\
\vdots \\
\nabla f_n(\mathbf{x})'
\end{pmatrix}.
$$
Its determinant, the **Jacobian determinant**, appears in the higher-dimensional version of **integration by substitution** or **change of variable**
$$
\int_{f(U)} \phi(\mathbf{v}) \, \operatorname{d} \mathbf{v} = \int_U \phi(f(\mathbf{u})) | \det \operatorname{D} f(\mathbf{u})| \, \operatorname{d} \mathbf{u}
$$
for function $\phi: \mathbb{R}^n \mapsto \mathbb{R}$. This result will be used in transformation of random variables in 202A.
For an example of $n=1$, an indefinite integral can be transformed to a definite integral over box [-1,1] via change of variable $v = u / (1-u^2)$:
$$
\int_{-\infty}^\infty f(v) \, dv = \int_{-1}^1 f\left(\frac{u}{1-u^2}\right) \frac{1+u^2}{(1-u^2)^2} \, du.
$$
## Some properties of determinant (important)
- The determinant of a **lower or upper triangular matrix** $\mathbf{A}$ is the product of the diagonal elements $\prod_{i=1}^n a_{ii}$. (Why?)
- Any square matrix $\mathbf{A}$ is singular if and only if $\det(\mathbf{A}) = 0$.
Proof (optional): see BR p287.
- Product rule: $\det(\mathbf{A} \mathbf{B}) = \det(\mathbf{A}) \det(\mathbf{B})$.
Proof (optional): see BR p288-289.
Product rule is extremely useful. For example, computer calculates the determinant of a square matrix $\mathbf{A}$ by first computing the LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U}$ and then $\det(\mathbf{A}) = \det(\mathbf{L}) \det(\mathbf{U})$.
- Determinant of an orthogonal matrix is 1 (**rotation**) or -1 (**reflection**).
This classifies orthogonal matrices into two classes: rotations and reflections.
```{julia}
# a rotator
θ = π/4
A = [cos(θ) -sin(θ);
sin(θ) cos(θ)]
```
```{julia}
det(A)
```
```{julia}
# a reflector
B = [cos(θ) sin(θ);
sin(θ) -cos(θ)]
```
```{julia}
B'B
```
```{julia}
det(B)
```
```{julia}
# 3 points for a triangle
X = [1 1 2 1; 1 3 1 1]
# rotation
Xrot = A * X
# reflection
Xref = B * X
```
```{julia}
plt = plot(X[1, :], X[2, :], color = :blue,
legend = :none, xlims = (-3, 3), ylims = (-3, 3),
xticks = -3:1:3, yticks = -3:1:3,
framestyle = :origin,
aspect_ratio = :equal)
plot!(plt, Xrot[1, :], Xrot[2, :])
plot!(plt, Xref[1, :], Xref[2, :],
annotations = [(-1.5, 2, "rotation"), (2, -1.75, "reflection")])
```
- $\det(\mathbf{A}') = \det(\mathbf{A})$.
- $\det(\mathbf{A}^{-1}) = 1/\det(\mathbf{A})$.
- $\det(c\mathbf{A}) = c^n \det(\mathbf{A})$.
- Determinant of a permutation matrix is the sign of the corresponding permutation.
- Determinant of triangular block matrix
\begin{eqnarray*}
\det \left( \begin{pmatrix}
\mathbf{A} & \mathbf{B} \\
\mathbf{O} & \mathbf{D}
\end{pmatrix} \right) = \det (\mathbf{A}) \det (\mathbf{D}).
\end{eqnarray*}
- For $\mathbf{A}$ and $\mathbf{D}$ square and nonsingular,
\begin{eqnarray*}
\det \left( \begin{pmatrix}
\mathbf{A} & \mathbf{B} \\
\mathbf{C} & \mathbf{D}
\end{pmatrix} \right) = \det (\mathbf{A}) \det (\mathbf{D} - \mathbf{C} \mathbf{A}^{-1} \mathbf{B}) = \det(\mathbf{D}) \det(\mathbf{A} - \mathbf{B} \mathbf{D}^{-1} \mathbf{C}).
\end{eqnarray*}
Proof: Take determinant on the both sides of the matrix identity
\begin{eqnarray*}
\begin{pmatrix}
\mathbf{A} & \mathbf{0} \\
\mathbf{0} & \mathbf{D} - \mathbf{C} \mathbf{A}^{-1} \mathbf{B}
\end{pmatrix} = \begin{pmatrix}
\mathbf{I} & \mathbf{0} \\ - \mathbf{C} \mathbf{A}^{-1} & \mathbf{I}
\end{pmatrix} \begin{pmatrix}
\mathbf{A} & \mathbf{B} \\
\mathbf{C} & \mathbf{D}
\end{pmatrix} \begin{pmatrix}
\mathbf{I} & - \mathbf{A}^{-1} \mathbf{B} \\
\mathbf{0} & \mathbf{I}
\end{pmatrix}.
\end{eqnarray*}
- Another interpretation of the determinant is the volume changing factor when operating on a set in $\mathbb{R}^n$. $\text{vol}(f(S)) = |\det(\mathbf{A})| \text{vol}(S)$ where $f: \mathbb{R}^n \mapsto \mathbb{R}^n$ is the linear mapping defined by $\mathbf{A}$.
- Recall that for differentiable function $f: \mathbb{R}^n \mapsto \mathbb{R}^n$, the **Jacobian matrix** $\operatorname{D} f(\mathbf{x}) \in \mathbb{R}^{n \times n}$ is
$$
\operatorname{D} f(\mathbf{x}) = \begin{pmatrix}
\frac{\partial f_1}{\partial x_1} (\mathbf{x}) & \frac{\partial f_1}{\partial x_2} (\mathbf{x}) & \cdots & \frac{\partial f_1}{\partial x_n} (\mathbf{x}) \\
\frac{\partial f_2}{\partial x_1} (\mathbf{x}) & \frac{\partial f_2}{\partial x_2} (\mathbf{x}) & \cdots & \frac{\partial f_2}{\partial x_n} (\mathbf{x}) \\
\vdots & \vdots & & \vdots \\
\frac{\partial f_n}{\partial x_1} (\mathbf{x}) & \frac{\partial f_n}{\partial x_2} (\mathbf{x}) & \cdots & \frac{\partial f_n}{\partial x_n} (\mathbf{x})
\end{pmatrix} = \begin{pmatrix}
\nabla f_1(\mathbf{x})' \\
\nabla f_2(\mathbf{x})' \\
\vdots \\
\nabla f_n(\mathbf{x})'
\end{pmatrix}.
$$
Its determinant, the **Jacobian determinant**, appears in the higher-dimensional version of **integration by substitution** or **change of variable**
$$
\int_{f(U)} \phi(\mathbf{v}) \, \operatorname{d} \mathbf{v} = \int_U \phi(f(\mathbf{u})) | \det \operatorname{D} f(\mathbf{u})| \, \operatorname{d} \mathbf{u}
$$
for function $\phi: \mathbb{R}^n \mapsto \mathbb{R}$. This result will be used in transformation of random variables in 202A.
For an example of $n=1$, an indefinite integral can be transformed to a definite integral over box [-1,1] via change of variable $v = u / (1-u^2)$:
$$
\int_{-\infty}^\infty f(v) \, dv = \int_{-1}^1 f\left(\frac{u}{1-u^2}\right) \frac{1+u^2}{(1-u^2)^2} \, du.
$$
## Some properties of determinant (important)
- The determinant of a **lower or upper triangular matrix** $\mathbf{A}$ is the product of the diagonal elements $\prod_{i=1}^n a_{ii}$. (Why?)
- Any square matrix $\mathbf{A}$ is singular if and only if $\det(\mathbf{A}) = 0$.
Proof (optional): see BR p287.
- Product rule: $\det(\mathbf{A} \mathbf{B}) = \det(\mathbf{A}) \det(\mathbf{B})$.
Proof (optional): see BR p288-289.
Product rule is extremely useful. For example, computer calculates the determinant of a square matrix $\mathbf{A}$ by first computing the LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U}$ and then $\det(\mathbf{A}) = \det(\mathbf{L}) \det(\mathbf{U})$.
- Determinant of an orthogonal matrix is 1 (**rotation**) or -1 (**reflection**).
This classifies orthogonal matrices into two classes: rotations and reflections.
```{julia}
# a rotator
θ = π/4
A = [cos(θ) -sin(θ);
sin(θ) cos(θ)]
```
```{julia}
det(A)
```
```{julia}
# a reflector
B = [cos(θ) sin(θ);
sin(θ) -cos(θ)]
```
```{julia}
B'B
```
```{julia}
det(B)
```
```{julia}
# 3 points for a triangle
X = [1 1 2 1; 1 3 1 1]
# rotation
Xrot = A * X
# reflection
Xref = B * X
```
```{julia}
plt = plot(X[1, :], X[2, :], color = :blue,
legend = :none, xlims = (-3, 3), ylims = (-3, 3),
xticks = -3:1:3, yticks = -3:1:3,
framestyle = :origin,
aspect_ratio = :equal)
plot!(plt, Xrot[1, :], Xrot[2, :])
plot!(plt, Xref[1, :], Xref[2, :],
annotations = [(-1.5, 2, "rotation"), (2, -1.75, "reflection")])
```
- $\det(\mathbf{A}') = \det(\mathbf{A})$.
- $\det(\mathbf{A}^{-1}) = 1/\det(\mathbf{A})$.
- $\det(c\mathbf{A}) = c^n \det(\mathbf{A})$.
- Determinant of a permutation matrix is the sign of the corresponding permutation.
- Determinant of triangular block matrix
\begin{eqnarray*}
\det \left( \begin{pmatrix}
\mathbf{A} & \mathbf{B} \\
\mathbf{O} & \mathbf{D}
\end{pmatrix} \right) = \det (\mathbf{A}) \det (\mathbf{D}).
\end{eqnarray*}
- For $\mathbf{A}$ and $\mathbf{D}$ square and nonsingular,
\begin{eqnarray*}
\det \left( \begin{pmatrix}
\mathbf{A} & \mathbf{B} \\
\mathbf{C} & \mathbf{D}
\end{pmatrix} \right) = \det (\mathbf{A}) \det (\mathbf{D} - \mathbf{C} \mathbf{A}^{-1} \mathbf{B}) = \det(\mathbf{D}) \det(\mathbf{A} - \mathbf{B} \mathbf{D}^{-1} \mathbf{C}).
\end{eqnarray*}
Proof: Take determinant on the both sides of the matrix identity
\begin{eqnarray*}
\begin{pmatrix}
\mathbf{A} & \mathbf{0} \\
\mathbf{0} & \mathbf{D} - \mathbf{C} \mathbf{A}^{-1} \mathbf{B}
\end{pmatrix} = \begin{pmatrix}
\mathbf{I} & \mathbf{0} \\ - \mathbf{C} \mathbf{A}^{-1} & \mathbf{I}
\end{pmatrix} \begin{pmatrix}
\mathbf{A} & \mathbf{B} \\
\mathbf{C} & \mathbf{D}
\end{pmatrix} \begin{pmatrix}
\mathbf{I} & - \mathbf{A}^{-1} \mathbf{B} \\
\mathbf{0} & \mathbf{I}
\end{pmatrix}.
\end{eqnarray*}
 - Interpretation of the (absolute value of) determinant as the **volume of the parallelotope** defined by the columns of the matrix. For example, if $\mathbf{X} \in \mathbb{R}^2$ has two columns $\mathbf{x}_1$ and $\mathbf{x}_2$, then
\begin{eqnarray*}
\text{area} &=& bh = \|\mathbf{x}_1\|\|\mathbf{x}_2\| \sin(\theta) \\
&=& \|\mathbf{x}_1\| \|\mathbf{x}_2\| \sqrt{1 - \left( \frac{\langle \mathbf{x}_1, \mathbf{x}_2 \rangle}{\|\mathbf{x}_1\| \|\mathbf{x}_2\|} \right)^2} \\
&=& \sqrt{\|\mathbf{x}_1\|^2 \|\mathbf{x}\|^2 - (\langle \mathbf{x}_1, \mathbf{x}_2\rangle)^2} \\
&=& \sqrt{(x_{11}^2 + x_{12}^2)(x_{21}^2+x_{22}^2) - (x_{11}x_{21} + x_{12}x_{22})^2} \\
&=& |x_{11} x_{22} - x_{12} x_{21}| \\
&=& |\det(\mathbf{X})|.
\end{eqnarray*}
- Interpretation of the (absolute value of) determinant as the **volume of the parallelotope** defined by the columns of the matrix. For example, if $\mathbf{X} \in \mathbb{R}^2$ has two columns $\mathbf{x}_1$ and $\mathbf{x}_2$, then
\begin{eqnarray*}
\text{area} &=& bh = \|\mathbf{x}_1\|\|\mathbf{x}_2\| \sin(\theta) \\
&=& \|\mathbf{x}_1\| \|\mathbf{x}_2\| \sqrt{1 - \left( \frac{\langle \mathbf{x}_1, \mathbf{x}_2 \rangle}{\|\mathbf{x}_1\| \|\mathbf{x}_2\|} \right)^2} \\
&=& \sqrt{\|\mathbf{x}_1\|^2 \|\mathbf{x}\|^2 - (\langle \mathbf{x}_1, \mathbf{x}_2\rangle)^2} \\
&=& \sqrt{(x_{11}^2 + x_{12}^2)(x_{21}^2+x_{22}^2) - (x_{11}x_{21} + x_{12}x_{22})^2} \\
&=& |x_{11} x_{22} - x_{12} x_{21}| \\
&=& |\det(\mathbf{X})|.
\end{eqnarray*}