---
title: Gaussian Elimination and LU Decomposition
subtitle: Biostat/Biomath M257
author: Dr. Hua Zhou @ UCLA
date: today
format:
html:
theme: cosmo
embed-resources: true
number-sections: true
toc: true
toc-depth: 4
toc-location: left
code-fold: false
jupyter:
jupytext:
formats: 'ipynb,qmd'
text_representation:
extension: .qmd
format_name: quarto
format_version: '1.0'
jupytext_version: 1.14.5
kernelspec:
display_name: Julia (8 threads) 1.8.5
language: julia
name: julia-_8-threads_-1.8
---
System information (for reproducibility):
```{julia}
versioninfo()
```
Load packages:
```{julia}
using Pkg
Pkg.activate(pwd())
Pkg.instantiate()
Pkg.status()
```
* Goal: solve linear equation
$$
\mathbf{A} \mathbf{x} = \mathbf{b}.
$$
For simplicity we consider a square matrix $\mathbf{A} \in \mathbb{R}^{n \times n}$.
* History: Chinese mathematical text [The Nine Chapters on the Mathematical Art](https://en.wikipedia.org/wiki/The_Nine_Chapters_on_the_Mathematical_Art), Issac Newton and Carl Friedrich Gauss.
 * A [toy example](https://en.wikipedia.org/wiki/Gaussian_elimination#Example_of_the_algorithm).
```{julia}
A = [2.0 1.0 -1.0; -3.0 -1.0 2.0; -2.0 1.0 2.0]
```
```{julia}
b = [8.0, -11.0, -3.0]
```
```{julia}
# Julia way to solve linear equation
# equivalent to `solve(A, b)` in R
A \ b
```
What happens when we call `A \ b` to solve a linear equation?
## Elementary operator matrix
* **Elementary operator matrix** is the identity matrix with the 0 in position $(j,k)$ replaced by $c$
$$
\mathbf{E}_{jk}(c) = \begin{pmatrix}
1 & & \\
& \ddots & \\
& & 1 & \\
& & & \ddots & \\
& & c & & 1 & \\
& & & & & \ddots \\
& & & & & & 1
\end{pmatrix} = \mathbf{I} + c \mathbf{e}_j \mathbf{e}_k^T.
$$
* $\mathbf{E}_{jk}(c)$ is unit triangular, full rank, and its inverse is
$$
\mathbf{E}_{jk}^{-1}(c) = \mathbf{E}_{jk}(-c).
$$
* $\mathbf{E}_{jk}(c)$ left-multiplies an $n \times m$ matrix $\mathbf{X}$ effectively replace its $j$-th row $\mathbf{x}_{j\cdot}$ by $c \mathbf{x}_{k \cdot} + \mathbf{x}_{j \cdot}$
$$
\mathbf{E}_{jk}(c) \times \mathbf{X} = \mathbf{E}_{jk}(c) \times \begin{pmatrix}
& & \\
\cdots & \mathbf{x}_{k\cdot} & \cdots \\
& & \\
\cdots & \mathbf{x}_{j\cdot} & \cdots \\
& &
\end{pmatrix} = \begin{pmatrix}
& & \\
\cdots & \mathbf{x}_{k\cdot} & \cdots \\
& & \\
\cdots & c \mathbf{x}_{k\cdot} + \mathbf{x}_{j\cdot} & \cdots \\
& &
\end{pmatrix}.
$$
$2m$ flops.
* Gaussian elimination applies a sequence of elementary operator matrices to transform the linear system $\mathbf{A} \mathbf{x} = \mathbf{b}$ to an upper triangular system
$$
\begin{eqnarray*}
\mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{A} \mathbf{x} &=& \mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{b} \\
\mathbf{U} \mathbf{x} &=& \mathbf{b}_{\text{new}}.
\end{eqnarray*}
$$
Column 1:
```{julia}
E21 = [1.0 0.0 0.0; 1.5 1.0 0.0; 0.0 0.0 1.0]
```
```{julia}
# zero (2, 1) entry
E21 * A
```
```{julia}
E31 = [1.0 0.0 0.0; 0.0 1.0 0.0; 1.0 0.0 1.0]
```
```{julia}
# zero (3, 1) entry
E31 * E21 * A
```
Column 2:
```{julia}
E32 = [1.0 0.0 0.0; 0.0 1.0 0.0; 0.0 -4.0 1.0]
```
```{julia}
# zero (3, 2) entry
E32 * E31 * E21 * A
```
## Gauss transformations
* For the first column,
$$
\mathbf{M}_1 = \mathbf{E}_{n1}(c_{n1}) \cdots \mathbf{E}_{31}(c_{31}) \mathbf{E}_{21}(c_{21}) = \begin{pmatrix}
1 & \\
c_{21} & \\
& \ddots & \\
c_{n1} & & 1
\end{pmatrix}
$$
For the $k$-th column,
$$
\mathbf{M}_k = \mathbf{E}_{nk}(c_{nk}) \cdots \mathbf{E}_{k+1,k}(c_{k+1,k}) = \begin{pmatrix}
1 & \\
& \ddots \\
& & 1 & \\
& & c_{k+1,k} & 1\\
& & \vdots & & \ddots \\
& & c_{n,k} & & & 1
\end{pmatrix}.
$$
* $\mathbf{M}_1, \ldots, \mathbf{M}_{n-1}$ are called the **Gauss transformations**.
```{julia}
M1 = E31 * E21
```
```{julia}
M2 = E32
```
* Gauss transformations $\mathbf{M}_k$ are unit triangular, full rank, with inverse
$$
\mathbf{M}_k^{-1} = \mathbf{E}_{k+1,k}^{-1}(c_{k+1,k}) \cdots \mathbf{E}_{nk}^{-1}(c_{nk}) = \begin{pmatrix}
1 & \\
& \ddots \\
& & 1 & \\
& & - c_{k+1,k}\\
& & \vdots & & \ddots \\
& & - c_{n,k} & & & 1
\end{pmatrix}.
$$
```{julia}
inv(M1)
```
```{julia}
inv(M2)
```
## LU decomposition
Gaussian elimination does
$$
\mathbf{M}_{n-1} \cdots \mathbf{M}_1 \mathbf{A} = \mathbf{U}.
$$
Let
\begin{equation*}
\mathbf{L} = \mathbf{M}_1^{-1} \cdots \mathbf{M}_{n-1}^{-1} = \begin{pmatrix}
1 & & & & \\
\,- c_{21} & \ddots & & & \\
& & 1 & & \\
\, - c_{k+1,1} & & - c_{k+1,k} & & \\
& & \vdots & & \ddots \\
\,- c_{n1} & & - c_{nk} & & & 1
\end{pmatrix}.
\end{equation*}
Thus we have the **LU decomposition**
$$
\mathbf{A} = \mathbf{L} \mathbf{U},
$$
where $\mathbf{L}$ is unit lower triangular and $\mathbf{U}$ is upper triangular.
```{julia}
# collect negative multipliers into a unit lower triangular matrix
L = [1 0 0; -3/2 1 0; -1 4 1]
```
```{julia}
# upper triangular matrix after Gaussian elimination
U = [2 1 -1; 0 1/2 1/2; 0 0 -1]
```
```{julia}
# recovers original matrix
L * U
```
* The whole LU algorithm is done in place, i.e., $\mathbf{A}$ is overwritten by $\mathbf{L}$ and $\mathbf{U}$.
* LU decomposition exists if the principal sub-matrix $\mathbf{A}[1:k, 1:k]$ is non-singular for $k=1,\ldots,n-1$.
* If the LU decomposition exists and $\mathbf{A}$ is non-singular, then the LU decmpositon is unique and
$$
\det(\mathbf{A}) = \det(\mathbf{L}) \det(\mathbf{U}) = \prod_{k=1}^n u_{kk}.
$$
* The LU decomposition costs
$$
2(n-1)^2 + 2(n-2)^2 + \cdots + 2 \cdot 1^2 \approx \frac 23 n^3 \quad \text{flops}.
$$
* A [toy example](https://en.wikipedia.org/wiki/Gaussian_elimination#Example_of_the_algorithm).
```{julia}
A = [2.0 1.0 -1.0; -3.0 -1.0 2.0; -2.0 1.0 2.0]
```
```{julia}
b = [8.0, -11.0, -3.0]
```
```{julia}
# Julia way to solve linear equation
# equivalent to `solve(A, b)` in R
A \ b
```
What happens when we call `A \ b` to solve a linear equation?
## Elementary operator matrix
* **Elementary operator matrix** is the identity matrix with the 0 in position $(j,k)$ replaced by $c$
$$
\mathbf{E}_{jk}(c) = \begin{pmatrix}
1 & & \\
& \ddots & \\
& & 1 & \\
& & & \ddots & \\
& & c & & 1 & \\
& & & & & \ddots \\
& & & & & & 1
\end{pmatrix} = \mathbf{I} + c \mathbf{e}_j \mathbf{e}_k^T.
$$
* $\mathbf{E}_{jk}(c)$ is unit triangular, full rank, and its inverse is
$$
\mathbf{E}_{jk}^{-1}(c) = \mathbf{E}_{jk}(-c).
$$
* $\mathbf{E}_{jk}(c)$ left-multiplies an $n \times m$ matrix $\mathbf{X}$ effectively replace its $j$-th row $\mathbf{x}_{j\cdot}$ by $c \mathbf{x}_{k \cdot} + \mathbf{x}_{j \cdot}$
$$
\mathbf{E}_{jk}(c) \times \mathbf{X} = \mathbf{E}_{jk}(c) \times \begin{pmatrix}
& & \\
\cdots & \mathbf{x}_{k\cdot} & \cdots \\
& & \\
\cdots & \mathbf{x}_{j\cdot} & \cdots \\
& &
\end{pmatrix} = \begin{pmatrix}
& & \\
\cdots & \mathbf{x}_{k\cdot} & \cdots \\
& & \\
\cdots & c \mathbf{x}_{k\cdot} + \mathbf{x}_{j\cdot} & \cdots \\
& &
\end{pmatrix}.
$$
$2m$ flops.
* Gaussian elimination applies a sequence of elementary operator matrices to transform the linear system $\mathbf{A} \mathbf{x} = \mathbf{b}$ to an upper triangular system
$$
\begin{eqnarray*}
\mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{A} \mathbf{x} &=& \mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{b} \\
\mathbf{U} \mathbf{x} &=& \mathbf{b}_{\text{new}}.
\end{eqnarray*}
$$
Column 1:
```{julia}
E21 = [1.0 0.0 0.0; 1.5 1.0 0.0; 0.0 0.0 1.0]
```
```{julia}
# zero (2, 1) entry
E21 * A
```
```{julia}
E31 = [1.0 0.0 0.0; 0.0 1.0 0.0; 1.0 0.0 1.0]
```
```{julia}
# zero (3, 1) entry
E31 * E21 * A
```
Column 2:
```{julia}
E32 = [1.0 0.0 0.0; 0.0 1.0 0.0; 0.0 -4.0 1.0]
```
```{julia}
# zero (3, 2) entry
E32 * E31 * E21 * A
```
## Gauss transformations
* For the first column,
$$
\mathbf{M}_1 = \mathbf{E}_{n1}(c_{n1}) \cdots \mathbf{E}_{31}(c_{31}) \mathbf{E}_{21}(c_{21}) = \begin{pmatrix}
1 & \\
c_{21} & \\
& \ddots & \\
c_{n1} & & 1
\end{pmatrix}
$$
For the $k$-th column,
$$
\mathbf{M}_k = \mathbf{E}_{nk}(c_{nk}) \cdots \mathbf{E}_{k+1,k}(c_{k+1,k}) = \begin{pmatrix}
1 & \\
& \ddots \\
& & 1 & \\
& & c_{k+1,k} & 1\\
& & \vdots & & \ddots \\
& & c_{n,k} & & & 1
\end{pmatrix}.
$$
* $\mathbf{M}_1, \ldots, \mathbf{M}_{n-1}$ are called the **Gauss transformations**.
```{julia}
M1 = E31 * E21
```
```{julia}
M2 = E32
```
* Gauss transformations $\mathbf{M}_k$ are unit triangular, full rank, with inverse
$$
\mathbf{M}_k^{-1} = \mathbf{E}_{k+1,k}^{-1}(c_{k+1,k}) \cdots \mathbf{E}_{nk}^{-1}(c_{nk}) = \begin{pmatrix}
1 & \\
& \ddots \\
& & 1 & \\
& & - c_{k+1,k}\\
& & \vdots & & \ddots \\
& & - c_{n,k} & & & 1
\end{pmatrix}.
$$
```{julia}
inv(M1)
```
```{julia}
inv(M2)
```
## LU decomposition
Gaussian elimination does
$$
\mathbf{M}_{n-1} \cdots \mathbf{M}_1 \mathbf{A} = \mathbf{U}.
$$
Let
\begin{equation*}
\mathbf{L} = \mathbf{M}_1^{-1} \cdots \mathbf{M}_{n-1}^{-1} = \begin{pmatrix}
1 & & & & \\
\,- c_{21} & \ddots & & & \\
& & 1 & & \\
\, - c_{k+1,1} & & - c_{k+1,k} & & \\
& & \vdots & & \ddots \\
\,- c_{n1} & & - c_{nk} & & & 1
\end{pmatrix}.
\end{equation*}
Thus we have the **LU decomposition**
$$
\mathbf{A} = \mathbf{L} \mathbf{U},
$$
where $\mathbf{L}$ is unit lower triangular and $\mathbf{U}$ is upper triangular.
```{julia}
# collect negative multipliers into a unit lower triangular matrix
L = [1 0 0; -3/2 1 0; -1 4 1]
```
```{julia}
# upper triangular matrix after Gaussian elimination
U = [2 1 -1; 0 1/2 1/2; 0 0 -1]
```
```{julia}
# recovers original matrix
L * U
```
* The whole LU algorithm is done in place, i.e., $\mathbf{A}$ is overwritten by $\mathbf{L}$ and $\mathbf{U}$.
* LU decomposition exists if the principal sub-matrix $\mathbf{A}[1:k, 1:k]$ is non-singular for $k=1,\ldots,n-1$.
* If the LU decomposition exists and $\mathbf{A}$ is non-singular, then the LU decmpositon is unique and
$$
\det(\mathbf{A}) = \det(\mathbf{L}) \det(\mathbf{U}) = \prod_{k=1}^n u_{kk}.
$$
* The LU decomposition costs
$$
2(n-1)^2 + 2(n-2)^2 + \cdots + 2 \cdot 1^2 \approx \frac 23 n^3 \quad \text{flops}.
$$
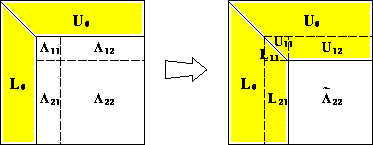 * Actual implementations can differ: outer product LU ($kij$ loop), block outer product LU (higher level-3 fraction), Crout's algorithm ($jki$ loop).
* Given LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U}$, solving $(\mathbf{L} \mathbf{U}) \mathbf{x} = \mathbf{b}$ for one right hand side costs $2n^2$ flops:
- One forward substitution ($n^2$ flops) to solve
$$
\mathbf{L} \mathbf{y} = \mathbf{b}
$$
- One back substitution ($n^2$ flops) to solve
$$
\mathbf{U} \mathbf{x} = \mathbf{y}
$$
* Therefore to solve $\mathbf{A} \mathbf{x} = \mathbf{b}$ via LU, we need a total of
$$
\frac 23 n^3 + 2n^2 \quad \text{flops}.
$$
* If there are multiple right hand sides, LU only needs to be done once.
## Matrix inversion
* For matrix inversion, we need to solve $\mathbf{A} \mathbf{X} = \mathbf{I}$, or $\mathbf{A} \mathbf{x}_i = \mathbf{e}_i$ for $i=1,\ldots,n$. There are $n$ right hand sides $\mathbf{e}_1, \ldots, \mathbf{e}_n$. Naively, we may need $\frac 23 n^3 + 2n^3$ flops. But taking advantage of 0s reduces the second term $2n^3$ to $\frac 43 n^3$.
* So **matrix inversion via LU** costs
$$
\frac 23 n^3 + \frac 43 n^3 = 2n^3 \quad \text{flops}.
$$
This is 3x more expensive than just solving one equation.
* **No inversion mentality**:
> **Whenever we see matrix inverse, we should think in terms of solving linear equations.**
* We do not compute matrix inverse unless
1. it is necessary to compute standard errors
2. number of right hand sides is much larger than $n$
3. $n$ is small
## Pivoting
* Let
$$
\mathbf{A} = \begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}.
$$
Is there a solution to $\mathbf{A} \mathbf{x} = \mathbf{b}$ for an arbitrary $\mathbf{b}$? Does GE/LU work for $\mathbf{A}$?
* What if, during LU procedure, the **pivot** $a_{kk}$ is 0 or nearly 0 due to underflow?
Solution: pivoting.
* **Partial pivoting**: before zeroing the $k$-th column, the row with $\max_{i=k}^n |a_{ik}|$ is moved into the $k$-th row.
* LU with partial pivoting yields
$$
\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U},
$$
where $\mathbf{P}$ is a permutation matrix, $\mathbf{L}$ is unit lower triangular with $|\ell_{ij}| \le 1$, and $\mathbf{U}$ is upper triangular.
* Complete pivoting: Do both row and column interchanges so that the largest entry in the sub matrix `A[k:n, k:n]` is permuted to the $(k,k)$-th entry. This yields the decomposition
$$
\mathbf{P} \mathbf{A} \mathbf{Q} = \mathbf{L} \mathbf{U},
$$
where $|\ell_{ij}| \le 1$.
* LU decomposition with partial pivoting is the most commonly used methods for solving **general** linear systems. Complete pivoting is the most stable but costs more computation. Partial pivoting is stable most of times.
## LAPACK and Julia implementation
* LAPACK: [?getrf](http://www.netlib.org/lapack/explore-html/dd/d9a/group__double_g_ecomputational_ga0019443faea08275ca60a734d0593e60.html#ga0019443faea08275ca60a734d0593e60) does $\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U}$ (LU decomposition with partial pivoting) in place.
* R: `solve()` implicitly performs LU decomposition (wrapper of LAPACK routine `dgesv`). `solve()` allows specifying a single or multiple right hand sides. If none, it computes the matrix inverse. The `matrix` package contains `lu()` function that outputs `L`, `U`, and `pivot`.
* Julia:
- [LinearAlgebra.lu](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.lu).
- [LinearAlgebra.lu!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.lu!). In-place version. Input matrix gets overwritten with L and U.
- Or call LAPACK wrapper function [getrf!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.getrf!) directly.
- Other LU-related LAPACK wrapper functions: [gesv](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.gesv!), [gesvx](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.gesvx!), [trtri](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.trtri!) (inverse of triangular matrix), [trtrs](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.trtrs!).
```{julia}
A
```
```{julia}
using LinearAlgebra
# second argument indicates partial pivoting (default) or not
alu = lu(A)
typeof(alu)
```
```{julia}
dump(alu)
```
```{julia}
alu.L
```
```{julia}
alu.U
```
```{julia}
alu.p
```
```{julia}
alu.P
```
```{julia}
alu.L * alu.U
```
```{julia}
A[alu.p, :]
```
```{julia}
# this is doing two triangular solves, 2n^2 flops
alu \ b
```
```{julia}
det(A) # this does LU! O(n^3)
```
```{julia}
det(alu) # this is cheap O(n)
```
```{julia}
inv(A) # this does LU! O(n^3)
```
```{julia}
inv(alu) # this is cheap O(n^2)
```
## Further reading
* Sections II.5.2 and II.5.3 of [Computational Statistics](http://ucla.worldcat.org/title/computational-statistics/oclc/437345409&referer=brief_results) by James Gentle (2010).
* A definite reference is Chapter 3 of the book [Matrix Computation](http://catalog.library.ucla.edu/vwebv/holdingsInfo?bibId=7122088) by Gene Golub and Charles Van Loan.
* Actual implementations can differ: outer product LU ($kij$ loop), block outer product LU (higher level-3 fraction), Crout's algorithm ($jki$ loop).
* Given LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U}$, solving $(\mathbf{L} \mathbf{U}) \mathbf{x} = \mathbf{b}$ for one right hand side costs $2n^2$ flops:
- One forward substitution ($n^2$ flops) to solve
$$
\mathbf{L} \mathbf{y} = \mathbf{b}
$$
- One back substitution ($n^2$ flops) to solve
$$
\mathbf{U} \mathbf{x} = \mathbf{y}
$$
* Therefore to solve $\mathbf{A} \mathbf{x} = \mathbf{b}$ via LU, we need a total of
$$
\frac 23 n^3 + 2n^2 \quad \text{flops}.
$$
* If there are multiple right hand sides, LU only needs to be done once.
## Matrix inversion
* For matrix inversion, we need to solve $\mathbf{A} \mathbf{X} = \mathbf{I}$, or $\mathbf{A} \mathbf{x}_i = \mathbf{e}_i$ for $i=1,\ldots,n$. There are $n$ right hand sides $\mathbf{e}_1, \ldots, \mathbf{e}_n$. Naively, we may need $\frac 23 n^3 + 2n^3$ flops. But taking advantage of 0s reduces the second term $2n^3$ to $\frac 43 n^3$.
* So **matrix inversion via LU** costs
$$
\frac 23 n^3 + \frac 43 n^3 = 2n^3 \quad \text{flops}.
$$
This is 3x more expensive than just solving one equation.
* **No inversion mentality**:
> **Whenever we see matrix inverse, we should think in terms of solving linear equations.**
* We do not compute matrix inverse unless
1. it is necessary to compute standard errors
2. number of right hand sides is much larger than $n$
3. $n$ is small
## Pivoting
* Let
$$
\mathbf{A} = \begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}.
$$
Is there a solution to $\mathbf{A} \mathbf{x} = \mathbf{b}$ for an arbitrary $\mathbf{b}$? Does GE/LU work for $\mathbf{A}$?
* What if, during LU procedure, the **pivot** $a_{kk}$ is 0 or nearly 0 due to underflow?
Solution: pivoting.
* **Partial pivoting**: before zeroing the $k$-th column, the row with $\max_{i=k}^n |a_{ik}|$ is moved into the $k$-th row.
* LU with partial pivoting yields
$$
\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U},
$$
where $\mathbf{P}$ is a permutation matrix, $\mathbf{L}$ is unit lower triangular with $|\ell_{ij}| \le 1$, and $\mathbf{U}$ is upper triangular.
* Complete pivoting: Do both row and column interchanges so that the largest entry in the sub matrix `A[k:n, k:n]` is permuted to the $(k,k)$-th entry. This yields the decomposition
$$
\mathbf{P} \mathbf{A} \mathbf{Q} = \mathbf{L} \mathbf{U},
$$
where $|\ell_{ij}| \le 1$.
* LU decomposition with partial pivoting is the most commonly used methods for solving **general** linear systems. Complete pivoting is the most stable but costs more computation. Partial pivoting is stable most of times.
## LAPACK and Julia implementation
* LAPACK: [?getrf](http://www.netlib.org/lapack/explore-html/dd/d9a/group__double_g_ecomputational_ga0019443faea08275ca60a734d0593e60.html#ga0019443faea08275ca60a734d0593e60) does $\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U}$ (LU decomposition with partial pivoting) in place.
* R: `solve()` implicitly performs LU decomposition (wrapper of LAPACK routine `dgesv`). `solve()` allows specifying a single or multiple right hand sides. If none, it computes the matrix inverse. The `matrix` package contains `lu()` function that outputs `L`, `U`, and `pivot`.
* Julia:
- [LinearAlgebra.lu](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.lu).
- [LinearAlgebra.lu!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.lu!). In-place version. Input matrix gets overwritten with L and U.
- Or call LAPACK wrapper function [getrf!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.getrf!) directly.
- Other LU-related LAPACK wrapper functions: [gesv](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.gesv!), [gesvx](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.gesvx!), [trtri](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.trtri!) (inverse of triangular matrix), [trtrs](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.trtrs!).
```{julia}
A
```
```{julia}
using LinearAlgebra
# second argument indicates partial pivoting (default) or not
alu = lu(A)
typeof(alu)
```
```{julia}
dump(alu)
```
```{julia}
alu.L
```
```{julia}
alu.U
```
```{julia}
alu.p
```
```{julia}
alu.P
```
```{julia}
alu.L * alu.U
```
```{julia}
A[alu.p, :]
```
```{julia}
# this is doing two triangular solves, 2n^2 flops
alu \ b
```
```{julia}
det(A) # this does LU! O(n^3)
```
```{julia}
det(alu) # this is cheap O(n)
```
```{julia}
inv(A) # this does LU! O(n^3)
```
```{julia}
inv(alu) # this is cheap O(n^2)
```
## Further reading
* Sections II.5.2 and II.5.3 of [Computational Statistics](http://ucla.worldcat.org/title/computational-statistics/oclc/437345409&referer=brief_results) by James Gentle (2010).
* A definite reference is Chapter 3 of the book [Matrix Computation](http://catalog.library.ucla.edu/vwebv/holdingsInfo?bibId=7122088) by Gene Golub and Charles Van Loan.


 * A [toy example](https://en.wikipedia.org/wiki/Gaussian_elimination#Example_of_the_algorithm).
```{julia}
A = [2.0 1.0 -1.0; -3.0 -1.0 2.0; -2.0 1.0 2.0]
```
```{julia}
b = [8.0, -11.0, -3.0]
```
```{julia}
# Julia way to solve linear equation
# equivalent to `solve(A, b)` in R
A \ b
```
What happens when we call `A \ b` to solve a linear equation?
## Elementary operator matrix
* **Elementary operator matrix** is the identity matrix with the 0 in position $(j,k)$ replaced by $c$
$$
\mathbf{E}_{jk}(c) = \begin{pmatrix}
1 & & \\
& \ddots & \\
& & 1 & \\
& & & \ddots & \\
& & c & & 1 & \\
& & & & & \ddots \\
& & & & & & 1
\end{pmatrix} = \mathbf{I} + c \mathbf{e}_j \mathbf{e}_k^T.
$$
* $\mathbf{E}_{jk}(c)$ is unit triangular, full rank, and its inverse is
$$
\mathbf{E}_{jk}^{-1}(c) = \mathbf{E}_{jk}(-c).
$$
* $\mathbf{E}_{jk}(c)$ left-multiplies an $n \times m$ matrix $\mathbf{X}$ effectively replace its $j$-th row $\mathbf{x}_{j\cdot}$ by $c \mathbf{x}_{k \cdot} + \mathbf{x}_{j \cdot}$
$$
\mathbf{E}_{jk}(c) \times \mathbf{X} = \mathbf{E}_{jk}(c) \times \begin{pmatrix}
& & \\
\cdots & \mathbf{x}_{k\cdot} & \cdots \\
& & \\
\cdots & \mathbf{x}_{j\cdot} & \cdots \\
& &
\end{pmatrix} = \begin{pmatrix}
& & \\
\cdots & \mathbf{x}_{k\cdot} & \cdots \\
& & \\
\cdots & c \mathbf{x}_{k\cdot} + \mathbf{x}_{j\cdot} & \cdots \\
& &
\end{pmatrix}.
$$
$2m$ flops.
* Gaussian elimination applies a sequence of elementary operator matrices to transform the linear system $\mathbf{A} \mathbf{x} = \mathbf{b}$ to an upper triangular system
$$
\begin{eqnarray*}
\mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{A} \mathbf{x} &=& \mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{b} \\
\mathbf{U} \mathbf{x} &=& \mathbf{b}_{\text{new}}.
\end{eqnarray*}
$$
Column 1:
```{julia}
E21 = [1.0 0.0 0.0; 1.5 1.0 0.0; 0.0 0.0 1.0]
```
```{julia}
# zero (2, 1) entry
E21 * A
```
```{julia}
E31 = [1.0 0.0 0.0; 0.0 1.0 0.0; 1.0 0.0 1.0]
```
```{julia}
# zero (3, 1) entry
E31 * E21 * A
```
Column 2:
```{julia}
E32 = [1.0 0.0 0.0; 0.0 1.0 0.0; 0.0 -4.0 1.0]
```
```{julia}
# zero (3, 2) entry
E32 * E31 * E21 * A
```
## Gauss transformations
* For the first column,
$$
\mathbf{M}_1 = \mathbf{E}_{n1}(c_{n1}) \cdots \mathbf{E}_{31}(c_{31}) \mathbf{E}_{21}(c_{21}) = \begin{pmatrix}
1 & \\
c_{21} & \\
& \ddots & \\
c_{n1} & & 1
\end{pmatrix}
$$
For the $k$-th column,
$$
\mathbf{M}_k = \mathbf{E}_{nk}(c_{nk}) \cdots \mathbf{E}_{k+1,k}(c_{k+1,k}) = \begin{pmatrix}
1 & \\
& \ddots \\
& & 1 & \\
& & c_{k+1,k} & 1\\
& & \vdots & & \ddots \\
& & c_{n,k} & & & 1
\end{pmatrix}.
$$
* $\mathbf{M}_1, \ldots, \mathbf{M}_{n-1}$ are called the **Gauss transformations**.
```{julia}
M1 = E31 * E21
```
```{julia}
M2 = E32
```
* Gauss transformations $\mathbf{M}_k$ are unit triangular, full rank, with inverse
$$
\mathbf{M}_k^{-1} = \mathbf{E}_{k+1,k}^{-1}(c_{k+1,k}) \cdots \mathbf{E}_{nk}^{-1}(c_{nk}) = \begin{pmatrix}
1 & \\
& \ddots \\
& & 1 & \\
& & - c_{k+1,k}\\
& & \vdots & & \ddots \\
& & - c_{n,k} & & & 1
\end{pmatrix}.
$$
```{julia}
inv(M1)
```
```{julia}
inv(M2)
```
## LU decomposition
Gaussian elimination does
$$
\mathbf{M}_{n-1} \cdots \mathbf{M}_1 \mathbf{A} = \mathbf{U}.
$$
Let
\begin{equation*}
\mathbf{L} = \mathbf{M}_1^{-1} \cdots \mathbf{M}_{n-1}^{-1} = \begin{pmatrix}
1 & & & & \\
\,- c_{21} & \ddots & & & \\
& & 1 & & \\
\, - c_{k+1,1} & & - c_{k+1,k} & & \\
& & \vdots & & \ddots \\
\,- c_{n1} & & - c_{nk} & & & 1
\end{pmatrix}.
\end{equation*}
Thus we have the **LU decomposition**
$$
\mathbf{A} = \mathbf{L} \mathbf{U},
$$
where $\mathbf{L}$ is unit lower triangular and $\mathbf{U}$ is upper triangular.
```{julia}
# collect negative multipliers into a unit lower triangular matrix
L = [1 0 0; -3/2 1 0; -1 4 1]
```
```{julia}
# upper triangular matrix after Gaussian elimination
U = [2 1 -1; 0 1/2 1/2; 0 0 -1]
```
```{julia}
# recovers original matrix
L * U
```
* The whole LU algorithm is done in place, i.e., $\mathbf{A}$ is overwritten by $\mathbf{L}$ and $\mathbf{U}$.
* LU decomposition exists if the principal sub-matrix $\mathbf{A}[1:k, 1:k]$ is non-singular for $k=1,\ldots,n-1$.
* If the LU decomposition exists and $\mathbf{A}$ is non-singular, then the LU decmpositon is unique and
$$
\det(\mathbf{A}) = \det(\mathbf{L}) \det(\mathbf{U}) = \prod_{k=1}^n u_{kk}.
$$
* The LU decomposition costs
$$
2(n-1)^2 + 2(n-2)^2 + \cdots + 2 \cdot 1^2 \approx \frac 23 n^3 \quad \text{flops}.
$$
* A [toy example](https://en.wikipedia.org/wiki/Gaussian_elimination#Example_of_the_algorithm).
```{julia}
A = [2.0 1.0 -1.0; -3.0 -1.0 2.0; -2.0 1.0 2.0]
```
```{julia}
b = [8.0, -11.0, -3.0]
```
```{julia}
# Julia way to solve linear equation
# equivalent to `solve(A, b)` in R
A \ b
```
What happens when we call `A \ b` to solve a linear equation?
## Elementary operator matrix
* **Elementary operator matrix** is the identity matrix with the 0 in position $(j,k)$ replaced by $c$
$$
\mathbf{E}_{jk}(c) = \begin{pmatrix}
1 & & \\
& \ddots & \\
& & 1 & \\
& & & \ddots & \\
& & c & & 1 & \\
& & & & & \ddots \\
& & & & & & 1
\end{pmatrix} = \mathbf{I} + c \mathbf{e}_j \mathbf{e}_k^T.
$$
* $\mathbf{E}_{jk}(c)$ is unit triangular, full rank, and its inverse is
$$
\mathbf{E}_{jk}^{-1}(c) = \mathbf{E}_{jk}(-c).
$$
* $\mathbf{E}_{jk}(c)$ left-multiplies an $n \times m$ matrix $\mathbf{X}$ effectively replace its $j$-th row $\mathbf{x}_{j\cdot}$ by $c \mathbf{x}_{k \cdot} + \mathbf{x}_{j \cdot}$
$$
\mathbf{E}_{jk}(c) \times \mathbf{X} = \mathbf{E}_{jk}(c) \times \begin{pmatrix}
& & \\
\cdots & \mathbf{x}_{k\cdot} & \cdots \\
& & \\
\cdots & \mathbf{x}_{j\cdot} & \cdots \\
& &
\end{pmatrix} = \begin{pmatrix}
& & \\
\cdots & \mathbf{x}_{k\cdot} & \cdots \\
& & \\
\cdots & c \mathbf{x}_{k\cdot} + \mathbf{x}_{j\cdot} & \cdots \\
& &
\end{pmatrix}.
$$
$2m$ flops.
* Gaussian elimination applies a sequence of elementary operator matrices to transform the linear system $\mathbf{A} \mathbf{x} = \mathbf{b}$ to an upper triangular system
$$
\begin{eqnarray*}
\mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{A} \mathbf{x} &=& \mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{b} \\
\mathbf{U} \mathbf{x} &=& \mathbf{b}_{\text{new}}.
\end{eqnarray*}
$$
Column 1:
```{julia}
E21 = [1.0 0.0 0.0; 1.5 1.0 0.0; 0.0 0.0 1.0]
```
```{julia}
# zero (2, 1) entry
E21 * A
```
```{julia}
E31 = [1.0 0.0 0.0; 0.0 1.0 0.0; 1.0 0.0 1.0]
```
```{julia}
# zero (3, 1) entry
E31 * E21 * A
```
Column 2:
```{julia}
E32 = [1.0 0.0 0.0; 0.0 1.0 0.0; 0.0 -4.0 1.0]
```
```{julia}
# zero (3, 2) entry
E32 * E31 * E21 * A
```
## Gauss transformations
* For the first column,
$$
\mathbf{M}_1 = \mathbf{E}_{n1}(c_{n1}) \cdots \mathbf{E}_{31}(c_{31}) \mathbf{E}_{21}(c_{21}) = \begin{pmatrix}
1 & \\
c_{21} & \\
& \ddots & \\
c_{n1} & & 1
\end{pmatrix}
$$
For the $k$-th column,
$$
\mathbf{M}_k = \mathbf{E}_{nk}(c_{nk}) \cdots \mathbf{E}_{k+1,k}(c_{k+1,k}) = \begin{pmatrix}
1 & \\
& \ddots \\
& & 1 & \\
& & c_{k+1,k} & 1\\
& & \vdots & & \ddots \\
& & c_{n,k} & & & 1
\end{pmatrix}.
$$
* $\mathbf{M}_1, \ldots, \mathbf{M}_{n-1}$ are called the **Gauss transformations**.
```{julia}
M1 = E31 * E21
```
```{julia}
M2 = E32
```
* Gauss transformations $\mathbf{M}_k$ are unit triangular, full rank, with inverse
$$
\mathbf{M}_k^{-1} = \mathbf{E}_{k+1,k}^{-1}(c_{k+1,k}) \cdots \mathbf{E}_{nk}^{-1}(c_{nk}) = \begin{pmatrix}
1 & \\
& \ddots \\
& & 1 & \\
& & - c_{k+1,k}\\
& & \vdots & & \ddots \\
& & - c_{n,k} & & & 1
\end{pmatrix}.
$$
```{julia}
inv(M1)
```
```{julia}
inv(M2)
```
## LU decomposition
Gaussian elimination does
$$
\mathbf{M}_{n-1} \cdots \mathbf{M}_1 \mathbf{A} = \mathbf{U}.
$$
Let
\begin{equation*}
\mathbf{L} = \mathbf{M}_1^{-1} \cdots \mathbf{M}_{n-1}^{-1} = \begin{pmatrix}
1 & & & & \\
\,- c_{21} & \ddots & & & \\
& & 1 & & \\
\, - c_{k+1,1} & & - c_{k+1,k} & & \\
& & \vdots & & \ddots \\
\,- c_{n1} & & - c_{nk} & & & 1
\end{pmatrix}.
\end{equation*}
Thus we have the **LU decomposition**
$$
\mathbf{A} = \mathbf{L} \mathbf{U},
$$
where $\mathbf{L}$ is unit lower triangular and $\mathbf{U}$ is upper triangular.
```{julia}
# collect negative multipliers into a unit lower triangular matrix
L = [1 0 0; -3/2 1 0; -1 4 1]
```
```{julia}
# upper triangular matrix after Gaussian elimination
U = [2 1 -1; 0 1/2 1/2; 0 0 -1]
```
```{julia}
# recovers original matrix
L * U
```
* The whole LU algorithm is done in place, i.e., $\mathbf{A}$ is overwritten by $\mathbf{L}$ and $\mathbf{U}$.
* LU decomposition exists if the principal sub-matrix $\mathbf{A}[1:k, 1:k]$ is non-singular for $k=1,\ldots,n-1$.
* If the LU decomposition exists and $\mathbf{A}$ is non-singular, then the LU decmpositon is unique and
$$
\det(\mathbf{A}) = \det(\mathbf{L}) \det(\mathbf{U}) = \prod_{k=1}^n u_{kk}.
$$
* The LU decomposition costs
$$
2(n-1)^2 + 2(n-2)^2 + \cdots + 2 \cdot 1^2 \approx \frac 23 n^3 \quad \text{flops}.
$$
 * Actual implementations can differ: outer product LU ($kij$ loop), block outer product LU (higher level-3 fraction), Crout's algorithm ($jki$ loop).
* Given LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U}$, solving $(\mathbf{L} \mathbf{U}) \mathbf{x} = \mathbf{b}$ for one right hand side costs $2n^2$ flops:
- One forward substitution ($n^2$ flops) to solve
$$
\mathbf{L} \mathbf{y} = \mathbf{b}
$$
- One back substitution ($n^2$ flops) to solve
$$
\mathbf{U} \mathbf{x} = \mathbf{y}
$$
* Therefore to solve $\mathbf{A} \mathbf{x} = \mathbf{b}$ via LU, we need a total of
$$
\frac 23 n^3 + 2n^2 \quad \text{flops}.
$$
* If there are multiple right hand sides, LU only needs to be done once.
## Matrix inversion
* For matrix inversion, we need to solve $\mathbf{A} \mathbf{X} = \mathbf{I}$, or $\mathbf{A} \mathbf{x}_i = \mathbf{e}_i$ for $i=1,\ldots,n$. There are $n$ right hand sides $\mathbf{e}_1, \ldots, \mathbf{e}_n$. Naively, we may need $\frac 23 n^3 + 2n^3$ flops. But taking advantage of 0s reduces the second term $2n^3$ to $\frac 43 n^3$.
* So **matrix inversion via LU** costs
$$
\frac 23 n^3 + \frac 43 n^3 = 2n^3 \quad \text{flops}.
$$
This is 3x more expensive than just solving one equation.
* **No inversion mentality**:
> **Whenever we see matrix inverse, we should think in terms of solving linear equations.**
* We do not compute matrix inverse unless
1. it is necessary to compute standard errors
2. number of right hand sides is much larger than $n$
3. $n$ is small
## Pivoting
* Let
$$
\mathbf{A} = \begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}.
$$
Is there a solution to $\mathbf{A} \mathbf{x} = \mathbf{b}$ for an arbitrary $\mathbf{b}$? Does GE/LU work for $\mathbf{A}$?
* What if, during LU procedure, the **pivot** $a_{kk}$ is 0 or nearly 0 due to underflow?
Solution: pivoting.
* **Partial pivoting**: before zeroing the $k$-th column, the row with $\max_{i=k}^n |a_{ik}|$ is moved into the $k$-th row.
* LU with partial pivoting yields
$$
\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U},
$$
where $\mathbf{P}$ is a permutation matrix, $\mathbf{L}$ is unit lower triangular with $|\ell_{ij}| \le 1$, and $\mathbf{U}$ is upper triangular.
* Complete pivoting: Do both row and column interchanges so that the largest entry in the sub matrix `A[k:n, k:n]` is permuted to the $(k,k)$-th entry. This yields the decomposition
$$
\mathbf{P} \mathbf{A} \mathbf{Q} = \mathbf{L} \mathbf{U},
$$
where $|\ell_{ij}| \le 1$.
* LU decomposition with partial pivoting is the most commonly used methods for solving **general** linear systems. Complete pivoting is the most stable but costs more computation. Partial pivoting is stable most of times.
## LAPACK and Julia implementation
* LAPACK: [?getrf](http://www.netlib.org/lapack/explore-html/dd/d9a/group__double_g_ecomputational_ga0019443faea08275ca60a734d0593e60.html#ga0019443faea08275ca60a734d0593e60) does $\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U}$ (LU decomposition with partial pivoting) in place.
* R: `solve()` implicitly performs LU decomposition (wrapper of LAPACK routine `dgesv`). `solve()` allows specifying a single or multiple right hand sides. If none, it computes the matrix inverse. The `matrix` package contains `lu()` function that outputs `L`, `U`, and `pivot`.
* Julia:
- [LinearAlgebra.lu](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.lu).
- [LinearAlgebra.lu!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.lu!). In-place version. Input matrix gets overwritten with L and U.
- Or call LAPACK wrapper function [getrf!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.getrf!) directly.
- Other LU-related LAPACK wrapper functions: [gesv](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.gesv!), [gesvx](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.gesvx!), [trtri](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.trtri!) (inverse of triangular matrix), [trtrs](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.trtrs!).
```{julia}
A
```
```{julia}
using LinearAlgebra
# second argument indicates partial pivoting (default) or not
alu = lu(A)
typeof(alu)
```
```{julia}
dump(alu)
```
```{julia}
alu.L
```
```{julia}
alu.U
```
```{julia}
alu.p
```
```{julia}
alu.P
```
```{julia}
alu.L * alu.U
```
```{julia}
A[alu.p, :]
```
```{julia}
# this is doing two triangular solves, 2n^2 flops
alu \ b
```
```{julia}
det(A) # this does LU! O(n^3)
```
```{julia}
det(alu) # this is cheap O(n)
```
```{julia}
inv(A) # this does LU! O(n^3)
```
```{julia}
inv(alu) # this is cheap O(n^2)
```
## Further reading
* Sections II.5.2 and II.5.3 of [Computational Statistics](http://ucla.worldcat.org/title/computational-statistics/oclc/437345409&referer=brief_results) by James Gentle (2010).
* A definite reference is Chapter 3 of the book [Matrix Computation](http://catalog.library.ucla.edu/vwebv/holdingsInfo?bibId=7122088) by Gene Golub and Charles Van Loan.
* Actual implementations can differ: outer product LU ($kij$ loop), block outer product LU (higher level-3 fraction), Crout's algorithm ($jki$ loop).
* Given LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U}$, solving $(\mathbf{L} \mathbf{U}) \mathbf{x} = \mathbf{b}$ for one right hand side costs $2n^2$ flops:
- One forward substitution ($n^2$ flops) to solve
$$
\mathbf{L} \mathbf{y} = \mathbf{b}
$$
- One back substitution ($n^2$ flops) to solve
$$
\mathbf{U} \mathbf{x} = \mathbf{y}
$$
* Therefore to solve $\mathbf{A} \mathbf{x} = \mathbf{b}$ via LU, we need a total of
$$
\frac 23 n^3 + 2n^2 \quad \text{flops}.
$$
* If there are multiple right hand sides, LU only needs to be done once.
## Matrix inversion
* For matrix inversion, we need to solve $\mathbf{A} \mathbf{X} = \mathbf{I}$, or $\mathbf{A} \mathbf{x}_i = \mathbf{e}_i$ for $i=1,\ldots,n$. There are $n$ right hand sides $\mathbf{e}_1, \ldots, \mathbf{e}_n$. Naively, we may need $\frac 23 n^3 + 2n^3$ flops. But taking advantage of 0s reduces the second term $2n^3$ to $\frac 43 n^3$.
* So **matrix inversion via LU** costs
$$
\frac 23 n^3 + \frac 43 n^3 = 2n^3 \quad \text{flops}.
$$
This is 3x more expensive than just solving one equation.
* **No inversion mentality**:
> **Whenever we see matrix inverse, we should think in terms of solving linear equations.**
* We do not compute matrix inverse unless
1. it is necessary to compute standard errors
2. number of right hand sides is much larger than $n$
3. $n$ is small
## Pivoting
* Let
$$
\mathbf{A} = \begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}.
$$
Is there a solution to $\mathbf{A} \mathbf{x} = \mathbf{b}$ for an arbitrary $\mathbf{b}$? Does GE/LU work for $\mathbf{A}$?
* What if, during LU procedure, the **pivot** $a_{kk}$ is 0 or nearly 0 due to underflow?
Solution: pivoting.
* **Partial pivoting**: before zeroing the $k$-th column, the row with $\max_{i=k}^n |a_{ik}|$ is moved into the $k$-th row.
* LU with partial pivoting yields
$$
\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U},
$$
where $\mathbf{P}$ is a permutation matrix, $\mathbf{L}$ is unit lower triangular with $|\ell_{ij}| \le 1$, and $\mathbf{U}$ is upper triangular.
* Complete pivoting: Do both row and column interchanges so that the largest entry in the sub matrix `A[k:n, k:n]` is permuted to the $(k,k)$-th entry. This yields the decomposition
$$
\mathbf{P} \mathbf{A} \mathbf{Q} = \mathbf{L} \mathbf{U},
$$
where $|\ell_{ij}| \le 1$.
* LU decomposition with partial pivoting is the most commonly used methods for solving **general** linear systems. Complete pivoting is the most stable but costs more computation. Partial pivoting is stable most of times.
## LAPACK and Julia implementation
* LAPACK: [?getrf](http://www.netlib.org/lapack/explore-html/dd/d9a/group__double_g_ecomputational_ga0019443faea08275ca60a734d0593e60.html#ga0019443faea08275ca60a734d0593e60) does $\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U}$ (LU decomposition with partial pivoting) in place.
* R: `solve()` implicitly performs LU decomposition (wrapper of LAPACK routine `dgesv`). `solve()` allows specifying a single or multiple right hand sides. If none, it computes the matrix inverse. The `matrix` package contains `lu()` function that outputs `L`, `U`, and `pivot`.
* Julia:
- [LinearAlgebra.lu](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.lu).
- [LinearAlgebra.lu!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.lu!). In-place version. Input matrix gets overwritten with L and U.
- Or call LAPACK wrapper function [getrf!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.getrf!) directly.
- Other LU-related LAPACK wrapper functions: [gesv](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.gesv!), [gesvx](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.gesvx!), [trtri](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.trtri!) (inverse of triangular matrix), [trtrs](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.trtrs!).
```{julia}
A
```
```{julia}
using LinearAlgebra
# second argument indicates partial pivoting (default) or not
alu = lu(A)
typeof(alu)
```
```{julia}
dump(alu)
```
```{julia}
alu.L
```
```{julia}
alu.U
```
```{julia}
alu.p
```
```{julia}
alu.P
```
```{julia}
alu.L * alu.U
```
```{julia}
A[alu.p, :]
```
```{julia}
# this is doing two triangular solves, 2n^2 flops
alu \ b
```
```{julia}
det(A) # this does LU! O(n^3)
```
```{julia}
det(alu) # this is cheap O(n)
```
```{julia}
inv(A) # this does LU! O(n^3)
```
```{julia}
inv(alu) # this is cheap O(n^2)
```
## Further reading
* Sections II.5.2 and II.5.3 of [Computational Statistics](http://ucla.worldcat.org/title/computational-statistics/oclc/437345409&referer=brief_results) by James Gentle (2010).
* A definite reference is Chapter 3 of the book [Matrix Computation](http://catalog.library.ucla.edu/vwebv/holdingsInfo?bibId=7122088) by Gene Golub and Charles Van Loan.

