---
title: Cholesky Decomposition
subtitle: Biostat/Biomath M257
author: Dr. Hua Zhou @ UCLA
date: today
format:
  html:
    theme: cosmo
    embed-resources: true
    number-sections: true
    toc: true
    toc-depth: 4
    toc-location: left
    code-fold: false
jupyter:
  jupytext:
    formats: 'ipynb,qmd'
    text_representation:
      extension: .qmd
      format_name: quarto
      format_version: '1.0'
      jupytext_version: 1.14.5
  kernelspec:
    display_name: Julia (8 threads) 1.8.5
    language: julia
    name: julia-_8-threads_-1.8
---

System information (for reproducibility):

```{julia}
versioninfo()
```

Load packages:

```{julia}
using Pkg

Pkg.activate(pwd())
Pkg.instantiate()
Pkg.status()
```

## Introduction

<img src="http://www.cerebralmastication.com/wp-content/uploads/2010/09/39-cholesky-250x300.jpg" width="200" align="center"/>

* A basic tenet in numerical analysis: 

> **The structure should be exploited whenever solving a problem.** 

  Common structures include: symmetry, positive (semi)definiteness, sparsity, Kronecker product, low rank, ...

* LU decomposition (Gaussian Elimination) is **not** used in statistics so often because most of time statisticians deal with positive (semi)definite matrix. 

* That's why we often criticize use of the `solve()` function in base R code, which inverts a matrix using LU decomposition. First, most likely we don't need a matrix inverse. Second, most likely we are dealing with a pd/psd matrix and should use Cholesky.

* For example, in the normal equation 
$$
    \mathbf{X}^T \mathbf{X} \beta = \mathbf{X}^T \mathbf{y}
$$
for linear regression, the coefficient matrix $\mathbf{X}^T \mathbf{X}$ is symmetric and positive semidefinite. How to exploit this structure?

## Cholesky decomposition

* **Theorem**: Let $\mathbf{A} \in \mathbb{R}^{n \times n}$ be symmetric and positive definite. Then $\mathbf{A} = \mathbf{L} \mathbf{L}^T$, where $\mathbf{L}$ is lower triangular with positive diagonal entries and is unique.  
**Proof** (by induction):  
If $n=1$, then $\ell = \sqrt{a}$. For $n>1$, the block equation
$$
\begin{eqnarray*}
\begin{pmatrix}
a_{11} & \mathbf{a}^T \\ \mathbf{a} & \mathbf{A}_{22}
\end{pmatrix} =
\begin{pmatrix}
	\ell_{11} & \mathbf{0}_{n-1}^T \\ \mathbf{l} & \mathbf{L}_{22}
\end{pmatrix}
\begin{pmatrix}
	\ell_{11} & \mathbf{l}^T \\ \mathbf{0}_{n-1} & \mathbf{L}_{22}^T
\end{pmatrix}
\end{eqnarray*}
$$
has solution
$$
\begin{eqnarray*}
	\ell_{11} &=& \sqrt{a_{11}} \\
	\mathbf{l} &=& \ell_{11}^{-1} \mathbf{a}	\\
	\mathbf{L}_{22} \mathbf{L}_{22}^T &=& \mathbf{A}_{22}  - \mathbf{l} \mathbf{l}^T = \mathbf{A}_{22}  - a_{11}^{-1} \mathbf{a} \mathbf{a}^T.
\end{eqnarray*}
$$  
Now $a_{11}>0$ (why?), so $\ell_{11}$ and $\mathbf{l}$ are uniquely determined. $\mathbf{A}_{22} - a_{11}^{-1} \mathbf{a} \mathbf{a}^T$ is positive definite because $\mathbf{A}$ is positive definite (why?). By induction hypothesis, $\mathbf{L}_{22}$ exists and is unique.

* The constructive proof completely specifies the algorithm: 

<img src="http://www.netlib.org/utk/papers/factor/_25826_figure440.gif" width="500" align="center"/>

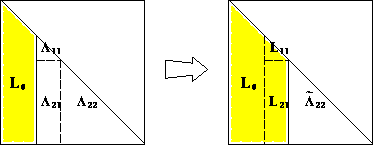* Computational cost: 
$$
\frac{1}{2} [2(n-1)^2 + 2(n-2)^2 + \cdots + 2 \cdot 1^2] \approx \frac{1}{3} n^3 \quad \text{flops}
$$ 
plus $n$ square roots. Half the cost of LU decomposition by utilizing symmetry.

* In general Cholesky decomposition is very stable. Failure of the decomposition simply means $\mathbf{A}$ is not positive definite. It is an efficient way to test positive definiteness. 

## Pivoting

* When $\mathbf{A}$ does not have full rank, e.g., $\mathbf{X}^T \mathbf{X}$ with a non-full column rank $\mathbf{X}$, we encounter $a_{kk} = 0$ during the procedure.

* **Symmetric pivoting**. At each stage $k$, we permute both row and column such that $\max_{k \le i \le n} a_{ii}$ becomes the pivot. If we encounter $\max_{k \le i \le n} a_{ii} = 0$, then $\mathbf{A}[k:n,k:n] = \mathbf{0}$ (why?) and the algorithm terminates.

* With symmetric pivoting: 
$$
\mathbf{P} \mathbf{A} \mathbf{P}^T = \mathbf{L} \mathbf{L}^T,
$$
where $\mathbf{P}$ is a permutation matrix and $\mathbf{L} \in \mathbb{R}^{n \times r}$, $r = \text{rank}(\mathbf{A})$.

## LAPACK and Julia implementation

* LAPACK functions: [?potrf](http://www.netlib.org/lapack/explore-html/d1/d7a/group__double_p_ocomputational_ga2f55f604a6003d03b5cd4a0adcfb74d6.html#ga2f55f604a6003d03b5cd4a0adcfb74d6) (without pivoting), [?pstrf](http://www.netlib.org/lapack/explore-html/da/dba/group__double_o_t_h_e_rcomputational_ga31cdc13a7f4ad687f4aefebff870e1cc.html#ga31cdc13a7f4ad687f4aefebff870e1cc) (with pivoting).

* Julia functions: [cholesky](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.cholesky), [cholesky!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.cholesky!), or call LAPACK wrapper functions [potrf!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.potrf!) and [pstrf!](https://docs.julialang.org/en/v1/stdlib/LinearAlgebra/#LinearAlgebra.LAPACK.pstrf!)

### Example: positive definite matrix

```{julia}
using LinearAlgebra

A = [4.0 12 -16; 12 37 -43; -16 -43 98]
```

```{julia}
# Cholesky without pivoting
Achol = cholesky(Symmetric(A))
```

```{julia}
typeof(Achol)
```

```{julia}
dump(Achol)
```

```{julia}
# retrieve the lower triangular Cholesky factor
Achol.L
```

```{julia}
# retrieve the upper triangular Cholesky factor
Achol.U
```

```{julia}
b = [1.0; 2.0; 3.0]
A \ b # this does LU; wasteful!!!; 2/3 n^3 + 2n^2
```

```{julia}
Achol \ b # two triangular solves; only 2n^2 flops
```

```{julia}
det(A) # this does LU; wasteful!!! (2/3) n^3
```

```{julia}
det(Achol) # cheap
```

```{julia}
inv(A) # this does LU! (2/3) n^3 + (4/3) n^3
```

```{julia}
inv(Achol) # (4/3) n^3
```

### Example: positive semi-definite matrix.

```{julia}
using Random

Random.seed!(123) # seed
A = randn(5, 3)
A = A * transpose(A) # A has rank 3
```

```{julia}
Achol = cholesky(A, Val(true)) # 2nd argument requests pivoting
```

```{julia}
Achol = cholesky(A, Val(true), check=false) # turn off checking pd
```

```{julia}
rank(Achol) # determine rank from Cholesky factor
```

```{julia}
rank(A) # determine rank from SVD (default), which is more numerically stable
```

```{julia}
Achol.L
```

```{julia}
Achol.U
```

```{julia}
Achol.p
```

```{julia}
# P A P' = L U
A[Achol.p, Achol.p] ≈ Achol.L * Achol.U
```

## Applications

* **No inversion** mentality: Whenever we see matrix inverse, we should think in terms of solving linear equations. If the matrix is positive (semi)definite, use Cholesky decomposition, which is twice cheaper than LU decomposition.

### Multivariate normal density 

Multivariate normal density $\text{MVN}(0, \Sigma)$, where $\Sigma$ is p.d., is
$$
\, - \frac{n}{2} \log (2\pi) - \frac{1}{2} \log \det \Sigma - \frac{1}{2} \mathbf{y}^T \Sigma^{-1} \mathbf{y}.
$$

* **Method 1**: (a) compute explicit inverse $\Sigma^{-1}$ ($2n^3$ flops), (b) compute quadratic form ($2n^2 + 2n$ flops), (c) compute determinant ($2n^3/3$ flops).
    
* **Method 2**: (a) Cholesky decomposition $\Sigma = \mathbf{L} \mathbf{L}^T$ ($n^3/3$ flops), (b) Solve $\mathbf{L} \mathbf{x} = \mathbf{y}$ by forward substitutions ($n^2$ flops), (c) compute quadratic form $\mathbf{x}^T \mathbf{x}$ ($2n$ flops), and (d) compute determinant from Cholesky factor ($n$ flops).  

**Which method is better?**

```{julia}
# this is a person w/o numerical analysis training
function logpdf_mvn_1(y::Vector, Σ::Matrix)
    n = length(y)
    - (n//2) * log(2π) - (1//2) * logdet(Symmetric(Σ)) - (1//2) * transpose(y) * inv(Σ) * y
end

# this is a computing-savvy person 
function logpdf_mvn_2(y::Vector, Σ::Matrix)
    n = length(y)
    Σchol = cholesky(Symmetric(Σ))
    - (n//2) * log(2π) - (1//2) * logdet(Σchol) - (1//2) * abs2(norm(Σchol.L \ y))
end

# better memory efficiency - input Σ is overwritten
function logpdf_mvn_3(y::Vector, Σ::Matrix)
    n = length(y)
    Σchol = cholesky!(Symmetric(Σ)) # Σ is overwritten
    - (n//2) * log(2π) - (1//2) * logdet(Σchol) - (1//2) * dot(y, Σchol \ y)
end
```

```{julia}
using BenchmarkTools, Distributions, Random

Random.seed!(257) # seed

n = 1000
# a pd matrix
Σ = convert(Matrix{Float64}, Symmetric([i * (n - j + 1) for i in 1:n, j in 1:n]))
y = rand(MvNormal(Σ)) # one random sample from N(0, Σ)

# at least they should give the same answer
@show logpdf_mvn_1(y, Σ)
@show logpdf_mvn_2(y, Σ)
Σc = copy(Σ)
@show logpdf_mvn_3(y, Σc);
```

```{julia}
@benchmark logpdf_mvn_1($y, $Σ)
```

```{julia}
@benchmark logpdf_mvn_2($y, $Σ)
```

```{julia}
@benchmark logpdf_mvn_3($y, $Σc) setup=(copy!(Σc, Σ)) evals=1
```

* To evaluate same multivariate normal density at many observations $y_1, y_2, \ldots$, we pre-compute the Cholesky decomposition ($n^3/3$ flops), then each evaluation costs $n^2$ flops.

### Linear regression

- Cholesky decomposition is **one** approach to solve linear regression  
$$
\widehat{\boldsymbol{\beta}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}.
$$

- Assume $\mathbf{X} \in \mathbb{R}^{n \times p}$ and $\mathbf{y} \in \mathbb{R}^n$.  
    - Compute $\mathbf{X}^T \mathbf{X}$: $np^2$ flops  
    - Compute $\mathbf{X}^T \mathbf{y}$: $2np$ flops  
    - Cholesky decomposition of $\mathbf{X}^T \mathbf{X}$: $\frac{1}{3} p^3$ flops  
    - Solve normal equation $\mathbf{X}^T \mathbf{X} \beta = \mathbf{X}^T \mathbf{y}$: $2p^2$ flops  
    - If need standard errors, another $(4/3)p^3$ flops

- Total computational cost is $np^2 + (1/3) p^3$ (without s.e.) or $np^2 + (5/3) p^3$ (with s.e.) flops.

## Further reading

* Section 7.7 of [Numerical Analysis for Statisticians](http://ucla.worldcat.org/title/numerical-analysis-for-statisticians/oclc/793808354&referer=brief_results) of Kenneth Lange (2010).

* Section II.5.3 of [Computational Statistics](http://ucla.worldcat.org/title/computational-statistics/oclc/437345409&referer=brief_results) by James Gentle (2010).

* Section 4.2 of [Matrix Computation](http://catalog.library.ucla.edu/vwebv/holdingsInfo?bibId=7122088) by Gene Golub and Charles Van Loan (2013).