{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Generative Adversarial Network\n",
"\n",
"In this notebook, we'll be building a generative adversarial network (GAN) trained on the MNIST dataset. From this, we'll be able to generate new handwritten digits!\n",
"\n",
"GANs were [first reported on](https://arxiv.org/abs/1406.2661) in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:\n",
"\n",
"* [Pix2Pix](https://affinelayer.com/pixsrv/) \n",
"* [CycleGAN & Pix2Pix in PyTorch, Jun-Yan Zhu](https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix)\n",
"* [A list of generative models](https://github.com/wiseodd/generative-models)\n",
"\n",
"The idea behind GANs is that you have two networks, a generator $G$ and a discriminator $D$, competing against each other. The generator makes \"fake\" data to pass to the discriminator. The discriminator also sees real training data and predicts if the data it's received is real or fake. \n",
"> * The generator is trained to fool the discriminator, it wants to output data that looks _as close as possible_ to real, training data. \n",
"* The discriminator is a classifier that is trained to figure out which data is real and which is fake. \n",
"\n",
"What ends up happening is that the generator learns to make data that is indistinguishable from real data to the discriminator.\n",
"\n",
" \n",
"\n",
"The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector that the generator uses to construct its fake images. This is often called a **latent vector** and that vector space is called **latent space**. As the generator trains, it figures out how to map latent vectors to recognizable images that can fool the discriminator.\n",
"\n",
"If you're interested in generating only new images, you can throw out the discriminator after training. In this notebook, I'll show you how to define and train these adversarial networks in PyTorch and generate new images!"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"\n",
"import numpy as np\n",
"import torch\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from torchvision import datasets\n",
"import torchvision.transforms as transforms\n",
"\n",
"# number of subprocesses to use for data loading\n",
"num_workers = 0\n",
"# how many samples per batch to load\n",
"batch_size = 64\n",
"\n",
"# convert data to torch.FloatTensor\n",
"transform = transforms.ToTensor()\n",
"\n",
"# get the training datasets\n",
"train_data = datasets.MNIST(root='data', train=True,\n",
" download=True, transform=transform)\n",
"\n",
"# prepare data loader\n",
"train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,\n",
" num_workers=num_workers)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Visualize the data"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAMgAAADFCAYAAAARxr1AAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAC9JJREFUeJzt3X+IVXUax/HPs7b+kWvZEDuJ6Zoi\nE5O0s2AarVDSzqaLYVMhDbQIivaHA7aEIP5TsRhC1m6SLLq7lkJrBtU6SayGmu7SMjSZ/bJ1i2hp\nZNJCzR/9kNFn/7hnYpr53u+9c++5d869vl8Qc+8zZ879HuzDOed7zn2OubsAhP1opAcAZBkBASII\nCBBBQIAIAgJEEBAggoAAEQQEiCAgQMRl5fyxmc2V9JSkUZL+4u5rCyzPZXtkhrtboWWs1FtNzGyU\npP9KapXUI+lNSe3ufjjyNwQEmVFMQMo5xJop6WN3/8Tdz0t6XtKCMtYHZE45AZkg6bMB73uS2g+Y\n2TIz6zaz7jI+CxgRZZ2DFMPdN0naJHGIhdpTzh7kqKSJA95fm9SAulFOQN6UNM3MrjOz0ZLuk9SZ\nzrCAbCj5EMvd+8ysQ9Iu5aZ5N7v7B6mNDMiAkqd5S/owzkGQIZWe5gXqHgEBIggIEEFAgAgCAkQQ\nECCCgAARBASIICBABAEBIggIEEFAgAgCAkQQECCCgAARBASIICBABAEBIggIEFHxvlgobNSoUcH6\nlVdemcr6Ozo6gvXLL798SK2pqSm47PLly4P1devWBevt7e3B+rfffhusr10bbuv86KOPBuvVUm7z\n6k8lnZF0QVKfu89IY1BAVqSxB5nj7l+msB4gczgHASLKDYhL2m1mb5nZstACNK9GLSv3EGu2ux81\ns59Kes3M/uPuBwYuQPNq1LKyAuLuR5Ofx83sZeWeGXIg/le1adKkScH66NGjg/VbbrllSG327NnB\nZceNGxes33PPPUWOLj09PT3B+vr164P1tra2YP3MmTPB+jvvvBOs79+/v4jRVV/Jh1hmNsbMxva/\nlvRrSe+nNTAgC8rZgzRKetnM+tfzN3f/RyqjAjKinO7un0j6eYpjATKHaV4ggoAAETwfZJCWlpZg\nfe/evcF6WvdLjYSLFy8OqS1evDi47NmzZ4e17t7e3mD95MmTwfqRI0eGtf408HwQoEwEBIggIEAE\nAQEiCAgQwSzWIA0NDcF6V1dXsD5lypRKDico31hOnToVrM+ZMydYP3/+/JBaLc/KDRezWECZCAgQ\nQUCACAICRBAQIIK+WIOcOHEiWF+5cmWwPn/+/GD97bffHlLL9628fA4dOhSst7a2Buvnzp0L1m+4\n4YZgfcWKFcMaz6WIPQgQQUCACAICRBAQIIKAABEF78Uys82S5ks67u7Tk1qDpO2SJkv6VNJCdw9/\nVeyH68r8vVjDdcUVVwTrob5QGzduDC67ZMmSYP3+++8P1rdt21bk6BCT1r1Yz0qaO6i2StIed58m\naU/yHqg7BQOStBIdfHFggaQtyestku5KeVxAJpR6obDR3fu/lf+5ck3kgpKm1sHG1kDWlX0l3d09\ndm5B82rUslIDcszMxrt7r5mNl3Q8zUHVktOnTxe97FdffTWsdS9dujRY3759e7AeauOD8pQ6zdsp\naVHyepGkHekMB8iWggExs22S/i2pycx6zGyJpLWSWs3sI0m/St4DdafgIZa7hx9XKt2e8liAzOFK\nOhBBQIAI2v5U0ZgxY4L1V155JVi/9dZbg/V58+YF67t37y5tYJco2v4AZSIgQAQBASIICBBBQIAI\nZrEyYOrUqcH6wYMHg/V8Tar37dsXrHd3dwfrGzZsGFKr5v8PI41ZLKBMBASIICBABAEBIggIEMEs\nVoa1tbUF688880ywPnbs2GGtf/Xq1UNqW7duDS7b29sbrNcyZrGAMhEQIIKAABEEBIggIEBEqc2r\nH5G0VNIXyWKr3f3Vgh/GLFYqpk+fHqw/+eSTwfrttxffXyNfg+01a9YE60ePHi163VlTyebVkvQH\nd29J/isYDqAWldq8GrgklHMO0mFm75rZZjO7Kt9CZrbMzLrNLHzPNZBhpQbkT5KmSmqR1CvpiXwL\nuvsmd5/h7jNK/CxgxJQUEHc/5u4X3P2ipD9LmpnusIBsKOpeLDObLGnngFms8f3PBzGz30ma5e73\nFbEeZrEqaNy4ccH6nXfeGayH7ukyC0/s7N27N1hvbW0tcnTZU8wsVsHevEnz6tskXW1mPZIelnSb\nmbVIcuWeUfhAWSMFMqrU5tV/rcBYgMzhSjoQQUCACAICRPCNwkvYd999N6R22WXh09K+vr5g/Y47\n7gjWX3/99ZLHVS18oxAoEwEBIggIEEFAgIiCFwqRPTfeeGOwfu+99wbrN910U7Ce74Q85PDhw8H6\ngQMHil5HLWIPAkQQECCCgAARBASIICBABLNYGdDU1BSsd3R0BOt33313sH7NNdeUPZYLFy4E6/ma\nV1+8eLHsz8wy9iBABAEBIggIEEFAgAgCAkQU09VkoqStkhqV62Kyyd2fMrMGSdslTVaus8lCdz9Z\nuaHWltCMUnt7qP9F/tmqyZMnpzmkIbq7hza7zNekurOzs6Jjyapi9iB9kh5y92ZJN0tabmbNklZJ\n2uPu0yTtSd4DdaWY5tW97n4weX1G0oeSJkhaIGlLstgWSXdVapDASBnWhcKkw+IvJHVJauzvrijp\nc+UOwUJ/s0zSstKHCIycok/Szewnkl6U9KC7nx74O891fgg2ZKB5NWpZUQExsx8rF47n3P2lpHzM\nzMYnvx8v6XhlhgiMnGJmsUy5VqMfuvvAZ3x1SlokaW3yc0dFRpgRjY3BI0g1NzcH608//fSQ2vXX\nX5/qmAbr6uoK1h9//PFgfceOof9k9X5v1XAVcw7yS0m/lfSemR1KaquVC8YLZrZE0v8kLazMEIGR\nU0zz6n9Jytdgq/inQwI1iCvpQAQBASIICBBxyX6jsKGhIVjfuHFjsN7S0hKsT5kyJbUxDfbGG28E\n6088EX5m6q5du4L1b775JrUxXWrYgwARBASIICBABAEBIggIEFE3s1izZs0K1leuXBmsz5w5M1if\nMGFCamMa7Ouvvw7W169fH6w/9thjwfq5c+dSGxPi2IMAEQQEiCAgQAQBASIICBBRN7NYbW1tw6oP\nV75n9O3cuTNY7+vrG1LLdw/VqVOnSh8YKoo9CBBBQIAIAgJEEBAgwnI93yIL5G9e/YikpZK+SBZd\n7e6vFlhX/MOAKnL3fM1IvldMQMZLGu/uB81srKS3lOvDu1DSWXdfV+yACAiypJiAFNP2p1dSb/L6\njJn1N68G6t6wzkEGNa+WpA4ze9fMNpvZVXn+ZpmZdZvZ0IdRABlX8BDr+wVzzav3S1rj7i+ZWaOk\nL5U7L/m9codhiwusg0MsZEYq5yDS982rd0raNag/b//vJ0va6e7TC6yHgCAziglIwUOsfM2r+zu7\nJ9okvV/KIIEsK2YWa7akf0p6T1J/6+/VktoltSh3iPWppAcGPFAn37rYgyAzUjvESgsBQZakcogF\nXMoICBBBQIAIAgJEEBAggoAAEQQEiCAgQAQBASKq3fbnS+WeqS5JVyfv6x3bmU0/K2ahqt5q8oMP\nNut29xkj8uFVxHbWNg6xgAgCAkSMZEA2jeBnVxPbWcNG7BwEqAUcYgERBASIqHpAzGyumR0xs4/N\nbFW1P7+SkvZHx83s/QG1BjN7zcw+Sn4G2yPVEjObaGb7zOywmX1gZiuSet1ta1UDYmajJG2QNE9S\ns6R2M2uu5hgq7FlJcwfVVkna4+7TJO1J3te6PkkPuXuzpJslLU/+HetuW6u9B5kp6WN3/8Tdz0t6\nXtKCKo+hYtz9gKQTg8oLJG1JXm9Rrm1rTXP3Xnc/mLw+I6m/22bdbWu1AzJB0mcD3veo/tuYNg7o\n9vK5ck3A68agbpt1t62cpFeR5+bU62ZePem2+aKkB9399MDf1cu2VjsgRyVNHPD+2qRWz471N9lL\nfh4f4fGkIum2+aKk59z9paRcd9ta7YC8KWmamV1nZqMl3Seps8pjqLZOSYuS14sk7RjBsaQiX7dN\n1eO2VvtKupn9RtIfJY2StNnd11R1ABVkZtsk3abcrd/HJD0s6e+SXpA0Sblb/Re6++AT+ZoS6bbZ\npXrbVm41AfLjJB2IICBABAEBIggIEEFAgAgCAkQQECDi/0Edkpqgj/uIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# obtain one batch of training images\n",
"dataiter = iter(train_loader)\n",
"images, labels = dataiter.next()\n",
"images = images.numpy()\n",
"\n",
"# get one image from the batch\n",
"img = np.squeeze(images[0])\n",
"\n",
"fig = plt.figure(figsize = (3,3)) \n",
"ax = fig.add_subplot(111)\n",
"ax.imshow(img, cmap='gray')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"# Define the Model\n",
"\n",
"A GAN is comprised of two adversarial networks, a discriminator and a generator."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Discriminator\n",
"\n",
"The discriminator network is going to be a pretty typical linear classifier. To make this network a universal function approximator, we'll need at least one hidden layer, and these hidden layers should have one key attribute:\n",
"> All hidden layers will have a [Leaky ReLu](https://pytorch.org/docs/stable/nn.html#torch.nn.LeakyReLU) activation function applied to their outputs.\n",
"\n",
"
\n",
"\n",
"The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector that the generator uses to construct its fake images. This is often called a **latent vector** and that vector space is called **latent space**. As the generator trains, it figures out how to map latent vectors to recognizable images that can fool the discriminator.\n",
"\n",
"If you're interested in generating only new images, you can throw out the discriminator after training. In this notebook, I'll show you how to define and train these adversarial networks in PyTorch and generate new images!"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"\n",
"import numpy as np\n",
"import torch\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"from torchvision import datasets\n",
"import torchvision.transforms as transforms\n",
"\n",
"# number of subprocesses to use for data loading\n",
"num_workers = 0\n",
"# how many samples per batch to load\n",
"batch_size = 64\n",
"\n",
"# convert data to torch.FloatTensor\n",
"transform = transforms.ToTensor()\n",
"\n",
"# get the training datasets\n",
"train_data = datasets.MNIST(root='data', train=True,\n",
" download=True, transform=transform)\n",
"\n",
"# prepare data loader\n",
"train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,\n",
" num_workers=num_workers)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Visualize the data"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAMgAAADFCAYAAAARxr1AAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAC9JJREFUeJzt3X+IVXUax/HPs7b+kWvZEDuJ6Zoi\nE5O0s2AarVDSzqaLYVMhDbQIivaHA7aEIP5TsRhC1m6SLLq7lkJrBtU6SayGmu7SMjSZ/bJ1i2hp\nZNJCzR/9kNFn/7hnYpr53u+9c++5d869vl8Qc+8zZ879HuzDOed7zn2OubsAhP1opAcAZBkBASII\nCBBBQIAIAgJEEBAggoAAEQQEiCAgQMRl5fyxmc2V9JSkUZL+4u5rCyzPZXtkhrtboWWs1FtNzGyU\npP9KapXUI+lNSe3ufjjyNwQEmVFMQMo5xJop6WN3/8Tdz0t6XtKCMtYHZE45AZkg6bMB73uS2g+Y\n2TIz6zaz7jI+CxgRZZ2DFMPdN0naJHGIhdpTzh7kqKSJA95fm9SAulFOQN6UNM3MrjOz0ZLuk9SZ\nzrCAbCj5EMvd+8ysQ9Iu5aZ5N7v7B6mNDMiAkqd5S/owzkGQIZWe5gXqHgEBIggIEEFAgAgCAkQQ\nECCCgAARBASIICBABAEBIggIEEFAgAgCAkQQECCCgAARBASIICBABAEBIggIEFHxvlgobNSoUcH6\nlVdemcr6Ozo6gvXLL798SK2pqSm47PLly4P1devWBevt7e3B+rfffhusr10bbuv86KOPBuvVUm7z\n6k8lnZF0QVKfu89IY1BAVqSxB5nj7l+msB4gczgHASLKDYhL2m1mb5nZstACNK9GLSv3EGu2ux81\ns59Kes3M/uPuBwYuQPNq1LKyAuLuR5Ofx83sZeWeGXIg/le1adKkScH66NGjg/VbbrllSG327NnB\nZceNGxes33PPPUWOLj09PT3B+vr164P1tra2YP3MmTPB+jvvvBOs79+/v4jRVV/Jh1hmNsbMxva/\nlvRrSe+nNTAgC8rZgzRKetnM+tfzN3f/RyqjAjKinO7un0j6eYpjATKHaV4ggoAAETwfZJCWlpZg\nfe/evcF6WvdLjYSLFy8OqS1evDi47NmzZ4e17t7e3mD95MmTwfqRI0eGtf408HwQoEwEBIggIEAE\nAQEiCAgQwSzWIA0NDcF6V1dXsD5lypRKDico31hOnToVrM+ZMydYP3/+/JBaLc/KDRezWECZCAgQ\nQUCACAICRBAQIIK+WIOcOHEiWF+5cmWwPn/+/GD97bffHlLL9628fA4dOhSst7a2Buvnzp0L1m+4\n4YZgfcWKFcMaz6WIPQgQQUCACAICRBAQIIKAABEF78Uys82S5ks67u7Tk1qDpO2SJkv6VNJCdw9/\nVeyH68r8vVjDdcUVVwTrob5QGzduDC67ZMmSYP3+++8P1rdt21bk6BCT1r1Yz0qaO6i2StIed58m\naU/yHqg7BQOStBIdfHFggaQtyestku5KeVxAJpR6obDR3fu/lf+5ck3kgpKm1sHG1kDWlX0l3d09\ndm5B82rUslIDcszMxrt7r5mNl3Q8zUHVktOnTxe97FdffTWsdS9dujRY3759e7AeauOD8pQ6zdsp\naVHyepGkHekMB8iWggExs22S/i2pycx6zGyJpLWSWs3sI0m/St4DdafgIZa7hx9XKt2e8liAzOFK\nOhBBQIAI2v5U0ZgxY4L1V155JVi/9dZbg/V58+YF67t37y5tYJco2v4AZSIgQAQBASIICBBBQIAI\nZrEyYOrUqcH6wYMHg/V8Tar37dsXrHd3dwfrGzZsGFKr5v8PI41ZLKBMBASIICBABAEBIggIEMEs\nVoa1tbUF688880ywPnbs2GGtf/Xq1UNqW7duDS7b29sbrNcyZrGAMhEQIIKAABEEBIggIEBEqc2r\nH5G0VNIXyWKr3f3Vgh/GLFYqpk+fHqw/+eSTwfrttxffXyNfg+01a9YE60ePHi163VlTyebVkvQH\nd29J/isYDqAWldq8GrgklHMO0mFm75rZZjO7Kt9CZrbMzLrNLHzPNZBhpQbkT5KmSmqR1CvpiXwL\nuvsmd5/h7jNK/CxgxJQUEHc/5u4X3P2ipD9LmpnusIBsKOpeLDObLGnngFms8f3PBzGz30ma5e73\nFbEeZrEqaNy4ccH6nXfeGayH7ukyC0/s7N27N1hvbW0tcnTZU8wsVsHevEnz6tskXW1mPZIelnSb\nmbVIcuWeUfhAWSMFMqrU5tV/rcBYgMzhSjoQQUCACAICRPCNwkvYd999N6R22WXh09K+vr5g/Y47\n7gjWX3/99ZLHVS18oxAoEwEBIggIEEFAgIiCFwqRPTfeeGOwfu+99wbrN910U7Ce74Q85PDhw8H6\ngQMHil5HLWIPAkQQECCCgAARBASIICBABLNYGdDU1BSsd3R0BOt33313sH7NNdeUPZYLFy4E6/ma\nV1+8eLHsz8wy9iBABAEBIggIEEFAgAgCAkQU09VkoqStkhqV62Kyyd2fMrMGSdslTVaus8lCdz9Z\nuaHWltCMUnt7qP9F/tmqyZMnpzmkIbq7hza7zNekurOzs6Jjyapi9iB9kh5y92ZJN0tabmbNklZJ\n2uPu0yTtSd4DdaWY5tW97n4weX1G0oeSJkhaIGlLstgWSXdVapDASBnWhcKkw+IvJHVJauzvrijp\nc+UOwUJ/s0zSstKHCIycok/Szewnkl6U9KC7nx74O891fgg2ZKB5NWpZUQExsx8rF47n3P2lpHzM\nzMYnvx8v6XhlhgiMnGJmsUy5VqMfuvvAZ3x1SlokaW3yc0dFRpgRjY3BI0g1NzcH608//fSQ2vXX\nX5/qmAbr6uoK1h9//PFgfceOof9k9X5v1XAVcw7yS0m/lfSemR1KaquVC8YLZrZE0v8kLazMEIGR\nU0zz6n9Jytdgq/inQwI1iCvpQAQBASIICBBxyX6jsKGhIVjfuHFjsN7S0hKsT5kyJbUxDfbGG28E\n6088EX5m6q5du4L1b775JrUxXWrYgwARBASIICBABAEBIggIEFE3s1izZs0K1leuXBmsz5w5M1if\nMGFCamMa7Ouvvw7W169fH6w/9thjwfq5c+dSGxPi2IMAEQQEiCAgQAQBASIICBBRN7NYbW1tw6oP\nV75n9O3cuTNY7+vrG1LLdw/VqVOnSh8YKoo9CBBBQIAIAgJEEBAgwnI93yIL5G9e/YikpZK+SBZd\n7e6vFlhX/MOAKnL3fM1IvldMQMZLGu/uB81srKS3lOvDu1DSWXdfV+yACAiypJiAFNP2p1dSb/L6\njJn1N68G6t6wzkEGNa+WpA4ze9fMNpvZVXn+ZpmZdZvZ0IdRABlX8BDr+wVzzav3S1rj7i+ZWaOk\nL5U7L/m9codhiwusg0MsZEYq5yDS982rd0raNag/b//vJ0va6e7TC6yHgCAziglIwUOsfM2r+zu7\nJ9okvV/KIIEsK2YWa7akf0p6T1J/6+/VktoltSh3iPWppAcGPFAn37rYgyAzUjvESgsBQZakcogF\nXMoICBBBQIAIAgJEEBAggoAAEQQEiCAgQAQBASKq3fbnS+WeqS5JVyfv6x3bmU0/K2ahqt5q8oMP\nNut29xkj8uFVxHbWNg6xgAgCAkSMZEA2jeBnVxPbWcNG7BwEqAUcYgERBASIqHpAzGyumR0xs4/N\nbFW1P7+SkvZHx83s/QG1BjN7zcw+Sn4G2yPVEjObaGb7zOywmX1gZiuSet1ta1UDYmajJG2QNE9S\ns6R2M2uu5hgq7FlJcwfVVkna4+7TJO1J3te6PkkPuXuzpJslLU/+HetuW6u9B5kp6WN3/8Tdz0t6\nXtKCKo+hYtz9gKQTg8oLJG1JXm9Rrm1rTXP3Xnc/mLw+I6m/22bdbWu1AzJB0mcD3veo/tuYNg7o\n9vK5ck3A68agbpt1t62cpFeR5+bU62ZePem2+aKkB9399MDf1cu2VjsgRyVNHPD+2qRWz471N9lL\nfh4f4fGkIum2+aKk59z9paRcd9ta7YC8KWmamV1nZqMl3Seps8pjqLZOSYuS14sk7RjBsaQiX7dN\n1eO2VvtKupn9RtIfJY2StNnd11R1ABVkZtsk3abcrd/HJD0s6e+SXpA0Sblb/Re6++AT+ZoS6bbZ\npXrbVm41AfLjJB2IICBABAEBIggIEEFAgAgCAkQQECDi/0Edkpqgj/uIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# obtain one batch of training images\n",
"dataiter = iter(train_loader)\n",
"images, labels = dataiter.next()\n",
"images = images.numpy()\n",
"\n",
"# get one image from the batch\n",
"img = np.squeeze(images[0])\n",
"\n",
"fig = plt.figure(figsize = (3,3)) \n",
"ax = fig.add_subplot(111)\n",
"ax.imshow(img, cmap='gray')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"# Define the Model\n",
"\n",
"A GAN is comprised of two adversarial networks, a discriminator and a generator."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Discriminator\n",
"\n",
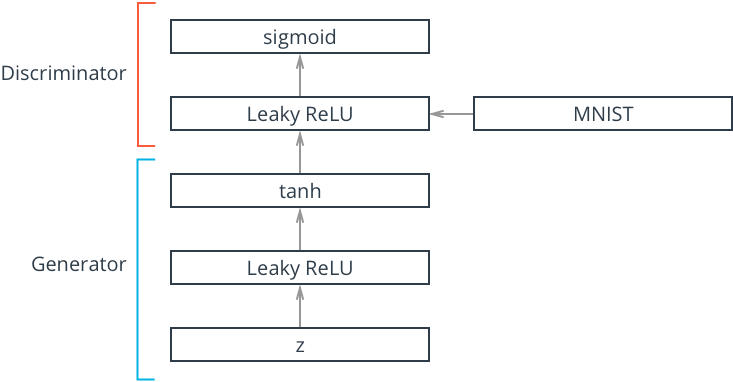
"The discriminator network is going to be a pretty typical linear classifier. To make this network a universal function approximator, we'll need at least one hidden layer, and these hidden layers should have one key attribute:\n",
"> All hidden layers will have a [Leaky ReLu](https://pytorch.org/docs/stable/nn.html#torch.nn.LeakyReLU) activation function applied to their outputs.\n",
"\n",
" \n",
"\n",
"#### Leaky ReLu\n",
"\n",
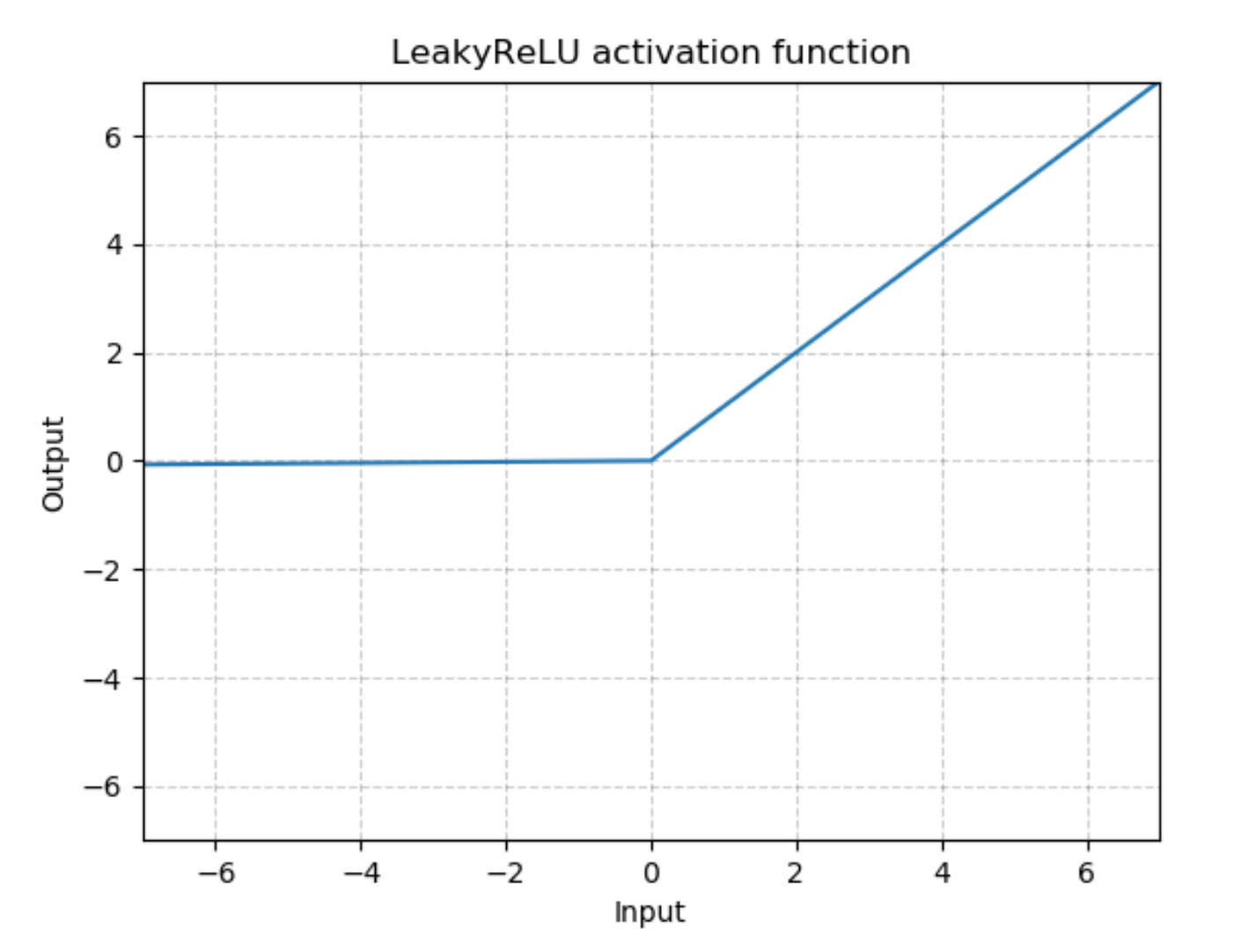
"We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.\n",
"\n",
"
\n",
"\n",
"#### Leaky ReLu\n",
"\n",
"We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.\n",
"\n",
" \n",
"\n",
"#### Sigmoid Output\n",
"\n",
"We'll also take the approach of using a more numerically stable loss function on the outputs. Recall that we want the discriminator to output a value 0-1 indicating whether an image is _real or fake_. \n",
"> We will ultimately use [BCEWithLogitsLoss](https://pytorch.org/docs/stable/nn.html#bcewithlogitsloss), which combines a `sigmoid` activation function **and** binary cross entropy loss in one function. \n",
"\n",
"So, our final output layer should not have any activation function applied to it."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"\n",
"class Discriminator(nn.Module):\n",
"\n",
" def __init__(self, input_size, hidden_dim, output_size):\n",
" super(Discriminator, self).__init__()\n",
" \n",
" # define hidden linear layers\n",
" self.fc1 = nn.Linear(input_size, hidden_dim*4)\n",
" self.fc2 = nn.Linear(hidden_dim*4, hidden_dim*2)\n",
" self.fc3 = nn.Linear(hidden_dim*2, hidden_dim)\n",
" \n",
" # final fully-connected layer\n",
" self.fc4 = nn.Linear(hidden_dim, output_size)\n",
" \n",
" # dropout layer \n",
" self.dropout = nn.Dropout(0.3)\n",
" \n",
" \n",
" def forward(self, x):\n",
" # flatten image\n",
" x = x.view(-1, 28*28)\n",
" # all hidden layers\n",
" x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc2(x), 0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc3(x), 0.2)\n",
" x = self.dropout(x)\n",
" # final layer\n",
" out = self.fc4(x)\n",
"\n",
" return out\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator\n",
"\n",
"The generator network will be almost exactly the same as the discriminator network, except that we're applying a [tanh activation function](https://pytorch.org/docs/stable/nn.html#tanh) to our output layer.\n",
"\n",
"#### tanh Output\n",
"The generator has been found to perform the best with $tanh$ for the generator output, which scales the output to be between -1 and 1, instead of 0 and 1. \n",
"\n",
"
\n",
"\n",
"#### Sigmoid Output\n",
"\n",
"We'll also take the approach of using a more numerically stable loss function on the outputs. Recall that we want the discriminator to output a value 0-1 indicating whether an image is _real or fake_. \n",
"> We will ultimately use [BCEWithLogitsLoss](https://pytorch.org/docs/stable/nn.html#bcewithlogitsloss), which combines a `sigmoid` activation function **and** binary cross entropy loss in one function. \n",
"\n",
"So, our final output layer should not have any activation function applied to it."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"\n",
"class Discriminator(nn.Module):\n",
"\n",
" def __init__(self, input_size, hidden_dim, output_size):\n",
" super(Discriminator, self).__init__()\n",
" \n",
" # define hidden linear layers\n",
" self.fc1 = nn.Linear(input_size, hidden_dim*4)\n",
" self.fc2 = nn.Linear(hidden_dim*4, hidden_dim*2)\n",
" self.fc3 = nn.Linear(hidden_dim*2, hidden_dim)\n",
" \n",
" # final fully-connected layer\n",
" self.fc4 = nn.Linear(hidden_dim, output_size)\n",
" \n",
" # dropout layer \n",
" self.dropout = nn.Dropout(0.3)\n",
" \n",
" \n",
" def forward(self, x):\n",
" # flatten image\n",
" x = x.view(-1, 28*28)\n",
" # all hidden layers\n",
" x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc2(x), 0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc3(x), 0.2)\n",
" x = self.dropout(x)\n",
" # final layer\n",
" out = self.fc4(x)\n",
"\n",
" return out\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator\n",
"\n",
"The generator network will be almost exactly the same as the discriminator network, except that we're applying a [tanh activation function](https://pytorch.org/docs/stable/nn.html#tanh) to our output layer.\n",
"\n",
"#### tanh Output\n",
"The generator has been found to perform the best with $tanh$ for the generator output, which scales the output to be between -1 and 1, instead of 0 and 1. \n",
"\n",
" \n",
"\n",
"Recall that we also want these outputs to be comparable to the *real* input pixel values, which are read in as normalized values between 0 and 1. \n",
"> So, we'll also have to **scale our real input images to have pixel values between -1 and 1** when we train the discriminator. \n",
"\n",
"I'll do this in the training loop, later on."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Generator(nn.Module):\n",
"\n",
" def __init__(self, input_size, hidden_dim, output_size):\n",
" super(Generator, self).__init__()\n",
" \n",
" # define hidden linear layers\n",
" self.fc1 = nn.Linear(input_size, hidden_dim)\n",
" self.fc2 = nn.Linear(hidden_dim, hidden_dim*2)\n",
" self.fc3 = nn.Linear(hidden_dim*2, hidden_dim*4)\n",
" \n",
" # final fully-connected layer\n",
" self.fc4 = nn.Linear(hidden_dim*4, output_size)\n",
" \n",
" # dropout layer \n",
" self.dropout = nn.Dropout(0.3)\n",
"\n",
" def forward(self, x):\n",
" # all hidden layers\n",
" x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc2(x), 0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc3(x), 0.2)\n",
" x = self.dropout(x)\n",
" # final layer with tanh applied\n",
" out = F.tanh(self.fc4(x))\n",
"\n",
" return out"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model hyperparameters"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Discriminator hyperparams\n",
"\n",
"# Size of input image to discriminator (28*28)\n",
"input_size = 784\n",
"# Size of discriminator output (real or fake)\n",
"d_output_size = 1\n",
"# Size of last hidden layer in the discriminator\n",
"d_hidden_size = 32\n",
"\n",
"# Generator hyperparams\n",
"\n",
"# Size of latent vector to give to generator\n",
"z_size = 100\n",
"# Size of discriminator output (generated image)\n",
"g_output_size = 784\n",
"# Size of first hidden layer in the generator\n",
"g_hidden_size = 32"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Build complete network\n",
"\n",
"Now we're instantiating the discriminator and generator from the classes defined above. Make sure you've passed in the correct input arguments."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Discriminator(\n",
" (fc1): Linear(in_features=784, out_features=128, bias=True)\n",
" (fc2): Linear(in_features=128, out_features=64, bias=True)\n",
" (fc3): Linear(in_features=64, out_features=32, bias=True)\n",
" (fc4): Linear(in_features=32, out_features=1, bias=True)\n",
" (dropout): Dropout(p=0.3)\n",
")\n",
"\n",
"Generator(\n",
" (fc1): Linear(in_features=100, out_features=32, bias=True)\n",
" (fc2): Linear(in_features=32, out_features=64, bias=True)\n",
" (fc3): Linear(in_features=64, out_features=128, bias=True)\n",
" (fc4): Linear(in_features=128, out_features=784, bias=True)\n",
" (dropout): Dropout(p=0.3)\n",
")\n"
]
}
],
"source": [
"# instantiate discriminator and generator\n",
"D = Discriminator(input_size, d_hidden_size, d_output_size)\n",
"G = Generator(z_size, g_hidden_size, g_output_size)\n",
"\n",
"# check that they are as you expect\n",
"print(D)\n",
"print()\n",
"print(G)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Discriminator and Generator Losses\n",
"\n",
"Now we need to calculate the losses. \n",
"\n",
"### Discriminator Losses\n",
"\n",
"> * For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_real_loss + d_fake_loss`. \n",
"* Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.\n",
"\n",
"
\n",
"\n",
"Recall that we also want these outputs to be comparable to the *real* input pixel values, which are read in as normalized values between 0 and 1. \n",
"> So, we'll also have to **scale our real input images to have pixel values between -1 and 1** when we train the discriminator. \n",
"\n",
"I'll do this in the training loop, later on."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Generator(nn.Module):\n",
"\n",
" def __init__(self, input_size, hidden_dim, output_size):\n",
" super(Generator, self).__init__()\n",
" \n",
" # define hidden linear layers\n",
" self.fc1 = nn.Linear(input_size, hidden_dim)\n",
" self.fc2 = nn.Linear(hidden_dim, hidden_dim*2)\n",
" self.fc3 = nn.Linear(hidden_dim*2, hidden_dim*4)\n",
" \n",
" # final fully-connected layer\n",
" self.fc4 = nn.Linear(hidden_dim*4, output_size)\n",
" \n",
" # dropout layer \n",
" self.dropout = nn.Dropout(0.3)\n",
"\n",
" def forward(self, x):\n",
" # all hidden layers\n",
" x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc2(x), 0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc3(x), 0.2)\n",
" x = self.dropout(x)\n",
" # final layer with tanh applied\n",
" out = F.tanh(self.fc4(x))\n",
"\n",
" return out"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model hyperparameters"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Discriminator hyperparams\n",
"\n",
"# Size of input image to discriminator (28*28)\n",
"input_size = 784\n",
"# Size of discriminator output (real or fake)\n",
"d_output_size = 1\n",
"# Size of last hidden layer in the discriminator\n",
"d_hidden_size = 32\n",
"\n",
"# Generator hyperparams\n",
"\n",
"# Size of latent vector to give to generator\n",
"z_size = 100\n",
"# Size of discriminator output (generated image)\n",
"g_output_size = 784\n",
"# Size of first hidden layer in the generator\n",
"g_hidden_size = 32"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Build complete network\n",
"\n",
"Now we're instantiating the discriminator and generator from the classes defined above. Make sure you've passed in the correct input arguments."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Discriminator(\n",
" (fc1): Linear(in_features=784, out_features=128, bias=True)\n",
" (fc2): Linear(in_features=128, out_features=64, bias=True)\n",
" (fc3): Linear(in_features=64, out_features=32, bias=True)\n",
" (fc4): Linear(in_features=32, out_features=1, bias=True)\n",
" (dropout): Dropout(p=0.3)\n",
")\n",
"\n",
"Generator(\n",
" (fc1): Linear(in_features=100, out_features=32, bias=True)\n",
" (fc2): Linear(in_features=32, out_features=64, bias=True)\n",
" (fc3): Linear(in_features=64, out_features=128, bias=True)\n",
" (fc4): Linear(in_features=128, out_features=784, bias=True)\n",
" (dropout): Dropout(p=0.3)\n",
")\n"
]
}
],
"source": [
"# instantiate discriminator and generator\n",
"D = Discriminator(input_size, d_hidden_size, d_output_size)\n",
"G = Generator(z_size, g_hidden_size, g_output_size)\n",
"\n",
"# check that they are as you expect\n",
"print(D)\n",
"print()\n",
"print(G)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Discriminator and Generator Losses\n",
"\n",
"Now we need to calculate the losses. \n",
"\n",
"### Discriminator Losses\n",
"\n",
"> * For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_real_loss + d_fake_loss`. \n",
"* Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.\n",
"\n",
" \n",
"\n",
"The losses will by binary cross entropy loss with logits, which we can get with [BCEWithLogitsLoss](https://pytorch.org/docs/stable/nn.html#bcewithlogitsloss). This combines a `sigmoid` activation function **and** and binary cross entropy loss in one function.\n",
"\n",
"For the real images, we want `D(real_images) = 1`. That is, we want the discriminator to classify the the real images with a label = 1, indicating that these are real. To help the discriminator generalize better, the labels are **reduced a bit from 1.0 to 0.9**. For this, we'll use the parameter `smooth`; if True, then we should smooth our labels. In PyTorch, this looks like `labels = torch.ones(size) * 0.9`\n",
"\n",
"The discriminator loss for the fake data is similar. We want `D(fake_images) = 0`, where the fake images are the _generator output_, `fake_images = G(z)`. \n",
"\n",
"### Generator Loss\n",
"\n",
"The generator loss will look similar only with flipped labels. The generator's goal is to get `D(fake_images) = 1`. In this case, the labels are **flipped** to represent that the generator is trying to fool the discriminator into thinking that the images it generates (fakes) are real!"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Calculate losses\n",
"def real_loss(D_out, smooth=False):\n",
" batch_size = D_out.size(0)\n",
" # label smoothing\n",
" if smooth:\n",
" # smooth, real labels = 0.9\n",
" labels = torch.ones(batch_size)*0.9\n",
" else:\n",
" labels = torch.ones(batch_size) # real labels = 1\n",
" \n",
" # numerically stable loss\n",
" criterion = nn.BCEWithLogitsLoss()\n",
" # calculate loss\n",
" loss = criterion(D_out.squeeze(), labels)\n",
" return loss\n",
"\n",
"def fake_loss(D_out):\n",
" batch_size = D_out.size(0)\n",
" labels = torch.zeros(batch_size) # fake labels = 0\n",
" criterion = nn.BCEWithLogitsLoss()\n",
" # calculate loss\n",
" loss = criterion(D_out.squeeze(), labels)\n",
" return loss"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Optimizers\n",
"\n",
"We want to update the generator and discriminator variables separately. So, we'll define two separate Adam optimizers."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true,
"scrolled": true
},
"outputs": [],
"source": [
"import torch.optim as optim\n",
"\n",
"# Optimizers\n",
"lr = 0.002\n",
"\n",
"# Create optimizers for the discriminator and generator\n",
"d_optimizer = optim.Adam(D.parameters(), lr)\n",
"g_optimizer = optim.Adam(G.parameters(), lr)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Training\n",
"\n",
"Training will involve alternating between training the discriminator and the generator. We'll use our functions `real_loss` and `fake_loss` to help us calculate the discriminator losses in all of the following cases.\n",
"\n",
"### Discriminator training\n",
"1. Compute the discriminator loss on real, training images \n",
"2. Generate fake images\n",
"3. Compute the discriminator loss on fake, generated images \n",
"4. Add up real and fake loss\n",
"5. Perform backpropagation + an optimization step to update the discriminator's weights\n",
"\n",
"### Generator training\n",
"1. Generate fake images\n",
"2. Compute the discriminator loss on fake images, using **flipped** labels!\n",
"3. Perform backpropagation + an optimization step to update the generator's weights\n",
"\n",
"#### Saving Samples\n",
"\n",
"As we train, we'll also print out some loss statistics and save some generated \"fake\" samples."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch [ 1/ 100] | d_loss: 1.3830 | g_loss: 0.6883\n",
"Epoch [ 1/ 100] | d_loss: 0.7668 | g_loss: 3.1404\n",
"Epoch [ 1/ 100] | d_loss: 1.0908 | g_loss: 2.6393\n",
"Epoch [ 2/ 100] | d_loss: 1.2982 | g_loss: 1.1008\n",
"Epoch [ 2/ 100] | d_loss: 1.1753 | g_loss: 1.1042\n",
"Epoch [ 2/ 100] | d_loss: 1.0874 | g_loss: 1.6588\n",
"Epoch [ 3/ 100] | d_loss: 0.9747 | g_loss: 2.9083\n",
"Epoch [ 3/ 100] | d_loss: 1.0724 | g_loss: 1.1101\n",
"Epoch [ 3/ 100] | d_loss: 1.4727 | g_loss: 0.4990\n",
"Epoch [ 4/ 100] | d_loss: 1.1590 | g_loss: 0.9996\n",
"Epoch [ 4/ 100] | d_loss: 1.1832 | g_loss: 1.0638\n",
"Epoch [ 4/ 100] | d_loss: 1.1652 | g_loss: 1.1463\n",
"Epoch [ 5/ 100] | d_loss: 1.2966 | g_loss: 1.0950\n",
"Epoch [ 5/ 100] | d_loss: 1.3616 | g_loss: 1.0312\n",
"Epoch [ 5/ 100] | d_loss: 1.2202 | g_loss: 1.1301\n",
"Epoch [ 6/ 100] | d_loss: 1.1609 | g_loss: 1.5148\n",
"Epoch [ 6/ 100] | d_loss: 1.1100 | g_loss: 1.2183\n",
"Epoch [ 6/ 100] | d_loss: 1.2376 | g_loss: 1.5296\n",
"Epoch [ 7/ 100] | d_loss: 1.2304 | g_loss: 1.1526\n",
"Epoch [ 7/ 100] | d_loss: 1.1684 | g_loss: 1.1339\n",
"Epoch [ 7/ 100] | d_loss: 1.0965 | g_loss: 1.3531\n",
"Epoch [ 8/ 100] | d_loss: 1.2527 | g_loss: 2.2266\n",
"Epoch [ 8/ 100] | d_loss: 1.2978 | g_loss: 1.6185\n",
"Epoch [ 8/ 100] | d_loss: 1.1493 | g_loss: 1.4873\n",
"Epoch [ 9/ 100] | d_loss: 0.9751 | g_loss: 2.6848\n",
"Epoch [ 9/ 100] | d_loss: 1.1574 | g_loss: 1.7639\n",
"Epoch [ 9/ 100] | d_loss: 0.9629 | g_loss: 2.2062\n",
"Epoch [ 10/ 100] | d_loss: 1.0279 | g_loss: 1.9386\n",
"Epoch [ 10/ 100] | d_loss: 1.1110 | g_loss: 1.0685\n",
"Epoch [ 10/ 100] | d_loss: 1.3441 | g_loss: 1.0324\n",
"Epoch [ 11/ 100] | d_loss: 1.1879 | g_loss: 1.0673\n",
"Epoch [ 11/ 100] | d_loss: 1.3366 | g_loss: 0.9610\n",
"Epoch [ 11/ 100] | d_loss: 1.1435 | g_loss: 1.0668\n",
"Epoch [ 12/ 100] | d_loss: 1.1189 | g_loss: 1.2501\n",
"Epoch [ 12/ 100] | d_loss: 1.2153 | g_loss: 1.0666\n",
"Epoch [ 12/ 100] | d_loss: 1.3179 | g_loss: 0.9101\n",
"Epoch [ 13/ 100] | d_loss: 1.1504 | g_loss: 1.4559\n",
"Epoch [ 13/ 100] | d_loss: 1.3358 | g_loss: 0.9763\n",
"Epoch [ 13/ 100] | d_loss: 1.1833 | g_loss: 1.0180\n",
"Epoch [ 14/ 100] | d_loss: 1.1839 | g_loss: 1.2705\n",
"Epoch [ 14/ 100] | d_loss: 1.3219 | g_loss: 1.0915\n",
"Epoch [ 14/ 100] | d_loss: 1.2945 | g_loss: 0.9335\n",
"Epoch [ 15/ 100] | d_loss: 1.3458 | g_loss: 0.9600\n",
"Epoch [ 15/ 100] | d_loss: 1.3445 | g_loss: 0.9098\n",
"Epoch [ 15/ 100] | d_loss: 1.3289 | g_loss: 1.3456\n",
"Epoch [ 16/ 100] | d_loss: 1.2725 | g_loss: 0.9085\n",
"Epoch [ 16/ 100] | d_loss: 1.1133 | g_loss: 1.0910\n",
"Epoch [ 16/ 100] | d_loss: 1.2564 | g_loss: 1.0233\n",
"Epoch [ 17/ 100] | d_loss: 1.3171 | g_loss: 0.9643\n",
"Epoch [ 17/ 100] | d_loss: 1.2932 | g_loss: 1.0311\n",
"Epoch [ 17/ 100] | d_loss: 1.2643 | g_loss: 0.9377\n",
"Epoch [ 18/ 100] | d_loss: 1.2226 | g_loss: 1.4327\n",
"Epoch [ 18/ 100] | d_loss: 1.3909 | g_loss: 0.9178\n",
"Epoch [ 18/ 100] | d_loss: 1.2430 | g_loss: 1.0297\n",
"Epoch [ 19/ 100] | d_loss: 1.3409 | g_loss: 1.1413\n",
"Epoch [ 19/ 100] | d_loss: 1.1607 | g_loss: 1.2019\n",
"Epoch [ 19/ 100] | d_loss: 1.4060 | g_loss: 1.1366\n",
"Epoch [ 20/ 100] | d_loss: 1.3076 | g_loss: 1.0200\n",
"Epoch [ 20/ 100] | d_loss: 1.2715 | g_loss: 0.9261\n",
"Epoch [ 20/ 100] | d_loss: 1.2959 | g_loss: 1.4079\n",
"Epoch [ 21/ 100] | d_loss: 1.2529 | g_loss: 1.4324\n",
"Epoch [ 21/ 100] | d_loss: 1.2907 | g_loss: 0.9551\n",
"Epoch [ 21/ 100] | d_loss: 1.2426 | g_loss: 1.2571\n",
"Epoch [ 22/ 100] | d_loss: 1.2168 | g_loss: 1.7557\n",
"Epoch [ 22/ 100] | d_loss: 1.2874 | g_loss: 1.0733\n",
"Epoch [ 22/ 100] | d_loss: 1.1758 | g_loss: 1.6449\n",
"Epoch [ 23/ 100] | d_loss: 1.3328 | g_loss: 0.9859\n",
"Epoch [ 23/ 100] | d_loss: 1.4189 | g_loss: 0.8197\n",
"Epoch [ 23/ 100] | d_loss: 1.3146 | g_loss: 0.9181\n",
"Epoch [ 24/ 100] | d_loss: 1.2752 | g_loss: 1.1507\n",
"Epoch [ 24/ 100] | d_loss: 1.1860 | g_loss: 1.0389\n",
"Epoch [ 24/ 100] | d_loss: 1.2692 | g_loss: 1.0240\n",
"Epoch [ 25/ 100] | d_loss: 1.2905 | g_loss: 0.8767\n",
"Epoch [ 25/ 100] | d_loss: 1.1643 | g_loss: 1.0650\n",
"Epoch [ 25/ 100] | d_loss: 1.3141 | g_loss: 0.8904\n",
"Epoch [ 26/ 100] | d_loss: 1.2288 | g_loss: 1.0190\n",
"Epoch [ 26/ 100] | d_loss: 1.2016 | g_loss: 0.9930\n",
"Epoch [ 26/ 100] | d_loss: 1.4220 | g_loss: 1.1657\n",
"Epoch [ 27/ 100] | d_loss: 1.2774 | g_loss: 1.0464\n",
"Epoch [ 27/ 100] | d_loss: 1.2179 | g_loss: 1.0301\n",
"Epoch [ 27/ 100] | d_loss: 1.2938 | g_loss: 1.1045\n",
"Epoch [ 28/ 100] | d_loss: 1.2736 | g_loss: 1.1921\n",
"Epoch [ 28/ 100] | d_loss: 1.1929 | g_loss: 1.1512\n",
"Epoch [ 28/ 100] | d_loss: 1.3188 | g_loss: 0.9897\n",
"Epoch [ 29/ 100] | d_loss: 1.3085 | g_loss: 1.4660\n",
"Epoch [ 29/ 100] | d_loss: 1.2663 | g_loss: 0.9120\n",
"Epoch [ 29/ 100] | d_loss: 1.3005 | g_loss: 0.9635\n",
"Epoch [ 30/ 100] | d_loss: 1.2953 | g_loss: 0.8053\n",
"Epoch [ 30/ 100] | d_loss: 1.3288 | g_loss: 0.9908\n",
"Epoch [ 30/ 100] | d_loss: 1.3487 | g_loss: 1.1090\n",
"Epoch [ 31/ 100] | d_loss: 1.2638 | g_loss: 1.0738\n",
"Epoch [ 31/ 100] | d_loss: 1.2856 | g_loss: 0.9346\n",
"Epoch [ 31/ 100] | d_loss: 1.2525 | g_loss: 1.1265\n",
"Epoch [ 32/ 100] | d_loss: 1.1938 | g_loss: 1.1639\n",
"Epoch [ 32/ 100] | d_loss: 1.2217 | g_loss: 0.9636\n",
"Epoch [ 32/ 100] | d_loss: 1.2105 | g_loss: 1.7308\n",
"Epoch [ 33/ 100] | d_loss: 1.1531 | g_loss: 1.5628\n",
"Epoch [ 33/ 100] | d_loss: 1.3260 | g_loss: 0.9161\n",
"Epoch [ 33/ 100] | d_loss: 1.2334 | g_loss: 0.9264\n",
"Epoch [ 34/ 100] | d_loss: 1.2336 | g_loss: 1.0195\n",
"Epoch [ 34/ 100] | d_loss: 1.2184 | g_loss: 1.3364\n",
"Epoch [ 34/ 100] | d_loss: 1.3039 | g_loss: 0.9413\n",
"Epoch [ 35/ 100] | d_loss: 1.3298 | g_loss: 1.1236\n",
"Epoch [ 35/ 100] | d_loss: 1.2562 | g_loss: 1.0155\n",
"Epoch [ 35/ 100] | d_loss: 1.3659 | g_loss: 1.2384\n",
"Epoch [ 36/ 100] | d_loss: 1.1759 | g_loss: 1.0545\n",
"Epoch [ 36/ 100] | d_loss: 1.2195 | g_loss: 1.0489\n",
"Epoch [ 36/ 100] | d_loss: 1.2799 | g_loss: 0.9530\n",
"Epoch [ 37/ 100] | d_loss: 1.2149 | g_loss: 1.0076\n",
"Epoch [ 37/ 100] | d_loss: 1.2700 | g_loss: 1.1004\n",
"Epoch [ 37/ 100] | d_loss: 1.3090 | g_loss: 0.9861\n",
"Epoch [ 38/ 100] | d_loss: 1.3035 | g_loss: 1.0189\n",
"Epoch [ 38/ 100] | d_loss: 1.2769 | g_loss: 1.0285\n",
"Epoch [ 38/ 100] | d_loss: 1.2371 | g_loss: 1.2829\n",
"Epoch [ 39/ 100] | d_loss: 1.2404 | g_loss: 1.0135\n",
"Epoch [ 39/ 100] | d_loss: 1.2708 | g_loss: 0.9378\n",
"Epoch [ 39/ 100] | d_loss: 1.2512 | g_loss: 0.9949\n",
"Epoch [ 40/ 100] | d_loss: 1.1768 | g_loss: 0.9511\n",
"Epoch [ 40/ 100] | d_loss: 1.3067 | g_loss: 0.9223\n",
"Epoch [ 40/ 100] | d_loss: 1.3625 | g_loss: 0.8471\n",
"Epoch [ 41/ 100] | d_loss: 1.2816 | g_loss: 1.0424\n",
"Epoch [ 41/ 100] | d_loss: 1.2974 | g_loss: 1.1541\n",
"Epoch [ 41/ 100] | d_loss: 1.1643 | g_loss: 1.2687\n",
"Epoch [ 42/ 100] | d_loss: 1.2976 | g_loss: 1.0265\n",
"Epoch [ 42/ 100] | d_loss: 1.3245 | g_loss: 1.1694\n",
"Epoch [ 42/ 100] | d_loss: 1.3458 | g_loss: 0.9364\n",
"Epoch [ 43/ 100] | d_loss: 1.1641 | g_loss: 1.6862\n",
"Epoch [ 43/ 100] | d_loss: 1.2706 | g_loss: 0.8405\n",
"Epoch [ 43/ 100] | d_loss: 1.3763 | g_loss: 0.9720\n",
"Epoch [ 44/ 100] | d_loss: 1.3490 | g_loss: 1.1244\n",
"Epoch [ 44/ 100] | d_loss: 1.2542 | g_loss: 1.3335\n",
"Epoch [ 44/ 100] | d_loss: 1.2833 | g_loss: 0.9767\n",
"Epoch [ 45/ 100] | d_loss: 1.3130 | g_loss: 0.9182\n",
"Epoch [ 45/ 100] | d_loss: 1.2353 | g_loss: 1.0782\n",
"Epoch [ 45/ 100] | d_loss: 1.3760 | g_loss: 0.9803\n",
"Epoch [ 46/ 100] | d_loss: 1.4026 | g_loss: 0.9744\n",
"Epoch [ 46/ 100] | d_loss: 1.3152 | g_loss: 0.9312\n",
"Epoch [ 46/ 100] | d_loss: 1.2657 | g_loss: 1.0664\n",
"Epoch [ 47/ 100] | d_loss: 1.2507 | g_loss: 1.2632\n",
"Epoch [ 47/ 100] | d_loss: 1.2343 | g_loss: 1.0100\n",
"Epoch [ 47/ 100] | d_loss: 1.2856 | g_loss: 0.9613\n",
"Epoch [ 48/ 100] | d_loss: 1.2589 | g_loss: 1.0631\n",
"Epoch [ 48/ 100] | d_loss: 1.2255 | g_loss: 1.3015\n",
"Epoch [ 48/ 100] | d_loss: 1.3112 | g_loss: 0.8649\n",
"Epoch [ 49/ 100] | d_loss: 1.2646 | g_loss: 0.9986\n",
"Epoch [ 49/ 100] | d_loss: 1.2757 | g_loss: 0.9732\n",
"Epoch [ 49/ 100] | d_loss: 1.1808 | g_loss: 1.4561\n",
"Epoch [ 50/ 100] | d_loss: 1.3849 | g_loss: 1.2169\n",
"Epoch [ 50/ 100] | d_loss: 1.2799 | g_loss: 1.4074\n",
"Epoch [ 50/ 100] | d_loss: 1.3711 | g_loss: 0.9860\n",
"Epoch [ 51/ 100] | d_loss: 1.2772 | g_loss: 1.2343\n",
"Epoch [ 51/ 100] | d_loss: 1.3022 | g_loss: 0.9042\n",
"Epoch [ 51/ 100] | d_loss: 1.3566 | g_loss: 0.8909\n",
"Epoch [ 52/ 100] | d_loss: 1.3641 | g_loss: 1.0716\n",
"Epoch [ 52/ 100] | d_loss: 1.2138 | g_loss: 1.2055\n",
"Epoch [ 52/ 100] | d_loss: 1.3753 | g_loss: 0.9283\n",
"Epoch [ 53/ 100] | d_loss: 1.2297 | g_loss: 1.1757\n",
"Epoch [ 53/ 100] | d_loss: 1.2801 | g_loss: 0.9982\n",
"Epoch [ 53/ 100] | d_loss: 1.2177 | g_loss: 0.9533\n",
"Epoch [ 54/ 100] | d_loss: 1.3590 | g_loss: 0.8750\n",
"Epoch [ 54/ 100] | d_loss: 1.2776 | g_loss: 1.3202\n",
"Epoch [ 54/ 100] | d_loss: 1.4154 | g_loss: 0.9770\n",
"Epoch [ 55/ 100] | d_loss: 1.3179 | g_loss: 1.1155\n",
"Epoch [ 55/ 100] | d_loss: 1.3786 | g_loss: 0.9604\n",
"Epoch [ 55/ 100] | d_loss: 1.3158 | g_loss: 0.9751\n",
"Epoch [ 56/ 100] | d_loss: 1.3204 | g_loss: 0.9898\n",
"Epoch [ 56/ 100] | d_loss: 1.4150 | g_loss: 1.0278\n",
"Epoch [ 56/ 100] | d_loss: 1.2821 | g_loss: 0.9324\n",
"Epoch [ 57/ 100] | d_loss: 1.2576 | g_loss: 1.2056\n",
"Epoch [ 57/ 100] | d_loss: 1.4449 | g_loss: 1.1794\n",
"Epoch [ 57/ 100] | d_loss: 1.3697 | g_loss: 1.1030\n",
"Epoch [ 58/ 100] | d_loss: 1.2824 | g_loss: 0.9524\n",
"Epoch [ 58/ 100] | d_loss: 1.2432 | g_loss: 1.1015\n",
"Epoch [ 58/ 100] | d_loss: 1.3309 | g_loss: 1.0080\n",
"Epoch [ 59/ 100] | d_loss: 1.3095 | g_loss: 1.0256\n",
"Epoch [ 59/ 100] | d_loss: 1.2653 | g_loss: 0.8913\n",
"Epoch [ 59/ 100] | d_loss: 1.3224 | g_loss: 1.0386\n",
"Epoch [ 60/ 100] | d_loss: 1.1556 | g_loss: 1.1556\n",
"Epoch [ 60/ 100] | d_loss: 1.2522 | g_loss: 1.0155\n",
"Epoch [ 60/ 100] | d_loss: 1.3123 | g_loss: 0.9344\n",
"Epoch [ 61/ 100] | d_loss: 1.2728 | g_loss: 1.1286\n",
"Epoch [ 61/ 100] | d_loss: 1.3303 | g_loss: 1.0562\n",
"Epoch [ 61/ 100] | d_loss: 1.3408 | g_loss: 0.8740\n",
"Epoch [ 62/ 100] | d_loss: 1.4031 | g_loss: 1.0154\n",
"Epoch [ 62/ 100] | d_loss: 1.1388 | g_loss: 1.3963\n",
"Epoch [ 62/ 100] | d_loss: 1.4201 | g_loss: 1.1908\n",
"Epoch [ 63/ 100] | d_loss: 1.2058 | g_loss: 1.1407\n",
"Epoch [ 63/ 100] | d_loss: 1.2444 | g_loss: 1.1547\n",
"Epoch [ 63/ 100] | d_loss: 1.3877 | g_loss: 1.0653\n",
"Epoch [ 64/ 100] | d_loss: 1.3246 | g_loss: 1.4514\n",
"Epoch [ 64/ 100] | d_loss: 1.3463 | g_loss: 1.0041\n",
"Epoch [ 64/ 100] | d_loss: 1.2426 | g_loss: 1.5180\n",
"Epoch [ 65/ 100] | d_loss: 1.3013 | g_loss: 1.0159\n",
"Epoch [ 65/ 100] | d_loss: 1.3368 | g_loss: 2.1512\n",
"Epoch [ 65/ 100] | d_loss: 1.3612 | g_loss: 0.9549\n",
"Epoch [ 66/ 100] | d_loss: 1.3277 | g_loss: 0.7320\n",
"Epoch [ 66/ 100] | d_loss: 1.2434 | g_loss: 0.9365\n",
"Epoch [ 66/ 100] | d_loss: 1.2326 | g_loss: 1.3177\n",
"Epoch [ 67/ 100] | d_loss: 1.2334 | g_loss: 1.4614\n",
"Epoch [ 67/ 100] | d_loss: 1.2690 | g_loss: 1.0928\n",
"Epoch [ 67/ 100] | d_loss: 1.3406 | g_loss: 1.0277\n",
"Epoch [ 68/ 100] | d_loss: 1.2498 | g_loss: 1.0917\n",
"Epoch [ 68/ 100] | d_loss: 1.3146 | g_loss: 1.0963\n",
"Epoch [ 68/ 100] | d_loss: 1.3215 | g_loss: 1.3057\n",
"Epoch [ 69/ 100] | d_loss: 1.3268 | g_loss: 1.1683\n",
"Epoch [ 69/ 100] | d_loss: 1.2631 | g_loss: 0.9922\n",
"Epoch [ 69/ 100] | d_loss: 1.3693 | g_loss: 1.0472\n",
"Epoch [ 70/ 100] | d_loss: 1.3476 | g_loss: 1.1509\n",
"Epoch [ 70/ 100] | d_loss: 1.2585 | g_loss: 1.2276\n",
"Epoch [ 70/ 100] | d_loss: 1.3906 | g_loss: 1.2750\n",
"Epoch [ 71/ 100] | d_loss: 1.2083 | g_loss: 0.9252\n",
"Epoch [ 71/ 100] | d_loss: 1.3743 | g_loss: 1.1076\n",
"Epoch [ 71/ 100] | d_loss: 1.2552 | g_loss: 0.9602\n",
"Epoch [ 72/ 100] | d_loss: 1.3761 | g_loss: 0.9666\n",
"Epoch [ 72/ 100] | d_loss: 1.3193 | g_loss: 0.9309\n",
"Epoch [ 72/ 100] | d_loss: 1.3079 | g_loss: 1.2341\n",
"Epoch [ 73/ 100] | d_loss: 1.4915 | g_loss: 1.0998\n",
"Epoch [ 73/ 100] | d_loss: 1.2271 | g_loss: 1.0882\n",
"Epoch [ 73/ 100] | d_loss: 1.2852 | g_loss: 1.0542\n",
"Epoch [ 74/ 100] | d_loss: 1.2105 | g_loss: 1.0388\n",
"Epoch [ 74/ 100] | d_loss: 1.2571 | g_loss: 1.2588\n",
"Epoch [ 74/ 100] | d_loss: 1.3393 | g_loss: 1.0764\n",
"Epoch [ 75/ 100] | d_loss: 1.2123 | g_loss: 1.2956\n",
"Epoch [ 75/ 100] | d_loss: 1.2723 | g_loss: 0.9174\n",
"Epoch [ 75/ 100] | d_loss: 1.4482 | g_loss: 1.0936\n",
"Epoch [ 76/ 100] | d_loss: 1.3366 | g_loss: 1.0978\n",
"Epoch [ 76/ 100] | d_loss: 1.2682 | g_loss: 1.2402\n",
"Epoch [ 76/ 100] | d_loss: 1.2431 | g_loss: 0.9709\n",
"Epoch [ 77/ 100] | d_loss: 1.3065 | g_loss: 0.9939\n",
"Epoch [ 77/ 100] | d_loss: 1.1876 | g_loss: 1.3299\n",
"Epoch [ 77/ 100] | d_loss: 1.2576 | g_loss: 1.1868\n",
"Epoch [ 78/ 100] | d_loss: 1.2706 | g_loss: 1.0540\n",
"Epoch [ 78/ 100] | d_loss: 1.2493 | g_loss: 0.9568\n",
"Epoch [ 78/ 100] | d_loss: 1.2227 | g_loss: 1.1633\n",
"Epoch [ 79/ 100] | d_loss: 1.3261 | g_loss: 0.9173\n",
"Epoch [ 79/ 100] | d_loss: 1.2312 | g_loss: 1.1450\n",
"Epoch [ 79/ 100] | d_loss: 1.3387 | g_loss: 1.2766\n",
"Epoch [ 80/ 100] | d_loss: 1.2280 | g_loss: 1.1469\n",
"Epoch [ 80/ 100] | d_loss: 1.2704 | g_loss: 1.1292\n",
"Epoch [ 80/ 100] | d_loss: 1.3570 | g_loss: 0.9845\n",
"Epoch [ 81/ 100] | d_loss: 1.2037 | g_loss: 1.1029\n",
"Epoch [ 81/ 100] | d_loss: 1.1613 | g_loss: 1.3356\n",
"Epoch [ 81/ 100] | d_loss: 1.3182 | g_loss: 1.0841\n",
"Epoch [ 82/ 100] | d_loss: 1.2307 | g_loss: 1.0811\n",
"Epoch [ 82/ 100] | d_loss: 1.2791 | g_loss: 0.8639\n",
"Epoch [ 82/ 100] | d_loss: 1.3174 | g_loss: 1.3110\n",
"Epoch [ 83/ 100] | d_loss: 1.3051 | g_loss: 0.9979\n",
"Epoch [ 83/ 100] | d_loss: 1.1558 | g_loss: 1.2926\n",
"Epoch [ 83/ 100] | d_loss: 1.2325 | g_loss: 1.0440\n",
"Epoch [ 84/ 100] | d_loss: 1.2974 | g_loss: 1.1218\n",
"Epoch [ 84/ 100] | d_loss: 1.2150 | g_loss: 1.0606\n",
"Epoch [ 84/ 100] | d_loss: 1.4180 | g_loss: 1.1683\n",
"Epoch [ 85/ 100] | d_loss: 1.3644 | g_loss: 1.2858\n",
"Epoch [ 85/ 100] | d_loss: 1.2591 | g_loss: 0.9795\n",
"Epoch [ 85/ 100] | d_loss: 1.1972 | g_loss: 0.9682\n",
"Epoch [ 86/ 100] | d_loss: 1.4219 | g_loss: 0.8627\n",
"Epoch [ 86/ 100] | d_loss: 1.1788 | g_loss: 1.4205\n",
"Epoch [ 86/ 100] | d_loss: 1.3966 | g_loss: 0.9346\n",
"Epoch [ 87/ 100] | d_loss: 1.2943 | g_loss: 0.9851\n",
"Epoch [ 87/ 100] | d_loss: 1.2265 | g_loss: 1.0192\n",
"Epoch [ 87/ 100] | d_loss: 1.2797 | g_loss: 1.3309\n",
"Epoch [ 88/ 100] | d_loss: 1.2280 | g_loss: 1.0253\n",
"Epoch [ 88/ 100] | d_loss: 1.2176 | g_loss: 1.2858\n",
"Epoch [ 88/ 100] | d_loss: 1.3786 | g_loss: 1.3351\n",
"Epoch [ 89/ 100] | d_loss: 1.3144 | g_loss: 1.1179\n",
"Epoch [ 89/ 100] | d_loss: 1.2299 | g_loss: 1.0613\n",
"Epoch [ 89/ 100] | d_loss: 1.3691 | g_loss: 1.0295\n",
"Epoch [ 90/ 100] | d_loss: 1.3526 | g_loss: 1.0230\n",
"Epoch [ 90/ 100] | d_loss: 1.2959 | g_loss: 1.1332\n",
"Epoch [ 90/ 100] | d_loss: 1.2445 | g_loss: 1.5470\n",
"Epoch [ 91/ 100] | d_loss: 1.3283 | g_loss: 1.0868\n",
"Epoch [ 91/ 100] | d_loss: 1.2901 | g_loss: 1.2393\n",
"Epoch [ 91/ 100] | d_loss: 1.4300 | g_loss: 1.1335\n",
"Epoch [ 92/ 100] | d_loss: 1.2987 | g_loss: 1.3160\n",
"Epoch [ 92/ 100] | d_loss: 1.2587 | g_loss: 1.0517\n",
"Epoch [ 92/ 100] | d_loss: 1.2881 | g_loss: 1.1046\n",
"Epoch [ 93/ 100] | d_loss: 1.2725 | g_loss: 1.1219\n",
"Epoch [ 93/ 100] | d_loss: 1.3230 | g_loss: 0.9735\n",
"Epoch [ 93/ 100] | d_loss: 1.3613 | g_loss: 0.9286\n",
"Epoch [ 94/ 100] | d_loss: 1.3035 | g_loss: 1.0815\n",
"Epoch [ 94/ 100] | d_loss: 1.2292 | g_loss: 1.0348\n",
"Epoch [ 94/ 100] | d_loss: 1.3835 | g_loss: 1.0981\n",
"Epoch [ 95/ 100] | d_loss: 1.2474 | g_loss: 1.1265\n",
"Epoch [ 95/ 100] | d_loss: 1.2481 | g_loss: 1.0578\n",
"Epoch [ 95/ 100] | d_loss: 1.3886 | g_loss: 0.8486\n",
"Epoch [ 96/ 100] | d_loss: 1.2996 | g_loss: 0.9993\n",
"Epoch [ 96/ 100] | d_loss: 1.2269 | g_loss: 0.9128\n",
"Epoch [ 96/ 100] | d_loss: 1.3136 | g_loss: 1.0670\n",
"Epoch [ 97/ 100] | d_loss: 1.3130 | g_loss: 0.9450\n",
"Epoch [ 97/ 100] | d_loss: 1.2538 | g_loss: 1.3591\n",
"Epoch [ 97/ 100] | d_loss: 1.2691 | g_loss: 0.9735\n",
"Epoch [ 98/ 100] | d_loss: 1.2483 | g_loss: 0.9697\n",
"Epoch [ 98/ 100] | d_loss: 1.1419 | g_loss: 1.9026\n",
"Epoch [ 98/ 100] | d_loss: 1.3835 | g_loss: 1.0033\n",
"Epoch [ 99/ 100] | d_loss: 1.2814 | g_loss: 0.9089\n",
"Epoch [ 99/ 100] | d_loss: 1.2866 | g_loss: 1.1416\n",
"Epoch [ 99/ 100] | d_loss: 1.5226 | g_loss: 1.1019\n",
"Epoch [ 100/ 100] | d_loss: 1.3635 | g_loss: 1.1240\n",
"Epoch [ 100/ 100] | d_loss: 1.3810 | g_loss: 0.9675\n",
"Epoch [ 100/ 100] | d_loss: 1.3214 | g_loss: 0.9679\n"
]
}
],
"source": [
"import pickle as pkl\n",
"\n",
"# training hyperparams\n",
"num_epochs = 100\n",
"\n",
"# keep track of loss and generated, \"fake\" samples\n",
"samples = []\n",
"losses = []\n",
"\n",
"print_every = 400\n",
"\n",
"# Get some fixed data for sampling. These are images that are held\n",
"# constant throughout training, and allow us to inspect the model's performance\n",
"sample_size=16\n",
"fixed_z = np.random.uniform(-1, 1, size=(sample_size, z_size))\n",
"fixed_z = torch.from_numpy(fixed_z).float()\n",
"\n",
"# train the network\n",
"D.train()\n",
"G.train()\n",
"for epoch in range(num_epochs):\n",
" \n",
" for batch_i, (real_images, _) in enumerate(train_loader):\n",
" \n",
" batch_size = real_images.size(0)\n",
" \n",
" ## Important rescaling step ## \n",
" real_images = real_images*2 - 1 # rescale input images from [0,1) to [-1, 1)\n",
" \n",
" # ============================================\n",
" # TRAIN THE DISCRIMINATOR\n",
" # ============================================\n",
" \n",
" d_optimizer.zero_grad()\n",
" \n",
" # 1. Train with real images\n",
"\n",
" # Compute the discriminator losses on real images \n",
" # smooth the real labels\n",
" D_real = D(real_images)\n",
" d_real_loss = real_loss(D_real, smooth=True)\n",
" \n",
" # 2. Train with fake images\n",
" \n",
" # Generate fake images\n",
" # gradients don't have to flow during this step\n",
" with torch.no_grad():\n",
" z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" z = torch.from_numpy(z).float()\n",
" fake_images = G(z)\n",
" \n",
" # Compute the discriminator losses on fake images \n",
" D_fake = D(fake_images)\n",
" d_fake_loss = fake_loss(D_fake)\n",
" \n",
" # add up loss and perform backprop\n",
" d_loss = d_real_loss + d_fake_loss\n",
" d_loss.backward()\n",
" d_optimizer.step()\n",
" \n",
" \n",
" # =========================================\n",
" # TRAIN THE GENERATOR\n",
" # =========================================\n",
" g_optimizer.zero_grad()\n",
" \n",
" # 1. Train with fake images and flipped labels\n",
" \n",
" # Generate fake images\n",
" z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" z = torch.from_numpy(z).float()\n",
" fake_images = G(z)\n",
" \n",
" # Compute the discriminator losses on fake images \n",
" # using flipped labels!\n",
" D_fake = D(fake_images)\n",
" g_loss = real_loss(D_fake) # use real loss to flip labels\n",
" \n",
" # perform backprop\n",
" g_loss.backward()\n",
" g_optimizer.step()\n",
"\n",
" # Print some loss stats\n",
" if batch_i % print_every == 0:\n",
" # print discriminator and generator loss\n",
" print('Epoch [{:5d}/{:5d}] | d_loss: {:6.4f} | g_loss: {:6.4f}'.format(\n",
" epoch+1, num_epochs, d_loss.item(), g_loss.item()))\n",
"\n",
" \n",
" ## AFTER EACH EPOCH##\n",
" # append discriminator loss and generator loss\n",
" losses.append((d_loss.item(), g_loss.item()))\n",
" \n",
" # generate and save sample, fake images\n",
" G.eval() # eval mode for generating samples\n",
" samples_z = G(fixed_z)\n",
" samples.append(samples_z)\n",
" G.train() # back to train mode\n",
"\n",
"\n",
"# Save training generator samples\n",
"with open('train_samples.pkl', 'wb') as f:\n",
" pkl.dump(samples, f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training loss\n",
"\n",
"Here we'll plot the training losses for the generator and discriminator, recorded after each epoch."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAEICAYAAACktLTqAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXd8m9W9/99Hy/J2vGM7sZ1N9nAS\nIClQZqFAWwqXtlxWJ1200EF/7W1Le2/npYNCC+0tBUpbaBs2hdIyAgQCWSQhezrx3panJEs6vz/O\n82hZtuWROBLn/XrlJUt6JD3R+Dyf53O+53uElBKNRqPRJBeWyd4BjUaj0Uw8Wtw1Go0mCdHirtFo\nNEmIFneNRqNJQrS4azQaTRKixV2j0WiSEC3umoRBCGEVQvQIIaZP5LYaTTIidJ275kQhhOgJu5oG\neAC/cf0zUso/n/y9Gj9CiP8ByqSUN0z2vmg0Q2Gb7B3QJC9SygzzbyFENfBJKeULQ20vhLBJKX0n\nY980mmRHxzKaSUMI8T9CiL8KIR4WQnQD/ymEOEMI8aYQolMI0SCE+JUQwm5sbxNCSCFEhXH9T8b9\nzwkhuoUQG4UQlaPd1rj/YiHEASGESwhxlxDidSHEDWP4Py0QQrxi7P87Qoj3h913qRBir/H6tUKI\nW4zbC4UQzxqPaRdCvBr2mDIhxONCiBYhxFEhxOfD7jtdCLFNCNElhGgSQvzvaPdXk7xocddMNh8C\n/gJkA38FfMCXgHxgDfA+4DPDPP5jwLeBXOA48N+j3VYIUQj8Dfia8bpHgVWj/Y8IIRzAM8A/gALg\nFuCvQohZxib3A5+QUmYCi4FXjNu/BhwxHlMM/JfxfBbj+TYDpcAFwNeEEOcZj7sL+F8pZRYwC1g3\n2n3WJC9a3DWTzQYp5dNSyoCUsl9KuVlK+ZaU0ielPAL8Djh7mMevk1JukVIOAH8Glo5h20uB7VLK\nJ437fgG0juH/sgZwoAR3wIigngM+Ytw/AMwXQmRKKdullNvCbi8BpkspvVJK07mfAWRJKX9o3H4I\nuC/q+WYLIfKklN1SyrfGsM+aJEWLu2ayqQm/IoSYJ4T4hxCiUQjRBXwf5aaHojHs7z4gY6gNh9m2\nJHw/pKoyqI1j36MpAY7LyCqFYyjXDeos5XLguBBivRBitXH7j43tXhRCHBZCfM24vRyYbsQ1nUKI\nTuDrKHcPcCMwH9gvhNgkhLhkDPusSVK0uGsmm+hyrd8Cu4BZRtzwHUCc4H1oAMrMK0IIQUiQR0M9\nMM14vMl0oA7AOCO5HChExS2PGLd3SSlvkVJWAB8EbhNCnI064ByUUuaE/cuUUl5mPG6/lPIjxvP9\nDHhUCOEcw35rkhAt7ppTjUzABfQKIU5j+Lx9ongGWC6EuEwIYUNl/gUjPMYqhHCG/UsB3kCNGXxF\nCGEXQpwLXILK3VOFEB8TQmQZ0U83EAAwXnemcVBwocpFA8BGwCuE+IrxGlYhxCIhxArjcdcKIfKl\nlAHjcdJ8To1Gi7vmVOMrwPUo8fstapD1hCKlbAKuBn4OtAEzgbdRdflD8Z9Af9i//VJKD3AZ8AFU\nZv8r4GNSyoPGY64Hjhlx0yeM5wCYC7wE9ACvA3dKKV8zykIvQQ3uVhvP+Vsgy3jcJcBeo9LoDuBq\nKaV37O+EJpnQk5g0miiEEFZUxHKllPK1yd4fjWYsaOeu0QBCiPcJIXKMeOXbqEqUTZO8WxrNmNHi\nrtEo1qJqzVuAi4APGTGLRpOQ6FhGo9FokhDt3DUajSYJmbTGYfn5+bKiomKyXl6j0WgSkq1bt7ZK\nKUcq1Z08ca+oqGDLli2T9fIajUaTkAghjsWz3YixjDF5YpMQYocQYrcQ4nsxtkkxuvsdEkK8ZXbi\n02g0Gs3kEE/m7gHOlVIuQTVaep8Q4vSobT4BdEgpZ6GaLv1kYndTo9FoNKNhRHGXCnNFHbvxL7rE\n5gPAg8bf64DzovpraDQajeYkElfmbszY24rqGf3rGK1FSzG66kkpfUIIF5BHVNtUIcSngU8DTJ+u\nl7bUaE4FBgYGqK2txe12T/auaMJwOp2UlZVht9vH9Pi4xF1K6QeWCiFygMeFEAullLtG+2JSyt+h\n+nNTVVWlC+w1mlOA2tpaMjMzqaioQJ9wnxpIKWlra6O2tpbKysqRHxCDUdW5Syk7gZdRq+OEUwdM\nA7W8GWpVnbYx7ZFGozmpuN1u8vLytLCfQgghyMvLG9fZVDzVMgWGY0cIkYpa6mtf1GZPoTreAVwJ\nvCT11FeNJmHQwn7qMd7PJB7nPhV4WQixE7WW47+llM8IIb4vhLjc2OY+IE8IcQi4FfjGuPYqXvw+\n2PYQBPwn5eU0Go0mUYinWmanlHKZlHKxlHKhlPL7xu3fkVI+ZfztllJeJaWcJaVcZax9eeI5vhGe\n+gLU6OZ9Gk0iY7VaWbp0KQsWLGDJkiX87Gc/IxBQ645s2bKFm2++edyvce+99/LHP/5xVI8588wz\nx/x6DzzwAPX19WN+/HiZtBmqE4LPaNrn06P8Gk0ik5qayvbt2wFobm7mYx/7GF1dXXzve9+jqqqK\nqqqqcT2/z+fjpptuGvXj3njjjTG/5gMPPMDChQspKSmJ+zF+vx+r1Trm1wwnsRuHBXyRlxqNJuEp\nLCzkd7/7HXfffTdSStavX8+ll14KwCuvvMLSpUtZunQpy5Yto7u7G4Cf/OQnLFq0iCVLlvCNb6hU\n+JxzzuHLX/4yVVVV3Hnnndx+++3ccccdwftuueUWqqqqOO2009i8eTNXXHEFs2fP5r/+67+C+5KR\nodZQX79+Peeccw5XXnkl8+bN45prrsEcVvz+97/PypUrWbhwIZ/+9KeRUrJu3Tq2bNnCNddcw9Kl\nS+nv7+fFF19k2bJlLFq0iI9//ON4PMqcVlRUcNttt7F8+XL+/ve/T9j7mNjOXYu7RjOhfO/p3eyp\n75rQ55xfksV3L1swqsfMmDEDv99Pc3NzxO133HEHv/71r1mzZg09PT04nU6ee+45nnzySd566y3S\n0tJob28Pbu/1eoM9rG6//faI53I4HGzZsoU777yTD3zgA2zdupXc3FxmzpzJLbfcQl5eXsT2b7/9\nNrt376akpIQ1a9bw+uuvs3btWr7whS/wne98B4Brr72WZ555hiuvvJK7776bO+64g6qqKtxuNzfc\ncAMvvvgic+bM4brrruOee+7hy1/+MgB5eXls27ZtVO/RSCSHc/cPTO5+aDSak8KaNWu49dZb+dWv\nfkVnZyc2m40XXniBG2+8kbS0NAByc3OD21999dVDPtfll6t6kEWLFrFgwQKmTp1KSkoKM2bMoKam\nZtD2q1atoqysDIvFwtKlS6murgbg5ZdfZvXq1SxatIiXXnqJ3bt3D3rs/v37qaysZM6cOQBcf/31\nvPrqq3Ht51hJEueuxV2jmQhG67BPFEeOHMFqtVJYWMjevXuDt3/jG9/g/e9/P88++yxr1qzh+eef\nH/Z50tPTh7wvJSUFAIvFEvzbvO7zDU4DwrexWq34fD7cbjef+9zn2LJlC9OmTeP2228fU236cPs5\nVpLEuetYRqNJFlpaWrjpppv4whe+MKjW+/DhwyxatIjbbruNlStXsm/fPi644ALuv/9++vr6ACJi\nmRONKeT5+fn09PSwbt264H2ZmZnBMYG5c+dSXV3NoUOHAHjooYc4++yzT+i+JYlz1+Ku0SQy/f39\nLF26lIGBAWw2G9deey233nrroO1++ctf8vLLL2OxWFiwYAEXX3wxKSkpbN++naqqKhwOB5dccgk/\n/OEPT8p+5+Tk8KlPfYqFCxdSXFzMypUrg/fdcMMN3HTTTaSmprJx40buv/9+rrrqKnw+HytXrhxT\n9c5omLQ1VKuqquS4F+vY+gA8/SW47E5YccNE7JZG865j7969nHbaaZO9G5oYxPpshBBbpZQj1oYm\nSSyjM3eNRqMJJ8HF3Wg7oGMZjUajiSDBxV1n7hqNRhOL5BB3HctoNBpNBIkt7qaoa+eu0Wg0ESS2\nuJuZu3buGo1GE0GCi7vO3DWaZKCpqYmPfexjzJgxgxUrVnDGGWfw+OOPT8q+rF+/flzdIE8VkkTc\ntXPXaBIVKSUf/OAHOeusszhy5Ahbt27lkUceoba29oS9Zqz2AiZjEffhnm+ySA5x1+0HNJqE5aWX\nXsLhcETM2CwvL+eLX/wifr+fr33ta6xcuZLFixfz29/+Fhi+Be/WrVs5++yzWbFiBRdddBENDQ3A\n4BbATz/9NKtXr2bZsmWcf/75NDU1UV1dzb333ssvfvELli5dymuvvUZ1dTXnnnsuixcv5rzzzuP4\n8eNAaAbq6tWr+frXv36S37WRSfD2A2adu3buGs2E8Nw3oPGdiX3O4kVw8Y+HvHv37t0sX7485n33\n3Xcf2dnZbN68GY/Hw5o1a7jwwguB2C14V69ezRe/+EWefPJJCgoK+Otf/8q3vvUt/vCHPwCRLYA7\nOjp48803EULw+9//np/+9Kf87Gc/46abbiIjI4OvfvWrAFx22WVcf/31XH/99fzhD3/g5ptv5okn\nngCgtraWN954Y8IW2JhIElzcdbWMRpNsfP7zn2fDhg04HA7Ky8vZuXNnsCGXy+Xi4MGDOByOYAte\nINiCNycnh127dnHBBRcAamWjqVOnBp87vLVubW0tV199NQ0NDXi9XiorK2Puz8aNG3nssccA1a89\n3KVfddVVp6SwQ8KLu45lNJoJZRiHfaJYsGABjz76aPD6r3/9a1pbW6mqqmL69OncddddXHTRRRGP\nWb9+fcwWvFJKFixYwMaNG2O+Vnhr3S9+8YvceuutXH755axfv37QYh7xcCJa9U4UyZG561hGo0lY\nzj33XNxuN/fcc0/wNrN970UXXcQ999zDwID6jR84cIDe3t4hn2vu3Lm0tLQExX1gYCDm4hmgzgJK\nS0sBePDBB4O3h7fqBbVI9iOPPALAn//8Z97znveM5b950klwcR9nnXtfO3j7Jm5/NBrNqBFC8MQT\nT/DKK69QWVnJqlWruP766/nJT37CJz/5SebPn8/y5ctZuHAhn/nMZ4atTHE4HKxbt47bbruNJUuW\nsHTp0iErX26//XauuuoqVqxYQX5+fvD2yy67jMcffzw4oHrXXXdx//33s3jxYh566CHuvPPOCX8P\nTgSJ3fL3sU/Dzr/CaZfD1Q+N/vH3rIEZ58BFPxjffmg0CYxu+Xvqolv+jnVAtacJuhsmbn80Go3m\nFCE5xH2ssYzfCwP9E7c/Go1Gc4qQ2OLuH6dz9/tgQGfuGs1kxbOaoRnvZ5LY4j7eWCYwoAdUNe96\nnE4nbW1tWuBPIaSUtLW14XQ6x/wcSVLnPoZYRkody2g0QFlZGbW1tbS0tEz2rmjCcDqdwUlaYyE5\nxH0sde5mGaWOZTTvcux2+5CzMzWJS4LHMuNYQ9U8IGhx12g0SUiCi/s42g/4vepSi7tGo0lCkkPc\nxxLLmAcEnblrNJokJMHF3RD1sQyoBh/r1Y3HNBpN0pHg4u6PvBwNZiwDOprRaDRJR4KL+3himbDH\n6GhGo9EkGckh7mOJZSLEXTt3jUaTXIwo7kKIaUKIl4UQe4QQu4UQX4qxzTlCCJcQYrvx7zsnZnej\nGFedu3buGo0meYlnEpMP+IqUcpsQIhPYKoT4t5RyT9R2r0kpL534XRyGcWXu2rlrNJrkZUTnLqVs\nkFJuM/7uBvYCpSd6x+LCP45qGS3uGo0miRlV5i6EqACWAW/FuPsMIcQOIcRzQogFQzz+00KILUKI\nLRPSx0LHMhqNRhOTuMVdCJEBPAp8WUrZFXX3NqBcSrkEuAt4ItZzSCl/J6WsklJWFRQUjHWfQ5ji\nLgMQCIzusdq5azSaJCYucRdC2FHC/mcp5WPR90spu6SUPcbfzwJ2IUR+9HYTTnjWPtr+MuHirtv+\najSaJCOeahkB3AfslVL+fIhtio3tEEKsMp63bSJ3NCbhgj7aaCagnbtGo0le4qmWWQNcC7wjhNhu\n3PZNYDqAlPJe4Ergs0IIH9APfESejM7/AR/YnOBzj35QVU9i0mg0ScyI4i6l3ACIEba5G7h7onYq\nbgI+cKQrcR9PLKPFXaPRJBmJO0M14Ack2FON66MU94hYpnfCdkuj0WhOBRJY3A0xt6Woy1HHMuGN\nw7Rz12g0yUXii7s9zbg+xszdYtcDqhqNJulIfHG3GauDj7Ynu/l4Z7Z27hqNJulIYHE3atzHmrmb\nsYwzS9e5azSapCOBxT0qcx9rLJOSpWMZjUaTdCSBuBvOXccyGo1GEyRxxd103nYjcx+1c/eCsIIj\nQ4u7RqNJOhJX3KOd+1gmMVkdKrPXde4ajSbJSGBxNwdUzWqZMWTuVrsh7tq5azSa5CKBxT2qFHIs\nM1QtNlUnrwdUNRpNkpH44m6WQo7JuTvAkaadu0ajSToSX9yDpZBjydztyrn7vaOvttFoNJpTmCQQ\nd3NAdQz93C22kPPX0YxGo0kiEl/c7WNsPxBeLQM6mtFoNElF4ov7WJ17MJZJV9e1c9doNElE4ou7\nfRzVMmYpJGhx12g0SUUCi7tR524bR7WMxR5qGaxjGY1Gk0QksLiP07n7tXPXaDTJS+KL+1jbD5ix\njEM7d41Gk3wkrribMcx4ltkLj2W8ur+MRqNJHhJX3Me9WIcvKpbRzl2j0SQPCSzu41wgOxA2QxV0\n5q7RaJKKxBd3i139G8syexYt7hqNJjlJAnG3qX+jnsQ0TCzTvBcad03Mfmo0Gs0kYJvsHRgz4eJu\ntY9hmT0jlrFYwZoS6dz/8RVAwI3/mLDd1Wg0mpNJAjt3Y0DVYh2jczdiGRi8YEdnDXh7JmY/NRqN\nZhJIYHE3xNx07mOqlnGovx3p4DWceyAA3Q3g80zcvmo0Gs1JJoHFPSpzH3VXSC9YjVTKnhqKZfra\n1IHD5564fdVoNJqTTPKI+5j6uceIZbrr1aV27hqNJoFJYHE3M3dzQHUU4i6lOjiYsUz4OqpdDepS\nO3eNRpPAJLC4+0BYwGIZfZ27eSAIxjJh4q6du0ajSQISW9wthjhbbKMT9+BgrBnLhC2SrZ27RqNJ\nApJD3K220cUyQeduxjJhA6pdhnOXfr1otkajSVgSV9z94c7dProB1aC4DzOgCtq9azSahCVxxT3g\nUxOYwIhl/KN4bJS4h9e5m7EM6Nxdo9EkLCOKuxBimhDiZSHEHiHEbiHEl2JsI4QQvxJCHBJC7BRC\nLD8xuxtGwBfKzMcay0SUQoYNqNqM1Z20c9doNAlKPM7dB3xFSjkfOB34vBBiftQ2FwOzjX+fBu6Z\n0L2MRWAiY5k09Xh3F7hdkFOubtfirtFoEpQRxV1K2SCl3Gb83Q3sBUqjNvsA8EepeBPIEUJMnfC9\nDSfgDxtQHWWde3QsY3aGbD+sLnMr1aXfO/791GgmCncX9HdO9l5oEoRRZe5CiApgGfBW1F2lQE3Y\n9VoGHwAQQnxaCLFFCLGlpaVldHsazXgyd1O0w0shAdpMcZ+hLrVz15xKPP0lePSTk70XmgQhbnEX\nQmQAjwJfllJ2jeXFpJS/k1JWSSmrCgoKxvIUIQIDUXXuo4lljBJH6xDiPsVw7npAVXMq0VUH3Y2T\nvReaBCEucRdC2FHC/mcp5WMxNqkDpoVdLzNuO3FE1LlPUCzTdkhdmrGMdu6aUwlvH/j0Wr+a+Iin\nWkYA9wF7pZQ/H2Kzp4DrjKqZ0wGXlLJhiG0nhvDMfdTtB4aIZdoPQ0oWpOWq69q5a04lvD0woA2H\nJj7iWYlpDXAt8I4QYrtx2zeB6QBSynuBZ4FLgENAH3DjxO9qFAFfqDeMxTrG3jJmP/ewWCZzqi6F\n1JyaeHvVzGmNJg5GFHcp5QZAjLCNBD4/UTsVF+OKZczMPayfO4C7E0qWhom7du6aUwhv72TvgSaB\nSOw1VMdc5z5ELAOQWQK2FPW3du6aU4VAAAZ6VSdUKUEM67c0mkRuPxBd5z6OWMZ07gBZJdq5a049\nzBnUMjC6s1TNu5bEFXf/QFid+1gzd9O5p4fuy5qqnbvm1MMUd9AVM5q4SFxxH08sE764NkQ698wS\nPaCqOfXw9oT+1hUzmjhIDnG32tXpaiAQ32OHjWWmGs8rdCyjOXUIH0zVzl0TBwks7v7IGaoQv3uP\njmUsVrAaUUxmiRqssjm1c9ecOoSLu3bumjhIYHH3xRD3OHP36BmqoGrdLTZIN9oi2FK0c9ecOoTH\nMtq5a+IgOUohTZGOt4ogup87qHJIe7pacBu0c9ecWmjnrhklySHupkjH69yjYxlQuXtqbui6LQV8\nuuWv5hTBq6tlNKMjScTdKImM17lHV8sATF2qatxNtHPXnEroahnNKElwcTdE3ToG526xR87yu/K+\nyG105q45ldDVMppRktgDqsFqF1Pc483cvZGRTCy0c9ecSujMXTNKElvcBw2oxlst44tD3LVz15xC\naOeuGSUJLO7+wZl73LGMN7JSJhbauWtOJbw9oQZ32rlr4iCBxT18DdXRxjIDodmpQ6Gdu+ZUYqAP\n0vLV39q5a+IgccXdPzDOWGaEsWTt3DWnEt5ecGaDsGrnromLxBR3KdWKNGNuPxBvLKOdu+YUwdsD\njnQ1H0ObDk0cJKa4B4ylxsbafiDuWEb/iDSnCN5eJe42JwzoWEYzMgkq7oaIj7X9QNyxzDDOve0w\nbP9LfK+n0YwXU9y1c9fESXKI+6jbD8QTy4zg3DffB098Vrco0JwcvL3gyNDOXRM3ySHupgsfTeOw\neGKZwEAoAorGVaMu+9rie02NZjx4e1XnUrse6NfER4KK+zgz93gnMcHQ0YyrVl32tcb3mhrNeAhm\n7qnauWviIkHF3Wz8NdY69zjbD8DQLskU996W+F5Toxkr/gHwe1Qso527Jk4SVNyHGlAdZeOw4TCd\nuz9Gpu7zQG+z+rtXxzKaE4zZekA7d80oSGxxDzYOG8Mye+Nx7l11ob91LHPycLsmew8mh3Bx185d\nEycJKu7jzdzjEfdhMndXmLjrWObkULcNflKhSlDfbQTFPUM7d03cJKi4m7FMVD/30VTLxDNDFWK7\nJDNvB+jVzv2k0H4EZAA6jk72npx8Bgxxt+tqGU38JLi4j2eG6jice5ch7rkztLifLPo7jMvOyd2P\nyWBQ5q7FXTMyySHuo56hOs7M3VWrOvRll+nM/WRh5u2myL+bCI9l7E7dFVITF4kp7v5ROncp1b/g\n40cTywyRuWeXKoHXmfvJwd0Zefluwlw/1XTufu/Qk+s0GoPEFPfozH249gP+AbhjDrzz98jb4pmh\nCkM79+xpkF6gSyFPFmYc826PZewjzL/QaAwSXNzNUkhD5GPFMm6Xqklv2Rf2+IH4GofBEJl7HWSV\nQno+eFy6NfDJwIxl3pXOvU9dms4ddO6uGZEEF3dDoIVQf8eqcw9mtWGiEG/jMBjskNwu8HSpvD3d\nWBknUfvL+Adg/3OTvRfx4X43O/ewWCbo3HXurhme5BB3UGIdK5bxdKtLU+QDAVVSN2IsM8Tpr1nj\nbmbukLi5+4F/wsMfgeZ9I2872Zii/m6cyOTtVd91q0M798micRc8+qn4izZOARJU3KMmMYGqfonV\nfmCQuBsfzoixzBClkGaNu5m5Q+KWQ5r7nQiCmWzOPRCA+y+B/f8ceVuzaZgQ2rlPFodfhHf+Bi37\nJ3tP4mZEcRdC/EEI0SyE2DXE/ecIIVxCiO3Gv+9M/G5GEd04DIaOZaLF3ewVM9ZJTGaNu5m5Q+LG\nMp4udWme9p/KJFvm7u6EY6+rfyNh9nIH7dwnC/P713ZocvdjFIxgXwF4ALgb+OMw27wmpbx0QvYo\nHmLGMrbYp0ymgJmiYG4zUixj3h/LuQsrZBaHnjtRYxm3sf8DfZO7HyMRCIT2NVmcuykWfe0jb2uu\nnwrauU8W5veu7eDk7scoGNG5SylfBeL4Bp5EYom71R679ndQLGM2HRvhuCYEWGOsxuSqg6wSddbg\nzFH7kKixTNC5n+Li7nEBEpzZ4O2Ov/vnqYxpNuI56xvoC4m7du6Tg6kfrYnj3Ccqcz9DCLFDCPGc\nEGLBBD3n0JgiHj7LdMhYxnTuUbHMSM4djHVUo1r+umpVpQyoA0AiT2QyD3xm75JTFfOzm1IReT2R\n6R+FuHt7wW6KuzkWpJ37ScWdhM49DrYB5VLKJcBdwBNDbSiE+LQQYosQYktLyzgEMXoSExgDqsNk\n7j63cjvmNiNl7hB7HdWuWpW3m6TnJ27m7k4Q524KYVDckyCaGY1zj4hltHOfFMzvYOuhyNnupzDj\nFncpZZeUssf4+1nALoTIH2Lb30kpq6SUVQUFBWN/0aEy95h17l1hf7sG94IfDpszMnMPBIzWA2Wh\n29LyEti5J0jm7o4S92TI3Ufr3IOxjM7cJwXzbNHjSpgYdtziLoQoFkII4+9VxnOeWCs7ZJ37MJk7\nqA8oGMuMwbn3tqgDSLi4pxckzIc9CPML602QWCan3LieBM3DwnvljFQ7HS7u2rlPDu5OVf4MCRPN\nxFMK+TCwEZgrhKgVQnxCCHGTEOImY5MrgV1CiB3Ar4CPSHmCz1uiG4eBGiAdLpYBQ9xHE8tEOfdg\njXu4uOcnrrgninOPjmWSybnDyJ0uI0ohtXM/6UiptKOsSl1vTQxxH7EUUkr50RHuvxtVKnnyiJW5\nW+wRsczR1l6m56Zh9XSpqhe/Rx19nTlqg7E4d1eNuozO3L3dykmZZWqJQqJk7tGxTDJl7qCimYzC\n2NtJGTuW0c795DHQr874ixbCvmdH79z9PrjvAjjnGzDnohOzjzFI0BmqUY3DwKhzV7c3dbk5/+ev\n8MzO+lAfGDAyd7POfQzO3Vw7NSJzNycyJZh7lzJxqmX6O9XcAvOgmmzOfbjc3ecB6QdHmrpusRgl\nutq5nzTMA3FaLuTNHH05ZH8H1G+D6g0Tv2/DkODiHhXLGLcfaOrGH5DUdvQrAQuKe+f4qmVctWqp\ns9QpodsStQWBzx060CVC5p6ao86MbKlJ4txd6rsEw4t7+EIdJnandu4nE3PMx5mtxH20zt2MP01z\neJJIOHHv8fhochlf+EEDqkqsqlvV/R29XiXuOcZASH+YuI/FuXc3qpmpavxYYbYgSDRxD68iSoRY\nxpmt/k7NSQ7n7u6E3Jnq72HBGa8mAAAgAElEQVTFPawjpIktVTv3k4n5fXPmQN5s6KgeXQMx8wy5\nq37Cd204Ek7cX9zbxMNvHlFXhqhzP9qqxKq916NELL1ACfWoY5kY1TIZRZHbmM490WIZT5i4jyaW\nOfhCfFPmJ5L+sLESZ05yOPf+Tsibof6Oy7mHibt27gBsOtqOe+AkrEgVdO45kD9bJQQdx+J/fFDc\ntXMfloLMFKwEkMIa6aAtoVimuk39ILp7e5WYp2Qq5zfeapme5pCYm6TlqctEde42Z/zO3d0Ff74S\nnvv6iduvmK9rxDKQXM49vRAcmcOv5hUrltHOnZZuD1f/biOPbDp+4l/MNBOphnOH0UUzQXFvUHNl\nThKJJ+4ZKdjxExDWyDvCxd2IZTy9xhE3JStM3EfTfiDKufc0Da5qcGarA0WiTWTyGO9NZnH8pZCu\nWkDCrkeh7fAJ27VBhMcyk+HcD/4bnv7SxD1fIBA6YKXlDu/cB7Rzj0WDqx8p4XDL2MaLXt7XzD93\nNcS3cUQsY0RpoymHNMU9MHBSdSLhxD0/IwVrLHE3YhmfP8DxdiVWA4PEvTP+xmEQ6dx9XvX46FhG\nCKMFwQl27tWvT2wvafMLlzk1/gFVs85fBuD1X07cvoxEeCyTmgP9J7m3zL5nYOuDE+e6vN3qPXRm\nqzO/eGIZc/AVDOf+7hb3pi71uzTP0kdDn9fHLX/bzv/8Y++w23W5B9h6rD0slslSB+O0vFE697AI\n9CRGMwkn7tmpdhwigD+6RN9Yiamusx9fQJLptOE3RSAl03B8rvj7uUOkczePuNGxDJz4iUzdjfCn\nD8Mzt07cc5qxzKicu3EKfNplsP3hkNifSMwJJKmTmLn3tABSifJEEO4E4xX3QdUy7+5YpqlL/S7H\nIu6PbKqhs2+A2o5+Ovu8Q27303/u4+rfvom3t129/+Y4Xd7sEc9cff4AP3x2L7UdfZETKU/ioGrC\nibvFIki3gy961y1WCPg4akQyy6ZPwTpgvKmxMvd4u0L6PUpgeprUbbEmm6SdYHF/9Q6Vsda8GVnl\nMh5MN5E51SiLjGNgylWrDooX/gCQ8PqvJmZfhmOgT53Ohjt3T9fJbfvb26wuJ+q9D89w0/KGH6Ae\nslpmEp373megeXjXe6JpNsS9rqMfry/yjMrrCzDUJHmvL8DvXztCdqoS6t31sT9Tj8/PU9vr8QUk\nPZ1toVgQIH/WiLHM/qZufvfqER5681iUuGvnPixK3GPHMmbevnx6DhkY7sYU9/7OUTYOMw4Afm/I\nuUfHMmA4d3X/0dZebn74bfq9EzSK31ENWx+AqUvUvh99ZWKe1xQq8/8Tj3t31ape9lPKYclHYNuD\napD5RBJ0uWGZO5zctr/m/9EzQeI+JucenblPonN/8vPwxsmdlB6NGcsEJModG0gpueAXr/DNx2Mu\nHMdTO+qpd7m5/fL5AOyqi/09emlvM11upRX9XW2h7x1A3ix1wB/mO1htVOyt39eixN2ZrQylFvfh\nSbfBgIx27qrOvbqtj4wUG7MLM0Pi7sxSLikilokzcwflkswfeMxYpiD4A31pXzNP7ahn2/EJam61\n/sfqrOTqP6nKioP/npjn9XSpU82UTHU9nooZV22oedLaW9V7ufWBidmfoQh3ueGXJzOaMQ/sE+bc\nDVFIzYH0PDVoOpRYxxL3MTr3Pu8EnO2YY08j9cM5wTR2ubFZVLXcsba+iNuPtfXx8KbjrN8faTwC\nAcm9rxxmXnEmH1xaSmlOKruGcO6PbqulMDMFh82Cr68j9L0DmFKpLocphzTjov1N3fT1dChxzyrR\nscxIpNkkA4FocVftB4609lKRn0ZuuoNMYXzo5oCq9IdcU7zVMqAGVYeNZfLU6fNAP/Wd6ke6o3YC\nxKd5L+x4BFZ9CnKmw4yz4dCLE9NP2t2lhN0UjXjWUXXVhiaE5c1UDqZhx/j3ZTjCa4zDL83P0dMN\nD1yqVqc/EXh6Qmc1E+Xc3VHOHYaOZry9SszD53SMwbk/vOk4i2//F09uH6dzNA507W1N43uecdLU\n5WZhqTqbC8/d9xhinem08f8ee4dud2iy0Qt7mzjU3MNnz5mJEIKFpVnsjuHcW3s8rN/fwoeWlzIj\nPx2L2xUZy5gaMEwRRXVrL3arOvi0tbUpDcoq1eI+Emk2iVdaCATCRM5oP1Dd2ktFXjq56Y7BsQyE\nPpB4Z6iCckm9LeoDMluuhhPWgqCuQ73mzpoJiA1e/qFy12uNgdTZF6jFQlr2jf+5PV3G/8eowhgp\nlvH71BczvK9O3uwTv2CwIeK7Oiz8x70b6ZDG/pptf2s2QfVrExdXRdMb5v4myrn3R2XuMLRQhDcN\nM7E5R+Xc23o8/OhZlZF/5W87eGnf2IXZ7VKPbWlu4uX9JziSG4bmbg/zS7LISLFFOPe9Deoz+s01\ny2nqcvOj5/bh8wd4ZNNxvvXELsqmpPL+RVMBWFiSzZHW3ogDAMDTO1TWfsWyMmYXZeLwdUXGMnG0\nHKlu62XZtCmU5qTS29WhNCir5OQUIRgkpLinWiU+acHVH/ahWOzIwAC1HX1U5qczJd1OpujHL+zK\ngZvi3tsKwhLphIYiKO6e2BOYTIItCFqoM5z7zvE690AADjwPy65R5VcAs85Xl2OIZgYNMHm6VFxl\nNqQaKZbpblBnPhHiPhPaj8Q3GDtWDJf71aeOsqm6nV1txsQ1UyAbd6rLE+WIesLqkj1xHrA93fCP\nrwx9MHAbjdAcGWHiPkTu7u0NfUYm9lTl3GOdwbUdhi33R9z0k3/uo3/Az7rPnsm8qZl89k/beOvI\n4NfzByQ/+9f+4GBlLGpqVBSRY+nlc3/axvaakz+hzOPz097rpTjLSXleWqRzb+iiIi+N98wu4BNr\nK/nLW8d578/W843H3qE0J5V7rlmBzapkz3T+exsiq6Ae3VbLwtIs5hZnMrswg7RALwOOzNAGYb/3\noTja2kdFfhpnzy3A199FwJGhxL375E1kSkhxd1olA1hp6QmbPWq1I2QAKQNU5KUzJU05d4/NKCEz\nj7y9LfGVQUIwlunt7VHiPlRb1mALgjbqO/uxWQT1Ljct3Z7Y2/d3wJ1LoGbz0K/dVasqdQpPC92W\nXQYFp8GhFwZtLqXkDxuOcsfzg2vh//LWcVb/8MXIH63bdO6GKxypBUGsXvb5s1Xu3jmKqdijpKGp\nEQCRppq17e8yxkrMaKPBFPcTNFA1Fud+/E3Y/Hs49kbs+/s7lWsXIo5YpieyDBIM0yFD40fhbP8z\nPPNlFScBW4918LcttXx8bSVLp+Xw4I2rKJuSyice3BIsJzQ50NTNXS8d4tl3hp7cU1+n2l4XWPvI\nz3Tw8Qc2c6QljkhvAjF/V8VZTiry0oNFFKBimdOmZgHwlQvnMq84k3SHjf+7rorHP3cmi8pC8cqC\nUrVd+KDq/sZudtV1ccUy9T2fk+8kU/TT7g87wDpzVAw8hLj3eHy09nioyE/nnDkFpMk+2gZSIKtM\nfWYnaVnOhBT3FKvEj5XWcPE0nLgdPxX56ditFnJtbtwW40MJd+7xRDIQdO7ffnSr+pEPJe7GD9Tb\n1Uxbr5c1s9SRPdq9D/iNI3bLAVUFc3wjAHWdg8u5aDf65+TOiLx99vnqcZ7QD8rnD/DNx9/h+8/s\n4e6XD0X82KSU/OH1ozR3e/jeM3tCzzNa5x4U9+mh24JTsU/MbNWjrb089aba59998lzKpqSypz3K\nuZuZ/wlz7mHiHm/mbj6mr5VGl5szf/Qirx0ME4LwGbdxOfeoWCa4GlOM3N18X3qa8Ack335iF8VZ\nTr60MgOe/xZ5KQF+8uHF9Hh8vFMbeSbS6FJi3zCMc+9oUQdRi9/NH69fCsDX1+0ccvvRIKWkrcfD\nztpONlcPXR5qVsoUZqVQnpdGbUc/A/4APR4fx9r7mG+Iu9Nu5dmb38M/v3wWF8wvQoS3KwEKM50U\nZqZEiPtfN9dgswguX1oCwJwp6uyo0Ru2VoMQxgpsscXdPNhU5KWzZlY+GcJNbZ9NOXc4aRUziSnu\nlgA+LJHO3XDjVvzMyFc/hilWN72MR9yVc69r6STQ3ax6gcTCcO5dbcrxXLigCIuAHWE/nl11LhZ8\n53l21HSGPtzO47T3ennvHeu56rcbI51UUNxnRr7WrAvU0f/oq4ByCZ94cAsPb6rhhjMrsFkED4f1\n29h2vJNDzT0sLM3iHzsbeHGvkbcOcu4jibvxnNlhC5XkG+J+Alam6ff6+eyftpIpewg4MpmWn8ms\nwgz2tg4YTeA61f+h3TiwdNXT4Ornx8/t41DzBDpJ4wfcZ0lHxjsz1vzR97Xxrz2N1LvcfP/pPfjM\ng3t0IzTEkOLe19tFv4haBCZ8LCgacwC6q55ndtazp6GL/7r0NNKq/w0b74Ztf2R6rvpN1LsiDw7m\n9YZOc+Je26DIrb+zMfh3ZdoAN587iy3HOoYV43jYdLSdRbf/ixX/8wKX3/06V927ka3HYlfkmGeg\nRYZz9wUk9Z397G/sQkqYX5IV3NZiETGfw2RhaTZH6uqhq4GWbg9/2XSMy5eUkJ+hfvvTUtXZUU1/\nVAHGMBMXzZioIi+d9BQbWZZ+DrqEFvd4cFgM594TdlpqCHae08KUdPVBZFnc9GC4HLMHu8cVdyzT\n41MRQKbow+LpHNq5p2SC1UF/hxLO2YWZzC7MjHDuD286jtcfYMuxDpW7AXQeZ19jF15fgJ21nVx2\n14ZQhtl2WP2IM6dGvtb0M5D2dA6/8Rif+/NWzvjhi2w41MqPrljE7Zcv4IL5RazbWovHp36Uf9tc\nQ5rDykMfX82cogy+/cQuej0+Y0A1M8y5xxHLpOZGusi0PCVOw0zFvm/DUW5/anforCVOvv3kLvY3\ndXNupROL8dnNLszgSEsP0mk0D2tSFTKBwoX4u+o5/46XufeVw9z88NshIR0vPc10i0yafRm0tcXZ\nFyRM3F/c20yKzcLB5h7+vtU4+3F3Ip05/HFjNfXdAyqiiSHuUkramuvZ2Rb1Mx3OuZvi3t3IO7Uu\nnHYLlyycGjqzeeMu8lMt2K2C+s7Ig4Mp6o0utxo3uHOxinkMOnq9ONxh++nu5OqV08lNd3DP+qHP\n3jr7vMGBzqF443ArvV4f3750Pnd9dBlCEHm2E0ZTmLiX56nvb3VbX7BSxoxl4mFhSRb/2XEPgQcv\n53evHsbrC/DF82YH77d71ft5tCdUOt3R6+W4Jx1/T+z9Mwd4K/LTwO/DKT3U9lppwDhLO0kVMwkp\n7jZ8BLBGZtqGYFfmpQRvyqIfV8D4IaSEfeBxOvfDnWrAtkQYR+ihxF0ISMtnoEuJe+mUVBaXZbOz\n1oWUEveAn6d2qA/0QGN36MN11ajrwAM3rsJhs/Afv93IG4dbof2oqqe1RH1ENgdv2FZRdOxpDh2t\n5v2Lp/K3z5zOR1epuOSjq6bT0TfA87ub6PX4eGZnPe9fNJUp6Q5+dMUi6l1ufvHP3cr1ObOHrJYZ\nNADrqo3M283/d/7sIZ27lJLfvnKYB96o5gt/2RaMnvwBySObjvP7147EfNzfNtewbmstXzx3NsV2\nN6Sqs67ZhZl4fAEGHFnKuRt5+0Ptp2GVfj4w28Z3L5vPnoYu7ttwNOZzjxaPq5FGfxZdpNHSOjpx\n93W3sPFIG9esLmdF+RR+/u8D9Hl9yP5OtrfCd57czV0vHVQznGOIe3VrD0WBZg558yLvMJz7wboY\n+2OORXQ3cNSoHLNYhPGdE+CqwbJ7HcXZzmDZrkmDEcvUu/pVFZS3B5pCUd6O2k7yCBPp/g5SHVZu\nOLOCl/Y1s68xtoB/+a/bufjO1/jwPW/w/O7GyCo3g6OtvZRkp/KJtZVctqSERaXZvH4ohjPuaabV\n1YXdKpiSZqfCOEs/1tbLnoYuctLsTM2Of7nLBaXZVIn9iLZDPPLmIT64rJTK/DADYxws97tCBRj3\nvnqYra1WWpvqYrYcPtraS2FmCmkOW7BlRQ+pvHDMr3RKO/ehEQE/wmqjtWdw5l6ZExLudPro9Bsf\ntNUWGpiKU9z3t6ozg6ocdZovh6qWAUjPR/a1YrUIijJTWDwth/ZeL3Wd/fxrTxPdbh9ZThv7m7oj\nnPuBpm6yU+2cNTufp76wlowUG+u21Kq4IW/moJeRUvKTvstJE16er9rKjz+8mBXlucH7187KZ1pu\nKg+/dZx/vNNAr9fP1StVbfqK8lyuWT2dx40cm5SssDr3kLhvONjKyh+8yINvVIdeOHwCUzjDlEMe\na+ujudvD6spcnt/dxGf/tJVNR9v54K9f5xuPvcMPnt2rFlQJY39jN99+chdrZ+XzpfNmR6x7O7NQ\nfX59lgzl3Bt34nHm81qfOrD98Nw8bjizggvmF/GLFw5wvC3OnjnD0NVaT6vMRqZk0d/dEV//cEPc\nO1ob8foCnDuvkG9eMo+Wbg//9+pRerva2N0uyE138Mr+FmRaXsxT/G279uAQfva6cyLPRAzn/pWH\n3+KB16MOYmHO/WhrLzMKjM+3qw5KV6h1QDf8ktKsFBpc0eKurjd1uQmYS8l1hUr3dta6yBcuAubS\nkka+f90Z5aQ5rPz2lcEH6111Ltbvb+H80wpp6nLzmYe28tH/e3OQeYjYV+DMmfm8fbxTnWWatB2G\nn83jlk3v5d+OryLWfZxCXwOpdivVrX3saehm/tQsxL5/xD0OtChPUmFpQhCgyN/MF8+dHbmB8X88\n2GXFPeDH6wvw6NZaBlLyyPB18JmHtgbPkk2qW3uDBx2z9UBaZg5P7miErKng0uI+NAEfFpsjQtwH\njHYE5VNCzj1V9tHmC10P5u5xxjJ7mpVzX5KhHEmDb5jTvfR8bP3tFGc5sVktLDFG5XfWuli3tZbS\nnFQ+uKyUg03dSJfh3L091DfUM6coAyHUj3359Bx2HG9Xzj23ctDLNLjc7PQUcbTkUsSW+wad4lks\ngo+snM7GI2385uVDzChIZ0V5aFnAz5w1k/TwmbtWu5rQZVTLbD3Wzqf+uIUezwDffWo3v3rxIDIQ\nQHbWUBPI40O/eZ1f/PtAKGbJn6UOVp7BTbXeOqrc6A8+tJD//uBCXtzXzH8YYwufO2cmUsIbhyMd\n61/eOoYQ8MuPLMVqEUY+rd7LWYa4d8p0w7nvoDZlFi3CEJuuOoQQfP8DC7BZLHzriXeG7DESL4Hu\nZnoduZQVF5Em+3h+d+PIDzJO1/s7m0h3WFlVmcuK8lzet6CYX764n5SBbmZML+OrF86l3uWm15od\ns1rm8EF1EK4JFARdNRB07mligNuf3sP/PLMn5IYNcQ901XO8vS/kQrvq1XjJ2lugdT8XWrcOjmWM\n1xjwS/oaD6gbw4RoR00nRdZuLPlzjNdSwpeT5uBjq6bz1I56atojD6i/WX+ITKeNn1+9lPVfPYdP\nrq3kraPtEZGqlJKjLb0RjnntrHx8Acmmo2Hvy5GXQfr5V8blNNmnwd6nEJt/T3leGodbetjX0MWy\nAgF/u071Y4qDqb2hOSNXz/RFuvaw97MzkM7hlh5e2tdEa4+XFfNnky48bDpQwxf+EhkDVrf1UZkX\nKe4LZ5Sx5VgH7tRiHcsMS8CH1WaLiGVa+9WXe/oUQ7ilJMXfiyvgDPV5MQex4pmdCuxqNrI9qX6s\nm1qHaVmQXkDqQDulOcpVzSvOwmG18K/djWw42MKHl5cyrziLXq8fv6sueBbR33KUOUWhGtql03Lo\nazPKIKMHU1HTmQF6Tv+K6jUT40t8VVUZNouguq2P/6iaFlElMD0vjeVFxsduRlX2NPD2srvexQ33\nb6Y428n6r76XK5aX8vN/H+D7j25EeLt5cI+fmvZ+7nzxIFf85g0ONXeHVcwMdu9vHW0nL93BzIIM\nrj29nF99dBk3nzebl756DrdeMIfMFBsbDoWiBSklL+5rZu2s/OCAVnhHyOxUO4WZKbT60lRFSss+\ntg2Uk19aobY1fjRTs1P5+vvm8trBVp7cPviH9M9dDaH2EDWboHbroG1ATddPH2gnM28qubn55Fj6\neWxbHK7LcO6iv521s/Nx2NT7/fX3zSXf4ccu/JwxfyZnz1VngnXe1EGxjM8foKNOvac1siBCNANW\nJe7vn5/DDWdW8PsNR/maWbFiiJGnow5fQFKZn6Hq4V11aobk/A/ClAou7nyYxq5+/MZBQUpJg6uf\nCiPDHmgyxN2IEKSU7KjpYAqu0EB6WAuCT7ynEouAX7xwIHhAPdTcw3O7GrnujHKynHZsVgvnzlPR\n5v7GkBlo6/XS7fFRkRcS1qqKKThslshopvp1yJzKz8UNPDD9h1CxFg6/REVeOm8dbcPjC/Ae6y41\nH6PxnZE/J0DUvx38+4qKGKXLxgGsizQONvXwyOYaVYJZXgHA7ecV8e89TTy3Sx30u90DtPZ4KM83\n4k5D3FfOLUcIODaQo2OZYQn4sNnsEc691qVc9qzcUCWBVfrolmm0m209TeceRy/3Ho+Pg+3qOVN6\n1Yfxcs0wI+9p+WT4XZTkqNd32CycNjWTJ7bXE5Dw4RVlzC3OACSipxHKqgDI8TZGifsUKiyGO4wu\ngwQOGuJePms+LL8Otv1RlVWGUZjp5PzTirBZBFcsLx30HOdVqn1s9BoHOUc6fT1dXHffJjJTbPzp\nk6spznZyx5VLuOHMCjZuU8KxZsUSNv6/c7nnmuXUdvRxya82sNFlREIxVoR/60g7qypzgweXy5eU\ncOsFc8hIsWGzWjh9Zh4bwn68B5t7qO3o59x5Yc3ZwmIZgNlFGTR4U1Q7iICPV1xTmVtZCdaUiB/N\nf64uZ3FZNj/9576IKOVQcw9f+MvbwRmbPHUz/PO2QfsOsGFvLRmin+KS6QhnNlOs/bx2sGXYST4E\nAkFxzwq4gmIGMKMggw03q/JBkZpDaU4qswszONCdosQ97CxjR62LPJ8aw6mT+dSENcdq96qz1LIM\nC7dfvoD/PH06j71dq+ZjGBU0sqvBeM10NXg+0KuqNaw2OPNmpvbu4TR5hOZutX1n3wDugQDLp6uz\nPGFWIfU0g0/Fi97eTmzSp9pOQMSKWFOzU/nke2bw2LY6vvXELvwBNd6SYrNw45rQGeicYvVdN00K\nEOzkWhkWyzjtVlZMn8Lr5pmdlHDsdahYS1O3h6IsJ8w8D5r3sDCzB/eAcs7zejep7Vv2qT44I1H/\nNu7McgZs6eR5YohufyfSYsdrcfLKgRZeOdDCf1SVYTXG366c56Qk28k6Y7DcHEyNdu55ufmcMSOP\nba40ZFf9xLQQGYEEFXc/Nrudth5v8HT0WIcS+mnZhnAbb2o3qaFcd5hYxh+QEadWexu6cEslfqK3\nhX5LOq9Vd8ccDAIIpOWThpvyrNABYHGZEqVVFbmU56UzuyiTKXRjDXhh2ukAlImWCHFfPC2bSjG0\nuO9v7KEwM4WcNAec9TU12/bV/x203fc/sIA/f3I1hZmDB5fOKFX/r1eOGQdHexr7a5ro9vh46JOr\ng2cfFovgu5fN5+cXqQG9965agd1q4eJFU3n+lrMom5LKTzcPqH2Iqpip7eijrrOf1ZW5DMXaWfnU\ntPdzzCgde3Gvqg8PCqLPqwZ6w5o2zS7M5Hhf6MxrZ6CclZV5g5oyWSyC/3fxadS73DwQNnbww2f3\n4gtIdtS68PR3Q+t+FYEBrr6BoNgBbHpHnbKXlZWDMwuHvw8pAzHPBoK4O0H6cduyyRZ9vHfWlIi7\nU8w21Mb/6ew5BezutKm2xmHR1msHW5hmaSGQXojPkhJcgAagtkd9B6emyeD7JSXsP2aIkz0dR38T\nIFVZsBmtmKV4lWcBMEfUBqMZM5JZVj4FkKR2VxtnlxK669lRo/J2QK0BkJI1qHnb1y+ay+fOmclf\n3jrOZx7awuNv1/GRldNDZ2GoxXby0h3BQgKAo8ZqSjOiIpG1s/PZ29ClTFzbIehpwlt2Bl1uH4VZ\nKcEZ2yv9yn07rILsuldVg73AgPpsR6J+O87pK7DnzwyVH4fjdiFSc6jIS+cJoy/PVVXTguXP1r5W\nrlhexmsHW2h0uUNlkMHM3RhkTsnkiuVl7O/LQvg9J2UiU4KKuw+73YEvIOk0WhAc7VACbhOGQBs/\nlB6ZSrsp7qlDxzLX/2ETX/rr9uD1XXUuvGELgvhSC2jv9UY4jnC6rOrAUZkWGqRabOTuV1apKpMs\np51FmUbJYeFpeK3plIlW5hSFZiBmOe0sTW9nALs6jY7iQFM3cw33Q1YJzLlIzYiMojDLyeoZeYNu\nB8i3KVH/1yElGP3CSXtnJzeuqWBmQeRsSCEE89OMH3XYgGphppNrTy/n7fo+vJllgypmzKx0VWXs\nfQD14wV47aBy7y/va2ZBSRbFZrVDdNMw1KBqq08dfDzWDGooZHn5lJhNmc6Ymcd58wr59cuH6Oj1\n8sqBFl7a18zqyly8vgBHdm1SKyL1tYKnm1v/tp2zfvoy67bW4vMH2H9YuVdrZhGkZCGQnFnq4A+v\nH+XjD2zm3J+t5z0/fSmy6sSYwHREqPeq0BY1qBtsGqa+G2fPLaA1YLznYT/4DQdbmevswDKlnJIc\nJzXtodc43qW+44WpStzNafSHjxsiXjAXW8BLeapHmQDzfckyqp1yypHCSqWlMTiIal4uKMmiyNZL\niq8byteo7V117KjtpNhqfPfT82OuZSuE4Ovvm8c3Lp7HC8aB+lNnDTYoc4sz2Rf2OzpiNNkyTYXJ\nmTPVd2fj4Tao3gBAc6464y3KdKrZ25klzHSp7//5eW2I7nqoulE9wUjRTG+rmr9RskwZqY4YFVbG\nhLM5RZlIaRYspIVaEPS18uEVZQQkPP52XXACk1miGTxgp2TyvoXFtFtC40MnmsQUd/8ADrsS6NYe\nD4GA5Gi7IeDmIg7GEbOHVDpGiGUCAcnWYx38Y2cDB4wv3a66LvIyUpGGy3fkFAPELs8CWvzqBzrN\nEfoxX7JoKre9bx6XLykJ3rYsx/iRZpXSZitihr2NvDBnA3BaSivHKUJGzagLBCQHm7sjnD6ZU0ff\nU914b95uDnCkpYdj3UUTzU0AACAASURBVJBl9fK5s2fF3t5Vow6IUdVCH1hait0qOEZppHM//BJ1\nu98gy2ljXnEmQzEjP52SbCcbDrbS2edly7F2zguLMSK6JxrMLszAJZUrOmydwbzibLXwQlZJRGWH\nyTcunkevx8cvXzjAfz+zh/K8NO78yDIAmg5uCW7X33yI1w62YrNY+Orfd3DdHzaR4jHENqMg+N25\nfsUU+rx+Glxu5hRm0tLt4TtP7goN3BqRzNtuI1qKbgjWH/l/WlmRS6/FbGqnDojd7gHerumkwtIK\nOdOZnpsW4dyPdqmYKceuLgsznRRnOaltMKqwCuYBsCzXODPrinLuNgeB7OlUisbgganecO4l2ams\nyDAGMQ2Hj6uW7TWdLMk1ejmlF6r9H6Lt701nz+Tujy3jxx9ePEiwAeYUZXKwKXQWfLS1h+m5acGe\nLyaLSrPJdNrUb+7Y65BeSJ1FGZ6iLKcqxZ11HrmNr2PFzyWpRmfQVZ9WnTRH6hRab5i5kmWqeKHj\n2OBFYNwucOYw2xjM/8hKY4Z2WH+Zyvx0VlZMYd3WGo629lGUZZRBQoS4Z6TYqJypBqO97Se+gVhi\ninvAj8NhiHu3h2PtfXSbPcQCxh9GH5BumRZy7kPEMvWufvqNXNYs59pV52JhaRbCqExIyS6iMj9d\nuYgYNPiUiE21hxxJeoqNz54zE6c9VCM7N12VVfrSi6iV+VRYBz9fmWzgsL8owq0B1HT04R4IMDdc\n3DMKjUx1FP29zfeGNL771G4a+yyUZ0J22hBVRK5a5Yyjau5z0x1cML+It7pykW2HVd7csh/+cjWn\nV/+aVZW5w84QFEKwdnY+bxxu5aV9zQQkvDdc3MO7JxrMKszAhRL3Te5prKowYo+skpiry88uyuTq\nldN4cOMxDjX38M1LTqM428nMgnRkfWja/MG97+D1B/jNNcv5wntn8cbhNootxil1eqGqLAIunJHG\nju9eyHNfeg/3XruCWy+Ywwt7m/mnMaDm61YH2oPSOMuJPv2O6k/vtFspLTO3VQeCN4+0IwN+srxN\nkDOdaVPSIhakONKhvqsWf+gzX1SWTWOzMfu4YC4A8zOMs0Szxj2zOLi9JX8WMy2NwVim0aV6IhVk\nprDIaZgFQ9wDrlo1wzrL+B2lFxjrIwzdNOzSxSVcuaIs5n3zijPp8/qpNTqoHm3tVQO/UdisFk6f\nkcfrh1rUYGrFGpqMKpuiLMMQzTofi7eLT1S0s0Zuh8IFqi110fxQU7mhMAdTpy5Rzj0wMNggGNVa\nly0p4ZrV07lgvnHQdqSr2d1GCeuVK8qoa2ln1Z4fsCgnrKGhKe5GAcUZyxYDcPDgBK6HPAQJKu4+\nUlKUuLf0eNhV5wqtzGQuo2e8qb0idbC4R8Uy5nT1xWXZPLm9jiMtPRxs7mZRaXaop3tGEWfPKeCV\nAy0xZ84d9yiHkieGX2ezwuEiIAXVnkwOeKYEK3FC/7cA2f01VMti3q6JdEZmhcHssBgnOLGqdxTu\n3eMCm5OlFQW8drAVaU8jP2WYhRxiTWAyuKpqGnsHihADfcrhP/l58HvJHWhi9TCRjMna2QV0uX3c\n/fIh8tIdLCkLa60ajGVCzZ7y0h34U5Sg7/BNp6rCyPSzStWPM0br3FvOn0Oaw8oZM/K40PhxrqzI\nJb9nH7JY/djqj+4h3WFl9YxcvnrRXP7yqdVct9g4tU4vCFUWRfWX+fiaSuZPzeK7T+3G1T/AU68r\nN3jO2veoDaLFvX/w2cj8mWrAsbVZxScbDrZQbndhkT7IKWdabhqtPd5gzffBNmOAOOyAvqg0mz6X\neq3+KcodznQa38WuOrXiVtj8DpE3iwrRSL1x0GjodFOU5cRqEcyyNqnfU+FpkDqFrqZq+rx+ZqYZ\nB5i0PDXju39ocR8Oc1C1uvoQgW1/orotssY9nLWz8hGdx6C7HirWBgezC7OM6G7GOSCsfLNiP1Na\nt6reSwDFi1QsM9zAZf3bqtrLmRUa34rO3d2qydvsokx+8KFFwconQC20YpypXbJoKmvt+7ma5znf\nEXbG4OlWYwCGMVq5YC4+rPS2nrhmeyYJK+5OhxLdlm4l7sJcWclcRs8Qd4szK0zczcw9MpYxxf0H\nH1yEBG57dCcBCQtKskN9PNILufXCOcwqzOCmh7YOWp7rcK8SghTP8D02iumghWzWH+rgqC8fp78n\n8kfS3YDF76HOUjyonaoZGc0Od+5mv5vRRDNGX5nLjLhoRkkBluEWfxhqAhNw1uwCOlLL1ZVnvwa1\nm+nJqKBUtIZctck76waVbq4xctUjLb28d15hpNPvN97LMCEUQtBfuIzvDVzLs4HVrDIHbIfp21GY\n5eT5L5/FfTdUBSt3Vk3PYrY8RnvBKmRqLu7mw5w5K58UmzIJZ87MZ05GP6Rkq8UxDOce3RnSZrXw\n4w8vorXHw6V3vUZt3XECWDjnzDPVBtGTk9wuQETMmF5xmorD/v7qDs740Yv88c1jXFBiRCo501XG\nC9R29BMISA63ewhgVevqGiwqyybLWJzmuEV9VtNsoT4zwffHJG8mqbjxdKoDSr2rPzjWMU02cFwW\n4hc2yCqjr0UJUYm9R7WgsNqGjWVGwowV03bcj+Wpz7M6sGNwfbnBufMKOdNiTLorX0tTlxun3UKW\n0/gNp+aoyrPNv1cH91lh4u7uHD7brn9bRTIQJu4xJoWF93IPJ6x5WKbTzqVTjUo2R9h3xGzzYWC1\n2Qhc/mtWvf8TQ+/XBJGw4u5wOHBYLbT2eNlV76I0Lyt4HxAUd2tqdozMPdK5H27pYUqanUVl2Vy+\npITN1epLu7A0K8y5F5DltPPAjavITrVz4wObI2qPq7vAi33EhbKzfS00ylye3lFPnTRyu85Qoy+z\nEZYlb+Ygcd/f1EPZlFQyUsIOThljEHdPNziz+MjK6fz+uiqmFxcM3fLXP6AmKeXEFnerRbBwyQp1\n5eDz+Ge/jxcyLscpBliQE1WKtu2PsPHXETflZaSwwGj0FJG3g5plKCyDXntGUTb3+y+mKDdHZa8Q\nJu5hg6r7/xm8Pi03LZSDAmfkdOAUA+ylAk/mdPK89bx3btTr9zSrvB2UyEPMzpCLy3K44cxKatr7\nOaMogEjPD2sDHXWwNztChkVc5SXF+LFSYu/hzJlqZu4nFxlnojnlwUZfx9v7aOp24/EF8FtTBjn3\nLNT38WB/Oh0ygwI6Qu9JDHEHSHEpp9rocgen7Rd6azkaKKatxwPZpYjuOtIdVrICYf2VzFhmDCV9\nGSk2yqakktKmylFvta2j0hyAjGJabhofyq2mTWbhSp9BU5eH4ixnZIfHWeerZnqOjGAVGkWL1OVQ\ng6rdjepswBT3jGJl5MKdu5QRk+gGEdUZ8owsdeY0zRp20PN0R4g7gGP5R2Hq4tjPOYEkqLj7ERYb\neRkOw7l3UV5gfADBWEa5FmdG1qBYpitKcw419wRnP37mbHUEz0mzq8Eg07kbC0kXZzt54OOr8Az4\nufGBzcEa6jqXmx5rzojibu1poNuez45aF7XSEABXTWgD48uVO20eu+u7IloBH2yKGkyFMcYyyrk7\nbBbOn1+EcKQN3fJ3z5OqosSclRiDS05fRo900kU6a3dfxj+OKxG1dUe5po5q5cajFhY+d97/b+/M\no+O46nz/ua1Wa2ntUmuXtcSOLduJ49gOdjZnISROIAsQAsMWyMAJk5BMHktgyGPgzTlzeDB5vDAD\nHAIJkFkSHmFJJoQQEsKYbGaczSReYnmRZVu2ZNmSLclabN33x69uV3V1tdaWWmrV5xwdqau71VVd\nVb/7u9/fcsvJDWVEs2eiHNkBRfVxq1+Z4NaaBkeapZGNjHE/3g4PfxCeuMtznyv7RfPceKKa/aqS\nenWYSxa72kv0ddozo6jn7t0Z8u4Ni/nxzWtYXXYKFY6IBJJd6B1QzXF5gkqRUdHMdeWHufcDK/jb\nd55JuZXjTmEtdcVy/G1H+6M54TqYHeO5l+VlUZ09yLDKpKVrmMO6mIJhy/AcPxCfeWXlqpcM7mdg\nWALEVYXZUVlwj66UIGtBDeGBwyyvKUT1ddqDVk6xGNRJLtS9uCKfSP8uhoL5rAy0sKR3U8LXrtRb\n2TSyhIdebuXw8QFbkjEsvFx+N663F7WvWAqoxEFVZzAVZLAtboz13If6pCDKfb4Mrs6QFUMyw6kZ\nw7jPFHPUuJ+CQAaR/CxebztGz8lh6mqsm9v0HR88ARlZ5IfzONYnBt/0ZN56OPaCdBr3JZUF3LCy\nhiuarf7PxnN3tPs9syKf7374XFo6ernv2Z1orTlw7CQDWSWjrqsIwPGDDIclsDWcZ91wMZ77bsjI\noumMJQydGol20xs+PcKuzt54425utgQd6jwZiJ0qEsoTQ+FeUam3U6SWmlWw7IaE/64hksfGhjt4\noPKrvP+SNXzkSpNC5whOnT5lP3YtLHzbpQt5+q6Lyc92BXQ7d0SDg05MzGGNU/bJLZNAufmM7U8A\nGt5+ytN7U4f+wrDK5DcH8vlLfwk1gS6q813FbTGeu7fmbsgKZnDpknIxgOY9uaXeAVWvaX7TJbBv\nk20su/eJN5mZTUk4RDiUwb6j/ew9IoNwIJQTF0RfEB7mhM5lT1c/3cEyMnoPybkePB7vuRfUcjoQ\nolG189bB4wyeGqGqMAdOtJNx+iR7dSWHek5yKr+aAn2CVdXZ1mBnDcDRtWwnJ80sL1NU6g7+VHoj\nB3SEwk3/5D0LONZKqPcAxyJrePCFPew72m/P1gxVK6H5WljzSXtbVr5ILYmCqgdfk1lh5Vn2Nnc6\npCttNY5wRIy72e9OcRiU6R0FvnGfMCPDEAhSlpfFLqsAonFRs5ycFmsJOutLLc0LRStUn2qx0r5O\nnI6mrnX1DnKsf5iF5fYJ+PZN5/CtG1fIg6jnHuvVXbQowgdW13L/xt28tLtL2gpkezeAijJ8Ega6\nCRaJUY9UVEvpv9O4d+2C4gbOsZqBGWlm75E+hk9rq8rVgVlC0Czg7cWL/wIPbpDlAsFeqMOQaB3V\nJz8vnQGv+96YyxJe/YmvcNett/K5dy1m/ZpzZaPTuB/fL14QxFXUZmdmUFvsmpafPiWFKx7GfW1T\nKfdc0xxdUAEQz6vA0dp22+Pi9Yfy4flvx+/woS305J/JgRPDvHQ0jwxGYs8DyGzIDOqZ2SLnJfDc\n7fc4vFsv455omt+4XlpOmJqF7lZZFB2JM9SVSMZMa1cfoYwAGaHcGM8doDpriGMjubzR1s1gTrkl\nPViGxu25BwIM5tfTpA7xqtU3vbooO9pGYreu4mD3AO1aYiKri/tjj814s6NkzIzG6hzZr992VfJo\n+IOog6/KspJuOkS6WbXuMo71D9PeM0BFfmzqMIEA3PSvtt5uqFyeWJY5sBnKFkOW434qsTx3k3Hl\nUWcRQzgitmigR+77k0cBJbNGg2/cJ8jIKcu4yxQsGFDi0S66UhaxGD4pHkt2AcW5IY71DaG15hfb\nRIfvGSKahrXTCqYazz0OD8/d8HdXN1OcG+LOR2SKF8iLjG7cLcMTjshNu7iyQG7gGM99D5Q0UV2Y\nTUNpLt99roXWrr5o8VSc5w4iGSWSZV76Hjz9Fdj3Iuy2FpEeOG5ryOC9GtPWx2Drr2H93VC+JPEx\neZFTLAOG07g7DbrLuHvS3SrT/rJ4456ZEeCvL2qK0dABu5Cpr0tS5866EdbcAm/9KrZLoNbQvoWM\nahnA945UxO/XqUG5aZ1tnrMLx15qr++Iw7iXyb44GfCQZQDqz5el23b/0Tr+fVBcH326zsp133Ok\njwWluajM7DjPvTSjnxPksrerX7z+3sPQbUl+bs8d0FbGjFkUo7IwJxrzORCopr3nJNv7xQlYnmPJ\naeY+MOsjJMqYOdYaNcxeLNQye3uxt5JdNdfKQPzHf4z33i3JcsmSs1jbJA5PnOeeiMqzxBN3N7Ub\nHpDrw+TxG0oaZcDsPRR7bAllGcdC2ZbXTtUKqzWG5cgMnohtNz6DzD3jPjIiGnBGJhFrBD+zIl9y\nyRddIb019j4fHTFLwlLJ+uKuLt48MsIIAU6RwSargrJlTOOebWdMuCjKDfH1a5dFG5hlFkRGl2Us\n415ZI6lvy2oKJAvFGPeT3dFWv0opfvDR1QydHuHDP9rExrc7CSjiKkgBueG8ZJnND8LvvgzN75EL\nbNtjsj3Oc3eto2oWeK5aARfcmfh4EqGUHJczlmCkGBUYn3HvtLr1eXjuCSmoFn15x5MyS2h+D6y7\nTTxup/fe0wYD3RQ2rSI/O8iRkOXVOqfkJlDmLNzKKhh9qb2hfpnpjOm5exiLrDyoPQ/2/JfMWo4f\niHruAHXFubQdPRnt0U4wJ85zL1D90QKvUHGNfAftlrZcGF/tnFWxiHp1iNda5ZqtLsyOLhITKKim\nvWeA13rk/0V6LUPtlmUSee6/uhX+4ybv54Dyk7s4rnM5SCkNkUJYd7ssmehu1dvdKn2DwhFuv1Qa\nltWVxBdGeWKCqoffit2+70X57oxWb3CnQ44pyzgWyjatDpouke/dJDj4nvsEMFP7QEa0Z8Vya6Fb\n6i8Qj3Hn09ERszhXvPsHnt9DZkaQoXV38ULmOv5staNt6eglN5QhF7YXuaUxHpSbq8+q5J3N4vmF\niytF2ki0qpE1Ra6uO4PHbruAa1fUxHruz3xNvNWzPwBImfZDnzyP7v5h/t/m/TSUhmMKoqLkReJl\nmR2/lWDimRvgfQ9Km4LtT0q/lqHeWG/C7bm3b5EL9tKvjH9JQjeFtS7jvlc804pl4zTu1s0ySiA3\nDtNfZtvj8r1WrRDPe+VH4Y1H7JmEtchHoGoFN62u44p3nG1lSjiMu7k5Yzz3gtE9d/eAEC6NbQim\ndWLPHaBpvQT6OrbK7NRh3BeU5HBy+DQtnb3SudHDcw8OHZeFTICCcivD6MCr8tu9ohcQjCwipE4T\n6jtAMKDkfuraBSVnUFkUpr1ngOcPW/2VTADSLct4ae4nDss6v92tsbM3BxkdW2kNNgBKGoYZ7dvd\nAqC7Ta6lQIALF5XxxGcvjN5vY1KZIGOm5VkZ8BsujN3uToccS5bJdRj3zrfF9tSdJ9tOWM3BZrNx\nV0o9qJTqUEp5hp2V8B2lVItSaotS6tzk76YDk+poae5g99YgM1u0y51PR/NLS6wl9/6wvYPLm8vJ\nvvKrZDaeH/Xcd3X2ckYkL27x3Cjv+gf40CMJd0cpxb0fWMGPb14jxh0SSzPRHh9VrKgrkn7lRQvk\nht/5e3jlx7D2b8QoWZxdW8SDN68hOzNAc3WC6V1eRfxivVsfE4/+xp9IBkHztaIJ7rR0TU/P3TLu\nxih7tBweN4W18bJMYZ38z/EY9yNvQ3517H6ORUGN6NYtz8jxmnN6wR2Ahkf+SqSpQ1tkBlGxjHve\nvZQvX70Mihti9ytqqB3G3e2593bAi/9sa7TmPWZAyC2V/Rmy1nQ9NSCDdyJj0XSJ7KdZ2s7puVvp\nkFpbTak8PHcGesgKi1xSWtUg2w5sFoMcdOnUEM2YaVSHqCjIlhqDrhYoPYOqwmxau/p4q2OA3sxS\nu5rTmS0D3rLMjt/IcQC0vhT/vNbQsZWjeeKJN5bl2WsXuK+NnraYVNjlNYVxbQoSUlAtefn7N8du\nb3lWZDD3wuMFtRKUN577uGUZy3MvXehIyW23nDw9e4078BPgqlGe3wAssn4+DXx/6rs1Cg7j3lyV\nT06mVB5GWXSFXCBHdornHrZz2m9YKVPTdzSW0NrVz6GegZhMGU9ySzyntE4KczKlbN7RTMiTE+0S\n4HOebHPh/vJTcjNf+ndxbzuvsYQn77iIr71nmff/DUesFgSOm/3obpE0jJy08HIxCK/9mzyOyZZx\nraNqdNoEVanjorBOLvpo9kerGNDiBpmpuDNz3HRuh8gEvHawg4Z6RCQZQ9ECeO/9Mug+dC288B2p\nTAw5grjuNLio5+6QZdye+5afwdP3wAGrH3x0QLCug1zrujTSjAluhl0pn4aaVZK59IblTBTZM0aT\n6w5IwY/bc9caBnooLy+XNMPqBus4Dnvq7UB08G5UhySYevqUeM6lZ1BVlM2R3iFOj2hO51WLJ+r8\nPkL5MkB6yTLbnrCD2ftejH++p02u1/JlBANKjievQq5PdxFR976YQW5CKCXXwdZf2w5Xz37o3Cbt\ngt1kBOWzju6Gbf8Jf7pXzmEizdx5fjvflvst3/qunQvYzFbjrrXeCIxWdnkd8JAWXgaKlFLxc8Bk\nYfLYA0EWluez9X9dGVuxuegK63WD4rlbskxRbiaXWEUqpiz+uR0dtPcMjG7cJ4IzwOKFVzGJuYFP\nHoNrvh3vTVg0RfKiMYY4vAqZju6OXckpFBYDv9PKJsoaJVumu1VuNo84w7hx550f22sb95Hh0Vej\n0dq6WSYYyDXGPa9C9Gsny98Hn30VrvqG3GxnXBb7vPHcXQ3AYj33wljP3SxQsue/XO9xBFTBDqq2\nvyG/nel3TjIyRVo0BtMxuDqziepLc8Ujdc7WrFnB4vpafnfXxdJvXFm3t0d3UQDyyhkM5NKo2iUN\ncs8fxXmKLJHgqjnsUodxNccWCIgW7ZZlTnZLUsPSa0Wi8PLcrXVZ1667iMduv0AavykVP3saPinH\nWDhJ4w4Sczk1IBWsALv+IL/dmTWGkiaJ2fzsI+LU3fybxJliwZDMwo7tlWywssXy/QSCcn3PduM+\nDmoAh7jKfmvb9GA8PqvdQJycUrQAIs3yd1Y+JXkhlIJrzqqK9oVorpIObQ//WbRuzyDlZDAj+ajG\n3TXuFTcASjI7FiW44MbCKrCK3uwDx+Vvdz/4pdfZMQun3OFeR7WnLWG7gXFjDFNPm1zk/V0Suyhu\nkO2jSTM9+yW4OxG9HeyBc8m74xcWBxms1n4GvrATNnwj9rmSRvlM8x32dogX7fTu3Z67Cf7t/ZP9\nHogNqILtuR98Tab95UsTH0PTJfI7vypGSskJSV1HKBigujBHrvOTR2HQknzcfXgygvbAlMhzV4rj\n4Xoa1SFq8xU8+UW5ZpZeH41BRfKzyCq1roVgtr0OMXj3l9n5tAzezddC/Trxkt1VuodF4c2qXi4t\nPgxu425kvQTV0eMisliy6P78QxksWp4R77q82fv1lWeJjVl/N/z1s4lfZwhHpGMlyEwzEJBMpRjP\nfR5kyyilPq2U2qyU2tzZOYGiGycOWSYhxnu32mz+8KOr+fy77KyLYEaAVfXFbNkvN0TyPfcEx3ai\n3Z62Rd9TJt7Be+6b+uca42KCUm7jvuhddkdMZypk1HN3yDJTuaHAfn93m50pYzx3GN24m8yDiWTK\ngAycG74FF31uYu8DkWVAZIH+o/Dmo1DpKhHPLpTV7I2DYTz3fS9L6mTfEZEiTEVt2G3cX5eAspf+\nbWhaL7+L4oP4C0pyqS/JFW3cSBUmPuLRZC3qSCQy7sBQYSONqp0rjj4imVrX3AuZ2eLJAytqC1Fm\noA5H7DgGiNfqlmW2/acYt5rVsMDqr+Neb6Bjq+y/O57inj2ZRIOpOhrn3y5S6ev/Abv+CAsviz0O\nJ+u/CP9jq8ij40kmCEfsa9mk7Zp6i+hCHUmyLxMkGcb9AOD89mutbXFore/XWq/WWq+ORCJeLxmb\n8Rj3M6+U39bF886lFTHaO8A7rJzZzAxlN9afKqGweDdemvvIaSkqcXvuAA0XJJRjxoW7BYEJCLmN\ne06RbTyyvbJl+iQ4mAzPPb8aUOJ9mYu/uEE8epUxunHvtNbvnKgsA/COT48ZI/EkGtDbA099SeSG\nq78Z+xpnlepgrwzWNatl2r//v+X7d2r0Uc/dqmI8+Lpd7p6I8qUio5h1Sh3cfdUS/t7EXYxxd6bR\nQmzwz2TIJJJlgMzyRdSoI5y99wFY9t6oXFVTlENAyZq+0fe7+vnHLdhhPOMl14gHW7NKslLcuvvh\nt6Q1rxv37Mkc22Q1d0PDRTJQP/M1aUuSSJIBGZgdrZHHxMRPVIZ9v+VXzQ3NfRw8DnzMyppZC/Ro\nrdvHetOkGY9xX7AOLv+qTM8TYJZ/aygNkzne6PtYKGWXJLvp6xRJxCMlbcq4PfdExh1g5UfEu8xz\npJNlOmSZvg7J6JjqDRUMyU3iNO5F9eINFdaOYdy3i6acKPA4HRQtAJTUBmz5mXj/bm3c2RnSrDF6\n7sdE297zp9gKTpDBIJApnvvR3WJYxjLuSsEnn5IsLRfnNZbY/Xfcxt0rbc8YqVE89/L6ZWQoTSCY\nBVf+Y3R7YW4mP791HZ+8sNGW2OKMe3Gs5r7rDxK3abbuu8xsqD43Vnc/NSjJDhUext09q+tpE6M5\n1XtGKTj/szIoq4AtfSUD852UNNl9bczaArPduCulHgZeAhYrpfYrpW5RSt2qlLrVesmTwG6gBfgh\n8DfTtrcQp7l7EsiQm3OUEfismiKyMwPJk2QMuQlaEHRYbUunkoGSiGCW3NRO455X6T0bWHYD3L03\n1nMPhsQIDffZmTJTNe5g57p3t4oMZNLn3NqqmyNvT1ySmSrBLPFQ2zaJ93zR5+Nf4/TcjSRTs0pS\nV/dslEIypwFUyr4eTCph9Tlj70vRAvu7SkS4XLziOOPukGWMBDiK507lctnVy+6Jm1Wuqi+RKuBE\nnrtbltn2hHx+w0X2tvp1UkhlMrE6d4iTMx7j3t0mnz2OBe3HZNkNkupYe97Y3+1EMN+J83rNrxL5\nzmQYpUhzH/Nb01p/aIznNXBb0vZoLKKe++i9TsYiFAxw3wdXxqSYJYVwWbwsozVsvFduSHfJc7LI\nK3fIMnu8vXaD181iOkN2W/r4VGUZEOPevkUMZ3G9rXMWN8D233i/R2vx3JdeN/XPnygljXJDXvcv\nthfmxOm5m2BqSZOc05e+J1P6BWtj35NbKhp+++tSaRkZI0A3XgKB2Cpgr2rKM6+0O2smomIZ3P5K\ntAWwJ/mVEkh1x2GMLKO1/Oz8ncR1nFr1gvOlOnj/ZpEEjZPjZdzNfpp0yKmkQbrJyISPP+65fvKU\nMLNLp3E3MyUjJdqFvAAACxNJREFUL4ZSo7knYUicYUbsVMipcuWyCWhr4yUcsasrDbufg9bnYcM3\np6atj/q55bGeu1ce72hkhsVzN8ZiqgFVEOOz/UmZCjv70xQ3RBeljpuy9h2Rqb5HT5lp5+IvQO/H\nxRv3wu25F9TKoNh4MbxwHwwOx3u3pkp18Lh4yV6DxmQpqov33J1eYtXZ8L4fjf1/yhKsnWsIZMCn\nnouPF+UUixc+eEKklv4uyUxxUnceoKD1RWmp8MzXZRbnVSCXmS2zDacsk0xnaLQBbLIY417m8txB\nBtZgdnLP+QSYe+0HxqO5pxIzDXeWnD/7D2LoVt08fZ+bZxn3oT4J5jhz3MdD1HNvk5s2GTphYZ3U\nG3S12FNucEy/PZYai2bKTDANMhk0rYezb0z8vPGKjedujEXdWvt6dLYrAOt66JBgatU4JJmJ4Gxd\nMSBLJ06pNmE0ImfGXxPO/jI7nwZUfL+WnCLx0jd+E379GQl2f+xXiaWWkkYx7maRmGTMIKeTqnNk\noKpfZ28znvuRnSnT22FOGndLc59sz5PpJhyRsnCjMe54Eg6+KilWo6XATZW8cgnoGa9nNFnGi8xc\nCYZ170veDRWNL+hYaWC0dEjTByQVnvtYGK94oAe6dkbL98nKk6wZiA8C55bJTGroxNjB1IlStMCu\nAh5tObjpItpfxjLutWukotvNsuvlmrrhB3DLM4lnRmDFY/aIl69HkjODnE5KGuGOV2PlI+O5D/en\n1LjPUvd3FJKkuU8b5sTev14KOXb8Vkb2FX81vZ9rWhBY1X8TNu6hsAxIfZ220ZoqzuBxsWMmMZpx\nf+MRSZObjsDzVDGa+7E9Ykyd31PjRdD2crwsY9IhIfnG3VRudrdZxj1B98LpwgwmR94WB+bSe7xf\nd/EX5Gc8FDeIx35kpzxOluY+k4RyrfbQPb5xnxCzXZZZdr00itr6mOiw+jS874HkRPxHw6Q2tlkF\nIxOVZTJzZXrd3QZNlyZnn2KMe4P9d06x6K5u437wNQk8bvhW4iKTVBLMEunDdFp0Gvfl74ddz8VX\nnxpPPpg9ubz90YgWMu2z12adSUzWyZu/kN+meHAqGCfAVP3OdlkmEfnVlnFPTaYM+MY9+QSzZIGI\nNbdIT5HObdIvZLoxWu++TSIFTPRGD+VKWfhwX/K8pZxiyRQY6oudXisl2TNu4/7KT8UIWi2PZyVZ\nBXaPGGeArnwJfOrZ+NcbmaLyrOQP8NEq4H1iSHJnsC4AbFlm5+/FuXBX9E4G4wTs2Si/Z+MMbjwU\nVMm972vuE2C2G3cn4VLpGT0TXqiRAw6/OXFJBiRbxvSET5bOqZTcnAXV8fGG4gbRrU3gebAX/vJz\nqZJM1GJ1NpBdIDGVQHB8g6CRZZItyYBIgIGgbdxTJcuMDMPCK7z7+UwUY9zb35BajemMU00npsbA\nN+4T4PQs19xTRbTiVE/OuDsbZCVzKlyz2l7AwMkZl4rn/vv/KY/f+qXIWdOZUZQMzDS7uGF8QX1T\nAFS7Jvn7EsiQwTNVmnsobPcqSoYkAyJjhfKsYOoc1NsNJm3U19wnQNRzn6XZMqnCGciblHF35N8n\n86a6/rve21d9QoK/L/6zyAnbHhdN2msgmE2YoOp4g85li+DmJ+OLm5KFWaZxoGfmZzxKyWf2H5XB\nOln/s7hBZqCzPVNmNPJ94z5x5pIsM5OY3tID3ZOXZUC8pmSWZydCKSnq6u+CZ/5etl31jdkZSHWS\nNUHjDtIYbrooqpdOjCOnZt5zBymeiyxJ7mcb4z5Xg6lg57r7xn0CFNbC2TfNbl02VeSVT964G1mm\nsG7mDGwgILnPAz3SVfHsxAsqzxqMEZuOasfJUFQnDckgNcb9vT9IvgEzuvtclmWinrufLTN+alfL\nj088eRWSczzRNEiwe7rP9FQ4GIIPPyotB7wKYGYbUeOepFqAqeI0gKkw7olWlZoK6WDcy86E+gun\nJ9YyTuaecfdJTF65SDOTMZJGc0/FVDgQsBe2mO1MRpaZTpznKxXGfTpouFDWuHUsFD/nCOXCJxI0\nx5shfOOeTlxwp6QSToao5z6HvaWZYNn1kskxHX35J0OqPffpoLwZPrs51Xsx5/GNezpRtWLy3o7x\n3OdyhsJMEFkMl3451XthU1AjC1ro0zPfW8ZnVjP38tx9pofypVCxXBYz8Jk7ZATtzAzfuPs48D13\nH6GwBj7zQqr3wmcyFC2Q3ufuBad95jW+5+7jM9cprJOYyWxtg+2TEnzP3cdnrnPep/z0YJ84fOPu\n4zPX8Ws/fDzwZRkfHx+fNMQ37j4+Pj5piG/cfXx8fNIQ37j7+Pj4pCG+cffx8fFJQ3zj7uPj45OG\n+Mbdx8fHJw3xjbuPj49PGqK0WX1+pj9YqU6gdZJvLwOOJHF35grz8bjn4zHD/Dzu+XjMMPHjrtda\nR8Z6UcqM+1RQSm3WWs+7krz5eNzz8Zhhfh73fDxmmL7j9mUZHx8fnzTEN+4+Pj4+achcNe73p3oH\nUsR8PO75eMwwP497Ph4zTNNxz0nN3cfHx8dndOaq5+7j4+PjMwq+cffx8fFJQ+accVdKXaWU2qGU\nalFKfSnV+zMdKKXqlFLPKaW2KqXeUkrdaW0vUUr9Xim10/pdnOp9nQ6UUhlKqdeUUk9YjxuVUpus\nc/4zpVQo1fuYTJRSRUqpR5VS25VS25RS6+bDuVZK3WVd328qpR5WSmWn47lWSj2olOpQSr3p2OZ5\nfpXwHev4tyilzp3s584p466UygC+C2wAlgIfUkotTe1eTQungM9prZcCa4HbrOP8EvCs1noR8Kz1\nOB25E9jmePy/gW9rrRcCx4BbUrJX08d9wFNa6yXACuTY0/pcK6VqgDuA1Vrr5UAG8EHS81z/BLjK\ntS3R+d0ALLJ+Pg18f7IfOqeMO3Ae0KK13q21HgIeAa5L8T4lHa11u9b6VevvE8jNXoMc60+tl/0U\nuD41ezh9KKVqgWuAH1mPFXAZ8Kj1krQ6bqVUIXAx8ACA1npIa93NPDjXyDKfOUqpIJALtJOG51pr\nvRE46tqc6PxeBzykhZeBIqVU1WQ+d64Z9xqgzfF4v7UtbVFKNQArgU1Ahda63XrqEFCRot2aTv4v\n8EVgxHpcCnRrrU9Zj9PtnDcCncCPLSnqR0qpMGl+rrXWB4B/AvYhRr0HeIX0PtdOEp3fpNm4uWbc\n5xVKqTzgF8Dfaq2PO5/TksOaVnmsSql3Ax1a61dSvS8zSBA4F/i+1nol0IdLgknTc12MeKmNQDUQ\nJl66mBdM1/mda8b9AFDneFxrbUs7lFKZiGH/d631L63Nh80Uzfrdkar9myYuAK5VSu1FJLfLED26\nyJq6Q/qd8/3Afq31Juvxo4ixT/dz/U5gj9a6U2s9DPwSOf/pfK6dJDq/SbNxc824/zewyIqoh5AA\nzOMp3qekY+nMDwDbtNb/x/HU48DHrb8/Djw20/s2nWitv6y1rtVaNyDn9g9a6w8DzwHvt16WVset\ntT4EtCmlFlubLge2kubnGpFj1iqlcq3r3Rx32p5rF4nO7+PAx6ysmbVAj0O+mRha6zn1A1wNvA3s\nAr6S6v2ZpmO8EJmmbQFet36uRvTnZ4GdwDNASar3dRq/g0uAJ6y/m4A/Ay3Az4GsVO9fko/1HGCz\ndb5/DRTPh3MNfB3YDrwJ/CuQlY7nGngYiSsMIzO1WxKdX0AhGYG7gL8g2UST+ly//YCPj49PGjLX\nZBkfHx8fn3HgG3cfHx+fNMQ37j4+Pj5piG/cfXx8fNIQ37j7+Pj4pCG+cffx8fFJQ3zj7uPj45OG\n/H9j49U4OAAHqgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots()\n",
"losses = np.array(losses)\n",
"plt.plot(losses.T[0], label='Discriminator')\n",
"plt.plot(losses.T[1], label='Generator')\n",
"plt.title(\"Training Losses\")\n",
"plt.legend()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator samples from training\n",
"\n",
"Here we can view samples of images from the generator. First we'll look at the images we saved during training."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# helper function for viewing a list of passed in sample images\n",
"def view_samples(epoch, samples):\n",
" fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)\n",
" for ax, img in zip(axes.flatten(), samples[epoch]):\n",
" img = img.detach()\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)\n",
" im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load samples from generator, taken while training\n",
"with open('train_samples.pkl', 'rb') as f:\n",
" samples = pkl.load(f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 1, 7, 3, 2. Since this is just a sample, it isn't representative of the full range of images this generator can make."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZkAAAGRCAYAAAC39s6jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJztvXn8lXP+//96CymkRSmkUBLKliUU\nJmGyDIOyqywZxjKDsYxlbB8fzIx1hrGTzBcjYhKRiSSStCplqyxtZAljff/++Pxez+6nrlfv63qf\n63Xe57x73P/pcbs65zrXeb2u5f18nOfz+aqqrq52QgghRAxWq+sDEEIIUX/RQ0YIIUQ09JARQggR\nDT1khBBCREMPGSGEENHQQ0YIIUQ09JARQggRDT1khBBCREMPGSGEENFYPcuLq6qqyrY9QFVVlXPO\nuXLoYLDaasue3T///HPia6qrq6vy+rxynpdKI6950ZzkyuLq6uqWeeyo3OalYcOGpr/77rs6PJJa\nkWpeMj1knHOuQYMGzjnnfvrppxW2OVd4U419w/cPFuecW2uttZxzzn377beJ/88bP489Bmuvvbbp\nr776ynTS2NVHVl992Wn1448/5rrvNA/wcqGc/vCpNHjtVldXz6nDQ4lKu3btTM+aNSvXffO+HOme\nk2peZJcJIYSIRuZIxj8R+ZdG1uhlub9STKf5KzX0V7KPYEL7TvMkD7036+sZvayxxhqmf/jhhxr3\nWR/IO3oheUUvJfgrL5cIppIitzxZVaK/vKMXUi6OiSIZIYQQ0dBDRgghRDQy22WeYsJZvjdku4UI\nWTG0FZI+Z/PNNzf97rvv1nhcaQh9D25fVSwyUgkWYblYCTVR1xZZVgt5VScPG7a+jbkiGSGEENHQ\nQ0YIIUQ0am2XZSVNCMjXhMLO0HtrshVCFllehI6rPmcHbbLJJqbnzZtnmhaZn1NaaN9//30Jjq5y\nKSbLkddNliy/Nddc0zTnpz7YNaWE9ypmwvLaX2+99Uz/97//Ne0zZOvbmCuSEUIIEQ09ZIQQQkQj\ns11W21YZfD1D+jQZWnlbLUmZaM5lt7O4H34n2kXcZyW1GUlj2bRv3970ZZddZvqYY44x7e0Djs8/\n/vEP0/vuu6/pHXfc0TT7OIWydOpbFo4n63fhOGSxyDgntMu4Dx5LMQXKqyI8b//whz+Yvvbaa003\nb97ctL+3NW3a1La1bLmsNdgOO+xg+vHHHzfNcab9xrno06eP6eHDh9d47HnOoyIZIYQQ0dBDRggh\nRDSqsoRCadpkh8IshuPUX3/9tWnaTwwTP//8c9PscHzggQea7tChg3Ou0AKgzTZ27FjTH3/8selW\nrVqZfv75503TrglZeqQW9mFZtPoPZb+FOms3adLE9IIFC0xzTpPGKE0B7sKFC0337t3b9PTp0xP3\nQ/IK78u51X8o45LZSl988UXq/TVr1sx0jx49TPN6e/XVVxM/s5Td1p1zb1RXV3fLY0fFzEtonGkb\nf/DBB6a32mor00888YRpf69yzrkZM2aYnjlzpnOu8D508MEHm27durXpTTfd1DTvbeeff77padOm\nmY5kY6aaF0UyQgghoqGHjBBCiGjkbpct9/rE7Qw7d911V9OTJ082TbuEIePOO+9smhaNz9II9Q37\n7LPPTL/11lum58xZtu7OFVdcYZpZGkuWLDGdxvZhxgg/l5SLXZYGFpXNnj3bNIsxQxl7teXTTz9N\n/Jxvvvkm189ZnnKzy0J94I4//njTw4YNM83xCWWJeduNVvGvf/1r07wmaLnQZi5xQW1Z2GUkVLzK\na4VjR0uN18ro0aNNb7DBBs455zp16pS4P74vlFFGy3n33Xc3/cknnyS+t0hklwkhhKhb9JARQggR\njai9y0LWEsP4SZMmmd5zzz1NX3LJJabvuusu0926LYvOfK8f55aFjFyVkjbX4MGDE/fBEJQZNiNH\njjTduHFj07QjQnYgP7dS4biwOIzbmW3EkH3u3Lmmly5d6pwrtHratm1resMNN0zcNy3HSy+91PQF\nF1yQ4VtUJjyvDj30UNMswKO1vM0225h+/fXXTdNq4Vytu+66zjnnunbtatt+97vfmW7YsKHpIUOG\nmP7zn/9sevHixWm+Sr0lZBdynG+//XbTvJ9NmTLF9E033WTaW2rHHXecbaNV7O205fnoo49M9+3b\n1zTvQ7yHMaO3FCiSEUIIEQ09ZIQQQkQjql3GsJ+hO0NNFpixuO/hhx82vcUWW5h+7LHHErc/++yz\nzjnnXn75ZdvGYjPaXGz7v/HGG5tm5to+++xjmllnDDWZYVLi4rTo8LvRsrn//vtNM2PlxRdfND1r\n1izT3nphcSsLamkB+GI05wrPndNPP900rbOsGU7lvGIn7YxQr77111/fNK8V2sZ8DW1pWid+Lmhr\nvv/++6aZ8fmrX/3K9I033pjmq6zSsFiZc8rCTN4LaXVtttlmzrnC+xr1VVddZZrZl/fcc49pXje0\nnBctWpThW+SLIhkhhBDR0ENGCCFENGrd6j9UiEhoGzF0D63kx0wK9gYKWQPMzPCFYtw3s2TWWWcd\n0wxBaU0wpGXBJq0GhsM8dmZXNWrUKHF7OdpooZ5GtLcefPBB07SZ+PpQO/6k1vOcW2b0hbL1OI/F\nUG4W2UYbbWR6/vz5ppllxxVHeQ77rL3lX8NCPtphvEb9OUnbhhmXtHm8heNcYUEhs8uyLC+wPOVs\nYS5Pmv5fX375pelrrrmmxtcTbz8zi5B9yd5+++1ETZhp2L17d9NDhw41TYuuFCiSEUIIEQ09ZIQQ\nQkQjs13mw768Vsbs2bNn4na2u2avM/ZVYtiXZNmttdZapkPLCzB7h325XnjhBdO0D2idhcJ7Wnrl\nTmgeQ1YnbbHa2n+0aVjgF4LzVYylQhuzruaIx8Dzlxl3PDYWXdI2DBXF0uYNLd3gLSpaa7zGaAvR\nzvrlL39pmkXUxdhl5W6RkTTnezGWuLcxmSHbrl0701z+hPTq1cv0gAEDTHP+x40bZ5pZoaGfOpjJ\ndvHFF9d47CtDkYwQQoho6CEjhBAiGlGLMQs+CBYJNYuEmCVDe4uFYszeSFrVkXZEmzZtTDPUpC1G\n+4v6nXfeSdweyq4iodUmK5VQy/gssDD2tNNOM92xY8fE1/NzWGxWjB1RDjZm6BhC/aRoXbGgOM1q\nrdxOS833i2M/v9A+mGVIC5s2c6RVF1c5/NjRomQWHwswW7RoYfrss882zT6DLFzne9Pck4q1yIgi\nGSGEENHQQ0YIIUQ0SmaXhYr1ZsyYYZrZYJdffrlp9hf75z//aXrMmDGm/Ypw++67r21jL7Lx48eb\nfuaZZ0yzIO7DDz80TRsvtCJdiPpgkZHQd6ZNwgw8WkJdunRxzhX2NvOt5pffB6FNc/7552c84vpD\n1oymkHVF/fnnnzvnCldtZQ85WsKHH364afb8k0WWP/4+w0w/2smcl/vuu880C2afe+4507wP8d5W\nahTJCCGEiIYeMkIIIaJRMruM0KJitlirVq1Ms9U+ezbtsMMOprkKprdouA/aNgw7mS3lbTbnCvsB\nhfpyMfOD4WjIDmQmXTFFa+UIw3q2hO/fv79p3zaeVmgIjvmxxx5rutLHLZRtGNtyCu3TZ4b98Y9/\ntG29e/c2zayzCRMmmGbBaMiKE7XHjyOLK3m+XHnllab5EwJtT/YZfOqpp0zXZdGrIhkhhBDRKFkk\nw7/m+KM6f3A88sgjE1/Dv6D41x9/QPZ/KbN9Bmtm/A/Qzjl39dVXm+YCW/yBeerUqaZDa6XzLzge\nCyOsSv8rfHk4/ttvv73pE0880fS2225rOksHZdYv8a+wSq87StOlPK+oJs17/TnJH4l5jfH8HThw\noGkmz7A1SdbF41Z1ONc8t30H5T59+ti2nXbayTTvMbyvTJw40TSvIdZV1SWKZIQQQkRDDxkhhBDR\nqBO7jD/Is53Gm2++abp169am2a32ySefNE2ry4f7/OGfFgDXqe/QoUPi59Da4Vrpvq5g+e9Ba4IW\nQ32G33n06NGmWZ908803m/Y/4POHf9oFtFpY18TPKeWP5XVFXXwXJt08/fTTprfeemvTbdu2NU0L\nm4tpiWR4rjIxhou/sePyCSec4JwrPBdYf8b74JZbbmmaCTh33XWX6T333NM057rU55oiGSGEENHQ\nQ0YIIUQ0am2Xpcn4ad68uWmu605oRTFLgiHgsGHDEveTlD3B7s20aLjGNdfeZlsbhpTM6uDCUWzP\nUJ/smtrA7+8XXHLOuQsuuMC0H/dbb73VtnFemKUUImSR1VfrLDa+1otWDK8rdvJlvdIHH3xgWuOd\nDOvoOL7dunUz3blzZ9OscXn88cedc4U1MB9//LFp1jJxvlg7yEUA+bMEaw3TWPt5ZnQqkhFCCBEN\nPWSEEEJEoypL2FtVVWUvZmHQ0qVLTYfsjJC1wfCSxZMsquT+a2qPwM/hPhguMoxl9gytNlpnCxYs\nSNweWkQqTSuZ6urq5PbDtYDzUg5wTn2BGe0CjhutSIbxtAnyWDQtLXnNS9Y5oT0cspaLgRbl8ccf\n75wrvA68VeOccz179jTNa5KZUDNnzjRdghYzb1RXV3er+WU1k9e1EiqM3GqrrUyfcsoppjmO/ImA\nltYhhxzinCu0nnl9MEOW80lri3Y+rU520Oa1VSSp5kWRjBBCiGjoISOEECIatc4uC1lkoawEWlfs\n/0X7K01XY1oxoT5iHtpWDEtbtmyZeLzHHHOMadpr7Eo7d+5c0yHLIHTslQTtrenTp5vmYmIha2SP\nPfYw7e2D/fff37Zx4TkW+B100EGmR40aZXrOnDk1fmbIjt1ll11Mv/baa4nvLQdi9P/i+b/jjjuu\noHm9DRo0yPTIkSNNM9OM80BrmfZO1uMq995+vG/xHGOG2L///W/T7H+44YYbmma3d97zzjzzTNMc\nFw97O9JyCxWFM6OXNv9uu+1m+rHHHkt87xlnnGH6lltuWeFYaosiGSGEENHQQ0YIIUQ0MttlPmQM\n2Rahwh1aSM2aNUvcTgsuZH+EssuS1orna2mzcTuLLhmuMkzt2rWraRZv8jMryQIIwV5vhx12mOlT\nTz3VNDPAuOgV7ZjFixeb3m677Zxzzo0bN862sdjsiiuuME07oEmTJqbZJ4uLaPE17Du33377mb7/\n/vtduRKykIshZKPQ0vILAjKjjX0D33jjDdNjxowxzX5+tJ9poZLQPaKSrg/OC60oLpPwxBNPmKbN\nRLuK95mQXZ80Xpwj3m+YoUY7+9VXXzXNjDJmnZEDDzww8djzRJGMEEKIaOghI4QQIhqZ7bKkkC6U\nURYq2KQtwt49fG8oY60maFvxc2gFcUVHtt1mbyB+PrNtWMgUsjhCVp8/nqzZOKWC87X33nubZng/\nZMgQ08w82myzzUyfd955prfYYgvnXKGlwvGhzcUiTY4Rs5pYDEvLYvjw4aZ/+9vfmi7nVTVjZCGG\nlkX49NNPTXs7c6ONNrJtnTp1Mk1rk7YYNa8nFnVynivJFgvRo0cP0yxGpVXLrFRa8bw+OF41Fa/S\nZmMmWJs2bRI/kz8/cC54LnDu+JkjRowwHcvyVyQjhBAiGnrICCGEiEate5eFCBUvMXSjXUUrZMmS\nJaZDdhktBu7fh4ksgGLmEsNeZlo8+uijpmnpcQVOhq8hyyV0jCFK3bsslDn2wAMPmGYrd1opIfsv\nZM3wHEiyOtNkHTEzhitmciVVWhYsZqTtltUuK2XvslBmUai3X019+xKOwTTH6p577nHOOdenTx/b\nxsLiAQMGmH7//fdNM7OwBP3KSEl7l3Xp0sU0MxuZZcmsRdpMPMdCxeicF9rC/j7DHmXMHAvNP/dd\nYotSvcuEEELULXrICCGEiEate5eFoFWU1IvHOeemTJlies899zTNcJyFT+z7Q33EEUeY9pYKe26x\nkIkW2dSpU00zY4S2GLPe0thfodeUS3YTbaYHH3ww8TU+E8y5QsuJ4TgJWSZJhbEcH2YgMZOJq5d6\nS8e5QiuMn8OW+Emf6Vz5ZZQRfhfamZwrWiSh7xgitNSGzxzk57P/1rx580y3aNHCNDP7KnllzJoK\nynl/oP3+l7/8xfS0adNM+4Jj5wrni+c872277rqraf5c4Mk6tuWexadIRgghRDT0kBFCCBGNzHaZ\nt07S2EMM+2i5sGDopZdeMs2CsBNOOME0V3gjbDfu98/QkQVo119/venRo0eb3mSTTUwzk4bQ9qtp\neYHlKUe7JrSKJ9uB07piC36uyBfKkqEF5oskadGxvX8xtgutHM51pcDvzsxGEsrsS/Mabqcd5z+L\nFs5TTz1lmrYYMz6zkubY64Isx8J5+c1vfmOa2ZfHHXecaVru7AGXJkusvqJIRgghRDT0kBFCCBGN\nWhdjhvpP0a4KZT1sueWWpll0x4KxVq1amT788MNNX3bZZaZpwfkMJPYWY3ttwqykUOhaUwvulW1P\nQ6mLMZd7PY/DdCgTjll6oQxAth7n/vO2BmIvqRCjGLMY2yg0J1ltNK58eckllzjnCotve/bsmfg5\nIfstzXmTIyUtxiRZv1u5WoSRUDGmEEKIukUPGSGEENHIbJclFTLlFSKGis1oyxBmhvkeT1zhj3ZK\n6BizZuzkRV3aZSHqw+qexVLK3mW12KfprOckCwBvu+0255xzgwcPtm133HGH6VCmWx1SZ3ZZCFr1\nIXtxFUB2mRBCiLpFDxkhhBDRyL3Vf17QGgi10U/K/EhjKTDULWZ1wmIK5crRLssKCzPLdbXPrJSz\nXVaLYzDNDMHWrVs75wrnb9KkSaU7sOyUnV0mnHOyy4QQQtQ1esgIIYSIRubeZTW1yW7Xrp3ppDbW\naeH+Q5ZWUnFUGvuvGIsslIEVyowrl2yTGAVzlWCRlXNxXAkyGE2zWJZaiNgokhFCCBENPWSEEEJE\nI2t22SLnXO09MOFpV11d3TKvnWleciO3edGc5IrmpTxJNS+ZHjJCCCFEFmSXCSGEiIYeMkIIIaKh\nh4wQQoho6CEjhBAiGnrICCGEiIYeMkIIIaKhh4wQQoho6CEjhBAiGnrICCGEiIYeMkIIIaKhh4wQ\nQoho6CEjhBAiGnrICCGEiIYeMkIIIaKRafnlqqoqrQuQE9XV1cnrNdeC1VZbrbpBgwbOucIloSuB\nRo0amf7222/r8Ej+j7zmRddKrizOcT0ZzUt+pJqXTA8ZUZ40aNDANW3a1Dnn3OLFixNfk3U9+djr\nz3s6depketKkSdE+x7n/GyfPTz/9FPWzRDpSnmf1dpExnpM///zzCv9fbut9rbbaMvPr559/TjUv\nssuEEEJEQ5FMPeDHH3+0CCb0l2Gav4gOPPBA008//XSm9y73F84K/7/66stONVp6U6dOrXHfxcDj\nCkUv/jVJxy3iUm5/qZcannN+LHjOphkfRkMkRrRem2tEkYwQQoho6CEjhBAiGrLL6hnF2A/Dhw+v\ncT8hOy4URtd11lua8F42mciLkG281lprmf7uu+9M13S9pkmMoC3Gz89KTZZ3rfeb256EEEKI5dBD\nRgghRDTK1i6LWafBsJBh7DfffJPr51QCjRs3Ns1iyFBNSfv27U2///77Ne4/KcMldr0Kzx3C86hU\ndUCifIlxDoRspv/+97+pj6GYYynG5oplGyuSEUIIEQ09ZIQQQkSjTuyyNHZJHuErbbH111/fNFuv\ndO3a1fS0adNMM7yNeYx5UFVVZcWOP/zwQ6rXe0IWIb+zb1njXKG92LZtW9Pz5s1b6WeGijFjkGZe\nymXu6pI11ljDNM8bbqeF0rp1a9Mff/yx6Uody7yOOy/bzd+vuD/a2ezzt2jRohXe51zhdctrrkWL\nFqYXLlxoer311jP9+eefm87TSlQkI4QQIhp6yAghhIhGVZZQqK7aZDMcZAj4/fffm/YhfqtWrWzb\n9OnTTY8ePdr00KFDTU+ZMsX0LbfcYnqzzTZL3M8HH3xgmqHpb37zm5q/CMiz1X9VVVW1D285n2mK\nqziefH3Dhg1NL1261PT9999v+rLLLjO99tprmz733HNN+3GfMWOGbfvkk09M02YrB9ulvrb6p/2x\nwQYbrPD//fv3N/3CCy+Y5rlPS43WDfX8+fOLPtYE3qiuru6Wx47SzEvouskrK5JzQe2vRY4nP3+r\nrbYyHcqUpP1Pi+zee+9N3M+4ceNMhzLgVkKqeVEkI4QQIhp6yAghhIhG2RZjEoaPa665pumDDjrI\n9HXXXeecc26TTTaxbQx7mVH2+uuvm2am07rrrmv6wQcfNM1Q89133zWdJpOrVCRZTWmKq/j9mVXE\nrDPaiLRDhg0bZnrBggWmGb7vt99+zjnntt56a9s2ZswY08yemT17tukYRZr8LH6/+tTqn2PPbLBt\nt93WdJMmTZxzzl1xxRW2jdmXPXv2NH3sscea5vlO62ivvfYy/f/+3/+r7aGXDTwPOJ7FnJMc3913\n3900LapPP/204F/nCm1oss4665hmUXTLlssWquQ80kY7++yzTdMWz9JTLQuKZIQQQkRDDxkhhBDR\nqIjsMhYM7bzzzqavv/56096OYRj/xRdfmD7ttNNMjxw50jQLkNq1a2eaGRjMxqFFxPdmLTDMO7ss\naXua7DLaAZ07dzbNDLCDDz7Y9N13323666+/Ns2+Z+edd57pgQMHOucKw3XakswQHDJkiGlmrtGK\ni52BFiO7LFYLdQ8zBGmjMLvo4YcfNu3Pbb6Px8V5HTFihGnazDz333777US9ZMmSDN9ipZQ0uywv\nOO/M2GvevLnpV1991bS/n4WKMXmP4X2O9httYFqkzArlHNGuq8W1pewyIYQQdYseMkIIIaJRttll\nDOUZGu6yyy6maW/5MPGJJ56wbTfffLPpmTNnmqZFwxBxzpw5pufOnWs6ZIWFWsqXO+w/xrH46KOP\nTB966KGmBwwYYDrU4+qRRx4xTZvGZ/sx7Of7qFkQyILZ559/3jSzC2nRZSW2hUVi7J/XRLduyxwL\njgn1rFmzTPtCY2Yx0cIke+yxh2naz8wiY1YgrbZVHdr8vC+ddNJJpnn9eUv5nXfesW1fffWVad6T\neH9ksfQ555xj+qijjjL9wAMPmC7muqkNimSEEEJEQw8ZIYQQ0Shbu4wWFcP0E044wTRD/PHjxzvn\nCgvMWMTJQipaDbR/aKEU0y6e9hILOUsBLTzaNAyvQ0VXLMxilgoz7UJh+sSJE00//vjjpn1m2B13\n3JF4XKEx5LzQduA88hwJzWOosI7ftdT2QR7wO06ePDnxNcwc+u1vf7vCdlqPXbp0MT1o0CDTvXv3\nNk1rh5mIb775pulyKlCuidjLT/D6YBYZ+yu+9957pvfcc0/nXGH2F4ufeYy8DliAzuJZzm+avmQs\n/OQ9otixUSQjhBAiGnrICCGEiEZZ2WWh1dhoDYQyw7bZZhvnXGF4z7b8LC5kIVno84vpU1Rqi4yE\n7Kc0GXK0yFiASjuJGS60SZ599lnT7BP35JNPOucKbYE//elPppkhSHuB34OWl7cUnHNuwoQJprlS\nYyibi/usRIssdH6msahoOfueZiyQPeCAA0z36NHDNMfJX2POFRZCc95Cx0vKYUkH5+Kv0Eq76rPP\nPjPNwkwWTPosyg8//NC2hbL1mCHKQkv+hMDrYP/99zfNZTcIX0/r7MsvvzRdm7lTJCOEECIaesgI\nIYSIRlnZZaFQjGEcLbBOnTqZ9pYaC51+//vfm2bhWYgY7eXLHVoaDMF9tp5zzj300EOm2T7+8ssv\nN02LjPPo7U0Wld14442mL7roItNjx441veOOOyYeLzNpaJelKa4sZQFmDLJmP5K+ffua9nZuaMVZ\n2m+0efr165e4PQSPkZmelWhVpoXXE619v7yCc4V2Fbd7G58WWWgVzVtvvdX0RhttZJpjTouUFl0I\nzkuRPc0KUCQjhBAiGnrICCGEiEZZ2WUhGNYze4xFlT6UfOaZZ2zbyy+/XIKjKy84JmnsP9pGzLZZ\nuHCh6UcffdT0NddcY5p2AHXS/ufNm2fbWPj39NNPm2ZGG3vUhWwX9j1LE9JXokVGaBVyNcQQtFeY\n8chCVA/Hj5r2czE2V322yAjHjtllXPagffv2ppmhucUWWzjnCpdr4Dn7l7/8xTT7/IUyREeNGmWa\nfRnTEMrurc01pEhGCCFENPSQEUIIEY2S2WUsEmKmURpC/bhYBOZXY2RhUqXbI7UhZBulCXmZUcKC\nVbZ7nzp1qmlmJBGG+z5Thp9Pi4BtzbnC3/bbb2+avcv4+mbNmplmdlult5vn+d6yZUvTWVeabNq0\nqWlai0nQWr3llltMv/jii6bT9L8KwfkP9Q6sb3AeeT1xSQ1al94uplVMe5rFsxxPWtssqp02bZpp\nzh3PhVKMvyIZIYQQ0cgcyfi/QrLWlDB6YT1Gmr+ONtxwQ9OvvPKKaXYrvfPOO51zhX+l84nNXHLW\nzPCHsvpQJxOKUtJEdfyrZtdddzW90047mWaOP6NTRpX8S9X/xcXEgEWLFplm3c0RRxyReFz77ruv\naS6+xciHrTg4p4yCQu2Eyg1GozxXOa5p2G677Uxz/P01xyQZzj2jVV4TvJ5CiR4k5EBwztkOqD7A\n7xzqds7XMNnFJ8Sw0zzbu3AfjNaPPPJI01OmTDHNOS0meizWEVIkI4QQIhp6yAghhIhGZrssD0sp\n6w+IDK9HjBhh+qabblrhuPhjNNe4/utf/2qaXUUPO+ww07QJ0nRoZdjLH7uzJjbkgT+WYlpAcG5p\n01CzrQ/tp1BCht+eZNc4VxjGhzoy+6QO55zr2LGjaVqn/AGV5wDnItTlu5zhuKaxLfgd+d2HDBli\n2v+YzFobjkfz5s1Ns07mvvvuM53GLguNcblYZDHOB1qKbBlDC5c283HHHWf6jDPOWGEftLZ4ffKn\ngtdee800k2F4n1t//fVNc+6YNNC4cWPTeSbPKJIRQggRDT1khBBCRKOs2srQOmFLBh9GOlfYkuS2\n224z7e2tXr162bYLLrjANLM0mHHE1jO0vNIQyvaoC/yxFGMB8L2zZ882zWwwjiPtGGbS1GSp8rim\nT59uesGCBab/+c9/mp44caJpLpzF8D60fx4Ls62YhVPO9VTFzGHPnj1Nc1E5b5OFvjetnVNOOcU0\nzwlmplUqWceWNmyaTt+8hzE0abRPAAAgAElEQVQTktma55xzjml//wstzEhb7JhjjjEd6ppNy5/X\nFgm1pMkTRTJCCCGioYeMEEKIaJSVXcYQlNlCDPvZTZThoA9l58+fb9u4INaAAQNMH3TQQaYZ0m68\n8cam2TU467HXJbSzaOGlsQb4Go7tv/71L9MM5dlZN8v3p6Ww5ZZbmua88PNpb7Zt29Y0sw6vuuqq\nxPfys1jIWSnZZcXAeQsVBiZBG5JjTLsxjV2WtSN4qUljLfM1zPpiN3hmObLom0XkvC9169bNNG0s\n/14eyxNPPGGai/qxjRLP99D3CBVgluI6UCQjhBAiGnrICCGEiEZZ2WW0NlhIxAwMZoCx8MhbKgxL\n2e306KOPTvxMhotpeluVe0FfXmtz096g7UbbhRZZlnFhsR/Dfob0zFyjXcqO0PwcFtvyWHjslbJw\nVjHnWGixqbPPPtv0pZde6pwrtFlobbHoknPF7sBpKEeLjITGlllk/A48P3nuDxw40DQLXFnozYJm\nFlKyR6A/P2lJjx8/3vTDDz9c47GnOXdKfd9SJCOEECIaesgIIYSIRsnsMtpc7EvF8C4UXjPDggsx\ntWjRwrQP/ZnRwcwxZnSECpDSFFSWo0Xm3LLvlKbnWk37cK7QPuEYcfy/+OIL01myy5gBt+2225qe\nMGGCac7XzjvvbJp24EMPPWSa2T7Dhg0zTcuoXOdueULrxKfpFxbq83fJJZeY9ktt8Fxp1aqV6X32\n2cc053XQoEE1fn6lwnM/dA1xXrh4Htv1/+53vzPdqVMn0xx/Folzn/78p+X/6KOPmub9iccbIs1r\nspJm8cMV3pP7UQghhBD/P3rICCGEiEZUu4xZGrRcQtkbocwI2gTszcOMjU022cQ5V2gX/M///I/p\n9u3bJ+578uTJpsuloLI25G0FcV4YInMu0lhRfjsthYMPPtg0swhZPMtMMK4UyM/Zc889Tffv3990\naKmF0Pnlv0cp5j+r3ZDm+iB33XWXabZ3p3Xz+uuvO+cKrx9amFxllL3LmAlY3+B40ioOLbXAwkwu\nUcHCYZ7DXA2YGWi05vy9iDYw75shS4/nVOyMvtpcI4pkhBBCREMPGSGEENGIapcxpGvUqJHp008/\n3fQDDzxgmsWQoUwahoYMWa+99lrnnHP7779/4mtZSPXWW2+ZZsFUMdSHPk1pLDd+N45/qDDT2zTM\nqDnyyCNN8xyZNGmSaWbVMNOMhWw83jR2R+j7ldImLeazaDMTZlmyYJIrM7Ivn1+ZsXPnzrZt5syZ\nptmWnpZaJdvJWeA5fvLJJ5t+8cUXTc+dO9c0MyR5TXAZEdpetMuYSTZ69GjnXOHKobwPUvMaizEv\nocy02tjyimSEEEJEQw8ZIYQQ0ShZMSbDL660+I9//MP08ccfbzq0SiUL83xGGbcz1GWWEbNkWPSX\nJmMmTUZQXVtkfnxj9Cui/cR5ZMYebZrLLrvMtG9fHrLWmF02atQo08ySotWQNSMrBO3bcuhpFrIz\n+V0233xz07TC+vbta5pZTDxv+/TpY7ply5bOOeduv/1228Y+gLRr6vq8rmt4HhKOM1dr/eSTT0x3\n6NDB9N/+9jfT7777rmn2JvPnNi1k6tBcxCgyDtlxtemrp0hGCCFENPSQEUIIEY2S2WW0PO6//37T\n7GM2ffp006GV3Ng765FHHjHtC5nYU+i6664zzSwZhp2hlSRJuWfVVFVV2UqioRUQmZmUtb8Zs1po\nY/7qV78yzXbntDG9ZcNj4TEeccQRppm9E8ocy4tysMhImrbzs2fPNk277+9//7tpFiN3797dNG3p\nHj16OOecu/fee20b2/vzc3it1BfrzNu/ab5Pv379TPOc4fizQJzzRYvYW5TOOTdy5MgVjoX7pM3P\n+2Bt+obVltD+lV0mhBCirNBDRgghRDSqsoQ/VVVVufsWDCl5LMze8OG9c4VZNc8++6xpb3VxH2ls\noTRFlDFWw6yurs6tDzfnheMWKmgNhcK0IlkYy+9PO4C9sWbNmmW6cePGK+x7zpw5ptlzbN68eYnH\nkpW8isfympcY10rWc9VbqM4VWpRHHXWUc66wt58vZnaucAVGWkEhQss/5GhzvlFdXd2t5pfVDOcl\nzXXN64nLTPC9vCfRcqellmaFzaTXljmp5kWRjBBCiGjoISOEECIadW6XrarkbZfVVIwZghkrtAZ8\nEaVzzr333numk1rkO1eYpXf99dev8PqbbrrJts2YMSPxWEq5cmXIKilnuywmMSzhHIlilxVDMdma\n9QjZZUIIIeoWPWSEEEJEo2TFmCIu3roKZaYwiy+U3cKCWfZX8q3hnSvMUmL2GrOK2Kbft5Dnyoxc\naqEYiilOK0NLqOSUsrivvpHGIguNbx7WZGjfWTMQS7GqpiIZIYQQ0dBDRgghRDRyzy5TCJ6OWMWY\noVCcq5Gy7XiIYkL9pNeEigRZ4BYizWeGjpdWH/vkrWRJhJJll7FvGy1GsQJll11WaeRVrLzctajs\nMiGEEHWLHjJCCCGikdUuW+Scm1PjC0VNtKuurm5Z88vSoXnJjdzmRXOSK5qX8iTVvGR6yAghhBBZ\nkF0mhBAiGnrICCGEiIYeMkIIIaKhh4wQQoho6CEjhBAiGnrICCGEiIYeMkIIIaKhh4wQQoho6CEj\nhBAiGnrICCGEiIYeMkIIIaKhh4wQQoho6CEjhBAiGnrICCGEiMbqWV68qi5dGoNYyy+L4ijl8sul\npFGjRqb9ktcVtMzH4hzXkynbL+2XNi7neWnQoIHpn376KdW8ZHrIOLdsLXWuo14O1HRcoTXg06xl\nT9KcAGnWpF9VKNfzhay++v9dBj/++GOu+63pu5fyPNliiy1Mv/322865ZQ+b5QldEyGK+R4pP2uV\nWGTMn4c//PCDbeNNnfz000817i/G+dWkSRPTS5YsSTUvssuEEEJEI3Mkk8dfpK1btza9YMEC03n8\nFcRt3F/ouENRTeg1aQh9j4022sg559zChQsz7a/SyPqXcE0sF6IXvb/lyTuC8SR991JGL/4vY+ec\nmzx5cp0eS4iQe1CfHQB+T2pGMJ5izvcYY7hkyZLM71EkI4QQIhp6yAghhIhGZrssCyHbpBiLjCTZ\nEcXYM8X8yLnGGmuYZtjL13/00Ue1Pra6JI39RWumJvspqy0SwyKrK0LfN4ZVFJqH9dZbzznn3Jdf\nfpn4/2uuuabpUHIAyevH/vpgkWWdx5qSjUL7CyUm8Tr8/vvva/x8krfNbfvNbU9CCCHEcughI4QQ\nIhpR7bI09Sih7bXNKEoTXma1LELZIHxNUmbIyj6rkkgTOoesmdpaAFnnrpxJc/wh65XjGnrvOuus\nY/rrr7+u8fXeJgud12kssmLIWstWCmKcY40bNzb97bff1rh/vz2U5Zr02uU1z5e11lrLNO+hoXMq\n1pgrkhFCCBENPWSEEEJEI3e7LBR2pimGJFkzimoKMdOEwFktGtoUZOnSpTV+Vt7Udd+j0Hh5zf/n\nXDEbhllN1F999ZVpnhchy4DvzZphkye1balD6zVUXEy++eabxNdwzGnd+DHs3r27bWOx5hdffFHj\nZxZjraS5R5TaIo2RIRc690KZYR5eE9w3bS5+PvfH19P2pAUb+iwee54ZnYpkhBBCREMPGSGEENHI\nbJcl2TLbbLON6enTp6/0fcu/t5i+VMye8PtniBojW4LHntUWi2lp1bTPrPYDw+iQRZXl8xneU6+/\n/vqmmzZtanrLLbc0/eGHH5pmAeG7775rmlZCKNOv1NR2ntNYZCF8fzznnOvatavpoUOHrvDazz77\nzDTttLvvvtv08OHDTS9atMj0O++8Y/q7777LdLx5vSYWoXtSaHvI3uLyCjw/OV6c63XXXdc5V2j3\n8nP4PmarkZBdGsr+THNtF4siGSGEENHQQ0YIIUQ0MttlSSHVtGnTavU+59JZZAxHqddee+0VtjMT\nidZZmky3ULZSiJAFVY69mbJ+dpowOk3xnB8jWg1c6oFzuPPOO5tevHixaWbxzZ8/f4V9L69JXRZ1\n1vYz0hQrUu+yyy6mR4wYYZoWGMffH1erVq1sG4s4+/Xrl/j5o0aNMs2W77RiaKmV80J1K4PnPs+Z\n0HbOM8ecbLXVVqY5Rsz66tKli3POuVmzZiXub7PNNks8lnHjxpn+5JNPEj8/BM8j7jPNYo5pz29F\nMkIIIaKhh4wQQohoRO1dRrKGWXw9s4723Xdf0zvssIPpzp07O+ecmzt3rm1jlsYHH3xg+oUXXjA9\nZcoU06FssZBNEcpiqkubIEvL/ZVRTEv6pMJLhv3bb7+9ac7tpptuavqEE04wfeKJJ5r++OOPTYes\nyPrU9ywEv9ftt99uOmSRcay8jRzqp9WwYUPTJ598sumtt97a9F133WWa1xDPOWYCpunBVu6ECopp\nM3FMmzRpYpo21iabbGJ63rx5pt9++23nXOFY9ezZM1EzK5PX/KOPPmo6ZOPRovv8889dEmr1L4QQ\noiLQQ0YIIUQ0otplxRRaspCJWRUXXXRR4naf7UILi//fp08f04cccojpgw8+2DTfy/CSIWUojGRh\naOxW6SsjjUWWl4VEyyBkzfgCszZt2tg2WmR77bWXaa4ceuedd5qmBZEmiyzN9kqHGXobbLCBac4J\nz0MWtF5wwQXOucLsMtpi3EenTp1Md+zY0TSvlQEDBph+6KGHTPO6adu2rWlaROU+P2nOq9A5SVuq\nW7duppkhyb5z/h7Gex+vq169epmmFUkLmfctZteG+uFltddrM1+KZIQQQkRDDxkhhBDRqHXvMoZx\nDLNCxUs17c+5wjCRmWFHHnmkaYbdzAbzdsCTTz5p22jLsBjKZ6I5Vxg6NmvWzHSaIkpaZNzPwIED\nTQ8ePNh0ufTUYhhfTCt8ZrhwHlnY58clTTEuezOx3XyHDh1M04JJsxpnXn3yiiEve5L76dGjh2me\nhyxiZfv+s846y/R7773nnHNuww03tG0sruT2M8880zQzN9mvcPbs2aZpr3E+H374YdM77bSTaWay\n0d4rRYZmmmLqUNZiaCVTbw87V3h98J7DcaQV7M9n3rc4PrxW+Tn8Hs2bNzfNok+OLd+bphdjsSuW\nKpIRQggRDT1khBBCRKPWvctCFllWO4DvZRjHfkwMr2kHjBkzxvRtt93mnHNu5syZto2WyKmnnmp6\n//33N3399debvvDCC00zAySUScJiK7ZNv+eee1wSpV69kvYjw/KsFlmoMDbUBp32gc92YQt6jj+t\nMNo0zJih1TljxgzTtB9DxX7lsEpmXhYZM4eOOuoo0ywuZtbRAw88YJrFyJ5PP/00cR+cP14HLVu2\nNP3qq6+aZuYUM9A4nzfffLNpzgltnFJnmhWz6ifnhTZ73759TTN7zxdaOldoY9GK8tYYM76YORha\nRZbwO/H64PFyzHlfCNlixVqXimSEEEJEQw8ZIYQQ0cilGLMYiyyU3cCMGWYUsWDvxhtvNO0zmmjb\n0IrZcccdTdPy2W233VbYh3PhgkoeL8PeNP2ySm0HhFbPSwO/QyiTkJkvnDvaOsccc4xzzrnDDz/c\ntrHn3IQJExL3wYwlwjEMZZcx7KdFVil9zJLa8jtXuCwCsyhpJ3IFTLaMT7JCmP3Fc59WDNvIc/xC\nfQHfeust0+w5d9lll5kOFdeWek6yFlBzXmhFM+OVBeC005llykw+WlF+NVhmiNGupF3GDDXehziP\nofFkASjHP1ZGnyIZIYQQ0dBDRgghRDRyscuyFuuECpmYrdS+fXvTzN5gK2v2Y/LhKy0cZquxjfyC\nBQtM01JgGJm1F1alWDFpCa06yVUqkwrJnCu0FbwFxvFn76rXXnvNNLPy2A6d1kCoADZNNkylzAuv\nA1qPXOaCY8/C1ZB1ktSmntlHtGI4rvwcZpf5gs7lP/OAAw4wPXbs2MTvxGu+LguUs/YY5HnFc5wr\nunK8WJhKq5NzStvR25e8D4UyWPlTAW1mah4jxzlUeBrrHqZIRgghRDT0kBFCCBGNWttlzNBiuJ6G\nUA+pkNU1bNgw0y+99FLia3xYydCd1g73zc8fPny46ZC9EMocC+lQX6xSFGOut956prPOCwlZTsyM\nCbU4Z2i+++67O+cKs7y4kuLjjz9umsWBXEmQWVBfffVV4jGmmS9uz2sF0Rjw/ORqiGzvT82MS9of\noVUyvaXC8eP7aOHwGnv//fdN8720nVhEe/fdd5tmhugjjzzikqgky5mFls8884zp/fbbzzTHlBlo\nHDtmkvlzm+c+rwlalLzGmOmW5qcLvobzW8z9YmUokhFCCBGNWkcyobWhQ4T+6g8toMNFq37xi1+Y\nZu0Lf2TjX7sePpn55Odf1U8//XTi8Wb94b9cEgLS/DWSdeGv0HrmhH8p77333itsZ/LG66+/bvrd\nd981zUiS8MdMfn7W6IWUW/RC2OGY57uPCp0rvFYmTZpkmnVfTGrh/Pgx53jzB2b+BczIlWPPBAxG\nl9tvv73phQsXmmadzIsvvmiakU+pohd/PqdJUgr91c8klSFDhpjmfWbkyJGmGflQMwr1Y80WTL17\n9zbN5BkutsiIlVEioyAmW4Q6zPMc4LlR7LWiSEYIIUQ09JARQggRjVzqZNKQZtEqhmUM10aNGmU6\n1HLDh4C0wtiRlt1h+QMaa2ayWltp7KWkH6fr+kfNNOuTh+A4st6lRYsWptu0aWP60EMPdc6FW2Iw\nROf8M9TnnIda3IS6MFcitJ9oOfFcZSILX8Nuv7y2WHvhbWbug+PHGiW2ieHrOW9MTuDYMwnlD3/4\nQ+L3qIsf+7O0T+FraWPecMMNpjlfvOewg3JooTL+7OCvEdpi7CrPljV77rmnaXas57XHnxzYvZ7J\nBrxfMuEgNBe1WfhPkYwQQoho6CEjhBAiGrnYZXnZTKHurAwpGa4xlPWhG9/HhZ2YgcHFlLgON0Pa\nYqiktiZpjonfh9YMx5Rrzp9++ukr7IOhOOeTNg3tlZBdxnMkzbFXSu0Fs3923XVX04MGDTJNy4Od\nl2lpTZw40TQtZ2Y9+Wsl1N5l8uTJpmlz0hLlWF5xxRWmWTNy9dVXm37qqadW+Hznstu1pYY1Q8yE\nY20KbSxmhrGWiYvCMUuNi7/5seZ19dxzz5nmPHMROO6P7+Vij5wXnhdsVZMmizStRUYUyQghhIiG\nHjJCCCGiUeeLljFEo3XCjA1SU7jG/THrhdtPPvlk0yyGKmc7pRSkWWyNWUq0W1hUmdTCh1YkLR3O\neah4lnOeJqQnWYs0Y5BmcSx+X2bt0c7dbrvtTHOhsPHjx5vmdcPMIeLtT2ZC8X2hRd/YMoWWKIsr\naaeGLLJKgvPCBcSYxcViWFpqLCIP3fPYwdnfi1iszPFkEedf//pX0wMHDjTNYtg33ngj8XhDPwuE\nOqkXO3eKZIQQQkRDDxkhhBDRqLVdFio4rKkQcfnXpAnFQn3PkvbPTItDDjnENLOS2NMp1rrW5UYa\nqyjNdto9tMuYYUOLx78+1Ck41FU5ZHMVs8hVXdmhWRfHeuedd0yzJx8zhzgm48aNM017i5lhSeMW\nWryK29k7bcCAAaa33npr08zA4rGzGJH7Z5YcP4tFgsx6KjWh4l+OLS1fjtH06dNNv/zyy6aZ6cWx\neOWVV0z7e1SoGzzHhNbdhRdeaJrXJM8L2m7MjON5wYXVQn0Ea4MiGSGEENHQQ0YIIUQ0am2XZbVc\nSPv27U0zo4hhNAnZbkkWnO+V5VxhqEvYO6mUFoq3FepiXfOsfdZIaMwJW49zTr3mkgq0LpnRQmuI\nx8vxSmOdkjTfr5SkOR6enyxQJbfffrtpFsKOGTPGNG0Rjrkfz5Al2bJlS9Pnnnuu6T322MM0i2VZ\naPjvf//bNLOY0izRUJcWGeG8pDmvuFAisy+ZZfnmm2+aDmVr+tdzWQxakXzf0KFDTdOWnDNnjmlm\nDxLat7y2Yt2XFMkIIYSIhh4yQggholEyu4zb2WqfIT0zI2ijpMmM8uFr//79E9/HEJEhaintsiSb\nIiZpVo5MYyGFCjNZZMisPs7dY4895pwrLMzj+DNjJ41dR9IcezlYZCRrr7gHHngg8TXMFmJhJq0T\nZqOxwNPPD60Y9vPjqo8sFiS8brl6JosRSdbW8TyfQoXZeZImKzZpaRHnCu0yvp4WJTP9QsWufv+0\nK1mAy6LXddZZxzTtVc4Lj5dzVIwtlqaweHkUyQghhIiGHjJCCCGiUbKVMQnD4lDmUCgbhZqhts/C\nYbjIkJatruuqj1KpiwFDn5e1hxdfT4uFY81COu5z7NixzrnCzDGOf5pC3hjjVld9zLJ+1oMPPmj6\n0ksvNc3Mre7du5tmO/4RI0aYpo3mW9Dvvffetu3MM880zYw2zgOXazj77LNNDx8+3HSaaytNX6xS\nWGQkzfIcoSLNkJ0c2n/oHuazy5YuXWrb3n///cTXcrkMFlHSfmMGYF6F8VkLi51TJCOEECIiesgI\nIYSIRp3YZQwpaaMQhnFpVs/r0qWLc865jTfe2LbRivvf//1f06XMOMqzZXZepCkwC41/586dTR92\n2GGmt9hiC9M+o8y5ZRZLaJ7ramXESlnWgZmYf/vb30x37drVNNu7t2vXzjSzy1hI6d/LLCaeE8yK\nGj16tOn77rvP9JQpU0xnPa/L5TpIA7PCQmMUusZD1xNfz4xab5eF+rwxK5NWNeF1yOLWkP2cZi5o\nkYeWj1gZimSEEEJEQw8ZIYQQ0chklzVq1MjaWk+bNs22Zy20IqH3hsJOwsIgn93EQsDBgwebZmZM\nKSlHayBUUBUa5x122MF0r169TPfr1880Q3lmPvmwnrZYaAW+ciucLBb/nbP2jeOYcNy4YiKtYGaG\n0S7p3bt34md5i4bHxWylAw880DSvc1o0zFyqNPxYZC3+TbOiL+eOVhuvOWaD0Yry+wxZ1SH77eij\njzZ9/fXXmw5lbmbNKKuNRUYUyQghhIiGHjJCCCGikcku+/bbb93UqVOdc+FV1NJYZAwj+Zo0fc9C\n2mfPcBtD/VDb6xBZW+CXS7ZSmuMOFVRxLpj1QpvGz79zzj3xxBOmaaOxDbnPcKG9E7JC04Tu5da6\nf2UknRM890P95DgOvnDSucJMo5kzZ5o+9dRTTTOj7OKLLzbtsy+dW9br7PLLL7dtzz//vGlanyS0\nvdLw503oXtWmTRvTXIGS80Urkssr8PzkdcZ579u3r+mDDjrItLe6eN9iXzL2c2O/tHvvvdcl0bRp\nU9O8/5X6ulEkI4QQIhp6yAghhIhGVRabp6qqqsYXhywkhpHFrKpJmLHh+zq9/fbbto1hLNuhp+k1\nFJvq6urcqhA5L8VYeGmsqFBxWoik14QyZkLviz1HzALLa17SXCs1HY9z4UyzUM8/ErLj/JjnlflY\ngoLjN6qrq7vlsaNi5iV0D0tTjMnXc2VgWnO+8JbLOKTJTGTfQBZgMustEqnmRZGMEEKIaOghI4QQ\nIhq522XMSgqF9KEwnqRpU8/eS77vD+EqfQxjN910U9NspV1KYtlleZE1uy6UbejnsZjlBbLaZcW8\nN695adCgQbUfk7za1oe+VyhjLbRchn9NmjlmhhILNrNSZCZmSe2yGPZfaGVM3rf8/TK0FArZZZdd\nTL/22mumS9wrUXaZEEKIukUPGSGEENGotV2Wxv6KbYvURMi6K4bQ8WZth13udlnelOOSB0nEyC7j\necjvziwjtvSPQV0UsTZr1sz0kiVLEo8lZaZnWWSXrWSfpsulKHtl5Hgtyi4TQghRt+ghI4QQIhpZ\n7bJFzrk58Q5nlaFddXV1y5pflg7NS27kNi+ak1zRvJQnqeYl00NGCCGEyILsMiGEENHQQ0YIIUQ0\n9JARQggRDT1khBBCREMPGSGEENHQQ0YIIUQ09JARQggRDT1khBBCREMPGSGEENHQQ0YIIUQ09JAR\nQggRDT1khBBCREMPGSGEENHQQ0YIIUQ09JARQggRjdWzvLgS1pKvFPJaS945zUue5DUv5Twnfk36\nClpLanGOi5ZVzJeuAFLNS6aHjBBZadCggXPOuZ9++inx//0Nz7n4N73VVlsWuP/8889RP8u58rqZ\n87v7Ofnxxx9tG48xzThx3kJzmOZ7p5z/eruSZSnP/wikmhc9ZEQuhC4W/3Ap5kaU5nPSUIoHC8nj\nprH66ssuUR5/mpt/iB9++GGF11KnGadmzZqZ/uqrr0zzwZWGCryx5sqq8P31m4wQQoho6CEjhBAi\nGrLLRO4kWTYhmyur/VVKe60c4G9ZWceHv61wHPxvMtzGz+H7Qtbm559/XuNrQr/tNGrUyPS33367\n0u+zKrHOOus455xbunRpHR9JviiSEUIIEQ09ZIQQQkRDdpkw0lhL3mpZnlCKcm0/J0TIAqIdU0z2\nWgyKSZ0OHX+azDBqvsYfD4/LWzXOOffll1/W+Pnc3rBhw8TXhKy+kEVWTLZbfaC+2WQeRTJCCCGi\noYeMEEKIaKySdtkaa6xh2hem1YZyylzKu7q8puLK5aGNlmRdJdk1y8PCw7XWWsv0119/nfj5/By+\nd+211zb93Xffma6rTKaQ3cNjTlPEGCq0DO2f48DX+DHkNo4T53Ldddc1/f333ye+ntdQ6Fi22247\n0x988IHpJUuWmC43m7MU1HQP4f83btzYNM/lNddc0/R///vfvA+xaBTJCCGEiIYeMkIIIaJRr+0y\nhprDhg0zff7555tm6M4QlO9l5g37NJVTSF/TsaQphsz6em4PWVebbrqpc865rl272rbevXubnjBh\ngumNNtrI9IYbbmia8zJq1KhEzWOhfUNbJ02RYZ4kWZgcPxYl8rwKHSctxJBFFdJ+Hpxzbuedd3bO\nOTdnzrL+hu+9957pjh07mt5mm21Mt2jRwjSvm+HDh5tetGhR4udPmjTJJZFXkW6l0qFDhxW2ffjh\nh6Zbt25t+sADDzS9yy67mL7rrrtMjx8/3vQ333yT+JmlHltFMkIIIaKhh4wQQoho1Gu77O233za9\nySabmN5///1N0w74+KQ12UQAAA+jSURBVOOPTdOiqQ9FUmmK6khN2WLOFWa10FLs1auX6YEDBzrn\nnNt8880T38fP2WCDDUy3b9/eNDNmaAfQbmIBYYhSZ+EkjS230SIjoSLKVq1amZ47d27iezmG7dq1\nM33SSSeZ9hYlLS/ab++++65pZoUdccQRpseMGWN69uzZphcvXmya35UWKjMEeYw8nvpmkXEeL7nk\nEtMXXXSR6fnz5zvnnHvuuedsG8+RI4880jSvG96revbsafrqq682HbqGS4EiGSGEENHQQ0YIIUQ0\n6p1dxswcFvHRKiHMeqGlVqkWWV6ZI6HiQO6fRa3du3c3PWDAANPebmFreGaF/etf/zK9xRZbmGaG\n01ZbbWWaVssvf/lL06+88orpefPmmaZNUFeFarQ2Qi31Q0WMnMOPPvoo8b0s0uMYnnzyyaaZZbdw\n4ULnXGEmGAst+Znjxo0zfe6555ru16+f6aFDh5qmLcZzJVT0TIusPnPllVeavvDCC01zrD/99FPn\nnHMTJ060bbwn0RbbeOONTR933HGmeU3+8Y9/NM1z/4033jDNTM8s/QezoEhGCCFENPSQEUIIEY16\nZ5eRl19+2TSzZAjD+88++yz6McUmduYIx4sFYYMGDTLNDJe33nrLOVdYADtr1izTDOPZx4pWzpQp\nUxI/n1k4tEY5Bnn1qSuGkA2RtYU9LczQqpbMLuM4s/DSZ13y80P2KLPYOCedO3c2femll5oePXp0\njfvMWhhcqZlmtDHPO+8806Hv6Qsv+/fvb9to83M+ue+WLVuapo3K91L36NHDNK3oadOmmc5zzBXJ\nCCGEiIYeMkIIIaJREXZZlp5T3MYCtBDMqgmFsZVE7L5E3P+OO+5oet999zVNC8xnuLz66quJ+2Pm\nVfPmzU2zqC9kGfhsHOcKbTG2p//iiy9Mjx071vQee+xhupQWY5qW/lmh7cXxbNq0qWkWWPrMSdqH\noRVHd9ttN9PMaOLnsP8cs9i4H44B33vYYYeZfuihh0xXqkVGQsXC66+/vml+z2bNmjnnCm1JXkuP\nPvqo6SeffNL05Zdfnrjv0P2M+wxl9+V5ziqSEUIIEQ09ZIQQQkSjIuyyNG3ZfWhIC4et0UPQfqkP\ndlle7dJDRZdbb7216YMOOihx/6+//rppH47z/2mXsKW/twucKyyGZfYU+9GFsshoB3D77rvv7uoC\n2g1pCjBDhJYJYF849pDjOC9YsGCF4wmd75wHFnQ2bNjQNK22O+64wzTnJPRduf8hQ4Ykvr5S7TKO\n6XXXXWeayySElsjwFvELL7xg22699VbTzH5lG38ukXH22WebZgYa4U8EzPq8+OKLTedp6yqSEUII\nEQ09ZIQQQkSjIuyyNPgslUceeaTG1zJcpb1WqSF6iGK+TygziCss0opiFhctLQ8LxtiPie9jpgt1\nqE08vx/ttVBb83IozMxqkRHOCe2Xvffe2/QOO+yQ+HoWunq7hHba2muvbZrFettuu61pZvw9+OCD\nppm5FrKC+Fm+d5pzhZZOaCXHciGN1clzjJl5IThePrvulltusW0cq9C5z+wyzhfPC54LN9xwg+mr\nrrqqxmMsFkUyQgghoqGHjBBCiGiUrV3GwjwWlb333numWaTHHjw10bZtW9P1zSLLC9obLPBibyyG\n4FzBj1lcvqcYx5n9sJjdxxbkzAykTcN256EW+oQWR11ZZHlBa4kZRUcddZRpjhszyrgEgF8ygBYZ\nM764AudLL71kmlbQvffea5pzQtJYZ7TIYhcSF0vIIuM5xkw/ji/PT2ZucfkE36OP1u96661nmuNG\n+5PzwmU2eK/kUht8L4+R/f/yRJGMEEKIaOghI4QQIhq1tsuOPfZY08w0yQuGpmzpfuqpp5pmVstp\np53mnAsXmDGL6ZNPPsntOCsdjhfDcY4/w3f2VeJSCocffrhpWmreymFI/9hjj5nmvPhW584VZtWw\nHxZJ00o+lBFEG4LHEINibKBQTzHOA+1M2sy0zji2PuuI40HruVu3bqY7dOhgevDgwaa5SmeaY2ch\nJ60jap4jLBgsF/h9CL8bYW89Xlu0bbmKqy+k/fWvf23bQhYW72FTp041zeU3zjnnHNOcxxdffLHG\n/eeJIhkhhBDRqHUkEyN6IQcccIBp/rXz+9//3jRbnPAHrCT4V28xtQrliv8rK+t3419n/MuX48Xt\nkydPNs2IhX9Zd+zY0bSPSPgDLyMj1s906dLF9JgxY0wXEwmEEgLYFTc2WVv98K9ejj3nlrVG//nP\nf0zvv//+ifvhdePXkGcLmtACcFxvnppRR5of/vnXe8htKPfEDH4fJmGwxc/RRx9tmvVirPtiJM+I\n0NfsMepglD1u3DjTbN3ERA3OP+t0eM1dcMEFphnBxooeFckIIYSIhh4yQggholG2dTLsPsrQlF17\naR/UZJcxvCz3fPzaUFsLkGNBm4RWC60lhtRMvLj//vtN84dQb8nwx3uuN9+9e3fTnOeRI0eazroO\nfE2dulf2mtik+VxaURw3bufYz58/3/Tw4cNN04ps3769ad82ht2qaZuwvmbo0KGmaf/Q2gq1/eF4\nh7aHEjOK6VadJ6HO0EwcoV02aNAg0xyvE0880TTrvvheP4+cT373adOmmWZ7pwceeMA06wV5Hb75\n5pumzzrrLNM33niji40iGSGEENHQQ0YIIUQ0ytYuO/TQQ01zHfB+/fqZZuZNko3CrBeGsQyBQ9lH\n9ZmQjRGyBphpxpoMbqelRrtl5syZzrlCS2XLLbc0zfqNrl27mp49e7ZpWjbF2FyVYo2GMvs4V1zA\nauzYsaY5nu3atTPNTMDRo0c75wotL9bG8DP32Wcf05MmTTLNbCVeZ3lZleWSAcrj4HjS/uK80Lan\nPvjgg03ffffdpmmH+ixBbgvZhttss41pWmShDL3bbrvN9D333JP4mlgokhFCCBENPWSEEEJEo2zt\nMi64w8yY7bbbzvTzzz9vunPnzivso3fv3qbZvqFSbJNYhLK1GI5zOzPKPvzwQ9PsZs1uvez46jOY\nWDBGa43ZNSTUfbYYe7OussvSfG5okTjOCW0s2lWvvfaa6V69eplmht7TTz9t2mfxHXTQQbaNNsse\ne+xhmsW3tMVYXJtmLNNkBZY7vIccf/zxplkYy+/DjswcL44j59fbpKHrk9cEC9GZJcgMzYEDB5p+\n6qmnkr9UCVAkI4QQIhp6yAghhIhG2dpl11xzjelOnTqZbtKkiWlmeySx7rrrmq6ksDwGIbsiDcxw\nYeYTu7+y+y87KPsQn0W0e+21l2kWifXt29c0ezbllQFYbgWYoTkJ2ZYce+6TduZbb71lmllHEyZM\nMO0zzWh3ss/VI488YpqLo4UKXkN2YJrvV0nQxkzzPWlp3nnnnaZ5PifNNReQ44J0zL7kzwm04tgN\nnXPOY8kKLe1Qn7qVoUhGCCFENPSQEUIIEY2ytctYkMTCvJ49e5quqTU4F9Va1QlZNmz3TtulRYsW\npkOhNnudhTJmfOjPUJ+WJ+0Y2myvvPJK4mdWOll7r4UKM9mXKjSGLNjkHPqsy1133dW2MXOKPbJo\nv3HfJI0Vm7UvWbn0LiO8PtjrLQSzwdh3jtmS3KfvNffwww/btp122sk055x28g033GCa97zQon5Z\nqY1FRhTJCCGEiIYeMkIIIaJRtnYZLQOGa2yfndTe/6uvvjJdivWry5lQ1g+zZDhGzCJh8ST7YU2Z\nMsU0w37aAaRp06bOucKMGWYy8bjYX4l2QOysMD9Opcg+S9M3jzZwaOVSZvPNnTs38TWcZ1qUv/jF\nL5xzhUV8tNaYlcQVHdNYW2kyAdOMcznaZeSMM84wPXjwYNO0tHj9caVf9oAjL7zwgnPOuTZt2tg2\n2mkcBxZFsyg9lIFYlyiSEUIIEQ09ZIQQQkSjbO0ywrDv1FNPNc2Q2of+p5xySuL7VkVC3z/NKoW0\nbGiLUXP/zLZh2/hjjz3WOVdYPEbr5tVXXzXN1R5p5aSxS0LWYMh2KWUfs9DSCmlez2NmzzdayNwn\n7ZIOHTqYvvLKK037TD8uycCMslAWWSgDjseY1QoLjUe5LMERypxjr77QEhkcF65AyXN74403Np1k\nOfN6oy120kknmeZKm+V4z1MkI4QQIhp6yAghhIhGRdhlzJg599xzTSdZISNGjCjdgdUDGF6zAJaa\nGWhJSyo459xxxx1n+uSTTzbtM9Zov82aNcv02WefbZoZM7RLaBmErLM0yxeEXh+brKtFhl5Pi4zz\nQ6uS/fq4eiPtSn/dMCtt1KhRpmnLheaB12QoizM0JyG7Ns0YlJrQd+D5zD6LHH9maPbp08c0My2J\nL5j9+9//btuYccn5yrr8RV0tc+GcIhkhhBAR0UNGCCFENCrCLttss81Mh1Zs9KFksX12KpWkLJhQ\nWMwiPWYjMez+5JNPTHfs2NE0Vxv905/+ZJor8iVZIyzwO/30002/8847pmlt0Q7IqwdTqfHjHDp+\nzg8zi0I9+UJZXNRcLmHbbbdNfI3fP/vDhQoEiS+sda4wMy3NeRaydLJaiXmS9TN4TtJS/POf/2y6\nf//+pnv06GGaPQL5ubSIn332Wedc4XXFTDQSOqdCNlpd2o+KZIQQQkRDDxkhhBDRqAi7jO3GR44c\nafqOO+4w/fjjjzvnwsVToaLDcin6KhYfDqf5/jUtkbA8M2bMME3rbPz48aZ333130wzlzzrrLOfc\nsvlxrrBPViiMT9MnK83r0xCrd5kfhzQrR4bsj6zZVxMnTjTNYkxmoF177bXOucJCWM5JKDtv/vz5\nia8JWTT8TllXZi2FXZZ1v2nm6Pbbbzf9n//8x/TFF19servttjO9ZMkS074fWjH3pHK8nymSEUII\nEQ09ZIQQQkSjKkvIWFVVVR4VUvWA6urqbP7BSijlvNAaYFtz2lh8jc/2K8d27UnkNS91da2wSJJz\nQqvH26V52VAxrK3l9vlGdXV1t5W8PMt+62Re6mLpghJYjqnmRZGMEEKIaOghI4QQIhoVkV0myoek\noj7nwqF5Fmsgr/A+zX7qspdTEqHsqzTHFnpvKIsyy/cNFe5mHb80dlHWflzlTmjs8iDN+JfDee2c\nIhkhhBAR0UNGCCFENGSXrSLkZUVkXeUxC6FCxTRhP7Oq2O+pGBuqrsh6bKHlGkJ9r7KQ1SLjeeaX\neXBuWRt758LWWX2wyEjMnnvFnL9t2rQxzR6FsVAkI4QQIhp6yAghhIhG1mLMRc65OfEOZ5WhXXV1\ndcu8dqZ5yY3c5kVzkiual/Ik1bxkesgIIYQQWZBdJoQQIhp6yAghhIiGHjJCCCGioYeMEEKIaOgh\nI4QQIhp6yAghhIiGHjJCCCGioYeMEEKIaOghI4QQIhr/H6927paNpD9KAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# -1 indicates final epoch's samples (the last in the list)\n",
"view_samples(-1, samples)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Below I'm showing the generated images as the network was training, every 10 epochs."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAKhCAYAAACGkQOuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXe4XFXV/z83NyEJTaoURUBpAiKg\nIL2L9KYiClhp8lJEf1hQbIi9AYJ0lKaCoqggYkMEK91CR5CitEAASSAh9/eHfrJn1r0nU+6ce4f3\nXd/nyXMzM2fO7L3O2ud8V90DQ0NDJBKJRCJRJyaM9wASiUQi8b8f+bBJJBKJRO3Ih00ikUgkakc+\nbBKJRCJRO/Jhk0gkEonakQ+bRCKRSNSOfNgkEolEonbkwyaRSCQStSMfNolEIpGoHRM7OXjChAlD\nEyaU59OcOXMAGBwcBCB2I/C1f/2urwcGBpr+er6qz+P7cRxVx8XPRePx//3XfMA8oCz8LX9j4sSJ\nTa9FlE2VLOLxrb4XUfV+u7JouAZdy8K/6kW3suhULyJGK4te6EWURRxTlE0rWUR9ez6skTiGXt0v\nno+yqLpfxLnXvUbi9yLquF909LBxwJMnT256f8qUKQA89dRTAMw///wAzJo1C4DnnnsOKAKbPXs2\nAPPNNx8ACy20UNN5Hn74YQBe8IIXAPDvf/+76XxO0PM48QUWWACAp59+uum131twwQWbzvfMM88A\n/1F+/98uVDhl4Rick7+hLJ599tkmWbjgoiwcY5TFIossMqIs/H5UtqlTpwIwc+bMJlk4DmU+kiw8\nZyeyAIbJwtfqRbweUS98P+qF53nkkUeA4XrheD2frx2X10BZRP30dxynMhoYGJh7TKey8PpFWTz5\n5JNAuc5VelElC6/rgw8+CMBiiy3WNPYo23gt43WP41h44YWbxqlejEYWVXrRShZV9wvHqIwfeugh\nABZddNGm81bphfB3q+4XVbLo9n7ROOZ27xeO2YdSlV60ul9EWXgeZawsZsyYMeI4lIV65vwnTpzY\ntl6kGy2RSCQStWOgk0acEydOHFpooYXmPtVkKD41fQr6fpVJKKKlsvjiize97+/41BYe71M7mqI+\n7R2XjDaOW5b45JNPMmvWLObMmdO2WTw4ODi0wAILzB3rpEmTmsYWZdHKlRTZuMykSrbxPMoijkO2\nJqNRFp5P2TZaIbNnz+5IFhMnThxacMEFh8nX34zvV7lPRLTWZO/t6oVMNepFK1k4Ps/75JNP9lwW\nVWtExNd+z7+tZCFj9vgqvWi1Rjyfa+SJJ57oeI20qxf+VpV7S3R6v6iSRaf3i7GQhXqhxdJKL5yz\n70e9iFa86NW9s9Gb1a4s0rJJJBKJRO3oyLKZMGHC0JQpU+Y+BfXz6UuXOfq0jD5SmYZ+af2FMfgl\nq/e46dOnN51HhiEL0KfqU/xf//oXUNicrEH4dJYBT506VUbfUcBv8uTJc5mJjGDatGlNY6wKkscA\nnn8j09BX6vvKIsZmoiy8NlEW0b+qLPTVzjfffDz99NM899xzHcsisuZHH30UKNdFWSizGHR0jiIG\nko3V+L5z9XerZKFeKosq/fR7ymLy5Mn8+9//7lgWjWvE62dcwbFUXQ/XgnOMa8a5ukZa6YXX94kn\nngDGfo304n7h56OVRaf3ixhX6YUsnKO6rCwci2OoipvGNRLvF543ysI1p8y9vn4e14hzrtILLZ7J\nkye3LYu0bBKJRCJROzrKRhM+fX26+dqnqRkLPgVjxsM666wDwPXXXw+Up/rrXvc6YPjT2M9f9KIX\nAXD55ZcDsNxyywGFNd5zzz1N41lmmWWAkqEho5Gx6POdb7755rLZTiED0Kfpb8u+Gi0GKLKQSay1\n1loA3HTTTU1z3WqrrYAiS1mcvlJl8Ytf/AKAF7/4xQDcd999QMlW8pq88IUvBIrlpc9W6POdMGFC\nx5k2opUsZIYe53VQL9Zee20AbrzxRqAw0m222QYo16+VXrzkJS8BCku79957m35XWWh5KWPHoywm\nTZo0V8c7RbQM/G2vh3OpWiOvetWrALj22mub5vra1762aczKQllFvfD1Aw88ABT98Nosu+yyQFkj\nURa9WCORDbd7v9BCrpKF9wuttipZxPuFa+Mf//hH03iiLDyv41IWkydP7rksXCNRFjHT1nuna8T3\nt956a2C4VefnSy21FAC/+tWvgOF6cf/99wPV9wv1NXqfJk2aNFfHWyEtm0QikUjUjo4sm4GBAQYH\nB+ey7BivkJGY7x5rPHz/7rvvBgqD3HbbbZu+L3v3Ke7xe+21F1BYov7ONddcE4A777wTKE9pn8qO\nN9ayPPbYY8B/WIVz6UQWjQVr+t6da/T3KgtZlzLTGlMWMlcZhueT3SmLN7/5zcDwWoNXvvKVANx6\n661AYfUynlhM5vkff/xx4D/XoBtZDA4OzmU9fl85KwvZUNQL/czKQj2pkoUWkMxUvYj1OGussQYA\nd911V5Msol7ILqMsJk6cWFn01koWsRZMWbS7RhyzbFpZyIDVo1e/+tUA3H777U2yUO/Ui1e84hVN\nxykL5+o1U9YxBtntGmn8nrLo9H7hulYWWjTqlWtg3XXXbTq+1f2iSi8cb6xl0RKeOHHiqO8XxkLi\nGnEt+Lmy8P7w97//vem1euFY1Qs9Jt4L3/jGNzZ9rvXmGvG+ouXr5/F+4Xi9nwwMDLQti7RsEolE\nIlE7OrZsJk+ePCw7TB99zNVecskl534PCnPYfvvtgfI01oJ52cteBsDKK68MlJjOaqut1vT9JZZY\nAoA3velNANx2220A3HLLLUDxL8pkfJoLz9PIZLthsJMnT57r13WOMd7hb0RZOEaZiexM1q4sXv7y\nlwNwzTXXAEUWWmWeV1lo0fztb38DSszAOcfaFM/jOKdPn15ZF1WFKAvRrl7IrmWsWihRL1ZddVUA\nrrvuOqCwMr9fpRfKxDiVc4564fvGBKZPn961XrS7RvSNa7HENeL10mJVFiuttBJQ1oiycw7KQkar\nRXPzzTcDRS9ixmB8v9ELULcs1AtZtGNQFl4vrTRlEO8Xvh9lseeeewJwxx13AOV+oV7EzDBl4fuO\nczSycI049xgTNHvRv1V6oYy05pZffnkAVl99dQBuuOGGptf+rhZRlIXWoLKIWbWO1/cbZdHu/SIt\nm0QikUjUjq6y0WIPIX2R0Xfn01ff6wYbbACUp6L+Zp+uO+64I1BYucfJ5r/3ve8BxeeqX9HfNcNC\nRiTDkR1eeeWVQMlGkREvtthic9lLp/DJH/s5ReYjQ9Enu9566wFFNrJ4GejOO+8MFFnIMGXzF1xw\nAVBYnnPWWjA7zbmuuOKKQJHFVVddBRTWJvtcbLHF5p6rUygLffNVeqEsjOG85jWvAQqbUzbqxU47\n7QQUWXhclV44JxmXeqG+aB1oQf3mN78BSnyjF7KIayRWxSsb14iycE2oJ77WOtthhx2Awso9Tgb7\n3e9+t+m1czYGYMaVerHRRhsBhc3/+te/bvq80ZvQ7RppJYtYT+Oc1l9//RFfO3f1QmvN+4Vz/8EP\nfgCUNeP4zSRTFr7vGnG8V1xxBTBcFksuueRcuXaKqvtF7BRhHDHeL9T9qBfGvbXm1W1lceGFFwIl\nlhPjU2armcG5ySabAOV+4RpRFlqNiy++eNt6kZZNIpFIJGpHx5bN7Nmzh1XHR+ZqfYsMQfhU1jer\nv1LmIfvacMMNgcLyzznnHKDkkstMfvvb3wKFlem7NavJ930qx06mjX3FOvXBDg0NMWvWrMquzrI1\nffJaJkLGIqN1TjIP/dobb7wxUNjbWWedBcB2220HlLx8Gann06pTFl4zZSZjif2meikLLRz1RPYU\n9UJGqm9dWUS9kIXL3s4++2yg1OHoY7/66qubfkdZmL2mLLTufB37TT399NMdywL+owPKwusY9SLK\nQobr9TPzSl+7FqwyVRYy27hGlMXvfvc7oFzvVVZZBRi+Rjyuao089dRTHWdgtSsL7xceF+tsvF8Y\nT6i6X6gXVbL4/e9/D5RYsTFAs9H8/XhfibJ48sknO5ZFXCMxbiWWXnppoNwvXDvKIna2Npannuol\n0Atw/vnnA7DFFlsA5X6hLByPeqEs1BeP01Iazf0iLZtEIpFI1I6OLJs5c+YwY8aMYQww9nHS7ydD\n0W+oL9x4gr5zLR79gfrgN9tsMwBWWGEFAP74xz8C5Snt+7K8Y489Fhi+V4f+xdjFtbH7bKcZWEND\nQzzzzDNzzxFl4dyNAziGl770pUBhrMYTZBbKwspeffDOWZnJ3rfccsum7yuLT37yk02/E/PjlYUs\nT3bSC1nE3Hz1QlkoI5mlLM3jtURk+erTRRddBAzXiz/84Q9AkZG+d2VxzDHHAMP31TFmFzvaOv6Z\nM2d2LIs5c+bw9NNPD2PDzk29UNd9bdah18cuCMrIMf/zn/8Eil5svvnmTXO2yl4ZqW9xjWg9qm/6\n3as6dHejF8oisuEoC+ekXlTJoup+0aksjB0rC/Ui9m6r0ovRrBHPETeS869rxJiK69p7WpSReqFF\nYixXWXivNYNTT4leIGNBVbIwZqkXyvuF6GSNpGWTSCQSidrRccxmwoQJwzqCxipp/YA+Nc368Okb\n/ZAy2D/96U9Ayfn2vDIZGYs55D6tjcnssssuQMlisno27ung7/u01p/aDaIs4k6YMg+zR/TJ6jOP\n/mnz4PUbG2ew15WykOXZI0nZKQszdYx7WXkc8+ZHkkWnO3WK2BstysLfrtILLSCPN66lRateeK38\nXAtHvZDRav2Z2ef3o49exH52c+bM6VoWsmFlEXeLVRZmWKkXVnCLqjVixXeUhXoRZWEm5q677gqU\n6nn1K8bRol7MmTOnqzUyYcKEYd2UlYm67HVQFuqFY4trxLlae6Zua1lX3S883iwz7xft6oWxn9Hc\nL6pk4ZxixxDjWd7LYm9F5+ocPc4YrjEe63CM5RiLUS922203oNyXlH2sy4v1hBMnTmx7jaRlk0gk\nEona0ZFlM2HCBCZPnjzX5xp3e/Rpp69V9iVTfP3rXw8UNu7TU/+kkCHrU5ddmV9/+OGHA8P3Bvn5\nz38OFB9/VXX/SDUwcW+VVrAiWFnEeFDsJKAsnMsee+wBlG7Pfu7Y494d+pFlV2YhHXHEEUBhzDLq\nSy+9tOl8sbo/7m7YWP/RqSwmTJjA1KlT545VyN7jb8ieol4oC/Ui1g55nY1/VemFsvDa/PSnPwVa\n60X0PXejF8rCsVbphWPwuruWZJiuEWVVJQvXiLJULw477DBg+D4pP/vZz4DCgKu6PvRijXi/iNZ/\nzMiqkoVW2J///GegyMI5e73Ued83vmF22qGHHgoUfYyyMD7qOLQexuJ+oSwaPQtQrCzXqfVVZqVq\njWnxxl1OY7fmv/zlL0C5XzgOZXfZZZcBRS+UpWvaazLSvlztyiItm0QikUjUjo526hwcHByaMmXK\n3Kedvrq4K6FP61j9aubVvvvuC8CPfvQjoFgy5vrvvffeQGGssrqDDz4YKH5rc8xPP/10oDAjn7Qy\nYP3WPq1lC437bXe7I2NVBbBzVxbKxjx4ZWH35p/85CdAYV3GbOxca+xFC+eQQw4BSj8o63NOPPFE\nYHgcRBnq29X6jLKYNWsWM2bM6EgW6oWyUC9kQc49+pn10Zsx43X/8Y9/DLSvF+9+97uBEsNTFqee\neipQGHGUhbKLstAymj17dse7llatEfVCH3pcIzFesc8++wDFQlUvjENFWchkXSNm6Nlr74wzzgBK\nfMNr5ZownuHrGG/rZo0MDg4OTZ06dZheKAtZeez+rSyMV7z1rW8F4JJLLgEKK1cv3vKWtzTJwnV/\n0EEHNcnCLh1nnnkmUOJWjk8Zer9QL3oli5HWSNQLra/YXUNZeD9wj56oF8pCq86MvagX3pNPO+00\noKwRoQxdU/He6TV77rnn2l4jadkkEolEonZ03PV50qRJw3L0fUrrH5Sh+LSWGeh7NVNChiLjsLeV\nT2MZr3nxcb+T6K80E0fmYhW2cFw+nZ3H7Nmzu+p0PDg4ONf32mgZQMlXjxk0/qaMwRoCWbdZa7Jz\ns5NkvMrCuEaUtTI1E+eb3/wmULLchOxdZqXPeNasWV1VzQ8ODs49R9QLfeixClrZGZ9wJ8XY0Va9\nsB7D46wc14qLXRmUqXohu7dTgWhkrNAsi270opM14nVRFsatXCPOQQvFmjXXiIxXBqzlou4rC6+z\nsrAThdX50TvRqzUyceLElrJwjMrC+8Vf//pXoOwuqbWoXthJQFnoLVAWrhGvt7/j71t3oyzs9iF6\nKQvHH9eIc1UWrkv1wxitMRctE+F9Qr0w/mR2o/cT14idKzy/llbV/SJ25o5r5Nlnn80OAolEIpHo\nH3TcQeDZZ5+dm8EQ98uWQejva9zXHsrT3KellosxGJ+Q9v2SUcj+ZRbGLYxz6GuVJbhHjGzObCTP\nF6u755tvvo7rKaxHMa6gLHwts2zsIAzDuz87RmVh/rtjs5urY5eBxD049Gdbgex87A/lazP2lPVI\nsuimN9rs2bPnZlw5Nv3Jzt1sH9maeqEsHINWnHEEZeSeLc6lSi+Mc9iZV9lFvdDv7flGkkWnPbDi\nGlEW6oVrRJ3Vyou1JI7BORqf0NJxjThmj4t7sMQ1UiULGbGfx/XQzRppdb/QqoqycI7GBWL3buuu\nhDqu3mr5xr15zLiKHUVcY8rCjKx4vxCjuV9UrRH1wvuFa8LPhWOOnQGUkdfVMVtfE2XhfUCr0Pls\ntdVWQJGFGZy+jvVFkydPTssmkUgkEv2Drro+61M3c0LG6mufyjIY/ZEf/ehHgZIpoU9Vf6M+eb8n\n9EPbJ8rYjX5D2YBWg3EO2ZqZP2ZUCFnG0NBQx3nz8J+nfdwT3rnKyvQTxxoR+3XZ7cBMOjPslIXn\nca4er79aX6y/qyy8RspYWTjOuHti7P/UKWbPnj1XFsrVMSl/ZeFvqTcf//jHgeF6EfdR9zxaMuqF\n+9rE+p2oF8pKtlalF419wbrVC+WvLJyrv6m1F9fQ0Ucf3TQ3M6aMW2m5xp521l3YMyvWdUW9cI2o\nZ7H2xfM2rsXRyiLO1d+MGXrqzUc+8pGmucT7hXqhjGXzys6+YlEWsZ7G8ygT15xrVYxWL+Z17zRW\no0dEWWj1feITnwBKVmq8X6gXsXN2vF+4RtQH/3p/UsZRL5RF1IuhoaFhu41WIS2bRCKRSNSOjups\nrC2J+5ToL9Yn69PZzqLu+iaDkJnY/0dfqjEdWYMdSn36mqkTMyp8yvv7/o5ZTjIWffgyX9nhE088\nwXPPPcfQ0FDHdTbKwjHrL3YssjY7GdulWZYt+zKzSh+7vnvHaO2BrC/KQjbmXD1OpqIslI2+W2XR\naIWOVhbqhT52/cXKQr3YdNNNm8Yk+zKDRlmoF7Ivs42co3MzA0fZyeI8Tpl7vNZelV70UhbG2tRl\n14jX387EjlkLRVkYX3JuVWvEuZlZpQUl21cvZa6xm4d6EWNNvVgjVbIwduMaURaua606s9CqZOH3\nZOGuEeMhylxrUVmoBx6vnhj3qlMW3jtjZp5rxE7mjklr3wxeZRG7Zpi16nmNc8XdSL3uWliuRWNB\nykbLKXaL70QWadkkEolEonZ0FLMZHBxkgQUWmJv5oK/Op6EsSgZhTr9ZRTIJn772+dl+++2Bkldv\ndondfM0uck8OGfLxxx8PDO+h5FPcp7e+3Jgh5HimTJkyl9W2C3tgCb8vE4i1A8abHJtxAtm6sog9\nkLSEzCqRychcZIVf+tKXANh9992BUh2v7ONulDFDqDFTqF0fbKMsGjvlKgvZs9crWjZWasf9bOxM\nq14oC1mesjDLMOrFcccdBxS9kLEqi7gDY9QL/3ajF1VrRAapPsi2XSPqRcxqjGtEHTcbTWZs1wVl\n4e+4RtQLLRl/T72IspDpOp6pU6fOtVC7lYWyjLKIeuHY1AvHpCycu/cLM7BiZ2O9BZ7/hBNOaJKF\nemHtivcL2btr00ys0dwvqvRCT4T3TPWiao14vdSDuEbcx0YPi2vELDMtIGVhj8bYGVuZx/6X6kA3\nskjLJpFIJBK1o+M6m6effnpupoNPY5/Svu9T2L0SfFobu2msY4Dhfbusio455XH/7AMOOKDpe+7k\nKEOOvnjHGXt3Oe5OZTFjxoy535Wl+Rv6kWXJ7qGhLIxXKAtlqez0mVpzoiz0xcswLr744iZZyEzc\n7VTfsLJwfMok7q7ZjSyGhoaaZBE7BPi+slAvnLOyiJkusT+TMRnPq56oF9aiKAutO/UidtBupRfd\nZBypF37X6+1vKQstBzsFaKEqC69LXCNWksdaElm9+uMa2X///YFi0bRaI1Ev/NsLWTjHeL8wdmOn\nAI/zfhH1wjFrmbhG1C9lE+MV++23H1BkqCw8b4xjOs4oi27vF433Tu8X0SqIeuHctNKEnhN1WV2P\n9VauGWWsXhx44IHA8Htn3FXX87jmYk+3mDk8L6Rlk0gkEona0XE22sSJE+f6MmVd8elmxoNPVZ/K\n+lLtOCpD0bevT16GYT8ombJMxXiFsRz3INd/qT/S42XIsoAYt5CBddLFdWBgYGhwcHCuLPyrT9Un\nv7KQxTtHfa5m5JlPb0WvmTXKwqwkGY1zU7Y/+MEPAPj+978PwDbbbAPAySefDJQYkVZAlIXX0rz5\nTmXRiV5E5qrvXb1wzsa/ol5YWyA7dE7qhd3Ete7sPGBHbI9XLzzvSLLoVC+q1khjTReUWI2WqrEW\n14jXO64RffLqi2vEzEznFrMbXSPGO0466SSg6IXMV0ar/jqPbtfIxIkT58ogykIYm40sXlm4RtRZ\n66TUH6+jeuEa0dJRL5TFhRdeCJT7RStZ9Op+MS+9iL3rXCNmG9rROuqFY1QvfO1xcb8cZWGMzzWi\nXrhGtLCUSezG4bg7kUVaNolEIpGoHV3V2UTox9OH7jEyWfeAN1dc9m6NgYwh9lgzl9zz2kNN37s+\nW/PmffpaNevv+HSW8ciYzdOfPn26nVw7YrAj+StlKDJWZaFPfaeddgJKFoqsOua/+z3Zu6xfWZhB\now/YrJW4s6OV5coi9qGK1fSjqS2JkAVZC+RvKAv1wmxGWZnszuM71Qv919ZpeN4oi6gXWg9m7Eyf\nPr1nsohrxLl53dULr59jNotRRqws1AsZrF4E4xMyZ2M1rhGtA187Z60D9cJrMto10sn9wi7M8X6h\njiqLaDnrNajSC2WnNyHuDRX1ok5ZeL81NqIs4v3CmiNlYQafsvDeqSfF+4B6oMUb+8kpC2WjjL13\nKgv1zzVirdto1khaNolEIpGoHR33RhsaGhrWCVc2LpP1qS178imp/1FWry9WxiBzMfvIXHOfwj51\nfdrKAmX1sobYq02mEvdAN+7RyT7ajZgzZ86wXmL+Ztz3wQpuLYtYMW5VvL53ZeHcZfu+to+Y/mVl\nLauPsjD7yPGaXeJ49W9PmDChq/5ojXrhbzfu5tf4m8pCZmm8Qr3QipNNKQuvs6zPzDstWfVCiyZ2\nxFUWsQ9c3A/euEe3soDhXZPjGlEv1GmZpb53maxV837fPnBe51ibomyVhcxV2Tkf9SbGDFwj/l6j\nXnSzRnp5v1AW3i9k91pvvq6ShXqh7MZTFlVrRJlEWRifirLwfuGaMLssykJrLt4vzMyLstACcjy9\nWCNp2SQSiUSidnQUsxkcHBwaqSI4MkX9hj519dHrAzULxO/HPkH6o92jRTYnm/DpLXOxbkM/ogw2\n7r3g01mmEzuXzpkzp6M9xeeff/5hspAdyWyVhQxGWTjHHXfcESiMQn+0/mv90dbT2D9MJhT7fP3y\nl79s+j2tN1mavl1lodXXGH965plnRiULWXvUC2M3MtMoC/XC3H6tMbOVPM5MGvuHCfVCBmutQmRj\nykJ98vVIsuhGL0ZaI43ZO1D0QustysLsoLhGrCHxODOstHCUWYxbuUYa4w4jyUK90AJvjLl0mqXY\nShbqsDEWZRGvt3oRe5QZj4iykOXLzrVwZfNXXXVVW7JQj3t1v2iUhToes1ddI8YR471TvVAWwuvv\nulcW3jsduxZu1Au/5xqJ9YLeS9WLbtZIWjaJRCKRqB0ddxCYMWPGsD0ZfFrL2vQ/mzcv65bZ+NS1\ng6m+WaGfMe4vEWM2+jNlAfqnZSyxElw24FNZhjR79uyOfbDKItbXRFkYl5C9mfEig9R6M3tEn71M\nwopfYzvKQqtOK84sEdmhMtfai+OKuyb6t1tZzJw5c9geLv6mrE1ZyOodo7JQL6yXiBXkZuB5nZV5\n9M2rF1rW6pGyiN0Sol74d9asWaPWC60qf1NZuEbsjqFeyK6jLKw9cTzKwtiOv+Maka0rc2VhZlWV\nLBp7XjXKotOdKRtl0en9Ql2WXVtPpyysFVEWrhFloexdM7FWxDWiXsT7hVZkr/Xi6aefrtQL5Vu1\nRrSEoiyMd/p9Y7pxDygtmVhDpF5U3TujXozmfpGWTSKRSCRqR0eWzYQJE5g8efKwvjjGBSJjMa/d\np6VPSZmLPlRzx316xp07rRnRErHPmOeLPlXZgcfHHkdaB512bm3EwMBA017ksjbn4NNemVglL6MU\nVbKQgWj9+b5zdW76XGPPLRlUlEXciTHKYmBggE7ieP52oyxijET4m8oi6oUsTln42vO4r4nvx7lF\nWcQ4WNQjZaFeOJ5GWXQK14iWacx8FMrCOJO/rexl3cpCy8fzGK+KtSFaJPYZi2vEucvy61wjURZV\n9wt/07o5ZSFk6Vptvtby8H7hGjGuEO8XXs+oF8oiji/KQuuiW72YMmXKsC4VjRmxMHyNaIU5FnVf\nS0VZeP2M3XicsvB+YLxKxPtF1AvH69rWEmrsAN7u/SItm0QikUjUjq7qbHwK+3STPcUak8bd3ABu\nvfVWoGRYyVhlZz69ZYP6H2OHVBmNzLRxbI2/K0uQHcj+PI/jnDBhQsdsXujfjWw4ykLmIJNxDspC\nC8esM7/n2M0uMj4lk4ldWf392DXY+Xk+WX5ktN2wNqEs4r4nMsMqvfB4r7Oy0a8cLSbra8zQqdKL\nKlmoFzJo2V/s/jw4ONiVXgwNDQ2ThWvEOUSGG9eI3RL8vj3vHI8WsmtEPVIWrq24Rpx71AsZq9Zi\nlEW3a6QTWcS9dKIsvL7eL6oDpZKVAAAgAElEQVRkoR4591ayaMwygyKLqBeNXZ97JQtfx/2mol54\n37BnmvGpeO/UsjXrTFn4e56nShYxa1LZGkuM907H3w7SskkkEolE7RhVbzSfwjIVs05kCjIEj5Nh\nyHR9mvt0NmMrsvW454pMx6e7v+PTNu6TLXwqO06PX2SRRZg2bRqzZs3qujeaT36f9P6NsvA4WVqU\nhWzefHvHXCULGW3MMnJuyl7Lyuvt+aIsFl54YR5//HFmz57ddQ+sWBneSi9kW469U1k4J1mc8Q6t\nuKgXVR0EvGaN/unHH3+8Y71olIXXW/m7Vjwm6q5MVlnI/o1HuEaiFRez3ey1ZUZWlSziGomy8Bot\nuuiiPProo6OSRdX9opUsXCP+bSWLuEaUhXGOqH9eo1ay8LjFFlts1LKIdW/+hsfE61V1v/DeaSZf\ntOLiGon93lqtERHvncqukzWSlk0ikUgkakfHHQTmn3/+YU/6uF913N/ep7U+chmLiLn8ka35NI3W\nQWQHPm0jQ5UdxrhJI+vspjp6ypQpc38r9hqLsvA3I3OpkkXsSeR1UhbK0uNit4TIqGU4js/3Y1W9\nsui0Onrq1KlzxxbZUfRDV+lFzNiKGTH+jXutKEvnEGWhHkQrrl1ZdKoX888//zBZONeoF5G9N3bT\nhWIdVumFayTKIh7nGoksPvYLjLGCsZBF1AvHEjuCuAZ6db/wddSLumTRuEa0FKpiNVVrxPdjfNo1\nEbMH1QtlWXW/iB6QKAvH7RptPL5dWaRlk0gkEona0ZFlMzAw8DBwT33DGVcsPzQ0tGS7B6csClIW\nBSmLgpRFQcqiw4dNIpFIJBLdIN1oiUQikagd+bBJJBKJRO3Ih00ikUgkakc+bBKJRCJRO/Jhk0gk\nEonakQ+bRCKRSNSOfNgkEolEonbkwyaRSCQStSMfNolEIpGoHR1tnjYwMPC/ut3A0NBQ2431UhYF\nKYuClEVByqIgZZGWTSKR6DMMDAyMasfYds/b7e/UMbb/C+h4W+hEIpHoBN6cW/VhrDqu1fc7/bzV\n61bjS3SHtGwSiUQiUTvSskn0HWSQ/o2bqLlJVtx22g2fqhhrdjgfH7Qr91aWiZueibihXNQLNyZz\nQ7H4uX/deKyVhdOP+uOY3R7eubqN9BJLLAHAa17zGgCuuOKKpuNE3O65jrmmZZNIJBKJ2pGWTZ9B\n9iYL+78A56wF4za/L3vZywD4+9//DhQW98IXvhCAadOmNX3fLbo9Tksn+to9XkabGF9UxVC8npF1\nL7300gA89NBDTZ9XbSPu+dzi2Oser79bIs+cObPp/X6waNRZLZWHH34YKDJ6/PHHm4537j/+8Y8B\n2HvvvQE444wzAPjHP/4BwMc//vGm83vfiX97MoeenSmRSCQSiQp0ui30qB7xMowll/zPDqKPPPJI\n0/sykylTpgDlqb3TTjsB8IMf/AAo/sgFFlig6XiZjuj0qTyWefOtMm9awbk//fTTTe97vtGy9zpl\nEX3va621FgCLLbYYAH/605+AwuL0vWvR+HfhhRcG4G9/+xsAjz32GAC77LILAFdddRUAN910E1D0\nQZloQYl5+OqznuK/qEMWMSajhbHMMssAJTYjG/f9yMZXXnlloFg+t9xyCwD33POf3Zi32247AP75\nz38CRS+0gD2fVkOM6UT9qFMvYlxpgw02AODPf/4zUKy5F73oRUDxAhxwwAEAvO51rwPKnNZZZx0A\nTj31VKCsqVe96lXOBYBPfvKTAJx99tlAkWErZJ1NIpFIJPoCY2rZ+JSVqSy66KJAYSarrbYaUJ6m\nq6++OgAXXnghABdccAEAe+yxBwDvfe97AfjLX/7S9DdaNB1kw4wZg63KrHGsyma99dYD4Be/+AUA\nr3zlK4HC7n//+98DJX7h95588klgeNbJeMpCS9W/Qkt31VVXBcrcPM7PtXS22GILANZYYw2gMNEH\nH3wQKHOWnf3hD38A4IEHHgCKRVNl9Y0lg32+oVNZDAwMtMwy0zPhGvC6LLTQQkC53nfffTcAm2yy\nSdNxWiZvf/vbgWL5/PGPfwRKzE89cc2oJ/fdd1/T547X83s/8XdEHXoR7wt6e7Rg9GRMnz4dKDJz\nLi9/+csB+O53vwvAi1/8YgB++tOfAsXi8R6qZfOVr3wFKGvuqaeeGnE8zz777IjjTssmkUgkEn2B\nMclGk5H6lHzLW94CFOa52WabAXDDDTcAsOaaawLlKerTXAbyjW98Ayg++Q033BCA22+/ven4mGc/\nnogZNrK2jTfeuOn9/fbbDyhxize84Q0AfPOb3wQKk5G1iSOOOKLp9Qte8AKgsLjISMYzw0a2tumm\nmwLwxBNPAEUvjOW9+93vBuDee+8FCvNcd911gSIL/ddadcZyTjnlFKCwu5i9Jnvrh2yjTrHUUksB\n8OijjwKFzbtG+mVOI40jxmi8fq6BV7/61UDRC2N5r3jFK4BiwWixet2XXXZZoFjGWr6uBa0D4x7R\n+ldP1Ldo2bTbaWA08LeUhVlld911FzC8tsi/eoE+8IEPAPCd73wHKDEcLRez0m6++WYAdt11V2B4\n/NJ7trFhrcrRIC2bRCKRSNSOWmM2ZoX4NJZ1+dSUafq5jERGs/baawPlaSyT0fK54447mj63SlbE\nyvE2KoR75oONWWXOUb+vMjjhhBOAkmnzxje+sWmMsnRlIguU7fm+fm9lIvvzc+MZMqFWWWq9lIUM\n1jHKILVUzBLafffdgZJV+NKXvhQojNZsRNlfzC7yOOsk/F3Zm5aMPnxlIcYj62ge52kaS7SIzaS6\n8847AXjHO94BwG233QYU61EZ+DfGHTrFaGQRM6xcE7JnsxKFY15llVUAWH755QHYcsstgWLJGIvz\nvFoyWvOeP8ZyDzroIKBYOGatyfI9n2soWjp1xjVjVwOhzGJmpV6B+++/HyiWkFabsvL633rrrQC8\n5z3vAYqXSIvHmJD3qT333BOAk08+uek8ImM2iUQikegL1GLZRAYTfbM+lX1K+1dLx0pfn87W1Vx7\n7bUAXH311UCpjpWhyohltp32xKrDsomxmpVWWgkozOF73/seUFi//udLLrkEKD75d77znUDxnWrd\neV4z+LQGrBT+2te+Bgxnf7GPWEQvZBGvv3P0fZnncsstB5RYzAc/+EGgWDJaxLI0Yzrbb789UHz8\nMmNjNTJV567eKPvIHueRnVa7ZdOqc4TW2Yc//GGgrAkztWTvO+64I1BkZHzil7/8JVDqNYxrdtqx\noheWjXU0WufGVtVFrTezU9V1rbfLL78cKDJ4yUteAhRW7/GuJV9fdNFFQFlD6oF6poWsZaN1qGUT\nq+rrWCPCteIcq75n1pleIOPgm2++OQCHHXYYUPTDWLCyNvbnHJ279+ToJRiN9Z+WTSKRSCRqRy3Z\naNGi8K9PV32kPiV9evv0tGOAcQxzx2WqxjW0fK677jqgMCaZkk/r6JsfSzh3x+Ycjj76aKD0NNpq\nq62AUgUvE5Vt/e53vwPgbW97G1BkaVzMWhR9+bI5rUnHMZY916LFENn0IossAsC73vUuoMx93333\nBeC1r30tUGqMtHi9rlpx3/rWt4BS/WxHAf3N1ibJ1n70ox8Bw2UyFtlGVagag3/VAz+Xze+zzz5A\nqZswUzOumeOPPx4oWWvGesZDH1wLrnuvp1a6Om1NiLr8m9/8BigdIo477jigxCm11rVIjF8deOCB\nQLFkYg+1bbbZBoBzzz0XKGtGfR0LvYhWdbwnapH+9re/BYo3wPtAtEy23XZboMkKA4Zn/nlePSnG\nzf/1r381nV8vRDxfJ0jLJpFIJBK1o9Y6G7NHtFB8Wvt0jH5KexuZD+/TW/Z/6KGHAqW/j0/jyGhk\nRsY7xFh0VI7ZI742q0zLREtElqcf2ayQyy67DIAFF1wQKIzELBJri8y88fvW4xj/kuGYRRJ9xHV2\nPo592mIcS7YkG9eHr4ysDVCPrH9wbsbw3vzmNwMlJqMV4N9o2Sp7Y3xaPDLfsYSZVVpjsmnrr/S9\nR33wup9++ukA/OxnPwPg05/+NFBYvbp+zDHHNH1/rNC4HqpiqMrfWI0WabxPGI9y3TsX9cLYnGvN\n7ER1X6tf685xaCGrf95vHI/nrcOyaXVOP9ez4XVXh42paIFo5ZmZqyUk/L73BTsLfPGLXwTg8MMP\nB4rFo9eoF3tCpWWTSCQSidpRa51NtCSqOhrrP9SHb7+eH/7wh02fmzVyyCGHAMWvWGWxxN9rg0XU\n1tHWuelTtdJXdiajleGaaefczaOXwbgPhd97//vfD5TMLDsKjJAP3/S3Cr3MtKnap8S5mHVk/Y0Z\nVGYTxSxDM/pWXHFFoFiHdr6V6cpQje35vhaVlrbXpMriHcs6G/VEa0yrz/iVWYcyT639k046CSi1\nRH/9618BOPLII4HSncO4WLfoRhatakXUAz0Tzs3OIu5Cqa573PXXXw8Ui0Xd13KJ3eRl6WZg6SUw\n3mG2o3VYWtDzWEM9XyMRsU5KK8yssthFwyzU973vfUDRcX9Ha00vknPzOK37GAMSo8leTcsmkUgk\nErWj1phN9NnH92UgMgh9tWaHyEgis7AaXoYcMy1kTOaqxz1fxhKOzblZC+Br/cQ33ngjUHzzMhY/\ntyPyXnvtBZSMO2Mu1iC86U1vAoos/FxZyN7GIuOqKmajNef1i9fZmhKtO2VgFqP1NMrE+IZ94LR4\nrGGSxcnqlb1sX1lVdbQdS8g8te7MpDP+FGVqfEu2HrtxnHfeeUCJf/YDtNocq3MxnuBc7CihRWrs\n7thjjwWKPjm3uK+Nlq56ZBabHhP1RitBC9nf0+KS7Y9FzEarTl1WN41DWUcTuz1r9ft5tJj0Gjhn\nOweoX2b8uUZi1pnXKGM2iUQikehrjIllU1U7oC/eKuiPfOQjwPDd42RCRx11FFAdo5EZywZ86suc\nx4O5OlZ9ovpcZS52qjabzPobWZ29iuzqGmtD9ENfeeWVTe/LdKJFE2udxgIxC83rITuTSRpbMRYn\nGxPW2dj3zWzDX//6101/rc/QwjEOJpuznkKWZ8ZOP1g2xmis/LZ7r6xfdq/stALPPPNMoMhY2Smr\nOrMOWyGyYXVUPfC169418pOf/AQoMRTXkllmdpbwOhvX0nLxc7/v9d5oo42Asga9/5x22mlNn19z\nzTXA2GQpOjfHJPRgeP/QKvceJ4yteLxrRX3RatMqVD/sNOFeYFtvvTVQ1qL9C3tRi5aWTSKRSCRq\nR62WjU/BqiwfLRGr5WXnPt1jFotMxae0T3PZu8zUHHT93OPJWJ2DufrGGWQOWjbOyQwqLRur57VE\n9MU7Ny0ea07izn5aCTIRs5XGEl7/FVZYASgdaLXazMBy7Fo66oc++bPOOguAc845Byhde9UX41la\nA1pzskAZqxZyqx07xxLWhtnh2No05yQ7l9WbhSaLr9qv6Atf+AIAl156KVCswX7Y78ZYqh1D9GBo\niaoXzs3aIeds9pndEz772c8CpYbEOSsDrUa7L/hXi+jrX/86UDoVuFbGch8b72XKwD15XCvGuYXW\nvNaZFrA67fo3BujnzsXuG2Yvej9xv6zRdAyISMsmkUgkErWj1jobGWXMJotMQT+j77s/jfELq2Jl\n+zIgM3eM/cgKjFcIz98qK63OegpZu4zD7BLZU6zsNUPGqniP9zx+zx5X1h5ZaRwRdwAcy/1svK7x\nOut/1udu3MrrZxaarH+99dYDCrvXl27tiXEM9UdLSCtQ61B/tllxsruqTth16oWWjKzd6/P5z38e\ngPe+971NYzJrSCZaBTsKqE+9Qi9k4Rz9qx543V3nrm8tXXVdz4Xf97p6vHU56pUyMBakrC+44IKm\n76snWgleA8fVzR4uot014j3THXrNTtWy9T4Qu3Bowfi5Gb5+38/NyDMG5Jqz36Sd1LWcfd97q96A\n7PqcSCQSib5ErZZNw/faei1jtY7GTAqZqFlDcX9un+bGO6r2XGiFOhms2SaxtkTInmRt9szSItHK\n8zhZ2+c+9zmgVJArS2UjG5P1x4risdi1VN+7mXBamLJ0r5tQBjGWE3tlmYllrzz1xFiNsQBlJsvT\n763vXxmNh2UTYcaUdVd2V5CBasVba2T1fLRclYk7wZptNFr0smre66DFq/zt6xV1VwvEuRhzkbV7\nvNdd69/uG1rC3i/c+dd6K+Oh3/72t4HC4rUeYo+9XupFrBHU02GvO/v/aWHEOhutMrt9+/k666wD\nFEtJvTDTTl3XC2DndO8TMW4lYhw+LZtEIpFI9AVqyUbzqSwTifU1VR0FYnaIe3GYcRErz2UqcefP\nbnchrBOxSj2yfMfo53Ya0A8dZSRLN5MvMtu4j7qsbCz3bPG31ANlYKacGXq77bYbUNi6mTBm6Fkf\nI4vXd681Z4af1dBaxjJg+0QZm9GCjjtEOs7omx9LGKMTZhla2e31tW+ca0Ar0LkcfPDBwPDdSPsh\nC805aNFqaRibU/f1bLjuY6zW42XhykQ9MT7h2vB6awVsuummQImPOg71zr9x/6067ifx3qg1bo/D\niy++GChdma0lc03ZOcAeiVpAWjJ2mlC31RvjZfvvvz8An/nMZ4AiU++pysrs2G6Qlk0ikUgkakct\nlo0dQ326xswnX+tj9+ls/YVM1q6vMhrPq6/Xug1rVWLHAi2s2D9oLBH3jYl7ZjjmmFkju3OHRS0Y\n8+CtHZDlx7nJSGIfqirWPpaMV1nYB8ouztbL6Hf2fbPNzDL66le/2nQe2VbcP11Z+XnMhlM/tIT6\nEV4XLRf1ZLvttgPKHLzOHr/nnnsCxZrrB4umCq5Pr58s2rVgjYlz9/qaVaa172stFGtLou5rQWv5\nqke+9vuuQS2ZOiyaGAsxPqmuet3dw8f7idfb18b6vv/97wOl9shYjWO3M0X8fT0s7pPl7/m+2Y2j\nQVo2iUQikagdtWSjabHEOIFxiuirPeWUU4Dir5Zp2r/HHRu1lGS8ZujIBmQsV1xxxYjjGo/9bGJ8\nSnYWxyT7ihlY9osyS+QTn/gEUGpOfB0zqbT+jHvF3xsLWTh3WZoV/M5VNma2kHohC7NzgP5l+zSZ\nRRRjMMZsZMpaNspc/7c1CMYCrGGoks1YZqNVIdasGZ9wLspAC9h4Rq/Z+GhkEWtJzDpcf/31gXLd\ntHi9Xxhj0cLxOjt3vQVmpXldtf48j54TWbpWobuYxn2OzMRS5jHLtZeZeXFPH2Ms3iPXXXddoOxW\n6hgcsx0nPI/r36xG16CysrO21qT32n333Rco3gNfn3/++UB1R4HMRkskEolEX6CnMZtY1SoTsILX\n3mcyVmsGZKjWXcjSzKxwfwotGbNRYu+kmDsexzUeqOp4K9v2tQzDuJQ1JPretWz0Q1tzZH8o2Z89\n17QOqzIBx9KHL9O0u4FsTUvHHRe1RGR3/pUBO2Z7XlmDYh8pe6UZx9Ii8nOZrJ/H7KLx1JNWiLE2\nWbd6c+GFFwKl7qofMjCr4HW0riVmH7r+XeeydbMOY1zKfm+XX345UDoFGHfwPqKVrx4YkzEuEWtK\nvK/EvaF6idjF/eSTTwZKNqFZp+7N4/rVCnRMzs09nL70pS8BxSJyV1IzQN/61rcCZc0pk9NPPx0o\n18J7cy/mnpZNIpFIJGpHLTGbuPOi/mW77RrT0Q9odbwsXabr01aWb5zC7CKZy+abb+74gO73Xqgz\nZhNZs+xeC0drT2vNfHer3LX6ZHFmjXiclo3xDJlJZGdek1bMtxeycAzKX0vGOoitttoKgA984ANA\nyUKLVdSyKmOAdue1+7PnVdbq0wEHHACUmIzZSlpKWj4y21ghLvohZtNwfqDI1CxE15xz1DqomlO3\n6EYWUfe1VNRNPR/GZLRM3LHXmJ6eEetn/L4xQGM4X/7yl4HSMdnP7fNlPMTYjPcbj9NadK8Xf2eE\nfbl61icuxlpdz1rvZtxpwVp3Y7cE67DiLsZajdZruaOvcS/XmHOP+uT9wrlXWTgZs0kkEolEX6AW\nyybmw/v0tE7CjqJaJO6TLsN1TFa/mlFhNokWjU9h97mRkXTrr66DwUZWJ/uWjZsVIqPZb7/9gJJx\nFyuKjdmYpWYmjb5a/c6yshEyaNqaXy9loYWjNSdT1FKVacpw49706pN6oLXn9dZS0j9t3Ouqq64C\nSqaOMvS8Vb3QIvrJshFausYj9LXvs88+QLHqeo1eZKMpf614YzNen5133hkoc1x77bWBskbi99QP\n4xHql9dVVm8djdmqrqXI5n0d10wdWYrKJFpV0SugN8j1bRxUq9zP/Z6Wjt6C2BsvWjRmerbRM7Hq\n/bRsEolEIjH+qLXrs09fs05knu5P8+EPfxgoPlyz02Tt5obbK83PG8YD9G73yTr2p4hZYP61s63d\nm82MsceR+fAyD9mbWWhmdrmnuFaDe3+MNhupDlkI9UEYX7CO6l3velfT57Iyj7NK2m69ZuDJ6mRt\nsjXZn+NQlu3u4NoPlo1jV0ZaZWYluVbMQoqV4r1CL+uvYpaXloyxNDuf20nAuixju64NM7XUfbNS\nje0ax/C83keMizgeLRv1ZQRLJr6uzRPi39jJvNOssHgfirHbquxU11LsTFGFtGwSiUQi0RcYk/1s\nRNyzQYtGVi7j8Dh9p77udWZNxFgw2MhQrdzVmtPXLsuSzZtVcu655wIlK834VczEGy3GopuCY467\nD8rSjb2oo/ro9Ue3Yl2t3m83W3E8LRtl5nV/97vf3fS+XXvVp9NOOw0oVfi9Rh0Wr2OP18MuCL5v\nL8S4F5SdQ6677jqgdBIw2yzqUey0Hmtd5hGjia9rs2xiT8V2d9itOp/fj9llcS2IOvYCS8smkUgk\nErVjTC2bfsdYWjZVu5XG/dmtv7FWxNd2U6irUrxOWTjXTv3CVedp1TFihPqIjn6nn2I2Ml4zN62z\n2muvvYBS8V0X6ozlOTctXWM1VZ0doh7FPl/GQWNsyOsf9a9Tz8lY6kW3+xFVWSxxr6/R7neUlk0i\nkUgk+gJp2TRgLC2bVtkhDWNq+ivq3oV0LGRRlQkzWgtntP7niH6wbPoFo+kgUHUd4vUyy0xLxDWi\n5RI7p2uhuIZiDUqMU1TtT9NKT+roIFA3em3BVCEtm0QikUj0BdKyacDzgamMFVIWBSmLgjosmxG+\nN+LxrWI3VVmGVT0TI9q1vJ5Pls1YIS2bRCKRSPQFOt3P5hHgnpZHPT+xfIfHpywKUhYFKYuCR4B7\nusj+G9X7nb7ucjypFwVtyaIjN1oikUgkEt0g3WiJRCKRqB35sEkkEolE7ciHTSKRSCRqRz5sEolE\nIlE78mGTSCQSidqRD5tEIpFI1I582CQSiUSiduTDJpFIJBK1Ix82iUQikagdHbWryWZyBSmLgpRF\nQZUs6mrt3up3ev27qRcFvZBFu1uFtGpO2u71bfV7rT6v+r12ZNFpb7TEKNHpXivtKlO3SpKoB16P\nuJd8vE5xL5YI93LxusXdJt3bJe57FPdF8jzqQTxP3AnU8TTuZjlWulOlq3Xv4TQWiHNYeumlAXjg\ngQeA1nszifj+AgssAMCMGTOavi/UE6/rfPPN1/Q6dsSeMmUKADNnzgRg8cUXB2DatGntTXQEpBst\nkUgkErUj97NpwHjs1FkXRmsup7ukoFNZNLLOqp1X4x4rI/wmUCySpZZaCiiM9GUvexkAV155JfAf\ny2Ok789jnE1/Pb7RkonHPffcc89LvajLIupGL6KFIbRM3F204Tf8ftPrEc4/z89bIVrijs/xaulU\njS/3s0kkEolEXyBjNmOMsfJ7RxYX2V38PGM6vcHAwAATJ04cZmkof+Urc5QxPvPMM02fa9FsscUW\nANx5550A/POf/2z63sILLwzAYostBsC9994LwAorrADAHXfc0fR7UQ+0lPx935fRNr4er1iJYzHO\nJFrp7KKLLgrAkUceCcBRRx0FwOWXXw7Atttu2/vBzgNDQ0PDYneO/d///nfTsVWW5zx2DR3V2Kru\nC47X8VXFkNpBWjaJRCKRqB0Zs2lANz7Y55sl0K7/+vnom68Lo9GLqVOnAvDss896rqa/MRtN5iib\nf/e73w3AOeec0/T65z//OQBf//rXAVhyySUBWHbZZQH46le/CsCOO+4IwAknnADAeeedB8ALXvAC\nAKZPnw6UrCPHEa2IwcFBZs+ePSpZtKt7xi8i228Xfl+Z3H333V2dpxV6cb/wOnvdYywnWjjKTsu3\nKosxQgtWPaz6vvro9Vd/52V5zZkzJ2M2iUQikegP9KVls8giiwCwww47AOWp/I1vfAOozvDxaR39\n5e1iNGx+vGoAquo2lIGfR7939NnLeMTzybKRZa255poA/PnPf+7p+TuRxeDg4NCUKVPmWgrqZJRv\nvG6xnuZFL3oRAA8//DAA888/PwAXXXQRACuuuCJQrvPyy/9nG3jnPnnyZACWWWYZoFz3T37ykwB8\n73vfA4q+aOH4N66lTrKORK/0wuvrnBzTbrvtBsCFF14IwGc/+1kA9tprLwBWWmmlpu8rA18vuOCC\nADz55JNdjasTWUyYMGFo0qRJc/UgrtP4WngdHPtyyy0HwD/+8Q9geGwt6lWM9ahH/k6sr9lggw0A\nuPrqq5vO531CNMYY07JJJBKJRN9gXCybqqe4T9df/epXQPEXvupVrwLKU9iag8cee6wXw5mLbnyw\nWl+XXHJJT8dSlWkjG9M3L6P961//CpQspbvuugsYzkxkVsrS4+P7zwfL5vrrrwdgrbXWAspcL7vs\nMgB23313oMQjZIEy5FgzUIVu9CJW5Pu6SudjXEPdt3J7k002AQpbP/XUUwHYY489gHLdVl55ZQAW\nWmghAHbdddem13/84x8BeNOb3gQUvbCCXdk4Dn31kyZNYtasWcyZM2fM9eLVr341AL/97W+BYsEc\nffTRQHX3BF/L5tWDCI937lbht0InejFp0qShJZZYgkcffbRpbFVZgq26KGy++eYAXHfddQBcccUV\nALzmNa9pmovXPcpCCw0A6eQAACAASURBVNkYoNffv+ussw4A1157LVDduaLh/bRsEolEIjH+6KuY\njf7If/3rX0BhGGbQvOMd7wDaj4tYZW2NQiuMJ5vXNxvrLn79618DZc4vfvGLgdJTyesnk3nkkUeA\nwnx++ctfAsV3HxlTVVZKP1o2L3/5ywFYf/31gRLDi3Bue+65JwDf//73geEZVu2iU1koUxhev9Cq\nNiRmJ5lZ5fXxOvt914i/qc6bffbCF74QKGtLZmtc481vfjMAr3/965vG6e+oh/7mWOhFVTzLWK73\nhxi7jTUgHrfddtsBcPPNNwPD42fx++3eE7uRhV4d0crSjdmJv/nNbwD4zne+A8DOO+8MwBe+8AUA\nbrvtNgAef/xxoNQYvf3tbwdK3dXqq68OwLe//W0A3vjGNwLlulujFK1G9cdro7WYlk0ikUgk+gJ9\n1UHA6mdxxhlnAMXP3Gn1arsWTS/RaVZazJ+XYWjF6YNt1RXY81hb8KUvfQmAr33ta03HxfP42tiA\nPuXxgOztkEMOAeC0004Dit9Yq67dWJ3V9d1aNN1i9uzZXWcnxoyrqi6+8X2Pl71vv/32AJx99tlA\n8cVvuummAHz5y18G4MYbb2z6Xc+rXnj+KVOmNFk5dSLK7E9/+hNQYnPxczOztOqXWGIJAJ544gkA\nHnroIWC4JRQxFjVzMRs0xj6qujkbszM2++CDDwKw7777AiX2tuqqqwLFAvKeqjVn/MvrfdBBBzWN\nx3utMrTLs5+rH9FCawdp2SQSiUSidvSVZSNiZ9t3vvOdQPHBmoVkn6h+quJv1zfv58ZeZAyyt403\n3hgoLF4fvDGcz3zmM0DxxceYjAzGuEarSuPR7FPRK5g5Y5xJ9qVMhO/LXCMblOWfeeaZ9Q12Hmgc\nT7v7F3mc1oOxO4/faqutgMJYtVRjfZXHv/a1rwXKWtFHrz5pLapPMmzPExn3WFuHjVCXZeHvfe97\ngaIXztn4wcEHHwwU6/7vf/87UPrHVSHu4VIHqvRho402AkrGndfB488//3yg3Cc+/OEPA+VeqUfC\n+hi/F+PfsW7n/vvvB4olc8EFFwClviuOM2ZVTpo0qe0uBmnZJBKJRKJ29KVl41P03HPPBWDrrbcG\nSqWv7K+fOxW3u+/ED3/4QwDWXnttoFggztHskmOOOQYoTNb8ePPsI7T6rChvJSvfn2+++bruwDBa\naIVZxWzc4YYbbgCGZ8bI0iNj7XX9VSew63OrDsUxpmNdjRbFu971LqBUx3sdrXuJFeLW32jh+r6y\nsfbIPmH+NWPvu9/9LgD33HMPMDwWOB46EeOMb33rW4HC8q2TiqzbNRFZfFUWmqjTohkcHOQFL3jB\nXN3UihJaNKussgpQ1r3xqPXWWw8oWWheZ9e5MvKvXoIf//jHQIl3fupTnwKKRWS9nrLUEraWUctI\nvRTq33/3OGpLBmnZJBKJRKJ29KVlY274scceCxTmYuaM/ZtaZZeMJWLVctXT3uPsfSX7kjnIIM2L\n15datc9EZMp+/4Mf/CAATz311DzHExl3K/ZXJ9ZYYw2gzFmWFWG9hdlmEdaWjAfsFVW1X1BVLzo/\nVy9korGexuPUGztXfO5znwNKHMusRDMyL730UqDEOazCNxaonsSuv6O1eEfTGV2WrnX2hz/8AShZ\nivG8vjaDS/zkJz8BSqwvxhjGIlbz3HPPMW3atLkWrNfTdeu+RV5X40yHHnooUCr+tWi87i95yUuA\ncn9wTahnXkezEY3FxN56jkPZ2kFAtOq51g76526dSCQSif+16EvL5v3vfz9Q2NZHP/pRoFg0Yrx2\nDhwJ7e4zYQ3JYYcdBsCJJ54IlGwhmY+9zXwtrOy19iB2tJUxGefQ51oVs+mHeJds2g4BsrAqGJ9o\nrNRvxFjVg1RhaGhomB40+rgbIQPVGvM4YzVV9RiydOss/B2Zb9wJ1IwuYwCHH344UHz4dlnYbLPN\ngNJ7TQvsv3vZdCiJ0emXYzcb1ZiNa0e2rSVsPY3xJ2Xlnj9V++NEi2a0++nMC7G3mH+vuuoqoKwF\n62rUAy0Q52jsx+8rC++ZXrfTTz8dgJe+9KVAsZijRWM22yte8Qpg+P3M46v212kHadkkEolEonb0\nlWVjxoy7CIpTTjllPIbTFqLFEC2auN+EvnPjT2ajycJk5fY8+ta3vgWUugmzhWQuZpFceeWVQGGs\nVhgrS3sltTuPsYRzt67KTJy4i6WZM7/73e/meT4zccYLEyZMqLRIfN+5yFRXWGEFoGSJ2avMeiqv\nnzLR4rXDhIzUOJed06NeqT8eb82KWVDq0UgdBLqJaYwmZmNXize84Q1A2d/qbW97G1DmpozUHzOp\n9A7YEbldtBvf7Aaxu7rXU8+G+wy57mMmnTEZvT2+Vj+M4Rinip1FjOmpZ8rMmiQtW3eCFVqZ6rP6\nlNloiUQikegr9JVlo2/Wp65P0Xb3lxhrNLK2aMEImYm+eX2fkeHIOPQXW2Pi/jU/+tGPADj++OOB\n0n1VX6tZJPrkRZVFE1naeMZu/G2rmTfccEMAjjjiCKBkWrV7nvGsdvf3q3aHjPvbbLPNNkCxOIwv\naOXHHRad47rrrguU2I3X3XoN2b2xO7OQZNIy2uiLv+mmm0Yc58yZM8c8ZnPyyScDJd4kW7fmSMvH\nfmDGdIxj+dt2tj7rrLOazq91GK2Hqn2ORrtGBgYG5t4noifkK1/5ClD26Kkaq9fDTN39998fKJax\nMomxHONPWijqjX+1tI1/RcvGccZYTydIyyaRSCQStaOv9rOR3Uefe7QK6kKde3VoschMXvnKVwJw\nwAEHAIVpyjQ+9KEPAcUy+fSnPw3AmmuuCZTaA1mZ2UyjzaDRWqtTFlXV9Ga+xBqEdhGtzF5Za53K\nYsKECZU7LMbuymaPabGqJ3brFtaYHHfccUDplfazn/0MKL5+j4tdNhotFCg7vMpY7ZjsGnOcWs4D\nAwNt7zXfKIt2j4XhNUj33XcfUFi2c7ZDgHGnW2+9FYBtt90WGF7t7px8311KL7744qbjquKuVRiN\nXrifkNlmxqWMmWmpVq2BTjvgV2WhKmt/T5kKP/eebLabseDp06e3fb9IyyaRSCQStaMvLJtWYzDj\nwtoS+4KZcdPDcXS813zDdzv6LX2n++yzT9P73/zmN5vO557y+qtlpLI1e1uZ1dZt7VGcy3js1Km/\neL/99gOKX7qVhaOV4PFageNl2Yz0vnOQXbuTqmxdi8RsoNVWWw0osrDjsWzf+ISs3roYLWG//4tf\n/AIoFo2+f7uKGyezYtzKdOs41ItVVlmFu+++mxkzZtSmFzFO5GutLmXnHLwfmJHXCq4NMwCtPZGl\nm8FZ106djVmKQmvO9+19Zi80YzDGqXxfeF29n1StlTgn7x/+rtltxo5aWXfeh+677z4z0tKySSQS\nicT4Y1yz0ewHFJ+6MplPfOITQGGu9vPRvx39i2ONDq3Cpu/ISKzwrYpjyFSr+n3J7nrVTaGXWWmd\n1iV43e3bJfv6/Oc/P+L5fO2uk9dccw1QGHC7vvdeY2BgYFgvKWMgsSremMhOO+0EwK677gqU/Uqs\nm4hxKHdgdH8bWbqWipZL7CRh9ptxEGOFWlZxB0bHfdttt9XWscPraMacc1YPHJMyPeecc4DiFTjp\npJOA4vGoimf4fbtw2ItPr4B96eqqOZszZ86wfYgck7ERd+r1HmcmnRm66snuu+8OFCvPWiOvszL0\n92KmpvoTfz/2xvNz9dIebepZdhBIJBKJRF9hXGM25rPHjrhbbrklUDIzhE9R+zhZZd0rdOqDnThx\nYm3sOfrQzVqK+9noqx8tRqi7GfOYTRW0cMywkm2pP3a4bndX0k7RjV5UWapm9TgXY3QyVmMlZivq\nG9ci8v1ddtkFgFtuuQUoWYj2DTO2I1O2FkVYt2X9TtwDqLFzABTvQh16YQaeXTWcs9a8e7bE/Yu8\nXzhXx2ycI9YmxWsie4/WnHU9WspV6CbGG++3/nbsped11XvTIP8Rz6+stFhid3D7DVqP49y9vlo2\nsS4s/l60GjvJUkzLJpFIJBK1o1bLxqdglQ/dp7W+WhlN1dNU/6RsIHaBrvp9z2e2k7GBiG5YW6/9\nu55P5moevgxFFlclq9FicHCw7ewSUZdloyzMErK/k5aMmTNaPnV1QRhNPYW6Lxt3DegDlz1rldkZ\nwF5VO+64IwB33HEHUNi9FpI7vMpIXSO33347UDpL6CXwOK1CrQMztMzM0vKS8f43Q7FWvdD6M/vU\nsdoN/MADDwRKhwljusZw7J1mHNN6HNd93P8odv2IrL3KImr4vGNZeO9SZ+NeOl5X92zSUmkFrTh3\nM/avMUGttVa72EYLK85d/dCSHhoaymy0RCKRSPQPas1G86loRot9f8y00Y9oxkUVM/X92LOo1d4K\nVVluvcJoOtqOdK5GaNnINP7f//t/QPUuhb1CP+xvE2H3XrOItOr0Z1977bXjM7AKNNZTxJ02ZaDW\nv1jF7h4906ZNA0rsxZiOmVLGdswy01cf+8HJPLVwYo88P49rSEYs427sTtxtLMzMqNi3L8Lfijt0\n+n33gorxBfvBRSvATDvjnfb/Un9a3S9avd8pBgYG5l5/vTKxk7byj9en3TEa47VnmjKqsmi0tMxe\ndFx2D4/WnZ9rFeZOnYlEIpHoK4xpNprV8LI3GYpP8/HGaPzRrXbobBfGaPTpy0xkdWeeeaZjHdXv\ntEI/xGz0ydslwYwqGa8sqx9lEetitBQ23XRToNS1yCBl27Ei3L3orSDfaKONALj66quBsvOiXgLr\nd7SkPJ/xEPXT8clsYxfyWK0/c+ZMd+scd73oFrGGpKpGJNYiVWE0Md6YgWuMrFNddk6eZ7fddgOK\nxWwvs7ivkhmA/l5VHDzq8WiyFNOySSQSiUTtGBPLJvY6Gu1+I3VV+I6GtbUaU9XnkZnIUM2ckYnq\nc9X/7Hn8ngy2V7IZTwZrBpaV3eqNsjGOcdRRR8VxAOOvF2b0wfB+XzLF5ZZbDiiZVVazuwulvn0r\nwt3X6Pe//z1QMvHMMjLbTAtI1l7F3qOv3XHZieDOO+8EimUjQ65DL8y8Mq7UKy+BUE/UJ9eS+tSt\nvvSizqbh86a/VddNPfA4rfy9994bKF3h7bFmPZX1eB5nl2n3PTr77LOB4TLXgoldw+MOwGnZJBKJ\nRKIv0BddnztFzFXvFcaCzceeWWYTmZ0kw43M0x0czeTTxysz0bff7TgixkIWke1rDdh3SStOyLq8\n/rI8uy2cd955QMle6hW6sWyUa1XdQmSMZpvpM3eXShmqlsXf/vY3oMjG62hGXtUuk/MYL1AsqVip\n3lgv1E39VTcZm6Nd38bBZO/W21jDpJ7YmzFmhLWL0cRs1Itu5+h1N0Z3yimnNH2uRayemc36xS9+\nESiy0DI55phjADj88MObxmc3hqqO2GYpzpkzJy2bRCKRSIw/nheWjQxW1lZX99lesvkqyyHuN+FO\nnSeeeOKIx3l9TjjhBKBUzxurMR9fq6Cf9nDpFLK+I488EijX3ddaQO7t8u1vfxsorN4sIi2jXqET\nWUyYMGFo4sSJcxlrjCPJGKPFE3tSNfz2iK9jDZuxlVYV4hEx2yhamY293UbbWaKumJp7Amn1a9no\nJbCHolmNsvSf/vSnwPAOAnXtZzMwMFDZTSWu9ziGGPtzbfi+HSA8vxaqVp0elA022KDpc61IM4Kr\n9M/sNbMWo0WWMZtEIpFI9AWeF5bNWGE0O++1y4q0SPS5W/Vsz7MYp7Br73e/+912h9YTjIdlY1bS\nW97yFgCOO+44oLA1ZRe79srqZWu9RjeyiBZs3MckWjLtWutV+5N0ysodX6y/qYqj9cKyEXvssQdQ\n9kbpFWJGlxlTxsF67RHpxrKp8njE7uBV7zs3rXjrrKzbeuKJJwC45557OphJ0SvhWosxvKqsubRs\nEolEItEXSMumAXWw+chkIjNQ/sYlzBbRN6pPvqo2qdW+E2NVQ9DVj7SJFf+7Q2unGXe9QjcMdoRz\nAK276rZx/qa/snd97tFSqYr5tNqrfqSYQbv7ljSMNe8X/0X0hETLseG4qt9qem1fQOuqjKkY1+50\n3ZuN6O8bC65C4zjb7Qaelk0ikUgkakdaNg3oBWtrVb8SISPRN2pFsPtQRCbaKrutV37pZLAFvegg\n0CqrLL6OaLeqvkpPqph0jAV4/ljV30/7HNWNVtbm/PPPz8yZM3nuuec6tmziuassyaoxxOsVr3fU\nu8au3Y3ns0OJNUaxPsvvV9UDNfZUyzqbRCKRSPQNOrVsHgY6S3N4/mD5oaGhJds9OGVRkLIoSFkU\npCwKUhYdPmwSiUQikegG6UZLJBKJRO3Ih00ikUgkakc+bBKJRCJRO/Jhk0gkEonakQ+bRCKRSNSO\nfNgkEolEonbkwyaRSCQStSMfNolEIpGoHfmwSSQSiUTtmNj6kILna2O9dvF/oclgu0hZFIznFtmd\nbj1Qd0eQ1IuClEVBbjFQIwYGBuZ2UoX/dEeNu91VfW+kzr5V77dCu79bNxrHvvTSS7P00kt39N1u\n5l4XJkyYULnfSztwr/nBwcG259bqN1vpzX/3FJn7vr/fLfrtmvxvQKM8R3t9no/Ih00ikUgkakfu\nZ9OAOs3iqn1L+q0Raif7U4hOZdHpnj/jjW70otUcZbVe/7iTa9QLd1J035F2rQ7P446e06dPj+Md\n8fiIBuspXUf/xf9lWYywL0+60RKJRCIx/kjLpgGj2VO8jeP9DWDs2X38vXntBDjee81Xjc33466D\n7k5o7OrZZ5/t5XA6loVWQDtodwfOEX4HgEUXXRQoFo/nWWihhYCy0+a8LJZ5fd54XFo2zUhZFKRl\nk0gkEom+QFo2DRiNZdOKIbZi674fM1SWWmopAKZMmQLAv//9b6Cw9yeffLLpeFl+t7GgbhlsJ2y+\nClpfkydPBmCBBRYAYMEFFwRg3XXXBeDII48E4MEHH2z6/r777gsUdh//dju+0TDYdi3Ydi0MLaG3\nve1tALz5zW9uOv/FF18MwIUXXggUvfnnP/8JFP2IehtRFVtMNl+QsihIyyaRSCQSfYHnhWUT2ZfM\nd+bMmT39nfFgKjJV5yQ+/vGPA4WJbrjhhgC8+tWvBuDPf/4zUBjqpz/9aQAuu+wyYHg8o9Pst7GU\nRawT+tOf/gTAj3/8YwA+8IEPNB3nnJ944gkAfvWrXwHwyCOPAHDzzTcDcO655wLFsomZWP0oi4bz\njPj34IMPBmDzzTcH4GUvexkAyyyzDADf+973gHLdTz75ZAAeeughAKZNmwYUCzpaXH6vCsnmC54P\nsjCLUe/AM8880/S3V/fQtGwSiUQi0RcY/9LzeWCrrbYCYI899gBg//33B2DttdcGCoPtB3TbXuSF\nL3whUOogvv71rwOw1lprAYWByPZlIquvvjpQso1e97rXAfCvf/0LgAceeACAhx9+GIBZs2Z1Pqma\nUFUp/8pXvhIoYzc2I5yD7Pupp54CYP311wdgxowZQInt/PCHP2w6X7/WNo0ELQ+tube//e0AbLbZ\nZgBssskmANx7771AsVx++ctfAnD33XcDcM899wCwzTbbAPDrX/8aKLLTsnk+yCTCeJR6seaaawLw\nt7/9ren9/0tQx43lutZ8/w9/+AMAZ5xxBgB33nknAH/84x+Bsrb8XitLtxOkZZNIJBKJ2tGXlo2+\n9je+8Y0AzDfffE2fH3TQQQAcfvjhYzuweaDT+pmG7B6gsLRVV1216TjrJfTRG3/Q4rn//vsBeMMb\n3gAUdvezn/0MgJNOOgkoTKfdivU6UZUJtfXWWwMl004rTXa+/PLLA3D00UcDZY7W3bz2ta8F4OUv\nfzkAH/vYxwD4whe+AMBf//pXYHxYfKdyVh+0cJRFtIS1eD/0oQ8BxdIxa1F9/MUvfgEU2Y82a7Ef\nEC1crUAtmh122AGAK664YuwHVzNiLM975GOPPTbi+8pkueWWA8qa2WKLLYAS79Qi7rTuqx2kZZNI\nJBKJ2jGulo2s3fjEVVddBZS4hE/jaNnceOONYzXEjtFuRwCZhQz1rW99K1CyR/xcli/zOPvss5ve\n1xevzIxXmH1ihflHP/rRpu/1U38yGalzk5VZZ3P88ccDJd4ga48W0m9/+1sAjjrqKABe9KIXASV2\noy9fjCWrb/e3tGS0XFdYYQUAPvjBDwLl+srqr7zySgD+/ve/A6WTgNfXv8q4lQ/++RDXmjp1KlAd\nlxDqgTLqB10fLdZZZx0A3vOe9wBw0003AfD5z38eKHM0TmlGpxmb3//+94HiBfD+8MUvfhEoXiNl\nG+v4RoO0bBKJRCJRO/qizkYWLzORhd13331AefqKW265BSi++V5hNHnzsnCZZZVcZa4veclLgJJx\ntddeewHF0pFRnH766UDxuVuPo8ysv/Gv47j99tsB+PCHPwzASiutBMDll18OlPjIT3/6U6Cww4Zq\n+55XzcfuCMrI673tttsChc1fcMEFQLHqYpwrQkvmrrvuAoqMZH9mcHmN2mW63chCXXbO7frAHbNj\nPeCAA4ASvxTG4r761a8CxdfunDyP+uDva9mYuRfRyuLth555n/jEJwA44ogjgGLpRP2yJu2OO+4A\nhtdZjRZ1yiJeh1gns+KKKwJl7h6vt8jY7TnnnAOUuFbMgv3a174GwC677ALAqaeeChTLqV29zTqb\nRCKRSPQF+iIbbffddwdK9bMMRTZuDYHvr7baak2ve5kL3i2MI1RBRiED0fdupsy73vUuoLBu89+1\n4n7zm98AJX6ltSezkbkstthiAGy00UZAqUlafPHFAebuoKlFI3PqpT+76lzxOikTs8x+//vfA8Wi\ntUNAu33FfvCDHwDDLWVlJSscC9+91le33Zyd+2677QaUMatn6r6++djLzGy2dro5jzTukY4brziO\na0Y27phdI2Zwen3tmuD73j+UaT/HoyKcq7FcY67Ofc899wTK2tGK876hBeua2G+//YDSU2/jjTcG\nShajvfXqQFo2iUQikagdfWHZ2KFWyFCOPfZYoNrX3w8WTafYYIMNgNIdwdf6k41byFBkMjJbLRsZ\ni3UW+uyVlZl8//M//wOUyuEtt9wSgG9961tN59e338pCaweddjA2o86sMfu+dXp9td78Xa1ELWat\njH7OuPI6nHfeecDwHT1vvfVWoGQXqRd+T5kZv/K19VjRAmoVo1lllVUAuO2220Y5s87hGLVU3v/+\n9wPwuc99Dihzc03YSeLQQw8FSrxytF2/xwMxnhkzNI3pXnrppU2fa8G4jo3haCGbdRazE+0Kbu1a\nu+hkT6+0bBKJRCJRO/rCsomMY+GFFwbgne9854jHf+UrX6l9TL2CTMO/WjL2edOfbPaY9TKyhVgV\nbWxGRqqv9R//+AdQspbe8Y53AMV3/9KXvhQo3aGN9WjZ9MKiEe0ySONLZshpiXRq0cT4lUzWGoNj\njjkGGM7iYy1KL6umu40nOhdlE3tUmY3odZfp+r7X+VOf+hQAH/nIR4CSzaQV8Je//AUY3vU3Wj7j\nYdHEsdgvMGaTmZWmrKy/83s777wzACeccEL9g+0x4nXwPuF9RF01LqUeaMmYvaonQxmqJ37fnmjG\nbjpFJ/HPtGwSiUQiUTv6wrKJ0B+phSN8iuqD72fISBzzEkssARR/shaFlotM0y7OxmRktjIamYnZ\nKTHDRgtIGcpkrT1ZeeWVAbj++ut7M9EGtLtbaWRXjz76aNPY43mUgdaCLG7JJZcE4LDDDgOKLO2l\npmUjI/ZaxDhIHX2gOrVonLPX3TnGDLrtt98eKHVar3nNa4AyB7tDqx/f+MY3ALjkkkuAYhFZZ2Xl\n+Qg7cnY0/jqgVW4ML45JGegBMU4lrFXS8jFzr59QtWasIXTMrg3/qsNaPN4Tzex1vXvfEeqRnpDX\nv/71vZpKS6Rlk0gkEona0VeWjSzcbs6yQ5/i7jFvD6x+hkxFi0T2bcaU7D72rjLuED+XucZuvpGJ\nulPnZz/7WaCwQy0a8++1rCJGU0/RyqIRxgmUzSKLLAKUzsax/kY2pgy0Dv2eLN49Om644Qag1N3E\nDrnqU5UMeoF261fi8bFL86te9Sqg1FW4M6fxLa+vccwzzzyz6XsxO8l6DGVWVWc1UnxrrHuLxa4H\nQllZh2fGZYTjtRNyt6gze7HqnF5vEWN3jsksM9fCPvvsA5QYXYxPWpdjPU23dWDdyCItm0QikUjU\njr6ybOxlZMZU3HXO2pDnE2Qisb+XTOO6664DSn67x+ubjTspKhNjO74vU/3ABz4AlE4BnifGLaoY\nSrfsbV4WUXw/doiIu0a++MUvBmC77bYDis9dBhvrad73vvcBsNNOOwGlO4L9o7TmRhrzSOPrBTo9\np8fb08oeeVr79ndbb731gOJzN/Zy4oknAuW6G+tR1laOb7rppgB85jOfAYolHXv6RStmPDomx+4Y\n8X3nrH5EuH/RaGNyYxm/Uie1up1r3HXU+4SZnMb4XP96SvQimKXq97qtURyNLNKySSQSiUTt6CvL\nxqp5Wb/szH3XO+2gO5bQZ6rFIUMxY8bq+Pe+971AYaxmYl199dXA8GyTeXTfbfqdaDFpSdlPSgak\nNRFrEkaLeZ0n+v9jDYdV6ksttRRQ6iOsEZHdGX+ImXdWx7tnjzI1BhR3Q42yrXPXSq+zTLWVRXnN\nNdcAxTrTwjF+JZv3fFo4Wq7OxU4DBx54IFDmbvzC/nOxm3BcW421SGO97vRoOHZl554uWoGuuZjl\nqN50e13jtasTVXpR1Z1baPXZScAu8ur4RRddBJS9nMxG7FQmWkqj0YG0bBKJRCJRO/rKsrGGIHau\nNftIltaPiBaNMZRp06YBJbvICt/IQJ2rFomsvd0Mr2WWWQYo2Sn67q3fsaLc8YyFHzrWGgkZp9XN\nVs1rofi5tQOveMUrgMKqYjaZfZ1kX84xMlO/XxUPqwPR114FZaWP/ctf/jIAZ511FlD0K3YMUF+q\nYnjK7sEHHwTKaeg7CAAAIABJREFUviXuyGidRtQnUUdX8E6hTLzuMRs17uGjHpiB1+31HQuLRnRr\naXj9jFtpubqGtHxjFlunv9cLqzYtm0QikUjUjr7YqbPh/MDwGgIZhj5a+4j1GnXsvCcTdc9va0Fk\nJlYI27FWFhcZcdzF1Iws2bv7rOvbf/jhh4HCaHfYYQeg+OpbXfc6ZKH/X9a9xhprAKVfnDUk1oLI\n2uwkYQ2Ru1eatbbssssC8LGPfQwovn5laofktdZaCyjdE/SHj4UsWvm8lY36ooxiDyxjbfZA04K1\nel6rzv2S7JTsWvrgBz8IlB0aXWvtYjx36qyCFvAee+zR9L7XV1m2QqesfzxkoX54T9RiMbanlef6\n/9CHPgSUnXzf8IY39GIYw5A7dSYSiUSiL9BXMZtDDjkEGL7LoH7nuiyabtFYW1LFiuzfpVXm3GSs\n1157LVDYuww4+uD1wWq52PdJC0hLR6bqDqBmoWjh9MNeLrHrgXEEM2fcidUqan30xqWsTTLGo16Y\naWMMSNZnBqDZjnYYWG655Zq+1yuZjFRzVJXlFV97fc3Us7eV1pp7/2gpi6hfxuqMZ7kHjNahbL9T\ny6afoC5bOyT0Dpjd2C7qXhOj6c7hfSF6fbyO1iia9Wp2q5bwqaee2uWoe4e0bBKJRCJRO/oiZqMf\n0swJMytkplVVtL3GaHywVRaD9TdmoWlx+L6M1up4Yziy7xVWWAEozMXsI7v9Whnu+Y3JyIBl/7Gm\nZB7zYmhoqBZ/tOzMGItxJK06d1bUCrNe5qijjgJKjZCdAbSEPF72bycBe+y574mZf3bUtTOuVkDD\nfIAmC6xrWbhPiEwzwuuvNWecwdfqvtffuVmbZMxOC8YMLBmuslUGxnT8nXZ7uNkbrZ9iNlo0rinn\nYn8410ZdGEtZxB6K6sHee+8NlJieemGNmTKyE3pdyJhNIpFIJPoCfWHZ2APLfdf1uWvx6IOt26fa\nKVPppBOuloj1Eeeffz5QYi0yTWsF3HddZqJVp2zMPjLrxLiEtQiyvf/P3pnHXTfW+//9POZ5zpTM\nJRkiY5KhzKWQ+WigOqco6aSkpAzRSSEy5JAh0qlwSiRDIUpkyFyEREhI5EjH8/vj19t17+99r2dP\na917PZ3v+/V6Xvez9157rXVd61p7fT/Xd7jieje9+myG6Ytux1DV6YO5/vrrgWK9xZp41j6LkXhG\n4BiJp6pTBahYYqVslZDv60+ZTrWGxixYFanX1z7RUrVOoOemb8Zx5By+1/mMM84Axq9uaV/2WhNr\nOpUOWqNsvJ5GZumD8/o2nRvUT19MnTp12iyzzDJ07o5t9rfS8eLvgn+NPnNs2ydNkcomSZIkaQUj\njUbTitdai9VbrevV9HzjoIy1nOKaKXEdCa1sI2RUbdY2cm5ey1NrXsvE/eqzOeWUU4CyjokWqH6O\nyV5xcaK+iGrKv3Et+csuuwwoVprzziqV/fbbD4AzzzwTKDkkWvFmTTtO7AP/xooDscpD3Wv7TPS9\n6Bvxtdc/Wul33nknUPIivEeOOeaYju1URuaY6JdS8fTqq5OqfKBhIqmaRvXnDIjXNVaLHiXTpk3r\nGGfe/6rrfvYDpc366hz7Xn/Hy3XXXTfEWddLKpskSZKkcUbqs9lll12AYpmaAyBGVGjxNk2TWfP2\ns34GKxub5a4FaxVet4/rUuy2225A8XM0Veusib6ICsdzNrN/o402AkrdrpNPPhko1pnWW1Qi9k1c\nkyVWmx6UOvpCdVW16mTsE1W/ilffnRFW+q1UzN/4xjeAMi48TtV6SFXKy/djZew6IvPqxr657777\ngBJ552qUF154YZOHr6UvqsZorOsXoxatDr7XXnsBJdrQcXP11VcDsOeeewLNVjb/x37TZ5MkSZKM\nnpEqG60nM8W1VPTVHHfccUCp76QF2xRN5NlIVDjR0nSe2dwT5+JdbdBKA35v0JX2qizsSJMWbKzz\nZiRWjEaz9pn5V1U5IYNaa23oi17Vl23Xco1+qBgJqGXsPTPo+Iy0Qdk4bsTcNHOaVMAxL6+Nircb\nXkfH6Dvf+U4A9thjD6BUCHEtJ9fP8vfEfL24Lo59MOjvSCSVTZIkSdIKWpFnI87Rf+ADHwAmfw2N\nOi2VNtQgm4hoFVZVIW6DBdsWJkPl9TpOelVjg44/v1dl+bZpXGy88cZAySmbbJrMy5vOfjr+ur+V\nV14ZKFGMk/27k8omSZIkaQWtUjajZhCrrSkF0/R+pc1z822hDX1R93gYIs9j5H3RFtrQF3X5n4Yl\nlU2SJEnSClq1ns2MxvQyxYe1QPvdr5F8Mepk2P3+X6ZNWfOD+l6MSooKppuiMR/Mag8zzTRTbZFL\nSX2MWtH0QyqbJEmSpHH6VTaPA+0sVDY8S/e5/ePTpk0b1xcNZuhO9/NuiqbP/fbdF/wTjot/9M0M\n2Rde1359MhLr1/1D1cyQfdEQ2ReFnvqirwCBJEmSJBmEnEZLkiRJGicfNkmSJEnj5MMmSZIkaZx8\n2CRJkiSNkw+bJEmSpHHyYZMkSZI0Tj5skiRJksbJh02SJEnSOPmwSZIkSRqnr3I1WTK8kH1RyL4o\n1N0XwxZKrfp+r4uwRXJcFLIvCrnEQAuZOnXqS2tQNLF90i6mTJnS8a+Kqus822yzMdtssw18/Jln\nnpmZZ5553PHnm2++lyo7N023tsfPq7bv9/26zi+ph1w8bQxNWCrRsuzXUnUZ56rlm6uOMyxptRX6\n6YvZZ5992tJLL82vf/3rnrZ3CYC5554bgMcee2y623udXVLir3/964SfdxtvVe/Hxbg8v+eee45p\n06b1PS6GWaah7oXB6rpHXN4575FCKpskSZKkFaSyGcMglkpd1pcKJs6hzzLLLAD87W9/62t/WnEr\nrLACAL/5zW+me1yVU1pt4xmkL1QEUXlMsL3H6Hg95tgd71cpmn6JPpt4XMf12M8HUTZj9z2soph1\n1lmBzrEKsOaaawJwww03dGzf6z0Z72FV5jPPPDPh58P0xT8rqWySJEmSVpDLQg9JXVFCH/3oRwHY\nfvvtAXjjG98I9K9o4nm9/OUvB4qyiceNvqA2LzOrhbnpppsCcNlll/W0/ViLFCZnCez/+Z//6Wm7\nKl+K57zgggsCsO+++wLw2c9+tmO7qv10Y+GFFwbg0UcfnfD7dS4BXVd/b7XVVgBceeWVQDlH/6ri\n77nnno7v2VequXnnnReAJ598csLjqGhkFONnWNp4rqlskiRJksZJn80YhpmD7deS0OrWZ+LfhRZa\nCIBHHnmkY3/dotF6pVeLuA3z0Z6rfaVl+8ILLwBw5513AqUNWqpapuuuuy4A11133VDnMUxf6Geo\nUqgx3HnrrbcG4E1vehMA73//+4Hiq3n++eeBYqV/5CMfAeCOO+4A4Nprr+04rr6daJ2PaVvH+92i\n00YxLvRbLrPMMgAsvvjiQOmT+eefH4BFFlkEgOuvvx6AddZZB4DzzjsPKG3Yb7/9gKIS7dOo6u2L\nqmvYhntkguMAxWfovWJfqWjvvfdeoPdo126kzyZJkiRpBa1WNjvttBMA3/nOd4BiwTz11FNA/f6F\nfiyVmWaaadrss89eGRWkBfH4449Pdz9ajlpb73vf+wA48sgjATj//POBYrFoXWmNDTq3rqXz3HPP\nTfh5E1Zbv1nrCyywAFCstB//+McArLjiikDxc5100klAaUubc4623XZboPSB/getZ9usde6Y75Z0\nqAV7//33A7DDDjsA8OyzzwLwwAMPALyUyLnYYosBRRG5fy1d7614rSZT/Uu00pdcckkAXve61wGl\nzSoZ93/XXXcBcNtttwHw9NNPd+x3iSWWAIr6M3n297//PdA9ErSJe2T22WcHevf5eY72jePo5ptv\nBmC33XYDiur/wx/+0LH9ZN4jqWySJEmSxmmlsll00UUB2GuvvQA45JBDgKICtDScu62KKumXJudg\no/9ho402AuAd73gHUBSNbfPvF7/4RQBOO+00oFhnWjT+/dOf/mQbJjx+VBXRIoqMcj46+rMuvfRS\noFiyf/nLX4Di19KirWrLsPTbF+Yq/eM1UNRYrCyw//77A7DFFlsA8PrXvx4o11+r3r6I6sDred99\n9wHwspe9DChz8ueeey4AX/rSl4CiWLSgPU58v8qyHmZcOAbH+H962o+zBMcffzxQfDMf//jHAfjt\nb38LwJ///OeO49g3qjgj71Qwnoev9VuodCbKNRp73m3y2Tg+HGc77rgjABtvvDEA++yzD1DU3ihm\nhVLZJEmSJI3TKmXz3ve+F4BTTz0VKH6FY489tuNzn8paMHXRj6UyderUabPMMsu4+dxeKwost9xy\nwPjM/j333BOA22+/veNzLU6vl3P5Khr/1sUorTZV16677grA6aefDhRfnRaqSkcrvKkcoX76YtFF\nF5228847c9xxx3W8X1UpwGx1rWmjzz73uc8Bpc0HHHAAADfddBMATzzxBFCsbi1bc5AcHz/84Q+B\nMlfvPROVUTfqzJrv1Xfj/a86s02qNNtW5VOxrSqXqFRe+cpXAvC73/0OKFGM5uuoFh1fbVQ2tukN\nb3gDUPxN+m6WXXZZoOTtOVPi+KmLVDZJkiRJK2iVspngeECpeWQNJOduP/ShD9V6vDoq2naz2ow2\nuvrqqwFYeeWVgWKdrb322kBRNtFa19qzL8whqSsPR0Zhtdl3zrF7fddff32gKB3/nnLKKcD4XJK6\nGWZceL3EiDnfj1azzDXXXB3ba41ryVblw+jfUBH5vTHWeMfffvtsMqLRVGn6r8w5Murs4osvBuCP\nf/wjMD6HyL4w2syIPPtaa9/qDFYcePjhh4Hx6i+q0VHmHEVsq1GGqjPvke222w4oas3fl16j3Xol\nlU2SJEnSClqtbCRadUYhGY1WF8NUtHVeuJvFYLTI3Xff7X6AYp2rfOI8tNtplb31rW8FSt+ccMIJ\nQH3W/SitNjPFtVwdo/aJ1ruWqX6ttkSjhdcdn3dbhyb6IeP1jJFW0bJdaaWVgNIXfn+VVVYBiv+j\nX8t29tln5/nnn+fFF1+szWcj8TdIf8MHPvABoKh/I/m+9rWvAUWxuD+j1PTlOT6soWe02qtf/Wqg\n+DccZ1J1D7XRZ1OFvsDoq7NCxU9+8pNaj5fKJkmSJGkFra76bJ2wWD9Ky6QNaOV0sxS1PJ07jdad\ncfBV1rkRWkcffTRQ5mad2z/rrLOAkoPS5urNVdgntq0qysyIK621WOW3DVRFJVZVbIjfc1z5etVV\nVwXgxBNPBODss88G4JxzzgGK1a/6s2+s/+X+rDzRL3XO8b/iFa8ASlUDiT4XlYjvW8FcZWsbjdR8\n85vfDMC73/1uAC666CIA3v72twOllp6+GcdZvEajrBZeF/aJvw9xBmUUpLJJkiRJGqdWn83yyy8P\nlOzlYdGycf2JaO3VTZNzsK997WuBElkX5971+cS8B+de9UuYaxAr1ZpzYC7SoBbMPPPMw7PPPsv/\n/u//jqy6r3+NsLNPtNasG2bbV1999Y7t6qafcTHrrLNOW3jhhV+aK9eijJFMESOwbLsVq1W6//qv\n/wrALrvs0rG/eC/YZ7EStnP01srq10qfddZZeeGFF/r22YxV8L1Gbi611FJAyQ15y1veApSK1uZZ\nXXHFFUDx1Rx22GFA8Wval94rZ5xxBlBUoSpQhRPHXdV5zzzzzPz973+v9ffCnJ9YYaJfHA+OE2c8\n/C21Okvd/s302SRJkiStoFafTV2KRlQ04lxtm9AS0TKJaLEaQWfki9bYrbfeChSL10ic3XffHSi5\nJDH2P9Z30o9l5E5cj72KqLD++te/jszf4zlodcVaWvorrL5gNfA2zaW/8MILPPLIIy9VpP7yl78M\ndD9HrWmt/U022QQoStWckSrcv+PN11aWOPjgg3s6jypeeOGFgb47bdq0l66XeTLdaqPpU7FiuvUA\nH3zwQaDkjuib2XDDDYESXaZPyHtJf5P3nO+bi6RirlrPJq75UndOGwyuaPTJGJlnjtrJJ58MFKVj\n7cWmIjZ7IZVNkiRJ0jitjkbTstCycd6xTURFE5WCVtChhx4KFGvKtl1zzTVAyQlwTv2YY44BiiXi\nfrSytFg8nn6LbuoyRsX98pe/7Pi8Kb9HL0TLUitf1eaKi+YYXX755UDv9egmi2nTpr0UNbjeeusB\npZ+jZVlVxdlaV1rjVbi/uB/HhXk3W265JVAi9waoHNDX9mOxKrNUrWsUIzT1pTz00ENAue5WTFfB\n6JPRqrdtziJ4j6nyrAumovH70SfseVbVXmsDnrv5efqrbINqUn/XKEllkyRJkjROKysIaMla90uL\npekY8TqjS2IUklaUa3BYaVbr3Plpo45UKq4yaM6R61Nosc4zzzxA6RvfNxoqWrDOV/t+1fzzKLOj\ntSjtO+el9W+5ZstrXvMaoFjOsYZVtwiwXhmkL6rUVq+rlXr9XcnT62wklvk6Rx11FFBUv8rl+9//\nPlD8nl7nz3zmM0CppN5r38w000z87//+71BVNnqNRrOPbLP5NUZYfeQjHwHKWj/uxzaaT2N1aPsi\n5u3o94w10FSLsa5cpA1rPtkH/r787Gc/83hAiejTZzzK+oGpbJIkSZLGaaWy+fnPfw6UXINPf/rT\nABx++OGNHrfJtTq0RJxT3X777YHim4m5RM7FVqk5s6W/9a1vAcXidYU+LVz3Y00urb+4OmHMbB9l\n1ecx5wAUZWtEzYEHHgiUNloLq6m59TqVzZjt3PeEn6tkzTlZY401ALjggguAYqXH/av6ttlmG6BY\n91HRrrbaakCJ4Oo1wmoYZTNmH3G7jvd97T1h/ot+zf/4j/8Aisp/7LHHgKJgLrzwQgDuuOMOoMwa\nxL6KykhF5b1gn3gtJ8i/aU1tNO/vd73rXR1/jYbU3znKXLRUNkmSJEnjtErZuH6F2c5aGsbpx1pK\ndVOHpRJj8kXryL9up8JQgcTaVVXXx7458sgjgfErOOoTcv5Z6y9Wyq2Ku2+T1eb1d85+iy22AODD\nH/4wAL/61a+A5vJthrHmnUs310MrvZsK8/rqv9RK7zbn7viyj1wLyBVAVUxGeK6zzjpA7zlydfhs\nYtWD6DOJbYlKR4Wz5JJLAmVsx1UqxTEeZwk222wzoPSFuWla/91UQJvuEdu81VZbASUK8rTTTgPG\nrwhcN6lskiRJklbQqjwbs2i1+rUstM6aVjZ1UDX3XZU1rdUV3+9mpbs/1/a4+eabgeLHMAM9VuuN\nETZtrmjruZkvYc6AalDL9JZbbpn8k+tCVTVwLdCq6y5eJ6MR+z3ujTfeCMAHP/hBoOTrqJzNPTFK\nKVLXuJhoNVtfq/r0kUQ/V6y6bN6NbVC9V62oqb/LXDhzl4zg++lPf9rxPa9JVF5tvkfEe+K4444D\nigr0uuvvHGUbUtkkSZIkjdMqZXPppZd2vFbhuAqlqwzOiFRF5GjBxhUa4/x2VXa9uSZazEZuXXXV\nVUBZB2XNNdcExlcM8Diuemp+ThuI+RBGUOnHsH7cV77yFaC7WhgFcc0VrXLzocwJ6UavVRJiZJX+\nLtWDPj3XqLeKuL68iDXZdthhh5ciH/thomvhOdoXjl1nBYysitdTf5N+JlfgdL0az89xor/Ce8La\nal/96leBEtFn33he0Vfj8b2XzPdqA56zv43mJMU6g/6WZm20JEmS5J+aVimbz33ucwCcf/75wHiL\nos0YZTSd6K6O11rrzun7ebRcqzLQrQ9lVWjRSnTOVmtQRVM1/9wmRSO2XcvTtX1sw9133w2UStda\nnKOs7xYxg9s1eLzu+tZiZWs/N1ot+i+qsE+sF3bJJZcA49dDciVX37fuWMTxYQVmfQGD4L1R1QYV\njSr9vvvuA0rfec7mUznG9dXpy/P9M888Eyg+G48fq8bHunLdaJOiEc9d/5W4Zo/Rql7vWJtxMkll\nkyRJkjROq5SNFo1oeVTNJ7eJXudCtUSioulmXcVcA1WgFotzslZ1ftvb3gaUSrfSJn9Gr1ih2hwC\n1YBRilrdqr244uIo22zOmD4X/RG2QWvcSCkVkLkkZr9X5eVYN+6AAw4ASu092+z+9cnpg4njIlJn\nBFa3lS9dPVKlanVnfTP6H13t1ut71113AXD77bcDpZ6cbbbPrUjy3e9+Fyh5OTEy0+1npHskVnf2\nd8jKERNUBpm8kwukskmSJEkap1XK5nvf+x5QInRco8EM338GomWhEjGHIOYMaLnEiB3XS7F6rzlI\nF198MVDyKGYkKy2i9e+cveNgmWWWAUoGubkERh2ZOzKKtk+ZMoXZZpvtJeVqG6JKN2rIdWY+9rGP\nAUVxWAPNGngqVWufmSFunpV1vqJ1rjIyV8kaet36ZqJs/kErBntOVb40M/uNnLMSgErlk5/8JFCi\nzLTWr7jiCgBWWWUVoFQgsaKE1cAPO+wwYHy0a2TQOnZtQH/XQQcdBMCrXvUqoFx37xXvpSZWG+1G\nKpskSZKkcVqlbJxXdg7W6q5xLfF/BrSStDSMQrKtWlNacSog3//xj38MwAYbbADAPvvsA5Sos14j\nstpktUW/lX3h3L25KnHVUi3hHXbYAYCTTjoJGM3KndOmTesYpzHiyQrmZ5xxBjC+lpWVIKxwripQ\n+Xbz7UVl7Phae+21O97vRqzxN2hfTpkypXJFzlgZQCXidVexup0qzkg7qz57/b/+9a8DxapXCbtK\n5aBjPSqziaoiTBYxj0ofoH3xi1/8AigKWF+gSlq/eCqbJEmS5J+SVlV99qltPad9990XKCv2qXx6\nXe2wX+qs4tot7yaiNefcu3OvRpUYnaTqMwN9ww03BMp8td/TojWuPtKtD9tU0VbsA9cAMgteP4Tj\nxvVM6lI2w/RF9KEYPabvRgWh38GILP9qkXaLWowrr5566qlA8XeYLd8Nx2FV9Fudaz5VVUVQ5ccK\nAvF9qx88+eSTHftxO4lRiR63273ZTQm14R7xN9EcIvOsll56aaDMDp111llAqcZSd85QVn1OkiRJ\nWkGrlM2Y4wDF2tPainW9Is5fxtjyXmmDpWLbtXhjhrnWWKwfZb6NFmzVGiHdMOqoDX1Rhb4b82zM\nZalqq4rIumD90kRfRL+F19fr7muvs9nw+ifcLvpyVE5VirbqPKSqD5daaikeeeQR/va3vzU+LqLy\nGXQGw1kCo916rS/XK228R2yj6s4ITfNwqq6vvx+Op35JZZMkSZK0glYqm1HRpAUbV2ismg+uWtXQ\niCyzoaP195nPfAaAgw8+eLr765U2Wm2RuO5IU9Fnw/RFt/6PUV9VK732Ol76OM/pfm+i1TT/8a+x\ncVGl9nolroMV2zhs5eO4vxnhHpGo8uomlU2SJEnSClLZjKFJZTO9uXAoa21It6iguA6JVpvH83uD\nxtPPCFbbZOUINdEXVf6DZZddFig5ZbEat/6qXnPO4nGG7bPJHBdV/qRukZ72kXXgYs3FyIzQF4MS\n1eKgvtxupLJJkiRJWkEqmzHUYal0m3NvesW8bpar0U0qnxkpz2ZUDNMXMZowovI48MADATj00EPj\n/jyH6X6/m8Xaq8+n2+s682y6tanpChBVyqnXPL68RwqpbJIkSZJW0K+y+SPwQHOnM1KWnjZt2iK9\nbpx9Uci+KGRfFLIvCtkXfT5skiRJkmQQchotSZIkaZx82CRJkiSNkw+bJEmSpHHyYZMkSZI0Tj5s\nkiRJksbJh02SJEnSOPmwSZIkSRonHzZJkiRJ4+TDJkmSJGmcmfvZOIvJFbIvCtkXheyLQvZFIfsi\nlU2S/FMyZcqUjqrGM80000vVjAdh1llnHVclOUn6GRP5sEmSJEkap69ptKS9xBUce12TI2k3ce2X\neF2jZdnr9t0K8MbtqlaMTf5v008h51Q2SZIkSeOkspnBmHPOOQF47rnngGKBPv/888D/n1sHmH/+\n+QH4y1/+0rF90k6qVqeMlqOf97vCZq+Kpuq4STIsqWySJEmSxpmhlM0rX/lKAOadd16gzEPfdNNN\nIzunutlkk00AuO6664Biyb7wwgsdf+2Dv/71rwAcdNBBAHzpS1/q2G6BBRYAii8nLdZ2oeKIimaW\nWWYBynXU9xIjyny94IILAkUhPf744wDMNddcQLn+zz77bMdx/b7Hmd55zmhjp0ot2mbbEz9PmiGV\nTZIkSdI4fS0LParEJC2Uhx56CIBnnnkGgM033xyA++67r5bjjCJJK1pfvvbve9/7XgBOP/10ABZf\nfHGgWKwzz/z/xemVV14JwLXXXgvAEkssAcDOO+8MwN133w2UqLVuPpxh+qJf/8Cw6Kd697vfDcBZ\nZ50F1OenGqYvvD5///vf43YTfn+hhRYC4OmnnwaKFe51W2aZZYAy9rfZZhsAfvWrXwFlfOiz+973\nvgeUe+SnP/0pUJRO9P11s/KbuEfmnntuoPgd7Stf66dcYYUVALjrrrsm3I/jwMi5qnFY1/ickZI6\nHUfvfOc7Abj99tsBuP7664HJ6YtUNkmSJEnjzBDKxvnoP/zhD0CxFh999FGgWPHDUoelMqzVpKKZ\nY445ALjiiisAWHLJJQG4+uqrAdhiiy2AYs1p+Tr3roVqX73qVa8CYNtttwXghhtuAIoSiswIVptt\nv/HGGwFYZJFFAPj1r38NwMEHHwzAT37yE2Dwufkm+iJa4SpVx43X3+023nhjAD74wQ8CsPrqqwNF\nofzyl78EYPnll+/Y3z333APAoYceCsDDDz8MwAMPPNBxfFFVTKQGpk2b1ui4UOGss846ABxyyCEA\nrLXWWgCsvPLKADz44INAGduqM1+7n9lmmw0ovxMxF21Y2niP+PujGlx11VUB+O53vwuUvvrUpz4F\nFN/w7373O6DZeySVTZIkSdI4rY5G8yn9mte8BihWv1x44YWTfk7dGFTRvPa1rwXggAMOAGDppZcG\nilUnO+64IwB33nknAIsuuigAf/rTn4ASpfbII48AsPDCCwPFEv76178OzBiVBrTOHQfrrbceAHvs\nsQdQrLA80kUBAAAgAElEQVTlllsOKCrgDW94AwBnn302AHvvvTcA55133mScdgdV+S7Rr6DFqUWq\nVa6C3X///Tv2o0WqMv3Rj34EFJ+O42G11VYDYKWVVgLKuNKSrbru0ac0Gf43/ZP6mzbYYIOOz/Uz\n2CeLLbYYALfeeisAr3jFK4CiZFRC+q309baRQWdE/J7Ri15XlbHjyd9Or/eZZ54JwKmnngqU8bHp\nppsO1oAeSGWTJEmSNE6rfTZa3TfffDNQnr6PPfYYUKJT2hB1NChacfpQtOb1P5gXYRuNKtOqU91p\noWjJ6qPxe/vssw9QFM6TTz453fMaRV94vQ888ECgqDj9ECoXr79W/dZbbw0UpaM198QTTwAlQitG\nhPXKZPSFlqdttE3mT+l7+cUvfgHAHXfcARRrP+bV2FbHl1a/KqBbNFqsVAA05rOJEZhV0WT77rsv\nUKxyx4vnutVWWwFwyimnAMW/+da3vhUY/PpXMUqfjQr14osvBspvo32mglHlOQ7++Mc/AuX3QyVk\nlJqKuV+FlT6bJEmSpBW02mdjBJYKxqe1Fs2MvL6G1RD++7//GyjW91NPPQWUygAf+tCHgGLB+rlR\nZ1rvoi/Hvll77bWB6mzqNuF8sZEyWt9a++eccw5QfDQ/+9nPgBJtdtRRRwElP+Owww4D6rdo6yRa\n7/pq9DupWO6//36gWLJGk9lHVopwP/q3rI1nHzi37/iqsmAnM1fKMamfQTy2EZTdfLRGXKl8jOBT\n1R9zzDH1nPAI8Hroc1WJxM/NQXI7FbD3hH5Lx4Pjx0i9Jq93KpskSZKkcVqpbLTCtdq19uQ//uM/\ngGKdzYjssssuQJk7PeKII4Biafz5z38G4JZbbgGKYlHdaYHEv+JrfUGf+cxnAPjCF74AwNFHHw3A\nfvvtV1+jBsSoIXNB5LLLLgPKueqjsW3mVagC9Gu8/OUvB8rc/SjpFtUV26KV7zhwTv3nP/85UHLN\nvEdUKs7Zq/r1zbndN7/5zY7j6quJUUqTXf1hLMsuuyxQVLuq7ve//31P348zH/apinlGVDZeH6tj\n7Lbbbh2f21fOBnz5y18Gxvvc9OV53Y1SdUblqquuauT8x5LKJkmSJGmcViobLVOtf/Fpfdxxx036\nOQ2LFsa6664LwEc+8hGgZDu/+tWvBopf4vLLLwfKXKv0a3Fq+Zp3Y2SfdebawG9+8xtgfD6VbTc7\nvmptlx/+8Icd3zvjjDOAdinfqpUz4+cqXati7LrrrkDxW/p9r6tz9PpsPv3pTwOl74488kigRB9W\nRZ9V+T8nU+lEv6RKxDHbja985SvA+LacfPLJdZ3ipGNbfvvb3wLluovXT/VftR6Ss0R+3/Fn1Opk\n+HJT2SRJkiSN0yplo9XmXO173vMeoDzdjRnvtvZGG7Ga71JLLQWUuHetbz93TtbqvOYcDGp52Fdr\nrrkmAKussgoA66+/PtCOKLU476xfSavdvlGNVfn0tNbczyiJOSASFU20wq0kodJ1PxtuuCFQKkZ8\n8YtfBODtb387UPwdRnRZNfplL3tZx/7t66rKBp7vZFaWiGsuGRnlvWBbu7Hnnnt2vDZH7ZJLLqnl\nPEeB/a+/0t8DFYqzP3GceT3/67/+q2N7cfsYzdokqWySJEmSxmmVstFi1aLVd6P11evcbZvQ0jz2\n2GOBUu9JRaPlctJJJwElgkbLREUS/RYx6zpGqYnZ9PPMM0/Hfo2/t5ZWG/jGN74BwOte9zoA3vzm\nNwNlrRYj6rSEtYDF7GgrDIySfhWBvjt9K3GFTiOyzLPZcsstgeKbMVrNisiOAyumu399Nt1mByaz\nVp5tPv/884HSZiueR+abbz6gRGyK95RK98QTTwSq86xGGXnXK56jFUXifbvZZpsBJddso402AoqP\nR59MRN/eZJLKJkmSJGmcVikbI3C0wnyqa5lst912ozmxIXCO3VwQ49pdWfP4448H4KKLLgKKAtGy\nvOmmm4Dq1QZVTs5Xqw608oyfj1EoMXdJZpppppFVgDbb3eq/KtxPfvKTQGmrfqfo7/jEJz4xKec5\nCN2saK+XfsnvfOc7AFxwwQVAsVj93KoKzr3rn3AO3grH/rUauOovRse1ocrCxz/+caCMUaskiPfG\nW97yFqBEbDq2/Wtb9P2qgFWBRvyZs9RmvE5edyMvVS5GG+61115A8Xt5vVWw7kdf8Lnnntv4uUdS\n2SRJkiSN0ypl4xoczsn6NLZ+WFxVsM1oTV1zzTVAUTRihIxtk16jQ1QmRmq5H603cxb8POZTVB1n\nlOvaRD+C1Z5tw7e//W2g5FNYBdhz/sEPfjAp5zkIMeqrqpKA1rgKVTVnvS+te1dgtPqCytnPzRC3\nRpZWv+NG6z9GMUVf4GQqHlcRrYqMtM22xXtMf6htl89//vNA8ZNaScDv6R+dLKZOnTpw1KfXwVVo\nrQvoyq3mHsZq8bbVWQPHg5UpJpNUNkmSJEnjtErZmC0tPp3Nt5mRMApMSyP6F5x7HRTn+K0GbITW\nRz/6UQBOOOEEAN7xjncAZZ0b1zXxvGYEVGGbb745UKx/rUTnr7ut0dMGosIRX+tj0ZL1HvD66qvR\n36CC0bfn9beWnsdTAdl3vu/+q9azmUycuaiKlDMaNSqUNdZYY8LtVQGu7Kkisu077bQTUHJRmqaO\nPrU6hrM/+uCM5FPhWlXePtU3N+zvzjCkskmSJEkapxUrdWpxxLpNPpWNTmvan1DnynuuoeF8snPg\nttFokV7nxKvm+mNUmmjl+3ncbnq5B02tyDgose2eu9aaa8wbrVi3VV5HX3iu/o1tqbpOMc/CcWOk\nlmu9qFicHVABXX/99R3bGwVphYFYoSLmcY319Y16XNh3VpLQl2cf+bmr2e68885AqXwefTSqQvN1\n+vVP1dEX/eb6xMoOKl4rnH/sYx8DitKN+XW+v9Zaa/V66j2RK3UmSZIkraAVPhujRXxqixFWo4yQ\nGhTP3fUltBS1MKziay5JN+JKeuYKWEtLq83qr2Ya+73Pfe5zHedRRRuzqaOfw8ga68u5+mCbVyGN\nykGqrof5EqJSVbF4r7hmvDlqRiNaQds1flQ2fr/fmnttGBf+Dpg9r7/CmQ/P0cojt912G1D8m6pC\nMefEvhoF/fZr/C00uvBd73oXUHxw66yzDlBUnveOeX2jIJVNkiRJ0jitUDZf+9rXOl779DaPYkao\nYRRxPlkLNc7Zq0i0PCRmdkerfu+99wbgoIMOAkrUm74g5+y32moroCgr525npFyliOpNH59WuWvP\ntwX9G/4fioKJGftV26lIVSJup3Lxr5as1Z/17RjBp7K59NJLO7avqvYsTdxrtsXr57lIr/e599RX\nv/pVAD784Q8DpaKAVaKN2IoVj8W6Yc6seC/GKgtRDbYJ16mK3HfffRO+b/Xw008/valTqiSVTZIk\nSdI4rVA2onV17733AtWVjGcEtJKsaeQ8s5ara7aoVJxftrqv+THGz/v5v/3bvwElWkn/hXO3Wovf\n+ta3gJKD0isbbrjhSxErbSP6PcxJUdW1hbHj1f977l4nrW0ViuPCz72+KiGt6ljR2v3aB+uttx4A\nZ511FlCy8j1OVDBV69fEe27mmWceupqAbfBvVDKxgnk3rFx86623AqXitfeebdZftdJKK3V836z7\n7bffHoD999+/43ziec9IxJwi0Xc7ClLZJEmSJI0z0jwb50JvvPFGoGS363dwnnmyLItB4ua7zTPr\nU9HCjBExce48WpZa70ZcuTKfaJmuuOKKQJlv9v255poLGD8/3o025dmI9eXMotZyfdvb3gY0F402\nSF9UrYDq9fDc9UO5oqZRZb52XKj2Vb764Lzuhx12GFAUjnXk7CvHVfQVVdVsm04Nt577Yu655562\nyiqrvBQxJ7bxqaeeAkq02LDEyD77/p3vfCdQlIzXIFZItkK76tK+dHYiUuc9Urdf2nvFnCT367ip\nq88l82ySJEmSVjBSZWPETVyd0IxfM8LjinxN0aQ1b2SMPpf3v//9QIla83OtKddmueyyy4CS7Wz0\nyeGHHw7AEUccAZTVLOMaQIPSRmVjXad1110XKH2lIm6qQnEdfaHV7f2m4vW1bfBesJad4yNGp7mK\nqRnk8T7eY489gOpKATEqrgllM1njolfMfXNVSysnX3vttUBRk66X5HZVtLkvnBVynHgdfV21Cuqg\npLJJkiRJWsFIlI1Wk9VWrVSqZaH1Zc6Ac7tN04SlUjV3L0Ydrb322kCpbGwUmtV73Y+WrRnCWjB1\nV1log9Xm/LIq71Of+hRQrDSj5lQ6bVQ2VYrB6x4rHBtNtuyyywKw5ZZbAqVysUpGP4JKyJwTc02c\nDYjRa/F+j+Oym++gDeNiUL7//e8DpU9Vd/rPYn3BboyyL2LVcK+XCtiq4Cpofz/Mv3PGZNjjjXmd\nyiZJkiQZPSP12fi0NQrE6BDXp7BirbkkTTMjWG3m65hToKIxqqku636UfaF19r73vQ8oK3PGsar1\nH9eqryLmkvRKv30xtoJAD9sD41fSlB133BEoFSeMLlLxWgfMGnv6IeLa83GlVhVyrMHWjRnhHqli\nySWXBErdQCOyzHk75phj+trfZPZFrCiiCvP1LbfcAhSfzLnnngsUZWv9t4022ggoUat1RfqmskmS\nJElaQSvWs2kLk2mpRF9Ov8rEKCWts2Gz6MfmKLz44osjtWD1S8SsefvKPKxLLrkEKDkFTa2rPoq+\niHXgVCoLLrggUPyYjhf7Ros3VgwYNI9Di3qWWWbh+eef58UXX5xhlU3dtGFtH6+vikZ/1DXXXNPx\nvtGvVb7CYUllkyRJkrSCViibQefS66bOqKPJpu7j99MXU6dOnTbzzDPXbi3F3JRR9e1k9kW8jiqc\nqvVwxpzjQMfrdvwJjpPK5h+04R6pYrJ/j1LZJEmSJK2gFcqmLaTVVsi+KIyiL7pZplUVk5terTTH\nRSH7opDKJkmSJGkF/a5n8zjQW1LDjMfSfW6ffVHIvijU0hfdZhy6VQJoiBwXheyLQk990dc0WpIk\nSZIMQk6jJUmSJI2TD5skSZKkcfJhkyRJkjROPmySJEmSxsmHTZIkSdI4+bBJkiRJGicfNkmSJEnj\n5MMmSZIkaZx82CRJkiSN01e5GovJvfKVrwTg17/+9VAHn6zigb0ySGE9l9eta3nVtpBFBgvZF4Xs\ni0L2RaGXvpjUqs9te7jIrLPOygsvvDDUKoRW4XVtnqoVN7tt56qTf/jDHyb8/pxzzgmUFTqbWrfi\nn/lG6rfP+u2LKVOmDHw9qu6RQdd8sq0y7Dhpw7jod1XbppiMvug2VmektcByGi1JkiRpnFzPZgx1\nWiqjXrlzWBXZBgu2LQzSF/32f6/jxe1cS/65557r+NzjVjGoBaxay3FRaGNfdFM6o5wJSWWTJEmS\nNE6/69m0mlGribF4DsceeywA++6776Qef9FFFwXg0UcfBdrhJ/vpT38KwBvf+EZg9OfU5Hx3t7Z5\n7Krtqsayr/XZxf35Pf0Z0WczqA+nDfdUpOr6tel3YFh6Vci2uZuicX9uN8ssswDwwgsvTPi9+Dsy\nDKlskiRJksaZFJ+NT0/DhOeaay4AHnvsMaBEl/j09q/bLbLIIgA8/PDDQLHa5p9/fgCeeuqpju9F\nfJr7tyqKZZA52H7Xgu93br7bdvvssw9QLJCNNtoIgI9//OMA/OIXvwBg9tlnB2CDDTYA4Oqrrwbg\nf/7nf8Ydd0afm7fvjOx76KGHAPjNb34DlND9XqkjGq3b9YwWZJXFGfcTlUq09r3u/l1llVUAuO66\n6zq2c3+O2+koq9aMC/1WCyywAACHH344UNIQPvaxjwHwl7/8pZHjt6kvoq+uX1+hf+P3elVW6bNJ\nkiRJWkEjPhutq/nmmw+AU089FYB3v/vdAJx99tkA/PznPwfgkUceAeDb3/42UHJJjjrqKAA23XRT\noFh7s802GwC//OUvAbjmmmsA+OxnPwvAs88+C4y31rpZbYPQ71rwg86R26frrrsuAB/84AcBeN3r\nXgcU1Xj99dcD8PzzzwPFovVaqHTsQ63DJ598sq/zayNaYfbF6quvDsDcc88NwCc+8QkA1llnHaCM\nH9vs96La65exfdhtrC200EIAPP744x3bd1M2ttW2LbHEEgCsvPLKHa8vuOACoCgnVZ6fP/DAAx37\nc5bB8fKnP/2plyaPhAUXXBCAAw44AIC1114bKH1qXx188MFA+Z3pd4y3yQcUz8XfBa9fnEVyFsft\n/V2IiraqbfE309+TGAXZC6lskiRJksYZSNl0e9L7uVbZ5ptvDsATTzwBlKeiT+OllloKgJe97GUA\nnH/++QDcdNNNAGyyySZAUTzuX6v+hhtuAMpcbZX/JM5P1mGp1J2hrWUZo0V22mknoPgh7LO77roL\ngK222gqAJZdcsuP1VVddBcD3vvc9AL7+9a8DxSL+85//PK49g7ah7sxu2/6GN7wBgMsvvxwoysPr\n/ZWvfAUovruTTjoJgHvuuQeAU045BYCdd94ZgN133x0ovhutQ62+OitddLtHqhSlysJzUIH6Wn+l\nKs0+0j/htXj/+98PwMILLwzACSecABTL1z57+umnO47jftpk1ctiiy0GwFprrQXArbfeCsBqq60G\nwB//+EcAtt56a6D8jnzzm98E4JlnngFKX3az7tvUdnHMqjS22WYboKg9VZ59deihhwKlr7yHeo3E\n9HjOiPgb3s/vRSqbJEmSpHEGUjZVTzKfoj/+8Y+B4oMxiszvfe1rXwPgxhtvBEr+hZaqVpnzxe96\n17uAYukapXbzzTcDRQnFp3S0TLtZMINQ5Vvp1WLQilaRaJVpueqb+eQnP9mx/Xe/+12gWMDxPFQX\nv/vd7wB49atf3XFeUdFUtacf6lI0Xv8111wTgMsuuwwYb4laCNZopGuvvRYoOSj33nsvANtttx1Q\n+m655ZYDSl/Ea9WEJeuxvV72v5ai52DbjSrUH7n88ssDJUdJVX/LLbcAcNtttwFw++23A2Ucau37\nfcfT0UcfDYz3T9l3bbLm7ZOYQ3TIIYcARY2p+p1RUcHsvffeQFFC/v7YV/bBKGut9Zr572+gf/3N\n9V7513/9V6CMr1/96lcAvP71rweKP/vOO++c7vlERevf+LvRzzhJZZMkSZI0Tq3RaD4Nt9xyS6DM\nI/s0Ne7dKCAtjxhxo4Xh93yKOz/pXPx+++0HlKi2UVQ+jRZAr5m5omVrX6ywwgoAnHvuuUCxwmPG\n+Zvf/GYA7r//fgC+8IUvAPD73/8eKHPyRvL9+7//OzA++qmNeP2dXzY/xvGgnyL64uwj8fP4viy9\n9NIAPPjggx3bN4HjQx+J40NUPm6n6jcv5rjjjgOKX1M/lX4Ir7sqwP3MO++8QLl3tt9+ewDWWGMN\noNxLEvtgbPTbqCo+2BbvjQ9/+MMALLvsskAZ6zEaUb+katK+OO+884DuWfeTSbdziApCH9yuu+4K\nwPrrrw8U/6RjWiU8zzzzAPCa17wGgLvvvrun48WKA8OQyiZJkiRpnFqVjT4Un54/+MEPALjjjjuA\nMr/cq4Xk09UIi/haa26UNbaq5iy7KZpoMSyzzDJAyQkwUkrrS3+WlrHzzVZX0H+h0vGv/ixV5f77\n799Ls0aCbdU6N+JFhWzbq6ys+H608iNaf0Y5qi7rJCpf1ZT5LnGceM7Ojbu96xsZTXbmmWcCpU88\njhas+VhGJcoPf/hDoFQqcHuP1y2jvE5UW1V5Td4jnuPxxx8PFD+U0a3eG/al/k8VjrMHKlz9W01V\nFuiFXmc+xOthWxwXV1xxBQAXX3wxUNRerKpi9Grskyq/ZdX1HyY6MZVNkiRJ0ji1KhuzlCPGuVcR\nrSmji4xSM/pM6+u//uu/gJIbMKqM4InmsbtFlWituZ0Z3694xSuA4u/SwtVqs+1aplr9Z511FlDm\noT3uy1/+cqBErakqjdzR/xEZJs9mUGLe1Ec/+lEAPv/5zwPw29/+FqiOFtJK1ALWL2UUW/SPxGsT\nKygPy0wzzTQuQ9vrbXRgfN9xZBv9vr4bLWDVvOMh+mYcP0azOctgnlXc34orrtjxfrdq03XSrVKD\nfaIVrjrXX+m9ceWVVwIlOs28O3PT4vGsmjDZjL237P9+ayVuttlmQLl/Vcj6YI0y06fzoQ99CCh9\n6ayQMx7xuNF3WBWVNgipbJIkSZLGGUrZOP+nheFT0DnwOJca0creYostgOJ/0LozmkQrTyvQLHiz\nryNV1kKdmeET7X/suUZsi4rECBmVh3OwttG2mROg1WY0khVuVXdRHaqMLr30UqCoBOduV1ppJaBY\nvDGHpR+mTp3KHHPMwUEHHQSUWlW9on9JdWd+jONIK00rLo4Hedvb3gaUCC5zEBxP9ok5TFXjwHHr\n+O6X6Y2LWCEifsfr5zgxN8SIPC1Yx5Pnqm/m05/+NFD8GSreiy66qGO/HkdfkH3hrILjr1/fQhPY\nZs9Jf6W+GcfJOeecA5S+iLMMRmqNionGhe/Ffo6/YY4bt1PhfPGLXwTK74BYDcMx7H708fh5r7Ud\n6/jtTGWTJEmSNM5QykarSnwaV/kDIkaVaAlr0Wp9OQ/tHKwWjVZeFTFGvNe1Ooahap0RX0dFY+2i\nqGjcXss0VsLWIrGa7yWXXAKU+WiPa06CkVwSI3nqUHkvvvgizz77bN+KRl+cas22W605WtNVNe9U\nPnvssQdQ/BX2hZWujcCqijqzjwdVNDK9Po0Ksmpb37/vvvuAUrFYX435E1ayts/sG9eKMhJUVWAE\nlm3U6revYk20UWbVS6zabt+pdF276T3veQ9QZkhEH82Xv/zlvo5b90zI9Kga616HuBZYrA/o9/Wb\nO/ujT85KFI6LfqnjtzKVTZIkSdI4tUaj9WoBaMWbM2BE1qte9SqgzCP7NHcOXqWj36Gqvle384lP\n6ZlnnnkgC27sfnpdqfMd73gHUHwwUQGpXP7lX/4FGB8lpGVjVJrbx9pJ9rHRam5n5I412CJNRqPF\ntnr9zbfQ6tLajtaeUUleK+u9We/L+k9+rtL61re+BZQ+qKLuqDQYXxXcNkQ/p+MlriqrstG/6dpQ\nWqwqY2cTrEOor87vOy48jkq7ahagTbXRqs7Fe8E+0N/keLKPVbZxJqYbk5m/V/W7EXONVPExElc1\nZ2WJCy+8EIC3v/3tQKlX6exRXNmz6vh1zgKlskmSJEkaZyhlE2tS9aoOVCoqGi0Rrb64lod/teas\nTGDW/LbbbguUecxua4hUVUjuh1lnnZUllljipfngqjl4LQYrBOy7775AmW+2rZ67OQTWjxP375x6\nzNfRytOCfd/73gcUBWQb9VtUMYgFs9JKK3H66aez3nrrTfi5VpnKwnN87Wtf23Fu1ryKK72uuuqq\nQKlcfOyxxwLj1zfyr+rtv//7v4HS15PFlClTximWuMaTc+uqOftIxaEV7ufmIKlw9HNp4Z522mlA\nibTzOptXYZ9bSd0+j3XFfH+Y6MTJwpkOr6+VAeLqtfp8e7XSY421YVduHbtfj+3103daFe3nb6Kq\n+6tf/SowPvLXlVeNTov+R9tkZQkrDnhPdpsFqmOtqlQ2SZIkSeMMpGzi/F6vTzufxuYOxPVr4jyi\nUWf6aLTOzI43zt5cFRVO1flMT/H0a8H97W9/4/777x83Jy8xn0KLVF+NdZ70J5g1b02jKqIVb1SS\nc/laTGZbn3HGGcD4PtH6iwpqEO66664JVU2MqFGxaNXbJx/5yEeAMs/sdda/9d73vhcoPhotWtuk\n707/hJWuR8W0adPGjSfzYrRQjS6zL7SeYz0339dqV7H4uTXSVLBG2lnN2VyjDTbYACgZ5nH/Y6s7\nj2Xs+B5U5TS12qfnbqSdStjjeS/ZR70S+6YuxqoHr6PXx/EgsSaiyqeq+oV/zVUzj05/ln1hlXDp\n9ZrUEZWYyiZJkiRpnIGUzaBRGlpNzqVbt8nMXp++Wne+NlfkS1/6ElBySOI67q79YkROtyq+dVhc\n8btmsZv/4pyr57zLLrsAcPnllwMlasi5217RwtEHpEVjmw477DCgqL4YaVWlaHbfffeX5nOHJao+\nx43XVWWqdW8fOa/sekVa9VprWpwqJf0an/rUp2o57ybQ16YPxTFudnyMFtOS1J+purfvrLDuSozu\nx9pp+vDc3lpYHkeLOUa/aUHXuY5Jr3W/er0PHTeqdnPHrEThPeWaLVr3ro8UzyuO06aU2ESoaGK1\ngxgVGM81+mzFavHO/qiojT713nIWoFcch1UKqxdS2SRJkiSNM6Wfp/eUKVM6Njbiod/8BOfq47Gr\n6vU4V6+1rl/CaDatNX1BRmb85Cc/6eu8pk2bNrEDZgJiX5jj4aqhWqi77747UPwSxsmfdNJJQMlq\n7lZ7SgtGpaRlE2uj2Xdae67ZEnOSquLqZ511Vl544QVefPHFgftizPsd5yRa9UbKxHpdvu92Yqa4\nVpp9qyIyT0ulW2MNvL77Irbd6xct06rqFmIfGImp5ep4saK665h4nLe+9a1AGWdasrFGW5yLr1I0\nYyzsocdFpNdMfdWa0WWqeceDKs8Zk5/97GdAidDy8wnOs6fjR5roi+iTHXOsCV/HaDOVjP7rI488\nsuN9f3tVe1YhH5Ze+iKVTZIkSdI4Q+XZDJtxrXVl9nNVlWYtlyOOOAIo1pjRS857nn322UCpjSWT\nMQd77bXXdrzWgrjrrrsAuP7664FSE016PSctGFWd69NEC8i5eNeAqbpGVVbcQw899FKuz7DYtpjR\nrdUclWxVFJAWrfWetFBV1o4Hr7uVjkdJvK62uSpTv6rSgPeIfqlY+UEfkKrOLHpz0KJy8XjRZxPX\n1YnbzzHHHLVHZ0nVGkvOWHidjSrTd6e602o34s7xYl5WrKUY+3yUK/1WrRdTNS7iuIrX0T70/tdv\nbQTnVVddVev5zzLLLD1HqqWySZIkSRpnKGXTb1VU51iPOuoooFQiPfnkk4Fi0cYM3rieida60SVa\nNPVZyPgAACAASURBVFp/bu98ZNW66nUqnuOOOw4oWfBapFbd3WSTTYBidWmFm2cT16SPUUJrrLEG\nAD/60Y869iO2Sb9Vv6rTOf9YMXcYtLL1yXiOqrNeK9Bq+cZVB+0bLWBXqRxW2ZiLsOuuuw61Hxi/\n+qx94VhX9Ym5IlqiKhwjq8Trv8466wBlVUqj1Ix21GdXNcZ9X+UV+zaur9ME0WcnXtc999wTKGNb\nq9373woTVunQ0nal31gTLVZYlzZVS+j3tyn+Bjt+4m+pSnjQ6s+RftY5SmWTJEmSNM5QyqbfKs/O\nJy6++OJAiRox2sy5eK05LRYjrswZ0Eo0r8anv/H1Khqj0qwi3aQlo9WtNaal6DmpYLRAVTa22ZU0\nzfC+7rrrgFLjzIoAzl+LFrJ5GOZb9Eu/cfe9EFdStRaa9GpdqRJ32GEHoMzRS8w5GpY6FI04xuwL\n2+I9oWXomHdsGz1YFRWm5aqaM6/CcWPNPon5G3F/VX6MqgoZdVDlM1HJOl6cHfD3Q6WiGjcLX2yr\nK3fat+Jrr8koFU03xdlvPTcxUjfW5Dv66KOB0fipUtkkSZIkjVPrejYRn6paGlakNcbbp++aa64J\nlIxx5639nsrG7FeteK051xw38kurMdZ9cr/d6o8NgxaE88cqGCO89Lk4p64SMofItjqXH/1UWnXO\nwW688cZA/4qmKspl0PVspvc9KwRYCWCLLbYAylobn/3sZyc8J3NFXIHR+eZ4zvrsmvQrDEqMPvO6\neT2jP9E2mrd12WWXdXzPv7bZmnT6ZhxX9kWVoqmiKjqqCar27RhXyajivvCFLwBlrL/pTW8CSu6R\natDPo18s1lKTyawYUEXV/VgVlRa3i1WgjcBz9sDxZgRoP76WukhlkyRJkjROLcqmyjKIr33Kmg/j\nHLzr2zjHqrWvBaKPRwtFq+3AAw8EivVo/L0r88V6Y1HRDFoBYXo436xl4TnrZ7DCgGhteS5GGRmB\no3KxSrRzreYQGJnTK/atETt1+bEm+p5WeFxDxwgqI6xUPmY7a91vs802wHirzorG1qFT0baRGN3l\nWNN3E3OFHA+OcdW/bbRa93bbbQfA97//faD4/szniitx2odxpVDPz2tVlTPR5AquEc/JOm/mDKnS\nrI5hX0X1Zp+odHw/9kmb6PecYiUK+8y+MFLP+nGqQH+DY428KvqNOJ7uvobeQ5IkSZJ0oRZl0+tT\n2WxWVwvUyle5uB99O/716WpVV300VneuyjxXZVSt4NnEmvNaT9FyMPfDtnhuWrgqGv0ZF110EVBW\nJXV7FZIqrWout8oi8XiTMWdbZQ0dfvjhE25nhWqtMd+3L10/ff/99+94PSNgW2KOh2NQBeznWu/6\n/rz+5pAZ5eg94OqkVda74yH6MWNUXIxqkslUAx7L3wnxXFXz5rZZUXvrrbcGSlX5qKhHWSmgG7Hq\nc6Sq/x0X/s7YF15PfcTOElnBxNkft6vaf519lsomSZIkaZyhqj5P8DnQuxWkle16Nc7N+n6MzKp6\nekeildDreQ1TxTUeI0bADIv7t2+ce7fqr1WBI9FHU8UEvpu++mKQOf1oXe+8885AmWv3+l5wwQVA\nsbLMPTLTv2mru87qvnFcxGg1lYw5YkZgrr/++kDx1ahoXM1Un02sNxfzvqp8Nr2sOfOPFUhrr3Tc\nL/aZ0aUqGu8FfYF1rMUzPersi26/UXEGo6qWXazm7eyQMyJef3MPjfirWk+nG/2Mi1Q2SZIkSeMM\npGwOPfRQAA466KCOz6vWyJhRGMRSiZaqFog5QOY/DEu0fIwe6hZNUvX9bozCgo3n6GtzTlzl1HVt\nJiuvZpC+GDSKJ1Zh3nDDDQG48cYbgfGWaswpcTYg+mK6RSFO0I6O102uZzMsVl0wss8q8DOSsumX\nKh9PjFJzVVPHyRvf+EagrCRcV+5hKpskSZKkFdTqsxn4JFqQwfuP4ze2OuWgGHVkxJ51u8w12XHH\nHQE466yzaj1uGy3YUVGH/6pfH16MCosZ5UYhmWv07W9/GygWr4q339paVZnrbVY2VefeNKP4veh1\neyvsW4FE1ae/u+5ZqFQ2SZIkSSuYFGVjbkCv9bvqjuTqlX4slTnnnHPaCius8FKV5qrqvJFhM3K7\n5Q51i9fvlTr8V93QjzCKOk39MBmRedHSHNbija97HXfdVoZso7LpRp1Z8GPppy9mm222aYsttti4\nCvbdMP8urmLaK71WSRl2RiaVTZIkSdIK+lU2fwQe6LrhjMnS06ZN63mZyuyLQvZFIfuikH1RyL7o\n82GTJEmSJIOQ02hJkiRJ4+TDJkmSJGmcfNgkSZIkjZMPmyRJkqRx8mGTJEmSNE4+bJIkSZLGyYdN\nkiRJ0jj5sEmSJEkaJx82SZIkSePM3M/GbSms1xQzYpHBpsi+KGRfFP4v9UW3orb/l/qiG1mIM/k/\nwZQpU8ZVKx4lg5zLoG1oW9sHYerUqePW7xmE2BfD9s0888zDPPPM80/Rx22gFYuntYW0VArZF4Vh\n+qJb6f+mGPQ43b43meOirr4adNmNuMTyBMuI1DYuZnRS2SRJkiStoC+fTdP0u4Rt3YshTSZ1t2Ge\neeYByiJLM1Lf9NoXcYGxrbbaCoCLL764p/2NwpqcYPGx6W7fb19obcdFtuaff36gLAM8Hb/DdI8z\nSpZYYgmgLG3cK2uttRYAN9xwAwAve9nLAPjDH/7Q134cL8MuRDgR/fZ7XYsijpJUNkmSJEnjtNJn\nM6r5zBnBT1HVN77v3yrLuNv3fX+Yvpgs5TlZx2myL6LjOV4/vz/munRsr8KZd955gbIk99xzzw0U\nZTPffPMB8Oijj3Z8v9s9FtXkIH3RbanpCb7Xcey4bPiofh9WXnllAO644w6PP/C46HdJ9Khku93n\nPZwPUBTwk08+2df347hOn02SJEnSChpVNtEqajv9WipTpkzp2brqZo3FOVlfR4u2yrL1/TnmmKPj\n89e85jUAXHfddRMep4o6VF7V9e/XqhtznAnft+1NzWs3qXi7+ZfGnANQ2qhSWXHFFQF48MEHATjg\ngAMA+Otf/wrAnXfeCcAvf/lLoFjl4nG7qQ/Hepui0aKar7pH6sLjzDvvvDzzzDP8/e9/b6wvurXd\neyiqwOeee27C7zleVLo77LADAM8//zwAP/rRj4CijPsllU2SJEnSChqNRjNC5umnn+54v80RMP3Q\nSztUGlocEi3aaNmOmQvt2D6+dm7+2GOPBYpl8tOf/hSAq666Cmg2sqaKqGiq5uAHRevOcab1Zh9E\n/0RUgaNU3F4//0ZVFnM7vH5zzjknAAsttBAAm222GQArrLACAC9/+csBuPvuu4GibK+//noAFlxw\nQaD0kcf1Hq2yqCfjnq1SKPF9+2a22WYDii9liy22AOAb3/gGUNSe2NZ43eO1iG31Gvj+008/PWm/\nYdtuuy0AF110EVCupz6WJ554AoDZZ5+946/K1javueaaACy11FIAHHTQQQBccsklQBkXZ599NjBe\nKdVBKpskSZKkcRpRNloIzg9qjWmBPvbYY9P9fpyL9eks0dprY+x5VDTdlIxW+t/+9jdgvFUn5tO8\n+tWvBuDTn/40AG9+85sB+NznPgeUOfpB52AHods887BKwv2af2FOyaabbgrAKqusAhSr/gc/+AFQ\nrsGYiCoAZp11VqBcizqVTq/+Iz/XkozvR+Wz5JJLAvCOd7wDKG3WJ6eStW333XcfAI8//jhQLF7n\n6rtFNdZhwffro+uhigEAiy66KFCUzGKLLQYU6/273/0uUNp+++23T3gc+9bX3oNVTIaqcTz85je/\nAeDoo48GiiLxHLz+Sy+9NFB+d379618DcP/99wPwyCOPAPDHP/4RgLvuuguAn/3sZwBceOGFQLkX\noqLpNdp1eqSySZIkSRqnEWXjU8851L333huAd73rXUB1vajXv/71QJk/VhHtuOOOQJlfvPrqq4F2\nRrnZlmgZVFkCWq7Rmop1mbbccksADjzwQABWW201oMxbu38tYi2baDnH7eqkyuLrNx9Gq7zq76te\n9Sqg9JnWvsr5T3/6EwDbb789UCzfxRdfHCiZ5H6/iSKLVf1bZbVX+RFs8zLLLAMUS/aZZ54B4NJL\nLwXgxhtv7Hhf/5XqT+vd8aLPR6XjPed2Kp86FE5UNDFKsddjeG4qFytHOB7cz1vf+lagqHvVXTwP\nj+f7VaquW65TncRjO1Y//OEPT3hOts17a/nllwfG+8lVNo75f/u3fwNg7bXXBspvrdekahZqmJy2\nVDZJkiRJ49SqbHzaalVdeeWVQLHKd9llFwC+9rWvASVywtpFCyywAFAUzsYbbwyUiBsVzmmnnQbA\niSeeCJSneL/+iSYykfvdV7dqwFocn/3sZwFYffXVgfHzzFrS9r3z5Foi0aqr8ilMnTp1ZHXVbIt+\nqWWXXRYo2fH6arzOTz31FFAi8lZddVUAFllkEQC++MUvAqUPtdImKy9jenTLHfH62BcqG6PNvM63\n3XYbUObmF154YQCWW245oEQtjc0RAfjd737XcVwtWv0ev//97wdq10TE/o65ZDLRWISixrTad9pp\np47PPXet9ssvvxyAe++9Fyi+425EX9Bxxx0HwG677Tbh+TVBjJSMUWVRAatA77nnHqCMA+8Nz1mF\nrGKxL7fZZhugKGL3Z3Tr4YcfDpRx9OMf/7jjPPshlU2SJEnSOLUqG2O1jf1+5zvfCcC//Mu/ACVq\nyKetfg0tUZ/e+mT23HNPoFgwWm3OyaqIDj30UKDMS/ZKnRZtryqpV6taa9yIKufqI6oQ5+bPO+88\nYLzKi/Pk0Zfj+02oml736bl43ffaay+gZMGrzozA03ozysgoNJW0ivj8888HSp9o3fv9Jul2vaOf\nQLwXYiUJ1Zn3zq9+9SugXH+te9WACsc8CxWvPr0Y/RgrI9dxj8R9xMjLqvpwMWrQtqy00kpAUa76\ngm+++WYALrvsMqCos6qI0Ijjz9+vT3ziE0AZL76/5JJLdo2oHRavu2M+9qFtcFYn+nLEcaBifdOb\n3gSUe8zfUCP2/vM//xMYr7C//OUvA2UcpbJJkiRJWkmtysYoIOc8tUDe8pa3AOPj3H06a5Foabqf\nPfbYAyi5A869Ot9odNFnPvOZOpsxEL0+6WONq2hlaZmY8W2kjXOpsbKAVr9+LF/7eawWG2lDRJ9t\nVuEecsghQGmz5+j8sZnh+vi0zrRwtc613lU09oHz4FK3726s36vXPJbou3N8aImq2t1Of6jqQOvb\n46qMVT6veMUrOs7D71VVEZ6gqm/vHdCFGHnZrVqBysQIOs/V62sbv/nNbwLwyle+EoDNN98cKDlJ\nZuOrAqUqz0r/h33pvdTv+jr90G/uYPz9sO/0h3/yk58Eim/Ptut7MZrN4+qbOfjggwH4/ve/D5QZ\nE/ugWy7SRKSySZIkSRqnVmUTrTPn+ZzrjFZXtDh9yjqna5SRFowROFpx1v+akdAyMMrIv2ussQYA\nRxxxBDA+d8A+EedqVTJaJGYQa6W1Qbl0w3Hzvve9r+O1ETJmOV9wwQVAUTwqGKPQzMPSajMfQ5Vg\nJJfKSOuv7ioLE/kEeq36LTGqzFwiLcqYB2MbnKNXvTkboP/CNjsO3U+3ChejxAiq9ddfHyhK1hwR\n/ZnmVRlJ9cEPfhAobX37298OlLyrbmrNz6MSqpMYFTqogvT6WUnA1Ur11VjVWYX8ne98Byg+IX9T\nHQ+qSOm1usJ0z3HgbyZJkiRJj9SqbLS+nWPV2orWtU9zLRGj2IyPf+CBB4AyZ6rCMTdApfSTn/yk\nY39txEiamOey++67A8Wa1zqL0STR0tHal4cffhgoPh4tGq37NhCt5vhapWuf6LMz6sxM8Bg5Zd6N\n+VdW/zVSSLWnNe9cu5auysccBWki76ZbtJCWrcrUHCP7yLapdJyDV/Wp2vRnqmgcL37/t7/9LTBe\nGVVV9RhlhfaYt6d17vW66aabgFIDzTarRMyz8ffB7bu1KdY1bLIvom+mW029eC6ObX97VX3e/zHv\nzqizqkhAFU78namjUnsqmyRJkqRxalU2Pv1i/kJ8GjsH62pxt9xyC1CeqkYlaaE6vxjzclyvpN/M\n3qZWdITxeStxjlNLxNwjM8OjxSv2nX2qCnD7rbfeGiiRf9/61rcAeO1rXwvADTfcMExzaiHO/2vN\n20f69pxfjhF5zjNrnRlZpfVm9KPj48gjjwSKUtLSjVWfrajbBL3Wg3N86LvzOtoXjvWYH+Ocur6d\nDTbYACjjSevftmrxOn5UefZNVDR1WfMzzTTTwBFtMbfoz3/+MwA///nPgTJz4uf6qTx3lYy+vF6j\nyKoqHtehbKr2FdcvqiJWPHfmxPHgDIl5NLvuuitQZoWcTVL1i/ekitff3DrVXCqbJEmSpHEaXalT\n4tPRp6f5FObTaH1puZ5++unAeJ9NXIVSH06vaD1YF8gs/Tqoiv5Szb373e8G4N///d+BMpduDomW\naqxIq1Wmf0sFZZ9p1Zl1/973vrdjuzZEpWnVGVWkZWoeRKxMrUWq9a/15px6zFlSNYr+DVc3dBXC\n6PuJ51eHNVelaHzfc1bB6HPRctXf4HjYZJNNgHId11lnHWB832ixul6JKzw6C6CaM/rRe0iq+mDK\nlCkD9cswswcez3FiBKZWuD43+9TfB5VJjMQb9LpOlAs3aLRe1Tl025/Kx9wyfzf0wfg7YY6R61vZ\nB/q77Mt4r7nOjdVYXDenTlLZJEmSJI0zKcomovXlHKzZqvpw/KsaiLkpWnfDrrlRp6KRqnNxzl3L\nxEi7a6+9FoAzzjij43MtGaNCtNKdm3e7ffbZBygWsVa/alF/iPtpUuFMzyqG4pMzIsr3zXsxXybm\nFsXKtVGZRKtQ1fC6170OgBNOOAEoKjBWPJa6rPmxbaj6vtZ5XHlVBaLvRUtUBWKb9FNFhSvmW6iE\n559/fqBk21tHzj71XmqTEhb7yjbst99+wPg6Xf6euM6NY79Xf0gVbYjM89hG6qpcPTev41e/+lWg\n3BP6eo866qiO92N0pL8nJ598MlDGQR1RaJLKJkmSJGmckSgbiU9Z55P1pcTKpz/84Q8BOPfcc4Hy\n9K2qMzYKqqwfLdVTTz0VKFaY22utO3eqxaIfwmx5LQ/n8rVAt9tuO6BE5mjNx0isJulm+Tl/rE9O\nK955YtfsUcVZS888G6OQrDRhLSz9Hvad0WjmYWkN9js+hrFku1UK8HqbB6HyjDkiXmf9EN4Lv/jF\nL4Bi3ccVW62dpoK2b7R03V4cb1XjZJRWvarLcaA6s4+0yvVD2beOt6r6g72uZ1RVcXkUOD7iORhl\n6L2gf9JZgypVpyJy/KmkqxRNv6vudny3728kSZIkSZ+MVNmoTKz7FOcLzbM45ZRTgJJDohV2zDHH\nAPCpT30KKJnndc4zTo9e5vRti3kP3WoLaTGoaLQkbFvMVdp///2B4t9QOWnJTsbqgt2IuRtGznmO\n1jwzbyZWZ46rF8bcJD9X8RrFWHfNs0Hotp6N1rmVIBwvsQK6uUZasI4nFa+vVU5WGFBBm8vm+WjJ\n9mvl98vYDPVB9+33jEY7/vjjgdIGK2Pr07EvVYNtqorQjW7n6O9DrA5uNGLMVVPZVKFqjJWtqxTM\nMKoulU2SJEnSOCNVNlqq5pA4x+7T+T3veQ9QImd82htho2VjRJYRF5OxAuPY85keWiAbbbQRANdd\ndx0wfm40RszYNyocI7m0ZPRfqHBUgd/73vc69tMrTVp9WkNGXhmNFtekr8qXivWbtOKMyHL/zulr\nrQ3KMPPSkar5fn01WpLOxetniPX+9LHor/AczUXS6rfigPkW7tfj6dOraludbYfBxlNUwnGNF6MJ\n4xo85p6ssMIKQFG6VQq31yi1yVREsc2Og9gH/rXtRvg6fsxFjKrO3xN/Y81hVAk32cZUNkmSJEnj\nTOnnSTZlypRGHns+dV15M66IFy0PIyhc88Us2rh+er9MmzZtSvet/j+99oXzyObBGDGjhWnElW1Q\n0Wh1mSUda6mZRyMrrrgiUOZoh7VM6+wLr6d+JduoquvVcvS6G7VoVJv7Mbdk2HEQqbMvtFQdDyoS\nr5dj3Si0qu+bT2UtNasyGJmlb1D/1a233goU1Ve1Omas0TfBSpC13yMSj61q9/pWVX5wHKjyHG/r\nrbceMN7fWRdNjAvHuApEpeK9o2ozklNFE6Mcq/bv9/XlOQsUV6/tl176IpVNkiRJ0jgj9dmI1pjz\nyj5tu9WXcs6+yeq9VUydOpU555xz3LoPES0ILRXVm221bpe+FjPBzSX52Mc+BpT1TayhpRq44447\ngKKMhrXeBs2an169qJiN3G3NniqlY8SMfeDn5pIYsTUscT2TfpmoL+JcvBapFquKw3GhJer6NM6t\n65fyeyoafTX6M7/97W8D41eArFI0UnXeTc7le4wYGWdbVKpV56b1H306dZ+f1NkX3u9GZnq9rZV4\nwAEHAHDSSScBRckaoWvFAMd+9NHEChP+1prLqJ97UPqpE5fKJkmSJGmcWpRNXdaPNdHMt6iaezcy\nx3pS5hho4YqrVjaxpsuLL77IM888My56R0vCczPmX1wH/cYbbwSKitMqe8Mb3gAUn4wWi8rnC1/4\nAlAsIefiq+az+6WuyrhjiX6CaClWnUOMoDGHKJ7jW97ylgnfH5RBFY1M1BcxcsoIqViF1+gxI+6M\nQvRzKwZsuummQPEB6stTEauc9OHFygBtyjWJeVSxZl7V2i+qwLjCq35O1eGwUWdNKht9t/pqVltt\nNaDkDrqujD48Izr33XdfoFTHOO200zr2418ri3zoQx8C4D//8z8BuOyyy4CikAfNTezHN5zKJkmS\nJGmcWpTNsJVxYz0nc0iqMJLnwAMPBEoOixFbonoY9uk9PeKTXetMxREj7bRAVG/6WrRUjR5ad911\ngaLKVHOqvy233BIo/gWtOXNY2kT02Qy6YqPqTQtVVRAVbZuIY1xrO+ZRidfZv/otbKNq3TGv+jfP\n6ktf+hJQVqmUaNVXqctRKp54Tt18gFr5m2++ecdr/aQxt6ibchl0rZk68N4455xzANh77707zs2o\nVhWL2HbvDdfJMpLPcaPS1ZcX1eRkkMomSZIkaZyRRqP5dNVvEbNeI8696tcwAueNb3wjAGeddRZQ\n1t/W8h1llVajR5xLV9HouznxxBOBMoeqheI6N+ZhaNEYkaWfQgvW7Hs/10/ShtpowypKra+Yi2S1\n6G715roxmRniXg+PGc9d5aM17tosqnOV0BFHHNHxvUsvvRQo4yVe917b1q2W2zD0288xOk202q0Y\ncOeddwJF8VxzzTVAuSe6HbdNtdN23HFHoNSJdMxbDcH72qrucQVffbpe/yuuuAIobYs5R463OC6b\n6INUNkmSJEnjtKKCQBVaNj59ncfWYtEq1OrTX2EkWL80kR3da62pOF8d/Rz2gfPQWnff+MY3gOIL\nOu+884BiAakCBljLpbFM8X5Rre22225AiT4yV8BxUDX/HK21fq23JvsiroxZNQ687v5VtRs5F+sB\nRmXiOKxSC70q4MmoIOBYjecs1n3z98DP9dk4HvTtWlU8jo+q4/V6r9TRF1X+ZH2xXmfv95jXV1X9\nWb+Vn8cIy7oj7LKCQJIkSdIKWq1sjC0398BKpdYFMvLGNcm1Agadd+zXUhlmjfoe9u85Tfi5dcC0\ndIxWcX2UYZlMZdNtTRVrX6nWtPZVuMPmxXRjkL7odwxWZdFXfR6VUFznJBL3161KQtX5T+a46GZ9\nmxUf82v0Y6iItfLNnjcyq1ei+hxzPpPeF1XjKZ5j3dW7u5HKJkmSJGkFrVY2kx0d0iY/Ra/zybGS\ncre+itEnVYyiL7pd71jvabJWZJ0MxWuUWawoEBVMrzki/b5fpS4niE7re1w0bWVHBWRfqtpiG7qd\nT6/+jCbukX7PVaoUcZt+O1PZJEmSJI0zEmUz2fOJvdLk3HyVoqiaDx42gmpY2qTynHsfds2NQamj\nL+pSIEYb6afotn2vxHtyFD6bWBl72N+HqFB6rVBQtZ9R+q/aTiqbJEmSpBX0W0HgceCBYQ/aNkXz\nD5buc/vHgQd6tSSrfCRVuSGjmnv9BwP1RRMnAqNTNP+glr7olr3e6/tR0XTbvlcmWJFzos0aHRd1\nVy2o6x4aRV/MYPTUF31NoyVJkiTJIOQ0WpIkSdI4+bBJkiRJGicfNkmSJEnj5MMmSZIkaZx82CRJ\nkiSNkw+bJEmSpHHyYZMkSZI0Tj5skiRJksbJh02SJEnSOH2Vq8licoWm+6LXpQCaYjL6YrKLi/aK\nywk//PDDQLvGxWSz6qqrAnDrrbcC/7f7IhYr/b/cF5Fe+qLV69n0S7cf6G6fNzF4XEEzrhHfNK7H\n/pe//GXCz7v90Dd5I7neiGvF91srz3N3DXpX8Kxqy/bbbw/AjTfeCMD999/f1/Ga7Aurfjsm+33w\n9vvA3myzzQC4/fbbgfJA7ZU61/apWjem13WN+q2gHY/TbQ2YbivITubDpqo6fFvIqs9JkiRJK2iF\nsulmQUwW/VoqU6dOfckqX2WVVQC47bbbGjm3QafVel3xM9JvX8w000xjpxemu31dU4Rx3HSziN3e\n41ZtP9988wFl7frJtGCXXHJJAB566KHpnmN8P670GberWiOm32sxjLLpdx2rqu095zHH6diuaszH\n/brSa1XfdltX5//SNFodMyGpbJIkSZLGGelKneJ8pDiXHy2UaIXVvZplGyyV5ZZbDhg/l77RRhsB\ncMkllwAw66yzdnxuX0U/yKB9Mkhf9Lui5vLLLw/Avffe63489oSvpdtc+1xzzdVxHnF/Ezh6p3ue\ng/RFv3Ps3Xx7VVZ+tz53nDguhmUy7pEqZeL1m3feeYGi4vwbx8viiy8OwHPPPQfA3HPPDZQ+djt9\nfl4rr53Kp4om+qKtQTPdSGWTJEmStIJJUTY+rWeZZRagREo9++yzQLEsVC5ur4XqdiqaKqs9asbH\ntgAAIABJREFUKqQ55pgDqI7IioxS2USre6mllgLgwAMPBIoK2HvvvTu2P+SQQ4ASovroo48CcNpp\npwFw5plnAt0tpdiXdUQdxUgrqZojjz6VPo7f8TrO6Tvenn766Qn3H1XIPvvsA8Dxxx/v+Q49LuJY\nrotulrBt8/PFFlsMKP4oz6fq+1E51dEXvVrvXkcVid975plnOl77e+D9Hn2/VdGL/rWP3I/jwPHo\n62HvkV637Qd9fJ6jfRDP/U1vehMwvu0XX3wxUNRfk7NCqWySJEmSxmlU2fh03WmnnQC48sorgfKU\nPfvsszu214rSEvVpqyXj/LPv93C+E74/itySbthX/v385z/vcQBYffXVgWKRbr755kDpmwcffBCA\nE088EYBzzjkHKPPO/foQBumLbj6XXvMgosKJitXva8UttNBCQJm7j4q529z7KHOO6sa+W3rp/78s\n/LLLLgvAaqutBsDVV18NwD333AOU8dQrTfaF564K9Lp5fePvgePC7y266KJA8X/ps7nhhhsAeOKJ\nJzq2d3zE6DNnYNy/x4u0YSZkxRVXBOCYY44BSh5VvGck+qdUrI6Tbsq76ncklU2SJEnSCvoqV9Mv\nzoFedtllQLWi0aI0YkYfi5atlkjMIZAqy7SuKLUmiBE35klorX/961/v2H6RRRYBSlSa1t9aa60F\nlDZq1cWImsnIPK7q/+i7iSrOc9ef8OSTTwJlzn7bbbfteF9rbIEFFgBKX7i/Cy+8sON4nkeV72h6\nmeqDjplRjTmPt8EGGwCw1157ASWC6wMf+AAAJ5xwAgDHHntsT/sdpi+qqMqv869jWV/L/2vvzKNv\nm+v//7hdraVhSZY0cS+SDJUpYwiZQ1mGlilEaLIyRAOhcFuJVomQuKKMGbuIDJE580wRKSINNNDC\n/f3R73Hfn8/r89n37HPO3udzru/r+c9nnfM55+z9fu33e+/n8zW99XzE7/v+iiuuCMByyy0HwOWX\nXw6U+SGrV6k4v2JWomvGz3dbH9QmHIvnusIKKwBFmfh+HFNciw888ABQ1twxxxwDwG677QZUZy/2\ncx9JZZNIJBKJ1tGKsonZZHvuuScAN9xwAwDzzTcfUHyoMgzZvU9lGUZ8Svv7fi8y5YUXXhgoT+9e\ns5x6gf7eTnGCmFHn5/U7y+Zkd6q6Cy+8ECh+6M033xwovlt/t6m6irqYPHlyZZaX75tV5DnG2hDP\n2UaYhxxyCAAbb7wxUGx0xBFHAHDTTTcBJctstdVWA+Css84CSqaedTyeh/PPHmna1vP1dT9MPn63\nikVXIcaxoq+86vsex/jmkksuCZSuCBdffDEA5557bo1RFDSpapzTXjfXp+fuGFdZZRWgqPfLLrsM\nKEpGD4gZWaq3Z555Bijzaf755wdKl4/rrrsOKPEqvQnGhOL5iCbWVL+K1zUzZcoUoCiTqBL/8pe/\nAHDzzTcDcM455wCw4YYbAuXe7Fx3fhjnUv09++yzPZ3neEhlk0gkEonW0aiyWXPNNYHyNJWBmCEh\nk5BR+loWb3feq6++Gij9oYSsQJZnho0Mx+P51PYp/eSTT/Y/uJqQfUe2VAWZiGzu8ccfBwq7j35k\n/dFmjaje/J6+emM+VZk0TWN2qlG1py2qelg5H1ZfffVR37N26JZbbgHg1FNPBWDBBRcECmOVtfl6\nr732AuCpp54C4MADDwSKMtpuu+2AogJU2mKhhRaa9d1e4ZztVlXLXFWsZo/JWLVl7KZhJuc666wD\nwAILLAAUFeHaNHuxLkb2AewXVvC7Pr2+/r7xSdezsRNZvbE717/r3WvlPPG1v+PaUOm6hqKydS3G\n8Y5Um33Uo4z7vtf54YcfHvf/3k+sv1t88cUBOOCAA4CiFr0XGoM544wzgDK39QbE+8Xyyy8PlPuM\na8nvx1hQL0hlk0gkEonW0ZeyibGTG2+8ESjV7vqLZWmPPvooUJ7ePi2NU8gs9KnLeCJ7k/Fus802\nQOkj5muZr0woKptBZJfUrQUS2kKVpw21iXU1jkXVJ+MxXnHwwQcDg4/ZjIeqquaqzsSyKmN7Kg5r\nQ6644gqgjM1aEjOuZGfORxWSNUvGjJwnHlemHZltt+x/PNTdc0U4t820c+04n2T18fecN8Y3Ntlk\nk1H/93frIp5nE2slxqGMB3juHkvFIns3e1UlIouXrauIn3jiCaCoOI+nLY3dxBhx7CdY1YuvzftF\nlaJxDcTeeXEN+f6ll14KwIwZM4CxezdpG9eCKtC57rUwy83fi/OuF6SySSQSiUTr6EvZxHiDDOCx\nxx4DYK211gLg+uuvBwozjZ+XmehHlJ099NBDoz4Xa0nMQpHBypRk/fq322BpoinWE1nfHnvsAcDS\nSy8NlM4A2sSMG330xm5kd7Fz9kTuFVQ3u0sbOjY7XMvKnTdmHX3mM58BSn2FUNFOnz4dKMz46aef\nHnUecZ+VNmqRxtkbZ7afl3V7XT1n14bs3s/51yr7E088ERhbk6Jtra/pdPwmMzerdsr0GB7T2Iue\nCmMrMaZiDMe5blwqVr97PVXM/q5Ku1Nn9Incmj1mxKlwnQcqD9eCikUFstJKKwHlHqgK1IbOR22g\njX/0ox8B5d6tR2WNNdYY9fs9jannbyYSiUQiURONZqP5FJZJnH322UBhW1XMUZ+6fkYzqMxK8Sls\n9pHK5/jjjwdKHYb+SRWPmVtN+N6r0LQfV4Yqy5PhGtc6//zzgWJrmbO1JZGt6fOVDQ4SdWsK/H9k\n637fegszrFQ+q666KlDmlWNUydi1WXVQlV1U9X4TKtC5W8XuI2TddoqQkTrmqGSMg+6///5Aud5+\nzuwk46edshPbYPGd4layaq9jzFY1XuXYVl55ZQDuuOMOoNhI27lm/D3nifPAGE7sGxjjnFVru41u\nChGek3Emz22rrbYCSpd3FY3XNXaQMI6uMnrkkUeA6j19pk2bBsCdd94JlLh51T5LU6ZMqZ2xmcom\nkUgkEq2jJ2UT4xQx4yV2Fq3yjcpUfErrj5StmS1iZo3sTKXi/81RP/roo4GSi+7nmt6tsE1EW2pr\nOwdElmc8TBYYuzP4Wt9tWzaYPHkyyy67LAC33norUF8ZxLiS52jGzMc//nGgxOasQdJHb3W07F9F\n3YlxxfNzPqkK+tl7RjW/6667jjpWVSfy2B/u9ttvB4pv3jltxwjfd0245lS6rj0Vr7aoe02aVHdV\nsY/Yv0/F4fuO2Risc977ifFM54+xm1in4/ecT84vlZFrJypqz8u16HHbjOE4FhXNQQcdBMBxxx0H\nlN5lnosq0H2uzOQzy8z5ZJ2WSqiqj6GK+rDDDgOK7d0XK8J7dq2x1f5kIpFIJBI9oidlE32ZUalE\nX2jcLyLuW2GfJjOujLnI1nx6ytJl8/po9UvKQKyS9nx8P+70OZFdoKt6X8nu9JXKcFVpcS8XfbHW\n35jB4+/IdNvuovDyyy/PUjRV6MTqowI25rbuuusCJU7h/DHrzF5XV111FVDGWtUlvArOt8UWWwz4\nHxvsdY6oaEQnpeD/nePuX6QNdtxxR6BkH8XdKz33uAbtgN0p8yrC/8uYjz322J5tUdVtW/WlovB6\nagPjTXHHTqFas8bM2jTXispHJeNxjd0suuiiQLl/RMSeilXzt0nE3mYqHOeBcWrn+DXXXDPq83YI\niJmWdTtZeL9x/qiomugvmcomkUgkEq2j0Ww0MxaquqxanapPVR+8vnZhvMEYwN133w2Up7OMZJ99\n9gHGMhn37Iixo5jJIxuYSDgmmbBZJO5qqlKJuxdq47333hsoNv32t78NwNprrw0UH28nVmqm15VX\nXtnXeMZDpx0747nJzmWsZhdFdhZZXrfV+vFz1utYJ9ak8u3UpTnGiawJ8bq7J9SWW2456py1hfUR\nn//854Gxe8/bMTl22q6Ca09m248tqjLx4nxQtRk7837iazsKqNaNPxhzWWqppYAS0/M6CjtM+L4x\nobvuugso8dB4v3A+qpTbzEazX5wxl5/97GdAWd9eD8euYq3KnKubLes1sCu4Yz3llFOA0knf+5E2\ndp7WQSqbRCKRSLSORpWNcQd9pzIGIUMwNmO9jE9p8+dlHmaLyN5UQDvttBNQMnFUNO466FPZjJ3b\nbrtt1HnEzgJzzTXXQHayhLF77jg2K3XNg7d6Xr+0MRozbPThO3bZn/UWX/ziF4HO++qINhSN7NhM\nmJjdFWN5sjDnkf5ox6jP3niW8+Yb3/gGUGoNNtpoI6A+G/dzxpx233134H+ds7uN+1TB66fartqd\n0r8q23vuuQcoFdwnnXQSUCq8VTyqf3/f4+nDr8pCrFJ/rj3VxHPPPdezJ6BKcboWvN7CWE3sPFG1\nRs2YcqwbbLABUO43Dz74IFBqR/SIqBKN6aoinV+xBmVkVX/b9wv7A3pu3ttUpv0qq7jLqR4SYTal\n6jLGfLtRNLOO2fU3EolEIpHoEo0qGxmLT0HZdqxa1jeu79W/O+ywAwCnn346UJimPc/MGbeaPmZa\nWCksZL7GimTOxgDs81OX/ddB3Z069c2q5syIMfMu9iDy3DfddFOgxGTinuRCm3Ri5m12tNW/W1W1\nLqONHQRk4SpZ2by7kwrnkXVWMlmzmeJ+SBGR1TsPO/UPq4OqKvmq+gbnqN1/nT/GI2XlMlGVj/FQ\nY33GL5z7fq7q+lYxZOfFyP6ETc2ReEzHaqw27lvlmI1bGGtxvhhrcZ7FXnjeh8zoUqEZEzS7Nda4\nxaxaX8+cObOxmI0K1H6PzgN7m+n52G+//WYdux9oS70O3n/swmKNo/OmydhUKptEIpFItI5GlU1k\nKD6lfTrri5Vxxv1OrJY111t/YdyNTtYljHNsu+22QGFx+lr19cv6mtiboQpR0cRMHJWI7EyGIUvT\nNmabycL23HNPAPbdd1+gsPAI2b9V9HU7LTeBONYqRRMzqSKTVcFab2XdlNfPrCU7T6hUhapPhltl\ng/h+k/OiSsFUISqfOMe1jXEvs8ucJ8Y/tY0dJ+IumHURP9+G8vU3nfvCNRTnhwrGeKd7rWg7Wbuq\nzs+rkI3RqGSMCaqIna8xHuP5NNlVQXiOjsHeZ9rGe2A/3SxGwnviaaedBpR+k843Fc0ll1wy6jwi\nerFFKptEIpFItI5GlE1ktD6lrWL36RzrJ9znWiVjbEafvbEZlYn74Zg5JcuPsRqftjIaMzi6raJu\nAh7D2p4jjzwSKFlEvi8Ll1XJ6sy4s0agqorZ/Wzc42UiuiPoU9dXHvfkELGHnv+Pu03a4Tr60h2b\n8yDuydEps67q+o8X9+rVjsYJPKdOsbF4HD/n92TXsneV7VFHHQWUjgPOn5NPPhmYmL1YIqrqrKqy\nEIVjN26lajOuqer3/hA7hejx8Hdda1//+teB0lfM36na76rJ+0VVn0av62abbQaMjU97fb1X9gpt\npSJ2fn7iE58AxnacqEIvtkhlk0gkEonW0aiyiU9D4w8+BfU7ylj0mcra9JnKcGVv1mncd999QKle\n3XnnnUcdLx5f366/K7Ox/qfJLLROMB5ghfcxxxwDwP333w/AeuutB8C1114LwCc/+UmgjNExV/U6\nsiurqqIT2lB38diyOBWPGXh+zhoiz2X77bcHih9beI5mmfm7KuPYQ8/YTkSs74i7HMYq6X5sE7MA\njTdGX3wnOFbPfZFFFgHgiCOOAMba9t577wXKmHpVNsbBjLP2g6pMSaHy8LrHXovazNoOx+TnrKcz\n9mttkB4NvQJ+X4+H86Xq/PTMaIMm7hdV9U6O3WywOPboBah7XZ3rxmZUwiop7z/GAD1e3GG2CaSy\nSSQSiUTrmNQNe5s0adK4H45MRWXSaXdI/dr+laXJAu0UoJ/SPkGyRllCjMX42kriq6++etzPR8yc\nObN2W9cqW0SopmRZKht7H9nLzE7Dfi72iYpKROZqT7ULLrgAqK6y7hbd2mK8Lgyes9cz7v2ur3zr\nrbcGSlX85ZdfDpRu4O6xIYM1trfmmmsCJQZo5wB99VW92OL5OV9H9r4a+flubPG6171u5iKLLDKL\nMcZjiU7rTgYbu+3aG8u9W7SBDNQ5b31Mv4hMutt5Mbv6HMcW7xceM3aNdx4Zm3G+OGbvH2Zk2tfL\njE9/z9okPS0qnar7VswQHNE1vvH7hbGaJ554Ahirpsy0VMHGztgqFufHFltsAZT7jgo4dhnvV8HU\nsUUqm0QikUi0jkZiNpFBRn91VQaVbElGLMN1tzmZbPRjyv5jd1YZh8wn+iEHgRgX0Ber/1c25U54\nSyyxBDB2N8EIbWrPsxkzZgBja5YmCrM7fqxfcYz6hR27ylVmqbrbZZddgOJ7N4an6tMXX9U3qlO3\n6SZt98ILL4xRNSOPXXcuxjFoCzPt7HxuDMd6mk5dE+qi2/Otwsjvx6xC7e7cjh2wXUPOD9eKCsfa\nM/d08lhmMapUtIk90pxfxnI9Tqf7Vpv3EY8VPRZmzqlIrBHSdnp9HIsqLtbhxbotd3D1eINAKptE\nIpFItI5GOwjU3TfEp6xPZzMlNtlkk1Gfs3bEaviY7RR97uakGwuoyvyI329j3xJVm2zbvyeccAJQ\nxnLggQcCMHXqVKD4amX/1uWY/27NwSAz6fpFZG1ef1/LyhyT8QbZvIxTVaiNzCqUqfr9qHTjdY71\nP1HZNDkf4rkI4wcxs0rEc9YXLzu367e/axZjpzhpXbRRp+WYRvYYg7FxqXh9fK2HwxieWYN2LDFW\nY5ara0U4j1RCVcqqaiffQdTneS5nnnkmUJSLvRM9R9WhPdQ6QdvaGaCpXmvdIJVNIpFIJFpHI9lo\nEXU7H0cGY+aWGRLua9NpD4fISKKvN9ZtiH6yjurawnOJcQKZrRla9kwz0yrW0VSxrRrn2dP3mrBF\n1bEde1X2mkrVONchhxwClOtpvZVxCquh7ffk+xFV8zLWlIxUHf+/w2/j86LG7wBlXjh2s4qMb2or\n67JUOHW9DN2y9zZs4fqNFfzRE2IcQpsYw1P1uQePnQGq7j+uOVWEvxd3v4wYRDaaMC5llphjt7vG\nRRddBJS5GjuoOxbnhWrP+0vTiiaz0RKJRCIxFGhF2fSLumw8Mo1YsV43M8ceWG0ylTb3jZkdBqVs\nXvOa14xRbyIqB1+rOKPS8bU1BbIzK77tAu3ulDJjY3xVjLbb6mtrh5qcF+64qQIZ5/vA2HiGcQbr\narSFNpo2bRrQef+ifuMOTdoinkvMUotZhM4LY3nGNV1TekDszhAVkgqoqp6nU5fykdfklVdeadUW\nnRA9JlVxyEHdb1LZJBKJRGIo0Kiy6ZU1+VTWTynzkPn2+nSuez6DUDaDQhUz7taGvdiik71j3UKs\n5fC1WYXrr78+UFSAWUdWjl988cWjvmf2oa+tw6mK2XXC1KlTefLJJ3nxxRcnjMFGxN54qsROvdaM\nU/RqC9HkvKib/eVfq+Krslp935hdVa1QVNLdrpFelc3suogPshN9G0hlk0gkEomhwITEbKr2t4h+\nyE5MQz+2/utujxsxJymbbuMP3aKNbLR4zlWMMlaSd/I/V8XuOtVZ1UU/tug1/tgJVT77OB+qMv96\nRRPzotPcrVLncR75vlmL1q7FfY+M4fk5O1oMU/xqxOf6OqeJ+v1UNolEIpEYCkxoNlq3nXB7RV12\nNycpm4imGcsgM/Oquob7fsxai5Xo0bdflRUXEav4rbeIWUkTOS+qOg3Ebhn+v9d5ENVg1X42g1B5\n8fNCxSKicu2kmKrmXVRQVbGgcXruDXxeWItovcyg0Y8tUtkkEolEonV0q2yeAR5r73QmFFNnzpz5\nlrofTlsUpC0K0hYFaYuCtEWXD5tEIpFIJHpButESiUQi0TryYZNIJBKJ1pEPm0QikUi0jnzYJBKJ\nRKJ15MMmkUgkEq0jHzaJRCKRaB35sEkkEolE68iHTSKRSCRaRz5sEolEItE65urmw8PWfLJpzMmN\nOJtG2qIgbVGQtihIWxTMsY04J0+ePKuD6zAjdqVtEm3bYNKkSa2e//9VTJo0adaumLPD3HPPPWsn\n0UR/mGuuuWZ1x24STa+Rpn9r5O/NCet5KB82iUQikXh1YUL3sxk2DJMsjntvuJeHr+vu0Bn3eqm7\nE+Qw2WKi0a0tJk+e3NoOquMcD+h+/5pevzfI/WwGhW53SRXDZIu4l0+/80LU/f4c60ZLJBKJxKsL\nzTs66Z0piE5P5WFlSOOh7rlGRhFt566BcbdCP9fp992J8YUXXuhwxq9+dLom/e6G+PLLLw9sjvb6\n+35v/vnnB8qOn22i6lxf//rXA/Dvf/+79XMYD1U7d7aJqmO4vt2FthO81/p78T4SY1lxl9tOv9uk\nQk9lk0gkEonW0aiyqatoon9xmWWWAeCNb3wjAIcffjgACyywAADveMc7gPL03nTTTYGyV/3tt98O\nwHPPPQfUZwWDQCeWFG2mDdwDfo011gAKQ1HhPPLIIwDcf//9o44TlYu/ry0ff/zxXofSNYZVgXY6\nnyb2dx/0mHu19eabbw7AD3/4w8bPqRPMxuukaN73vvcBcM899wAwdepUoNwXpk+fDpT7ikrJub/b\nbrsB8K9//QuA6667DoD//ve/QLkPDcM89d7leve+4F9Vtzbba6+9APjnP/8JlLHecsstQLlHzjvv\nvADsuuuuACy22GIAXH/99aN+X3httFm8//SCVDaJRCKRaB2tZqMZJ/Bp7bFkJOuttx4AK6+8MgBr\nr702UJ6mKh6fqn5fJhKf+h7nrW99KwBvecv/tsWuy+YHmYElE5VBLLfccgAsuOCCAHzsYx8DYOml\nlwbg/e9/P1DG+tvf/hYoKlBms8QSSwDw+9//HoDzzjsPKIonXu+q6z+M2WhV7L1tBTWMtqhCZPdC\nRvriiy8CzKoFkiGrAi6//HIA1llnnXF/v01bHHrooQAccMABo95fdtllgTLXXecbbLABAM888wwA\nb3/72wHG1Kd5v/B7TzzxBADf//73Afje974HlPvF008/HccBjLt2+rZF/G2vwzzzzAOUdf2mN70J\ngB//+McArLnmmkC5f0QlJKJq+9WvfjXq7y9+8Qug2OTPf/4zUGzovOmkbDIbLZFIJBJDgVaVjU/p\nEd8f9b4sfsaMGUCJvSy11FIAvOc97xn1PZ+6+i1lb/5fH+zGG28MwNVXXw2Up3onRtwGa6uq6vV9\n/dF/+9vfgMJY9Ctvt912AHz4wx8Giq20hazPMT/22GMA7L333gD89a9/BQpbq5t5Mwxs3nnidXUs\nKuZ7770XKGrO+fSf//yn0fMYBluM+H2gXDdt4Ty66qqrRn3uDW94A1AYrmvq73//OwCrrbYaUJju\n888/DxQmu8MOOwBw8skne9zWbFGVWeVrYzUPPvggAI8++ihQ1Nriiy8OFFbuvIkxYjO+rr32WqB4\nWOreCydNmsTMmTMbtUWM3X7wgx8EivLcfvvtgaK+9IQ4Zj9nVqGKyPuBsd13vetdAPz6178G4Mwz\nzwTGxruj1ygi2jSVTSKRSCSGAgPpIBD9yLKmddddFyiMQpbu01n/oKxLJrPhhhsC8M1vfhOARRZZ\nZNTvPPzww0CJdwyyaj6ysU7Kxiwxs0VULNpKxRNZvjbUFjIcGcoZZ5wx6nW3WSQTweYds8xT9l1l\nSxWM7F4l67xqChOpbByzytZ4p4pjpZVWAorv3rXmfInz0XjItGnTgJKtpM1VNpG5ijbWSBUcg3+3\n3XZbAFZccUWgrHNZu3FJ57xK2PuDYzn77LMBuOGGGwDYZpttgLK26qINW2h371neH1RfKliv0wUX\nXAAUz4VjFyoVbWhdlTG7GM966qmnRr1fF6lsEolEIjEU6FrZ6K+s+flRf2VfsiljM+b633fffQDc\ndtttAPzpT38CxjJcv3/ppZcC8IEPfAAozEamctdddwHwxz/+EehcB9Qkg40s3HMWMYvEc5ely1xi\n5l38fetydtppJwDOOussoGTodFJ1bWbadPF9oNjCOhfHFs9RRht99f/4xz8AOO644wA46KCD+jmt\nWejGFksuueTM6dOns8oqq/R1TMd88MEHA7D77rsDhekK50esGTFW45zXViroTp0kZL4x/tXtvOjm\nflEF18R3vvMdoMQnn3zySQC23HJLoKwp/xrj8b5iJpdxK22qOugW3dhi8uTJM+eee+7aXRK0vx4J\nx6QC8X1t2ykWq2Iy3m3Mx7WkLb3eVfHtqh6LqWwSiUQiMRTouoPAyCeeT9sqluTTWXblU9On60Yb\nbQSM9bGff/75wNhsEo9ndb3ZSGZWWA1rlon+yW47HjcB7aQNPHezRGI/KPPo/b8sX1+6zNQx+H/r\nIQ488EAAzj333J7OcyLhOcja9M2rULbYYgugsLDI1n/5y18CsOSSSwJlHtRFE9XR4oEHHuhb1UCx\nySabbAKU2rH4/9/85jcAfOQjHwFgoYUWAuDGG28EiqK+6aabgGIzEZmwXoHTTz+97zGM/F1gll08\ntyrEczJOYZzKNeVasCZFJWNMR8+IcU8zOa0lssakE5qYH6+88sooVVOlQJzb3lN9be1hPKeqfXxi\n3Y42c37oTbK2KSqlqt/rZ8+cVDaJRCKRaB099Ubz6dbJ7+uTPPr7jMHIVH06x9iOT+GFF14YKCzf\nWhTZ2mmnnQYUxSPTsTOBjNnYjbjmmmtG/V6TcAz60GP9gtD/fMkllwDw3ve+FyiZeWaZ/OEPfwCK\nzawpOfroo4Hi137b29426nuyv5jlIoZB2UTYv8l4hddZOA/0vVs57nXWVnWznppQNE3DMdo5Io7B\nbMNddtkFKIpFG6ho/J627NRBQkVjHOyhhx4C/qec9CB0C1l1J0UTz8nr96EPfWjU78jW9ZDoFTji\niCOAch8w4+6d73wnULJZL7roIqCshVgPWNVxXU+La60XdJqT8djxdczo9X5h5q394zyOisj6HD0h\n3ltj54GYxVgVCzLmY21kHaSySSQSiUTr6EnZdLs3S8w2kn2bRWKGjU/dO++8EyhP41uWDLD/AAAN\nXUlEQVRvvRWAKVOmAKXvl/3BZB5mI+m7t5Ot9TgyHc+/qv9TE5BpRlWn0vFcZYuysa9+9atAySa6\n++67gZIxo03s9qq69PtVefJVO/D1ujNfG5BVWa1uv6YIx6Yvfr755gMKc7VOaxhVW10cdthhwFim\n6bw555xzgLHZYjfffPOo1/7fWrW6UNEI4x29oNeODmbOGY+s2pvFWI6K9sgjjwSKF0Avg2rN+4Xz\nZtVVVwVKJ2Q9Jda8Cf/fD3rdOTN6fewwoG28X1hr5jxQeaiQnT96ebw2UcHoHdILFf9vvLwbpLJJ\nJBKJROvoqYNA3Z00RezjJDv/whe+ABSfrOxJNnfMMccA5akts7Ay2B5JVRkdK6ywAgB33HEHUFRA\nVaypl9qSWLtjbCT6PGN/Nv8fK75VZbGTQKwMtkO27M+MLPPlVVbxePG4VXv/TETVvOpMdmb9VMSb\n3/xmoKg9v7fZZpsBZWwqnbqw0jx+r4l50S2M8VlrZLxAn7zZZypZffAqYdeMrN8YT10Y74zxskHO\nC9ev2aXGbJzTDzzwwKjPm7VorFgFE5XM6quvDpQ6PJWwayd2wm6yLq/XzDa/Z3xSNWZGrzFce6Gd\ndNJJQJnTqjpjOCof973xnlgVo+mU0Zt1NolEIpEYCrQSs5ERxBqRWEVv/rwKxhoRn7Kybp+qPrVj\nJwGPZwzIzAw7pRqrcf+KJlG1f0TsYFuVBSTD8fMyUyGL93Pa5IorrgCKzzVWkmsz1WQ83jBmYHnd\nvY5xXxJVn0xX/7Vjs17LTLxulU23n58delU0zgOVTVS2/l9fvczU2iQ/71pR8XaLqGgmAiqVqmyx\nL33pS0CZD8bwYnd5P2+s2HllHMtOJK4hM/yMVzSJuuuuynvkWFSy9nczI8/7hfVSZgBeeOGFQFHC\n2sYxR89HRBPxz1Q2iUQikWgdPSmbToh+P9mWf9/97ncDcOyxxwIlYyKydNFpPxp7YMkG9VObcSGj\niUynzR0eq865CvGchOrws5/9LFB8rdYIVfVA8ndiV19t7N+2d7nsBrFORj+0PnR3VLTv26KLLgoU\n26lozWabE+F1mD59OlD6d8lYrS2xDkumrCqUue6zzz5AiUcMA+rOtardJ/WQuAZUbbHfWNzRV6hU\n9HS4JjbddFMA1lhjjVHHEU12mKiL2AFAG3idnR/eUz0397Ey+8y4tvdC15j3CeNgZqn52msVs9Wq\nuoHXQSqbRCKRSLSOVpRN7HVl5oxPw5133hmAT3/600BRJN36M2Uc66+/PlDqMowBxTz9qrhJE51p\nI3r9vZj9YQxGZqtfWh+ttovZZzIUM7WMY2jjYVI0EbGORgVjXZRjifudmJ00jGOqC8/danhZt9cx\nMsvYd9A5f/HFFzd6Xq997Wv7ZvZ1r8unPvUpAPbYYw+gKJ3LLrsMKHU0dTsoC23o2vF8rNszzhXr\nguK4e7VFE/cZr78xvFjPd+WVV476qwqM+xRZR+Nrax1Vf967o4IZr36v7phS2SQSiUSidbSibHzK\nWidhrys7A8Ruq516rFVBZSO7Mwfdp/0JJ5wAdGZUyy677Jic/bbQraJQ0bi7oHEMGWzMk49MN/bI\n6uRzbYLB9gvPVT9y7L9krO9rX/saUPzJJ5544qBOsXXIMO1B9bnPfQ4o8UmZpxlV7uRp9qEs3pq0\nflFVj1UHdee8MZR9990XGLubpPGq6667rqfzML4RUVWvJ/qJU4xEN6omZuB5XePOu56T9VjaUGUT\nY7PeM1WL3kdUd75f9x4wzzzzzOpU33FMtT6VSCQSiUQfaEXZCOslZN/uoXDUUUcBY+MMEVW53z71\n9b0+8sgjQNmf/bvf/S4wtk6n6jjddC7tFVUVuVXnJgOxAlh/tT2J3JHT7ggi1u3EyuDImCL6YbCD\nwtZbbz3qtVXRc3KsJiLWRZmJd+qppwLF527807UmYseJftFPvKHu92TnMWPKuastuu21FnuoxUxR\n15b730RERTPINRJrCj0X7w/GdFU03mu9N2ozbanijbWQdtY3a83j+v+qMet9qINUNolEIpFoHX0p\nmypWrh/QLDR3TjRW89Of/hTo7AONv+/T3b/uU2Edjb2yZEiR3fXrc+0GsYo5Hjt2U4iQUVhFfdVV\nVwGF0Votb/wiKhfjV/p67fukT7aN6ui2oU2XWGKJUe/r4381Q2Zqhp6xmGWWWWbU51wrTdeGDEI1\nureT11nPh3GpnXbaqadzca3Zg9E1IlvXS1AFz8d+c3VjFL0gdvmO9S6eg/NBBeN8UKHETgFxl2Oz\n06x5vP/++4EyX7z/VGWv9tL7L5VNIpFIJFpHX8qmKs4gqzbDwVhNtztixviGXVut9FW5mKnl09ie\na1bZDxJmvEQfZ/S1ygh8HT9v3rvxKG1h11/ZVczIc696r4E20rfba+bfMMAxRZx55pkDPpP2oBJ1\nvjhPqnzmKlzhPIlV8HMC3LdKJaKa7zXLUA+L8S7jn64BO6uvt956AJxyyimjvh/ZfBuKJsajo1JQ\nycTPqWyih+LZZ58d9Ttm9Hnv9P6k98fX888//6i/2r7ujqJ1kMomkUgkEq2j0Wy0H/zgB0Dpwirr\nMlvo/PPPB8ouc/a4itkhPrV9+rrP9lprrQWUSl/9ku5F7x4PZuz41O5UadxkBwF9q9YExDx42blK\nxD01Ym80mYj+apWJe/pccsklwNhMLOty3M/iW9/6FlBsbfZIZCbD3FFAxI7YsR6nKTg/e63n6Aba\n3flhNwz3KbGKfrwqdhgb++u12/REIO4ftPzyywMlDmk/wB133BEocQezR2PHCNeUnSaswzKmGxXN\n8ccfD8BPfvKTrs578uTJjcV/Y4zN3/X6Oi/8v7EZla4x3JihayzGfYm8V5q9av/B2267DSi91Nz9\nWEVUpeZGdrXPDgKJRCKRGBo0qmzceVO2rkLR7ygzMQ5hPEElZIdaFYrV8j69hXuLf/SjHx31vS9/\n+ctAeYrXfeI2yeb9LcemElHV+b79vdw3xA621tFMmTIFKH3BZCSyP22ojz/2SJK1Pf7448DY7q1V\n5z3M0AcvzD5sGoNQNEK7O8fNJvr5z38OlOsbs4JUA3HPH1VeVSxwIhHVs2OQvbtWjJ3Yxdv+cP51\nDsvyvX+oBr3PeDwVzf777w+U6+uaqlIpMWZc1U26CcT9r7y32XXF7DEzMVUs7sBp3EmoSPz/fffd\nB5T7irWOUV0aE9aTUrUvV8ZsEolEIjGUmNQNo+20p7h7hstAzD5Tqci24p4rkUFEyCTMkJgxYwZQ\n/I0qKVldVa1BVVzCmE2T+6vrcxX2rrJfm7EVxyYbU/lcdNFFQPFP60t1571YOezYzNzRVqeffjow\nNlZTtaf4vPPOy/PPP89LL700sL3mO2GrrbYCxtZDyIiNW7WFJudFFYwvOi+E80KFct555wGlZ1qc\n04cffjgwtm9cU2jSFo4tZtzpCdlggw0AOOyww4DC0kf8/myP77pXAe+3335AyZKNtonV8p2q55u0\nhffEGHuJ3p1VVlkFgK985StAsWHMYvSvHQHMzDXO5U6/rh3j4NrE+0unvb/mmmsuXnrppVq2SGWT\nSCQSidbRaMzGPHm7qBpb0Ueq0rFOpkpV+VSWjRuLsYeRcYhOrC1m8FQdr414hWxIpmL3BHdYNNtD\nxmLGjVkk55xzDgC/+93vgMJQIvPwrzazb1jsKBBtVTXmYeosEPf0iXA+OJ/mpEysCDMmja3JqqdO\nnQqUmJ9ZQ5HVW19hzVGvthhkVmLsVO5aUN2r4ozF2DHEtaMaiLEUu2VY36d3oJNNooIZZLzLczcu\n6Xzwengv8/7hfcFMXG3oPNCDYmcAu7hoG8cW6/66jel206EilU0ikUgkWkejMZsqxIwaq1R9mus3\n9CltloldWPvN/qjL1gbhmxdRccgwPNeYZdaJecReSvFvtzt0DtIWnaB/+tBDD/V4QMk6tNt3W2x8\nImwhe1epWiuiDZwHjtn4Vdt7ETVpi273uYkZUY7ZjCo9Kt12hY7otH9NGzHeKnif8P4gYh2MNoox\nm073i6bWTMZsEolEIjEUaETZNLWT3URjmNj8iOMAnbv5xn1q+o1fDJMt4t4dUQ32C/3bu+2227j/\nn0hbxMpy54MKZ9q0aUCpw+gXbWRgxTlsd4ymdhGdKDQxL9qOkQ0qBpfKJpFIJBJDgYHEbOYUDBOb\nr4u2mMsw2kLWbTyr7foaMQhb6IPvNt7Q6/d6RZu26GWPlIrjAv2viU6/M4xrpGk0GeNNZZNIJBKJ\n1jEhymZ2lfzjvd/W8SLmBKYS6yvq2qrb780JthgUJsIWva6FhRZaCChdfTshdqAwVjNMbH5YO5IP\n4xqJMd2q3mZ1UVdtprJJJBKJxFCg23SevwCP9XvQQVbyd/G7U7v82UZs0S16tVGX35sjbDEgTIgt\ner3OdRWN6LJKfo6yRcsYyjUSs1T7jX/V/H4tW3TlRkskEolEohekGy2RSCQSrSMfNolEIpFoHfmw\nSSQSiUTryIdNIpFIJFpHPmwSiUQi0TryYZNIJBKJ1pEPm0QikUi0jnzYJBKJRKJ15MMmkUgkEq3j\n/wEP0qPq0cr5CgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"rows = 10 # split epochs into 10, so 100/10 = every 10 epochs\n",
"cols = 6\n",
"fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)\n",
"\n",
"for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):\n",
" for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):\n",
" img = img.detach()\n",
" ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise like 1s and 9s."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sampling from the generator\n",
"\n",
"We can also get completely new images from the generator by using the checkpoint we saved after training. **We just need to pass in a new latent vector $z$ and we'll get new samples**!"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZkAAAGRCAYAAAC39s6jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJztnWm4FdWVhveNcWIScEBBBBRBUVEB\nBYdGjVPHiVbj1BgHNImtJumgSWur7ZDY2q3RjlOMQ7TFJI5xwqgxYsQRFQFFQVQEZJJBAXGM5vSP\nfmr5HqjFrbqn9hku3/vre4q6dar2rjrF+s5aazeVSqUghBBCxOAbtT4BIYQQrRe9ZIQQQkRDLxkh\nhBDR0EtGCCFENPSSEUIIEQ29ZIQQQkRDLxkhhBDR0EtGCCFENPSSEUIIEY1v5tm5qalJ7QEqoKmp\nKYQQQqlUCqVSqanA42peCqKoedGcFMqiUqm0YREH0rwUSqZ5yfWSaWSSL/gQ/v9LvhasueaaIYQQ\n/va3v9Xk84VoUGZW88NifFdkOeY3v/n/X8dfffVV6t/9/e9/z/WZa6yxhmkesxK+8Y2vza+///3v\nmeZFdpkQQoho1CSSKep/Ciu8VVe5b5bPyXO8lvDFF18UfkwhRMvwvodiOB08Jj+X3zlffvllxZ/D\nYxcVvZCWfC8qkhFCCBENvWSEEEJEoyZ2WXM/fIXgh45Z9mkpMSwyIWpFPSS71DNZxiTLGHIf7/ie\nRZZmafEHe+87yTuvepxzRTJCCCGioZeMEEKIaNRVnUwW+6u5jAmGorEzRoSoZ3TPZydvplkWu6pt\n27amWRvHLFNaY8lxaJHx3/n96J0Xt2epk6mGvaZIRgghRDT0khFCCBGNurLLstBcSJclGyNp77Kq\nv/WOw+3t2rUzvXz58lWel0iH8+JlDhaVBSSyMXjwYNMcy8mTJ5v+5JNPqnpORcIeggme5UW4j3ev\nesWQ3GettdYyTXs/0Rz/JUuWmJ40aVKzn+99h3nWWefOnVM/q8hCTkUyQgghoqGXjBBCiGgUbpfl\n7f9VlM2RhIM8Bj+f4WWHDh1M9+zZ0/TWW29tesCAAaYvu+wy03PnzjUtiyyd9u3bmz7xxBNDCCF8\n9NFHtm3EiBGmR40aZXrmzJmpeurUqc1+piyyyuC9/+STT5qeNWuW6WXLlpnebbfdTDdaV/G0eyXL\n99A666xj+vPPPze9ySabmH7//fdNr7322qb5vcjx4nfRt7/97RBCCH379rVt06ZNM7106VLTfD74\n3cZje9Ydt3/wwQemYxV1KpIRQggRDb1khBBCRKNwuyxG/68soVtaNgT/jqEr7a9tttnGNK2wsWPH\nml60aFGLz6u1sd5665led911TZ9wwgmmN910U9Pf//73Qwjl2S0cN9ouHMPFixebPuCAA0y/8sor\npvPea7Q7Pvvss1x/2xphltO4ceNM81np06eP6V/+8pem119/fdO0iBr1OchSdMl7hvcSr59Wsbc/\n2WqrrUwn30U8BuHnkLw9HHmtzLSl1cbMWVrdLUGRjBBCiGjoJSOEECIaLbbLimq574WpDONotbDv\nT3M9hpjRwYyNI444wjT7C40ePdr0NddcY9rLnmlUayAvHMcjjzzS9LvvvmuaduWee+5pOpk7b61y\nr9cSi8TOOuss08cdd5xpzkuW4k1ZZD6cE68YkVmB5513nunW8BzkbenP7yGOHTPAvP1pM7/11lum\n58yZE0Iov5ffeecd016GGPGeLT7DfM6877ZKLTKiSEYIIUQ09JIRQggRjRbbZUWvShmC38eK2z3b\npbl9/+Vf/sU0Mz0Yxp599tmmGUa2BjsgLxy7Tp06mX7++edN09KidUYLcv78+SGEEC688ELbRotg\nww03NH3uueeaZpHsXnvtZfq//uu/TP/oRz/KcCVfk7dQuLXTsWNH0xwb7xkbM2aMaRYjtgaytM7P\nexyOKb9zevfubXr27Nmm//znP4cQQjjooINsG6396dOnm164cKFp2mj8TA9+t1XjmVAkI4QQIhp6\nyQghhIhGXbX6Z5jOQrHu3bubZi+ftOwy2my0c1j0x/CSPYBYdLk6WmQetEZoi7Hv0dtvv216yJAh\nphcsWBBC8MeT88x9LrnkEtNdunQx7dmoWUL9DTbYYKXzam3kKRDmmDHjyeORRx4x7a3Y2Ejwmj/9\n9FPTWVr9e2PLcWFRKy0y9oDj5ybbWcy88847m+7fv7/p8ePHpx6Pc8rvOc9Sq0Z/SUUyQgghoqGX\njBBCiGgUYpcVVZhJ62SzzTYzzYIkL7xLijdZxMnMJVphPPZ9991nmmFnXphRRXupllZCJWEuw372\nK9tiiy1Mz5s3z/R7771n2iuYTeD9svvuu5s+44wzTG+88camGeqzYJZksQDqwSKL3e8uzzG/853v\nmOacEJ4v7wlmSzXqkhe0qkjeeeG9R2uXBeATJ040ze8EZnol40hbl73NeF7sb8bCSW6nnZ3lvivq\ne3xFFMkIIYSIhl4yQgghotFiu4zhVyWhFUPwXXfd1XSWjAmeQ7du3UII5RllLGqincUQ9e677zad\n9zqYnfLxxx/n+ttqUIkdw1bu++23n+k2bdqYpk1AO5LjmMwdrdDDDz/cNNvH05bj/jwebZq82WX1\nQD1kLXbt2jWEEMJ1113X7L7s9/bb3/7WdKOM96qopBCR31uetfzhhx+apqXI+5n3cPL9R0s6KdAM\nodz+8o7nWf7efccx8M5LK2MKIYSoW/SSEUIIEY0W22VFhf0MDTt06GB6k002Mc3MDELrJgn12Gae\nGUq0tiZMmGCa2Rheu3OGlLTrWlv/JsJwnHN05plnmub1c9W+ffbZx3SS+fKLX/zCth144IGmaS8Q\njv8nn3xieuuttzZ9//33m64HG6pRSGzkLO3ie/XqZdrbv1F7wlVyrt7qkmz17y0HQGgLb7fddiGE\nELbddlvb5j0ftMWyFIl6cE5jrRyrSEYIIUQ09JIRQggRjRbbZV4xUF5mzZplmpZWjx49TDMcZWjO\njLGLL744hFBeYJWEnyseg8WdtM68VeWomb1GG8cLL2MX3xUJz5UZeE888YRprlLJ3ky0OqdMmWJ6\nxowZIYRyy43ZOJ4Fw8+/8sorTXPFUlqX9QzvPW8lwthwnDmHaVx00UWmWcBaVDv81gCvmd8DXias\nB5+F5PuP32tLliwx7WWUkUp6kXn2v3qXCSGEqFtaHMlUEr14/2Pmj1zstsz/MfNvTz31VNNJncxO\nO+1k29544w3TjFiY7+/9T9qDue88L49G+l+e1xqHY8Ruy3369Ek9DiPSpLWGt5gc4Vi9+eabpvkj\np3de9TzOtYpeCBee4w/SCRy/1157LXV7ayFxQ/L+r5/PO+9DRiN555rHGTt2bAihfFG/V155xTSj\nSs918Z6JLN9zvA7+baWOgSIZIYQQ0dBLRgghRDSqtmiZF8ZRT5o0yfRPf/pT01dffbVp1sFsueWW\npocOHRpCKA/tuMAW16ZnCxS2g/HWtecPt/zxzevi2qjw2phg8cwzz5geMGCA6ZEjR5pmywtaBskC\nZmwZtPnmm5tmiM65Y1sbtj/xfvBsFOusmrCrLhMzmISRwHF99tln455YjclTH5PlXuLxeD+zC/zC\nhQtT/5bPWZLsRNuatrG3sJpX68Lt/J7zbDTPgiMt6dSsSEYIIUQ09JIRQggRjarZZVly7GnXsDsv\nQz3W5wwaNMh0kjHDfbmQ1nPPPWd68eLFpmnRJN1pQygPb7O0cGhtdg1DZ2YjUbNVjMeNN94YQgih\nXbt2tm2PPfYw/R//8R+mmWnzwAMPmJZF1jI4Pux8nVg6HLMrrrjCNO/91X2MaWfx3qdtRL3LLruY\nvvTSS02PGjXKNGsD+X118sknhxDKFy1LsmZDKLftN9poo9RjsGaHx/FaZvFveXzONe3vlnTcVyQj\nhBAiGnrJCCGEiEbV7DLiheC0rmidMRwdM2aM6eOPP950YnUxu+LRRx81nbQ3CaG8kJSf79loWYqR\nVkcrIQ8cw/Hjx5v+53/+Z9Ncc54Fsx5ZFmJqpK7ARcNrv/DCC00nzx/H75JLLkn9u9Udz2ZiYaaX\nXcYu8bS92IKKHcmTwmXaU4899php2vncp0uXLs1+Prtp0w6dPHly6jFZGM/WNi1BkYwQQoho6CUj\nhBAiGjWxy/IWODF0S4r7Qgihe/fuphM7hiHtvHnzTNN+82D2SEuyKBqF2HYSw/Rvf/vbIYQQjjvu\nONtGa4Z9smgNMKOvkn5MqxscE9ooLPBLyNKBd3UkS289Pjfs1UdbnlYYs2KZGfbUU0+ZToot58+f\nb9tmz55tmt9h7NHIvowHH3yw6Tlz5phm4fro0aNN86cILvLIz60URTJCCCGioZeMEEKIaNTELssC\nsySoL7/8ctPsl5WErOzvw3Xns6y3XYl11EhFa7xOWmdeH7G8LdG5bvmtt94aQii3Lpndws/n8g48\nHovEiHderdnqbA6OFbP40mxGto6XXZYO708+E8zEohU2ffp008xA41jPnDkzdf/EomKfPxZUMitt\n3Lhxpmmj/eEPfzDN55A2HovU+QxxGZMiv8MUyQghhIiGXjJCCCGiUbd2GS0PZitx1TiGo08//XQI\nodxOY4ZS7AKzerfIaD8xHGdbd2bJcP8smXmERWOJBce25z/60Y9Mc768nlme/dW/f3/TEydOzHWO\nrRVaN+wXlzae/fr1s231fv/GJotVzDHkPrTCOI7sI8bj8zhcdiSxzmjt87mZMmWKae+Z5Hfl4MGD\nTT/xxBOp58Xz5XNG25XWYEsyUxXJCCGEiIZeMkIIIaJRt3YZQ8qlS5ea5uqZe++9t+mXX345hFCe\nUZal59jqCDNNuALlgw8+aPo3v/mN6bvuuss0Q2fO0bBhw0xfddVVphNLk0VfI0aMMM1Csvvuu880\n+8t5Ybkssv+HY7vjjjuapnVCWyRZ9sLL2lsd4XdF3uJfz2r0Vp2kHcbnL7GLaRt37tw59XM8TSvs\nkUceMU0rjJYXYYahd00t+dlBkYwQQoho6CUjhBAiGnVllzG8ZJYMezCxN8/UqVNNJ5YaQ9FaUY+F\nmTwPFkaSc845x/QNN9xg+txzzzXNeeGyCh06dDDNcDz53Kuvvtq23XTTTaaZMSOyw3l46KGHTO++\n++6mvUyg5Bnh0hYiHRY00nLyss48e42WZtrzwePzO4yWJv+OzxsL0HmO3nehd+4elfY6VCQjhBAi\nGnrJCCGEiEZUu4whYpZ+Usy02GeffUyfd955phm+Mrvo7bffDiHEL7r0ipRIvVhkHuyHxEwW9i46\n5ZRTTN98882m2abcy1LhXJ988skhhBBGjRpl27TyYnZYIMtxvfvuu00PGjTItDcnLExOimFX1+zL\nZIy8+5BjyIJvz37i8+5ZYRxrrzAzOR/2KOMyJ506dTJNq5PnyExcj7xZcpU+r4pkhBBCREMvGSGE\nENFoymPtNDU1FeIDMVxkeEk7gD17Ro4caXr48OGmEysmhBDGjBkTQvAtrLzktfryUiqVClvWMcu8\nMET2isS43Svk4/iOHTvW9MCBA01z7LbaaqsQQnkb/3qmqHkp6lkhHFfaL5wf7vPjH//Y9LXXXmua\ndkyDML5UKg1qfrfm4bx4z3iWvl0dO3Y0vWTJEtO08znO/Fvuw/5yiV3tLS/A702vKJr3QpbMuArJ\nNC+KZIQQQkRDLxkhhBDRqIldlsWK8lpvV1oYVC9U2y4rCs7Lsccea/p73/ue6QsuuMD0k08+GULI\nlslUD0Ws9WyXrcZEscta8LemvaLLWty3zPhktmgVzkV2mRBCiNqil4wQQoho1MQuW+GYprOcC7Oe\n2Na6FlQSJjeqXZaFWtsHlSC7rC6pC7usEjybP+1ZyfL8FLVyZZ7zSkF2mRBCiNqil4wQQoho1LzV\nf147pdYWGamnDJN6ohbX74X97P3FluhCVPOZ9ayrtM/Nci5e0XkWi8wrxs57DllRJCOEECIaeskI\nIYSIRl67bFEIYWaME2l0coaXPQr++NV+XrywP6dFVuS8rPZzUiBR5mV1tbULvO5M85IrhVkIIYTI\ng+wyIYQQ0dBLRgghRDT0khFCCBENvWSEEEJEQy8ZIYQQ0dBLRgghRDT0khFCCBENvWSEEEJEQy8Z\nIYQQ0dBLRgghRDT0khFCCBENvWSEEEJEQy8ZIYQQ0dBLRgghRDRyrSfT1NSkdQEKolQqNTW/Vzbq\nbV769+9v+tVXX13lvt6yybWiqHmptzkhyfK7DbTMx6JSqbRhEQfSvBRKpnnJu2hZ3dKAE1TXVLL+\n+SOPPGK6W7duqzz2uuuua/rjjz9u9tjf/ObXt+yXX36Z67zqAV47qeZ9u/baa4cQQvjss89s2xpr\nrGGaL3vvvCq5P7Kwwn8+Cl38LTk2r5OfR6r5H5/k3v7b3/5m2/LeL5zHr776qsXnknF+M82L7DIh\nhBDRaDWRTBH/m4r9v7NGIsv1e+PF6CXtf4j832GW6IX/O2vE6IXU6r7iPDCCSeB51cO9HzOCSDt2\nUdef9zuE85JEMDwGdZYxKWruirwHFMkIIYSIhl4yQggholFXdpkXaub58atWP6y2ZqvNywDzrnOD\nDTYw/eGHH4YQQrj88stt28iRI0337dvX9NSpU1OPV8kPmK2JSqwYzltyHP47j9emTRvTtCf5g/RG\nG21k+v3332/2XMg666xjOs26qwW1spmamxfe+7Sh586dm/qZlVxHUUkDK6JIRgghRDT0khFCCBGN\nurLLvFAvTwiYxWbzbIdKQs16sciKKm70xqhXr16mly1bZnrQoEGmN9lkE9Mbb7xxCCGE73//+7bt\nkEMOMT18+HDTlYTr9WjBpFGJrertn6XGI80a47nQIvv0009TP5P7L1y40DTt0Q8++CB1f85nPc/P\nqshi53vb82SJ8d9ZR+ZZZITbvdon71xi2dKKZIQQQkRDLxkhhBDRqLldVnRWFm0BhotrrbWWaYbr\n3nYexwv7vSyQWlJUERvnYs011zT90UcfmeZ4TZ482fTdd9+90vnw72gBLF261LRnb2aB5+LdUxMm\nTDC94447tvizspLWviTvPU4b8PPPP0/dx7M/vHs4oV27dqa9Ilf+XdKOJoRyS2358uWm2faH2Wi0\n4zj/ixcvTv3cmKTNC8lip3uZefxbz/7lPmlWZ2Ixh1A+nrQoCT+f8+J9Jq+bzzbvNT6vlaJIRggh\nRDT0khFCCBGNVmOXJaEpQ1SGmixk2m233Uz36dPH9GuvvWb6ueeeMz1//nzThx12mOlx48aZnjmz\n0EaxVSPL+NP24PgeddRRprt37266bdu2phM7gMe+9tprTTMTjUV9tNHyWpHedVTDIiPNWZe0KjjG\nHL9PPvkkdf8vvvii2c/h3NIW7tixYwih3Kpp3769adpynAd+Po/Hc+d50V7jZ9XCIiPNzYt3//D7\nxLMlea969y3tQmZlHn300SGEchuTGZwLFiww/dJLL6XuM378eNO0kD1LjzapZ5FV+h2tSEYIIUQ0\n9JIRQggRjZrbZVnCL4aX3J+hXhJishfWdtttZ7pDhw6mhw0bZvqJJ54wTcuHx9lhhx1Mz5kzxzSt\nBJ6jF6bWO17xFrcff/zxpn/+85+bppVCEmvk9NNPt20PPfSQ6c0228z0t771LdNPP/206by9sRoF\n2ky0XLj8gTcnHrwP+bedOnUyndhxvDdpBc2bNy/1vGiFeZmYhPt7mU477bST6RdffDF1n1o+Q15m\nKcfLuzZqZm7RmvzHf/xH04mlz4LW9957z/Qf/vCH1HOkzcUxz7sQHaGlfdpppzW7/6pQJCOEECIa\neskIIYSIRt3aZV6oye3MwunatWsIIYQDDzzQtjGLjBliLFjadtttTbOIkMdesmRJ6vl6WRqNZJFl\nOdfOnTubPvfcc0172TajRo0yfc4554QQyvsuEWbMcC5oJa0OePOQxebgfei142d/scQK5tjTluG9\nzAwxPhO09Lz9eX8wS47XQYuM1MszlCXj0sMrDOf3Ep+LrbfeOoQQwltvvWXb+J3E+erSpYvpnj17\nmubfMkuwuT52IZTfRz/84Q9Tr6klKJIRQggRDb1khBBCRKPmdpkHw0tmTLCocuDAgaaPPfbYEEK5\nFcYsjccee8w0Q9Tp06ebZgbaWWedZZqFmddff71pr5iuUWGWDDNg9t5779T9GYKfccYZpq+55prU\nfdJght7DDz9smvbK6kAWK8yzNlgYyUI+2igsgEzsX2b2JSuYhlBup9By4f0+ZMgQ0ywGfOONN1L/\nltaZ1w+sXiyyLGTJfqN1mFhhIZTP0csvv2w6ef44b9S0/JlRxixaFhxzHm+77TbT/D7lnBbV93BF\nFMkIIYSIhl4yQgghohHVLqukoIqhG60bWmS9e/c2nWS73H777bZt6tSpppkh5hVVHXrooab32GMP\n07QSvLbatPeSTLcQyrN2GgnaVcwo41i8+uqrplm81VzY7WUIMmOpNZDYFSyEpG1FO4NFlBwHb6VD\nr9CO9zbvvaRfGf+WWYPsQ3fDDTeY5n3A6xg5cqTp0aNHm2b/P9p43ncBMwonTZqUek2xoG3F5QoI\nvx+yZJDyOmlFsYibxcW8zsS+3HLLLW0bi1WnTJlimssBcG65Ai3n4o477kg9d2+c+T3LPmnqXSaE\nEKKu0EtGCCFENKLaZZVki7AAc/vttze9+eabm+7Ro4fp119/PYRQXrDEsJShLrPIdt99d9O0hbgP\nQ1baFMwoY1jN0Lg1sOGGG5qeNm2aaVosLbU3aMd4PbCKotr9sJIxydLa3rMKPfuFhZa8FtrCzG5i\nBtLBBx8cQii/95khRnuE80OLZvDgwaYvueSS1PPl8+H1SeNqpbHnf0U8i4x4K4Z68NoIx5f7cI6S\nfnDs4ccMWRY589y9zNYxY8aY9no+csz5nev1kWsJimSEEEJEQy8ZIYQQ0airYkzPzlh//fVNz549\n2zQLM5MsJfb0YTEYC5l23XVX01zpMi10DaG8MJPHJF4IWm2Y0cOiq7zQmuG4cCVLL+uuObzsFlqR\n3vIOvCavDXuWz60mtCF4X/HavRbxvJe4nfZLmzZtTDPTiNlT6623nunknueYPf/886a5yiv3oaV3\n8sknm2a/rCzzwDn0srcaCe97i/cz9+H1895ICsr5M8Af//hH08xmZTHmX//6V9OcOy7Z4BU38x7k\n/Bb1PRKCIhkhhBAR0UtGCCFENOrWLqNFM2PGDNPbbLON6bffftv0Pvvss9LxaBfsv//+ptl3iVky\n7LvE0JT9hbJYLtUoJPOoJLSlRXX44YebZq832iGeddgcnJdBgwaZvvLKK01zbn/zm9+YZh85wvni\n8Wkr1ApaZB7efeVlZXlFwSwoPu6441L/NslG4vM2fvx405zjyZMnm2bGJZcO4P5ZihRpI9XSIisq\n29ArqmXx6oABA0zz+2TTTTc1nRTHehlqfN6oee6zZs0yzXs/y/V5q6BWiiIZIYQQ0dBLRgghRDTq\nyi7z2n4zo4xhXK9evUwnLeNpf7GoicdgpgVb1NOKYTYa7Y68ITatgSyZN7WEtguz9Gj/sQhwiy22\nMM0iTZKMF7Ob2Ods3333NU2bi3YAixmHDh1q+vjjjzfNDMQHH3zQNJcdqAeytO5nZh81x4TWBvfh\n+LAvGDONknub481/5+ewDx/Pl89HFmvFW42RVDvTLEa2Ia+TReTDhg0zTduRhZTJPcB5effdd01z\nTPi9Qrh0hpeJ6d2Dns1faaaZIhkhhBDRqFokkyUC4P8CsixaxU7Jyf+CuDgQ/0fL/6k99NBDpt95\n5x3TrD3g/xoq+YGw3qMXwutkuw9GjPyfDGsr+IPzwoULTR9wwAEhhBD+7d/+zbYxqYPjzJYoP//5\nz02ff/75pvm/qvvuu8/0xRdfbPqggw4y7f1YXo15Se5n/g/Ru3/4P1NeI8ee9Sg8JiPtP/3pT6Zf\neeUV02x1lNznrHninDAZg7UT7Oq7aNEi097/br16H1LtOakEr70KtzNiT+t8HUL588FIJYFjwnnj\nnHv3lNf5Osu5ewkZqpMRQghRt+glI4QQIhpVs8vy/kjOH79oedAO22WXXUwntgzDcoaltMv4Q2mW\n7rc8pheyVrvDbwx43hzbJ554wnQyziGUd7ympcWxTmqSrrjiCtvWt29f01z4jHVKY8eONc26gief\nfNI0LTL+mEoLtHv37qFW5Fm8jVYRr+XNN99MPR7vYR7n4YcfTv0sHj+5n7kePOvMeDy2LKGlxnFl\nTRPPkc8Nn2HPFvNastSjjeb9YE67jD/833rrrabHjRtnmlZn0jWedWm0rbOcC60tLgjImhlvjrLU\n97Xke06RjBBCiGjoJSOEECIadVUnw7CYWRLDhw83nSy4FEK5pZOEbsx6oRXGzByufU7bgTnreVvD\nNKpF5kHLi9lG3M52L6eccoppWinJuuSso/n1r39tmnPE8J42AjNdmI3DzCvaAZdddplphvfsVuzZ\npNWE9wzvQy62xwwl7s86JtoybCvCZ4E6sb1+8IMf2DbWl7GOqV+/fqZpjzKz0OsUzWvifHK7R71Y\nZFnqmvhdxUUVmf3KRcAIrzNZiIzWIrs0swbGqzvi8Widccz5PHn1SF7NUku+5xTJCCGEiIZeMkII\nIaJRE7vMKwzy1pvmQjz8W25P1h/nQlpPPfWUaXZyZtZZFovMyyJrzTz++OOm+/TpY/rUU081/cMf\n/tA0w3FmBiVtTn71q1+lfg7XmWdWGMN1Ho8dtHm//OQnPzH96KOPmt5hhx1MT5w4MfUcYpMlI8fr\nZLzzzjubZiuX5H4Pobx9Ei2Vl156yTS7LP/DP/xDCKHcWmOGGNv40Gb2Mi7ZeZia88ZWNbRxsrSb\niUWWDDbvnPj9xIwyZr/yb70FxDimSddmZhfSZvTO17PxvCJRQmuWFDkXimSEEEJEQy8ZIYQQ0ahJ\n7zJPewVmDKlvvvlm0z/72c9MJ1YCC8a4IBCL/rJkjGTZXo8U1cmWx7nqqqtM77nnnqbZ5ZeZW7QX\nk35k/fv3t23smMweZVzkiR2h2dOM9gE/M7GAQijvTUd773vf+16oBd49w8wxz06iJXzkkUeaZpHm\n5ZdfbppZYl6B56RJk0IIX2f9NRHhAAAgAElEQVQzhVD+jCUZgSGUF85yATPuz8JpzhXvvywFzdXG\n+2yvcNSbR2Zf8v4cOXKk6ddff900v+c4Lokdxn/fcMMNTfMeoXXmFWByYbmBAweaZnGz933B6670\n+0+RjBBCiGjoJSOEECIaVbPLGN4x/GJ4R0uF4T17Wh122GGmmW2ThPgsymPhHkNjb8EfhoJegVm9\nFIl5FLXYE20aFlcyZGeo7VmgSaHad7/7XdvGJRWY9eJl7NDWoaXGzzn66KNN8z6ijVYP8Jy9Ndg5\nrsxE4nPw2GOPpR7/3nvvNc37nPdzUsjJTCgWp/K54jnSCqItxs/hdfCY3vVVY3Eyjyy90jzb3MuK\n++Mf/2iazw3H0SuSTKx+FnfyeePnZymW5FIOzDpk9iD/tnPnzqY/+OCD1GO2BEUyQgghoqGXjBBC\niGgUbpdlaZHPdeKZmcHCPBaHsdcYQ02uGpdkzDBzgqEms84YOmah3i2yovAsAPa9Ouqoo0wz64yr\nUabZJ8wEY38nWjO0Tvn5zLChvfDCCy+Ynjp1qmlmHfL+4v61wrNeveJGjgNXevUygbwVNvksJMfk\n2B977LGmmdnHTDOeF59DPs/MQPNsliwWWd4W9JXirTSZJSv2z3/+c+pxWPTN6+F3EfdPxoXfd8zg\nZEEtrUgeb6eddjL905/+1PQxxxxjmvYzYSF7kZm2imSEEEJEQy8ZIYQQ0SjcLmMIxewKZhQx5GIx\nHtuXs3cW7YB9993X9OzZs00n4SMtF2ZLsE05bQRm7/Dciyq6rMdCTi+TxuvRRvuE4zVixAjTzHZh\nVktige62226pn8lVN3mPsB/XaaedZpot5vfee2/TXobNP/3TP5mulV3GsfTGmNs5lrS5SN4iYhZ+\nJvPPLCPakFxC4ZVXXjHNZ4iWM/tyeZZSlnvfG49qkGU8aRfyfuP+fLaYIel9t3BeEhuZ35u0uR55\n5JFUze9B9qvjsiieHUiyjL+KMYUQQtQVeskIIYSIRlOe8KepqSlXrORlmrGnGHv6sNirffv2ptmS\nnGE6V/AbN25cCKE8pKd1Nnfu3NRzrHTVt5ZSKpUKWzMg77zkJUtL9OZgoWWW5RWYMcMVBp955hnT\nlaxumbZkQ6lUKmxessyJ17fPy77i/UwLk2PF49DeIYldTFuOxaxjx441zRVNaWfyWc1rhbXgORtf\nKpUGNb9b8+R9Vnjve5YT7XeOOVfu3X///U3zu2ibbbYxnbTd53dfz549Td9+++2maXVOmDDBNDNB\ns1iO1ZgXRTJCCCGioZeMEEKIaOTOLktsryyhGFfvo82V1nY8hBB23XVX0wzdWOzFYksWFSVZT8x+\nYv8dr7irXjK+YlNJWFxEMWpaMeCqoKXm9emqhGrMe55nJUu/LNqD3v1Me4ct+LlPMrYsqKQVw8/k\n88RMKGaUedA6or1Wa5Lr8+6BLN8VHCPeq7Qrn332WdO8/9lbr2vXrqZ79+4dQghh9OjRto2r+zKL\njD8zeJaeR7ULXRXJCCGEiIZeMkIIIaKR2y5Lwqss9osXUrO/0UknnWSamRFDhgwxzbCb2S7sXZbY\ncV62WIxCy0bCu+ZKMsfyWHBFWXTdunUzzfmvR5JnhfevlxVG64p4BXLUtGKY6cRstAEDBphO7Bja\nbzwvb5kFWmeE9gvhMT1qUaycfE4WmynLc+PNBZk4caJprgzLjL2k5x4zZNlfLu+SI2kZlCuebzXG\nX5GMEEKIaOglI4QQIhpRizFXcRzT3ufnLd5LjpO3RXWteovVYzGmV+xX7T5SITT+vOQtxqzkGr1+\nYSy2pKWVPE9e5pS3oiYzp5gtFuP+WCEDqmbFmBmPmbq96CJV73M4X1VeaVTFmEIIIWqLXjJCCCGi\nUXir/yxkCSO94j0vkyXZxzt23u1ZqMc2/nnxiv1qTex5KaIfW6UUdc9kWYGS1llib9H+8ixpFgty\nxUbvOfTI+6zUwqJtKVnuMe7TXDF4lmJQzmclFpmyy4QQQjQ0eskIIYSIRk3ssix4oVutw+jWYJGR\n2NfQpk2bEIJfyFcJlfSjq5VFRirJSvLwio7Tij29AlCOKy2yvCtXFmXpVJuinvGW3mNZxraS8fRs\n0lgokhFCCBENvWSEEEJEI69dtiiEMDPGiTQKBdlLPYo4CKjbeYlhkyVEsE6LnJdm56Re7da8fbw8\nCrTINC8FUqBFlmleclX8CyGEEHmQXSaEECIaeskIIYSIhl4yQgghoqGXjBBCiGjoJSOEECIaeskI\nIYSIhl4yQgghoqGXjBBCiGjoJSOEECIaeskIIYSIhl4yQgghoqGXjBBCiGjoJSOEECIaeskIIYSI\nRq71ZJqamhp2XYB6Wza5VCqlr73bAhp5XvISex6LmpfVaU6qwKJSqbRhEQfSvBRKpnnJu2hZw8L1\nxr1Fe+rtRZSHZF32CAt5VcQaa6wRQsi/3jnngnjrk1cyXy09x0YlGdsGusfrckE+kW1eZJcJIYSI\nRtRIxosM2rRpY/rTTz9N3aelJP+jD6H8f/VZlhzl3/JciooOYkYbRRyzW7dupufOnWs677xw3lsa\nHfAzOS8FLum70vHrLQpcEe/e9vCev0Q3cuRea0499VTT1113XQ3PpLq0b9/e9EcffZTpbxTJCCGE\niIZeMkIIIaLRlCdMLiozwwvTvR97uU/yI20I5ZZBYiV41+PZC55F5h0ny7lnGdN6zC6rtX3ifT7n\nnPZblvulS5cupt9//33TnvVUz9llWa6XNGeveeNah4wvlUqDijiQsssKJdO8KJIRQggRDb1khBBC\nRKNqdTIM9akZ0jNk90J5L6xPtvPYffv2Nf3BBx+YXrRokWlaDW3btjX9ySefmN50001Nf/jhh6aX\nL1+eepxGJYtFmGX/PGSx6Lw596xTHocWGan3TLI0sthiXlZk2jNX5xaZaCUokhFCCBENvWSEEEJE\no/DssqIylPIWnjV3DJ4XW5N88cUXqft4VkLXrl1NDx061PT9999v+vPPPzftjUHR2WXNtQrJO55F\nFf6lWW3evzdXPBhCCGuttZZpzh3ZYostTC9evNj0kiVL/Av4+rPqNrusBedgep111jGdFLRyLD/+\n+GPT6623nmkW3HFc33nnndTPjGRDKrssEttvv73pSZMm5f1zZZcJIYSoLXrJCCGEiEYhdllRRV1F\nWG20eYiXicTP5Pa8YX/eDKxq2GUciw4dOpimbeSNObtWr7vuuqa9fkUcX5L8LY/HzD1u5zFoabK/\nHc+XxymKerbL8lqYtMOoBw36f4djwYIFtm3p0qUr/fuKf7f//vubfu2110yPHTvW9MSJE5s9rxY8\n2w1plxVh+dc5ssuEEELUFr1khBBCRKOQYsyiiroqyUZLbJS1117bttF+oS3D7BkWZn722We5PpM2\nUt6/LZq0sWOI7mVWZen15llkvH7acSyC3WabbUII5UWs/DvOFy0yFlE+/vjjppctW5Z6LiRvD7RG\nIYvlst1225k+5JBDTPfp08f09OnTQwjlY7Pjjjua7tWrl+mOHTuanjZtmukbb7zR9Pz58023hqLk\nomilFlluFMkIIYSIhl4yQgghotFiu6yolvd5P4uWB3uNHXrooSGEEA4++GDbxpUeZ8+ebZpZNTNn\nfr1MNVe4Y18ywowRZj3VC0XNixfqe3MxbNgw08cee6zpZLzGjRtn2/r37296woQJpjfffHPTbNHP\nvnNjxoxp9tzz9kCLDW3ALCu05oVW8DHHHGN6p512Mt2jR4+VNAswt9pqK9MbbLCBaRZxdurUyXTn\nzp1NM9Os1stFNDLJs+IV0bL4mKsLDx8+3PRNN92Uun8tUSQjhBAiGnrJCCGEiEaL7bIYFhmtKBaB\n0eZg5gszXIYMGRJCKLewJk+ebJrZTcy0uvPOO02z55i3BEFey6Xa9sEqij8LOT6vp3fv3qb//d//\n3TStlGQO2BfphRdeMH3AAQeYHjBggGlaQOeff75p2mvsS+YR26rKQuzP3WSTTUxzTpIeZSGEcNtt\nt5lOMvr4rKy//vqm33vvPdM777yzae5PO5nXJ4ssHVrL2267remTTjrJdGL1M/t14cKFpnv27Gma\nzwefycsuu8z0UUcdZXr06NHNnmOs7ypFMkIIIaKhl4wQQohoFJ5dlhfaGcw6oqXFgrDrr7/eNDNi\nEquLtswll1xi+vnnnzfNYkEWY+bF601US4ummvYcLTLO0Ztvvmn62muvDSGE8OCDD6Yegxbl4Ycf\nnrqPN7ZZoL3J4sSHHnrIdKNbPLRULrjgAtO0E1n0msCxfO6550wn1nMIIWy88cam58yZY5qWz8sv\nv2yaFl0WS70e7MwVydKH0NuHNlZSiBxCCOPHjzft9VdMuw/5XGU5R2ad0Trj0gxTpkxp9vN/9rOf\nmf7v//7v1P2zokhGCCFENPSSEUIIEY1Cssvat29v2utz5cGeVxdffLFphpS//OUvTbO9O4sqX3rp\npRBCCKeffrpto13AMJb9nWjFvPHGG6Zps3gFiCxao2VBy6DaxLB+eM20tPbee+/UfdjuPbEJmJnE\nArOrrrrKNItryYwZM0xXYm96ll2jw6I7WpV8htq1a2c6scP4fLAvGZ8rFjTvsccepmk9PvDAA6bZ\nc47PFu/Lfv36pe7PottqW5g8V8/OIjw/rpB7+eWXm2YxbJbjJNYxx4R2Gb8rs7DRRhuZ9lYy9ajU\nIiOKZIQQQkRDLxkhhBDRKKTVf16LzOs/lrQgD6E8G4Z2wKhRo0zTOkuyYxhy0+ZiqLnXXnuZ7tq1\nq+m5c+ea5nG8rBfaCgy3G72l/IqwNT/tSG5nlhjnKGnNz31ZGLbpppuapk3BMT/66KNN5x3P1aHd\nuneNtGKYJZZkoHFFS9pszD5icScLmp988knTtIe9LDIWV9OWrheyWGTcZ4sttjDN551WPK+f31Uc\n6x/84AemkzFi5t5BBx1kmiuT8jP5OVxyhM9qLZ8DRTJCCCGioZeMEEKIaBRil+UtAGQBFgsm2Q6e\n/a/mzZtnmgVhDA0Ty45ZZGwdf+WVV5reeuutTb/77rum2frcs2UYdjLzgys21jK7LAbdu3c3PXDg\nQNO0NJldx3FM7JYtt9zStm2//famee/QcqOVM3XqVNONXjhZTWip3HvvvaaTVTK5WiYzAmfNmmWa\n9ziPd99995lmxp83P7S8G3U5AD77tPaZdUebl+PFpSv4fKTB3n6333676XPPPdc0nwkWXdKW5Hdb\nLW17RTJCCCGioZeMEEKIaLTYLttss81MM7z2YGYG24pfccUVpmmpvPXWW6YZjtOWou2WhOAsDD3x\nxBNN77nnnqnnxawbkqU3EbPq6iWLjNl6zYXlK+JdM4/j9Zpipt3ZZ59tOrHXaBfQRqC1yGOwd1KM\nzBiv71xrgjYns8SS8WfGHy1MPkNcOfaMM84wzeUA8o6fZ5FV20bjM8t7Mu/f/u53vzN95JFHmqbV\nmGcVXY4nLWQWpbMAlt+nLORkFlstbUlFMkIIIaLR4kgmS/RC+D9Hr5spj8lcfa+tC4+ZaC7gxAiI\nP9Txf9Vsp8H/2fF/7zxfr91MjEXcWkLe6IXwvDm2HFPWSrD2iD8iM88/+SGS48AIkOebdGwOofyH\nzRi01uiFczhy5EjTvN7kR3gm0TAyYe3YRRddZJr7x4jcq/2s5I1eCMeZi4mNGTPGNKPDPPDZY3LN\nEUccYXrQoEGpf8saNXayryWKZIQQQkRDLxkhhBDRKKROxoMhJcM+/sBL64Thq7duOH945/ZksZ75\n8+fbtnvuucc08/R3331302xxwuOxay3PhTYBf5TLQjIejVAbwOvkD4ivvvqqae/HfLbcSIP1TbQo\nn376adOcr6JobuGs1lDftOGGG5r2ugAnFiUtMta9cFG/pUuXmi5qfBq1TobwGpikdOONN5o+5ZRT\nTNM6Y/LM5MmTTSc2GWtdWNPHBen4fcp5ob1ZL2OrSEYIIUQ09JIRQggRjah2GWGeOK2V5cuXm2ZW\nBUNKWmRciIedkpOsJ9o8XhfYXr16mWabFGaa0RZiaEzrzAv7vTC1XsJXD14PNTPA2PqHc7fPPvuY\nZg1VkuHCzrs77rijadqSv/3tb01znXlaNpWMofe39bK2fB44P6z1uvDCC03z3ub+iU12zTXX2DZa\nPrSQubAZF5vLU/fRGmG2HjXHiwt/8T4/9NBDTTPrNW1M2TKG9jRhh+d6/I5RJCOEECIaeskIIYSI\nRtWyywizIbxCR8KiP9petHGSkJXWGhfE+td//VfTzDpjphMtA56jZ8F58BwaKWMpy+JX559/vmlm\nkXERK87X+PHjQwjlWTK0Y2id3nXXXaZpxdWjBVAtvMW02Pplhx12MH3MMceY5tjyPk8sHY4xMz5p\n2zCLic9eJXYZ57M1t/ehDcvCSNrCad+RzERjYSzh9wrt0nq0MRXJCCGEiIZeMkIIIaLRYrvM68br\nWWTeds8KYWjOjDIWb6b9LTNq/vSnP6Xuu9tuu5lmrx+GmlksMi+7rJEsMsLroXXhXT8XKuvUqZNp\nFlUm48h7hHaa9zmtzTppKV4hMu9Pr88fC1ppS91xxx0r/TuLYvmZJ598sulbbrkl/wWkkBROh1Ce\nGdWa4ZjSxuQ8brXVViGEr+cnhBC6detmmr3jkn1DqE+LjCiSEUIIEQ29ZIQQQkSjxXaZV8DmWS4M\nx72/ZUhPu4xFYJtvvrnpefPmmU4yyR5++GHbRluGn8kiNBYJshdZloymvFlPyfXFtII8C8/L4smy\nOJu3P7OTuJ54mg1zwAEHNHuOtAmqaZfVc085L/uSliwX5ON9zmfu8ccfN/3QQw+FEMptK2aRfetb\n3zJ94IEHmv6f//mf3OefxupikXl4WbTnnXdeCKHcIuNzy2xaPnv1jiIZIYQQ0dBLRgghRDQKL8b0\nbA4vA4K2GC0a7v/666+bpr3FgrQzzzwzhBDCeuutl/o5PMbtt99uOm+hZSVUwwLKW+jm9VyjfUIL\nxuvZtGzZstTPTQrFjjvuONtGu4wWJVvPV5N6tssIx61t27amaaNQ02a+9NJLTSd2FXvCcXVHZnNe\nf/31plnQ6Z1XvY9hvcEs3cSm9FYRZkFzI6FIRgghRDT0khFCCBGNqvUu88Jo2lW0X7iddg0tgBNO\nOMH0iBEjVjrGokWLTO+6666miyqW9Iqq6oVK7DlaI174zu3UgwYNMp0sq0B7h+fFTDRmO1WSPZO3\n8LeeCz95LbS0dtllF9NcDZOZW96YJ23nmcVE7rzzTtO037x7XBZZy+nXr5/pjh07hhDKx3n27Nmm\n6/k+XRWKZIQQQkRDLxkhhBDRiGqXZen5lSXriXjtsxOYRTZs2DDTMfr7ZLHImD1Ha6je8YoAvYw1\nbqc1efDBB4cQyrPVaFdOnDjRdFEFZq3JvuG13HzzzaZpLbJvHJ8P9pZjT78ePXqEEMrnjPYo5ySL\nRaPssnzQZucSGclPARzzm266qXon5lDp/CqSEUIIEQ29ZIQQQkQjt12WhNheEV/ZwZ0VIosKqefO\nnWv6yiuvDCGEcMUVV9g2ZpfVimpYZGussYZlDLHAzsMr5MsC545ZTV26dDFNizBZmmHy5Mm2bf78\n+aYfeOAB08wcbA39rfL0qqOFwqwv9t/jvZ3c7yGUr4zI4lb29ps2bZrp7bbbLoRQbrldd911plkg\nmKWfnyyyfAwZMsQ07/kEfmewz2KtqHR+FckIIYSIhl4yQgghopHbLktCf6/gjXhFj3mzFWi7EfYu\nS+wiWjWV0EhZYV999ZXZZBwTriLKMc9rkZEsx2GL+aeeeiqE8PVSDCGEcNttt5lesGCB6SzZZd6K\nrN45Zrm/YvUuy1M8xwy+WbNmmfaWvOjbt69pWpUbbLCB6f3228/0uHHjTCfWJa1V9p4jWa7BW7Gz\n3m20LL39ioI9FZnpx2clgc9BI7X091AkI4QQIhp6yQghhIhGi4sxqxkKMwRPCslCKLcPLrroohBC\ntuyqLHhWDKnHIjTPIivq/Ly+Y2+++abpq6++2nRSBMtiP+9cWLDpkWVe6mUuioDjPWHCBNN8Jlh0\nOWfOHNOTJk1KPWaerMssllJRvQCrTWyLjN9P7DtHS5PnkFjH99xzj21rVCuSKJIRQggRDb1khBBC\nRCNq7zKPLD3NvH2GDh1qevDgwaYffPDBEEJ5SOkdjxkdXk+zLOFovYesPD9mnTErLEtRrQfHmmH9\n4sWLW3RMFh5W0msur01Yz/NIK8rL6Gxp9mMWK6wSS4nny2JT75rqZR68IvK80CKmdfniiy+a5jXP\nmDEjhBDChRdemHqMRkWRjBBCiGjoJSOEECIaTXlC1KampprEs1lC6rQ+UdUMxfMWdpVKpearWTPS\n1NRUSrNSYlxzNQvYmoPX7C0fkaV4kxQ1L96zUo/2UCwKLGgeXyqVBjW/W/PU6juspVTzfmnBZ2Wa\nF0UyQgghoqGXjBBCiGjkzS5bFEKYGeNEVkWW0C3NuqmmHZHTOurR/C65WFQqlaoyL7W2yEiWzLgs\nFhkocl5Sn5XWbpGRAnv+RZ+XeqWa90sLPivTvOT6TUYIIYTIg+wyIYQQ0dBLRgghRDT0khFCCBEN\nvWSEEEJEQy8ZIYQQ0dBLRgghRDT0khFCCBENvWSEEEJEQy8ZIYQQ0dBLRgghRDT0khFCCBENvWSE\nEEJEQy8ZIYQQ0dBLRgghRDT0khFCCBGNXIuWNdr62PVMUWvJh6B5KZKi5kVzUiiLSqXShkUcqN7m\npampaSXNhQG/8Y2v44B6WDBwhfPJNC95V8YUQohq0zArWeblm9/8+it4zTXXDCGE8Mknn9i2Nm3a\nmP74449NZ1lski8wkuVvvZcbz2f58uWZ5kUvGZEKb1Ctntr41Nv/iOuBSr6EK4EvFi4PnmjO1fLl\ny3Mde4011jD91VdfNbu/Nwa8R7hP3vMJQb/JCCGEiIheMkIIIaIhu0ykQssgi9WS+MkhlIfpyf6y\n36oP5y2N1X1OKrlmb+yy2FVffvll6vZkvvr27Wvbpk2blvo53nPIOc9il2UZg0rvDUUyQgghoqGX\njBBCiGg0hF227bbbmp48eXLqPknGBsNIZdEUQ5Zx9CyAddZZJ4QQwmeffVboOYl08mQXxbbI6t2O\nq+T8vP35rKy77rqms9z/yd9OmTIl17kQZqsRph7zXLI825XOoyIZIYQQ0dBLRgghRDQawi6jRUY7\nIK39wrXXXmvbFi9ebPrHP/6x6dNPP930ww8/bHrBggUFnfHqB7NaOEeJjcZtDLk5/iNGjDBNq0fz\nsmpoZ2TJKErmokOHDrYtsTVDCGHp0qWmP//881zHJpznYcOGmR49enSLj1kklVh4a621lmlaVHwO\nvvjii9S/9eyntMLIvNliHuwiQLznslevXqbfeeed1HPMOn6KZIQQQkRDLxkhhBDRaMoTMtaqgylD\nxo033tj0Bx98YHr48OEhhBBOPfVU27bDDjukHoM22/z580337t3bNDMwYmTGrC5dmJNwnMWaHTt2\nND1p0qSV9g2hvBngYYcdZnrChAmmY2QPxu7CXEmmTt7+Y9x/7bXXNp08KwcffHDqeb3//vumL774\nYtPsW7Vs2TLTtIsiZZGNL5VKg4o4UJZnxcvQ433L6ye8fn6fzJgxwzTnjjbl+uuvH0IIoXPnzqnH\nmznz636U3ufnfSa8eyrjfZppXhTJCCGEiIZeMkIIIaJRV9llXttpZnIsWrTINMP0//3f/w0hhNCu\nXTvb1r9/f9MMC6l/97vfmWYmTT0Wj9Ub3nylbWd783322cc0rYn11lvP9MKFC03TJmj0ecl7/hzL\nvIVzZO+99za92267hRDKLUk+E+eee65pPhPcnzZSJRZgt27dTM+ZMyfX38bCy+JasmSJaY5Xz549\nTXOMmNHVr18/04ceeqhpzsuAAQNCCOVZaePHjzd9zz33mH755ZdN8ztx1qxZprPcL8ww5PV5KLtM\nCCFEXaGXjBBCiGjUlV3mhV9Z+v4kRX833HCDbTviiCNM77rrrql/t+WWW5puDb3OaC16xWBFwYwx\nkmTJhBDCp59+GkIoD7PTijVDKLcpevTokbp/o9tleamkpxZ7Z7399tumP/rooxBCCI888ohte/bZ\nZ02ziJk2JzU/p5IiwXqxyDyyWPi0c2k/de/e3TTHn5b+hx9+aDoZizvuuMO2sdX/a6+9lnqMrl27\nmp47d65p/pzgXYdnkXn3nXqXCSGEqCv0khFCCBGNurLLioAWEUNRwpCP4WVrILZFRuuqS5cupnfe\neWfTL730kunEjvSK937961+bZiHtu+++a1rLBGSH80Pb8r333jN9wQUXhBDKi5X5d4R2Ji0iUlR/\nrXrEsx+Zdcfr573NMd9xxx1N9+nTxzTt+vPPPz+EEMKjjz5q21is2b59+9Rjcx8WjHpWWFGZgVlR\nJCOEECIaeskIIYSIRquzyxj+sXeQt0+S/RRCvlUFGxlmhXkr6XlwXGgZPPXUU6n7zJ49e6VtL7zw\nguntt9/e9BNPPLHS34UQwgYbbGCabegbBdpWzNyKAa0b2sWc57Zt2650XiwWTAqbQ/CtSmaa8T7I\nAp8/tpSfPn16ruPEwrOQvNVf2Rduv/32M00r/uyzzzY9dOhQ07SWn3vuuRBC+XcSx59zSOuMthgt\nPT7nLBIdPHiwaRZ7etenlTGFEELULXrJCCGEiEars8tYmMQsDq8HFG0cZmkwvGxt5LXIPNhfzCu2\nZPieQHvlrbfeMj1kyBDTzLphGH/RRRelHscL42m1McMtdhYeqaZF5lkeHJ+kRxyz+ZiV9Pvf/z71\n73hs2mV5s/94T9S7RUZ4/dz/mGOOMc1eZFxRkvchbUyu0pv0HePn81niZ/Jc+F3FZ9v7KYCZm1l+\nFqg060yRjBBCiGjoJSOEECIarcYuS8LBN954w7bRRmDIx3CVWR+rW1+sSuF4UdN2TNqa0yIZMWKE\n6Xvvvdf0RhttZJorlgeQFzQAAAn/SURBVLJ/kzenHmyD3lrxxsHrxZcUYw4a9PWihnfddVfqvrRl\naDHmzSgjbIFfS/JmWdKu4rIUzNJr06aN6cMPP9z0zTffbDrJIgshhDfffNN02jzyM3mO3vjzmrx9\nuKKwZxPmXYV1VSiSEUIIEQ29ZIQQQkSj1dhlJ554YgihPFwltE2YueRZPqLlbL755qbPOeecEMLX\nBYAhhLB8+XLT7J/FsJwWxIQJE0xXMyusUfBsDm7n6o3JyqR8Vg477DDTF198seks/f8albzFh8zQ\noiV8yCGHmGaRJHu9sQDyL3/5i2lm6SVzx22bbLKJaRYi8xni53jWlvc9t9lmm5nOu6pmVhTJCCGE\niIZeMkIIIaLR0HYZMyn+8z//M4Tgh7rDhw833Yj9r+odjvt3vvMd08lyAMyMYXjPFf5uueUW0ywI\nZNGnZ3GIleGcsBgwGXNaa3yWvOejNVhkJMvqjxwj2ljMHLv//vtNH3300aZpEW+33XamDzzwQNMP\nPvig6WTFUh6DlibnhVmZtPGoWSTLZ4jnVUmWYFYUyQghhIhG1Egm9oI4/B9xWp47f7x65ZVXCv98\n8TWsgznqqKNMJ/9T4v8CJ06caPqvf/2r6WuvvdY0f+BvzR2xi4bPGZ8/1o8lzwLb+IwePdo0u/q2\ntuilEljHxXE54ogjTHfo0MH0lClTTDNi2GOPPUwzISOJZE466STbxudmwYIFptkSiFEqO2hfeuml\npvld6bUB4vWxFVKlbagUyQghhIiGXjJCCCGiEdUuix1qMwRkXUUCw/4kFBXFwR9F2Spmiy22MJ2E\n+7QuR40aZfqxxx4zzTBeNk12aIsRr9s4fxxOeOCBB1L3rRXVWHs+y2eTpL4ohBAefvhh0/vuu69p\nLlTG54AdkV9//XXT/A7bf//9Qwjl18uOyVzgjMk1TA6g1cbnkwsFvvjii6ZptT3//POm0+6REMrt\nu6xJOIpkhBBCREMvGSGEENFo6DoZ5psnYSdD/bPOOst0UQt1re6wnmLYsGGmr7jiitR9Eth59557\n7jHNbsuyyFrG9ttvb/r99983zQy9rbbaynS/fv1CCOV2Cus+7rzzTtNFthfJQzXuBc+So+7bt69p\n2km0dtlJ+eSTTzZNO4l21dChQ03feuutppPssaeeeir17zhfe+21l2laW5zz448/3vTaa69teurU\nqaaZdUsrLMvCbVlRJCOEECIaeskIIYSIRkPbZRdeeOFK21j0dPfdd1fzdFottBXYtfXqq682nWaR\nEdqVyiKrHM5Jp06dTPfu3dv0M888Y5qdxxPbhcfgc8O2I605KzNLBhutMMLCxaefftr0wIEDTbOD\nMhc5W7ZsmWnacY8++mgIoXxRM44/5+W6664zfdFFF5lmphktarakoaVKO5TPKLtJV3oPKJIRQggR\nDb1khBBCRKMh7DKGtcyA6NWr10r7MPzjvtRekZpoHq4PztCcY8osmCTbhX2XaO+wYJbIRls1vJ9f\ne+010+ydRQuTPeJefvnlEEJ5D60DDjgg9dhZLKVaFk5WQpbMOe96+Bww64zWGe/z/fbbzzRt/jvu\nuMN0UnjJBcmYOcZ56dGjh2l+h3ldm1nUmSzwGEIIv/jFL0xzITaeQ6UokhFCCBENvWSEEEJEo67s\nMobdtFyY6cD22SQJfe+77z7bxiwOkjekZxjJLJxGsgaKgnPB9d9p0zB8P+2000IIIUyfPt22cQEl\nzjP16lY861lO3M6COhbdffzxx6Z5z3v9ypJ9eGzaljx2FvI+B41qrxGOLbO4eN9yHy5Oxn59tKWS\neeSyGZ6lxyJK9lRjL7K//OUvppnpxuUA+Fk83yLnRZGMEEKIaOglI4QQIhp1tTKmZxOwkInhIPdJ\nwtQLLrjAtjG7hi21WVzEY3Tu3Nk07QXaQo0a3lcCr5lZNew71r17d9PTpk0z/eSTT4YQQpg5c2az\nn1OrPln1QJb15r0VDdlGPgvJfU5rh8egXZblfq/kOa8XaNXmzTrziotphXF8+d2SNha053letEK5\nuuyECRNMc6kBtvTnzwyLFi1KPXfCc6SN9t3vftc0l+xYFYpkhBBCREMvGSGEENGoycqYWcJr2i8/\n+clPTHuhZtK+es8997RtXO2PISiXCHj11VdNM3Rk8RLbW7eGzJi8MGRngRnHhSH1G2+8sdL2jh07\n2jbaj14Rp8hOlnuSWYFJJhkzJTknfMY4x1ksvUaC41aJVZvl+vl8UPOeTzK9aFdyLni+M2bMMH3l\nlVea5vIb7733nmmuxulldHJ1YVrh5Pbbb0/dvir0VAshhIiGXjJCCCGiUZPsMmpmfR199NGmTzjh\nBNO777576t8y7HzppZdCCOUZFWxLz+MNHjzYNLMl3nnnHdNe+Nyo1kBeevbsaZoZewMGDDDdrVs3\n07RVGGon+3OFP1qXLCRcnbPL8sJny9PsdbXLLruY3mGHHUII5fcy+1xxHjzrrDWQN3POG4tKLHTu\nn1YEy+84ZgMyc5ZZsVx18/e//33qcTi/1J5FxkLOefPmpe6zKhTJCCGEiIZeMkIIIaJRV9lls2fP\nNs1VLTfeeGPTm266qWmuIPerX/0qhBDC22+/bdsYCp511lmmWdzJVeJWFyuMYT9JbJQQysduyJAh\nptlinOPFTKV77rnHdJKxQjuGvZ54L7Q2kmuLUdBIOFc8Trt27Ux36dLFdJJJ9vjjj9s29rMqqodc\no2Zi8vo9e55wH+9v+czxJwLun8wRv5O8MaRdd9JJJ5k+88wzTTPLs5LnrCUWGVEkI4QQIhp6yQgh\nhIhGU54wtqmpqeYxb3NhX1Fhed5eRnkplUqF+URFzQuvmasmJv3HQihvDd62bVvTRx55pOnrr7/e\ndDIfRc2L11OpKIqaF85JUeecxX7iHNIWPvzww00nqzFy/mjRxKBC62x8qVQaVNB5lKBT98mSRUbb\nmP3CvP1Z6MgMTRaDJ/cGe57RWubcMrts4MCBppnFyc/0ltfgd1useVEkI4QQIhp6yQghhIhGw9ll\nrYV6tMtYJMnCMC97qeiMIVpxedvXF0UMu0xUTBS7rCiyWOueNZdWSJvXwmrTpo1pPje0Q1n0XMlz\nu8LzL7tMCCFEbdFLRgghRDSiFmOKxoJLHXjhfcyiOob6ldhyjVoEKBqTvCtpZtneHCNGjDB9yy23\nmOa9z8y0SpZdIS05X0UyQgghoqGXjBBCiGgou6xG1GN2mVB2WZ0SvRizKDspJnmLcb2s0KJWBA0q\nxhRCCFFr9JIRQggRjbzZZYtCCDNjnMhqRo/md8mF5qUYipwXzUlxRJmXWNlUschyLllW9C3wmjLN\nS67fZIQQQog8yC4TQggRDb1khBBCREMvGSGEENHQS0YIIUQ09JIRQggRDb1khBBCREMvGSGEENHQ\nS0YIIUQ09JIRQggRjf8DCGGm5rjhC7AAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# randomly generated, new latent vectors\n",
"sample_size=16\n",
"rand_z = np.random.uniform(-1, 1, size=(sample_size, z_size))\n",
"rand_z = torch.from_numpy(rand_z).float()\n",
"\n",
"G.eval() # eval mode\n",
"# generated samples\n",
"rand_images = G(rand_z)\n",
"\n",
"# 0 indicates the first set of samples in the passed in list\n",
"# and we only have one batch of samples, here\n",
"view_samples(0, [rand_images])"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
\n",
"\n",
"The losses will by binary cross entropy loss with logits, which we can get with [BCEWithLogitsLoss](https://pytorch.org/docs/stable/nn.html#bcewithlogitsloss). This combines a `sigmoid` activation function **and** and binary cross entropy loss in one function.\n",
"\n",
"For the real images, we want `D(real_images) = 1`. That is, we want the discriminator to classify the the real images with a label = 1, indicating that these are real. To help the discriminator generalize better, the labels are **reduced a bit from 1.0 to 0.9**. For this, we'll use the parameter `smooth`; if True, then we should smooth our labels. In PyTorch, this looks like `labels = torch.ones(size) * 0.9`\n",
"\n",
"The discriminator loss for the fake data is similar. We want `D(fake_images) = 0`, where the fake images are the _generator output_, `fake_images = G(z)`. \n",
"\n",
"### Generator Loss\n",
"\n",
"The generator loss will look similar only with flipped labels. The generator's goal is to get `D(fake_images) = 1`. In this case, the labels are **flipped** to represent that the generator is trying to fool the discriminator into thinking that the images it generates (fakes) are real!"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Calculate losses\n",
"def real_loss(D_out, smooth=False):\n",
" batch_size = D_out.size(0)\n",
" # label smoothing\n",
" if smooth:\n",
" # smooth, real labels = 0.9\n",
" labels = torch.ones(batch_size)*0.9\n",
" else:\n",
" labels = torch.ones(batch_size) # real labels = 1\n",
" \n",
" # numerically stable loss\n",
" criterion = nn.BCEWithLogitsLoss()\n",
" # calculate loss\n",
" loss = criterion(D_out.squeeze(), labels)\n",
" return loss\n",
"\n",
"def fake_loss(D_out):\n",
" batch_size = D_out.size(0)\n",
" labels = torch.zeros(batch_size) # fake labels = 0\n",
" criterion = nn.BCEWithLogitsLoss()\n",
" # calculate loss\n",
" loss = criterion(D_out.squeeze(), labels)\n",
" return loss"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Optimizers\n",
"\n",
"We want to update the generator and discriminator variables separately. So, we'll define two separate Adam optimizers."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true,
"scrolled": true
},
"outputs": [],
"source": [
"import torch.optim as optim\n",
"\n",
"# Optimizers\n",
"lr = 0.002\n",
"\n",
"# Create optimizers for the discriminator and generator\n",
"d_optimizer = optim.Adam(D.parameters(), lr)\n",
"g_optimizer = optim.Adam(G.parameters(), lr)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Training\n",
"\n",
"Training will involve alternating between training the discriminator and the generator. We'll use our functions `real_loss` and `fake_loss` to help us calculate the discriminator losses in all of the following cases.\n",
"\n",
"### Discriminator training\n",
"1. Compute the discriminator loss on real, training images \n",
"2. Generate fake images\n",
"3. Compute the discriminator loss on fake, generated images \n",
"4. Add up real and fake loss\n",
"5. Perform backpropagation + an optimization step to update the discriminator's weights\n",
"\n",
"### Generator training\n",
"1. Generate fake images\n",
"2. Compute the discriminator loss on fake images, using **flipped** labels!\n",
"3. Perform backpropagation + an optimization step to update the generator's weights\n",
"\n",
"#### Saving Samples\n",
"\n",
"As we train, we'll also print out some loss statistics and save some generated \"fake\" samples."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch [ 1/ 100] | d_loss: 1.3830 | g_loss: 0.6883\n",
"Epoch [ 1/ 100] | d_loss: 0.7668 | g_loss: 3.1404\n",
"Epoch [ 1/ 100] | d_loss: 1.0908 | g_loss: 2.6393\n",
"Epoch [ 2/ 100] | d_loss: 1.2982 | g_loss: 1.1008\n",
"Epoch [ 2/ 100] | d_loss: 1.1753 | g_loss: 1.1042\n",
"Epoch [ 2/ 100] | d_loss: 1.0874 | g_loss: 1.6588\n",
"Epoch [ 3/ 100] | d_loss: 0.9747 | g_loss: 2.9083\n",
"Epoch [ 3/ 100] | d_loss: 1.0724 | g_loss: 1.1101\n",
"Epoch [ 3/ 100] | d_loss: 1.4727 | g_loss: 0.4990\n",
"Epoch [ 4/ 100] | d_loss: 1.1590 | g_loss: 0.9996\n",
"Epoch [ 4/ 100] | d_loss: 1.1832 | g_loss: 1.0638\n",
"Epoch [ 4/ 100] | d_loss: 1.1652 | g_loss: 1.1463\n",
"Epoch [ 5/ 100] | d_loss: 1.2966 | g_loss: 1.0950\n",
"Epoch [ 5/ 100] | d_loss: 1.3616 | g_loss: 1.0312\n",
"Epoch [ 5/ 100] | d_loss: 1.2202 | g_loss: 1.1301\n",
"Epoch [ 6/ 100] | d_loss: 1.1609 | g_loss: 1.5148\n",
"Epoch [ 6/ 100] | d_loss: 1.1100 | g_loss: 1.2183\n",
"Epoch [ 6/ 100] | d_loss: 1.2376 | g_loss: 1.5296\n",
"Epoch [ 7/ 100] | d_loss: 1.2304 | g_loss: 1.1526\n",
"Epoch [ 7/ 100] | d_loss: 1.1684 | g_loss: 1.1339\n",
"Epoch [ 7/ 100] | d_loss: 1.0965 | g_loss: 1.3531\n",
"Epoch [ 8/ 100] | d_loss: 1.2527 | g_loss: 2.2266\n",
"Epoch [ 8/ 100] | d_loss: 1.2978 | g_loss: 1.6185\n",
"Epoch [ 8/ 100] | d_loss: 1.1493 | g_loss: 1.4873\n",
"Epoch [ 9/ 100] | d_loss: 0.9751 | g_loss: 2.6848\n",
"Epoch [ 9/ 100] | d_loss: 1.1574 | g_loss: 1.7639\n",
"Epoch [ 9/ 100] | d_loss: 0.9629 | g_loss: 2.2062\n",
"Epoch [ 10/ 100] | d_loss: 1.0279 | g_loss: 1.9386\n",
"Epoch [ 10/ 100] | d_loss: 1.1110 | g_loss: 1.0685\n",
"Epoch [ 10/ 100] | d_loss: 1.3441 | g_loss: 1.0324\n",
"Epoch [ 11/ 100] | d_loss: 1.1879 | g_loss: 1.0673\n",
"Epoch [ 11/ 100] | d_loss: 1.3366 | g_loss: 0.9610\n",
"Epoch [ 11/ 100] | d_loss: 1.1435 | g_loss: 1.0668\n",
"Epoch [ 12/ 100] | d_loss: 1.1189 | g_loss: 1.2501\n",
"Epoch [ 12/ 100] | d_loss: 1.2153 | g_loss: 1.0666\n",
"Epoch [ 12/ 100] | d_loss: 1.3179 | g_loss: 0.9101\n",
"Epoch [ 13/ 100] | d_loss: 1.1504 | g_loss: 1.4559\n",
"Epoch [ 13/ 100] | d_loss: 1.3358 | g_loss: 0.9763\n",
"Epoch [ 13/ 100] | d_loss: 1.1833 | g_loss: 1.0180\n",
"Epoch [ 14/ 100] | d_loss: 1.1839 | g_loss: 1.2705\n",
"Epoch [ 14/ 100] | d_loss: 1.3219 | g_loss: 1.0915\n",
"Epoch [ 14/ 100] | d_loss: 1.2945 | g_loss: 0.9335\n",
"Epoch [ 15/ 100] | d_loss: 1.3458 | g_loss: 0.9600\n",
"Epoch [ 15/ 100] | d_loss: 1.3445 | g_loss: 0.9098\n",
"Epoch [ 15/ 100] | d_loss: 1.3289 | g_loss: 1.3456\n",
"Epoch [ 16/ 100] | d_loss: 1.2725 | g_loss: 0.9085\n",
"Epoch [ 16/ 100] | d_loss: 1.1133 | g_loss: 1.0910\n",
"Epoch [ 16/ 100] | d_loss: 1.2564 | g_loss: 1.0233\n",
"Epoch [ 17/ 100] | d_loss: 1.3171 | g_loss: 0.9643\n",
"Epoch [ 17/ 100] | d_loss: 1.2932 | g_loss: 1.0311\n",
"Epoch [ 17/ 100] | d_loss: 1.2643 | g_loss: 0.9377\n",
"Epoch [ 18/ 100] | d_loss: 1.2226 | g_loss: 1.4327\n",
"Epoch [ 18/ 100] | d_loss: 1.3909 | g_loss: 0.9178\n",
"Epoch [ 18/ 100] | d_loss: 1.2430 | g_loss: 1.0297\n",
"Epoch [ 19/ 100] | d_loss: 1.3409 | g_loss: 1.1413\n",
"Epoch [ 19/ 100] | d_loss: 1.1607 | g_loss: 1.2019\n",
"Epoch [ 19/ 100] | d_loss: 1.4060 | g_loss: 1.1366\n",
"Epoch [ 20/ 100] | d_loss: 1.3076 | g_loss: 1.0200\n",
"Epoch [ 20/ 100] | d_loss: 1.2715 | g_loss: 0.9261\n",
"Epoch [ 20/ 100] | d_loss: 1.2959 | g_loss: 1.4079\n",
"Epoch [ 21/ 100] | d_loss: 1.2529 | g_loss: 1.4324\n",
"Epoch [ 21/ 100] | d_loss: 1.2907 | g_loss: 0.9551\n",
"Epoch [ 21/ 100] | d_loss: 1.2426 | g_loss: 1.2571\n",
"Epoch [ 22/ 100] | d_loss: 1.2168 | g_loss: 1.7557\n",
"Epoch [ 22/ 100] | d_loss: 1.2874 | g_loss: 1.0733\n",
"Epoch [ 22/ 100] | d_loss: 1.1758 | g_loss: 1.6449\n",
"Epoch [ 23/ 100] | d_loss: 1.3328 | g_loss: 0.9859\n",
"Epoch [ 23/ 100] | d_loss: 1.4189 | g_loss: 0.8197\n",
"Epoch [ 23/ 100] | d_loss: 1.3146 | g_loss: 0.9181\n",
"Epoch [ 24/ 100] | d_loss: 1.2752 | g_loss: 1.1507\n",
"Epoch [ 24/ 100] | d_loss: 1.1860 | g_loss: 1.0389\n",
"Epoch [ 24/ 100] | d_loss: 1.2692 | g_loss: 1.0240\n",
"Epoch [ 25/ 100] | d_loss: 1.2905 | g_loss: 0.8767\n",
"Epoch [ 25/ 100] | d_loss: 1.1643 | g_loss: 1.0650\n",
"Epoch [ 25/ 100] | d_loss: 1.3141 | g_loss: 0.8904\n",
"Epoch [ 26/ 100] | d_loss: 1.2288 | g_loss: 1.0190\n",
"Epoch [ 26/ 100] | d_loss: 1.2016 | g_loss: 0.9930\n",
"Epoch [ 26/ 100] | d_loss: 1.4220 | g_loss: 1.1657\n",
"Epoch [ 27/ 100] | d_loss: 1.2774 | g_loss: 1.0464\n",
"Epoch [ 27/ 100] | d_loss: 1.2179 | g_loss: 1.0301\n",
"Epoch [ 27/ 100] | d_loss: 1.2938 | g_loss: 1.1045\n",
"Epoch [ 28/ 100] | d_loss: 1.2736 | g_loss: 1.1921\n",
"Epoch [ 28/ 100] | d_loss: 1.1929 | g_loss: 1.1512\n",
"Epoch [ 28/ 100] | d_loss: 1.3188 | g_loss: 0.9897\n",
"Epoch [ 29/ 100] | d_loss: 1.3085 | g_loss: 1.4660\n",
"Epoch [ 29/ 100] | d_loss: 1.2663 | g_loss: 0.9120\n",
"Epoch [ 29/ 100] | d_loss: 1.3005 | g_loss: 0.9635\n",
"Epoch [ 30/ 100] | d_loss: 1.2953 | g_loss: 0.8053\n",
"Epoch [ 30/ 100] | d_loss: 1.3288 | g_loss: 0.9908\n",
"Epoch [ 30/ 100] | d_loss: 1.3487 | g_loss: 1.1090\n",
"Epoch [ 31/ 100] | d_loss: 1.2638 | g_loss: 1.0738\n",
"Epoch [ 31/ 100] | d_loss: 1.2856 | g_loss: 0.9346\n",
"Epoch [ 31/ 100] | d_loss: 1.2525 | g_loss: 1.1265\n",
"Epoch [ 32/ 100] | d_loss: 1.1938 | g_loss: 1.1639\n",
"Epoch [ 32/ 100] | d_loss: 1.2217 | g_loss: 0.9636\n",
"Epoch [ 32/ 100] | d_loss: 1.2105 | g_loss: 1.7308\n",
"Epoch [ 33/ 100] | d_loss: 1.1531 | g_loss: 1.5628\n",
"Epoch [ 33/ 100] | d_loss: 1.3260 | g_loss: 0.9161\n",
"Epoch [ 33/ 100] | d_loss: 1.2334 | g_loss: 0.9264\n",
"Epoch [ 34/ 100] | d_loss: 1.2336 | g_loss: 1.0195\n",
"Epoch [ 34/ 100] | d_loss: 1.2184 | g_loss: 1.3364\n",
"Epoch [ 34/ 100] | d_loss: 1.3039 | g_loss: 0.9413\n",
"Epoch [ 35/ 100] | d_loss: 1.3298 | g_loss: 1.1236\n",
"Epoch [ 35/ 100] | d_loss: 1.2562 | g_loss: 1.0155\n",
"Epoch [ 35/ 100] | d_loss: 1.3659 | g_loss: 1.2384\n",
"Epoch [ 36/ 100] | d_loss: 1.1759 | g_loss: 1.0545\n",
"Epoch [ 36/ 100] | d_loss: 1.2195 | g_loss: 1.0489\n",
"Epoch [ 36/ 100] | d_loss: 1.2799 | g_loss: 0.9530\n",
"Epoch [ 37/ 100] | d_loss: 1.2149 | g_loss: 1.0076\n",
"Epoch [ 37/ 100] | d_loss: 1.2700 | g_loss: 1.1004\n",
"Epoch [ 37/ 100] | d_loss: 1.3090 | g_loss: 0.9861\n",
"Epoch [ 38/ 100] | d_loss: 1.3035 | g_loss: 1.0189\n",
"Epoch [ 38/ 100] | d_loss: 1.2769 | g_loss: 1.0285\n",
"Epoch [ 38/ 100] | d_loss: 1.2371 | g_loss: 1.2829\n",
"Epoch [ 39/ 100] | d_loss: 1.2404 | g_loss: 1.0135\n",
"Epoch [ 39/ 100] | d_loss: 1.2708 | g_loss: 0.9378\n",
"Epoch [ 39/ 100] | d_loss: 1.2512 | g_loss: 0.9949\n",
"Epoch [ 40/ 100] | d_loss: 1.1768 | g_loss: 0.9511\n",
"Epoch [ 40/ 100] | d_loss: 1.3067 | g_loss: 0.9223\n",
"Epoch [ 40/ 100] | d_loss: 1.3625 | g_loss: 0.8471\n",
"Epoch [ 41/ 100] | d_loss: 1.2816 | g_loss: 1.0424\n",
"Epoch [ 41/ 100] | d_loss: 1.2974 | g_loss: 1.1541\n",
"Epoch [ 41/ 100] | d_loss: 1.1643 | g_loss: 1.2687\n",
"Epoch [ 42/ 100] | d_loss: 1.2976 | g_loss: 1.0265\n",
"Epoch [ 42/ 100] | d_loss: 1.3245 | g_loss: 1.1694\n",
"Epoch [ 42/ 100] | d_loss: 1.3458 | g_loss: 0.9364\n",
"Epoch [ 43/ 100] | d_loss: 1.1641 | g_loss: 1.6862\n",
"Epoch [ 43/ 100] | d_loss: 1.2706 | g_loss: 0.8405\n",
"Epoch [ 43/ 100] | d_loss: 1.3763 | g_loss: 0.9720\n",
"Epoch [ 44/ 100] | d_loss: 1.3490 | g_loss: 1.1244\n",
"Epoch [ 44/ 100] | d_loss: 1.2542 | g_loss: 1.3335\n",
"Epoch [ 44/ 100] | d_loss: 1.2833 | g_loss: 0.9767\n",
"Epoch [ 45/ 100] | d_loss: 1.3130 | g_loss: 0.9182\n",
"Epoch [ 45/ 100] | d_loss: 1.2353 | g_loss: 1.0782\n",
"Epoch [ 45/ 100] | d_loss: 1.3760 | g_loss: 0.9803\n",
"Epoch [ 46/ 100] | d_loss: 1.4026 | g_loss: 0.9744\n",
"Epoch [ 46/ 100] | d_loss: 1.3152 | g_loss: 0.9312\n",
"Epoch [ 46/ 100] | d_loss: 1.2657 | g_loss: 1.0664\n",
"Epoch [ 47/ 100] | d_loss: 1.2507 | g_loss: 1.2632\n",
"Epoch [ 47/ 100] | d_loss: 1.2343 | g_loss: 1.0100\n",
"Epoch [ 47/ 100] | d_loss: 1.2856 | g_loss: 0.9613\n",
"Epoch [ 48/ 100] | d_loss: 1.2589 | g_loss: 1.0631\n",
"Epoch [ 48/ 100] | d_loss: 1.2255 | g_loss: 1.3015\n",
"Epoch [ 48/ 100] | d_loss: 1.3112 | g_loss: 0.8649\n",
"Epoch [ 49/ 100] | d_loss: 1.2646 | g_loss: 0.9986\n",
"Epoch [ 49/ 100] | d_loss: 1.2757 | g_loss: 0.9732\n",
"Epoch [ 49/ 100] | d_loss: 1.1808 | g_loss: 1.4561\n",
"Epoch [ 50/ 100] | d_loss: 1.3849 | g_loss: 1.2169\n",
"Epoch [ 50/ 100] | d_loss: 1.2799 | g_loss: 1.4074\n",
"Epoch [ 50/ 100] | d_loss: 1.3711 | g_loss: 0.9860\n",
"Epoch [ 51/ 100] | d_loss: 1.2772 | g_loss: 1.2343\n",
"Epoch [ 51/ 100] | d_loss: 1.3022 | g_loss: 0.9042\n",
"Epoch [ 51/ 100] | d_loss: 1.3566 | g_loss: 0.8909\n",
"Epoch [ 52/ 100] | d_loss: 1.3641 | g_loss: 1.0716\n",
"Epoch [ 52/ 100] | d_loss: 1.2138 | g_loss: 1.2055\n",
"Epoch [ 52/ 100] | d_loss: 1.3753 | g_loss: 0.9283\n",
"Epoch [ 53/ 100] | d_loss: 1.2297 | g_loss: 1.1757\n",
"Epoch [ 53/ 100] | d_loss: 1.2801 | g_loss: 0.9982\n",
"Epoch [ 53/ 100] | d_loss: 1.2177 | g_loss: 0.9533\n",
"Epoch [ 54/ 100] | d_loss: 1.3590 | g_loss: 0.8750\n",
"Epoch [ 54/ 100] | d_loss: 1.2776 | g_loss: 1.3202\n",
"Epoch [ 54/ 100] | d_loss: 1.4154 | g_loss: 0.9770\n",
"Epoch [ 55/ 100] | d_loss: 1.3179 | g_loss: 1.1155\n",
"Epoch [ 55/ 100] | d_loss: 1.3786 | g_loss: 0.9604\n",
"Epoch [ 55/ 100] | d_loss: 1.3158 | g_loss: 0.9751\n",
"Epoch [ 56/ 100] | d_loss: 1.3204 | g_loss: 0.9898\n",
"Epoch [ 56/ 100] | d_loss: 1.4150 | g_loss: 1.0278\n",
"Epoch [ 56/ 100] | d_loss: 1.2821 | g_loss: 0.9324\n",
"Epoch [ 57/ 100] | d_loss: 1.2576 | g_loss: 1.2056\n",
"Epoch [ 57/ 100] | d_loss: 1.4449 | g_loss: 1.1794\n",
"Epoch [ 57/ 100] | d_loss: 1.3697 | g_loss: 1.1030\n",
"Epoch [ 58/ 100] | d_loss: 1.2824 | g_loss: 0.9524\n",
"Epoch [ 58/ 100] | d_loss: 1.2432 | g_loss: 1.1015\n",
"Epoch [ 58/ 100] | d_loss: 1.3309 | g_loss: 1.0080\n",
"Epoch [ 59/ 100] | d_loss: 1.3095 | g_loss: 1.0256\n",
"Epoch [ 59/ 100] | d_loss: 1.2653 | g_loss: 0.8913\n",
"Epoch [ 59/ 100] | d_loss: 1.3224 | g_loss: 1.0386\n",
"Epoch [ 60/ 100] | d_loss: 1.1556 | g_loss: 1.1556\n",
"Epoch [ 60/ 100] | d_loss: 1.2522 | g_loss: 1.0155\n",
"Epoch [ 60/ 100] | d_loss: 1.3123 | g_loss: 0.9344\n",
"Epoch [ 61/ 100] | d_loss: 1.2728 | g_loss: 1.1286\n",
"Epoch [ 61/ 100] | d_loss: 1.3303 | g_loss: 1.0562\n",
"Epoch [ 61/ 100] | d_loss: 1.3408 | g_loss: 0.8740\n",
"Epoch [ 62/ 100] | d_loss: 1.4031 | g_loss: 1.0154\n",
"Epoch [ 62/ 100] | d_loss: 1.1388 | g_loss: 1.3963\n",
"Epoch [ 62/ 100] | d_loss: 1.4201 | g_loss: 1.1908\n",
"Epoch [ 63/ 100] | d_loss: 1.2058 | g_loss: 1.1407\n",
"Epoch [ 63/ 100] | d_loss: 1.2444 | g_loss: 1.1547\n",
"Epoch [ 63/ 100] | d_loss: 1.3877 | g_loss: 1.0653\n",
"Epoch [ 64/ 100] | d_loss: 1.3246 | g_loss: 1.4514\n",
"Epoch [ 64/ 100] | d_loss: 1.3463 | g_loss: 1.0041\n",
"Epoch [ 64/ 100] | d_loss: 1.2426 | g_loss: 1.5180\n",
"Epoch [ 65/ 100] | d_loss: 1.3013 | g_loss: 1.0159\n",
"Epoch [ 65/ 100] | d_loss: 1.3368 | g_loss: 2.1512\n",
"Epoch [ 65/ 100] | d_loss: 1.3612 | g_loss: 0.9549\n",
"Epoch [ 66/ 100] | d_loss: 1.3277 | g_loss: 0.7320\n",
"Epoch [ 66/ 100] | d_loss: 1.2434 | g_loss: 0.9365\n",
"Epoch [ 66/ 100] | d_loss: 1.2326 | g_loss: 1.3177\n",
"Epoch [ 67/ 100] | d_loss: 1.2334 | g_loss: 1.4614\n",
"Epoch [ 67/ 100] | d_loss: 1.2690 | g_loss: 1.0928\n",
"Epoch [ 67/ 100] | d_loss: 1.3406 | g_loss: 1.0277\n",
"Epoch [ 68/ 100] | d_loss: 1.2498 | g_loss: 1.0917\n",
"Epoch [ 68/ 100] | d_loss: 1.3146 | g_loss: 1.0963\n",
"Epoch [ 68/ 100] | d_loss: 1.3215 | g_loss: 1.3057\n",
"Epoch [ 69/ 100] | d_loss: 1.3268 | g_loss: 1.1683\n",
"Epoch [ 69/ 100] | d_loss: 1.2631 | g_loss: 0.9922\n",
"Epoch [ 69/ 100] | d_loss: 1.3693 | g_loss: 1.0472\n",
"Epoch [ 70/ 100] | d_loss: 1.3476 | g_loss: 1.1509\n",
"Epoch [ 70/ 100] | d_loss: 1.2585 | g_loss: 1.2276\n",
"Epoch [ 70/ 100] | d_loss: 1.3906 | g_loss: 1.2750\n",
"Epoch [ 71/ 100] | d_loss: 1.2083 | g_loss: 0.9252\n",
"Epoch [ 71/ 100] | d_loss: 1.3743 | g_loss: 1.1076\n",
"Epoch [ 71/ 100] | d_loss: 1.2552 | g_loss: 0.9602\n",
"Epoch [ 72/ 100] | d_loss: 1.3761 | g_loss: 0.9666\n",
"Epoch [ 72/ 100] | d_loss: 1.3193 | g_loss: 0.9309\n",
"Epoch [ 72/ 100] | d_loss: 1.3079 | g_loss: 1.2341\n",
"Epoch [ 73/ 100] | d_loss: 1.4915 | g_loss: 1.0998\n",
"Epoch [ 73/ 100] | d_loss: 1.2271 | g_loss: 1.0882\n",
"Epoch [ 73/ 100] | d_loss: 1.2852 | g_loss: 1.0542\n",
"Epoch [ 74/ 100] | d_loss: 1.2105 | g_loss: 1.0388\n",
"Epoch [ 74/ 100] | d_loss: 1.2571 | g_loss: 1.2588\n",
"Epoch [ 74/ 100] | d_loss: 1.3393 | g_loss: 1.0764\n",
"Epoch [ 75/ 100] | d_loss: 1.2123 | g_loss: 1.2956\n",
"Epoch [ 75/ 100] | d_loss: 1.2723 | g_loss: 0.9174\n",
"Epoch [ 75/ 100] | d_loss: 1.4482 | g_loss: 1.0936\n",
"Epoch [ 76/ 100] | d_loss: 1.3366 | g_loss: 1.0978\n",
"Epoch [ 76/ 100] | d_loss: 1.2682 | g_loss: 1.2402\n",
"Epoch [ 76/ 100] | d_loss: 1.2431 | g_loss: 0.9709\n",
"Epoch [ 77/ 100] | d_loss: 1.3065 | g_loss: 0.9939\n",
"Epoch [ 77/ 100] | d_loss: 1.1876 | g_loss: 1.3299\n",
"Epoch [ 77/ 100] | d_loss: 1.2576 | g_loss: 1.1868\n",
"Epoch [ 78/ 100] | d_loss: 1.2706 | g_loss: 1.0540\n",
"Epoch [ 78/ 100] | d_loss: 1.2493 | g_loss: 0.9568\n",
"Epoch [ 78/ 100] | d_loss: 1.2227 | g_loss: 1.1633\n",
"Epoch [ 79/ 100] | d_loss: 1.3261 | g_loss: 0.9173\n",
"Epoch [ 79/ 100] | d_loss: 1.2312 | g_loss: 1.1450\n",
"Epoch [ 79/ 100] | d_loss: 1.3387 | g_loss: 1.2766\n",
"Epoch [ 80/ 100] | d_loss: 1.2280 | g_loss: 1.1469\n",
"Epoch [ 80/ 100] | d_loss: 1.2704 | g_loss: 1.1292\n",
"Epoch [ 80/ 100] | d_loss: 1.3570 | g_loss: 0.9845\n",
"Epoch [ 81/ 100] | d_loss: 1.2037 | g_loss: 1.1029\n",
"Epoch [ 81/ 100] | d_loss: 1.1613 | g_loss: 1.3356\n",
"Epoch [ 81/ 100] | d_loss: 1.3182 | g_loss: 1.0841\n",
"Epoch [ 82/ 100] | d_loss: 1.2307 | g_loss: 1.0811\n",
"Epoch [ 82/ 100] | d_loss: 1.2791 | g_loss: 0.8639\n",
"Epoch [ 82/ 100] | d_loss: 1.3174 | g_loss: 1.3110\n",
"Epoch [ 83/ 100] | d_loss: 1.3051 | g_loss: 0.9979\n",
"Epoch [ 83/ 100] | d_loss: 1.1558 | g_loss: 1.2926\n",
"Epoch [ 83/ 100] | d_loss: 1.2325 | g_loss: 1.0440\n",
"Epoch [ 84/ 100] | d_loss: 1.2974 | g_loss: 1.1218\n",
"Epoch [ 84/ 100] | d_loss: 1.2150 | g_loss: 1.0606\n",
"Epoch [ 84/ 100] | d_loss: 1.4180 | g_loss: 1.1683\n",
"Epoch [ 85/ 100] | d_loss: 1.3644 | g_loss: 1.2858\n",
"Epoch [ 85/ 100] | d_loss: 1.2591 | g_loss: 0.9795\n",
"Epoch [ 85/ 100] | d_loss: 1.1972 | g_loss: 0.9682\n",
"Epoch [ 86/ 100] | d_loss: 1.4219 | g_loss: 0.8627\n",
"Epoch [ 86/ 100] | d_loss: 1.1788 | g_loss: 1.4205\n",
"Epoch [ 86/ 100] | d_loss: 1.3966 | g_loss: 0.9346\n",
"Epoch [ 87/ 100] | d_loss: 1.2943 | g_loss: 0.9851\n",
"Epoch [ 87/ 100] | d_loss: 1.2265 | g_loss: 1.0192\n",
"Epoch [ 87/ 100] | d_loss: 1.2797 | g_loss: 1.3309\n",
"Epoch [ 88/ 100] | d_loss: 1.2280 | g_loss: 1.0253\n",
"Epoch [ 88/ 100] | d_loss: 1.2176 | g_loss: 1.2858\n",
"Epoch [ 88/ 100] | d_loss: 1.3786 | g_loss: 1.3351\n",
"Epoch [ 89/ 100] | d_loss: 1.3144 | g_loss: 1.1179\n",
"Epoch [ 89/ 100] | d_loss: 1.2299 | g_loss: 1.0613\n",
"Epoch [ 89/ 100] | d_loss: 1.3691 | g_loss: 1.0295\n",
"Epoch [ 90/ 100] | d_loss: 1.3526 | g_loss: 1.0230\n",
"Epoch [ 90/ 100] | d_loss: 1.2959 | g_loss: 1.1332\n",
"Epoch [ 90/ 100] | d_loss: 1.2445 | g_loss: 1.5470\n",
"Epoch [ 91/ 100] | d_loss: 1.3283 | g_loss: 1.0868\n",
"Epoch [ 91/ 100] | d_loss: 1.2901 | g_loss: 1.2393\n",
"Epoch [ 91/ 100] | d_loss: 1.4300 | g_loss: 1.1335\n",
"Epoch [ 92/ 100] | d_loss: 1.2987 | g_loss: 1.3160\n",
"Epoch [ 92/ 100] | d_loss: 1.2587 | g_loss: 1.0517\n",
"Epoch [ 92/ 100] | d_loss: 1.2881 | g_loss: 1.1046\n",
"Epoch [ 93/ 100] | d_loss: 1.2725 | g_loss: 1.1219\n",
"Epoch [ 93/ 100] | d_loss: 1.3230 | g_loss: 0.9735\n",
"Epoch [ 93/ 100] | d_loss: 1.3613 | g_loss: 0.9286\n",
"Epoch [ 94/ 100] | d_loss: 1.3035 | g_loss: 1.0815\n",
"Epoch [ 94/ 100] | d_loss: 1.2292 | g_loss: 1.0348\n",
"Epoch [ 94/ 100] | d_loss: 1.3835 | g_loss: 1.0981\n",
"Epoch [ 95/ 100] | d_loss: 1.2474 | g_loss: 1.1265\n",
"Epoch [ 95/ 100] | d_loss: 1.2481 | g_loss: 1.0578\n",
"Epoch [ 95/ 100] | d_loss: 1.3886 | g_loss: 0.8486\n",
"Epoch [ 96/ 100] | d_loss: 1.2996 | g_loss: 0.9993\n",
"Epoch [ 96/ 100] | d_loss: 1.2269 | g_loss: 0.9128\n",
"Epoch [ 96/ 100] | d_loss: 1.3136 | g_loss: 1.0670\n",
"Epoch [ 97/ 100] | d_loss: 1.3130 | g_loss: 0.9450\n",
"Epoch [ 97/ 100] | d_loss: 1.2538 | g_loss: 1.3591\n",
"Epoch [ 97/ 100] | d_loss: 1.2691 | g_loss: 0.9735\n",
"Epoch [ 98/ 100] | d_loss: 1.2483 | g_loss: 0.9697\n",
"Epoch [ 98/ 100] | d_loss: 1.1419 | g_loss: 1.9026\n",
"Epoch [ 98/ 100] | d_loss: 1.3835 | g_loss: 1.0033\n",
"Epoch [ 99/ 100] | d_loss: 1.2814 | g_loss: 0.9089\n",
"Epoch [ 99/ 100] | d_loss: 1.2866 | g_loss: 1.1416\n",
"Epoch [ 99/ 100] | d_loss: 1.5226 | g_loss: 1.1019\n",
"Epoch [ 100/ 100] | d_loss: 1.3635 | g_loss: 1.1240\n",
"Epoch [ 100/ 100] | d_loss: 1.3810 | g_loss: 0.9675\n",
"Epoch [ 100/ 100] | d_loss: 1.3214 | g_loss: 0.9679\n"
]
}
],
"source": [
"import pickle as pkl\n",
"\n",
"# training hyperparams\n",
"num_epochs = 100\n",
"\n",
"# keep track of loss and generated, \"fake\" samples\n",
"samples = []\n",
"losses = []\n",
"\n",
"print_every = 400\n",
"\n",
"# Get some fixed data for sampling. These are images that are held\n",
"# constant throughout training, and allow us to inspect the model's performance\n",
"sample_size=16\n",
"fixed_z = np.random.uniform(-1, 1, size=(sample_size, z_size))\n",
"fixed_z = torch.from_numpy(fixed_z).float()\n",
"\n",
"# train the network\n",
"D.train()\n",
"G.train()\n",
"for epoch in range(num_epochs):\n",
" \n",
" for batch_i, (real_images, _) in enumerate(train_loader):\n",
" \n",
" batch_size = real_images.size(0)\n",
" \n",
" ## Important rescaling step ## \n",
" real_images = real_images*2 - 1 # rescale input images from [0,1) to [-1, 1)\n",
" \n",
" # ============================================\n",
" # TRAIN THE DISCRIMINATOR\n",
" # ============================================\n",
" \n",
" d_optimizer.zero_grad()\n",
" \n",
" # 1. Train with real images\n",
"\n",
" # Compute the discriminator losses on real images \n",
" # smooth the real labels\n",
" D_real = D(real_images)\n",
" d_real_loss = real_loss(D_real, smooth=True)\n",
" \n",
" # 2. Train with fake images\n",
" \n",
" # Generate fake images\n",
" # gradients don't have to flow during this step\n",
" with torch.no_grad():\n",
" z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" z = torch.from_numpy(z).float()\n",
" fake_images = G(z)\n",
" \n",
" # Compute the discriminator losses on fake images \n",
" D_fake = D(fake_images)\n",
" d_fake_loss = fake_loss(D_fake)\n",
" \n",
" # add up loss and perform backprop\n",
" d_loss = d_real_loss + d_fake_loss\n",
" d_loss.backward()\n",
" d_optimizer.step()\n",
" \n",
" \n",
" # =========================================\n",
" # TRAIN THE GENERATOR\n",
" # =========================================\n",
" g_optimizer.zero_grad()\n",
" \n",
" # 1. Train with fake images and flipped labels\n",
" \n",
" # Generate fake images\n",
" z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" z = torch.from_numpy(z).float()\n",
" fake_images = G(z)\n",
" \n",
" # Compute the discriminator losses on fake images \n",
" # using flipped labels!\n",
" D_fake = D(fake_images)\n",
" g_loss = real_loss(D_fake) # use real loss to flip labels\n",
" \n",
" # perform backprop\n",
" g_loss.backward()\n",
" g_optimizer.step()\n",
"\n",
" # Print some loss stats\n",
" if batch_i % print_every == 0:\n",
" # print discriminator and generator loss\n",
" print('Epoch [{:5d}/{:5d}] | d_loss: {:6.4f} | g_loss: {:6.4f}'.format(\n",
" epoch+1, num_epochs, d_loss.item(), g_loss.item()))\n",
"\n",
" \n",
" ## AFTER EACH EPOCH##\n",
" # append discriminator loss and generator loss\n",
" losses.append((d_loss.item(), g_loss.item()))\n",
" \n",
" # generate and save sample, fake images\n",
" G.eval() # eval mode for generating samples\n",
" samples_z = G(fixed_z)\n",
" samples.append(samples_z)\n",
" G.train() # back to train mode\n",
"\n",
"\n",
"# Save training generator samples\n",
"with open('train_samples.pkl', 'wb') as f:\n",
" pkl.dump(samples, f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training loss\n",
"\n",
"Here we'll plot the training losses for the generator and discriminator, recorded after each epoch."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAEICAYAAACktLTqAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXd8m9W9/99Hy/J2vGM7sZ1N9nAS\nIClQZqFAWwqXtlxWJ1200EF/7W1Le2/npYNCC+0tBUpbaBs2hdIyAgQCWSQhezrx3panJEs6vz/O\n82hZtuWROBLn/XrlJUt6JD3R+Dyf53O+53uElBKNRqPRJBeWyd4BjUaj0Uw8Wtw1Go0mCdHirtFo\nNEmIFneNRqNJQrS4azQaTRKixV2j0WiSEC3umoRBCGEVQvQIIaZP5LYaTTIidJ275kQhhOgJu5oG\neAC/cf0zUso/n/y9Gj9CiP8ByqSUN0z2vmg0Q2Gb7B3QJC9SygzzbyFENfBJKeULQ20vhLBJKX0n\nY980mmRHxzKaSUMI8T9CiL8KIR4WQnQD/ymEOEMI8aYQolMI0SCE+JUQwm5sbxNCSCFEhXH9T8b9\nzwkhuoUQG4UQlaPd1rj/YiHEASGESwhxlxDidSHEDWP4Py0QQrxi7P87Qoj3h913qRBir/H6tUKI\nW4zbC4UQzxqPaRdCvBr2mDIhxONCiBYhxFEhxOfD7jtdCLFNCNElhGgSQvzvaPdXk7xocddMNh8C\n/gJkA38FfMCXgHxgDfA+4DPDPP5jwLeBXOA48N+j3VYIUQj8Dfia8bpHgVWj/Y8IIRzAM8A/gALg\nFuCvQohZxib3A5+QUmYCi4FXjNu/BhwxHlMM/JfxfBbj+TYDpcAFwNeEEOcZj7sL+F8pZRYwC1g3\n2n3WJC9a3DWTzQYp5dNSyoCUsl9KuVlK+ZaU0ielPAL8Djh7mMevk1JukVIOAH8Glo5h20uB7VLK\nJ437fgG0juH/sgZwoAR3wIigngM+Ytw/AMwXQmRKKdullNvCbi8BpkspvVJK07mfAWRJKX9o3H4I\nuC/q+WYLIfKklN1SyrfGsM+aJEWLu2ayqQm/IoSYJ4T4hxCiUQjRBXwf5aaHojHs7z4gY6gNh9m2\nJHw/pKoyqI1j36MpAY7LyCqFYyjXDeos5XLguBBivRBitXH7j43tXhRCHBZCfM24vRyYbsQ1nUKI\nTuDrKHcPcCMwH9gvhNgkhLhkDPusSVK0uGsmm+hyrd8Cu4BZRtzwHUCc4H1oAMrMK0IIQUiQR0M9\nMM14vMl0oA7AOCO5HChExS2PGLd3SSlvkVJWAB8EbhNCnI064ByUUuaE/cuUUl5mPG6/lPIjxvP9\nDHhUCOEcw35rkhAt7ppTjUzABfQKIU5j+Lx9ongGWC6EuEwIYUNl/gUjPMYqhHCG/UsB3kCNGXxF\nCGEXQpwLXILK3VOFEB8TQmQZ0U83EAAwXnemcVBwocpFA8BGwCuE+IrxGlYhxCIhxArjcdcKIfKl\nlAHjcdJ8To1Gi7vmVOMrwPUo8fstapD1hCKlbAKuBn4OtAEzgbdRdflD8Z9Af9i//VJKD3AZ8AFU\nZv8r4GNSyoPGY64Hjhlx0yeM5wCYC7wE9ACvA3dKKV8zykIvQQ3uVhvP+Vsgy3jcJcBeo9LoDuBq\nKaV37O+EJpnQk5g0miiEEFZUxHKllPK1yd4fjWYsaOeu0QBCiPcJIXKMeOXbqEqUTZO8WxrNmNHi\nrtEo1qJqzVuAi4APGTGLRpOQ6FhGo9FokhDt3DUajSYJmbTGYfn5+bKiomKyXl6j0WgSkq1bt7ZK\nKUcq1Z08ca+oqGDLli2T9fIajUaTkAghjsWz3YixjDF5YpMQYocQYrcQ4nsxtkkxuvsdEkK8ZXbi\n02g0Gs3kEE/m7gHOlVIuQTVaep8Q4vSobT4BdEgpZ6GaLv1kYndTo9FoNKNhRHGXCnNFHbvxL7rE\n5gPAg8bf64DzovpraDQajeYkElfmbszY24rqGf3rGK1FSzG66kkpfUIIF5BHVNtUIcSngU8DTJ+u\nl7bUaE4FBgYGqK2txe12T/auaMJwOp2UlZVht9vH9Pi4xF1K6QeWCiFygMeFEAullLtG+2JSyt+h\n+nNTVVWlC+w1mlOA2tpaMjMzqaioQJ9wnxpIKWlra6O2tpbKysqRHxCDUdW5Syk7gZdRq+OEUwdM\nA7W8GWpVnbYx7ZFGozmpuN1u8vLytLCfQgghyMvLG9fZVDzVMgWGY0cIkYpa6mtf1GZPoTreAVwJ\nvCT11FeNJmHQwn7qMd7PJB7nPhV4WQixE7WW47+llM8IIb4vhLjc2OY+IE8IcQi4FfjGuPYqXvw+\n2PYQBPwn5eU0Go0mUYinWmanlHKZlHKxlHKhlPL7xu3fkVI+ZfztllJeJaWcJaVcZax9eeI5vhGe\n+gLU6OZ9Gk0iY7VaWbp0KQsWLGDJkiX87Gc/IxBQ645s2bKFm2++edyvce+99/LHP/5xVI8588wz\nx/x6DzzwAPX19WN+/HiZtBmqE4LPaNrn06P8Gk0ik5qayvbt2wFobm7mYx/7GF1dXXzve9+jqqqK\nqqqqcT2/z+fjpptuGvXj3njjjTG/5gMPPMDChQspKSmJ+zF+vx+r1Trm1wwnsRuHBXyRlxqNJuEp\nLCzkd7/7HXfffTdSStavX8+ll14KwCuvvMLSpUtZunQpy5Yto7u7G4Cf/OQnLFq0iCVLlvCNb6hU\n+JxzzuHLX/4yVVVV3Hnnndx+++3ccccdwftuueUWqqqqOO2009i8eTNXXHEFs2fP5r/+67+C+5KR\nodZQX79+Peeccw5XXnkl8+bN45prrsEcVvz+97/PypUrWbhwIZ/+9KeRUrJu3Tq2bNnCNddcw9Kl\nS+nv7+fFF19k2bJlLFq0iI9//ON4PMqcVlRUcNttt7F8+XL+/ve/T9j7mNjOXYu7RjOhfO/p3eyp\n75rQ55xfksV3L1swqsfMmDEDv99Pc3NzxO133HEHv/71r1mzZg09PT04nU6ee+45nnzySd566y3S\n0tJob28Pbu/1eoM9rG6//faI53I4HGzZsoU777yTD3zgA2zdupXc3FxmzpzJLbfcQl5eXsT2b7/9\nNrt376akpIQ1a9bw+uuvs3btWr7whS/wne98B4Brr72WZ555hiuvvJK7776bO+64g6qqKtxuNzfc\ncAMvvvgic+bM4brrruOee+7hy1/+MgB5eXls27ZtVO/RSCSHc/cPTO5+aDSak8KaNWu49dZb+dWv\nfkVnZyc2m40XXniBG2+8kbS0NAByc3OD21999dVDPtfll6t6kEWLFrFgwQKmTp1KSkoKM2bMoKam\nZtD2q1atoqysDIvFwtKlS6murgbg5ZdfZvXq1SxatIiXXnqJ3bt3D3rs/v37qaysZM6cOQBcf/31\nvPrqq3Ht51hJEueuxV2jmQhG67BPFEeOHMFqtVJYWMjevXuDt3/jG9/g/e9/P88++yxr1qzh+eef\nH/Z50tPTh7wvJSUFAIvFEvzbvO7zDU4DwrexWq34fD7cbjef+9zn2LJlC9OmTeP2228fU236cPs5\nVpLEuetYRqNJFlpaWrjpppv4whe+MKjW+/DhwyxatIjbbruNlStXsm/fPi644ALuv/9++vr6ACJi\nmRONKeT5+fn09PSwbt264H2ZmZnBMYG5c+dSXV3NoUOHAHjooYc4++yzT+i+JYlz1+Ku0SQy/f39\nLF26lIGBAWw2G9deey233nrroO1++ctf8vLLL2OxWFiwYAEXX3wxKSkpbN++naqqKhwOB5dccgk/\n/OEPT8p+5+Tk8KlPfYqFCxdSXFzMypUrg/fdcMMN3HTTTaSmprJx40buv/9+rrrqKnw+HytXrhxT\n9c5omLQ1VKuqquS4F+vY+gA8/SW47E5YccNE7JZG865j7969nHbaaZO9G5oYxPpshBBbpZQj1oYm\nSSyjM3eNRqMJJ8HF3Wg7oGMZjUajiSDBxV1n7hqNRhOL5BB3HctoNBpNBIkt7qaoa+eu0Wg0ESS2\nuJuZu3buGo1GE0GCi7vO3DWaZKCpqYmPfexjzJgxgxUrVnDGGWfw+OOPT8q+rF+/flzdIE8VkkTc\ntXPXaBIVKSUf/OAHOeusszhy5Ahbt27lkUceoba29oS9Zqz2AiZjEffhnm+ySA5x1+0HNJqE5aWX\nXsLhcETM2CwvL+eLX/wifr+fr33ta6xcuZLFixfz29/+Fhi+Be/WrVs5++yzWbFiBRdddBENDQ3A\n4BbATz/9NKtXr2bZsmWcf/75NDU1UV1dzb333ssvfvELli5dymuvvUZ1dTXnnnsuixcv5rzzzuP4\n8eNAaAbq6tWr+frXv36S37WRSfD2A2adu3buGs2E8Nw3oPGdiX3O4kVw8Y+HvHv37t0sX7485n33\n3Xcf2dnZbN68GY/Hw5o1a7jwwguB2C14V69ezRe/+EWefPJJCgoK+Otf/8q3vvUt/vCHPwCRLYA7\nOjp48803EULw+9//np/+9Kf87Gc/46abbiIjI4OvfvWrAFx22WVcf/31XH/99fzhD3/g5ptv5okn\nngCgtraWN954Y8IW2JhIElzcdbWMRpNsfP7zn2fDhg04HA7Ky8vZuXNnsCGXy+Xi4MGDOByOYAte\nINiCNycnh127dnHBBRcAamWjqVOnBp87vLVubW0tV199NQ0NDXi9XiorK2Puz8aNG3nssccA1a89\n3KVfddVVp6SwQ8KLu45lNJoJZRiHfaJYsGABjz76aPD6r3/9a1pbW6mqqmL69OncddddXHTRRRGP\nWb9+fcwWvFJKFixYwMaNG2O+Vnhr3S9+8YvceuutXH755axfv37QYh7xcCJa9U4UyZG561hGo0lY\nzj33XNxuN/fcc0/wNrN970UXXcQ999zDwID6jR84cIDe3t4hn2vu3Lm0tLQExX1gYCDm4hmgzgJK\nS0sBePDBB4O3h7fqBbVI9iOPPALAn//8Z97znveM5b950klwcR9nnXtfO3j7Jm5/NBrNqBFC8MQT\nT/DKK69QWVnJqlWruP766/nJT37CJz/5SebPn8/y5ctZuHAhn/nMZ4atTHE4HKxbt47bbruNJUuW\nsHTp0iErX26//XauuuoqVqxYQX5+fvD2yy67jMcffzw4oHrXXXdx//33s3jxYh566CHuvPPOCX8P\nTgSJ3fL3sU/Dzr/CaZfD1Q+N/vH3rIEZ58BFPxjffmg0CYxu+Xvqolv+jnVAtacJuhsmbn80Go3m\nFCE5xH2ssYzfCwP9E7c/Go1Gc4qQ2OLuH6dz9/tgQGfuGs1kxbOaoRnvZ5LY4j7eWCYwoAdUNe96\nnE4nbW1tWuBPIaSUtLW14XQ6x/wcSVLnPoZYRkody2g0QFlZGbW1tbS0tEz2rmjCcDqdwUlaYyE5\nxH0sde5mGaWOZTTvcux2+5CzMzWJS4LHMuNYQ9U8IGhx12g0SUiCi/s42g/4vepSi7tGo0lCkkPc\nxxLLmAcEnblrNJokJMHF3RD1sQyoBh/r1Y3HNBpN0pHg4u6PvBwNZiwDOprRaDRJR4KL+3himbDH\n6GhGo9EkGckh7mOJZSLEXTt3jUaTXIwo7kKIaUKIl4UQe4QQu4UQX4qxzTlCCJcQYrvx7zsnZnej\nGFedu3buGo0meYlnEpMP+IqUcpsQIhPYKoT4t5RyT9R2r0kpL534XRyGcWXu2rlrNJrkZUTnLqVs\nkFJuM/7uBvYCpSd6x+LCP45qGS3uGo0miRlV5i6EqACWAW/FuPsMIcQOIcRzQogFQzz+00KILUKI\nLRPSx0LHMhqNRhOTuMVdCJEBPAp8WUrZFXX3NqBcSrkEuAt4ItZzSCl/J6WsklJWFRQUjHWfQ5ji\nLgMQCIzusdq5azSaJCYucRdC2FHC/mcp5WPR90spu6SUPcbfzwJ2IUR+9HYTTnjWPtr+MuHirtv+\najSaJCOeahkB3AfslVL+fIhtio3tEEKsMp63bSJ3NCbhgj7aaCagnbtGo0le4qmWWQNcC7wjhNhu\n3PZNYDqAlPJe4Ergs0IIH9APfESejM7/AR/YnOBzj35QVU9i0mg0ScyI4i6l3ACIEba5G7h7onYq\nbgI+cKQrcR9PLKPFXaPRJBmJO0M14Ack2FON66MU94hYpnfCdkuj0WhOBRJY3A0xt6Woy1HHMuGN\nw7Rz12g0yUXii7s9zbg+xszdYtcDqhqNJulIfHG3GauDj7Ynu/l4Z7Z27hqNJulIYHE3atzHmrmb\nsYwzS9e5azSapCOBxT0qcx9rLJOSpWMZjUaTdCSBuBvOXccyGo1GEyRxxd103nYjcx+1c/eCsIIj\nQ4u7RqNJOhJX3KOd+1gmMVkdKrPXde4ajSbJSGBxNwdUzWqZMWTuVrsh7tq5azSa5CKBxT2qFHIs\nM1QtNlUnrwdUNRpNkpH44m6WQo7JuTvAkaadu0ajSToSX9yDpZBjydztyrn7vaOvttFoNJpTmCQQ\nd3NAdQz93C22kPPX0YxGo0kiEl/c7WNsPxBeLQM6mtFoNElF4ov7WJ17MJZJV9e1c9doNElE4ou7\nfRzVMmYpJGhx12g0SUUCi7tR524bR7WMxR5qGaxjGY1Gk0QksLiP07n7tXPXaDTJS+KL+1jbD5ix\njEM7d41Gk3wkrribMcx4ltkLj2W8ur+MRqNJHhJX3Me9WIcvKpbRzl2j0SQPCSzu41wgOxA2QxV0\n5q7RaJKKxBd3i139G8syexYt7hqNJjlJAnG3qX+jnsQ0TCzTvBcad03Mfmo0Gs0kYJvsHRgz4eJu\ntY9hmT0jlrFYwZoS6dz/8RVAwI3/mLDd1Wg0mpNJAjt3Y0DVYh2jczdiGRi8YEdnDXh7JmY/NRqN\nZhJIYHE3xNx07mOqlnGovx3p4DWceyAA3Q3g80zcvmo0Gs1JJoHFPSpzH3VXSC9YjVTKnhqKZfra\n1IHD5564fdVoNJqTTPKI+5j6uceIZbrr1aV27hqNJoFJYHE3M3dzQHUU4i6lOjiYsUz4OqpdDepS\nO3eNRpPAJLC4+0BYwGIZfZ27eSAIxjJh4q6du0ajSQISW9wthjhbbKMT9+BgrBnLhC2SrZ27RqNJ\nApJD3K220cUyQeduxjJhA6pdhnOXfr1otkajSVgSV9z94c7dProB1aC4DzOgCtq9azSahCVxxT3g\nUxOYwIhl/KN4bJS4h9e5m7EM6Nxdo9EkLCOKuxBimhDiZSHEHiHEbiHEl2JsI4QQvxJCHBJC7BRC\nLD8xuxtGwBfKzMcay0SUQoYNqNqM1Z20c9doNAlKPM7dB3xFSjkfOB34vBBiftQ2FwOzjX+fBu6Z\n0L2MRWAiY5k09Xh3F7hdkFOubtfirtFoEpQRxV1K2SCl3Gb83Q3sBUqjNvsA8EepeBPIEUJMnfC9\nDSfgDxtQHWWde3QsY3aGbD+sLnMr1aXfO/791GgmCncX9HdO9l5oEoRRZe5CiApgGfBW1F2lQE3Y\n9VoGHwAQQnxaCLFFCLGlpaVldHsazXgyd1O0w0shAdpMcZ+hLrVz15xKPP0lePSTk70XmgQhbnEX\nQmQAjwJfllJ2jeXFpJS/k1JWSSmrCgoKxvIUIQIDUXXuo4lljBJH6xDiPsVw7npAVXMq0VUH3Y2T\nvReaBCEucRdC2FHC/mcp5WMxNqkDpoVdLzNuO3FE1LlPUCzTdkhdmrGMdu6aUwlvH/j0Wr+a+Iin\nWkYA9wF7pZQ/H2Kzp4DrjKqZ0wGXlLJhiG0nhvDMfdTtB4aIZdoPQ0oWpOWq69q5a04lvD0woA2H\nJj7iWYlpDXAt8I4QYrtx2zeB6QBSynuBZ4FLgENAH3DjxO9qFAFfqDeMxTrG3jJmP/ewWCZzqi6F\n1JyaeHvVzGmNJg5GFHcp5QZAjLCNBD4/UTsVF+OKZczMPayfO4C7E0qWhom7du6aUwhv72TvgSaB\nSOw1VMdc5z5ELAOQWQK2FPW3du6aU4VAAAZ6VSdUKUEM67c0mkRuPxBd5z6OWMZ07gBZJdq5a049\nzBnUMjC6s1TNu5bEFXf/QFid+1gzd9O5p4fuy5qqnbvm1MMUd9AVM5q4SFxxH08sE764NkQ698wS\nPaCqOfXw9oT+1hUzmjhIDnG32tXpaiAQ32OHjWWmGs8rdCyjOXUIH0zVzl0TBwks7v7IGaoQv3uP\njmUsVrAaUUxmiRqssjm1c9ecOoSLu3bumjhIYHH3xRD3OHP36BmqoGrdLTZIN9oi2FK0c9ecOoTH\nMtq5a+IgOUohTZGOt4ogup87qHJIe7pacBu0c9ecWmjnrhklySHupkjH69yjYxlQuXtqbui6LQV8\nuuWv5hTBq6tlNKMjScTdKImM17lHV8sATF2qatxNtHPXnEroahnNKElwcTdE3ToG526xR87yu/K+\nyG105q45ldDVMppRktgDqsFqF1Pc483cvZGRTCy0c9ecSujMXTNKElvcBw2oxlst44tD3LVz15xC\naOeuGSUJLO7+wZl73LGMN7JSJhbauWtOJbw9oQZ32rlr4iCBxT18DdXRxjIDodmpQ6Gdu+ZUYqAP\n0vLV39q5a+IgccXdPzDOWGaEsWTt3DWnEt5ecGaDsGrnromLxBR3KdWKNGNuPxBvLKOdu+YUwdsD\njnQ1H0ObDk0cJKa4B4ylxsbafiDuWEb/iDSnCN5eJe42JwzoWEYzMgkq7oaIj7X9QNyxzDDOve0w\nbP9LfK+n0YwXU9y1c9fESXKI+6jbD8QTy4zg3DffB098Vrco0JwcvL3gyNDOXRM3ySHupgsfTeOw\neGKZwEAoAorGVaMu+9rie02NZjx4e1XnUrse6NfER4KK+zgz93gnMcHQ0YyrVl32tcb3mhrNeAhm\n7qnauWviIkHF3Wz8NdY69zjbD8DQLskU996W+F5Toxkr/gHwe1Qso527Jk4SVNyHGlAdZeOw4TCd\nuz9Gpu7zQG+z+rtXxzKaE4zZekA7d80oSGxxDzYOG8Mye+Nx7l11ob91LHPycLsmew8mh3Bx185d\nEycJKu7jzdzjEfdhMndXmLjrWObkULcNflKhSlDfbQTFPUM7d03cJKi4m7FMVD/30VTLxDNDFWK7\nJDNvB+jVzv2k0H4EZAA6jk72npx8Bgxxt+tqGU38JLi4j2eG6jice5ch7rkztLifLPo7jMvOyd2P\nyWBQ5q7FXTMyySHuo56hOs7M3VWrOvRll+nM/WRh5u2myL+bCI9l7E7dFVITF4kp7v5ROncp1b/g\n40cTywyRuWeXKoHXmfvJwd0Zefluwlw/1XTufu/Qk+s0GoPEFPfozH249gP+AbhjDrzz98jb4pmh\nCkM79+xpkF6gSyFPFmYc826PZewjzL/QaAwSXNzNUkhD5GPFMm6Xqklv2Rf2+IH4GofBEJl7HWSV\nQno+eFy6NfDJwIxl3pXOvU9dms4ddO6uGZEEF3dDoIVQf8eqcw9mtWGiEG/jMBjskNwu8HSpvD3d\nWBknUfvL+Adg/3OTvRfx4X43O/ewWCbo3HXurhme5BB3UGIdK5bxdKtLU+QDAVVSN2IsM8Tpr1nj\nbmbukLi5+4F/wsMfgeZ9I2872Zii/m6cyOTtVd91q0M798micRc8+qn4izZOARJU3KMmMYGqfonV\nfmCQuBsfzoixzBClkGaNu5m5Q+KWQ5r7nQiCmWzOPRCA+y+B/f8ceVuzaZgQ2rlPFodfhHf+Bi37\nJ3tP4mZEcRdC/EEI0SyE2DXE/ecIIVxCiO3Gv+9M/G5GEd04DIaOZaLF3ewVM9ZJTGaNu5m5Q+LG\nMp4udWme9p/KJFvm7u6EY6+rfyNh9nIH7dwnC/P713ZocvdjFIxgXwF4ALgb+OMw27wmpbx0QvYo\nHmLGMrbYp0ymgJmiYG4zUixj3h/LuQsrZBaHnjtRYxm3sf8DfZO7HyMRCIT2NVmcuykWfe0jb2uu\nnwrauU8W5veu7eDk7scoGNG5SylfBeL4Bp5EYom71R679ndQLGM2HRvhuCYEWGOsxuSqg6wSddbg\nzFH7kKixTNC5n+Li7nEBEpzZ4O2Ov/vnqYxpNuI56xvoC4m7du6Tg6kfrYnj3Ccqcz9DCLFDCPGc\nEGLBBD3n0JgiHj7LdMhYxnTuUbHMSM4djHVUo1r+umpVpQyoA0AiT2QyD3xm75JTFfOzm1IReT2R\n6R+FuHt7wW6KuzkWpJ37ScWdhM49DrYB5VLKJcBdwBNDbSiE+LQQYosQYktLyzgEMXoSExgDqsNk\n7j63cjvmNiNl7hB7HdWuWpW3m6TnJ27m7k4Q524KYVDckyCaGY1zj4hltHOfFMzvYOuhyNnupzDj\nFncpZZeUssf4+1nALoTIH2Lb30kpq6SUVQUFBWN/0aEy95h17l1hf7sG94IfDpszMnMPBIzWA2Wh\n29LyEti5J0jm7o4S92TI3Ufr3IOxjM7cJwXzbNHjSpgYdtziLoQoFkII4+9VxnOeWCs7ZJ37MJk7\nqA8oGMuMwbn3tqgDSLi4pxckzIc9CPML602QWCan3LieBM3DwnvljFQ7HS7u2rlPDu5OVf4MCRPN\nxFMK+TCwEZgrhKgVQnxCCHGTEOImY5MrgV1CiB3Ar4CPSHmCz1uiG4eBGiAdLpYBQ9xHE8tEOfdg\njXu4uOcnrrgninOPjmWSybnDyJ0uI0ohtXM/6UiptKOsSl1vTQxxH7EUUkr50RHuvxtVKnnyiJW5\nW+wRsczR1l6m56Zh9XSpqhe/Rx19nTlqg7E4d1eNuozO3L3dykmZZWqJQqJk7tGxTDJl7qCimYzC\n2NtJGTuW0c795DHQr874ixbCvmdH79z9PrjvAjjnGzDnohOzjzFI0BmqUY3DwKhzV7c3dbk5/+ev\n8MzO+lAfGDAyd7POfQzO3Vw7NSJzNycyJZh7lzJxqmX6O9XcAvOgmmzOfbjc3ecB6QdHmrpusRgl\nutq5nzTMA3FaLuTNHH05ZH8H1G+D6g0Tv2/DkODiHhXLGLcfaOrGH5DUdvQrAQuKe+f4qmVctWqp\ns9QpodsStQWBzx060CVC5p6ao86MbKlJ4txd6rsEw4t7+EIdJnandu4nE3PMx5mtxH20zt2MP01z\neJJIOHHv8fhochlf+EEDqkqsqlvV/R29XiXuOcZASH+YuI/FuXc3qpmpavxYYbYgSDRxD68iSoRY\nxpmt/k7NSQ7n7u6E3Jnq72HBGa8mAAAgAElEQVTFPawjpIktVTv3k4n5fXPmQN5s6KgeXQMx8wy5\nq37Cd204Ek7cX9zbxMNvHlFXhqhzP9qqxKq916NELL1ACfWoY5kY1TIZRZHbmM490WIZT5i4jyaW\nOfhCfFPmJ5L+sLESZ05yOPf+Tsibof6Oy7mHibt27gBsOtqOe+AkrEgVdO45kD9bJQQdx+J/fFDc\ntXMfloLMFKwEkMIa6aAtoVimuk39ILp7e5WYp2Qq5zfeapme5pCYm6TlqctEde42Z/zO3d0Ff74S\nnvv6iduvmK9rxDKQXM49vRAcmcOv5hUrltHOnZZuD1f/biOPbDp+4l/MNBOphnOH0UUzQXFvUHNl\nThKJJ+4ZKdjxExDWyDvCxd2IZTy9xhE3JStM3EfTfiDKufc0Da5qcGarA0WiTWTyGO9NZnH8pZCu\nWkDCrkeh7fAJ27VBhMcyk+HcD/4bnv7SxD1fIBA6YKXlDu/cB7Rzj0WDqx8p4XDL2MaLXt7XzD93\nNcS3cUQsY0RpoymHNMU9MHBSdSLhxD0/IwVrLHE3YhmfP8DxdiVWA4PEvTP+xmEQ6dx9XvX46FhG\nCKMFwQl27tWvT2wvafMLlzk1/gFVs85fBuD1X07cvoxEeCyTmgP9J7m3zL5nYOuDE+e6vN3qPXRm\nqzO/eGIZc/AVDOf+7hb3pi71uzTP0kdDn9fHLX/bzv/8Y++w23W5B9h6rD0slslSB+O0vFE697AI\n9CRGMwkn7tmpdhwigD+6RN9Yiamusx9fQJLptOE3RSAl03B8rvj7uUOkczePuNGxDJz4iUzdjfCn\nD8Mzt07cc5qxzKicu3EKfNplsP3hkNifSMwJJKmTmLn3tABSifJEEO4E4xX3QdUy7+5YpqlL/S7H\nIu6PbKqhs2+A2o5+Ovu8Q27303/u4+rfvom3t129/+Y4Xd7sEc9cff4AP3x2L7UdfZETKU/ioGrC\nibvFIki3gy961y1WCPg4akQyy6ZPwTpgvKmxMvd4u0L6PUpgeprUbbEmm6SdYHF/9Q6Vsda8GVnl\nMh5MN5E51SiLjGNgylWrDooX/gCQ8PqvJmZfhmOgT53Ohjt3T9fJbfvb26wuJ+q9D89w0/KGH6Ae\nslpmEp373megeXjXe6JpNsS9rqMfry/yjMrrCzDUJHmvL8DvXztCdqoS6t31sT9Tj8/PU9vr8QUk\nPZ1toVgQIH/WiLHM/qZufvfqER5681iUuGvnPixK3GPHMmbevnx6DhkY7sYU9/7OUTYOMw4Afm/I\nuUfHMmA4d3X/0dZebn74bfq9EzSK31ENWx+AqUvUvh99ZWKe1xQq8/8Tj3t31ape9lPKYclHYNuD\napD5RBJ0uWGZO5zctr/m/9EzQeI+JucenblPonN/8vPwxsmdlB6NGcsEJModG0gpueAXr/DNx2Mu\nHMdTO+qpd7m5/fL5AOyqi/09emlvM11upRX9XW2h7x1A3ix1wB/mO1htVOyt39eixN2ZrQylFvfh\nSbfBgIx27qrOvbqtj4wUG7MLM0Pi7sxSLikilokzcwflkswfeMxYpiD4A31pXzNP7ahn2/EJam61\n/sfqrOTqP6nKioP/npjn9XSpU82UTHU9nooZV22oedLaW9V7ufWBidmfoQh3ueGXJzOaMQ/sE+bc\nDVFIzYH0PDVoOpRYxxL3MTr3Pu8EnO2YY08j9cM5wTR2ubFZVLXcsba+iNuPtfXx8KbjrN8faTwC\nAcm9rxxmXnEmH1xaSmlOKruGcO6PbqulMDMFh82Cr68j9L0DmFKpLocphzTjov1N3fT1dChxzyrR\nscxIpNkkA4FocVftB4609lKRn0ZuuoNMYXzo5oCq9IdcU7zVMqAGVYeNZfLU6fNAP/Wd6ke6o3YC\nxKd5L+x4BFZ9CnKmw4yz4dCLE9NP2t2lhN0UjXjWUXXVhiaE5c1UDqZhx/j3ZTjCa4zDL83P0dMN\nD1yqVqc/EXh6Qmc1E+Xc3VHOHYaOZry9SszD53SMwbk/vOk4i2//F09uH6dzNA507W1N43uecdLU\n5WZhqTqbC8/d9xhinem08f8ee4dud2iy0Qt7mzjU3MNnz5mJEIKFpVnsjuHcW3s8rN/fwoeWlzIj\nPx2L2xUZy5gaMEwRRXVrL3arOvi0tbUpDcoq1eI+Emk2iVdaCATCRM5oP1Dd2ktFXjq56Y7BsQyE\nPpB4Z6iCckm9LeoDMluuhhPWgqCuQ73mzpoJiA1e/qFy12uNgdTZF6jFQlr2jf+5PV3G/8eowhgp\nlvH71BczvK9O3uwTv2CwIeK7Oiz8x70b6ZDG/pptf2s2QfVrExdXRdMb5v4myrn3R2XuMLRQhDcN\nM7E5R+Xc23o8/OhZlZF/5W87eGnf2IXZ7VKPbWlu4uX9JziSG4bmbg/zS7LISLFFOPe9Deoz+s01\ny2nqcvOj5/bh8wd4ZNNxvvXELsqmpPL+RVMBWFiSzZHW3ogDAMDTO1TWfsWyMmYXZeLwdUXGMnG0\nHKlu62XZtCmU5qTS29WhNCir5OQUIRgkpLinWiU+acHVH/ahWOzIwAC1HX1U5qczJd1OpujHL+zK\ngZvi3tsKwhLphIYiKO6e2BOYTIItCFqoM5z7zvE690AADjwPy65R5VcAs85Xl2OIZgYNMHm6VFxl\nNqQaKZbpblBnPhHiPhPaj8Q3GDtWDJf71aeOsqm6nV1txsQ1UyAbd6rLE+WIesLqkj1xHrA93fCP\nrwx9MHAbjdAcGWHiPkTu7u0NfUYm9lTl3GOdwbUdhi33R9z0k3/uo3/Az7rPnsm8qZl89k/beOvI\n4NfzByQ/+9f+4GBlLGpqVBSRY+nlc3/axvaakz+hzOPz097rpTjLSXleWqRzb+iiIi+N98wu4BNr\nK/nLW8d578/W843H3qE0J5V7rlmBzapkz3T+exsiq6Ae3VbLwtIs5hZnMrswg7RALwOOzNAGYb/3\noTja2kdFfhpnzy3A199FwJGhxL375E1kSkhxd1olA1hp6QmbPWq1I2QAKQNU5KUzJU05d4/NKCEz\nj7y9LfGVQUIwlunt7VHiPlRb1mALgjbqO/uxWQT1Ljct3Z7Y2/d3wJ1LoGbz0K/dVasqdQpPC92W\nXQYFp8GhFwZtLqXkDxuOcsfzg2vh//LWcVb/8MXIH63bdO6GKxypBUGsXvb5s1Xu3jmKqdijpKGp\nEQCRppq17e8yxkrMaKPBFPcTNFA1Fud+/E3Y/Hs49kbs+/s7lWsXIo5YpieyDBIM0yFD40fhbP8z\nPPNlFScBW4918LcttXx8bSVLp+Xw4I2rKJuSyice3BIsJzQ50NTNXS8d4tl3hp7cU1+n2l4XWPvI\nz3Tw8Qc2c6QljkhvAjF/V8VZTiry0oNFFKBimdOmZgHwlQvnMq84k3SHjf+7rorHP3cmi8pC8cqC\nUrVd+KDq/sZudtV1ccUy9T2fk+8kU/TT7g87wDpzVAw8hLj3eHy09nioyE/nnDkFpMk+2gZSIKtM\nfWYnaVnOhBT3FKvEj5XWcPE0nLgdPxX56ditFnJtbtwW40MJd+7xRDIQdO7ffnSr+pEPJe7GD9Tb\n1Uxbr5c1s9SRPdq9D/iNI3bLAVUFc3wjAHWdg8u5aDf65+TOiLx99vnqcZ7QD8rnD/DNx9/h+8/s\n4e6XD0X82KSU/OH1ozR3e/jeM3tCzzNa5x4U9+mh24JTsU/MbNWjrb089aba59998lzKpqSypz3K\nuZuZ/wlz7mHiHm/mbj6mr5VGl5szf/Qirx0ME4LwGbdxOfeoWCa4GlOM3N18X3qa8Ack335iF8VZ\nTr60MgOe/xZ5KQF+8uHF9Hh8vFMbeSbS6FJi3zCMc+9oUQdRi9/NH69fCsDX1+0ccvvRIKWkrcfD\nztpONlcPXR5qVsoUZqVQnpdGbUc/A/4APR4fx9r7mG+Iu9Nu5dmb38M/v3wWF8wvQoS3KwEKM50U\nZqZEiPtfN9dgswguX1oCwJwp6uyo0Ru2VoMQxgpsscXdPNhU5KWzZlY+GcJNbZ9NOXc4aRUziSnu\nlgA+LJHO3XDjVvzMyFc/hilWN72MR9yVc69r6STQ3ax6gcTCcO5dbcrxXLigCIuAHWE/nl11LhZ8\n53l21HSGPtzO47T3ennvHeu56rcbI51UUNxnRr7WrAvU0f/oq4ByCZ94cAsPb6rhhjMrsFkED4f1\n29h2vJNDzT0sLM3iHzsbeHGvkbcOcu4jibvxnNlhC5XkG+J+Alam6ff6+eyftpIpewg4MpmWn8ms\nwgz2tg4YTeA61f+h3TiwdNXT4Ornx8/t41DzBDpJ4wfcZ0lHxjsz1vzR97Xxrz2N1LvcfP/pPfjM\ng3t0IzTEkOLe19tFv4haBCZ8LCgacwC6q55ndtazp6GL/7r0NNKq/w0b74Ztf2R6rvpN1LsiDw7m\n9YZOc+Je26DIrb+zMfh3ZdoAN587iy3HOoYV43jYdLSdRbf/ixX/8wKX3/06V927ka3HYlfkmGeg\nRYZz9wUk9Z397G/sQkqYX5IV3NZiETGfw2RhaTZH6uqhq4GWbg9/2XSMy5eUkJ+hfvvTUtXZUU1/\nVAHGMBMXzZioIi+d9BQbWZZ+DrqEFvd4cFgM594TdlpqCHae08KUdPVBZFnc9GC4HLMHu8cVdyzT\n41MRQKbow+LpHNq5p2SC1UF/hxLO2YWZzC7MjHDuD286jtcfYMuxDpW7AXQeZ19jF15fgJ21nVx2\n14ZQhtl2WP2IM6dGvtb0M5D2dA6/8Rif+/NWzvjhi2w41MqPrljE7Zcv4IL5RazbWovHp36Uf9tc\nQ5rDykMfX82cogy+/cQuej0+Y0A1M8y5xxHLpOZGusi0PCVOw0zFvm/DUW5/anforCVOvv3kLvY3\ndXNupROL8dnNLszgSEsP0mk0D2tSFTKBwoX4u+o5/46XufeVw9z88NshIR0vPc10i0yafRm0tcXZ\nFyRM3F/c20yKzcLB5h7+vtU4+3F3Ip05/HFjNfXdAyqiiSHuUkramuvZ2Rb1Mx3OuZvi3t3IO7Uu\nnHYLlyycGjqzeeMu8lMt2K2C+s7Ig4Mp6o0utxo3uHOxinkMOnq9ONxh++nu5OqV08lNd3DP+qHP\n3jr7vMGBzqF443ArvV4f3750Pnd9dBlCEHm2E0ZTmLiX56nvb3VbX7BSxoxl4mFhSRb/2XEPgQcv\n53evHsbrC/DF82YH77d71ft5tCdUOt3R6+W4Jx1/T+z9Mwd4K/LTwO/DKT3U9lppwDhLO0kVMwkp\n7jZ8BLBGZtqGYFfmpQRvyqIfV8D4IaSEfeBxOvfDnWrAtkQYR+ihxF0ISMtnoEuJe+mUVBaXZbOz\n1oWUEveAn6d2qA/0QGN36MN11ajrwAM3rsJhs/Afv93IG4dbof2oqqe1RH1ENgdv2FZRdOxpDh2t\n5v2Lp/K3z5zOR1epuOSjq6bT0TfA87ub6PX4eGZnPe9fNJUp6Q5+dMUi6l1ufvHP3cr1ObOHrJYZ\nNADrqo3M283/d/7sIZ27lJLfvnKYB96o5gt/2RaMnvwBySObjvP7147EfNzfNtewbmstXzx3NsV2\nN6Sqs67ZhZl4fAEGHFnKuRt5+0Ptp2GVfj4w28Z3L5vPnoYu7ttwNOZzjxaPq5FGfxZdpNHSOjpx\n93W3sPFIG9esLmdF+RR+/u8D9Hl9yP5OtrfCd57czV0vHVQznGOIe3VrD0WBZg558yLvMJz7wboY\n+2OORXQ3cNSoHLNYhPGdE+CqwbJ7HcXZzmDZrkmDEcvUu/pVFZS3B5pCUd6O2k7yCBPp/g5SHVZu\nOLOCl/Y1s68xtoB/+a/bufjO1/jwPW/w/O7GyCo3g6OtvZRkp/KJtZVctqSERaXZvH4ohjPuaabV\n1YXdKpiSZqfCOEs/1tbLnoYuctLsTM2Of7nLBaXZVIn9iLZDPPLmIT64rJTK/DADYxws97tCBRj3\nvnqYra1WWpvqYrYcPtraS2FmCmkOW7BlRQ+pvHDMr3RKO/ehEQE/wmqjtWdw5l6ZExLudPro9Bsf\ntNUWGpiKU9z3t6ozg6ocdZovh6qWAUjPR/a1YrUIijJTWDwth/ZeL3Wd/fxrTxPdbh9ZThv7m7oj\nnPuBpm6yU+2cNTufp76wlowUG+u21Kq4IW/moJeRUvKTvstJE16er9rKjz+8mBXlucH7187KZ1pu\nKg+/dZx/vNNAr9fP1StVbfqK8lyuWT2dx40cm5SssDr3kLhvONjKyh+8yINvVIdeOHwCUzjDlEMe\na+ujudvD6spcnt/dxGf/tJVNR9v54K9f5xuPvcMPnt2rFlQJY39jN99+chdrZ+XzpfNmR6x7O7NQ\nfX59lgzl3Bt34nHm81qfOrD98Nw8bjizggvmF/GLFw5wvC3OnjnD0NVaT6vMRqZk0d/dEV//cEPc\nO1ob8foCnDuvkG9eMo+Wbg//9+pRerva2N0uyE138Mr+FmRaXsxT/G279uAQfva6cyLPRAzn/pWH\n3+KB16MOYmHO/WhrLzMKjM+3qw5KV6h1QDf8ktKsFBpc0eKurjd1uQmYS8l1hUr3dta6yBcuAubS\nkka+f90Z5aQ5rPz2lcEH6111Ltbvb+H80wpp6nLzmYe28tH/e3OQeYjYV+DMmfm8fbxTnWWatB2G\nn83jlk3v5d+OryLWfZxCXwOpdivVrX3saehm/tQsxL5/xD0OtChPUmFpQhCgyN/MF8+dHbmB8X88\n2GXFPeDH6wvw6NZaBlLyyPB18JmHtgbPkk2qW3uDBx2z9UBaZg5P7miErKng0uI+NAEfFpsjQtwH\njHYE5VNCzj1V9tHmC10P5u5xxjJ7mpVzX5KhHEmDb5jTvfR8bP3tFGc5sVktLDFG5XfWuli3tZbS\nnFQ+uKyUg03dSJfh3L091DfUM6coAyHUj3359Bx2HG9Xzj23ctDLNLjc7PQUcbTkUsSW+wad4lks\ngo+snM7GI2385uVDzChIZ0V5aFnAz5w1k/TwmbtWu5rQZVTLbD3Wzqf+uIUezwDffWo3v3rxIDIQ\nQHbWUBPI40O/eZ1f/PtAKGbJn6UOVp7BTbXeOqrc6A8+tJD//uBCXtzXzH8YYwufO2cmUsIbhyMd\n61/eOoYQ8MuPLMVqEUY+rd7LWYa4d8p0w7nvoDZlFi3CEJuuOoQQfP8DC7BZLHzriXeG7DESL4Hu\nZnoduZQVF5Em+3h+d+PIDzJO1/s7m0h3WFlVmcuK8lzet6CYX764n5SBbmZML+OrF86l3uWm15od\ns1rm8EF1EK4JFARdNRB07mligNuf3sP/PLMn5IYNcQ901XO8vS/kQrvq1XjJ2lugdT8XWrcOjmWM\n1xjwS/oaD6gbw4RoR00nRdZuLPlzjNdSwpeT5uBjq6bz1I56atojD6i/WX+ITKeNn1+9lPVfPYdP\nrq3kraPtEZGqlJKjLb0RjnntrHx8Acmmo2Hvy5GXQfr5V8blNNmnwd6nEJt/T3leGodbetjX0MWy\nAgF/u071Y4qDqb2hOSNXz/RFuvaw97MzkM7hlh5e2tdEa4+XFfNnky48bDpQwxf+EhkDVrf1UZkX\nKe4LZ5Sx5VgH7tRiHcsMS8CH1WaLiGVa+9WXe/oUQ7ilJMXfiyvgDPV5MQex4pmdCuxqNrI9qX6s\nm1qHaVmQXkDqQDulOcpVzSvOwmG18K/djWw42MKHl5cyrziLXq8fv6sueBbR33KUOUWhGtql03Lo\nazPKIKMHU1HTmQF6Tv+K6jUT40t8VVUZNouguq2P/6iaFlElMD0vjeVFxsduRlX2NPD2srvexQ33\nb6Y428n6r76XK5aX8vN/H+D7j25EeLt5cI+fmvZ+7nzxIFf85g0ONXeHVcwMdu9vHW0nL93BzIIM\nrj29nF99dBk3nzebl756DrdeMIfMFBsbDoWiBSklL+5rZu2s/OCAVnhHyOxUO4WZKbT60lRFSss+\ntg2Uk19aobY1fjRTs1P5+vvm8trBVp7cPviH9M9dDaH2EDWboHbroG1ATddPH2gnM28qubn55Fj6\neWxbHK7LcO6iv521s/Nx2NT7/fX3zSXf4ccu/JwxfyZnz1VngnXe1EGxjM8foKNOvac1siBCNANW\nJe7vn5/DDWdW8PsNR/maWbFiiJGnow5fQFKZn6Hq4V11aobk/A/ClAou7nyYxq5+/MZBQUpJg6uf\nCiPDHmgyxN2IEKSU7KjpYAqu0EB6WAuCT7ynEouAX7xwIHhAPdTcw3O7GrnujHKynHZsVgvnzlPR\n5v7GkBlo6/XS7fFRkRcS1qqKKThslshopvp1yJzKz8UNPDD9h1CxFg6/REVeOm8dbcPjC/Ae6y41\nH6PxnZE/J0DUvx38+4qKGKXLxgGsizQONvXwyOYaVYJZXgHA7ecV8e89TTy3Sx30u90DtPZ4KM83\n4k5D3FfOLUcIODaQo2OZYQn4sNnsEc691qVc9qzcUCWBVfrolmm0m209TeceRy/3Ho+Pg+3qOVN6\n1Yfxcs0wI+9p+WT4XZTkqNd32CycNjWTJ7bXE5Dw4RVlzC3OACSipxHKqgDI8TZGifsUKiyGO4wu\ngwQOGuJePms+LL8Otv1RlVWGUZjp5PzTirBZBFcsLx30HOdVqn1s9BoHOUc6fT1dXHffJjJTbPzp\nk6spznZyx5VLuOHMCjZuU8KxZsUSNv6/c7nnmuXUdvRxya82sNFlREIxVoR/60g7qypzgweXy5eU\ncOsFc8hIsWGzWjh9Zh4bwn68B5t7qO3o59x5Yc3ZwmIZgNlFGTR4U1Q7iICPV1xTmVtZCdaUiB/N\nf64uZ3FZNj/9576IKOVQcw9f+MvbwRmbPHUz/PO2QfsOsGFvLRmin+KS6QhnNlOs/bx2sGXYST4E\nAkFxzwq4gmIGMKMggw03q/JBkZpDaU4qswszONCdosQ97CxjR62LPJ8aw6mT+dSENcdq96qz1LIM\nC7dfvoD/PH06j71dq+ZjGBU0sqvBeM10NXg+0KuqNaw2OPNmpvbu4TR5hOZutX1n3wDugQDLp6uz\nPGFWIfU0g0/Fi97eTmzSp9pOQMSKWFOzU/nke2bw2LY6vvXELvwBNd6SYrNw45rQGeicYvVdN00K\nEOzkWhkWyzjtVlZMn8Lr5pmdlHDsdahYS1O3h6IsJ8w8D5r3sDCzB/eAcs7zejep7Vv2qT44I1H/\nNu7McgZs6eR5YohufyfSYsdrcfLKgRZeOdDCf1SVYTXG366c56Qk28k6Y7DcHEyNdu55ufmcMSOP\nba40ZFf9xLQQGYEEFXc/Nrudth5v8HT0WIcS+mnZhnAbb2o3qaFcd5hYxh+QEadWexu6cEslfqK3\nhX5LOq9Vd8ccDAIIpOWThpvyrNABYHGZEqVVFbmU56UzuyiTKXRjDXhh2ukAlImWCHFfPC2bSjG0\nuO9v7KEwM4WcNAec9TU12/bV/x203fc/sIA/f3I1hZmDB5fOKFX/r1eOGQdHexr7a5ro9vh46JOr\ng2cfFovgu5fN5+cXqQG9965agd1q4eJFU3n+lrMom5LKTzcPqH2Iqpip7eijrrOf1ZW5DMXaWfnU\ntPdzzCgde3Gvqg8PCqLPqwZ6w5o2zS7M5Hhf6MxrZ6CclZV5g5oyWSyC/3fxadS73DwQNnbww2f3\n4gtIdtS68PR3Q+t+FYEBrr6BoNgBbHpHnbKXlZWDMwuHvw8pAzHPBoK4O0H6cduyyRZ9vHfWlIi7\nU8w21Mb/6ew5BezutKm2xmHR1msHW5hmaSGQXojPkhJcgAagtkd9B6emyeD7JSXsP2aIkz0dR38T\nIFVZsBmtmKV4lWcBMEfUBqMZM5JZVj4FkKR2VxtnlxK669lRo/J2QK0BkJI1qHnb1y+ay+fOmclf\n3jrOZx7awuNv1/GRldNDZ2GoxXby0h3BQgKAo8ZqSjOiIpG1s/PZ29ClTFzbIehpwlt2Bl1uH4VZ\nKcEZ2yv9yn07rILsuldVg73AgPpsR6J+O87pK7DnzwyVH4fjdiFSc6jIS+cJoy/PVVXTguXP1r5W\nrlhexmsHW2h0uUNlkMHM3RhkTsnkiuVl7O/LQvg9J2UiU4KKuw+73YEvIOk0WhAc7VACbhOGQBs/\nlB6ZSrsp7qlDxzLX/2ETX/rr9uD1XXUuvGELgvhSC2jv9UY4jnC6rOrAUZkWGqRabOTuV1apKpMs\np51FmUbJYeFpeK3plIlW5hSFZiBmOe0sTW9nALs6jY7iQFM3cw33Q1YJzLlIzYiMojDLyeoZeYNu\nB8i3KVH/1yElGP3CSXtnJzeuqWBmQeRsSCEE89OMH3XYgGphppNrTy/n7fo+vJllgypmzKx0VWXs\nfQD14wV47aBy7y/va2ZBSRbFZrVDdNMw1KBqq08dfDzWDGooZHn5lJhNmc6Ymcd58wr59cuH6Oj1\n8sqBFl7a18zqyly8vgBHdm1SKyL1tYKnm1v/tp2zfvoy67bW4vMH2H9YuVdrZhGkZCGQnFnq4A+v\nH+XjD2zm3J+t5z0/fSmy6sSYwHREqPeq0BY1qBtsGqa+G2fPLaA1YLznYT/4DQdbmevswDKlnJIc\nJzXtodc43qW+44WpStzNafSHjxsiXjAXW8BLeapHmQDzfckyqp1yypHCSqWlMTiIal4uKMmiyNZL\niq8byteo7V117KjtpNhqfPfT82OuZSuE4Ovvm8c3Lp7HC8aB+lNnDTYoc4sz2Rf2OzpiNNkyTYXJ\nmTPVd2fj4Tao3gBAc6464y3KdKrZ25klzHSp7//5eW2I7nqoulE9wUjRTG+rmr9RskwZqY4YFVbG\nhLM5RZlIaRYspIVaEPS18uEVZQQkPP52XXACk1miGTxgp2TyvoXFtFtC40MnmsQUd/8ADrsS6NYe\nD4GA5Gi7IeDmIg7GEbOHVDpGiGUCAcnWYx38Y2cDB4wv3a66LvIyUpGGy3fkFAPELs8CWvzqBzrN\nEfoxX7JoKre9bx6XLykJ3rYsx/iRZpXSZitihr2NvDBnA3BaSivHKUJGzagLBCQHm7sjnD6ZU0ff\nU914b95uDnCkpYdj3UUTzU0AACAASURBVJBl9fK5s2fF3t5Vow6IUdVCH1hait0qOEZppHM//BJ1\nu98gy2ljXnEmQzEjP52SbCcbDrbS2edly7F2zguLMSK6JxrMLszAJZUrOmydwbzibLXwQlZJRGWH\nyTcunkevx8cvXzjAfz+zh/K8NO78yDIAmg5uCW7X33yI1w62YrNY+Orfd3DdHzaR4jHENqMg+N25\nfsUU+rx+Glxu5hRm0tLt4TtP7goN3BqRzNtuI1qKbgjWH/l/WlmRS6/FbGqnDojd7gHerumkwtIK\nOdOZnpsW4dyPdqmYKceuLgsznRRnOaltMKqwCuYBsCzXODPrinLuNgeB7OlUisbgganecO4l2ams\nyDAGMQ2Hj6uW7TWdLMk1ejmlF6r9H6Lt701nz+Tujy3jxx9ePEiwAeYUZXKwKXQWfLS1h+m5acGe\nLyaLSrPJdNrUb+7Y65BeSJ1FGZ6iLKcqxZ11HrmNr2PFzyWpRmfQVZ9WnTRH6hRab5i5kmWqeKHj\n2OBFYNwucOYw2xjM/8hKY4Z2WH+Zyvx0VlZMYd3WGo629lGUZZRBQoS4Z6TYqJypBqO97Se+gVhi\ninvAj8NhiHu3h2PtfXSbPcQCxh9GH5BumRZy7kPEMvWufvqNXNYs59pV52JhaRbCqExIyS6iMj9d\nuYgYNPiUiE21hxxJeoqNz54zE6c9VCM7N12VVfrSi6iV+VRYBz9fmWzgsL8owq0B1HT04R4IMDdc\n3DMKjUx1FP29zfeGNL771G4a+yyUZ0J22hBVRK5a5Yyjau5z0x1cML+It7pykW2HVd7csh/+cjWn\nV/+aVZW5w84QFEKwdnY+bxxu5aV9zQQkvDdc3MO7JxrMKszAhRL3Te5prKowYo+skpiry88uyuTq\nldN4cOMxDjX38M1LTqM428nMgnRkfWja/MG97+D1B/jNNcv5wntn8cbhNootxil1eqGqLAIunJHG\nju9eyHNfeg/3XruCWy+Ywwt7m/mnMaDm61YH2oPSOMuJPv2O6k/vtFspLTO3VQeCN4+0IwN+srxN\nkDOdaVPSIhakONKhvqsWf+gzX1SWTWOzMfu4YC4A8zOMs0Szxj2zOLi9JX8WMy2NwVim0aV6IhVk\nprDIaZgFQ9wDrlo1wzrL+B2lFxjrIwzdNOzSxSVcuaIs5n3zijPp8/qpNTqoHm3tVQO/UdisFk6f\nkcfrh1rUYGrFGpqMKpuiLMMQzTofi7eLT1S0s0Zuh8IFqi110fxQU7mhMAdTpy5Rzj0wMNggGNVa\nly0p4ZrV07lgvnHQdqSr2d1GCeuVK8qoa2ln1Z4fsCgnrKGhKe5GAcUZyxYDcPDgBK6HPAQJKu4+\nUlKUuLf0eNhV5wqtzGQuo2e8qb0idbC4R8Uy5nT1xWXZPLm9jiMtPRxs7mZRaXaop3tGEWfPKeCV\nAy0xZ84d9yiHkieGX2ezwuEiIAXVnkwOeKYEK3FC/7cA2f01VMti3q6JdEZmhcHssBgnOLGqdxTu\n3eMCm5OlFQW8drAVaU8jP2WYhRxiTWAyuKpqGnsHihADfcrhP/l58HvJHWhi9TCRjMna2QV0uX3c\n/fIh8tIdLCkLa60ajGVCzZ7y0h34U5Sg7/BNp6rCyPSzStWPM0br3FvOn0Oaw8oZM/K40PhxrqzI\nJb9nH7JY/djqj+4h3WFl9YxcvnrRXP7yqdVct9g4tU4vCFUWRfWX+fiaSuZPzeK7T+3G1T/AU68r\nN3jO2veoDaLFvX/w2cj8mWrAsbVZxScbDrZQbndhkT7IKWdabhqtPd5gzffBNmOAOOyAvqg0mz6X\neq3+KcodznQa38WuOrXiVtj8DpE3iwrRSL1x0GjodFOU5cRqEcyyNqnfU+FpkDqFrqZq+rx+ZqYZ\nB5i0PDXju39ocR8Oc1C1uvoQgW1/orotssY9nLWz8hGdx6C7HirWBgezC7OM6G7GOSCsfLNiP1Na\nt6reSwDFi1QsM9zAZf3bqtrLmRUa34rO3d2qydvsokx+8KFFwconQC20YpypXbJoKmvt+7ma5znf\nEXbG4OlWYwCGMVq5YC4+rPS2nrhmeyYJK+5OhxLdlm4l7sJcWclcRs8Qd4szK0zczcw9MpYxxf0H\nH1yEBG57dCcBCQtKskN9PNILufXCOcwqzOCmh7YOWp7rcK8SghTP8D02iumghWzWH+rgqC8fp78n\n8kfS3YDF76HOUjyonaoZGc0Od+5mv5vRRDNGX5nLjLhoRkkBluEWfxhqAhNw1uwCOlLL1ZVnvwa1\nm+nJqKBUtIZctck76waVbq4xctUjLb28d15hpNPvN97LMCEUQtBfuIzvDVzLs4HVrDIHbIfp21GY\n5eT5L5/FfTdUBSt3Vk3PYrY8RnvBKmRqLu7mw5w5K58UmzIJZ87MZ05GP6Rkq8UxDOce3RnSZrXw\n4w8vorXHw6V3vUZt3XECWDjnzDPVBtGTk9wuQETMmF5xmorD/v7qDs740Yv88c1jXFBiRCo501XG\nC9R29BMISA63ewhgVevqGiwqyybLWJzmuEV9VtNsoT4zwffHJG8mqbjxdKoDSr2rPzjWMU02cFwW\n4hc2yCqjr0UJUYm9R7WgsNqGjWVGwowV03bcj+Wpz7M6sGNwfbnBufMKOdNiTLorX0tTlxun3UKW\n0/gNp+aoyrPNv1cH91lh4u7uHD7brn9bRTIQJu4xJoWF93IPJ6x5WKbTzqVTjUo2R9h3xGzzYWC1\n2Qhc/mtWvf8TQ+/XBJGw4u5wOHBYLbT2eNlV76I0Lyt4HxAUd2tqdozMPdK5H27pYUqanUVl2Vy+\npITN1epLu7A0K8y5F5DltPPAjavITrVz4wObI2qPq7vAi33EhbKzfS00ylye3lFPnTRyu85Qoy+z\nEZYlb+Ygcd/f1EPZlFQyUsIOThljEHdPNziz+MjK6fz+uiqmFxcM3fLXP6AmKeXEFnerRbBwyQp1\n5eDz+Ge/jxcyLscpBliQE1WKtu2PsPHXETflZaSwwGj0FJG3g5plKCyDXntGUTb3+y+mKDdHZa8Q\nJu5hg6r7/xm8Pi03LZSDAmfkdOAUA+ylAk/mdPK89bx3btTr9zSrvB2UyEPMzpCLy3K44cxKatr7\nOaMogEjPD2sDHXWwNztChkVc5SXF+LFSYu/hzJlqZu4nFxlnojnlwUZfx9v7aOp24/EF8FtTBjn3\nLNT38WB/Oh0ygwI6Qu9JDHEHSHEpp9rocgen7Rd6azkaKKatxwPZpYjuOtIdVrICYf2VzFhmDCV9\nGSk2yqakktKmylFvta2j0hyAjGJabhofyq2mTWbhSp9BU5eH4ixnZIfHWeerZnqOjGAVGkWL1OVQ\ng6rdjepswBT3jGJl5MKdu5QRk+gGEdUZ8owsdeY0zRp20PN0R4g7gGP5R2Hq4tjPOYEkqLj7ERYb\neRkOw7l3UV5gfADBWEa5FmdG1qBYpitKcw419wRnP37mbHUEz0mzq8Eg07kbC0kXZzt54OOr8Az4\nufGBzcEa6jqXmx5rzojibu1poNuez45aF7XSEABXTWgD48uVO20eu+u7IloBH2yKGkyFMcYyyrk7\nbBbOn1+EcKQN3fJ3z5OqosSclRiDS05fRo900kU6a3dfxj+OKxG1dUe5po5q5cajFhY+d97/b+/M\no+O46nz/ua1Wa2ntUmuXtcSOLduJ49gOdjZnISROIAsQAsMWyMAJk5BMHktgyGPgzTlzeDB5vDAD\nHAIJkFkSHmFJJoQQEsKYbGaczSReYnmRZVu2ZNmSLclabN33x69uV3V1tdaWWmrV5xwdqau71VVd\nVb/7u9/fcsvJDWVEs2eiHNkBRfVxq1+Z4NaaBkeapZGNjHE/3g4PfxCeuMtznyv7RfPceKKa/aqS\nenWYSxa72kv0ddozo6jn7t0Z8u4Ni/nxzWtYXXYKFY6IBJJd6B1QzXF5gkqRUdHMdeWHufcDK/jb\nd55JuZXjTmEtdcVy/G1H+6M54TqYHeO5l+VlUZ09yLDKpKVrmMO6mIJhy/AcPxCfeWXlqpcM7mdg\nWALEVYXZUVlwj66UIGtBDeGBwyyvKUT1ddqDVk6xGNRJLtS9uCKfSP8uhoL5rAy0sKR3U8LXrtRb\n2TSyhIdebuXw8QFbkjEsvFx+N663F7WvWAqoxEFVZzAVZLAtboz13If6pCDKfb4Mrs6QFUMyw6kZ\nw7jPFHPUuJ+CQAaR/CxebztGz8lh6mqsm9v0HR88ARlZ5IfzONYnBt/0ZN56OPaCdBr3JZUF3LCy\nhiuarf7PxnN3tPs9syKf7374XFo6ernv2Z1orTlw7CQDWSWjrqsIwPGDDIclsDWcZ91wMZ77bsjI\noumMJQydGol20xs+PcKuzt54425utgQd6jwZiJ0qEsoTQ+FeUam3U6SWmlWw7IaE/64hksfGhjt4\noPKrvP+SNXzkSpNC5whOnT5lP3YtLHzbpQt5+q6Lyc92BXQ7d0SDg05MzGGNU/bJLZNAufmM7U8A\nGt5+ytN7U4f+wrDK5DcH8vlLfwk1gS6q813FbTGeu7fmbsgKZnDpknIxgOY9uaXeAVWvaX7TJbBv\nk20su/eJN5mZTUk4RDiUwb6j/ew9IoNwIJQTF0RfEB7mhM5lT1c/3cEyMnoPybkePB7vuRfUcjoQ\nolG189bB4wyeGqGqMAdOtJNx+iR7dSWHek5yKr+aAn2CVdXZ1mBnDcDRtWwnJ80sL1NU6g7+VHoj\nB3SEwk3/5D0LONZKqPcAxyJrePCFPew72m/P1gxVK6H5WljzSXtbVr5ILYmCqgdfk1lh5Vn2Nnc6\npCttNY5wRIy72e9OcRiU6R0FvnGfMCPDEAhSlpfFLqsAonFRs5ycFmsJOutLLc0LRStUn2qx0r5O\nnI6mrnX1DnKsf5iF5fYJ+PZN5/CtG1fIg6jnHuvVXbQowgdW13L/xt28tLtL2gpkezeAijJ8Ega6\nCRaJUY9UVEvpv9O4d+2C4gbOsZqBGWlm75E+hk9rq8rVgVlC0Czg7cWL/wIPbpDlAsFeqMOQaB3V\nJz8vnQGv+96YyxJe/YmvcNett/K5dy1m/ZpzZaPTuB/fL14QxFXUZmdmUFvsmpafPiWFKx7GfW1T\nKfdc0xxdUAEQz6vA0dp22+Pi9Yfy4flvx+/woS305J/JgRPDvHQ0jwxGYs8DyGzIDOqZ2SLnJfDc\n7fc4vFsv455omt+4XlpOmJqF7lZZFB2JM9SVSMZMa1cfoYwAGaHcGM8doDpriGMjubzR1s1gTrkl\nPViGxu25BwIM5tfTpA7xqtU3vbooO9pGYreu4mD3AO1aYiKri/tjj814s6NkzIzG6hzZr992VfJo\n+IOog6/KspJuOkS6WbXuMo71D9PeM0BFfmzqMIEA3PSvtt5uqFyeWJY5sBnKFkOW434qsTx3k3Hl\nUWcRQzgitmigR+77k0cBJbNGg2/cJ8jIKcu4yxQsGFDi0S66UhaxGD4pHkt2AcW5IY71DaG15hfb\nRIfvGSKahrXTCqYazz0OD8/d8HdXN1OcG+LOR2SKF8iLjG7cLcMTjshNu7iyQG7gGM99D5Q0UV2Y\nTUNpLt99roXWrr5o8VSc5w4iGSWSZV76Hjz9Fdj3Iuy2FpEeOG5ryOC9GtPWx2Drr2H93VC+JPEx\neZFTLAOG07g7DbrLuHvS3SrT/rJ4456ZEeCvL2qK0dABu5Cpr0tS5866EdbcAm/9KrZLoNbQvoWM\nahnA945UxO/XqUG5aZ1tnrMLx15qr++Iw7iXyb44GfCQZQDqz5el23b/0Tr+fVBcH326zsp133Ok\njwWluajM7DjPvTSjnxPksrerX7z+3sPQbUl+bs8d0FbGjFkUo7IwJxrzORCopr3nJNv7xQlYnmPJ\naeY+MOsjJMqYOdYaNcxeLNQye3uxt5JdNdfKQPzHf4z33i3JcsmSs1jbJA5PnOeeiMqzxBN3N7Ub\nHpDrw+TxG0oaZcDsPRR7bAllGcdC2ZbXTtUKqzWG5cgMnohtNz6DzD3jPjIiGnBGJhFrBD+zIl9y\nyRddIb019j4fHTFLwlLJ+uKuLt48MsIIAU6RwSargrJlTOOebWdMuCjKDfH1a5dFG5hlFkRGl2Us\n415ZI6lvy2oKJAvFGPeT3dFWv0opfvDR1QydHuHDP9rExrc7CSjiKkgBueG8ZJnND8LvvgzN75EL\nbNtjsj3Oc3eto2oWeK5aARfcmfh4EqGUHJczlmCkGBUYn3HvtLr1eXjuCSmoFn15x5MyS2h+D6y7\nTTxup/fe0wYD3RQ2rSI/O8iRkOXVOqfkJlDmLNzKKhh9qb2hfpnpjOm5exiLrDyoPQ/2/JfMWo4f\niHruAHXFubQdPRnt0U4wJ85zL1D90QKvUHGNfAftlrZcGF/tnFWxiHp1iNda5ZqtLsyOLhITKKim\nvWeA13rk/0V6LUPtlmUSee6/uhX+4ybv54Dyk7s4rnM5SCkNkUJYd7ssmehu1dvdKn2DwhFuv1Qa\nltWVxBdGeWKCqoffit2+70X57oxWb3CnQ44pyzgWyjatDpouke/dJDj4nvsEMFP7QEa0Z8Vya6Fb\n6i8Qj3Hn09ERszhXvPsHnt9DZkaQoXV38ULmOv5staNt6eglN5QhF7YXuaUxHpSbq8+q5J3N4vmF\niytF2ki0qpE1Ra6uO4PHbruAa1fUxHruz3xNvNWzPwBImfZDnzyP7v5h/t/m/TSUhmMKoqLkReJl\nmR2/lWDimRvgfQ9Km4LtT0q/lqHeWG/C7bm3b5EL9tKvjH9JQjeFtS7jvlc804pl4zTu1s0ySiA3\nDtNfZtvj8r1WrRDPe+VH4Y1H7JmEtchHoGoFN62u44p3nG1lSjiMu7k5Yzz3gtE9d/eAEC6NbQim\ndWLPHaBpvQT6OrbK7NRh3BeU5HBy+DQtnb3SudHDcw8OHZeFTICCcivD6MCr8tu9ohcQjCwipE4T\n6jtAMKDkfuraBSVnUFkUpr1ngOcPW/2VTADSLct4ae4nDss6v92tsbM3BxkdW2kNNgBKGoYZ7dvd\nAqC7Ta6lQIALF5XxxGcvjN5vY1KZIGOm5VkZ8BsujN3uToccS5bJdRj3zrfF9tSdJ9tOWM3BZrNx\nV0o9qJTqUEp5hp2V8B2lVItSaotS6tzk76YDk+poae5g99YgM1u0y51PR/NLS6wl9/6wvYPLm8vJ\nvvKrZDaeH/Xcd3X2ckYkL27x3Cjv+gf40CMJd0cpxb0fWMGPb14jxh0SSzPRHh9VrKgrkn7lRQvk\nht/5e3jlx7D2b8QoWZxdW8SDN68hOzNAc3WC6V1eRfxivVsfE4/+xp9IBkHztaIJ7rR0TU/P3TLu\nxih7tBweN4W18bJMYZ38z/EY9yNvQ3517H6ORUGN6NYtz8jxmnN6wR2Ahkf+SqSpQ1tkBlGxjHve\nvZQvX70Mihti9ytqqB3G3e2593bAi/9sa7TmPWZAyC2V/Rmy1nQ9NSCDdyJj0XSJ7KdZ2s7puVvp\nkFpbTak8PHcGesgKi1xSWtUg2w5sFoMcdOnUEM2YaVSHqCjIlhqDrhYoPYOqwmxau/p4q2OA3sxS\nu5rTmS0D3rLMjt/IcQC0vhT/vNbQsZWjeeKJN5bl2WsXuK+NnraYVNjlNYVxbQoSUlAtefn7N8du\nb3lWZDD3wuMFtRKUN577uGUZy3MvXehIyW23nDw9e4078BPgqlGe3wAssn4+DXx/6rs1Cg7j3lyV\nT06mVB5GWXSFXCBHdornHrZz2m9YKVPTdzSW0NrVz6GegZhMGU9ySzyntE4KczKlbN7RTMiTE+0S\n4HOebHPh/vJTcjNf+ndxbzuvsYQn77iIr71nmff/DUesFgSOm/3obpE0jJy08HIxCK/9mzyOyZZx\nraNqdNoEVanjorBOLvpo9kerGNDiBpmpuDNz3HRuh8gEvHawg4Z6RCQZQ9ECeO/9Mug+dC288B2p\nTAw5grjuNLio5+6QZdye+5afwdP3wAGrH3x0QLCug1zrujTSjAluhl0pn4aaVZK59IblTBTZM0aT\n6w5IwY/bc9caBnooLy+XNMPqBus4Dnvq7UB08G5UhySYevqUeM6lZ1BVlM2R3iFOj2hO51WLJ+r8\nPkL5MkB6yTLbnrCD2ftejH++p02u1/JlBANKjievQq5PdxFR976YQW5CKCXXwdZf2w5Xz37o3Cbt\ngt1kBOWzju6Gbf8Jf7pXzmEizdx5fjvflvst3/qunQvYzFbjrrXeCIxWdnkd8JAWXgaKlFLxc8Bk\nYfLYA0EWluez9X9dGVuxuegK63WD4rlbskxRbiaXWEUqpiz+uR0dtPcMjG7cJ4IzwOKFVzGJuYFP\nHoNrvh3vTVg0RfKiMYY4vAqZju6OXckpFBYDv9PKJsoaJVumu1VuNo84w7hx550f22sb95Hh0Vej\n0dq6WSYYyDXGPa9C9Gsny98Hn30VrvqG3GxnXBb7vPHcXQ3AYj33wljP3SxQsue/XO9xBFTBDqq2\nvyG/nel3TjIyRVo0BtMxuDqziepLc8Ujdc7WrFnB4vpafnfXxdJvXFm3t0d3UQDyyhkM5NKo2iUN\ncs8fxXmKLJHgqjnsUodxNccWCIgW7ZZlTnZLUsPSa0Wi8PLcrXVZ1667iMduv0AavykVP3saPinH\nWDhJ4w4Sczk1IBWsALv+IL/dmTWGkiaJ2fzsI+LU3fybxJliwZDMwo7tlWywssXy/QSCcn3PduM+\nDmoAh7jKfmvb9GA8PqvdQJycUrQAIs3yd1Y+JXkhlIJrzqqK9oVorpIObQ//WbRuzyDlZDAj+ajG\n3TXuFTcASjI7FiW44MbCKrCK3uwDx+Vvdz/4pdfZMQun3OFeR7WnLWG7gXFjDFNPm1zk/V0Suyhu\nkO2jSTM9+yW4OxG9HeyBc8m74xcWBxms1n4GvrATNnwj9rmSRvlM8x32dogX7fTu3Z67Cf7t/ZP9\nHogNqILtuR98Tab95UsTH0PTJfI7vypGSskJSV1HKBigujBHrvOTR2HQknzcfXgygvbAlMhzV4rj\n4Xoa1SFq8xU8+UW5ZpZeH41BRfKzyCq1roVgtr0OMXj3l9n5tAzezddC/Trxkt1VuodF4c2qXi4t\nPgxu425kvQTV0eMisliy6P78QxksWp4R77q82fv1lWeJjVl/N/z1s4lfZwhHpGMlyEwzEJBMpRjP\nfR5kyyilPq2U2qyU2tzZOYGiGycOWSYhxnu32mz+8KOr+fy77KyLYEaAVfXFbNkvN0TyPfcEx3ai\n3Z62Rd9TJt7Be+6b+uca42KCUm7jvuhddkdMZypk1HN3yDJTuaHAfn93m50pYzx3GN24m8yDiWTK\ngAycG74FF31uYu8DkWVAZIH+o/Dmo1DpKhHPLpTV7I2DYTz3fS9L6mTfEZEiTEVt2G3cX5eAspf+\nbWhaL7+L4oP4C0pyqS/JFW3cSBUmPuLRZC3qSCQy7sBQYSONqp0rjj4imVrX3AuZ2eLJAytqC1Fm\noA5H7DgGiNfqlmW2/acYt5rVsMDqr+Neb6Bjq+y/O57inj2ZRIOpOhrn3y5S6ev/Abv+CAsviz0O\nJ+u/CP9jq8ij40kmCEfsa9mk7Zp6i+hCHUmyLxMkGcb9AOD89mutbXFore/XWq/WWq+ORCJeLxmb\n8Rj3M6+U39bF886lFTHaO8A7rJzZzAxlN9afKqGweDdemvvIaSkqcXvuAA0XJJRjxoW7BYEJCLmN\ne06RbTyyvbJl+iQ4mAzPPb8aUOJ9mYu/uEE8epUxunHvtNbvnKgsA/COT48ZI/EkGtDbA099SeSG\nq78Z+xpnlepgrwzWNatl2r//v+X7d2r0Uc/dqmI8+Lpd7p6I8qUio5h1Sh3cfdUS/t7EXYxxd6bR\nQmzwz2TIJJJlgMzyRdSoI5y99wFY9t6oXFVTlENAyZq+0fe7+vnHLdhhPOMl14gHW7NKslLcuvvh\nt6Q1rxv37Mkc22Q1d0PDRTJQP/M1aUuSSJIBGZgdrZHHxMRPVIZ9v+VXzQ3NfRw8DnzMyppZC/Ro\nrdvHetOkGY9xX7AOLv+qTM8TYJZ/aygNkzne6PtYKGWXJLvp6xRJxCMlbcq4PfdExh1g5UfEu8xz\npJNlOmSZvg7J6JjqDRUMyU3iNO5F9eINFdaOYdy3i6acKPA4HRQtAJTUBmz5mXj/bm3c2RnSrDF6\n7sdE297zp9gKTpDBIJApnvvR3WJYxjLuSsEnn5IsLRfnNZbY/Xfcxt0rbc8YqVE89/L6ZWQoTSCY\nBVf+Y3R7YW4mP791HZ+8sNGW2OKMe3Gs5r7rDxK3abbuu8xsqD43Vnc/NSjJDhUext09q+tpE6M5\n1XtGKTj/szIoq4AtfSUD852UNNl9bczaArPduCulHgZeAhYrpfYrpW5RSt2qlLrVesmTwG6gBfgh\n8DfTtrcQp7l7EsiQm3OUEfismiKyMwPJk2QMuQlaEHRYbUunkoGSiGCW3NRO455X6T0bWHYD3L03\n1nMPhsQIDffZmTJTNe5g57p3t4oMZNLn3NqqmyNvT1ySmSrBLPFQ2zaJ93zR5+Nf4/TcjSRTs0pS\nV/dslEIypwFUyr4eTCph9Tlj70vRAvu7SkS4XLziOOPukGWMBDiK507lctnVy+6Jm1Wuqi+RKuBE\nnrtbltn2hHx+w0X2tvp1UkhlMrE6d4iTMx7j3t0mnz2OBe3HZNkNkupYe97Y3+1EMN+J83rNrxL5\nzmQYpUhzH/Nb01p/aIznNXBb0vZoLKKe++i9TsYiFAxw3wdXxqSYJYVwWbwsozVsvFduSHfJc7LI\nK3fIMnu8vXaD181iOkN2W/r4VGUZEOPevkUMZ3G9rXMWN8D233i/R2vx3JdeN/XPnygljXJDXvcv\nthfmxOm5m2BqSZOc05e+J1P6BWtj35NbKhp+++tSaRkZI0A3XgKB2Cpgr2rKM6+0O2smomIZ3P5K\ntAWwJ/mVEkh1x2GMLKO1/Oz8ncR1nFr1gvOlOnj/ZpEEjZPjZdzNfpp0yKmkQbrJyISPP+65fvKU\nMLNLp3E3MyUjJdqFvAAACxNJREFUL4ZSo7knYUicYUbsVMipcuWyCWhr4yUcsasrDbufg9bnYcM3\np6atj/q55bGeu1ce72hkhsVzN8ZiqgFVEOOz/UmZCjv70xQ3RBeljpuy9h2Rqb5HT5lp5+IvQO/H\nxRv3wu25F9TKoNh4MbxwHwwOx3u3pkp18Lh4yV6DxmQpqov33J1eYtXZ8L4fjf1/yhKsnWsIZMCn\nnouPF+UUixc+eEKklv4uyUxxUnceoKD1RWmp8MzXZRbnVSCXmS2zDacsk0xnaLQBbLIY417m8txB\nBtZgdnLP+QSYe+0HxqO5pxIzDXeWnD/7D2LoVt08fZ+bZxn3oT4J5jhz3MdD1HNvk5s2GTphYZ3U\nG3S12FNucEy/PZYai2bKTDANMhk0rYezb0z8vPGKjedujEXdWvt6dLYrAOt66JBgatU4JJmJ4Gxd\nMSBLJ06pNmE0ImfGXxPO/jI7nwZUfL+WnCLx0jd+E379GQl2f+xXiaWWkkYx7maRmGTMIKeTqnNk\noKpfZ28znvuRnSnT22FOGndLc59sz5PpJhyRsnCjMe54Eg6+KilWo6XATZW8cgnoGa9nNFnGi8xc\nCYZ170veDRWNL+hYaWC0dEjTByQVnvtYGK94oAe6dkbL98nKk6wZiA8C55bJTGroxNjB1IlStMCu\nAh5tObjpItpfxjLutWukotvNsuvlmrrhB3DLM4lnRmDFY/aIl69HkjODnE5KGuGOV2PlI+O5D/en\n1LjPUvd3FJKkuU8b5sTev14KOXb8Vkb2FX81vZ9rWhBY1X8TNu6hsAxIfZ220ZoqzuBxsWMmMZpx\nf+MRSZObjsDzVDGa+7E9Ykyd31PjRdD2crwsY9IhIfnG3VRudrdZxj1B98LpwgwmR94WB+bSe7xf\nd/EX5Gc8FDeIx35kpzxOluY+k4RyrfbQPb5xnxCzXZZZdr00itr6mOiw+jS874HkRPxHw6Q2tlkF\nIxOVZTJzZXrd3QZNlyZnn2KMe4P9d06x6K5u437wNQk8bvhW4iKTVBLMEunDdFp0Gvfl74ddz8VX\nnxpPPpg9ubz90YgWMu2z12adSUzWyZu/kN+meHAqGCfAVP3OdlkmEfnVlnFPTaYM+MY9+QSzZIGI\nNbdIT5HObdIvZLoxWu++TSIFTPRGD+VKWfhwX/K8pZxiyRQY6oudXisl2TNu4/7KT8UIWi2PZyVZ\nBXaPGGeArnwJfOrZ+NcbmaLyrOQP8NEq4H1iSHJnsC4AbFlm5+/FuXBX9E4G4wTs2Si/Z+MMbjwU\nVMm972vuE2C2G3cn4VLpGT0TXqiRAw6/OXFJBiRbxvSET5bOqZTcnAXV8fGG4gbRrU3gebAX/vJz\nqZJM1GJ1NpBdIDGVQHB8g6CRZZItyYBIgIGgbdxTJcuMDMPCK7z7+UwUY9zb35BajemMU00npsbA\nN+4T4PQs19xTRbTiVE/OuDsbZCVzKlyz2l7AwMkZl4rn/vv/KY/f+qXIWdOZUZQMzDS7uGF8QX1T\nAFS7Jvn7EsiQwTNVmnsobPcqSoYkAyJjhfKsYOoc1NsNJm3U19wnQNRzn6XZMqnCGciblHF35N8n\n86a6/rve21d9QoK/L/6zyAnbHhdN2msgmE2YoOp4g85li+DmJ+OLm5KFWaZxoGfmZzxKyWf2H5XB\nOln/s7hBZqCzPVNmNPJ94z5x5pIsM5OY3tID3ZOXZUC8pmSWZydCKSnq6u+CZ/5etl31jdkZSHWS\nNUHjDtIYbrooqpdOjCOnZt5zBymeiyxJ7mcb4z5Xg6lg57r7xn0CFNbC2TfNbl02VeSVT964G1mm\nsG7mDGwgILnPAz3SVfHsxAsqzxqMEZuOasfJUFQnDckgNcb9vT9IvgEzuvtclmWinrufLTN+alfL\nj088eRWSczzRNEiwe7rP9FQ4GIIPPyotB7wKYGYbUeOepFqAqeI0gKkw7olWlZoK6WDcy86E+gun\nJ9YyTuaecfdJTF65SDOTMZJGc0/FVDgQsBe2mO1MRpaZTpznKxXGfTpouFDWuHUsFD/nCOXCJxI0\nx5shfOOeTlxwp6QSToao5z6HvaWZYNn1kskxHX35J0OqPffpoLwZPrs51Xsx5/GNezpRtWLy3o7x\n3OdyhsJMEFkMl3451XthU1AjC1ro0zPfW8ZnVjP38tx9pofypVCxXBYz8Jk7ZATtzAzfuPs48D13\nH6GwBj7zQqr3wmcyFC2Q3ufuBad95jW+5+7jM9cprJOYyWxtg+2TEnzP3cdnrnPep/z0YJ84fOPu\n4zPX8Ws/fDzwZRkfHx+fNMQ37j4+Pj5piG/cfXx8fNIQ37j7+Pj4pCG+cffx8fFJQ3zj7uPj45OG\n+Mbdx8fHJw3xjbuPj49PGqK0WX1+pj9YqU6gdZJvLwOOJHF35grz8bjn4zHD/Dzu+XjMMPHjrtda\nR8Z6UcqM+1RQSm3WWs+7krz5eNzz8Zhhfh73fDxmmL7j9mUZHx8fnzTEN+4+Pj4+achcNe73p3oH\nUsR8PO75eMwwP497Ph4zTNNxz0nN3cfHx8dndOaq5+7j4+PjMwq+cffx8fFJQ+accVdKXaWU2qGU\nalFKfSnV+zMdKKXqlFLPKaW2KqXeUkrdaW0vUUr9Xim10/pdnOp9nQ6UUhlKqdeUUk9YjxuVUpus\nc/4zpVQo1fuYTJRSRUqpR5VS25VS25RS6+bDuVZK3WVd328qpR5WSmWn47lWSj2olOpQSr3p2OZ5\nfpXwHev4tyilzp3s584p466UygC+C2wAlgIfUkotTe1eTQungM9prZcCa4HbrOP8EvCs1noR8Kz1\nOB25E9jmePy/gW9rrRcCx4BbUrJX08d9wFNa6yXACuTY0/pcK6VqgDuA1Vrr5UAG8EHS81z/BLjK\ntS3R+d0ALLJ+Pg18f7IfOqeMO3Ae0KK13q21HgIeAa5L8T4lHa11u9b6VevvE8jNXoMc60+tl/0U\nuD41ezh9KKVqgWuAH1mPFXAZ8Kj1krQ6bqVUIXAx8ACA1npIa93NPDjXyDKfOUqpIJALtJOG51pr\nvRE46tqc6PxeBzykhZeBIqVU1WQ+d64Z9xqgzfF4v7UtbVFKNQArgU1Ahda63XrqEFCRot2aTv4v\n8EVgxHpcCnRrrU9Zj9PtnDcCncCPLSnqR0qpMGl+rrXWB4B/AvYhRr0HeIX0PtdOEp3fpNm4uWbc\n5xVKqTzgF8Dfaq2PO5/TksOaVnmsSql3Ax1a61dSvS8zSBA4F/i+1nol0IdLgknTc12MeKmNQDUQ\nJl66mBdM1/mda8b9AFDneFxrbUs7lFKZiGH/d631L63Nh80Uzfrdkar9myYuAK5VSu1FJLfLED26\nyJq6Q/qd8/3Afq31Juvxo4ixT/dz/U5gj9a6U2s9DPwSOf/pfK6dJDq/SbNxc824/zewyIqoh5AA\nzOMp3qekY+nMDwDbtNb/x/HU48DHrb8/Djw20/s2nWitv6y1rtVaNyDn9g9a6w8DzwHvt16WVset\ntT4EtCmlFlubLge2kubnGpFj1iqlcq3r3Rx32p5rF4nO7+PAx6ysmbVAj0O+mRha6zn1A1wNvA3s\nAr6S6v2ZpmO8EJmmbQFet36uRvTnZ4GdwDNASar3dRq/g0uAJ6y/m4A/Ay3Az4GsVO9fko/1HGCz\ndb5/DRTPh3MNfB3YDrwJ/CuQlY7nGngYiSsMIzO1WxKdX0AhGYG7gL8g2UST+ly//YCPj49PGjLX\nZBkfHx8fn3HgG3cfHx+fNMQ37j4+Pj5piG/cfXx8fNIQ37j7+Pj4pCG+cffx8fFJQ3zj7uPj45OG\n/H9j49U4OAAHqgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots()\n",
"losses = np.array(losses)\n",
"plt.plot(losses.T[0], label='Discriminator')\n",
"plt.plot(losses.T[1], label='Generator')\n",
"plt.title(\"Training Losses\")\n",
"plt.legend()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator samples from training\n",
"\n",
"Here we can view samples of images from the generator. First we'll look at the images we saved during training."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# helper function for viewing a list of passed in sample images\n",
"def view_samples(epoch, samples):\n",
" fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)\n",
" for ax, img in zip(axes.flatten(), samples[epoch]):\n",
" img = img.detach()\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)\n",
" im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Load samples from generator, taken while training\n",
"with open('train_samples.pkl', 'rb') as f:\n",
" samples = pkl.load(f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 1, 7, 3, 2. Since this is just a sample, it isn't representative of the full range of images this generator can make."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZkAAAGRCAYAAAC39s6jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJztvXn8lXP+//96CymkRSmkUBLKliUU\nJmGyDIOyqywZxjKDsYxlbB8fzIx1hrGTzBcjYhKRiSSStCplqyxtZAljff/++Pxez+6nrlfv63qf\n63Xe57x73P/pcbs65zrXeb2u5f18nOfz+aqqrq52QgghRAxWq+sDEEIIUX/RQ0YIIUQ09JARQggR\nDT1khBBCREMPGSGEENHQQ0YIIUQ09JARQggRDT1khBBCREMPGSGEENFYPcuLq6qqyrY9QFVVlXPO\nuXLoYLDaasue3T///HPia6qrq6vy+rxynpdKI6950ZzkyuLq6uqWeeyo3OalYcOGpr/77rs6PJJa\nkWpeMj1knHOuQYMGzjnnfvrppxW2OVd4U419w/cPFuecW2uttZxzzn377beJ/88bP489Bmuvvbbp\nr776ynTS2NVHVl992Wn1448/5rrvNA/wcqGc/vCpNHjtVldXz6nDQ4lKu3btTM+aNSvXffO+HOme\nk2peZJcJIYSIRuZIxj8R+ZdG1uhlub9STKf5KzX0V7KPYEL7TvMkD7036+sZvayxxhqmf/jhhxr3\nWR/IO3oheUUvJfgrL5cIppIitzxZVaK/vKMXUi6OiSIZIYQQ0dBDRgghRDQy22WeYsJZvjdku4UI\nWTG0FZI+Z/PNNzf97rvv1nhcaQh9D25fVSwyUgkWYblYCTVR1xZZVgt5VScPG7a+jbkiGSGEENHQ\nQ0YIIUQ0am2XZSVNCMjXhMLO0HtrshVCFllehI6rPmcHbbLJJqbnzZtnmhaZn1NaaN9//30Jjq5y\nKSbLkddNliy/Nddc0zTnpz7YNaWE9ypmwvLaX2+99Uz/97//Ne0zZOvbmCuSEUIIEQ09ZIQQQkQj\ns11W21YZfD1D+jQZWnlbLUmZaM5lt7O4H34n2kXcZyW1GUlj2bRv3970ZZddZvqYY44x7e0Djs8/\n/vEP0/vuu6/pHXfc0TT7OIWydOpbFo4n63fhOGSxyDgntMu4Dx5LMQXKqyI8b//whz+Yvvbaa003\nb97ctL+3NW3a1La1bLmsNdgOO+xg+vHHHzfNcab9xrno06eP6eHDh9d47HnOoyIZIYQQ0dBDRggh\nRDSqsoRCadpkh8IshuPUX3/9tWnaTwwTP//8c9PscHzggQea7tChg3Ou0AKgzTZ27FjTH3/8selW\nrVqZfv75503TrglZeqQW9mFZtPoPZb+FOms3adLE9IIFC0xzTpPGKE0B7sKFC0337t3b9PTp0xP3\nQ/IK78u51X8o45LZSl988UXq/TVr1sx0jx49TPN6e/XVVxM/s5Td1p1zb1RXV3fLY0fFzEtonGkb\nf/DBB6a32mor00888YRpf69yzrkZM2aYnjlzpnOu8D508MEHm27durXpTTfd1DTvbeeff77padOm\nmY5kY6aaF0UyQgghoqGHjBBCiGjkbpct9/rE7Qw7d911V9OTJ082TbuEIePOO+9smhaNz9II9Q37\n7LPPTL/11lum58xZtu7OFVdcYZpZGkuWLDGdxvZhxgg/l5SLXZYGFpXNnj3bNIsxQxl7teXTTz9N\n/Jxvvvkm189ZnnKzy0J94I4//njTw4YNM83xCWWJeduNVvGvf/1r07wmaLnQZi5xQW1Z2GUkVLzK\na4VjR0uN18ro0aNNb7DBBs455zp16pS4P74vlFFGy3n33Xc3/cknnyS+t0hklwkhhKhb9JARQggR\njai9y0LWEsP4SZMmmd5zzz1NX3LJJabvuusu0926LYvOfK8f55aFjFyVkjbX4MGDE/fBEJQZNiNH\njjTduHFj07QjQnYgP7dS4biwOIzbmW3EkH3u3Lmmly5d6pwrtHratm1resMNN0zcNy3HSy+91PQF\nF1yQ4VtUJjyvDj30UNMswKO1vM0225h+/fXXTdNq4Vytu+66zjnnunbtatt+97vfmW7YsKHpIUOG\nmP7zn/9sevHixWm+Sr0lZBdynG+//XbTvJ9NmTLF9E033WTaW2rHHXecbaNV7O205fnoo49M9+3b\n1zTvQ7yHMaO3FCiSEUIIEQ09ZIQQQkQjql3GsJ+hO0NNFpixuO/hhx82vcUWW5h+7LHHErc/++yz\nzjnnXn75ZdvGYjPaXGz7v/HGG5tm5to+++xjmllnDDWZYVLi4rTo8LvRsrn//vtNM2PlxRdfND1r\n1izT3nphcSsLamkB+GI05wrPndNPP900rbOsGU7lvGIn7YxQr77111/fNK8V2sZ8DW1pWid+Lmhr\nvv/++6aZ8fmrX/3K9I033pjmq6zSsFiZc8rCTN4LaXVtttlmzrnC+xr1VVddZZrZl/fcc49pXje0\nnBctWpThW+SLIhkhhBDR0ENGCCFENGrd6j9UiEhoGzF0D63kx0wK9gYKWQPMzPCFYtw3s2TWWWcd\n0wxBaU0wpGXBJq0GhsM8dmZXNWrUKHF7OdpooZ5GtLcefPBB07SZ+PpQO/6k1vOcW2b0hbL1OI/F\nUG4W2UYbbWR6/vz5ppllxxVHeQ77rL3lX8NCPtphvEb9OUnbhhmXtHm8heNcYUEhs8uyLC+wPOVs\nYS5Pmv5fX375pelrrrmmxtcTbz8zi5B9yd5+++1ETZhp2L17d9NDhw41TYuuFCiSEUIIEQ09ZIQQ\nQkQjs13mw768Vsbs2bNn4na2u2avM/ZVYtiXZNmttdZapkPLCzB7h325XnjhBdO0D2idhcJ7Wnrl\nTmgeQ1YnbbHa2n+0aVjgF4LzVYylQhuzruaIx8Dzlxl3PDYWXdI2DBXF0uYNLd3gLSpaa7zGaAvR\nzvrlL39pmkXUxdhl5W6RkTTnezGWuLcxmSHbrl0701z+hPTq1cv0gAEDTHP+x40bZ5pZoaGfOpjJ\ndvHFF9d47CtDkYwQQoho6CEjhBAiGlGLMQs+CBYJNYuEmCVDe4uFYszeSFrVkXZEmzZtTDPUpC1G\n+4v6nXfeSdweyq4iodUmK5VQy/gssDD2tNNOM92xY8fE1/NzWGxWjB1RDjZm6BhC/aRoXbGgOM1q\nrdxOS833i2M/v9A+mGVIC5s2c6RVF1c5/NjRomQWHwswW7RoYfrss882zT6DLFzne9Pck4q1yIgi\nGSGEENHQQ0YIIUQ0SmaXhYr1ZsyYYZrZYJdffrlp9hf75z//aXrMmDGm/Ypw++67r21jL7Lx48eb\nfuaZZ0yzIO7DDz80TRsvtCJdiPpgkZHQd6ZNwgw8WkJdunRxzhX2NvOt5pffB6FNc/7552c84vpD\n1oymkHVF/fnnnzvnCldtZQ85WsKHH364afb8k0WWP/4+w0w/2smcl/vuu880C2afe+4507wP8d5W\nahTJCCGEiIYeMkIIIaJRMruM0KJitlirVq1Ms9U+ezbtsMMOprkKprdouA/aNgw7mS3lbTbnCvsB\nhfpyMfOD4WjIDmQmXTFFa+UIw3q2hO/fv79p3zaeVmgIjvmxxx5rutLHLZRtGNtyCu3TZ4b98Y9/\ntG29e/c2zayzCRMmmGbBaMiKE7XHjyOLK3m+XHnllab5EwJtT/YZfOqpp0zXZdGrIhkhhBDRKFkk\nw7/m+KM6f3A88sgjE1/Dv6D41x9/QPZ/KbN9Bmtm/A/Qzjl39dVXm+YCW/yBeerUqaZDa6XzLzge\nCyOsSv8rfHk4/ttvv73pE0880fS2225rOksHZdYv8a+wSq87StOlPK+oJs17/TnJH4l5jfH8HThw\noGkmz7A1SdbF41Z1ONc8t30H5T59+ti2nXbayTTvMbyvTJw40TSvIdZV1SWKZIQQQkRDDxkhhBDR\nqBO7jD/Is53Gm2++abp169am2a32ySefNE2ry4f7/OGfFgDXqe/QoUPi59Da4Vrpvq5g+e9Ba4IW\nQ32G33n06NGmWZ908803m/Y/4POHf9oFtFpY18TPKeWP5XVFXXwXJt08/fTTprfeemvTbdu2NU0L\nm4tpiWR4rjIxhou/sePyCSec4JwrPBdYf8b74JZbbmmaCTh33XWX6T333NM057rU55oiGSGEENHQ\nQ0YIIUQ0am2Xpcn4ad68uWmu605oRTFLgiHgsGHDEveTlD3B7s20aLjGNdfeZlsbhpTM6uDCUWzP\nUJ/smtrA7+8XXHLOuQsuuMC0H/dbb73VtnFemKUUImSR1VfrLDa+1otWDK8rdvJlvdIHH3xgWuOd\nDOvoOL7dunUz3blzZ9OscXn88cedc4U1MB9//LFp1jJxvlg7yEUA+bMEaw3TWPt5ZnQqkhFCCBEN\nPWSEEEJEoypL2FtVVWUvZmHQ0qVLTYfsjJC1wfCSxZMsquT+a2qPwM/hPhguMoxl9gytNlpnCxYs\nSNweWkQqTSuZ6urq5PbDtYDzUg5wTn2BGe0CjhutSIbxtAnyWDQtLXnNS9Y5oT0cspaLgRbl8ccf\n75wrvA68VeOccz179jTNa5KZUDNnzjRdghYzb1RXV3er+WU1k9e1EiqM3GqrrUyfcsoppjmO/ImA\nltYhhxzinCu0nnl9MEOW80lri3Y+rU520Oa1VSSp5kWRjBBCiGjoISOEECIatc4uC1lkoawEWlfs\n/0X7K01XY1oxoT5iHtpWDEtbtmyZeLzHHHOMadpr7Eo7d+5c0yHLIHTslQTtrenTp5vmYmIha2SP\nPfYw7e2D/fff37Zx4TkW+B100EGmR40aZXrOnDk1fmbIjt1ll11Mv/baa4nvLQdi9P/i+b/jjjuu\noHm9DRo0yPTIkSNNM9OM80BrmfZO1uMq995+vG/xHGOG2L///W/T7H+44YYbmma3d97zzjzzTNMc\nFw97O9JyCxWFM6OXNv9uu+1m+rHHHkt87xlnnGH6lltuWeFYaosiGSGEENHQQ0YIIUQ0MttlPmQM\n2Rahwh1aSM2aNUvcTgsuZH+EssuS1orna2mzcTuLLhmuMkzt2rWraRZv8jMryQIIwV5vhx12mOlT\nTz3VNDPAuOgV7ZjFixeb3m677Zxzzo0bN862sdjsiiuuME07oEmTJqbZJ4uLaPE17Du33377mb7/\n/vtduRKykIshZKPQ0vILAjKjjX0D33jjDdNjxowxzX5+tJ9poZLQPaKSrg/OC60oLpPwxBNPmKbN\nRLuK95mQXZ80Xpwj3m+YoUY7+9VXXzXNjDJmnZEDDzww8djzRJGMEEKIaOghI4QQIhqZ7bKkkC6U\nURYq2KQtwt49fG8oY60maFvxc2gFcUVHtt1mbyB+PrNtWMgUsjhCVp8/nqzZOKWC87X33nubZng/\nZMgQ08w82myzzUyfd955prfYYgvnXKGlwvGhzcUiTY4Rs5pYDEvLYvjw4aZ/+9vfmi7nVTVjZCGG\nlkX49NNPTXs7c6ONNrJtnTp1Mk1rk7YYNa8nFnVynivJFgvRo0cP0yxGpVXLrFRa8bw+OF41Fa/S\nZmMmWJs2bRI/kz8/cC54LnDu+JkjRowwHcvyVyQjhBAiGnrICCGEiEate5eFCBUvMXSjXUUrZMmS\nJaZDdhktBu7fh4ksgGLmEsNeZlo8+uijpmnpcQVOhq8hyyV0jCFK3bsslDn2wAMPmGYrd1opIfsv\nZM3wHEiyOtNkHTEzhitmciVVWhYsZqTtltUuK2XvslBmUai3X019+xKOwTTH6p577nHOOdenTx/b\nxsLiAQMGmH7//fdNM7OwBP3KSEl7l3Xp0sU0MxuZZcmsRdpMPMdCxeicF9rC/j7DHmXMHAvNP/dd\nYotSvcuEEELULXrICCGEiEate5eFoFWU1IvHOeemTJlies899zTNcJyFT+z7Q33EEUeY9pYKe26x\nkIkW2dSpU00zY4S2GLPe0thfodeUS3YTbaYHH3ww8TU+E8y5QsuJ4TgJWSZJhbEcH2YgMZOJq5d6\nS8e5QiuMn8OW+Emf6Vz5ZZQRfhfamZwrWiSh7xgitNSGzxzk57P/1rx580y3aNHCNDP7KnllzJoK\nynl/oP3+l7/8xfS0adNM+4Jj5wrni+c872277rqraf5c4Mk6tuWexadIRgghRDT0kBFCCBGNzHaZ\nt07S2EMM+2i5sGDopZdeMs2CsBNOOME0V3gjbDfu98/QkQVo119/venRo0eb3mSTTUwzk4bQ9qtp\neYHlKUe7JrSKJ9uB07piC36uyBfKkqEF5oskadGxvX8xtgutHM51pcDvzsxGEsrsS/Mabqcd5z+L\nFs5TTz1lmrYYMz6zkubY64Isx8J5+c1vfmOa2ZfHHXecaVru7AGXJkusvqJIRgghRDT0kBFCCBGN\nWhdjhvpP0a4KZT1sueWWpll0x4KxVq1amT788MNNX3bZZaZpwfkMJPYWY3ttwqykUOhaUwvulW1P\nQ6mLMZd7PY/DdCgTjll6oQxAth7n/vO2BmIvqRCjGLMY2yg0J1ltNK58eckllzjnCotve/bsmfg5\nIfstzXmTIyUtxiRZv1u5WoSRUDGmEEKIukUPGSGEENHIbJclFTLlFSKGis1oyxBmhvkeT1zhj3ZK\n6BizZuzkRV3aZSHqw+qexVLK3mW12KfprOckCwBvu+0255xzgwcPtm133HGH6VCmWx1SZ3ZZCFr1\nIXtxFUB2mRBCiLpFDxkhhBDRyL3Vf17QGgi10U/K/EhjKTDULWZ1wmIK5crRLssKCzPLdbXPrJSz\nXVaLYzDNDMHWrVs75wrnb9KkSaU7sOyUnV0mnHOyy4QQQtQ1esgIIYSIRubeZTW1yW7Xrp3ppDbW\naeH+Q5ZWUnFUGvuvGIsslIEVyowrl2yTGAVzlWCRlXNxXAkyGE2zWJZaiNgokhFCCBENPWSEEEJE\nI2t22SLnXO09MOFpV11d3TKvnWleciO3edGc5IrmpTxJNS+ZHjJCCCFEFmSXCSGEiIYeMkIIIaKh\nh4wQQoho6CEjhBAiGnrICCGEiIYeMkIIIaKhh4wQQoho6CEjhBAiGnrICCGEiIYeMkIIIaKhh4wQ\nQoho6CEjhBAiGnrICCGEiIYeMkIIIaKRafnlqqoqrQuQE9XV1cnrNdeC1VZbrbpBgwbOucIloSuB\nRo0amf7222/r8Ej+j7zmRddKrizOcT0ZzUt+pJqXTA8ZUZ40aNDANW3a1Dnn3OLFixNfk3U9+djr\nz3s6depketKkSdE+x7n/GyfPTz/9FPWzRDpSnmf1dpExnpM///zzCv9fbut9rbbaMvPr559/TjUv\nssuEEEJEQ5FMPeDHH3+0CCb0l2Gav4gOPPBA008//XSm9y73F84K/7/66stONVp6U6dOrXHfxcDj\nCkUv/jVJxy3iUm5/qZcannN+LHjOphkfRkMkRrRem2tEkYwQQoho6CEjhBAiGrLL6hnF2A/Dhw+v\ncT8hOy4URtd11lua8F42mciLkG281lprmf7uu+9M13S9pkmMoC3Gz89KTZZ3rfeb256EEEKI5dBD\nRgghRDTK1i6LWafBsJBh7DfffJPr51QCjRs3Ns1iyFBNSfv27U2///77Ne4/KcMldr0Kzx3C86hU\ndUCifIlxDoRspv/+97+pj6GYYynG5oplGyuSEUIIEQ09ZIQQQkSjTuyyNHZJHuErbbH111/fNFuv\ndO3a1fS0adNMM7yNeYx5UFVVZcWOP/zwQ6rXe0IWIb+zb1njXKG92LZtW9Pz5s1b6WeGijFjkGZe\nymXu6pI11ljDNM8bbqeF0rp1a9Mff/yx6Uody7yOOy/bzd+vuD/a2ezzt2jRohXe51zhdctrrkWL\nFqYXLlxoer311jP9+eefm87TSlQkI4QQIhp6yAghhIhGVZZQqK7aZDMcZAj4/fffm/YhfqtWrWzb\n9OnTTY8ePdr00KFDTU+ZMsX0LbfcYnqzzTZL3M8HH3xgmqHpb37zm5q/CMiz1X9VVVW1D285n2mK\nqziefH3Dhg1NL1261PT9999v+rLLLjO99tprmz733HNN+3GfMWOGbfvkk09M02YrB9ulvrb6p/2x\nwQYbrPD//fv3N/3CCy+Y5rlPS43WDfX8+fOLPtYE3qiuru6Wx47SzEvouskrK5JzQe2vRY4nP3+r\nrbYyHcqUpP1Pi+zee+9N3M+4ceNMhzLgVkKqeVEkI4QQIhp6yAghhIhG2RZjEoaPa665pumDDjrI\n9HXXXeecc26TTTaxbQx7mVH2+uuvm2am07rrrmv6wQcfNM1Q89133zWdJpOrVCRZTWmKq/j9mVXE\nrDPaiLRDhg0bZnrBggWmGb7vt99+zjnntt56a9s2ZswY08yemT17tukYRZr8LH6/+tTqn2PPbLBt\nt93WdJMmTZxzzl1xxRW2jdmXPXv2NH3sscea5vlO62ivvfYy/f/+3/+r7aGXDTwPOJ7FnJMc3913\n3900LapPP/204F/nCm1oss4665hmUXTLlssWquQ80kY7++yzTdMWz9JTLQuKZIQQQkRDDxkhhBDR\nqIjsMhYM7bzzzqavv/56096OYRj/xRdfmD7ttNNMjxw50jQLkNq1a2eaGRjMxqFFxPdmLTDMO7ss\naXua7DLaAZ07dzbNDLCDDz7Y9N13323666+/Ns2+Z+edd57pgQMHOucKw3XakswQHDJkiGlmrtGK\ni52BFiO7LFYLdQ8zBGmjMLvo4YcfNu3Pbb6Px8V5HTFihGnazDz333777US9ZMmSDN9ipZQ0uywv\nOO/M2GvevLnpV1991bS/n4WKMXmP4X2O9httYFqkzArlHNGuq8W1pewyIYQQdYseMkIIIaJRttll\nDOUZGu6yyy6maW/5MPGJJ56wbTfffLPpmTNnmqZFwxBxzpw5pufOnWs6ZIWFWsqXO+w/xrH46KOP\nTB966KGmBwwYYDrU4+qRRx4xTZvGZ/sx7Of7qFkQyILZ559/3jSzC2nRZSW2hUVi7J/XRLduyxwL\njgn1rFmzTPtCY2Yx0cIke+yxh2naz8wiY1YgrbZVHdr8vC+ddNJJpnn9eUv5nXfesW1fffWVad6T\neH9ksfQ555xj+qijjjL9wAMPmC7muqkNimSEEEJEQw8ZIYQQ0Shbu4wWFcP0E044wTRD/PHjxzvn\nCgvMWMTJQipaDbR/aKEU0y6e9hILOUsBLTzaNAyvQ0VXLMxilgoz7UJh+sSJE00//vjjpn1m2B13\n3JF4XKEx5LzQduA88hwJzWOosI7ftdT2QR7wO06ePDnxNcwc+u1vf7vCdlqPXbp0MT1o0CDTvXv3\nNk1rh5mIb775pulyKlCuidjLT/D6YBYZ+yu+9957pvfcc0/nXGH2F4ufeYy8DliAzuJZzm+avmQs\n/OQ9otixUSQjhBAiGnrICCGEiEZZ2WWh1dhoDYQyw7bZZhvnXGF4z7b8LC5kIVno84vpU1Rqi4yE\n7Kc0GXK0yFiASjuJGS60SZ599lnT7BP35JNPOucKbYE//elPppkhSHuB34OWl7cUnHNuwoQJprlS\nYyibi/usRIssdH6msahoOfueZiyQPeCAA0z36NHDNMfJX2POFRZCc95Cx0vKYUkH5+Kv0Eq76rPP\nPjPNwkwWTPosyg8//NC2hbL1mCHKQkv+hMDrYP/99zfNZTcIX0/r7MsvvzRdm7lTJCOEECIaesgI\nIYSIRlnZZaFQjGEcLbBOnTqZ9pYaC51+//vfm2bhWYgY7eXLHVoaDMF9tp5zzj300EOm2T7+8ssv\nN02LjPPo7U0Wld14442mL7roItNjx441veOOOyYeLzNpaJelKa4sZQFmDLJmP5K+ffua9nZuaMVZ\n2m+0efr165e4PQSPkZmelWhVpoXXE619v7yCc4V2Fbd7G58WWWgVzVtvvdX0RhttZJpjTouUFl0I\nzkuRPc0KUCQjhBAiGnrICCGEiEZZ2WUhGNYze4xFlT6UfOaZZ2zbyy+/XIKjKy84JmnsP9pGzLZZ\nuHCh6UcffdT0NddcY5p2AHXS/ufNm2fbWPj39NNPm2ZGG3vUhWwX9j1LE9JXokVGaBVyNcQQtFeY\n8chCVA/Hj5r2czE2V322yAjHjtllXPagffv2ppmhucUWWzjnCpdr4Dn7l7/8xTT7/IUyREeNGmWa\nfRnTEMrurc01pEhGCCFENPSQEUIIEY2S2WUsEmKmURpC/bhYBOZXY2RhUqXbI7UhZBulCXmZUcKC\nVbZ7nzp1qmlmJBGG+z5Thp9Pi4BtzbnC3/bbb2+avcv4+mbNmplmdlult5vn+d6yZUvTWVeabNq0\nqWlai0nQWr3llltMv/jii6bT9L8KwfkP9Q6sb3AeeT1xSQ1al94uplVMe5rFsxxPWtssqp02bZpp\nzh3PhVKMvyIZIYQQ0cgcyfi/QrLWlDB6YT1Gmr+ONtxwQ9OvvPKKaXYrvfPOO51zhX+l84nNXHLW\nzPCHsvpQJxOKUtJEdfyrZtdddzW90047mWaOP6NTRpX8S9X/xcXEgEWLFplm3c0RRxyReFz77ruv\naS6+xciHrTg4p4yCQu2Eyg1GozxXOa5p2G677Uxz/P01xyQZzj2jVV4TvJ5CiR4k5EBwztkOqD7A\n7xzqds7XMNnFJ8Sw0zzbu3AfjNaPPPJI01OmTDHNOS0meizWEVIkI4QQIhp6yAghhIhGZrssD0sp\n6w+IDK9HjBhh+qabblrhuPhjNNe4/utf/2qaXUUPO+ww07QJ0nRoZdjLH7uzJjbkgT+WYlpAcG5p\n01CzrQ/tp1BCht+eZNc4VxjGhzoy+6QO55zr2LGjaVqn/AGV5wDnItTlu5zhuKaxLfgd+d2HDBli\n2v+YzFobjkfz5s1Ns07mvvvuM53GLguNcblYZDHOB1qKbBlDC5c283HHHWf6jDPOWGEftLZ4ffKn\ngtdee800k2F4n1t//fVNc+6YNNC4cWPTeSbPKJIRQggRDT1khBBCRKOs2srQOmFLBh9GOlfYkuS2\n224z7e2tXr162bYLLrjANLM0mHHE1jO0vNIQyvaoC/yxFGMB8L2zZ882zWwwjiPtGGbS1GSp8rim\nT59uesGCBab/+c9/mp44caJpLpzF8D60fx4Ls62YhVPO9VTFzGHPnj1Nc1E5b5OFvjetnVNOOcU0\nzwlmplUqWceWNmyaTt+8hzE0abRPAAAgAElEQVQTktma55xzjml//wstzEhb7JhjjjEd6ppNy5/X\nFgm1pMkTRTJCCCGioYeMEEKIaJSVXcYQlNlCDPvZTZThoA9l58+fb9u4INaAAQNMH3TQQaYZ0m68\n8cam2TU467HXJbSzaOGlsQb4Go7tv/71L9MM5dlZN8v3p6Ww5ZZbmua88PNpb7Zt29Y0sw6vuuqq\nxPfys1jIWSnZZcXAeQsVBiZBG5JjTLsxjV2WtSN4qUljLfM1zPpiN3hmObLom0XkvC9169bNNG0s\n/14eyxNPPGGai/qxjRLP99D3CBVgluI6UCQjhBAiGnrICCGEiEZZ2WW0NlhIxAwMZoCx8MhbKgxL\n2e306KOPTvxMhotpeluVe0FfXmtz096g7UbbhRZZlnFhsR/Dfob0zFyjXcqO0PwcFtvyWHjslbJw\nVjHnWGixqbPPPtv0pZde6pwrtFlobbHoknPF7sBpKEeLjITGlllk/A48P3nuDxw40DQLXFnozYJm\nFlKyR6A/P2lJjx8/3vTDDz9c47GnOXdKfd9SJCOEECIaesgIIYSIRsnsMtpc7EvF8C4UXjPDggsx\ntWjRwrQP/ZnRwcwxZnSECpDSFFSWo0Xm3LLvlKbnWk37cK7QPuEYcfy/+OIL01myy5gBt+2225qe\nMGGCac7XzjvvbJp24EMPPWSa2T7Dhg0zTcuoXOdueULrxKfpFxbq83fJJZeY9ktt8Fxp1aqV6X32\n2cc053XQoEE1fn6lwnM/dA1xXrh4Htv1/+53vzPdqVMn0xx/Folzn/78p+X/6KOPmub9iccbIs1r\nspJm8cMV3pP7UQghhBD/P3rICCGEiEZUu4xZGrRcQtkbocwI2gTszcOMjU022cQ5V2gX/M///I/p\n9u3bJ+578uTJpsuloLI25G0FcV4YInMu0lhRfjsthYMPPtg0swhZPMtMMK4UyM/Zc889Tffv3990\naKmF0Pnlv0cp5j+r3ZDm+iB33XWXabZ3p3Xz+uuvO+cKrx9amFxllL3LmAlY3+B40ioOLbXAwkwu\nUcHCYZ7DXA2YGWi05vy9iDYw75shS4/nVOyMvtpcI4pkhBBCREMPGSGEENGIapcxpGvUqJHp008/\n3fQDDzxgmsWQoUwahoYMWa+99lrnnHP7779/4mtZSPXWW2+ZZsFUMdSHPk1pLDd+N45/qDDT2zTM\nqDnyyCNN8xyZNGmSaWbVMNOMhWw83jR2R+j7ldImLeazaDMTZlmyYJIrM7Ivn1+ZsXPnzrZt5syZ\nptmWnpZaJdvJWeA5fvLJJ5t+8cUXTc+dO9c0MyR5TXAZEdpetMuYSTZ69GjnXOHKobwPUvMaizEv\nocy02tjyimSEEEJEQw8ZIYQQ0ShZMSbDL660+I9//MP08ccfbzq0SiUL83xGGbcz1GWWEbNkWPSX\nJmMmTUZQXVtkfnxj9Cui/cR5ZMYebZrLLrvMtG9fHrLWmF02atQo08ySotWQNSMrBO3bcuhpFrIz\n+V0233xz07TC+vbta5pZTDxv+/TpY7ply5bOOeduv/1228Y+gLRr6vq8rmt4HhKOM1dr/eSTT0x3\n6NDB9N/+9jfT7777rmn2JvPnNi1k6tBcxCgyDtlxtemrp0hGCCFENPSQEUIIEY2S2WW0PO6//37T\n7GM2ffp006GV3Ng765FHHjHtC5nYU+i6664zzSwZhp2hlSRJuWfVVFVV2UqioRUQmZmUtb8Zs1po\nY/7qV78yzXbntDG9ZcNj4TEeccQRppm9E8ocy4tysMhImrbzs2fPNk277+9//7tpFiN3797dNG3p\nHj16OOecu/fee20b2/vzc3it1BfrzNu/ab5Pv379TPOc4fizQJzzRYvYW5TOOTdy5MgVjoX7pM3P\n+2Bt+obVltD+lV0mhBCirNBDRgghRDSqsoQ/VVVVufsWDCl5LMze8OG9c4VZNc8++6xpb3VxH2ls\noTRFlDFWw6yurs6tDzfnheMWKmgNhcK0IlkYy+9PO4C9sWbNmmW6cePGK+x7zpw5ptlzbN68eYnH\nkpW8isfympcY10rWc9VbqM4VWpRHHXWUc66wt58vZnaucAVGWkEhQss/5GhzvlFdXd2t5pfVDOcl\nzXXN64nLTPC9vCfRcqellmaFzaTXljmp5kWRjBBCiGjoISOEECIadW6XrarkbZfVVIwZghkrtAZ8\nEaVzzr333numk1rkO1eYpXf99dev8PqbbrrJts2YMSPxWEq5cmXIKilnuywmMSzhHIlilxVDMdma\n9QjZZUIIIeoWPWSEEEJEo2TFmCIu3roKZaYwiy+U3cKCWfZX8q3hnSvMUmL2GrOK2Kbft5Dnyoxc\naqEYiilOK0NLqOSUsrivvpHGIguNbx7WZGjfWTMQS7GqpiIZIYQQ0dBDRgghRDRyzy5TCJ6OWMWY\noVCcq5Gy7XiIYkL9pNeEigRZ4BYizWeGjpdWH/vkrWRJhJJll7FvGy1GsQJll11WaeRVrLzctajs\nMiGEEHWLHjJCCCGikdUuW+Scm1PjC0VNtKuurm5Z88vSoXnJjdzmRXOSK5qX8iTVvGR6yAghhBBZ\nkF0mhBAiGnrICCGEiIYeMkIIIaKhh4wQQoho6CEjhBAiGnrICCGEiIYeMkIIIaKhh4wQQoho6CEj\nhBAiGnrICCGEiIYeMkIIIaKhh4wQQoho6CEjhBAiGnrICCGEiMbqWV68qi5dGoNYyy+L4ijl8sul\npFGjRqb9ktcVtMzH4hzXkynbL+2XNi7neWnQoIHpn376KdW8ZHrIOLdsLXWuo14O1HRcoTXg06xl\nT9KcAGnWpF9VKNfzhay++v9dBj/++GOu+63pu5fyPNliiy1Mv/322865ZQ+b5QldEyGK+R4pP2uV\nWGTMn4c//PCDbeNNnfz000817i/G+dWkSRPTS5YsSTUvssuEEEJEI3Mkk8dfpK1btza9YMEC03n8\nFcRt3F/ouENRTeg1aQh9j4022sg559zChQsz7a/SyPqXcE0sF6IXvb/lyTuC8SR991JGL/4vY+ec\nmzx5cp0eS4iQe1CfHQB+T2pGMJ5izvcYY7hkyZLM71EkI4QQIhp6yAghhIhGZrssCyHbpBiLjCTZ\nEcXYM8X8yLnGGmuYZtjL13/00Ue1Pra6JI39RWumJvspqy0SwyKrK0LfN4ZVFJqH9dZbzznn3Jdf\nfpn4/2uuuabpUHIAyevH/vpgkWWdx5qSjUL7CyUm8Tr8/vvva/x8krfNbfvNbU9CCCHEcughI4QQ\nIhpR7bI09Sih7bXNKEoTXma1LELZIHxNUmbIyj6rkkgTOoesmdpaAFnnrpxJc/wh65XjGnrvOuus\nY/rrr7+u8fXeJgud12kssmLIWstWCmKcY40bNzb97bff1rh/vz2U5Zr02uU1z5e11lrLNO+hoXMq\n1pgrkhFCCBENPWSEEEJEI3e7LBR2pimGJFkzimoKMdOEwFktGtoUZOnSpTV+Vt7Udd+j0Hh5zf/n\nXDEbhllN1F999ZVpnhchy4DvzZphkye1balD6zVUXEy++eabxNdwzGnd+DHs3r27bWOx5hdffFHj\nZxZjraS5R5TaIo2RIRc690KZYR5eE9w3bS5+PvfH19P2pAUb+iwee54ZnYpkhBBCREMPGSGEENHI\nbJcl2TLbbLON6enTp6/0fcu/t5i+VMye8PtniBojW4LHntUWi2lp1bTPrPYDw+iQRZXl8xneU6+/\n/vqmmzZtanrLLbc0/eGHH5pmAeG7775rmlZCKNOv1NR2ntNYZCF8fzznnOvatavpoUOHrvDazz77\nzDTttLvvvtv08OHDTS9atMj0O++8Y/q7777LdLx5vSYWoXtSaHvI3uLyCjw/OV6c63XXXdc5V2j3\n8nP4PmarkZBdGsr+THNtF4siGSGEENHQQ0YIIUQ0MttlSSHVtGnTavU+59JZZAxHqddee+0VtjMT\nidZZmky3ULZSiJAFVY69mbJ+dpowOk3xnB8jWg1c6oFzuPPOO5tevHixaWbxzZ8/f4V9L69JXRZ1\n1vYz0hQrUu+yyy6mR4wYYZoWGMffH1erVq1sG4s4+/Xrl/j5o0aNMs2W77RiaKmV80J1K4PnPs+Z\n0HbOM8ecbLXVVqY5Rsz66tKli3POuVmzZiXub7PNNks8lnHjxpn+5JNPEj8/BM8j7jPNYo5pz29F\nMkIIIaKhh4wQQohoRO1dRrKGWXw9s4723Xdf0zvssIPpzp07O+ecmzt3rm1jlsYHH3xg+oUXXjA9\nZcoU06FssZBNEcpiqkubIEvL/ZVRTEv6pMJLhv3bb7+9ac7tpptuavqEE04wfeKJJ5r++OOPTYes\nyPrU9ywEv9ftt99uOmSRcay8jRzqp9WwYUPTJ598sumtt97a9F133WWa1xDPOWYCpunBVu6ECopp\nM3FMmzRpYpo21iabbGJ63rx5pt9++23nXOFY9ezZM1EzK5PX/KOPPmo6ZOPRovv8889dEmr1L4QQ\noiLQQ0YIIUQ0otplxRRaspCJWRUXXXRR4naf7UILi//fp08f04cccojpgw8+2DTfy/CSIWUojGRh\naOxW6SsjjUWWl4VEyyBkzfgCszZt2tg2WmR77bWXaa4ceuedd5qmBZEmiyzN9kqHGXobbLCBac4J\nz0MWtF5wwQXOucLsMtpi3EenTp1Md+zY0TSvlQEDBph+6KGHTPO6adu2rWlaROU+P2nOq9A5SVuq\nW7duppkhyb5z/h7Gex+vq169epmmFUkLmfctZteG+uFltddrM1+KZIQQQkRDDxkhhBDRqHXvMoZx\nDLNCxUs17c+5wjCRmWFHHnmkaYbdzAbzdsCTTz5p22jLsBjKZ6I5Vxg6NmvWzHSaIkpaZNzPwIED\nTQ8ePNh0ufTUYhhfTCt8ZrhwHlnY58clTTEuezOx3XyHDh1M04JJsxpnXn3yiiEve5L76dGjh2me\nhyxiZfv+s846y/R7773nnHNuww03tG0sruT2M8880zQzN9mvcPbs2aZpr3E+H374YdM77bSTaWay\n0d4rRYZmmmLqUNZiaCVTbw87V3h98J7DcaQV7M9n3rc4PrxW+Tn8Hs2bNzfNok+OLd+bphdjsSuW\nKpIRQggRDT1khBBCRKPWvctCFllWO4DvZRjHfkwMr2kHjBkzxvRtt93mnHNu5syZto2WyKmnnmp6\n//33N3399debvvDCC00zAySUScJiK7ZNv+eee1wSpV69kvYjw/KsFlmoMDbUBp32gc92YQt6jj+t\nMNo0zJih1TljxgzTtB9DxX7lsEpmXhYZM4eOOuoo0ywuZtbRAw88YJrFyJ5PP/00cR+cP14HLVu2\nNP3qq6+aZuYUM9A4nzfffLNpzgltnFJnmhWz6ifnhTZ73759TTN7zxdaOldoY9GK8tYYM76YORha\nRZbwO/H64PFyzHlfCNlixVqXimSEEEJEQw8ZIYQQ0cilGLMYiyyU3cCMGWYUsWDvxhtvNO0zmmjb\n0IrZcccdTdPy2W233VbYh3PhgkoeL8PeNP2ySm0HhFbPSwO/QyiTkJkvnDvaOsccc4xzzrnDDz/c\ntrHn3IQJExL3wYwlwjEMZZcx7KdFVil9zJLa8jtXuCwCsyhpJ3IFTLaMT7JCmP3Fc59WDNvIc/xC\nfQHfeust0+w5d9lll5kOFdeWek6yFlBzXmhFM+OVBeC005llykw+WlF+NVhmiNGupF3GDDXehziP\nofFkASjHP1ZGnyIZIYQQ0dBDRgghRDRyscuyFuuECpmYrdS+fXvTzN5gK2v2Y/LhKy0cZquxjfyC\nBQtM01JgGJm1F1alWDFpCa06yVUqkwrJnCu0FbwFxvFn76rXXnvNNLPy2A6d1kCoADZNNkylzAuv\nA1qPXOaCY8/C1ZB1ktSmntlHtGI4rvwcZpf5gs7lP/OAAw4wPXbs2MTvxGu+LguUs/YY5HnFc5wr\nunK8WJhKq5NzStvR25e8D4UyWPlTAW1mah4jxzlUeBrrHqZIRgghRDT0kBFCCBGNWttlzNBiuJ6G\nUA+pkNU1bNgw0y+99FLia3xYydCd1g73zc8fPny46ZC9EMocC+lQX6xSFGOut956prPOCwlZTsyM\nCbU4Z2i+++67O+cKs7y4kuLjjz9umsWBXEmQWVBfffVV4jGmmS9uz2sF0Rjw/ORqiGzvT82MS9of\noVUyvaXC8eP7aOHwGnv//fdN8720nVhEe/fdd5tmhugjjzzikqgky5mFls8884zp/fbbzzTHlBlo\nHDtmkvlzm+c+rwlalLzGmOmW5qcLvobzW8z9YmUokhFCCBGNWkcyobWhQ4T+6g8toMNFq37xi1+Y\nZu0Lf2TjX7sePpn55Odf1U8//XTi8Wb94b9cEgLS/DWSdeGv0HrmhH8p77333itsZ/LG66+/bvrd\nd981zUiS8MdMfn7W6IWUW/RC2OGY57uPCp0rvFYmTZpkmnVfTGrh/Pgx53jzB2b+BczIlWPPBAxG\nl9tvv73phQsXmmadzIsvvmiakU+pohd/PqdJUgr91c8klSFDhpjmfWbkyJGmGflQMwr1Y80WTL17\n9zbN5BkutsiIlVEioyAmW4Q6zPMc4LlR7LWiSEYIIUQ09JARQggRjVzqZNKQZtEqhmUM10aNGmU6\n1HLDh4C0wtiRlt1h+QMaa2ayWltp7KWkH6fr+kfNNOuTh+A4st6lRYsWptu0aWP60EMPdc6FW2Iw\nROf8M9TnnIda3IS6MFcitJ9oOfFcZSILX8Nuv7y2WHvhbWbug+PHGiW2ieHrOW9MTuDYMwnlD3/4\nQ+L3qIsf+7O0T+FraWPecMMNpjlfvOewg3JooTL+7OCvEdpi7CrPljV77rmnaXas57XHnxzYvZ7J\nBrxfMuEgNBe1WfhPkYwQQoho6CEjhBAiGrnYZXnZTKHurAwpGa4xlPWhG9/HhZ2YgcHFlLgON0Pa\nYqiktiZpjonfh9YMx5Rrzp9++ukr7IOhOOeTNg3tlZBdxnMkzbFXSu0Fs3923XVX04MGDTJNy4Od\nl2lpTZw40TQtZ2Y9+Wsl1N5l8uTJpmlz0hLlWF5xxRWmWTNy9dVXm37qqadW+Hznstu1pYY1Q8yE\nY20KbSxmhrGWiYvCMUuNi7/5seZ19dxzz5nmPHMROO6P7+Vij5wXnhdsVZMmizStRUYUyQghhIiG\nHjJCCCGiUeeLljFEo3XCjA1SU7jG/THrhdtPPvlk0yyGKmc7pRSkWWyNWUq0W1hUmdTCh1YkLR3O\neah4lnOeJqQnWYs0Y5BmcSx+X2bt0c7dbrvtTHOhsPHjx5vmdcPMIeLtT2ZC8X2hRd/YMoWWKIsr\naaeGLLJKgvPCBcSYxcViWFpqLCIP3fPYwdnfi1iszPFkEedf//pX0wMHDjTNYtg33ngj8XhDPwuE\nOqkXO3eKZIQQQkRDDxkhhBDRqLVdFio4rKkQcfnXpAnFQn3PkvbPTItDDjnENLOS2NMp1rrW5UYa\nqyjNdto9tMuYYUOLx78+1Ck41FU5ZHMVs8hVXdmhWRfHeuedd0yzJx8zhzgm48aNM017i5lhSeMW\nWryK29k7bcCAAaa33npr08zA4rGzGJH7Z5YcP4tFgsx6KjWh4l+OLS1fjtH06dNNv/zyy6aZ6cWx\neOWVV0z7e1SoGzzHhNbdhRdeaJrXJM8L2m7MjON5wYXVQn0Ea4MiGSGEENHQQ0YIIUQ0am2XZbVc\nSPv27U0zo4hhNAnZbkkWnO+V5VxhqEvYO6mUFoq3FepiXfOsfdZIaMwJW49zTr3mkgq0LpnRQmuI\nx8vxSmOdkjTfr5SkOR6enyxQJbfffrtpFsKOGTPGNG0Rjrkfz5Al2bJlS9Pnnnuu6T322MM0i2VZ\naPjvf//bNLOY0izRUJcWGeG8pDmvuFAisy+ZZfnmm2+aDmVr+tdzWQxakXzf0KFDTdOWnDNnjmlm\nDxLat7y2Yt2XFMkIIYSIhh4yQggholEyu4zb2WqfIT0zI2ijpMmM8uFr//79E9/HEJEhaintsiSb\nIiZpVo5MYyGFCjNZZMisPs7dY4895pwrLMzj+DNjJ41dR9IcezlYZCRrr7gHHngg8TXMFmJhJq0T\nZqOxwNPPD60Y9vPjqo8sFiS8brl6JosRSdbW8TyfQoXZeZImKzZpaRHnCu0yvp4WJTP9QsWufv+0\nK1mAy6LXddZZxzTtVc4Lj5dzVIwtlqaweHkUyQghhIiGHjJCCCGiUbKVMQnD4lDmUCgbhZqhts/C\nYbjIkJatruuqj1KpiwFDn5e1hxdfT4uFY81COu5z7NixzrnCzDGOf5pC3hjjVld9zLJ+1oMPPmj6\n0ksvNc3Mre7du5tmO/4RI0aYpo3mW9Dvvffetu3MM880zYw2zgOXazj77LNNDx8+3HSaaytNX6xS\nWGQkzfIcoSLNkJ0c2n/oHuazy5YuXWrb3n///cTXcrkMFlHSfmMGYF6F8VkLi51TJCOEECIiesgI\nIYSIRp3YZQwpaaMQhnFpVs/r0qWLc865jTfe2LbRivvf//1f06XMOMqzZXZepCkwC41/586dTR92\n2GGmt9hiC9M+o8y5ZRZLaJ7ramXESlnWgZmYf/vb30x37drVNNu7t2vXzjSzy1hI6d/LLCaeE8yK\nGj16tOn77rvP9JQpU0xnPa/L5TpIA7PCQmMUusZD1xNfz4xab5eF+rwxK5NWNeF1yOLWkP2cZi5o\nkYeWj1gZimSEEEJEQw8ZIYQQ0chklzVq1MjaWk+bNs22Zy20IqH3hsJOwsIgn93EQsDBgwebZmZM\nKSlHayBUUBUa5x122MF0r169TPfr1880Q3lmPvmwnrZYaAW+ciucLBb/nbP2jeOYcNy4YiKtYGaG\n0S7p3bt34md5i4bHxWylAw880DSvc1o0zFyqNPxYZC3+TbOiL+eOVhuvOWaD0Yry+wxZ1SH77eij\njzZ9/fXXmw5lbmbNKKuNRUYUyQghhIiGHjJCCCGikcku+/bbb93UqVOdc+FV1NJYZAwj+Zo0fc9C\n2mfPcBtD/VDb6xBZW+CXS7ZSmuMOFVRxLpj1QpvGz79zzj3xxBOmaaOxDbnPcKG9E7JC04Tu5da6\nf2UknRM890P95DgOvnDSucJMo5kzZ5o+9dRTTTOj7OKLLzbtsy+dW9br7PLLL7dtzz//vGlanyS0\nvdLw503oXtWmTRvTXIGS80Urkssr8PzkdcZ579u3r+mDDjrItLe6eN9iXzL2c2O/tHvvvdcl0bRp\nU9O8/5X6ulEkI4QQIhp6yAghhIhGVRabp6qqqsYXhywkhpHFrKpJmLHh+zq9/fbbto1hLNuhp+k1\nFJvq6urcqhA5L8VYeGmsqFBxWoik14QyZkLviz1HzALLa17SXCs1HY9z4UyzUM8/ErLj/JjnlflY\ngoLjN6qrq7vlsaNi5iV0D0tTjMnXc2VgWnO+8JbLOKTJTGTfQBZgMustEqnmRZGMEEKIaOghI4QQ\nIhq522XMSgqF9KEwnqRpU8/eS77vD+EqfQxjN910U9NspV1KYtlleZE1uy6UbejnsZjlBbLaZcW8\nN695adCgQbUfk7za1oe+VyhjLbRchn9NmjlmhhILNrNSZCZmSe2yGPZfaGVM3rf8/TK0FArZZZdd\nTL/22mumS9wrUXaZEEKIukUPGSGEENGotV2Wxv6KbYvURMi6K4bQ8WZth13udlnelOOSB0nEyC7j\necjvziwjtvSPQV0UsTZr1sz0kiVLEo8lZaZnWWSXrWSfpsulKHtl5Hgtyi4TQghRt+ghI4QQIhpZ\n7bJFzrk58Q5nlaFddXV1y5pflg7NS27kNi+ak1zRvJQnqeYl00NGCCGEyILsMiGEENHQQ0YIIUQ0\n9JARQggRDT1khBBCREMPGSGEENHQQ0YIIUQ09JARQggRDT1khBBCREMPGSGEENHQQ0YIIUQ09JAR\nQggRDT1khBBCREMPGSGEENHQQ0YIIUQ09JARQggRjdWzvLgS1pKvFPJaS945zUue5DUv5Twnfk36\nClpLanGOi5ZVzJeuAFLNS6aHjBBZadCggXPOuZ9++inx//0Nz7n4N73VVlsWuP/8889RP8u58rqZ\n87v7Ofnxxx9tG48xzThx3kJzmOZ7p5z/eruSZSnP/wikmhc9ZEQuhC4W/3Ap5kaU5nPSUIoHC8nj\nprH66ssuUR5/mpt/iB9++GGF11KnGadmzZqZ/uqrr0zzwZWGCryx5sqq8P31m4wQQoho6CEjhBAi\nGrLLRO4kWTYhmyur/VVKe60c4G9ZWceHv61wHPxvMtzGz+H7Qtbm559/XuNrQr/tNGrUyPS33367\n0u+zKrHOOus455xbunRpHR9JviiSEUIIEQ09ZIQQQkRDdpkw0lhL3mpZnlCKcm0/J0TIAqIdU0z2\nWgyKSZ0OHX+azDBqvsYfD4/LWzXOOffll1/W+Pnc3rBhw8TXhKy+kEVWTLZbfaC+2WQeRTJCCCGi\noYeMEEKIaKySdtkaa6xh2hem1YZyylzKu7q8puLK5aGNlmRdJdk1y8PCw7XWWsv0119/nfj5/By+\nd+211zb93Xffma6rTKaQ3cNjTlPEGCq0DO2f48DX+DHkNo4T53Ldddc1/f333ye+ntdQ6Fi22247\n0x988IHpJUuWmC43m7MU1HQP4f83btzYNM/lNddc0/R///vfvA+xaBTJCCGEiIYeMkIIIaJRr+0y\nhprDhg0zff7555tm6M4QlO9l5g37NJVTSF/TsaQphsz6em4PWVebbrqpc865rl272rbevXubnjBh\ngumNNtrI9IYbbmia8zJq1KhEzWOhfUNbJ02RYZ4kWZgcPxYl8rwKHSctxJBFFdJ+Hpxzbuedd3bO\nOTdnzrL+hu+9957pjh07mt5mm21Mt2jRwjSvm+HDh5tetGhR4udPmjTJJZFXkW6l0qFDhxW2ffjh\nh6Zbt25t+sADDzS9yy67mL7rrrtMjx8/3vQ333yT+JmlHltFMkIIIaKhh4wQQoho1Gu77O233za9\nySabmN5///1N0w74+KQ12UQAAA+jSURBVOOPTdOiqQ9FUmmK6khN2WLOFWa10FLs1auX6YEDBzrn\nnNt8880T38fP2WCDDUy3b9/eNDNmaAfQbmIBYYhSZ+EkjS230SIjoSLKVq1amZ47d27iezmG7dq1\nM33SSSeZ9hYlLS/ab++++65pZoUdccQRpseMGWN69uzZphcvXmya35UWKjMEeYw8nvpmkXEeL7nk\nEtMXXXSR6fnz5zvnnHvuuedsG8+RI4880jSvG96revbsafrqq682HbqGS4EiGSGEENHQQ0YIIUQ0\n6p1dxswcFvHRKiHMeqGlVqkWWV6ZI6HiQO6fRa3du3c3PWDAANPebmFreGaF/etf/zK9xRZbmGaG\n01ZbbWWaVssvf/lL06+88orpefPmmaZNUFeFarQ2Qi31Q0WMnMOPPvoo8b0s0uMYnnzyyaaZZbdw\n4ULnXGEmGAst+Znjxo0zfe6555ru16+f6aFDh5qmLcZzJVT0TIusPnPllVeavvDCC01zrD/99FPn\nnHMTJ060bbwn0RbbeOONTR933HGmeU3+8Y9/NM1z/4033jDNTM8s/QezoEhGCCFENPSQEUIIEY16\nZ5eRl19+2TSzZAjD+88++yz6McUmduYIx4sFYYMGDTLNDJe33nrLOVdYADtr1izTDOPZx4pWzpQp\nUxI/n1k4tEY5Bnn1qSuGkA2RtYU9LczQqpbMLuM4s/DSZ13y80P2KLPYOCedO3c2femll5oePXp0\njfvMWhhcqZlmtDHPO+8806Hv6Qsv+/fvb9to83M+ue+WLVuapo3K91L36NHDNK3oadOmmc5zzBXJ\nCCGEiIYeMkIIIaJREXZZlp5T3MYCtBDMqgmFsZVE7L5E3P+OO+5oet999zVNC8xnuLz66quJ+2Pm\nVfPmzU2zqC9kGfhsHOcKbTG2p//iiy9Mjx071vQee+xhupQWY5qW/lmh7cXxbNq0qWkWWPrMSdqH\noRVHd9ttN9PMaOLnsP8cs9i4H44B33vYYYeZfuihh0xXqkVGQsXC66+/vml+z2bNmjnnCm1JXkuP\nPvqo6SeffNL05Zdfnrjv0P2M+wxl9+V5ziqSEUIIEQ09ZIQQQkSjIuyyNG3ZfWhIC4et0UPQfqkP\ndlle7dJDRZdbb7216YMOOihx/6+//rppH47z/2mXsKW/twucKyyGZfYU+9GFsshoB3D77rvv7uoC\n2g1pCjBDhJYJYF849pDjOC9YsGCF4wmd75wHFnQ2bNjQNK22O+64wzTnJPRduf8hQ4Ykvr5S7TKO\n6XXXXWeayySElsjwFvELL7xg22699VbTzH5lG38ukXH22WebZgYa4U8EzPq8+OKLTedp6yqSEUII\nEQ09ZIQQQkSjIuyyNPgslUceeaTG1zJcpb1WqSF6iGK+TygziCss0opiFhctLQ8LxtiPie9jpgt1\nqE08vx/ttVBb83IozMxqkRHOCe2Xvffe2/QOO+yQ+HoWunq7hHba2muvbZrFettuu61pZvw9+OCD\nppm5FrKC+Fm+d5pzhZZOaCXHciGN1clzjJl5IThePrvulltusW0cq9C5z+wyzhfPC54LN9xwg+mr\nrrqqxmMsFkUyQgghoqGHjBBCiGiUrV3GwjwWlb333numWaTHHjw10bZtW9P1zSLLC9obLPBibyyG\n4FzBj1lcvqcYx5n9sJjdxxbkzAykTcN256EW+oQWR11ZZHlBa4kZRUcddZRpjhszyrgEgF8ygBYZ\nM764AudLL71kmlbQvffea5pzQtJYZ7TIYhcSF0vIIuM5xkw/ji/PT2ZucfkE36OP1u96661nmuNG\n+5PzwmU2eK/kUht8L4+R/f/yRJGMEEKIaOghI4QQIhq1tsuOPfZY08w0yQuGpmzpfuqpp5pmVstp\np53mnAsXmDGL6ZNPPsntOCsdjhfDcY4/w3f2VeJSCocffrhpWmreymFI/9hjj5nmvPhW584VZtWw\nHxZJ00o+lBFEG4LHEINibKBQTzHOA+1M2sy0zji2PuuI40HruVu3bqY7dOhgevDgwaa5SmeaY2ch\nJ60jap4jLBgsF/h9CL8bYW89Xlu0bbmKqy+k/fWvf23bQhYW72FTp041zeU3zjnnHNOcxxdffLHG\n/eeJIhkhhBDRqHUkEyN6IQcccIBp/rXz+9//3jRbnPAHrCT4V28xtQrliv8rK+t3419n/MuX48Xt\nkydPNs2IhX9Zd+zY0bSPSPgDLyMj1s906dLF9JgxY0wXEwmEEgLYFTc2WVv98K9ejj3nlrVG//nP\nf0zvv//+ifvhdePXkGcLmtACcFxvnppRR5of/vnXe8htKPfEDH4fJmGwxc/RRx9tmvVirPtiJM+I\n0NfsMepglD1u3DjTbN3ERA3OP+t0eM1dcMEFphnBxooeFckIIYSIhh4yQggholG2dTLsPsrQlF17\naR/UZJcxvCz3fPzaUFsLkGNBm4RWC60lhtRMvLj//vtN84dQb8nwx3uuN9+9e3fTnOeRI0eazroO\nfE2dulf2mtik+VxaURw3bufYz58/3/Tw4cNN04ps3769ad82ht2qaZuwvmbo0KGmaf/Q2gq1/eF4\nh7aHEjOK6VadJ6HO0EwcoV02aNAg0xyvE0880TTrvvheP4+cT373adOmmWZ7pwceeMA06wV5Hb75\n5pumzzrrLNM33niji40iGSGEENHQQ0YIIUQ0ytYuO/TQQ01zHfB+/fqZZuZNko3CrBeGsQyBQ9lH\n9ZmQjRGyBphpxpoMbqelRrtl5syZzrlCS2XLLbc0zfqNrl27mp49e7ZpWjbF2FyVYo2GMvs4V1zA\nauzYsaY5nu3atTPNTMDRo0c75wotL9bG8DP32Wcf05MmTTLNbCVeZ3lZleWSAcrj4HjS/uK80Lan\nPvjgg03ffffdpmmH+ixBbgvZhttss41pWmShDL3bbrvN9D333JP4mlgokhFCCBENPWSEEEJEo2zt\nMi64w8yY7bbbzvTzzz9vunPnzivso3fv3qbZvqFSbJNYhLK1GI5zOzPKPvzwQ9PsZs1uvez46jOY\nWDBGa43ZNSTUfbYYe7OussvSfG5okTjOCW0s2lWvvfaa6V69eplmht7TTz9t2mfxHXTQQbaNNsse\ne+xhmsW3tMVYXJtmLNNkBZY7vIccf/zxplkYy+/DjswcL44j59fbpKHrk9cEC9GZJcgMzYEDB5p+\n6qmnkr9UCVAkI4QQIhp6yAghhIhG2dpl11xzjelOnTqZbtKkiWlmeySx7rrrmq6ksDwGIbsiDcxw\nYeYTu7+y+y87KPsQn0W0e+21l2kWifXt29c0ezbllQFYbgWYoTkJ2ZYce+6TduZbb71lmllHEyZM\nMO0zzWh3ss/VI488YpqLo4UKXkN2YJrvV0nQxkzzPWlp3nnnnaZ5PifNNReQ44J0zL7kzwm04tgN\nnXPOY8kKLe1Qn7qVoUhGCCFENPSQEUIIEY2ytctYkMTCvJ49e5quqTU4F9Va1QlZNmz3TtulRYsW\npkOhNnudhTJmfOjPUJ+WJ+0Y2myvvPJK4mdWOll7r4UKM9mXKjSGLNjkHPqsy1133dW2MXOKPbJo\nv3HfJI0Vm7UvWbn0LiO8PtjrLQSzwdh3jtmS3KfvNffwww/btp122sk055x28g033GCa97zQon5Z\nqY1FRhTJCCGEiIYeMkIIIaJRtnYZLQOGa2yfndTe/6uvvjJdivWry5lQ1g+zZDhGzCJh8ST7YU2Z\nMsU0w37aAaRp06bOucKMGWYy8bjYX4l2QOysMD9Opcg+S9M3jzZwaOVSZvPNnTs38TWcZ1qUv/jF\nL5xzhUV8tNaYlcQVHdNYW2kyAdOMcznaZeSMM84wPXjwYNO0tHj9caVf9oAjL7zwgnPOuTZt2tg2\n2mkcBxZFsyg9lIFYlyiSEUIIEQ09ZIQQQkSjbO0ywrDv1FNPNc2Q2of+p5xySuL7VkVC3z/NKoW0\nbGiLUXP/zLZh2/hjjz3WOVdYPEbr5tVXXzXN1R5p5aSxS0LWYMh2KWUfs9DSCmlez2NmzzdayNwn\n7ZIOHTqYvvLKK037TD8uycCMslAWWSgDjseY1QoLjUe5LMERypxjr77QEhkcF65AyXN74403Np1k\nOfN6oy120kknmeZKm+V4z1MkI4QQIhp6yAghhIhGRdhlzJg599xzTSdZISNGjCjdgdUDGF6zAJaa\nGWhJSyo459xxxx1n+uSTTzbtM9Zov82aNcv02WefbZoZM7RLaBmErLM0yxeEXh+brKtFhl5Pi4zz\nQ6uS/fq4eiPtSn/dMCtt1KhRpmnLheaB12QoizM0JyG7Ns0YlJrQd+D5zD6LHH9maPbp08c0My2J\nL5j9+9//btuYccn5yrr8RV0tc+GcIhkhhBAR0UNGCCFENCrCLttss81Mh1Zs9KFksX12KpWkLJhQ\nWMwiPWYjMez+5JNPTHfs2NE0Vxv905/+ZJor8iVZIyzwO/30002/8847pmlt0Q7IqwdTqfHjHDp+\nzg8zi0I9+UJZXNRcLmHbbbdNfI3fP/vDhQoEiS+sda4wMy3NeRaydLJaiXmS9TN4TtJS/POf/2y6\nf//+pnv06GGaPQL5ubSIn332Wedc4XXFTDQSOqdCNlpd2o+KZIQQQkRDDxkhhBDRqAi7jO3GR44c\nafqOO+4w/fjjjzvnwsVToaLDcin6KhYfDqf5/jUtkbA8M2bMME3rbPz48aZ333130wzlzzrrLOfc\nsvlxrrBPViiMT9MnK83r0xCrd5kfhzQrR4bsj6zZVxMnTjTNYkxmoF177bXOucJCWM5JKDtv/vz5\nia8JWTT8TllXZi2FXZZ1v2nm6Pbbbzf9n//8x/TFF19servttjO9ZMkS074fWjH3pHK8nymSEUII\nEQ09ZIQQQkSjKkvIWFVVVR4VUvWA6urqbP7BSijlvNAaYFtz2lh8jc/2K8d27UnkNS91da2wSJJz\nQqvH26V52VAxrK3l9vlGdXV1t5W8PMt+62Re6mLpghJYjqnmRZGMEEKIaOghI4QQIhoVkV0myoek\noj7nwqF5Fmsgr/A+zX7qspdTEqHsqzTHFnpvKIsyy/cNFe5mHb80dlHWflzlTmjs8iDN+JfDee2c\nIhkhhBAR0UNGCCFENGSXrSLkZUVkXeUxC6FCxTRhP7Oq2O+pGBuqrsh6bKHlGkJ9r7KQ1SLjeeaX\neXBuWRt758LWWX2wyEjMnnvFnL9t2rQxzR6FsVAkI4QQIhp6yAghhIhG1mLMRc65OfEOZ5WhXXV1\ndcu8dqZ5yY3c5kVzkiual/Ik1bxkesgIIYQQWZBdJoQQIhp6yAghhIiGHjJCCCGioYeMEEKIaOgh\nI4QQIhp6yAghhIiGHjJCCCGioYeMEEKIaOghI4QQIhr/H6927paNpD9KAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# -1 indicates final epoch's samples (the last in the list)\n",
"view_samples(-1, samples)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Below I'm showing the generated images as the network was training, every 10 epochs."
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAKhCAYAAACGkQOuAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXe4XFXV/z83NyEJTaoURUBpAiKg\nIL2L9KYiClhp8lJEf1hQbIi9AYJ0lKaCoqggYkMEK91CR5CitEAASSAh9/eHfrJn1r0nU+6ce4f3\nXd/nyXMzM2fO7L3O2ud8V90DQ0NDJBKJRCJRJyaM9wASiUQi8b8f+bBJJBKJRO3Ih00ikUgkakc+\nbBKJRCJRO/Jhk0gkEonakQ+bRCKRSNSOfNgkEolEonbkwyaRSCQStSMfNolEIpGoHRM7OXjChAlD\nEyaU59OcOXMAGBwcBCB2I/C1f/2urwcGBpr+er6qz+P7cRxVx8XPRePx//3XfMA8oCz8LX9j4sSJ\nTa9FlE2VLOLxrb4XUfV+u7JouAZdy8K/6kW3suhULyJGK4te6EWURRxTlE0rWUR9ez6skTiGXt0v\nno+yqLpfxLnXvUbi9yLquF909LBxwJMnT256f8qUKQA89dRTAMw///wAzJo1C4DnnnsOKAKbPXs2\nAPPNNx8ACy20UNN5Hn74YQBe8IIXAPDvf/+76XxO0PM48QUWWACAp59+uum131twwQWbzvfMM88A\n/1F+/98uVDhl4Rick7+hLJ599tkmWbjgoiwcY5TFIossMqIs/H5UtqlTpwIwc+bMJlk4DmU+kiw8\nZyeyAIbJwtfqRbweUS98P+qF53nkkUeA4XrheD2frx2X10BZRP30dxynMhoYGJh7TKey8PpFWTz5\n5JNAuc5VelElC6/rgw8+CMBiiy3WNPYo23gt43WP41h44YWbxqlejEYWVXrRShZV9wvHqIwfeugh\nABZddNGm81bphfB3q+4XVbLo9n7ROOZ27xeO2YdSlV60ul9EWXgeZawsZsyYMeI4lIV65vwnTpzY\ntl6kGy2RSCQStWOgk0acEydOHFpooYXmPtVkKD41fQr6fpVJKKKlsvjiize97+/41BYe71M7mqI+\n7R2XjDaOW5b45JNPMmvWLObMmdO2WTw4ODi0wAILzB3rpEmTmsYWZdHKlRTZuMykSrbxPMoijkO2\nJqNRFp5P2TZaIbNnz+5IFhMnThxacMEFh8nX34zvV7lPRLTWZO/t6oVMNepFK1k4Ps/75JNP9lwW\nVWtExNd+z7+tZCFj9vgqvWi1Rjyfa+SJJ57oeI20qxf+VpV7S3R6v6iSRaf3i7GQhXqhxdJKL5yz\n70e9iFa86NW9s9Gb1a4s0rJJJBKJRO3oyLKZMGHC0JQpU+Y+BfXz6UuXOfq0jD5SmYZ+af2FMfgl\nq/e46dOnN51HhiEL0KfqU/xf//oXUNicrEH4dJYBT506VUbfUcBv8uTJc5mJjGDatGlNY6wKkscA\nnn8j09BX6vvKIsZmoiy8NlEW0b+qLPTVzjfffDz99NM899xzHcsisuZHH30UKNdFWSizGHR0jiIG\nko3V+L5z9XerZKFeKosq/fR7ymLy5Mn8+9//7lgWjWvE62dcwbFUXQ/XgnOMa8a5ukZa6YXX94kn\nngDGfo304n7h56OVRaf3ixhX6YUsnKO6rCwci2OoipvGNRLvF543ysI1p8y9vn4e14hzrtILLZ7J\nkye3LYu0bBKJRCJROzrKRhM+fX26+dqnqRkLPgVjxsM666wDwPXXXw+Up/rrXvc6YPjT2M9f9KIX\nAXD55ZcDsNxyywGFNd5zzz1N41lmmWWAkqEho5Gx6POdb7755rLZTiED0Kfpb8u+Gi0GKLKQSay1\n1loA3HTTTU1z3WqrrYAiS1mcvlJl8Ytf/AKAF7/4xQDcd999QMlW8pq88IUvBIrlpc9W6POdMGFC\nx5k2opUsZIYe53VQL9Zee20AbrzxRqAw0m222QYo16+VXrzkJS8BCku79957m35XWWh5KWPHoywm\nTZo0V8c7RbQM/G2vh3OpWiOvetWrALj22mub5vra1762aczKQllFvfD1Aw88ABT98Nosu+yyQFkj\nURa9WCORDbd7v9BCrpKF9wuttipZxPuFa+Mf//hH03iiLDyv41IWkydP7rksXCNRFjHT1nuna8T3\nt956a2C4VefnSy21FAC/+tWvgOF6cf/99wPV9wv1NXqfJk2aNFfHWyEtm0QikUjUjo4sm4GBAQYH\nB+ey7BivkJGY7x5rPHz/7rvvBgqD3HbbbZu+L3v3Ke7xe+21F1BYov7ONddcE4A777wTKE9pn8qO\nN9ayPPbYY8B/WIVz6UQWjQVr+t6da/T3KgtZlzLTGlMWMlcZhueT3SmLN7/5zcDwWoNXvvKVANx6\n661AYfUynlhM5vkff/xx4D/XoBtZDA4OzmU9fl85KwvZUNQL/czKQj2pkoUWkMxUvYj1OGussQYA\nd911V5Msol7ILqMsJk6cWFn01koWsRZMWbS7RhyzbFpZyIDVo1e/+tUA3H777U2yUO/Ui1e84hVN\nxykL5+o1U9YxBtntGmn8nrLo9H7hulYWWjTqlWtg3XXXbTq+1f2iSi8cb6xl0RKeOHHiqO8XxkLi\nGnEt+Lmy8P7w97//vem1euFY1Qs9Jt4L3/jGNzZ9rvXmGvG+ouXr5/F+4Xi9nwwMDLQti7RsEolE\nIlE7OrZsJk+ePCw7TB99zNVecskl534PCnPYfvvtgfI01oJ52cteBsDKK68MlJjOaqut1vT9JZZY\nAoA3velNANx2220A3HLLLUDxL8pkfJoLz9PIZLthsJMnT57r13WOMd7hb0RZOEaZiexM1q4sXv7y\nlwNwzTXXAEUWWmWeV1lo0fztb38DSszAOcfaFM/jOKdPn15ZF1WFKAvRrl7IrmWsWihRL1ZddVUA\nrrvuOqCwMr9fpRfKxDiVc4564fvGBKZPn961XrS7RvSNa7HENeL10mJVFiuttBJQ1oiycw7KQkar\nRXPzzTcDRS9ixmB8v9ELULcs1AtZtGNQFl4vrTRlEO8Xvh9lseeeewJwxx13AOV+oV7EzDBl4fuO\nczSycI049xgTNHvRv1V6oYy05pZffnkAVl99dQBuuOGGptf+rhZRlIXWoLKIWbWO1/cbZdHu/SIt\nm0QikUjUjq6y0WIPIX2R0Xfn01ff6wYbbACUp6L+Zp+uO+64I1BYucfJ5r/3ve8BxeeqX9HfNcNC\nRiTDkR1eeeWVQMlGkREvtthic9lLp/DJH/s5ReYjQ9Enu9566wFFNrJ4GejOO+8MFFnIMGXzF1xw\nAVBYnnPWWjA7zbmuuOKKQJHFVVddBRTWJvtcbLHF5p6rUygLffNVeqEsjOG85jWvAQqbUzbqxU47\n7QQUWXhclV44JxmXeqG+aB1oQf3mN78BSnyjF7KIayRWxSsb14iycE2oJ77WOtthhx2Awso9Tgb7\n3e9+t+m1czYGYMaVerHRRhsBhc3/+te/bvq80ZvQ7RppJYtYT+Oc1l9//RFfO3f1QmvN+4Vz/8EP\nfgCUNeP4zSRTFr7vGnG8V1xxBTBcFksuueRcuXaKqvtF7BRhHDHeL9T9qBfGvbXm1W1lceGFFwIl\nlhPjU2armcG5ySabAOV+4RpRFlqNiy++eNt6kZZNIpFIJGpHx5bN7Nmzh1XHR+ZqfYsMQfhU1jer\nv1LmIfvacMMNgcLyzznnHKDkkstMfvvb3wKFlem7NavJ930qx06mjX3FOvXBDg0NMWvWrMquzrI1\nffJaJkLGIqN1TjIP/dobb7wxUNjbWWedBcB2220HlLx8Gann06pTFl4zZSZjif2meikLLRz1RPYU\n9UJGqm9dWUS9kIXL3s4++2yg1OHoY7/66qubfkdZmL2mLLTufB37TT399NMdywL+owPKwusY9SLK\nQobr9TPzSl+7FqwyVRYy27hGlMXvfvc7oFzvVVZZBRi+Rjyuao089dRTHWdgtSsL7xceF+tsvF8Y\nT6i6X6gXVbL4/e9/D5RYsTFAs9H8/XhfibJ48sknO5ZFXCMxbiWWXnppoNwvXDvKIna2Npannuol\n0Atw/vnnA7DFFlsA5X6hLByPeqEs1BeP01Iazf0iLZtEIpFI1I6OLJs5c+YwY8aMYQww9nHS7ydD\n0W+oL9x4gr5zLR79gfrgN9tsMwBWWGEFAP74xz8C5Snt+7K8Y489Fhi+V4f+xdjFtbH7bKcZWEND\nQzzzzDNzzxFl4dyNAziGl770pUBhrMYTZBbKwspeffDOWZnJ3rfccsum7yuLT37yk02/E/PjlYUs\nT3bSC1nE3Hz1QlkoI5mlLM3jtURk+erTRRddBAzXiz/84Q9AkZG+d2VxzDHHAMP31TFmFzvaOv6Z\nM2d2LIs5c+bw9NNPD2PDzk29UNd9bdah18cuCMrIMf/zn/8Eil5svvnmTXO2yl4ZqW9xjWg9qm/6\n3as6dHejF8oisuEoC+ekXlTJoup+0aksjB0rC/Ui9m6r0ovRrBHPETeS869rxJiK69p7WpSReqFF\nYixXWXivNYNTT4leIGNBVbIwZqkXyvuF6GSNpGWTSCQSidrRccxmwoQJwzqCxipp/YA+Nc368Okb\n/ZAy2D/96U9Ayfn2vDIZGYs55D6tjcnssssuQMlisno27ung7/u01p/aDaIs4k6YMg+zR/TJ6jOP\n/mnz4PUbG2ew15WykOXZI0nZKQszdYx7WXkc8+ZHkkWnO3WK2BstysLfrtILLSCPN66lRateeK38\nXAtHvZDRav2Z2ef3o49exH52c+bM6VoWsmFlEXeLVRZmWKkXVnCLqjVixXeUhXoRZWEm5q677gqU\n6nn1K8bRol7MmTOnqzUyYcKEYd2UlYm67HVQFuqFY4trxLlae6Zua1lX3S883iwz7xft6oWxn9Hc\nL6pk4ZxixxDjWd7LYm9F5+ocPc4YrjEe63CM5RiLUS922203oNyXlH2sy4v1hBMnTmx7jaRlk0gk\nEona0ZFlM2HCBCZPnjzX5xp3e/Rpp69V9iVTfP3rXw8UNu7TU/+kkCHrU5ddmV9/+OGHA8P3Bvn5\nz38OFB9/VXX/SDUwcW+VVrAiWFnEeFDsJKAsnMsee+wBlG7Pfu7Y494d+pFlV2YhHXHEEUBhzDLq\nSy+9tOl8sbo/7m7YWP/RqSwmTJjA1KlT545VyN7jb8ieol4oC/Ui1g55nY1/VemFsvDa/PSnPwVa\n60X0PXejF8rCsVbphWPwuruWZJiuEWVVJQvXiLJULw477DBg+D4pP/vZz4DCgKu6PvRijXi/iNZ/\nzMiqkoVW2J///GegyMI5e73Ued83vmF22qGHHgoUfYyyMD7qOLQexuJ+oSwaPQtQrCzXqfVVZqVq\njWnxxl1OY7fmv/zlL0C5XzgOZXfZZZcBRS+UpWvaazLSvlztyiItm0QikUjUjo526hwcHByaMmXK\n3Kedvrq4K6FP61j9aubVvvvuC8CPfvQjoFgy5vrvvffeQGGssrqDDz4YKH5rc8xPP/10oDAjn7Qy\nYP3WPq1lC437bXe7I2NVBbBzVxbKxjx4ZWH35p/85CdAYV3GbOxca+xFC+eQQw4BSj8o63NOPPFE\nYHgcRBnq29X6jLKYNWsWM2bM6EgW6oWyUC9kQc49+pn10Zsx43X/8Y9/DLSvF+9+97uBEsNTFqee\neipQGHGUhbKLstAymj17dse7llatEfVCH3pcIzFesc8++wDFQlUvjENFWchkXSNm6Nlr74wzzgBK\nfMNr5ZownuHrGG/rZo0MDg4OTZ06dZheKAtZeez+rSyMV7z1rW8F4JJLLgEKK1cv3vKWtzTJwnV/\n0EEHNcnCLh1nnnkmUOJWjk8Zer9QL3oli5HWSNQLra/YXUNZeD9wj56oF8pCq86MvagX3pNPO+00\noKwRoQxdU/He6TV77rnn2l4jadkkEolEonZ03PV50qRJw3L0fUrrH5Sh+LSWGeh7NVNChiLjsLeV\nT2MZr3nxcb+T6K80E0fmYhW2cFw+nZ3H7Nmzu+p0PDg4ONf32mgZQMlXjxk0/qaMwRoCWbdZa7Jz\ns5NkvMrCuEaUtTI1E+eb3/wmULLchOxdZqXPeNasWV1VzQ8ODs49R9QLfeixClrZGZ9wJ8XY0Va9\nsB7D46wc14qLXRmUqXohu7dTgWhkrNAsi270opM14nVRFsatXCPOQQvFmjXXiIxXBqzlou4rC6+z\nsrAThdX50TvRqzUyceLElrJwjMrC+8Vf//pXoOwuqbWoXthJQFnoLVAWrhGvt7/j71t3oyzs9iF6\nKQvHH9eIc1UWrkv1wxitMRctE+F9Qr0w/mR2o/cT14idKzy/llbV/SJ25o5r5Nlnn80OAolEIpHo\nH3TcQeDZZ5+dm8EQ98uWQejva9zXHsrT3KellosxGJ+Q9v2SUcj+ZRbGLYxz6GuVJbhHjGzObCTP\nF6u755tvvo7rKaxHMa6gLHwts2zsIAzDuz87RmVh/rtjs5urY5eBxD049Gdbgex87A/lazP2lPVI\nsuimN9rs2bPnZlw5Nv3Jzt1sH9maeqEsHINWnHEEZeSeLc6lSi+Mc9iZV9lFvdDv7flGkkWnPbDi\nGlEW6oVrRJ3Vyou1JI7BORqf0NJxjThmj4t7sMQ1UiULGbGfx/XQzRppdb/QqoqycI7GBWL3buuu\nhDqu3mr5xr15zLiKHUVcY8rCjKx4vxCjuV9UrRH1wvuFa8LPhWOOnQGUkdfVMVtfE2XhfUCr0Pls\ntdVWQJGFGZy+jvVFkydPTssmkUgkEv2Drro+61M3c0LG6mufyjIY/ZEf/ehHgZIpoU9Vf6M+eb8n\n9EPbJ8rYjX5D2YBWg3EO2ZqZP2ZUCFnG0NBQx3nz8J+nfdwT3rnKyvQTxxoR+3XZ7cBMOjPslIXn\nca4er79aX6y/qyy8RspYWTjOuHti7P/UKWbPnj1XFsrVMSl/ZeFvqTcf//jHgeF6EfdR9zxaMuqF\n+9rE+p2oF8pKtlalF419wbrVC+WvLJyrv6m1F9fQ0Ucf3TQ3M6aMW2m5xp521l3YMyvWdUW9cI2o\nZ7H2xfM2rsXRyiLO1d+MGXrqzUc+8pGmucT7hXqhjGXzys6+YlEWsZ7G8ygT15xrVYxWL+Z17zRW\no0dEWWj1feITnwBKVmq8X6gXsXN2vF+4RtQH/3p/UsZRL5RF1IuhoaFhu41WIS2bRCKRSNSOjups\nrC2J+5ToL9Yn69PZzqLu+iaDkJnY/0dfqjEdWYMdSn36mqkTMyp8yvv7/o5ZTjIWffgyX9nhE088\nwXPPPcfQ0FDHdTbKwjHrL3YssjY7GdulWZYt+zKzSh+7vnvHaO2BrC/KQjbmXD1OpqIslI2+W2XR\naIWOVhbqhT52/cXKQr3YdNNNm8Yk+zKDRlmoF7Ivs42co3MzA0fZyeI8Tpl7vNZelV70UhbG2tRl\n14jX387EjlkLRVkYX3JuVWvEuZlZpQUl21cvZa6xm4d6EWNNvVgjVbIwduMaURaua606s9CqZOH3\nZOGuEeMhylxrUVmoBx6vnhj3qlMW3jtjZp5rxE7mjklr3wxeZRG7Zpi16nmNc8XdSL3uWliuRWNB\nykbLKXaL70QWadkkEolEonZ0FLMZHBxkgQUWmJv5oK/Op6EsSgZhTr9ZRTIJn772+dl+++2Bkldv\ndondfM0uck8OGfLxxx8PDO+h5FPcp7e+3Jgh5HimTJkyl9W2C3tgCb8vE4i1A8abHJtxAtm6sog9\nkLSEzCqRychcZIVf+tKXANh9992BUh2v7ONulDFDqDFTqF0fbKMsGjvlKgvZs9crWjZWasf9bOxM\nq14oC1mesjDLMOrFcccdBxS9kLEqi7gDY9QL/3ajF1VrRAapPsi2XSPqRcxqjGtEHTcbTWZs1wVl\n4e+4RtQLLRl/T72IspDpOp6pU6fOtVC7lYWyjLKIeuHY1AvHpCycu/cLM7BiZ2O9BZ7/hBNOaJKF\nemHtivcL2btr00ys0dwvqvRCT4T3TPWiao14vdSDuEbcx0YPi2vELDMtIGVhj8bYGVuZx/6X6kA3\nskjLJpFIJBK1o+M6m6effnpupoNPY5/Svu9T2L0SfFobu2msY4Dhfbusio455XH/7AMOOKDpe+7k\nKEOOvnjHGXt3Oe5OZTFjxoy535Wl+Rv6kWXJ7qGhLIxXKAtlqez0mVpzoiz0xcswLr744iZZyEzc\n7VTfsLJwfMok7q7ZjSyGhoaaZBE7BPi+slAvnLOyiJkusT+TMRnPq56oF9aiKAutO/UidtBupRfd\nZBypF37X6+1vKQstBzsFaKEqC69LXCNWksdaElm9+uMa2X///YFi0bRaI1Ev/NsLWTjHeL8wdmOn\nAI/zfhH1wjFrmbhG1C9lE+MV++23H1BkqCw8b4xjOs4oi27vF433Tu8X0SqIeuHctNKEnhN1WV2P\n9VauGWWsXhx44IHA8Htn3FXX87jmYk+3mDk8L6Rlk0gkEona0XE22sSJE+f6MmVd8elmxoNPVZ/K\n+lLtOCpD0bevT16GYT8ombJMxXiFsRz3INd/qT/S42XIsoAYt5CBddLFdWBgYGhwcHCuLPyrT9Un\nv7KQxTtHfa5m5JlPb0WvmTXKwqwkGY1zU7Y/+MEPAPj+978PwDbbbAPAySefDJQYkVZAlIXX0rz5\nTmXRiV5E5qrvXb1wzsa/ol5YWyA7dE7qhd3Ete7sPGBHbI9XLzzvSLLoVC+q1khjTReUWI2WqrEW\n14jXO64RffLqi2vEzEznFrMbXSPGO0466SSg6IXMV0ar/jqPbtfIxIkT58ogykIYm40sXlm4RtRZ\n66TUH6+jeuEa0dJRL5TFhRdeCJT7RStZ9Op+MS+9iL3rXCNmG9rROuqFY1QvfO1xcb8cZWGMzzWi\nXrhGtLCUSezG4bg7kUVaNolEIpGoHV3V2UTox9OH7jEyWfeAN1dc9m6NgYwh9lgzl9zz2kNN37s+\nW/PmffpaNevv+HSW8ciYzdOfPn26nVw7YrAj+StlKDJWZaFPfaeddgJKFoqsOua/+z3Zu6xfWZhB\now/YrJW4s6OV5coi9qGK1fSjqS2JkAVZC+RvKAv1wmxGWZnszuM71Qv919ZpeN4oi6gXWg9m7Eyf\nPr1nsohrxLl53dULr59jNotRRqws1AsZrF4E4xMyZ2M1rhGtA187Z60D9cJrMto10sn9wi7M8X6h\njiqLaDnrNajSC2WnNyHuDRX1ok5ZeL81NqIs4v3CmiNlYQafsvDeqSfF+4B6oMUb+8kpC2WjjL13\nKgv1zzVirdto1khaNolEIpGoHR33RhsaGhrWCVc2LpP1qS178imp/1FWry9WxiBzMfvIXHOfwj51\nfdrKAmX1sobYq02mEvdAN+7RyT7ajZgzZ86wXmL+Ztz3wQpuLYtYMW5VvL53ZeHcZfu+to+Y/mVl\nLauPsjD7yPGaXeJ49W9PmDChq/5ojXrhbzfu5tf4m8pCZmm8Qr3QipNNKQuvs6zPzDstWfVCiyZ2\nxFUWsQ9c3A/euEe3soDhXZPjGlEv1GmZpb53maxV837fPnBe51ibomyVhcxV2Tkf9SbGDFwj/l6j\nXnSzRnp5v1AW3i9k91pvvq6ShXqh7MZTFlVrRJlEWRifirLwfuGaMLssykJrLt4vzMyLstACcjy9\nWCNp2SQSiUSidnQUsxkcHBwaqSI4MkX9hj519dHrAzULxO/HPkH6o92jRTYnm/DpLXOxbkM/ogw2\n7r3g01mmEzuXzpkzp6M9xeeff/5hspAdyWyVhQxGWTjHHXfcESiMQn+0/mv90dbT2D9MJhT7fP3y\nl79s+j2tN1mavl1lodXXGH965plnRiULWXvUC2M3MtMoC/XC3H6tMbOVPM5MGvuHCfVCBmutQmRj\nykJ98vVIsuhGL0ZaI43ZO1D0QustysLsoLhGrCHxODOstHCUWYxbuUYa4w4jyUK90AJvjLl0mqXY\nShbqsDEWZRGvt3oRe5QZj4iykOXLzrVwZfNXXXVVW7JQj3t1v2iUhToes1ddI8YR471TvVAWwuvv\nulcW3jsduxZu1Au/5xqJ9YLeS9WLbtZIWjaJRCKRqB0ddxCYMWPGsD0ZfFrL2vQ/mzcv65bZ+NS1\ng6m+WaGfMe4vEWM2+jNlAfqnZSyxElw24FNZhjR79uyOfbDKItbXRFkYl5C9mfEig9R6M3tEn71M\nwopfYzvKQqtOK84sEdmhMtfai+OKuyb6t1tZzJw5c9geLv6mrE1ZyOodo7JQL6yXiBXkZuB5nZV5\n9M2rF1rW6pGyiN0Sol74d9asWaPWC60qf1NZuEbsjqFeyK6jLKw9cTzKwtiOv+Maka0rc2VhZlWV\nLBp7XjXKotOdKRtl0en9Ql2WXVtPpyysFVEWrhFloexdM7FWxDWiXsT7hVZkr/Xi6aefrtQL5Vu1\nRrSEoiyMd/p9Y7pxDygtmVhDpF5U3TujXozmfpGWTSKRSCRqR0eWzYQJE5g8efKwvjjGBSJjMa/d\np6VPSZmLPlRzx316xp07rRnRErHPmOeLPlXZgcfHHkdaB512bm3EwMBA017ksjbn4NNemVglL6MU\nVbKQgWj9+b5zdW76XGPPLRlUlEXciTHKYmBggE7ieP52oyxijET4m8oi6oUsTln42vO4r4nvx7lF\nWcQ4WNQjZaFeOJ5GWXQK14iWacx8FMrCOJO/rexl3cpCy8fzGK+KtSFaJPYZi2vEucvy61wjURZV\n9wt/07o5ZSFk6Vptvtby8H7hGjGuEO8XXs+oF8oiji/KQuuiW72YMmXKsC4VjRmxMHyNaIU5FnVf\nS0VZeP2M3XicsvB+YLxKxPtF1AvH69rWEmrsAN7u/SItm0QikUjUjq7qbHwK+3STPcUak8bd3ABu\nvfVWoGRYyVhlZz69ZYP6H2OHVBmNzLRxbI2/K0uQHcj+PI/jnDBhQsdsXujfjWw4ykLmIJNxDspC\nC8esM7/n2M0uMj4lk4ldWf392DXY+Xk+WX5ktN2wNqEs4r4nMsMqvfB4r7Oy0a8cLSbra8zQqdKL\nKlmoFzJo2V/s/jw4ONiVXgwNDQ2ThWvEOUSGG9eI3RL8vj3vHI8WsmtEPVIWrq24Rpx71AsZq9Zi\nlEW3a6QTWcS9dKIsvL7eL6oDpZKVAAAgAElEQVRkoR4591ayaMwygyKLqBeNXZ97JQtfx/2mol54\n37BnmvGpeO/UsjXrTFn4e56nShYxa1LZGkuM907H3w7SskkkEolE7RhVbzSfwjIVs05kCjIEj5Nh\nyHR9mvt0NmMrsvW454pMx6e7v+PTNu6TLXwqO06PX2SRRZg2bRqzZs3qujeaT36f9P6NsvA4WVqU\nhWzefHvHXCULGW3MMnJuyl7Lyuvt+aIsFl54YR5//HFmz57ddQ+sWBneSi9kW469U1k4J1mc8Q6t\nuKgXVR0EvGaN/unHH3+8Y71olIXXW/m7Vjwm6q5MVlnI/o1HuEaiFRez3ey1ZUZWlSziGomy8Bot\nuuiiPProo6OSRdX9opUsXCP+bSWLuEaUhXGOqH9eo1ay8LjFFlts1LKIdW/+hsfE61V1v/DeaSZf\ntOLiGon93lqtERHvncqukzWSlk0ikUgkakfHHQTmn3/+YU/6uF913N/ep7U+chmLiLn8ka35NI3W\nQWQHPm0jQ5UdxrhJI+vspjp6ypQpc38r9hqLsvA3I3OpkkXsSeR1UhbK0uNit4TIqGU4js/3Y1W9\nsui0Onrq1KlzxxbZUfRDV+lFzNiKGTH+jXutKEvnEGWhHkQrrl1ZdKoX888//zBZONeoF5G9N3bT\nhWIdVumFayTKIh7nGoksPvYLjLGCsZBF1AvHEjuCuAZ6db/wddSLumTRuEa0FKpiNVVrxPdjfNo1\nEbMH1QtlWXW/iB6QKAvH7RptPL5dWaRlk0gkEona0ZFlMzAw8DBwT33DGVcsPzQ0tGS7B6csClIW\nBSmLgpRFQcqiw4dNIpFIJBLdIN1oiUQikagd+bBJJBKJRO3Ih00ikUgkakc+bBKJRCJRO/Jhk0gk\nEonakQ+bRCKRSNSOfNgkEolEonbkwyaRSCQStSMfNolEIpGoHR1tnjYwMPC/ut3A0NBQ2431UhYF\nKYuClEVByqIgZZGWTSKR6DMMDAyMasfYds/b7e/UMbb/C+h4W+hEIpHoBN6cW/VhrDqu1fc7/bzV\n61bjS3SHtGwSiUQiUTvSskn0HWSQ/o2bqLlJVtx22g2fqhhrdjgfH7Qr91aWiZueibihXNQLNyZz\nQ7H4uX/deKyVhdOP+uOY3R7eubqN9BJLLAHAa17zGgCuuOKKpuNE3O65jrmmZZNIJBKJ2pGWTZ9B\n9iYL+78A56wF4za/L3vZywD4+9//DhQW98IXvhCAadOmNX3fLbo9Tksn+to9XkabGF9UxVC8npF1\nL7300gA89NBDTZ9XbSPu+dzi2Oser79bIs+cObPp/X6waNRZLZWHH34YKDJ6/PHHm4537j/+8Y8B\n2HvvvQE444wzAPjHP/4BwMc//vGm83vfiX97MoeenSmRSCQSiQp0ui30qB7xMowll/zPDqKPPPJI\n0/sykylTpgDlqb3TTjsB8IMf/AAo/sgFFlig6XiZjuj0qTyWefOtMm9awbk//fTTTe97vtGy9zpl\nEX3va621FgCLLbYYAH/605+AwuL0vWvR+HfhhRcG4G9/+xsAjz32GAC77LILAFdddRUAN910E1D0\nQZloQYl5+OqznuK/qEMWMSajhbHMMssAJTYjG/f9yMZXXnlloFg+t9xyCwD33POf3Zi32247AP75\nz38CRS+0gD2fVkOM6UT9qFMvYlxpgw02AODPf/4zUKy5F73oRUDxAhxwwAEAvO51rwPKnNZZZx0A\nTj31VKCsqVe96lXOBYBPfvKTAJx99tlAkWErZJ1NIpFIJPoCY2rZ+JSVqSy66KJAYSarrbYaUJ6m\nq6++OgAXXnghABdccAEAe+yxBwDvfe97AfjLX/7S9DdaNB1kw4wZg63KrHGsyma99dYD4Be/+AUA\nr3zlK4HC7n//+98DJX7h95588klgeNbJeMpCS9W/Qkt31VVXBcrcPM7PtXS22GILANZYYw2gMNEH\nH3wQKHOWnf3hD38A4IEHHgCKRVNl9Y0lg32+oVNZDAwMtMwy0zPhGvC6LLTQQkC53nfffTcAm2yy\nSdNxWiZvf/vbgWL5/PGPfwRKzE89cc2oJ/fdd1/T547X83s/8XdEHXoR7wt6e7Rg9GRMnz4dKDJz\nLi9/+csB+O53vwvAi1/8YgB++tOfAsXi8R6qZfOVr3wFKGvuqaeeGnE8zz777IjjTssmkUgkEn2B\nMclGk5H6lHzLW94CFOa52WabAXDDDTcAsOaaawLlKerTXAbyjW98Ayg++Q033BCA22+/ven4mGc/\nnogZNrK2jTfeuOn9/fbbDyhxize84Q0AfPOb3wQKk5G1iSOOOKLp9Qte8AKgsLjISMYzw0a2tumm\nmwLwxBNPAEUvjOW9+93vBuDee+8FCvNcd911gSIL/ddadcZyTjnlFKCwu5i9Jnvrh2yjTrHUUksB\n8OijjwKFzbtG+mVOI40jxmi8fq6BV7/61UDRC2N5r3jFK4BiwWixet2XXXZZoFjGWr6uBa0D4x7R\n+ldP1Ldo2bTbaWA08LeUhVlld911FzC8tsi/eoE+8IEPAPCd73wHKDEcLRez0m6++WYAdt11V2B4\n/NJ7trFhrcrRIC2bRCKRSNSOWmM2ZoX4NJZ1+dSUafq5jERGs/baawPlaSyT0fK54447mj63SlbE\nyvE2KoR75oONWWXOUb+vMjjhhBOAkmnzxje+sWmMsnRlIguU7fm+fm9lIvvzc+MZMqFWWWq9lIUM\n1jHKILVUzBLafffdgZJV+NKXvhQojNZsRNlfzC7yOOsk/F3Zm5aMPnxlIcYj62ge52kaS7SIzaS6\n8847AXjHO94BwG233QYU61EZ+DfGHTrFaGQRM6xcE7JnsxKFY15llVUAWH755QHYcsstgWLJGIvz\nvFoyWvOeP8ZyDzroIKBYOGatyfI9n2soWjp1xjVjVwOhzGJmpV6B+++/HyiWkFabsvL633rrrQC8\n5z3vAYqXSIvHmJD3qT333BOAk08+uek8ImM2iUQikegL1GLZRAYTfbM+lX1K+1dLx0pfn87W1Vx7\n7bUAXH311UCpjpWhyohltp32xKrDsomxmpVWWgkozOF73/seUFi//udLLrkEKD75d77znUDxnWrd\neV4z+LQGrBT+2te+Bgxnf7GPWEQvZBGvv3P0fZnncsstB5RYzAc/+EGgWDJaxLI0Yzrbb789UHz8\nMmNjNTJV567eKPvIHueRnVa7ZdOqc4TW2Yc//GGgrAkztWTvO+64I1BkZHzil7/8JVDqNYxrdtqx\noheWjXU0WufGVtVFrTezU9V1rbfLL78cKDJ4yUteAhRW7/GuJV9fdNFFQFlD6oF6poWsZaN1qGUT\nq+rrWCPCteIcq75n1pleIOPgm2++OQCHHXYYUPTDWLCyNvbnHJ279+ToJRiN9Z+WTSKRSCRqRy3Z\naNGi8K9PV32kPiV9evv0tGOAcQxzx2WqxjW0fK677jqgMCaZkk/r6JsfSzh3x+Ycjj76aKD0NNpq\nq62AUgUvE5Vt/e53vwPgbW97G1BkaVzMWhR9+bI5rUnHMZY916LFENn0IossAsC73vUuoMx93333\nBeC1r30tUGqMtHi9rlpx3/rWt4BS/WxHAf3N1ibJ1n70ox8Bw2UyFtlGVagag3/VAz+Xze+zzz5A\nqZswUzOumeOPPx4oWWvGesZDH1wLrnuvp1a6Om1NiLr8m9/8BigdIo477jigxCm11rVIjF8deOCB\nQLFkYg+1bbbZBoBzzz0XKGtGfR0LvYhWdbwnapH+9re/BYo3wPtAtEy23XZboMkKA4Zn/nlePSnG\nzf/1r381nV8vRDxfJ0jLJpFIJBK1o9Y6G7NHtFB8Wvt0jH5KexuZD+/TW/Z/6KGHAqW/j0/jyGhk\nRsY7xFh0VI7ZI742q0zLREtElqcf2ayQyy67DIAFF1wQKIzELBJri8y88fvW4xj/kuGYRRJ9xHV2\nPo592mIcS7YkG9eHr4ysDVCPrH9wbsbw3vzmNwMlJqMV4N9o2Sp7Y3xaPDLfsYSZVVpjsmnrr/S9\nR33wup9++ukA/OxnPwPg05/+NFBYvbp+zDHHNH1/rNC4HqpiqMrfWI0WabxPGI9y3TsX9cLYnGvN\n7ER1X6tf685xaCGrf95vHI/nrcOyaXVOP9ez4XVXh42paIFo5ZmZqyUk/L73BTsLfPGLXwTg8MMP\nB4rFo9eoF3tCpWWTSCQSidpRa51NtCSqOhrrP9SHb7+eH/7wh02fmzVyyCGHAMWvWGWxxN9rg0XU\n1tHWuelTtdJXdiajleGaaefczaOXwbgPhd97//vfD5TMLDsKjJAP3/S3Cr3MtKnap8S5mHVk/Y0Z\nVGYTxSxDM/pWXHFFoFiHdr6V6cpQje35vhaVlrbXpMriHcs6G/VEa0yrz/iVWYcyT639k046CSi1\nRH/9618BOPLII4HSncO4WLfoRhatakXUAz0Tzs3OIu5Cqa573PXXXw8Ui0Xd13KJ3eRl6WZg6SUw\n3mG2o3VYWtDzWEM9XyMRsU5KK8yssthFwyzU973vfUDRcX9Ha00vknPzOK37GAMSo8leTcsmkUgk\nErWj1phN9NnH92UgMgh9tWaHyEgis7AaXoYcMy1kTOaqxz1fxhKOzblZC+Br/cQ33ngjUHzzMhY/\ntyPyXnvtBZSMO2Mu1iC86U1vAoos/FxZyN7GIuOqKmajNef1i9fZmhKtO2VgFqP1NMrE+IZ94LR4\nrGGSxcnqlb1sX1lVdbQdS8g8te7MpDP+FGVqfEu2HrtxnHfeeUCJf/YDtNocq3MxnuBc7CihRWrs\n7thjjwWKPjm3uK+Nlq56ZBabHhP1RitBC9nf0+KS7Y9FzEarTl1WN41DWUcTuz1r9ft5tJj0Gjhn\nOweoX2b8uUZi1pnXKGM2iUQikehrjIllU1U7oC/eKuiPfOQjwPDd42RCRx11FFAdo5EZywZ86suc\nx4O5OlZ9ovpcZS52qjabzPobWZ29iuzqGmtD9ENfeeWVTe/LdKJFE2udxgIxC83rITuTSRpbMRYn\nGxPW2dj3zWzDX//6101/rc/QwjEOJpuznkKWZ8ZOP1g2xmis/LZ7r6xfdq/stALPPPNMoMhY2Smr\nOrMOWyGyYXVUPfC169418pOf/AQoMRTXkllmdpbwOhvX0nLxc7/v9d5oo42Asga9/5x22mlNn19z\nzTXA2GQpOjfHJPRgeP/QKvceJ4yteLxrRX3RatMqVD/sNOFeYFtvvTVQ1qL9C3tRi5aWTSKRSCRq\nR62WjU/BqiwfLRGr5WXnPt1jFotMxae0T3PZu8zUHHT93OPJWJ2DufrGGWQOWjbOyQwqLRur57VE\n9MU7Ny0ea07izn5aCTIRs5XGEl7/FVZYASgdaLXazMBy7Fo66oc++bPOOguAc845Byhde9UX41la\nA1pzskAZqxZyqx07xxLWhtnh2No05yQ7l9WbhSaLr9qv6Atf+AIAl156KVCswX7Y78ZYqh1D9GBo\niaoXzs3aIeds9pndEz772c8CpYbEOSsDrUa7L/hXi+jrX/86UDoVuFbGch8b72XKwD15XCvGuYXW\nvNaZFrA67fo3BujnzsXuG2Yvej9xv6zRdAyISMsmkUgkErWj1jobGWXMJotMQT+j77s/jfELq2Jl\n+zIgM3eM/cgKjFcIz98qK63OegpZu4zD7BLZU6zsNUPGqniP9zx+zx5X1h5ZaRwRdwAcy/1svK7x\nOut/1udu3MrrZxaarH+99dYDCrvXl27tiXEM9UdLSCtQ61B/tllxsruqTth16oWWjKzd6/P5z38e\ngPe+971NYzJrSCZaBTsKqE+9Qi9k4Rz9qx543V3nrm8tXXVdz4Xf97p6vHU56pUyMBakrC+44IKm\n76snWgleA8fVzR4uot014j3THXrNTtWy9T4Qu3Bowfi5Gb5+38/NyDMG5Jqz36Sd1LWcfd97q96A\n7PqcSCQSib5ErZZNw/faei1jtY7GTAqZqFlDcX9un+bGO6r2XGiFOhms2SaxtkTInmRt9szSItHK\n8zhZ2+c+9zmgVJArS2UjG5P1x4risdi1VN+7mXBamLJ0r5tQBjGWE3tlmYllrzz1xFiNsQBlJsvT\n763vXxmNh2UTYcaUdVd2V5CBasVba2T1fLRclYk7wZptNFr0smre66DFq/zt6xV1VwvEuRhzkbV7\nvNdd69/uG1rC3i/c+dd6K+Oh3/72t4HC4rUeYo+9XupFrBHU02GvO/v/aWHEOhutMrt9+/k666wD\nFEtJvTDTTl3XC2DndO8TMW4lYhw+LZtEIpFI9AVqyUbzqSwTifU1VR0FYnaIe3GYcRErz2UqcefP\nbnchrBOxSj2yfMfo53Ya0A8dZSRLN5MvMtu4j7qsbCz3bPG31ANlYKacGXq77bYbUNi6mTBm6Fkf\nI4vXd681Z4af1dBaxjJg+0QZm9GCjjtEOs7omx9LGKMTZhla2e31tW+ca0Ar0LkcfPDBwPDdSPsh\nC805aNFqaRibU/f1bLjuY6zW42XhykQ9MT7h2vB6awVsuummQImPOg71zr9x/6067ifx3qg1bo/D\niy++GChdma0lc03ZOcAeiVpAWjJ2mlC31RvjZfvvvz8An/nMZ4AiU++pysrs2G6Qlk0ikUgkakct\nlo0dQ326xswnX+tj9+ls/YVM1q6vMhrPq6/Xug1rVWLHAi2s2D9oLBH3jYl7ZjjmmFkju3OHRS0Y\n8+CtHZDlx7nJSGIfqirWPpaMV1nYB8ouztbL6Hf2fbPNzDL66le/2nQe2VbcP11Z+XnMhlM/tIT6\nEV4XLRf1ZLvttgPKHLzOHr/nnnsCxZrrB4umCq5Pr58s2rVgjYlz9/qaVaa172stFGtLou5rQWv5\nqke+9vuuQS2ZOiyaGAsxPqmuet3dw8f7idfb18b6vv/97wOl9shYjWO3M0X8fT0s7pPl7/m+2Y2j\nQVo2iUQikagdtWSjabHEOIFxiuirPeWUU4Dir5Zp2r/HHRu1lGS8ZujIBmQsV1xxxYjjGo/9bGJ8\nSnYWxyT7ihlY9osyS+QTn/gEUGpOfB0zqbT+jHvF3xsLWTh3WZoV/M5VNma2kHohC7NzgP5l+zSZ\nRRRjMMZsZMpaNspc/7c1CMYCrGGoks1YZqNVIdasGZ9wLspAC9h4Rq/Z+GhkEWtJzDpcf/31gXLd\ntHi9Xxhj0cLxOjt3vQVmpXldtf48j54TWbpWobuYxn2OzMRS5jHLtZeZeXFPH2Ms3iPXXXddoOxW\n6hgcsx0nPI/r36xG16CysrO21qT32n333Rco3gNfn3/++UB1R4HMRkskEolEX6CnMZtY1SoTsILX\n3mcyVmsGZKjWXcjSzKxwfwotGbNRYu+kmDsexzUeqOp4K9v2tQzDuJQ1JPretWz0Q1tzZH8o2Z89\n17QOqzIBx9KHL9O0u4FsTUvHHRe1RGR3/pUBO2Z7XlmDYh8pe6UZx9Ii8nOZrJ/H7KLx1JNWiLE2\nWbd6c+GFFwKl7qofMjCr4HW0riVmH7r+XeeydbMOY1zKfm+XX345UDoFGHfwPqKVrx4YkzEuEWtK\nvK/EvaF6idjF/eSTTwZKNqFZp+7N4/rVCnRMzs09nL70pS8BxSJyV1IzQN/61rcCZc0pk9NPPx0o\n18J7cy/mnpZNIpFIJGpHLTGbuPOi/mW77RrT0Q9odbwsXabr01aWb5zC7CKZy+abb+74gO73Xqgz\nZhNZs+xeC0drT2vNfHer3LX6ZHFmjXiclo3xDJlJZGdek1bMtxeycAzKX0vGOoitttoKgA984ANA\nyUKLVdSyKmOAdue1+7PnVdbq0wEHHACUmIzZSlpKWj4y21ghLvohZtNwfqDI1CxE15xz1DqomlO3\n6EYWUfe1VNRNPR/GZLRM3LHXmJ6eEetn/L4xQGM4X/7yl4HSMdnP7fNlPMTYjPcbj9NadK8Xf2eE\nfbl61icuxlpdz1rvZtxpwVp3Y7cE67DiLsZajdZruaOvcS/XmHOP+uT9wrlXWTgZs0kkEolEX6AW\nyybmw/v0tE7CjqJaJO6TLsN1TFa/mlFhNokWjU9h97mRkXTrr66DwUZWJ/uWjZsVIqPZb7/9gJJx\nFyuKjdmYpWYmjb5a/c6yshEyaNqaXy9loYWjNSdT1FKVacpw49706pN6oLXn9dZS0j9t3Ouqq64C\nSqaOMvS8Vb3QIvrJshFausYj9LXvs88+QLHqeo1eZKMpf614YzNen5133hkoc1x77bWBskbi99QP\n4xHql9dVVm8djdmqrqXI5n0d10wdWYrKJFpV0SugN8j1bRxUq9zP/Z6Wjt6C2BsvWjRmerbRM7Hq\n/bRsEolEIjH+qLXrs09fs05knu5P8+EPfxgoPlyz02Tt5obbK83PG8YD9G73yTr2p4hZYP61s63d\nm82MsceR+fAyD9mbWWhmdrmnuFaDe3+MNhupDlkI9UEYX7CO6l3velfT57Iyj7NK2m69ZuDJ6mRt\nsjXZn+NQlu3u4NoPlo1jV0ZaZWYluVbMQoqV4r1CL+uvYpaXloyxNDuf20nAuixju64NM7XUfbNS\nje0ax/C83keMizgeLRv1ZQRLJr6uzRPi39jJvNOssHgfirHbquxU11LsTFGFtGwSiUQi0RcYk/1s\nRNyzQYtGVi7j8Dh9p77udWZNxFgw2MhQrdzVmtPXLsuSzZtVcu655wIlK834VczEGy3GopuCY467\nD8rSjb2oo/ro9Ue3Yl2t3m83W3E8LRtl5nV/97vf3fS+XXvVp9NOOw0oVfi9Rh0Wr2OP18MuCL5v\nL8S4F5SdQ6677jqgdBIw2yzqUey0Hmtd5hGjia9rs2xiT8V2d9itOp/fj9llcS2IOvYCS8smkUgk\nErVjTC2bfsdYWjZVu5XG/dmtv7FWxNd2U6irUrxOWTjXTv3CVedp1TFihPqIjn6nn2I2Ml4zN62z\n2muvvYBS8V0X6ozlOTctXWM1VZ0doh7FPl/GQWNsyOsf9a9Tz8lY6kW3+xFVWSxxr6/R7neUlk0i\nkUgk+gJp2TRgLC2bVtkhDWNq+ivq3oV0LGRRlQkzWgtntP7niH6wbPoFo+kgUHUd4vUyy0xLxDWi\n5RI7p2uhuIZiDUqMU1TtT9NKT+roIFA3em3BVCEtm0QikUj0BdKyacDzgamMFVIWBSmLgjosmxG+\nN+LxrWI3VVmGVT0TI9q1vJ5Pls1YIS2bRCKRSPQFOt3P5hHgnpZHPT+xfIfHpywKUhYFKYuCR4B7\nusj+G9X7nb7ucjypFwVtyaIjN1oikUgkEt0g3WiJRCKRqB35sEkkEolE7ciHTSKRSCRqRz5sEolE\nIlE78mGTSCQSidqRD5tEIpFI1I582CQSiUSiduTDJpFIJBK1Ix82iUQikagdHbWryWZyBSmLgpRF\nQZUs6mrt3up3ev27qRcFvZBFu1uFtGpO2u71bfV7rT6v+r12ZNFpb7TEKNHpXivtKlO3SpKoB16P\nuJd8vE5xL5YI93LxusXdJt3bJe57FPdF8jzqQTxP3AnU8TTuZjlWulOlq3Xv4TQWiHNYeumlAXjg\ngQeA1nszifj+AgssAMCMGTOavi/UE6/rfPPN1/Q6dsSeMmUKADNnzgRg8cUXB2DatGntTXQEpBst\nkUgkErUj97NpwHjs1FkXRmsup7ukoFNZNLLOqp1X4x4rI/wmUCySpZZaCiiM9GUvexkAV155JfAf\ny2Ok789jnE1/Pb7RkonHPffcc89LvajLIupGL6KFIbRM3F204Tf8ftPrEc4/z89bIVrijs/xaulU\njS/3s0kkEolEXyBjNmOMsfJ7RxYX2V38PGM6vcHAwAATJ04cZmkof+Urc5QxPvPMM02fa9FsscUW\nANx5550A/POf/2z63sILLwzAYostBsC9994LwAorrADAHXfc0fR7UQ+0lPx935fRNr4er1iJYzHO\nJFrp7KKLLgrAkUceCcBRRx0FwOWXXw7Atttu2/vBzgNDQ0PDYneO/d///nfTsVWW5zx2DR3V2Kru\nC47X8VXFkNpBWjaJRCKRqB0Zs2lANz7Y55sl0K7/+vnom68Lo9GLqVOnAvDss896rqa/MRtN5iib\nf/e73w3AOeec0/T65z//OQBf//rXAVhyySUBWHbZZQH46le/CsCOO+4IwAknnADAeeedB8ALXvAC\nAKZPnw6UrCPHEa2IwcFBZs+ePSpZtKt7xi8i228Xfl+Z3H333V2dpxV6cb/wOnvdYywnWjjKTsu3\nKosxQgtWPaz6vvro9Vd/52V5zZkzJ2M2iUQikegP9KVls8giiwCwww47AOWp/I1vfAOozvDxaR39\n5e1iNGx+vGoAquo2lIGfR7939NnLeMTzybKRZa255poA/PnPf+7p+TuRxeDg4NCUKVPmWgrqZJRv\nvG6xnuZFL3oRAA8//DAA888/PwAXXXQRACuuuCJQrvPyy/9nG3jnPnnyZACWWWYZoFz3T37ykwB8\n73vfA4q+aOH4N66lTrKORK/0wuvrnBzTbrvtBsCFF14IwGc/+1kA9tprLwBWWmmlpu8rA18vuOCC\nADz55JNdjasTWUyYMGFo0qRJc/UgrtP4WngdHPtyyy0HwD/+8Q9geGwt6lWM9ahH/k6sr9lggw0A\nuPrqq5vO531CNMYY07JJJBKJRN9gXCybqqe4T9df/epXQPEXvupVrwLKU9iag8cee6wXw5mLbnyw\nWl+XXHJJT8dSlWkjG9M3L6P961//CpQspbvuugsYzkxkVsrS4+P7zwfL5vrrrwdgrbXWAspcL7vs\nMgB23313oMQjZIEy5FgzUIVu9CJW5Pu6SudjXEPdt3J7k002AQpbP/XUUwHYY489gHLdVl55ZQAW\nWmghAHbdddem13/84x8BeNOb3gQUvbCCXdk4Dn31kyZNYtasWcyZM2fM9eLVr341AL/97W+BYsEc\nffTRQHX3BF/L5tWDCI937lbht0InejFp0qShJZZYgkcffbRpbFVZgq26KGy++eYAXHfddQBcccUV\nALzmNa9pmovXPcpCCw0A6eQAACAASURBVNkYoNffv+ussw4A1157LVDduaLh/bRsEolEIjH+6KuY\njf7If/3rX0BhGGbQvOMd7wDaj4tYZW2NQiuMJ5vXNxvrLn79618DZc4vfvGLgdJTyesnk3nkkUeA\nwnx++ctfAsV3HxlTVVZKP1o2L3/5ywFYf/31gRLDi3Bue+65JwDf//73geEZVu2iU1koUxhev9Cq\nNiRmJ5lZ5fXxOvt914i/qc6bffbCF74QKGtLZmtc481vfjMAr3/965vG6e+oh/7mWOhFVTzLWK73\nhxi7jTUgHrfddtsBcPPNNwPD42fx++3eE7uRhV4d0crSjdmJv/nNbwD4zne+A8DOO+8MwBe+8AUA\nbrvtNgAef/xxoNQYvf3tbwdK3dXqq68OwLe//W0A3vjGNwLlulujFK1G9cdro7WYlk0ikUgk+gJ9\n1UHA6mdxxhlnAMXP3Gn1arsWTS/RaVZazJ+XYWjF6YNt1RXY81hb8KUvfQmAr33ta03HxfP42tiA\nPuXxgOztkEMOAeC0004Dit9Yq67dWJ3V9d1aNN1i9uzZXWcnxoyrqi6+8X2Pl71vv/32AJx99tlA\n8cVvuummAHz5y18G4MYbb2z6Xc+rXnj+KVOmNFk5dSLK7E9/+hNQYnPxczOztOqXWGIJAJ544gkA\nHnroIWC4JRQxFjVzMRs0xj6qujkbszM2++CDDwKw7777AiX2tuqqqwLFAvKeqjVn/MvrfdBBBzWN\nx3utMrTLs5+rH9FCawdp2SQSiUSidvSVZSNiZ9t3vvOdQPHBmoVkn6h+quJv1zfv58ZeZAyyt403\n3hgoLF4fvDGcz3zmM0DxxceYjAzGuEarSuPR7FPRK5g5Y5xJ9qVMhO/LXCMblOWfeeaZ9Q12Hmgc\nT7v7F3mc1oOxO4/faqutgMJYtVRjfZXHv/a1rwXKWtFHrz5pLapPMmzPExn3WFuHjVCXZeHvfe97\ngaIXztn4wcEHHwwU6/7vf/87UPrHVSHu4VIHqvRho402AkrGndfB488//3yg3Cc+/OEPA+VeqUfC\n+hi/F+PfsW7n/vvvB4olc8EFFwClviuOM2ZVTpo0qe0uBmnZJBKJRKJ29KVl41P03HPPBWDrrbcG\nSqWv7K+fOxW3u+/ED3/4QwDWXnttoFggztHskmOOOQYoTNb8ePPsI7T6rChvJSvfn2+++bruwDBa\naIVZxWzc4YYbbgCGZ8bI0iNj7XX9VSew63OrDsUxpmNdjRbFu971LqBUx3sdrXuJFeLW32jh+r6y\nsfbIPmH+NWPvu9/9LgD33HMPMDwWOB46EeOMb33rW4HC8q2TiqzbNRFZfFUWmqjTohkcHOQFL3jB\nXN3UihJaNKussgpQ1r3xqPXWWw8oWWheZ9e5MvKvXoIf//jHQIl3fupTnwKKRWS9nrLUEraWUctI\nvRTq33/3OGpLBmnZJBKJRKJ29KVlY274scceCxTmYuaM/ZtaZZeMJWLVctXT3uPsfSX7kjnIIM2L\n15datc9EZMp+/4Mf/CAATz311DzHExl3K/ZXJ9ZYYw2gzFmWFWG9hdlmEdaWjAfsFVW1X1BVLzo/\nVy9korGexuPUGztXfO5znwNKHMusRDMyL730UqDEOazCNxaonsSuv6O1eEfTGV2WrnX2hz/8AShZ\nivG8vjaDS/zkJz8BSqwvxhjGIlbz3HPPMW3atLkWrNfTdeu+RV5X40yHHnooUCr+tWi87i95yUuA\ncn9wTahnXkezEY3FxN56jkPZ2kFAtOq51g76526dSCQSif+16EvL5v3vfz9Q2NZHP/pRoFg0Yrx2\nDhwJ7e4zYQ3JYYcdBsCJJ54IlGwhmY+9zXwtrOy19iB2tJUxGefQ51oVs+mHeJds2g4BsrAqGJ9o\nrNRvxFjVg1RhaGhomB40+rgbIQPVGvM4YzVV9RiydOss/B2Zb9wJ1IwuYwCHH344UHz4dlnYbLPN\ngNJ7TQvsv3vZdCiJ0emXYzcb1ZiNa0e2rSVsPY3xJ2Xlnj9V++NEi2a0++nMC7G3mH+vuuoqoKwF\n62rUAy0Q52jsx+8rC++ZXrfTTz8dgJe+9KVAsZijRWM22yte8Qpg+P3M46v212kHadkkEolEonb0\nlWVjxoy7CIpTTjllPIbTFqLFEC2auN+EvnPjT2ajycJk5fY8+ta3vgWUugmzhWQuZpFceeWVQGGs\nVhgrS3sltTuPsYRzt67KTJy4i6WZM7/73e/meT4zccYLEyZMqLRIfN+5yFRXWGEFoGSJ2avMeiqv\nnzLR4rXDhIzUOJed06NeqT8eb82KWVDq0UgdBLqJaYwmZmNXize84Q1A2d/qbW97G1DmpozUHzOp\n9A7YEbldtBvf7Aaxu7rXU8+G+wy57mMmnTEZvT2+Vj+M4Rinip1FjOmpZ8rMmiQtW3eCFVqZ6rP6\nlNloiUQikegr9JVlo2/Wp65P0Xb3lxhrNLK2aMEImYm+eX2fkeHIOPQXW2Pi/jU/+tGPADj++OOB\n0n1VX6tZJPrkRZVFE1naeMZu/G2rmTfccEMAjjjiCKBkWrV7nvGsdvf3q3aHjPvbbLPNNkCxOIwv\naOXHHRad47rrrguU2I3X3XoN2b2xO7OQZNIy2uiLv+mmm0Yc58yZM8c8ZnPyyScDJd4kW7fmSMvH\nfmDGdIxj+dt2tj7rrLOazq91GK2Hqn2ORrtGBgYG5t4noifkK1/5ClD26Kkaq9fDTN39998fKJax\nMomxHONPWijqjX+1tI1/RcvGccZYTydIyyaRSCQStaOv9rOR3Uefe7QK6kKde3VoschMXvnKVwJw\nwAEHAIVpyjQ+9KEPAcUy+fSnPw3AmmuuCZTaA1mZ2UyjzaDRWqtTFlXV9Ga+xBqEdhGtzF5Za53K\nYsKECZU7LMbuymaPabGqJ3brFtaYHHfccUDplfazn/0MKL5+j4tdNhotFCg7vMpY7ZjsGnOcWs4D\nAwNt7zXfKIt2j4XhNUj33XcfUFi2c7ZDgHGnW2+9FYBtt90WGF7t7px8311KL7744qbjquKuVRiN\nXrifkNlmxqWMmWmpVq2BTjvgV2WhKmt/T5kKP/eebLabseDp06e3fb9IyyaRSCQStaMvLJtWYzDj\nwtoS+4KZcdPDcXS813zDdzv6LX2n++yzT9P73/zmN5vO557y+qtlpLI1e1uZ1dZt7VGcy3js1Km/\neL/99gOKX7qVhaOV4PFageNl2Yz0vnOQXbuTqmxdi8RsoNVWWw0osrDjsWzf+ISs3roYLWG//4tf\n/AIoFo2+f7uKGyezYtzKdOs41ItVVlmFu+++mxkzZtSmFzFO5GutLmXnHLwfmJHXCq4NMwCtPZGl\nm8FZ106djVmKQmvO9+19Zi80YzDGqXxfeF29n1StlTgn7x/+rtltxo5aWXfeh+677z4z0tKySSQS\nicT4Y1yz0ewHFJ+6MplPfOITQGGu9vPRvx39i2ONDq3Cpu/ISKzwrYpjyFSr+n3J7nrVTaGXWWmd\n1iV43e3bJfv6/Oc/P+L5fO2uk9dccw1QGHC7vvdeY2BgYFgvKWMgsSremMhOO+0EwK677gqU/Uqs\nm4hxKHdgdH8bWbqWipZL7CRh9ptxEGOFWlZxB0bHfdttt9XWscPraMacc1YPHJMyPeecc4DiFTjp\npJOA4vGoimf4fbtw2ItPr4B96eqqOZszZ86wfYgck7ERd+r1HmcmnRm66snuu+8OFCvPWiOvszL0\n92KmpvoTfz/2xvNz9dIebepZdhBIJBKJRF9hXGM25rPHjrhbbrklUDIzhE9R+zhZZd0rdOqDnThx\nYm3sOfrQzVqK+9noqx8tRqi7GfOYTRW0cMywkm2pP3a4bndX0k7RjV5UWapm9TgXY3QyVmMlZivq\nG9ci8v1ddtkFgFtuuQUoWYj2DTO2I1O2FkVYt2X9TtwDqLFzABTvQh16YQaeXTWcs9a8e7bE/Yu8\nXzhXx2ycI9YmxWsie4/WnHU9WspV6CbGG++3/nbsped11XvTIP8Rz6+stFhid3D7DVqP49y9vlo2\nsS4s/l60GjvJUkzLJpFIJBK1o1bLxqdglQ/dp7W+WhlN1dNU/6RsIHaBrvp9z2e2k7GBiG5YW6/9\nu55P5moevgxFFlclq9FicHCw7ewSUZdloyzMErK/k5aMmTNaPnV1QRhNPYW6Lxt3DegDlz1rldkZ\nwF5VO+64IwB33HEHUNi9FpI7vMpIXSO33347UDpL6CXwOK1CrQMztMzM0vKS8f43Q7FWvdD6M/vU\nsdoN/MADDwRKhwljusZw7J1mHNN6HNd93P8odv2IrL3KImr4vGNZeO9SZ+NeOl5X92zSUmkFrTh3\nM/avMUGttVa72EYLK85d/dCSHhoaymy0RCKRSPQPas1G86loRot9f8y00Y9oxkUVM/X92LOo1d4K\nVVluvcJoOtqOdK5GaNnINP7f//t/QPUuhb1CP+xvE2H3XrOItOr0Z1977bXjM7AKNNZTxJ02ZaDW\nv1jF7h4906ZNA0rsxZiOmVLGdswy01cf+8HJPLVwYo88P49rSEYs427sTtxtLMzMqNi3L8Lfijt0\n+n33gorxBfvBRSvATDvjnfb/Un9a3S9avd8pBgYG5l5/vTKxk7byj9en3TEa47VnmjKqsmi0tMxe\ndFx2D4/WnZ9rFeZOnYlEIpHoK4xpNprV8LI3GYpP8/HGaPzRrXbobBfGaPTpy0xkdWeeeaZjHdXv\ntEI/xGz0ydslwYwqGa8sqx9lEetitBQ23XRToNS1yCBl27Ei3L3orSDfaKONALj66quBsvOiXgLr\nd7SkPJ/xEPXT8clsYxfyWK0/c+ZMd+scd73oFrGGpKpGJNYiVWE0Md6YgWuMrFNddk6eZ7fddgOK\nxWwvs7ivkhmA/l5VHDzq8WiyFNOySSQSiUTtGBPLJvY6Gu1+I3VV+I6GtbUaU9XnkZnIUM2ckYnq\nc9X/7Hn8ngy2V7IZTwZrBpaV3eqNsjGOcdRRR8VxAOOvF2b0wfB+XzLF5ZZbDiiZVVazuwulvn0r\nwt3X6Pe//z1QMvHMMjLbTAtI1l7F3qOv3XHZieDOO+8EimUjQ65DL8y8Mq7UKy+BUE/UJ9eS+tSt\nvvSizqbh86a/VddNPfA4rfy9994bKF3h7bFmPZX1eB5nl2n3PTr77LOB4TLXgoldw+MOwGnZJBKJ\nRKIv0BddnztFzFXvFcaCzceeWWYTmZ0kw43M0x0czeTTxysz0bff7TgixkIWke1rDdh3SStOyLq8\n/rI8uy2cd955QMle6hW6sWyUa1XdQmSMZpvpM3eXShmqlsXf/vY3oMjG62hGXtUuk/MYL1AsqVip\n3lgv1E39VTcZm6Nd38bBZO/W21jDpJ7YmzFmhLWL0cRs1Itu5+h1N0Z3yimnNH2uRayemc36xS9+\nESiy0DI55phjADj88MObxmc3hqqO2GYpzpkzJy2bRCKRSIw/nheWjQxW1lZX99lesvkqyyHuN+FO\nnSeeeOKIx3l9TjjhBKBUzxurMR9fq6Cf9nDpFLK+I488EijX3ddaQO7t8u1vfxsorN4sIi2jXqET\nWUyYMGFo4sSJcxlrjCPJGKPFE3tSNfz2iK9jDZuxlVYV4hEx2yhamY293UbbWaKumJp7Amn1a9no\nJbCHolmNsvSf/vSnwPAOAnXtZzMwMFDZTSWu9ziGGPtzbfi+HSA8vxaqVp0elA022KDpc61IM4Kr\n9M/sNbMWo0WWMZtEIpFI9AWeF5bNWGE0O++1y4q0SPS5W/Vsz7MYp7Br73e/+912h9YTjIdlY1bS\nW97yFgCOO+44oLA1ZRe79srqZWu9RjeyiBZs3MckWjLtWutV+5N0ysodX6y/qYqj9cKyEXvssQdQ\n9kbpFWJGlxlTxsF67RHpxrKp8njE7uBV7zs3rXjrrKzbeuKJJwC45557OphJ0SvhWosxvKqsubRs\nEolEItEXSMumAXWw+chkIjNQ/sYlzBbRN6pPvqo2qdW+E2NVQ9DVj7SJFf+7Q2unGXe9QjcMdoRz\nAK276rZx/qa/snd97tFSqYr5tNqrfqSYQbv7ljSMNe8X/0X0hETLseG4qt9qem1fQOuqjKkY1+50\n3ZuN6O8bC65C4zjb7Qaelk0ikUgkakdaNg3oBWtrVb8SISPRN2pFsPtQRCbaKrutV37pZLAFvegg\n0CqrLL6OaLeqvkpPqph0jAV4/ljV30/7HNWNVtbm/PPPz8yZM3nuuec6tmziuassyaoxxOsVr3fU\nu8au3Y3ns0OJNUaxPsvvV9UDNfZUyzqbRCKRSPQNOrVsHgY6S3N4/mD5oaGhJds9OGVRkLIoSFkU\npCwKUhYdPmwSiUQikegG6UZLJBKJRO3Ih00ikUgkakc+bBKJRCJRO/Jhk0gkEonakQ+bRCKRSNSO\nfNgkEolEonbkwyaRSCQStSMfNolEIpGoHfmwSSQSiUTtmNj6kILna2O9dvF/oclgu0hZFIznFtmd\nbj1Qd0eQ1IuClEVBbjFQIwYGBuZ2UoX/dEeNu91VfW+kzr5V77dCu79bNxrHvvTSS7P00kt39N1u\n5l4XJkyYULnfSztwr/nBwcG259bqN1vpzX/3FJn7vr/fLfrtmvxvQKM8R3t9no/Ih00ikUgkakfu\nZ9OAOs3iqn1L+q0Raif7U4hOZdHpnj/jjW70otUcZbVe/7iTa9QLd1J035F2rQ7P446e06dPj+Md\n8fiIBuspXUf/xf9lWYywL0+60RKJRCIx/kjLpgGj2VO8jeP9DWDs2X38vXntBDjee81Xjc33466D\n7k5o7OrZZ5/t5XA6loVWQDtodwfOEX4HgEUXXRQoFo/nWWihhYCy0+a8LJZ5fd54XFo2zUhZFKRl\nk0gkEom+QFo2DRiNZdOKIbZi674fM1SWWmopAKZMmQLAv//9b6Cw9yeffLLpeFl+t7GgbhlsJ2y+\nClpfkydPBmCBBRYAYMEFFwRg3XXXBeDII48E4MEHH2z6/r777gsUdh//dju+0TDYdi3Ydi0MLaG3\nve1tALz5zW9uOv/FF18MwIUXXggUvfnnP/8JFP2IehtRFVtMNl+QsihIyyaRSCQSfYHnhWUT2ZfM\nd+bMmT39nfFgKjJV5yQ+/vGPA4WJbrjhhgC8+tWvBuDPf/4zUBjqpz/9aQAuu+wyYHg8o9Pst7GU\nRawT+tOf/gTAj3/8YwA+8IEPNB3nnJ944gkAfvWrXwHwyCOPAHDzzTcDcO655wLFsomZWP0oi4bz\njPj34IMPBmDzzTcH4GUvexkAyyyzDADf+973gHLdTz75ZAAeeughAKZNmwYUCzpaXH6vCsnmC54P\nsjCLUe/AM8880/S3V/fQtGwSiUQi0RcY/9LzeWCrrbYCYI899gBg//33B2DttdcGCoPtB3TbXuSF\nL3whUOogvv71rwOw1lprAYWByPZlIquvvjpQso1e97rXAfCvf/0LgAceeACAhx9+GIBZs2Z1Pqma\nUFUp/8pXvhIoYzc2I5yD7Pupp54CYP311wdgxowZQInt/PCHP2w6X7/WNo0ELQ+tube//e0AbLbZ\nZgBssskmANx7771AsVx++ctfAnD33XcDcM899wCwzTbbAPDrX/8aKLLTsnk+yCTCeJR6seaaawLw\nt7/9ren9/0tQx43lutZ8/w9/+AMAZ5xxBgB33nknAH/84x+Bsrb8XitLtxOkZZNIJBKJ2tGXlo2+\n9je+8Y0AzDfffE2fH3TQQQAcfvjhYzuweaDT+pmG7B6gsLRVV1216TjrJfTRG3/Q4rn//vsBeMMb\n3gAUdvezn/0MgJNOOgkoTKfdivU6UZUJtfXWWwMl004rTXa+/PLLA3D00UcDZY7W3bz2ta8F4OUv\nfzkAH/vYxwD4whe+AMBf//pXYHxYfKdyVh+0cJRFtIS1eD/0oQ8BxdIxa1F9/MUvfgEU2Y82a7Ef\nEC1crUAtmh122AGAK664YuwHVzNiLM975GOPPTbi+8pkueWWA8qa2WKLLYAS79Qi7rTuqx2kZZNI\nJBKJ2jGulo2s3fjEVVddBZS4hE/jaNnceOONYzXEjtFuRwCZhQz1rW99K1CyR/xcli/zOPvss5ve\n1xevzIxXmH1ihflHP/rRpu/1U38yGalzk5VZZ3P88ccDJd4ga48W0m9/+1sAjjrqKABe9KIXASV2\noy9fjCWrb/e3tGS0XFdYYQUAPvjBDwLl+srqr7zySgD+/ve/A6WTgNfXv8q4lQ/++RDXmjp1KlAd\nlxDqgTLqB10fLdZZZx0A3vOe9wBw0003AfD5z38eKHM0TmlGpxmb3//+94HiBfD+8MUvfhEoXiNl\nG+v4RoO0bBKJRCJRO/qizkYWLzORhd13331AefqKW265BSi++V5hNHnzsnCZZZVcZa4veclLgJJx\ntddeewHF0pFRnH766UDxuVuPo8ysv/Gv47j99tsB+PCHPwzASiutBMDll18OlPjIT3/6U6Cww4Zq\n+55XzcfuCMrI673tttsChc1fcMEFQLHqYpwrQkvmrrvuAoqMZH9mcHmN2mW63chCXXbO7frAHbNj\nPeCAA4ASvxTG4r761a8CxdfunDyP+uDva9mYuRfRyuLth555n/jEJwA44ogjgGLpRP2yJu2OO+4A\nhtdZjRZ1yiJeh1gns+KKKwJl7h6vt8jY7TnnnAOUuFbMgv3a174GwC677ALAqaeeChTLqV29zTqb\nRCKRSPQF+iIbbffddwdK9bMMRTZuDYHvr7baak2ve5kL3i2MI1RBRiED0fdupsy73vUuoLBu89+1\n4n7zm98AJX6ltSezkbkstthiAGy00UZAqUlafPHFAebuoKlFI3PqpT+76lzxOikTs8x+//vfA8Wi\ntUNAu33FfvCDHwDDLWVlJSscC9+91le33Zyd+2677QaUMatn6r6++djLzGy2dro5jzTukY4brziO\na0Y27phdI2Zwen3tmuD73j+UaT/HoyKcq7FcY67Ofc899wTK2tGK876hBeua2G+//YDSU2/jjTcG\nShajvfXqQFo2iUQikagdfWHZ2KFWyFCOPfZYoNrX3w8WTafYYIMNgNIdwdf6k41byFBkMjJbLRsZ\ni3UW+uyVlZl8//M//wOUyuEtt9wSgG9961tN59e338pCaweddjA2o86sMfu+dXp9td78Xa1ELWat\njH7OuPI6nHfeecDwHT1vvfVWoGQXqRd+T5kZv/K19VjRAmoVo1lllVUAuO2220Y5s87hGLVU3v/+\n9wPwuc99Dihzc03YSeLQQw8FSrxytF2/xwMxnhkzNI3pXnrppU2fa8G4jo3haCGbdRazE+0Kbu1a\nu+hkT6+0bBKJRCJRO/rCsomMY+GFFwbgne9854jHf+UrX6l9TL2CTMO/WjL2edOfbPaY9TKyhVgV\nbWxGRqqv9R//+AdQspbe8Y53AMV3/9KXvhQo3aGN9WjZ9MKiEe0ySONLZshpiXRq0cT4lUzWGoNj\njjkGGM7iYy1KL6umu40nOhdlE3tUmY3odZfp+r7X+VOf+hQAH/nIR4CSzaQV8Je//AUY3vU3Wj7j\nYdHEsdgvMGaTmZWmrKy/83s777wzACeccEL9g+0x4nXwPuF9RF01LqUeaMmYvaonQxmqJ37fnmjG\nbjpFJ/HPtGwSiUQiUTv6wrKJ0B+phSN8iuqD72fISBzzEkssARR/shaFlotM0y7OxmRktjIamYnZ\nKTHDRgtIGcpkrT1ZeeWVAbj++ut7M9EGtLtbaWRXjz76aNPY43mUgdaCLG7JJZcE4LDDDgOKLO2l\npmUjI/ZaxDhIHX2gOrVonLPX3TnGDLrtt98eKHVar3nNa4AyB7tDqx/f+MY3ALjkkkuAYhFZZ2Xl\n+Qg7cnY0/jqgVW4ML45JGegBMU4lrFXS8jFzr59QtWasIXTMrg3/qsNaPN4Tzex1vXvfEeqRnpDX\nv/71vZpKS6Rlk0gkEona0VeWjSzcbs6yQ5/i7jFvD6x+hkxFi0T2bcaU7D72rjLuED+XucZuvpGJ\nulPnZz/7WaCwQy0a8++1rCJGU0/RyqIRxgmUzSKLLAKUzsax/kY2pgy0Dv2eLN49Om644Qag1N3E\nDrnqU5UMeoF261fi8bFL86te9Sqg1FW4M6fxLa+vccwzzzyz6XsxO8l6DGVWVWc1UnxrrHuLxa4H\nQllZh2fGZYTjtRNyt6gze7HqnF5vEWN3jsksM9fCPvvsA5QYXYxPWpdjPU23dWDdyCItm0QikUjU\njr6ybOxlZMZU3HXO2pDnE2Qisb+XTOO6664DSn67x+ubjTspKhNjO74vU/3ABz4AlE4BnifGLaoY\nSrfsbV4WUXw/doiIu0a++MUvBmC77bYDis9dBhvrad73vvcBsNNOOwGlO4L9o7TmRhrzSOPrBTo9\np8fb08oeeVr79ndbb731gOJzN/Zy4oknAuW6G+tR1laOb7rppgB85jOfAYolHXv6RStmPDomx+4Y\n8X3nrH5EuH/RaGNyYxm/Uie1up1r3HXU+4SZnMb4XP96SvQimKXq97qtURyNLNKySSQSiUTt6CvL\nxqp5Wb/szH3XO+2gO5bQZ6rFIUMxY8bq+Pe+971AYaxmYl199dXA8GyTeXTfbfqdaDFpSdlPSgak\nNRFrEkaLeZ0n+v9jDYdV6ksttRRQ6iOsEZHdGX+ImXdWx7tnjzI1BhR3Q42yrXPXSq+zTLWVRXnN\nNdcAxTrTwjF+JZv3fFo4Wq7OxU4DBx54IFDmbvzC/nOxm3BcW421SGO97vRoOHZl554uWoGuuZjl\nqN50e13jtasTVXpR1Z1baPXZScAu8ur4RRddBJS9nMxG7FQmWkqj0YG0bBKJRCJRO/rKsrGGIHau\nNftIltaPiBaNMZRp06YBJbvICt/IQJ2rFomsvd0Mr2WWWQYo2Sn67q3fsaLc8YyFHzrWGgkZp9XN\nVs1rofi5tQOveMUrgMKqYjaZfZ1kX84xMlO/XxUPqwPR114FZaWP/ctf/jIAZ511FlD0K3YMUF+q\nYnjK7sEHHwTKaeg7CAAAIABJREFUviXuyGidRtQnUUdX8E6hTLzuMRs17uGjHpiB1+31HQuLRnRr\naXj9jFtpubqGtHxjFlunv9cLqzYtm0QikUjUjr7YqbPh/MDwGgIZhj5a+4j1GnXsvCcTdc9va0Fk\nJlYI27FWFhcZcdzF1Iws2bv7rOvbf/jhh4HCaHfYYQeg+OpbXfc6ZKH/X9a9xhprAKVfnDUk1oLI\n2uwkYQ2Ru1eatbbssssC8LGPfQwovn5laofktdZaCyjdE/SHj4UsWvm8lY36ooxiDyxjbfZA04K1\nel6rzv2S7JTsWvrgBz8IlB0aXWvtYjx36qyCFvAee+zR9L7XV1m2QqesfzxkoX54T9RiMbanlef6\n/9CHPgSUnXzf8IY39GIYw5A7dSYSiUSiL9BXMZtDDjkEGL7LoH7nuiyabtFYW1LFiuzfpVXm3GSs\n1157LVDYuww4+uD1wWq52PdJC0hLR6bqDqBmoWjh9MNeLrHrgXEEM2fcidUqan30xqWsTTLGo16Y\naWMMSNZnBqDZjnYYWG655Zq+1yuZjFRzVJXlFV97fc3Us7eV1pp7/2gpi6hfxuqMZ7kHjNahbL9T\ny6afoC5bOyT0Dpjd2C7qXhOj6c7hfSF6fbyO1iia9Wp2q5bwqaee2uWoe4e0bBKJRCJRO/oiZqMf\n0swJMytkplVVtL3GaHywVRaD9TdmoWlx+L6M1up4Yziy7xVWWAEozMXsI7v9Whnu+Y3JyIBl/7Gm\nZB7zYmhoqBZ/tOzMGItxJK06d1bUCrNe5qijjgJKjZCdAbSEPF72bycBe+y574mZf3bUtTOuVkDD\nfIAmC6xrWbhPiEwzwuuvNWecwdfqvtffuVmbZMxOC8YMLBmuslUGxnT8nXZ7uNkbrZ9iNlo0rinn\nYn8410ZdGEtZxB6K6sHee+8NlJieemGNmTKyE3pdyJhNIpFIJPoCfWHZ2APLfdf1uWvx6IOt26fa\nKVPppBOuloj1Eeeffz5QYi0yTWsF3HddZqJVp2zMPjLrxLiEtQiyvf/P3pnHXTfW+//9POZ5zpTM\nJRkiY5KhzKWQ+WigOqco6aSkpAzRSSEy5JAh0qlwSiRDIUpkyFyEREhI5EjH8/vj19t17+99r2dP\na917PZ3v+/V6Xvez9157rXVd61p7fT/Xd7jieje9+myG6Ytux1DV6YO5/vrrgWK9xZp41j6LkXhG\n4BiJp6pTBahYYqVslZDv60+ZTrWGxixYFanX1z7RUrVOoOemb8Zx5By+1/mMM84Axq9uaV/2WhNr\nOpUOWqNsvJ5GZumD8/o2nRvUT19MnTp12iyzzDJ07o5t9rfS8eLvgn+NPnNs2ydNkcomSZIkaQUj\njUbTitdai9VbrevV9HzjoIy1nOKaKXEdCa1sI2RUbdY2cm5ey1NrXsvE/eqzOeWUU4CyjokWqH6O\nyV5xcaK+iGrKv3Et+csuuwwoVprzziqV/fbbD4AzzzwTKDkkWvFmTTtO7AP/xooDscpD3Wv7TPS9\n6Bvxtdc/Wul33nknUPIivEeOOeaYju1URuaY6JdS8fTqq5OqfKBhIqmaRvXnDIjXNVaLHiXTpk3r\nGGfe/6rrfvYDpc366hz7Xn/Hy3XXXTfEWddLKpskSZKkcUbqs9lll12AYpmaAyBGVGjxNk2TWfP2\ns34GKxub5a4FaxVet4/rUuy2225A8XM0Veusib6ICsdzNrN/o402AkrdrpNPPhko1pnWW1Qi9k1c\nkyVWmx6UOvpCdVW16mTsE1W/ilffnRFW+q1UzN/4xjeAMi48TtV6SFXKy/djZew6IvPqxr657777\ngBJ552qUF154YZOHr6UvqsZorOsXoxatDr7XXnsBJdrQcXP11VcDsOeeewLNVjb/x37TZ5MkSZKM\nnpEqG60nM8W1VPTVHHfccUCp76QF2xRN5NlIVDjR0nSe2dwT5+JdbdBKA35v0JX2qizsSJMWbKzz\nZiRWjEaz9pn5V1U5IYNaa23oi17Vl23Xco1+qBgJqGXsPTPo+Iy0Qdk4bsTcNHOaVMAxL6+Nircb\nXkfH6Dvf+U4A9thjD6BUCHEtJ9fP8vfEfL24Lo59MOjvSCSVTZIkSdIKWpFnI87Rf+ADHwAmfw2N\nOi2VNtQgm4hoFVZVIW6DBdsWJkPl9TpOelVjg44/v1dl+bZpXGy88cZAySmbbJrMy5vOfjr+ur+V\nV14ZKFGMk/27k8omSZIkaQWtUjajZhCrrSkF0/R+pc1z822hDX1R93gYIs9j5H3RFtrQF3X5n4Yl\nlU2SJEnSClq1ns2MxvQyxYe1QPvdr5F8Mepk2P3+X6ZNWfOD+l6MSooKppuiMR/Mag8zzTRTbZFL\nSX2MWtH0QyqbJEmSpHH6VTaPA+0sVDY8S/e5/ePTpk0b1xcNZuhO9/NuiqbP/fbdF/wTjot/9M0M\n2Rde1359MhLr1/1D1cyQfdEQ2ReFnvqirwCBJEmSJBmEnEZLkiRJGicfNkmSJEnj5MMmSZIkaZx8\n2CRJkiSNkw+bJEmSpHHyYZMkSZI0Tj5skiRJksbJh02SJEnSOPmwSZIkSRqnr3I1WTK8kH1RyL4o\n1N0XwxZKrfp+r4uwRXJcFLIvCrnEQAuZOnXqS2tQNLF90i6mTJnS8a+Kqus822yzMdtssw18/Jln\nnpmZZ5553PHnm2++lyo7N023tsfPq7bv9/26zi+ph1w8bQxNWCrRsuzXUnUZ56rlm6uOMyxptRX6\n6YvZZ5992tJLL82vf/3rnrZ3CYC5554bgMcee2y623udXVLir3/964SfdxtvVe/Hxbg8v+eee45p\n06b1PS6GWaah7oXB6rpHXN4575FCKpskSZKkFaSyGcMglkpd1pcKJs6hzzLLLAD87W9/62t/WnEr\nrLACAL/5zW+me1yVU1pt4xmkL1QEUXlMsL3H6Hg95tgd71cpmn6JPpt4XMf12M8HUTZj9z2soph1\n1lmBzrEKsOaaawJwww03dGzf6z0Z72FV5jPPPDPh58P0xT8rqWySJEmSVpDLQg9JXVFCH/3oRwHY\nfvvtAXjjG98I9K9o4nm9/OUvB4qyiceNvqA2LzOrhbnpppsCcNlll/W0/ViLFCZnCez/+Z//6Wm7\nKl+K57zgggsCsO+++wLw2c9+tmO7qv10Y+GFFwbg0UcfnfD7dS4BXVd/b7XVVgBceeWVQDlH/6ri\n77nnno7v2VequXnnnReAJ598csLjqGhkFONnWNp4rqlskiRJksZJn80YhpmD7deS0OrWZ+LfhRZa\nCIBHHnmkY3/dotF6pVeLuA3z0Z6rfaVl+8ILLwBw5513AqUNWqpapuuuuy4A11133VDnMUxf6Geo\nUqgx3HnrrbcG4E1vehMA73//+4Hiq3n++eeBYqV/5CMfAeCOO+4A4Nprr+04rr6daJ2PaVvH+92i\n00YxLvRbLrPMMgAsvvjiQOmT+eefH4BFFlkEgOuvvx6AddZZB4DzzjsPKG3Yb7/9gKIS7dOo6u2L\nqmvYhntkguMAxWfovWJfqWjvvfdeoPdo126kzyZJkiRpBa1WNjvttBMA3/nOd4BiwTz11FNA/f6F\nfiyVmWaaadrss89eGRWkBfH4449Pdz9ajlpb73vf+wA48sgjATj//POBYrFoXWmNDTq3rqXz3HPP\nTfh5E1Zbv1nrCyywAFCstB//+McArLjiikDxc5100klAaUubc4623XZboPSB/getZ9usde6Y75Z0\nqAV7//33A7DDDjsA8OyzzwLwwAMPALyUyLnYYosBRRG5fy1d7614rSZT/Uu00pdcckkAXve61wGl\nzSoZ93/XXXcBcNtttwHw9NNPd+x3iSWWAIr6M3n297//PdA9ErSJe2T22WcHevf5eY72jePo5ptv\nBmC33XYDiur/wx/+0LH9ZN4jqWySJEmSxmmlsll00UUB2GuvvQA45JBDgKICtDScu62KKumXJudg\no/9ho402AuAd73gHUBSNbfPvF7/4RQBOO+00oFhnWjT+/dOf/mQbJjx+VBXRIoqMcj46+rMuvfRS\noFiyf/nLX4Di19KirWrLsPTbF+Yq/eM1UNRYrCyw//77A7DFFlsA8PrXvx4o11+r3r6I6sDred99\n9wHwspe9DChz8ueeey4AX/rSl4CiWLSgPU58v8qyHmZcOAbH+H962o+zBMcffzxQfDMf//jHAfjt\nb38LwJ///OeO49g3qjgj71Qwnoev9VuodCbKNRp73m3y2Tg+HGc77rgjABtvvDEA++yzD1DU3ihm\nhVLZJEmSJI3TKmXz3ve+F4BTTz0VKH6FY489tuNzn8paMHXRj6UyderUabPMMsu4+dxeKwost9xy\nwPjM/j333BOA22+/veNzLU6vl3P5Khr/1sUorTZV16677grA6aefDhRfnRaqSkcrvKkcoX76YtFF\nF5228847c9xxx3W8X1UpwGx1rWmjzz73uc8Bpc0HHHAAADfddBMATzzxBFCsbi1bc5AcHz/84Q+B\nMlfvPROVUTfqzJrv1Xfj/a86s02qNNtW5VOxrSqXqFRe+cpXAvC73/0OKFGM5uuoFh1fbVQ2tukN\nb3gDUPxN+m6WXXZZoOTtOVPi+KmLVDZJkiRJK2iVspngeECpeWQNJOduP/ShD9V6vDoq2naz2ow2\nuvrqqwFYeeWVgWKdrb322kBRNtFa19qzL8whqSsPR0Zhtdl3zrF7fddff32gKB3/nnLKKcD4XJK6\nGWZceL3EiDnfj1azzDXXXB3ba41ryVblw+jfUBH5vTHWeMfffvtsMqLRVGn6r8w5Murs4osvBuCP\nf/wjMD6HyL4w2syIPPtaa9/qDFYcePjhh4Hx6i+q0VHmHEVsq1GGqjPvke222w4oas3fl16j3Xol\nlU2SJEnSClqtbCRadUYhGY1WF8NUtHVeuJvFYLTI3Xff7X6AYp2rfOI8tNtplb31rW8FSt+ccMIJ\nQH3W/SitNjPFtVwdo/aJ1ruWqX6ttkSjhdcdn3dbhyb6IeP1jJFW0bJdaaWVgNIXfn+VVVYBiv+j\nX8t29tln5/nnn+fFF1+szWcj8TdIf8MHPvABoKh/I/m+9rWvAUWxuD+j1PTlOT6soWe02qtf/Wqg\n+DccZ1J1D7XRZ1OFvsDoq7NCxU9+8pNaj5fKJkmSJGkFra76bJ2wWD9Ky6QNaOV0sxS1PJ07jdad\ncfBV1rkRWkcffTRQ5mad2z/rrLOAkoPS5urNVdgntq0qysyIK621WOW3DVRFJVZVbIjfc1z5etVV\nVwXgxBNPBODss88G4JxzzgGK1a/6s2+s/+X+rDzRL3XO8b/iFa8ASlUDiT4XlYjvW8FcZWsbjdR8\n85vfDMC73/1uAC666CIA3v72twOllp6+GcdZvEajrBZeF/aJvw9xBmUUpLJJkiRJGqdWn83yyy8P\nlOzlYdGycf2JaO3VTZNzsK997WuBElkX5971+cS8B+de9UuYaxAr1ZpzYC7SoBbMPPPMw7PPPsv/\n/u//jqy6r3+NsLNPtNasG2bbV1999Y7t6qafcTHrrLNOW3jhhV+aK9eijJFMESOwbLsVq1W6//qv\n/wrALrvs0rG/eC/YZ7EStnP01srq10qfddZZeeGFF/r22YxV8L1Gbi611FJAyQ15y1veApSK1uZZ\nXXHFFUDx1Rx22GFA8Wval94rZ5xxBlBUoSpQhRPHXdV5zzzzzPz973+v9ffCnJ9YYaJfHA+OE2c8\n/C21Okvd/s302SRJkiStoFafTV2KRlQ04lxtm9AS0TKJaLEaQWfki9bYrbfeChSL10ic3XffHSi5\nJDH2P9Z30o9l5E5cj72KqLD++te/jszf4zlodcVaWvorrL5gNfA2zaW/8MILPPLIIy9VpP7yl78M\ndD9HrWmt/U022QQoStWckSrcv+PN11aWOPjgg3s6jypeeOGFgb47bdq0l66XeTLdaqPpU7FiuvUA\nH3zwQaDkjuib2XDDDYESXaZPyHtJf5P3nO+bi6RirlrPJq75UndOGwyuaPTJGJlnjtrJJ58MFKVj\n7cWmIjZ7IZVNkiRJ0jitjkbTstCycd6xTURFE5WCVtChhx4KFGvKtl1zzTVAyQlwTv2YY44BiiXi\nfrSytFg8nn6LbuoyRsX98pe/7Pi8Kb9HL0TLUitf1eaKi+YYXX755UDv9egmi2nTpr0UNbjeeusB\npZ+jZVlVxdlaV1rjVbi/uB/HhXk3W265JVAi9waoHNDX9mOxKrNUrWsUIzT1pTz00ENAue5WTFfB\n6JPRqrdtziJ4j6nyrAumovH70SfseVbVXmsDnrv5efqrbINqUn/XKEllkyRJkjROKysIaMla90uL\npekY8TqjS2IUklaUa3BYaVbr3Plpo45UKq4yaM6R61Nosc4zzzxA6RvfNxoqWrDOV/t+1fzzKLOj\ntSjtO+el9W+5ZstrXvMaoFjOsYZVtwiwXhmkL6rUVq+rlXr9XcnT62wklvk6Rx11FFBUv8rl+9//\nPlD8nl7nz3zmM0CppN5r38w000z87//+71BVNnqNRrOPbLP5NUZYfeQjHwHKWj/uxzaaT2N1aPsi\n5u3o94w10FSLsa5cpA1rPtkH/r787Gc/83hAiejTZzzK+oGpbJIkSZLGaaWy+fnPfw6UXINPf/rT\nABx++OGNHrfJtTq0RJxT3X777YHim4m5RM7FVqk5s6W/9a1vAcXidYU+LVz3Y00urb+4OmHMbB9l\n1ecx5wAUZWtEzYEHHgiUNloLq6m59TqVzZjt3PeEn6tkzTlZY401ALjggguAYqXH/av6ttlmG6BY\n91HRrrbaakCJ4Oo1wmoYZTNmH3G7jvd97T1h/ot+zf/4j/8Aisp/7LHHgKJgLrzwQgDuuOMOoMwa\nxL6KykhF5b1gn3gtJ8i/aU1tNO/vd73rXR1/jYbU3znKXLRUNkmSJEnjtErZuH6F2c5aGsbpx1pK\ndVOHpRJj8kXryL9up8JQgcTaVVXXx7458sgjgfErOOoTcv5Z6y9Wyq2Ku2+T1eb1d85+iy22AODD\nH/4wAL/61a+A5vJthrHmnUs310MrvZsK8/rqv9RK7zbn7viyj1wLyBVAVUxGeK6zzjpA7zlydfhs\nYtWD6DOJbYlKR4Wz5JJLAmVsx1UqxTEeZwk222wzoPSFuWla/91UQJvuEdu81VZbASUK8rTTTgPG\nrwhcN6lskiRJklbQqjwbs2i1+rUstM6aVjZ1UDX3XZU1rdUV3+9mpbs/1/a4+eabgeLHMAM9VuuN\nETZtrmjruZkvYc6AalDL9JZbbpn8k+tCVTVwLdCq6y5eJ6MR+z3ujTfeCMAHP/hBoOTrqJzNPTFK\nKVLXuJhoNVtfq/r0kUQ/V6y6bN6NbVC9V62oqb/LXDhzl4zg++lPf9rxPa9JVF5tvkfEe+K4444D\nigr0uuvvHGUbUtkkSZIkjdMqZXPppZd2vFbhuAqlqwzOiFRF5GjBxhUa4/x2VXa9uSZazEZuXXXV\nVUBZB2XNNdcExlcM8Diuemp+ThuI+RBGUOnHsH7cV77yFaC7WhgFcc0VrXLzocwJ6UavVRJiZJX+\nLtWDPj3XqLeKuL68iDXZdthhh5ciH/thomvhOdoXjl1nBYysitdTf5N+JlfgdL0az89xor/Ce8La\nal/96leBEtFn33he0Vfj8b2XzPdqA56zv43mJMU6g/6WZm20JEmS5J+aVimbz33ucwCcf/75wHiL\nos0YZTSd6K6O11rrzun7ebRcqzLQrQ9lVWjRSnTOVmtQRVM1/9wmRSO2XcvTtX1sw9133w2UStda\nnKOs7xYxg9s1eLzu+tZiZWs/N1ot+i+qsE+sF3bJJZcA49dDciVX37fuWMTxYQVmfQGD4L1R1QYV\njSr9vvvuA0rfec7mUznG9dXpy/P9M888Eyg+G48fq8bHunLdaJOiEc9d/5W4Zo/Rql7vWJtxMkll\nkyRJkjROq5SNFo1oeVTNJ7eJXudCtUSioulmXcVcA1WgFotzslZ1ftvb3gaUSrfSJn9Gr1ih2hwC\n1YBRilrdqr244uIo22zOmD4X/RG2QWvcSCkVkLkkZr9X5eVYN+6AAw4ASu092+z+9cnpg4njIlJn\nBFa3lS9dPVKlanVnfTP6H13t1ut71113AXD77bcDpZ6cbbbPrUjy3e9+Fyh5OTEy0+1npHskVnf2\nd8jKERNUBpm8kwukskmSJEkap1XK5nvf+x5QInRco8EM338GomWhEjGHIOYMaLnEiB3XS7F6rzlI\nF198MVDyKGYkKy2i9e+cveNgmWWWAUoGubkERh2ZOzKKtk+ZMoXZZpvtJeVqG6JKN2rIdWY+9rGP\nAUVxWAPNGngqVWufmSFunpV1vqJ1rjIyV8kaet36ZqJs/kErBntOVb40M/uNnLMSgErlk5/8JFCi\nzLTWr7jiCgBWWWUVoFQgsaKE1cAPO+wwYHy0a2TQOnZtQH/XQQcdBMCrXvUqoFx37xXvpSZWG+1G\nKpskSZKkcVqlbJxXdg7W6q5xLfF/BrSStDSMQrKtWlNacSog3//xj38MwAYbbADAPvvsA5Sos14j\nstpktUW/lX3h3L25KnHVUi3hHXbYAYCTTjoJGM3KndOmTesYpzHiyQrmZ5xxBjC+lpWVIKxwripQ\n+Xbz7UVl7Phae+21O97vRqzxN2hfTpkypXJFzlgZQCXidVexup0qzkg7qz57/b/+9a8DxapXCbtK\n5aBjPSqziaoiTBYxj0ofoH3xi1/8AigKWF+gSlq/eCqbJEmS5J+SVlV99qltPad9990XKCv2qXx6\nXe2wX+qs4tot7yaiNefcu3OvRpUYnaTqMwN9ww03BMp8td/TojWuPtKtD9tU0VbsA9cAMgteP4Tj\nxvVM6lI2w/RF9KEYPabvRgWh38GILP9qkXaLWowrr5566qlA8XeYLd8Nx2FV9Fudaz5VVUVQ5ccK\nAvF9qx88+eSTHftxO4lRiR63273ZTQm14R7xN9EcIvOsll56aaDMDp111llAqcZSd85QVn1OkiRJ\nWkGrlM2Y4wDF2tPainW9Is5fxtjyXmmDpWLbtXhjhrnWWKwfZb6NFmzVGiHdMOqoDX1Rhb4b82zM\nZalqq4rIumD90kRfRL+F19fr7muvs9nw+ifcLvpyVE5VirbqPKSqD5daaikeeeQR/va3vzU+LqLy\nGXQGw1kCo916rS/XK228R2yj6s4ITfNwqq6vvx+Op35JZZMkSZK0glYqm1HRpAUbV2ismg+uWtXQ\niCyzoaP195nPfAaAgw8+eLr765U2Wm2RuO5IU9Fnw/RFt/6PUV9VK732Ol76OM/pfm+i1TT/8a+x\ncVGl9nolroMV2zhs5eO4vxnhHpGo8uomlU2SJEnSClLZjKFJZTO9uXAoa21It6iguA6JVpvH83uD\nxtPPCFbbZOUINdEXVf6DZZddFig5ZbEat/6qXnPO4nGG7bPJHBdV/qRukZ72kXXgYs3FyIzQF4MS\n1eKgvtxupLJJkiRJWkEqmzHUYal0m3NvesW8bpar0U0qnxkpz2ZUDNMXMZowovI48MADATj00EPj\n/jyH6X6/m8Xaq8+n2+s682y6tanpChBVyqnXPL68RwqpbJIkSZJW0K+y+SPwQHOnM1KWnjZt2iK9\nbpx9Uci+KGRfFLIvCtkXfT5skiRJkmQQchotSZIkaZx82CRJkiSNkw+bJEmSpHHyYZMkSZI0Tj5s\nkiRJksbJh02SJEnSOPmwSZIkSRonHzZJkiRJ4+TDJkmSJGmcmfvZOIvJFbIvCtkXheyLQvZFIfsi\nlU2S/FMyZcqUjqrGM80000vVjAdh1llnHVclOUn6GRP5sEmSJEkap69ptKS9xBUce12TI2k3ce2X\neF2jZdnr9t0K8MbtqlaMTf5v008h51Q2SZIkSeOkspnBmHPOOQF47rnngGKBPv/888D/n1sHmH/+\n+QH4y1/+0rF90k6qVqeMlqOf97vCZq+Kpuq4STIsqWySJEmSxpmhlM0rX/lKAOadd16gzEPfdNNN\nIzunutlkk00AuO6664Biyb7wwgsdf+2Dv/71rwAcdNBBAHzpS1/q2G6BBRYAii8nLdZ2oeKIimaW\nWWYBynXU9xIjyny94IILAkUhPf744wDMNddcQLn+zz77bMdx/b7Hmd55zmhjp0ot2mbbEz9PmiGV\nTZIkSdI4fS0LParEJC2Uhx56CIBnnnkGgM033xyA++67r5bjjCJJK1pfvvbve9/7XgBOP/10ABZf\nfHGgWKwzz/z/xemVV14JwLXXXgvAEkssAcDOO+8MwN133w2UqLVuPpxh+qJf/8Cw6Kd697vfDcBZ\nZ50F1OenGqYvvD5///vf43YTfn+hhRYC4OmnnwaKFe51W2aZZYAy9rfZZhsAfvWrXwFlfOiz+973\nvgeUe+SnP/0pUJRO9P11s/KbuEfmnntuoPgd7Stf66dcYYUVALjrrrsm3I/jwMi5qnFY1/ickZI6\nHUfvfOc7Abj99tsBuP7664HJ6YtUNkmSJEnjzBDKxvnoP/zhD0CxFh999FGgWPHDUoelMqzVpKKZ\nY445ALjiiisAWHLJJQG4+uqrAdhiiy2AYs1p+Tr3roVqX73qVa8CYNtttwXghhtuAIoSiswIVptt\nv/HGGwFYZJFFAPj1r38NwMEHHwzAT37yE2Dwufkm+iJa4SpVx43X3+023nhjAD74wQ8CsPrqqwNF\nofzyl78EYPnll+/Y3z333APAoYceCsDDDz8MwAMPPNBxfFFVTKQGpk2b1ui4UOGss846ABxyyCEA\nrLXWWgCsvPLKADz44INAGduqM1+7n9lmmw0ovxMxF21Y2niP+PujGlx11VUB+O53vwuUvvrUpz4F\nFN/w7373O6DZeySVTZIkSdI4rY5G8yn9mte8BihWv1x44YWTfk7dGFTRvPa1rwXggAMOAGDppZcG\nilUnO+64IwB33nknAIsuuigAf/rTn4ASpfbII48AsPDCCwPFEv76178OzBiVBrTOHQfrrbceAHvs\nsQdQrLA80kUBAAAgAElEQVTlllsOKCrgDW94AwBnn302AHvvvTcA55133mScdgdV+S7Rr6DFqUWq\nVa6C3X///Tv2o0WqMv3Rj34EFJ+O42G11VYDYKWVVgLKuNKSrbru0ac0Gf43/ZP6mzbYYIOOz/Uz\n2CeLLbYYALfeeisAr3jFK4CiZFRC+q309baRQWdE/J7Ri15XlbHjyd9Or/eZZ54JwKmnngqU8bHp\nppsO1oAeSGWTJEmSNE6rfTZa3TfffDNQnr6PPfYYUKJT2hB1NChacfpQtOb1P5gXYRuNKtOqU91p\noWjJ6qPxe/vssw9QFM6TTz453fMaRV94vQ888ECgqDj9ECoXr79W/dZbbw0UpaM198QTTwAlQitG\nhPXKZPSFlqdttE3mT+l7+cUvfgHAHXfcARRrP+bV2FbHl1a/KqBbNFqsVAA05rOJEZhV0WT77rsv\nUKxyx4vnutVWWwFwyimnAMW/+da3vhUY/PpXMUqfjQr14osvBspvo32mglHlOQ7++Mc/AuX3QyVk\nlJqKuV+FlT6bJEmSpBW02mdjBJYKxqe1Fs2MvL6G1RD++7//GyjW91NPPQWUygAf+tCHgGLB+rlR\nZ1rvoi/Hvll77bWB6mzqNuF8sZEyWt9a++eccw5QfDQ/+9nPgBJtdtRRRwElP+Owww4D6rdo6yRa\n7/pq9DupWO6//36gWLJGk9lHVopwP/q3rI1nHzi37/iqsmAnM1fKMamfQTy2EZTdfLRGXKl8jOBT\n1R9zzDH1nPAI8Hroc1WJxM/NQXI7FbD3hH5Lx4Pjx0i9Jq93KpskSZKkcVqpbLTCtdq19uQ//uM/\ngGKdzYjssssuQJk7PeKII4Biafz5z38G4JZbbgGKYlHdaYHEv+JrfUGf+cxnAPjCF74AwNFHHw3A\nfvvtV1+jBsSoIXNB5LLLLgPKueqjsW3mVagC9Gu8/OUvB8rc/SjpFtUV26KV7zhwTv3nP/85UHLN\nvEdUKs7Zq/r1zbndN7/5zY7j6quJUUqTXf1hLMsuuyxQVLuq7ve//31P348zH/apinlGVDZeH6tj\n7Lbbbh2f21fOBnz5y18Gxvvc9OV53Y1SdUblqquuauT8x5LKJkmSJGmcViobLVOtf/Fpfdxxx036\nOQ2LFsa6664LwEc+8hGgZDu/+tWvBopf4vLLLwfKXKv0a3Fq+Zp3Y2SfdebawG9+8xtgfD6VbTc7\nvmptlx/+8Icd3zvjjDOAdinfqpUz4+cqXati7LrrrkDxW/p9r6tz9PpsPv3pTwOl74488kigRB9W\nRZ9V+T8nU+lEv6RKxDHbja985SvA+LacfPLJdZ3ipGNbfvvb3wLluovXT/VftR6Ss0R+3/Fn1Opk\n+HJT2SRJkiSN0yplo9XmXO173vMeoDzdjRnvtvZGG7Ga71JLLQWUuHetbz93TtbqvOYcDGp52Fdr\nrrkmAKussgoA66+/PtCOKLU476xfSavdvlGNVfn0tNbczyiJOSASFU20wq0kodJ1PxtuuCFQKkZ8\n8YtfBODtb387UPwdRnRZNfplL3tZx/7t66rKBp7vZFaWiGsuGRnlvWBbu7Hnnnt2vDZH7ZJLLqnl\nPEeB/a+/0t8DFYqzP3GceT3/67/+q2N7cfsYzdokqWySJEmSxmmVstFi1aLVd6P11evcbZvQ0jz2\n2GOBUu9JRaPlctJJJwElgkbLREUS/RYx6zpGqYnZ9PPMM0/Hfo2/t5ZWG/jGN74BwOte9zoA3vzm\nNwNlrRYj6rSEtYDF7GgrDIySfhWBvjt9K3GFTiOyzLPZcsstgeKbMVrNisiOAyumu399Nt1mByaz\nVp5tPv/884HSZiueR+abbz6gRGyK95RK98QTTwSq86xGGXnXK56jFUXifbvZZpsBJddso402AoqP\nR59MRN/eZJLKJkmSJGmcVikbI3C0wnyqa5lst912ozmxIXCO3VwQ49pdWfP4448H4KKLLgKKAtGy\nvOmmm4Dq1QZVTs5Xqw608oyfj1EoMXdJZpppppFVgDbb3eq/KtxPfvKTQGmrfqfo7/jEJz4xKec5\nCN2saK+XfsnvfOc7AFxwwQVAsVj93KoKzr3rn3AO3grH/rUauOovRse1ocrCxz/+caCMUaskiPfG\nW97yFqBEbDq2/Wtb9P2qgFWBRvyZs9RmvE5edyMvVS5GG+61115A8Xt5vVWw7kdf8Lnnntv4uUdS\n2SRJkiSN0ypl4xoczsn6NLZ+WFxVsM1oTV1zzTVAUTRihIxtk16jQ1QmRmq5H603cxb8POZTVB1n\nlOvaRD+C1Z5tw7e//W2g5FNYBdhz/sEPfjAp5zkIMeqrqpKA1rgKVTVnvS+te1dgtPqCytnPzRC3\nRpZWv+NG6z9GMUVf4GQqHlcRrYqMtM22xXtMf6htl89//vNA8ZNaScDv6R+dLKZOnTpw1KfXwVVo\nrQvoyq3mHsZq8bbVWQPHg5UpJpNUNkmSJEnjtErZmC0tPp3Nt5mRMApMSyP6F5x7HRTn+K0GbITW\nRz/6UQBOOOEEAN7xjncAZZ0b1zXxvGYEVGGbb745UKx/rUTnr7ut0dMGosIRX+tj0ZL1HvD66qvR\n36CC0bfn9beWnsdTAdl3vu/+q9azmUycuaiKlDMaNSqUNdZYY8LtVQGu7Kkisu077bQTUHJRmqaO\nPrU6hrM/+uCM5FPhWlXePtU3N+zvzjCkskmSJEkapxUrdWpxxLpNPpWNTmvan1DnynuuoeF8snPg\nttFokV7nxKvm+mNUmmjl+3ncbnq5B02tyDgose2eu9aaa8wbrVi3VV5HX3iu/o1tqbpOMc/CcWOk\nlmu9qFicHVABXX/99R3bGwVphYFYoSLmcY319Y16XNh3VpLQl2cf+bmr2e68885AqXwefTSqQvN1\n+vVP1dEX/eb6xMoOKl4rnH/sYx8DitKN+XW+v9Zaa/V66j2RK3UmSZIkraAVPhujRXxqixFWo4yQ\nGhTP3fUltBS1MKziay5JN+JKeuYKWEtLq83qr2Ya+73Pfe5zHedRRRuzqaOfw8ga68u5+mCbVyGN\nykGqrof5EqJSVbF4r7hmvDlqRiNaQds1flQ2fr/fmnttGBf+Dpg9r7/CmQ/P0cojt912G1D8m6pC\nMefEvhoF/fZr/C00uvBd73oXUHxw66yzDlBUnveOeX2jIJVNkiRJ0jitUDZf+9rXOl779DaPYkao\nYRRxPlkLNc7Zq0i0PCRmdkerfu+99wbgoIMOAkrUm74g5+y32moroCgr525npFyliOpNH59WuWvP\ntwX9G/4fioKJGftV26lIVSJup3Lxr5as1Z/17RjBp7K59NJLO7avqvYsTdxrtsXr57lIr/e599RX\nv/pVAD784Q8DpaKAVaKN2IoVj8W6Yc6seC/GKgtRDbYJ16mK3HfffRO+b/Xw008/valTqiSVTZIk\nSdI4rVA2onV17733AtWVjGcEtJKsaeQ8s5ara7aoVJxftrqv+THGz/v5v/3bvwElWkn/hXO3Wovf\n+ta3gJKD0isbbrjhSxErbSP6PcxJUdW1hbHj1f977l4nrW0ViuPCz72+KiGt6ljR2v3aB+uttx4A\nZ511FlCy8j1OVDBV69fEe27mmWceupqAbfBvVDKxgnk3rFx86623AqXitfeebdZftdJKK3V836z7\n7bffHoD999+/43ziec9IxJwi0Xc7ClLZJEmSJI0z0jwb50JvvPFGoGS363dwnnmyLItB4ua7zTPr\nU9HCjBExce48WpZa70ZcuTKfaJmuuOKKQJlv9v255poLGD8/3o025dmI9eXMotZyfdvb3gY0F402\nSF9UrYDq9fDc9UO5oqZRZb52XKj2Vb764Lzuhx12GFAUjnXk7CvHVfQVVdVsm04Nt577Yu655562\nyiqrvBQxJ7bxqaeeAkq02LDEyD77/p3vfCdQlIzXIFZItkK76tK+dHYiUuc9Urdf2nvFnCT367ip\nq88l82ySJEmSVjBSZWPETVyd0IxfM8LjinxN0aQ1b2SMPpf3v//9QIla83OtKddmueyyy4CS7Wz0\nyeGHHw7AEUccAZTVLOMaQIPSRmVjXad1110XKH2lIm6qQnEdfaHV7f2m4vW1bfBesJad4yNGp7mK\nqRnk8T7eY489gOpKATEqrgllM1njolfMfXNVSysnX3vttUBRk66X5HZVtLkvnBVynHgdfV21Cuqg\npLJJkiRJWsFIlI1Wk9VWrVSqZaH1Zc6Ac7tN04SlUjV3L0Ydrb322kCpbGwUmtV73Y+WrRnCWjB1\nV1log9Xm/LIq71Of+hRQrDSj5lQ6bVQ2VYrB6x4rHBtNtuyyywKw5ZZbAqVysUpGP4JKyJwTc02c\nDYjRa/F+j+Oym++gDeNiUL7//e8DpU9Vd/rPYn3BboyyL2LVcK+XCtiq4Cpofz/Mv3PGZNjjjXmd\nyiZJkiQZPSP12fi0NQrE6BDXp7BirbkkTTMjWG3m65hToKIxqqku636UfaF19r73vQ8oK3PGsar1\nH9eqryLmkvRKv30xtoJAD9sD41fSlB133BEoFSeMLlLxWgfMGnv6IeLa83GlVhVyrMHWjRnhHqli\nySWXBErdQCOyzHk75phj+trfZPZFrCiiCvP1LbfcAhSfzLnnngsUZWv9t4022ggoUat1RfqmskmS\nJElaQSvWs2kLk2mpRF9Ov8rEKCWts2Gz6MfmKLz44osjtWD1S8SsefvKPKxLLrkEKDkFTa2rPoq+\niHXgVCoLLrggUPyYjhf7Ros3VgwYNI9Di3qWWWbh+eef58UXX5xhlU3dtGFtH6+vikZ/1DXXXNPx\nvtGvVb7CYUllkyRJkrSCViibQefS66bOqKPJpu7j99MXU6dOnTbzzDPXbi3F3JRR9e1k9kW8jiqc\nqvVwxpzjQMfrdvwJjpPK5h+04R6pYrJ/j1LZJEmSJK2gFcqmLaTVVsi+KIyiL7pZplUVk5terTTH\nRSH7opDKJkmSJGkF/a5n8zjQW1LDjMfSfW6ffVHIvijU0hfdZhy6VQJoiBwXheyLQk990dc0WpIk\nSZIMQk6jJUmSJI2TD5skSZKkcfJhkyRJkjROPmySJEmSxsmHTZIkSdI4+bBJkiRJGicfNkmSJEnj\n5MMmSZIkaZx82CRJkiSN01e5GovJvfKVrwTg17/+9VAHn6zigb0ySGE9l9eta3nVtpBFBgvZF4Xs\ni0L2RaGXvpjUqs9te7jIrLPOygsvvDDUKoRW4XVtnqoVN7tt56qTf/jDHyb8/pxzzgmUFTqbWrfi\nn/lG6rfP+u2LKVOmDHw9qu6RQdd8sq0y7Dhpw7jod1XbppiMvug2VmektcByGi1JkiRpnFzPZgx1\nWiqjXrlzWBXZBgu2LQzSF/32f6/jxe1cS/65557r+NzjVjGoBaxay3FRaGNfdFM6o5wJSWWTJEmS\nNE6/69m0mlGribF4DsceeywA++6776Qef9FFFwXg0UcfBdrhJ/vpT38KwBvf+EZg9OfU5Hx3t7Z5\n7Krtqsayr/XZxf35Pf0Z0WczqA+nDfdUpOr6tel3YFh6Vci2uZuicX9uN8ssswDwwgsvTPi9+Dsy\nDKlskiRJksaZFJ+NT0/DhOeaay4AHnvsMaBEl/j09q/bLbLIIgA8/PDDQLHa5p9/fgCeeuqpju9F\nfJr7tyqKZZA52H7Xgu93br7bdvvssw9QLJCNNtoIgI9//OMA/OIXvwBg9tlnB2CDDTYA4Oqrrwbg\nf/7nf8Ydd0afm7fvjOx76KGHAPjNb34DlND9XqkjGq3b9YwWZJXFGfcTlUq09r3u/l1llVUAuO66\n6zq2c3+O2+koq9aMC/1WCyywAACHH344UNIQPvaxjwHwl7/8pZHjt6kvoq+uX1+hf+P3elVW6bNJ\nkiRJWkEjPhutq/nmmw+AU089FYB3v/vdAJx99tkA/PznPwfgkUceAeDb3/42UHJJjjrqKAA23XRT\noFh7s802GwC//OUvAbjmmmsA+OxnPwvAs88+C4y31rpZbYPQ71rwg86R26frrrsuAB/84AcBeN3r\nXgcU1Xj99dcD8PzzzwPFovVaqHTsQ63DJ598sq/zayNaYfbF6quvDsDcc88NwCc+8QkA1llnHaCM\nH9vs96La65exfdhtrC200EIAPP744x3bd1M2ttW2LbHEEgCsvPLKHa8vuOACoCgnVZ6fP/DAAx37\nc5bB8fKnP/2plyaPhAUXXBCAAw44AIC1114bKH1qXx188MFA+Z3pd4y3yQcUz8XfBa9fnEVyFsft\n/V2IiraqbfE309+TGAXZC6lskiRJksYZSNl0e9L7uVbZ5ptvDsATTzwBlKeiT+OllloKgJe97GUA\nnH/++QDcdNNNAGyyySZAUTzuX6v+hhtuAMpcbZX/JM5P1mGp1J2hrWUZo0V22mknoPgh7LO77roL\ngK222gqAJZdcsuP1VVddBcD3vvc9AL7+9a8DxSL+85//PK49g7ah7sxu2/6GN7wBgMsvvxwoysPr\n/ZWvfAUovruTTjoJgHvuuQeAU045BYCdd94ZgN133x0ovhutQ62+OitddLtHqhSlysJzUIH6Wn+l\nKs0+0j/htXj/+98PwMILLwzACSecABTL1z57+umnO47jftpk1ctiiy0GwFprrQXArbfeCsBqq60G\nwB//+EcAtt56a6D8jnzzm98E4JlnngFKX3az7tvUdnHMqjS22WYboKg9VZ59deihhwKlr7yHeo3E\n9HjOiPgb3s/vRSqbJEmSpHEGUjZVTzKfoj/+8Y+B4oMxiszvfe1rXwPgxhtvBEr+hZaqVpnzxe96\n17uAYukapXbzzTcDRQnFp3S0TLtZMINQ5Vvp1WLQilaRaJVpueqb+eQnP9mx/Xe/+12gWMDxPFQX\nv/vd7wB49atf3XFeUdFUtacf6lI0Xv8111wTgMsuuwwYb4laCNZopGuvvRYoOSj33nsvANtttx1Q\n+m655ZYDSl/Ea9WEJeuxvV72v5ai52DbjSrUH7n88ssDJUdJVX/LLbcAcNtttwFw++23A2Ucau37\nfcfT0UcfDYz3T9l3bbLm7ZOYQ3TIIYcARY2p+p1RUcHsvffeQFFC/v7YV/bBKGut9Zr572+gf/3N\n9V7513/9V6CMr1/96lcAvP71rweKP/vOO++c7vlERevf+LvRzzhJZZMkSZI0Tq3RaD4Nt9xyS6DM\nI/s0Ne7dKCAtjxhxo4Xh93yKOz/pXPx+++0HlKi2UVQ+jRZAr5m5omVrX6ywwgoAnHvuuUCxwmPG\n+Zvf/GYA7r//fgC+8IUvAPD73/8eKHPyRvL9+7//OzA++qmNeP2dXzY/xvGgnyL64uwj8fP4viy9\n9NIAPPjggx3bN4HjQx+J40NUPm6n6jcv5rjjjgOKX1M/lX4Ir7sqwP3MO++8QLl3tt9+ewDWWGMN\noNxLEvtgbPTbqCo+2BbvjQ9/+MMALLvsskAZ6zEaUb+katK+OO+884DuWfeTSbdziApCH9yuu+4K\nwPrrrw8U/6RjWiU8zzzzAPCa17wGgLvvvrun48WKA8OQyiZJkiRpnFqVjT4Un54/+MEPALjjjjuA\nMr/cq4Xk09UIi/haa26UNbaq5iy7KZpoMSyzzDJAyQkwUkrrS3+WlrHzzVZX0H+h0vGv/ixV5f77\n799Ls0aCbdU6N+JFhWzbq6ys+H608iNaf0Y5qi7rJCpf1ZT5LnGceM7Ojbu96xsZTXbmmWcCpU88\njhas+VhGJcoPf/hDoFQqcHuP1y2jvE5UW1V5Td4jnuPxxx8PFD+U0a3eG/al/k8VjrMHKlz9W01V\nFuiFXmc+xOthWxwXV1xxBQAXX3wxUNRerKpi9Grskyq/ZdX1HyY6MZVNkiRJ0ji1KhuzlCPGuVcR\nrSmji4xSM/pM6+u//uu/gJIbMKqM4InmsbtFlWituZ0Z3694xSuA4u/SwtVqs+1aplr9Z511FlDm\noT3uy1/+cqBErakqjdzR/xEZJs9mUGLe1Ec/+lEAPv/5zwPw29/+FqiOFtJK1ALWL2UUW/SPxGsT\nKygPy0wzzTQuQ9vrbXRgfN9xZBv9vr4bLWDVvOMh+mYcP0azOctgnlXc34orrtjxfrdq03XSrVKD\nfaIVrjrXX+m9ceWVVwIlOs28O3PT4vGsmjDZjL237P9+ayVuttlmQLl/Vcj6YI0y06fzoQ99CCh9\n6ayQMx7xuNF3WBWVNgipbJIkSZLGGUrZOP+nheFT0DnwOJca0creYostgOJ/0LozmkQrTyvQLHiz\nryNV1kKdmeET7X/suUZsi4rECBmVh3OwttG2mROg1WY0khVuVXdRHaqMLr30UqCoBOduV1ppJaBY\nvDGHpR+mTp3KHHPMwUEHHQSUWlW9on9JdWd+jONIK00rLo4Hedvb3gaUCC5zEBxP9ok5TFXjwHHr\n+O6X6Y2LWCEifsfr5zgxN8SIPC1Yx5Pnqm/m05/+NFD8GSreiy66qGO/HkdfkH3hrILjr1/fQhPY\nZs9Jf6W+GcfJOeecA5S+iLMMRmqNionGhe/Ffo6/YY4bt1PhfPGLXwTK74BYDcMx7H708fh5r7Ud\n6/jtTGWTJEmSNM5QykarSnwaV/kDIkaVaAlr0Wp9OQ/tHKwWjVZeFTFGvNe1Ooahap0RX0dFY+2i\nqGjcXss0VsLWIrGa7yWXXAKU+WiPa06CkVwSI3nqUHkvvvgizz77bN+KRl+cas22W605WtNVNe9U\nPnvssQdQ/BX2hZWujcCqijqzjwdVNDK9Po0Ksmpb37/vvvuAUrFYX435E1ayts/sG9eKMhJUVWAE\nlm3U6revYk20UWbVS6zabt+pdF276T3veQ9QZkhEH82Xv/zlvo5b90zI9Kga616HuBZYrA/o9/Wb\nO/ujT85KFI6LfqnjtzKVTZIkSdI4tUaj9WoBaMWbM2BE1qte9SqgzCP7NHcOXqWj36Gqvle384lP\n6ZlnnnkgC27sfnpdqfMd73gHUHwwUQGpXP7lX/4FGB8lpGVjVJrbx9pJ9rHRam5n5I412CJNRqPF\ntnr9zbfQ6tLajtaeUUleK+u9We/L+k9+rtL61re+BZQ+qKLuqDQYXxXcNkQ/p+MlriqrstG/6dpQ\nWqwqY2cTrEOor87vOy48jkq7ahagTbXRqs7Fe8E+0N/keLKPVbZxJqYbk5m/V/W7EXONVPExElc1\nZ2WJCy+8EIC3v/3tQKlX6exRXNmz6vh1zgKlskmSJEkaZyhlE2tS9aoOVCoqGi0Rrb64lod/teas\nTGDW/LbbbguUecxua4hUVUjuh1lnnZUllljipfngqjl4LQYrBOy7775AmW+2rZ67OQTWjxP375x6\nzNfRytOCfd/73gcUBWQb9VtUMYgFs9JKK3H66aez3nrrTfi5VpnKwnN87Wtf23Fu1ryKK72uuuqq\nQKlcfOyxxwLj1zfyr+rtv//7v4HS15PFlClTximWuMaTc+uqOftIxaEV7ufmIKlw9HNp4Z522mlA\nibTzOptXYZ9bSd0+j3XFfH+Y6MTJwpkOr6+VAeLqtfp8e7XSY421YVduHbtfj+3103daFe3nb6Kq\n+6tf/SowPvLXlVeNTov+R9tkZQkrDnhPdpsFqmOtqlQ2SZIkSeMMpGzi/F6vTzufxuYOxPVr4jyi\nUWf6aLTOzI43zt5cFRVO1flMT/H0a8H97W9/4/777x83Jy8xn0KLVF+NdZ70J5g1b02jKqIVb1SS\nc/laTGZbn3HGGcD4PtH6iwpqEO66664JVU2MqFGxaNXbJx/5yEeAMs/sdda/9d73vhcoPhotWtuk\n707/hJWuR8W0adPGjSfzYrRQjS6zL7SeYz0339dqV7H4uTXSVLBG2lnN2VyjDTbYACgZ5nH/Y6s7\nj2Xs+B5U5TS12qfnbqSdStjjeS/ZR70S+6YuxqoHr6PXx/EgsSaiyqeq+oV/zVUzj05/ln1hlXDp\n9ZrUEZWYyiZJkiRpnIGUzaBRGlpNzqVbt8nMXp++Wne+NlfkS1/6ElBySOI67q79YkROtyq+dVhc\n8btmsZv/4pyr57zLLrsAcPnllwMlasi5217RwtEHpEVjmw477DCgqL4YaVWlaHbfffeX5nOHJao+\nx43XVWWqdW8fOa/sekVa9VprWpwqJf0an/rUp2o57ybQ16YPxTFudnyMFtOS1J+purfvrLDuSozu\nx9pp+vDc3lpYHkeLOUa/aUHXuY5Jr3W/er0PHTeqdnPHrEThPeWaLVr3ro8UzyuO06aU2ESoaGK1\ngxgVGM81+mzFavHO/qiojT713nIWoFcch1UKqxdS2SRJkiSNM6Wfp/eUKVM6Njbiod/8BOfq47Gr\n6vU4V6+1rl/CaDatNX1BRmb85Cc/6eu8pk2bNrEDZgJiX5jj4aqhWqi77747UPwSxsmfdNJJQMlq\n7lZ7SgtGpaRlE2uj2Xdae67ZEnOSquLqZ511Vl544QVefPHFgftizPsd5yRa9UbKxHpdvu92Yqa4\nVpp9qyIyT0ulW2MNvL77Irbd6xct06rqFmIfGImp5ep4saK665h4nLe+9a1AGWdasrFGW5yLr1I0\nYyzsocdFpNdMfdWa0WWqeceDKs8Zk5/97GdAidDy8wnOs6fjR5roi+iTHXOsCV/HaDOVjP7rI488\nsuN9f3tVe1YhH5Ze+iKVTZIkSdI4Q+XZDJtxrXVl9nNVlWYtlyOOOAIo1pjRS857nn322UCpjSWT\nMQd77bXXdrzWgrjrrrsAuP7664FSE016PSctGFWd69NEC8i5eNeAqbpGVVbcQw899FKuz7DYtpjR\nrdUclWxVFJAWrfWetFBV1o4Hr7uVjkdJvK62uSpTv6rSgPeIfqlY+UEfkKrOLHpz0KJy8XjRZxPX\n1YnbzzHHHLVHZ0nVGkvOWHidjSrTd6e602o34s7xYl5WrKUY+3yUK/1WrRdTNS7iuIrX0T70/tdv\nbQTnVVddVev5zzLLLD1HqqWySZIkSRpnKGXTb1VU51iPOuoooFQiPfnkk4Fi0cYM3rieida60SVa\nNPVZyPgAACAASURBVFp/bu98ZNW66nUqnuOOOw4oWfBapFbd3WSTTYBidWmFm2cT16SPUUJrrLEG\nAD/60Y869iO2Sb9Vv6rTOf9YMXcYtLL1yXiOqrNeK9Bq+cZVB+0bLWBXqRxW2ZiLsOuuuw61Hxi/\n+qx94VhX9Ym5IlqiKhwjq8Trv8466wBlVUqj1Ix21GdXNcZ9X+UV+zaur9ME0WcnXtc999wTKGNb\nq9373woTVunQ0nal31gTLVZYlzZVS+j3tyn+Bjt+4m+pSnjQ6s+RftY5SmWTJEmSNM5QyqbfKs/O\nJy6++OJAiRox2sy5eK05LRYjrswZ0Eo0r8anv/H1Khqj0qwi3aQlo9WtNaal6DmpYLRAVTa22ZU0\nzfC+7rrrgFLjzIoAzl+LFrJ5GOZb9Eu/cfe9EFdStRaa9GpdqRJ32GEHoMzRS8w5GpY6FI04xuwL\n2+I9oWXomHdsGz1YFRWm5aqaM6/CcWPNPon5G3F/VX6MqgoZdVDlM1HJOl6cHfD3Q6WiGjcLX2yr\nK3fat+Jrr8koFU03xdlvPTcxUjfW5Dv66KOB0fipUtkkSZIkjVPrejYRn6paGlakNcbbp++aa64J\nlIxx5639nsrG7FeteK051xw38kurMdZ9cr/d6o8NgxaE88cqGCO89Lk4p64SMofItjqXH/1UWnXO\nwW688cZA/4qmKspl0PVspvc9KwRYCWCLLbYAylobn/3sZyc8J3NFXIHR+eZ4zvrsmvQrDEqMPvO6\neT2jP9E2mrd12WWXdXzPv7bZmnT6ZhxX9kWVoqmiKjqqCar27RhXyajivvCFLwBlrL/pTW8CSu6R\natDPo18s1lKTyawYUEXV/VgVlRa3i1WgjcBz9sDxZgRoP76WukhlkyRJkjROLcqmyjKIr33Kmg/j\nHLzr2zjHqrWvBaKPRwtFq+3AAw8EivVo/L0r88V6Y1HRDFoBYXo436xl4TnrZ7DCgGhteS5GGRmB\no3KxSrRzreYQGJnTK/atETt1+bEm+p5WeFxDxwgqI6xUPmY7a91vs802wHirzorG1qFT0baRGN3l\nWNN3E3OFHA+OcdW/bbRa93bbbQfA97//faD4/szniitx2odxpVDPz2tVlTPR5AquEc/JOm/mDKnS\nrI5hX0X1Zp+odHw/9kmb6PecYiUK+8y+MFLP+nGqQH+DY428KvqNOJ7uvobeQ5IkSZJ0oRZl0+tT\n2WxWVwvUyle5uB99O/716WpVV300VneuyjxXZVSt4NnEmvNaT9FyMPfDtnhuWrgqGv0ZF110EVBW\nJXV7FZIqrWout8oi8XiTMWdbZQ0dfvjhE25nhWqtMd+3L10/ff/99+94PSNgW2KOh2NQBeznWu/6\n/rz+5pAZ5eg94OqkVda74yH6MWNUXIxqkslUAx7L3wnxXFXz5rZZUXvrrbcGSlX5qKhHWSmgG7Hq\nc6Sq/x0X/s7YF15PfcTOElnBxNkft6vaf519lsomSZIkaZyhqj5P8DnQuxWkle16Nc7N+n6MzKp6\nekeildDreQ1TxTUeI0bADIv7t2+ce7fqr1WBI9FHU8UEvpu++mKQOf1oXe+8885AmWv3+l5wwQVA\nsbLMPTLTv2mru87qvnFcxGg1lYw5YkZgrr/++kDx1ahoXM1Un02sNxfzvqp8Nr2sOfOPFUhrr3Tc\nL/aZ0aUqGu8FfYF1rMUzPersi26/UXEGo6qWXazm7eyQMyJef3MPjfirWk+nG/2Mi1Q2SZIkSeMM\npGwOPfRQAA466KCOz6vWyJhRGMRSiZaqFog5QOY/DEu0fIwe6hZNUvX9bozCgo3n6GtzTlzl1HVt\nJiuvZpC+GDSKJ1Zh3nDDDQG48cYbgfGWaswpcTYg+mK6RSFO0I6O102uZzMsVl0wss8q8DOSsumX\nKh9PjFJzVVPHyRvf+EagrCRcV+5hKpskSZKkFdTqsxn4JFqQwfuP4ze2OuWgGHVkxJ51u8w12XHH\nHQE466yzaj1uGy3YUVGH/6pfH16MCosZ5UYhmWv07W9/GygWr4q339paVZnrbVY2VefeNKP4veh1\neyvsW4FE1ae/u+5ZqFQ2SZIkSSuYFGVjbkCv9bvqjuTqlX4slTnnnHPaCius8FKV5qrqvJFhM3K7\n5Q51i9fvlTr8V93QjzCKOk39MBmRedHSHNbija97HXfdVoZso7LpRp1Z8GPppy9mm222aYsttti4\nCvbdMP8urmLaK71WSRl2RiaVTZIkSdIK+lU2fwQe6LrhjMnS06ZN63mZyuyLQvZFIfuikH1RyL7o\n82GTJEmSJIOQ02hJkiRJ4+TDJkmSJGmcfNgkSZIkjZMPmyRJkqRx8mGTJEmSNE4+bJIkSZLGyYdN\nkiRJ0jj5sEmSJEkaJx82SZIkSePM3M/GbSms1xQzYpHBpsi+KGRfFP4v9UW3orb/l/qiG1mIM/k/\nwZQpU8ZVKx4lg5zLoG1oW9sHYerUqePW7xmE2BfD9s0888zDPPPM80/Rx22gFYuntYW0VArZF4Vh\n+qJb6f+mGPQ43b43meOirr4adNmNuMTyBMuI1DYuZnRS2SRJkiStoC+fTdP0u4Rt3YshTSZ1t2Ge\neeYByiJLM1Lf9NoXcYGxrbbaCoCLL764p/2NwpqcYPGx6W7fb19obcdFtuaff36gLAM8Hb/DdI8z\nSpZYYgmgLG3cK2uttRYAN9xwAwAve9nLAPjDH/7Q134cL8MuRDgR/fZ7XYsijpJUNkmSJEnjtNJn\nM6r5zBnBT1HVN77v3yrLuNv3fX+Yvpgs5TlZx2myL6LjOV4/vz/munRsr8KZd955gbIk99xzzw0U\nZTPffPMB8Oijj3Z8v9s9FtXkIH3RbanpCb7Xcey4bPiofh9WXnllAO644w6PP/C46HdJ9Khku93n\nPZwPUBTwk08+2df347hOn02SJEnSChpVNtEqajv9WipTpkzp2brqZo3FOVlfR4u2yrL1/TnmmKPj\n89e85jUAXHfddRMep4o6VF7V9e/XqhtznAnft+1NzWs3qXi7+ZfGnANQ2qhSWXHFFQF48MEHATjg\ngAMA+Otf/wrAnXfeCcAvf/lLoFjl4nG7qQ/Hepui0aKar7pH6sLjzDvvvDzzzDP8/e9/b6wvurXd\neyiqwOeee27C7zleVLo77LADAM8//zwAP/rRj4CijPsllU2SJEnSChqNRjNC5umnn+54v80RMP3Q\nSztUGlocEi3aaNmOmQvt2D6+dm7+2GOPBYpl8tOf/hSAq666Cmg2sqaKqGiq5uAHRevOcab1Zh9E\n/0RUgaNU3F4//0ZVFnM7vH5zzjknAAsttBAAm222GQArrLACAC9/+csBuPvuu4GibK+//noAFlxw\nQaD0kcf1Hq2yqCfjnq1SKPF9+2a22WYDii9liy22AOAb3/gGUNSe2NZ43eO1iG31Gvj+008/PWm/\nYdtuuy0AF110EVCupz6WJ554AoDZZ5+946/K1javueaaACy11FIAHHTQQQBccsklQBkXZ599NjBe\nKdVBKpskSZKkcRpRNloIzg9qjWmBPvbYY9P9fpyL9eks0dprY+x5VDTdlIxW+t/+9jdgvFUn5tO8\n+tWvBuDTn/40AG9+85sB+NznPgeUOfpB52AHods887BKwv2af2FOyaabbgrAKqusAhSr/gc/+AFQ\nrsGYiCoAZp11VqBcizqVTq/+Iz/XkozvR+Wz5JJLAvCOd7wDKG3WJ6eStW333XcfAI8//jhQLF7n\n6rtFNdZhwffro+uhigEAiy66KFCUzGKLLQYU6/273/0uUNp+++23T3gc+9bX3oNVTIaqcTz85je/\nAeDoo48GiiLxHLz+Sy+9NFB+d379618DcP/99wPwyCOPAPDHP/4RgLvuuguAn/3sZwBceOGFQLkX\noqLpNdp1eqSySZIkSRqnEWXjU8851L333huAd73rXUB1vajXv/71QJk/VhHtuOOOQJlfvPrqq4F2\nRrnZlmgZVFkCWq7Rmop1mbbccksADjzwQABWW201oMxbu38tYi2baDnH7eqkyuLrNx9Gq7zq76te\n9Sqg9JnWvsr5T3/6EwDbb789UCzfxRdfHCiZ5H6/iSKLVf1bZbVX+RFs8zLLLAMUS/aZZ54B4NJL\nLwXgxhtv7Hhf/5XqT+vd8aLPR6XjPed2Kp86FE5UNDFKsddjeG4qFytHOB7cz1vf+lagqHvVXTwP\nj+f7VaquW65TncRjO1Y//OEPT3hOts17a/nllwfG+8lVNo75f/u3fwNg7bXXBspvrdekahZqmJy2\nVDZJkiRJ49SqbHzaalVdeeWVQLHKd9llFwC+9rWvASVywtpFCyywAFAUzsYbbwyUiBsVzmmnnQbA\niSeeCJSneL/+iSYykfvdV7dqwFocn/3sZwFYffXVgfHzzFrS9r3z5Foi0aqr8ilMnTp1ZHXVbIt+\nqWWXXRYo2fH6arzOTz31FFAi8lZddVUAFllkEQC++MUvAqUPtdImKy9jenTLHfH62BcqG6PNvM63\n3XYbUObmF154YQCWW245oEQtjc0RAfjd737XcVwtWv0ev//97wdq10TE/o65ZDLRWISixrTad9pp\np47PPXet9ssvvxyAe++9Fyi+425EX9Bxxx0HwG677Tbh+TVBjJSMUWVRAatA77nnHqCMA+8Nz1mF\nrGKxL7fZZhugKGL3Z3Tr4YcfDpRx9OMf/7jjPPshlU2SJEnSOLUqG2O1jf1+5zvfCcC//Mu/ACVq\nyKetfg0tUZ/e+mT23HNPoFgwWm3OyaqIDj30UKDMS/ZKnRZtryqpV6taa9yIKufqI6oQ5+bPO+88\nYLzKi/Pk0Zfj+02oml736bl43ffaay+gZMGrzozA03ozysgoNJW0ivj8888HSp9o3fv9Jul2vaOf\nQLwXYiUJ1Zn3zq9+9SugXH+te9WACsc8CxWvPr0Y/RgrI9dxj8R9xMjLqvpwMWrQtqy00kpAUa76\ngm+++WYALrvsMqCos6qI0Ijjz9+vT3ziE0AZL76/5JJLdo2oHRavu2M+9qFtcFYn+nLEcaBifdOb\n3gSUe8zfUCP2/vM//xMYr7C//OUvA2UcpbJJkiRJWkmtysYoIOc8tUDe8pa3AOPj3H06a5Foabqf\nPfbYAyi5A869Ot9odNFnPvOZOpsxEL0+6WONq2hlaZmY8W2kjXOpsbKAVr9+LF/7eawWG2lDRJ9t\nVuEecsghQGmz5+j8sZnh+vi0zrRwtc613lU09oHz4FK3726s36vXPJbou3N8aImq2t1Of6jqQOvb\n46qMVT6veMUrOs7D71VVEZ6gqm/vHdCFGHnZrVqBysQIOs/V62sbv/nNbwLwyle+EoDNN98cKDlJ\nZuOrAqUqz0r/h33pvdTv+jr90G/uYPz9sO/0h3/yk58Eim/Ptut7MZrN4+qbOfjggwH4/ve/D5QZ\nE/ugWy7SRKSySZIkSRqnVmUTrTPn+ZzrjFZXtDh9yjqna5SRFowROFpx1v+akdAyMMrIv2ussQYA\nRxxxBDA+d8A+EedqVTJaJGYQa6W1Qbl0w3Hzvve9r+O1ETJmOV9wwQVAUTwqGKPQzMPSajMfQ5Vg\nJJfKSOuv7ioLE/kEeq36LTGqzFwiLcqYB2MbnKNXvTkboP/CNjsO3U+3ChejxAiq9ddfHyhK1hwR\n/ZnmVRlJ9cEPfhAobX37298OlLyrbmrNz6MSqpMYFTqogvT6WUnA1Ur11VjVWYX8ne98Byg+IX9T\nHQ+qSOm1usJ0z3HgbyZJkiRJj9SqbLS+nWPV2orWtU9zLRGj2IyPf+CBB4AyZ6rCMTdApfSTn/yk\nY39txEiamOey++67A8Wa1zqL0STR0tHal4cffhgoPh4tGq37NhCt5vhapWuf6LMz6sxM8Bg5Zd6N\n+VdW/zVSSLWnNe9cu5auysccBWki76ZbtJCWrcrUHCP7yLapdJyDV/Wp2vRnqmgcL37/t7/9LTBe\nGVVV9RhlhfaYt6d17vW66aabgFIDzTarRMyz8ffB7bu1KdY1bLIvom+mW029eC6ObX97VX3e/zHv\nzqizqkhAFU78namjUnsqmyRJkqRxalU2Pv1i/kJ8GjsH62pxt9xyC1CeqkYlaaE6vxjzclyvpN/M\n3qZWdITxeStxjlNLxNwjM8OjxSv2nX2qCnD7rbfeGiiRf9/61rcAeO1rXwvADTfcMExzaiHO/2vN\n20f69pxfjhF5zjNrnRlZpfVm9KPj48gjjwSKUtLSjVWfrajbBL3Wg3N86LvzOtoXjvWYH+Ocur6d\nDTbYACjjSevftmrxOn5UefZNVDR1WfMzzTTTwBFtMbfoz3/+MwA///nPgTJz4uf6qTx3lYy+vF6j\nyKoqHtehbKr2FdcvqiJWPHfmxPHgDIl5NLvuuitQZoWcTVL1i/ekitff3DrVXCqbJEmSpHEaXalT\n4tPRp6f5FObTaH1puZ5++unAeJ9NXIVSH06vaD1YF8gs/Tqoiv5Szb373e8G4N///d+BMpduDomW\naqxIq1Wmf0sFZZ9p1Zl1/973vrdjuzZEpWnVGVWkZWoeRKxMrUWq9a/15px6zFlSNYr+DVc3dBXC\n6PuJ51eHNVelaHzfc1bB6HPRctXf4HjYZJNNgHId11lnHWB832ixul6JKzw6C6CaM/rRe0iq+mDK\nlCkD9cswswcez3FiBKZWuD43+9TfB5VJjMQb9LpOlAs3aLRe1Tl025/Kx9wyfzf0wfg7YY6R61vZ\nB/q77Mt4r7nOjdVYXDenTlLZJEmSJI0zKcomovXlHKzZqvpw/KsaiLkpWnfDrrlRp6KRqnNxzl3L\nxEi7a6+9FoAzzjij43MtGaNCtNKdm3e7ffbZBygWsVa/alF/iPtpUuFMzyqG4pMzIsr3zXsxXybm\nFsXKtVGZRKtQ1fC6170OgBNOOAEoKjBWPJa6rPmxbaj6vtZ5XHlVBaLvRUtUBWKb9FNFhSvmW6iE\n559/fqBk21tHzj71XmqTEhb7yjbst99+wPg6Xf6euM6NY79Xf0gVbYjM89hG6qpcPTev41e/+lWg\n3BP6eo866qiO92N0pL8nJ598MlDGQR1RaJLKJkmSJGmckSgbiU9Z55P1pcTKpz/84Q8BOPfcc4Hy\n9K2qMzYKqqwfLdVTTz0VKFaY22utO3eqxaIfwmx5LQ/n8rVAt9tuO6BE5mjNx0isJulm+Tl/rE9O\nK955YtfsUcVZS888G6OQrDRhLSz9Hvad0WjmYWkN9js+hrFku1UK8HqbB6HyjDkiXmf9EN4Lv/jF\nL4Bi3ccVW62dpoK2b7R03V4cb1XjZJRWvarLcaA6s4+0yvVD2beOt6r6g72uZ1RVcXkUOD7iORhl\n6L2gf9JZgypVpyJy/KmkqxRNv6vudny3728kSZIkSZ+MVNmoTKz7FOcLzbM45ZRTgJJDohV2zDHH\nAPCpT30KKJnndc4zTo9e5vRti3kP3WoLaTGoaLQkbFvMVdp///2B4t9QOWnJTsbqgt2IuRtGznmO\n1jwzbyZWZ46rF8bcJD9X8RrFWHfNs0Hotp6N1rmVIBwvsQK6uUZasI4nFa+vVU5WGFBBm8vm+WjJ\n9mvl98vYDPVB9+33jEY7/vjjgdIGK2Pr07EvVYNtqorQjW7n6O9DrA5uNGLMVVPZVKFqjJWtqxTM\nMKoulU2SJEnSOCNVNlqq5pA4x+7T+T3veQ9QImd82htho2VjRJYRF5OxAuPY85keWiAbbbQRANdd\ndx0wfm40RszYNyocI7m0ZPRfqHBUgd/73vc69tMrTVp9WkNGXhmNFtekr8qXivWbtOKMyHL/zulr\nrQ3KMPPSkar5fn01WpLOxetniPX+9LHor/AczUXS6rfigPkW7tfj6dOraludbYfBxlNUwnGNF6MJ\n4xo85p6ssMIKQFG6VQq31yi1yVREsc2Og9gH/rXtRvg6fsxFjKrO3xN/Y81hVAk32cZUNkmSJEnj\nTOnnSTZlypRGHns+dV15M66IFy0PIyhc88Us2rh+er9MmzZtSvet/j+99oXzyObBGDGjhWnElW1Q\n0Wh1mSUda6mZRyMrrrgiUOZoh7VM6+wLr6d+JduoquvVcvS6G7VoVJv7Mbdk2HEQqbMvtFQdDyoS\nr5dj3Si0qu+bT2UtNasyGJmlb1D/1a233goU1Ve1Omas0TfBSpC13yMSj61q9/pWVX5wHKjyHG/r\nrbceMN7fWRdNjAvHuApEpeK9o2ozklNFE6Mcq/bv9/XlOQsUV6/tl176IpVNkiRJ0jgj9dmI1pjz\nyj5tu9WXcs6+yeq9VUydOpU555xz3LoPES0ILRXVm221bpe+FjPBzSX52Mc+BpT1TayhpRq44447\ngKKMhrXeBs2an169qJiN3G3NniqlY8SMfeDn5pIYsTUscT2TfpmoL+JcvBapFquKw3GhJer6NM6t\n65fyeyoafTX6M7/97W8D41eArFI0UnXeTc7le4wYGWdbVKpV56b1H306dZ+f1NkX3u9GZnq9rZV4\nwAEHAHDSSScBRckaoWvFAMd+9NHEChP+1prLqJ97UPqpE5fKJkmSJGmcWpRNXdaPNdHMt6iaezcy\nx3pS5hho4YqrVjaxpsuLL77IM888My56R0vCczPmX1wH/cYbbwSKitMqe8Mb3gAUn4wWi8rnC1/4\nAlAsIefiq+az+6WuyrhjiX6CaClWnUOMoDGHKJ7jW97ylgnfH5RBFY1M1BcxcsoIqViF1+gxI+6M\nQvRzKwZsuummQPEB6stTEauc9OHFygBtyjWJeVSxZl7V2i+qwLjCq35O1eGwUWdNKht9t/pqVltt\nNaDkDrqujD48Izr33XdfoFTHOO200zr2418ri3zoQx8C4D//8z8BuOyyy4CikAfNTezHN5zKJkmS\nJGmcWpTNsJVxYz0nc0iqMJLnwAMPBEoOixFbonoY9uk9PeKTXetMxREj7bRAVG/6WrRUjR5ad911\ngaLKVHOqvy233BIo/gWtOXNY2kT02Qy6YqPqTQtVVRAVbZuIY1xrO+ZRidfZv/otbKNq3TGv+jfP\n6ktf+hJQVqmUaNVXqctRKp54Tt18gFr5m2++ecdr/aQxt6ibchl0rZk68N4455xzANh77707zs2o\nVhWL2HbvDdfJMpLPcaPS1ZcX1eRkkMomSZIkaZyRRqP5dNVvEbNeI8696tcwAueNb3wjAGeddRZQ\n1t/W8h1llVajR5xLV9HouznxxBOBMoeqheI6N+ZhaNEYkaWfQgvW7Hs/10/ShtpowypKra+Yi2S1\n6G715roxmRniXg+PGc9d5aM17tosqnOV0BFHHNHxvUsvvRQo4yVe917b1q2W2zD0288xOk202q0Y\ncOeddwJF8VxzzTVAuSe6HbdNtdN23HFHoNSJdMxbDcH72qrucQVffbpe/yuuuAIobYs5R463OC6b\n6INUNkmSJEnjtKKCQBVaNj59ncfWYtEq1OrTX2EkWL80kR3da62pOF8d/Rz2gfPQWnff+MY3gOIL\nOu+884BiAakCBljLpbFM8X5Rre22225AiT4yV8BxUDX/HK21fq23JvsiroxZNQ687v5VtRs5F+sB\nRmXiOKxSC70q4MmoIOBYjecs1n3z98DP9dk4HvTtWlU8jo+q4/V6r9TRF1X+ZH2xXmfv95jXV1X9\nWb+Vn8cIy7oj7LKCQJIkSdIKWq1sjC0398BKpdYFMvLGNcm1Agadd+zXUhlmjfoe9u85Tfi5dcC0\ndIxWcX2UYZlMZdNtTRVrX6nWtPZVuMPmxXRjkL7odwxWZdFXfR6VUFznJBL3161KQtX5T+a46GZ9\nmxUf82v0Y6iItfLNnjcyq1ei+hxzPpPeF1XjKZ5j3dW7u5HKJkmSJGkFrVY2kx0d0iY/Ra/zybGS\ncre+itEnVYyiL7pd71jvabJWZJ0MxWuUWawoEBVMrzki/b5fpS4niE7re1w0bWVHBWRfqtpiG7qd\nT6/+jCbukX7PVaoUcZt+O1PZJEmSJI0zEmUz2fOJvdLk3HyVoqiaDx42gmpY2qTynHsfds2NQamj\nL+pSIEYb6afotn2vxHtyFD6bWBl72N+HqFB6rVBQtZ9R+q/aTiqbJEmSpBX0W0HgceCBYQ/aNkXz\nD5buc/vHgQd6tSSrfCRVuSGjmnv9BwP1RRMnAqNTNP+glr7olr3e6/tR0XTbvlcmWJFzos0aHRd1\nVy2o6x4aRV/MYPTUF31NoyVJkiTJIOQ0WpIkSdI4+bBJkiRJGicfNkmSJEnj5MMmSZIkaZx82CRJ\nkiSNkw+bJEmSpHHyYZMkSZI0Tj5skiRJksbJh02SJEnSOH2Vq8licoWm+6LXpQCaYjL6YrKLi/aK\nywk//PDDQLvGxWSz6qqrAnDrrbcC/7f7IhYr/b/cF5Fe+qLV69n0S7cf6G6fNzF4XEEzrhHfNK7H\n/pe//GXCz7v90Dd5I7neiGvF91srz3N3DXpX8Kxqy/bbbw/AjTfeCMD999/f1/Ga7Aurfjsm+33w\n9vvA3myzzQC4/fbbgfJA7ZU61/apWjem13WN+q2gHY/TbQ2YbivITubDpqo6fFvIqs9JkiRJK2iF\nsulmQUwW/VoqU6dOfckqX2WVVQC47bbbGjm3QafVel3xM9JvX8w000xjpxemu31dU4Rx3HSziN3e\n41ZtP9988wFl7frJtGCXXHJJAB566KHpnmN8P670GberWiOm32sxjLLpdx2rqu095zHH6diuaszH\n/brSa1XfdltX5//SNFodMyGpbJIkSZLGGelKneJ8pDiXHy2UaIXVvZplGyyV5ZZbDhg/l77RRhsB\ncMkllwAw66yzdnxuX0U/yKB9Mkhf9Lui5vLLLw/Avffe63489oSvpdtc+1xzzdVxHnF/Ezh6p3ue\ng/RFv3Ps3Xx7VVZ+tz53nDguhmUy7pEqZeL1m3feeYGi4vwbx8viiy8OwHPPPQfA3HPPDZQ+djt9\nfl4rr53Kp4om+qKtQTPdSGWTJEmStIJJUTY+rWeZZRagREo9++yzQLEsVC5ur4XqdiqaKqs9asbH\ntgAAIABJREFUKqQ55pgDqI7IioxS2USre6mllgLgwAMPBIoK2HvvvTu2P+SQQ4ASovroo48CcNpp\npwFw5plnAt0tpdiXdUQdxUgrqZojjz6VPo7f8TrO6Tvenn766Qn3H1XIPvvsA8Dxxx/v+Q49LuJY\nrotulrBt8/PFFlsMKP4oz6fq+1E51dEXvVrvXkcVid975plnOl77e+D9Hn2/VdGL/rWP3I/jwPHo\n62HvkV637Qd9fJ6jfRDP/U1vehMwvu0XX3wxUNRfk7NCqWySJEmSxmlU2fh03WmnnQC48sorgfKU\nPfvsszu214rSEvVpqyXj/LPv93C+E74/itySbthX/v385z/vcQBYffXVgWKRbr755kDpmwcffBCA\nE088EYBzzjkHKPPO/foQBumLbj6XXvMgosKJitXva8UttNBCQJm7j4q529z7KHOO6sa+W3rp/78s\n/LLLLgvAaqutBsDVV18NwD333AOU8dQrTfaF564K9Lp5fePvgePC7y266KJA8X/ps7nhhhsAeOKJ\nJzq2d3zE6DNnYNy/x4u0YSZkxRVXBOCYY44BSh5VvGck+qdUrI6Tbsq76ncklU2SJEnSCvoqV9Mv\nzoFedtllQLWi0aI0YkYfi5atlkjMIZAqy7SuKLUmiBE35klorX/961/v2H6RRRYBSlSa1t9aa60F\nlDZq1cWImsnIPK7q/+i7iSrOc9ef8OSTTwJlzn7bbbfteF9rbIEFFgBKX7i/Cy+8sON4nkeV72h6\nmeqDjplRjTmPt8EGGwCw1157ASWC6wMf+AAAJ5xwAgDHHntsT/sdpi+qqMqv869jWV/L/2vvzKNv\nm+v//7hdraVhSZY0cS+SDJUpYwiZQ1mGlilEaLIyRAOhcFuJVomQuKKMGbuIDJE580wRKSINNNDC\n/f3R73Hfn8/r89n37HPO3udzru/r+c9nnfM55+z9fu33e+/n8zW99XzE7/v+iiuuCMByyy0HwOWX\nXw6U+SGrV6k4v2JWomvGz3dbH9QmHIvnusIKKwBFmfh+HFNciw888ABQ1twxxxwDwG677QZUZy/2\ncx9JZZNIJBKJ1tGKsonZZHvuuScAN9xwAwDzzTcfUHyoMgzZvU9lGUZ8Svv7fi8y5YUXXhgoT+9e\ns5x6gf7eTnGCmFHn5/U7y+Zkd6q6Cy+8ECh+6M033xwovlt/t6m6irqYPHlyZZaX75tV5DnG2hDP\n2UaYhxxyCAAbb7wxUGx0xBFHAHDTTTcBJctstdVWA+Css84CSqaedTyeh/PPHmna1vP1dT9MPn63\nikVXIcaxoq+86vsex/jmkksuCZSuCBdffDEA5557bo1RFDSpapzTXjfXp+fuGFdZZRWgqPfLLrsM\nKEpGD4gZWaq3Z555Bijzaf755wdKl4/rrrsOKPEqvQnGhOL5iCbWVL+K1zUzZcoUoCiTqBL/8pe/\nAHDzzTcDcM455wCw4YYbAuXe7Fx3fhjnUv09++yzPZ3neEhlk0gkEonW0aiyWXPNNYHyNJWBmCEh\nk5BR+loWb3feq6++Gij9oYSsQJZnho0Mx+P51PYp/eSTT/Y/uJqQfUe2VAWZiGzu8ccfBwq7j35k\n/dFmjaje/J6+emM+VZk0TWN2qlG1py2qelg5H1ZfffVR37N26JZbbgHg1FNPBWDBBRcECmOVtfl6\nr732AuCpp54C4MADDwSKMtpuu+2AogJU2mKhhRaa9d1e4ZztVlXLXFWsZo/JWLVl7KZhJuc666wD\nwAILLAAUFeHaNHuxLkb2AewXVvC7Pr2+/r7xSdezsRNZvbE717/r3WvlPPG1v+PaUOm6hqKydS3G\n8Y5Um33Uo4z7vtf54YcfHvf/3k+sv1t88cUBOOCAA4CiFr0XGoM544wzgDK39QbE+8Xyyy8PlPuM\na8nvx1hQL0hlk0gkEonW0ZeyibGTG2+8ESjV7vqLZWmPPvooUJ7ePi2NU8gs9KnLeCJ7k/Fus802\nQOkj5muZr0woKptBZJfUrQUS2kKVpw21iXU1jkXVJ+MxXnHwwQcDg4/ZjIeqquaqzsSyKmN7Kg5r\nQ6644gqgjM1aEjOuZGfORxWSNUvGjJwnHlemHZltt+x/PNTdc0U4t820c+04n2T18fecN8Y3Ntlk\nk1H/93frIp5nE2slxqGMB3juHkvFIns3e1UlIouXrauIn3jiCaCoOI+nLY3dxBhx7CdY1YuvzftF\nlaJxDcTeeXEN+f6ll14KwIwZM4CxezdpG9eCKtC57rUwy83fi/OuF6SySSQSiUTr6EvZxHiDDOCx\nxx4DYK211gLg+uuvBwozjZ+XmehHlJ099NBDoz4Xa0nMQpHBypRk/fq322BpoinWE1nfHnvsAcDS\nSy8NlM4A2sSMG330xm5kd7Fz9kTuFVQ3u0sbOjY7XMvKnTdmHX3mM58BSn2FUNFOnz4dKMz46aef\nHnUecZ+VNmqRxtkbZ7afl3V7XT1n14bs3s/51yr7E088ERhbk6Jtra/pdPwmMzerdsr0GB7T2Iue\nCmMrMaZiDMe5blwqVr97PVXM/q5Ku1Nn9Incmj1mxKlwnQcqD9eCikUFstJKKwHlHqgK1IbOR22g\njX/0ox8B5d6tR2WNNdYY9fs9jannbyYSiUQiURONZqP5FJZJnH322UBhW1XMUZ+6fkYzqMxK8Sls\n9pHK5/jjjwdKHYb+SRWPmVtN+N6r0LQfV4Yqy5PhGtc6//zzgWJrmbO1JZGt6fOVDQ4SdWsK/H9k\n637fegszrFQ+q666KlDmlWNUydi1WXVQlV1U9X4TKtC5W8XuI2TddoqQkTrmqGSMg+6///5Aud5+\nzuwk46edshPbYPGd4layaq9jzFY1XuXYVl55ZQDuuOMOoNhI27lm/D3nifPAGE7sGxjjnFVru41u\nChGek3Emz22rrbYCSpd3FY3XNXaQMI6uMnrkkUeA6j19pk2bBsCdd94JlLh51T5LU6ZMqZ2xmcom\nkUgkEq2jJ2UT4xQx4yV2Fq3yjcpUfErrj5StmS1iZo3sTKXi/81RP/roo4GSi+7nmt6tsE1EW2pr\nOwdElmc8TBYYuzP4Wt9tWzaYPHkyyy67LAC33norUF8ZxLiS52jGzMc//nGgxOasQdJHb3W07F9F\n3YlxxfNzPqkK+tl7RjW/6667jjpWVSfy2B/u9ttvB4pv3jltxwjfd0245lS6rj0Vr7aoe02aVHdV\nsY/Yv0/F4fuO2Risc977ifFM54+xm1in4/ecT84vlZFrJypqz8u16HHbjOE4FhXNQQcdBMBxxx0H\nlN5lnosq0H2uzOQzy8z5ZJ2WSqiqj6GK+rDDDgOK7d0XK8J7dq2x1f5kIpFIJBI9oidlE32ZUalE\nX2jcLyLuW2GfJjOujLnI1nx6ytJl8/po9UvKQKyS9nx8P+70OZFdoKt6X8nu9JXKcFVpcS8XfbHW\n35jB4+/IdNvuovDyyy/PUjRV6MTqowI25rbuuusCJU7h/DHrzF5XV111FVDGWtUlvArOt8UWWwz4\nHxvsdY6oaEQnpeD/nePuX6QNdtxxR6BkH8XdKz33uAbtgN0p8yrC/8uYjz322J5tUdVtW/WlovB6\nagPjTXHHTqFas8bM2jTXispHJeNxjd0suuiiQLl/RMSeilXzt0nE3mYqHOeBcWrn+DXXXDPq83YI\niJmWdTtZeL9x/qiomugvmcomkUgkEq2j0Ww0MxaquqxanapPVR+8vnZhvMEYwN133w2Up7OMZJ99\n9gHGMhn37Iixo5jJIxuYSDgmmbBZJO5qqlKJuxdq47333hsoNv32t78NwNprrw0UH28nVmqm15VX\nXtnXeMZDpx0747nJzmWsZhdFdhZZXrfV+vFz1utYJ9ak8u3UpTnGiawJ8bq7J9SWW2456py1hfUR\nn//854Gxe8/bMTl22q6Ca09m248tqjLx4nxQtRk7837iazsKqNaNPxhzWWqppYAS0/M6CjtM+L4x\nobvuugso8dB4v3A+qpTbzEazX5wxl5/97GdAWd9eD8euYq3KnKubLes1sCu4Yz3llFOA0knf+5E2\ndp7WQSqbRCKRSLSORpWNcQd9pzIGIUMwNmO9jE9p8+dlHmaLyN5UQDvttBNQMnFUNO466FPZjJ3b\nbrtt1HnEzgJzzTXXQHayhLF77jg2K3XNg7d6Xr+0MRozbPThO3bZn/UWX/ziF4HO++qINhSN7NhM\nmJjdFWN5sjDnkf5ox6jP3niW8+Yb3/gGUGoNNtpoI6A+G/dzxpx233134H+ds7uN+1TB66fartqd\n0r8q23vuuQcoFdwnnXQSUCq8VTyqf3/f4+nDr8pCrFJ/rj3VxHPPPdezJ6BKcboWvN7CWE3sPFG1\nRs2YcqwbbLABUO43Dz74IFBqR/SIqBKN6aoinV+xBmVkVX/b9wv7A3pu3ttUpv0qq7jLqR4SYTal\n6jLGfLtRNLOO2fU3EolEIpHoEo0qGxmLT0HZdqxa1jeu79W/O+ywAwCnn346UJimPc/MGbeaPmZa\nWCksZL7GimTOxgDs81OX/ddB3Z069c2q5syIMfMu9iDy3DfddFOgxGTinuRCm3Ri5m12tNW/W1W1\nLqONHQRk4SpZ2by7kwrnkXVWMlmzmeJ+SBGR1TsPO/UPq4OqKvmq+gbnqN1/nT/GI2XlMlGVj/FQ\nY33GL5z7fq7q+lYxZOfFyP6ETc2ReEzHaqw27lvlmI1bGGtxvhhrcZ7FXnjeh8zoUqEZEzS7Nda4\nxaxaX8+cObOxmI0K1H6PzgN7m+n52G+//WYdux9oS70O3n/swmKNo/OmydhUKptEIpFItI5GlU1k\nKD6lfTrri5Vxxv1OrJY111t/YdyNTtYljHNsu+22QGFx+lr19cv6mtiboQpR0cRMHJWI7EyGIUvT\nNmabycL23HNPAPbdd1+gsPAI2b9V9HU7LTeBONYqRRMzqSKTVcFab2XdlNfPrCU7T6hUhapPhltl\ng/h+k/OiSsFUISqfOMe1jXEvs8ucJ8Y/tY0dJ+IumHURP9+G8vU3nfvCNRTnhwrGeKd7rWg7Wbuq\nzs+rkI3RqGSMCaqIna8xHuP5NNlVQXiOjsHeZ9rGe2A/3SxGwnviaaedBpR+k843Fc0ll1wy6jwi\nerFFKptEIpFItI5GlE1ktD6lrWL36RzrJ9znWiVjbEafvbEZlYn74Zg5JcuPsRqftjIaMzi6raJu\nAh7D2p4jjzwSKFlEvi8Ll1XJ6sy4s0agqorZ/Wzc42UiuiPoU9dXHvfkELGHnv+Pu03a4Tr60h2b\n8yDuydEps67q+o8X9+rVjsYJPKdOsbF4HD/n92TXsneV7VFHHQWUjgPOn5NPPhmYmL1YIqrqrKqy\nEIVjN26lajOuqer3/hA7hejx8Hdda1//+teB0lfM36na76rJ+0VVn0av62abbQaMjU97fb1X9gpt\npSJ2fn7iE58AxnacqEIvtkhlk0gkEonW0aiyiU9D4w8+BfU7ylj0mcra9JnKcGVv1mncd999QKle\n3XnnnUcdLx5f366/K7Ox/qfJLLROMB5ghfcxxxwDwP333w/AeuutB8C1114LwCc/+UmgjNExV/U6\nsiurqqIT2lB38diyOBWPGXh+zhoiz2X77bcHih9beI5mmfm7KuPYQ8/YTkSs74i7HMYq6X5sE7MA\njTdGX3wnOFbPfZFFFgHgiCOOAMba9t577wXKmHpVNsbBjLP2g6pMSaHy8LrHXovazNoOx+TnrKcz\n9mttkB4NvQJ+X4+H86Xq/PTMaIMm7hdV9U6O3WywOPboBah7XZ3rxmZUwiop7z/GAD1e3GG2CaSy\nSSQSiUTrmNQNe5s0adK4H45MRWXSaXdI/dr+laXJAu0UoJ/SPkGyRllCjMX42kriq6++etzPR8yc\nObN2W9cqW0SopmRZKht7H9nLzE7Dfi72iYpKROZqT7ULLrgAqK6y7hbd2mK8Lgyes9cz7v2ur3zr\nrbcGSlX85ZdfDpRu4O6xIYM1trfmmmsCJQZo5wB99VW92OL5OV9H9r4a+flubPG6171u5iKLLDKL\nMcZjiU7rTgYbu+3aG8u9W7SBDNQ5b31Mv4hMutt5Mbv6HMcW7xceM3aNdx4Zm3G+OGbvH2Zk2tfL\njE9/z9okPS0qnar7VswQHNE1vvH7hbGaJ554Ahirpsy0VMHGztgqFufHFltsAZT7jgo4dhnvV8HU\nsUUqm0QikUi0jkZiNpFBRn91VQaVbElGLMN1tzmZbPRjyv5jd1YZh8wn+iEHgRgX0Ber/1c25U54\nSyyxBDB2N8EIbWrPsxkzZgBja5YmCrM7fqxfcYz6hR27ylVmqbrbZZddgOJ7N4an6tMXX9U3qlO3\n6SZt98ILL4xRNSOPXXcuxjFoCzPt7HxuDMd6mk5dE+qi2/Otwsjvx6xC7e7cjh2wXUPOD9eKCsfa\nM/d08lhmMapUtIk90pxfxnI9Tqf7Vpv3EY8VPRZmzqlIrBHSdnp9HIsqLtbhxbotd3D1eINAKptE\nIpFItI5GOwjU3TfEp6xPZzMlNtlkk1Gfs3bEaviY7RR97uakGwuoyvyI329j3xJVm2zbvyeccAJQ\nxnLggQcCMHXqVKD4amX/1uWY/27NwSAz6fpFZG1ef1/LyhyT8QbZvIxTVaiNzCqUqfr9qHTjdY71\nP1HZNDkf4rkI4wcxs0rEc9YXLzu367e/axZjpzhpXbRRp+WYRvYYg7FxqXh9fK2HwxieWYN2LDFW\nY5ara0U4j1RCVcqqaiffQdTneS5nnnkmUJSLvRM9R9WhPdQ6QdvaGaCpXmvdIJVNIpFIJFpHI9lo\nEXU7H0cGY+aWGRLua9NpD4fISKKvN9ZtiH6yjurawnOJcQKZrRla9kwz0yrW0VSxrRrn2dP3mrBF\n1bEde1X2mkrVONchhxwClOtpvZVxCquh7ffk+xFV8zLWlIxUHf+/w2/j86LG7wBlXjh2s4qMb2or\n67JUOHW9DN2y9zZs4fqNFfzRE2IcQpsYw1P1uQePnQGq7j+uOVWEvxd3v4wYRDaaMC5llphjt7vG\nRRddBJS5GjuoOxbnhWrP+0vTiiaz0RKJRCIxFGhF2fSLumw8Mo1YsV43M8ceWG0ylTb3jZkdBqVs\nXvOa14xRbyIqB1+rOKPS8bU1BbIzK77tAu3ulDJjY3xVjLbb6mtrh5qcF+64qQIZ5/vA2HiGcQbr\narSFNpo2bRrQef+ifuMOTdoinkvMUotZhM4LY3nGNV1TekDszhAVkgqoqp6nU5fykdfklVdeadUW\nnRA9JlVxyEHdb1LZJBKJRGIo0Kiy6ZU1+VTWTynzkPn2+nSuez6DUDaDQhUz7taGvdiik71j3UKs\n5fC1WYXrr78+UFSAWUdWjl988cWjvmf2oa+tw6mK2XXC1KlTefLJJ3nxxRcnjMFGxN54qsROvdaM\nU/RqC9HkvKib/eVfq+Krslp935hdVa1QVNLdrpFelc3suogPshN9G0hlk0gkEomhwITEbKr2t4h+\nyE5MQz+2/utujxsxJymbbuMP3aKNbLR4zlWMMlaSd/I/V8XuOtVZ1UU/tug1/tgJVT77OB+qMv96\nRRPzotPcrVLncR75vlmL1q7FfY+M4fk5O1oMU/xqxOf6OqeJ+v1UNolEIpEYCkxoNlq3nXB7RV12\nNycpm4imGcsgM/Oquob7fsxai5Xo0bdflRUXEav4rbeIWUkTOS+qOg3Ebhn+v9d5ENVg1X42g1B5\n8fNCxSKicu2kmKrmXVRQVbGgcXruDXxeWItovcyg0Y8tUtkkEolEonV0q2yeAR5r73QmFFNnzpz5\nlrofTlsUpC0K0hYFaYuCtEWXD5tEIpFIJHpButESiUQi0TryYZNIJBKJ1pEPm0QikUi0jnzYJBKJ\nRKJ15MMmkUgkEq0jHzaJRCKRaB35sEkkEolE68iHTSKRSCRaRz5sEolEItE65urmw8PWfLJpzMmN\nOJtG2qIgbVGQtihIWxTMsY04J0+ePKuD6zAjdqVtEm3bYNKkSa2e//9VTJo0adaumLPD3HPPPWsn\n0UR/mGuuuWZ1x24STa+Rpn9r5O/NCet5KB82iUQikXh1YUL3sxk2DJMsjntvuJeHr+vu0Bn3eqm7\nE+Qw2WKi0a0tJk+e3NoOquMcD+h+/5pevzfI/WwGhW53SRXDZIu4l0+/80LU/f4c60ZLJBKJxKsL\nzTs66Z0piE5P5WFlSOOh7rlGRhFt566BcbdCP9fp992J8YUXXuhwxq9+dLom/e6G+PLLLw9sjvb6\n+35v/vnnB8qOn22i6lxf//rXA/Dvf/+79XMYD1U7d7aJqmO4vt2FthO81/p78T4SY1lxl9tOv9uk\nQk9lk0gkEonW0aiyqatoon9xmWWWAeCNb3wjAIcffjgACyywAADveMc7gPL03nTTTYGyV/3tt98O\nwHPPPQfUZwWDQCeWFG2mDdwDfo011gAKQ1HhPPLIIwDcf//9o44TlYu/ry0ff/zxXofSNYZVgXY6\nnyb2dx/0mHu19eabbw7AD3/4w8bPqRPMxuukaN73vvcBcM899wAwdepUoNwXpk+fDpT7ikrJub/b\nbrsB8K9//QuA6667DoD//ve/QLkPDcM89d7leve+4F9Vtzbba6+9APjnP/8JlLHecsstQLlHzjvv\nvADsuuuuACy22GIAXH/99aN+X3httFm8//SCVDaJRCKRaB2tZqMZJ/Bp7bFkJOuttx4AK6+8MgBr\nr702UJ6mKh6fqn5fJhKf+h7nrW99KwBvecv/tsWuy+YHmYElE5VBLLfccgAsuOCCAHzsYx8DYOml\nlwbg/e9/P1DG+tvf/hYoKlBms8QSSwDw+9//HoDzzjsPKIonXu+q6z+M2WhV7L1tBTWMtqhCZPdC\nRvriiy8CzKoFkiGrAi6//HIA1llnnXF/v01bHHrooQAccMABo95fdtllgTLXXecbbLABAM888wwA\nb3/72wHG1Kd5v/B7TzzxBADf//73Afje974HlPvF008/HccBjLt2+rZF/G2vwzzzzAOUdf2mN70J\ngB//+McArLnmmkC5f0QlJKJq+9WvfjXq7y9+8Qug2OTPf/4zUGzovOmkbDIbLZFIJBJDgVaVjU/p\nEd8f9b4sfsaMGUCJvSy11FIAvOc97xn1PZ+6+i1lb/5fH+zGG28MwNVXXw2Up3onRtwGa6uq6vV9\n/dF/+9vfgMJY9Ctvt912AHz4wx8Giq20hazPMT/22GMA7L333gD89a9/BQpbq5t5Mwxs3nnidXUs\nKuZ7770XKGrO+fSf//yn0fMYBluM+H2gXDdt4Ty66qqrRn3uDW94A1AYrmvq73//OwCrrbYaUJju\n888/DxQmu8MOOwBw8skne9zWbFGVWeVrYzUPPvggAI8++ihQ1Nriiy8OFFbuvIkxYjO+rr32WqB4\nWOreCydNmsTMmTMbtUWM3X7wgx8EivLcfvvtgaK+9IQ4Zj9nVqGKyPuBsd13vetdAPz6178G4Mwz\nzwTGxruj1ygi2jSVTSKRSCSGAgPpIBD9yLKmddddFyiMQpbu01n/oKxLJrPhhhsC8M1vfhOARRZZ\nZNTvPPzww0CJdwyyaj6ysU7Kxiwxs0VULNpKxRNZvjbUFjIcGcoZZ5wx6nW3WSQTweYds8xT9l1l\nSxWM7F4l67xqChOpbByzytZ4p4pjpZVWAorv3rXmfInz0XjItGnTgJKtpM1VNpG5ijbWSBUcg3+3\n3XZbAFZccUWgrHNZu3FJ57xK2PuDYzn77LMBuOGGGwDYZpttgLK26qINW2h371neH1RfKliv0wUX\nXAAUz4VjFyoVbWhdlTG7GM966qmnRr1fF6lsEolEIjEU6FrZ6K+s+flRf2VfsiljM+b633fffQDc\ndtttAPzpT38CxjJcv3/ppZcC8IEPfAAozEamctdddwHwxz/+EehcB9Qkg40s3HMWMYvEc5ely1xi\n5l38fetydtppJwDOOussoGTodFJ1bWbadPF9oNjCOhfHFs9RRht99f/4xz8AOO644wA46KCD+jmt\nWejGFksuueTM6dOns8oqq/R1TMd88MEHA7D77rsDhekK50esGTFW45zXViroTp0kZL4x/tXtvOjm\nflEF18R3vvMdoMQnn3zySQC23HJLoKwp/xrj8b5iJpdxK22qOugW3dhi8uTJM+eee+7aXRK0vx4J\nx6QC8X1t2ykWq2Iy3m3Mx7WkLb3eVfHtqh6LqWwSiUQiMRTouoPAyCeeT9sqluTTWXblU9On60Yb\nbQSM9bGff/75wNhsEo9ndb3ZSGZWWA1rlon+yW47HjcB7aQNPHezRGI/KPPo/b8sX1+6zNQx+H/r\nIQ488EAAzj333J7OcyLhOcja9M2rULbYYgugsLDI1n/5y18CsOSSSwJlHtRFE9XR4oEHHuhb1UCx\nySabbAKU2rH4/9/85jcAfOQjHwFgoYUWAuDGG28EiqK+6aabgGIzEZmwXoHTTz+97zGM/F1gll08\ntyrEczJOYZzKNeVasCZFJWNMR8+IcU8zOa0lssakE5qYH6+88sooVVOlQJzb3lN9be1hPKeqfXxi\n3Y42c37oTbK2KSqlqt/rZ8+cVDaJRCKRaB099Ubz6dbJ7+uTPPr7jMHIVH06x9iOT+GFF14YKCzf\nWhTZ2mmnnQYUxSPTsTOBjNnYjbjmmmtG/V6TcAz60GP9gtD/fMkllwDw3ve+FyiZeWaZ/OEPfwCK\nzawpOfroo4Hi137b29426nuyv5jlIoZB2UTYv8l4hddZOA/0vVs57nXWVnWznppQNE3DMdo5Io7B\nbMNddtkFKIpFG6ho/J627NRBQkVjHOyhhx4C/qec9CB0C1l1J0UTz8nr96EPfWjU78jW9ZDoFTji\niCOAch8w4+6d73wnULJZL7roIqCshVgPWNVxXU+La60XdJqT8djxdczo9X5h5q394zyOisj6HD0h\n3ltj54GYxVgVCzLmY21kHaSySSQSiUTr6EnZdLs3S8w2kn2bRWKGjU/dO++8EyhP41uWDLD/AAAN\nXUlEQVRvvRWAKVOmAKXvl/3BZB5mI+m7t5Ot9TgyHc+/qv9TE5BpRlWn0vFcZYuysa9+9atAySa6\n++67gZIxo03s9qq69PtVefJVO/D1ujNfG5BVWa1uv6YIx6Yvfr755gMKc7VOaxhVW10cdthhwFim\n6bw555xzgLHZYjfffPOo1/7fWrW6UNEI4x29oNeODmbOGY+s2pvFWI6K9sgjjwSKF0Avg2rN+4Xz\nZtVVVwVKJ2Q9Jda8Cf/fD3rdOTN6fewwoG28X1hr5jxQeaiQnT96ebw2UcHoHdILFf9vvLwbpLJJ\nJBKJROvoqYNA3Z00RezjJDv/whe+ABSfrOxJNnfMMccA5akts7Ay2B5JVRkdK6ywAgB33HEHUFRA\nVaypl9qSWLtjbCT6PGN/Nv8fK75VZbGTQKwMtkO27M+MLPPlVVbxePG4VXv/TETVvOpMdmb9VMSb\n3/xmoKg9v7fZZpsBZWwqnbqw0jx+r4l50S2M8VlrZLxAn7zZZypZffAqYdeMrN8YT10Y74zxskHO\nC9ev2aXGbJzTDzzwwKjPm7VorFgFE5XM6quvDpQ6PJWwayd2wm6yLq/XzDa/Z3xSNWZGrzFce6Gd\ndNJJQJnTqjpjOCof973xnlgVo+mU0Zt1NolEIpEYCrQSs5ERxBqRWEVv/rwKxhoRn7Kybp+qPrVj\nJwGPZwzIzAw7pRqrcf+KJlG1f0TsYFuVBSTD8fMyUyGL93Pa5IorrgCKzzVWkmsz1WQ83jBmYHnd\nvY5xXxJVn0xX/7Vjs17LTLxulU23n58delU0zgOVTVS2/l9fvczU2iQ/71pR8XaLqGgmAiqVqmyx\nL33pS0CZD8bwYnd5P2+s2HllHMtOJK4hM/yMVzSJuuuuynvkWFSy9nczI8/7hfVSZgBeeOGFQFHC\n2sYxR89HRBPxz1Q2iUQikWgdPSmbToh+P9mWf9/97ncDcOyxxwIlYyKydNFpPxp7YMkG9VObcSGj\niUynzR0eq865CvGchOrws5/9LFB8rdYIVfVA8ndiV19t7N+2d7nsBrFORj+0PnR3VLTv26KLLgoU\n26lozWabE+F1mD59OlD6d8lYrS2xDkumrCqUue6zzz5AiUcMA+rOtardJ/WQuAZUbbHfWNzRV6hU\n9HS4JjbddFMA1lhjjVHHEU12mKiL2AFAG3idnR/eUz0397Ey+8y4tvdC15j3CeNgZqn52msVs9Wq\nuoHXQSqbRCKRSLSOVpRN7HVl5oxPw5133hmAT3/600BRJN36M2Uc66+/PlDqMowBxTz9qrhJE51p\nI3r9vZj9YQxGZqtfWh+ttovZZzIUM7WMY2jjYVI0EbGORgVjXZRjifudmJ00jGOqC8/danhZt9cx\nMsvYd9A5f/HFFzd6Xq997Wv7ZvZ1r8unPvUpAPbYYw+gKJ3LLrsMKHU0dTsoC23o2vF8rNszzhXr\nguK4e7VFE/cZr78xvFjPd+WVV476qwqM+xRZR+Nrax1Vf967o4IZr36v7phS2SQSiUSidbSibHzK\nWidhrys7A8Ruq516rFVBZSO7Mwfdp/0JJ5wAdGZUyy677Jic/bbQraJQ0bi7oHEMGWzMk49MN/bI\n6uRzbYLB9gvPVT9y7L9krO9rX/saUPzJJ5544qBOsXXIMO1B9bnPfQ4o8UmZpxlV7uRp9qEs3pq0\nflFVj1UHdee8MZR9990XGLubpPGq6667rqfzML4RUVWvJ/qJU4xEN6omZuB5XePOu56T9VjaUGUT\nY7PeM1WL3kdUd75f9x4wzzzzzOpU33FMtT6VSCQSiUQfaEXZCOslZN/uoXDUUUcBY+MMEVW53z71\n9b0+8sgjQNmf/bvf/S4wtk6n6jjddC7tFVUVuVXnJgOxAlh/tT2J3JHT7ggi1u3EyuDImCL6YbCD\nwtZbbz3qtVXRc3KsJiLWRZmJd+qppwLF527807UmYseJftFPvKHu92TnMWPKuastuu21FnuoxUxR\n15b730RERTPINRJrCj0X7w/GdFU03mu9N2ozbanijbWQdtY3a83j+v+qMet9qINUNolEIpFoHX0p\nmypWrh/QLDR3TjRW89Of/hTo7AONv+/T3b/uU2Edjb2yZEiR3fXrc+0GsYo5Hjt2U4iQUVhFfdVV\nVwGF0Votb/wiKhfjV/p67fukT7aN6ui2oU2XWGKJUe/r4381Q2Zqhp6xmGWWWWbU51wrTdeGDEI1\nureT11nPh3GpnXbaqadzca3Zg9E1IlvXS1AFz8d+c3VjFL0gdvmO9S6eg/NBBeN8UKHETgFxl2Oz\n06x5vP/++4EyX7z/VGWv9tL7L5VNIpFIJFpHX8qmKs4gqzbDwVhNtztixviGXVut9FW5mKnl09ie\na1bZDxJmvEQfZ/S1ygh8HT9v3rvxKG1h11/ZVczIc696r4E20rfba+bfMMAxRZx55pkDPpP2oBJ1\nvjhPqnzmKlzhPIlV8HMC3LdKJaKa7zXLUA+L8S7jn64BO6uvt956AJxyyimjvh/ZfBuKJsajo1JQ\nycTPqWyih+LZZ58d9Ttm9Hnv9P6k98fX888//6i/2r7ujqJ1kMomkUgkEq2j0Wy0H/zgB0Dpwirr\nMlvo/PPPB8ouc/a4itkhPrV9+rrP9lprrQWUSl/9ku5F7x4PZuz41O5UadxkBwF9q9YExDx42blK\nxD01Ym80mYj+apWJe/pccsklwNhMLOty3M/iW9/6FlBsbfZIZCbD3FFAxI7YsR6nKTg/e63n6Aba\n3flhNwz3KbGKfrwqdhgb++u12/REIO4ftPzyywMlDmk/wB133BEocQezR2PHCNeUnSaswzKmGxXN\n8ccfD8BPfvKTrs578uTJjcV/Y4zN3/X6Oi/8v7EZla4x3JihayzGfYm8V5q9av/B2267DSi91Nz9\nWEVUpeZGdrXPDgKJRCKRGBo0qmzceVO2rkLR7ygzMQ5hPEElZIdaFYrV8j69hXuLf/SjHx31vS9/\n+ctAeYrXfeI2yeb9LcemElHV+b79vdw3xA621tFMmTIFKH3BZCSyP22ojz/2SJK1Pf7448DY7q1V\n5z3M0AcvzD5sGoNQNEK7O8fNJvr5z38OlOsbs4JUA3HPH1VeVSxwIhHVs2OQvbtWjJ3Yxdv+cP51\nDsvyvX+oBr3PeDwVzf777w+U6+uaqlIpMWZc1U26CcT9r7y32XXF7DEzMVUs7sBp3EmoSPz/fffd\nB5T7irWOUV0aE9aTUrUvV8ZsEolEIjGUmNQNo+20p7h7hstAzD5Tqci24p4rkUFEyCTMkJgxYwZQ\n/I0qKVldVa1BVVzCmE2T+6vrcxX2rrJfm7EVxyYbU/lcdNFFQPFP60t1571YOezYzNzRVqeffjow\nNlZTtaf4vPPOy/PPP89LL700sL3mO2GrrbYCxtZDyIiNW7WFJudFFYwvOi+E80KFct555wGlZ1qc\n04cffjgwtm9cU2jSFo4tZtzpCdlggw0AOOyww4DC0kf8/myP77pXAe+3335AyZKNtonV8p2q55u0\nhffEGHuJ3p1VVlkFgK985StAsWHMYvSvHQHMzDXO5U6/rh3j4NrE+0unvb/mmmsuXnrppVq2SGWT\nSCQSidbRaMzGPHm7qBpb0Ueq0rFOpkpV+VSWjRuLsYeRcYhOrC1m8FQdr414hWxIpmL3BHdYNNtD\nxmLGjVkk55xzDgC/+93vgMJQIvPwrzazb1jsKBBtVTXmYeosEPf0iXA+OJ/mpEysCDMmja3JqqdO\nnQqUmJ9ZQ5HVW19hzVGvthhkVmLsVO5aUN2r4ozF2DHEtaMaiLEUu2VY36d3oJNNooIZZLzLczcu\n6Xzwengv8/7hfcFMXG3oPNCDYmcAu7hoG8cW6/66jel206EilU0ikUgkWkejMZsqxIwaq1R9mus3\n9CltloldWPvN/qjL1gbhmxdRccgwPNeYZdaJecReSvFvtzt0DtIWnaB/+tBDD/V4QMk6tNt3W2x8\nImwhe1epWiuiDZwHjtn4Vdt7ETVpi273uYkZUY7ZjCo9Kt12hY7otH9NGzHeKnif8P4gYh2MNoox\nm073i6bWTMZsEolEIjEUaETZNLWT3URjmNj8iOMAnbv5xn1q+o1fDJMt4t4dUQ32C/3bu+2227j/\nn0hbxMpy54MKZ9q0aUCpw+gXbWRgxTlsd4ymdhGdKDQxL9qOkQ0qBpfKJpFIJBJDgYHEbOYUDBOb\nr4u2mMsw2kLWbTyr7foaMQhb6IPvNt7Q6/d6RZu26GWPlIrjAv2viU6/M4xrpGk0GeNNZZNIJBKJ\n1jEhymZ2lfzjvd/W8SLmBKYS6yvq2qrb780JthgUJsIWva6FhRZaCChdfTshdqAwVjNMbH5YO5IP\n4xqJMd2q3mZ1UVdtprJJJBKJxFCg23SevwCP9XvQQVbyd/G7U7v82UZs0S16tVGX35sjbDEgTIgt\ner3OdRWN6LJKfo6yRcsYyjUSs1T7jX/V/H4tW3TlRkskEolEohekGy2RSCQSrSMfNolEIpFoHfmw\nSSQSiUTryIdNIpFIJFpHPmwSiUQi0TryYZNIJBKJ1pEPm0QikUi0jnzYJBKJRKJ15MMmkUgkEq3j\n/wEP0qPq0cr5CgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"rows = 10 # split epochs into 10, so 100/10 = every 10 epochs\n",
"cols = 6\n",
"fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)\n",
"\n",
"for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):\n",
" for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):\n",
" img = img.detach()\n",
" ax.imshow(img.reshape((28,28)), cmap='Greys_r')\n",
" ax.xaxis.set_visible(False)\n",
" ax.yaxis.set_visible(False)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise like 1s and 9s."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Sampling from the generator\n",
"\n",
"We can also get completely new images from the generator by using the checkpoint we saved after training. **We just need to pass in a new latent vector $z$ and we'll get new samples**!"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZkAAAGRCAYAAAC39s6jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJztnWm4FdWVhveNcWIScEBBBBRBUVEB\nBYdGjVPHiVbj1BgHNImtJumgSWur7ZDY2q3RjlOMQ7TFJI5xwqgxYsQRFQFFQVQEZJJBAXGM5vSP\nfmr5HqjFrbqn9hku3/vre4q6dar2rjrF+s5aazeVSqUghBBCxOAbtT4BIYQQrRe9ZIQQQkRDLxkh\nhBDR0EtGCCFENPSSEUIIEQ29ZIQQQkRDLxkhhBDR0EtGCCFENPSSEUIIEY1v5tm5qalJ7QEqoKmp\nKYQQQqlUCqVSqanA42peCqKoedGcFMqiUqm0YREH0rwUSqZ5yfWSaWSSL/gQ/v9LvhasueaaIYQQ\n/va3v9Xk84VoUGZW88NifFdkOeY3v/n/X8dfffVV6t/9/e9/z/WZa6yxhmkesxK+8Y2vza+///3v\nmeZFdpkQQoho1CSSKep/Ciu8VVe5b5bPyXO8lvDFF18UfkwhRMvwvodiOB08Jj+X3zlffvllxZ/D\nYxcVvZCWfC8qkhFCCBENvWSEEEJEoyZ2WXM/fIXgh45Z9mkpMSwyIWpFPSS71DNZxiTLGHIf7/ie\nRZZmafEHe+87yTuvepxzRTJCCCGioZeMEEKIaNRVnUwW+6u5jAmGorEzRoSoZ3TPZydvplkWu6pt\n27amWRvHLFNaY8lxaJHx3/n96J0Xt2epk6mGvaZIRgghRDT0khFCCBGNurLLstBcSJclGyNp77Kq\nv/WOw+3t2rUzvXz58lWel0iH8+JlDhaVBSSyMXjwYNMcy8mTJ5v+5JNPqnpORcIeggme5UW4j3ev\nesWQ3GettdYyTXs/0Rz/JUuWmJ40aVKzn+99h3nWWefOnVM/q8hCTkUyQgghoqGXjBBCiGgUbpfl\n7f9VlM2RhIM8Bj+f4WWHDh1M9+zZ0/TWW29tesCAAaYvu+wy03PnzjUtiyyd9u3bmz7xxBNDCCF8\n9NFHtm3EiBGmR40aZXrmzJmpeurUqc1+piyyyuC9/+STT5qeNWuW6WXLlpnebbfdTDdaV/G0eyXL\n99A666xj+vPPPze9ySabmH7//fdNr7322qb5vcjx4nfRt7/97RBCCH379rVt06ZNM7106VLTfD74\n3cZje9Ydt3/wwQemYxV1KpIRQggRDb1khBBCRKNwuyxG/68soVtaNgT/jqEr7a9tttnGNK2wsWPH\nml60aFGLz6u1sd5665led911TZ9wwgmmN910U9Pf//73Qwjl2S0cN9ouHMPFixebPuCAA0y/8sor\npvPea7Q7Pvvss1x/2xphltO4ceNM81np06eP6V/+8pem119/fdO0iBr1OchSdMl7hvcSr59Wsbc/\n2WqrrUwn30U8BuHnkLw9HHmtzLSl1cbMWVrdLUGRjBBCiGjoJSOEECIaLbbLimq574WpDONotbDv\nT3M9hpjRwYyNI444wjT7C40ePdr0NddcY9rLnmlUayAvHMcjjzzS9LvvvmuaduWee+5pOpk7b61y\nr9cSi8TOOuss08cdd5xpzkuW4k1ZZD6cE68YkVmB5513nunW8BzkbenP7yGOHTPAvP1pM7/11lum\n58yZE0Iov5ffeecd016GGPGeLT7DfM6877ZKLTKiSEYIIUQ09JIRQggRjRbbZUWvShmC38eK2z3b\npbl9/+Vf/sU0Mz0Yxp599tmmGUa2BjsgLxy7Tp06mX7++edN09KidUYLcv78+SGEEC688ELbRotg\nww03NH3uueeaZpHsXnvtZfq//uu/TP/oRz/KcCVfk7dQuLXTsWNH0xwb7xkbM2aMaRYjtgaytM7P\nexyOKb9zevfubXr27Nmm//znP4cQQjjooINsG6396dOnm164cKFp2mj8TA9+t1XjmVAkI4QQIhp6\nyQghhIhGXbX6Z5jOQrHu3bubZi+ftOwy2my0c1j0x/CSPYBYdLk6WmQetEZoi7Hv0dtvv216yJAh\nphcsWBBC8MeT88x9LrnkEtNdunQx7dmoWUL9DTbYYKXzam3kKRDmmDHjyeORRx4x7a3Y2Ejwmj/9\n9FPTWVr9e2PLcWFRKy0y9oDj5ybbWcy88847m+7fv7/p8ePHpx6Pc8rvOc9Sq0Z/SUUyQgghoqGX\njBBCiGgUYpcVVZhJ62SzzTYzzYIkL7xLijdZxMnMJVphPPZ9991nmmFnXphRRXupllZCJWEuw372\nK9tiiy1Mz5s3z/R7771n2iuYTeD9svvuu5s+44wzTG+88camGeqzYJZksQDqwSKL3e8uzzG/853v\nmOacEJ4v7wlmSzXqkhe0qkjeeeG9R2uXBeATJ040ze8EZnol40hbl73NeF7sb8bCSW6nnZ3lvivq\ne3xFFMkIIYSIhl4yQgghotFiu4zhVyWhFUPwXXfd1XSWjAmeQ7du3UII5RllLGqincUQ9e677zad\n9zqYnfLxxx/n+ttqUIkdw1bu++23n+k2bdqYpk1AO5LjmMwdrdDDDz/cNNvH05bj/jwebZq82WX1\nQD1kLXbt2jWEEMJ1113X7L7s9/bb3/7WdKOM96qopBCR31uetfzhhx+apqXI+5n3cPL9R0s6KdAM\nodz+8o7nWf7efccx8M5LK2MKIYSoW/SSEUIIEY0W22VFhf0MDTt06GB6k002Mc3MDELrJgn12Gae\nGUq0tiZMmGCa2Rheu3OGlLTrWlv/JsJwnHN05plnmub1c9W+ffbZx3SS+fKLX/zCth144IGmaS8Q\njv8nn3xieuuttzZ9//33m64HG6pRSGzkLO3ie/XqZdrbv1F7wlVyrt7qkmz17y0HQGgLb7fddiGE\nELbddlvb5j0ftMWyFIl6cE5jrRyrSEYIIUQ09JIRQggRjRbbZV4xUF5mzZplmpZWjx49TDMcZWjO\njLGLL744hFBeYJWEnyseg8WdtM68VeWomb1GG8cLL2MX3xUJz5UZeE888YRprlLJ3ky0OqdMmWJ6\nxowZIYRyy43ZOJ4Fw8+/8sorTXPFUlqX9QzvPW8lwthwnDmHaVx00UWmWcBaVDv81gCvmd8DXias\nB5+F5PuP32tLliwx7WWUkUp6kXn2v3qXCSGEqFtaHMlUEr14/2Pmj1zstsz/MfNvTz31VNNJncxO\nO+1k29544w3TjFiY7+/9T9qDue88L49G+l+e1xqHY8Ruy3369Ek9DiPSpLWGt5gc4Vi9+eabpvkj\np3de9TzOtYpeCBee4w/SCRy/1157LXV7ayFxQ/L+r5/PO+9DRiN555rHGTt2bAihfFG/V155xTSj\nSs918Z6JLN9zvA7+baWOgSIZIYQQ0dBLRgghRDSqtmiZF8ZRT5o0yfRPf/pT01dffbVp1sFsueWW\npocOHRpCKA/tuMAW16ZnCxS2g/HWtecPt/zxzevi2qjw2phg8cwzz5geMGCA6ZEjR5pmywtaBskC\nZmwZtPnmm5tmiM65Y1sbtj/xfvBsFOusmrCrLhMzmISRwHF99tln455YjclTH5PlXuLxeD+zC/zC\nhQtT/5bPWZLsRNuatrG3sJpX68Lt/J7zbDTPgiMt6dSsSEYIIUQ09JIRQggRjarZZVly7GnXsDsv\nQz3W5wwaNMh0kjHDfbmQ1nPPPWd68eLFpmnRJN1pQygPb7O0cGhtdg1DZ2YjUbNVjMeNN94YQgih\nXbt2tm2PPfYw/R//8R+mmWnzwAMPmJZF1jI4Pux8nVg6HLMrrrjCNO/91X2MaWfx3qdtRL3LLruY\nvvTSS02PGjXKNGsD+X118sknhxDKFy1LsmZDKLftN9poo9RjsGaHx/FaZvFveXzONe3vlnTcVyQj\nhBAiGnrJCCGEiEbV7DLiheC0rmidMRwdM2aM6eOPP950YnUxu+LRRx81nbQ3CaG8kJSf79loWYqR\nVkcrIQ8cw/Hjx5v+53/+Z9Ncc54Fsx5ZFmJqpK7ARcNrv/DCC00nzx/H75JLLkn9u9Udz2ZiYaaX\nXcYu8bS92IKKHcmTwmXaU4899php2vncp0uXLs1+Prtp0w6dPHly6jFZGM/WNi1BkYwQQoho6CUj\nhBAiGjWxy/IWODF0S4r7Qgihe/fuphM7hiHtvHnzTNN+82D2SEuyKBqF2HYSw/Rvf/vbIYQQjjvu\nONtGa4Z9smgNMKOvkn5MqxscE9ooLPBLyNKBd3UkS289Pjfs1UdbnlYYs2KZGfbUU0+ZToot58+f\nb9tmz55tmt9h7NHIvowHH3yw6Tlz5phm4fro0aNN86cILvLIz60URTJCCCGioZeMEEKIaNTELssC\nsySoL7/8ctPsl5WErOzvw3Xns6y3XYl11EhFa7xOWmdeH7G8LdG5bvmtt94aQii3Lpndws/n8g48\nHovEiHderdnqbA6OFbP40mxGto6XXZYO708+E8zEohU2ffp008xA41jPnDkzdf/EomKfPxZUMitt\n3Lhxpmmj/eEPfzDN55A2HovU+QxxGZMiv8MUyQghhIiGXjJCCCGiUbd2GS0PZitx1TiGo08//XQI\nodxOY4ZS7AKzerfIaD8xHGdbd2bJcP8smXmERWOJBce25z/60Y9Mc768nlme/dW/f3/TEydOzHWO\nrRVaN+wXlzae/fr1s231fv/GJotVzDHkPrTCOI7sI8bj8zhcdiSxzmjt87mZMmWKae+Z5Hfl4MGD\nTT/xxBOp58Xz5XNG25XWYEsyUxXJCCGEiIZeMkIIIaJRt3YZQ8qlS5ea5uqZe++9t+mXX345hFCe\nUZal59jqCDNNuALlgw8+aPo3v/mN6bvuuss0Q2fO0bBhw0xfddVVphNLk0VfI0aMMM1Csvvuu880\n+8t5Ybkssv+HY7vjjjuapnVCWyRZ9sLL2lsd4XdF3uJfz2r0Vp2kHcbnL7GLaRt37tw59XM8TSvs\nkUceMU0rjJYXYYahd00t+dlBkYwQQoho6CUjhBAiGnVllzG8ZJYMezCxN8/UqVNNJ5YaQ9FaUY+F\nmTwPFkaSc845x/QNN9xg+txzzzXNeeGyCh06dDDNcDz53Kuvvtq23XTTTaaZMSOyw3l46KGHTO++\n++6mvUyg5Bnh0hYiHRY00nLyss48e42WZtrzwePzO4yWJv+OzxsL0HmO3nehd+4elfY6VCQjhBAi\nGnrJCCGEiEZUu4whYpZ+Usy02GeffUyfd955phm+Mrvo7bffDiHEL7r0ipRIvVhkHuyHxEwW9i46\n5ZRTTN98882m2abcy1LhXJ988skhhBBGjRpl27TyYnZYIMtxvfvuu00PGjTItDcnLExOimFX1+zL\nZIy8+5BjyIJvz37i8+5ZYRxrrzAzOR/2KOMyJ506dTJNq5PnyExcj7xZcpU+r4pkhBBCREMvGSGE\nENFoymPtNDU1FeIDMVxkeEk7gD17Ro4caXr48OGmEysmhBDGjBkTQvAtrLzktfryUiqVClvWMcu8\nMET2isS43Svk4/iOHTvW9MCBA01z7LbaaqsQQnkb/3qmqHkp6lkhHFfaL5wf7vPjH//Y9LXXXmua\ndkyDML5UKg1qfrfm4bx4z3iWvl0dO3Y0vWTJEtO08znO/Fvuw/5yiV3tLS/A702vKJr3QpbMuArJ\nNC+KZIQQQkRDLxkhhBDRqIldlsWK8lpvV1oYVC9U2y4rCs7Lsccea/p73/ue6QsuuMD0k08+GULI\nlslUD0Ws9WyXrcZEscta8LemvaLLWty3zPhktmgVzkV2mRBCiNqil4wQQoho1MQuW+GYprOcC7Oe\n2Na6FlQSJjeqXZaFWtsHlSC7rC6pC7usEjybP+1ZyfL8FLVyZZ7zSkF2mRBCiNqil4wQQoho1LzV\nf147pdYWGamnDJN6ohbX74X97P3FluhCVPOZ9ayrtM/Nci5e0XkWi8wrxs57DllRJCOEECIaeskI\nIYSIRl67bFEIYWaME2l0coaXPQr++NV+XrywP6dFVuS8rPZzUiBR5mV1tbULvO5M85IrhVkIIYTI\ng+wyIYQQ0dBLRgghRDT0khFCCBENvWSEEEJEQy8ZIYQQ0dBLRgghRDT0khFCCBENvWSEEEJEQy8Z\nIYQQ0dBLRgghRDT0khFCCBENvWSEEEJEQy8ZIYQQ0dBLRgghRDRyrSfT1NSkdQEKolQqNTW/Vzbq\nbV769+9v+tVXX13lvt6yybWiqHmptzkhyfK7DbTMx6JSqbRhEQfSvBRKpnnJu2hZ3dKAE1TXVLL+\n+SOPPGK6W7duqzz2uuuua/rjjz9u9tjf/ObXt+yXX36Z67zqAV47qeZ9u/baa4cQQvjss89s2xpr\nrGGaL3vvvCq5P7Kwwn8+Cl38LTk2r5OfR6r5H5/k3v7b3/5m2/LeL5zHr776qsXnknF+M82L7DIh\nhBDRaDWRTBH/m4r9v7NGIsv1e+PF6CXtf4j832GW6IX/O2vE6IXU6r7iPDCCSeB51cO9HzOCSDt2\nUdef9zuE85JEMDwGdZYxKWruirwHFMkIIYSIhl4yQggholFXdpkXaub58atWP6y2ZqvNywDzrnOD\nDTYw/eGHH4YQQrj88stt28iRI0337dvX9NSpU1OPV8kPmK2JSqwYzltyHP47j9emTRvTtCf5g/RG\nG21k+v3332/2XMg666xjOs26qwW1spmamxfe+7Sh586dm/qZlVxHUUkDK6JIRgghRDT0khFCCBGN\nurLLvFAvTwiYxWbzbIdKQs16sciKKm70xqhXr16mly1bZnrQoEGmN9lkE9Mbb7xxCCGE73//+7bt\nkEMOMT18+HDTlYTr9WjBpFGJrertn6XGI80a47nQIvv0009TP5P7L1y40DTt0Q8++CB1f85nPc/P\nqshi53vb82SJ8d9ZR+ZZZITbvdon71xi2dKKZIQQQkRDLxkhhBDRqLldVnRWFm0BhotrrbWWaYbr\n3nYexwv7vSyQWlJUERvnYs011zT90UcfmeZ4TZ482fTdd9+90vnw72gBLF261LRnb2aB5+LdUxMm\nTDC94447tvizspLWviTvPU4b8PPPP0/dx7M/vHs4oV27dqa9Ilf+XdKOJoRyS2358uWm2faH2Wi0\n4zj/ixcvTv3cmKTNC8lip3uZefxbz/7lPmlWZ2Ixh1A+nrQoCT+f8+J9Jq+bzzbvNT6vlaJIRggh\nRDT0khFCCBGNVmOXJaEpQ1SGmixk2m233Uz36dPH9GuvvWb6ueeeMz1//nzThx12mOlx48aZnjmz\n0EaxVSPL+NP24PgeddRRprt37266bdu2phM7gMe+9tprTTMTjUV9tNHyWpHedVTDIiPNWZe0KjjG\nHL9PPvkkdf8vvvii2c/h3NIW7tixYwih3Kpp3769adpynAd+Po/Hc+d50V7jZ9XCIiPNzYt3//D7\nxLMlea969y3tQmZlHn300SGEchuTGZwLFiww/dJLL6XuM378eNO0kD1LjzapZ5FV+h2tSEYIIUQ0\n9JIRQggRjZrbZVnCL4aX3J+hXhJishfWdtttZ7pDhw6mhw0bZvqJJ54wTcuHx9lhhx1Mz5kzxzSt\nBJ6jF6bWO17xFrcff/zxpn/+85+bppVCEmvk9NNPt20PPfSQ6c0228z0t771LdNPP/206by9sRoF\n2ky0XLj8gTcnHrwP+bedOnUyndhxvDdpBc2bNy/1vGiFeZmYhPt7mU477bST6RdffDF1n1o+Q15m\nKcfLuzZqZm7RmvzHf/xH04mlz4LW9957z/Qf/vCH1HOkzcUxz7sQHaGlfdpppzW7/6pQJCOEECIa\neskIIYSIRt3aZV6oye3MwunatWsIIYQDDzzQtjGLjBliLFjadtttTbOIkMdesmRJ6vl6WRqNZJFl\nOdfOnTubPvfcc0172TajRo0yfc4554QQyvsuEWbMcC5oJa0OePOQxebgfei142d/scQK5tjTluG9\nzAwxPhO09Lz9eX8wS47XQYuM1MszlCXj0sMrDOf3Ep+LrbfeOoQQwltvvWXb+J3E+erSpYvpnj17\nmubfMkuwuT52IZTfRz/84Q9Tr6klKJIRQggRDb1khBBCRKPmdpkHw0tmTLCocuDAgaaPPfbYEEK5\nFcYsjccee8w0Q9Tp06ebZgbaWWedZZqFmddff71pr5iuUWGWDDNg9t5779T9GYKfccYZpq+55prU\nfdJght7DDz9smvbK6kAWK8yzNlgYyUI+2igsgEzsX2b2JSuYhlBup9By4f0+ZMgQ0ywGfOONN1L/\nltaZ1w+sXiyyLGTJfqN1mFhhIZTP0csvv2w6ef44b9S0/JlRxixaFhxzHm+77TbT/D7lnBbV93BF\nFMkIIYSIhl4yQgghohHVLqukoIqhG60bWmS9e/c2nWS73H777bZt6tSpppkh5hVVHXrooab32GMP\n07QSvLbatPeSTLcQyrN2GgnaVcwo41i8+uqrplm81VzY7WUIMmOpNZDYFSyEpG1FO4NFlBwHb6VD\nr9CO9zbvvaRfGf+WWYPsQ3fDDTeY5n3A6xg5cqTp0aNHm2b/P9p43ncBMwonTZqUek2xoG3F5QoI\nvx+yZJDyOmlFsYibxcW8zsS+3HLLLW0bi1WnTJlimssBcG65Ai3n4o477kg9d2+c+T3LPmnqXSaE\nEKKu0EtGCCFENKLaZZVki7AAc/vttze9+eabm+7Ro4fp119/PYRQXrDEsJShLrPIdt99d9O0hbgP\nQ1baFMwoY1jN0Lg1sOGGG5qeNm2aaVosLbU3aMd4PbCKotr9sJIxydLa3rMKPfuFhZa8FtrCzG5i\nBtLBBx8cQii/95khRnuE80OLZvDgwaYvueSS1PPl8+H1SeNqpbHnf0U8i4x4K4Z68NoIx5f7cI6S\nfnDs4ccMWRY589y9zNYxY8aY9no+csz5nev1kWsJimSEEEJEQy8ZIYQQ0airYkzPzlh//fVNz549\n2zQLM5MsJfb0YTEYC5l23XVX01zpMi10DaG8MJPHJF4IWm2Y0cOiq7zQmuG4cCVLL+uuObzsFlqR\n3vIOvCavDXuWz60mtCF4X/HavRbxvJe4nfZLmzZtTDPTiNlT6623nunknueYPf/886a5yiv3oaV3\n8sknm2a/rCzzwDn0srcaCe97i/cz9+H1895ICsr5M8Af//hH08xmZTHmX//6V9OcOy7Z4BU38x7k\n/Bb1PRKCIhkhhBAR0UtGCCFENOrWLqNFM2PGDNPbbLON6bffftv0Pvvss9LxaBfsv//+ptl3iVky\n7LvE0JT9hbJYLtUoJPOoJLSlRXX44YebZq832iGeddgcnJdBgwaZvvLKK01zbn/zm9+YZh85wvni\n8Wkr1ApaZB7efeVlZXlFwSwoPu6441L/NslG4vM2fvx405zjyZMnm2bGJZcO4P5ZihRpI9XSIisq\n29ArqmXx6oABA0zz+2TTTTc1nRTHehlqfN6oee6zZs0yzXs/y/V5q6BWiiIZIYQQ0dBLRgghRDTq\nyi7z2n4zo4xhXK9evUwnLeNpf7GoicdgpgVb1NOKYTYa7Y68ITatgSyZN7WEtguz9Gj/sQhwiy22\nMM0iTZKMF7Ob2Ods3333NU2bi3YAixmHDh1q+vjjjzfNDMQHH3zQNJcdqAeytO5nZh81x4TWBvfh\n+LAvGDONknub481/5+ewDx/Pl89HFmvFW42RVDvTLEa2Ia+TReTDhg0zTduRhZTJPcB5effdd01z\nTPi9Qrh0hpeJ6d2Dns1faaaZIhkhhBDRqFokkyUC4P8CsixaxU7Jyf+CuDgQ/0fL/6k99NBDpt95\n5x3TrD3g/xoq+YGw3qMXwutkuw9GjPyfDGsr+IPzwoULTR9wwAEhhBD+7d/+zbYxqYPjzJYoP//5\nz02ff/75pvm/qvvuu8/0xRdfbPqggw4y7f1YXo15Se5n/g/Ru3/4P1NeI8ee9Sg8JiPtP/3pT6Zf\neeUV02x1lNznrHninDAZg7UT7Oq7aNEi097/br16H1LtOakEr70KtzNiT+t8HUL588FIJYFjwnnj\nnHv3lNf5Osu5ewkZqpMRQghRt+glI4QQIhpVs8vy/kjOH79oedAO22WXXUwntgzDcoaltMv4Q2mW\n7rc8pheyVrvDbwx43hzbJ554wnQyziGUd7ympcWxTmqSrrjiCtvWt29f01z4jHVKY8eONc26gief\nfNI0LTL+mEoLtHv37qFW5Fm8jVYRr+XNN99MPR7vYR7n4YcfTv0sHj+5n7kePOvMeDy2LKGlxnFl\nTRPPkc8Nn2HPFvNastSjjeb9YE67jD/833rrrabHjRtnmlZn0jWedWm0rbOcC60tLgjImhlvjrLU\n97Xke06RjBBCiGjoJSOEECIadVUnw7CYWRLDhw83nSy4FEK5pZOEbsx6oRXGzByufU7bgTnreVvD\nNKpF5kHLi9lG3M52L6eccoppWinJuuSso/n1r39tmnPE8J42AjNdmI3DzCvaAZdddplphvfsVuzZ\npNWE9wzvQy62xwwl7s86JtoybCvCZ4E6sb1+8IMf2DbWl7GOqV+/fqZpjzKz0OsUzWvifHK7R71Y\nZFnqmvhdxUUVmf3KRcAIrzNZiIzWIrs0swbGqzvi8Widccz5PHn1SF7NUku+5xTJCCGEiIZeMkII\nIaJRE7vMKwzy1pvmQjz8W25P1h/nQlpPPfWUaXZyZtZZFovMyyJrzTz++OOm+/TpY/rUU081/cMf\n/tA0w3FmBiVtTn71q1+lfg7XmWdWGMN1Ho8dtHm//OQnPzH96KOPmt5hhx1MT5w4MfUcYpMlI8fr\nZLzzzjubZiuX5H4Pobx9Ei2Vl156yTS7LP/DP/xDCKHcWmOGGNv40Gb2Mi7ZeZia88ZWNbRxsrSb\niUWWDDbvnPj9xIwyZr/yb70FxDimSddmZhfSZvTO17PxvCJRQmuWFDkXimSEEEJEQy8ZIYQQ0ahJ\n7zJPewVmDKlvvvlm0z/72c9MJ1YCC8a4IBCL/rJkjGTZXo8U1cmWx7nqqqtM77nnnqbZ5ZeZW7QX\nk35k/fv3t23smMweZVzkiR2h2dOM9gE/M7GAQijvTUd773vf+16oBd49w8wxz06iJXzkkUeaZpHm\n5ZdfbppZYl6B56RJk0IIX2f9NRHhAAAgAElEQVQzhVD+jCUZgSGUF85yATPuz8JpzhXvvywFzdXG\n+2yvcNSbR2Zf8v4cOXKk6ddff900v+c4Lokdxn/fcMMNTfMeoXXmFWByYbmBAweaZnGz933B6670\n+0+RjBBCiGjoJSOEECIaVbPLGN4x/GJ4R0uF4T17Wh122GGmmW2ThPgsymPhHkNjb8EfhoJegVm9\nFIl5FLXYE20aFlcyZGeo7VmgSaHad7/7XdvGJRWY9eJl7NDWoaXGzzn66KNN8z6ijVYP8Jy9Ndg5\nrsxE4nPw2GOPpR7/3nvvNc37nPdzUsjJTCgWp/K54jnSCqItxs/hdfCY3vVVY3Eyjyy90jzb3MuK\n++Mf/2iazw3H0SuSTKx+FnfyeePnZymW5FIOzDpk9iD/tnPnzqY/+OCD1GO2BEUyQgghoqGXjBBC\niGgUbpdlaZHPdeKZmcHCPBaHsdcYQ02uGpdkzDBzgqEms84YOmah3i2yovAsAPa9Ouqoo0wz64yr\nUabZJ8wEY38nWjO0Tvn5zLChvfDCCy+Ynjp1qmlmHfL+4v61wrNeveJGjgNXevUygbwVNvksJMfk\n2B977LGmmdnHTDOeF59DPs/MQPNsliwWWd4W9JXirTSZJSv2z3/+c+pxWPTN6+F3EfdPxoXfd8zg\nZEEtrUgeb6eddjL905/+1PQxxxxjmvYzYSF7kZm2imSEEEJEQy8ZIYQQ0SjcLmMIxewKZhQx5GIx\nHtuXs3cW7YB9993X9OzZs00n4SMtF2ZLsE05bQRm7/Dciyq6rMdCTi+TxuvRRvuE4zVixAjTzHZh\nVktige62226pn8lVN3mPsB/XaaedZpot5vfee2/TXobNP/3TP5mulV3GsfTGmNs5lrS5SN4iYhZ+\nJvPPLCPakFxC4ZVXXjHNZ4iWM/tyeZZSlnvfG49qkGU8aRfyfuP+fLaYIel9t3BeEhuZ35u0uR55\n5JFUze9B9qvjsiieHUiyjL+KMYUQQtQVeskIIYSIRlOe8KepqSlXrORlmrGnGHv6sNirffv2ptmS\nnGE6V/AbN25cCKE8pKd1Nnfu3NRzrHTVt5ZSKpUKWzMg77zkJUtL9OZgoWWW5RWYMcMVBp955hnT\nlaxumbZkQ6lUKmxessyJ17fPy77i/UwLk2PF49DeIYldTFuOxaxjx441zRVNaWfyWc1rhbXgORtf\nKpUGNb9b8+R9Vnjve5YT7XeOOVfu3X///U3zu2ibbbYxnbTd53dfz549Td9+++2maXVOmDDBNDNB\ns1iO1ZgXRTJCCCGioZeMEEKIaOTOLktsryyhGFfvo82V1nY8hBB23XVX0wzdWOzFYksWFSVZT8x+\nYv8dr7irXjK+YlNJWFxEMWpaMeCqoKXm9emqhGrMe55nJUu/LNqD3v1Me4ct+LlPMrYsqKQVw8/k\n88RMKGaUedA6or1Wa5Lr8+6BLN8VHCPeq7Qrn332WdO8/9lbr2vXrqZ79+4dQghh9OjRto2r+zKL\njD8zeJaeR7ULXRXJCCGEiIZeMkIIIaKR2y5Lwqss9osXUrO/0UknnWSamRFDhgwxzbCb2S7sXZbY\ncV62WIxCy0bCu+ZKMsfyWHBFWXTdunUzzfmvR5JnhfevlxVG64p4BXLUtGKY6cRstAEDBphO7Bja\nbzwvb5kFWmeE9gvhMT1qUaycfE4WmynLc+PNBZk4caJprgzLjL2k5x4zZNlfLu+SI2kZlCuebzXG\nX5GMEEKIaOglI4QQIhpRizFXcRzT3ufnLd5LjpO3RXWteovVYzGmV+xX7T5SITT+vOQtxqzkGr1+\nYSy2pKWVPE9e5pS3oiYzp5gtFuP+WCEDqmbFmBmPmbq96CJV73M4X1VeaVTFmEIIIWqLXjJCCCGi\nUXir/yxkCSO94j0vkyXZxzt23u1ZqMc2/nnxiv1qTex5KaIfW6UUdc9kWYGS1llib9H+8ixpFgty\nxUbvOfTI+6zUwqJtKVnuMe7TXDF4lmJQzmclFpmyy4QQQjQ0eskIIYSIRk3ssix4oVutw+jWYJGR\n2NfQpk2bEIJfyFcJlfSjq5VFRirJSvLwio7Tij29AlCOKy2yvCtXFmXpVJuinvGW3mNZxraS8fRs\n0lgokhFCCBENvWSEEEJEI69dtiiEMDPGiTQKBdlLPYo4CKjbeYlhkyVEsE6LnJdm56Re7da8fbw8\nCrTINC8FUqBFlmleclX8CyGEEHmQXSaEECIaeskIIYSIhl4yQgghoqGXjBBCiGjoJSOEECIaeskI\nIYSIhl4yQgghoqGXjBBCiGjoJSOEECIaeskIIYSIhl4yQgghoqGXjBBCiGjoJSOEECIaeskIIYSI\nRq71ZJqamhp2XYB6Wza5VCqlr73bAhp5XvISex6LmpfVaU6qwKJSqbRhEQfSvBRKpnnJu2hZw8L1\nxr1Fe+rtRZSHZF32CAt5VcQaa6wRQsi/3jnngnjrk1cyXy09x0YlGdsGusfrckE+kW1eZJcJIYSI\nRtRIxosM2rRpY/rTTz9N3aelJP+jD6H8f/VZlhzl3/JciooOYkYbRRyzW7dupufOnWs677xw3lsa\nHfAzOS8FLum70vHrLQpcEe/e9vCev0Q3cuRea0499VTT1113XQ3PpLq0b9/e9EcffZTpbxTJCCGE\niIZeMkIIIaLRlCdMLiozwwvTvR97uU/yI20I5ZZBYiV41+PZC55F5h0ny7lnGdN6zC6rtX3ifT7n\nnPZblvulS5cupt9//33TnvVUz9llWa6XNGeveeNah4wvlUqDijiQsssKJdO8KJIRQggRDb1khBBC\nRKNqdTIM9akZ0jNk90J5L6xPtvPYffv2Nf3BBx+YXrRokWlaDW3btjX9ySefmN50001Nf/jhh6aX\nL1+eepxGJYtFmGX/PGSx6Lw596xTHocWGan3TLI0sthiXlZk2jNX5xaZaCUokhFCCBENvWSEEEJE\no/DssqIylPIWnjV3DJ4XW5N88cUXqft4VkLXrl1NDx061PT9999v+vPPPzftjUHR2WXNtQrJO55F\nFf6lWW3evzdXPBhCCGuttZZpzh3ZYostTC9evNj0kiVL/Av4+rPqNrusBedgep111jGdFLRyLD/+\n+GPT6623nmkW3HFc33nnndTPjGRDKrssEttvv73pSZMm5f1zZZcJIYSoLXrJCCGEiEYhdllRRV1F\nWG20eYiXicTP5Pa8YX/eDKxq2GUciw4dOpimbeSNObtWr7vuuqa9fkUcX5L8LY/HzD1u5zFoabK/\nHc+XxymKerbL8lqYtMOoBw36f4djwYIFtm3p0qUr/fuKf7f//vubfu2110yPHTvW9MSJE5s9rxY8\n2w1plxVh+dc5ssuEEELUFr1khBBCRKOQYsyiiroqyUZLbJS1117bttF+oS3D7BkWZn722We5PpM2\nUt6/LZq0sWOI7mVWZen15llkvH7acSyC3WabbUII5UWs/DvOFy0yFlE+/vjjppctW5Z6LiRvD7RG\nIYvlst1225k+5JBDTPfp08f09OnTQwjlY7Pjjjua7tWrl+mOHTuanjZtmukbb7zR9Pz58023hqLk\nomilFlluFMkIIYSIhl4yQgghotFiu6yolvd5P4uWB3uNHXrooSGEEA4++GDbxpUeZ8+ebZpZNTNn\nfr1MNVe4Y18ywowRZj3VC0XNixfqe3MxbNgw08cee6zpZLzGjRtn2/r37296woQJpjfffHPTbNHP\nvnNjxoxp9tzz9kCLDW3ALCu05oVW8DHHHGN6p512Mt2jR4+VNAswt9pqK9MbbLCBaRZxdurUyXTn\nzp1NM9Os1stFNDLJs+IV0bL4mKsLDx8+3PRNN92Uun8tUSQjhBAiGnrJCCGEiEaL7bIYFhmtKBaB\n0eZg5gszXIYMGRJCKLewJk+ebJrZTcy0uvPOO02z55i3BEFey6Xa9sEqij8LOT6vp3fv3qb//d//\n3TStlGQO2BfphRdeMH3AAQeYHjBggGlaQOeff75p2mvsS+YR26rKQuzP3WSTTUxzTpIeZSGEcNtt\nt5lOMvr4rKy//vqm33vvPdM777yzae5PO5nXJ4ssHVrL2267remTTjrJdGL1M/t14cKFpnv27Gma\nzwefycsuu8z0UUcdZXr06NHNnmOs7ypFMkIIIaKhl4wQQohoFJ5dlhfaGcw6oqXFgrDrr7/eNDNi\nEquLtswll1xi+vnnnzfNYkEWY+bF601US4ummvYcLTLO0Ztvvmn62muvDSGE8OCDD6Yegxbl4Ycf\nnrqPN7ZZoL3J4sSHHnrIdKNbPLRULrjgAtO0E1n0msCxfO6550wn1nMIIWy88cam58yZY5qWz8sv\nv2yaFl0WS70e7MwVydKH0NuHNlZSiBxCCOPHjzft9VdMuw/5XGU5R2ad0Trj0gxTpkxp9vN/9rOf\nmf7v//7v1P2zokhGCCFENPSSEUIIEY1Cssvat29v2utz5cGeVxdffLFphpS//OUvTbO9O4sqX3rp\npRBCCKeffrpto13AMJb9nWjFvPHGG6Zps3gFiCxao2VBy6DaxLB+eM20tPbee+/UfdjuPbEJmJnE\nArOrrrrKNItryYwZM0xXYm96ll2jw6I7WpV8htq1a2c6scP4fLAvGZ8rFjTvsccepmk9PvDAA6bZ\nc47PFu/Lfv36pe7PottqW5g8V8/OIjw/rpB7+eWXm2YxbJbjJNYxx4R2Gb8rs7DRRhuZ9lYy9ajU\nIiOKZIQQQkRDLxkhhBDRKKTVf16LzOs/lrQgD6E8G4Z2wKhRo0zTOkuyYxhy0+ZiqLnXXnuZ7tq1\nq+m5c+ea5nG8rBfaCgy3G72l/IqwNT/tSG5nlhjnKGnNz31ZGLbpppuapk3BMT/66KNN5x3P1aHd\nuneNtGKYJZZkoHFFS9pszD5icScLmp988knTtIe9LDIWV9OWrheyWGTcZ4sttjDN551WPK+f31Uc\n6x/84AemkzFi5t5BBx1kmiuT8jP5OVxyhM9qLZ8DRTJCCCGioZeMEEKIaBRil+UtAGQBFgsm2Q6e\n/a/mzZtnmgVhDA0Ty45ZZGwdf+WVV5reeuutTb/77rum2frcs2UYdjLzgys21jK7LAbdu3c3PXDg\nQNO0NJldx3FM7JYtt9zStm2//famee/QcqOVM3XqVNONXjhZTWip3HvvvaaTVTK5WiYzAmfNmmWa\n9ziPd99995lmxp83P7S8G3U5AD77tPaZdUebl+PFpSv4fKTB3n6333676XPPPdc0nwkWXdKW5Hdb\nLW17RTJCCCGioZeMEEKIaLTYLttss81MM7z2YGYG24pfccUVpmmpvPXWW6YZjtOWou2WhOAsDD3x\nxBNN77nnnqnnxawbkqU3EbPq6iWLjNl6zYXlK+JdM4/j9Zpipt3ZZ59tOrHXaBfQRqC1yGOwd1KM\nzBiv71xrgjYns8SS8WfGHy1MPkNcOfaMM84wzeUA8o6fZ5FV20bjM8t7Mu/f/u53vzN95JFHmqbV\nmGcVXY4nLWQWpbMAlt+nLORkFlstbUlFMkIIIaLR4kgmS/RC+D9Hr5spj8lcfa+tC4+ZaC7gxAiI\nP9Txf9Vsp8H/2fF/7zxfr91MjEXcWkLe6IXwvDm2HFPWSrD2iD8iM88/+SGS48AIkOebdGwOofyH\nzRi01uiFczhy5EjTvN7kR3gm0TAyYe3YRRddZJr7x4jcq/2s5I1eCMeZi4mNGTPGNKPDPPDZY3LN\nEUccYXrQoEGpf8saNXayryWKZIQQQkRDLxkhhBDRKKROxoMhJcM+/sBL64Thq7duOH945/ZksZ75\n8+fbtnvuucc08/R3331302xxwuOxay3PhTYBf5TLQjIejVAbwOvkD4ivvvqqae/HfLbcSIP1TbQo\nn376adOcr6JobuGs1lDftOGGG5r2ugAnFiUtMta9cFG/pUuXmi5qfBq1TobwGpikdOONN5o+5ZRT\nTNM6Y/LM5MmTTSc2GWtdWNPHBen4fcp5ob1ZL2OrSEYIIUQ09JIRQggRjah2GWGeOK2V5cuXm2ZW\nBUNKWmRciIedkpOsJ9o8XhfYXr16mWabFGaa0RZiaEzrzAv7vTC1XsJXD14PNTPA2PqHc7fPPvuY\nZg1VkuHCzrs77rijadqSv/3tb01znXlaNpWMofe39bK2fB44P6z1uvDCC03z3ub+iU12zTXX2DZa\nPrSQubAZF5vLU/fRGmG2HjXHiwt/8T4/9NBDTTPrNW1M2TKG9jRhh+d6/I5RJCOEECIaeskIIYSI\nRtWyywizIbxCR8KiP9petHGSkJXWGhfE+td//VfTzDpjphMtA56jZ8F58BwaKWMpy+JX559/vmlm\nkXERK87X+PHjQwjlWTK0Y2id3nXXXaZpxdWjBVAtvMW02Pplhx12MH3MMceY5tjyPk8sHY4xMz5p\n2zCLic9eJXYZ57M1t/ehDcvCSNrCad+RzERjYSzh9wrt0nq0MRXJCCGEiIZeMkIIIaLRYrvM68br\nWWTeds8KYWjOjDIWb6b9LTNq/vSnP6Xuu9tuu5lmrx+GmlksMi+7rJEsMsLroXXhXT8XKuvUqZNp\nFlUm48h7hHaa9zmtzTppKV4hMu9Pr88fC1ppS91xxx0r/TuLYvmZJ598sulbbrkl/wWkkBROh1Ce\nGdWa4ZjSxuQ8brXVViGEr+cnhBC6detmmr3jkn1DqE+LjCiSEUIIEQ29ZIQQQkSjxXaZV8DmWS4M\nx72/ZUhPu4xFYJtvvrnpefPmmU4yyR5++GHbRluGn8kiNBYJshdZloymvFlPyfXFtII8C8/L4smy\nOJu3P7OTuJ54mg1zwAEHNHuOtAmqaZfVc085L/uSliwX5ON9zmfu8ccfN/3QQw+FEMptK2aRfetb\n3zJ94IEHmv6f//mf3OefxupikXl4WbTnnXdeCKHcIuNzy2xaPnv1jiIZIYQQ0dBLRgghRDQKL8b0\nbA4vA4K2GC0a7v/666+bpr3FgrQzzzwzhBDCeuutl/o5PMbtt99uOm+hZSVUwwLKW+jm9VyjfUIL\nxuvZtGzZstTPTQrFjjvuONtGu4wWJVvPV5N6tssIx61t27amaaNQ02a+9NJLTSd2FXvCcXVHZnNe\nf/31plnQ6Z1XvY9hvcEs3cSm9FYRZkFzI6FIRgghRDT0khFCCBGNqvUu88Jo2lW0X7iddg0tgBNO\nOMH0iBEjVjrGokWLTO+6666miyqW9Iqq6oVK7DlaI174zu3UgwYNMp0sq0B7h+fFTDRmO1WSPZO3\n8LeeCz95LbS0dtllF9NcDZOZW96YJ23nmcVE7rzzTtO037x7XBZZy+nXr5/pjh07hhDKx3n27Nmm\n6/k+XRWKZIQQQkRDLxkhhBDRiGqXZen5lSXriXjtsxOYRTZs2DDTMfr7ZLHImD1Ha6je8YoAvYw1\nbqc1efDBB4cQyrPVaFdOnDjRdFEFZq3JvuG13HzzzaZpLbJvHJ8P9pZjT78ePXqEEMrnjPYo5ySL\nRaPssnzQZucSGclPARzzm266qXon5lDp/CqSEUIIEQ29ZIQQQkQjt12WhNheEV/ZwZ0VIosKqefO\nnWv6yiuvDCGEcMUVV9g2ZpfVimpYZGussYZlDLHAzsMr5MsC545ZTV26dDFNizBZmmHy5Mm2bf78\n+aYfeOAB08wcbA39rfL0qqOFwqwv9t/jvZ3c7yGUr4zI4lb29ps2bZrp7bbbLoRQbrldd911plkg\nmKWfnyyyfAwZMsQ07/kEfmewz2KtqHR+FckIIYSIhl4yQgghopHbLktCf6/gjXhFj3mzFWi7EfYu\nS+wiWjWV0EhZYV999ZXZZBwTriLKMc9rkZEsx2GL+aeeeiqE8PVSDCGEcNttt5lesGCB6SzZZd6K\nrN45Zrm/YvUuy1M8xwy+WbNmmfaWvOjbt69pWpUbbLCB6f3228/0uHHjTCfWJa1V9p4jWa7BW7Gz\n3m20LL39ioI9FZnpx2clgc9BI7X091AkI4QQIhp6yQghhIhGi4sxqxkKMwRPCslCKLcPLrroohBC\ntuyqLHhWDKnHIjTPIivq/Ly+Y2+++abpq6++2nRSBMtiP+9cWLDpkWVe6mUuioDjPWHCBNN8Jlh0\nOWfOHNOTJk1KPWaerMssllJRvQCrTWyLjN9P7DtHS5PnkFjH99xzj21rVCuSKJIRQggRDb1khBBC\nRCNq7zKPLD3NvH2GDh1qevDgwaYffPDBEEJ5SOkdjxkdXk+zLOFovYesPD9mnTErLEtRrQfHmmH9\n4sWLW3RMFh5W0msur01Yz/NIK8rL6Gxp9mMWK6wSS4nny2JT75rqZR68IvK80CKmdfniiy+a5jXP\nmDEjhBDChRdemHqMRkWRjBBCiGjoJSOEECIaTXlC1KampprEs1lC6rQ+UdUMxfMWdpVKpearWTPS\n1NRUSrNSYlxzNQvYmoPX7C0fkaV4kxQ1L96zUo/2UCwKLGgeXyqVBjW/W/PU6juspVTzfmnBZ2Wa\nF0UyQgghoqGXjBBCiGjkzS5bFEKYGeNEVkWW0C3NuqmmHZHTOurR/C65WFQqlaoyL7W2yEiWzLgs\nFhkocl5Sn5XWbpGRAnv+RZ+XeqWa90sLPivTvOT6TUYIIYTIg+wyIYQQ0dBLRgghRDT0khFCCBEN\nvWSEEEJEQy8ZIYQQ0dBLRgghRDT0khFCCBENvWSEEEJEQy8ZIYQQ0dBLRgghRDT0khFCCBENvWSE\nEEJEQy8ZIYQQ0dBLRgghRDT0khFCCBGNXIuWNdr62PVMUWvJh6B5KZKi5kVzUiiLSqXShkUcqN7m\npampaSXNhQG/8Y2v44B6WDBwhfPJNC95V8YUQohq0zArWeblm9/8+it4zTXXDCGE8Mknn9i2Nm3a\nmP74449NZ1lski8wkuVvvZcbz2f58uWZ5kUvGZEKb1Ctntr41Nv/iOuBSr6EK4EvFi4PnmjO1fLl\ny3Mde4011jD91VdfNbu/Nwa8R7hP3vMJQb/JCCGEiIheMkIIIaIhu0ykQssgi9WS+MkhlIfpyf6y\n36oP5y2N1X1OKrlmb+yy2FVffvll6vZkvvr27Wvbpk2blvo53nPIOc9il2UZg0rvDUUyQgghoqGX\njBBCiGg0hF227bbbmp48eXLqPknGBsNIZdEUQ5Zx9CyAddZZJ4QQwmeffVboOYl08mQXxbbI6t2O\nq+T8vP35rKy77rqms9z/yd9OmTIl17kQZqsRph7zXLI825XOoyIZIYQQ0dBLRgghRDQawi6jRUY7\nIK39wrXXXmvbFi9ebPrHP/6x6dNPP930ww8/bHrBggUFnfHqB7NaOEeJjcZtDLk5/iNGjDBNq0fz\nsmpoZ2TJKErmokOHDrYtsTVDCGHp0qWmP//881zHJpznYcOGmR49enSLj1kklVh4a621lmlaVHwO\nvvjii9S/9eyntMLIvNliHuwiQLznslevXqbfeeed1HPMOn6KZIQQQkRDLxkhhBDRaMoTMtaqgylD\nxo033tj0Bx98YHr48OEhhBBOPfVU27bDDjukHoM22/z580337t3bNDMwYmTGrC5dmJNwnMWaHTt2\nND1p0qSV9g2hvBngYYcdZnrChAmmY2QPxu7CXEmmTt7+Y9x/7bXXNp08KwcffHDqeb3//vumL774\nYtPsW7Vs2TLTtIsiZZGNL5VKg4o4UJZnxcvQ433L6ye8fn6fzJgxwzTnjjbl+uuvH0IIoXPnzqnH\nmznz636U3ufnfSa8eyrjfZppXhTJCCGEiIZeMkIIIaJRV9llXttpZnIsWrTINMP0//3f/w0hhNCu\nXTvb1r9/f9MMC6l/97vfmWYmTT0Wj9Ub3nylbWd783322cc0rYn11lvP9MKFC03TJmj0ecl7/hzL\nvIVzZO+99za92267hRDKLUk+E+eee65pPhPcnzZSJRZgt27dTM+ZMyfX38bCy+JasmSJaY5Xz549\nTXOMmNHVr18/04ceeqhpzsuAAQNCCOVZaePHjzd9zz33mH755ZdN8ztx1qxZprPcL8ww5PV5KLtM\nCCFEXaGXjBBCiGjUlV3mhV9Z+v4kRX833HCDbTviiCNM77rrrql/t+WWW5puDb3OaC16xWBFwYwx\nkmTJhBDCp59+GkIoD7PTijVDKLcpevTokbp/o9tleamkpxZ7Z7399tumP/rooxBCCI888ohte/bZ\nZ02ziJk2JzU/p5IiwXqxyDyyWPi0c2k/de/e3TTHn5b+hx9+aDoZizvuuMO2sdX/a6+9lnqMrl27\nmp47d65p/pzgXYdnkXn3nXqXCSGEqCv0khFCCBGNurLLioAWEUNRwpCP4WVrILZFRuuqS5cupnfe\neWfTL730kunEjvSK937961+bZiHtu+++a1rLBGSH80Pb8r333jN9wQUXhBDKi5X5d4R2Ji0iUlR/\nrXrEsx+Zdcfr573NMd9xxx1N9+nTxzTt+vPPPz+EEMKjjz5q21is2b59+9Rjcx8WjHpWWFGZgVlR\nJCOEECIaeskIIYSIRquzyxj+sXeQt0+S/RRCvlUFGxlmhXkr6XlwXGgZPPXUU6n7zJ49e6VtL7zw\nguntt9/e9BNPPLHS34UQwgYbbGCabegbBdpWzNyKAa0b2sWc57Zt2650XiwWTAqbQ/CtSmaa8T7I\nAp8/tpSfPn16ruPEwrOQvNVf2Rduv/32M00r/uyzzzY9dOhQ07SWn3vuuRBC+XcSx59zSOuMthgt\nPT7nLBIdPHiwaRZ7etenlTGFEELULXrJCCGEiEars8tYmMQsDq8HFG0cZmkwvGxt5LXIPNhfzCu2\nZPieQHvlrbfeMj1kyBDTzLphGH/RRRelHscL42m1McMtdhYeqaZF5lkeHJ+kRxyz+ZiV9Pvf/z71\n73hs2mV5s/94T9S7RUZ4/dz/mGOOMc1eZFxRkvchbUyu0pv0HePn81niZ/Jc+F3FZ9v7KYCZm1l+\nFqg060yRjBBCiGjoJSOEECIarcYuS8LBN954w7bRRmDIx3CVWR+rW1+sSuF4UdN2TNqa0yIZMWKE\n6Xvvvdf0RhttZJorlgeQFzQAAAn/SURBVLJ/kzenHmyD3lrxxsHrxZcUYw4a9PWihnfddVfqvrRl\naDHmzSgjbIFfS/JmWdKu4rIUzNJr06aN6cMPP9z0zTffbDrJIgshhDfffNN02jzyM3mO3vjzmrx9\nuKKwZxPmXYV1VSiSEUIIEQ29ZIQQQkSj1dhlJ554YgihPFwltE2YueRZPqLlbL755qbPOeecEMLX\nBYAhhLB8+XLT7J/FsJwWxIQJE0xXMyusUfBsDm7n6o3JyqR8Vg477DDTF198seks/f8albzFh8zQ\noiV8yCGHmGaRJHu9sQDyL3/5i2lm6SVzx22bbLKJaRYi8xni53jWlvc9t9lmm5nOu6pmVhTJCCGE\niIZeMkIIIaLR0HYZMyn+8z//M4Tgh7rDhw833Yj9r+odjvt3vvMd08lyAMyMYXjPFf5uueUW0ywI\nZNGnZ3GIleGcsBgwGXNaa3yWvOejNVhkJMvqjxwj2ljMHLv//vtNH3300aZpEW+33XamDzzwQNMP\nPvig6WTFUh6DlibnhVmZtPGoWSTLZ4jnVUmWYFYUyQghhIhG1Egm9oI4/B9xWp47f7x65ZVXCv98\n8TWsgznqqKNMJ/9T4v8CJ06caPqvf/2r6WuvvdY0f+BvzR2xi4bPGZ8/1o8lzwLb+IwePdo0u/q2\ntuilEljHxXE54ogjTHfo0MH0lClTTDNi2GOPPUwzISOJZE466STbxudmwYIFptkSiFEqO2hfeuml\npvld6bUB4vWxFVKlbagUyQghhIiGXjJCCCGiEdUuix1qMwRkXUUCw/4kFBXFwR9F2Spmiy22MJ2E\n+7QuR40aZfqxxx4zzTBeNk12aIsRr9s4fxxOeOCBB1L3rRXVWHs+y2eTpL4ohBAefvhh0/vuu69p\nLlTG54AdkV9//XXT/A7bf//9Qwjl18uOyVzgjMk1TA6g1cbnkwsFvvjii6ZptT3//POm0+6REMrt\nu6xJOIpkhBBCREMvGSGEENFo6DoZ5psnYSdD/bPOOst0UQt1re6wnmLYsGGmr7jiitR9Eth59557\n7jHNbsuyyFrG9ttvb/r99983zQy9rbbaynS/fv1CCOV2Cus+7rzzTtNFthfJQzXuBc+So+7bt69p\n2km0dtlJ+eSTTzZNO4l21dChQ03feuutppPssaeeeir17zhfe+21l2laW5zz448/3vTaa69teurU\nqaaZdUsrLMvCbVlRJCOEECIaeskIIYSIRkPbZRdeeOFK21j0dPfdd1fzdFottBXYtfXqq682nWaR\nEdqVyiKrHM5Jp06dTPfu3dv0M888Y5qdxxPbhcfgc8O2I605KzNLBhutMMLCxaefftr0wIEDTbOD\nMhc5W7ZsmWnacY8++mgIoXxRM44/5+W6664zfdFFF5lmphktarakoaVKO5TPKLtJV3oPKJIRQggR\nDb1khBBCRKMh7DKGtcyA6NWr10r7MPzjvtRekZpoHq4PztCcY8osmCTbhX2XaO+wYJbIRls1vJ9f\ne+010+ydRQuTPeJefvnlEEJ5D60DDjgg9dhZLKVaFk5WQpbMOe96+Bww64zWGe/z/fbbzzRt/jvu\nuMN0UnjJBcmYOcZ56dGjh2l+h3ldm1nUmSzwGEIIv/jFL0xzITaeQ6UokhFCCBENvWSEEEJEo67s\nMobdtFyY6cD22SQJfe+77z7bxiwOkjekZxjJLJxGsgaKgnPB9d9p0zB8P+2000IIIUyfPt22cQEl\nzjP16lY861lO3M6COhbdffzxx6Z5z3v9ypJ9eGzaljx2FvI+B41qrxGOLbO4eN9yHy5Oxn59tKWS\neeSyGZ6lxyJK9lRjL7K//OUvppnpxuUA+Fk83yLnRZGMEEKIaOglI4QQIhp1tTKmZxOwkInhIPdJ\nwtQLLrjAtjG7hi21WVzEY3Tu3Nk07QXaQo0a3lcCr5lZNew71r17d9PTpk0z/eSTT4YQQpg5c2az\nn1OrPln1QJb15r0VDdlGPgvJfU5rh8egXZblfq/kOa8XaNXmzTrziotphXF8+d2SNha053letEK5\nuuyECRNMc6kBtvTnzwyLFi1KPXfCc6SN9t3vftc0l+xYFYpkhBBCREMvGSGEENGoycqYWcJr2i8/\n+clPTHuhZtK+es8997RtXO2PISiXCHj11VdNM3Rk8RLbW7eGzJi8MGRngRnHhSH1G2+8sdL2jh07\n2jbaj14Rp8hOlnuSWYFJJhkzJTknfMY4x1ksvUaC41aJVZvl+vl8UPOeTzK9aFdyLni+M2bMMH3l\nlVea5vIb7733nmmuxulldHJ1YVrh5Pbbb0/dvir0VAshhIiGXjJCCCGiUZPsMmpmfR199NGmTzjh\nBNO777576t8y7HzppZdCCOUZFWxLz+MNHjzYNLMl3nnnHdNe+Nyo1kBeevbsaZoZewMGDDDdrVs3\n07RVGGon+3OFP1qXLCRcnbPL8sJny9PsdbXLLruY3mGHHUII5fcy+1xxHjzrrDWQN3POG4tKLHTu\nn1YEy+84ZgMyc5ZZsVx18/e//33qcTi/1J5FxkLOefPmpe6zKhTJCCGEiIZeMkIIIaJRV9lls2fP\nNs1VLTfeeGPTm266qWmuIPerX/0qhBDC22+/bdsYCp511lmmWdzJVeJWFyuMYT9JbJQQysduyJAh\nptlinOPFTKV77rnHdJKxQjuGvZ54L7Q2kmuLUdBIOFc8Trt27Ux36dLFdJJJ9vjjj9s29rMqqodc\no2Zi8vo9e55wH+9v+czxJwLun8wRv5O8MaRdd9JJJ5k+88wzTTPLs5LnrCUWGVEkI4QQIhp6yQgh\nhIhGU54wtqmpqeYxb3NhX1Fhed5eRnkplUqF+URFzQuvmasmJv3HQihvDd62bVvTRx55pOnrr7/e\ndDIfRc2L11OpKIqaF85JUeecxX7iHNIWPvzww00nqzFy/mjRxKBC62x8qVQaVNB5lKBT98mSRUbb\nmP3CvP1Z6MgMTRaDJ/cGe57RWubcMrts4MCBppnFyc/0ltfgd1useVEkI4QQIhp6yQghhIhGw9ll\nrYV6tMtYJMnCMC97qeiMIVpxedvXF0UMu0xUTBS7rCiyWOueNZdWSJvXwmrTpo1pPje0Q1n0XMlz\nu8LzL7tMCCFEbdFLRgghRDSiFmOKxoJLHXjhfcyiOob6ldhyjVoEKBqTvCtpZtneHCNGjDB9yy23\nmOa9z8y0SpZdIS05X0UyQgghoqGXjBBCiGgou6xG1GN2mVB2WZ0SvRizKDspJnmLcb2s0KJWBA0q\nxhRCCFFr9JIRQggRjbzZZYtCCDNjnMhqRo/md8mF5qUYipwXzUlxRJmXWNlUschyLllW9C3wmjLN\nS67fZIQQQog8yC4TQggRDb1khBBCREMvGSGEENHQS0YIIUQ09JIRQggRDb1khBBCREMvGSGEENHQ\nS0YIIUQ09JIRQggRjf8DCGGm5rjhC7AAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# randomly generated, new latent vectors\n",
"sample_size=16\n",
"rand_z = np.random.uniform(-1, 1, size=(sample_size, z_size))\n",
"rand_z = torch.from_numpy(rand_z).float()\n",
"\n",
"G.eval() # eval mode\n",
"# generated samples\n",
"rand_images = G(rand_z)\n",
"\n",
"# 0 indicates the first set of samples in the passed in list\n",
"# and we only have one batch of samples, here\n",
"view_samples(0, [rand_images])"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
 \n",
"\n",
"#### Leaky ReLu\n",
"\n",
"We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.\n",
"\n",
"
\n",
"\n",
"#### Leaky ReLu\n",
"\n",
"We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.\n",
"\n",
" \n",
"\n",
"#### Sigmoid Output\n",
"\n",
"We'll also take the approach of using a more numerically stable loss function on the outputs. Recall that we want the discriminator to output a value 0-1 indicating whether an image is _real or fake_. \n",
"> We will ultimately use [BCEWithLogitsLoss](https://pytorch.org/docs/stable/nn.html#bcewithlogitsloss), which combines a `sigmoid` activation function **and** binary cross entropy loss in one function. \n",
"\n",
"So, our final output layer should not have any activation function applied to it."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"\n",
"class Discriminator(nn.Module):\n",
"\n",
" def __init__(self, input_size, hidden_dim, output_size):\n",
" super(Discriminator, self).__init__()\n",
" \n",
" # define hidden linear layers\n",
" self.fc1 = nn.Linear(input_size, hidden_dim*4)\n",
" self.fc2 = nn.Linear(hidden_dim*4, hidden_dim*2)\n",
" self.fc3 = nn.Linear(hidden_dim*2, hidden_dim)\n",
" \n",
" # final fully-connected layer\n",
" self.fc4 = nn.Linear(hidden_dim, output_size)\n",
" \n",
" # dropout layer \n",
" self.dropout = nn.Dropout(0.3)\n",
" \n",
" \n",
" def forward(self, x):\n",
" # flatten image\n",
" x = x.view(-1, 28*28)\n",
" # all hidden layers\n",
" x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc2(x), 0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc3(x), 0.2)\n",
" x = self.dropout(x)\n",
" # final layer\n",
" out = self.fc4(x)\n",
"\n",
" return out\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator\n",
"\n",
"The generator network will be almost exactly the same as the discriminator network, except that we're applying a [tanh activation function](https://pytorch.org/docs/stable/nn.html#tanh) to our output layer.\n",
"\n",
"#### tanh Output\n",
"The generator has been found to perform the best with $tanh$ for the generator output, which scales the output to be between -1 and 1, instead of 0 and 1. \n",
"\n",
"
\n",
"\n",
"#### Sigmoid Output\n",
"\n",
"We'll also take the approach of using a more numerically stable loss function on the outputs. Recall that we want the discriminator to output a value 0-1 indicating whether an image is _real or fake_. \n",
"> We will ultimately use [BCEWithLogitsLoss](https://pytorch.org/docs/stable/nn.html#bcewithlogitsloss), which combines a `sigmoid` activation function **and** binary cross entropy loss in one function. \n",
"\n",
"So, our final output layer should not have any activation function applied to it."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"\n",
"class Discriminator(nn.Module):\n",
"\n",
" def __init__(self, input_size, hidden_dim, output_size):\n",
" super(Discriminator, self).__init__()\n",
" \n",
" # define hidden linear layers\n",
" self.fc1 = nn.Linear(input_size, hidden_dim*4)\n",
" self.fc2 = nn.Linear(hidden_dim*4, hidden_dim*2)\n",
" self.fc3 = nn.Linear(hidden_dim*2, hidden_dim)\n",
" \n",
" # final fully-connected layer\n",
" self.fc4 = nn.Linear(hidden_dim, output_size)\n",
" \n",
" # dropout layer \n",
" self.dropout = nn.Dropout(0.3)\n",
" \n",
" \n",
" def forward(self, x):\n",
" # flatten image\n",
" x = x.view(-1, 28*28)\n",
" # all hidden layers\n",
" x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc2(x), 0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc3(x), 0.2)\n",
" x = self.dropout(x)\n",
" # final layer\n",
" out = self.fc4(x)\n",
"\n",
" return out\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Generator\n",
"\n",
"The generator network will be almost exactly the same as the discriminator network, except that we're applying a [tanh activation function](https://pytorch.org/docs/stable/nn.html#tanh) to our output layer.\n",
"\n",
"#### tanh Output\n",
"The generator has been found to perform the best with $tanh$ for the generator output, which scales the output to be between -1 and 1, instead of 0 and 1. \n",
"\n",
" \n",
"\n",
"Recall that we also want these outputs to be comparable to the *real* input pixel values, which are read in as normalized values between 0 and 1. \n",
"> So, we'll also have to **scale our real input images to have pixel values between -1 and 1** when we train the discriminator. \n",
"\n",
"I'll do this in the training loop, later on."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Generator(nn.Module):\n",
"\n",
" def __init__(self, input_size, hidden_dim, output_size):\n",
" super(Generator, self).__init__()\n",
" \n",
" # define hidden linear layers\n",
" self.fc1 = nn.Linear(input_size, hidden_dim)\n",
" self.fc2 = nn.Linear(hidden_dim, hidden_dim*2)\n",
" self.fc3 = nn.Linear(hidden_dim*2, hidden_dim*4)\n",
" \n",
" # final fully-connected layer\n",
" self.fc4 = nn.Linear(hidden_dim*4, output_size)\n",
" \n",
" # dropout layer \n",
" self.dropout = nn.Dropout(0.3)\n",
"\n",
" def forward(self, x):\n",
" # all hidden layers\n",
" x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc2(x), 0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc3(x), 0.2)\n",
" x = self.dropout(x)\n",
" # final layer with tanh applied\n",
" out = F.tanh(self.fc4(x))\n",
"\n",
" return out"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model hyperparameters"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Discriminator hyperparams\n",
"\n",
"# Size of input image to discriminator (28*28)\n",
"input_size = 784\n",
"# Size of discriminator output (real or fake)\n",
"d_output_size = 1\n",
"# Size of last hidden layer in the discriminator\n",
"d_hidden_size = 32\n",
"\n",
"# Generator hyperparams\n",
"\n",
"# Size of latent vector to give to generator\n",
"z_size = 100\n",
"# Size of discriminator output (generated image)\n",
"g_output_size = 784\n",
"# Size of first hidden layer in the generator\n",
"g_hidden_size = 32"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Build complete network\n",
"\n",
"Now we're instantiating the discriminator and generator from the classes defined above. Make sure you've passed in the correct input arguments."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Discriminator(\n",
" (fc1): Linear(in_features=784, out_features=128, bias=True)\n",
" (fc2): Linear(in_features=128, out_features=64, bias=True)\n",
" (fc3): Linear(in_features=64, out_features=32, bias=True)\n",
" (fc4): Linear(in_features=32, out_features=1, bias=True)\n",
" (dropout): Dropout(p=0.3)\n",
")\n",
"\n",
"Generator(\n",
" (fc1): Linear(in_features=100, out_features=32, bias=True)\n",
" (fc2): Linear(in_features=32, out_features=64, bias=True)\n",
" (fc3): Linear(in_features=64, out_features=128, bias=True)\n",
" (fc4): Linear(in_features=128, out_features=784, bias=True)\n",
" (dropout): Dropout(p=0.3)\n",
")\n"
]
}
],
"source": [
"# instantiate discriminator and generator\n",
"D = Discriminator(input_size, d_hidden_size, d_output_size)\n",
"G = Generator(z_size, g_hidden_size, g_output_size)\n",
"\n",
"# check that they are as you expect\n",
"print(D)\n",
"print()\n",
"print(G)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Discriminator and Generator Losses\n",
"\n",
"Now we need to calculate the losses. \n",
"\n",
"### Discriminator Losses\n",
"\n",
"> * For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_real_loss + d_fake_loss`. \n",
"* Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.\n",
"\n",
"
\n",
"\n",
"Recall that we also want these outputs to be comparable to the *real* input pixel values, which are read in as normalized values between 0 and 1. \n",
"> So, we'll also have to **scale our real input images to have pixel values between -1 and 1** when we train the discriminator. \n",
"\n",
"I'll do this in the training loop, later on."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Generator(nn.Module):\n",
"\n",
" def __init__(self, input_size, hidden_dim, output_size):\n",
" super(Generator, self).__init__()\n",
" \n",
" # define hidden linear layers\n",
" self.fc1 = nn.Linear(input_size, hidden_dim)\n",
" self.fc2 = nn.Linear(hidden_dim, hidden_dim*2)\n",
" self.fc3 = nn.Linear(hidden_dim*2, hidden_dim*4)\n",
" \n",
" # final fully-connected layer\n",
" self.fc4 = nn.Linear(hidden_dim*4, output_size)\n",
" \n",
" # dropout layer \n",
" self.dropout = nn.Dropout(0.3)\n",
"\n",
" def forward(self, x):\n",
" # all hidden layers\n",
" x = F.leaky_relu(self.fc1(x), 0.2) # (input, negative_slope=0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc2(x), 0.2)\n",
" x = self.dropout(x)\n",
" x = F.leaky_relu(self.fc3(x), 0.2)\n",
" x = self.dropout(x)\n",
" # final layer with tanh applied\n",
" out = F.tanh(self.fc4(x))\n",
"\n",
" return out"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Model hyperparameters"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Discriminator hyperparams\n",
"\n",
"# Size of input image to discriminator (28*28)\n",
"input_size = 784\n",
"# Size of discriminator output (real or fake)\n",
"d_output_size = 1\n",
"# Size of last hidden layer in the discriminator\n",
"d_hidden_size = 32\n",
"\n",
"# Generator hyperparams\n",
"\n",
"# Size of latent vector to give to generator\n",
"z_size = 100\n",
"# Size of discriminator output (generated image)\n",
"g_output_size = 784\n",
"# Size of first hidden layer in the generator\n",
"g_hidden_size = 32"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Build complete network\n",
"\n",
"Now we're instantiating the discriminator and generator from the classes defined above. Make sure you've passed in the correct input arguments."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Discriminator(\n",
" (fc1): Linear(in_features=784, out_features=128, bias=True)\n",
" (fc2): Linear(in_features=128, out_features=64, bias=True)\n",
" (fc3): Linear(in_features=64, out_features=32, bias=True)\n",
" (fc4): Linear(in_features=32, out_features=1, bias=True)\n",
" (dropout): Dropout(p=0.3)\n",
")\n",
"\n",
"Generator(\n",
" (fc1): Linear(in_features=100, out_features=32, bias=True)\n",
" (fc2): Linear(in_features=32, out_features=64, bias=True)\n",
" (fc3): Linear(in_features=64, out_features=128, bias=True)\n",
" (fc4): Linear(in_features=128, out_features=784, bias=True)\n",
" (dropout): Dropout(p=0.3)\n",
")\n"
]
}
],
"source": [
"# instantiate discriminator and generator\n",
"D = Discriminator(input_size, d_hidden_size, d_output_size)\n",
"G = Generator(z_size, g_hidden_size, g_output_size)\n",
"\n",
"# check that they are as you expect\n",
"print(D)\n",
"print()\n",
"print(G)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Discriminator and Generator Losses\n",
"\n",
"Now we need to calculate the losses. \n",
"\n",
"### Discriminator Losses\n",
"\n",
"> * For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_real_loss + d_fake_loss`. \n",
"* Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.\n",
"\n",
" \n",
"\n",
"The losses will by binary cross entropy loss with logits, which we can get with [BCEWithLogitsLoss](https://pytorch.org/docs/stable/nn.html#bcewithlogitsloss). This combines a `sigmoid` activation function **and** and binary cross entropy loss in one function.\n",
"\n",
"For the real images, we want `D(real_images) = 1`. That is, we want the discriminator to classify the the real images with a label = 1, indicating that these are real. To help the discriminator generalize better, the labels are **reduced a bit from 1.0 to 0.9**. For this, we'll use the parameter `smooth`; if True, then we should smooth our labels. In PyTorch, this looks like `labels = torch.ones(size) * 0.9`\n",
"\n",
"The discriminator loss for the fake data is similar. We want `D(fake_images) = 0`, where the fake images are the _generator output_, `fake_images = G(z)`. \n",
"\n",
"### Generator Loss\n",
"\n",
"The generator loss will look similar only with flipped labels. The generator's goal is to get `D(fake_images) = 1`. In this case, the labels are **flipped** to represent that the generator is trying to fool the discriminator into thinking that the images it generates (fakes) are real!"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Calculate losses\n",
"def real_loss(D_out, smooth=False):\n",
" batch_size = D_out.size(0)\n",
" # label smoothing\n",
" if smooth:\n",
" # smooth, real labels = 0.9\n",
" labels = torch.ones(batch_size)*0.9\n",
" else:\n",
" labels = torch.ones(batch_size) # real labels = 1\n",
" \n",
" # numerically stable loss\n",
" criterion = nn.BCEWithLogitsLoss()\n",
" # calculate loss\n",
" loss = criterion(D_out.squeeze(), labels)\n",
" return loss\n",
"\n",
"def fake_loss(D_out):\n",
" batch_size = D_out.size(0)\n",
" labels = torch.zeros(batch_size) # fake labels = 0\n",
" criterion = nn.BCEWithLogitsLoss()\n",
" # calculate loss\n",
" loss = criterion(D_out.squeeze(), labels)\n",
" return loss"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Optimizers\n",
"\n",
"We want to update the generator and discriminator variables separately. So, we'll define two separate Adam optimizers."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true,
"scrolled": true
},
"outputs": [],
"source": [
"import torch.optim as optim\n",
"\n",
"# Optimizers\n",
"lr = 0.002\n",
"\n",
"# Create optimizers for the discriminator and generator\n",
"d_optimizer = optim.Adam(D.parameters(), lr)\n",
"g_optimizer = optim.Adam(G.parameters(), lr)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Training\n",
"\n",
"Training will involve alternating between training the discriminator and the generator. We'll use our functions `real_loss` and `fake_loss` to help us calculate the discriminator losses in all of the following cases.\n",
"\n",
"### Discriminator training\n",
"1. Compute the discriminator loss on real, training images \n",
"2. Generate fake images\n",
"3. Compute the discriminator loss on fake, generated images \n",
"4. Add up real and fake loss\n",
"5. Perform backpropagation + an optimization step to update the discriminator's weights\n",
"\n",
"### Generator training\n",
"1. Generate fake images\n",
"2. Compute the discriminator loss on fake images, using **flipped** labels!\n",
"3. Perform backpropagation + an optimization step to update the generator's weights\n",
"\n",
"#### Saving Samples\n",
"\n",
"As we train, we'll also print out some loss statistics and save some generated \"fake\" samples."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch [ 1/ 100] | d_loss: 1.3830 | g_loss: 0.6883\n",
"Epoch [ 1/ 100] | d_loss: 0.7668 | g_loss: 3.1404\n",
"Epoch [ 1/ 100] | d_loss: 1.0908 | g_loss: 2.6393\n",
"Epoch [ 2/ 100] | d_loss: 1.2982 | g_loss: 1.1008\n",
"Epoch [ 2/ 100] | d_loss: 1.1753 | g_loss: 1.1042\n",
"Epoch [ 2/ 100] | d_loss: 1.0874 | g_loss: 1.6588\n",
"Epoch [ 3/ 100] | d_loss: 0.9747 | g_loss: 2.9083\n",
"Epoch [ 3/ 100] | d_loss: 1.0724 | g_loss: 1.1101\n",
"Epoch [ 3/ 100] | d_loss: 1.4727 | g_loss: 0.4990\n",
"Epoch [ 4/ 100] | d_loss: 1.1590 | g_loss: 0.9996\n",
"Epoch [ 4/ 100] | d_loss: 1.1832 | g_loss: 1.0638\n",
"Epoch [ 4/ 100] | d_loss: 1.1652 | g_loss: 1.1463\n",
"Epoch [ 5/ 100] | d_loss: 1.2966 | g_loss: 1.0950\n",
"Epoch [ 5/ 100] | d_loss: 1.3616 | g_loss: 1.0312\n",
"Epoch [ 5/ 100] | d_loss: 1.2202 | g_loss: 1.1301\n",
"Epoch [ 6/ 100] | d_loss: 1.1609 | g_loss: 1.5148\n",
"Epoch [ 6/ 100] | d_loss: 1.1100 | g_loss: 1.2183\n",
"Epoch [ 6/ 100] | d_loss: 1.2376 | g_loss: 1.5296\n",
"Epoch [ 7/ 100] | d_loss: 1.2304 | g_loss: 1.1526\n",
"Epoch [ 7/ 100] | d_loss: 1.1684 | g_loss: 1.1339\n",
"Epoch [ 7/ 100] | d_loss: 1.0965 | g_loss: 1.3531\n",
"Epoch [ 8/ 100] | d_loss: 1.2527 | g_loss: 2.2266\n",
"Epoch [ 8/ 100] | d_loss: 1.2978 | g_loss: 1.6185\n",
"Epoch [ 8/ 100] | d_loss: 1.1493 | g_loss: 1.4873\n",
"Epoch [ 9/ 100] | d_loss: 0.9751 | g_loss: 2.6848\n",
"Epoch [ 9/ 100] | d_loss: 1.1574 | g_loss: 1.7639\n",
"Epoch [ 9/ 100] | d_loss: 0.9629 | g_loss: 2.2062\n",
"Epoch [ 10/ 100] | d_loss: 1.0279 | g_loss: 1.9386\n",
"Epoch [ 10/ 100] | d_loss: 1.1110 | g_loss: 1.0685\n",
"Epoch [ 10/ 100] | d_loss: 1.3441 | g_loss: 1.0324\n",
"Epoch [ 11/ 100] | d_loss: 1.1879 | g_loss: 1.0673\n",
"Epoch [ 11/ 100] | d_loss: 1.3366 | g_loss: 0.9610\n",
"Epoch [ 11/ 100] | d_loss: 1.1435 | g_loss: 1.0668\n",
"Epoch [ 12/ 100] | d_loss: 1.1189 | g_loss: 1.2501\n",
"Epoch [ 12/ 100] | d_loss: 1.2153 | g_loss: 1.0666\n",
"Epoch [ 12/ 100] | d_loss: 1.3179 | g_loss: 0.9101\n",
"Epoch [ 13/ 100] | d_loss: 1.1504 | g_loss: 1.4559\n",
"Epoch [ 13/ 100] | d_loss: 1.3358 | g_loss: 0.9763\n",
"Epoch [ 13/ 100] | d_loss: 1.1833 | g_loss: 1.0180\n",
"Epoch [ 14/ 100] | d_loss: 1.1839 | g_loss: 1.2705\n",
"Epoch [ 14/ 100] | d_loss: 1.3219 | g_loss: 1.0915\n",
"Epoch [ 14/ 100] | d_loss: 1.2945 | g_loss: 0.9335\n",
"Epoch [ 15/ 100] | d_loss: 1.3458 | g_loss: 0.9600\n",
"Epoch [ 15/ 100] | d_loss: 1.3445 | g_loss: 0.9098\n",
"Epoch [ 15/ 100] | d_loss: 1.3289 | g_loss: 1.3456\n",
"Epoch [ 16/ 100] | d_loss: 1.2725 | g_loss: 0.9085\n",
"Epoch [ 16/ 100] | d_loss: 1.1133 | g_loss: 1.0910\n",
"Epoch [ 16/ 100] | d_loss: 1.2564 | g_loss: 1.0233\n",
"Epoch [ 17/ 100] | d_loss: 1.3171 | g_loss: 0.9643\n",
"Epoch [ 17/ 100] | d_loss: 1.2932 | g_loss: 1.0311\n",
"Epoch [ 17/ 100] | d_loss: 1.2643 | g_loss: 0.9377\n",
"Epoch [ 18/ 100] | d_loss: 1.2226 | g_loss: 1.4327\n",
"Epoch [ 18/ 100] | d_loss: 1.3909 | g_loss: 0.9178\n",
"Epoch [ 18/ 100] | d_loss: 1.2430 | g_loss: 1.0297\n",
"Epoch [ 19/ 100] | d_loss: 1.3409 | g_loss: 1.1413\n",
"Epoch [ 19/ 100] | d_loss: 1.1607 | g_loss: 1.2019\n",
"Epoch [ 19/ 100] | d_loss: 1.4060 | g_loss: 1.1366\n",
"Epoch [ 20/ 100] | d_loss: 1.3076 | g_loss: 1.0200\n",
"Epoch [ 20/ 100] | d_loss: 1.2715 | g_loss: 0.9261\n",
"Epoch [ 20/ 100] | d_loss: 1.2959 | g_loss: 1.4079\n",
"Epoch [ 21/ 100] | d_loss: 1.2529 | g_loss: 1.4324\n",
"Epoch [ 21/ 100] | d_loss: 1.2907 | g_loss: 0.9551\n",
"Epoch [ 21/ 100] | d_loss: 1.2426 | g_loss: 1.2571\n",
"Epoch [ 22/ 100] | d_loss: 1.2168 | g_loss: 1.7557\n",
"Epoch [ 22/ 100] | d_loss: 1.2874 | g_loss: 1.0733\n",
"Epoch [ 22/ 100] | d_loss: 1.1758 | g_loss: 1.6449\n",
"Epoch [ 23/ 100] | d_loss: 1.3328 | g_loss: 0.9859\n",
"Epoch [ 23/ 100] | d_loss: 1.4189 | g_loss: 0.8197\n",
"Epoch [ 23/ 100] | d_loss: 1.3146 | g_loss: 0.9181\n",
"Epoch [ 24/ 100] | d_loss: 1.2752 | g_loss: 1.1507\n",
"Epoch [ 24/ 100] | d_loss: 1.1860 | g_loss: 1.0389\n",
"Epoch [ 24/ 100] | d_loss: 1.2692 | g_loss: 1.0240\n",
"Epoch [ 25/ 100] | d_loss: 1.2905 | g_loss: 0.8767\n",
"Epoch [ 25/ 100] | d_loss: 1.1643 | g_loss: 1.0650\n",
"Epoch [ 25/ 100] | d_loss: 1.3141 | g_loss: 0.8904\n",
"Epoch [ 26/ 100] | d_loss: 1.2288 | g_loss: 1.0190\n",
"Epoch [ 26/ 100] | d_loss: 1.2016 | g_loss: 0.9930\n",
"Epoch [ 26/ 100] | d_loss: 1.4220 | g_loss: 1.1657\n",
"Epoch [ 27/ 100] | d_loss: 1.2774 | g_loss: 1.0464\n",
"Epoch [ 27/ 100] | d_loss: 1.2179 | g_loss: 1.0301\n",
"Epoch [ 27/ 100] | d_loss: 1.2938 | g_loss: 1.1045\n",
"Epoch [ 28/ 100] | d_loss: 1.2736 | g_loss: 1.1921\n",
"Epoch [ 28/ 100] | d_loss: 1.1929 | g_loss: 1.1512\n",
"Epoch [ 28/ 100] | d_loss: 1.3188 | g_loss: 0.9897\n",
"Epoch [ 29/ 100] | d_loss: 1.3085 | g_loss: 1.4660\n",
"Epoch [ 29/ 100] | d_loss: 1.2663 | g_loss: 0.9120\n",
"Epoch [ 29/ 100] | d_loss: 1.3005 | g_loss: 0.9635\n",
"Epoch [ 30/ 100] | d_loss: 1.2953 | g_loss: 0.8053\n",
"Epoch [ 30/ 100] | d_loss: 1.3288 | g_loss: 0.9908\n",
"Epoch [ 30/ 100] | d_loss: 1.3487 | g_loss: 1.1090\n",
"Epoch [ 31/ 100] | d_loss: 1.2638 | g_loss: 1.0738\n",
"Epoch [ 31/ 100] | d_loss: 1.2856 | g_loss: 0.9346\n",
"Epoch [ 31/ 100] | d_loss: 1.2525 | g_loss: 1.1265\n",
"Epoch [ 32/ 100] | d_loss: 1.1938 | g_loss: 1.1639\n",
"Epoch [ 32/ 100] | d_loss: 1.2217 | g_loss: 0.9636\n",
"Epoch [ 32/ 100] | d_loss: 1.2105 | g_loss: 1.7308\n",
"Epoch [ 33/ 100] | d_loss: 1.1531 | g_loss: 1.5628\n",
"Epoch [ 33/ 100] | d_loss: 1.3260 | g_loss: 0.9161\n",
"Epoch [ 33/ 100] | d_loss: 1.2334 | g_loss: 0.9264\n",
"Epoch [ 34/ 100] | d_loss: 1.2336 | g_loss: 1.0195\n",
"Epoch [ 34/ 100] | d_loss: 1.2184 | g_loss: 1.3364\n",
"Epoch [ 34/ 100] | d_loss: 1.3039 | g_loss: 0.9413\n",
"Epoch [ 35/ 100] | d_loss: 1.3298 | g_loss: 1.1236\n",
"Epoch [ 35/ 100] | d_loss: 1.2562 | g_loss: 1.0155\n",
"Epoch [ 35/ 100] | d_loss: 1.3659 | g_loss: 1.2384\n",
"Epoch [ 36/ 100] | d_loss: 1.1759 | g_loss: 1.0545\n",
"Epoch [ 36/ 100] | d_loss: 1.2195 | g_loss: 1.0489\n",
"Epoch [ 36/ 100] | d_loss: 1.2799 | g_loss: 0.9530\n",
"Epoch [ 37/ 100] | d_loss: 1.2149 | g_loss: 1.0076\n",
"Epoch [ 37/ 100] | d_loss: 1.2700 | g_loss: 1.1004\n",
"Epoch [ 37/ 100] | d_loss: 1.3090 | g_loss: 0.9861\n",
"Epoch [ 38/ 100] | d_loss: 1.3035 | g_loss: 1.0189\n",
"Epoch [ 38/ 100] | d_loss: 1.2769 | g_loss: 1.0285\n",
"Epoch [ 38/ 100] | d_loss: 1.2371 | g_loss: 1.2829\n",
"Epoch [ 39/ 100] | d_loss: 1.2404 | g_loss: 1.0135\n",
"Epoch [ 39/ 100] | d_loss: 1.2708 | g_loss: 0.9378\n",
"Epoch [ 39/ 100] | d_loss: 1.2512 | g_loss: 0.9949\n",
"Epoch [ 40/ 100] | d_loss: 1.1768 | g_loss: 0.9511\n",
"Epoch [ 40/ 100] | d_loss: 1.3067 | g_loss: 0.9223\n",
"Epoch [ 40/ 100] | d_loss: 1.3625 | g_loss: 0.8471\n",
"Epoch [ 41/ 100] | d_loss: 1.2816 | g_loss: 1.0424\n",
"Epoch [ 41/ 100] | d_loss: 1.2974 | g_loss: 1.1541\n",
"Epoch [ 41/ 100] | d_loss: 1.1643 | g_loss: 1.2687\n",
"Epoch [ 42/ 100] | d_loss: 1.2976 | g_loss: 1.0265\n",
"Epoch [ 42/ 100] | d_loss: 1.3245 | g_loss: 1.1694\n",
"Epoch [ 42/ 100] | d_loss: 1.3458 | g_loss: 0.9364\n",
"Epoch [ 43/ 100] | d_loss: 1.1641 | g_loss: 1.6862\n",
"Epoch [ 43/ 100] | d_loss: 1.2706 | g_loss: 0.8405\n",
"Epoch [ 43/ 100] | d_loss: 1.3763 | g_loss: 0.9720\n",
"Epoch [ 44/ 100] | d_loss: 1.3490 | g_loss: 1.1244\n",
"Epoch [ 44/ 100] | d_loss: 1.2542 | g_loss: 1.3335\n",
"Epoch [ 44/ 100] | d_loss: 1.2833 | g_loss: 0.9767\n",
"Epoch [ 45/ 100] | d_loss: 1.3130 | g_loss: 0.9182\n",
"Epoch [ 45/ 100] | d_loss: 1.2353 | g_loss: 1.0782\n",
"Epoch [ 45/ 100] | d_loss: 1.3760 | g_loss: 0.9803\n",
"Epoch [ 46/ 100] | d_loss: 1.4026 | g_loss: 0.9744\n",
"Epoch [ 46/ 100] | d_loss: 1.3152 | g_loss: 0.9312\n",
"Epoch [ 46/ 100] | d_loss: 1.2657 | g_loss: 1.0664\n",
"Epoch [ 47/ 100] | d_loss: 1.2507 | g_loss: 1.2632\n",
"Epoch [ 47/ 100] | d_loss: 1.2343 | g_loss: 1.0100\n",
"Epoch [ 47/ 100] | d_loss: 1.2856 | g_loss: 0.9613\n",
"Epoch [ 48/ 100] | d_loss: 1.2589 | g_loss: 1.0631\n",
"Epoch [ 48/ 100] | d_loss: 1.2255 | g_loss: 1.3015\n",
"Epoch [ 48/ 100] | d_loss: 1.3112 | g_loss: 0.8649\n",
"Epoch [ 49/ 100] | d_loss: 1.2646 | g_loss: 0.9986\n",
"Epoch [ 49/ 100] | d_loss: 1.2757 | g_loss: 0.9732\n",
"Epoch [ 49/ 100] | d_loss: 1.1808 | g_loss: 1.4561\n",
"Epoch [ 50/ 100] | d_loss: 1.3849 | g_loss: 1.2169\n",
"Epoch [ 50/ 100] | d_loss: 1.2799 | g_loss: 1.4074\n",
"Epoch [ 50/ 100] | d_loss: 1.3711 | g_loss: 0.9860\n",
"Epoch [ 51/ 100] | d_loss: 1.2772 | g_loss: 1.2343\n",
"Epoch [ 51/ 100] | d_loss: 1.3022 | g_loss: 0.9042\n",
"Epoch [ 51/ 100] | d_loss: 1.3566 | g_loss: 0.8909\n",
"Epoch [ 52/ 100] | d_loss: 1.3641 | g_loss: 1.0716\n",
"Epoch [ 52/ 100] | d_loss: 1.2138 | g_loss: 1.2055\n",
"Epoch [ 52/ 100] | d_loss: 1.3753 | g_loss: 0.9283\n",
"Epoch [ 53/ 100] | d_loss: 1.2297 | g_loss: 1.1757\n",
"Epoch [ 53/ 100] | d_loss: 1.2801 | g_loss: 0.9982\n",
"Epoch [ 53/ 100] | d_loss: 1.2177 | g_loss: 0.9533\n",
"Epoch [ 54/ 100] | d_loss: 1.3590 | g_loss: 0.8750\n",
"Epoch [ 54/ 100] | d_loss: 1.2776 | g_loss: 1.3202\n",
"Epoch [ 54/ 100] | d_loss: 1.4154 | g_loss: 0.9770\n",
"Epoch [ 55/ 100] | d_loss: 1.3179 | g_loss: 1.1155\n",
"Epoch [ 55/ 100] | d_loss: 1.3786 | g_loss: 0.9604\n",
"Epoch [ 55/ 100] | d_loss: 1.3158 | g_loss: 0.9751\n",
"Epoch [ 56/ 100] | d_loss: 1.3204 | g_loss: 0.9898\n",
"Epoch [ 56/ 100] | d_loss: 1.4150 | g_loss: 1.0278\n",
"Epoch [ 56/ 100] | d_loss: 1.2821 | g_loss: 0.9324\n",
"Epoch [ 57/ 100] | d_loss: 1.2576 | g_loss: 1.2056\n",
"Epoch [ 57/ 100] | d_loss: 1.4449 | g_loss: 1.1794\n",
"Epoch [ 57/ 100] | d_loss: 1.3697 | g_loss: 1.1030\n",
"Epoch [ 58/ 100] | d_loss: 1.2824 | g_loss: 0.9524\n",
"Epoch [ 58/ 100] | d_loss: 1.2432 | g_loss: 1.1015\n",
"Epoch [ 58/ 100] | d_loss: 1.3309 | g_loss: 1.0080\n",
"Epoch [ 59/ 100] | d_loss: 1.3095 | g_loss: 1.0256\n",
"Epoch [ 59/ 100] | d_loss: 1.2653 | g_loss: 0.8913\n",
"Epoch [ 59/ 100] | d_loss: 1.3224 | g_loss: 1.0386\n",
"Epoch [ 60/ 100] | d_loss: 1.1556 | g_loss: 1.1556\n",
"Epoch [ 60/ 100] | d_loss: 1.2522 | g_loss: 1.0155\n",
"Epoch [ 60/ 100] | d_loss: 1.3123 | g_loss: 0.9344\n",
"Epoch [ 61/ 100] | d_loss: 1.2728 | g_loss: 1.1286\n",
"Epoch [ 61/ 100] | d_loss: 1.3303 | g_loss: 1.0562\n",
"Epoch [ 61/ 100] | d_loss: 1.3408 | g_loss: 0.8740\n",
"Epoch [ 62/ 100] | d_loss: 1.4031 | g_loss: 1.0154\n",
"Epoch [ 62/ 100] | d_loss: 1.1388 | g_loss: 1.3963\n",
"Epoch [ 62/ 100] | d_loss: 1.4201 | g_loss: 1.1908\n",
"Epoch [ 63/ 100] | d_loss: 1.2058 | g_loss: 1.1407\n",
"Epoch [ 63/ 100] | d_loss: 1.2444 | g_loss: 1.1547\n",
"Epoch [ 63/ 100] | d_loss: 1.3877 | g_loss: 1.0653\n",
"Epoch [ 64/ 100] | d_loss: 1.3246 | g_loss: 1.4514\n",
"Epoch [ 64/ 100] | d_loss: 1.3463 | g_loss: 1.0041\n",
"Epoch [ 64/ 100] | d_loss: 1.2426 | g_loss: 1.5180\n",
"Epoch [ 65/ 100] | d_loss: 1.3013 | g_loss: 1.0159\n",
"Epoch [ 65/ 100] | d_loss: 1.3368 | g_loss: 2.1512\n",
"Epoch [ 65/ 100] | d_loss: 1.3612 | g_loss: 0.9549\n",
"Epoch [ 66/ 100] | d_loss: 1.3277 | g_loss: 0.7320\n",
"Epoch [ 66/ 100] | d_loss: 1.2434 | g_loss: 0.9365\n",
"Epoch [ 66/ 100] | d_loss: 1.2326 | g_loss: 1.3177\n",
"Epoch [ 67/ 100] | d_loss: 1.2334 | g_loss: 1.4614\n",
"Epoch [ 67/ 100] | d_loss: 1.2690 | g_loss: 1.0928\n",
"Epoch [ 67/ 100] | d_loss: 1.3406 | g_loss: 1.0277\n",
"Epoch [ 68/ 100] | d_loss: 1.2498 | g_loss: 1.0917\n",
"Epoch [ 68/ 100] | d_loss: 1.3146 | g_loss: 1.0963\n",
"Epoch [ 68/ 100] | d_loss: 1.3215 | g_loss: 1.3057\n",
"Epoch [ 69/ 100] | d_loss: 1.3268 | g_loss: 1.1683\n",
"Epoch [ 69/ 100] | d_loss: 1.2631 | g_loss: 0.9922\n",
"Epoch [ 69/ 100] | d_loss: 1.3693 | g_loss: 1.0472\n",
"Epoch [ 70/ 100] | d_loss: 1.3476 | g_loss: 1.1509\n",
"Epoch [ 70/ 100] | d_loss: 1.2585 | g_loss: 1.2276\n",
"Epoch [ 70/ 100] | d_loss: 1.3906 | g_loss: 1.2750\n",
"Epoch [ 71/ 100] | d_loss: 1.2083 | g_loss: 0.9252\n",
"Epoch [ 71/ 100] | d_loss: 1.3743 | g_loss: 1.1076\n",
"Epoch [ 71/ 100] | d_loss: 1.2552 | g_loss: 0.9602\n",
"Epoch [ 72/ 100] | d_loss: 1.3761 | g_loss: 0.9666\n",
"Epoch [ 72/ 100] | d_loss: 1.3193 | g_loss: 0.9309\n",
"Epoch [ 72/ 100] | d_loss: 1.3079 | g_loss: 1.2341\n",
"Epoch [ 73/ 100] | d_loss: 1.4915 | g_loss: 1.0998\n",
"Epoch [ 73/ 100] | d_loss: 1.2271 | g_loss: 1.0882\n",
"Epoch [ 73/ 100] | d_loss: 1.2852 | g_loss: 1.0542\n",
"Epoch [ 74/ 100] | d_loss: 1.2105 | g_loss: 1.0388\n",
"Epoch [ 74/ 100] | d_loss: 1.2571 | g_loss: 1.2588\n",
"Epoch [ 74/ 100] | d_loss: 1.3393 | g_loss: 1.0764\n",
"Epoch [ 75/ 100] | d_loss: 1.2123 | g_loss: 1.2956\n",
"Epoch [ 75/ 100] | d_loss: 1.2723 | g_loss: 0.9174\n",
"Epoch [ 75/ 100] | d_loss: 1.4482 | g_loss: 1.0936\n",
"Epoch [ 76/ 100] | d_loss: 1.3366 | g_loss: 1.0978\n",
"Epoch [ 76/ 100] | d_loss: 1.2682 | g_loss: 1.2402\n",
"Epoch [ 76/ 100] | d_loss: 1.2431 | g_loss: 0.9709\n",
"Epoch [ 77/ 100] | d_loss: 1.3065 | g_loss: 0.9939\n",
"Epoch [ 77/ 100] | d_loss: 1.1876 | g_loss: 1.3299\n",
"Epoch [ 77/ 100] | d_loss: 1.2576 | g_loss: 1.1868\n",
"Epoch [ 78/ 100] | d_loss: 1.2706 | g_loss: 1.0540\n",
"Epoch [ 78/ 100] | d_loss: 1.2493 | g_loss: 0.9568\n",
"Epoch [ 78/ 100] | d_loss: 1.2227 | g_loss: 1.1633\n",
"Epoch [ 79/ 100] | d_loss: 1.3261 | g_loss: 0.9173\n",
"Epoch [ 79/ 100] | d_loss: 1.2312 | g_loss: 1.1450\n",
"Epoch [ 79/ 100] | d_loss: 1.3387 | g_loss: 1.2766\n",
"Epoch [ 80/ 100] | d_loss: 1.2280 | g_loss: 1.1469\n",
"Epoch [ 80/ 100] | d_loss: 1.2704 | g_loss: 1.1292\n",
"Epoch [ 80/ 100] | d_loss: 1.3570 | g_loss: 0.9845\n",
"Epoch [ 81/ 100] | d_loss: 1.2037 | g_loss: 1.1029\n",
"Epoch [ 81/ 100] | d_loss: 1.1613 | g_loss: 1.3356\n",
"Epoch [ 81/ 100] | d_loss: 1.3182 | g_loss: 1.0841\n",
"Epoch [ 82/ 100] | d_loss: 1.2307 | g_loss: 1.0811\n",
"Epoch [ 82/ 100] | d_loss: 1.2791 | g_loss: 0.8639\n",
"Epoch [ 82/ 100] | d_loss: 1.3174 | g_loss: 1.3110\n",
"Epoch [ 83/ 100] | d_loss: 1.3051 | g_loss: 0.9979\n",
"Epoch [ 83/ 100] | d_loss: 1.1558 | g_loss: 1.2926\n",
"Epoch [ 83/ 100] | d_loss: 1.2325 | g_loss: 1.0440\n",
"Epoch [ 84/ 100] | d_loss: 1.2974 | g_loss: 1.1218\n",
"Epoch [ 84/ 100] | d_loss: 1.2150 | g_loss: 1.0606\n",
"Epoch [ 84/ 100] | d_loss: 1.4180 | g_loss: 1.1683\n",
"Epoch [ 85/ 100] | d_loss: 1.3644 | g_loss: 1.2858\n",
"Epoch [ 85/ 100] | d_loss: 1.2591 | g_loss: 0.9795\n",
"Epoch [ 85/ 100] | d_loss: 1.1972 | g_loss: 0.9682\n",
"Epoch [ 86/ 100] | d_loss: 1.4219 | g_loss: 0.8627\n",
"Epoch [ 86/ 100] | d_loss: 1.1788 | g_loss: 1.4205\n",
"Epoch [ 86/ 100] | d_loss: 1.3966 | g_loss: 0.9346\n",
"Epoch [ 87/ 100] | d_loss: 1.2943 | g_loss: 0.9851\n",
"Epoch [ 87/ 100] | d_loss: 1.2265 | g_loss: 1.0192\n",
"Epoch [ 87/ 100] | d_loss: 1.2797 | g_loss: 1.3309\n",
"Epoch [ 88/ 100] | d_loss: 1.2280 | g_loss: 1.0253\n",
"Epoch [ 88/ 100] | d_loss: 1.2176 | g_loss: 1.2858\n",
"Epoch [ 88/ 100] | d_loss: 1.3786 | g_loss: 1.3351\n",
"Epoch [ 89/ 100] | d_loss: 1.3144 | g_loss: 1.1179\n",
"Epoch [ 89/ 100] | d_loss: 1.2299 | g_loss: 1.0613\n",
"Epoch [ 89/ 100] | d_loss: 1.3691 | g_loss: 1.0295\n",
"Epoch [ 90/ 100] | d_loss: 1.3526 | g_loss: 1.0230\n",
"Epoch [ 90/ 100] | d_loss: 1.2959 | g_loss: 1.1332\n",
"Epoch [ 90/ 100] | d_loss: 1.2445 | g_loss: 1.5470\n",
"Epoch [ 91/ 100] | d_loss: 1.3283 | g_loss: 1.0868\n",
"Epoch [ 91/ 100] | d_loss: 1.2901 | g_loss: 1.2393\n",
"Epoch [ 91/ 100] | d_loss: 1.4300 | g_loss: 1.1335\n",
"Epoch [ 92/ 100] | d_loss: 1.2987 | g_loss: 1.3160\n",
"Epoch [ 92/ 100] | d_loss: 1.2587 | g_loss: 1.0517\n",
"Epoch [ 92/ 100] | d_loss: 1.2881 | g_loss: 1.1046\n",
"Epoch [ 93/ 100] | d_loss: 1.2725 | g_loss: 1.1219\n",
"Epoch [ 93/ 100] | d_loss: 1.3230 | g_loss: 0.9735\n",
"Epoch [ 93/ 100] | d_loss: 1.3613 | g_loss: 0.9286\n",
"Epoch [ 94/ 100] | d_loss: 1.3035 | g_loss: 1.0815\n",
"Epoch [ 94/ 100] | d_loss: 1.2292 | g_loss: 1.0348\n",
"Epoch [ 94/ 100] | d_loss: 1.3835 | g_loss: 1.0981\n",
"Epoch [ 95/ 100] | d_loss: 1.2474 | g_loss: 1.1265\n",
"Epoch [ 95/ 100] | d_loss: 1.2481 | g_loss: 1.0578\n",
"Epoch [ 95/ 100] | d_loss: 1.3886 | g_loss: 0.8486\n",
"Epoch [ 96/ 100] | d_loss: 1.2996 | g_loss: 0.9993\n",
"Epoch [ 96/ 100] | d_loss: 1.2269 | g_loss: 0.9128\n",
"Epoch [ 96/ 100] | d_loss: 1.3136 | g_loss: 1.0670\n",
"Epoch [ 97/ 100] | d_loss: 1.3130 | g_loss: 0.9450\n",
"Epoch [ 97/ 100] | d_loss: 1.2538 | g_loss: 1.3591\n",
"Epoch [ 97/ 100] | d_loss: 1.2691 | g_loss: 0.9735\n",
"Epoch [ 98/ 100] | d_loss: 1.2483 | g_loss: 0.9697\n",
"Epoch [ 98/ 100] | d_loss: 1.1419 | g_loss: 1.9026\n",
"Epoch [ 98/ 100] | d_loss: 1.3835 | g_loss: 1.0033\n",
"Epoch [ 99/ 100] | d_loss: 1.2814 | g_loss: 0.9089\n",
"Epoch [ 99/ 100] | d_loss: 1.2866 | g_loss: 1.1416\n",
"Epoch [ 99/ 100] | d_loss: 1.5226 | g_loss: 1.1019\n",
"Epoch [ 100/ 100] | d_loss: 1.3635 | g_loss: 1.1240\n",
"Epoch [ 100/ 100] | d_loss: 1.3810 | g_loss: 0.9675\n",
"Epoch [ 100/ 100] | d_loss: 1.3214 | g_loss: 0.9679\n"
]
}
],
"source": [
"import pickle as pkl\n",
"\n",
"# training hyperparams\n",
"num_epochs = 100\n",
"\n",
"# keep track of loss and generated, \"fake\" samples\n",
"samples = []\n",
"losses = []\n",
"\n",
"print_every = 400\n",
"\n",
"# Get some fixed data for sampling. These are images that are held\n",
"# constant throughout training, and allow us to inspect the model's performance\n",
"sample_size=16\n",
"fixed_z = np.random.uniform(-1, 1, size=(sample_size, z_size))\n",
"fixed_z = torch.from_numpy(fixed_z).float()\n",
"\n",
"# train the network\n",
"D.train()\n",
"G.train()\n",
"for epoch in range(num_epochs):\n",
" \n",
" for batch_i, (real_images, _) in enumerate(train_loader):\n",
" \n",
" batch_size = real_images.size(0)\n",
" \n",
" ## Important rescaling step ## \n",
" real_images = real_images*2 - 1 # rescale input images from [0,1) to [-1, 1)\n",
" \n",
" # ============================================\n",
" # TRAIN THE DISCRIMINATOR\n",
" # ============================================\n",
" \n",
" d_optimizer.zero_grad()\n",
" \n",
" # 1. Train with real images\n",
"\n",
" # Compute the discriminator losses on real images \n",
" # smooth the real labels\n",
" D_real = D(real_images)\n",
" d_real_loss = real_loss(D_real, smooth=True)\n",
" \n",
" # 2. Train with fake images\n",
" \n",
" # Generate fake images\n",
" # gradients don't have to flow during this step\n",
" with torch.no_grad():\n",
" z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" z = torch.from_numpy(z).float()\n",
" fake_images = G(z)\n",
" \n",
" # Compute the discriminator losses on fake images \n",
" D_fake = D(fake_images)\n",
" d_fake_loss = fake_loss(D_fake)\n",
" \n",
" # add up loss and perform backprop\n",
" d_loss = d_real_loss + d_fake_loss\n",
" d_loss.backward()\n",
" d_optimizer.step()\n",
" \n",
" \n",
" # =========================================\n",
" # TRAIN THE GENERATOR\n",
" # =========================================\n",
" g_optimizer.zero_grad()\n",
" \n",
" # 1. Train with fake images and flipped labels\n",
" \n",
" # Generate fake images\n",
" z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" z = torch.from_numpy(z).float()\n",
" fake_images = G(z)\n",
" \n",
" # Compute the discriminator losses on fake images \n",
" # using flipped labels!\n",
" D_fake = D(fake_images)\n",
" g_loss = real_loss(D_fake) # use real loss to flip labels\n",
" \n",
" # perform backprop\n",
" g_loss.backward()\n",
" g_optimizer.step()\n",
"\n",
" # Print some loss stats\n",
" if batch_i % print_every == 0:\n",
" # print discriminator and generator loss\n",
" print('Epoch [{:5d}/{:5d}] | d_loss: {:6.4f} | g_loss: {:6.4f}'.format(\n",
" epoch+1, num_epochs, d_loss.item(), g_loss.item()))\n",
"\n",
" \n",
" ## AFTER EACH EPOCH##\n",
" # append discriminator loss and generator loss\n",
" losses.append((d_loss.item(), g_loss.item()))\n",
" \n",
" # generate and save sample, fake images\n",
" G.eval() # eval mode for generating samples\n",
" samples_z = G(fixed_z)\n",
" samples.append(samples_z)\n",
" G.train() # back to train mode\n",
"\n",
"\n",
"# Save training generator samples\n",
"with open('train_samples.pkl', 'wb') as f:\n",
" pkl.dump(samples, f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training loss\n",
"\n",
"Here we'll plot the training losses for the generator and discriminator, recorded after each epoch."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"
\n",
"\n",
"The losses will by binary cross entropy loss with logits, which we can get with [BCEWithLogitsLoss](https://pytorch.org/docs/stable/nn.html#bcewithlogitsloss). This combines a `sigmoid` activation function **and** and binary cross entropy loss in one function.\n",
"\n",
"For the real images, we want `D(real_images) = 1`. That is, we want the discriminator to classify the the real images with a label = 1, indicating that these are real. To help the discriminator generalize better, the labels are **reduced a bit from 1.0 to 0.9**. For this, we'll use the parameter `smooth`; if True, then we should smooth our labels. In PyTorch, this looks like `labels = torch.ones(size) * 0.9`\n",
"\n",
"The discriminator loss for the fake data is similar. We want `D(fake_images) = 0`, where the fake images are the _generator output_, `fake_images = G(z)`. \n",
"\n",
"### Generator Loss\n",
"\n",
"The generator loss will look similar only with flipped labels. The generator's goal is to get `D(fake_images) = 1`. In this case, the labels are **flipped** to represent that the generator is trying to fool the discriminator into thinking that the images it generates (fakes) are real!"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"# Calculate losses\n",
"def real_loss(D_out, smooth=False):\n",
" batch_size = D_out.size(0)\n",
" # label smoothing\n",
" if smooth:\n",
" # smooth, real labels = 0.9\n",
" labels = torch.ones(batch_size)*0.9\n",
" else:\n",
" labels = torch.ones(batch_size) # real labels = 1\n",
" \n",
" # numerically stable loss\n",
" criterion = nn.BCEWithLogitsLoss()\n",
" # calculate loss\n",
" loss = criterion(D_out.squeeze(), labels)\n",
" return loss\n",
"\n",
"def fake_loss(D_out):\n",
" batch_size = D_out.size(0)\n",
" labels = torch.zeros(batch_size) # fake labels = 0\n",
" criterion = nn.BCEWithLogitsLoss()\n",
" # calculate loss\n",
" loss = criterion(D_out.squeeze(), labels)\n",
" return loss"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Optimizers\n",
"\n",
"We want to update the generator and discriminator variables separately. So, we'll define two separate Adam optimizers."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true,
"scrolled": true
},
"outputs": [],
"source": [
"import torch.optim as optim\n",
"\n",
"# Optimizers\n",
"lr = 0.002\n",
"\n",
"# Create optimizers for the discriminator and generator\n",
"d_optimizer = optim.Adam(D.parameters(), lr)\n",
"g_optimizer = optim.Adam(G.parameters(), lr)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"## Training\n",
"\n",
"Training will involve alternating between training the discriminator and the generator. We'll use our functions `real_loss` and `fake_loss` to help us calculate the discriminator losses in all of the following cases.\n",
"\n",
"### Discriminator training\n",
"1. Compute the discriminator loss on real, training images \n",
"2. Generate fake images\n",
"3. Compute the discriminator loss on fake, generated images \n",
"4. Add up real and fake loss\n",
"5. Perform backpropagation + an optimization step to update the discriminator's weights\n",
"\n",
"### Generator training\n",
"1. Generate fake images\n",
"2. Compute the discriminator loss on fake images, using **flipped** labels!\n",
"3. Perform backpropagation + an optimization step to update the generator's weights\n",
"\n",
"#### Saving Samples\n",
"\n",
"As we train, we'll also print out some loss statistics and save some generated \"fake\" samples."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"scrolled": true
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Epoch [ 1/ 100] | d_loss: 1.3830 | g_loss: 0.6883\n",
"Epoch [ 1/ 100] | d_loss: 0.7668 | g_loss: 3.1404\n",
"Epoch [ 1/ 100] | d_loss: 1.0908 | g_loss: 2.6393\n",
"Epoch [ 2/ 100] | d_loss: 1.2982 | g_loss: 1.1008\n",
"Epoch [ 2/ 100] | d_loss: 1.1753 | g_loss: 1.1042\n",
"Epoch [ 2/ 100] | d_loss: 1.0874 | g_loss: 1.6588\n",
"Epoch [ 3/ 100] | d_loss: 0.9747 | g_loss: 2.9083\n",
"Epoch [ 3/ 100] | d_loss: 1.0724 | g_loss: 1.1101\n",
"Epoch [ 3/ 100] | d_loss: 1.4727 | g_loss: 0.4990\n",
"Epoch [ 4/ 100] | d_loss: 1.1590 | g_loss: 0.9996\n",
"Epoch [ 4/ 100] | d_loss: 1.1832 | g_loss: 1.0638\n",
"Epoch [ 4/ 100] | d_loss: 1.1652 | g_loss: 1.1463\n",
"Epoch [ 5/ 100] | d_loss: 1.2966 | g_loss: 1.0950\n",
"Epoch [ 5/ 100] | d_loss: 1.3616 | g_loss: 1.0312\n",
"Epoch [ 5/ 100] | d_loss: 1.2202 | g_loss: 1.1301\n",
"Epoch [ 6/ 100] | d_loss: 1.1609 | g_loss: 1.5148\n",
"Epoch [ 6/ 100] | d_loss: 1.1100 | g_loss: 1.2183\n",
"Epoch [ 6/ 100] | d_loss: 1.2376 | g_loss: 1.5296\n",
"Epoch [ 7/ 100] | d_loss: 1.2304 | g_loss: 1.1526\n",
"Epoch [ 7/ 100] | d_loss: 1.1684 | g_loss: 1.1339\n",
"Epoch [ 7/ 100] | d_loss: 1.0965 | g_loss: 1.3531\n",
"Epoch [ 8/ 100] | d_loss: 1.2527 | g_loss: 2.2266\n",
"Epoch [ 8/ 100] | d_loss: 1.2978 | g_loss: 1.6185\n",
"Epoch [ 8/ 100] | d_loss: 1.1493 | g_loss: 1.4873\n",
"Epoch [ 9/ 100] | d_loss: 0.9751 | g_loss: 2.6848\n",
"Epoch [ 9/ 100] | d_loss: 1.1574 | g_loss: 1.7639\n",
"Epoch [ 9/ 100] | d_loss: 0.9629 | g_loss: 2.2062\n",
"Epoch [ 10/ 100] | d_loss: 1.0279 | g_loss: 1.9386\n",
"Epoch [ 10/ 100] | d_loss: 1.1110 | g_loss: 1.0685\n",
"Epoch [ 10/ 100] | d_loss: 1.3441 | g_loss: 1.0324\n",
"Epoch [ 11/ 100] | d_loss: 1.1879 | g_loss: 1.0673\n",
"Epoch [ 11/ 100] | d_loss: 1.3366 | g_loss: 0.9610\n",
"Epoch [ 11/ 100] | d_loss: 1.1435 | g_loss: 1.0668\n",
"Epoch [ 12/ 100] | d_loss: 1.1189 | g_loss: 1.2501\n",
"Epoch [ 12/ 100] | d_loss: 1.2153 | g_loss: 1.0666\n",
"Epoch [ 12/ 100] | d_loss: 1.3179 | g_loss: 0.9101\n",
"Epoch [ 13/ 100] | d_loss: 1.1504 | g_loss: 1.4559\n",
"Epoch [ 13/ 100] | d_loss: 1.3358 | g_loss: 0.9763\n",
"Epoch [ 13/ 100] | d_loss: 1.1833 | g_loss: 1.0180\n",
"Epoch [ 14/ 100] | d_loss: 1.1839 | g_loss: 1.2705\n",
"Epoch [ 14/ 100] | d_loss: 1.3219 | g_loss: 1.0915\n",
"Epoch [ 14/ 100] | d_loss: 1.2945 | g_loss: 0.9335\n",
"Epoch [ 15/ 100] | d_loss: 1.3458 | g_loss: 0.9600\n",
"Epoch [ 15/ 100] | d_loss: 1.3445 | g_loss: 0.9098\n",
"Epoch [ 15/ 100] | d_loss: 1.3289 | g_loss: 1.3456\n",
"Epoch [ 16/ 100] | d_loss: 1.2725 | g_loss: 0.9085\n",
"Epoch [ 16/ 100] | d_loss: 1.1133 | g_loss: 1.0910\n",
"Epoch [ 16/ 100] | d_loss: 1.2564 | g_loss: 1.0233\n",
"Epoch [ 17/ 100] | d_loss: 1.3171 | g_loss: 0.9643\n",
"Epoch [ 17/ 100] | d_loss: 1.2932 | g_loss: 1.0311\n",
"Epoch [ 17/ 100] | d_loss: 1.2643 | g_loss: 0.9377\n",
"Epoch [ 18/ 100] | d_loss: 1.2226 | g_loss: 1.4327\n",
"Epoch [ 18/ 100] | d_loss: 1.3909 | g_loss: 0.9178\n",
"Epoch [ 18/ 100] | d_loss: 1.2430 | g_loss: 1.0297\n",
"Epoch [ 19/ 100] | d_loss: 1.3409 | g_loss: 1.1413\n",
"Epoch [ 19/ 100] | d_loss: 1.1607 | g_loss: 1.2019\n",
"Epoch [ 19/ 100] | d_loss: 1.4060 | g_loss: 1.1366\n",
"Epoch [ 20/ 100] | d_loss: 1.3076 | g_loss: 1.0200\n",
"Epoch [ 20/ 100] | d_loss: 1.2715 | g_loss: 0.9261\n",
"Epoch [ 20/ 100] | d_loss: 1.2959 | g_loss: 1.4079\n",
"Epoch [ 21/ 100] | d_loss: 1.2529 | g_loss: 1.4324\n",
"Epoch [ 21/ 100] | d_loss: 1.2907 | g_loss: 0.9551\n",
"Epoch [ 21/ 100] | d_loss: 1.2426 | g_loss: 1.2571\n",
"Epoch [ 22/ 100] | d_loss: 1.2168 | g_loss: 1.7557\n",
"Epoch [ 22/ 100] | d_loss: 1.2874 | g_loss: 1.0733\n",
"Epoch [ 22/ 100] | d_loss: 1.1758 | g_loss: 1.6449\n",
"Epoch [ 23/ 100] | d_loss: 1.3328 | g_loss: 0.9859\n",
"Epoch [ 23/ 100] | d_loss: 1.4189 | g_loss: 0.8197\n",
"Epoch [ 23/ 100] | d_loss: 1.3146 | g_loss: 0.9181\n",
"Epoch [ 24/ 100] | d_loss: 1.2752 | g_loss: 1.1507\n",
"Epoch [ 24/ 100] | d_loss: 1.1860 | g_loss: 1.0389\n",
"Epoch [ 24/ 100] | d_loss: 1.2692 | g_loss: 1.0240\n",
"Epoch [ 25/ 100] | d_loss: 1.2905 | g_loss: 0.8767\n",
"Epoch [ 25/ 100] | d_loss: 1.1643 | g_loss: 1.0650\n",
"Epoch [ 25/ 100] | d_loss: 1.3141 | g_loss: 0.8904\n",
"Epoch [ 26/ 100] | d_loss: 1.2288 | g_loss: 1.0190\n",
"Epoch [ 26/ 100] | d_loss: 1.2016 | g_loss: 0.9930\n",
"Epoch [ 26/ 100] | d_loss: 1.4220 | g_loss: 1.1657\n",
"Epoch [ 27/ 100] | d_loss: 1.2774 | g_loss: 1.0464\n",
"Epoch [ 27/ 100] | d_loss: 1.2179 | g_loss: 1.0301\n",
"Epoch [ 27/ 100] | d_loss: 1.2938 | g_loss: 1.1045\n",
"Epoch [ 28/ 100] | d_loss: 1.2736 | g_loss: 1.1921\n",
"Epoch [ 28/ 100] | d_loss: 1.1929 | g_loss: 1.1512\n",
"Epoch [ 28/ 100] | d_loss: 1.3188 | g_loss: 0.9897\n",
"Epoch [ 29/ 100] | d_loss: 1.3085 | g_loss: 1.4660\n",
"Epoch [ 29/ 100] | d_loss: 1.2663 | g_loss: 0.9120\n",
"Epoch [ 29/ 100] | d_loss: 1.3005 | g_loss: 0.9635\n",
"Epoch [ 30/ 100] | d_loss: 1.2953 | g_loss: 0.8053\n",
"Epoch [ 30/ 100] | d_loss: 1.3288 | g_loss: 0.9908\n",
"Epoch [ 30/ 100] | d_loss: 1.3487 | g_loss: 1.1090\n",
"Epoch [ 31/ 100] | d_loss: 1.2638 | g_loss: 1.0738\n",
"Epoch [ 31/ 100] | d_loss: 1.2856 | g_loss: 0.9346\n",
"Epoch [ 31/ 100] | d_loss: 1.2525 | g_loss: 1.1265\n",
"Epoch [ 32/ 100] | d_loss: 1.1938 | g_loss: 1.1639\n",
"Epoch [ 32/ 100] | d_loss: 1.2217 | g_loss: 0.9636\n",
"Epoch [ 32/ 100] | d_loss: 1.2105 | g_loss: 1.7308\n",
"Epoch [ 33/ 100] | d_loss: 1.1531 | g_loss: 1.5628\n",
"Epoch [ 33/ 100] | d_loss: 1.3260 | g_loss: 0.9161\n",
"Epoch [ 33/ 100] | d_loss: 1.2334 | g_loss: 0.9264\n",
"Epoch [ 34/ 100] | d_loss: 1.2336 | g_loss: 1.0195\n",
"Epoch [ 34/ 100] | d_loss: 1.2184 | g_loss: 1.3364\n",
"Epoch [ 34/ 100] | d_loss: 1.3039 | g_loss: 0.9413\n",
"Epoch [ 35/ 100] | d_loss: 1.3298 | g_loss: 1.1236\n",
"Epoch [ 35/ 100] | d_loss: 1.2562 | g_loss: 1.0155\n",
"Epoch [ 35/ 100] | d_loss: 1.3659 | g_loss: 1.2384\n",
"Epoch [ 36/ 100] | d_loss: 1.1759 | g_loss: 1.0545\n",
"Epoch [ 36/ 100] | d_loss: 1.2195 | g_loss: 1.0489\n",
"Epoch [ 36/ 100] | d_loss: 1.2799 | g_loss: 0.9530\n",
"Epoch [ 37/ 100] | d_loss: 1.2149 | g_loss: 1.0076\n",
"Epoch [ 37/ 100] | d_loss: 1.2700 | g_loss: 1.1004\n",
"Epoch [ 37/ 100] | d_loss: 1.3090 | g_loss: 0.9861\n",
"Epoch [ 38/ 100] | d_loss: 1.3035 | g_loss: 1.0189\n",
"Epoch [ 38/ 100] | d_loss: 1.2769 | g_loss: 1.0285\n",
"Epoch [ 38/ 100] | d_loss: 1.2371 | g_loss: 1.2829\n",
"Epoch [ 39/ 100] | d_loss: 1.2404 | g_loss: 1.0135\n",
"Epoch [ 39/ 100] | d_loss: 1.2708 | g_loss: 0.9378\n",
"Epoch [ 39/ 100] | d_loss: 1.2512 | g_loss: 0.9949\n",
"Epoch [ 40/ 100] | d_loss: 1.1768 | g_loss: 0.9511\n",
"Epoch [ 40/ 100] | d_loss: 1.3067 | g_loss: 0.9223\n",
"Epoch [ 40/ 100] | d_loss: 1.3625 | g_loss: 0.8471\n",
"Epoch [ 41/ 100] | d_loss: 1.2816 | g_loss: 1.0424\n",
"Epoch [ 41/ 100] | d_loss: 1.2974 | g_loss: 1.1541\n",
"Epoch [ 41/ 100] | d_loss: 1.1643 | g_loss: 1.2687\n",
"Epoch [ 42/ 100] | d_loss: 1.2976 | g_loss: 1.0265\n",
"Epoch [ 42/ 100] | d_loss: 1.3245 | g_loss: 1.1694\n",
"Epoch [ 42/ 100] | d_loss: 1.3458 | g_loss: 0.9364\n",
"Epoch [ 43/ 100] | d_loss: 1.1641 | g_loss: 1.6862\n",
"Epoch [ 43/ 100] | d_loss: 1.2706 | g_loss: 0.8405\n",
"Epoch [ 43/ 100] | d_loss: 1.3763 | g_loss: 0.9720\n",
"Epoch [ 44/ 100] | d_loss: 1.3490 | g_loss: 1.1244\n",
"Epoch [ 44/ 100] | d_loss: 1.2542 | g_loss: 1.3335\n",
"Epoch [ 44/ 100] | d_loss: 1.2833 | g_loss: 0.9767\n",
"Epoch [ 45/ 100] | d_loss: 1.3130 | g_loss: 0.9182\n",
"Epoch [ 45/ 100] | d_loss: 1.2353 | g_loss: 1.0782\n",
"Epoch [ 45/ 100] | d_loss: 1.3760 | g_loss: 0.9803\n",
"Epoch [ 46/ 100] | d_loss: 1.4026 | g_loss: 0.9744\n",
"Epoch [ 46/ 100] | d_loss: 1.3152 | g_loss: 0.9312\n",
"Epoch [ 46/ 100] | d_loss: 1.2657 | g_loss: 1.0664\n",
"Epoch [ 47/ 100] | d_loss: 1.2507 | g_loss: 1.2632\n",
"Epoch [ 47/ 100] | d_loss: 1.2343 | g_loss: 1.0100\n",
"Epoch [ 47/ 100] | d_loss: 1.2856 | g_loss: 0.9613\n",
"Epoch [ 48/ 100] | d_loss: 1.2589 | g_loss: 1.0631\n",
"Epoch [ 48/ 100] | d_loss: 1.2255 | g_loss: 1.3015\n",
"Epoch [ 48/ 100] | d_loss: 1.3112 | g_loss: 0.8649\n",
"Epoch [ 49/ 100] | d_loss: 1.2646 | g_loss: 0.9986\n",
"Epoch [ 49/ 100] | d_loss: 1.2757 | g_loss: 0.9732\n",
"Epoch [ 49/ 100] | d_loss: 1.1808 | g_loss: 1.4561\n",
"Epoch [ 50/ 100] | d_loss: 1.3849 | g_loss: 1.2169\n",
"Epoch [ 50/ 100] | d_loss: 1.2799 | g_loss: 1.4074\n",
"Epoch [ 50/ 100] | d_loss: 1.3711 | g_loss: 0.9860\n",
"Epoch [ 51/ 100] | d_loss: 1.2772 | g_loss: 1.2343\n",
"Epoch [ 51/ 100] | d_loss: 1.3022 | g_loss: 0.9042\n",
"Epoch [ 51/ 100] | d_loss: 1.3566 | g_loss: 0.8909\n",
"Epoch [ 52/ 100] | d_loss: 1.3641 | g_loss: 1.0716\n",
"Epoch [ 52/ 100] | d_loss: 1.2138 | g_loss: 1.2055\n",
"Epoch [ 52/ 100] | d_loss: 1.3753 | g_loss: 0.9283\n",
"Epoch [ 53/ 100] | d_loss: 1.2297 | g_loss: 1.1757\n",
"Epoch [ 53/ 100] | d_loss: 1.2801 | g_loss: 0.9982\n",
"Epoch [ 53/ 100] | d_loss: 1.2177 | g_loss: 0.9533\n",
"Epoch [ 54/ 100] | d_loss: 1.3590 | g_loss: 0.8750\n",
"Epoch [ 54/ 100] | d_loss: 1.2776 | g_loss: 1.3202\n",
"Epoch [ 54/ 100] | d_loss: 1.4154 | g_loss: 0.9770\n",
"Epoch [ 55/ 100] | d_loss: 1.3179 | g_loss: 1.1155\n",
"Epoch [ 55/ 100] | d_loss: 1.3786 | g_loss: 0.9604\n",
"Epoch [ 55/ 100] | d_loss: 1.3158 | g_loss: 0.9751\n",
"Epoch [ 56/ 100] | d_loss: 1.3204 | g_loss: 0.9898\n",
"Epoch [ 56/ 100] | d_loss: 1.4150 | g_loss: 1.0278\n",
"Epoch [ 56/ 100] | d_loss: 1.2821 | g_loss: 0.9324\n",
"Epoch [ 57/ 100] | d_loss: 1.2576 | g_loss: 1.2056\n",
"Epoch [ 57/ 100] | d_loss: 1.4449 | g_loss: 1.1794\n",
"Epoch [ 57/ 100] | d_loss: 1.3697 | g_loss: 1.1030\n",
"Epoch [ 58/ 100] | d_loss: 1.2824 | g_loss: 0.9524\n",
"Epoch [ 58/ 100] | d_loss: 1.2432 | g_loss: 1.1015\n",
"Epoch [ 58/ 100] | d_loss: 1.3309 | g_loss: 1.0080\n",
"Epoch [ 59/ 100] | d_loss: 1.3095 | g_loss: 1.0256\n",
"Epoch [ 59/ 100] | d_loss: 1.2653 | g_loss: 0.8913\n",
"Epoch [ 59/ 100] | d_loss: 1.3224 | g_loss: 1.0386\n",
"Epoch [ 60/ 100] | d_loss: 1.1556 | g_loss: 1.1556\n",
"Epoch [ 60/ 100] | d_loss: 1.2522 | g_loss: 1.0155\n",
"Epoch [ 60/ 100] | d_loss: 1.3123 | g_loss: 0.9344\n",
"Epoch [ 61/ 100] | d_loss: 1.2728 | g_loss: 1.1286\n",
"Epoch [ 61/ 100] | d_loss: 1.3303 | g_loss: 1.0562\n",
"Epoch [ 61/ 100] | d_loss: 1.3408 | g_loss: 0.8740\n",
"Epoch [ 62/ 100] | d_loss: 1.4031 | g_loss: 1.0154\n",
"Epoch [ 62/ 100] | d_loss: 1.1388 | g_loss: 1.3963\n",
"Epoch [ 62/ 100] | d_loss: 1.4201 | g_loss: 1.1908\n",
"Epoch [ 63/ 100] | d_loss: 1.2058 | g_loss: 1.1407\n",
"Epoch [ 63/ 100] | d_loss: 1.2444 | g_loss: 1.1547\n",
"Epoch [ 63/ 100] | d_loss: 1.3877 | g_loss: 1.0653\n",
"Epoch [ 64/ 100] | d_loss: 1.3246 | g_loss: 1.4514\n",
"Epoch [ 64/ 100] | d_loss: 1.3463 | g_loss: 1.0041\n",
"Epoch [ 64/ 100] | d_loss: 1.2426 | g_loss: 1.5180\n",
"Epoch [ 65/ 100] | d_loss: 1.3013 | g_loss: 1.0159\n",
"Epoch [ 65/ 100] | d_loss: 1.3368 | g_loss: 2.1512\n",
"Epoch [ 65/ 100] | d_loss: 1.3612 | g_loss: 0.9549\n",
"Epoch [ 66/ 100] | d_loss: 1.3277 | g_loss: 0.7320\n",
"Epoch [ 66/ 100] | d_loss: 1.2434 | g_loss: 0.9365\n",
"Epoch [ 66/ 100] | d_loss: 1.2326 | g_loss: 1.3177\n",
"Epoch [ 67/ 100] | d_loss: 1.2334 | g_loss: 1.4614\n",
"Epoch [ 67/ 100] | d_loss: 1.2690 | g_loss: 1.0928\n",
"Epoch [ 67/ 100] | d_loss: 1.3406 | g_loss: 1.0277\n",
"Epoch [ 68/ 100] | d_loss: 1.2498 | g_loss: 1.0917\n",
"Epoch [ 68/ 100] | d_loss: 1.3146 | g_loss: 1.0963\n",
"Epoch [ 68/ 100] | d_loss: 1.3215 | g_loss: 1.3057\n",
"Epoch [ 69/ 100] | d_loss: 1.3268 | g_loss: 1.1683\n",
"Epoch [ 69/ 100] | d_loss: 1.2631 | g_loss: 0.9922\n",
"Epoch [ 69/ 100] | d_loss: 1.3693 | g_loss: 1.0472\n",
"Epoch [ 70/ 100] | d_loss: 1.3476 | g_loss: 1.1509\n",
"Epoch [ 70/ 100] | d_loss: 1.2585 | g_loss: 1.2276\n",
"Epoch [ 70/ 100] | d_loss: 1.3906 | g_loss: 1.2750\n",
"Epoch [ 71/ 100] | d_loss: 1.2083 | g_loss: 0.9252\n",
"Epoch [ 71/ 100] | d_loss: 1.3743 | g_loss: 1.1076\n",
"Epoch [ 71/ 100] | d_loss: 1.2552 | g_loss: 0.9602\n",
"Epoch [ 72/ 100] | d_loss: 1.3761 | g_loss: 0.9666\n",
"Epoch [ 72/ 100] | d_loss: 1.3193 | g_loss: 0.9309\n",
"Epoch [ 72/ 100] | d_loss: 1.3079 | g_loss: 1.2341\n",
"Epoch [ 73/ 100] | d_loss: 1.4915 | g_loss: 1.0998\n",
"Epoch [ 73/ 100] | d_loss: 1.2271 | g_loss: 1.0882\n",
"Epoch [ 73/ 100] | d_loss: 1.2852 | g_loss: 1.0542\n",
"Epoch [ 74/ 100] | d_loss: 1.2105 | g_loss: 1.0388\n",
"Epoch [ 74/ 100] | d_loss: 1.2571 | g_loss: 1.2588\n",
"Epoch [ 74/ 100] | d_loss: 1.3393 | g_loss: 1.0764\n",
"Epoch [ 75/ 100] | d_loss: 1.2123 | g_loss: 1.2956\n",
"Epoch [ 75/ 100] | d_loss: 1.2723 | g_loss: 0.9174\n",
"Epoch [ 75/ 100] | d_loss: 1.4482 | g_loss: 1.0936\n",
"Epoch [ 76/ 100] | d_loss: 1.3366 | g_loss: 1.0978\n",
"Epoch [ 76/ 100] | d_loss: 1.2682 | g_loss: 1.2402\n",
"Epoch [ 76/ 100] | d_loss: 1.2431 | g_loss: 0.9709\n",
"Epoch [ 77/ 100] | d_loss: 1.3065 | g_loss: 0.9939\n",
"Epoch [ 77/ 100] | d_loss: 1.1876 | g_loss: 1.3299\n",
"Epoch [ 77/ 100] | d_loss: 1.2576 | g_loss: 1.1868\n",
"Epoch [ 78/ 100] | d_loss: 1.2706 | g_loss: 1.0540\n",
"Epoch [ 78/ 100] | d_loss: 1.2493 | g_loss: 0.9568\n",
"Epoch [ 78/ 100] | d_loss: 1.2227 | g_loss: 1.1633\n",
"Epoch [ 79/ 100] | d_loss: 1.3261 | g_loss: 0.9173\n",
"Epoch [ 79/ 100] | d_loss: 1.2312 | g_loss: 1.1450\n",
"Epoch [ 79/ 100] | d_loss: 1.3387 | g_loss: 1.2766\n",
"Epoch [ 80/ 100] | d_loss: 1.2280 | g_loss: 1.1469\n",
"Epoch [ 80/ 100] | d_loss: 1.2704 | g_loss: 1.1292\n",
"Epoch [ 80/ 100] | d_loss: 1.3570 | g_loss: 0.9845\n",
"Epoch [ 81/ 100] | d_loss: 1.2037 | g_loss: 1.1029\n",
"Epoch [ 81/ 100] | d_loss: 1.1613 | g_loss: 1.3356\n",
"Epoch [ 81/ 100] | d_loss: 1.3182 | g_loss: 1.0841\n",
"Epoch [ 82/ 100] | d_loss: 1.2307 | g_loss: 1.0811\n",
"Epoch [ 82/ 100] | d_loss: 1.2791 | g_loss: 0.8639\n",
"Epoch [ 82/ 100] | d_loss: 1.3174 | g_loss: 1.3110\n",
"Epoch [ 83/ 100] | d_loss: 1.3051 | g_loss: 0.9979\n",
"Epoch [ 83/ 100] | d_loss: 1.1558 | g_loss: 1.2926\n",
"Epoch [ 83/ 100] | d_loss: 1.2325 | g_loss: 1.0440\n",
"Epoch [ 84/ 100] | d_loss: 1.2974 | g_loss: 1.1218\n",
"Epoch [ 84/ 100] | d_loss: 1.2150 | g_loss: 1.0606\n",
"Epoch [ 84/ 100] | d_loss: 1.4180 | g_loss: 1.1683\n",
"Epoch [ 85/ 100] | d_loss: 1.3644 | g_loss: 1.2858\n",
"Epoch [ 85/ 100] | d_loss: 1.2591 | g_loss: 0.9795\n",
"Epoch [ 85/ 100] | d_loss: 1.1972 | g_loss: 0.9682\n",
"Epoch [ 86/ 100] | d_loss: 1.4219 | g_loss: 0.8627\n",
"Epoch [ 86/ 100] | d_loss: 1.1788 | g_loss: 1.4205\n",
"Epoch [ 86/ 100] | d_loss: 1.3966 | g_loss: 0.9346\n",
"Epoch [ 87/ 100] | d_loss: 1.2943 | g_loss: 0.9851\n",
"Epoch [ 87/ 100] | d_loss: 1.2265 | g_loss: 1.0192\n",
"Epoch [ 87/ 100] | d_loss: 1.2797 | g_loss: 1.3309\n",
"Epoch [ 88/ 100] | d_loss: 1.2280 | g_loss: 1.0253\n",
"Epoch [ 88/ 100] | d_loss: 1.2176 | g_loss: 1.2858\n",
"Epoch [ 88/ 100] | d_loss: 1.3786 | g_loss: 1.3351\n",
"Epoch [ 89/ 100] | d_loss: 1.3144 | g_loss: 1.1179\n",
"Epoch [ 89/ 100] | d_loss: 1.2299 | g_loss: 1.0613\n",
"Epoch [ 89/ 100] | d_loss: 1.3691 | g_loss: 1.0295\n",
"Epoch [ 90/ 100] | d_loss: 1.3526 | g_loss: 1.0230\n",
"Epoch [ 90/ 100] | d_loss: 1.2959 | g_loss: 1.1332\n",
"Epoch [ 90/ 100] | d_loss: 1.2445 | g_loss: 1.5470\n",
"Epoch [ 91/ 100] | d_loss: 1.3283 | g_loss: 1.0868\n",
"Epoch [ 91/ 100] | d_loss: 1.2901 | g_loss: 1.2393\n",
"Epoch [ 91/ 100] | d_loss: 1.4300 | g_loss: 1.1335\n",
"Epoch [ 92/ 100] | d_loss: 1.2987 | g_loss: 1.3160\n",
"Epoch [ 92/ 100] | d_loss: 1.2587 | g_loss: 1.0517\n",
"Epoch [ 92/ 100] | d_loss: 1.2881 | g_loss: 1.1046\n",
"Epoch [ 93/ 100] | d_loss: 1.2725 | g_loss: 1.1219\n",
"Epoch [ 93/ 100] | d_loss: 1.3230 | g_loss: 0.9735\n",
"Epoch [ 93/ 100] | d_loss: 1.3613 | g_loss: 0.9286\n",
"Epoch [ 94/ 100] | d_loss: 1.3035 | g_loss: 1.0815\n",
"Epoch [ 94/ 100] | d_loss: 1.2292 | g_loss: 1.0348\n",
"Epoch [ 94/ 100] | d_loss: 1.3835 | g_loss: 1.0981\n",
"Epoch [ 95/ 100] | d_loss: 1.2474 | g_loss: 1.1265\n",
"Epoch [ 95/ 100] | d_loss: 1.2481 | g_loss: 1.0578\n",
"Epoch [ 95/ 100] | d_loss: 1.3886 | g_loss: 0.8486\n",
"Epoch [ 96/ 100] | d_loss: 1.2996 | g_loss: 0.9993\n",
"Epoch [ 96/ 100] | d_loss: 1.2269 | g_loss: 0.9128\n",
"Epoch [ 96/ 100] | d_loss: 1.3136 | g_loss: 1.0670\n",
"Epoch [ 97/ 100] | d_loss: 1.3130 | g_loss: 0.9450\n",
"Epoch [ 97/ 100] | d_loss: 1.2538 | g_loss: 1.3591\n",
"Epoch [ 97/ 100] | d_loss: 1.2691 | g_loss: 0.9735\n",
"Epoch [ 98/ 100] | d_loss: 1.2483 | g_loss: 0.9697\n",
"Epoch [ 98/ 100] | d_loss: 1.1419 | g_loss: 1.9026\n",
"Epoch [ 98/ 100] | d_loss: 1.3835 | g_loss: 1.0033\n",
"Epoch [ 99/ 100] | d_loss: 1.2814 | g_loss: 0.9089\n",
"Epoch [ 99/ 100] | d_loss: 1.2866 | g_loss: 1.1416\n",
"Epoch [ 99/ 100] | d_loss: 1.5226 | g_loss: 1.1019\n",
"Epoch [ 100/ 100] | d_loss: 1.3635 | g_loss: 1.1240\n",
"Epoch [ 100/ 100] | d_loss: 1.3810 | g_loss: 0.9675\n",
"Epoch [ 100/ 100] | d_loss: 1.3214 | g_loss: 0.9679\n"
]
}
],
"source": [
"import pickle as pkl\n",
"\n",
"# training hyperparams\n",
"num_epochs = 100\n",
"\n",
"# keep track of loss and generated, \"fake\" samples\n",
"samples = []\n",
"losses = []\n",
"\n",
"print_every = 400\n",
"\n",
"# Get some fixed data for sampling. These are images that are held\n",
"# constant throughout training, and allow us to inspect the model's performance\n",
"sample_size=16\n",
"fixed_z = np.random.uniform(-1, 1, size=(sample_size, z_size))\n",
"fixed_z = torch.from_numpy(fixed_z).float()\n",
"\n",
"# train the network\n",
"D.train()\n",
"G.train()\n",
"for epoch in range(num_epochs):\n",
" \n",
" for batch_i, (real_images, _) in enumerate(train_loader):\n",
" \n",
" batch_size = real_images.size(0)\n",
" \n",
" ## Important rescaling step ## \n",
" real_images = real_images*2 - 1 # rescale input images from [0,1) to [-1, 1)\n",
" \n",
" # ============================================\n",
" # TRAIN THE DISCRIMINATOR\n",
" # ============================================\n",
" \n",
" d_optimizer.zero_grad()\n",
" \n",
" # 1. Train with real images\n",
"\n",
" # Compute the discriminator losses on real images \n",
" # smooth the real labels\n",
" D_real = D(real_images)\n",
" d_real_loss = real_loss(D_real, smooth=True)\n",
" \n",
" # 2. Train with fake images\n",
" \n",
" # Generate fake images\n",
" # gradients don't have to flow during this step\n",
" with torch.no_grad():\n",
" z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" z = torch.from_numpy(z).float()\n",
" fake_images = G(z)\n",
" \n",
" # Compute the discriminator losses on fake images \n",
" D_fake = D(fake_images)\n",
" d_fake_loss = fake_loss(D_fake)\n",
" \n",
" # add up loss and perform backprop\n",
" d_loss = d_real_loss + d_fake_loss\n",
" d_loss.backward()\n",
" d_optimizer.step()\n",
" \n",
" \n",
" # =========================================\n",
" # TRAIN THE GENERATOR\n",
" # =========================================\n",
" g_optimizer.zero_grad()\n",
" \n",
" # 1. Train with fake images and flipped labels\n",
" \n",
" # Generate fake images\n",
" z = np.random.uniform(-1, 1, size=(batch_size, z_size))\n",
" z = torch.from_numpy(z).float()\n",
" fake_images = G(z)\n",
" \n",
" # Compute the discriminator losses on fake images \n",
" # using flipped labels!\n",
" D_fake = D(fake_images)\n",
" g_loss = real_loss(D_fake) # use real loss to flip labels\n",
" \n",
" # perform backprop\n",
" g_loss.backward()\n",
" g_optimizer.step()\n",
"\n",
" # Print some loss stats\n",
" if batch_i % print_every == 0:\n",
" # print discriminator and generator loss\n",
" print('Epoch [{:5d}/{:5d}] | d_loss: {:6.4f} | g_loss: {:6.4f}'.format(\n",
" epoch+1, num_epochs, d_loss.item(), g_loss.item()))\n",
"\n",
" \n",
" ## AFTER EACH EPOCH##\n",
" # append discriminator loss and generator loss\n",
" losses.append((d_loss.item(), g_loss.item()))\n",
" \n",
" # generate and save sample, fake images\n",
" G.eval() # eval mode for generating samples\n",
" samples_z = G(fixed_z)\n",
" samples.append(samples_z)\n",
" G.train() # back to train mode\n",
"\n",
"\n",
"# Save training generator samples\n",
"with open('train_samples.pkl', 'wb') as f:\n",
" pkl.dump(samples, f)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Training loss\n",
"\n",
"Here we'll plot the training losses for the generator and discriminator, recorded after each epoch."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"