{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Introduction\n",
"\n",
"This notebook combines the excellent [illustration](http://jalammar.github.io/illustrated-transformer/) of the [transfomer](https://arxiv.org/abs/1706.03762) by Jay Alammar and the [code annonation](http://nlp.seas.harvard.edu/2018/04/03/attention.html) by `harvardnlp` lab."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"import numpy as np\n",
"import torch\n",
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"import math, copy, time\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"## Part 1: Components of the transformer model\n",
"\n",
"### Step 1: EncoderDecoder and Generator models\n",
"\n",
"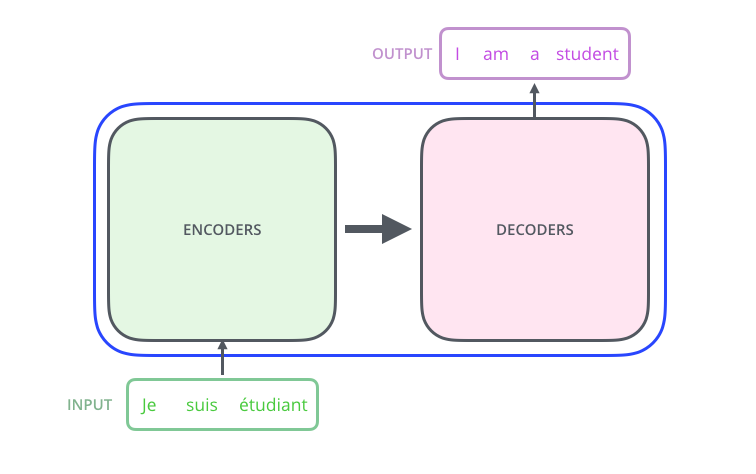\n",
"\n",
"At this point now we don't bother about how `self.decoder` and `self.encoder` are implemented."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class EncoderDecoder(nn.Module):\n",
" '''\n",
" A standard Encoder-Decoder architecture. Base for this and many \n",
" other models.\n",
" '''\n",
" def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):\n",
" super(EncoderDecoder, self).__init__()\n",
" self.encoder = encoder\n",
" self.decoder = decoder\n",
" self.src_embed = src_embed\n",
" self.tgt_embed = tgt_embed\n",
" self.generator = generator\n",
" \n",
" def encode(self, src, src_mask):\n",
" return self.encoder(self.src_embed(src), src_mask)\n",
" \n",
" def decode(self, memory, src_mask, tgt, tgt_mask):\n",
" return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)\n",
" \n",
" def forward(self, src, tgt, src_mask, tgt_mask):\n",
" memory = self.encoder(self.src_embed(src), src_mask)\n",
" return self.decoder(memory, src_mask, tgt, tgt_mask)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"### Step 2: Encoder and decoder stacks\n",
"\n",
"The encoder and decoder shown above are actually stacks of multiple (six to be precise) encoders and decoders:\n",
"\n",
"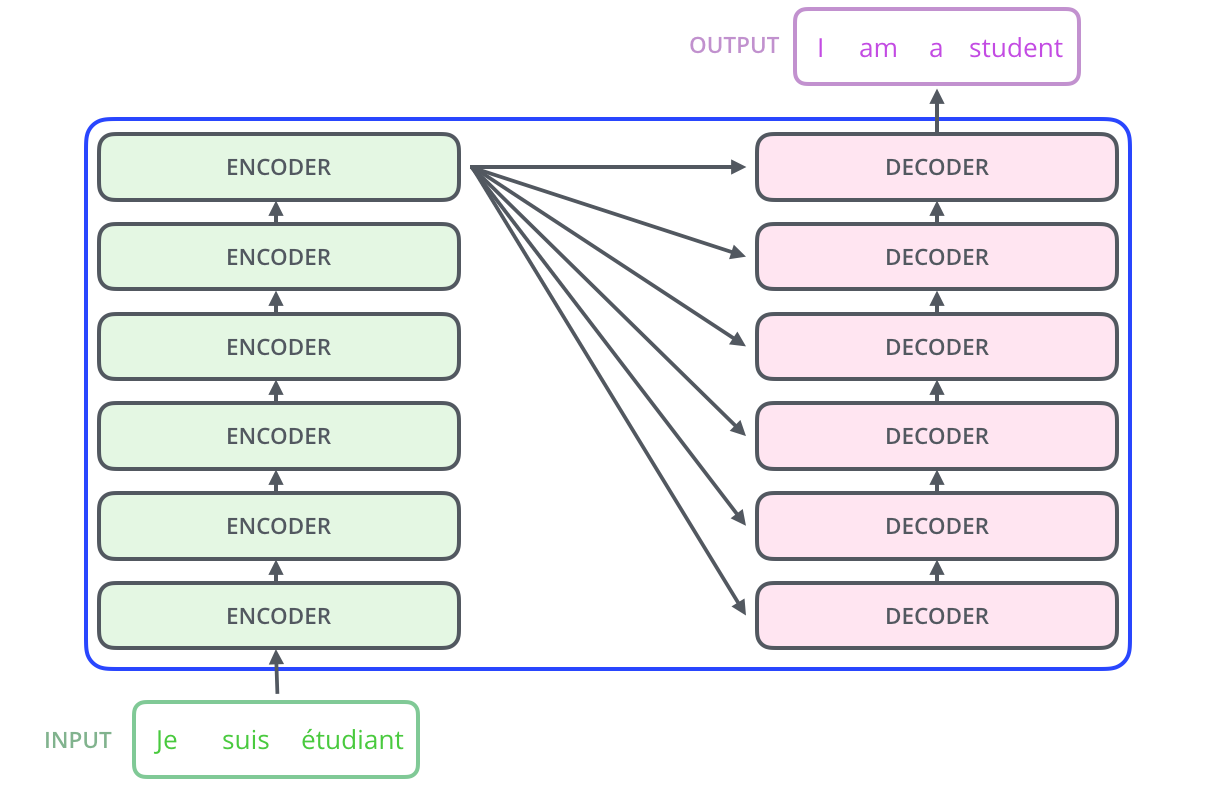\n",
"\n",
"Since the layers are identical, we first write a function to create identical copies of any `module`:"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def clones(module, N):\n",
" return nn.ModuleList([ copy.deepcopy(module) for _ in range(N) ])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Then we implement the encoder. It is simply a stack of `N=6` identical layers plus a `LayerNorm` layer. Don't worry about it for now. We will see later how it is implemented."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Encoder(nn.Module):\n",
" def __init__(self, layer, N):\n",
" super(Encoder, self).__init__()\n",
" self.layers = clones(layer, N)\n",
" self.norm = LayerNorm(layer.size)\n",
" \n",
" def forward(self, x, mask):\n",
" for layer in self.layers:\n",
" x = layer(x, mask)\n",
" return self.norm(x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"A decoder does the same thing at a high level:"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Decoder(nn.Module):\n",
" def __init__(self, layer, N):\n",
" super(Decoder, self).__init__()\n",
" self.layers = clones(layer, N)\n",
" self.norm = LayerNorm(layer.size)\n",
" \n",
" def forward(self, x, memory, src_mask, tgt_mask):\n",
" for layer in self.layers:\n",
" x = layer(x, memory, src_mask, tgt_mask)\n",
" return self.norm(x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"### Step 3: Looking into an encoder\n",
"\n",
"An encoder has two sub-layers (self-attention and feed forward) like so:\n",
"\n",
"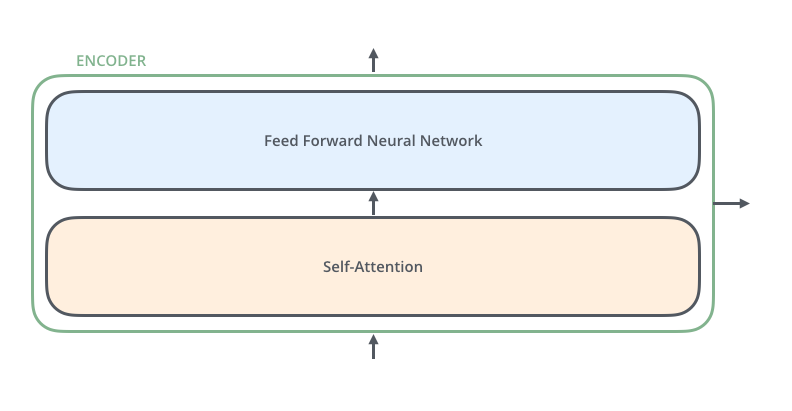\n",
"\n",
"The feed forward layer simply is a collection of linear layers:\n",
"\n",
"\n",
"\n",
"Note that the self-attention layer uses the inputs x1, x2, ... to calculate how much attention to pay to each input. However the linear transformations z1 → r1, z2 → r2, ... are all independent of each other. Hence this part can be parallelized.\n",
"\n",
"#### 3.1 Residuals and normalization\n",
"\n",
"After each sub-layer of an encoder, we add to the output the input and then apply layer normalization to it:\n",
"\n",
"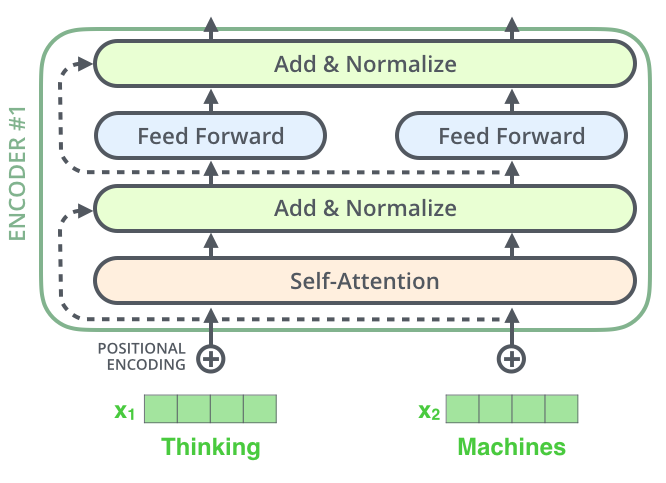\n",
"\n",
"> ### To facilitate these residual connections, all sub-layers in the model, as well as the embedding layers, produce outputs of dimension dmodel=512. \n",
"[source](http://nlp.seas.harvard.edu/2018/04/03/attention.html)\n",
"\n",
"Let's implement the `LayerNorm` now:"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class LayerNorm(nn.Module):\n",
" def __init__(self, features_size, eps=1e-6):\n",
" super(LayerNorm, self).__init__()\n",
" self.scale = nn.Parameter(torch.ones(features_size))\n",
" self.shift = nn.Parameter(torch.zeros(features_size))\n",
" self.eps = eps\n",
" \n",
" def forward(self, x):\n",
" mean = x.mean(-1, keepdims=True)\n",
" std = x.std(-1, keepdims=True)\n",
" return (x - mean) * scale / (std + self.eps) + shift"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Next we implement the layer in green above which says `Add & Normalize`. It takes as function a `sublayer` and the input `x` to the sublayer. Then it calculates `x + sublayer(x)` and then normalizes it. However we do two things differently here:\n",
"\n",
"1. We apply layer normalization to `x` before feeding it to `sublayer`.\n",
"2. We apply dropout to the output of `sublayer` before adding `x` to it."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class SubLayerConnection(nn.Module):\n",
" def __init__(self, features_size, dropout):\n",
" super(SubLayerConnection, self).__init__()\n",
" self.norm = LayerNorm(features_size)\n",
" self.dropout = nn.Dropout(dropout)\n",
" \n",
" def forward(self, x, sublayer):\n",
" return x + self.dropout(sublayer(self.norm(x)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now let's create the encoder layer which contains the following layers as shown below:\n",
"- Self attention layer\n",
"- Add and normalize layer\n",
"- Feed forward layer\n",
"- Another add and normalize layer"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class EncoderLayer(nn.Module):\n",
" def __init__(self, size, self_attn, feed_forward, dropout):\n",
" super(EncoderLayer, self).__init__()\n",
" self.size = size\n",
" self.self_attn = self_attn\n",
" self.feed_forward = feed_forward\n",
" self.sublayers = clones(SubLayerConnection(size, dropout), 2)\n",
" \n",
" def forward(self, x, mask):\n",
" attn_function = lambda x: self.self_attn(x, x, x, mask)\n",
" x = self.sublayers[0](x, attn_function)\n",
" return self.sublayers[1](x, self.feed_forward)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Note that `mask` is only used by the `self_attn` layer in the class above. We still don't know how `self_attn` works. Let's look into how it works.\n",
"\n",
"---\n",
"\n",
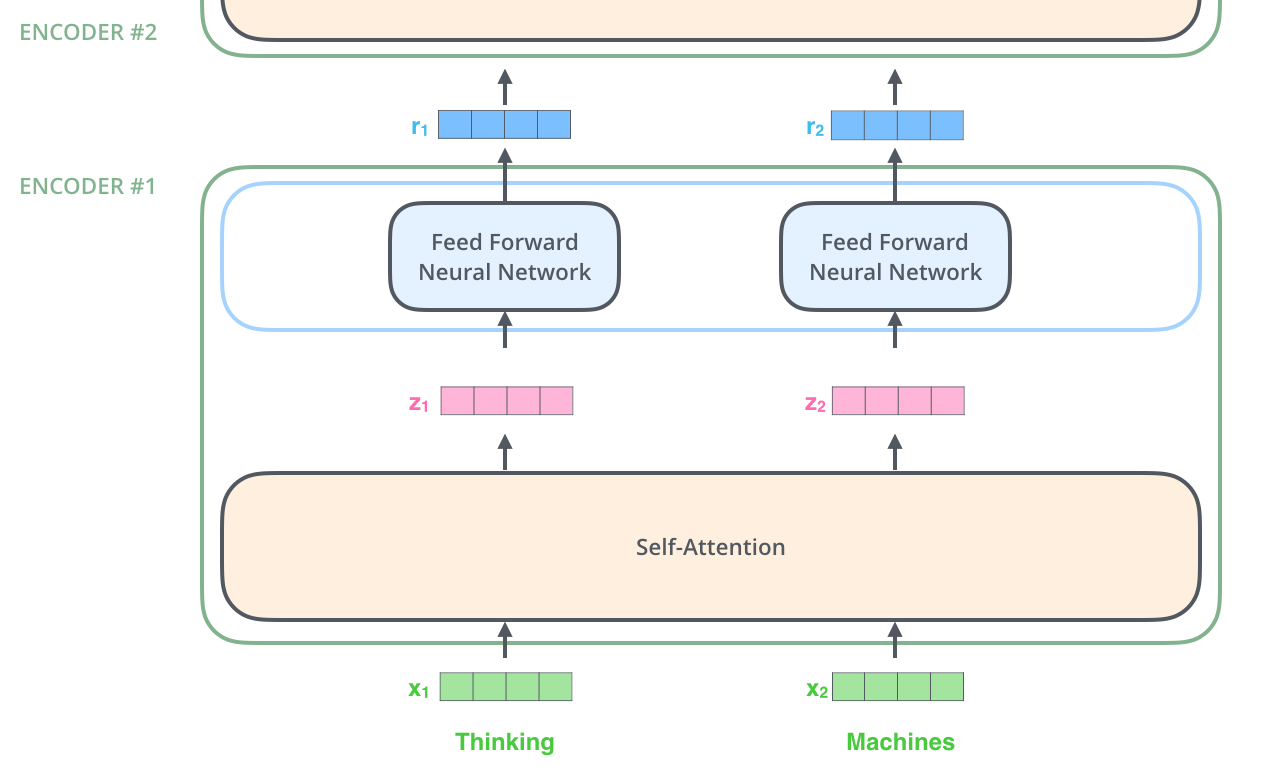
"### Step 4: Self attention\n",
"\n",
"Each input vector vi to an encoder layer undergoes three different linear transformations to create three different vectors: queryi, keyi and valuei.\n",
"\n",
"To calculate the attention for the word corresponding to the first index `(i=0)`, we calculate:\n",
"\n",
"< query0, keyi > * valuei for all `i` where `` represents a dot product.\n",
"\n",
"Then we add all these vectors up:\n",
"\n",
"Σi valuei * < query0, keyi >\n",
"\n",
"However there are some details between these steps:\n",
"- While the input (and output) vectors have dimension = 512, queryi, keyi and valuei vectors have dimension = 64\n",
"- After calculating the dot product < query0, keyi >, the output is divided by √(dimension of output vector) = √64 = 8 \n",
"\n",
" Scale values by < query0, keyi > / 8\n",
" \n",
"\n",
"- [Optional] A mask is applied to the values above. As we will see below, the mask is required only by the decoder, not by the encoder.\n",
"- A softmax is taken over all values < query0, keyi > / 8\n",
"- The output of the softmax is then multiplied elementwise to the valuei vectors.\n",
"\n",
"This is shown nicely in the illustration below:\n",
"\n",
"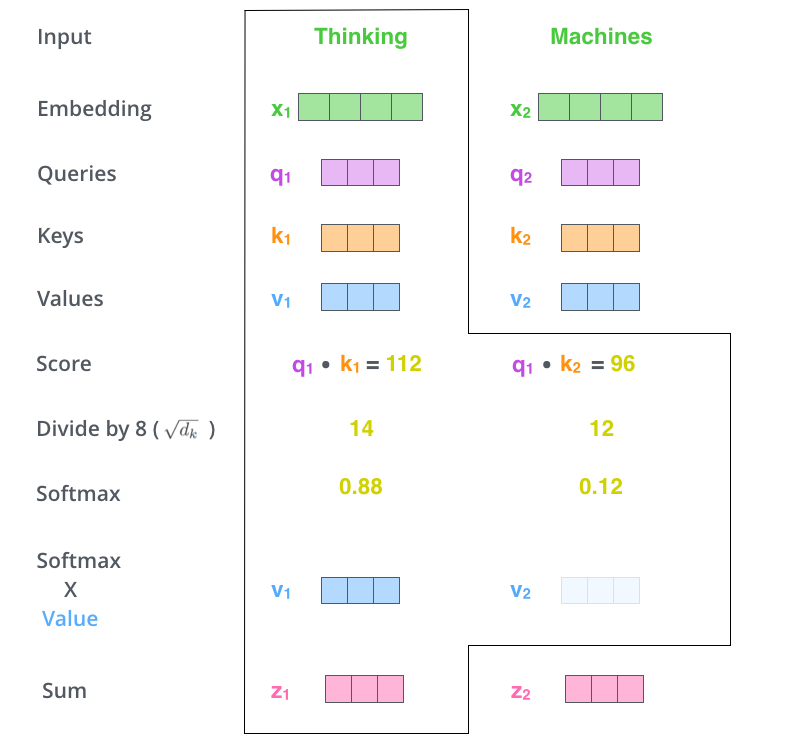\n",
"\n",
"\n",
"All of this can be condensed into one step as shown (here a vector is represented in a row form):\n",
"\n",
"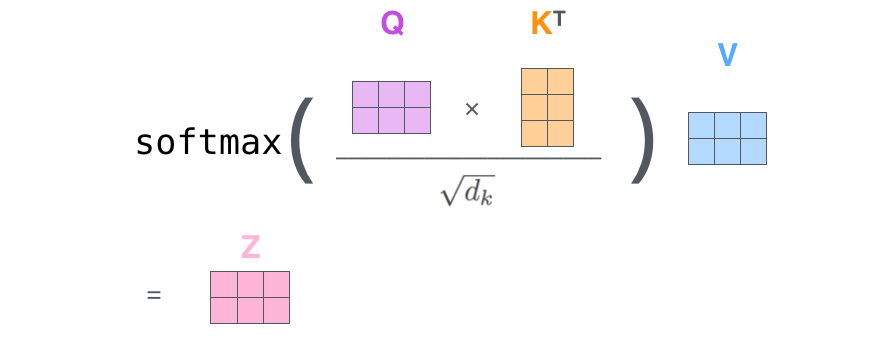\n",
"\n",
"Now let's implement this. Assuming we have `query`, `key` and `value` vectors, we implement the visual shown below:\n",
"\n",
"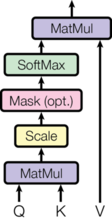"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def attention(query, key, value, mask=None, dropout=None):\n",
" '''\n",
" query, key and value contain vectors corresponding to each word in the input\n",
" '''\n",
" sqrt_d_k = math.sqrt(query.size(-1))\n",
" scores = torch.matmul(query, key.transpose(-2,-1)) / sqrt_d_k\n",
" \n",
" if mask is not None:\n",
" scores = scores.masked_fill(mask == 0, -1e9)\n",
" \n",
" prob_scores = F.softmax(scores, dim=-1)\n",
" \n",
" if dropout is not None:\n",
" p_attn = dropout(prob_scores)\n",
" \n",
" scaled_value = torch.matmul(prob_scores, value)\n",
" return scaled_value, prob_scores"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"### Step 5: Multi-headed attention\n",
"\n",
"Note that the output vector (`value`) corresponding to each input vector has dimension = 64. We know that the input and output vectors of the `EncoderLayer` have dimension = 512. So what happens after the self-attention step? \n",
"\n",
"Well, we have eight copies of self-attention which produce eight output vectors each of dimension = 64 for each input vector of dimension = 512. When we concatenate them, we get an output vector of dimension = 64 * 8 = 512. This is then fed to a linear layer called Wo.\n",
"\n",
"Each \"copy\" is self-attention is called an attention head. We have eight attention heads here. Each attention head learns a different attention.\n",
"\n",
"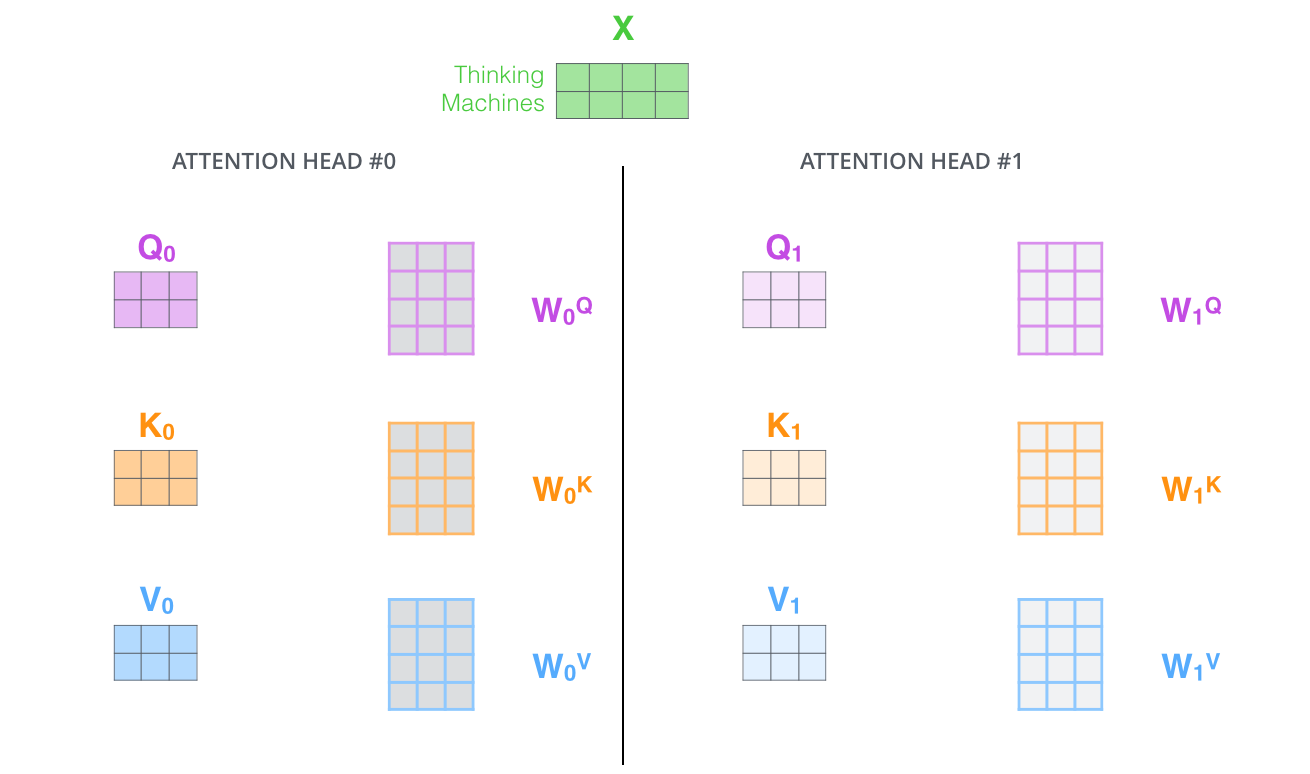\n",
"\n",
"---\n",
"\n",
"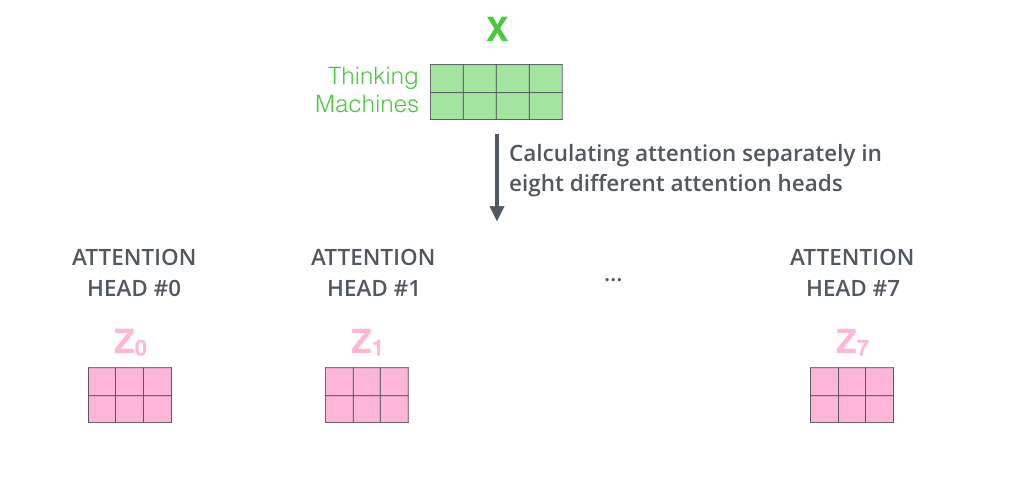\n",
"\n",
"---\n",
"\n",
"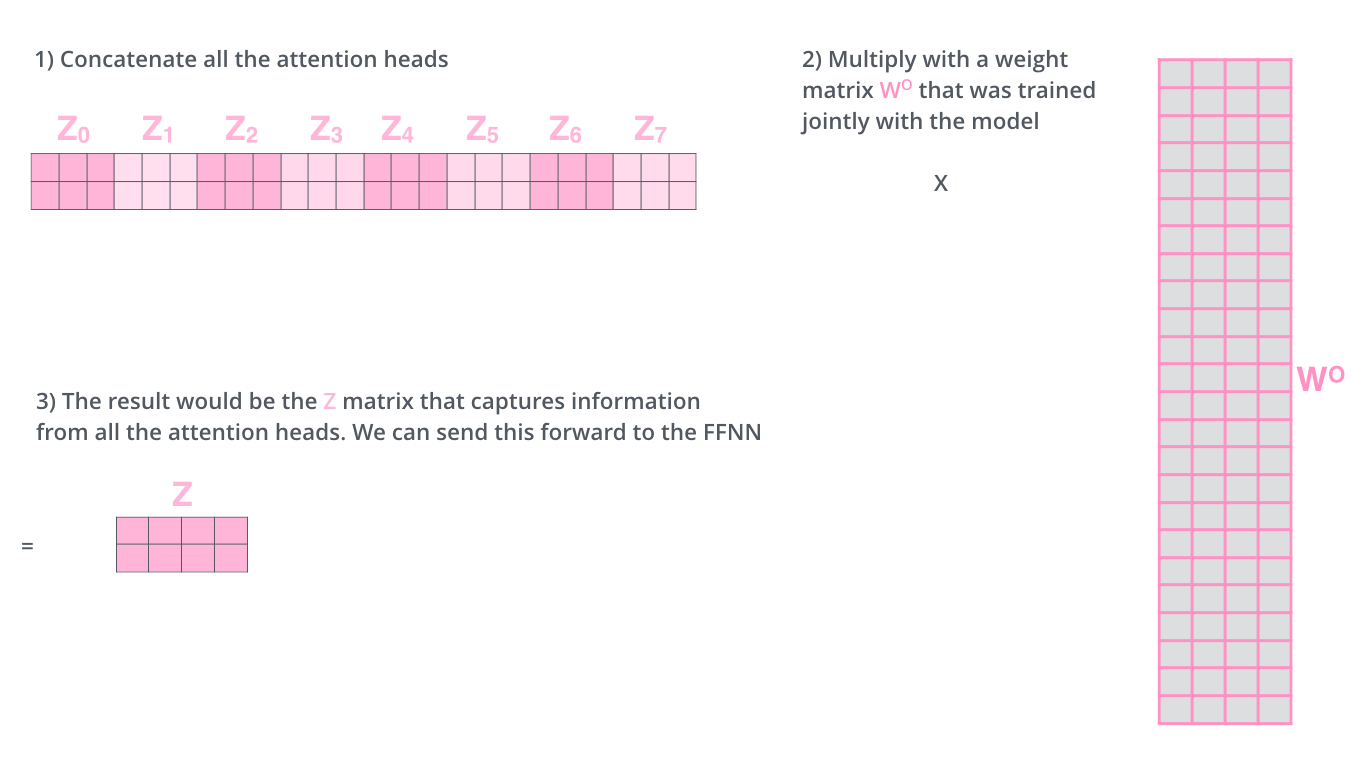\n",
"\n",
"\n",
"This can also be shown as:\n",
"\n",
"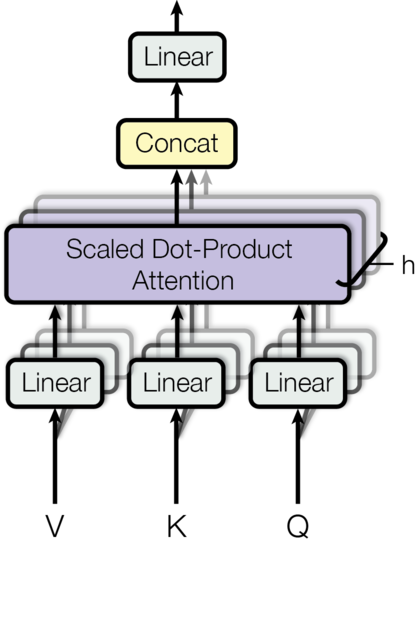\n",
"\n",
"Note that for each attention head, we have an input with shape _something_ like:\n",
"```\n",
"(batch size, words in each input, 64)\n",
"```\n",
"\n",
"Now that we have multiple heads, we want the input tensor to have _something_ like:\n",
"```\n",
"(batch size, number of attention heads, words in each input, 64)\n",
"```\n",
"\n",
"This is how it is done:\n",
"\n",
"- `head 1` converts `x` (dim=512) into `query1` (dim=64). This is a linear transformation `nn.Linear(512, 64)`\n",
"- `head 2` converts `x` (dim=512) into `query2` (dim=64). This is a linear transformation `nn.Linear(512, 64)`\n",
"...\n",
"- `head 8` converts `x` (dim=512) into `query8` (dim=64). This is a linear transformation `nn.Linear(512, 64)`\n",
"\n",
"We can do implement of the above individual head calculations using a single linear transformation `nn.Linear(512, 512)`. This will give us a vector with `query1, query2, ..., query8` concatenated in a vector of dimension = 512. Let's call the layer that does this transformation `L1`.\n",
"\n",
"Similarly we can do another linear transformation `nn.Linear(512, 512)` which gives us a vector with `key1, key2, ..., key8` concatenated. Let's call this layer `L2`.\n",
"\n",
"And a third linear transformation `nn.Linear(512, 512)` which gives us a vector with `value1, value2, ..., value8` concatenated. Let's call this layer `L3`.\n",
"\n",
"For each output (`query`, `key` and `value`) we perform the following steps:\n",
"\n",
"- We change the shape of each output tensor to \n",
"```\n",
"(batch size, words in each input, number of attention heads, 64)\n",
"```\n",
"\n",
"- Then we transpose the dimensions of the tensor to get a tensor with size:\n",
"```\n",
"(batch size, number of attention heads, words in each input, 64)\n",
"```\n",
"\n",
"Then we perform attention by calling the `attention` function above."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class MultiHeadedAttention(nn.Module):\n",
" def __init__(self, num_heads, dim_input=512, dropout=0.1):\n",
" super(MultiHeadedAttention, self).__init__()\n",
" assert dim_input % num_heads == 0\n",
" self.num_heads = num_heads\n",
" self.dropout = nn.Dropout(p=dropout)\n",
" self.d_k = dim_input // num_heads\n",
" \n",
" # L1, L2, L3 and W0: four linear layers in all\n",
" self.linears = clones(nn.Linear(dim_input, dim_input), 4)\n",
" \n",
" # this is used to store the prob_scores, just for visualization\n",
" self.attn = None\n",
" \n",
" # helper function to resize the tensor as described above\n",
" self.resize_tensor = lambda tensor: tensor.view(batch_size, -1, self.num_heads, self.d_k).transpose(1,2)\n",
" \n",
" def forward(self, query, key, value, mask=None):\n",
" if mask is not None:\n",
" mask = mask.unsqueeze(1) # same mask is applied to all heads\n",
" batch_size = query.size(0)\n",
" \n",
" # use the first three linear layers to transform query, key and value\n",
" zipped = zip(self.linears, (query, key, value))\n",
" query, key, value = [self.resize_tensor(linear(x)) for (linear, x) in zipped]\n",
" \n",
" # apply self attention\n",
" scaled_value, self.attn = attention(query, key, value, mask, self.dropout)\n",
" scaled_value = scaled_value.transpose(1,2).contiguous().view(batch_size, -1, self.num_heads * self.d_k)\n",
" return self.linears[-1](scaled_value)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"At this point let us take a pause and take a stock of things we have and have not covered yet.\n",
"\n",
"Things we have covered:\n",
"- An encoder has two layers: self-attention and feed-forward\n",
"- How self-attention works\n",
"- How multi-headed self-attention works\n",
"\n",
"Things we have not covered:\n",
"- How many layers does a decoder have\n",
"- How do those layers work?\n",
"\n",
"Let's start by looking into a decoder\n",
"\n",
"### Step 6: Looking into a decoder\n",
"\n",
"Each decoder has three sub-layers:\n",
"1. Self-attention\n",
"2. Encoder-decoder attention\n",
"3. Feed forward\n",
"\n",
"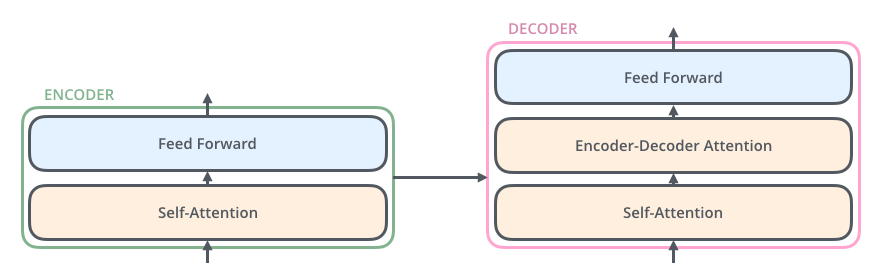\n",
"\n",
"As in an encoder layer, we perform `Add + Layernormalize` operation after each of these layers. Here is how the whole picture looks:\n",
"\n",
"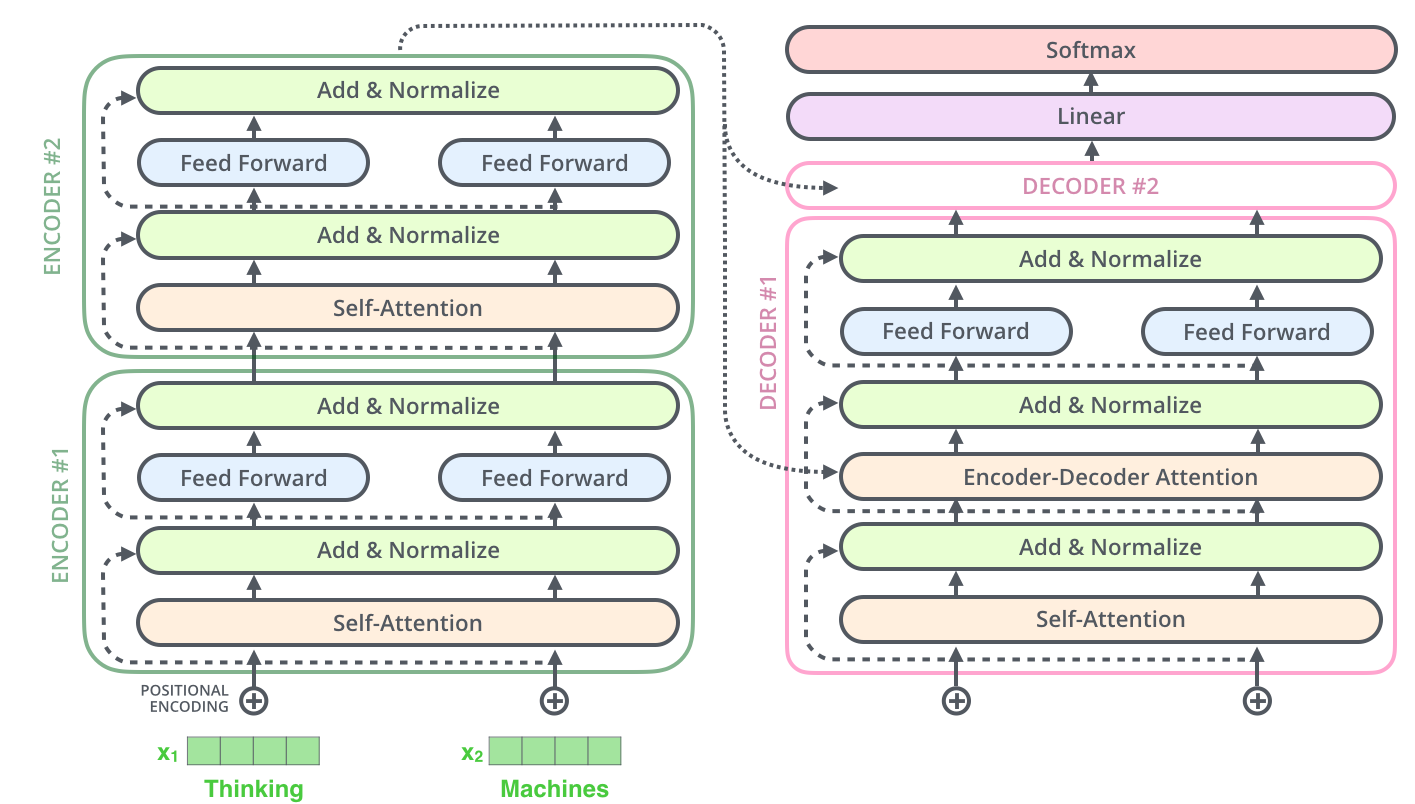\n",
"\n",
"Let's not worry about how each sub-layer inside a decoder works and just implement how these layers interact with each other inside a decoder:"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class DecoderLayer(nn.Module):\n",
" def __init__(self, size, self_attn, enc_dec_attn, feed_forward, dropout):\n",
" super(DecoderLayer, self).__init__()\n",
" # enc_dec_attn is also called src_attn in the harvardnlp implementation\n",
" self.self_attn = self_attn\n",
" self.enc_dec_attn = enc_dec_attn\n",
" self.feed_forward = feed_forward\n",
" self.sublayers = clones(SubLayerConnection(size, dropout), 3)\n",
" # we need to store size because it is used by LayerNorm in Decoder\n",
" self.size = size\n",
" \n",
" def forward(self, x, encoder_outputs, src_mask, tgt_mask):\n",
" # encoder_outputs are also called `memory` in the paper\n",
" x = self.sublayers[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))\n",
" x = self.sublayers[1](x, lambda x: self.enc_dec_attn(x, encoder_outputs, encoder_outputs, src_mask))\n",
" return self.subayers[2](x, self.feed_forward)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### 6.1 Understanding self-attention mask in a decoder layer\n",
"\n",
"Note the first step:\n",
"```python\n",
"x = self.sublayers[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))\n",
"```\n",
"\n",
"It looks the self-attention in encoder. The only difference here is how the `tgt_mask` is defined. When the decoder is decoding at time step `t`, it should not attend to any vectors which are ahead in time (`time > t`). Thus, when decoding for the first time step, it should not consider any vectors at time steps `2,3,..`. We implement this using a mask (`tgt_mask`). \n",
"\n",
"> We also modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions. This masking, combined with fact that the output embeddings are offset by one position, ensures that the predictions for position _i_ can depend only on the known outputs at positions less than _i_.\n",
"[source](http://nlp.seas.harvard.edu/2018/04/03/attention.html)\n",
"\n",
"This is how it is implemented:"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAP8AAAD8CAYAAAC4nHJkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAADKdJREFUeJzt3W+sZHV9x/H3p7tQC1JZRBTYbRca\nQkJNU8iGoDbWlPJHSlgf+GCJtlsxIaaxhaaNQkhq0ke1NvZPamoI2NKUgBGhEgOFDWqaJmUV1uWf\ni7BSCuuuQLUBtWlx228fzFlzuc7dvcycc3aW3/uV3MyZOb/Z+e6Z+7m/mTPnzDdVhaT2/NThLkDS\n4WH4pUYZfqlRhl9qlOGXGmX4pUYZfqlRhl9qlOGXGrV2zAc78YQ1tXHDUa/6fk88fMwA1UivPf/N\nD3m5/ierGTtq+DduOIqv3rPhVd/volN+eYBqpNee7XXfqsf6sl9qlOGXGjVX+JNcnOSbSXYnuaav\noiQNb+bwJ1kDfAp4N3AWcHmSs/oqTNKw5pn5zwV2V9VTVfUycCuwuZ+yJA1tnvCfCjy75Pqe7jZJ\nR4B5wj/ts8Sf+FqgJFcmeSDJAy9893/neDhJfZon/HuApR/arwf2Lh9UVddX1aaq2vSmN66Z4+Ek\n9Wme8H8NOCPJaUmOBrYAd/ZTlqShzXyEX1XtT/Jh4B5gDfCZqnqst8okDWquw3ur6i7grp5qkTQi\nj/CTGmX4pUaNelbfrO7Zu3Pm+3pGoDSdM7/UKMMvNcrwS40y/FKjDL/UKMMvNcrwS40y/FKjDL/U\nKMMvNcrwS40y/FKjDL/UqCPirL55eEagNJ0zv9Qowy81yvBLjZqnV9+GJF9OsivJY0mu6rMwScOa\nZ4fffuAPqmpHkuOAB5Nsq6pv9FSbpAHNPPNX1b6q2tEtfx/Yhb36pCNGL+/5k2wEzga29/HvSRre\n3OFP8nrg88DVVfXSlPU26pQW0FzhT3IUk+DfXFW3Txtjo05pMc2ztz/AjcCuqvpkfyVJGsM8M/87\ngN8Efi3Jzu7nkp7qkjSwebr0/guQHmuRNCKP8JMaZfilRr3mT+mdx6ynA3sqsI4EzvxSowy/1CjD\nLzXK8EuNMvxSowy/1CjDLzXK8EuNMvxSowy/1CjDLzXK8EuNMvxSozyrbwA2B9WRwJlfapThlxpl\n+KVG9dG0Y02Sryf5Yh8FSRpHHzP/VUz69Ek6gszbsWc98BvADf2UI2ks8878fwF8BPi/HmqRNKJ5\n2nVdCjxfVQ8eYpyNOqUFNG+7rsuSPA3cyqRt1z8sH2SjTmkxzRz+qrq2qtZX1UZgC/Clqnp/b5VJ\nGpSf80uN6uXY/qr6CvCVPv4tSeNw5pcaZfilRnlK74KxOajG4swvNcrwS40y/FKjDL/UKMMvNcrw\nS40y/FKjDL/UKMMvNcrwS40y/FKjDL/UKMMvNcqz+l4jbA6qV8uZX2qU4ZcaZfilRs3bruv4JLcl\neTzJriRv66swScOad4ffXwL/VFXvTXI0cEwPNUkawczhT/KzwDuB3waoqpeBl/spS9LQ5nnZfzrw\nAvC3Sb6e5IYkx/ZUl6SBzRP+tcA5wN9U1dnAD4Frlg+yUae0mOYJ/x5gT1Vt767fxuSPwSvYqFNa\nTPM06vwO8GySM7ubzge+0UtVkgY3797+3wVu7vb0PwV8YP6SJI1hrvBX1U5gU0+1SBqRR/hJjTL8\nUqM8pVc2B22UM7/UKMMvNcrwS40y/FKjDL/UKMMvNcrwS40y/FKjDL/UKMMvNcrwS40y/FKjDL/U\nKM/q08xsDnpkc+aXGmX4pUYZfqlR8zbq/P0kjyV5NMktSV7XV2GShjVz+JOcCvwesKmq3gqsAbb0\nVZikYc37sn8t8DNJ1jLp0Lt3/pIkjWGejj3fBv4MeAbYB7xYVff2VZikYc3zsn8dsBk4DTgFODbJ\n+6eMs1GntIDmedn/68C/VdULVfUj4Hbg7csH2ahTWkzzhP8Z4LwkxyQJk0adu/opS9LQ5nnPv51J\nW+4dwCPdv3V9T3VJGti8jTo/Bnysp1okjcgj/KRGGX6pUZ7Sq8PC5qCHnzO/1CjDLzXK8EuNMvxS\nowy/1CjDLzXK8EuNMvxSowy/1CjDLzXK8EuNMvxSowy/1CjP6tMRxeag/XHmlxpl+KVGGX6pUYcM\nf5LPJHk+yaNLbjshybYkT3aX64YtU1LfVjPz/x1w8bLbrgHuq6ozgPu665KOIIcMf1X9M/C9ZTdv\nBm7qlm8C3tNzXZIGNut7/jdX1T6A7vKk/kqSNIbBd/jZqFNaTLOG/7kkJwN0l8+vNNBGndJimjX8\ndwJbu+WtwBf6KUfSWFbzUd8twL8CZybZk+SDwJ8AFyR5Eriguy7pCHLIY/ur6vIVVp3fcy2SRuQR\nflKjDL/UKE/pVTNsDvpKzvxSowy/1CjDLzXK8EuNMvxSowy/1CjDLzXK8EuNMvxSowy/1CjDLzXK\n8EuNMvxSozyrTzqE12pzUGd+qVGGX2qU4ZcaNWujzk8keTzJw0nuSHL8sGVK6tusjTq3AW+tql8C\nngCu7bkuSQObqVFnVd1bVfu7q/cD6weoTdKA+njPfwVwdw//jqQRzRX+JNcB+4GbDzLGRp3SApo5\n/Em2ApcC76uqWmmcjTqlxTTTEX5JLgY+CvxqVf1XvyVJGsOsjTr/GjgO2JZkZ5JPD1ynpJ7N2qjz\nxgFqkTQij/CTGmX4pUZ5Sq80oEVuDurMLzXK8EuNMvxSowy/1CjDLzXK8EuNMvxSowy/1CjDLzXK\n8EuNMvxSowy/1CjDLzXKs/qkBTTr2YDnXrT6b9Vz5pcaZfilRhl+qVEzNepcsu4Pk1SSE4cpT9JQ\nZm3USZINwAXAMz3XJGkEMzXq7Pw58BFgxW49khbXTO/5k1wGfLuqHuq5HkkjedWf8yc5BrgOuHCV\n468ErgT4uVM9rEBaFLPM/L8AnAY8lORpYD2wI8lbpg22Uae0mF71VFxVjwAnHbje/QHYVFX/0WNd\nkgY2a6NOSUe4WRt1Ll2/sbdqJI3GI/ykRhl+qVGpGu8YnSQvAP++wuoTgUXaabho9cDi1WQ9B3c4\n6vn5qnrTagaOGv6DSfJAVW063HUcsGj1wOLVZD0Ht2j1LOfLfqlRhl9q1CKF//rDXcAyi1YPLF5N\n1nNwi1bPKyzMe35J41qkmV/SiEYPf5KLk3wzye4k10xZ/9NJPtut355k44C1bEjy5SS7kjyW5Kop\nY96V5MUkO7ufPxqqniWP+XSSR7rHe2DK+iT5q24bPZzknAFrOXPJ/31nkpeSXL1szKDbaNq3SSU5\nIcm2JE92l+tWuO/WbsyTSbYOWM8nkjzePR93JDl+hfse9LkdVVWN9gOsAb4FnA4cDTwEnLVszO8A\nn+6WtwCfHbCek4FzuuXjgCem1PMu4Isjb6engRMPsv4S4G4gwHnA9hGfv+8w+Sx5tG0EvBM4B3h0\nyW1/ClzTLV8DfHzK/U4Anuou13XL6waq50Jgbbf88Wn1rOa5HfNn7Jn/XGB3VT1VVS8DtwKbl43Z\nDNzULd8GnJ8kQxRTVfuqake3/H1gF3DqEI/Vs83A39fE/cDxSU4e4XHPB75VVSsdqDWImv5tUkt/\nT24C3jPlrhcB26rqe1X1n8A2pnwlXR/1VNW9VbW/u3o/k1PdF9rY4T8VeHbJ9T38ZNh+PKbbmC8C\nbxy6sO7txdnA9imr35bkoSR3J/nFoWth8tVo9yZ5sPsylOVWsx2HsAW4ZYV1Y2+jN1fVPpj8EWfJ\naeZLHK7tdAWTV2bTHOq5Hc3YX60zbQZf/nHDasb0Ksnrgc8DV1fVS8tW72DyMvcHSS4B/hE4Y8h6\ngHdU1d4kJwHbkjzezTY/LnnKfYbeRkcDlwHXTll9OLbRahyO7XQdsB+4eYUhh3puRzP2zL8H2LDk\n+npg70pjkqwF3sD0LxDtRZKjmAT/5qq6ffn6qnqpqn7QLd8FHDX0V5VX1d7u8nngDiZvl5ZazXbs\n27uBHVX13PIVh2MbAc8deKvTXT4/Zcyo26nboXgp8L7q3uAvt4rndjRjh/9rwBlJTutmki3AncvG\n3Akc2Cv7XuBLK23IeXX7Em4EdlXVJ1cY85YD+xySnMtkm313iHq6xzg2yXEHlpnsSFreM+FO4Le6\nvf7nAS8eeAk8oMtZ4SX/2Nuos/T3ZCvwhSlj7gEuTLKu+zTgwu623iW5GPgocFlVTW2Yt8rndjxj\n72Fksqf6CSZ7/a/rbvtjJhsN4HXA54DdwFeB0wes5VeYvAx8GNjZ/VwCfAj4UDfmw8BjTD6ZuB94\n+8Db5/TusR7qHvfANlpaU4BPddvwESZfozZkTccwCfMbltw22jZi8kdnH/AjJrP5B5nsB7oPeLK7\nPKEbuwm4Ycl9r+h+l3YDHxiwnt1M9i8c+D068InVKcBdB3tuD9ePR/hJjfIIP6lRhl9qlOGXGmX4\npUYZfqlRhl9qlOGXGmX4pUb9P6Vn+gT3i/23AAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"subsequent_mask = lambda size: torch.from_numpy(np.tril(np.ones((1,size,size)))) > 0\n",
"\n",
"# Let's take a look at how it looks\n",
"plt.imshow(subsequent_mask(15)[0])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Now refer back to the below lines in the implementation of `attention` function:\n",
"\n",
"```python\n",
" if mask is not None:\n",
" scores = scores.masked_fill(mask == 0, -1e9)\n",
" \n",
" prob_scores = F.softmax(scores, dim=-1)\n",
"```\n",
"\n",
"Thus after the softmax operation all the position which are 0 in the mask will be zero as well. The corresponding `value` vectors will then become zero vectors.\n",
"\n",
"\n",
"### 6.2 Understanding encoder-decoder attention in a decoder layer\n",
"\n",
"Now look at the below line of code:\n",
"\n",
"```python\n",
"x = self.sublayers[1](x, lambda x: self.enc_dec_attn(x, encoder_outputs, encoder_outputs, src_mask))\n",
"```\n",
"\n",
"In this case the `query` vector is the vector `x` that will eventually predict the output word. The `key` and `value` vectors come from the output of the encoder stack. Thus we are still scaling the encoder output vectors but they are _queried_ by `x`.\n",
"\n",
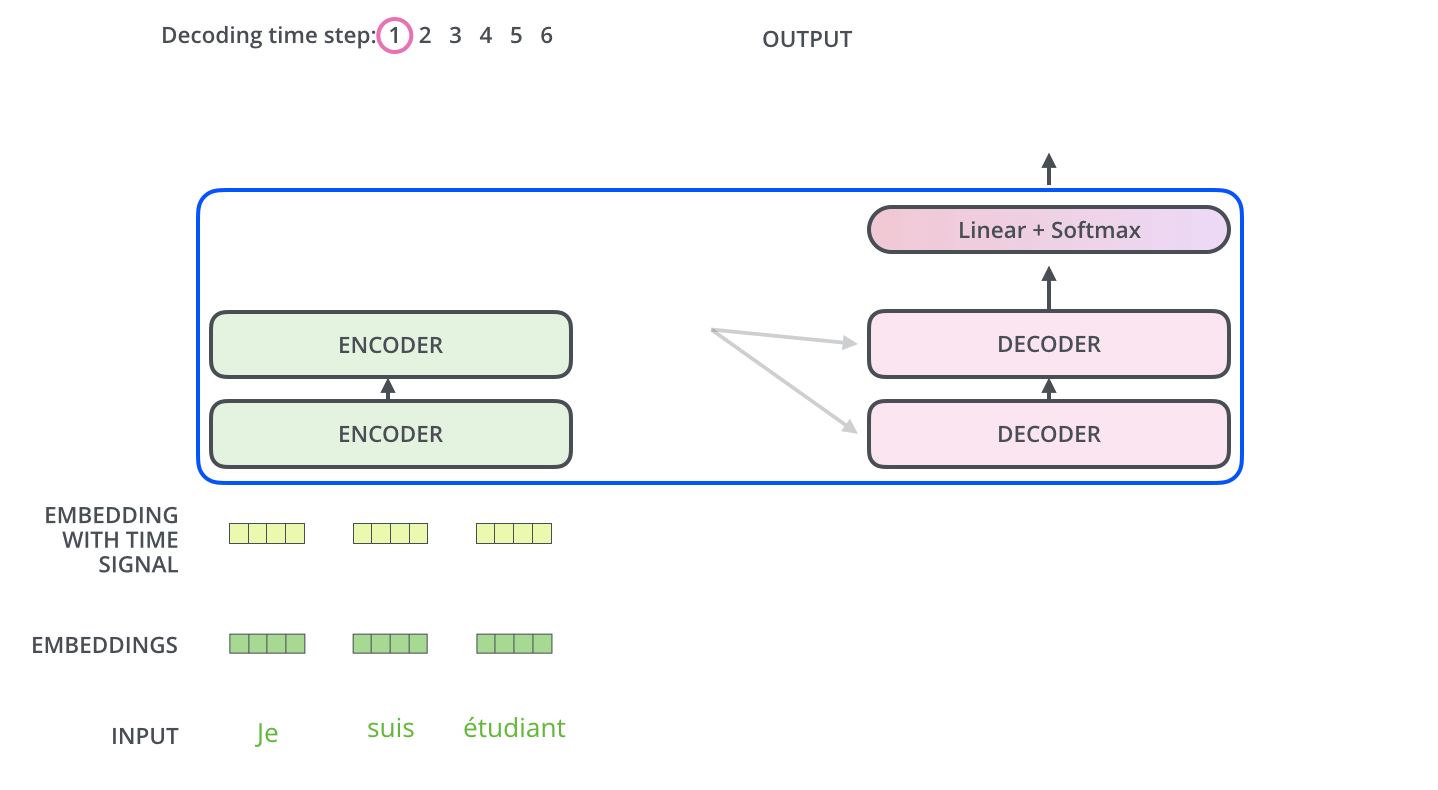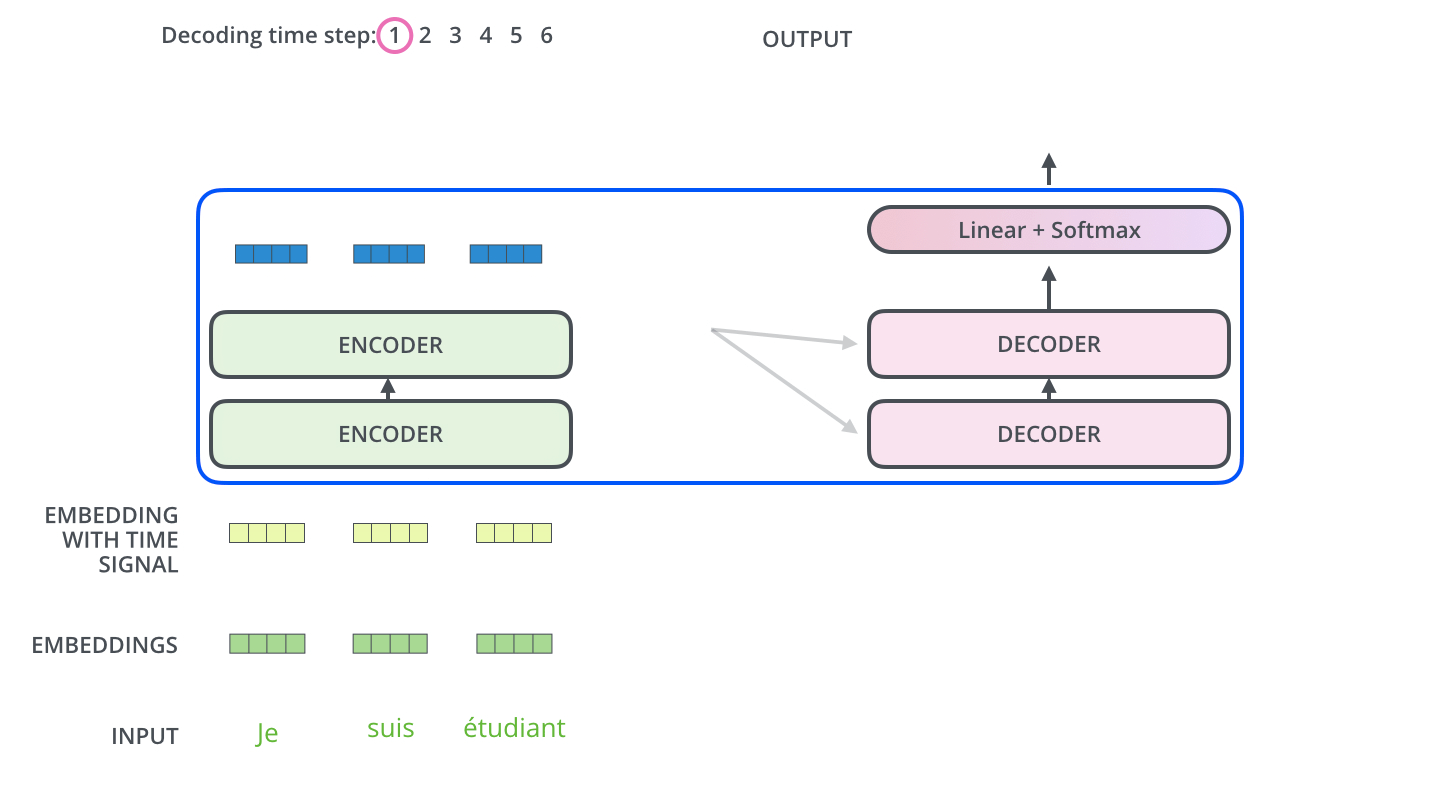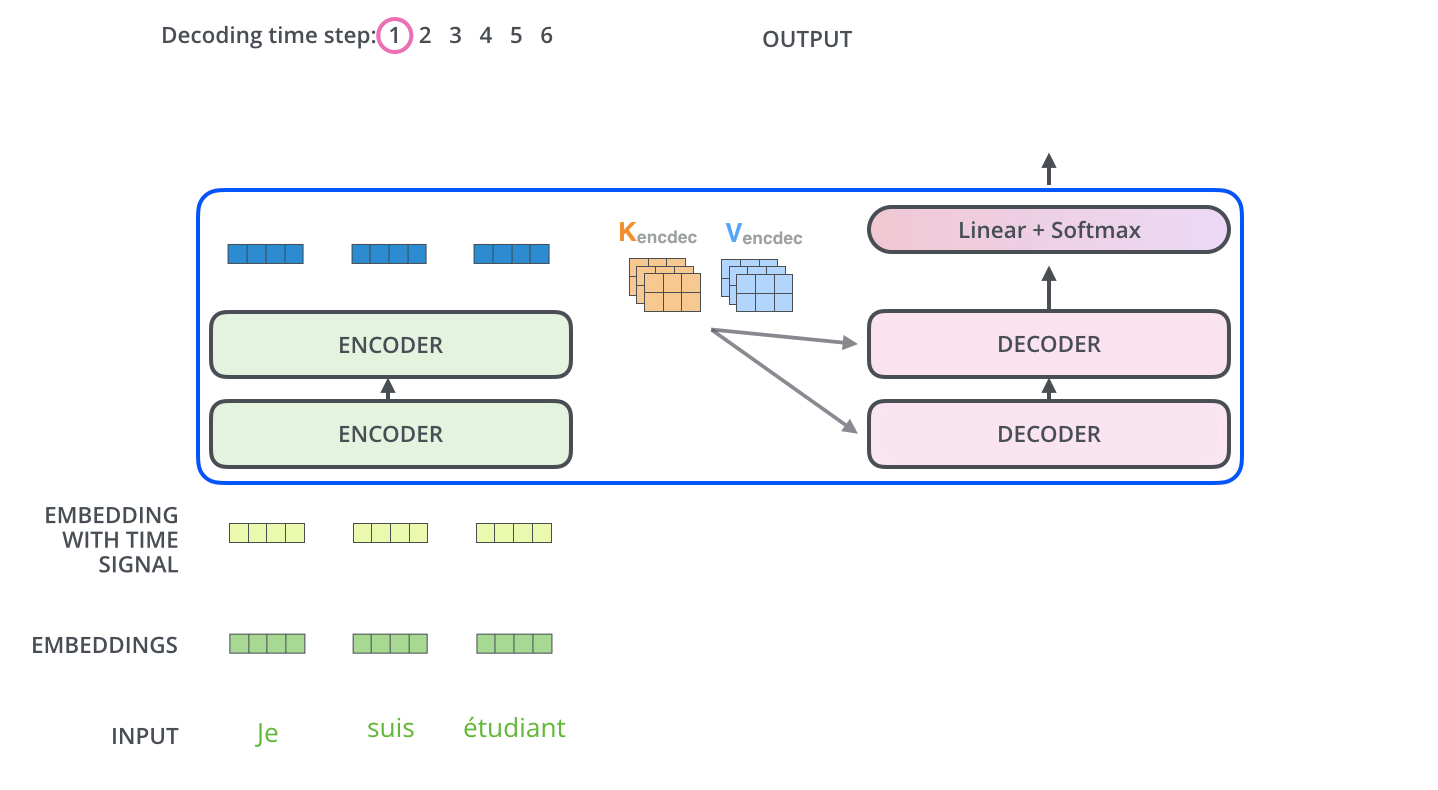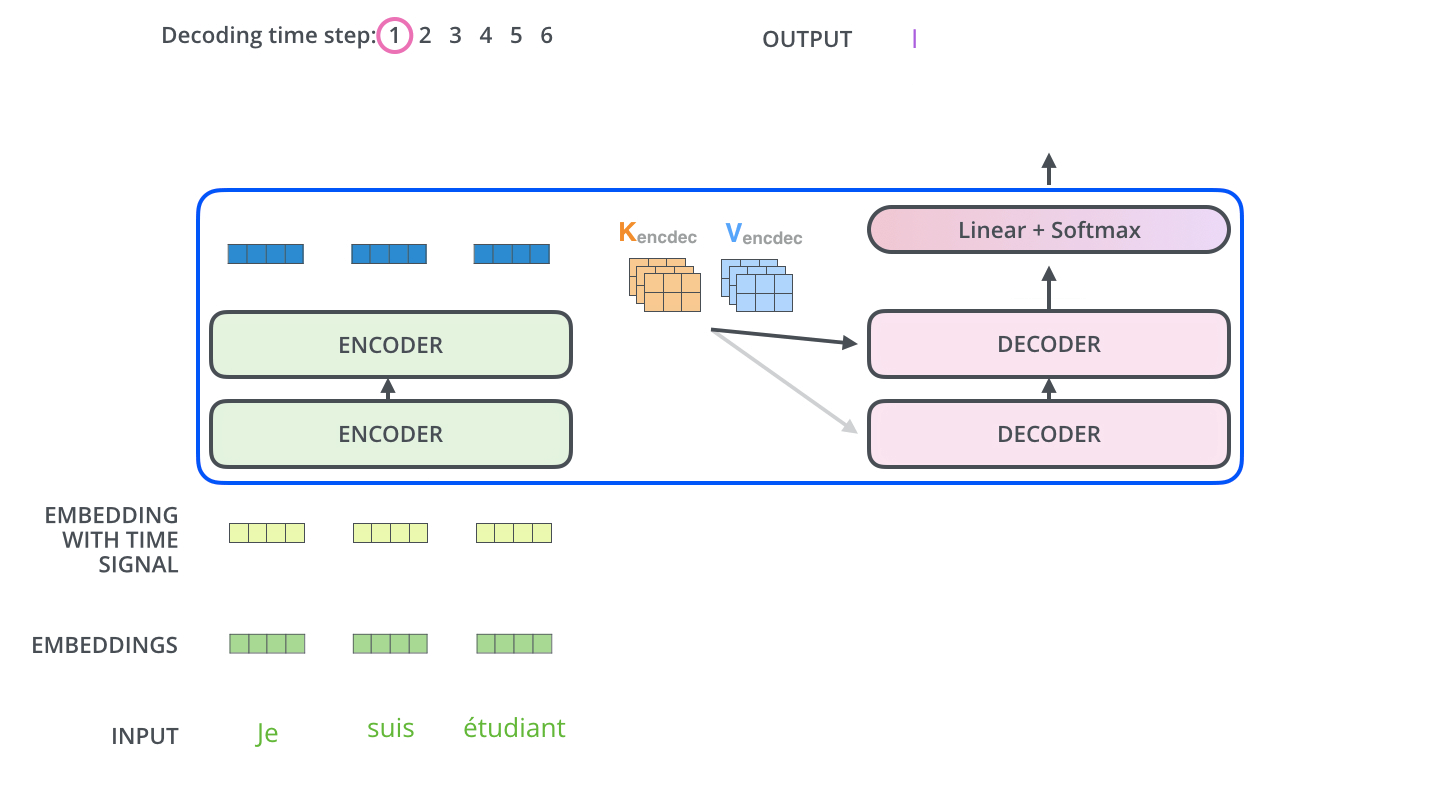
"> The encoder start by processing the input sequence. The output of the top encoder is then transformed into a set of attention vectors K and V. These are to be used by each decoder in its “encoder-decoder attention” layer which helps the decoder focus on appropriate places in the input sequence.\n",
"\n",
"> ...\n",
"\n",
"> The “Encoder-Decoder Attention” layer works just like multiheaded self-attention, except it creates its Queries matrix from the layer below it, and takes the Keys and Values matrix from the output of the encoder stack.\n",
"[source](http://jalammar.github.io/illustrated-transformer/)\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"### Step 7: Linear + Softmax on the output of decoder layer\n",
"\n",
"Notice the `Linear + Softmax` layer in the `.gif` image above? It simply maps each _decoded_ vector to another vector whose dimension = vocabulary size. Then a softmax operation simply tells us which word to pick.\n",
"\n",
"The `[Linear + Softmax]` layer takes as input the output from decoders. It is implemented in class `Generator` below."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Generator(nn.Module):\n",
" '''Linear + Softmax generation step'''\n",
" def __init__(self, d_model, vocab_len):\n",
" super(Generator, self).__init__()\n",
" self.proj = nn.Linear(d_model, vocab_len)\n",
" \n",
" def forward(self, x):\n",
" return F.log_softmax(self.proj(x), dim=-1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"### Step 8: Feed forward sub-layer in encoders and decoders\n",
"\n",
"The feed-forward sub-layer in each encoder and decoder is actually a set where each item is `[Linear layer, ReLU, Linear layer]`. Each item i vt performs this transformation for the corresponding vector vt for all time steps `t`:\n",
"\n",
"\n",
"\n",
"> In addition to attention sub-layers, each of the layers in our encoder and decoder contains a fully connected feed-forward network, which is applied to each position separately and identically. This consists of two linear transformations with a ReLU activation in between.\n",
"[source](http://nlp.seas.harvard.edu/2018/04/03/attention.html)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class PositionWiseFeedForward(nn.Module):\n",
" def __init__(self, input_size=512, output_size=2048, dropout=0.1):\n",
" super(PositionWiseFeedForward, self).__init__()\n",
" self.linear1 = nn.Linear(input_size, output_size)\n",
" self.linear2 = nn.Linear(output_size, input_size)\n",
" self.dropout = nn.Dropout(dropout)\n",
" \n",
" def forward(self, x):\n",
" return self.linear2(self.dropout(F.relu(self.linear1(x))))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"### Step 9: Positional Encoding\n",
"\n",
"> One thing that’s missing from the model as we have described it so far is a way to account for the order of the words in the input sequence.\n",
"[source](http://jalammar.github.io/illustrated-transformer/)\n",
"\n",
"> Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence. To this end, we add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension `dim_model` as the embeddings, so that the two can be summed. There are many choices of positional encodings, learned and fixed.\n",
"\n",
"> ...\n",
"\n",
"> We also experimented with using learned positional embeddings (cite) instead, and found that the two versions produced nearly identical results. We chose the sinusoidal version because it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training.\n",
"[source](http://nlp.seas.harvard.edu/2018/04/03/attention.html/)\n",
"\n",
"This is shown in the visual below:\n",
"\n",
"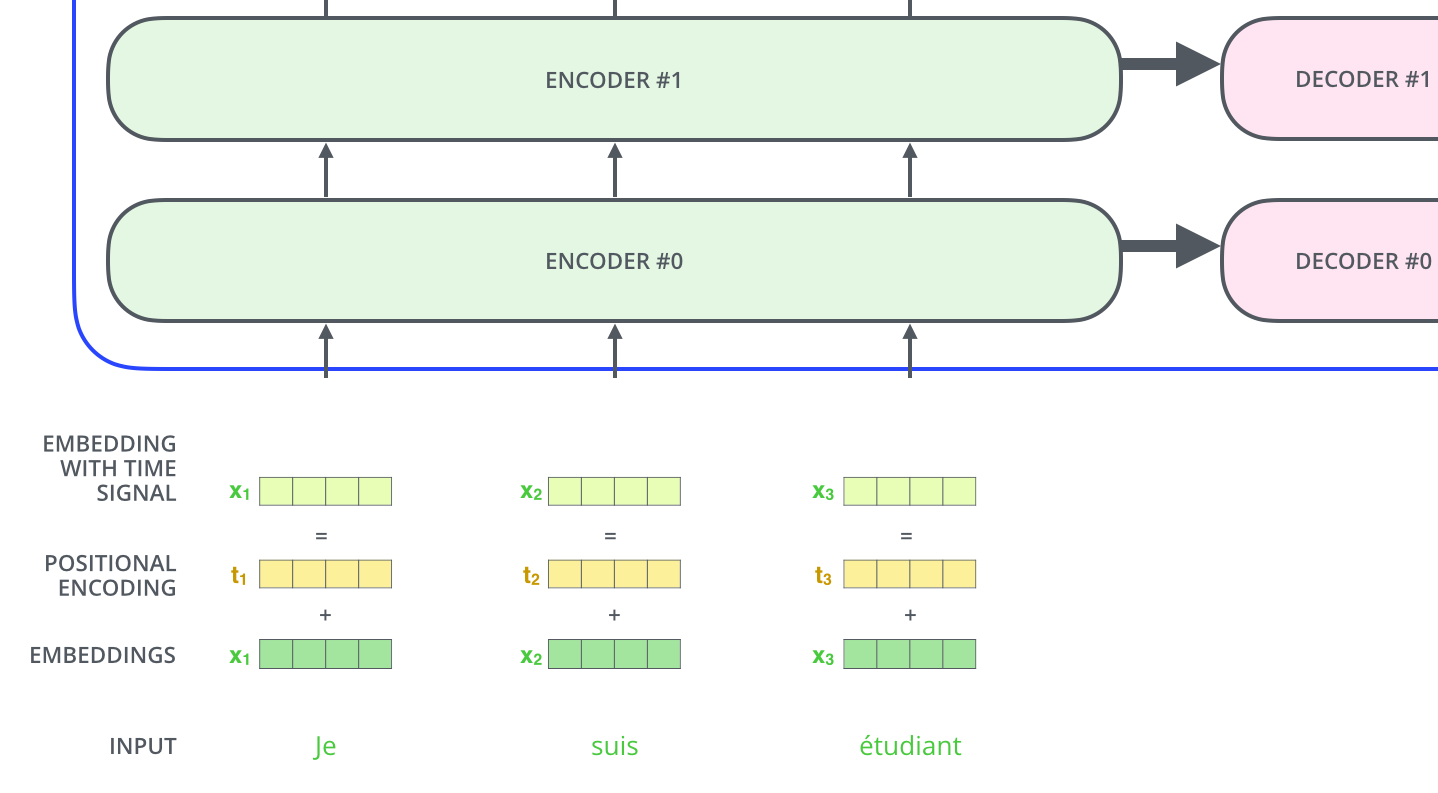\n",
"\n",
"One thing that is not shown in the visual above is that we apply dropout to the sum of embedding and positional encoding.\n",
"\n",
"For implementing positional encoding we need to know three things:\n",
"1. Length of word embedding `(= 512)`\n",
"2. Dropout rate `(= 0.1)`\n",
"3. Maximum length of sequence.\n",
"\n",
"### 9.1 Formulae for positional encoding \n",
"\n",
"Given an embedding at position `pos`, \n",
"\n",
"* an even index (`2i`-th index) of the corresponding positional encoding is given by:\n",
" * PEpos, 2i = sin(pos * C-2i/(len_of_embedding)) \n",
" \n",
" \n",
"* an odd index (`2i+1`-th index) of the corresponding positional encoding is given by:\n",
" * PEpos, 2i+1 = cos(pos * C-2i/(len_of_embedding)) \n",
" \n",
"where `C` = 10000 and `pos` is zero-indexed (i.e. counting the position starts from 0)\n",
"\n",
"Let us simply by saying `L` = `len_of_embedding` and `C` = 1000.\n",
"\n",
"Then we have:\n",
"\n",
"log ( C-2i/(len_of_embedding) ) = -(2i/N) \\* log(C) = 2i \\* (-log(C) / N)\n",
"\n",
"Therefore:
\n",
"C-2i/(len_of_embedding) = exp( 2i \\* (-log(C) / N) )\n",
"\n",
"This is how we calculate the arguments to `sin` and `cosine` functions. Also we want to store the positional embeddings in the state dict even though it is not something that is learable (i.e. it is not a parameter). We can do so by calling `register_buffer`:"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class PositionalEncoding(nn.Module):\n",
" def __init__(self, dim_embedding, dropout, max_len=5000):\n",
" super(PositionalEncoding, self).__init__()\n",
" self.dropout = nn.Dropout(dropout)\n",
" positional_encodings = torch.zeros(max_len, dim_embedding)\n",
" positions = torch.arange(0, max_len).unsqueeze(1).float()\n",
" \n",
" # calculate the arguments for sin and cos functions\n",
" scale = -(math.log(10000) / dim_embedding)\n",
" arguments = torch.arange(0, dim_embedding, 2).float() * scale\n",
" arguments = torch.exp(arguments)\n",
" arguments = positions * arguments\n",
" \n",
" # define the encodings here\n",
" positional_encodings[:, 0::2] = torch.sin(arguments)\n",
" positional_encodings[:, 1::2] = torch.cos(arguments)\n",
" \n",
" positional_encodings = positional_encodings.unsqueeze(0)\n",
" self.register_buffer('positional_encodings', positional_encodings)\n",
" \n",
" def forward(self, x):\n",
" pos_enc = self.positional_encodings[:, :x.size(1)]\n",
" pos_enc.requires_grad_(False)\n",
" x = x + pos_enc\n",
" return self.dropout(x)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's take a look at some of the positional encodings:"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3wAAAEyCAYAAACh2dIXAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzs3XV0FefWwOHfnLh7QoiQBHd3t+Lu\nDqWFFiq3XqqUW6hQ2lKseCktbsUpVtwtSIC4AnG3I/P9MZSP3iIBjiW8z1pZCTlzZnZCcjL7lb0l\nWZYRBEEQBEEQBEEQyh6VqQMQBEEQBEEQBEEQDEMkfIIgCIIgCIIgCGWUSPgEQRAEQRAEQRDKKJHw\nCYIgCIIgCIIglFEi4RMEQRAEQRAEQSijRMInCIIgCIIgCIJQRomETxAEQRAEQRAEoYwSCZ8gCIIg\nCIIgCEIZJRI+QRAEQRAEQRCEMsrS1AE8DU9PTzkoKMjUYQiCIAiCIAiCIJjEuXPnUmVZ9nrccaUy\n4QsKCuLs2bOmDkMQBEEQBEEQBMEkJEmKLclxYkmnIAiCIAiCIAhCGSUSPkEQBEEQBEEQhDJKJHyC\nIAiCIAiCIAhllEj4BEEQBEEQBEEQyiiR8AmCIAiCIAiCIJRRIuETBEEQBEEQBEEoo0TCJwiCIAiC\nIAiCUEbpJeGTJGmZJEnJkiRdecjjkiRJP0mSFCFJUqgkSQ3ue2yMJEnhd9/G6CMeQRAEQRAEQRAE\nQX8zfL8AXR/xeDeg8t23CcACAEmS3IHPgaZAE+BzSZLc9BSTIAiCIAiCIAjCc81SHyeRZfmwJElB\njzikD/CrLMsycFKSJFdJknyBdsBeWZbTASRJ2ouSOK7WR1zGlDXvY2SVLZJ3ZVQunkg2NkjWNqhs\nrJWPbW2xdHdH5eyMJEmmDtekCoq1RKbkEpWah5+rLbX9XLG2FKuLzVW+Op+0wjSyi7Ip0hah1qlR\n69QUa4vvvdfoNADYWdpha2mrvFnY/v+/LWxxs3XD2sLaxF+N8ECyDOp8KMyGomxQWYJ7CDznr1WP\notXJqLW6u28y9tYW2FpZmDosQXi+ZMRCzi2w9wQHT7B1Ea9bj6DW6rgQl0mhWoufmx1+rnbidesB\n5OJitNnZaLOy7r1Z+flhW6WKqUN7anpJ+ErAD4i/798Jdz/3sM//iyRJE1BmBwkMDDRMlE9Llkle\nthFN3uNfZCRrayw9PbH08sLS2wuLux9b+ZTDOiQYm5AQLFxcjBC04RVrdNy4ncPNOzmEJ+cSfvd9\nfEY+svz/x9lYqqgX4EqTYHcaB7nToIIbjjbG+tF8vuWr84nOjiYmK4a47DiSC5JJL0gnrTCNtII0\n0grTKNAU6O16bjZueNl74W3vjbe9N152ysflHMoR7ByMn5MfKkkk/waj08KNnXD+V+Um6e8ErygH\n7ibt93hWhVoDlDfPSqaJ1wxEpuSy8kQsOy/fIr9Yey/J08n/PM7WSkW3Wr4MauhPsxAPVCpx0ykI\neifLkHwNwrZB2Ha4c/mfj6uslMTPwRMcvJS3qt2hem9QPZ9/WxIy8jl0M4VDN1I4HplGbtE/X+s9\nHa3xc7W7lwAGutvTvbYvHo42JorYsLS5eagTE1DHx1Mcf/d9Qjya5JR7yZ2cn/+v53m8NB7bd981\nQcT6Icmy/PijSnIiZYZvuyzLtR7w2A7gK1mWj979937gfaADYCPL8pd3P/8pkC/L8qxHXatRo0by\n2bNn9RK3vmgSo9HFX0JOvIycdBX51nV0GYnIOglZK6Gz9kJTrjUa22C0aWloUlLuvqWizcz8x7ks\nPD2xCQnBumIINsHKe9tq1bD08DDRV/dkdDqZbaFJfLPrOklZhQBYWUgEezpQ2ceJyt6OVPZ2ItjT\ngbj0PE5HZ3AmJp2rSVnoZFBJUKO8My0qejKhTQieZfRFx5hyi3O5knaFiIwIYrJjiM5SkrzkguR7\nx0hIuNm64W7rjoedBx62HnjYeSj/tvW4N0NnpbLCSmV17+O/3+tkHUXaIgo1hRRoCijUFlKkKaJA\nW0C+Op/0wnRS8lNIzk8muSCZlPwU0grT0Mm6ezHYWtgS7BJMiGsIlVwrEeKivPdz9MNCJUYhn5q6\nEC6thhNzIS0CXALBpwbYOIOt8/+8d4H8dLi2BWKPAzL41lUSv5r9wTXA1F+NwWl1MgevJ7PiRAxH\nwlOxspB4oUY5fJxtsbKUsLZQYalS3fexRHhyLlsvJZFTqMHfzY4BDfwZ2NCfAHd7U385glC66XSQ\ncAau303yMqIBCQKaQvVe4F1Nec3KS7nvLVV5nxkPecnKAFbrd5TXMYuyPaCs1uo4EZnGoZsp/HUj\nmciUPAD8XO1oW9WLNpW9cLO3IjGzgMSMAuX9fR8XaXTYW1swvlUwL7UOwcXOysRf0dPRFRVRdPMm\nhVevUXjtGkU3blAcH482Pf0fx6mcnLAOCMDSxwcLV1csXFywcHFG5eJy92NXLFycsfL1xdLT00Rf\nzcNJknROluVGjz3OSAnfQuAvWZZX3/33DZTlnO2AdrIsT3zQcQ9jjgnfAxVmwa1LkHRRGVWPO6Hc\nOPX4Hvz///9GV1yM5tYtiqKiKI6KUt5HKu912dn3jrMKDMSubl3s6tXFrl49bKtWRbI0rxeuszHp\n/HdHGJfiM6nl58yENhWp4etEBQ8HrCwePbqWW6ThQlwGZ6LTOROTwdnYdBxsLPm4e3UGNvR/7pfC\nlpRGpyEyM5LQ1FAup1wmNCWUqKwoZJTfdSdrJ4KdgwlyCSLIOYhgl2CCnIMIcA7AxsK4ybVGpyGt\nII1bebeIyooiMjNSecuK5Hbe7XvH2VvaU8erDvW961PPqx51vOrgaO1o1FhLpfx0OLsUTi1Sbnp8\n60HLN5XR7pLc9GQlKonflY2QeE75XEBTaDpRuXEqYzLzi1l3Np6VJ2OJTy/Ax9mGkU0rMLRJIF5O\nj//dKFRr2XP1NuvPJnAsMhVZhhYVPRjUyJ9utXzF0ilBeBKyDBdXwf5pkHtbmb0LaQvVeiqzdk4+\njz+HTqu8hh3+TpkZdAuG1m9DnaFgWfa2GITdyuaddZe4disba0sVzUI8aFvFi7ZVvKjo5fDY+yhZ\nlglPzmX2/nB2hN7Cxc6KiW1DGNsiCHtr87rfvJ+sVlN49SoFV65SeO0ahVevUhQZCRplNlPl4oJt\ntWpYV6iAVYA/1gEBWPkHYB3gX+pX1ZlbwtcDeA3ojlKg5SdZlpvcLdpyDvi7aud5oOHfe/oeptQk\nfPeTZeWm6c9PlKVU9UdBp6nKsoOHPkVGm5ZGUUSk8oN88SIFFy+iSUkBQLKzw65WLezq18eheTPs\nGjZEZW2aF7D49Hy+3n2dHaG38HG24b0u1ehf3++ZljVFJOcwZdNlzsRk0DzEgxn9axPs6aDHqMsG\nrU7L5dTLHE86zpnbZ7iadvXeMkxXG1dqe9amtldt6njWoap7VTxsPUpF8pxbnHsvCbyadpWLyRcJ\nzwxHJ+uQkKjsVllJAL3r0bRcU7zsvUwdsvnISoDjc5Wlm+o8qNRJSfSCWj/9/pb0aLi6CULXQcp1\nqDscus8Em9KfeBeqtXy96zprzsRRqNbRJNidMc2DeKGmz2MHqh4mMbOAjecS2HAugbj0fKr4OLJg\nZEMqepX+75cgGFx+Omx/S0nWAptDo/FQ5QVlBcLT0Ong5i449C3cugjO/tDqP8q9mJWtfmM3AY1W\nx8LDUfy47yYudtZ81qsGnav7YGf99INMV5OymPXnTQ5cT8bT0YbJ7SsyvGkgNpamH7iSdTqKrl8n\n7+Qp8k6dpODMWXR3l2FauLtjW7MmtjVrYFujBrY1amLlV75U3Pc8DaMmfJIkrUaZrfME7qBU3rQC\nkGX5Z0n5Ls9FKciSD4yTZfns3ee+CHx091TTZVle/rjrlcqE729FOXDoGzi5AKwdoeOn0HAclHC5\nmizLaJKSyL94kYKLlyi4eJHCsDDQaJDs7XFo1gzH1q1waN0Ga/8HbofUq5xCNfMORrLsWDQqCSa2\nqcjEtiF6GwnS6WTWnInnq11hFGl0vNmxMhPahDz1TVhZcTvvNscSj3Es6Rgnb50kpzgHCYkaHjWo\n61X3XoIX4BRQpl7kcotzCU0N5VLyJS4kXyA0NZQ8tbJcpbp7dVr7t6a1X2tqe9Z+fpeARh6EdWOU\nRK/WQGjxOpT71zjc09Nq4PC3yo2TRyUYtBzK1dbf+Y3sVlYBE1eeIzQhi8GN/BnbIpga5Z31dn6d\nTubA9WTe3xhKkVrLzEF16V7bV2/nF4QyJ/owbH4Fcu9Ah0+V1zB9vZ7LMkTsV17D4k+Bky8MWgGB\nTfVzfhOISM7lnfWXuBSfSc86vkzrUwt3B/0N/p+LTWfmnhucjErHz9WOtzpXYUADP6PfWxTHxZF7\n9Cj5J0+Rf+oU2qwsAKyDg3Fo3gz7Jk2xq18PS2/vMnXf8zhGn+EzplKd8P0t+Trsek95YXvAMs8n\nocvLI+/UaXKPHCbv8BHUiYmA8kvg2KY1jm3bYt+kid6Xfx4JT+E/ay6SlldM/wZ+vNelKr4udnq9\nxt+SswuZuu0qOy/fpqqPE18NqE2DwOeng4dO1hGaEsre2L0cTTxKVFYUAN523rTwa0HL8i1p5tsM\nV1tXE0dqXFqdlvDMcI4mHuVIwhEupVxCK2txtXGlpV9LWvu1pmX5ls/P9+XcL7D9bfCqCkN/Vypt\nGkr0Ydj4MhRkQJfp0PilUlcd71xsOhNXnqegWMOPQ+vTuUYJlog9paTMAiavOs+FuExebBnMlO7V\nnvuBK0H4B00xHJwOx2aDR0UYsATK1zfMtWQZYo7AtjeVpesDFkONPoa5loFodTLLj0Uzc88N7K0t\n+G/fWvSsU94g15JlmWMRacz88waX4jMZ2yKIz3rWMGhxKlmWKbp5k5y9+8jZu5eiGzcAsCzvi0Oz\n5jg0a4p906ZY+Rjudbs0EAlfaSDLyhKpPR8rm4sHLIWafZ/xlDLF0THkHTlM7uEj5J85g1xcjIWb\nG05du+DSvTt2DRsiPWO1qt1XbvPG6guEeDnw7cA61PE3zg313mt3+OyPK9zOLmRC6xA+6FqtzFbD\nk2WZq2lX2R29mz2xe7iddxsrlRWNfBrR0q8lLcq3oJJrpedqJOtxsoqyOJF0giOJRziaeJT0wnQs\nJAua+Taje0h3OgR0KJt7/3Ra2PuZUpSlUicYuFwpwmJouSmw5RWI2KcUT+g9B+xKx0DMujPxfLLl\nCr6utiwe3YgqPk4Gv2axRseMnWH8cjyGRhXcmDu8AeVcSv9yMkF4ZqnhsHG8Uveg4VjoMgOsjbCF\nIy8N1gyD+NPKwFWzSaVi4Co2LY9311/iTEwGnar7MKN/LbydDP9aotPJfLkjjGXHoulVtzyzBtXV\na1stWaejMDSU7L17ydm7D3VcHEgSdg0b4Ny5M47t22MVULZWLj0rkfCVJoVZ8PtgpQrVgMV6LYag\nKygg9+hRsnfuJPfgX8iFhVj6+ODcrRvOPbpjW6vWE//ibL6QwLvrQ6nt58KKcU1wsTduBaecQjUz\ndl5n9ek4RjWrwLQ+NcvML78sy1xPv87umN3sidlDYm4ilipLWpZvSZegLrQPaF82ExYD0Mk6rqZe\n5UD8AXZF7yIxNxEbCxva+LehR3APWvm3MnqRGoMoyoVNLyuFoZpMgC5fGbcKnU6nJJr7vwCn8jBw\nKQQ0Md71n5Baq2P6DiXpal3ZkznD6uNqb9y9z1svJfHhxlDsrS34aVh9WlQ0v8pvgmA051bA7g/B\n0lYZNKre07jXVxfApgkQthWaTISuX+lvCakBHI9M5aUVZ7FQSUztVZP+Rl5eKcsyPx+K4pvd12lV\nyZOfRzV85lZaReHhZG7aTPaOHWiSk8HKCodmzXDq3AmnDh3MsjqmuRAJX2lTlAurBiuVPPsthDqD\n9X4JXV4eOQf/UpK/I0dArcYqIACX3r1xHTgAK9/H7yv5/VQsn2y5QrNgDxaPaWSyfnmyLPP1russ\nPBzF2BZBfN6rRqlO+jIKM9gauZWN4RuJzorGUrKkafmmdA3qSvuA9rjYlO4qUqYmyzKXUi6xM3on\ne2L2kF6YjpOVE50qdKJXxV408mlUOn9+shJh9RC4cxW6fq1UzzSVhLOwYZwSU7+fDfIa9qwy8oqZ\nvOo8xyPTGN8qmCndqmFpomWV4XdyeOW3c0Sn5vFul6q82rZi6fwZFIRncfJn2P0BhLSDvj+Ds4n2\nt+p0sPdTZfCqag9lOam1+bVUOR+Xwcglp/B3s2PFi00Mto2mJNadjWfKpsvULO/MsrGNn7iFljY7\nm+ydO8ncuInCy5fB0hLHtm1x7toFx7ZtsXA2wiqVMkAkfKVRcR6sGgIxR6HvfKg33GCX0mZlkbNv\nH9k7dpB34iRIEo7t2uE2ZDAOrVohWfx7dGvx4Sim7wyjQzVv5o9oYPIS47KsLC1YejSa8a2C+aRH\n9VJ1wyTLMmfvnGX9zfXsi92HWqemnlc9+lTqQ6fATs/PvjMj0+g0nLp1ip3RO9kXu498TT7BLsEM\nrjKY3pV642xdSv7IJF2A1cOUwaKBy5QKdqZWkAlrRyoDV8PXKstLzcTNOzmMX3GGO9lFzOhXm4EN\n/U0dErlFGj7YGMqO0Fu82q4iH3StZuqQBMF4QtcpqxOq91IKp5jDrNqphbDrA/BrAMPWgqP5VH8O\nu5XNkIUncHOwZv3E5ng7m345+P6wO0xedR5fFzt+fbHJY/uOyjodeSdOkLVpMzn79iEXFWFTpQou\n/fvh0qtXqek3bU5EwldaFecr68mjDkHvn6DBaMNfMiGBzHXrydy4EW1aGlbly+M6eDCuA/pj6eWF\nLMv8uC+c2fvD6VHblx+G1NPrmu1nIcsyX2y7xi/HY5jYJoQPu1Uz+6QvvTCdrRFb2RC+gdjsWJys\nnehdsTcDKg+gsltlU4f3XCnUFPJn7J+svb6W0NRQbC1s6RbcjSFVh1DTs6apw3u4yAOwZgTYeyiJ\nlY8ZxVqYDcu7Q3oUjN2u3DiZ2K2sAvrMPYYMLBrVkPpmVPBJlmU+2nyF1afjmNGvNsObBpo6JEEw\nvJt/Kvc6gc1hxAbzao1wfQdsGA+O3jByI3ia/u9yZEouQxaewMpCxfpXmuPvZj6zj+di03nxl7NY\nW6pYMa7JA6sca7OyyNywgYzfV6FOSkLl7IxLzx649B+Abc3SvULL1ETCV5qpC5RR8oh90PMHaPSi\nUS4rFxeTc+AAGWvXkn/iJFha4tSxA9sqteGbRFsGNfTn6wF1sDCzIimyLPPZH1dZeTKWSe0q8l6X\nqmb54nEj/QYrrq5gV8wuNDoNDbwbMLDKQDpX6IytpRn9sXtOhaWFsfbGWnZG76RAU0BNj5oMqTqE\nbsHdzOv/J+UmLOkIroEwclPJmg8bW85tWNpZGcAa/6dScc9E8oo0DPr5BHHp+Wx8tQVVyxm+OMuT\n0mh1vPzrWQ6Hp7JkdCPaV/M2dUiCYDhxJ+HXvuBVBcZsN06BqSeVcFZZcSWpYMJf4GL4NlcPDSUj\nn0E/n0Ct1bFuYnNCzLCXZ/idHEYvO01uoYYlYxrRNESZqSuKiibjt5Vkbt6CXFCAfePGuA0bimPH\njqhsysAeejMgEr7STl0I60ZD+B7o/h00edmoly+OiSFj3TpurV6PTUEuqRWqUufd13Du2OGZK3wa\ngk4n88kfV1h1Ko43OlTi7ReqmjokQElGT9w6wYqrKziedBw7Szv6V+7PoCqDqOhquptg4eFyinPY\nFrmNdTfWEZkVibutOyOqj2BI1SGm30tZkAGLO0JRNrx8EFwDTBvPo6RGwLIXlH6j4/eaJDHV6WQm\n/naO/WF3WDqmsVknUnlFGgYvPEF0ah7rJjanlp/YtyuUQXeuwvJu4OAF43ab1ZLJf0kOgyWdwLMK\njNtlklnI5OxCBi08QUZeMWsmNNdrj1B9S8osYNTSU6RkF7KluTVWm9eRe+gQkpUVzj174j56FLbV\nq5s6zDJHJHxlgaYI1o+DGzugxyylz5URLT4cxXdbLzHNJpqGJ3eiTkzEOjgYj/Ev4ty7Nypr41a2\nexydTmbKpsusPRvPW52q8GYn0y3DUOvU7InZw4qrK7iefh1PO09GVB/BoCqDTJ80CCXy9x7L5VeW\ncyTxCPaW9gyqMohRNUbh42CCWTWtBn4fADHHlKWSgc2MH8OTSjgLK3opDdrH7QQb486ufbUrjIWH\novi8Vw3GtQw26rWfxp3sQvrPP06xVsfmSS3MatmWIDyzjBhY2kWZNRu/R1mlYO7CtsPaEVB3uFJb\nwYirhzLyihmy6AQJGQX89lJTs+89LKvVRK/eSMS8hQRk3Ubl7o778OG4DR0iqmwakEj4ygpNMawb\npSzvHLcbAhob5bJnYtIZuugknav7sGBkA9Bqyd6zh7SlSym6FoallxfuY0bjOmQIFk7ms0RKp5N5\nf2MoG84lmOQmL1+dz4abG1gZtpLbebcJcQlhbM2x9AjpgbWFeSXIQsndSL/BsivL2B2zG5WkonfF\n3oytOZZgFyP+fO36EE4tgN5zocEo4133Wd38E1YPheDWMHw9WBrn92DdmXje3xjKyGaB/LfPk7ef\nMZWbd3IYsOA45Zxt2fBqC1zsjNv2RhAMIjcZlr6grFJ4cTd4l6KZnoNfwaGvodu3RquEnFOoZsSS\nU1y/ncMv4xqbdesWubiYzD/+IG3hItQJCaiDKjLHvRFO3bsza0TjUvPaW1qJhK8sKciEha1BBl45\nbPDGxqm5RfT46Qi2VhZse70Vzrb/f8MhyzJ5x4+TvnQpecdPoHJ0xH3cWNzHjMHC0TzWlWt1Mq/8\ndo6/biSz8dUWRmkKX6QtYt2NdSy5vIT0wnQa+jRkXM1xtPZvjUoyvyWwwtOJz4lnxdUVbInYQrG2\nmE4VOvFK3Veo4lbFsBc+/ytsfR2avgrdvjbstQzhwu/wxySoPQj6LQIDLws/EZnGqKWnaF7Rg2Vj\nG2NlotYLT+t4RCpjlp+mUQV3VrzYxGyKZAnCUynMgl96QFokjN5qtIFrvdHplLoKN3fD6C0Q3Mag\nl9NodYxaepozMeksGt2QDtXMcJ82dxO9TZtJW7QIdVIStrVq4Tl5Eo7t2jH3QASz9t5kaq8ajC0F\nqytKM5HwlTUJ55T9MJW7wNDfDbasQKuTGbPsNKdj0tk8qQU1yz98+WHB1aukLlhA7r79WLi64vHy\nS7gNH47KznR9Yf6WmV9M99lHsLZUsf2N1gbrF6jWqtkUvolFlxeRnJ9Mk3JNmFxvMg18TF+ZUDCc\ntII0fg/7nTXX15CrzqVbcDcm15tMoLMBlijFnlCWRQa1UqrZGbOpuj4dmQX7p0Hz16DLdINdJjo1\nj37zj+HhYM2mSS1L7QzZpvMJvL3uEv3r+zFrcF0xSi6UTjqdshQ9+rDS5qCy+bRqeSKF2cp+vrwU\npYiLWwWDXWrO/nBm7b3JzIF1GNTI/PZp64qLydq4kdRFi9HcuoVt3Tp4TZ6MQ+vW916ndDqZCSvP\n8teNFFZPaEbjIHcTR112iYSvLDo+F/78WGmw3OxVg1zi+703+Wl/ON8MqM2QxiW7eS24fIWU2bPJ\nO3oUCy9PPCe+guvgQSbf43c6Op2hi07Qp54fPwypp9dzq3VqtkVuY+GlhSTlJVHfuz6v1XuNJr5N\n9HodwbxlFWWx/Mpyfg/7HbVOTb/K/ZhYZyLlHMrp5wKZcbCoPdi6wMv7DT67b1CyDLveh9OLlJ5b\nNfvq/RJZ+Wr6zT9GRn4xWya3pIKHg96vYUx/3/iZUyEqQXgifzdW7/E9NB5v6mieTWoELO4AboHw\n4p8Gacx+IS6DgT+foGcdX2YPra/38z8LWaMhc9MmUucvQHP7Nnb16uE5eTIOrVo+cEAqu1BNn7nH\nyC3SsP31VviYQd/AskgkfGWRLCuNliP2KaXO9dzf6vDNFMYsP03/+v58N6jOE48o5589S8qPs8k/\nexbL8r54TZ6MS58+SJamm5H4cd9NftwXzqxBdRmgh0bLOlnHzuidzL84n/iceGp51OK1+q/RonwL\nMQL/HEvJT2Hx5cWsv7keFSqGVhvK+Nrjcbd9hlHN4jylwEFmLLy0XylhXtpp1co+nowYmHRSr5U7\n1VodY5ef5nR0Or+/1IwmwaV/RFmWZd7fEMr6cwmseqkpLSqZ7z4eQfiX5OuwqC0Et1X6hZaFv5Hh\ne+H3QVCrPwxYqtevKbdIQ4+fjqDRyux8s7XZrE6QZZncv/4iedYsiiMisatbF883XsehxePve27c\nzqHvvGPUKO/M6pebieXpBiASvrIqPx1+bq0s65p4WBn514OkzAJ6/HQEH2dbNk9qiZ21xVOdR5Zl\n8o4dJ2X2bAovX8Y6OBifDz/AsW1bvcT5pLQ6mWGLT3IlMYvtr7d6pv41F5Iv8O3pb7mSdoWqblWZ\nXG8y7QLaiURPuCcxN5EFFxewLWobtha2jKk5hrE1x2Jv9YQjwbKstGW5vh2Gr4PKnQ0TsCmk3FT2\nJIe0g2Fr9HbD9PfqBH0N7piLgmIt3X86QrFGx5632hhsebog6JWmGJZ2gqwEePWEefYLfVpHvof9\nX0DnadDyTb2d9v0Nl9hwLoE1E5qbzYBVweUrJM+cSf7p01hXqIDXO2/j1LnzE933bLuUxOurLzCm\neQW+6FPLgNE+n0qa8IlUu7Sxd4eByyAzXinioIeEXa3V8dqq8xRrdMwb0eCpkz0ASZJwbNWSoHVr\n8Z87B3Q64ie+QtzLEyiKjHzmWJ+UhUpi9tB6WFuqeGPNBYo02ic+R2JuIu8eepfRu0aTnJ/M9FbT\nWddrHe0D24tkT/gHP0c/vmz1JZt7b6alX0sWXFpA7y292RG1gycaXDv3C4RthU5flK1kD5SZyo6f\nKwUQLvyml1NeS8pm/sEI+tf3K1PJHoCdtQXfDapDUlYBM3aGmTocQSiZQ9/ArUvQa3bZSvYAWr0F\nNfvBvqkQeUAvp9x5+RbrziYwqV0ls0j2ihMSSXznXWIGDaIoPByfTz8hZPs2nF944Ynve3rVLc9L\nrYJZcSKWTecTDBSx8Dhihq+0Ovoj7PtcL03Z/7v9GkuPRjN3eH161imvpwAVcnEx6atWkTpvPrr8\nfNyGDcPrtclYuBq+cub9/rw8Fjg/AAAgAElEQVR6mwkrzzG+VTCf9qxRoufkFuey5PISVl5biUpS\nMa7WuKebrRGeW+fvnOfr018Tlh5GPa96fNjkQ2p61nz0k7KTYF5T8K0LY7aVjWVQ/0ung197Q9JF\nePXYMxVAUGt19J13jDvZhex9qy1uDmWz/cmMnWEsOhzFry82oU0VM25WLQhxp2B517u96+aZOhrD\nKM5T9vMV5cDkU8/UY/RWVgFdfzxCkIc9G15tYdKqwtqcHFIX/EzGypWgUuE+diweL7/0zFXYNVod\nI5ac4mJ8Jlsmt6S6r/k2kC9txAxfWdfiDajUGfZ8pIyiPaXdV26x9Gg0Y1sE6T3ZA5CsrfEYO5aK\ne3bjOngQGatWEdGlK+krf0NWq/V+vYd5oWY5xjSvwNKj0Ry8nvzIY7U6LRtubqDH5h4svbKULkFd\n2NZvG5PqTRLJnvBEGvg0YHWP1UxrMY24nDiG7RjGp8c+JbUg9cFPkGXY8S5oi5WR8bKY7IHSlqHP\n3RvBLZOUBPApLTocxdWkbP7bp1aZTfYA3u5chYpeDny4MZTsQuO9dgrCEynKhc0TwMUfun5l6mgM\nx9pB6YmanQQHvnzq0+h0Mm+vvYRaq+PHofVNluzJskzWtm1Edu9O+vLlOPfsScU9u/F+6z96abll\naaFi7vAGONla8sHGULS60jfZVNqJhK+0Uqmg30Kw94T1Y5WSwU8oI6+YKZsuU9ffhY+6G7YJqqW7\nO76ff07wls3Y1azBnenTierbj7wTJwx63ftN6V6dauWceHf9JZKzCx94zJXUKwzbMYwvTnxBBecK\nrO6xmhmtZ+iv6qLw3LFQWdCvcj929NvB2Jpj2R61nZ6be7LsyjKKtcX/PPjaH3BjB7SbAh4VTROw\nsbhVUG4IY4/CqZ+f6hQRyTnM3hdO99rl6FbbV88BmhdbKwu+G1SX29mFzNghlnYKZmrPR5ARq9yf\n2JbxWZyAxsoKq1MLIeHpVp0tPhLFiag0Pu9Vg2BP01QVLrx5k7hRo0l6732sfMoRtG4t5b+agVU5\n/d73eDnZ8GnPGoQmZPHbyVi9nlt4PJHwlWYOHjBwqVLx7ilGmL7dc53sQg3fDKxjtMpJtlWqELB0\nKf7z5yNr1MSNe5HE999Hk5Zm+GtbWTB3eH3yi7W8te4iuvtGmHKKc5h+cjrDdwwntSCVmW1msqLr\nCmp5ig3Ggn44WjvydqO32dJnC419GvPDuR8YsHUAZ26fUQ7IT4ed7ylLOZu/ZtpgjaX+SKjSVSmA\nkHLziZ6q1SkVLO1tLPii9/Pxe1o/0I2JbSuy5kw8f9149EoFQTC6G7vg/AqlkEmFFqaOxjg6fApO\nvrD1DaUK8RO4kpjFd3/eoGvNcgw2Qb89bW4ed775luh+/SkKD6fcF18QtHYNdrVrG+yaveuWp3Vl\nT2buucHtrAcPvAuGIRK+0q5CC2g0Hs4shluhJX7a+bgMVp+O58WWQVQrZ9xROEmScOrQnpCtW/Gc\nNInsXbuJ7N6DjPXrkZ9haVdJVPJ2YmrvGhyLSGP1mThkWWZ39G56b+nNupvrGFZtGFv7bqVrcFdR\nkEUwiArOFZjTcQ4LOi1ArVPz4p4X+ezYZ2Tt/hDy05RlQqW1ufqTkiTo9RNY2SvLwJ7ghumX4zGc\nj8tkaq+aeDnZGDBI8/KfTpWp4uPIhxsvk1UglnYKZiI3RSkk51Mb2n9k6miMx9YZesyC5KtwfE6J\nn1ZQrOXNNRdwd7Dmq/61jXq/IcsyWTt2ENW9O+m//IJr//6E7N6F25DBSBZPX7SvJCRJ4su+tVBr\ndUzbftWg1xL+SSR8ZUGHj8HOHXa+W6K9MBqtjo83X6Gcsy3/6WS63l4qGxu83nidkC2bsa1cmduf\nfkbsqNEURUQY9LqDGwXQNNidmfuPMX7PBN47/B7e9t6s6r6KKU2n4Gj97OvVBeFxWvm1YnOfzbxY\n60W2RvxB78yjbK/fF7mc4UZXzZKTD/T8HpIuKOXOSyA2LY+Ze67ToZo3ferpf++xObOxVJZ2puQW\n8d/t10wdjiAoe4+3vQmFWdB/EVg+PwMwAFTrDtV7K5VJ00pWjfy7P28QmZLHrEH1jLr3uDg+nrgX\nXyTpnXex9PIiaM1qfP87DUs3N6PFUMHDgTc6Vmbn5dvsD7tjtOs+70TCVxbYuUHnLyD+FISueezh\nv56IJexWNp/3qoGDGfR0sqlYkcCVv+I7fTrFERFE9etP8g8/ois0zHS/RqehTq0zaHxncuHOJaY0\nmcKq7qseXz1REPTMztKOt2pPYG22Dj/ZkikZZ3hl3yvEZ8ebOjTjqtkPag+Cw98qid8j6HQyH2wM\nxUqlYnq/Ws/lTHwdf1cmtavIhnMJ4oZJML3Qtcre446fg0/JqmCXOd1ngoUNbP/PY9tlhd/J4Zfj\nMQxrEkiryp5GCU/WaklfsYKo3n0oDL2Mz2efErRuLXZ16xrl+v/r5dYhVPZ25LM/rpJfrDFJDM8b\nvSR8kiR1lSTphiRJEZIkffiAx3+QJOni3bebkiRl3veY9r7HtuojnudS3eHg3wT+/BQKMh962J3s\nQr7fe5O2VbzoWst8CpFIkoTrgP6E7NqJS48epC1cSFTvPuSdPq3X61xLu8aQHUNYE7GYAJtGZEe8\nRV2XHlioDLuMQRAe6uAMqqbFsbLDXKY0mcKllEv029qPJZeXoNY9R0v2us8EBy/44zXQPbxf5qrT\ncZyMSufjHtXxdbEzYoDm5fUOlalWzokpmy6TmV/8+CcIgiEU5cLez8CvITSbZOpoTMepHHSeCtGH\n4eKqhx4myzLTtl/D3tqCd18wzgqroshIYkeM5M5XX2PfpDEh27fhPny4wZdvPoq1pYrp/WqTmFnA\n7H3hJovjefLMCZ8kSRbAPKAbUAMYJknSP4Z4ZFl+S5blerIs1wPmAJvue7jg78dkWe79rPE8t1Qq\n6PEdFKTDwekPPey/269RrNUxrU9NsxwZt3R3p/zXXxH4yy8AxI0ew+3pM9AVFDzTedVaNfMuzmPE\njhFkFGYwp8Mc1vSdj4u1J1O3Xn2yptiCoC+J5+DkfGg4FovgNgyvPpw/+vxBK79WzD4/m5E7RxKR\nYdglzmbDzk2p2nnnClxY+cBDEjML+GpnGC0reTCksfGLHJgTa0sV3w2qS3peMdNF1U7BVI7+ALl3\noOs3yn3I86zBWAhsDn9+rOxpfIB9YckcCU/lrU5V8HA07NJXWa0m9eeFRPftR3F0NOW//YaAn3/G\nytc8Kho3CXZnaOMAlhyN5lrSk1eaF56MPn47mwARsixHybJcDKwB+jzi+GHAaj1cV/hfvnWh8Utw\nZskDC7gcCU9he+gtJrerRAUP05T/LSmHZk0J2bIZt5EjyVi5kqi+fck/f/6pznU9/TrDdgzj50s/\n0y24G1v6bKFdQDtc7K14v0tVzsRk8MfFJD1/BYLwGFq1UtnN0Qc6T7v3aR8HH35s/yPft/ueW7m3\nGLx9MMuvLEf7iFmvMqNGXwhoplQd/p9WM7Is89Gmy+hk+Lp/HbMcsDK2Wn4ujG8VzIbzCVxNyjJ1\nOMLzJjNOKVRSe5DSouB5p1Ip/VOL82DPlH89XKTR8uWOa1T0cmBU8woGDaXw2jWiBw8h5ccfcezY\nkZAd23Hp3dvsXjc/7FYNVzsrPtp8WfTmMzB9JHx+wP0bThLufu5fJEmqAAQDB+77tK0kSWclSTop\nSVLfh11EkqQJd487m5Ly4JETAWj/4AIuRRotn/1xlSAPeya2DTFhgCWnsren3CcfE7hiBWi0ypKE\nb74t8d4+tVbN/IvzGbZ9GGmFafzU/idmtJ6Bi43LvWMGNwqgrr8LM3aGkVsk1pELRnTsR2U2q8cs\nsHX518OdK3Rmc5/NtPFvw/fnvmfs7rHEZpfx3kWSBF1nQF6KMnNwnwPXkzl0M4V3u1QlwN3eRAGa\nn0ntK+FqZ8X0HWFipYJgXHs/B0kFnaaaOhLz4VUVWr8Dl9dD+L5/PLT8WAyxafl81qumwRqsy2o1\nKT/NIXrQYDSpKfjN+Qn/H3/A0tM4ewWflKu9NZ/0rM7F+ExWnY4zdThlmj5+4h40XPCwvzpDgQ2y\nLN8/VB0oy3IjYDjwoyRJD+w2LMvyIlmWG8my3MjLy+vZIi7L7FyV2YL4U3Dp/ydSFx6KIjo1j2l9\namFrVbr2qzk0bULwH3/gOmQw6cuXE92vPwWXLj3yOTfSbzBsxzAWXFpAl+AubOmzhfaB7f91nEol\nMbV3TZJzipizX6wjF4wkOwkOz1Iqu1Xr8dDDPOw8+KHdD3zV+isisyIZuHUgv4f9jk42bPsSk/Jr\nCHWGwIl5SgNnlMrCX++6TrCnA6MNPDJe2rjYWfFmx8ocj0zjoOjNJxhL3Em4uglavgEu/qaOxry0\negs8q8COt5TZPiA5u5A5+8PpVN2btlUMcw9bFB1NzPARpM6fj0vPHlTcvh3nzp0Nci196lvPj5aV\nPPh213WSs0VvPkPRR8KXANy/mcIfeNj6uKH8z3JOWZaT7r6PAv4C6ushpudb3WEQ0FTZSF2QQWxa\nHnMPRtCjji9tDPRCY2gWjg74Tp1KwNIl6AoLiRk2nORZ3yMX/7NYgU7W8cuVXxi6YyipBanMbj+b\nr1t//Y9Zvf9VP9CNQQ39WXYsmsiUXEN/KYIAf30FOg288N/HHipJEj1DerK592YalWvE16e/5uU/\nXyYxN9EIgZpIx8+UmYP9XwCw4VwC4cm5vN+lqsFGxkuzEc0qEOzpwIyd19Foy/BggGAedDrY9QE4\nlVearAv/ZGmjLO3MjIMT8wH4ds8NirU6Pu6h/yqmsiyTsWYt0f0HUBwXh9+PP1L+m2+wcHn4fY85\nUXrz1aZIq2OaaDVjMPr4y3kGqCxJUrAkSdYoSd2/qm1KklQVcANO3Pc5N0mSbO5+7Am0BMT/9rNS\nqaC7UsBFPjCdqVuvYqWS+NQALzTG5tiyJSFb/8ClX1/SFi8mZvgIimNiALiTd4cJeycw69ws2vq3\nZUufLXQI7FCi877ftRq2lhaigItgeCk34MJvyn5bt6ASP83HwYf5HecztflUrqReYcDWAWyP2m64\nOE3JxR9avA5XNlIYdYLv996kQaCrWVUWNidWFio+7FaNiORc1px5zlp6CMYXugZuXVSWclqbdz0A\nk6nQAqr1hGOzuRwexYZzCbzYKphgT/1+vzSpqSS8OonbU6diX78+IVv/wLlrF71ewxiCPR2Y3K4S\n20NvcTo63dThlEnPnPDJsqwBXgP2AGHAOlmWr0qSNE2SpPurbg4D1sj/vJuuDpyVJOkScBD4WpZl\nkfDpg2+duwVclpJ88wxvv1CVci62po5KLyycnCg/fTp+s2dTHB9PVP8BHF8ynQFb+xOaEsrU5lP5\nod0PuNq6lvicXk42vNW5CkfCU/nzmuhrJRjQ/mlg5QBt3n3ip0qSxIAqA9jUZxNV3Kow5cgUPj76\nMXnqPAMEamIt3wTHcmRufpeUnAI+6l7d7AoOmJMXavjQJNidH/fdJKfwOWrnIRhXUS7s+0JZel17\nkKmjMW8dP0NW5xG1aRqejja81r6SXk+fc+CA0r7q+HF8PvqIgCWLsfLx0es1jGlCmxC8nWz4dvd1\nMfBuAHpZGyPL8k5ZlqvIslxRluXpdz/3mSzLW+87Zqosyx/+z/OOy7JcW5blunffL9VHPIJC2+4j\nMiUnvrVbwZhmgaYOR++cu7yA74ZV3AlwwO2733jjDy1r2i5lQJUBT3VjOKp5Bar4OPLf7dcoVD8H\nFREF44s7Bde3K8mMw9Nvovdz9GNZl2W8UvcVtkdtZ/C2wVxNvarHQM2AjSM5LadQLucKHweG0SjI\n3dQRmTVJkvikR3VSc4v5+VCkqcMRyqpjP0Lubej6tWjD8DheVYkN6EvX/G1MbeuMk62VXk6ry8/n\n1qefkTBpMpY+PgRv3ID76FFIpfz/w87agjc6VuZsbIbYj2wApfunQ3ikP67nMaN4CDV1N7AM32nq\ncPQuLC2MEWff5I2+Gdwc1Ijal3PRjf4P+ecvPNX5rCxUTO1dk4SMAhYeitJztMJzT5Zh3+dKG4bm\nz96g2FJlyeR6k1nWZRnFumJG7hzJ8ivLy1RBl+/uNOCKLogx+ctB/Wy9OJ8Hdfxd6VuvPEuORJOU\nKb5fgp793Yah1kAIaGLqaMxeXpGG1291QZIkeqQu18s5i8LDiR48mMwNG/B4+SWC167BpnJlvZzb\nHAxpHEAFD3tm7rmJTrRp0CuR8JVRaq2OH/eFc927B7JHZTg44x9tGkozWZb59eqvDN85nHx1Pou6\nLqHPf1cS9PtvoFIRO3IkKfPmIWuevM1Ci4qe9Kjty4JDEaTkFBkgeuG5dWMXxJ2Adh/qdd9LQ5+G\nbOi1gfaB7fn+3Pe8svcVUgtS9XZ+U4lKyeX30wmcqvw2VrlJStVO4bHe7VIVGfhuzw1ThyKUNfum\nAhJ0/sLUkZQK8/+K4HKOE+k1xyKFroHksKc+lyzLZG7YQPSgwWgzswhcugTvd95BsrbWY8SmZ2Wh\n4u3OVQi7lc22UNEfWZ9EwldGrTsbT1x6Pm93qYHU7kNIvqaUUC7lsouz+c/B/zDz7Exa+7VmY++N\nNPVtCoBdvXoEb9mMc48epM6ZS9y4F1EnP/mygHdeqEKxRsdCsSxK0BetRqk46VEJ6o/S++ldbFyY\n1XYWnzX/jAvJFxiwdQBHE4/q/TrGNHPPDawtVfTuO1QpfnD0B8gR+2sfx9/NnvGtgtl0IZEriaIZ\nu6AncafgykbRhqGE4tPzWXwkmn71/SjX4yOwdlT2bz8FbW4eSe9/wK1PPsWufj1CNm/CoUULPUds\nPnrVKU+1ck58v/cmalF1WG9EwlcGFaq1zNkfQcMKbrSr6gU1+4N3Dfjra+XGs5S6mnaVwdsGczjh\nMO83fp/Z7Wf/qzCLhaMjfjO/xferryi4fJno/gPIO3X6ia4T4uVIv/r+rDwZK3rCCPpxaTWkXFfa\nDVjoZx/H/5IkiUFVBrGm5xo87Tx5dd+rzLkwB62u9O1HPRebwa4rt5nYpiJeTjZKb1FNERz80tSh\nlQqvtquIu4M1X+64JoofCM9Op4PdH4KTr2jDUEJzD0QA8H7XqmDvrnzfbuxU+hc+gcLr14kZOJDs\nHTvwfON1ApcswbKM96JWqSTe61KV2LR81p0VVYf1RSR8ZdBvJ2O5nV3Iuy9UVYqXqFTQ/iNIC4fL\n60wd3hOTZZm119cyaucoNDoNy7suZ1SNUY8szOLary9B69Zi4eRE3LhxpC5chPwES1rf6FgJjU5m\n/l9ilk94RuoCZUm1X0Ol0bqBVXStyO/df6dfpX4sCl3ExH0TSStIM/h19UWWZb7aGYaXkw0vtQ5W\nPulREZpMgPMr4fZl0wZYCjjbWvFWp8qcjEpnf5gofiA8o+vbIOm8MmAl2jA8VlxaPhvPJzC8SSC+\nLnbKJ5u9quzf3jdV2c/9GEpvvTXEDB6CLj+fwF+W4zVpEpKFhWGDNxMdqnnTsIIbs/eFU1Bc+gYt\nzZFI+MqYvCINC/6KpFUlT5pX9Pj/B6r1BN+6d2f5Sk/J7jx1Hh8c+YAvT31JU9+mrO+1nnre9Ur0\nXNsqVQhavx7nrl1I+eEH4l99FW1mZomeW8HDgYEN/Fl1Oo5bWaL4gfAMTi2EnCRllspIbQVsLW2Z\n1nIa01pM42LyRQZvH8zF5ItGufaz+vPaHc7GZvBWpyo42Fj+/wNt3wNbFyV5Fh5raJNAQrwcmLEr\nTCyLEp6eTgeHvlWWo9cZYupoSoV5ByNQqSReaVvx/z9p7QBtP1D2cd/c88jn6/LySHrnHW5P/QL7\nJk0I3rIZhybPV5EcSZJ4v0tVknOKWHEixtThlAki4Stjlh+LJi2vmHe7VP3nA5IE7T+BzFil6XMp\ncDPjJkO3D2VPzB7ebPAm8zrOw83W7YnOYeHoQPlZs/D59BPyjp8guv8ACkJDS/Tc1zpUQqeTmX9Q\nzPIJTyk/HY5+D5VfgKBWRr98v8r9+K37b9hY2DBu9zh+vfqrWS/xU2t1fLPrOhW9HBjc6H/2Cdm5\nQfPJyrKoW5dME2ApYmWh4qNu1YlKyWPDuQRThyOUVjd2wp0r0OY9UD0fs0vP4v7ZvX/1Pm4wGtxD\nlP3cD1lqXxQdTfSQIWTv3oPXW28RsGghlu7PZ0uapiEetK3ixYK/IskqKD0TFeZKJHxlSFa+moWH\no+hU3Yd6AQ9oOl65M/g3hsPfKfthzNj2qO2M2DGCXHUuS15Ywku1X0IlPd2PqyRJuI8YQdCq3wGI\nGTGS9N9+f+yNb4C7PYMbB7DmTByJosS58DSO/gCF2dDxc5OFUM29Gmt7rqVtQFtmnp3JO4feIbc4\n12TxPMraM/FEpebxYbfqWFo84Pe9yQSwcYbDM40fXCnUsbo3dQNcmf9XhJjlE56cLMOhb5QkpdZA\nU0dTKsw9GI5KJfFqu4r/ftDCCjp8ohTRu7z+Xw/n7N9PzKDBaNPSCVy6BM+JE0p9b71n9V6XqmQV\nqFl8WLTKelbP909SGbPoSCS5RRreeaHKgw+QJGj/MWQnwLkVxg2uhDQ6Dd+c/oYpR6ZQ07Mm63ut\np3G5xno5t13t2gRv2ohjixbc+fJLbn34IbrCRxdlmdy+EhLSvQ3YglBimfHKcs66w6BcLZOG4mTt\nxA/tfuDdRu9yIO4AQ3cMJTwj3KQx/a8ijZa5ByJoHORGp+reDz7IzhWavgJh2+DONeMGWApJksTr\n7SsRn17A1ouixLnwhG7uhtuh0PpdsLB8/PHPOWV2L5HhTQLxcbZ98EE1+inbaw5MvzfwLmu1JM+e\nTcLk17AOCiJ44wYcmjc3YuTmq5afCz3r+LLsWLRolfWMRMJXRqTmFrH8WAw965Snuq/zww8MaQcV\nWsGR76A431jhlUh6YToT9k7gt7DfGFF9BItfWIynnader2Hh6or/gvl4vvE6WX9sJXbESNRJD78R\n8nO1Y2iTANafjSc+3by+X4KZOzwTkKH9FFNHAig3/2NqjmFpl6XkqfMYsXME+2P3mzqsezadT+R2\ndiGvd6j8yIJMNHtVKXEuZvlKpGN1b6r7OjPvrwi0opGxUFKyrOz5dwuCOoNNHU2pMPdgOBYPm937\nm0oFnaZCVhycXYY2M5P4ia+QtuBnXAYOoMLvv2FVvryxQi4V3nmhKkUaHfMOioH3ZyESvjJi/sFI\nijQ63upU+dEHShJ0+Bhy78DZpcYJrgSupV1j6PahXEq+xPRW0/mwyYdYqQxUvl6lwmvSJPznz6c4\nNpbogYPIO/3w1g2T2lVCpZKYc8C8ZkQEM5adBBdXKT33XANNHc0/NPRpyNqea6nsWpn//PUf5l2c\nh0427XI/jVbHgr8iqePvQuvKjxnksXdXlnZe3Qwporn440iSxOsdKhGVksfOy7dMHY5QWoT/Cbcu\nQut3DNZKpiwp0eze3yp2gOC2FG6eRfSAgeSfOkW5aV9Q/ssvUdnYGCfgUiTYU9nT/fupWDHw/gxE\nwlcGJGUW8NupWAY08CPEy/HxT6jQQnnBOfoDFOUYPsDH2Ba5jdG7RiMj82v3X+ld0fCl6wGcOrRX\nWje4uBD34viH7usr52LL8CaBbDyfSExqnlFiE0q543NB1ilNis2Qt703y7ouo2+lvvx86WfePPim\nSff1bQ+9RVx6vrKEuiSVTJtPBis7ODLL8MGVAV1rlqOStyNzD0SgE7N8wuP8vXfPNVBZki48Volm\n9+6TpWtHzHZL5PwsKvy2ErfBYhb1Ud7oqKz8mL1fDLw/LZHwlQFzDoQjyzJvdHzM7N792n8C+WnK\nHiMT+Xu/3kdHP6K2Z23W9FhDTY+aRo3BJiSEoHVrcWzVStnX9/En6Ir+vU58UruKWKokfhKzfMLj\n5KfDueVQe6CyHMpM2VjYMK3FNKY0mcKRhCOM2DmCmKwYo8eh08nM/yuCKj6OdK7uU7InOXhC4/FK\n4YM0UUX3cVQqicntK3LjTg77wu6YOhzB3EXsh8RzYnavhJ5kdk/WakmeNYukbxZjV96W4F752NWq\nYaRISy9fFztGNA1k84VEEjLELN/TEAlfKRefns+6s0oJYH83+5I/0b8hVOkGx3+CgpL1ptOnzMJM\nJu6dyG9hvzGy+kgWvbAIDzuPxz/RACycnPCfPw/PSZPI2rSJ2FGjUd/5502Rt7Mto5pVYMuFRCJT\nzLPCoWAmTv0M6nxo9ZapI3ksSZIYXn04i19YTEZhBsN3DOdIwhGjxrA37A437+Qyub2ydLrEWrwB\nFtZilq+EetUpTwUPe+YciDDr1hyCickyHPoaXAKg7nBTR1MqlHR2T5ubS8Lk10hbvATXoUMInD0D\ny+IEuLzBSJGWbi+3DkEClhyJNnUopZJI+Eq5JUeiUEnwartKT/7k9h9BYRacnK//wB4hKiuK4TuH\nczH5ItNbTeeDJh8YbL9eSUkqFV5vvI7/3DkUR0QQPXDgv/r1TWxbERtLC34SSwqEhynKURK+aj3B\nu7qpoymxxuUas6bnGvyc/Ji8fzJLLi8xSlIgyzLzDkYQ6G5Pj9q+T/ZkR29oOA4urYGMGIPEV5ZY\nWqiY1K4ilxOzOHQzxdThCOYq6iAknFEGrCytTR2N2Svp7F5xfDyxw4aRe+QIPp99iu/UqUjVu4FP\nLWV7jU60TXmc8q529K3vx5ozcaTnFZs6nFJHJHylWHpeMWvPxtO3nt+/G3yWhG8d5cb01M9QZJxZ\nq+OJxxm5YyR56jyWdllqtP16JeXUqRNBa9egsrEldtRosnfuvPeYl5MNo1tUYOulJMLvmH7vo2CG\nzi5XBlFavW3qSJ5Yecfy/NrtV7oGdWX2+dl8fPRjirWG/aN6JDyV0IQsXm1X8cF99x6n5ZugsoQj\n3+s/uDKoX31//FztxCyf8GCyDH99A85+UH+kqaMpFeYeDMdSJTHpEbN7eadOEzNoMOrkFAKXLMZ9\n+N2ZU0lSEuvUG0qDey50y60AACAASURBVOGxXmkbQqFaxy/HY0wdSqkjEr5SbMXxGArVOia2DXn6\nk7R6S7lBPf+r/gJ7iFVhq5i0fxK+jr6s7rGaet71DH7Np2FTuTJB69ZiW7MmiW+/Q8q8efdujia2\nqYidlQVzRXlg4X+pC+HEXAhuqyyZLoXsLO34ps03TK43mW1R23j5z5fJKMww2PXmHoygnLMt/Rv4\nPd0JnH2hwWilImpmvH6DK4OsLVW80jaEc7EZnIhKM3U4grmJPgTxJ+/O7olqkY9zb3avaSDeD5nd\ny1i7jrjx47Fwdyd43dp/99er0VfZ6330eyXhFh6pkrcTnWv48OuJGPKKNKYOp1QRCV8plV+s4dcT\nMXSq7kMlb6enP5F/IwhsoSzr1Kr1Ft/9NDoNX578kq9Of0Vrv9b82u1Xyjuad58ZS3d3An9Zjkuf\nPqTOmUvSu++hKyzE3cGaYU0C2R56i8TMAlOHKZiTS//H3nmHR1Xlb/xzZ9I76SGZNJp0SKN3EbGt\nDaSHqmJby+pPd1fddXVXXXUVRUSkgxTbqosCYkGkJST0HkIy6b23yczc3x83QQQkA5mZOzO5n+fh\nEWfuPfd9EE/u95zved+PpbiTEfa3u3cxgiDwYP8H+ffIf3O87DjTtkwjszLT7M9JzSon5Xw594+M\nxdVJff0DDX9c+ufut80jzMGZlKAhyNuV935QFq0ULmHn6+AdJsXJKLRJ6+7ewlGX7+6Jej2F/3iZ\nwhdfxHPoEKI3bcQlKuryQdRO0nnkvDTIsu75aXtl4eguVNY3szFVWeS7FpSCz0755EAuFfXNPNie\n3b1Whv0RqnLg+H/bP9YlVOuqWbhjIZtOb2JO7zm8PeZtPJ09zf4cS6BycSHs1X8R9OSTVG/ZQnZy\nMvqSEuYOjwFgxS/KwWGFFgx6+OVtCI+XdvgcgJtjbmbFhBU06BuY8c0M9uTvMev4i3/MuLCA0i58\nI2DgdKlLoTrfPOIcGDdnNQ+MjGXPuTLSssvllqNgK5zfBdm7pd095+s4ItLByK9s4PP0PKYmXb67\nZ6itJWfhQ1SsX4//3LlolixB7X2VhfkB08ErRGlNN5G4yE4kxfjz0a5MdHrl7KOpKAWfHaI3GFm2\nK5P4qE4kRPu3f8BuN0FgD9j9jllbCrTVWqZvmc6BogO8NPQlnkx4ErWqHSv5MiAIAoH3LyB80Ts0\nnT7D+cn3EVCk5bZ+YWxM0VLVYJldUQU74/jnUJkt2ZibkiNnJ/QL6sfHt35MqFcoD+14iE2nNpll\n3GN5Vfx0uoR5w2NwdzHDnDD8SSn3cPc77R+rAzBtUCT+ni68q+zyKbTy8+tS0RE3S24ldsGqPVmI\nwPwRMb/5vLmggOxp06nbs4fQf7xEyDNPI6jbmOOc3WDwQ5JhTv5By4l2IBaO7kJBVSNfHVYW+UxF\nKfjskC1HC8itaODBK7QRXBcqFQx9FIqOShOOGThYfJDp30ynsqmSZeOXcVe3u8wyrlz43HQTUevW\ngcFA1tRpLHDKp05nYEOKVm5pCnJjNEoua0E3SFEnDkZnr86snbiWYeHDeHn/y7yW8hoGo6FdYy7+\nMQNvNydmDrlCi9P10CkK+k+BtFVQW2yeMR0YDxcn5g2P4afTJRzNrZJbjoLcFByG8z/DkIfB2V1u\nNTZPTWMzG/Zrmdgn9DdxWA3Hj5M1+T6a8/PRfLiUTpMmmT5owlxw9VV2+UxkdPcgbgj15oOd5zAa\nlbOPpqAUfHaGKIos3ZlJlyBPxt0QbL6B+00Gr1DYvajdQ23L2sb8bfPxdfVl/S3rSQhNMINA+XHv\n05voTzbjGh2N+oVneLT2MCt3n1daCjo6Z7ZC8Qlpl0nlmFOqp7Mni8YsYmavmaw7uY7HfnyM+ubr\nC7/NKK5h6/FCkodE4+NmxjiW4U+CvglSPzLfmA7MrCFR+Lg58e4PSsxMh2fvYnDxgrhkuZXYBZtS\nc6hp0rNgxK9Hamp++JHsmbPA2YnoDR/jNWzYtQ3q5gNJ8+Hk11Cq/D/ZFoIg5R5mFNey42RR2zco\nmKfgEwThZkEQTguCkCEIwrNX+H62IAglgiAcavk1/6LvkgVBONvyS5lt2mDX2VJOFFTzwMgu1xZS\n3BZOrjD4QWmHr+DwdQ0hiiKrjq3iTzv/RO/A3qyduJZIn3aez7ExnENCiFq7Bq8RI7hlx1pu3fsZ\nXx3MlVuWglyIohT87RcJfe6RW41FUavUPJP4DM8Pfp5f8n5hzrY5lDaUXvM47/90Djcn9YWzsGYj\noAv0mCgVfM2KoVJbeLs5M3tYDNtPFJFRrMTMdFiq8+HYZ5JRi7uf3GpsHr3ByMrdWSTF+NNfI/15\nla9dR+4jj+AaG0vMpk24dut2fYMPWii9iykGVCZxa98wNP7uLNl5TomZMYF2F3yCIKiBxcBEoBcw\nVRCEXle4dJMoigNafn3Ucq8/8CIwCEgCXhQEoVN7NTkyS38+R4iPK38YaAGXy/g50irfnnev+Va9\nUc8r+1/hzbQ3uSnqJpbdtIxObo75n1Ll6UnE4vfwu28yk87+RNPf/oqhqUluWQpykLUL8g5Ixkdq\nJ7nVWIXJPSbz7th3OV91nhnfzCCzynQHz5zyer48lH/hDJnZGfwQ1JfBEfOcNXR0Zg2JwsVJxcrd\nWXJLUZCL/Uul86+DH5RbiV3wzbFC8iobWDAiFtFgoPCVf1L0yit4jRlD1JrVOAUFXf/gXkHSGcrD\nm6Aqz3yiHRQntYr7R8RyUFtJynnFgKotzLHDlwRkiKKYKYqiDtgI/MHEeycA34miWC6KYgXwHXCz\nGTQ5JEdzq9idUcbcYTHtszH/Pdz9IH42HPscKk0/m1bfXM/jPz5+wYnz36P+javasTN8BCcnQv/2\nN4qmzCPuXCrHpiVjqKyUW5aCtdn1JngGw4COFVI8MmIkKyespEHfwMxvZpJelG7SfSt2n0cl8JtW\nKLMSPRxC+8He95VMKxMI9HLlzgGd+Sw9l4o6ndxyFKxNUy2krYSet0tZcApXRRRFPtqVSWygJ2Oi\nvMl99DEq1q7FPzmZiEXvoPLwaHuQthjyiFSA732v/WN1ACYlaAjwdGHJznNyS7F5zFHwhQMXh2Hk\ntnx2KfcIgnBEEIRPBUHQXOO9CIJwvyAIBwRBOFBSUmIG2fbHBz+fw9vViamDLNgmOXih5DK4932T\nLi9tKGXOtjnsytvFXwb9hScTnkQlOOY5pksRBIGhf32SJSOSUZ06Tta06ehylfbODkP+Qcj8qcXo\noOPZmPcO7M26W9bh7+bPgu0L2Jq19arX1zQ288mBXG7r15lQXwv9eQmC9N+j9DRkfG+ZZzgYc4fH\n0Nhs5GPFgKrjcehjaKySigyFNkk5X86R3CoW9Pcnd+5can/8kZC//pWQ555t24nTVDpFQd9JkgFV\nvbJr1RZuzmrmDIvmp9MlnCyolluOTWOON/MrHSS7dGn1ayBaFMV+wA5g9TXcK30oih+KopggimJC\nUHu2zO2U7LI6vj1awPTBUeY1OrgU3wjoc6+UadXGZJNZmcn0LdM5X3WeRWMWMeWGKZbTZaO4OKno\nOX0Sfx6ygKbiErKmTKXh6DG5ZSlYg31LpBbohDlyK5ENjbeGtRPX0juwN0/vfJrVx1f/7lmKzQdy\nqW3SM3eYmc/uXUrvuyUDKmWF3CRuCPVheNdA1uzNUgyoOhJGA+xbDBGJoEmSW41dsGzXebobq0l4\n4/9oPHWK8EXv4D9juvkfNPxxaK6X2m0V2mTm4Gg8XdR8oOzyXRVzFHy5gOaif48AfhOMIYpimSiK\nrYeclgHxpt6rIPHRrvM4qVTMHRZt+YcNfRSa6+DA8t+95FDxIWZtnUWToYmVE1YySuMYYdPXw7RB\nkWR27s7m5BdQubiQPWsWtTt3yi1LwZLUFEqtzwOmg5uv3Gpkxc/Nj2U3LWN81HjeOPAGr6a8ells\ng8EosmrPeRKjO9E3wsJ/Xk4uMOh+yYCq6IRln+UgzBseQ1F1E98cLZBbioK1OP0NVGQpu3smkllS\ny/l96bz207sYKyuIXLkCn/HjLfOw4J7QbYL0DqZX/AHawtfDmemDo/j6cD7asutzj+4ImKPgSwW6\nCYIQIwiCCzAF+OriCwRBCLvoX+8ATrb8fhtwkyAInVrMWm5q+UzhIkprm9h8IIe748IJ9rFC61ho\nH+gyDvZ/CM2Nl329M2cnC7YvwNfFl7W3SKv7HRlfd2emJEWytkCF67JVuMREk/PQw1T+979yS1Ow\nFAdWgFEPgx6QW4lN4Kp25Y1RbzCz10w+PvUxf9r5J5oMv76o7DhZRE55g+V391qJnwNO7tIOhkKb\njOoeRGyQJ8t/Oa+43XUU9i6W3IVvuE1uJXbBllVf8vqu9/FwdyV6/To84uIs+8DBD0JdibSwqNAm\n84bHoFYJrNh9Xm4pNku7Cz5RFPXAI0iF2klgsyiKxwVBeEkQhDtaLntMEITjgiAcBh4DZrfcWw78\nA6loTAVeavlM4SLW7MlCZzCyYKSFjA6uxLA/Ql0xHNn4m4+/OPsFf/zxj8T6xbJm4ho03prfGaBj\n0Woxv/pkDVFr1uCRlEjBs89RtnyFzMoUzE5zo1TwdZ8gRQEoAKASVDyT+AxPJzzNDu0OFu5YSI1O\nsvtf8ct5wv3cGd8rxDpiPPxhwDQ4slkJYjcBlUpg7rAYjuZVcSC7Qm45CpYmNw20e6UYgA7iLtwe\n8j75nNEr/kljYAixmzfi2rWr5R8aOwYCe8D+JYoBlQmE+LhxW7/OfJqWS01js9xybBKzuGuIoviN\nKIrdRVHsIoriKy2fvSCK4lctv39OFMXeoij2F0VxjCiKpy66d4Uoil1bfq00hx5HorHZwNp92dzY\nM4QuQV7We3DMSAjrL0U0GI2IosiyI8t4Yc8LJIUmsWLCCgLcA6ynx8YJ93Pntn5hbEjRUqt2RbN0\nKd4Tb6b43/+m6LXXEY3K2RiH4dhn0srrIMXG/ErM6j2Lfw7/JweLDjJ321x+ycxk//lykodG4aS2\noqHT4IfAoIPU329NV/iVe+Ii8PNwZvkuZYXc4dn7Hrj6QNxMuZXYNKIoUrZ8OdXP/4XjATEEr1iF\nc4iVFq0EQeogKTgMOfut80w7J3loNLVNej5LU8zzrkTHsFO0Y746nE9FfTNzrHF272IEAYY+BmUZ\nGE79j3+l/ItFBxdxS8wtLB63GE9nT+vqsQMWjIilTmdgQ4oWlYsL4W++Safp0ylfuZL8Z59FbFZW\nneweUZRWXIN6QuxoudXYLLd3uZ13x71LdnU2T/6yAA+PCu5LsKC78JUI7Ardb1aC2E3E3UXNtKRI\ntp8oJKdcOQfjsFRq4cSXEJ8Mrt5yq7FZRKOR4ldfpfjfb7AvKo4dyc/RLTas7RvNSf8p0hnxfUus\n+1w7ZYDGjwEaP9bszcZoVHZFL0Up+GwYURRZvSeLHiHeDImVYTet153ofCJ4JvUVNpzawKxes/jX\niH/hrLagS6gd0yfcl2FdA1i5+zw6vRFBpSLkr38h6PHHqf7qa3IWPoSxrk5umQrtIXsPFB6VVl6F\nK5kMK7QyPHw4bwxfQr2+Fo/oJeQ1nLW+iCEPQ32p1Nqp0CazhkSjEgQliN2RaXV+TFLOH/8eYnMz\n+c8+S/nqNZTcdCcvDZjC3DE9rC/ExVMKYj/5NVQpu1amMGdYNJmldfx8tmPGt10NpeCzYdKyKzie\nX03y0GgEGV4uaw2NLAzvzHbqearHTJ5OfLrDZOxdLwtGxFJU3cSWo5LZrCAIBD74AGEv/4O6PXvI\nnj0HfblyTNVu2b8E3DtBv/vkVmIXpJ/1pj7rQXxcPZi7bS77C6zcmhQ9AkL7wj4liN0UQn3duLVf\nGJsP5CjnYByRxmopcqn3XeCnnL+/EsbGRnIffYzqr74m8LHHeClqAr3C/RjSRaYjLIkLAFHqVFBo\nk4l9wgjydmXVniy5pdgcytu7DbNyTxY+bk7cObCz1Z9d0VjB/O3zSWsq5p+lVcwuLbS6BntkZLcg\nYgM9WbM3+zef+917LxHvvUvTmTNkT5tOc76SPmJ3VGTDqS0QlwwuHnKrsXma9AbW7ctmdGwfNty2\njjDPMBbuWMi2LCsaMQsCDH4YSk7BOSWI3RTmDY+htknPptQcuaUomJuDa6GpWtr5VrgMQ3U12vnz\nqd25k9C/vcixsfeQUVLHghGxsiy6A1IQe49bpCB2pTW9TVycVMwYFMVPp0vILKmVW45NoRR8Nkph\nVSNbjxVyX6IGDxfrumgV1hWSvDWZjMoM3h7zDrfH3gqHN0JjlVV12CMqlcDMIVEc1FZyJLfyN995\njx1L5Irl6MvKyJo+g6ZMxRzBrkhdBgiQtEBuJXbB14cLKK3VMXdYDCGeIay6eRV9Avvw9M6n2Xza\nii2Wfe5pCWJXIhpMoV+EH4nRnVi1JwuDcg7GcTDoYd8HEDkUwi0cKWCH6EtKyJ6VTMPhI4S/9Sad\npkxh+S/nCfWRdr1lZfBCaKhQWtNNZNqgSJzVwmUL7x0dpeCzUdbvz8YoiswcHG3V52ZVZTHr21kU\n1xez5MYljNaMlkKMm+vg0MdW1WKv3BMfgYeL+oqTjUd8PFFrViPqdGTPmEHD8eMyKFS4ZnR1UitU\nrzvAN0JuNTaPKIqs+OU83UO8GNZVaoXydfVl6filDA8fzj/2/YMVx6wUWeLkAknz4dwPShC7icwb\nHkNuRQPfnVA6OxyGU19DlVbZ3bsCutxcsqbPQJedjWbJEnwmTuRcSS2/ZJQyY3AkztZ0F74SUcMg\npK90/lJpTW+TIG9XbuvXmU+U1vTfoBR8NkiTXnJ6HHdDMJEB1msdO1V+iuStyTTqG1kxYQWJoYnS\nF50HQkQipCwDJV6gTXzcnLk7LpyvDudTXqe77Hu3nj2JWrcWwc0VbfJs6g8ckEGlwjVxeIO0wz1o\nodxK7IL958s5UVDNnGExv2mFcndy550x7zAxeiL/SfsPb6e9bZ2g7/i5LUHs71v+WQ7A+F6haPzd\nWf6L0oXgMOz/EDpFQ4+JciuxKRpPnyF76jQMVVVErVyB1/BhAKzdm42zWuC+RCu7C1+J1oiG4uOQ\ntUtuNXbB7KHR1OkMfKpENFxAKfhskC1HpFao5KHRVntmelE6c7bOwUXtwqqJq+gV0Ou3FyQ9AOXn\nIPMHq2myZ2YNiUanN7L5wJXPwbjGxBC9fj1OwcFo50lnBhRsFKNRWlntPBA0SXKrsQtW/HKeTh7O\n3DUw/LLvnNXO/GvEv5jUfRLLjy3n5X0vYxQtvJDkGSBZnB/9BOoV06S2UKsEZg+NITWr4rLWdAU7\npOg4aPdAwjxQqeVWYzPUHzxI9syZIAhEr1uL+4ABANS1ZLnd0lcyALEJ+k4Cj4BfXVYVrkp/jR8D\nI/1YvSdLiWhoQSn4bJDVe7LoEuTJ8K6BVnnez7k/88B3DxDoHsiam9cQ6xt7+UW9/gCewdIqoUKb\ndA/xZnCsP2v3Zv/uORjnsDCi1q3FtUsXch5+hKr/bbGySgWTOPcDlJ6RdveUKIY20ZbV893JIqYN\nisTN+covl2qVmucHP8/cPnPZfGYzz+16jmajhVtvEueDvhEOrbfscxyEyQkReLk6Kbt8jkDqR+Dk\nBgNnyK3EZqjbuxftvPmoO/kR9fHHuHbrduG7/x7Ko6ZJz6whUTIqvARnN4ifLRmHVWTJrcYumD00\nmqyyenYqEQ2AUvDZHAe1FRzOrbJaFMPW81v54w9/JMY3hlU3ryLM63cOJzu5SJPN2e1QnmlxXY5A\n8pBo8iob+OFU8e9e4+TvT+TqVXgMGED+009TsXGjFRUqmMT+JeAVIlmZK7TJ6r1ZqAWhzfPHgiDw\nRPwT/DHuj3xz/hue+PEJGvWNlhMW2gcih0DqcqU13QS83Zy5Nz6Cb44WUFrbJLccheulsQoOb5LM\nizz85VZjE9T88CM5DzyIS3g40evW4RLxayeCKIqs3ZtNrzAf4iI7yajyCiTOB0ElHa9RaJOJfcII\n9nZllZIrCigFn82xek8WXq5O3B1neWOIz89+zjM/P0P/4P4sn7CcAPc2cmYS5krtIKnLLa7NERjf\nK4QwXzfW7M266nVqb280Hy3Da+RICv/2d0o/VCZzm6HkDGTskFqhnFzkVmPz1Dbp2Zyaw639wgj1\ndTPpnvl95/P84Of5OfdnFu5YSK3OglbaifOh4ry0a6vQJjMGR9FsEH+3NV3BDji8STJdS5wvtxKb\noOp/W8h99FFce/Qgau0anIKCfvN9alYFpwprmDUkSr4oht/Dp7PUbZW+FpqUyIG2cHFSMWNwFDvP\nlHBOiWhQCj5borimkS1HC7g3XmqlsSTrT67nxT0vMjR8KEtuXIK3i3fbN/mEQc/bpSwfXZ1F9TkC\nTmoV0wdFsutsaZuTjcrNjYj33sXn1lspeestit+2kpmFwtVJWQpqF0iYI7cSu+C/B1tboaKv6b7J\nPSbz6ohXOVR8iPnb51PZaKFzYz3vAM8gJcTYRLoGezEkNoD1+7RKRIM9IrYEdneOU6IYgIrNm8l/\n+mk8Bg4kcuUK1H5+l12zZq+Uf/yHAZefP7YJBi+Epio4onQDmcLUpEhc1CrWKEHsSsFnS2zYn0Oz\nQbR43/hHRz/i1ZRXGRc5jkVjFuHu5G76zUkPSC0iSh6MSUxpmWzWmpAHIzg70/n11/C99x7KPlhK\n8auvKkWfnDRWw6EN0Ode8AqWW43NI4oi6/a1tkJd/iLVFrfE3sLbY97mbMVZ5m6fS2lDqflFOrlA\nXDKc2QoVSkaTKcwcEkVeZQM/nf791nQFGyVrF5SeVrJDgbKVqyh84UU8RwxHs+xD1F5el11TXC3l\nH09K0ODuYqPmNhGJkoHY/qVKa7oJSBENYXyalkt1B49oUAo+G0GnN7J+fzajugcRG3T5RGQORFFk\nUfoi3kl/h1tjb+WNUW/gor7GNrXIwVIeTMoyJQ/GBAK9XLmlbyifpeVS26Rv83pBrSbspZfoNHMm\n5avXUPji3xCVSV0ejrS0QiUprVCmkK6VWqFmDL7+VqhRmlG8N+49cmtymbN1DoV1FsiBi58tme+k\nrTL/2A7I+F4hBHu7sm6fUiDbHSnLwL1Thz5/LIoiJe++R/Frr+E9YQKa995D5X7lRe4NKTnojSIz\nB9uQWculCIJkIFZ6BjJ/lFuNXZDcGtFwoGNHNCgFn42w9XghxTVNzLZQFIMoiryW+hrLji7j3u73\n8s/h/8RJdR1to4IgBbEXH4fsPeYX6oDMGhpNTZOeLw7mmXS9oFIR8ufnCLj/fio3byb/2WcR9W0X\niwpmRBThwAoI6y+1Qym0ybp9WrxcnfjDgM7tGmdI5yF8cOMHlDSUMHvrbHJrzPxD2k8D3SdC+hrQ\nK2YkbeGsVjElKZKfzpSgLauXW46CqVTnS46OA2eC8zV08TgQoihS/NrrlC5ejO9ddxH+5hsILlde\n5G42/LroHh3oaWWl10jvO8EjUPoZpdAm/TV+xEX6sWZvx45oUAo+G2H1niyiAzwY1T2o7YuvEYPR\nwN/2/o31J9czs9dMXhj8AiqhHf/p+9wLbn7S+SaFNhmo8aNvuC9r9mSZ3KIpCALBTz5B0OOPU/3V\n1+Q9+RSi7vIQdwULod0HxScksxZbO7hvg5TX6dhypIC748LxNMP547iQOD666SNqdDUkb03mfJWZ\nowES50F9KZz4yrzjOihTkzSoBIH1Kcoun92QtgpEo2S21gERjUYKX3qJ8lWr6DR9OmGvvIzg9Ptz\n0/bjRRTXNNlWFMPv4eQqRWyc/lYq7BXaJFmJaFAKPlvgWF4VadkVzBwSjUpl3pfLZmMzz/3yHJ+f\n/ZwH+z/I0wlPt995ysUD4mbCyf9BlWm7Vh0ZQRCYNSSKs8W17M0su6Z7Ax98gJDnnqVm+3ZyHn0U\nY6MFbesVfuXAcnD1gb73yq3ELvjkQA46g5EZZmyF6hPYhxUTVqA36pm9dTZnKs6YbWxix4B/F0hV\nHHFNIczXnfE9Q/jkQC6NzQa55Si0haFZKvi6jQf/GLnVWB3RYKDgr89TuWEjAfPnEfLXvyCorv66\nu2ZvFhGd3Bndw07Oa8fPBtEgdSootMnEPmEEeLrw8X6t3FJkQyn4bIA1e7Nwd1YzKcG8UQzNhmae\n3vk0357/lifin+DhAQ+bz2Y4cb60eqi0FJjE7f0708nD2STzlkvxT04m9KW/U/fzLnIeeBBjneKQ\nalHqSuHEl9B/CrjYeGuPDWA0inycoiUp2p/uISa4/V4DPfx7sPLmlTgJTszdNpfjpcfNM7BKJe3y\n5eyHgiPmGdPBmTE4ivI6Hd8eK5BbikJbnPwaaosgseOZtYh6Pfn/9yxVn39O4EMPEfTUU22+95wu\nrGH/+XJmDI5CbeZFd4vhHwNdxkHaajAoRz7awsVJxeREDd+fLKKgqkFuObKgFHwyU9XQzNeHC7hz\nYGd83JzNNm6ToYnHf3qc77Xf81zSc8ztY+a2jk7R0P1maRVROQfTJm7OaiYnath+ooj8ymufbDpN\nnkzn11+n/sABtAvux1CrZMpYjIPrwKDrsK1Q18qujFKyy+qZPjjSIuPH+sayauIqvJy9mL99PoeK\nD5ln4AHTwMld2s1VaJOhXQKIDfS8rkUrBSuT+hH4RUHXcXIrsSqiTkfek09R/b//EfTEEwQ99qhJ\ni9xr92VJBUGCxgoqzUjiPKjJl1yHFdpkamIkIrAxpWPmiioFn8z892AeDc0GpiWZrxWqQd/AYz88\nxs+5P/PCkBeY1nOa2cb+DUkLpHMwJ7+2zPgOxoxBURhF8bpbCnxvv43wt96i4cgRtPPmYaiuNrNC\nBYxGSFsJUcMguKfcauyCdfuyCfB04eY+oRZ7hsZbw6qbVxHgHsD9393PgcID7R/UvRP0vUeKmGms\nav94Do5KJTB9cBTp2kqO5yt/XjZL0QnI3i0VAyobjRawAMamJnIf+yM127cT8tyzBD5wv0n31TQ2\n80V6Hrf364y/OcCpRgAAIABJREFU5zW6lstNtwng3VnptDKRyAAPRnYLYmOqFr2h47mfKwWfjIgt\nL//9InzpG+FrljHrm+t55PtH2Ju/l5eGvsSk7pPMMu4ViR0j7fQdWGm5ZzgQGn8Pxt0QwoYULU36\n6zsH4zPhJiIWvUPjiZNoZ8/BUGmhgOqOSuYPUJGl7O6ZSF5lA9+fLGJyogZXJ8u+XIZ6hrJywkrC\nPMNYuGMh+wr2tX/QxPnQXA+HlRBjU7g3LgI3ZxXr9nXcczA2T+pHoHaV3Dk7CMaGBnIfepjan34i\n9MUX8E9ONvnez9PzqNMZ7MOs5VLUThCfDOe+h3IzG1s5KNMHRVJU3cQPpzperqhS8MlIWnYFp4tq\nmJZknlaoWl0tC3cs5EDRAf454p/c1c3C2TsqlRRinP0LlJjRUMGBmTE4krI6HduPF133GN5jx6J5\n712aMjLITp6NvrzcjAo7OKkrJLvrnrfLrcQu2JiiRQSzzWFtEeQRxIoJK9D4aHjk+0fYnbe7fQN2\nHgjh8dJLspIr2ia+Hs7c0b8z/z2Y1+FDjG2SxmopP7TPPeDhL7caq2CsqyPngQep27OHsFdeptPU\nqSbfK4oia/dl0z/Cl/4aPwuqtCBxs0BQS50pCm0y9oZgQn3cWN8BzVvMUvAJgnCzIAinBUHIEATh\n2St8/6QgCCcEQTgiCML3giBEXfSdQRCEQy2/OpRH9sf7tXi7OnF7//blVgFU66p54LsHOFJyhNdH\nvs5tsbeZQaEJDJwBKiclxNhERnYLIqKTe7udorxGjSJiyfvosrPJnjULfUnHtRo2G1W5cOZbyYHW\nyVVuNTZPs8HIxtQcxvQIRuPvYbXnBrgHsPym5cT4xvDoD4+yM2dn+wZMXCCFGJ//2TwCHZyZg6Np\naDbwRbri0GxzHNkEulpImi+3EqtgqK1Fu+B+6tPS6Pz66/jdc8813b83s4yM4lpmDom2jEBr4NMZ\nekyUzp4rfgpt4qRWMSVJw89nO16uaLsLPkEQ1MBiYCLQC5gqCEKvSy47CCSIotgP+BR4/aLvGkRR\nHNDy64726rEXKup0/O9oAXcObH9uVVVTFQu2L+BE+QneHP0mE6InmEmlCXgFww23weGPobljOh9d\nCyqVwNSkSPZmlpFZ0j7jFa9hw9AsXUpzfgHZs5JpLrr+XUMFJHtrUZTsrhXaZPvxIkpqmphhIbOW\nq9HJrRMf3fQR3Tt1v2BOdd30vks6z5f6kfkEOjB9I3zpH+HL2n3ZJueKKlgBUZT+DrfuWjs4hpoa\ncubNp+HIEcLffBPf2699kXv9fi2+7s7c1i/MAgqtSOI8qC9T/BRM5L5EDQKwIbVj7fKZY4cvCcgQ\nRTFTFEUdsBH4w8UXiKL4oyiKraX0PsC8+QN2yGfpuej0RqYNat/LUnljOfO2zSOjIoN3xrzD2Mix\nZlJ4DSTMgYYKycpeoU0mJUTgpBLYmNp+pyjPQUlELvsQfXEx2TNn0ZyvhLBeF4Zmyd66643SuVSF\nNlm3L5twP3dGdZcnt8rX1ZdlNy2jV0Av/vTTn9iWte36BnJ2k847ndqihBibyIzBUWQU17IvU2kn\ntxmy90DJKelcqoNjqK5GO28+DSdOEPH2f/C5+doXuUtrm9h+vJB74iJwc7Zzc5uY0dApBlIVx2FT\nCPN1Z1zPEDan5qDTdxzzFnMUfOHAxW+uuS2f/R7zgG8v+nc3QRAOCIKwTxCEO3/vJkEQ7m+57kCJ\nnbeviaKUWxUX6UfPMJ/rHqesoYx52+aRVZ3Fu2PfZWTESDOqvAaiR0ohxop5i0kEe7txY88QPk3L\nvW7zlovxiI8ncvlHGCoqyJ45C12u0mp1zZz+BmoLFbMWE8kormVvZhnTBkXKmlvl7eLN0huX0i+o\nH8/8/AxbMrdc30AJc6Rc0bTV5hXooNzevzO+7s6s269ENNgMaSvB1Rd63y23EotiqKxEO2cujSdP\nEvHOO3jfeON1jfNZWi7NBpFpg+wsiuFKqFTSHKbdA8Un5VZjF0wfJPkpbDteKLcUq2GOgu9KP+2v\n2OchCMIMIAH490UfR4qimABMA94WBKHLle4VRfFDURQTRFFMCAoKaq9mWdmXWU5mSR3TB12/K1Rp\nQynzts0jtyaX98a9x9DwoWZUeI2oVFIbXM4+ZbIxkWmDIimv07H1mHkmG/cBA4hcsUI60zBrFrrc\nXLOM22E4sAJ8IqC7Fduh7Zj1+7NxVgvclyj/y5KXixdLblxCfEg8z+16jq/PXUdbk38sdBkLB9cq\nIcYm4OasZlJ8BNuOFVJc3Si3HIX6cqnDpv8UcLHeeVpro6+oIHvuXJrOnCHi3UV4jx1zXeMYjSIb\nUrQkRfvTNdjbzCplYsAMULsoEQ0m0uqnsL4DLVqZo+DLBS7+qR8BXNYXIwjCjcBfgDtEUbxwslQU\nxfyWf2YCPwEDzaDJplm/Pxtfd2duvc6+8dZiL78un8XjFjM4bLCZFV4HA6a3TDbKLp8pDO8aSKS/\nR7vNWy7GvW8fIlcsx1BXR/asWehyOma46DVTdg4yf5IWLTpQbtX10qAz8FlaLjf3CSPQyzbMbTyc\nPVg8bjGDwgbxl1/+wpcZ19FenjAHqvMgY4f5BTog0wdHoTeKbDJDa7pCOzm8AQw6yaLfQdGXl6Od\nPQddxjki3l+M9+jR1z3WvswyssrqmeoIu3uteAZArzuliBldndxqbB6VSmDaoEj2ZZaTUdw+PwV7\nwRwFXyrQTRCEGEEQXIApwG/cNgVBGAgsRSr2ii/6vJMgCK4tvw8EhgEnzKDJZimtbWLb8ULujgu/\nrr7xkvoS5mydQ0FdAYvHLSYpLMkCKq8DzwDoeUfLZNOxnI+uB5VKYEqShv3nzTvZuPfuTdTKFYh1\n9VJ7p7ZjHUq+Lg6skJxm4zpOblV7+PpwPtWNema08/yxuXF3cufdse8yOGwwz+9+ni/OfnFtA3S/\nGbxCFMdhE4kJ9GRY1wA2puZgNCrmLbIhitLf2YgkCOkttxqLoC8rQ5s8G11WFhFL3sdrxIh2jbc+\nRTJrmdjHzs1aLiVhLjRVw7HP5FZiF0yK1+CsFsy68G7LtLvgE0VRDzwCbANOAptFUTwuCMJLgiC0\num7+G/ACPrkkfqEncEAQhMPAj8Croig6dMH3yQGpb3z6dbwsFdUVMXfbXIrri1ly4xISQxMtoLAd\nJMyBpio4fo0vWh2USfEanFQCG1LMO9m49epF5OpViI2NUtGXlWXW8R2K5gY4tB5uuBW8Q+VWYxes\n359Nt2AvkmJsL+fLzcmNRWMXMaTzEF7c8yKfn/3c9JvVzlLMzNltUKWcgzWFKYmR5FU2sCujVG4p\nHRftXilWxEHdhfWlpWQnJ6PLyUGz9AO8hg1r13gOZdZyKZGDIbiXYt5iIkHerkzoHcqnaTk0Nrff\nT8HWMUsOnyiK34ii2F0UxS6iKL7S8tkLoih+1fL7G0VRDLk0fkEUxT2iKPYVRbF/yz8d+m/phb7x\nmGvvGy+sK7xQ7H0w/gPiQ2zQdjlqGAR2VwJATaR1svksPdfsk43bDTdIRZ9OR/asZJrOnzfr+A7D\n8f9KDrMJ8+RWYhccz6/icG4V0wZFIgjymbVcjdaib2j4UF7c8yKfnvnU9JvjZknmLQfXWU6gA3FT\n7xD8PV3Y0EFWyG2StFUtZi13ya3E7OhLSshOnk1zXj6aD5fiObj9x1c+dSSzlksRBGmXr+AQ5KXL\nrcYumD4oiupGPf87UiC3FItjloJPwTR+yShFW15/zbt7rcVeWWMZS8cvZWCwjR5zFASInwO5qVB4\nVG41dsG0QZFU1jebzbzlYtx69JCKPr0e7axkmjKVou8y0lZKDrMxMjnc2hkbU3JwdVJx18CrGTHL\nj6valXfGvMPw8OH8fe/f+eTMJ6bd2ClaMm9JXwNGx1/xbS+uTmrujY9gx8kiimsU8xarU18uLVr1\nm+xwZi0Xir2CAiI/XIpnUvuPrxiNIhsdzazlUvpNBmcPOODQ+ydmY3CsP7FBnh3CvEUp+KzIx/u1\n+Hu6cHMf01vHCmoLmLN1DhWNFSwdv5QBwQMsqNAM9J8CalfFvMVEhsQGEBVgXvOWi3Hr3p2o1asQ\njUayk2fRdO6cRZ5jlxSfhJz9UiuUje5W2RL1Oj3/PZjHLX3D8PNwkVtOm7QWfSMjRvLS3pfYfHqz\naTfGz4bqXMhoR5h7B2JKoga9UeTTNMUZ2Ooc3giGJuk4hQPRXFwsFXuFhUR+uBSPRPMcX9nbYtbS\n3vxjm8bNF/pOgqOfQUOl3GpsHkEQmD4oioPaSk7kV8stx6IoBZ+VKKpu5LuTRUyKj8DVybS+8YLa\nAuZum0tlUyUfjv+Q/kH9LazSDHj4S60lRzZDU8dwPmoPKpXA1KRIUrLKOVtUY5FnuHbrRtTqVSBC\ndvJsmjIzLfIcuyNtNaicYcA0uZXYBVuOFFDTpGdqkv28LLmoXfjP6P8wKmIU/9j3Dzae2tj2TT1u\nAc9gxbzFRGKDvBgc68/GFMW8xapcMGtJdCizlubiYrSz5/xa7CUkmG3sj1O0+Hk4X9Oiu10SPxv0\nDXDUxM6GDs49ceG4OqkcfpdPKfisxObUHAxG0eSXpdY2ztZir29QXwsrNCMJc0BXozhFmci98RGS\nU5SZzVsuxrVrV6noA+lMX0cv+pob4chGyazFM1BuNXbBhhQtXYI8SYzuJLeUa8JF7cJbo99itGY0\nr+x/hU2nNl39BrUzDJwOZ7ZC9WUJQwpXYGpSJNryevacK5NbSsdBuw9KTzuUWUtzcTHai3f2zFjs\nObRZy6V0HgihfSF9tbQwoHBV/DxcuK1fZ748lE9dk+PmsCoFnxUwtJi1DO8aSHSgZ5vXF9YVMmfr\nHPss9gA0gyCop2LeYiKBXi3mLWnmN2+5GNcuXX4t+pI7eNF38mvJrMWBXpYsyenCGtK1lUxNsl2z\nlqvhonbhrVFvMTpiNC/vf7nt9s64WSAa4OB66wi0cyb0DsXPw5kNqYp5i9VIWwWuPg5j1nKh2Csq\nInLZh2Yt9uBXs5apSQ5o1nIpggBxyZKXQv5BudXYBVOTNNQ26dniwOYtSsFnBX4+U0J+VaNJfeN2\nvbPXiiBIu3z5B5XJxkSmDYqkutHyk41rly5ErVrZ0t7ZgYu+tFXgFwUxo+RWYhdsSNHiolZxd1yE\n3FKuG2e1M2+OfvNCe+dViz7/WIgdrZi3mIibs5p74iLYfryQ0tomueU4PvXlUvxRv8ng0vYisq3T\nXFyMdlYy+tZiL968LuQdwqzlUvpNBid3aZdPoU3iozrRNdjLoRetlILPCmxI0RLg6cKNPUOuel1r\nsVfRWGG/xV4r/e6TJhvFvMUkhsQGEBvoadG2zlZcu3aVij6j2FL0dTD3ztIMyP5F2sVRKVNgWzQ2\nG/jiYB4T+oTi72n7Zi1Xo7W906SiL342VGnh3I9W02fPTE3S0GwQ+Uwxb7E8RzZJZi0O0KFwodgr\nLkZjgWIPOohZy6W4+UKfu+Hop4qfggkIgsCURA0HtZWcKnRM8xblbcfCFFc38v2pYu6Nj8DF6ff/\nuC8u9paOX2rfxR6Au5802Rz7TJlsTEAQJPOWtOwKThdaxrzlYi6c6TOKaDta0Ze+GgS1FLKt0Cbf\nHiugqqGZqYmO0QrVWvSNjBjJP/b94/cjG3rcCh6BSmu6iXQN9iYxuhMbUrSIyrkhy9Fq1hKeIJ3T\nsmP0JSVSG6cFiz3oQGYtlxKXDLpaxU/BRO6Oi8BFrWJjSo7cUiyCUvBZmE/ScjEYRe67ysvSpcVe\nv6B+VlRoQZTJ5pq4J16abDZYYZcPfi36RKOx4xR9eh0c+hh6TATvDvbD/zrZsD+H6AAPBscGyC3F\nbLS6d7ZGNlyx6HNykcxbTn8LNebPyXREpiZFklVWz95MxbzFYuTsh5JTdr+7py8tlaIXLNTG2UqH\nMmu5FE0SBN2gtHWaiL+nCxP6hPJ5umX9FORCKfgsiNEosik1h0Ex/sQGeV3xmqK6IuZtm+d4xR4o\nk801Isdk09reeaHoO+/gRd/pLVBfKi1GKLRJRnEtKVnl3JcYiUplf2YtV6O16BsRPoKX9r7Ep2c+\nvfyiuOQW85Z11hdoh9zSNwwfNyeHXSG3CdJWgYu31EFjp1wo9lrdOC1U7EEHM2u5lFbzlrw0KDwm\ntxq7YGqihupGPd8eczzzFqXgsyB7M8vQltf/bhRDcX0x87bPo6yxjA/Gf+BYxR4ok811IMdk49qt\n20VF32x0WVlWe7bVSVsNPhHQdZzcSuyCjSlanFQC98bbr1nL1XBRu/CfMf9hePhw/r7373x25pJu\nhIAuEDNSWrQyGuURaUe4Oau5Oy6CrccKKa/TyS3H8WiosHuzFn1ZGdmzZ9Ocn4/mgyVmd+O8mAtm\nLTEdyKzlUvpPAbWrsvBuIoNjA4gK8GCDAy5aKQWfBdmQosXX/cp94yX1JczbNo+S+hI+uPED+whV\nvx76TwG1i+R2p9Amck02rt26EblyBWJzM9nJs9FpHdCpqvw8ZP4IcTNB1cFae66DJr2Bz9JzGd8r\nhCBvV7nlWAxXtStvj3mbYeHD+Pvev/PF2S9+e0H8bKjUSn93FNpkalIkOoORz9MV8xazc3gT6Bvt\ntp1TX16OdvZsmnPz0HzwAZ5JSRZ93r4Ws5YOubvXioc/9LpD+rujq5dbjc2jUgncl6gh5Xw550oc\ny39CKfgsRHmdju3Hi7hrYPhlfeOlDaXM2z6PovoiPhj/AQOCB8ik0gp4+EPPO6SQ6+YGudXYPBdP\nNplWnmzcuncnctUqxKYmqejLcbAVroNrQVApZi0msu14ERX1zb/boeBIuKpdeWfMOwzpPIQX97zI\nlxlf/vrlDbeBR4DUSqfQJj1CvYmL9ONjxbzFvFwwa4mHMPvrBpKKvTnocnLRfLAEz0GWLfYANqbm\n4OPmxMQ+YRZ/lk0TlwxNVXDiy7avVeDe+AicVAKbUh3rHUgp+CzE5+m56AzGy16WShtKmbdtHoV1\nhSy5cQkDgwfKpNCKxM2Cxio48ZXcSuyCe+MiUMs02bj16E7kqpWI9fVkJyejy82zugaLYGiWQrS7\njgdfx2xPNDcbU7REdHJneNdAuaVYhdaib1DYIJ7f/Txfn/ta+sLJFQZMg9PfQE2RvCLthKlJkWSW\n1JGaVSG3FMchNxVKTko/T+0MfUUF2jlz0WVno1nyPp6DB1v8mRV1OrYeK+TujmjWcinRw8G/i9LW\naSLB3m6M6xnMZ2m56PSO08qvFHwWQBRFNqbmMDDSjx6hv/aNlzWUsWD7AgrqClg8bjHxIZY7qGxT\nRI+ATjHKZGMiwT5ujLshmE9lmmzcbriByFUrMdbVo501i+Y8Byj6zmyD2kKIV8xaTOF8aR17zpUx\nJVHjcGYtV8PNyY1FYxeRFJrEX3f/lS2ZW6Qv4maDUQ+HP5ZVn71wW7/OeLs5Wc1xuEOQvhqcPaHP\nPXIruSYuFHtZWVKxN2SIVZ77+cE8dAbjVR3SOwyCIP3s0+6FktNyq7ELpiRFUlan47sTjrPIpxR8\nFiAtu4KM4lqmJv66u1feWM787fPJrcll8bjFJIYmyqjQyqhU0qpk9m4p9FqhTaa2TDbfn5RnsnHr\n2ZPIFcsx1NaSPSuZ5vx8WXSYjfTV4BUK3SbIrcQu2JiqRa0SmJTQ8V6W3J3ceXfcu8SHxPPnX/7M\nt+e/hcCuEDVMOoustCm2ibuLmrsGhrPlaAGV9Yp5S7tprIZjn0Pfe8DVfsxHDJWVaOfNQ5eZScTi\nxXgOHWqV54qiyKZULf01fvQM87HKM22e/tNA5az4KZjIyG5BhPu5szHVcRatlILPAmxIycHL1Ylb\n+0l94xWNFczfPp+cmhzeG/dexyr2WhkwXQq7Vnb5TGJk9yDCfN3YIGMPuXvv3kQuX46hulqy0C6w\nU5viyhzI2CGd3VM7ya3G5tHpjXyWlsvYG4IJ8XGTW44suDu5897Y9xgYPJDndj3H1qyt0qJVeSZk\n/SK3PLtgSmIkOr2RLw46QIeA3Bz7FJrrpZ1mO8FQXY123nx0ZzOIeO9dvIYPs9qz07WVnCmqZaqy\nu/crXkFwwy1SDq2+SW41No+04BnBrrOl5JQ7htmNUvCZmaqGZrYczef2/p3xdHWisrGSBdsXoK3W\n8u7YdxkUNkhuifLgHSKFXR/6WAq/Vrgqrbsru86WyDrZuPftQ+TyjzBUVFwIybU7Dq4D0Si5cyq0\nyY6TRZTW6jq2sx3g4ezB++Pep39Qf579+Vm2e3mBq6+yaGUivTr70C/Cl40pOYp5S3tJXwPBvSE8\nTm4lJmGoqUE7bz6NZ84QvugdvEaOtOrzN6Zo8XRRc3v/zlZ9rs0TlwwN5XDya7mV2AWTEzSoBBzG\nvEUp+MzMV4fyaGw2MjVJQ1VTFfd/dz/nq86zaMwihnS2Tu+6zRKXLIVen/5GbiV2weQEyVzkkwPy\nTjbu/fpJRV9ZGdpZyTQXFcuq55owtoRmdxkLnaLlVmMXbEzNIczXjVHdg+WWIjsezh68f+P79Avq\nx//tfp7ve4ySzKfqy+WWZhdMSYzkdFENh3Iq5ZZivxQcgfyD0hkswfbP0xpqa8mZv4DGU6eIeOdt\nvMeMserzaxqb+d+RgguL7goXETsG/CKVRSsT6eznzqjuQWw+kIPeYP/mLUrBZ0ZEUWRDSg69wnyI\nChK4/7v7yajM4O0xbzM03Dq96zZN13FS6LXSQ24SEZ08GNEtiM0HcjEY5V0hd+/fH82yZehLSqQc\npWI7KfoyvofqXGmxQaFNcsrr2XW2hEkJGtQdyKzlang6e/L+uPfpHdibP9Ue5QdXFRzZLLcsu+D2\n/mG4O6vZ6IAhxlYjfY0UnN13ktxK2sRQW0fOgvtpOH6c8LfexHvsWKtr+OpwPg3NBqZ0gDiZa6bV\nT+H8z1J7ukKbTEmKpLimiR9O2ck7z1VQCj4zcjSvihMF1dwd78/CHQs5U3GG/4z+DyMiRsgtzTZQ\nqaVzVOd+gIpsudXYBVMTNRRWN7LzjPyTjUfcQDTLPqS5qAjtnLnoS0vlltQ26avBIxB63CK3Erug\ndTe5dXdZQcLLxYslNy6hZ0AvngoOYufh5Yp5iwl4uzlze/8wvj6ST22TXm459oeuXlpc6PUHKdPW\nhjHW1ZHzwAM0HDlC+Jtv4jN+vCw6NqbkcEOoN/0jfGV5vs0zYIbkp5Cm7PKZwtgbggnydmWjA7R1\nKgWfGdmQkoObi44dla9wsuwkb416i1GaUXLLsi1aQ68PrpNXh50wrmcIgV4ubLCRFXKP+Hgil35A\nc34+2jlz0JeVyS3p96kphNPfwoCp4OQitxqbx2AU2XwglxHdgojo5CG3HJvD28WbD8Z/QA/3EJ5w\nbWDX4ZVyS7IL7kuMpF5n4OvDdu70KwcnvpQCs208TsZYX0/OAw/ScOgQ4W/8G58JN8mi41heFUfz\nqpiSqEGwg/ZXWfAJg+4TJD8FQ7PcamweZ7WKSfER/HS6mIKqBrnltAuzFHyCINwsCMJpQRAyBEF4\n9grfuwqCsKnl+/2CIERf9N1zLZ+fFgTBbj3T65r0fHX4HEHd1nK6/CRvjHqDMZHW7V23C/w0Umvn\nwXVgUFZ828LFScU9cRH8cKqY4upGueUA4JGYiGbJEnQ5udJOX4WNhisf+hhEg9LOaSI7zxRTWN2o\nONtdBR8XH5bespquzQYeP/w2u/N2yy3J5omL9KN7iJdDrJBbnfQ1UmB2lPUcLq8VY0MDOQsfoj49\nnc6vvYbPxImyadmUmoOrk4q7BiodClclLhnqiuHMVrmV2AX3JWowirA5NVduKe2i3QWfIAhqYDEw\nEegFTBUEodcll80DKkRR7Ar8B3it5d5ewBSgN3Az8H7LeHbHF4cyMYYup9qYyWsjX2Nc1Di5Jdku\ncclQky9Z5Su0yX2JGgxGkU/SbGey8Rw8CM2S99FlZ9tm0Wc0Si9LUcMgsJvcauyCjSk5BHq5MK5n\niNxSbBpf73A+DBxBjK6ZP/74GHvz98otyaYRBIEpiZEczqnkZEG13HLsh5IzoN0jnbmy0d0qY2Mj\nOQ89RH1KCp1f/Re+t90qm5YGnYH/Hsrjlr5h+Ho4y6bDLuh6I3iHKW2dJhIV4MlT47szrGuA3FLa\nhTl2+JKADFEUM0VR1AEbgT9ccs0fgNa/WZ8C4wRpv/0PwEZRFJtEUTwPZLSMZ1c06htZdPw5nNyz\neXXEv7gpWp52Bruhx0TwDFbMW0wkNsiLQTH+bErNwSizecvFeA4ZQsTixegyM9HOm4ehqkpuSb+S\n/QtUnJdelhTapLi6ke9PFXNPXAQuTkqnf1v4JSxgWUEhkU4+PPbDY+wv2C+3JJvmroHhuKhVbExx\nnBBji5O+GlROMGCa3EquiLGpidyHH6F+337C/vVPfO+4Q1Y93xwtoKZRz31Kh0LbqJ2k4zUZO6DK\ndhaSbZlHx3UjIdq2z9G2hTl+socDF/dq5LZ8dsVrRFHUA1VAgIn3AiAIwv2CIBwQBOFASUmJGWSb\nDxVOhHlE84fwPzExVr52BrtB7Sz9EDuzVTpnpdAmU5Mi0ZbXszfTts7MeQ0fRsR776I7m4F27jwM\n1Taygp+2Gtx8JbMDhTb5JE1yglVelkwkIoFOAT34qNpIhHcEj3z/CKmFqXKrslk6ebpwc59QvjiY\nR2OzQW45to9eB4c3SIujXrYXj2LU6ch99FHqdu8m7OWX8bvzTrklsTFVS0ygJ4Ni7Pul3GoMbMml\nVfwUOgzmKPiu1Gtw6TbE711jyr3Sh6L4oSiKCaIoJgQFBV2jRMvi4uTEl1Pe5OXxym6CycTNks5X\nKZONSdzcJxQfNyebPAfjNXIk4e8uovHMGbTzF2CoqZFXUH05nPwK+t0Hzu7yarEDjEaRzQdyGBTj\nT2yQl9xy7ANBgPhk/PMPsWzAU3T26szD3z9MWlGa3MpslimJGqob9Xx7rEBuKbbP6S1QXwZxs+VW\nchlGnY5MENYiAAAgAElEQVS8Rx+j7uddhP7jJfzuuVtuSWQU15CaVcF9ilmL6XSKgtjRkL5WyqtV\ncHjMUfDlAhcvC0cAl9pxXbhGEAQnwBcoN/FeBUckoAtEj5DaOo32H2hpadyc1dwdF8G2Y4WU1+nk\nlnMZ3qNHE/HO2zSePEnO/AUYamvlE3NkExh0SjuniezLLCO7rJ4pScru3jXR7z5QuxB4/EuWT1hO\niEcID+14iIPFB+VWZpMMjg0gKsBDyeQzhfQ14KuBLrZl/CbqdOQ9/gS1O3cS+re/0WmSbWQDbkrN\nwUklcE+cYtZyTcQnSzm1536UW4mCFTBHwZcKdBMEIUYQBBckE5avLrnmK6DVKu9e4AdRFMWWz6e0\nuHjGAN2AFDNoUrAH4pKhMhvO75RbiV0wJUmDzmDk83Tb7Ln3HjuW8LfepOH4cXIW3I+hts76IkRR\naufsHAehfa3/fDtkY2oOPm5OTOwTJrcU+8LDH3reAUc2EejkyfIJywnyCGLhjoUcLjkstzqbQ6US\nmJygYf/5cjJLZFwQsnUqsqUX8IEzpOxaG0Fsbibvqaeo/eEHQp7/K52m3Ce3JACa9AY+S89jfK8Q\ngrxd5ZZjX/S4VcqpTV8ltxKb5wftD5Q3lssto120u+BrOZP3CLANOAlsFkXxuCAILwmC0HqKdzkQ\nIAhCBvAk8GzLvceBzcAJYCvwsCiKyt5yR6Hn7eDeSTqcrtAmN4T6MEDjx8bUHEQbDX32GT+e8Dff\npOHIEXIeeABjnZWLvtxUKDlp87lVtkJFnY6txwq5Oy4CN2fbebm0G+KTobEKTnxFsEcwy29ajr+b\nPw9+9yBHS47Krc7mmBQfgVolsMkGW9NthoNrpX+2ZtbaAKJeT96fnqbmux2E/PnP+E+fLrekC3x3\noojyOp1y/vh6cHKRcmpPfwu1xXKrsVm2ZG7hiZ+e4P1D78stpV2YxY5NFMVvRFHsLopiF1EUX2n5\n7AVRFL9q+X2jKIqTRFHsKopikiiKmRfd+0rLfT1EUfzWHHoU7ARnN+g3BU7+D+pK5VZjF0xN0pBR\nXEtato3FIFyEz4SbCH/j3zQcOkTOgwsx1tdb7+Hpq8HZE/rcY71n2jGfH8xDZzAqL0vXS9Rw6BRz\nYdEqxDOEFRNW4OfqxwPfPcDx0uMyC7Qtgn3cGHdDMJ+l56LTK638l2HQw8H1km2+r220J4p6PXlP\nP03Ntm0E/9//4T9rptySfsOm1BzC/dwZ0c22vB3shoGzwKiHQ+vlVmKTfHv+W/78y5+JD4nnqYSn\n5JbTLhT/bQV5iU8GY7PkSKbQJrf164yni5qPbdze3GfiRDq/9hr1aWnkLHwIY0OD5R/aWA3HPoc+\nd4Ort+WfZ+eIosimVC39NX70DPORW459olJJZ0Wzd0NpBgChnqGsmLACH1cfFny3gBNlJ2QWaVtM\nSdJQWqvj+5NFckuxPTJ2SBm1NtKhIOr15P/fs9R8u5Xgp58mYM5suSX9Bm1ZPbvOljI5QYNapZi1\nXBdB3SFyqHRu1EY7h+RiW9Y2ntv1HAODB/Le2Pdwd7JvEzil4FOQl+CeoBkknbtSJps28XR14o4B\n4XxztICqhma55VwV39tupfOr/6I+JYXchx/G2Nho2Qce+wya6yF+tmWf4yCkays5U1TLFGV3r30M\nmAaC+jet6WFeYSyfsBwvZy/u/+5+TpefllGgbTGqezChPm5sUNo6Lyd9tZRR2/1muZUgGgzkP/dn\nqrdsIeipJwmYN1duSZex6YAWlQCTE21jN9RuiU+G8kzI+kVuJTbDd9nf8X8//x/9g/rz/rj38XD2\nkFtSu1EKPgX5iUuGsrOg3Su3ErtgapKGxmYjXx7Kk1tKm/jecQdh//ondXv3kfvwIxibmiz3sPTV\nENwLwuMt9wwHYlOqFg8XNbf37yy3FPvGO1TKSzv0sZSf1kK4VzjLJyzH3cmd+dvnK0VfC2qVwOSE\nCHadLSG3wort3rZOdT6c2QYDp0tZtTIiGgwU/PkvVH/9NUGPP07gggWy6rkSzQYjmw/kMqZHMGG+\n9r3zIjs97wBXX8VPoYXvs7/nmZ3P0DewL+/f6BjFHigFn4It0PtOcPWBtFVyK7EL+ob70ivMhw0p\ntmvecjF+d95J2MsvU7dnD7mPPGqZoq/gCOQflBYPlBymNqlpbObrwwXc0b8zXq5Ocsuxf+KSob4U\nTn/zm4813hpW3LQCF7ULC7Yv4GzFWZkE2haTEqRd5c0HbNNxWBYOrpeyaWWOkxGNRgr++jxVX35J\n0B8fI/DBB2TV83v8cKqYkpompiRFyi3F/nHxgH6T4cRXUo5tB+ZH7Y/8aeef6BXYiyU3LsHT2VNu\nSWZDKfgU5MfFE/pOghNfQoPtmpHYCoIgMHVQJCcLqjmSWyW3HJPwu+duwv7xEnW7dpH72GMYdWbO\nEkxfA2pX6YeWQpt8dTifhmaDYtZiLrqOA5+IKy5aaXw0rJiwAmeVM/O3zyejIsP6+mwMjb8HI7oF\nsTk1B71BMW/BaJTmsJhR/8/efYdHUb1tHP/OpvfeIA1C75DQmyJVARtKh0AAqdJEsSGCWFGsoLTQ\nQQT5KUqRLh1C7z2dJEBI79l5/5jgCwokIbuZ3c35XFeuQHZ25o6SzZ455zwPuFZVLYas1XJz2jRS\nN2zAfexY3EeNUi1LcdYcicbL0Yqna4piLToRPBgKc+H0WrWTqGZPzB4m7ZlEbbfa/NjxR+wt7dWO\npFNiwCcYhuDBUJBToV9sSuP5RpWwsTBjzVHDLt5yP+devfCe8SGZe/4mbpwOB315Wcq/mzo9ld5o\nQrF+PhpDLW8HGvk5qx3FNGjMlJmZ67sg+cZ/Hg5wDGBRl0WYSWaE/RXGtZRrKoQ0LP2a+ZGQlsOe\ny7fUjqK+6zshNVrV/ceyVkvC9A9JXbce99Gj8Bg7RrUsxYlLyWb35Vu8GuKHuZl4G6sT3vWhUmNl\nWacRrBzStb2xe5m4eyI1XWryY6cfcbA0vcJv4idFMAw+DcGnkSjeUkKO1hY818CH30/Gk5FboHac\nEnN59VW8p08nY88e4sZPQNbFoO/8b5CbqiyrE4p1Lj6V07Gp9G7qhySWv+pO4wEgaZSZmocIdApk\nUZdFaCQNYVvDuJ56/aHHVRTP1PbC3d6K1QZecbhcHFsCtm5Q6zlVLi/LMgkzZ5Kydi1ur72G+7hx\nquQoqbVFBX9eDRErFHSqyWBIOg+xEWonKVf74vYxYdcEqjlX46dOP+FoaZpVq8WATzAcwYMh6RzE\nHVM7iVHo28yPzLxCNp6KVztKqbj06Y33B9PI2LWL2ImTyj7oO75MWQYV2EY3AU3c6iPRWJlreKmx\nqGynU06VoXpnpZ9V4cMr6FZxqsKiLosACNsaxo3U/84GVhQWZhpeCfFl58UkbqaWQ9sWQ5WeqDS+\nbtQPzK3K/fKyLJMwYwYpq9fgNnwYHhPGG/SNoEKtzNqIGNpW98DP1TSKaRiM+r2UPrYVqHjL/rj9\njN85niDnIBZ0XoCTlZPakfRGDPgEw1GvF1jYiuItJdTE34XqnvasMcI75C59++L1/ntk7NhB3OTJ\nyPlP2GLi1iWIPqAspzPgNymGIjO3gP+diOe5Bj442apbCdAkBYdCRiJc3vLIQ6o6VWVRl0VoZS1h\nW8OITI0st3iGpk9TP7QyrD1agYu3nFypNL5WYYWCLMskzpypDPaGheExaZJBD/YA9lxO4mZqDn3F\n/mPds3JQ+tie/RVy09VOo3cH4g7w+s7Xqepc1eQHeyAGfIIhsXasUC82ZSVJEn2a+XMqNpXz8Wlq\nxyk11/798Xr3XdK3bSdu8htPNug7thQ0FtBogO4DmqA/TitLgPuJynb6Ua0TOFQq9qZVkHMQizov\nolAuJGxrGFFpUeWTz8AEuNnRppo7Px+NplBbAZfy3yvWEtAG3KuX66WVwd5H3F21GtewoXhMnmzw\ngz2A1UdicLe3omMdL7WjmKYmgyE/E878onYSvToQf4DXdxUN9jqZ/mAPxIBPMDRNQotebNapncQo\nvNS4MpbmGqMq3nI/14ED8Hp7Kul//UXcG1NKN+jLz4FTq6B2d7AXldpKYtWRGKp72hMc4KJ2FNNk\nZg5NBsLVHXD38YO4ai7VWNh5IfnafIZuHUp0mnH+DJdV32b+xKfm8PeVCli8JfJvuHuj3Iu1yLJM\n4kezuLtqFa5Dh+L5xhtGMdhLTMth58UkegX7YiGKteiHbwh41jXplVYH4w/y+s7XCXQMZEGnBThb\nV4ziZeInRjAsviFK8+wKtIa8LFzsLOlWz5sNJ+LIzitUO84TcR08GM+pb5G+dWvpBn332nioWNnO\nmJyLT+VUTAr9mvsbxZs7o9W4aLb5xIpiD63uUp2FXRaSX5jPkK1DKuSgr1MdL9zsLFl9uOJ97xxb\nAjYuULtHuV1SlmUSZ33M3ZUrcQ0NxXOKcQz2AH6JiKFQK9NHLOfUH0mCkCFw8xTEHVc7jc4dunmI\ncTvHEeAYwILOFWewB2LAJxgaSVKWFMSfUJppC8Xq09Sf9JwCNp25qXaUJ+YWGlr6Qd+xJUXFWtrp\nPZ8puFes5cXGldWOYtqc/aFaRzixHAqLr6Bbw6UGCzovqLCDPktzDb1CfNlxMYnEtBy145SfzNtw\n4Q9o2BcsrMvlkrIsk/jxJ9xdsUK50fbWm0Yz2NNqZdYcjaFVkBuB7qbTDNsgNXi1qJ5CuNpJdOrw\nzcOM2zEOf0d/FnZeiIt1xVrpIgZ8guFp8KrSRFvM8pVIi6quVHG3M/ry5qUa9CVdLCrWMhg04mWs\nOFl5RcVa6vvgbGupdhzTFxwK6Tfhyl8lOryma80KPejr09SfQq3MLxExakcpPydXgTa/3Iq1yLJM\n4iefcHf5clwHD8Jz6ltGM9gD2Hf1NrF3s+kj9h/rn7WTUk/hzHrIMb76AA9z5OYRxu4Yi6+Db4Uc\n7IEY8AmGyNYV6jyvNNPOy1I7jcGTJIneTf2IiLrLlUTjLnZT4kHf8XvFWvqXb0Aj9cepm2TkFtC3\nuXizVC5qdAF771LdtPr3oK8iFXKp4m5HqyA3Vh+JQVsRirfIsvJvw68FeNYqh8vJJH36KXeXLcdl\n0EA8p041qsEewJqj0bjYWtClrijWUi6Ch5hM8ZbDNw8zZseYfwZ7rtauakdShRjwCYYpOBRy0+Dc\nr2onMQovN/HFXCOx5qjx3yEvdtCXn63cHRfFWkps1ZFoqnvaEyKKtZQPMwto3F+Z4UstecuBmq41\n/9nTN3Tr0Ao16OvbzJ+4lGz2Xr2tdhT9i9oPd64qvWf17N7MXvLSZbgMGojX228b3WDvVnouf51L\n5OUmvliZm6kdp2KoHAxe9ZVlnbLx3oQ5dPPQP4O9RV0W4WbjpnYk1YgBn2CYAlqBe02IWKx2EqPg\n4WBF57pe/Ho8lpx84yzecr/HDvrO/w45KcodSKFY5+PTOBmTQt9molhLuWoyCGRtiYq33K+GS40K\nOejrXNcL14pSvOXYUrBygjov6PUy/xRoWbYc18GDjXKwB7D+eCwFWlks5yxPkgQhoZBwBuKNs3jL\nwfiDjN0xFn9HfxZ1WVRhZ/buEQM+wTDdqxQVd0ypFiUUq28zf+5m5bPlbILaUXTikYO+Y+FKsZYq\nolhLSaw+Eo2luYaXmohiLeXKJRCCOsDx5aAt3U2YijjoszI3o1ewL9svJJJkysVbspKVCsMNXgVL\nW71d5p/WCytWKNU4jWzP3j2yLLPmSDTNAl2p5mmvdpyKpX5R8ZYI4yveciDuwD/VOCvyMs77iQGf\nYLga9gFza6N8sVFD6yB3At1sWXnYdN4cPjDomzQZOe4MRB9Ulvwa4ZuX8qYUa4kTxVrUEhwKabFK\nX75SemDQt2UokamROo9naPo09aNAK/PLsZIvgzU6p3+Gwly9LudUmqrPVFovDB1qVNU4/+3g9TtE\n3smiTzPRiqHcWTtCvZfh7HrISVU7TYntj9vPuJ3jCHQMFIO9+4gBn2C4bFyUF5szv0CucRcjKQ8a\njUS/5v4cjbzLpQTT+e/lFhqK1ztvk75tG7HjX0eWRbGWkvrj9E3ScwvoK5ZCqaPms2Dn+cRNjGu4\n1GBRl0UUyAUM3TqU66nXdZvPwFT1sKdFVVfWHI02zeItsqz8W6gcDN719XMJrZaEGTO4u2o1bsPC\njKrP3sOsPByNk40Fz9b3UTtKxRQyBPKzlCJ6RmBf3D5e3/k6VZyqVNhqnI8iBnyCYQsZCnkZRvNi\no7ZewX5YmmlYZUKzfACugwbh9fabZJxNIPZkdbQWjmpHMgqrDkdTzdOepoHil54qzCygUT+4vAXS\n4p/oFNVdqrOo8yIK5UKGbhnKtZRrOg5pWPo28ycmOZv910yweEvMYbh1UW+tGGStloQPZ5Cyeg1u\nw4fjMXmyUQ/2ktJz2Ho2gV7BvlhbiGItqqjUBLwbKDcqDLx4y764fYzfOZ6qzlVZ2HlhhWqqXhJl\nGvBJkuQqSdI2SZKuFH3+z7sKSZIaSZJ0UJKkc5IknZYkqfd9jy2RJOmGJEkniz4alSWPYILu3QmN\nMO5KUeXF1c6SZ+t78+vxODJzi2/6bExcG9ngHZxCxqUUYseNQ5ubq3YkgyaKtRiIJoNALix18Zb7\nVXOpRniXcCRJYujWoVy5e0WHAQ1Ll7reuNhaGH1f0Yc6ugisHKF+L52fWtZqSZj+ISk//4zbiBF4\nTJpo9D/3v0QoxVr6i3Yy6rlXTyHxrFJTwUD9Hfs3r+98nSDnIBZ0WiAGew9R1hm+qcAOWZarAzuK\n/v5vWcAgWZbrAl2BryVJuv//xBRZlhsVfZwsYx7B1EiSMsuXeAZiI9ROYxQGtAggPbeAjaeebEbB\nYEWE49LcB+8Pp5O5529ix4pB3+OsOVpUrKWxKNaiKrcgqPqUUpmxlMVb7lfVuSqLuyzGTDIjbGsY\nl5Iv6SyiIbG2MOPlJr78dS6RW+km9POdeRvO/w8a9gVLO52eWi4s5Ob775Oydi1uI1/DY+IEox/s\nFWplVh2OpnU1N6p6iGItqqrXCyzsDLaews7onYzfNZ7qLtVZ0FkM9h6lrAO+54F7nWWXAv+pMSzL\n8mVZlq8U/TkeSAJE8yyh5Oq/Apb2SnVGoVjBAS7U9HJgpSmVN0+6ADGHIDgUl9698floJpn79hE7\najTaHBOu6PeEsvMK2XA8jmfreeNiJ4q1qC4kTCnecnlrmU5TxakK4V3DsTCzIOyvMC4mX9RRQMPS\np5l/UfEW4+8r+o8Ty6EwT7mBqUNyYSE333mH1PW/4j5mDB7jxxv9YA9g96Uk4lKyGdA8QO0ognXR\nrPTZ9ZCdonaaB2yL2sbk3ZOp7VqbBZ0X4GTlpHYkg1XWAZ+XLMs3AYo+ez7uYEmSmgGWwP2bEGYV\nLfWcI0mSVRnzCKbIykEpYX12PWTfVTuNwZMkif4t/DkTl8rpWMN6cX5ix5aAmeU/xVqce/XCZ9Ys\nMg8eJGbUKLTZ2ermMzAbT8eTnltAP/FmyTDUfBYcfODowjKfKsAxgCVdlmBjbkPY1jDO3zmvg4CG\npZqnUrxl1eFoCk2heItWq8yOBLQBz1o6O61cUED8m2+R+tvveIx/HY9xY01isAew4lAUng5WdKzj\npXYUAZRlnQXZShE9A7Hlxham7JlCXfe6/NTpJxwtxd7+xyl2wCdJ0nZJks4+5OP50lxIkiQfYDkw\nRJZlbdGX3wZqAU0BV+Ctxzx/hCRJEZIkRdy6das0lxZMQfAQKMiBU2vUTmIUXmhcGRsLM1YcMoHi\nLfnZcGo11O4Bdm7/fNn5pRfx+eRjsg4dJua1kWgzM1UMaVhWHY4myMNOFGsxFGbmSouGazsgueyV\nNv0c/QjvEo69hT3D/hrG2dtny57RwAxsEUjs3Wx2X0pSO0rZXdsBKVHQVHeze3J+PnGT3yDtzz/x\nfGMy7qNG6ezcaotJzmL35Vv0aeqHhZmoLWgQKjUGn0YGU0/hj+t/8Nbet2jo0ZCfOv2Eg6WD2pEM\nXrE/SbIsd5Rlud5DPn4DEosGcvcGdA99ZZYkyRH4E3hPluVD9537pqzIBcKBZo/JMV+W5RBZlkM8\nPMSK0ArHpwFUDoGIxQbxYmPoHK0teKFxJX4/FU9qdr7accrm3P+UHkDBQ/7zkPMLL1Dp88/JOnaM\n6OEjKMzIUCGgYTkbl8rJmBT6Nw8wmbv9JqHJYJDMlNcwHfB18GVx18U4Wjoy/K/hnEwyrS3wnet6\n4elgxXJTuGl1dKHSnqNWD52cTs7LI3biRNK3bsVz6lu4DRumk/MaitVHopFQlvYKBiQ4FJLOQexR\nVWP8dvU33tn7DiFeIczrOA87C93uiTVVZb118jtwr77wYOC3fx8gSZIlsAFYJsvyL/967N5gUULZ\n/2d6tykF3QkZCrcvQ9R+tZMYhX7NAsjJ17LhuJE3MY5YDG7VILDNQx926tGdyl9+Sfbp00QPDaMw\n1XgaxOrDsoOR2FiY8XKwr9pRhPs5+kDt7kq1znzdLEGubF+ZJV2X4GrtyohtIziaoO4bMV2yMNPQ\nt5k/ey7fIuqOEc/ep0QrezebDALzsu+n1ebmEjvudTK278DrvfdwCw0te0YDklegZW1EDM/U9qKS\ns43acYT71e+l1FNQsXjL+svreX//+7TwacH3z3yPrYWtalmMTVkHfJ8CnSRJugJ0Kvo7kiSFSJJ0\nb7PCq0A7IPQh7RdWSpJ0BjgDuAMflTGPYMrqvgjWTjq7Q27q6vs60dDXiZWHo5GNdVY0/iTEHoGm\nw5SKrY/g2LULvt9+Q+6FC0QNGULB3Yq51zMlK4/fTsbzQuPKONlYqB1H+LeQMGUf8rn/6eyU3nbe\nLOm6BB87H0ZvH83B+IM6O7fa+jbzRyNJrDLmAlTHliivXcGhZT6VNieH2DFjydizB+/p03Ed0L/M\n5zQ0W84lcDsjT7RiMERWDkoRvXO/qlJP4eeLPzP94HRaVW7Fd898h425uCFQGmUa8MmyfEeW5Wdk\nWa5e9Dm56OsRsiwPK/rzClmWLe5rvfBP+wVZljvIsly/aInoAFmWxXos4dEsbaFhPzj/O2SIfZwl\n0b9FAFeSMjgaaaQDoKMLwMJWKWVeDIcOHfCd+wN5164TPTiUgtsm2Li5GOuOxZJboGVgC1GsxSBV\naQdu1SFikU5P62HrweIui/Fz9GPsjrH8Hfu3Ts+vFm8nazrX8eLniBhy8p+8pYVqCvLg+DKo3gWc\n/cp0Km1WFjGjRpG5fz8+sz7CpU/v4p9khFYcisLf1ZZ21cXWHYPUNEypp3BiZbledtm5ZXx0+CPa\n+7bn26e/xcpM1HgsLbEbVjAuIUNAmw8ny/fFxlj1aFAJB2tz4yzekpUMZ9YpFVptStZXx75tW/x+\nnEdedDRRgwaTn2gCBR9KSKuVWX4oipAAF+pUEtXKDJIkKW+YYo8qs9c65GbjxuLOiwlyDmL8rvHs\niN6h0/OrZWCLAFKy8vnz9E21o5Tehd8h85ayQqEMCjMyiB4+gqzDR/D55GOcX35ZRwENy+XEdI7c\nSKZfc380GrH/2CB51wf/lsrNWK22+ON1YP7p+XwR8QWdAjox56k5WJqJVkNPQgz4BOPiUVMpbX0s\nvNxebIyZjaXSxHjz2ZvczjCyJsYnVyp3EpsOL9XT7Fq2xH/BfAoSEogaNJD8m0b4RvEJ/H3lFlF3\nshjYUszuGbSGfcHcRuezfADO1s4s7LKQOq51mLx7MltubNH5NcpbyyA3qnrYGWfxlojF4BIIQR2e\n+BSFKSlEDxlK9qlTVP7qS5xf+E+7Y5Ox6nA0lmYaXhH7jw1bs+FwNxKubtfrZWRZ5tvj3/Ldie/o\nXrU7n7f7HAszsVXhSYkBn2B8QoYoLzbXd6mdxCj0b+5PfqHMumNGVLxFq1Uq2/m3BO96pX66bdOm\n+C1aSOGdZKIGDCQvxoQaOD/CikNRuNtb0q2ej9pRhMexcVaKH5xZp5cmxo6WjszvPJ+GHg15a+9b\nbLy2UefXKE+SJDGwRQAnY1I4E2tEBZmSLigFxoKHgObJ3moV3LlD1OBQci9exPfbb3Hs2lXHIQ1H\nVl4B64/F8mx9b9zsxXI9g1arB9h7KbN8eiLLMl9EfMGCMwt4ufrLzGozC3ONud6uVxGIAZ9gfGr3\nAFt3UbylhKp7OdC8itLEWGssTYyvblcG9c1KN7t3P9vGjfEPD0ebkUFU/wHkXrumu3wGJiY5ix0X\nk+jT1B9Lc/GybvCaDoP8LL31FbWzsGNex3k09WrKu/veZd3ldXq5Tnl5qYmv8fUVPboIzCyh8YAn\nenp+YhJRAweRFxWF74/zcOjwtI4DGpbfT8aTnltAf7H/2PCZWyo3Mq5sgzu6/72qlbV8dOgjlp9f\nTv/a/fmg5QdoJPF7razEf0HB+JhbKb9EL22CFNOfudGF/i0CiE7OYu9VIylkcnSBcgexjH2rbOrX\nw3/ZMmStlqgBA8m5cEFHAQ3LysNK36p+orKdcajUCCoHK8s69VRB19bClu+f+Z42ldvw4cEPWXpu\nqV6uUx6cbJS+or+diiM1ywj6iuZmKIP5ui+CnXupn54fF0fUwIEUJCTgv2A+9q1b6yGk4ZBlmRWH\no6jp5UBIgIvacYSSCA4Fje76it5TqC3k/f3vs/byWobWG8pbTd8S/WR1RAz4BON0bxP80YWPP04A\noEtdL9zsLI3jDnnyDeXOYXCoTvpWWdesQcDyZUjW1kQNDiX7pGk1qM7JL2RtRAyd6oi+VUal6TCl\nr2jkXr1dwtrcmm+e/oZOAZ2YHTGbeSfnGW2LlgEtlL6i64yhr+iZXyAvXWnDUUp5kZFEDhhIYUoK\n/uGLsW3aVA8BDcup2FTOxqUxoIW/eHNvLBx9lNVWJ5ZDXpZOTpmvzWfq3qn8fu13RjcazYQmE8S/\nBx0SAz7BODn7Qa3ucHypzpoYmzIrczP6NvNn+4VEYpJ18+KsNxGLQNLopG/VPVZVqhC4YjlmLs5E\nDZp9GBsAACAASURBVA0j89BhnZ1bbZvO3CQ5M49BLQPVjiKURt0XwcZFWfqnRxZmFnze7nN6BvVk\n7qm5fBnxpVEO+upWcqKJvzMrDkUZ9tJ0WVZew7zqgV+zUj019+pVIgcORM7JIWDpEmwaNtRTSMOy\n8lAUtpZmvNC4stpRhNJoNgJyUpUbHGWUW5jLpF2T2BK5hUnBkxjVcJQY7OmYGPAJxqv5a0rzTx28\n2FQEA1oEoJEklh2MVDvKo+VlwfHlyp1Dx0o6PbVF5coELF+OZeVKxLz2Ghl79uj0/GpZdjCKqh52\ntApyUzuKUBoWNtCoP1z8A9IT9Hopc405M1vPpE/NPiw9v5SZh2ailY2vyvHAlgHcuJ3JgWt31I7y\naLFHIeEMhAxV2nCUUPaZs0QNGAhAwPJlWNeura+EBiUlK4+Np+N5vlFlHKxFBUaj4t9SubFxZEGZ\nlqZn5mcyevtodsfu5t3m7zKk3hAdhhTuEQM+wXgFtFZebA7/pLd9MKbE28mabvW8WXM0hszcArXj\nPNzZ9ZCTUqZiLY9j4emJ/7JlWAUFETN2HGlbturlOuXlTGwqJ2NSGNgiQNwNNUYhQ0FboDTn1jON\npOGd5u8QVi+MXy7/wjv73qFAa6CvA4/QrZ4PrnaWLD8UqXaURzu6CCztlf6hJZR55AjRoaFo7OwI\nXLkSq2rV9BjQsKw+EkNOvpZBop2M8ZEkZWl64hmIebJVM6m5qYz4awTHEo/xcZuP6VOrj45DCveI\nAZ9gvCRJmeVLPAtRB9ROYxSGtK5Cek4Bv56IUzvKf8myUqzFo7YymNcTcxcX/JcuwaZ+feImTSJl\nw//0di19W34oEltLM14WfauMk1uQ0qMtIhwK9T/4kiSJCcETeL3x6/x5/U8m755MXmGe3q+rK9YW\nZrwa4se284ncTDXApfwZt+DcBmjYB6wcSvSU9N27iRk+AnNvbwJWrcTSv+IUXioo1LL8YCStgtyo\n7eOodhzhSTR4Fayc4Mj8Uj/1dvZthmwdwoXkC3z11Ff0CCpbkTbh8cSATzBu9V9R9sEc/lHtJEah\nib8zDXydWLL/huHt44mNgJunoNmwUi2FehJmDg74L1yAXYvm3Hz7bZKX6X+GRddSsvL47WQ8LzSu\njKNYCmW8mg6D9Hi49Ge5XXJ4g+FMbTaVnTE7GbtjLFn5Br6v9z79m/sjA6sPR6sd5b8iFkNhLjR7\nrUSHp/7xJ7Fjx2FVrRoBK5Zj4eWl54CGZeu5ROJTcxjSuoraUYQnZWmnVE0//1uplqbHZcQxaPMg\nYtNjmdtxLh38O+gxpABiwCcYOwsbaDJY2QcjWjQUS5IkhrQO5NqtTPZeMbAWDUcXgKUDNOhdLpfT\n2Nri++OPOHTqROLHn3Dr228NbxD8GL9ExJJboGWg6Ftl3Gp0BWd/ODSvXC/bv3Z/ZrSaweGEwwzf\nNpzUXONoau7nasvTNT1ZdSSGvAID2odYkKtUja7WCTxqFHv43TU/Ez9litIvdOkSzF0qXjuCxftv\n4O9qS4danmpHEcqiaZiyNP1YyVq/XE+9zuDNg0nJTWF+p/m08Gmh54ACiAGfYApEi4ZSeba+D+72\nViw5EKl2lP93bylUo34lXgqlCxpLSyrP+Qqnl1/i9tx5JM78CFlrQG8iH0GrVfpWNQ10EUuhjJ3G\nDJqPhOiDEHe8XC/9YvUX+bL9l1y4c4HQLaEkZSWV6/Wf1MCWAdzOyGXTmZtqR/l/Z3+FzCRoMarY\nQ+8sXEjC9OnYt2uH34L5mNnbl0NAw3I6NoVjUXcZ3CoQM43Yf2zU3IKgWseiGe7H98m8cOcCQ7YM\nIV+bT3iXcBp5NiqnkIIY8AnGz9kPaj0nWjSUkJW5Gf2b+7PzYhI3bmeqHUdxfCkU5v3/4L0cSebm\n+Hz0Ea5Dh3J31Sri33wLOd+wmzv/feUWUXeyGChaMZiGxgOV2e1ynuUD6BjQkbkd5xKfEc+gzYOI\nTjPApZL/0r66B0Eedizcd90wZuVlGQ7NBfeayp7MRx4mkzTna5Jmf4njs8/i+/13aKytyzGo4Qjf\nH4m9lTmvhoj9xyah6XDISFBWWz1CREIEYVvDsDSzZGnXpdR0rVmOAQUx4BNMQ/ORokVDKfRv4Y+F\nmcRSQ5jlKyxQilZUaV+ipVD6IEkSnlPewGPSJNL++IPYsePQZhvuzYPw/ZF4OFjRta632lEEXbB2\nVPbBnPsV0uLL/fItfFqwqMsiMvMzGbR5EJeSL5V7htLQaCSGtqnC2bg0jtxIVjuOUjQs4bQyu/eI\n/cdyYSEJH0znzk8/4dy7N5W++BzJomLuvU1Ky+GP0/H0CvYVrRhMRfVO4BygtGh4iJ3RO3lt22u4\n2bixrOsyAp0CyzefIAZ8gokQLRpKxdPBmu4NKrHuWCzpOSrPZl3eDGmxemvFUFKSJOE+Yjje06eT\n8fffRA8bTmFamqqZHuZyYjp7Lt9icMsALM3FS7jJaP4aaAtVW5pez70eS7suxVxjzpAtQzieWL7L\nS0vrpca+ONtasGjfDbWjKLN7Ni6P3H+szc0lbsJEUtauxW3ECLynf4BkZlbOIQ3HikNRFGhlQlsF\nqh1F0BWNmbJCJ2o/JJ574KENVzYwcfdEarjUYFm3ZfjY+6gUsmIT7xYE0yBJ0GyEaNFQCqGtAsnI\nLWDdsVh1gxz4XilaUaObujmKuPTpTeUvZ5N9+jRRgwZTcNuwitss2nsDawsN/ZuLYi0mxbWKsjQ9\nYjHkqVM1s6pzVZZ3W46bjRuvbXuNv2P/ViVHSdhYmjGgeQDbLiQSqebS9OQbcPFPCB4Clrb/ebgw\nI4OY4SNI37YNr3fexnPSxArdMzMnv5CVh6N5ppYnge52ascRdKnxADC3fqBFw+Kzi5l2YBrNvZuz\nqMsiXKwrXnEiQyEGfILpEC0aSqWhnzNN/J1ZeiASrValWdGYoxBzCFqMATNzdTI8hOOzz+I3dy55\nUVFE9utPXrRh7Gu6lZ7LhhNx9Ar2xcXOUu04gq61GK0sTT/9s2oRfOx9WNptKVWcqjB+53j+vF5+\n7SJKa1DLAMw1kroFqI4s+P/ZjX8puH2bqEGDyDp+nEpffIHroEEqBDQsG0/FcyczT7RiMEW2rkpf\nvlNr0GYk8WXEl8w5NoeugV354ZkfsLX47w0RofyIAZ9gOixtRYuGUgptXYXIO1nsvqxSdb6D34G1\nk3Jn0MDYt21DQPhitGlpRPbtR/bZc8U/Sc+WH4oiX6tlqHizZJoCWoFPQ6V4i4pL012tXVncZTGN\nvRozde9Ulp4rWbn18ubpaE2PhpVYGxFDarYKS9Nz0uD4MqjzAjhVfuChvJgY5WbRjUj85s3FqUf3\n8s9nYGRZJnx/JDW9HGgV5KZ2HEEfWo4lvyCH97cMZ8m5JfSt1ZfP2n2GhZnYq6k2MeATTEvTMOVz\nxCJ1cxiJbvW88XK0Inx/ZPlfPPkGXNioLIWyMsyy5DaNGhGwahUaKyuiBw0iY/9+1bLk5Bey4lAU\nz9TyoqqHYf73EspIkpRZvtuX4OoOVaPYW9ozr+M8Ogd0ZnbEbL44+gVa2fBaloS1qUJWXiFrjqgw\nC39yFeSlK//P7pNz4QKRffuhTU0lYEk49m3bln82A3T4RjLnb6YR2jqwQi9rNWXZLv5MrFqH3zOv\nM6b+a7zd7G00khhqGALxf0EwLc7+yj6YY0tEi4YSsDDTMLBFAHuv3OZqUnr5XvzQPJDMlGIVBsyq\nahUCVq/Gws+PmNdGkrpxoyo5fj0eR3JmHsPbitk9k1b3JbD3VgqBqMzKzIov2n9Bv1r9WHZ+GVP3\nTiWvME/tWA+oW8mJllXdWHogkvzCchyQaguV7QO+zcA3+J8vZx45QtTAQUgWFgSsWolNw4bll8nA\nhe+/gYutBS82rlz8wYLRSclJYcRfI/hbzuS928mM1NqKgb0BEQM+wfTca9Fweq3aSYxC32b+WJpr\nyncfTPZdOLEC6vcCx0rld90nZOHlScCK5dg2aUL8lDe5szi8XK+v1cos3Hed+pWdaFbFtVyvLZQz\nc0toNgyu7YCki2qnQSNpmNpsKhOaTGDzjc2M3j6ajLwMtWM9IKxNFeJTc9h8NqH8Lnp5K9y9AS3/\nf3YvbfNmYsKGYe7lReCqlVgFBZVfHgMXk5zFtvOJ9G3mj7VFxa1Qaqpi02MZuHkg5++cZ3b7L+jt\nUEMpyKYtVDuaUKRMAz5JklwlSdomSdKVos8PLb8jSVKhJEkniz5+v+/rVSRJOlz0/J8lSRJVCISy\nC2gN3vXh4PegNbwlSIbGzd6K5xtWYv2xuPLbBxMRDvmZ0HJs+VxPB8wcHPBbuACHrl1J+vxzEj/9\nDLmc/n3tupTE9VuZDGtbRdwxrQiChyrV7g6XfyP2h5EkibD6YcxqM4tjiccI3RLKraxbasf6R4da\nnlRxt2PR3nJsxH5oLjj6Qq0eyLLMnfAlxE2chHWDBgSuXIGFjyg9f7+lByKRJImBLUV1YVNz7s45\nBmwaQHJOMvM7z6dzYBdoNQ6Sr8GlzWrHE4qUdYZvKrBDluXqwI6ivz9MtizLjYo+et739c+AOUXP\nvwuElTGPICj7YFpPgNuX4dImtdMYhdDWgWTnF7LqcDnsgynIU/olVn0avOvp/3o6pLG0pPKXs3Hp\n35/kJUuIf/Mt5Dz9L3FbuPcGPk7WPFtfvImsEOzclJ5up9ZA5h210/yjZ1BPvnvmO6LToxm4eSA3\nUg2gBx5FjdhbB3IqNpVjUXf1f8GEMxC5F5qPQEYi8ZNPSPrsMxy6dMF/8SLMnJ31n8GIZOYW8HNE\nDN3qeePjZKN2HEGH9sXtY8iWIViaWbK823KCvYqWN9fuqWyxOfCdugGFf5R1wPc8cK9811LghZI+\nUVJuU3cA1j3J8wXhseq8AM4BsG+OaMReAnUrOdGmmjuL998gJ1/PSzDOroOMBGhlPLN795PMzPB6\n7108Jk0i7Y8/iB4+gsLUVL1d72xcKgev32FI60AszMQq/AqjxSgoyIFji9VO8oA2ldsQ3iWc7IJs\nBm0exMmkk2pHAuDlYF+cbMqpEfuhH8HCFm2d3sRNnMTdZctxHTyYynO+QmNlpf/rG5n1x2NJzylg\naBux/9iUbLiygbE7xhLgGMCKZ1dQ1bnq/z9oZq60W4o5BDFH1Asp/KOs7x68ZFm+CVD02fMRx1lL\nkhQhSdIhSZLuDercgBRZlguK/h4LiJ28gm6YmStLCuIiIEq9yorGZPRTQdxKz2X9cT02YpdlZV2/\nZx0IekZ/19EzSZJwHzGcSp9/Rtbx40r59dg4vVxr0b4b2Fma0bupv17OLxgoz9oQ1AGOLFRmxQ1I\nXfe6LO+2HAdLB8K2hrE1cqvakbC1NKdfc3+2nksgJlmPjeszbsGZtRRU70X06ElKQ/W3p+L19lQk\njbgh828FhVoW77tR1PdVNN02BbIsM+/UPKYdmEYz72aEdwnH0/Yhb/8bD1DaLolZPoNQ7KuTJEnb\nJUk6+5CP50txHX9ZlkOAfsDXkiQFAQ/biPLIqRhJkkYUDRojbt0ynL0DggFrPABs3WHf12onMQot\ng9xo6OvET3uuU6CvanfXdkLSOWXvngnsRXPq2RP/hQspuHWLyD59yD5zVqfnv5mazcZT8fRu6o+T\njehjVOG0GKPMhp/boHaS//B39GfFsyuo41aHN/a8weKzi8tv/9wjDG4ZiEaS9NtmJmIReamFRC24\nQM65c1SeMwfXwYP1dz0jt+lsApF3shjVXhSwMQUF2gI+PPghc0/OpWdQT37o+AP2lo9oE2RlDyFh\nSvul5OvlG1T4j2IHfLIsd5Rlud5DPn4DEiVJ8gEo+vzQ7s2yLMcXfb4O7AYaA7cBZ0mSzIsO8wXi\nH5NjvizLIbIsh3h4eJTiWxQqLAsbaDESrm6DBN2+ETdFkiQx6qlqRCdn6a/a3YHvlJLz9Xvp5/wq\nsGvejMDVSq++qEGDSN+5U2fnXnogCq0sM6R1oM7OKRiRoA7gXgMO/WCQS9NdrV1Z2GUhXQK7MOfY\nHGYemkmBtqD4J+qJt5M13Rv4sDYihrQcPRSgys0g+8+fiNxVmYK0DPzDF+PYtYvur2MiZFlm7q6r\nVPO0p3MdL7XjCGWUkZfB2B1jWX9lPSMajOCj1h9hoSnmRmTz18DMAg6q32amoivr+oPfgXu3tgYD\nv/37AEmSXCRJsir6szvQGjgvK7cCdwG9Hvd8QSiTpsPA0h72i1m+kuhcx4sgDzvm7r6m+7v1CWfh\n+i5oPgLMTWufi1VQEIFrVmMVFETsmLEkL19R5nNm5haw6nAU3er54Odqq4OUgtHRaKDlGLh5Spkd\nN0BWZlZ83u5zhtYbyi+Xf2HszrFk5meqliesTVUycgtYezRG5+dOm/8eUZss0Tg4E7h6FbbBwcU/\nqQLbeTGJiwnpjH4qCI3G+Fd0VGTxGfEM3DyQwzcP80HLDxjXeFzJKkY7eEODV5U2TFnJ+g8qPFJZ\nB3yfAp0kSboCdCr6O5IkhUiStLDomNpAhCRJp1AGeJ/Ksny+6LG3gEmSJF1F2dO3qIx5BOFBNi4Q\nHApnf4W7UWqnMXgajcTI9kFcuJnGnss6Xjp98AewsIPgIbo9r4Ew9/AgYNlS7Dt0IHHWLBI/+RS5\n8MkL4PwSEUNaTgFhotF6xdawLzhWhr9nq53kkTSShonBE/mg5Qccij/E4M2DScgsx55496nvq/Sq\nXLzvBnkFulmaLssyt3+cR9wPW7H2siFw3QasqlYt/okVmCzLfL/rKr4uNvRoaPi9VoVHO33rNH3/\n7EtiZiLzOs2jV41SrtBpORYKsuHowuKPFfSmTAM+WZbvyLL8jCzL1Ys+Jxd9PUKW5WFFfz4gy3J9\nWZYbFn1edN/zr8uy3EyW5WqyLL8iy3Ju2b4dQXiIlmNA0ih9+YRiPd+oMj5O1szdfU13J027CWd+\nKdpXabqNwzW2tvh++w0uAweSvHQpsePHo80qfQGJQq3M4v2RBAe4iEIHFZ25FbQeD9EHINKwC1D1\nqtGLH575gdiMWPr/2Z+Lyeo0jh/9VBDxqTn8qoMCVHJeHjffe49bX3+Lo38W/nNnY+7uroOUpu3Q\n9WRORKfwWruqorqwEdsauZWhW4diY27DimdX0MKnRelP4lkbqndW2jHl5+g+pFAi4qdQMH2OlZSe\nVseXQ+ZttdMYPEtzDcPbVuXIjWSOReloCcaRn0AuVErNmzjJzAzvd9/B6523ydi5i8j+A8i/ebNU\n5/jzzE2ik7MYJsqYCwBNBoGdB/z9hdpJitW6cmuWdl2KJEkM3jyY3TG7yz1D+xoeNPB14ofdV8kv\nQwGqwpQUoocNJ3X9r7g3kaj0SnU0NY23unB5mrv7Ku72VrwS4qd2FOEJyLLMwjMLeWPPG9R2rc2q\n51Y92HahtFqNg6zbcHqN7kIKpSKpXVXrSYSEhMgREREPfC0/P5/Y2Fhycire3QNra2t8fX2xsBBV\n/B7p1iX4oTm0mwId3lU7jcHLyiug9ac7CQ5wYeHgpmU7WU4afF0Pqj4Fry7TRTyjkbFnD3GTJiPZ\n2OD3w/fYNGxY7HO0WpkuX/+NJMGW8e3E3hdBsf8b2DYNhu0A3xC10xQrMTOR13e9zoU7F5gQPIEh\ndYeUbM+Pjmw/n8iwZRHMfqUhvYJ9S/38vMhIYl4bSX58PD7Dn8UpeR70Wws1RJGW4pyOTaHn9/uZ\n2q0WI0V1TqOTX5jPhwc/5Ldrv9GtSjdmtp6JlVkZ993LMsxvD3lZMOaIsj9Z0AlJko4VdUJ4LPPi\nDjAWsbGxODg4EBgYWK6/VNQmyzJ37twhNjaWKlXEbMAjedSEWs/BkfnK8iirR5QRFgClp1VoqyrM\n2X6ZSwnp1PR2ePKTHfkJclKh9QTdBTQS9u3bE7hmNTGjRhM1cBA+s2bh1KP7Y5+z6exNriRl8F3f\nxmKwJ/y/kKGwb46yl6+f4d8l97LzYknXJby//33mHJvDtZRrTGs5rexvHEvomdqe1PFxZO6uq7zY\nuDJmpfhZyjx8hNjXX0fSaPBfvAjbQyPBu76yLE0o1txd13C0Nqd/c9E71Nik5KQwac8kjiYcZVTD\nUYxqOEo376klCVq9DuvD4PJm5f2YUK5MZoidk5ODm5tbhRrsgVJK383NrULObJZa6wmQkwLHl6qd\nxCgMbhWAraUZP+4pw16+nDSl0XqNrlC5ie7CGRGr6tUJ/GUtNg0aED9lCklff42sffgyM61W5tsd\nV6jmac+z9X3KOalg0KwcoMVo5c3SzdNqpykRG3Mbvmj3BWMajeH3a78TtjWM29nls6xekiTGdajG\n9duZ/HH6kR2f/uPu2rVEDxuGuZsbgWt/xtYmBu5chbaTTaJ3qL5dSUxny7kEQlsF4mAtVh0Zk8t3\nL9Pnzz6cTDrJx20+ZnSj0bp9T13nBXCpAns+M8g2M6bOZAZ8QIUb7N1TUb/vUvNrCgFtlGqRBXlq\npzF4zraW9Gvmz++n4olJLn3hEUDZpJ2TAk9N1W04I2Pu4oL/4kU49XqZOz/+RNz4CQ8t5rLlXAKX\nEzMY16FaqWYkhAqi2QiwcoS9X6qdpMQkSWJkw5F82f5LLiVfou+ffblw50K5XLtLXW9qeNnz/c6r\naLWPf4Mp5+eTMGMGCdM+wK5ZMwLXrMbS1xf2fgVu1aF2z3LJbOzm7bmGjYUZoa3FiiNjsiN6BwM2\nDSCvMI8lXZfQI6iH7i9iZg7t31TazFzapPvzC49lUgM+QzJ9+nRmz1bKaE+bNo3t27eX6XyFhYU0\nbtyY7t0fvxxMKEabCZAWp1SMFIoV1rYKGgkW7L1e+ifnpCqVUWt0g0qNdR/OyEiWlvjMnInX21NJ\n37GDyAEPFnO5N7sX5GFH9waijLnwEDbO0Gw4nP9N2ZdsRDoHdmZpt6XIsszgLYPZHlW234klodFI\njO1QnStJGWw59+g2EQXJyUQPGcrdVatxHToUv59+xMzRES5vhcQz0HYSaMz0ntfYxSRn8dvJePo1\n98fVzlLtOEIJaGUt807NY8KuCVRzrsaa7mto4NFAfxes/yq4BsGuT+ARK10E/RADvnIwY8YMOnbs\nWKZzfPPNN9SuXVtHiSqwah3Bq55SAEG82BTLx8mGlxr78vPRGG5nlLJripjd+w9JknAdPBi/H+eR\nHxXNjV6vkHX0KAB/nU/gYkI64zpUF7N7wqO1GA0WNsrMk5Gp41aH1c+tprpzdSbunsi8U/PQyvp9\nHX6uvg9VPez4budVHlakLufCBW706kX26dNU+vwzvN6cgmRuriw52zsbnP2h/it6zWgq5v99HY0E\nw9uKHoXGICs/izf2vMHck3PpUbUH4V3D8bT11O9Fzcyh/VvKjZSLf+j3WsIDxIBPh2bNmkXNmjXp\n2LEjly79/93X0NBQ1q1bB0BgYCDvvPMOLVu2JCQkhOPHj9OlSxeCgoL48ccfH3re2NhY/vzzT4YN\nG1Yu34dJkyRlL9/tS3Dhd7XTGIUR7auSV6glfP+Nkj/p3uxezWehUiP9hTNS9u3aEbj2Z8wcHYka\nMpQ7S5fxzfYrVHW3E02Khcezc1cKuJz5BZKfYOZdZR62HizuupjuVbsz9+RcJuyaQHpeut6uZ6aR\nGPNUNS7cTGP7haQHHkvbvJnIvv2gUEvAypU49bxv2eaNvyH2qFLky0zsRStOUnoOP0fE0CvYF28n\na7XjCMWIy4hj4OaB7IjewRshbzCrzaxyK6hE/V7KMundYpavPJlMlc77fbjxHOfj03R6zjqVHPmg\nR91HPn7s2DHWrFnDiRMnKCgooEmTJgQHBz/0WD8/Pw4ePMjEiRMJDQ1l//795OTkULduXUaOHPmf\n4ydMmMDnn39Oerr+filWKPVeUvpZ7ZoFtbord5yERwrysKdbPW+WHYxiRLsgnGxK8ObncFFlzvZv\n6T+gkbIKCiJw7c/EvzWVpE8+4Vm/YHxnfihm94TitRoHRxbAvq+h57dqpyk1KzMrPm7zMXXd6jI7\nYjb9/uzH109/TZCzfkr4P9+oEt/suMK3O67QsbYnaLXc+uZb7syfj03jxvh++w3mHh4PPmnvbLD3\nhkYD9JLJ1Czad4OCQi2vtRNtGAzd0YSjTN49mQK5gLnPzKV15dblG0Bjpqz8WR8GF36Dui+W7/Ur\nKDHDpyN79+7lxRdfxNbWFkdHR3r2fPQG73uP1a9fn+bNm+Pg4ICHhwfW1takpKQ8cOwff/yBp6fn\nIwePwhPQmEGH9+D2ZdEEtITGPF2N9JwC5v9dgoqd2SlFs3vPidm9Ypg5OFD5u2/Z0qwnHWKO0/Cz\nKeTHxakdSzB0Dt5KM/aTqyAlRu00T0SSJAbUGcCCzgtIy0uj35/92Ba1TS/XMjfTMObpIM7EpbLn\n+HViR4/hzvz5OL/SC/+lS/472Is5oszwtRoHFmK2qjipWfmsPBTNcw0qEehup3Yc4RFkWWbpuaUM\n/2s4ztbOrHp2VfkP9u6p+yK414Tdn4K2UJ0MFYxJTm08biZOn0paLdPKSpk212g0//z53t8LCgoe\nOHb//v38/vvvbNq0iZycHNLS0hgwYAArVqzQXfCKqHYPqNREebGp/wqYl9NSBiNVt5ITPRtWYvG+\nSAa3DMTT8TFvgu7N7j0lZvdKYsel23xTqR2132hGlZ8+48bLvaj89RzsWrRQO5pgyFqPh2PhcOBb\nePYLtdM8sabeTfm5+89M3j2ZSbsnMbTeUF5v/DpmOi6S8mJjXzas3YXFqFAyslPwmvY+Ln37Pvz3\n9t+zwcYVQoboNIOpWrT/Bhm5BYx+SszuGaqMvAymHZjGtqhtdPTvyMzWM7G3VLEf8b1ZvnVD4NwG\nZZmnoFdihk9H2rVrx4YNG8jOziY9PZ2NGzfq5LyffPIJsbGxREZGsmbNGjp06CAGe7ogSfDMNEiN\ngYjFaqcxCpM71yC/UMu3O688+qDsFKXtRa3u4NOw/MIZKVmW+WbHZQLcbOk45EWq/LIWM3c30SMA\nswAAIABJREFUooeGcWdx+EOLTAgCAM5+0LAvHFsK6YlqpykTbztvwruG06tGLxafXcyo7aNIyUkp\n/omlkPW/X3l/85do8/JJ/fg7XPv1e/hg7+YpuLJVKY5jKWaripOUnsPCvdd5roEPtX0c1Y4jPMTV\nu1fp+2dfdkbv5I2QN/jqqa/UHezdU+cF8Kyj9OUTs3x6JwZ8OtKkSRN69+5No0aNePnll2nbtq3a\nkYTiVH0KAtsqd3NzM9ROY/AC3Ozo28yfNUdiiLyd+fCDDv8IuWLvXkntvJjE2bg0xjxdDXMzDZaB\ngQSu+RmHjh1J+vxz4sZPoFDs3RUepc1E0OYrs3xGztLMkg9afsD0ltOJSIyg9x+9OXfnXJnPq83J\nIf7dd7n53vvYhQQzo+dUvop/zIqObR+AjYvS/kIo1jfbr5BXoGVK55pqRxEeYtP1TfTb1I/0vHQW\ndF7A4LqDDad3s0ajzPLdvgxn16udxuRJxngHOSQkRI6IiHjgaxcuXKjQbQsq+vf/xGKOwqKO8PR7\n0H6K2mkMXlJ6Du0/303HOl581/dfvfWyU+DrBlClLfRZqU5AIyLLMs//sJ+7WXnsnPwUFmaaBx5L\nXhxO0ldfYVGpEpW/noNNXXWWqgsG7n+jlYqdYyPAJUDtNDpx5tYZJu6eSHJOMlOaTqFPzT5P9CY1\nLzqa2PETyL1wAbdRI/EYO5Ylh6L5cON51oxoQYuqbg8+4eoOWPESdPkEWo7W0Xdjuq7fyqDTnL/p\n39yfGc/XUzuOcJ/8wnxmR8xm1cVVNPFswhftv9B/y4UnodXCT20hPxvGHBFF9J6AJEnHZFkOKe44\nMcMnVGx+TZXiIge+haxktdMYPE8Ha8LaVGHjqXjOxqU++OCheWJ2rxR2X7rF6dhUxj5d7YHBHij7\ngd3ChhKwfDlyfj5RffqSvGqVWOIp/NfT74KkgZ0z1U6iM/U96vNLj19o4dOCjw9/zOQ9k0vduiF9\n505uvNyL/Ph4fH+ch+f48UhmZvRt5o+ngxWfbbn44M+TthC2TQPnAGgapuPvyDR9sfUS1uYaXn+m\nutpRhPskZCYwZOsQVl1cxcA6A1nYZaFhDvagaJbvbUi+pty4EvRGDPgEocN7kJsO++aoncQojGhf\nFWdbC77Y+v+9JslOUQZ8tbqDTwP1whkJrVbm6+2X8XWx4aUmvo88zrZJY6ps+BXbli1InDGT+MmT\nKcwQy4+F+zhVhpZjlTdLccfUTqMzLtYufP/M90wMnsjO6J28uvHVEi3xlPPzSZo9m9jRY7D086PK\n+nU4PPXUP49bW5jxRueanIhO4Y/TN///iad/hsSz0PEDUcSrBI5H32Xz2QSGt6uKu73472Uo9sTs\n4ZWNr3D57mW+aP8FbzZ9EwuNgfeRrPUceDdQ9vIVFhR/vPBExIBPELzqQINX4ch8SLtZ/PEVnKO1\nBaOfCmLP5VscvHZH+eKhucrs3lNT1Q1nJH47Fcep2FQmdKzxn9m9fzN3ccHvxx/xmDSJtK1/Efly\nL3IuXCinpIJRaDMB7Dzgr/fBhGaBNZKGofWGEt41nHxtPgM3DWT1xdWPnOnOi4khsv8A7ixchHPv\n3gSsXoWl739vqLwc7EttH0c+3XyRnPxCZTnZzo+Uys11X9L3t2X0ZFnm000Xcbe3YnjbqmrHEYC8\nwjw+O/IZY3eOxdvOm7Xd19I1sKvasUpGkuDpd+DuDdEqS4/EgE8QQFlSoC2Avz9XO4lRGNQyEB8n\na2VZVGosHPgO6jwP3vXVjmbwsvIK+GzzJRr4OvFS48oleo6k0eA+YjgBS5egzc4msncf7q75WSzx\nFBRWDsprWNR+uLRJ7TQ619izcbFLPFP/+JMbL7xI3o0bVP56Dj4fTkdj9fCZJzONxHvP1SYuJZvw\n/ZHK6oS0OOj8kfLmU3isnReTOBKZzPiO1bGzEnuu1BaVFsWATQNYcWEF/Wv3Z+WzKwl0ClQ7VunU\n6AqVGiuzfAV5aqcxSWLAJwgArlUgOBSOL4Pk62qnMXjWFmZM6FidkzEp3Fz3lrL/pdMMtWMZhR/3\nXCchLYdp3eug0ZTuzaVtSIiyxLNpUxKmTyfu9dcpuHtXT0kFo9JkMLjXUPahFearnUbn7i3xnBQ8\n6Z8lnqdunUKbmUn8O+8S/8YbWNWoQdX/bcCxa/EzG62rudOxtierdh1Hu/crqPksBKrUhNqIFGpl\nPttykSrudvRp6qd2nApv47WNvLrxVeIz4/n26W+Z2mwqlmaWascqPUlSttekRMPheWqnMUliwCcI\n97SbAhoL2PWJ2kmMwstNfOnpEk2lmD/QthwHLoFqRzJ4cSnZ/LTnGj0aViIk0PWJzmHu5obfgvl4\nvvkm6bv3cOP5F8g8cEDHSQWjY2YOnWbCnatwbInaafRCI2kYUm8I4V3D0cpapi0ZyIkenUjdsAG3\nUSMJWL4Mi8olmzUHePvZ2oRp1yHnZUHH6XrLbUrWH4/lcmIGU7rULHY5uqA/WflZvLvvXd7Z9w61\nXGuxrsc6nvZ/Wu1YZVOtozLTt+dzSE9QO43JET+tgnCPgzc0f00pfpBY9v5Pps5ckplptYx42ZUN\n9q+qHccofLr5IgBTu9Uq03kkjQa3oUOo8vMaNPb2RA8NI/Gzz9HmiaUwFVqNLkpv0d2fQE5q8ccb\nqUYejQhPf4VZSwvJSbvL8pHVyB3yEpJ56ZYXBmkSGWi2jZ8Ln+KytpKe0pqOnPxC5my7TEM/Z7rV\n81Y7ToV19vZZev/Rm43XNjKy4UgWdVmEt52J/P/o8jEU5in9MAWdEgM+PZk+fTqzZ88GYNq0aWzf\nvv2JzxUYGEj9+vVp1KgRISHFttoQyqL1eLByhB1ieWKxTqzAKeU8qxyH8eWuWKX4gfBIx6KS2Xgq\nntfaVaWys41Ozmldpw5V1q/DpV9fksPDiXy1N7lXr+rk3IIRkiRlH1rWHZOtOpyfmEjM8BGkfvYl\nTm3bk7FwBrs9btNrYy82XNlQun2tO2agsbBigVlvZv0pCiEVJ3x/JDdTc3i7Wy3Dad5dgeRr85l7\nci4DNg0gqyCLRV0WMabRGMw1JrSP0i0IWo1TirdEH1Y7jUkp04BPkiRXSZK2SZJ0peizy0OOeVqS\npJP3feRIkvRC0WNLJEm6cd9jjcqSx1DNmDGDjh07lukcu3bt4uTJk/y74bygY7au0HYiXN4Cl7ao\nncZwZacog2L/lrR6fgTxqTksPxildiqDpdXKfLjxPN6O1ox8Kkin59bY2OA9bRq+8+ZSkJTEjZd7\niZ59FVmlRtCgDxycCykxaqfRGVmWSf39d6736EnWsWN4TXsf37k/0KXRK6zvuZ667nWZdmAak3ZP\nIiUnpfgTxhyF8/9Daj2e/s80Zc/lW+y+lKT/b8RIpWTlMXf3VTrU8vxvw3pB766nXGfApgHMOzWP\nblW6seH5DTT1bqp2LP1oOxkcKsGmN5T6AIJOlPW2wFRghyzLn0qSNLXo7w90XZZleRfQCJQBInAV\n+Ou+Q6bIsryujDketHkqJJzR6Snxrg/dPn3sIbNmzWLZsmX4+fnh4eFBcHAwAKGhoXTv3p1evXoR\nGBhIv3792LVrF/n5+cyfP5+3336bq1evMmXKFEaOHKnb3ELptRgDp9bApilQpS1Y2qmdyPDs+VyZ\nRej2K618PGhXw4Nvd1yhZ6NKeDlaq53O4Px6Io7TsanM6d0QW0v93I11ePppbH77H/HvvEvijJlk\n7NqNz8wZWHibyFIfoeQ6vAfn/6c0Y39pvtppyqwgOZmED6aTvm0bNo0bU+nTT7AMCPjncR97HxZ0\nWsDS80v57sR3nPr9FB+1/ohWlVs9/ISyDNveB3svaDmWQWa2rDgUxcebLtCmmjvmYm/af/yw6yoZ\nuQW82bWm2lEqFK2sZdWFVXx9/GtszG34sv2XdA7srHYs/bK0g84zYX0YHF8KIUPVTmQSyvqq9jyw\ntOjPS4EXijm+F7BZluWsMl7X4Bw7dow1a9Zw4sQJfv31V44ePfrIY/38/Dh48CBt27YlNDSUdevW\ncejQIaZNm/bQ4yVJonPnzgQHBzN/vvH/8jZ45pbQfQ6kRislgoUH3boER36CJoPApyEAH/asS26h\nlg83ir2P/5aZW8DnWy7S0M+Z5xuWvKDEkzD38MBv/k94vfceWRERXO/eg5R168RsX0Xj7ActRivN\nxONPqJ2mTNJ37OD/2rvv8Ciq9YHj37O76T0Q0gktEEJPkF5EehEIoDQLiop69QqKBf2JgpVrvxYs\nIApXmvSiUqWjQEIntIRAgBBCCqRnN3t+f0xAUEogm+xmcz7Psw+7k9nZd8hkdt4557wn8d7+5GzY\nQI3xLxD2v1nXJHuX6XV6Hm38KLP7zMbD0YMxa8fw5rY3/zF9AwCHV8Kp7dpUFk7uOBp0vNK7IUdT\nc5i3y35aRS0l6UIuP247yeCoECICPK0dTpWRkpPC46sfZ8rOKbQJbMPiAYvtP9m7rPFgCOsA696C\nvAxrR2MXynqr2V9KmQIgpUwRQtS4xfrDgI//tuwdIcREYB3wipSysIwx3bIlrjxs3ryZmJgYXF1d\nAejfv/8N1738syZNmpCTk4OHhwceHh44OzuTlZWFt7f3Netv3bqVoKAgzp8/T/fu3YmIiKBTp07l\ntzMKhLWDFg/A9i+h6VDwb2TtiGyDlPDbBHBwg65/3aCoXd2N57qG88GqI6w5lEr3SH8rBmlbpm5I\n4Hx2IV8/GH3b0zDcCSEEvg+MxL1TR1L+73VS/u91Lv36m9baF6QKU1QZHcZp08ysfh0eXl7p5pcr\nvnSJ1Hfe5eLSpTg1bEjQ99/j3KD+Ld/XsFpD5vWbx1d7v+LHgz+y+cxm3mj7Bp1CSr4zTYWw9g2o\n3gBaPHjlfT0b+dOqti8frz5K/2ZBeDg7lNeuVSpSSl5ZtA8ng47xPVTrXkWQUrI0YSlTdkzBLM1M\najeJmHoxVWvcpBDQewp80xF+fxf6fmjtiCq9W7bwCSHWCiEOXOcx4HY+SAgRCDQBVl21eAIQAdwF\n+PK37qB/e/8TQohdQohdaWlpt/PRFaa0f4xOJZPB6nS6K88vvzaZTP9YP6jkIq1GjRrExMSwY8cO\nC0Sr3FL3t8DZC5aPBbPZ2tHYhqO/QcI6uPsVcKt+zY8e71iHBv4eTFx6gJzCfx7HVVFyRh7fbk5k\nYPMgomr+Y4hzuXKsWZOaP8zAf+Lr5O3eTeK9/cmcN1+19lUVzp7a32nSZohfZu1obkv2+t9J7D+A\niytWUP3pp6g9b26pkr3LnA3OPB/9PD/1+QlPR0/+te5fvLr5VS4WXtS6o6cfh17valNZlBBC8Hrf\nSNJzi/hqQ0J57FalNHdnMn8kZvBq34YEeKnu+uUtOTuZMWvG8PrW16nvU5+F/RcyKHxQ1Ur2Lgto\nDHc9BrumW36YVhV0y4RPStlNStn4Oo+lQGpJInc5obvZiOf7gcVSyiszwkopU6SmEJgBtLpJHN9K\nKVtKKVv6+fmVdv8qTKdOnVi8eDH5+flkZ2ezfPlyi2w3NzeX7OzsK89Xr15N48aNLbJt5RZcfbWK\nd6d3aP3IqzpToda6V70BtHr8Hz92NOh4d1ATzl0q4KPVR6wQoO15/9fD6AS81Kts0zDcKaHT4Tti\nBHWWLcW5SRPOvfEGyaNHU3T6jFXiUSpY9Cit2/XKFyA33drR3JLx/HlOjx3H6aefRu/hQa05s/H7\n978Rjnc2kXTj6o2Z128eY5qO4dcTvzJgUV/WxU2F5iO1Ob/+pkmIF4Oigpm+5QRJF3LLujuV3rmL\nBby7Mp42dXzVJOvlzGQ28cOBHxi0dBD7LuzjtdavMaPXDEI8QqwdmnXdPQGcveGXl7QeRsodK+sY\nvmXAwyXPHwaW3mTd4cCcqxdclSwKtPF/B8oYj9VERUUxdOhQmjdvzuDBg+nYsaNFtpuamkqHDh1o\n1qwZrVq1om/fvvTq1csi21ZKodlwbV6rtW9AThWv4PbHV5B5Anq9B/rrd3eKDvPhgdZh/LAtiT3J\npaiUZ8f+TExn5f4UnuxclyALTcNwpxxDQqg543sCJk0if89eTvTvT8bMmcjr9ChQ7IjeAQZO1arq\n/vqitaO5IWk2kzlvPol9+5Gzfj1+Y8dSe+ECXJo2LfO2HfWOPNPiGeb0molfQTZja1RjvKeB9Pzr\nJ8Av94rA2aBj/M97KTZX3QtMKSWvLz1AUbGZ9wc1rZotTBUkPj2eEStH8FHsR7QJbMOSAUsYFjEM\nnVDFg3D11YaPnNoGBxZaO5pKTZSle48QohowH6gJnALuk1JmCCFaAk9KKR8rWa8WsBUIlVKar3r/\nesAPEMCekvfk3OpzW7ZsKf8+PUF8fDwNGza8432p7Kr6/pertKMwtR00ioHB31k7GuvIPgefR0Pt\nTjB8zk1XvVRgpPvHG/F1c2LZM+1xqIIV7/KKTPT97xaKTGbWPt8ZF0e9tUO6wnjmDCmTJpG7aTNO\nDRsS+MZEXJrb5Yw4ymUbP4Df34b7Z0HkjceXW0NhYiIpEyeSvysW11atCJj0Jk61a1v+gzZMwbjh\nXWZ0fJypZ9fhYnDhuRbPMaT+EPS6a/8+F+8+zbh5e5nQO4IxnS07jUplsXJfCv+aHVel/w/KW74p\nn6l7pzLz4Ey8nbyZ0HoCPcJ6qOT678zF8F0XyEmDZ3aCk7u1I7IpQohYKeUtJ+ku05WYlDJdStlV\nShle8m9GyfJdl5O9ktdJUsrgq5O9kuX3SCmblHQRfaA0yZ6iVDi/+loBhP3zIeF3a0dT8aSE5c9B\nsVHr4noLns4OTOrfmPiUS0zfcqICArQ976yMJyk9lw/ua2pTyR6AQ3Awod98Q/Bnn1GckUHS8BGk\nTHyD4qyq3SJr1zqM1bp2rhgHuResHQ0A5qIi0r78khMDBlJ47DiB77xNzR9/KJ9kL/UgbPoAhyb3\n8UTXD1nYfyGRvpG8/efbjPxlJAcvXFtdeGDzYHo28uej1Uc5mnqdKp92LjO3iDeWHaBJsBejO5TD\n70Nh29ltDF42mBkHZjCg3gCWDlxKz1o9VbJ3PTo99P4Ass/CZlW85U5VvVvvinInOr4AvnW0sTDG\nAmtHU7F2TtOKtXSfBNVKd6e3V+MAekT68+nao5xKt7tZWG5q/eFUfvrzFI91qE27utVv/QYrEELg\n2bMHdVauxPehh8hauJCEPn3JWrxEFXWxR5e7dhZc1CYztrKcTZs4MWAgFz7/Ao/u3am7cgXegweX\nz8VusQmWPA0u3tD7PwDU8arDdz2+Y0rHKaTmpTJ85XDe/uNtragL2t/HOzFN8HA28Pz8PRiLq1bR\nrrdXxpOVZ2TK4KZqTkILO519mrG/j2XMmjEIBNN7TGdSu0l4OXlZOzTbVrM1NH8Atn4Gp/6wdjSV\nkvpLVpTScHCGvh9DRgJs+fvMInbsfDys/j+twEHrJ2/rrZMGNMKg0/Hakv1VJolIzynkpQX7iQjw\nYHxP2y9hrnd3w3/CK9ReuADHmjVJmTCBUw8+ROGxY9YOTbE0/0Zw98twcDEcXGKVEIqSkkh+8imS\nnxgDZjOh335D8McfYahejjdGtv0XUvZAnw+18UAlhBD0qdOHZQOXMbLhSH4++jP9l/Rn6fGlSCmp\n7u7EOzFNOHDmEl+sP15+8dmYTUfTWBh3mic71yUySM25Zyn5pny+3PMlA5cOZNvZbTwX9RyLByym\nVeANaxUqf9frPfCuCQsfg/xMa0dT6aiET1FKq24XaHIfbPkELlSBC2JjgXZidXTXWgdu8+57oJcL\nL/ZswOZjF1i652w5BWk7tPmq9nMp38inw5rjZLCtrpw34xwRQdjsnwiYPImCY8dIjBnEubfexpSp\nvlTtSvtxENi8pGpnxXXtLM7J5fyHH5Jwb3/yduygxovjqbN8Ge7lPZ9s2hHY8B5EDoBGA6+7ioej\nBy+3epl5/eYR6hHK/239P0b9NoqD6Qfp1TiAQS2C+eL34+w7bf9dnnMLTUxYtJ86fm48c089a4dj\nF6SUrE5azYAlA/h679fcU/Melg1cxmNNHsNRf2fVZ6ssZ08Y/D1kp2jDTKrIjWRLUQmfotyOnu+C\ngwssetz+u3aumwSpB2DgV+Be44428UCbMJqHejN5xSEyc4ssHKBtmb8rmTWHUnmxZwMiAirfnXGh\n0+Fz//3U/fUXvIcMJnPOHBJ69CR9+veYi+z7d1dl6A3azZvCS1rSV86k2UzW4iUk9O5F+rTpePXt\nS53ffqXa6NF3PNVCqZmLYem/tBtWfW497ifCN4KZvWcyqd0kTlw8wbAVw5iweQJjuvri5+7E8/P3\nUmAsLt+YrezD1Uc4ezGf/wxuirND5blhZauOZx7n8dWP88LGF/Bw9GBGzxn8p9N/CHALsHZolVdI\nNNzzf3BoKcTNtHY0lYpK+MrJm2++yYcfal8yEydOZO3atXe8raysLIYMGUJERAQNGzZk+/btlgpT\nuV3uNbQLprO74beXrR1N+Tm2VpuG4a7HoX7PO96MXid4f3ATLuUbGf/zXsx2Wub8ZHouk5Yfom2d\napW+yIHB15fAN9+kztIluLRozvkPPiCxT18u/baqynTNtWv+kdD5ZTi0ROveWU7y4naTNHw4KRMm\n4BAYRK15cwl6/z0catzZzaPb9sdUOL1TG7dXyhtWOqFjUPggVg5ayejGo1mdtJqRvw2ifasdHL9w\nwa7nF409mckP25J4sE0YLWv53voNyg2dzzvPpO2TGLJ8CPEZ8bzW+jXm9ZtHy4BbFlJUSqPdc1Dn\nbvj1Za0VXykVlfBVgMmTJ9Ot2z8neS2t5557jl69enH48GH27t2rpl+wtoi+0OF5iP0B4mZZOxrL\ny70AS54Cv4bQ460yby4iwJOJ90ay7vB5Pl1nf11hTcVmxs3bg14n+Oj+Zuh09lFlzSk8nJrffkvo\ntGnoXFw4M3YsJ0c+QP6+fdYOTSmr9mMhqIXWypeTZtFNFxw5QvKTT3FyxAiMZ88S+N571Jo7B5dm\nzSz6OTeVngDr34IGfaDJkNt+u4ejB2Ojx7IiZgXdw7qz+sxsqkV8zA8HZrMtwf7mY71YckMu0NOZ\nl3pFWDucSutS0SU+jf2Uvov6suT4Eu5vcD8rYlYwLGIYBp3B2uHZD50OYr4BR1dY8Kj997ayEJXw\nWdA777xDgwYN6NatG0eO/HXXYdSoUSxYsACAWrVq8eqrr9K2bVtatmxJXFwcPXv2pG7dunz99df/\n2OalS5fYtGkTo0ePBsDR0RFvb++K2SHlxu75P+0O08oXtNY+eyGl1g2q4CIMnqZ1X7WAB9uEcV90\nCP9dd4xVB89ZZJu24uuNCcSdyuLtgY2tPsF6eXDv0J7aSxYTMHkSRadOkXT/UE6PG0dhQoK1Q1Pu\n1JWundmw8nmLjIUpSk7mzIsvcWJgDHmxsfiNG0e9VavwjhmI0FXgpUZRrnYRqHfSCm2VofJnoHsg\n73V8j7l959KoejjOAUt5asMIfk1YYzet3aZiM8/MjuN0Zh6fDmuBu5NKTG5XgamAGQdm0Hthb6Yf\nmH5lnN6rrV/Fx9nH2uHZJ48A7RyWegDWTLR2NJWCXf5lT9kxhcMZhy26zQjfCF5udeMufLGxscyd\nO5fdu3djMpmIiooiOjr6uuuGhoayfft2xo0bx6hRo9i6dSsFBQU0atSIJ5+8thJiYmIifn5+PPLI\nI+zdu5fo6Gg+++wz3NzcLLp/ym3S6WHwdPimM8x7CMZsvKYCXKV1eQqGXu9DQGOLbVYIwVsDG3P0\nfA7Pz9vDkn+1J9zfw2Lbt5Z9p7P4dO0x7m0WxIDmwdYOp9wIvR6f++/Hs09f0qdPI+PHmWT/tgrP\nfv2o/vRT5TN3mlK+ajSELq/B2je0QlQdn7+jzZjS0rgwdSqZ839G6PVUe2w01UaPRm+NG5NmMywe\nAyl7Yfgc8Ay0yGYbVW/Ej71n8F3sCj6L+4SXtjzPjEMNebr503QO6Vyp505755d4Nh+7wJTBTWhV\n2w6+wyqQyWxiecJyvtzzJal5qbQPbs/YqLFE+KpW0gpRvye0fgr+nKoV1WvQ29oR2TTVwmchmzdv\nJiYmBldXVzw9Penfv/8N1738syZNmtC6dWs8PDzw8/PD2dmZrL9NfmwymYiLi+Opp55i9+7duLm5\n8f7775frviil5FYdhs6EnHNaNUtzJR/Qf3kKhrpdodUYi2/e2UHP1w9E4eKo54lZsVzMN1r8MypS\nXpGJsfP24OfhxNsDLJcc2zK9uxs1nnuOemvXUG30o2SvXUti336cffkVik6etHZ4yu1q/5xWeXjd\nJNi/4LbeasrM5PzHn3C8R08y583He8hg6q5eTY0XXrBOsgfafsQv14prWfjiTwjBEy3vZWTIf8k/\nO4SzlzJ5dv2zDFs5jI3JGytli9+cHaeYsTWJ0R1qM/SumtYOp9Iwmo0sT1jOoGWDmLhtIjVca/B9\nz+/5utvXKtmraN0nQUATba7NSynWjsam2WUL381a4spTae/yOTk5AaDT6a48v/zaZDJds25ISAgh\nISG0bt0agCFDhqiEz5YER0OfD7QSwRveh3tes3ZEd6Yo99opGMqpC1aglwtfjYxmxHd/MG7eHqY9\n1LJSjnkrMpl58n9xJF3IZdbo1ni5Olg7pApl8PWlxvjx+I4aRfq06WTOmcPFFSvwGjiA6k89hWNI\niLVDVEpDCBjwJVw8o43b9QyGsLY3fYsxJYX0GTPI+nkBMj8fzz598Pv3szjWqlUxMd9I3EzY+im0\nfBTaPFVuH/Nyr0acSi/kt/0tGNUjnT8z5/PM+meIrBbJ082eplNIp0rR4vdHYjqvLzlAp/p+TOit\nkpTSKCwuZOnxpXx/4HvO5Jyhvk99Prn7E7rW7Fopfud2yeCkTdXwbWetevpDS7UeWMo/qBY+C+nU\nqROLFy8mPz+f7Oxsli9fbpHtBgQEEBoaemVM4Lp164iMjLTIthULiXoYWjwAm/4DR35uFTCzAAAe\naUlEQVS1djS3z1gAc4bD+UNasufhX64f16q2L2/cG8n6w+f5ZO3Rcv2s8lBsljw/fw+bjqbxbkwT\n2tcrx0mjbZyhenX8X3mZumtW4zNyBJeWryChV2/OvvwKBUdU9bRKweAEw34C7zCYOxwuXH+S8cLE\nE5x99TWtRe+n2Xj26EGdFcsJ/vgj6yd7JzbBinFQ9x6tKmc5XnzrdYJPhzXnrlrVmb0ugFebzmBy\nu8lcLLzIM+ufYfjK4aw7uY5iG+7xkZyRx1P/i6VmNVc+H94Cg15dCt5MnjGPHw/+SO+FvXnrj7eo\n5lyNz+/5nAX3LqBbWDeV7FmbX33oPQWSNmtd1Ctha3tFsMsWPmuIiopi6NChNG/enLCwMDp27Gix\nbX/++eeMHDmSoqIi6tSpw4wZMyy2bcUChNDmeTq3HxaNgSd+h2p1rR1V6ZiK4OeH4cRGLdmr36NC\nPvaBNmHsP3ORz9cfp1GQJ70aW2asTXmTUjJx6QFW7Evhld4RDGulukEBONSoQcCrr1Jt9GjSp00n\na+FCLi5dilu7dvg+8ghuHdqriyJb5uoLI3+Gad3gpyHw2FqtyzqQf/Ag6d9+R/bq1QhHR3zuv59q\njz6CQ7CNjFm9cAzmPQjV6sF9P4C+/FvbnR30THvoLoZ8vY2n/7eXn5/qyvKYfqxIWME3+75h7Iax\nhLiH8EDkA8TUi8HVwbXcYyqt7AIjo3/ciVnC9IfvwsulavVOuB0XCy8y5/Acfor/iazCLFoFtOLd\nju/SOqC1Op/ZmhYPwtk9sO1zMLhU3t5W5UhUxn7nLVu2lLt27bpmWXx8fJWerqCq779NyDypdSvw\nCILRq8HJ3doR3Zy5WKtmd2gJ9P0I7nqsQj++wFjM0G//4FhqNkv+1Z76laCIy4erjvDF78cZ07kO\nE3qrv7cbKb54kcx588mcNQtTWhpO4eH4PvIInv36oivvCbeVO5e8E37sh6zRmJyaL5A5fwG527aj\nc3fHZ8QIfB9+CEO1ataO8i95GfDdPVq10cfXgU+tCv34M1n5DP5qGxLJoqfbE+ztgslsYv2p9cw6\nNIs9aXvwcPBgSP0hjGg4wuoTbhebJU/M3MWGo2n8+EgrOoRX3d4JN3Mk4whzDs9hZeJKCooL6BTS\nicebPE7zGs2tHZpyM2YzLP837J6lFaTq/JK1I6oQQohYKeUtJ3lUCZ+dqOr7bzOOr4Wf7tPmuBrx\nM7jZ0MXR1cxmWPYM7PkJur8F7f9tlTDOXSyg3+dbcHfSM29MW/w9na0SR2lM25zI2yvjGXZXKO8N\naqLu8JaCLCri4spfyJgxg8KjR9H7Vcd35Ei8Bw/G4Odn7fCUvzFduEDWV2+RueRXTHl6DAEB+IwY\ngc/wYeg9bOyGjKkQZg6EM7EwagWEtrJKGIfPXeK+qdvx93JmwZNt8Xb964bG3rS9zDo0izUn1yAQ\n9AjrwUONHqJxdesUeXr/18N8vTGByQMa8VDbWlaJwVYZzUbWn1rP7PjZxJ2Pw0nvRN86fRkRMYIG\nvg2sHZ5SWmYzLH0a9s6Bbm9Ch3HWjqjcqYSviqnq+29TDq+Enx8BnzB4cDF42VgBCynhlxdh53fQ\n+RXoMsGq4cSezOCh6TvwcnHgh0db2WRL34LY04z/eS+9GwfwxYgo9JWw0Iw1SSnJ3bqNjBkzyN26\nFfR63Lvcjc999+HWoQNCrwbZW4uUkvzdu8mcPYdLq1aB0YhrwxB8qu3DY/BoRO93rR3iP0mpFZnZ\nO0ebHucOJle3pG0JFxj1/U6ahXoxa3RrnB2uPZ7P5JxhdvxsFh1bRI4xh4a+DYkJj6FP7T54OXlV\nSIw/bkvijWUHGdm6Jm8PbKxuWJW4kH+BBUcX8PORnzmff55g92CGNRhGTHhMhf1uFAszF8OiJ+DA\nAq1ib9t/WTuicqUSviqmqu+/zUnaohVCcfLQkj4/G7lDKKU2qHnrZ9DuWa11zwa++A+cucgjP+yk\n0FjMtw+1pE0d22kZXX3wHE/9FEfbOtWYPqolTgaVnJRFYeIJshYu4OLiJRRnZGAICMB7UAxegwbj\nGGIj48KqAFN6Opd++ZWshQspPHwYnbs7XjEx+Awfps2rePmmUI+3oe0zNnGeALSWvZXPw+7/wd2v\nwt3Wqcr9d8v3nuXZObvp1SiAL0de/6ZQTlEOyxKWsfj4Yg5nHMZR50i3sG7EhMfQKqAVOmH54imm\nYjNvr4znh21JdGtYg6kPRONQxYu0FBUXsen0JpYnLGfTmU2YzCbaBbVjRMQIOgR3QK+qPFZ+xSZY\n8AjEL9NqLLR63NoRlRuV8FUxVX3/bVLKPvjfYDCbYOQCCIm2dkSw8QP4/W2tdHnfj23nIg6tctyo\nGTtIzsjno/ubcW+zIGuHxPaEdB6esYOGgZ7Mfqw1bk6qzpWlyKIisn/fQNaCBeRu2QKAW7t2eMXE\n4NHlbnRublaO0P6Y8/LIXreei8uXkbt1GxQX4xQRgc+wYXjd2+/a//NiEywYpc1r13ykNs7XwcVq\nsQPaPFvzHoAzu6DTS9DlVZs6h03fcoK3Vhyib9NApgxuivtNzheH0g+x6Ngifkn8hWxjNsHuwQys\nN5ABdQcQ6G6ZIlaXCow8M3s3m46mMbpDbV7t07DK9k6QUrI3bS/LE5bzW9JvXCq6RDXnavSp04f7\n6t9Hba/a1g5RsbRiI8x/GI6shH6fQstHrB1RuVAJXxVT1fffZmUkwqwYyEmDobOgXlfrxGE2w5aP\nYP3b0Gw4DPiq3ObaK4usvCKemBnLjqQMXuvTkMc61rZK1yMpJTO3n+TdX+Kp6evK/DFt8XFTxUbK\ni/HMGbIWLSZr0SJMKSkIJyfcO3XEo2cv3O++G727Sv7ulDSZyN2+nYvLl5O9dh0yLw9DYCBe/frh\neW8/nOvXv/GbzcWw8T+w8X1tcuP7Z4GvlS6Mk3doyV5hDsR8DZH9rRPHLXy9MYH//HaYsGpufDGi\nBY2Cbt4tsMBUwLpT61h8bDF/nvsTgKZ+TeleszvdwroR4nFnQwJOpecx+sednLiQy1sDGzO8ilYU\nPnXpFCsTV7I8cTnJ2ck46525p+Y93Fv3XtoEtsGgUzfx7JqpUKvie2wV9P8Coh60dkQWpxK+Kqaq\n779Nyz4H/xsCaYe1C5WKHm+SkQhLn4GTW6HxYIj5FvS2+yVXYCzmhfl7Wbk/hVHtavF6v8gKvSt9\n/lIBLy7Yx8ajaXRp4McH9zWjurtThX1+VSaLi8mPi+PSb6vIXr0aU1oawskJt44d8OzVWyV/pVSc\nk0vutq3kbNhIzoYNFGdkoPP0xLNnT7z634tLdDTidm74HF2lTWqMgEHfVdj0LVfE/ggrXwCvYBg2\nB/xtey7aPxPT+ffc3WTmGXm9XyQPtK5ZqhtXydnJ/HbiN9acXEN8RjwADX0b0qNWD7rV7EYtr1ql\n+vydSRmMmRVLsVky9YEo2tWtOtU4i83F7L+wnw3JG9iQvIGEiwkIBK0CWtGvbj+6h3XHzUGdQ6oU\nY4E2x2jCeq0aedc3wNnT2lFZjEr4qpiqvv82Lz9LG9N3ajv0fAdaPwnlPU7AbNbG4Kx9E3QG6PWe\n1jXLhrpA3YjZLHn3l3imbTlBz0b+fDasxT8KIZSH3w6cY8KifeQbi3mtb+kv1BTLk2bzX8nfqlVa\n8ufoiGurVri1b49bu3Y41Q9Xv58SRcnJ5Py+gZwNG8jduROMRnSenrh36IBH7164d+5ctikxMk5o\nd8pTD0Dnl7VHefcSMBXBqgmwc5o2qfrg6dqcgZVAek4hz8/fy8ajafRtGsh7g5rg6Vz6Oe+Ss5NZ\nd3Ida06tYV/aPgDqedejS2gX2gS2oVmNZjjp/3kjamHsaSYs2k+IjwvTR91F7er2n9zkGfPYfnY7\nG05vYNPpTWQUZGAQBqL9o+kc2pnuYd2tPiWGYmXGfFg3Gf6YCp5B2pCWBr2sHZVFqITPyt58803c\n3d0ZP348EydOpFOnTnTr1u22t3PkyBGGDh165XViYiKTJ09m7Nix16xna/uvXIcxHxaM1vqT14iE\nrhOhfq/yScAyTpS06m2Bet3g3v9qd8crmelbTvD2ykM08PdgXPf69Ij0L5cL/NxCE5OXH2LermQa\nB3vy6dAW1Kth4/MoViHSbCZ/924urVpF7patFCUmAmDw88OtXVstAWzbtkpN9WBKTycvLo78XbHk\nbNlCUUICAI516uB+9924390Z1xYtEA4WnFi7KE9rads7G+p1h0Hfll8ClpMG8x+CU9ug/XPaXflK\nVkzDbJZ8symRD1cfIcTHhS+GR9Ek5PYrP57LPce6U+tYc3INe87voVgW46R3IqpGFG2C2tAmsA21\nPML577oEvt6YQLu61Zg6MhovV/ucVL3AVMD+C/uJTY0lNjWWuNQ4isxFeDh40CGkA11Cu9A+uD2e\njvbTiqNYyOldsOxZOH9I6/HUawq4V+7vDZXwWdnVCZ+lFBcXExwczJ9//klYWNg1P7O1/VduwGyG\nQ4th/TuQkQChrbULmVrtLbf9XdNhTcnFUc93oMWDlaJV70bWHkrlrZWHOJmeR8NAT/59Tz16NgpA\nZ6FunnGnMhk3bw+nMvJ4+u66PNe1Po4G2xvfqPzFmJJC7rbt5G7dSu727RRnZgLgFB6OS/PmODdp\njEvTpjjVq4cw2G735dKSUmI8eZK82Djy4mLJj42jKCkJAOHoiEt0FB5duuDeuTOOf/tuKIdgIHYG\n/PISeAZq56+IfuBgoTk0s1Mh7kfY8Z02ofqAL6w+7UJZ7UrK4Nk5u0nPKWJCnwgebBOG4Q4rZeYa\nc4lNjWX72e38kfIHx7OOaz8odsWYW4dmfs0Y27ELTfwa4e5oHzetcopy2JO250qCd+DCAYxmIwJB\nfZ/63BVwF11Cu9DCvwUOOvtMchULMhXB1k9h0wfg6KZN3dBseKW9TqqQhE8IcR/wJtAQaCWl3HWD\n9XoBnwF6YJqU8v2S5bWBuYAvEAc8KKUsutXn3irhO/fuuxTGH77Dvbo+p4YRBLz66k3Xeeedd5g5\ncyahoaH4+fkRHR3N+PHjGTVqFP369WPIkCHUqlWLESNG8Pvvv2M0Gvn222+ZMGECx48f58UXX+TJ\nJ5+84fZXr17NpEmT2Lp16z9+phK+SqbYqJUV3zgFslO0u+VdJ0Jg0zvbnqkQTv2hncCSNmvdn/p/\nbntzAN4hU7GZZXvP8sX64yReyKWBvwfPdq1Hn8aBd5T45RcVs/lYGqsOprJkzxkCPJ35ZGhzWtWu\nHN3FlL9Is5mC+Hhyt20j788d5O/fj/niRQCEszPOkZG4NGmMc5OmOEc2xDEkBFGWro3lzFxYSFFC\nAoXHjlF47BgFx45RcPAQxRcuAKDz8sI1KgrX6ChcoqJxbtyobF0179TpXdq4voxEcPaGZsO0m0sB\ndzCpuJRwcpvWdTN+mVbZuO490G3SnZ8TbUxmbhHjf97LusPnqe7uSL+mQfRvHkSLUO876rWQkJbD\ntM0nWLT3EMVOxwgNOoN0PkZ6YeqVdWp51qJR9UY0qtaIyGqRRPhG2PT4NSklZ3PPcjTjKEcz/3qc\nyj6FWZoxCAOR1SKJ9o8m2j+a5jWaq7nylDuXdgSW/RuS/4A6XaD3FKhev9IlfqVN+Mp66/MAMAj4\n5iaB6IEvge7AaWCnEGKZlPIQMAX4REo5VwjxNTAamFrGmKwiNjaWuXPnsnv3bkwmE1FRUURHX78M\nf2hoKNu3b2fcuHGMGjWKrVu3UlBQQKNGjW6a8M2dO5fhw4eX1y4oFUnvoJUIbjYMdnwLmz+Gbzpq\nXQyajwCf2uAVCoYbXMhJqRWBSVivPZK2gikfHD207ptRD1W6k9bNGPQ6BkWFMKB5MCv2neW/647x\nzOzdhNc4xrNdw+lc3w9PZ8NNL5wu5BSyPv48qw+lsuV4GgVGMx7OBobdFcrLvSNua3yNYjuETodL\no0a4NGoEjz+utYYlJ5O/bz8F+/eTv38/mfPmI3+cqb1Bp8MhKAjHWrVwDAvTHrW15wZ/f3RO5Vug\nR0qJOScH07lzGM+lYko9h/FsCoXHj1N47BhFJ09qLfUADg441amDW7u2uEZF4xodhWPdurdXcKW8\nhLSEZ2LhxEbYPQt2fQ9/fg1BUVolvMZDbl0YoTAb9s6FndMhLR6cvbTxzS0fhWp1K2Y/KoiPmyPT\nHm7JmkOpLN1zljk7TvHDtiRq+royoHkQA5oHUa+Gx023IaXkzxMZfLcpkXWHz+No0DE4qiGjO/S9\n0gU9oyCDQ+mHOHjhIAfTD7Lz3E5WJq68so3qLtWp6VGTUI9QQj1CqelZU3vtGVohXSCNxUZS81JJ\nyU3hXO45UnJTOJtzloSsBI5lHSPXmHtl3VCPUMK9w+lduzdR/lE0rd4UVwfXco9RqSL8GsAjv2q9\nota+CV+2As8QrcdVWHuo1QF869jNtZRFunQKITYA46/XwieEaAu8KaXsWfJ6QsmP3gfSgAAppenv\n692MLXbp/PTTT8nIyGDy5MkAPP/88wQFBV23hW/r1q0EBwfz/fffs337dr777jsAatasyb59+/D2\n9v7H9ouKiggKCuLgwYP4+/v/4+fW3n+ljPKzYNvn8MdXYMzTlgkdeASBTxj41ALvMHCrDmditSQv\nO0Vbr3p97W54nS7aCcrJPrrx3EyxWbJyfwqfrzvGsfM5ADgadPi5O+Hn8dejhocTeiHYeDSN2FOZ\nSAnB3i50j/Sne6Q/rWr7VvlJiKsCaTJdaTErSkqiKOkkRSdPUpSUhDk395p1da6u6KtVQ+/rg8HH\nF72vLwZfH/Q+PggHRzDoEQYDwuCAcDAg9HowGECCOT8Pc14eMi8Pc14+5ry8K4/ijHQtwTt3DnNe\n3rUBCoFjzZo41Q/HKTwcp/r1cQoPx7FmTcuOwStPeRmwbz7EzYTzB8Hgok1DY3DWWuxksTbNg7lY\ne202aeeyohwIbAZ3Pa7d8HKsGhf02QVGVh1MZemeM2w9fgGzhMhAT9rVrUahyUxuoYncIhO5hcXk\nFJrILTRxMd/I+exCfN0cebBNGA+2DStVBeG0vDQOpR/iaOZRkrOTOZV9iuRLyZzPP3/Nei4GF7yd\nvK95eDl54ePsg5eTFw46B/RCj07o0OtK/hV69EKPRJJnzCPXmEuOMecfzzMKMkjJTeFC/gUk1153\n+jj5UMe7DuHe4dT3rU99n/rU865n062Rip25dBbiV2h1D05ug9w0bbl7AIS105LAuvdoCaCNqagW\nvtIIBpKven0aaA1UA7KklKarlt+wqoQQ4gngCdASI1tU2m4ZTiV3kHU63ZXnl1+bTKbrvufXX38l\nKirqusmeYgdcvKHr69DuGUg9BFknITMJMk9qz69O8Fx8oM7dfyV53qFWDNw69DpB/2ZB9GsSyMaj\naSSk5ZCWXag9cgpJzsgj7mQm6blaD/FGQZ481zWc7pH+RAZ6qsqOVYwwGHBu2BDnv90Uk1JSnJ6u\nJYEnT2JKS8OUkUFxRibFGRkYU1MpiI+nOCMDaTTe/ue6uqJzdUXn4oLB1xen8HDcO3bA4B+AQ4A/\nhoAADDX8cajhZ9PdTEvF1RfaPAmtx8DZOIibpbX+IbTxxDoDCH3Jc732PHKA1poXHG03d9FLy8PZ\ngSHRIQyJDiEtu5AV+86yZM9ZZv1xEldHPW5OBtwcDbg56fFwNhDg6Yybk4HoMB8GRQXfVtViP1c/\nOrt2pnNo52uW55vyOZ19+koCmJafRlZh1pXHmZwzZBVmcano0m3vn5PeCTcHN1wNrrg7uuPt5E2H\n4A4EugUS4BZAgFsAgW6B+Lv542Jwue3tK4pFeQZB6ye0h5Rw4ZiW/CVt1aa0OrhIKx7VfbK1I71j\nt0z4hBBrgevVs31NSrm0FJ9xvbO4vMny65JSfgt8C1oLXyk+t0J16tSJUaNG8corr2AymVi+fDlj\nxoyx2PbnzJmjunNWBS4+JQVcrlPExVgAuefBM7jSVasrLzqdoEtEDbpE1Ljuz43FZvKNxaq7pnJd\nQggM1atjqF4d15Y3vkEqpUTm5SGNRqTJVPIoBtNfrxHiSnKnc3VFODvbRtfLiiaElsAFX39Ig/JP\nfh5OPNK+No+0r9hJ7V0MLoT7hBPuE37T9UxmE9lF2RjNRszSTLEsxmwu+bfkNYCbg5uW5Dm4quIp\nSuUlBPjV1x4tH9USwIxE0Ffum3K3TPiklLc/l8C1TgNXN0GEAGeBC4C3EMJQ0sp3eXmlFBUVxdCh\nQ2nevDlhYWF07NjRYtvOy8tjzZo1fPPNDYdKKlWBgzN422brtq1y0OtUl02lzIQQCDfVvUypmgw6\nAz7OPtYOQ1GsQwi7GFNcEWP4DMBRoCtwBtgJjJBSHhRC/AwsvKpoyz4p5Ve3+jxbHMNnbVV9/xVF\nURRFURSlKintGL4y3foWQsQIIU4DbYGVQohVJcuDhBC/AJS03j0DrALigflSyoMlm3gZeF4IcRxt\nTN/0ssSjKIqiKIqiKIqi/KVMRVuklIuBxddZfhboc9XrX4BfrrNeItCqLDEoiqIoiqIoiqIo12dX\ng1ss0T21Mqqq+60oiqIoiqIoys3ZTcLn7OxMenp6lUt+pJSkp6fj7Oxs7VAURVEURVEURbExFTEP\nX4UICQnh9OnTpKWlWTuUCufs7ExISIi1w1AURVEURVEUxcbYTcLn4OBA7doVO4eNoiiKoiiKoiiK\nLbObLp2KoiiKoiiKoijKtVTCpyiKoiiKoiiKYqdUwqcoiqIoiqIoimKnRGWsaimESANOWjuO66gO\nXLB2EIrdU8eZUt7UMaZUBHWcKRVBHWdKebPmMRYmpfS71UqVMuGzVUKIXVLKltaOQ7Fv6jhTyps6\nxpSKoI4zpSKo40wpb5XhGFNdOhVFURRFURRFUeyUSvgURVEURVEURVHslEr4LOtbawegVAnqOFPK\nmzrGlIqgjjOlIqjjTClvNn+MqTF8iqIoiqIoiqIodkq18CmKoiiKoiiKotgplfApiqIoiqIoiqLY\nKZXwWYAQopcQ4ogQ4rgQ4hVrx6PYByFEqBDidyFEvBDioBDiuZLlvkKINUKIYyX/+lg7VqVyE0Lo\nhRC7hRArSl7XFkL8WXKMzRNCOFo7RqVyE0J4CyEWCCEOl5zT2qpzmWJpQohxJd+XB4QQc4QQzup8\nppSVEOJ7IcR5IcSBq5Zd9/wlNP8tyQn2CSGirBf5X1TCV0ZCCD3wJdAbiASGCyEirRuVYidMwAtS\nyoZAG+BfJcfWK8A6KWU4sK7ktaKUxXNA/FWvpwCflBxjmcBoq0Sl2JPPgN+klBFAM7TjTZ3LFIsR\nQgQD/wZaSikbA3pgGOp8ppTdD0Cvvy270fmrNxBe8ngCmFpBMd6USvjKrhVwXEqZKKUsAuYCA6wc\nk2IHpJQpUsq4kufZaBdIwWjH148lq/0IDLROhIo9EEKEAH2BaSWvBXAPsKBkFXWMKWUihPAEOgHT\nAaSURVLKLNS5TLE8A+AihDAArkAK6nymlJGUchOQ8bfFNzp/DQBmSs0fgLcQIrBiIr0xlfCVXTCQ\nfNXr0yXLFMVihBC1gBbAn4C/lDIFtKQQqGG9yBQ78CnwEmAueV0NyJJSmkpeq3OaUlZ1gDRgRknX\n4WlCCDfUuUyxICnlGeBD4BRaoncRiEWdz5TycaPzl03mBSrhKztxnWVqrgvFYoQQ7sBCYKyU8pK1\n41HshxCiH3BeShl79eLrrKrOaUpZGIAoYKqUsgWQi+q+qVhYyRiqAUBtIAhwQ+te93fqfKaUJ5v8\nDlUJX9mdBkKveh0CnLVSLIqdEUI4oCV7P0kpF5UsTr3cPaDk3/PWik+p9NoD/YUQSWjd0e9Ba/Hz\nLukSBeqcppTdaeC0lPLPktcL0BJAdS5TLKkbcEJKmSalNAKLgHao85lSPm50/rLJvEAlfGW3Ewgv\nqQLliDZAeJmVY1LsQMlYqulAvJTy46t+tAx4uOT5w8DSio5NsQ9SyglSyhApZS20c9d6KeVI4Hdg\nSMlq6hhTykRKeQ5IFkI0KFnUFTiEOpcplnUKaCOEcC35/rx8nKnzmVIebnT+WgY8VFKtsw1w8XLX\nT2sSUlq9lbHSE0L0Qbsrrge+l1K+Y+WQFDsghOgAbAb289f4qlfRxvHNB2qifcHdJ6X8+2BiRbkt\nQoi7gfFSyn5CiDpoLX6+wG7gASlloTXjUyo3IURztMJAjkAi8AjaTWd1LlMsRggxCRiKVuV6N/AY\n2vgpdT5T7pgQYg5wN1AdSAXeAJZwnfNXyc2GL9CqeuYBj0gpd1kj7quphE9RFEVRFEVRFMVOqS6d\niqIoiqIoiqIodkolfIqiKIqiKIqiKHZKJXyKoiiKoiiKoih2SiV8iqIoiqIoiqIodkolfIqiKIqi\nKIqiKHZKJXyKoiiKoiiKoih2SiV8iqIoiqIoiqIodur/AV+pxnbDP75sAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=(15, 5))\n",
"pe = PositionalEncoding(20,0)\n",
"y = pe(torch.zeros(1,100,20))\n",
"plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())\n",
"plt.legend([\"dim %d\"%p for p in [4,5,6,7]])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"This is what these positional encodings look with dropout:"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3YAAAEyCAYAAAC2+0LeAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsnXd8U+X+x98nOx1JJ6uMtuy9RFDB\ngShLQREEBfde1/G7qKjXdfV6r3tvBRRElqCgCIgoONhLhqyyV1vaNOlIs87vj9PTMjpy0rRp4Xm/\nXn2lpGc8Kc2T5/N8vkOSZRmBQCAQCAQCgUAgENRfdJEegEAgEAgEAoFAIBAIqocQdgKBQCAQCAQC\ngUBQzxHCTiAQCAQCgUAgEAjqOULYCQQCgUAgEAgEAkE9Rwg7gUAgEAgEAoFAIKjnCGEnEAgEAoFA\nIBAIBPUcIewEAoFAIBAIBAKBoJ4jhJ1AIBAIBAKBQCAQ1HOEsBMIBAKBQCAQCASCeo4h0gOoiKSk\nJDk1NTXSwxAIBAKBQCAQCASCiLB27dpsWZaTgzm2zgq71NRU1qxZE+lhCAQCgUAgEAgEAkFEkCRp\nX7DHilBMgUAgEAgEAoFAIKjnCGEnEAgEAoFAIBAIBPUcIewEAoFAIBAIBAKBoJ4jhJ1AIBAIBAKB\nQCAQ1HOEsBMIBAKBQCAQCASCeo4QdgKBQCAQCAQCgUBQzxHCTiAQCAQCgUAgEAjqOULYCQQCgUAg\nEAgEAkE9Rwg7gUAgEAgEAoFAIKjnGCI9gPqEd/cm8md/hq7FOUj2ZCSTGclsQmc2I5nNSCYzuuho\nDMlJ6MzmSA9XIAiagBwgrziPHHcO+d58vH4v3kDJl9+LJ+Ap/d6kN2ExWLDoLVgMFqwGa+n30cZo\n7GY7OknsGdV5il2gM4DRGumR1FlkWcYXkPH6A3j9Mj5/gPgoEzqdFOmhCQRnF5l/g68IopIgOhmM\nlkiPqE4jyzJ/7j6O2agjJS6KBrFmMW9VgffoUdybNxPVpw/6mJhIDydkhLDTgGfjCo5+vghYVOWx\nOpsNQ3IyhqSkkx6NTZtibpmOqXlzJJOp5gddC/gDMjoJJElMGnURWZbJKspib95e9jr3ctB1kOPu\n4xwvOl76mOvOxSf7wnI/g85AsjWZ5KhkGlgb0CCqgfJ9VANSYlJoaW9JnCUuLPcSVINp10F8Kgx/\nN9IjiTj+gMzPf2fyxZ972XQwD68/gM8v4/EHTju2WYKVa3o0ZWTPpjSNj6r9wQoEZxvFLviwLwS8\nZc+ZYiE6qeQrGeKawzm3QnLbyI2zDrHtiIvrP11Z+m+jXqKx3UpKnJWUeOWxfWMbl3VoiF4IPgAK\nV6/h8PjxpC/4QQi7swVrz560GnYUedAbyM0uIFDsQfYUIxcXEyguRi72EMh34cvKxpeVpXxlZ1O0\ncSO+rCxkt7vsYno9pmbNMLVsiTk9HVN6OuZWLTG3bYuungg+R6GHt5bs5Ms/9/He2B4M7NhI8zXW\n7c/lQE4hV3ZpInaTqoksyxzKP8SW41vIyMsoFXL7nPso8BaUHmfSmUi0JpJoSaRhVEPaJ7Qv/Xei\nNZFoYzQmvQmjzohJZ8KoL3nUGTHoDHgDXop8Rbj9bop9xbj9buXfPjf53nyyCrPIKsoiszCTjLwM\nVh5ZicvrOmmsCZYEWsW1It2erjzGKY/xlvja/rWdveTujfQIIk5ugYcZaw7w5Yp9HMwtorHdwpVd\nG2Mx6DEadBj1Oow6qfR7WZb5ZXsWby3ZyVtLdnJ+y0RG9WzGwI6NsJr0kX45AsGZSeFxRdSdexc0\n7AgFWVCQDYXZyveO/bD7Z1j5EXQYDheOh0adIj3qiJKVXwzAhMHtiDIbOJRbxCFHEYdyC1m+M4tM\nVzGyDG0axvDIZW0Z2LFhvd2c9x0/jnvrVtxbtuLeupWoXr1IuGGc5uv4XU4A9DZbuIdYqwhhpwGd\nLQldVADiDdC6taZzZVkmkJ+PZ/9+PBkZFO/ejWd3BsV7Mshftgy8yk6UZDRi6dABa7duWLt3w9qt\nG8ZG2gVTTeLxBfhyxT7eXrITl9tLQIZdmfkM7Kj9Wm8s3sHyndl8+ec+XhrRmdYNY8M/4DOUfE8+\nm49vZlPWJv7K+otN2ZvIcecAICHROLoxqfZUurXsRqo9lVRbKmn2NBpENaj1UMlCbyFZRVkccB1g\nt2N36de8jHknic6UmBS6Jnele4PudGvQjdZxrdHrxIK5RnDnKV9nIVsO5/HFH/uYu+EQxb4AvdMS\neHJIey7r0BCDvvL3xu390jmYW8jstYeYte4AD03fQKzZwBVdmzC6VzO6NRNutEAQVtR5Kv0iaDe0\n/GMKsmHF+7DyY9g6F9oOgQv/CSk9a2+cdQiXW1lTXtKuAW3KWVd5fAEWbT3K64t3cPeUtXRpauef\nl7elX+ukOi3w/A4HhevWK0Ku5Mt39GjZAUYjnn37QhJ2AaeyAa2Lrd/rUCHstGCxK48hLIYkSUIf\nG4u1Y0esHU9WQLLXi+fAQYp37qRo00aKNmwk9+uvyZk8GQBDo0ZYu3Ujqkd3ovv2w5SWGpE3nizL\nLN56jJcW/M2e7AL6tU7iyaHtGfbu7zjd3qovUA6OQi8pcVZ2ZeUz5O3l3HNxK+69uCUWo1jMV8QX\nW77gm53fkJGXgYwMQJo9jb4pfemS1IVOyZ1It6djNdSd3KkoYxQtjC1oYWtB35S+pc/LssyxwmPs\nduxml2MXG7M2svroan7Y84NyniGKLsld6N6gO90bdKdHwx6Y9SJ/tZTcvRDXArTOBwE/FDvPOmH3\n91En/5q7mdV7c7Ea9Yzo0ZSbzm9Bu0badmibxkfx4IDWPNC/FSv35DBzzQHmrD/ItFX7uaFPC566\noj1mg5jDBIKwoM5T6hqsPKKT4NKn4fwHFHG34n34pD+0vFRx8FqcVztjrSM4i5TUCpvFWO7PTQYd\nV3RpwqCOjZiz/hBv/rSTGz9fxblpCYwf2JZeqQm1OdwK8ecXULRuLQV/rqBg5QqKt/0NsgyShCk9\nnahevbB06FDy1Z5jL/6HglUrq75wefdyOZHM5noTNVcRQthpwWwDpLAvhiSjEXN6Gub0NGwDLwdA\n9nhwb99O0foNFG3cSNGGDbh+/BF4CWNKCtEX9iOmXz+ie/dGFx0d1vGUx5bDebwwfxt/ZhynZXI0\nE2/uxcVtk5EkCZvFWDqJaMXp9nJOajxPX9GBF77fxttLdjJ/02FeurozvdMTw/wqzgy+3PYlRp2R\ne7vdS5ekLnRM6ojdXMkHXh1GkiQaRTeiUXQjLki5AFDE3uGCw6zPXM+GzA1syNzAR5s+IiAHsBqs\n9G7Um35N+9EvpR+NYxpH+BVEiIAfFj4JKz+AG+ZCy0u0nV+shJycTcJuwV9H+L+ZG4k2G3hqaHtG\n9WyGPar8RU+w6HQS57VM5LyWiTw3vCNvL9nJJ8v3sOlQHu+P7UFKXN3ZXBEI6i3BCDsVazxc/Bic\ndy+s/hT+eBcmDoI2g2HEx2Cp32F2waJuttuslS/zDXodo85pxrBuTZi++gDv/LyLUR/+ycVtk3ly\nSPtaj6KSfT4K162j4M8/KVyxkqK//gKfD8loxNq9O0kP3E/0uediad++3LWvzhZb6rxpJeB0obPV\nb7cOhLDThk6niLtQF0POI2COBXPVSZmSyYS1c2esnTsDNwDgOXiIgt+Wk79sOXnffodj2tfKH/s5\nPYnp24+Y/pdgTksLbWwV4A/IvPj9Nib+sYc4q5Hnh3fkunObYzwhXMluNYTs2DmLvNgsRhJjzLwx\nuhtXdU/hyTl/MfrjFYzp1YwJg9tXe/F1puHyuLi61dXc3fXuSA+lRpAkiZSYFFJiUrgi/QpACTtd\nl7mO5QeXs/zQcn45+AsAreJa0a9pPy5MuZCuDbpi1J0FfyvFLph1G+xcqPzbeVj7NdQ5rNgJgYAy\nt52hBAIyby7ZydtLdtK9eRwfjetJA1v4K+rFWow8ObQDPVvE88+Zm7ji7eW8OaY7F7VJDvu9BIKz\nCnW+MmsQZeZY6Puwkpe36mNY8jxMHAJjZ4CtSc2Msw7hLPJi0ElYg4x+Mhv03HheKqN6NmPyn3v5\n8NfdXP3+H3x8Y0/Ob5lUo2MNFBdT8McfuBb/RP7PP+N3OECvx9qpE4m33UZ0n95Yu3dHZ6l63tbb\n7ATy85H9fiS9tqgJv8uFPrb+C38h7LRisYcu7CZfqYRM3TQPYrXnzZmapmAaM4b4MWMIeDwUrVtH\n/rLlFCxfRuYrr5D5yitYOnTANnQItsGDMTap3uTl9Qf458yNfLvhMOP6NGf8wHbYracvnG1WI84i\n7cJOlmWcbt9JO0oXtUlm0cMX8tZPO/n0tz38tC2Tt6/rVuMTS33BF/BR4C3AZqr/k48WYkwxXNj0\nQi5seiGyLLPHuUcReQeX8+WWL5m4eSJx5jgub3E5Q9KH0L1B9zOz5ULeQfhqNGRuU8KOljwf2nyk\nniMHwJN/xu5i5xf7eGT6BhZtPcbInk154apONR7mPahTY9o0jOWeKeu4eeIqHry0Nf/o31oUhxII\nQkWLY3cqpijo+5BSTGXGTfDpABg7UynCcgbjdHuxWY2a03asJj13X9SS4d2acONnq7j589W8OaYb\nQzqHNzrGn19AwbJfcS5eTMGvywgUFqKLjSXmkouJHTCA6PPOQx9Crpu+xHEL5Oejt2v7ewk4nSHd\ns64hhJ1WLNVx7A6DtwAmDVXEXTV2jXQmE9F9+hDdpw88Oh7v4cM4Fy3C+f0PZL7yKpmvvIq1Rw9s\nQ4ZgGzQQQ5I2YeT2+nlg2noWbz3G+IFtue+SVhUea7MYcRR6NL+GQo8ff0A+LQY8ymRgwpD2XNm1\nCQ9P38Ctk1Yz8eZzOa+lCM3M9+QDYNOyc3mGIUkS6fZ00u3p3NTxJvI9+fx55E8W713Md7u/Y8aO\nGTSKbsTgtMEMTRtKm/g2dToZPGgOrVVaFHiLlF3n9P6w5N/gdmi/1olzmDvvjBR2+44XcMcXa9id\nVcDTV3TglgtqLzc5PTmGOfedz1NzNvPmTztZv9/Bm6O7ER9dv3M3BIKQKc6HY5uheR/t57rzAEmb\nY3cqrQbALQvgq2vh80Ew+ktIvzj069Uwsizz7/nb2HHMxZTbe2s+31nkw2YJfYnf2G5l5t3ncdvk\nNdz31TqeH96JG/q0CPl6oNSTyF+2DMecORQsW47s8aBPTMR2xRXEXnYZ0b3PrXYbMF2J4+Z3uTQL\nO7/LhT6u/he/OgO3tGuYUB07v1cRdW0GgeuoEhKQdzBswzI2aULizTeTNnMGLRctJPmhhwjk53Ps\nhRfYeeFF7LvlFvLmzSfgqVqAFXp83PHFGhZvPcZzwzpWKuqgxLFza8+xK4sBLz98rlOKnWl39qFZ\nfBS3TlrNqj05mu9R19hyfAvP/fkcQ78ZygHnAc3nuzxK7Hisqf7vKoWLGFMMl7W4jJcveplfR//K\nS/1eonVca77Y8gUj543k6m+v5uNNH3O04GjVF6urbJkLE4eCwQy3LVIWKdUJDT9V2J1h/L4rm+Hv\n/c4xZzGTbzmXW/um1bq4jzIZeO3arrx4dSf+3H2cK975jY0HQhDhAkF9x1MIU65RBFVRiBtRZlv1\nQ8Ybd4HbfwJ7M2U8G76q3vVqCFmWeWnB33z++x5W7clBlmXN11Adu+oQF2Viym296d+2Af+au5nX\nF+8IaSzuHTs49t//sfPiSzh43/0UbdxI/HVjaDF1Cq2X/Urj558jpl/fsPR2LnXsnE7N554pjp0Q\ndloJVdipk1nLS+GGOUpflolDlP4rYcbUvDlJd99F+nffkj7vOxLvuhPvgYMcHj+eXRddzLGXX8Gz\nd2+55zrdXm78bBW/78rmlZFduOn81CrvZ7MYQgrFzCs5p6KqTQBJMWa+uqMPTeIs3DxxFWv21j9x\nl+/JZ8b2GVw771rGzB/DnJ1z2O/az7acbZqv5fQok1Wssf5PPjVBlDGKK9Kv4P0B7/PztT/zVO+n\nsJvtvLP+HQbOHsgDPz/Ab4d+IyCf3ni6TiLLsPw1mHkTNOoMt/8MDdqX/dxqD32hVN73ZwCTft/D\njZ+vokGsme/uv4C+rSMXxi1JEmN7t2Dm3UpFvus+WcFfB8+s37dAUCl+rzJ/HVgByMraRyvuvNDC\nMMvD3hRuXQCpfWHuPfDLf5V5tg7x7s+7+HhZBg1izXj8Adxe7Z9Xav2C6mI16fnohp6M6tmUt5fs\n5Mm5m/EHqv59+fPyyJ02jT0jR7Fn2HBypkwhqkcPmn7wPq2XLqXhhAlE9eypOQ+uKtRWBf4QhJ3f\ndWYUTxHCTiuhCjs1XMoaB83OVSrZuR3KLnwNNgo2t25NgwcfpOWihTT77FOizjmHnMmT2T1oMPtv\nvRXnjwuRS3ro5RR4GPvJSjYccPDOdT0YdU6zoO6hOHZezTs5aiXN8vL2TiQ51sy0O/rQyGbh5omr\nWbc/V9N9IoEsy2zO3syzfzxL/5n9+feKf+OX/TzR+wlmXjkTKBNpWlDPOZtDMYMlwZLA6HajmTx4\nMgtGLODWTreyKWsT9/x0D0O/Gcrnmz8n112H/5ZkGeY9qOTRdRqphG/HnFKII+T56MwUdjNWH+DZ\neVvp364B39x7AS0Sa75icDB0bRbHnHvPJz7KxK2TV3MwtzDSQxIIap5AAObeCzsXQTulEFbIoePh\nEnagXOv6mdD1evjlJfj2PvBpTyepCT77bQ+vLd7BiB4pPHCp0i85L4SN81PrF1QHg17HyyO7cO/F\nLflq5X7um7oOt9df7rHubds4POEJdva7kKPPPY/s8dBwwuO0XvYrTd95m9hLLkEy1FwWmNpcXKuw\nk2VZFE85a6nuQspSEr/btCfc+C18cZUi7m76DhJbhm+cpyDpdMRccAExF1yA91gmed/MJnfmTA49\n9BD65CRMI8dwh78T+3MK+eTGc7ikXYOgr22zGPH6ZdzeAFZT8LsvqssXzOTTwGbhqzv6MObjP7np\ns1VMub03XetgI2BvwMuivYuYvGUy23K2YTVYGZw2mJGtR9IpqROSJFHoVRZ11RF2IhRTG01jm/Jg\njwe5t+u9/LT/J6Zvn84ba9/g3fXvcnnq5YxpO4auyV3rVi7eb2/AuslwwUMw4Nnye9VZ4sKTY3cG\n8Ofu4zwx5y/6tU7i/bE9TqrcWxdoYLMw6ZZejPjgD26euJrZd58vKv4KzlxkGRY+AX/NUAo9NT8P\n/p4feoRBOIUdgMEEV70Pcc3h1/9Coy7QJ7KVpqev3s+/529lUMdGvHxNF37coqQP5BV5aWTXVsk3\nXI6diiRJPDqoHUkxZp6fv5WbPl/FpzedQ6zFiOz3k//LL+RM/oLCVauQrFbsI64mbuQoLB071Orn\nqhpKGXBpa3kgFxeD1yscu7MSi72kRHj5uxUVok5mJ05OTboru/DeQph0BWTvCt84K8HYsAFJ99xD\nq8WLafrhB0iNmlD0wbvkZR5n0i3nahJ1UCbMtLY8KM2xC3LyaWS3MO3OPsRHm7jhs5V1KqSpwFvA\nl1u/ZOg3Q3l8+eO4/W6e6v0UP4/6mefOf47OyZ1LJzerwYpBMuAs1i7s1By7s60qZrgw6o0MThvM\npEGTmDNsDiPbjOTXA79yw4IbuGHBDSzdv7RuhGluX1Dm1A14tuIG5NXaaJJO+L5+sye7gHumrqVF\nYhTvXl/3RJ1K64axfHRDT/YdL+CuKWso9mn8HBEI6gvLX1X6bPa5D/o+UrapXRccOxVJgksmgCkG\nHPvCf30NzNt4mMe/+YuL2iTz1nXdMOh1pdFMoTl21c+xK49b+6bx1phurNmXy2NfruD45C/YPXgI\nB++7H8+BAzQY/09a/7KUxs8+i7VTx1rfLNWVOnbahJ3q8J0Jjl3d/PSry6iTS7HGBognhmKeSOMu\ncPN88HuUapk5e6o/xiCR9HpiL76YzT0vBeCjq1qHVHlSFWZa8+zKHLvgJ5/GdivT7uyDzWpk3Gcr\n2XwosovSrMIs3lz7JpfNuoyXV79M4+jGvNP/HeYOn8vodqOJMZ3es1CSJGxmW0iOnRB24aNVfCue\n6P0ES0Yt4YneT5BdlM0/lv6DEd+O4Ntd3+INhNabsdoc2wqzb4fGXWH4uxWLOlDmk1CFXWzjsu/r\nMXmFXm6btBoJ+PzmXlWGdkea81sm8crIrqzIyOGxWZtCKkYgENRpVn8GP78AXcbA5S8oc5i69qkr\njt2JWOJCG1eYWLLtGA9P30Cv1AQ+HNcTs0GJfApV2BX7/Li9gWpVxayMIY2NfOz6jVvf+geZL72E\nITGRlDffoNXiRSTedpvmapThRBcdDTodAZe29ZXq8OmFY3cWok4uWhdDRSW5PJZywgcbdoSbvwdf\nEcy8GXzF1RqiVhx6xeJvF2I6iirMtDt2So5drMbJJyXOyrQ7+hBjNjDus5XsP177+Sp78vbw9O9P\nM3D2QCZumUifxn2YOmQqkwdP5uJmF1fZQ81mCk3YOT1ODJIBq8Ea6tAFpxBljOK6dtcx/+r5/Lff\nf9HpdDz1+1MM+WYIU7ZOKQ2drRUKc2DaGDBFw5ivwFjF/3OoCxJ3HkQlKjvV9VjYef0B7pm6lgO5\nhXx0wzl1JqeuKq7qnsI/L2/D3A2HeW3RjkgPRyAIH1vmwPf/B60HKhtTaiXLuujYqVjjy9Zotcwf\nu7K5Z+o6OjSx8dlN55yUzhKqsHOVrq3Cu8nlPXqUo8//m92XXUaTn7/jcLsePHTRP9j33FvYBg2q\n0dy5YJF0OnSxsSE7djrh2J2FhCrsqmqw2aAdDH8fjmyAxU+HPr4QyNEpws7vCG2Bp+4KqcVQgiWv\nyEuUSR9S2FSzhCim3t4bf0Dmga/X4/XXTvjcAecBnvztSa769ioW7FnAiNYjmH/VfF6/+HW6JHcJ\n+jo2ky3kUMxYU2zdygU7QzDoDAxNH8rsK2fz3qXvkRKTwv9W/4/LZ1/O3F1za34Afi/MuFFphzJ6\nKthTqj7HEqe0UfFrdBfVhVKooZx1AFmWefrbLfyx+zgvjejCuWkJkR6SJu67pBVjejXj3aW7+HpV\n+KsjCwS1zu6fYfYdSq+6UZNAf4KwMFpBb9a+ERXwK+kvNSrsQsxVribbjji5/Ys1pCVGM/mWc08T\nYqEKOy31C4LBe/gwR557jt2XXU7ujBnYhw+j5cIfGfDVR0jtO/Lg1+s5kFN3CkLpY2OFYyfQQMjC\nzgEGCxgrSYBtfwX0vhtWfgjb5oU+Ro1k6cwA+J2hLfDsoTp2Rd5qhU2lJkXzv2u6sPGAo8Z3vY/k\nH+HZP55l2NxhLNy7kHHtx/HjNT/yVJ+naGYLrnroicSaY0Nz7IqdonBKDSNJEhc2vZBJgybx5eAv\naRTViDfXvlnzN/7xcdi7HK58C5r1Cu6c6mw0lQq7GljQOA4oXzXIZ7/tYdqq/dx7cUtG9mxao/eq\nCSRJ4t9XdeLCNsk8OXczv2zPjPSQBILQyd4JX4+DpDZw3ddgijr552o4ptb5Rt0ArWlhV8uOndvr\n58Gv1xNtNvDlbecSH316D7fYUNNcShy76hZP8Rw8xJGnn2HXwEE4Zs3GfvXVtPzxRxr/+9+YmjYl\nymTgw3E98Qdk7vpybYWVMmsbnS0Wf5629ZXq8AnH7mwk5FBMR/lhmKdy2fPQuJtSfje3dpJ5s+QS\nYZcXomNnDXXyqX7VpiGdG3Pduc358NfdLN+ZVa1rlUdmYSYvrniRoXOG8t3u7xjVdhQ/jPiB8b3G\nk2jVno+oEnIoptcp8utqkW4NutE3pS95nryazYVa/Rms/hTOfwC6XRf8eWreSkjCzhZ6g/Oq+PZe\n+OzyGlssLdl2jBd/2Magjo345+Vta+QetYFRr+P9sT1o2zCW+6auY8vh+umeCs5y/F745k6l0uS4\nWafXElAJJXTcXQvCLgI5dv9d8Dc7juXz6qiuNLCVv+Gv10nEWgwhhGJqr19wIt7MTI48/Qy7Bw0i\nb84c4kZeQ6uFP9L4+ecwNT05kiQ1KZq3xnRj6xEnT8z5q07kDOtjbfg1VsVUHT7h2J2NVMexq2iy\nOxGDWQlhkGWYdUut9FY5Kitv/kAIDR2hLEdOe7hAePqsPH1FB1o3iOHh6RvJcoUnP9HhdvDK6lcY\n8s0QZu2YxfBWw/n+6u95ovcTNIjSVjW0PGwmG3nF2hdxaiimoPawm+34Aj6KfEU1c4M9y2HBo9Dq\nMhjwnLZz1flI82KphkMxnUfAdRh+eDTsl952xMk/pq2nUxM7b4zuhk5Xv8OSY8wGJt7Si1iLkQem\nra8zu94CQdAsexUOr4Mr3gRbk4qPC8WxqyqNJRzUco7d0u2ZTPpjL7dekMZFbZIrPdZuNYZQmC40\nxy5QUEDW2++we+AgHN98Q/y1o2i5aCGNn3kGY5OK/1/7t2vIg5e25pt1h5iyIrLVRUERZ1rXs2WO\nXf1fXwlhp5VqhT4F2XctIQ2GvQOH1sISjQu9EMjxgNdkDinHLuB2c3DYMCasnYr3yFFN54bDsQOw\nmvS8c313XG4v/5y5kUAg9B0jr9/LF1u+YMicIUzZNoWBqQP57urveOa8Z2gc07jaY1WxmWy4PC7N\npfWdxU7RnLyWsZuV97yjuAZ2dHP3Knl1Cekw8jPQBd8HEgitIMGJOStq+5ZwU5QLplilh9XWb8N2\nWbfXz31T1xFjMfDpKYUG6jMNbRZeHdWVjKwCXlu0PdLDEQiC5+AaWPaKUgGz41WVHxuSY1dLws5f\nDN4a2rw7gez8YsbP3ES7RrE8OqjqaAO71ah909ytLcdO9vnI/Xo6uwYOIvv994m56CJafj+fRk8/\njbFxcOueBy9tzSVtk3l+/lbW7svRNN5wowvRsZNMJnRmcw2NqvYQwk4r6qI6pFBMDRNTx6ug1+3w\n57uw/Udt99KIo9CLNyompFBM37FjeDIyuPDAegb8936y3n6HQGFwSbTh7LPSrpGNp67owK87svjs\nN+0tI2RZ5uf9P3P1d1fzyppX6JzUmdlXzubFvi/SLFZ7Dl1V2M12ZGTyvfmazhOOXe2jCrtQHNZK\nCQTgm7sUoXXd16EtXEo3mjQsltRWLTXl2MmyIuzOuUXp1TnvIXAdC8ul3/hpBxnZBbx+bTcaVhC+\nVF/p2zqJsb2b8+lve1izN7JHKas2AAAgAElEQVQLI4EgKDwFSgimrQkMebnq4+usY6e2YqhZ106W\nZR6btQmn28ubY7phMVa9MRWSsCsKrkewLMu4fl5KxvCrOPrss5iaNyf162k0ffMNTC1aaLqnTifx\n5ujuNLZbuWfKOjJdbk3nhxO9zRaSY6f2wKvvCGGnFZ1e2YmuqVDME7n8RWjUGebeDXkHtZ0b7LC8\nfoq8fvzRsaXlXrXgdyiT9PS+17GndXey33+f3YOHkDdvHnKgcjcqr9Ab1j4r43o3Z2DHhry88G82\nHQz+w2N7znZuX3Q7Dy59EJ2k471L3+PDAR/SKr5V2MZ2KmqenJbKmLIs4/SI4im1jd1UIuw8YRZA\naz6DAytg8H8hsWVo1wglx+7EhZIq7MKZF1HsBNkPMQ3g6o+Uxd+8B6t9j40HHHyyLIMxvZpxQauk\nMA22bjFhSHtS4qz8c+ZGijwiJFNQx1n0L8jJgKs+CE54WeKgKNSK4jW46LbGK481nGc3ZeV+lvyd\nyYTB7WjXKLjXE6pjp9dJRFUS0eA9epT9N97EwXvvBb+fpu++Q4upU7B266bpXieNNcrIRzf0xOn2\ncv/U9firET1VHXS2WAKFhci+4Cu1+11O9GdAGCaESdhJkvS5JEmZkiRtruDnkiRJb0uStEuSpE2S\nJPUIx30jRii73EUaQjFVjBYYNVlJTJ51q/aS5kFQGrsdE4s/T/ukpgq7nCZpzBhyDy2mTsGQlMTh\n8Y+y97rrKNq4sdzzAgEZV7EvrM2EJUnif9d0ITnGzAPT1pNfXPmbOrsom2f+eIZR80axPXc7E86d\nwOxhs7mw6YU13k5ADafUUkCl2F+MN+AVxVNqmRpx7BwH4KdnIf0S6KqhWMqphJJjd6qwkwPg0eYc\nV0phidtkTYDktjDgGdixADZMDfmSxT4/42dtpEGshSeGtg/TQOseMWYDL4/swt7jhby88O9ID0cg\nqJidi5XNqfPvh7R+wZ1jjYPiPCVKIVhqw7Gz1LxjtyvTxQvzt3JRm2RuPj816PNsllAcOx82i6HS\ndUzu1KkUrltHo2eeJn3ed8QOGBCWdU/7xjZeuKozq/bm8OWfe6t9vVDQl1S21BKOGXC60J0BhVMg\nfI7dJGBQJT8fDLQu+boT+CBM940MWoVdIKDsYmt17EDZyb/yLTiwEn5+Qfv5VeAomTAku52AxvKw\nUCbs9HY7TreXqJ49SZ05g8b/+Q/ew4fZO3oMhx59FF/WyRUr8z0+ZDn0qk0VERdl4s0x3TmQU8i/\n5pa7z1DKTQtu4rtd3zGuwzi+v/p7rm9/PUZdeMdTEaWOnQZhpx4rhF3tUl1h5/GfUgBJluH7RxRB\ndeWbShnwUFF7Q1XHsTvxuXCgLo7UXfDe90CLvrDgcXCE1q/tvaW72XEsnxev7hSWvNy6zPktk7jp\nvBZM+mMvKzOOR3o4AsHpFBxXKnc36Aj9/xX8eZZqRBjUZG65OlfVUC+7Yp+ff0zbQLTZwCujumgS\nUPao0By7qtZWvuM5GJKSiL/uOiRjeOfUa3qk0K91Eq8u2sHRvNoPyVQrW2oJx/S7XKWCsL4TFmEn\ny/IyoLKkgOHAF7LCCiBOkqTwVaKobbQKu+I8QA59x6nzSOh8rZJvp2WnKwjUCcNgt4eUY6cKO0N8\nfKn7J+l0xI24mlY//kjiXXfhWvAju4cMJffr6aXhmcHGgIfCuWkJPHhpG+asP8TsteWHsBb5itjv\n2s9dXe/i0V6Pli7ea4tQQjFdHtdJ5wpqh+oIuwxHBr2n9ma3Y3fZk5tnw85F0P8piE+t/gC19qKr\nLWEXVdIwXKeDq94HZJh7r7LRpYFtR5y8v3QXV3dP4dL2DcM3zjrMY4Pb0Sw+ivGzNlHoCT6cSCCo\ncWQZ5j+ovM9HfKxU8g6W0tBxjfOV2aa9sJQWajjH7vVFO9h6xMn/rulCg1htucF2q5FiX0BTtVxn\nUdWF6fwOB/r4eE1jCRZJknjhqk54/QGem7elRu5RGWovOrXSZTAEnM4zotUB1F6OXQpwYrfagyXP\nnYQkSXdKkrRGkqQ1WVnh70kWNiz2ErEWJGqYlNZQzBNJ6QkBX9hjwB2FisAyxceFVjzF4QCdDnOc\nrbQppoouOpoGDz9E2nffYunYkaPPPsu+68fi3r6jrBxvGNodlMf9/VtxbloCz363pdwWCOoivTq9\n6KqDKha0OHaqsBM5drWLWW/GarCGJOz25O3BJ/vYk1dS0KfguNLaIKUn9L47PAO0xtVtxw4gvgUM\neklpwL7qo6Av5fMHGD9rI3FRRp6+okP4xljHiTIZeHVUVw7kFvK/BSIkU1CH2Pg1bJunbEw16qTt\n3NKQR43CribDMKFGc+x+35XNR8syGNu7OZd10L4xFUqfYKe76lZS/txc9HHVWJNWQYvEaP5xaWsW\nbD7Kkm3hKZ4VLKWOnUubY3cmNCeH2hN25fnOp2VVyrL8sSzL58iyfE5ycuW9PSKKVsdO3Z0KJRRT\nJapEgBSGNzTHUaiEiVkS4pCLiwm4tdnmfocDvc2GLcqMs8hbbnNKc1oazSd+TpP//RfPvn3sueYa\nij94G7PPU2NhVXqdxEsjOuP2+Xn5x9MXRmrp+nhzzexYVUV1QjGFsKt9bCZbSMVTcotzT3pk4QRl\n7hj2Tvh2oC326uXYnfhcOCgVdgknP9/9Bmg9UMktzNoR1KU+Xp7B5kNOnh/eifhoU/jGWA84Ny2B\nW85PY/Kf+/hjd3akhyMQQO4++GE8tLgAzrtf+/mhOnY1LexMsSDpwu7YFRT7+OfMjaQnR/PU0NA2\nptQ6BFrCMYN27GpQ2AHc0S+d1g1iePrbLbUaeRCSY+dyCcdOIweBE2vGNwUO19K9w49mYacupKoj\n7EoWSWEWdupkEZWoCBy/xjw7dXKwW434AjJFFYQLSJKEffhw0n/4HvvwYVhmTuXDn1/Btml19V5A\nJbRMjuHWvmnMXHuQ9ftPnrBz3cq/48w1O7FVhNVgxSAZNIViihy7yBFnjgupj516jsPtgJ0/wabp\n0PdhaNgxfIOzhOjYmW01I+xKi6ec8t6SJBj2tpIXOOcu8Ff+Qb8r08WbP+1kcKdGDOlcfyP3q8P4\ngW1JS4rm0VmbqiwGJRDUOD9OUB6v+iC0jam66tjpdCXzaHgdu/d/2cWRPDevjOwScs/NkIRdED2C\nlVDMml3/mAw6/jOiM4ccRbz5084avdeJqALNH6RjFyguRvZ4hGOnke+AG0uqY/YB8mRZPlJL9w4/\nFju4ncHnipSGYlZjcqohxy6vqKQsbomwCzi1LfACeXno4+JOCBeofPFhiI+nyYsvkvHUq3h0RvRP\nPMKhRx7Bl1szse0P9G9Ng1gzz3y35aTG5eqCO1LCTpIkbGabNseuWDh2kcJutmsS4SrqBkJuYSbM\nfwiS2sCF48M7uFBy7NSclVCKGVSF2pxcX87CIrYRDH0dDq+Dv2ZWeAl/QObRWZuIMul5bngYRXA9\nw2rS8+qoLhxyFPHSD9siPRzB2c6xzdB2sBJaHQp11bEDZWxhdOz2Hy/kk+V7uKpbE3q2SKj6hAoI\nzbGrPBRTDgTwl6zdappeqQmM6dWMz37bw9bD2j9DQ0Ff0o8uEKRjpxZZEY7dCUiSNA34E2grSdJB\nSZJukyTpbkmS1CSSH4AMYBfwCXBvOO4bMSx2QAZPkDZvWEIxSyaGovA2rnUUerFbjRhK3uBa8+x8\nJY6dujsU7ORzNLUD91/yCLH33Idz8U9kXHElrp9+0jb4IIgxG3hiSHs2HcxjxpqyNM9SYVcdF7Wa\n2Ew2TXlbonhK5LCb7SHl2Kl/Z3n7liu9KIe9o63YQDCEkmOnLpTU3lBhFXY5EFVJiHP7Ycpj7t4K\nD5n0x17W7XfwzJUdNBcbONPo2SKBO/qlM3XlflaIKpmCSFJ4HKKrkSZTVx07UPLswphj9+IPW9FL\nEo8Prl57Fq3CzuMLUOT1E1uJYxdwKsaEoYaKp5zK44PbEWc18sScv2qlt50UFQV6fdCOndoWQSf6\n2JUhy/J1siw3lmXZKMtyU1mWP5Nl+UNZlj8s+bksy/J9siy3lGW5syzLa8Jx34ihNXwpHMVTairH\nrshLnNWIzqa8Jq3CTg3FVHeHnO7gJh9nkRev3kDjB+4jbdZMDA0bcPD+Bzg0/tHSSpvhYni3JvRK\njeflhdvJKykW4ygR27VdDfNEbCaNjp3HidVgxVieEyKoUWwmW7VCMXNzdkGv26F5n3APrSzHLtgG\n4CculPRGMEaH37GzVrJg0BuUubCCuWz/8UJeXbidS9omc1W302psnZU8clkbUuKsvPD91pMiDwSC\nWsPrVvpdRoXuPintWUx107GzhM+x+31XNgu3HOO+S1rSyF69jSmtws7lViuOV+zYqRFSteHYgdKG\n6qkr2rPhgIOvVu6r8ftJkoQ+Njbodgdljt2ZsWleW6GYZxZahZ3bAToDmKJDv6cxCgyWGimeYrMa\n0cepwk5rjl3eSY5dsJWbnG4vsWYDep2EpW1b0qZPJ+n++3EuWMDuK6/EtXSpthdSCZIk8eywjjgK\nPby+eDugFLOINcbWWt+68tAaiunyuEQYZoSIM8eR58krtzhQZThKHHaH0aI06q4JLHEg+8FTENzx\npy6UtIZyVkVhzumFU04lOgkKyy8I8tKCbUgSvHh157A0zD0TsBj1jB/Yls2HnHy78VCkhyM4G1HX\nHlHVqCQtSSUCKsj5Ru0BXFuOXRjmQZ8/wPPzttI03srt/dKrfT1VoJ0q7DwHD3HwwYdw/vDDSc+r\n1ckr62NX2n+4loQdwFXdUrigVSIv/7idTGfN97bT2WxBF09RHTu9cOzOYjQLu5KFVHUWKZKkTKiF\n4Q3FzCvyEhdlRG/X7tgFPB7kwkL0cfayHLugHTvfSROPZDSSfP99pE7/GkN8AgfvuZfDj0/AX8mO\niyzLpTlMVdGxiZ2xvVvw5Yp9bDvixFHsiGgYJpQ4dhr72IkwzMhgN9vxBXwU+Yo0nZdbcFR5jE4A\ncw19aJTOR0EuSsoVdrXo2IEylxWcLuzW7stlweaj3HlhOk3irOEb0xnAsK5N6NLUzis/btfU00og\nCAuqsItOqt51tOSyFTupVg9gLYSaY3dsC+xYWPrPr1btZ/sxF08NbY/FWP3Kxwa9jhizoVTYybKM\nY+5c9gwfjmvhQpyLF590fJljF4Swq6VQTFB723Wm2B/guflba/x++tjY4EMxS9aZIhTzbCaUUMxw\niIiohJoRdlYjuuho0Onwayie4s8t2/VRd5WqKp5y4n3L21GyduxI6qyZJN59F3nz5pFx5TDyf//9\ntOOyi7K556d76D+zP0dLFs9V8X+Xt8FuNfLMd1twuB0RK5yiEkoopnDsIkOoTcodXmUn0BE4vZdi\nMATlEIa60XTi+WHPsavCsYtKOm0uk2WZl37YRlKMmTvCsNN9pqHTSTwxpD2H89x89tueSA9HcLah\nOuzVcexAW/XJE1uz1DTWeOV+wRbFU1n2Knx9PeTsIbfAw2uLdnBeeiIDOzYK29DsViN5RV58ubkc\neuhhjjw+AXO7dphatsSfc7IYLesRXImwy619xw4gLSma+y9pxfebjrB0e2aN3ktniw2+eIrIsROE\nFIpZncIpKtaEGgjF9BIXZULS6dDbbAQ0OHYn2vmxIYRiVhQDrjOZaPDQQ6R+PQ1ddDQHbrudYy+/\nguxReu79euBXrvnuGn4//Du+gI8DrgPlXudU4qJM/HNgW1btyWGvIyvyws5sw+VxEZCD+yARjl3k\nsJuU97yWPDtvwIvLX4wpIJPvK8TrD76qmcpti25j7A9jOeCs5G9cnVuCDW+qSWEXCCjjqMqxi048\nLRRz0dZjrNmXy8OXtSbaXHlz3bOVPumJXNahIR/8spvs/NA2CwSCkFA3YqLC4dgFOVepES21lWMn\nB8ruGSz5mRDwwdIXeeOnHbjcXp4Z1iGsYeQ2q5H4LevZM2w4rp9/JvmRR2jxxWTM6Wn4c05eE6pR\nU5VVxYxEKKbKXRel0zI5mn/P24rPr1FEa0Afa9Pg2JWEYoocu7OYiDl2iWEVdv6ArAiskp0dnd2G\n3xGasDMZdFiNek3FUyrbUQKwdu5M2uxZxI0ZTc7nn5MxZgxvzX2M+3++n2RrMq9c9ApA0OGYAGN6\nNadTio2jruPEGiNXOAUUx05GJt+bH9TxwrGLHKWOnYYm5aq718Ln03yuypbsLWzK2sSo+aOYnzG/\n/IO0zEfl5ayEU9i5HYBcdY6dOpeVOJJef4D/LfiblsnRjD6nWeXnnuVMGNwOt9fPmz8F1+RdIAgL\n4cixg7rt2IH2PLvCbECCv2ayduWvjO3dgnaNwicQAm43o1fMYOT0l9HZbKRN/5qkO+9A0uvRxyfg\nO82xCzIU02BAFxMTtnEGi9mg57FB7cjILmDW2oM1dh9tjp0TyWhEMoe5YnWEEMIuFMwaS4S788Lj\n2IVZ2LncXmQZ4koElt4eV2lO26mcuutjsxqCDsV0uX1VNtAE0FmtNH72WaSXHsexdzsX/us7nsjq\nzdQhUzmn4TkA5LiDD0/V6ySeG9aJgC6fjMzIVpdT3bdg8+ycHqdw7CJEKKGYauXV1IAyzWrZgAAo\n8hVR6CtkdNvRtI1vy4TlE3hi+RMUeE8pklLaiy6IBUl5OSvhFHZqjkqVOXZJyi53yX2nrz5ARnYB\njw9uj0EvPpYqIz05hrG9mzNt1QF2ZQbZckcgqC4F2SDpqr+WscZBkYa1E9Rejh1oz7MryELuNIJ8\nKYYJphk8clmbsA3J/fff7Bk5kt7rf+LXTv1Jmz0LS4cOpT/XJ8Tjz81FPiF8tMyxqywUMxd9XFzE\nilNd1qEh3ZvH8daSnTWWL6y32UuLolSF3+lCZ7OdMcW6xCdoKOgNYIrRFooZjokpKlG5pz848VQV\njpLS/3FRqrCzayqe4s87RdhZjBodu6rDrWRZZsrWKYzNf5t/35uIvmM7un36O1njHyfWrbwJtQg7\ngI4pViSdl7/2+9iTHWQlwRrAVrJBEEyeXUAOkO/JF45dhAhF2OUWKwuENJ1SBERruwRVCHZM7Mhn\nAz/j3q738v2e7xk1bxSbszeXHajFsVOPMZ+wQWCxgdsZfLuEylAXRVXl2KkFGAqPk1/s482fdnBu\nagID2jeo/hjOAh4c0IYoo56Xfvg70kMRnC0UHlc2bHTVLAhiiYPiPAgEsaCPhGOnpZddwA+FOez2\nN+Jtz5X0ZQPxmSurPRRZlsmdNo29144mkOdk4U0TmNRjBDrLya0TDAmJUNJsXMVZ5EMnQbSp4v8n\npU1V5CKWJEli/MC2HMlzM2VFzbQ/0NtikYuKSlN4KiPgcp4xFTFBCLvQsdiVxVBVyHJ4i6cgh600\nuVplqVTY2WzahF1J2KYq7OzW4ISdPyDjKq7asctx53Dvknv53+r/cV6T8/h83Fw6T51F8iOP4Fr8\nE/uvGcU5R6M1Czt1gW2QY3n5x8gtjEoduyCEXb43HxlZCLsIEZJjV/J3llby/6zVsVP/rhMsCRh0\nBu7pdg8TB07EG/Byww83MHHzRCU/U130BLMgKW+hZLFra5dQGUE7diXhXAXZfLIsg+x8DxOGtDtj\ndkxrmoRoE/f1b8WSvzP5Y1f5bSMEgrBSmF39/Dooc8ZC3YiqKSwhOHaFOYDMd7s8/JE4AtnWBH56\nplqbZH6Xi0MPP8LR554nqndv0r6dS37nc8rtY6dPUDbQ/DllayA1vaayudTvcGCIq72KmOVxfssk\n+rVO4r2lu0oreYYTtRBKMK6d6tidKQhhFyrB9n7y5CuLpnCFYkLYwjEdJROF3WoCFMdOa/EUyWIp\n3UWyWY1BhWKqb2J7JaEC6zPXM2reKFYdWcWTvZ/knf7vkGBJQNLrSbrzDlK/mopkMPLPSXk0n7P6\npFCEqlAX3P1bp7Jg81G2HtaYLB0mtIRiujyuk84R1C5mvRmrwarNsSsRcmkWxYXS6tidKOxUejTs\nwawrZ3FJ80t4fe3r3LX4LrKLc5WFTzALpfKKEWjNGa4MtcBCMDl2gOP4ET5ZnsHQzo3p3jyyC436\nxs3np5Y0Ld8mmpYLap7CnOrn14G20PHaFHah5NgVZAGwu8DKhGE9kC6eAIfWwt8V5ENXQdFfm9kz\n4hpcixeT/H+P0OyjDzEkJGC3Giny+vH4Tl7nGBKVedZ3vGxN6CzyVrlp7nfkoo+PbPE4gPED25Jb\n6OXT5eGv8qsWQgkmvcgvHDsBEHxeSukOebgcO8In7AoVi9p+YvEUpzNokaTY+WWvy2YxlLurdCqV\nleOVZZlJmydxy4+3YNabmTJkCmPajTlt98napQtp33zD9m6J9Pp2BwfuuQdfbnA7beoCe0S3tsRa\nDBErQqClIIcq/oSwixw2ky2k4imp0SmAdmF3vEh5nyecIpLsZjuvXfQaz573LBsyN3DtvGtZGxNk\nQYKKHLsTf1YdgnXsSkIxl6zdhscXYPzAttW/91mGxajn0UFt2XrEyTfrRdNyQQ1TkK1Us60uWqr4\nuvPAFKukv9Q0IeTYFeQeAaB5s+Zc0CoJul4PSW1gyfOaUmZkWSbniy/Ze/31yD4fLb78kqQ77kDS\nKUt0e0lU1anrqzLHrmzMTrevyjQX3ylrt0jRpWkcgzs14tPlGRwPc5Vf1bELBOHYBZwudDYh7ATB\nCjt18gpXjh2ErZfdaaGYdjvIMoH84Ko0+h2O0sbmUOLYBWGplyb3ntLuIK84j38s/QevrX2N/s37\nM/2K6bRPbF/hdfQx0fx+57nMGZ5MwR9/sueaayjauLHK+6tFLVJsidzeN51FW4/x18Ew9vEKkpAc\nu9rYuRSUi91s1+bYFR0nKhAgOrYx0cZozaGYx90lws5yuvslSRLXtLmGqUOnEmWM4rZYmFSwu+q+\nd7Um7KpYNJTMZbv37mVcnxakJkVX/95nIcO6NqFrszheXbidIo9oWi6oQQqPR8axq438OgCjFQwW\nTTl2yzcoqRxX9+2mPKE3QP9/QfYO2PhVUNfw5+Vx8IEHOPaf/xDTty9p38wmqkf3k45RN99PE3Yl\nDcb9uSeEYlbh2MmyjN+Rhz7CoZgq/3d5G4q8ft5bujus1y1z7IIIxXS50MeeOWsrIexCJWjHrmSS\nCFcfOwijY3dySKTerowx2Dy70x07I84ib5WLy9JyvCc4dluytzB6/mh+O/gbj/V6jNcuei2ofLJ4\nawI/dA8ooZlI7B13AzlTplY6BrWoRbwlnlv6pmK3GiPi2lkNVgw6Q1A5duoxIscucmgVdo6CY8T7\nAxCdSJw5LqRQzChDFFaDtcJj2sS34euhX9OfKF7zH+WhpQ9V/vdU48IuR7leVQUWTNEUS2Ya6PN5\noH+r6t/3LEWSJJ4a2p6jTjefLs+I9HAEZyqBQImwC2OOXbCOXW0JO1BEZ5COndPtZcPfuwBok55W\n9oP2V0LKObD0JfAWVXqNor82s+fqEeT/8isNHn+Mpu+/hyH+dMFlq0DYqcf6jp+SY1eJsAsUFIDX\nWyccO4BWDWK5pkdTpqzYxyFH5b8vLehLHbsgitO5XOiFYyfQ7tjVvRy7vCIvMWYDxpLy4np7yQ5H\nkL3sThN2VgMBGQqq2Dkuc+yMyLLMtL+nccOCGwjIASYNnsS4DuOCLqKQaEkkrzgPQ8d2pH0zm5gL\nLuDYCy9w6JFH8OeXXwxCXWDbzXZsFiN3XpjOkr8z2XAgPEVpgkWSJGwmW1DCTuTYRZ44c5xGxy6L\nuIAfopOJN8eXbigES447p1y37lRiTDG8Zm7JY8Vmlh1cxpj5Y/g7p4KiQOVWxdRQzKAqinKrzq8D\nVu3JISsQS59GMokxZ0bvoEjRKzWBQR0b8eGvu8ktqLoCnECgmeI8pVbAmezYgRJCHqSwm/z7XqJ8\nOciS7uTQc0mCAc+C6zCs+rjC8x2zZ7Nv7FhkZFK/mkrizTdXuO5RN9+dpwg7yWhEZ7efXDylqPJQ\nzNI2VeUIyEjxUEmLiLfCuMGusyl/N1U5doHiYuTiYnTCsRNgsSuFCKrKR1MXS+Fw7ExRYLCG1bE7\nsYCJGlbpd4bu2MHpk8+pqDl2JqOXx5Y/xn9W/oc+jfsw44oZdE3uquk1qAvfvOI89HFxNH3/PZL/\n7xFcCxexd+RI3NtPnygcbgcxxhiMOmW8N52fSnyUkTcW175rZzPZggrFFI5d5NGaY+dw5xLnD0BU\nEnGWuNIQ4GDJKco5Lb+uIiRrPOPyi5g4aCLF/mLGfj+Wb3Z+c/qB5eWshLt4ShX5dbIs858ftpGv\ns9E6Jrx5FWcrj1zehgKPn4m/h78IgUBAQcmaIzocjp2GtgLhahUVLNa4oOZBp9vLJ8sz6BrvRYpK\nPD1CIa0ftBoAy18/7XUGPB6OPP0MR558iqhzepI2ezbWLl0qvV9FoZiguHa+U6pixlbWnLykFkFd\ncewAUuKsjO3TnFlrD7IrM7hUoKpQHbiq1rNqDp5w7AQlJcIDStXLylAXc+GanKISw5hj5zlZ2JXE\nJAdTGVOWZfx5eac4diXCroo8u7wiL5LxOON/v4Mf9/zIgz0e5N1L3yUuBFdTXfiqhSYknY6kO+6g\n+aSJ+Avy2TtmDM4FC046x1HsIM5cdq8Ys4G7LmrJrzuyWLsvPL/bYLGZg3PsnB4nEhLRRpGLFCnU\nUMwq89hKyPU4iQsEIDo55FDMYBw7oLRKb7cG3Zh55Ux6NOzBM388w79+/xfF/hPEU3k74Kp7Fy7H\nrooedr9sz2LDAQf2xMboi2r3/Xam0qZhLIM6NmLiH3uD7iUqEASNuplcVX/KYDBaQW+q147dpN/3\n4nT76Jborzg89dJnlNf4+1ulT3mPHmXfuBtwzJhB4p130uyTT8oNvTyVyoSdPjGx1LHz+gMUevyV\nhmKWOnZ1SNgB3HdJK6xGPa8v3h6W60kWCxiNBKpw7FRHTzh2guB3uYscgATmcAm7eCWPJQw4Cr2l\nhVMAdKWOXXAxyfj9FbDNYKIAACAASURBVDh2lVeD+jtvDdFp73Ks6CgfDPiA2zvfjk4K7U8x3qxM\niqf2sos+91zSv/kGS/v2HHr4ETJfew3Zr4SIOoodxFtOnkxvPK8FidEm3li8M6RxhIqWUMxYU2zI\nvydB9Ykzx+ENeCnyBZcHkOcrJN7vr1aOXaIlyNAna5yyyeT3kWBJ4MMBH3JXl7uYu2sut/x4C8cK\njinHlbdQMpjAGBWe/phFlTt2sizz7tJdpMRZadg4RemNJQgL9/dvhcvt48s/a6bhr+AsRn2fhiPH\nTpJKctnqoLALYlxOt5dPl2cwoH1D7H5HxS5m4y7QeRSs+ACcRyhYuYo9I67Bs2sXKW+/RYNHHkbS\nB9fsvVLHLiG+tHiKy61WHA8mFLNuCbukGDO39Uvnh7+OhqWYnSRJ6GNj8VeRY6fm4AnHThC8sHM7\nwGIDXZh+1VGJYe1jd6KwKw3FDCLHTi2wcmqOHVQciinLMp9v/pxFOS8g+e1MHzqdC1IuCHn8UObY\nldek3JCcTItJE4kbM5rjn3zKgbvuxp+XR647t7TVgEqUycDdF7Xkt13ZrMwIz+83GLSEYoowzMii\npUm51+8lP+AhTgYsccRb4inwFuDxB5cDFZAD5LpztTl2UDof6XV67u9+P29d8ha7HbsZPX80GzI3\nVLxQCjZnuCqqyLFbkZHD2n253HVROrropLIQL0G16ZRip3+7Bny6PIOC4uBLrQsEVVLq2IUhxw5K\nQh6rEHaBALiddc6xU926hwa0VvrYRSdXfPAlTyL7fRz/933sv/VW9HFxpM6aie3yyzUNy6jXEWXS\nV9CkPLG0eEppYbp6Foqpcke/NOKjjLy8sIIccY3oY2ODd+xizpz1lRB2oRK0sMsLT+EUlTAKu7wi\nb2lzcgCd2YxksQRVFbPMzj+h3YGl4lDMQm8hjy57lDfWvkFD3bnYHY/QzNasui+h1NGoqJS8ZDLR\n+NlnafTccxSsXMmeUddi3Z9V6vSdyLg+LUiKMfNGLVbI1OLYicIpkcVuCr7voOrOxeujQJJKQ3+D\nde1cHhc+2adB2JVfkKB/8/58NfQroo3R3LLwFmZ5M2tO2Pl9yjUqcezeW7qLpBgz157TTJnLvAVV\nVo4TBM99l7Qit9DLVyv3R3oogjOJAtWxC5OwC8ax87gAufaFnbcAfOVvwJ3o1nVKsStOZiXCLmBt\nxOEtHcmct43YCy8gdcYMzOnpIQ3NbjVWIOzi8TscyH7/CY5dFaGYklSaelOXiLUYuffiVizfmc2K\nMGyw62w2/FX0sROOnaCMYPNSisKc/BsmYSfLMnmnFE8BxbULpnhKeXHaFVVuOuA6wLgF41i0bxEP\n93yY5v47sZtjqvsSAKWYiEEylOvYnUj86GtpMXkygaJCHvrwKO3+Ov1DxWrSc+/FLVmRkcMfu2sn\nRMxmtuHyuAjIlRfhcRY7hbCLMGoPwWAcO7UCZlzJ/5ka+htsL7vKetiVS+lG0+l/1y3jWvLV0K/o\n3bg3z5mKeIFsvH7v6edXV9iVFooqX9htOODgt13Z3NEvDYtRXxbCFKaNKgH0bBHPBa0S+Xh5Bm6v\n6GsnCBOFx5VwbVNUeK4XjGNXXmuWmsZa/gaZyklunc+jjLGCUEzvkSPsHTsW519ZJHdxkjKiMfqY\n0HPkKxJ2hvgECATw5+VV2CP4RNT+w8GGgdY2N5zXguRYM+8t3VXtaymOXeUb5yLHTlCGOtlUFUbn\ndoSlIubE3/cw4PVfka0JymTir16oTZHXj8cfOCkUE0qEnRbHzl722mJLJhOnu2xsGY4Mxswfw7GC\nY3xw6Qfc2ulWpRxvJaECWtBJOuIt8VUKO4CoHt1JmfEV+5Oh19tLyXzrLeRTqppe37s5DW1m3li8\nI+giGdXBZrIhI5e2M6gINcdOEDm0uG5qBcz4kvBNrY5dTkkebbBVMcsWJOW/d+1mO+/1f49b891M\n9x7j9kW3k110wuZFOISdmvtbQYGF95buwm41MrZPi5Ljwtu+RaDwQP/WZLmKmb76QKSHIjhTCFdz\ncpVgHLuICLuKK3aW69ZBucKuaMMG9oy6Fu++/TT94H2SRl6KtOazas2xtoocu0RlvvXn5JTbI/hU\nfLm5dTIMU8Vi1HPrBWks35nN5kPV+0wKxrHzC8dOUEqwvZ+KHNUOxXR7/bzz8y52ZeZTZCiZ5ILs\ntQJAwA+//BdcR0ufUpuTx53q2NlsBPKqDg30556egGvQ64g+JQ582cFlOD1OvhzyJeennA8oE+Sp\nTmF1iLfElzocVZFvM/HsWD05A7pz/IMPOXj/A0rDzhIsRj33XdKK1Xtz+W1Xzbt2qgtXVTimy+Mq\ndYwEkUFLjp3q2NmtymJIFXbB9rJTNyo0O3aVLJb0SDyclcX/Es5j6/GtjJk/hi3Ht5SdX21hV/La\nynHs/j7qZPHWY9x8fiox5pLdZLUQQ4EooBJOeqcl0Cs1ng9/3Y3HV0U7HoEgGMIt7IJy7Eo+E2u7\neAqUu746ya2DsnnrlFBMx9y57LvhRnRRUaRO/5rYiy+Gvo8oJsCaz0Memt1qLLd+gSFB+Yzw5eSU\nOXZVhGLWZWEHMLZPc2LNBj74dXe1rqO32aounuJ0gdGoVNE8QxDCLlQsQYZiuvOq7djNXHuQnJLG\ns7mU7Cpo2eXO3Aq/vARLXyx9ShVfpzp2ujgNjl05cdq2UyafY4XHsBqspNnSSp+rqoGmVhIsCUE5\ndqA4Jj6DRMH/3UTDp54i/5df2Dt2HN7Dh0uPGd2rGY3tFl6vBddOFQtVCTunx0ms8czZUaqPBCvC\noUz8xUc1VB5LQjHzghRP2oVdEBtNJTkrQxK78MXgL9BJOm5ecDOL9y0Oj7BT27CU4zK+v3Q30SY9\nt1yQWvakCMWsESRJ4v7+rTmS52b2uoORHo7gTKAgO/yOnbuKPsCRdOxOEZ2qW3dZhxK3DpTCKVC6\nQSX7/WS++ipHHp+AtUcPUqd/jblVK+WYJt2gZX/48/2Qc4orEnb6BOX/RXHsSnLsKg3FzKtTzcnL\nw2ZRIjsW/HWEvdkFVZ9QAXpbbJVGhd/lRB8bW2Fz+PqIEHahojeCMTrIqpihT0w+f4BPlmWUvlGz\nAiW5aVoWQ84S0bLxa3ApZc9Vx+7E4ikA+v9n773j4zrr7P/3nT6SpkmyJFu2JDsusdNjJ3YCIZQQ\nEtgfkIUF0h2nQAKEErLAsrDsd+t34bu7QFhSHKc4jbqQEIg3JEuaExOTXm3HlmQVq07v5f7+eOZO\nvTNzR9JYLve8Xnk51rRre+aZ5zznfM5xaid2BqezzKfttJmLwlPGI+N0NnUWfWgCseScWTFBbH61\nzi7lQi3srbRecjFLbrmZ5NAQ+z71aaIvvwyA1WTkC+9fzouDvoardjmyUMXSm0gniKVjumI3z7CZ\nbNiMNk1F496I+NJ3O7qAPIGvR7GTkIr6FqtfXOUZuxwKNkqr21Zz30fuY2XrSr76x6+yOTGCHPPD\nbA4ycopd8TX3T4b57SsjXLKhF3dTwXqjWzEbhvesaOekxS7+6497SKV11U7HLBGZmptycgV2NyBD\nNffDfM7YlSh2ilr3pQ+syP+wQLFLh0IMXfd5pjbfjueiC+nZrNJP9+6vQHgcXrp3RpdWccauVbyO\notgZJGi2VCF2h7gVU8Gmd/VhMhq49am9M34Og8OJnEiQiccr3icTCGJ0HFmH5jqxmw2ypcAVkYxB\nKjYrK+Yjrx9gcDrCl85ZCcCBZHb4tp4uO4XYpRPwp1sAUU4OVAhP0WDF9PmKEjEVOO2moh678cg4\nHU0dud/nCjTn0IpZj2KXC7XIbphbzjqLvgfux2CzMXDZ5fgffhiAT65dzAKHlVufnPmiogUKWaum\nAim36TN28w+X1aUtFTN0gJZMBnOLIHZmgxmH2aF9xi42jdvqxmTQqGznSn+1b5Ta7e1s+dAWzl96\nPj8IvMbftrlI1GPxLkWFGbubn3gHk9HAlWctLb6/zQ2SUbdiNgCKard/OsqDL4/UfoAOHdXQiBk7\nqD5nd4jM2KmqdZBT7BLeOP2f+Qyhp5+m6+++Q9d3voNkVtnf9J0F3evgmR/OKCPBZTcTTqRJlhzU\nKCQtPSVm7Bw2MwZDZfUp7fMd8oodQIfTxifXLuYXO4cYD8Rm9BzK3Fy1AJV0MIjhEEwInQ10Yjcb\n1LIvKaRvhlZMWZa55Ym9LGtv5uL1PQAMxbM+4HpOuYOjIBlg1Ufg+c0QD+Zn7FTCU+RolEyiet9W\nJZ+2mmJXSOxycbxVrAL1otXWSjgZJpaq/eFX1JZCJcS6fDl9P/sptuOPZ+SGrzFx04+xGA1sPLOP\np3ZP8sZIbaI7U2ix9ynBKnoq5vzDZXVpm7GLjONOp4sKfd02t2ZleTo2rd2GCdnSX1fdGyWr0cr/\nPev/cl3HmTzoaOHqxz+v+RrLEPWKdaagI3LEF+WXLwzxmdOW0OEomWEwGAQJ1EvKG4JzVndwbJeD\nm/53D+lM44OgdByhSMYgEZr7GTvQ5jA4mE6V3Kxyfg2857mBcrUOIDJJZMpO/2VXk56YpOf22/Fc\neGHl55YkOOur4BuA1/+77ktT9kyldkzJbBYH8t5pArHqYy6ZaBQ5FjssFDuAa85aRiqTYcsz/TN6\nvJJ0WS1AJRMI6IqdjgLUInbKJmuGit32d6Z4ddjP1e9Zhs1spL3FwmDULm6sy4o5DM0dYlGJ+eGF\nrfgqzNgZXeKDkKlhx6xI7Ox5YpeRM4xHi4mdYiVwNc2tYgfaouQVxaTU4mZqbaXnji24PvYxJm+6\niZEbvsZFJ3XQZDGyeRZWgFrQYsVUiJ2u2M0/tBI7X2wadyZTNFjvtro1K3ZT0SntiZgKbO66FDsF\nkiRxbc95/Nv4JK953+bi313MXv8M3vORaXENhvzXyq1P7kWW4Zr3VOhumsNeTh3FkCSJL75/BXsn\nwvz+tdH5vhwdhyvmupwctCt2lhYwzt0hcE0YjOJgKks4E6kMd23v593L24vVOiCw/TUGH3djdDrp\n++kDNG9YX/v5V54PC46Fp/+jbtu7smdS77JrJTXtJRCtPuai1j98KKOvvZnzT1jIvc8NqPYj14Ku\n2OmoHzUVO2UjNTNid/MT77DAYeWCU7oB6HDYGAoh+mQi9VgxR8G5CBavg54z4bn/IhiOYjEasJuL\nZ+SMLvGBrzVnl/b7MakqdnkrpjfmJZVJFRG7XBzvHM/YAUzHa/+d+OI+WswtmI3lr2+wWFj4r//C\ngq9+lcDvfofv2qu5dJWDB18eYdTfmBJlu8mOyWDSZMXUFbv5h8uiUbGL+3CnM0VzKW5rAxU7qG0N\nr2Ztsrk4Pxxhy8k3EE6GueThS3h25Nn6Xj/qLUrEnAzFeeD5QT5+SjeLPRX6r5raIVwnsdtxK/zh\n7+t7zFGK847v4pgFzdz0+B4yumqnYyZQiN2cz9hRe706mDZMBXZXTrF76OURxgJxriqwkcuyzOQt\ntzJ83+vYOs30PnA/lr4+bc9tMMC7vgzjr8OubXVdljI2U6nyID01VTO/IEfsDgMrpoJrzz6GYDzF\nvc8N1v1YQ1aJq6rYBfUZOx2FaKAV8/URP0/tnuSKd/WJMl+gy2XjgD+WPeWuc8bOuUj8/7u+BP79\n9Ixuw2k3lyUBGZwaiV0VxS4YS5LJyIxHxgHozCYDAprieOuFomxMa5g79Ma8uSALNUiSRPs1V9P9\nwx8Qf3sXF9z+dywMjHHHDK0AtSBJEk6LU7diHibQOmPnT4bxlBA7j82jiRTCDImdfWaKHZCzT55k\nbef+j9xPZ3Mn1/7hWl6ZeEX760e9RfN1tz+9j3gqw7XvPabyY5rb6rdivvozceI9Nbso7KMBRoPE\n59+3nLcOBPnDm2PzfTk6Dkcon8+GKHZVDrpmGTw3Y9g9EPUhyzK3PbWXlZ0tnL1SOC/kZJLRb3+b\nif/4D5zH2um5dFl5SEotnPBJcPWINawOVCN2Jk8rKe90zcTxtFf8fasdyh+qOL7bxVkr2rn96X3E\nkum6HpsTKmoqdjqx06GggVbMW57YS4vVxMXre3M/63TaGAvExMJT14xdAbFbcS60r+LMsXtxqywA\necWu8gdBTiTIhMMYXCrhKTYzGRnCiVSO2BUrdqnc/eYKOcVOQ4CKP+7HY629EDvPPZfeu+/CEIvy\nw6d/zAu//eOMrABa4LQ4q1oxldt0K+b8Q7Fi1qrB8KajuGW5aD7EbXVrSsVMppMEEoGZKXZVrU3Z\n95jazEouVdPPopZFbD53M2k5zYvjL2p//eh0TrHzR5NsfXaAD5+wkGMWtFR+zEysmP5hQIYdN9f3\nuKMUHz1pET2tTbPuhNJxlEI5RG5qgGJXy4o5H8TO5oaol2f2TPHWgSBXnbUMSZJIBwIMXnMN/l/8\nkvbrrmXR2UkMzo7az1cKoxnO/CLsfw4Gtmt+WFXFrrWV9LSXQEyEp1RC3op5+BA7EKrdZCjOr14Y\nrutxihJXyYqZSSTEzKHjyDo014ndbKAQu0qbvBkqdvunIzz86igXre8pSq3sctqYCifI2Fu1b4YS\nYXGNjoXi9wYDnPlFliTe4T3G18rurnivqyl2ym1qi4NyvYFYirGIOCEuInY5xW5uw1NAG7Hzxr24\nNH5Z2E88UXTRtLfx7T/+F4/9132zus5KcFprKHbJYO5+OuYXLquLZCZJNFXZmhtPx4nIKTxGuxiY\nz8Jj8xBNRWuG/Cjkb2ZWzBqKXaWZlQJiB9Bmb6PF3MJIqI5Exag312F39/Z+QvEUn3/v8uqPaWoX\nG8eMxpPYdFKEQRlM8OK91U/8dQBgMhrY9K4+Xhz08cKg/velo040YsbO3AQG8yFqxfRAzMetT+1l\ngcPKx05eRHJ4mP6LLiLy/E4W/vM/s+D665EiU2Xl5JpxyiVi7Xvq3zU/RHE5qZaUt7WS9noJheNV\nD81Th6EVE+CMY9o4abGLW558p64gKGV2Lh1Qt2JmshZNXbHTkYfNBXJGJEapYYZxvbc/vQ+DBJve\nVRwP3uWyAhA116HYBbJD84piB3Dip5iSWvlk7Jdld1cKx9P+yguucuqjOmNnzyc3jUfGMUgG2u35\nk75GzNg1mZqwGq2a5pe0KnYKLEuWsPLnD3Cgq49jb/1XxjffPuel5U6Ls6pFLxAPYDFYsBqtc/q6\nOuqHErpT7d8rl7xqLlaqlMfWClBRDijabHVupGxusVGqeNBUZaNkyx4aFGy0upq7GA3XEboRETN2\nsWSau57t532rFrBmUY3DiOZ2QNZO0AIj4v7rroRkGP58l/brO4rxyXVLcFhNbHl633xfio7DDeFJ\nkXY7w3RvVUiSeL5DUbGzu0mFp3ly1wSXn9FL5q232Pfpz5AaG6dn8224//ICSETE+jPTuUNLE2z4\nHOx5FEa12d2rKnaeVpBlDOGgJiumUcVtdShDkiSufe8xDExF6gqCMlitSBYLmaD6wbli0dRn7HTk\nkTvlrqC2RH2ixFwlqKMSpsMJEThwcjddruJ48E6n+H3I6NQ+YxfMnrgXEjuTlZ8aP8Ka2Asw+nLR\n3Q0OB0hS9RShKnK+QtgUYtdmayvq4vJHk5gMEk0WY9ljZwpJkmi1tTIVq012vTGv9tLnLEweD+b/\n/DFPLjqRqe9/n7F/+EfkdH1e72qoNWMXSAR0G+YhApdFfOarzdnlk1eLvzy1ErupqHgf15+K6YJM\nCpIR9durzayYrGCyFyl+i1oWcSB8QNtrp5OQCEJTKw+9PMJkKMFVZ1VIwixEvSXl/iHx66rzYOl7\nYMct4rV1VEWL1cRnTl/C7187wLCvMUFQOo5QRKaEimWYu+9sIH8QVQnzrNjZzBKfTA8xcNllGCwW\n+h64n+YNG8R9lLnD2QTKnHY1WBzwzH9qurvVZMRmNlSwYorDalc8VCM8xY+hpUW9Z+8QxwfXdLGs\nvZmbn3inrsN1g9NZW7HTiZ2OHErsS2WI+eo+5br72X5iyYxqPLhC9Hw4IO7XtqFRyskdi4p+vDX5\nfuKGJlGWWQDJYBAfBF/+z/Tw3od5auip3O9T1YhdwalSaYcdCCumWmjLbKGlpDyRThBJReomdgDv\nPX4Jv/jI5/jfk87Fe999DH3hi2QiFTbQdcJlddUMT9FtmIcGlH+HqoqdQuxKrJT1KnYzCk+Byqfg\ntTZKJVbOhc0LtSt2WcVNtrnZ8kw/qzodnHmMBsVRIXZaS8oVYudaAmd8QRxcvfEbbY89ynH5mX3I\nsszd2/vn+1J0HE6ITM7tfJ2CaopdJgPxwLwQu5DUgklO8U35LbxfuR5Lby+9D9yP9ZiCEKhsOfmM\nrZgg/vynbRKddtPa6mVcdrN6eEqbWEdd8VDVYLrDpZxcDUaDxGfPXsZrwwGe3qM9cMvocJCuqNgJ\nYmfU6w505JCzL1XY5EV9dQWnRBNp7trezzmrO1jRWX6C0JVV7CbTWYuXFvuSQuycC3M/SqYzjMat\nvL7wArGo+IpjZI0uF+lAAFmW+cELP+AbT32Dm1/OBxVoUuyyM3ZlxC6amtNycgUem6cmsVM21B5b\n/QubwSBx9XuW829LzyX82S8TeuIJBi7fSGq6jnTSCnBanIQSITJyRvV2XbE7dKAkqlYjdsqMnKfk\nva+873zVTqmZjRWz1kFTfcSuq7kLX9xHpJICWIjsWrQ7aOHN0QCb3t2n7fBGOfHWmozp3y9+dXbD\n8g9C2wp49qa6O6GORiz2NHH+8Qu570+DhOOp+b4cHYcLItNzO1+noJpilwiJMZd5IHbPDKWYfKOF\n039xG02nraN3692YO0pCUpSDqNkQO4AN1wmb659u03T3SsTO6BGHgK5EuOr+Ku31HnbBKYX4+Cnd\ndDqt/OSP2oOgDE4HmYqKnW7F1FEKLRupOhS7n+3cjzeS5HNnq8eDu+xmrCYD4+lm8QMt9qXAiLhO\nS3PuR8rCsPeYy4TX/dn/KnqI0eUi5fPyne3fYfOrm3FYHAyFhnK3VyV2JTN2lRS7uYYWxU6ZwZuJ\nYgfwsVMWscBh5QfOk1n8ox8S37WLgYsuJjFUX1JTKZwWJzJyrtagFMFEUK86OESgRXXzZU9z3c2d\nRT9XHlsrGXMqNoXFYKHZ3Fz1fmVQDpEqbZZmoNgB2uyYWWv4w3titDZb+NjJ3ZouuW4rZmBYPMbS\nJIKgNlwLIy/CYJ2de0cpNr17KcFYil/8eaj2nXXoAEFimup0D2hBNcVuhvkEs0U4Gif4i+1MvOLE\nec676bnlFowtKqm+4TmqgHB0wXEXwIv3QLxy15qCyoqd+Pdxa1HsDmNiZzUZufLdS9n+zhSvDWur\nDjI6nBV77BTFTi8o15FHbiNVxYqpcWFKpTPc9tRe1vZ6WNenvohKkkSn08ZwPFv2q2UzFBwts2H6\nImJhMLcugeM/CS/cVTyz52hm7/5X+fWeX3PtSddyxXFXMB2bzp3cZ/x+JIsFyW4ve7kWqyB209EQ\ngUSgqMMOBOGby+AUBW22Nrwxb1XvdX72aWYLm9VkZOOZfTy1e5KhNafRc8cWUtPTDFx4IbG3357R\nc0Le3lfJjqkrdocOFIJdzTrrzSZJupzF5EZR+2oqdtFpWu2t9duV51ixW9Qi1g1NdsysYvf4YJKL\n1/fkujdrImfFrGPGzrU4//uTLhQzMc/+WNvjj3Ks7fVw8hI3dzyzTy8s16ENkam5LSdXUE2xmwdi\nl4nFeOmqz3Pc7t20Hhti0VcuQbJY1O88F1ZMBeuvFbbTl2qnbgtiV662K2St5oyd14vRc/gSO4BP\nn9ZDk8XInRot5Uank0yFlHddsdNRjlobqTqsmP/zxhhD3qjqbF0hupw2BmLZUBUtASqF5eRZKCc+\n7iaL6FNJRmDn7YDYdP45+jaZQIBvb/g21518Hd0tYoOqRJ+nsqc+ahtPk9FAi9XEeHbhK1fsqhdo\nzhSttlYRM5+qbBvLzz7NfGG7eL1YVG57ai9Np55K3733gMHAwCWXEnn++Rk9Zy2yoCt2hw5sJhs2\no636jF14DEc6g7lEsTMZTDgsjpqK3YzKyaH6jJ2WmZUKip02YifWoiAOLtnQW+POBTBZRa+eZivm\nEDgLiJ2lCdZtgrce1jyncrTjyncvpX8qwuNvjc/3peg41JHJCGLXCCum3S2C5zIqIwhKr+tBInZp\nv5/BTVfi/vN2tr/rHDpPDiBVWeMJT4iwKUudrgo1LF4L3etEEJTa30UBnHazat2BZDKRanHgToSq\np2Ie5oodCHL7l6d28+DLI0yF4jXvb3A6qit2JpOqSHE4Qyd2s4G1xoxdHeEpd27vZ7HHzjmrO6ve\nr9NlY184G3uv1YpZMF8H4I8mgGx8btfxsPwc2HELo4H9XPbIZYwYgnSmm/nUqk8B0O0QxG44JCyH\naZ+valyu02ZiMlZeTi5eO1nUzTdXUBIEp6OVya6ilNRTd1AKd5OFT61bwoMvjTDqj2JdsYK+++/D\ntGABg1deReDRR+t+zhyxUykpl2VZJ3aHGJzW6vUU3ugk7kxa9TTXY/VomrGbEbGr5iDQMrNSQuza\n7e0YJaOmLrtYQBCz9cctz6X3akZTHb2cpYodiHQ5gwme0wvLteD847tY5LJxu159oKMW4n6Q040J\nT7G5AVm8RikOomKXPHCA/osvJvLKq/zraRfTd/XG7DVUWaeVDru5CoHbcC1MvwN7/lD1bpWsmACJ\nFheueLiiFVNOJMiEw5gO0/CUQlx+Rh+JVIYHnt9f876KFVPNzZUOBjA6HHMe5jff0IndbGCyiKJN\ntQUgnRKbKQ3q0BsjAf60b5rLz+jDaKj+ButyWtkVzNoDam2G0kkIjYmggQIoVky3sgCs+Ti7Ej4u\n+f0lTEQmOHv1hzGGosjZ0yNFsVPm7Gqd+jjtZrxxodgdLCumQtaqVR7M1oqp4Mp3LyUjy9z5TD8A\n5kWL6L33HmyrVzP8pS/jfeCndT1fNStmJBUhLad1K+YhBLfVXXXGzh/z4UlnoLn8lNttq/5YmAWx\ns5Z30eWgZaOkj+Q7JAAAIABJREFUELvsF6DJYKKjqUPTjN3b+wZIyQYufs9x9V612DRqScWM+cVJ\nfimxcy6EEz4p5lSq9WLpAISr4rIz+3h27xSvj2ibU9FxlEKxSDdKsQP1z+xBInbxffvov+giUqMH\nuOOjX2bf8Wdw9onLs9dVxVkRnlBd32eM1R+Fli7YUf1wymU3E4qnSKXLlb1YsxNXIkSLRV2xq5Zm\nfrhhRaeDs1a0s/XZAZIqfxeFMDgdkEwix2Jlt2UCwSOunBx0Yjd7lJxy51DHwnTX9n7sZiOfWrek\n5n07nTYCKROyuam2FTM0BsjgKFbscsSuSRCsF4wyGxd2IqdT3HnenSzuXg2ZDJlwGBDza3aTvVix\nq0bsbGaCKfGFUKjYxZJp4qlMY8JTsopdtZJyX9xHs7kZcx29gmpY0trEh09YyH078ulyJo+Hnju2\n0HLWWRz47neZ+PGPNXetVLNiKoEqumJ36MBldVVX7JJB3JlMZcWuCrGTZZnp2HT9iZgARpPoRZrp\neqTSg6el8iCdkekfGiZscHDikhmcBje3a7Ni+rMhRaXEDkS6XDIs5oV11MSFp/VgNxvZ8nT/fF+K\njkMZyuHxXJIYBdXCnpT1yto4Yhd9/XUGLr4EORYn+m838fNMJ1e+eykmu1M4AKodEoUn5ma+ToHJ\nAqddBe88BhO7Kt5NcTsFY+VzduEmJ62JMIYK4kC10LvDERvP7ONAIMa216sfPBodYu+k1mUnFLsj\nb281J8ROkqTzJEl6W5KkPZIkfUPl9o2SJE1IkvRS9r+r5uJ1DwlUJHbZRaGGFdMbTvDrl4b5+Cnd\nuJpqEw6lyy5lbc3NtVREILshK1XsokkkCRw2M08OPclnX/0hbek0W3v+klWtq3KdHunswKkkSSxq\nXsRwUCF2/hqKnYlwepomUxMtlnyilLIYNaLuQNkIV0vG9MbrLyevhCve1UcwnuLXL+UTMQ1NTSy+\n6Ue4Pv5xJn90kygyr+GZh+pWTIVA6IrdoQOXpXrvoC8Vxp0BLOVpam6ru+qMXSQVIZ6Oz0yxg+zc\nyiyIXeF9gYUttYndY2+OYYp7MbbkN3+RZERbTQIINUDLvHBhh10pFp4IfWfpheUa4Woy81frFvPQ\nyyOMB8tPsnXoAPIHLvOm2DVm0x3e8ScGL7scg81G7733cNsBC06bSRyuS5IgnVUVu6m5JXYAazeC\n0QJ/uqXiXRS3k5odM2htwRUPV3xsjtgdAVZMgPet6qC3rSnnnKoEY1aRy6h02WUCwdztRxJmTewk\nSTICPwbOB9YAF0qStEblrj+VZfnk7H+bZ/u6hwwqETtlsaphxfzpzv3EUxkuP1Nb4IDSZRczu2pb\nMYPlHXYg7JAOq4lt/b/nS49/iaWupdw5GaA7JJ7P6BYbvHRBklC3o5vh0DCyLGuyYsZkr2rVgXL7\nXEPpCKtG7Hxx35wRu1N7PBy3yMnd2weKlDnJbGbhv/wzrVduwnvffYx8/RvIyeobTbvJjslgwp8o\nfx/lFDu9oPyQgcvqql53kI7jMdpU5y88tuozdsqMqKJA1w2ba+bWJjVi17yQsfAY6Uy64sO2PLOP\nTnOUZld+DuerT3yVC35zAQOBgdrX3NQmrJi1FG6lw85VoUrhjC+IOgS9sFwTrnjXUpKZDPc8q+Hf\nSMfRCWWP0bAZOyorduZmmKW7Rg3BP/yB/VdfjWlhF73338ekp4vfvzbKhet7aM6memP3VJ6xk2Wh\n2M012W1ZACf8Fbx0f0W1UFHs1Iid39pMczyMnFZfq9PeI0uxMxgkLjujj50DXl4dquygMVRV7IK5\n248kzIVidzqwR5blvbIsJ4AHgI/NwfMeHpiFYpfOyGx9doANy1o5tkvbm0sJJggZNRA7pZy8rO4g\ngb1tB9946huc1HESt39oC22uvlyqnBKMUhgR290iiF06FIJUqqYVM4VXdb5OuX2uYTVaaTY3Vyd2\nMd+sEjELIUkSl5/Rx9tjQXbsmy67rfPGG1nw1a8SeOghhr54PRkVf3fh/V0Wl6pipyhDumJ36ECx\nYqpZbaOpKFEyuE3qKVsuq4tYOkY0FVW9XZkRnbFiZ5tjxa55ISk5xWRU3Sr5+oif5/ZO09cURyrY\n6Lw19RYj4REu//3lvD1dowqkuR3ScTGTXA3+IWGRaqkQMLXiXGhbrheWa8TS9mY+cGwH9+wYJJas\nTNx1HGbY/iN4+/dz81xz1demBntWOVI9iNJeFVUPfL/8FUPXfwnr6mPp3boVc2cn9z4nDjYuO6Ov\n4NqqKHbxoFiv5lqxA1j/WWEpf/Ee1ZsVV5casZs2t2BAzilzpTjSrJgAf7Vucc3qA6NLIXbl34uZ\noK7YVUI3UBhNM5T9WSk+IUnSK5Ik/UKSJNVhMkmSrpEkaackSTsnJibm4NIOAmyufDRvIRRiV2Vx\n+sObYwz7omw8s0/zy3U4RSKmX3JqI3ZGa1G5qCzLvBn9NRHnzzlr8VncfM7NgjS0Ls0RO6WsMR3I\n/7m6W7oJJUP4x4UdqpZilzH6WdBUvPApi1EjFDsQm+Fa4SlzpdgBfPTkRbibzNz9bL/q7e3XXE3X\n332H0BNPsP/qawQprgCn1Vl9xs585J0qHa5wWV0kM0lVcqZYZ90VZiKVkJ9Kqp1yMDFzYueqEZ5S\n5f2vkqpZq/LgjmfEfHCrFM5t1IKJIFOxKS5YfgFGg5Ertl3BS+MvVX5drSXl/iFR3WKo0JFXVFj+\nXPXn0gGIwvLpcILfFFjKdRzGkGX447/C83NkiopMiYA4S9PcPF8h7DUUuzkmdlO3b2H0W9+iecMG\nerdsweTxEE+l+enz+/nA6k663QWHcXZP5Rm7ueywK8XCk6DnTGHHVHFJVFPsJrOHielp9cPtI5HY\nOW1mPnGqsJRPVqg+MDgUK6au2NUDtUnN0uPSh4A+WZZPBP4AqE64y7J8qyzL62RZXrdgQQM+NI3A\nLKyYd23vZ5HLVrPioBBWk5HWZgvTcgtEqvdh5aoOspYwWZb59z//OyOGX+HJrOc/3/ef2EzZaPLW\nZeDth0wGo0tcc9qX/3MtbhGBBQdGxWBvtZJLh9WAZArgthT/GwayM3auBvTYgdgM1wpPmU3VQSls\n2cCbba+PccCvrsh5LryQRd/7HpEXX2Tw8o2kKiy6TksNYqdbMQ8ZuCxiw6H276VYNCu9zxTFuJKV\nc9bErtaMXbX3UQXFDlBNxpwIxnnwpRE+uXYxhpgvd4Ck2C/PXnI2d59/Nx6rh2sevYbtI9vVX1ex\nedUqKQ8Mq8/XFeKkC8WaW2VORUceZyxrY/VCJ7c/vU9z2JOOQxjBUaF8T1YO4KgLjeqwA0EYDebK\n1vE5InayLDP+//6d8e99D8f557H45p9gaBb9c797dZSpcILLzigZhak2Y5cLlGmAPRVgw+fANwi7\nHim7qRqxGzMI8p2aqkDsvF4kux2Drc46mkMcl5/ZSyKd4f4dg6q3G1WEChD1D3I0qit2FTAEFH7b\nLgaKio9kWZ6SZVmh07cBa+fgdQ8NlESE51DDirlrLMj2d6a45IxeTMb6/hk6nTbGU82i/6VaUEBw\nNBecks6k+e6z3+XO1+/EFj2LE63XYjYUKGety4S9IDiSl65LZuwAJsfEpq3aqY/REkGSMjhMxV8I\njbRigtgMV7JiJtNJwsnwnCp2AJes7yUjy9y3o/KciusvPsLim35EfM8eBi65lORoufrhtDirWjFb\nzOVBHDrmB8p7SI2cKQcL7gozKQrhqxSgMieKXaWNkqVFJGdWe6xy3yy6mrsAGAmXd9ndt2OQRDrD\nxg0LhX0ou9b1B/oBWOpcSndLN3edfxdLHEv4wmNf4A8DKj1NygapVjKmf796ImYhLM1wyiXw5kMQ\nrF3TcLRDkiSufPdSdo2FeHqPxpJ4HYcuJneLX337Ialu964LjSR2kpQ9iGocsZMzGcb+4R+Yuu02\n3J/+NN3f/z4GiyV3+93PDrCsvZl3HVOyXlebscspdg0idqs+Ig6wnvtJ2U3ViN0BKavYeSsrdkeS\nWqdgeYeoPrhnh3r1QSXFTnFQGVp0YqeG54EVkiQtlSTJAnwGeLDwDpIkFaZ3fBR4cw5e99CASkQ4\nIBYmoxXM6rM2d23vx2Iy8JnTeup+yS6nlZFE1hpRLU0uMAyOhSTSCW588kZ+tftXfPbEz5Ka+Dju\nJkvxfVuXil+n92Kw2ZCs1iJPstJl558QrttqBeUZg3ic3VisWjQyPAWqE7u56rArRU9bE+9f1cF9\nfxoknqo8p+J473vp2XwbqbEx+i++mER/f9Ht1ayYLeYWjJXsZzoOOhT1VK3ywBceA8DTrK7C5xS7\nKlZMh9mBxWhRvb0mbG5IBEWPZiG0bJSUBLoCYtdiacFhcTAaKj6MiKfSbH1ugPetWsAxzdlNRjbw\npd/fj0EysNghSFi7vZ0tH9rCmrY13PDEDfx6z6+LX1exilezYmbSWQdCheCUQqzbJNbkF+6ufV8d\n/H8nLaSt2cJWPUTl8EdOqZNh6p3ZP194snHEDrLKWGOInZxKMfrNb+K9735ar9xE13f/DsmY/x59\nbdjPi4M+LtnQW14RoDgf1EKjGmnFBHH4dtpV0P8UjL1edJPNbMRiMuQOyRWkMzKjUjYxvYoVs5rT\n6nDGFe/qYywQ55HXyg/zDBYLks1WFp6SySp4umKnAlmWU8AXgG0IwvYzWZZflyTp/0iS9NHs3a6X\nJOl1SZJeBq4HNs72dQ8ZWMs3Q4BYrCosTP5okl+9MMzHTlpEa3P9G7gul43BWJYwVtoMyTIERok6\nFnD9/17PowOPcuO6G7nupM/jjyRx20uJ3TLxa0GASqFi57A4cFqchCfFB6fayU8SoUZYKVYdAtEU\nFqMBq6kx9YmKFTMjl5/aKArJXIWnFOKyM/uYDCVUF5VCNJ12Gj1334UcjdF/8SXE3nord1slK2Yg\nEdCDUw4xuLLdSmrEzhsUM6iuloVlt0H+YKGiYhednnkiJuTXnFL1N+arbsMEMFnBZCtbyxY1Lyqz\nYj7y2gEmQ3GueNfS/OFSdsZuIDDAouZFReTUZXVx6wdvZX3Xer79zLfZ+sbW/JPlrJhVFKPQmCBr\ntRQ7gLZj4Jj3w847ygmujjJYTUY+ddoS/vDmGKP+OVB5dMwfpvYU/P/u2T9fZKpxyhQ0TLHLJBIM\nf+Wr+H/zIAu+dD0dX/saUklK8d3PivngT6xVWVOUYBc1W3suUKaBfy+nXgYmu2phuctuLlPsQrEU\nAUsTsiSRrmLFNB2Bih3Ae1dmqw8qhKgYHY6yuoN0VsFTFL0jCXOyw5Zl+XeyLK+UZfkYWZb/Kfuz\n78iy/GD2/78py/JxsiyfJMvy+2RZfqv6Mx5GULEvid/7Ktowf75zP9FkmsvrCE0pRKfTxkAtYhf1\nEs4kuM7/ItuHt/P3Z/49lx13GaFEioycLyfPwdktOlSm9wEiSSjjL/4gdLd0E5uezN5eedGNyWLT\napKL//yBWBKn3VS2wM4VWm2tpOV0bi6tEIpCMteKHcBZy9tZ2t7MXVWSmRTYjzuO3nvvQTKZGLh8\nI9FXXgEEsQslQmWkNJAI6OXkjYYsl52MVoMyY6dWT+ELCQLkcqrPgjktTiSkqjN2M7ZhQuVAgnhA\n20ZJZWZYraT8xUEfzRYj717enp9FKZix63P1lT11k7mJmz5wE+f0nMO/Pf9vPDb4mLjB6hBrTzUr\nZrUOOzWcdrWoe3n7d9ruf5TjotN7kKHinIqOwwSTu6B9Vfb/54jYHWzFTpZnRewy0ShD132e4KOP\n0vk336T92mvL9hy+SILfvDQi+oPVHES5xE6VA7jwJFgcYG7grFpTK5z0aXjlZ2WuLDViF4glyRiM\npJsdpI4yKybkqw/+PODllaHy71aD01mm2KVzit2Rt79qjHRyNKESsYv6VINTMhmZrc8NsK7Xw/Hd\nM1u4upw2fHJ25qpCSbl/6m2u6ergxegB/vWsf+UvV/yl+HlELAhli5nBCJ6+fDJmiWIHgtilfV4M\nDgeSqfKsTiQ9hSxLyKniuTB/NNkwGybk55LUkjEbZcUEsahcuqGXFwZ9vDZcuU9FgXXZMnrvvQej\nw8HgFZuI7NyJ0+JERi4jpYG4rtg1HC/fDz85E0Zf0XT3qopdZAJnOo2pQiS/yWDCaXVWtGJOxaZm\nR+yU9ah0s6R1o6RC7Lqau8pm7N4+EGR5p0NYmKJ5xU6WZfoD/fQ5+1Sf3mK08L2zv4fdZOf5A8+L\nH0pStqS8ihUz12GnQbEDWPkhQQLnKh3wCMeS1ibet6qD+5/frzqnouMwweQekazoWjJ7YpeMiSCW\nRhI7NcUuEQI5MyNilw4GGbzqasLPPMPCf/pHWi+7TPV+P985RDyVKQ9NUaDs3dRsouGJxqqYCk7/\nLKRi8Oc7i36sRuyU38sud0XFLuXzYXQfGeXkaqhWfWB0OMrqDjK6YqejIlQiwnO/V1Hs/rhrnIGp\nyIzVOoBOl41pOftmVNkMTUWnuPK57/Km1cK/n/B5Przsw7nblAVA9ZTKs7RAsXOrEjvJH6p56hNI\nTiGnHITixYEygWiyYcEpkC91nlYhu7m0QltjFrZPrF2M3WysWH1QCsvixfTeew+mzk4Gr7qarjfE\nbFapHTOYDOrErtH4063i15EXNd3dZrJhM9pUiZ0/5sWTyVT94vdYPY1T7KqtRzNV7FoWEkwECRX0\nzO0eD7KqUzlcyp5q21sZj4wTTUXpdVbYMCHI7XL3cnZ7CzaeTe3VUzH92Th+rcTOYIS1G2HfEzAx\nRwmBRzgu3dDLRDDO/7w+Nt+XomMmSETAPwjtK0Sf42ytmLly8oOs2Gnp3FRByutlcOMVRF9+me7/\n933cn/iE6v2Uw/XT+1pZvbCCWpOzYqopdhONm68rROcaWHq2OJwqsJRXUuwAJE+rat2BnE6TCQSO\nWMUORCjfJ9cu5rcvjzIRLK4+MLicZHTFTodmVLNiqixMd24foNNp5bzju2b8kl1OGz6ym6oSYjcW\nHuOKbVcwEB3nprEJ3n/Mh4tu92UVu7LwFBBzdtN7QZYxOp1l8bDdjm6aIhlkZ3PV6/PGJ5FTzrIB\n30As1VDFTkkcVAtQyaUVNkCxA7HYXnBqN795aQRvOKHpMebOTnq33o2lt5fF/+du1u7OlBO7RFC3\nYjYSwy/kCd34G5of5rQ61RW7hB93OlN1/sJtdavO2KUzaXxx39wodqWn4LMhdiWVB5OhOJOhBCs7\nlcOlvGKnVB2oWTELscKzgt3e3fmI/ea22lZMqzMf8KIFp14m4tR3btH+mKMY71m5gMUeO1uf65/v\nS9ExE0xnw1LaV0D7SqHYzabC4mAQu1xISYFKPANilxwfZ+DSS4nv3s3im36E88MfrnjfJ3ZNMDgd\n4dJKap1yXaCu2DV67rAQp18tQvB2/0/uR6rELiqIn7HVQ8qr8t0SCIh9nefIVexAlMwn0hnu/1Ox\npdzocOZm6hQoip1RV+x0lKEOK+Y7EyGe3DXBxet7MddZcVCITqeNOBYSxqYi//VQcIjLH7mc8cg4\nNy84mzOjcSixhPmignSUzdiBIHbJMITGy8JTQCh2LVGZRIu16vVNRMcxZty5UyQFwWgSp60xHXYA\nbXbxBaTWZeeL+2gyNc08bVADLjujl3gqw8927tf8GFNbG7133UlmeQ9f+2WGyCOPFt2uWzEbjJ1b\nRJ/SgmPrm7OzutRTMZMhPDIidr8C3Da3qhXTF/eRkTNzNGNXcG31zKxUIXbKnN2uMfGFmCN2Ua+Y\nkbM056oOKlkxFSx3L8cb9+Zt0zWtmEPa1ToFLR2w5mPw0n2QCNf32KMQRoPExet7eW7vNLvHyueU\ndRziUKyXbSsEuUuEZlf5oRy0NJLE2NyAXBz2VCexS46OMnDppSRHRlly66043vveqve/+9l+Fjis\nfOi4KofrVWfsDpIVE2Dl+eBYWHQ4VU2xM7e1kZ4qX0fTWbJ3JCt2AMs7WjhrRTv37hggVWApNzod\nuRRMBelAEIxGpKamg32ZDYdO7GaLXER4wUYtk1G1Ym59dgCL0cCFp9dfcVAIT5MZi8lAxOjMEbt9\n/n1c/sjlhJIhNp+7mbWJlCB1xmICl1Ps1JQzJRnTuw+jy4kciSAn8urT4pbFOGIQbqr+thmLjGHG\nkztFUiDCUxqn2ClqnJpi54v7GmbDVHBsl5P1S1vZ+twA6Yz2k1Kj243lR//M24uh+Z9uxffLXwGQ\nyqSIpCJ6OXmjEPXBq7+AEz4JS04XxE7jCbfb6lbvsUvHcBksYm6symPVFLtch91cpGIWnjTXM7Oi\ngdjtHhOWzFVdCrGbFhshSaI/0I/NaKOjqaPqy6zwrBDPpdgxa1oxNXTYqeH0q0Xf56s/r/+xRyE+\ntW4xFqOBe/UQlcMPk7sBSaTCti3P/mwWNmTl0LjRih0U759i2Q24hvUqMTTEwCWXkp6apmfzZpo3\nrK96/8GpCH/cNcGFp/dgqZbOXWnGLpMR4SkHw4oJovrg1Mthzx/A2w+IuqhgLFW0x1DcUbYFbaT9\nfuRU8d4r7RN/jiOd2IGwlI8F4jz21njuZ4asYicXfL9nggGMDkfDwvzmEzqxmy1MVhFLW7gZigcA\nuUixk2WZh14e4UPHd7HAUV3xqgVJkuh0WgkYnBCZYrd3Nxsf2Ugqk2LLh7ZwfPvx2c6n8sh15aRH\nlWAVdtllUy8L7ZiLWhbhiELAVnnzG01FCSaC2A2eolMlWZYJRFPqs31zBJPBhNvqVg1P8ca9udCL\nRuLyM/sY8kb549vjte9cAJeni3/+tJHQicsY/da3mL733lyQim7FbBBe+SmkoqL3rPN4QVBC2uaL\nXBaXaj2FT07iMap3VyrwWD34Yr6iLxnIE7s22yw2UuYmMJiK16N6TsAVYldwbe32dkySKUfs3h4L\n4rKb6VDWsag312E3EBig19mLQar+1bLcLTaee3zZePamNkHA0uXFu8DMFDuAJevFv+3zm2dnSztK\n0NZi5cMndPHLPw8RjutVEYcVpnaDe4nozm1fmf/ZTHEwYv1zBKrgoEvjehXft0+QulCInjvuoOnU\nU2q+3D07BjBIEhfVOlw3WcDcrGJp94GcPnjEDoSlXDLkQlSUPVSwwBEViKVEBtWCdpDlHJFTkCN2\nR7gVE+D9x3bQ5bQVHU4ZnQ5Ip5Ej+b7pdCCI4QicrwOd2M0NSk+5VRamYV+UqXCC05fO4jS+AF1O\nEaDyVnSMTds2YZJM3Hnenaz0ZBf04Khqma8/msRmNmAzqxReu3tAMsL03lydQaEd0yobaYrDtLny\nDNl4RBCaFmNbkRUzlsyQSGcaGp4CIhxFTbHzx/y5GbxG4oNrOul0WrmrzrJfp9VJwizx6l//BS0f\n+ABj//CPTN9xJ4BuxWwEZBmevx0WnQqLToGONeLnGu2YalbMaCpKHBm3uaXCowTcNjeJTIJoqrgz\nbE6InSSJzVLRCXidxC6ThGT+2owGI53NnXkr5oEgKztb8iedEW/OutTv768anKKg3d5Oq601r9g1\nZ//ManbMRESQ7pkQO0mC066EA6/C0PP1P/4oxKVn9BKMp/jNSyO176zj0MHkLmHDBHAuEsRkNsmY\nkSlAqljbNCdQm2XLrVeVXze+Zw8Dl12GnEjQe9ed2E84vuZLxZJpfrZzPx86rpMul4aqAru73Ip5\nMMhuKVzdsOp8eGErpOI5YlfoiApEk7RYTZjbxTpaWlJ+tFgxAUxGA585fQlP7ppgcEoQOSX5snDO\nLp1V7I5E6MRuLmBz5e0DkN9UFSyISgz+CTOsOChFp9PGCwYzV5p82E127jzvTpa6lubvEBgW3uwS\n+CKJ8nJyBUazOPGb3ovRqRC7/J9LUe/GzZVLbBVi57K0F4WnKCTPaW/cjB2IygPV8JS4tyHl5KUw\nGw1cvL6XJ3dNsHciVPsBWdiMNswGM345wuL//A8c559H4ge38vHtGV2xawQGnoHJt8WmH6DzOPGr\nxgAVJTylUHVT5uY8NQJ6lAOGUitnzoo5mxk70HTQVPWxhY/JYmHzQkZDo8iyzK6xYH6+DsTmp6mV\nZDrJcGhYE7EDodrlFbsqJeUBJRFTY4ddKU74lOid0qsPNOHUHg+rFzq557mBMlVZxyEKWRZVB4pS\nJ0nQvnz2xK6pVSTMNgo2NSumsl6pf+/F3nqLgUsvQ0Ki9+67sB17rKaXevDlEXyRJJdu6NN2bXZP\nuRUzPCF+PVgzdgrWXSFmHt98KEfs/CX7K6fNjNEjvjvS08WE9GiyYgJ85rQejAaJ+7IhKkryZeF+\nNhMIYnDqxE5HJZRupJTFoIBIvDrsx2SQOLZrbt5IJvsgP15wAEcmzR3n3cGSwkLkRFhcj3NR2eN8\nkaR6cIqCbDKm0a0Qu/zCpiwOw8bKg/VjEWFla7UuIBgrPlECGq7YtdpaVcNT/HF/wxIxS/GZ05dg\nNkpsfU67aidJEk6Lk0A8gGQ20/297xE/ZwMXPZHBc9+j+gZrrrFzi/jcHif6HWlqFQchGhU7t7Vc\ndfNmiZm7xoyc8j4snbObik5hlIyzn6m0uyucgM+S2IVHGQvECcRS+fk6yM7YuRkKDZGW08UHTFWw\nwrOCPb49ZORMfo5HTbFTOuxUHAiaYG2Bky+E1/9bnTjqKIIkSVyyoYc3RgO8MKhey6HjEENgRASf\ntS/P/6xtxSyJ3WRj5+uggmLnE5ZyY/leIfrqqwxcvhHJaqV3691Yly8vu48aZFlm67MDrOxsYcMy\njQdnNhXFLhcocxCtmADL3i96hnfekQugKyJ2UZE4bmpTiF3xOpr2+ZDMZgzNR15QiBq6XDY+cGwH\nP9+5n0Qqk1PsMsECYhcKYnQcmYfmOrGbC5SdkJcrdq8OB1jR6VC3QNaJnQd28mTwn7Clzdw5coBu\nW8kiExCWKVViF01Wn3NrXQbT+wpOOPJ/LoXYDRn8pDLq8xeKYtfetKCCYtd4Yleq2CXTSULJ0EEj\ndh0OGx8MSZMVAAAgAElEQVQ6TsypxJJpzY9zWp25uS3JZGLsK5/if0+QsNzxKyb+8wc6uZsrhMbh\njQfhpIvAUvBF17FGuxXTIghQ4ZydLyQS6Nw1gkMU5bg0GXM6No3H5qk5n1YTDVDsupq7GI+M88YB\ncc0rOkoUO3sr/f5+AM2K3Qr3CqKpKMOh4fwJuFrlgX9I/DoTK6aCdVdCOgEvbp35cxxF+PjJ3bRY\nTdxTx+GUjnmEMkunKHbK//v3CyvzTBCZbrzlsJJip7JWRV54kcErNmF0OOi9ZyuWvj7NL/PSfh+v\nDvu5dEOv9rAMtfL0+VLsDAZYewUMPM2CmOgaLlXsHDYTxlZB7FIlil3K68Xodh+RQSGVcPGGXqbC\nCba9fiDvQCvoskvrip2OqqixkZJlmdeG/ZzQPfvTgedGn+O6x67DbVnAGftPoyudFifmhQhmZyNU\nrJj+SA1i51kKMR9GiyARhRGxCrHz2zK5TqtSjEfGaTY302Z3Eoznk5sUP3gj6w5AzCf54r4i4qlY\n3g4WsQO4aH0PgViKh18Z1fwYp8VZRBQC6RA3f8SA5S//gqlbbmH8e9/Xyd1c4MWtYo5s3RXFP+9c\nAxNvF5XBVoISxFM4Z+cNCGXJ3Vz+uStEJcVu1uXkCirO2Gl4/1coOF/YspC0nOblEbHRX6mUkyci\nkIoVddhptmJ6xGn7bu/uAiummmI3BEiqB1Wa0XEs9J0Fz2+BjPbDlqMVzVYTnzi1m4dfGWVaYy+n\njnlEYdWBgvblgJzvt6sX4UnhZGgkLM0i7KnUYVBC7CLPP8/gVVeJeqB7tmJZXN8hz9bnBmixmrjg\n1DoeV3XGrsFKphpOuQSMFjp33Q+UKnZZK6bbDZKkqtgdLTZMBWctb2dJq517dwyI8BSKFbt0UFfs\ndFRDDSvmiD/GdDjBCYtn98F6ZvgZvvDYF+hu6eZvTv0hkZRyyl2yGcopdurhKTWtmIAhMSEWCF+5\nYheyw0hIfbB+PDJOR1NHTpkLZe2YimLXyFRMIFdpUDi/lCN2B2HGTsEZy9pY1t5cVpRZDYoVU0Ew\nEUSWJLq++108F1/M9JYtjP3zv+jkbjbIpEW6WN9ZsGBV8W0dx0E6rmkjpBC7ovdZNlzE46y+ecjN\n2KkodnND7CodNGn4Equg2C1qFqTq9bFB2lustLUUJGIC2D30B/pptbVqTp9VkjF3e3fne6NUrZjZ\neWEVa1ZdOO0q8A/C7kdr31cHF2/oJZGur5dTxzxhcreYI3UUdLMp6t1M7ZgHo4i7UthTAbELP7eD\nwWs+i3nhQnq23o25q0r/nAp8kQS/fWWUj5+yiBZrHQfLlWbs7J7Zr0UzQXM7rPkYTW/+DBvxImIX\njKVw2k1IRiNGt1slPMV3VCRiFsJgkLjw9B6e2zvNQFw45RTFTk4mkSMRDI7qQWeHK3RiNxewOYsj\nwmM+kS5pFacErw7NPjjlif1P8MXHv8hS11K2fGgLK9sW4SUrI0dKFDslbECl7sAXTeBuqlLSnSV2\nkr8fg8NRVHegELugHWGfUsFYZEwQu6wypxC6qjULcwhlY1xox1Q23wcjFVOBJIlFZeeAN1foXAuF\nVkwQ5eQmyUSTuYnOv/0WrRs34t26lQN///fImUyVZ9JREXseA9+gqDgohRKgosGOqabY+cLjSLKM\ns0bIh8PiwCAZVMNT5oTYKTN2ufXILxLytGxGcsSu+NqULrt9vv15tQ7yxK6plf6AtkRMBc3mZrpb\nukWAitEkNkyqVswZdtiV4tiPQEuXHqKiESs7Haxf2sq9OwbI1NHLqWMeMLVbKHSFVrvWY7K37an/\n+TKZbHjKQVCm1GaCs+tQ+Nln2f+5z2FZ3E3vXXdi7qhuc1fDr14YJpHKcNHp2tcmQBDOVBSSsfzP\nwpMHNxGzFOs2IcUDXGB6VlWxAzC2tqqGpxxtih3AX60VeQcPvCH2g+msYpcOiWA7XbHTURmlEeFR\nn/hZdpF9ddg3q+CUxwcf58t//DIrPSvZfO5mPDYPHU4rXlkhdiWn3MFR8fqW5qIfx5JpYslMDStm\nHyBlS8pd5TN2JhNJq5Gh0JDqw8cj43Q2deYInLL4KPN2jgZbMdWInRKmcjCtmACfWCvKfu/TWPar\nptg5LKJAU5IkOr7+17RdfTW+B37K6Le/rZO7mWDn7dDcAcf+RfltC1aJAxkNyZjKjJ0/UWDFjE7h\nymQwtnRWfazRYMRlcTWO2JWuRzGftvk6ACW4RWXGDuBA5EBJImb2c5a1YtZD7EDM2RWXlFeYsXPl\n3QepTEoErtQLoxnWbhRlv9P76n/8UYhLz+hl/3SUJ3ZPzPel6KiGyd3FNkwQ88OuJTMrKY/7RV/b\nwSAxFRS70NPPsP9z12Lp6aHnrrswtdd/LbIsc/+fBjl5iZs1i+rcxCsugsJrO5jl5GroOQMWrOYS\n0+O5vVU6IxOMp3J7LlNrKyndignAAoeVDx3Xxc9fGkWy28lkFTtlxMioz9jpqIhS+1LMP2fBKY8N\nPMYNf7yB1a2rufXcW3NKgc1sJGOrYF8KjICjfB5FWQiqWjHNNmHhnN6L0eksS8U0etx0NnepKnYZ\nOcNkZJKOpo5810pWsQvEUtjMBqymBkYnA63ZRMLpaLlid7CJXWuzhfOO7+KXLwwRTdSe63FZXQST\nQdLZGaBgIliUkChJEgu++hXar7sW/y9/xei3/hY5rc8LaYZvEHZtg1MvFQW0pTBZoW35zBW7uBd3\nOqNpM+S2uYvSW2OpGOFkmDb7HJyQlwYSVAgjUIXZBiZbGbFrMjfhMDtJGbwliZjizxAy25iMTtLn\n7KvrUld4VjAQGCCRTgh1oHQtk+WycvLvbv8uH/31RxkNaZ9fzWHt5eLA7YW763/sUYhz13TR3mLl\nnjp7OXUcRCQiQtUuDE5R0D7DZExl1nWeFLvQvjhD112HZelSeu66E1PrzA68dg542T0eql1IXum6\noHjOLjxx8INTCiFJsG4Tx7EHl/c1AELx4vyCUsVOzhaWH21WTAUXr+8lEEuRsDXnHGiKJdOgK3Y6\nKqKM2PnmJDjl0YFH+doTX2NN+xpu+eAtZX1mVmf25KjMijmibsOMaJxza12aKynPFPbY+fwYXS66\nHd0MB8uJ3XRsmpScyloxi0s0C60CjUSrtbIV82DO2Cm4aH0PwViK375Su+xX+fcNJYVNIJAI4DAX\nnyhJksSC66+n/QtfwP/f/83o33xLJ3da8ee7xK9rN1a+T+dxmoidzWTDZrQVE7tkCLdMcdJmBbit\n7iLFTiF5c6bYQfFBk1Zipzy+QDlW4DR3YDD5iq2Y2bVnIBUGqJvYLXcvJyWn2OffJzZMpcQuPCnm\nHrP21lQmxWODjzEQGOCKbVdUnPWtCOciWHkevHgPpJO173+Uw2IycOHpS3j87XGGvDNMV9TRWChW\ny3aV6P+2FeL2eueylc9h80EgdoWKnSwTfCfK0J0vYF2+nN4778A0C0Jy/45BHFYTf3FS9UArVSiK\nXSHpjMyzYgdw0qeJYWX99G+Agiopu2LF9JAumLHLBIOQTh+Vih3AhmWtLFvQzLRkyYWnKL/qip2O\nyijdSEV95cEpdc7Xbevfxo1P3Mjx7cdzyzm34LCUvwHb3A4ikl1dsVNJkMspdpUKyhUoxM5dbsU0\nut10t3SrKnZKh50IT8nO2ClWzFiy4fN1IObUjJKxjNjZTXasRmvDX78U65e2csyC5lxRZjUoxE6x\nY5YqdoVY8IXP0379F/H/5jeMfPObOrmrhVRCqDQrzgV3ldPbzjXgG4B47blIpaRcgTcVwS1pe4+7\nre6iVMw5KyeH8m6omRC7EsUOwCy3Ipm9rCgtJwf6k+K16rZieoR9bI9vj1AHSq2YSoddVrF7fep1\nQskQVxx/BYFEgE3bNlWc962ItRshPA5v/76+xx2l+PRpglT/bKe6/V7HPEOt6kBB+wpIhMR4Rj2I\nHMT0xwLFLrjtdww97ca6uI2eO7bMioz4Igl+++ooHz+lmybLDEZAbCWKXTolDrLmU7EDsLnY0fI+\nzgg/DjF/vkrKplgx20j7fMgpcaieKyf3HJ3ETpIkLl7fy4RkJTAh/i11xU5HbZRGhMd8uc2VEpxy\nfB3E7pF9j/D1J7/OSQtO4uYP3kyLRT25p8tpE3N2hXUH6ZTYtKhYMX0REVtd1YoJIkAlPIGh2V4W\nnqIQu4noBLFUrOhh42HRYVc4Y5ezYkZTDU/EBDBIBjw2TzGxi/kOanBKIZQQlRcHfbw5Wq6CFCJH\n7LIBKoFEQJXQK1hw3XUs+PKXCDz4ECNf/0ZuIdehgrcfFp+L066sfr+ObIDK+Fs1n9JldRUrdpk4\nHqNN0+V4bJ6iVMypmDicOWQUOxVil0q4MFr8xcp7dBpMNgbCo0hI9Djrszz1OfswSaZs5UHWilmo\nLihBUFlit2N0BwAbj9vIbefeRjARZNMjmxgK1kE6lp8j7OZ/vrOuaz1asdjTxHtWLOBnz+8nldbn\neg85TO4GpFzwWRHas3N39c7ZKYfFB23Gzk9g2zaGbvg6Nk+Snr+5CKNr5mFzkA9NuXAmNkwon7GL\nTgPy/Ct2wJ/aL8BGHF7+ab5Kyq5YMcV1K4Qu7RVk5mhV7AA+cWo3UYsd73hxiIqu2OmoDNWNlPgQ\nvTbsx2iQWL1Q28nAw3sf5utPCVL3k3N+QrO5ueJ9O502JjMtZApPuUNjIGcqlpODFium+IIwWmTS\nfn8uXr+Q2AGMhIttUEo5eUdTBy0WE5KUV+z80WTDO+xyl19SUu6NezVHsDcCn1y7GIvJULP6QFHn\nlECOWsQOoP1zn2PBV75C4Le/ZeSvv66Tu0p4/nZw9YhNfTXkkjFfq/mULosr928lyzI+OY3bVPnz\nWgjFiql8tuZUsVOdsavjZNLqVCV2wVALGGIEEwVqZkE5+aKWRViMNdwAJTAbzfS5+tjt2y1OwuV0\ncViBUk7uzBO7Y1uPpdXWynFtx3HbubcRSobYtG0T+4MaY/kNRjj1MnjncfD213W9RysuPL2HA4EY\nf3xbD1E55DC5W7gQzPby22ZaeXAw+9rsbgL7rQzfcAP21cvpee8UxrbqAVS1IMsy9800NKXguoC8\nYqf8ncy3YgcEPcfzGsfAzi0EouLAPq/YZUvKp7IkJkvwTEcxsXM3WXB3tJL0+wnFU7kQFV2x01EZ\nCrGLZysPlFRM4NVhPys6WjQFpzz0zkP8zdN/w6kdp/KTc35Ck7n6rE6XSyh2qVABsQtkyZaaFTOi\nITwFREk5YDTFIZ0mEw7nBnBNbjeLHWKTVTpnNxYZwygZabO1YTBIOKwmAgU9dgfDignlxM4f9+f6\n7eYD7iYLHzlhIf/9wjCRRGXiVajYybJMIBEom6tUQ/tnr6HjazcQ+N3vGL7xRp3clWJyD/Q/BWsv\nE5v6anD3iD4oDcmYbqs7p9hFU1ESEngqWGdL4bF6SGaSRFJibqkxxC67HsUCs1bsUukMkz5BWkfD\nBbauiDfXYVfvfJ2CFe4V7PHuUS8p9w+ByQ5NrURTUV4cf5H1XetzN69pW8PmczcTSUUEuQtoJHen\nXJINUdk6o2s+2vCB1R0scFh54HntvZw6DhImd+WVuVI4FoKlpX5iF5kSnzsN88KzReCVAwxv92Bf\nvYol/3A9RrNc33qlgp0DXvbMNDRFgdUFSHlLezh7qDGfdQdZuOxmtibfDxNvYhnekfsZgLFVkPG0\nt5jYHa3hKQqW9nXRlIjym5eGhWJnMGBobvz7ez6gE7u5QGFEeDIiosbt7oLglNqL1EPvPMS3nv4W\n6zrX8eMP/LgmqQNhxZzGgVy4EQpmiZ1DvcPOaJBql3S2ZokdIsQj4/cjRyLIyWSRYlc62zIeGafN\n3oYxu3l22s35GbuDFJ4ClFkxvTHvQU/ELMWFp/cQjKf47cuVZx0KZ+xi6RipTKqmYqeg7aqr6Ljx\nRoK/f4ThG76GnNSDIXJ44S5RY3DKpbXvK0nQsRrGNFQeFFgxvdn3m9aAHkVBVkJTpqPT2E12TZ/7\nmih0ECTCQgWbJbEbmI6QiIn3Z1EaZdSL3CSqDvpcfTO63BWeFYyERwgp9SyFM8NKh50k8eL4iyQz\nSdYvXF/0+NVtq7n93NuJpWJcse0KBgMayIdrsZi31ENUNMFsNPCpdYt5/K1xRv3R+b4cHQoyGRGO\nojZfB2I9a1uen8PTioNRTg4EHtnG8A9/jb0twZJ/+RpGY/azOEtid99sQlMUGAziOnKKXZbYHQJW\nTJfdzIPpM5CtTpbsewAoVOyyVsxsgEpKt2IC0LmwneZUjPuf6ycdCGJ0iCqpIxE6sZsLFEaEK6c7\nNjej/hhT4QQnLK6+SCmk7vSu07npAzdp3tx1OK345BYMBbHpecWuu+z+/mgSl91c+81sdUBzB0Y5\n69H2+/OnPm437fZ2LAaLKrHrbMpbKJw2M4FYUqhPsVTOA95otNnaiqLkfXHfvBO70/o8LO9o4d4q\ndkzFihlIBHJ2Ny2KnYK2KzfR8Y2vE9y2jeGv3aiTOxChKS/dB6vOB0eXtsd0rhFWzBpJckp4iizL\n+LLqtduu7UtfUZCVZMw567ADUfZtaRFrkULQZkLsCv78uw4EkVPiM1Sk2EWnmbC1EElF6g5OUZAL\nUJGzqYuFJeUFVQc7Rndgkkys7Vxb9hyrWlex+dzNJNIJrth2BQMBDfH8azdC6ICowNBRE585rYeM\nDD97Xg9ROWQQHBGHyW0qiZgK2lcI10I9iExB0xytRxUQeGSbsF8eu5QlZ09jNMQL1qvZhaY8PJvQ\nlELYPXlreM6KOf/Ezmk3E8VGaNUn6Bt7DBchWpS6gzah2BVZMQ0GDI4jc55MK4xOJwZZZu/gBFMH\nJjE4j0wbJujEbu6gbIaUhcnu5tXh2sEphaTuRx/4EXaTik++ArqcNqZlB+ZUGFJx8cPACBitqouy\nL5LErdUO2boMQ0osZOlAgFQBsTNIBha1LFIldh1NHbnfO+0mAtEUkUSadEY+aIpdq62VUDJEPB0n\nmUkSSobmpeqgEJIkcdHpPby838frI+XzSwA2ow2zwUwgEcglY9ZD7ADaNm7UyV0h3n5YEIVTL9f+\nmM7jxZd5jSQ5l8VFIpMglo7h9QvC7mnWRh6Vg4acYjeXxA5ygQQzJnbpBBSEI+0aC0G6BbPBXELs\nvAyYxVzdTIndcrfYlO5OlGygAPzDRcTuxAUnVjz4WtW6is0f2kwynWTTtk21lbvlHxQhU3qIiiYs\naW3irBXt/PT5QdKZOuPzdTQGisWykhUTROWBf1D03WlFeLKhlsPAI48IUnfyySz5/t8J++VMD6JK\nMOvQlELY3XnFLjIJkiEfqjKPUGyXY8s/jUlOcKF1O0aDOLA3ulwgSUVWTKPbjWQ4urf7SlDKAhKM\nDE9gPIKJ7tH9Lz2XyBE7X+73rw6J4JQ1FYJTZkPqQBRgBwzZ51a67IKjosNORZXzR5O4as3X5Z58\nGcaEUP/SvmLFDqDb0V2WRFdG7LKKnV9raMscQdkge2PenFVuvlIxC/GJUxdjNRm4b4f6hlOSJJwW\nJ4F4gGCyfsVOQRG5u/Gvj25y9+e7RPDG8g9of0zHGvFrDTumQs78cT/ebJ+a21GulKuhVLGbik3N\nMbFzibVopsQOiuyYu8aC9LS20NXclSd2sgyRafqNYq1Z6lw6o0td1LKIJlMTe6KiLiVnxUzFhaLm\nWoI/7ueNqTfYsHBD1eda6VmZI3c1bZlGkyir3/MHUV6voyYuPL2HEX+MJ3frISqHBHIddhWsmJAn\nfdPvaH/eyFTDglMCv/89wzd8TZC6W27B2Ja1S8Z8+f2TxlnlUsxJaEoh7J7iGbumNmHRnGfkiF3T\nCgZtx/Ipw2M5h4VkNGJ0u/OKndd31NswIR+U8uGlLYQmfcgt6mnzRwLm/x16pEAhdgVWzGrBKQ+9\n8xB/+8zfzpjUgSACGXt2M6hshgIjqlUHIBQ7zeSqdSnGxAGgxIqZjSBe3LK4KBUzkowQTAZLFDsx\nY5frWTlIxE7ZNE/FpnKR8vNtxQRwNZn5yIkL+c1LI4Tj6gEnTquzSLHTOmNXiraNG+n4+tcJPvLI\n0UvupvfB3v8Vm/daoSmF6FSIXfVkTGVOzh/34w+Lz4onW6RdC8r7MWfFjM6xYmefpWIHRcTu7bHg\n/8/eece3VZ9r/Hu0ZU3LO7GdvUnIIAFaRsNsb9tLB7Sh7NVLobRQRkv3HrS9bW8XELgN3FJoyy2X\nDWWEFgoZZBCgQPaw421Na0vn/vHTkWRbknVkOVaons+HT4x1ztGRfHT0e97neZ+XOY02WiwtmR67\n6BAkY+yXYhi1RpospSXZaSQNs52z2eXbB/qa4fcyAMdUNndvRkYe1V+XC3Nr57L2rLVEE9GxlTul\n77IaolIUzljQRL3VwP15ilNVHGH07xRhT9YCn71SRh5MUI+d78kn6bzp5gyps1qy5sWlClE6M+jU\npesqKEtoSjZMzuGpmBVgw4QMsfOFYqy3/hsz5UPQsTn9uLbOle6xUxS7f3VoHYLYvX+6FVMsRHfy\nyKxHJwNVYlcujFDsZJMzb3DKY3sf46v/+Corm1aWTOoUaC2pqpoyyy7PcHIQip0aK6bWkBpz4POm\nB5WnFTvrVLwRL4GoCFhRRh1k99g5zHp84XhmzsoRtGKCUOyUIdCTbcVUcMHx7QQicR557XDOxx0G\nB76ILz3LrlRiB1B32Qhy96+Wlrntf4R1ZtmF6vYz14oe1TGSMbOJnTvYj0aWsRU5x81msKGRNLjD\nbmRZngArpmOEtUnF9T9iLmcknmB//xDzmkcodql7zoFEiHZ7Oxqp9K+TObVz2OXehVxTn7FiKqMO\nHK1s6NqAWWdmcf3ioo6n9NxFEpHCaZnONphzprhWEv9in48SYNBpOHdFG8+93UuPLzz2DlVMLPp3\nCeJWqG/eNQuQiu+zi4XFUPMy99hlk7r2O1OkDsBgAY0u4zAYhw2zLKEp2RjZY1cBow4gUyT3hmI8\npz2ZkGQW7pQUdLUu4ooV0+3+l0/EBNI9hjNMSZyJCLsC7147eZXYlQvK7KfUYqg7ZsoZnPLY3sfS\n6ZfjJXUABnuqgqQM9vUdFlbMHPAEozhriqyEuWYgaWUkvY5kDsVuZDJm9gw7BXaTnkAkzuBQas7K\nEQxPAdG3pCgilWDFBFjeXsu8JlvemXaKYpcOTynRkqKg7rJLabzllhS5+xcahZCIwbb7RB9VqkdL\nFRoXjmnFTBO7qBdPeBBHMonG2lhwHwUaSZOeZeeL+ojL8crqsYP0vvv6h4gnZeY2CcWuL9RHLBlL\nV7IPxLwljzpQMNs5G0/Ew0CNM6PYpYldGxu7NrKiaQV6bfHFoWxyd9nTl+UndysuFRb2XX8d12v4\nV8GalW0kkjJ/frXI0RJVTBwUYlcIhhpwtBWv2E3AcHLfU08PI3UaS9a8T0lKKWPjI3ZlDU1RYE6d\nlyynrJiVQewcWcSuL6pnk3U1vPG/6Xu2tq6OxEC2Yjd5c3wrBdpUWErSH8AeD9MR0/FGZ+68g6Md\nVWJXLoywYu7oF9WA7OCUx/c+niZ1vzr9V+MmdQA1DrGQlIcGxEIrEclpxUwkRTJl8VbMmUgSaGoM\naSumxmJBMghiODXVS9QREIuvnqDojxkZngLQ6RHx2EdMsUvZUwdDGWI3mQPKsyFJEuevamNHhzfn\nTcVuSFkxy6DYKai7/DJB7p78FyJ3O58W/VkrVISmZKNpIfS9XTAK32EQ15Qn4sEd9eNMkntIcB4o\nxC49w848gT12agoEI4jdO92iyDC3ycYU6xSScpK+YB8EB4kBHZHBcRM7JRlzZ40lk4rpE/eWbp2W\n/b79Y/bX5cIw5e6veYaYzzkbrM3VEJUiMb3ewntm1fHA5kMkqyEqk4fokPiMjEXsQGxT7MiDNLEr\nT4+d7+m/iqCUY4+l7Y4RpE6B2Tluxe5/yxmakj6vWjEuJuKvKCumxaBFq5HwhmL4QjG21v07xEPw\n+p8BMfIgMTiYmT9cVezSYSkJtxttJETYaM5bYD/aUSV25UK2FdNo543DgWHBKU/sfYIvv/TlspI6\nALtLWB8jvj7wpVIqc1gxlXlyYw4nV2CuBXMtWpOGhNc3yqfdah0+pDyXFVMhch1ukcZ1pHrsanQ1\nGLVGodhVUI+dgo+mQlRy3VTS4SlRP2adGb2mPO9Z3eWXpefcHb7lX8CWufUesVifc3Zp+zcuEvMo\nB/Lbl7KtmJ54gFpJRR8f4pp0h93lHU6uwOyEiE/YJfU16npW0sROfHZ29Yh72cwGC82p1M/DgcMQ\nctOp0xGXkyUnYipIjzzQ6zMDyr0dYGlgY99rACURO8iQu1A8JGyZI8ldOkTlGfBUVahicP6qdjrc\nIV7a3T/2xlVMDJR7U12RxK5/95gjXIBMYaUMtkPfM88IUrdkCW133pmxX47EOBU7WZa5v5yhKQqU\nBMxAL0S8FUPsJEnCYdYLYheO4a1dDE2L03ZMba2LhNdL0u9HjkarPXaAJhWWEusUa9bp05p5ePth\ngtF331qoSuzKBSUi3N81KjjlqX1PcetLt7KiaQW/PG389stsNNTa8MlmQt4+8KV6X3IQO08pyZS1\nM9DqE2nFLvvmYDfYsegtw6yYVr11WBS5QuQODSqK3ZGxYkqSRK2ploHwAO6IG7POjElnOiLPXQwc\nZj0fXNyS86ZiN9rxx/x4Ip6yqHXZqLvichpvvhnfE09y+ItfeveSO88hkXS47EKxaC8FTYvEvz1v\n5t3EpDNh1BrxRXx4EhGcGnUN/7Wm2mGKnWIhLguUxZHnoPqF0kjFrsfPjHoLRp2WFouweXcNdaVG\nHYj3t9Th5ApcJhcuk4tdUmK4FdM+lY1dG6k11qbJXynIJndXPH3FqERfll0kFr3bfj+OV/Gvg7MW\nNeGyGN61Fe+jAulRBwUSMRXUz4HYUCaQqBCUhO1xKnb+Z5+l84YvYD7mGNrWFiB1MG7FLh2acnwZ\n1altmdgAACAASURBVDrI9BsrJNoyMUmhpcBh1uMJxghE4mKtteIS6N4Bh7ehrRNFwuj+/UB1ODmA\npNOhsVjSxG7ZwjYCkTiP7Sg81uhoRJXYlQtZCynZ7OCNTi/HTHXw9P6n+dKLX2JZ4zJ+dVrxw8eL\nRZNNDCmP+vvEsFLISey8ahU7EAEq2jAJn4+Exzvs5iBJElOtU4cRu2wbJmSIXIc7iMWgRac9cpeb\ny+RKjzuoJLVOwZpV7TlvKsp4g8OBwyWNOhgLdVdcTuNNN+J7/HEO3/pl5ESi7M8x6dj2e5CTQoUp\nFfVzRUN/EQEq3qgXTzJGrVbdZzttxUyFkNSZy0nsUtd8KcRObxKzMFPEbmePn7lNotqpKHbdQ90Q\nGmS/XtxPxmvFBKHa7ZZDYgEaC4G3AzlF7Fa1rBpXOAvAfNd81p65lqHYEFc8fcXwOZy108RIjGqI\nSlEw6rR8fPlUnvlnD73+aojKpKB/FyCBa+bY2yqqXjF9dkp40Tj6yfzPPUfH9TdgXrSItrvWoh0r\nWn6cit39SmjKkjKFpihQFDvlfasQxQ5E4bzTE0KWU0X0JZ8QiaJb1qFzCWIX2bMXoBqekoLGbk8T\nu9kzm5nVYOGBd2FxqkrsyoUsYhfV2egPRDHa3+CLf/8ixzYcy29O/03ZSR1As8PEIDbRY+c7DEg5\no489QRFg4jCrUBVcM9FqgiQ8npyRuWMSu5Ri1+kOHTEbpgKXycVgeBB32F2RxG7l9FpmNlj44+bh\n1i+FzHUGOieE2AHUXXklDTfcgO/RR+n68ruM3CUTgtjNXA2100s/js4gFkMFFDsQxM4T9uCWkjhU\nKqxOoxNP2MNAeCD9/2VD+n50oLSelZS1PBRNcHAwyNwm8drMOjMukyul2HnYbzTjNDrL0sM6xzmH\nPVEPSRCLS28H+6wuekO9RY05KAYL6haw9qy1+GN+rnj6iszoBhAhKr5OofZWMSbWrGonnpR5cEvH\n2BtXUTy634AfzYD9LxXebmAXONtFIWYsKH14BazlaQQHAEmoaCXA//x6Oq6/AdPChcWROsgMAi+B\n2HlDMR5/vYt/XzqlfKEp2ecFmf7ECiJ2DrM+0+Zi0ov3bdFH4fUH0dqEKyy6V8wurCp2AtosYqez\n21mzsp2tBz3s7PFP8pmVF1ViVy4oFfLgAB7Zgs72Bo/3/JglDUv4zRkTQ+oAmuwm3LINTWhQEDtr\nI+RIjitZsTMkSI5B7GRZpifYk5fY+SPxIxacokAhdpWq2EmSxJqVbWw54B52U1HIXPdQd9mtmNmo\n/49P03D95/E+/AhdX/0acjI5Yc91RLH7OREosOLS8R+radHYyZgGB4cDh4lLErUqr7NaUy1xOc5B\n/0GcRic6TRkXJdl2ynEQu929AWQZ5jVlrsVmS7OYYRkc5IDRWBa1DoRiF5LjdOp0YphyNMAGrVDP\nSu2vy4WFdQtZe+ZafBEflz19mVAfAea+XxTFtvyubM/1bsasBivHz3Dxx2qISnmxea3ojX3kc2L0\nQD707yzOhglgawGDNWPfLITggBh1oGb2Zwr+9evp+PznMc2fT/tda9OBFWPClLJiJuOq71cPb+8k\nUu7QFAVpxS5FiCskFRMEsesPjEgcX3EJRAPoBrYAWYpdldgBIkAlGRRkWGO387HlU9FrpXedpbxK\n7MqFrJvRE8kIpql/YGHdIn5z+m+w6At4y8f7tHotAa0DfcRdcIadJ1hCj51rBhp9kmQoRNLnS486\nUNBqayUUDzEQHqA/1D8sOAWG99QdqVEHChRiNxgerJgZdiPx8eWt6LUSD2zKqHbKeAMZecIUOwX1\nV19N/XWfxfvQQ3R97V1C7rasE1++8/5t/MdqWgjeg8MGdY+Ew+jggG8/AE6VVkql4LDXs7e8wSkw\nvNo+DmL3TqroMCeL2LVYWugOdIseO51m3MEpCuY4U8mYBj10icCUjbFBplqn0mYrbvB7sVhUv4g7\nz7oTb8TL5U9fLsidVg9LLxBjD4rpRaqCTx3fzoGBIK/sHZjsU3l3IBKA1x8UQRiDe+DFn+TeLpmE\ngT3FJWKCGClQN7s4K2awv6T+usDf/07n5z6Pad482u++Kx0vXxRKvF+J0JRDHDPVPiyBvGwwjVTs\nKonYZa2vlMJ52/HQMB/tvkcAiO5JKXZVKyYgyJwCrc1GndXIWYuaeWhbJ+HYu8e5VCV25ULqZrS+\nxswvjAcwJKZx55l3YDUUYUMYJ2JGJ+a4VwS35Bh1AKUSu5lojZnFfi7FDmBH3w4ScmKUYmcx6NCk\n5qaqet4ywGVyEUlE6An2VMwMu5Gosxo5a2Ezf9nWQSQubirZZG4iFTsFDddeS/011+D937/Q/Y1v\nHN3kzt8NO5+CpZ9SlwKZD42pAJXet/Ju4jQ6CSVEVb22ZrQFuhBqTeK63OfdV35il704KpnY+djV\n48eg1TC9LuM4aLG00DXUxVCon15JHndwioJZzlkA7Dbo4fB2EsDmwIGy2TBH4pj6Y7jjzDsYDA9y\n5V+vFMm+yy8S/Znb7puQ53y34exFzThr9PzhXVbxnjS8+ZAYDv7Bn8CSNfDSz3K7BvyHIRYsntiB\nUPeKsmIOqlamAi++RMdnr8M4Z456UgcZAgWq7levd3p5q8vHJ1dOgFoHYnyN1ihm2Gn04xqeXm5k\nr6nSrS6SBMsvQTuwDTQS0Q5hk1b993iXIltBVkje+Svb8QRjPP1m92SdVtlRJXblgsnB38wmvtBY\nT13UwknWW48IqQNImlyY5BC4D+RV7LyhGFajDr2aABNLA9qsnjxtbW5it613G8AoYqfRSNhSlaTJ\nsGICxJKxirRiKvjkyrbUTUXMAcwmduMdTl4s6q/7LHVX/weePz9I9ze/dfSSu22/FzOHlpc4u24k\nikjGzP4bOW3Nqg6vXJfhRHgCiF35FLtZjdZhwUctlhaC8SCvR0XoS7msmDX6GlotU9ilF4rdWwYD\n/niQ45snhtgBLGlYwu1n3E5fsI8rnr6CPpMNZpwC2+4VqkgVBWHSa/nYslb++mY3A4HIZJ/O0Y+t\n90D9PKG8nP09MX/ysetHX4uK8lbMqAMF9XPAe0jMvyuEoX5hxSwSQy+/TMe112KYNYv2/757lLOn\nKJSo2N2/6RBmvZZzluZe94wbUlavoaVB/H+FYBixy15fHbsGSW9AW6OHRAKN3Y6kO7KOqUpFWrHT\naNDUiGLle2bV0eZ6d820qxK7MuHvA29wQ1MD86JRjju0jOWt6hZ544FGsQfEhsCeOxXKE4qqV80k\nCW19RoXIp9ht7d0KMMqKCZmbz2SEpyioVCsmwEmz62mtNaeTmbJDKGz6iVfsQPT7NXz+89R9+tN4\n/vQnur/zHeRi5h1VEpJJ2HovTD8Z6meX55iOVjA6CiZjKkPKAZwq7YLZBYeyEzuDBZS5ejkWSuFY\ngi8/9Do//es7ufujUsRuZ3cmEVNBi1XcY16RRa9CuayYALNr57LLYIDBPWxIffGuallVtuPnwtLG\npdx+5u30BHu4/OnL6V/8cZEmuu+FCX3edwvWrGojlpB5aFvn2BtXkR89/4SOzbD8YkEgLPVw9vfh\n0MbRfZ9Kz1exPXaQFaCyp/B2wYGirZhDGzZw6DPXYJg+XZC6Unu5hhWiijvGUCTOI9s7+eCSlokt\nHCt9dhU06gBGKnZZxK3GBQv+Ha1OOElGFuT/laEodhqbDUkj6I9GI7FmZTsb9g6yty8wmadXNlSJ\nXRnwj85/cMOLtzA7FueO7l5CCSeLW4+cZK+3ZSU15bFieoMxdcEpKWgbWzM/j7hp1+hrcJlc/HNA\nLHxHKnaQueEcqRl2ClzmLGJXwYqdRiPxyePaeHnPAAcGhjDpTBhS89COhBVTgSRJNNxwPXVXXoHn\n/gfo+e73ji5yt+8FkQBZjtAUBZIEjQsKKnbZRNzpUEdwsgsO2ddrWZBdaR5B7HzhGJf89yb+sPEg\nv3x+Nzf8aTvR+AhFwORADns57A2nEzEVKLPsXtHJSEC7vXw2qDm1czig1xEFNljtzKmdQ7154vta\nljUu47dn/JaeYA9XHPgL/RZXethvFYUxt8nG8nYn9286eHTdMyoNW+8FrQGOPT/zu2PXwIxT4dlv\nZubUglDsjHYRllYsihl5kEwKYldEL9nQxk0cuvozGNrbaV/3O3Tj6eMqQbF7fEcXQ9EEa1aWt/92\nFExZil0FIZvYWY0j1lcrLkFnEO031eCUDDR28V02MtTnvBWtaDXSqJTyoxVVYjdOvHL4FT6//vPM\ndM5krTeBIynjlywsbDlyxM7syLrh5AtPCcVK6nPTNk3P/JzjBjHVOpV4Mo5W0uZUHZRK2hFX7IxH\nB7EDOPe4VjQS6ZuKYu87UlZMBZIk0XDjjbguuwz3fffR84MfHD0LtS33iMrq/A+V97hNC0UlPc/7\noFxbWlnG5lRH7Gx6G9qUqlbW4eQKlAVS1nXU6wvzyTs2sOWAm1+sWcot75/Hw9sPc8U9mwlEsua3\nmexIiQhGosMSMSEzy+5tg54pOhtGrbFspzyndg4JSeJto4HtOmlCbZgjsaJpBb8+/dd0Bbu5qqWF\nwZ1PZmZ6VVEQa1a2s6dviC0H3JN9KkcnYmHY8YC4f2UrQ5IEH/oZJKLw5C2Z3w/sEgqcGmtg3SxA\nKtxnF/EKO/sYil1w82YOXX01+tapgtS5xlmYKsE6fv/mg8xutLJi2gT30KcVu8oidsqaymrUjZ4R\nPP3k9MiDKrHLQGsT34UKwVPQaDdx2vxGHtzSMbrIeRSiSuzGgY1dG7nu+etot7dz55l3pqv3DmcD\nZoP6qOBSYa3NqtrlTcWMlqTYaaZmrB75iB1AvbkebY54ZPsk9dgpwRQjf65EtDjMrJ7XyJ+3dBBL\nJNN9dhOdipkLkiTReMvN1F58Ee57/4feH91W+eRuqB/eflxUuouZ6aQGTYvEYseX22aW/swnZTR6\ns6pDS5KUJoZlt2JCZrGUWijt6x/iY799mQMDQ/z3pSs5Z+lUrnnfbG47dwkv7xngU2s3ZPqkUvvY\nCY5S7OpMdRg0emRJYpqpvGqakoz5oM1KRJLLOuagGKxsXsmvTvsVHXKEK5tqcW+tjj4oBh9c0oLV\nqOP+Te+OivcRx9uPiTluyy8e/VjdLDj1FnjrEXj7CfG7/l3q+utABIE42wordkOpdNMC4SnBrVs5\n+B9Xo29pYdrvfoeurgxFqWGK3djfe+90+9l20MOalW1IE933ppxbBY06gKw2l1xuKElC174AAJ35\nyK1FKx1ah7i2FIKXjfNXtTEwFOXZt3qO9GmVHVViVyI2d2/ms899ljZbG3eddRe1plrk1A2ppfnI\n9dcBOOuzns+Wu8fOG4qrG06egrZ1QeoHDZocg0YVYpervw6yrJhHWLEz6UzpMROVrtiBGPbb54/w\n/Nu9k0rsQBCOpltvpfaCCxhct46+n/60ssnd9j9AMpZ7UTReNBYOUFH+RrUl3kqVosPEELtU5dvk\nZEeHh3N/+zLBaIL7rzqBU+Zmqs+fOK6NOy9awc4eP+fe/gqHBoNpUtigD9NaO5ywSpJES+p8p1ty\n329KxTTHNHRIPG6xoEViRdOKsh6/GKxqWcV/nf4rDuoNXLXrf/CGPUf8HI42WIw6PnzsFB5//XB6\nZmoVKrBlHTinCdtlLrznc9C4EJ64Cfw9otBUSi9x3ZzCs+yCCrHLTdaC27Zx6Mqr0Dc2CqWuoUwq\nlsEqeoJ1JtCN7QB4YPNBDFoNH1veOua240ZasatMYmfLUzTXzhG9ydpwtdiiQKModrbRa9lT5zbS\n4jC9K0JUykLsJEl6vyRJ70iStFuSpC/leNwoSdIfU49vlCRpejmed7KwpWcL1z53LVOsU1h71tr0\noiyqE5XtaVMnKKEpD+obW1LPbwXj6AtWlmW8odIUO6lhNhp9Eq3FlLMyNtUmiF2u/jrItmIe+VQm\n5e+S3QdVqVg9r4FGm5E/bj6UtmAeyR67kZAkiaavfgXn+WsYuOtu+n7288okd7IselNaV4l+uHJD\nOWYeYqdcW06ptMLFhCp2qUrzqz0J1ty5AbNBy4NXn8ixbaMLHacvaOK+K49ncCjKx377MgeHxOtZ\n5JLRaEZ/7pv14nWXMzgFQK/RM0NrIaqRWGxuOWLJwiNx4pQT+a+Zn2CflOSqxz+FN5J/lmEVAuev\naiMcS/LIa9UZgKowsAf2vyhGbWjyLMm0evjwL8R8xf+9QvxOTXCKAmXkQb7E12DKepwjKCT02msc\nuvIqtA31tN+zDn2jiv6+saD0BBdhwwzHEjy0rZOzFjXhspRhrM1YqNAeO7u58NpK2yxIr9b/NsSr\nibUA2nSP3eiiuVYjcd5xbby0u18UN49ijJvYSZKkBX4NfABYCJwvSdLCEZtdAbhlWZ4N/Az40Xif\nd7KwrXcb1zx7DU01Tdx99t3DGvvdSVHZnjv9CFSRsuCyWfDLZrz63DfaYDRBLCGXNkvO1oLWKKPN\nI+cril1eYmeeHCsmCDXErDNj1qmzyE0GdFoN5x3Xygvv9KJHKI2TSexAkLvmr30N5yc+wcCdd9L/\ny19O6vnkxMFXRL/JijKNOBgJsxMcbXmTMRVi5tSWdo2liV25w1MgvUi69i97aHfV8JfPvIeZDfmJ\n0oppLh68+kR0GokvPymqlnMduReALTqRWDk9NXuunJhjFIvK4+uOKfux1eA9J3yBnw8G2B3o4D+e\n+Q98Ud+knk+lY/FUBwtb7OmE3yqKxLb/EWrV0gsLb9e2ClZeKUggqLdiglD5YkExBy8X8ih2oddf\n5+AVV6J1uZh2zz3om9TN7CwKpuKI3dNvduMJxjh/1QTNrhuJClXsrKk5wfnWVjqX+BtqpYBoVagi\nrdhp7bnXVp9c2cY175t+RFupJgLlkFFWAbtlWd4LIEnSA8A5QPZK6Bzgm6mfHwR+JUmSJFekBJAf\nD77xD769+Xo0sg1f75V84jdvDHv8s4E475eNLGg9spUdjUbCp7GzP2Tjkz99YdTjiVSceUnETqNB\nW6NHkj3wy+NGPdwqyWCDxt3rIWEV83dajk3bKRT/97DnDg5Cx6sixrljE7SdAKd9Rf25jQGXyVW6\nWuc7DA9fCx+/W9VMn/Hgk8e18+v1e+h2a9BImrSVtKzY/w949b/hY2vzV4ezIGk0NH/zG8jJBP2/\n+S0Pv97De7/9RRa05LCJdm6Bv/8UzltXngHhWdjdG+D7T7zFby5YjkmfddPdei8YbLDoo2V9vmFo\nXAhvPZbz+jcBRquM05T7bxXr6aHjmmtJBnNXAM8N9DG/MYnt4vKT+L0BPTOB2W1T+O2lJ45aAPT+\n9Kf4n31u2O80wLqkTJ/Hz16pgXNPug1+eeeoY7doh8CiY3rdyBre+DHHMgWCBzh+yntU7yvLMh3X\nXEt0//6822jtdtruvgttDmv5MBgsnDz3I/zsnb9wveYdrn7mau44846SCy5/eudP7HTv5KsnfDX3\nBk/cAu3HwzEfH/VQwuul8ws30vK976I/wlb/sdB/+x1oLBZcF13ImlVtfP3hN3m9w1tUMvTLT77E\noV/8mrtOu4KEdvRy5KPRR1nWbOSky74/6rFEMsEtf7+FCxdeyLLGZarP+y9/vZ7O/S9wXSTPMkjS\nwJnfgnkfUH3ssXDO/TdyUuuJ3Pyec2DbfTD37Lyjiobh9K/zwt7H+bsU5uuumTk3+cbDb/Di7tyh\nP0vjQf4TiK09C72xZvQGoVT4TRaxC735piB1TifT7lmX9/oLxxJcfPcm+odKU4d+NaSlxqjHFY6N\nulfFk3Fu+fstXLboMh7YNESby8yJM4vv7bvvrft44O0H8j6ulbTcsvIW3jM1xz1HIXZ5euwe3fMo\nuzy7+MKKLxR9Pgr6gn189R9f5Qcn/0C1a0OjkXCY9XnbXEJW8fsfT3Xx+pbvwi71/cIXLLiANfPX\nqN5vS88W7nvrPn58yo9zZi+MB6/1vcY3X/4m8WQ87zant5/O9SuuH/V7hdBpcih2AN277+G5w7/m\nI32/oN56WnlOeBJQDmI3Fcg28XYAI6PM0tvIshyXJMkL1AHD7j6SJH0a+DRAe/sRqsaowBRrE07t\nHOZpL8fYNPpDuDv8cV41reSUSWD7B4+9ga19OhZacl+wK6bV8r55pRHOuos/gdS9DZpHh5C0yjLX\nxDp4/2A37EotWLQGmLIM2lZxTt1ytCcYaN3/ILy4CQ5tgv53xHaSVlhHe96E1V8u+/DPixZcRE+w\nxEbYgxtgz/PQvQNmvq+cp5UX7XU1nDS7nt37F3Hzvy1GI01AC+zuZ+GNB+Hfflw0YZU0Glq+/W28\ngQjvfeovHPiFlQU/vHX0hnueh3ceF1afpvIu+DfuG+D5t3vZPzDE/ObUNR7ywJv/JyLBDRNAghWc\neG3B498c72PRkotyPhba/hrhN9/EcsrJOYlE8tUg7/1ngGA4isVcvnRJgPtCJ2DXxrj7ipOGk+EU\nfE8+BYB5yeJRj+lDYSLrB4glp0Hz6AXnh5JhNPoELQ2LynrOAB9afg3Bl70sm/Nh1fsmh4YIrF+P\nceECjNOnj3o83ttH8NVXie7bh3nx6Nc9Cssv5tQtv+Onyz7FjZ1Pc/WzV3PHGXeotoiuP7ie72z4\nDgCXLLyENvuIiPZ4BDavhaHenMQu/NbbDP3jH4S2v4b+/ZVF7LyPPYrW7sB10YWcs3Qq33v8LR7Y\nfJDFrYXf38OeEE/e8wif2r+dVTVRvDmSFU/d/RKWQyFgNLEbDA/y1wN/ZYZjRknE7q9dr7BXF+O6\n2jz77noG/vnwhBC7PeHniRwMc3O9SfzNi+0PNtn52/zTeOjwi3xNZyTXN+bjr3djNWo5ZupoYh2M\nrOC+Padzit1AW20el0H9nPT9LvzWWxy8/Aq0VqsgdVPyt5ns6Quwaf8gq6a7aLSrv5et913Ea4c8\nvPVfL/LL85ezNMsyPhAa4JkDz9BsmsUre6dz89nzclrE8x774Hp8UR+rmnPPxHz2wLNs6NqQm9jN\nPh1OugGmLM277/a+7SURux19O3j58Mu80f8Gp7Seonr/L31gPrMbc9+L9rbqeOEECe/CZuYH9sGU\nE1R9T27u3sxT+58qidg9f/B5njnwDAf8B5jpyF2AKBVP73+aA74DnN5+es7H+0J93P3G3SxvWj7q\nPdXYbDTc+AVsZ5wxar9YIsa3dz+AnIgzVeVM2kpDOYhdrk/XSCWumG2QZflO4E6A4447ruLUvPdM\nn83fp/+hwBbLj9i5jMSJH/kMJ07Qse1XfiPvYxrgM8r/+HuEAndooyBwG++gNhHlIoDtiMpX6ypY\n8gloP0GQv233wZM3C4XMMbWs5z2uwcZKzHnoyMZ3f3JlG9fd30+bboKGMitBEMFBVUqkpNHQ9x83\n8tqbXZzxf/fSP7Oe+k9fNXyjQK/4dwKInRLI4AtlVele/zPEQxNnw1Qw81TxXx58ssCu8W4xe2rK\nj36Uc87T/177Pc587vfs23OYY46ZMd4zTUOWZR4+7OCUuZflJHUAicFBnOedR9Oto9qikaNR3l5y\nLJq5H4Hzrh71eDsw+rflQXPzUj73sT+WtG/SK3rhXBdcgPPjowlScMsWDlxwIQlfkbbKKcugeTGn\n7foHP/7Aj7npbzfxmWc/w+1n3l60or7bvZsvvfglptuns9+3n+cPPc8li0ZcswO7QU6Ke2gOJPzi\nfBO+yuv1S3i9kOUK+eDiFh7efpivfHABNYbcS4x4Isn1D2xnWUgMBP7Ke1qoWT6aYPX9MEIy5EOW\n5VE93gNhYRv0REoLt3EnI3i0Wjgvj5Jx70eg962Sjl0IntAQkiZOKD4EW+8RgWezzyx6f7/BTAKZ\nUDxEjX646ibLMr5QjHNXtPKlD8wfvW84xuJvXsGX58/n06cUtlGH33mHg5ddjqamhvZ770E/tfD3\nc69fKHVf/MD8EkcQLGfLgUE+d/92zv3ty9x89jyuOnkmGo2EP+oH4NVDnWg1Mzh3hbp2F1/UxzH1\nx/DjU3+c8/HT/3Q63miez1aNC874Zt5je6NePBEPSTmpuhjrjoj1xUBoQNV+Cj65Mr8A0p/w8ofV\nWh474/tMu+v9ML8FTv1a0cf+yktfYWPXxpLOq8PfAcBO986yE7sdfTtYXL84798ymohy3qPn8b0N\n3+O4c44b9hmRJIn6q67Kud/v3vwdeyMD/GpgkBpbZRXP1KIckkAHkE1vW4GRBu70NpIk6QAHMFiG\n566ikmBrggUfhrO+C1f8FW7tgCuegY/dBdduhpv3wgV/glNugukniepRyxKxb/eOyT33kRjqE/+G\njmwi3lmLmqit0U9cn4ryeoLqv0h6hmL8bPkn2XfsSfT9538ycPd/D98gm9iVGRlil0rck2Uxu655\nMbTkrqRWAmJd3UgmU95ZQl0a8aXTsS/3OIVSsbd/iP5AlFUzcpP3ZCRCMhhEm2eosGQwoKmpIeGp\nPCJRCAm/WABq7LmdC5rUYNpkarsxIUmw/BLo3sEZ+jpuO+U2Xu9/nWuevYZgbOwGe2/Ey+fWfw6z\nzszas9Yyp3YO6w+tH71h39vi30BuYpdMEdGiz/sIQZZlkh4vCXemALZmVTuBSJzHd3Tl3e+/ntvF\npv2DvK9ZWLbjA7mtgzVyACcBBgOj7X3KYngwXNpSwi3HCSETTURzb9C4APreyR80UiI6/eK8E4lB\n4aBYegHksKHmgy8iroVcPZ+ReJJoIpm37cJq1GHQaRgI5HnNKYR37uTgpZchGY1Mu2cdhtaxiVSf\nT/yNGm2lOw9WTHPxxOdO5owFTfzgybe5bN1m+gOR9Gt9p7eX1fMaabKrG2vji/oKpkzbjfaSA5K8\nES9JOZkmn2qgFCVKvYYLQfl81DUsgtlnwPb7IJHfvjgSrbZWeoO9RBLqrbWHAsLEt3OwwGiNEhBL\nxHhr4C0W1+d3Axi0Br52wtc4PHSY23fcXtRxD/oOcueOOznT3Mqp4ahIaT2KUQ5itxmYI0nSgWOh\n5wAAIABJREFUDEmSDMAa4JER2zwCKCXKc4Hnj7b+uipKgM4oGr6XnAcNc3P3dDUdA0jQVanE7sgq\ndkadlo8vb+WZf/bQ55+AJKtw6cSu1x8hKWl44kOfxv5vH6D3xz9mYN26zAbKezawZ/znOQKKUucL\np4jd4W3Q87pYdE/0HKNxINbVhb65Oe+spUOSWKD0HihvkuCmfWKhkI/YKQtxrSt/ZV3jdAg15iiC\nosTlSj0D0V+XvV1RWHwe6Myw5R7Omn4WPzz5h2zv2861z11bkNzFk3Fu+ttNdA118fPVP6fZ0szq\nttVs692GOzzivtKXsqfnIXYJn1g0JryVFeAiB4PIsRgJrxc5kQBg5fRaZjZYeGBz7pj1l/f088v1\nu/n48lZaNYJgJAZyL2xNcT9GKUbXwOgC27gUO1nGk/pI5l3QN8wXjgDPfvXHL4Buv/jbG5O9QqVd\nntvGnQ8KgchFJJQCWL6kREmSqLMYGBjKT+wiu3cLUqfXC1JXZFtMjy8MQMM4iB2Ao0bPby9cznc+\ncgyv7B3gA794kY0HROErkhzi/FXqbXJjETun0Vmy8qtcP6M+00VA2WciiF1/qB+TNjX2afkl4O+C\n3c8UvX+brQ0ZmU6/uqKjLMvDFLty4h33O0STUZY0LCm43XHNx/GxOR/j3jfv5Z3BdwpuK8sy393w\nXXQaHV8yzRIBPhW8pigG4yZ2sizHgc8CTwNvAX+SZflNSZK+LUnSv6c2uxuokyRpN/AFYLT3p4p/\nTRitYgBrxSp2R5bYAaxZ1UY8KfO/WzvKf/C0Ype7Ql4Iyhf3YDjBlNtuw3b22fT+8EcM3vs/YgNl\nUToBip2i1PnDqYrj1nvEYnvxeWV/rnIi1t2FfkruUIREUuagLPpcvJ3lHYq6ed8g9VYjM+pz2wXT\nxC6PYgegdThJeI6uGW6KspUv9UyrVrEDkYy66CPw+oMQHeL9M97P90/6Plt7t3Ld89cRiody7vbT\nV3/Khq4NfP2Er7O0UajKp7WdRlJO8veOvw/fWFHsogGIBEa/rgq1YqaJfzKZJsuSJLFmZRtbDrjZ\n2TP8fR4IRLj+ge3MqLfw7XMWpa/D+GCOQlM8gjYh7jn9vaPVP0WRKGVBHQr2E0r1aOVd0Dem7OS9\nb6s+fiH0DIlFvCT5YeZqqJ2uan9Fvcql2Cn3yUJBaXVWAwM5FFCAyN69HLj0MtBqaF+3DkOOPtV8\n6PVHcNbo81q/1UCSJC46YRoPX/te7CYd//ncawAYDRFOnasuKyApJwlEA+kxQrngMDpKUuxkWU7v\nVwoxVPZRihTlRH+4nzpznSgqzj0brE3C5VIkWq1Cpe0IqFuHDIQHCMVDaCRN2Ynda33iOhiL2AF8\nYcUXcBgdfHvDt0nK+VX3J/Y9wStdr/D55Z+nMRYpKpm10lGWdAZZlp+QZXmuLMuzZFn+Xup3X5dl\n+ZHUz2FZls+TZXm2LMurlATNKqoAoHlJBSp2KeIzCcOJZzfaWDm9lgc2HSz/7Lhw6surFMUuZbVx\nB2NIOh1Tf/JjbGeeSc/3v8/gffdBQFHsJoDYhbOsmJGAWGQv+kh6VlulIt7VjS5H+AiAOxhlQC8s\nH6HevrI+78Z9gxw/w5VXKYwPisWlLkdghQKt42hU7BQrZu4vZ6mmBrTatGWzaCy/GKJ+ePMhAD44\n84N8973fZXP3Zj73/OcIx8PDNv+/3f/H79/6PRcsuICPzskkti6sW0hjTeNoO2bfO6Rb0XOodsrr\nSqpRGo8Asq+PhDtzr/zY8lb0Wok/Zql2yaTMjX9+DU8oxq/OX47FqEsTu5yKXTjzWj0D3aMeVlSO\nUoidx51ZguRX7OaJf/vK22fXNyTepyENxYemZEEhdAUVuwLjhVwWI4M5FLvIvn0cvORSkGWmrVuH\ncaa6nt9ef3hcNsxcWNBi59HrTmL5dHHcWlscnVbdstUf9SMjF1TsSiV2oXiIaFK8l+NS7EITo9il\nx3Fp9bD0U7DraZFnUATaUgEih/zqBpwrat2yxmV0DXWVdUzMjr4dNNY00mwZuwfOYXRw03E3saNv\nBw/ufDDnNt6Il9s238bi+sV8Yu4nxPqoSuyqqKIMaFkC3oMi0KNSMImKHcCale3sHwjyyt4yV/LG\nYcXs8YvFqzu1KJD0eqb+9CdYTz+dnu98F/ebMTGLKNhf9vct3WMXjonFdTQg7CUVDDkaJd7Xlzce\nvM8fYUhvIqbREe8fKBuJ73AH6fSEWDk9vxqnLMILK3ZHI7ET55tPsZMkCa3NRtKnkti1nyjmhm29\nN/2rD8/6MN9573fY2LWRz6//fLoXZXvvdr79yrc5vuV4bjruplHPv7ptNS8ffjlDBuNRUQxRUvdy\nEjvxuirNipmt6CY8mc98vdXImQub+MvWDiJxYdG8+6V9vPBOH1/74AIWThGL7Hhq/5yKXVZRLeDu\nHfWwoth5Ih7Vnx23L7NYzbugN9nB3lr2AJWBlGsioNEQn3O2qn1lWS5oxVQKYPki8IGcVszo/v0c\nvORS5ESCafeswzhL/XzKHl+ERpu63rdiUGPQsXqh+DwbDerbExRiUQyxU3sdZZOW8Sh2E9Vjlz1n\nmeUXC+vv9vuK2t9lcmHWmdNErVgoRFBJrdzl3qVq/0LY0beDYxuOLXr7D838EMe3HM/Pt/ycvuDo\n4unPt/4cb8TL10/8uhjLUCV2VVRRJjQrASqvT+55ZCOdijk5VrR/W9yCzaTjgU3qqmUFIctZVkz1\nXyQZxS6zKJAMBlp/9p9Y33s83a86cffNFQ8MlFeU92WnYm69F+rnimTVCkastw9kOa8Vsz8QAUki\nbHVgDfro9oVzbqcWm/cr/XX55zwlUordu43YJX1+kCQ0BWbUaex29YqdJImF0aGNwxb658w+h2+9\n51u8fPhlrl9/PYf8h7jhhRtoqmniJ6f8BJ1mdK/TaW2nEYqH2NC1QfxicC8k4zAjFc2dg9gpRFRV\nb+ARwHDFbngxZ83KdtzBGE+/2cP2Qx5+9NTbnL2oiQtPmAaAHI+nU0wT/bmIXebYYd9o67hiX0vI\nCdWqgDtrsZo3DRGgcX7ZrZiBQMZW2hNR95kPxoMkZEGUc71mbzFWTIthWHhK9OBBDlxyKXIsRvu6\n32GcPVvVOSno80dKGnNQDAqR2bGgvE+F5k86DA6iySjhhLq/R3ZRQEm4VANFsZsIK+YoYueaKe4x\nW/+nqEAgSZJos7WVpNhJSLyv7X1A+frsBkIDdAQ6WFI/tg1TgSRJfPX4rxJJRLht823DHtvWu40H\ndz7IhQsuZL4rlSAb9ori9FGOKrGrYvLRkqrAVEqfXSwMyg17koid2aDlo8um8tQb3WmFbNyIBiC1\nKFCr2CWTMr3+MHqtRCSeJBRNpB+TDAamfuVqLC1huh/vwLPXXHY7prJgsXh3ipEayy+u+AZnZdRB\nPiumEo6jqXPhjPjZ2zdUlufdtG8Qu0nHvOb8C5mExw0aTTpMJBcUYnc05Vwl/H40NhtSrqCmFIRi\nVwJBWvop0OiHqXYAH53zUb5x4jd4qfMlPvrwRwnGgvzytF/izLNAWNm8EqvemrFjKv11M1IjNXKM\nPFCIaMVZMT35id1Js+uZ6jSz7h/7uO7+rTTZTdz28WPT9uBsUqhYg4ch694bC4y+X2VHxKtVS9yB\njLWz4L6NC6B/p6o0wbGgc29J/9zlV1dgUxIxIY9ilwqZspvyp2y6rAZCsQTBaJzooUOC1EUitK/7\nHaa5c1WdjwJZllNWzPIrdpBF7GJ+EsnEGFsPh/KejRWeAgXU2zzIvnY8JbRtKPu7w+6CfWBqEUvG\ncEfc1JlHFPeWXwKeA7DvhaKOUwqxO+Q/RJOliVZrKw6jo2zE7vV+Ufhf3FDE/NEsTHdM56olV/HU\n/qd4seNFIDWz7pVv02Jp4Zql12Q2rip2VVRRJljqwTalcvrslGARSTNpVkwQFe9oIslftpUpCj+b\npKokdu5glFhCZlaDNf3/2dDE3LSeNIjluMV0bXLieezpcZ+uAlmW8aVCU1a6HxWL62PPL9vxJwqx\nLkHs9C35rZgA1uYmaiMB9vaNDs0oBZv2DbJyugttgQG+8cFBtA4HkjZ/0IHW6YBYDDk4dqx/pSDp\n86YDUvJBY7epV+xA3KfmfxBeu18Uf7Jw7txz+doJX0MrafnByT9gdm1+1UOv1XPS1JN44dALYpGq\n9Ne1HQ8aHQRG95MphK7iFLssK2Z8BLHTaCQ+ubKNrQc9HPaE+a/zl+KoyShJChHUOBwkBgpbMeUc\nDoOB8EC610Ztf5M7lFEACxK7hgWQiIB7n6rj50UyiXEok9LXE1B33tkqXeFUzPyKXb1FqGp9u/Zz\n4JJLkINB2n/335jmzVN1LtlwB2PEEnLZe+wUZL/uQEzdfTJtxRwjPAXUE7vxKHaxRIxALIDT6BSq\nc6R8n22lZ6/ONILYzf+QmCdcZIhKq7WVzkCnKtLZEeigzdaGJEnMrZ1btpEHO/p2oJW0LKxTPyP3\n8mMuZ4ZjBt/b+D1C8RD3/PMednt285XjvzJ8FmTYUyV2VVRRNrQsqRzFTumvc7ZPKrFbOMXOsW3O\n8oWoKAslnSljNS0SPSkbpqICjSR2BHrQaKH1pz/A0qah6/ev4Hno/8Z9ygBD0QSJpIyRKO8deg4W\nfEgssiscsS6xQC/UY2fWa7G3NFIbDbCnDIpdfyDCnr6hvGMOFCTcHrQFglNAKHbAUWXHTPj8aBz5\nF3AAWqstnTKpGisuFfeEtx4d9dAn5n2Cl89/mdPaTxvzMKvbVjMYHhRV6L63xb3GaBXJdYHR/WSJ\nLGJXSQpqwutFMpmQjMZh4SkKzjuulTqLgVs/MJ8V04ZfbwqxM86aRcLjQY6PUMWyrJiGqCfdqwci\n6dAddjPLKXrBVBO78CBaWabOVFd4Qd2YsmiVq89u/4tE5EyhRAlSKRbZBCdfKmaNQYu+QMCIy2Kg\nMTjI0LWfJjmUInULFqg6j5HoTfVfq50vVyyySaxa262y71g9dqBe+VW2d5lcqhU7ZV/lGi6nHbM/\nLL7fh1kxAfQmURR9+/Gi1gBttjYiiUjO/rR8OOQ/lE7UnFs7l12eXWVRI3f072Bu7VzMOrPqfQ1a\nA18/4et0Bjr51ivf4vbXbufMaWdyatupmY3iUYgFq1bMKqooG5qXCMtLtALUAeWGVz8XYkPiAz9J\nOH9lG7t6A2w9WAaCqSh2rpmqe+yU4JQ0sRuKDd8glYipqWul9VPzsbTp6fryl/E+MnKkpXooVeiz\nNa9il/0lJclNBuLdXWgcDjSW3CMH+gMR6m0GdPX1KSvm+IdPb07Nr1s5FrEbHERbW/gLTHNUEjtf\n3hl2CjR2WzplUjVmnCri6besy/mwVlNc1PvJrSej0+h4/tDzQrFrSBEIaxP4Ryt2Cb9fzAFNJEgO\nVcA9MoWE14vW6URbWzvKignQ4jCz8cunc+XJM0c9pih8Sk/XqP1TC+WwwUWtFKDbm1FJPREPCTnB\nLMes9P+rgSfqwyFDral2DMUu9XfpK1Of3dZ7cGsNyEmhqPUHSyN2ElJexa5Qfx1AXdDND1+6Hdnv\np/3uuzEtVK+AjIRS+JvIHjuNJJaraoldseEpoF6xU449zT5NtWKnbK9cw+UMUFFsyqOIHYjvz2RM\nOA/GQKtN3ciDYCxIf6g/nag5r3YeoXhIdQDLSCSSCd7of6OoMQf5cFzzcXxk9kd4fO/j6DQ6vrjy\ni8M3UAo8VcWuiirKhJYlIrGp95+TfSYZxa4+1W8wCSMPFHz42ClYDFruL0eISjiL2EW8kIgV3j4L\nvalgjwXN4ssxl2KHyQE6I5rmubS+t5+a41dx+Eu34n10tLqhBkpwykXGF+igEWa8b1zHO1KIdXXn\nVesA+gIRGqxGdPV1aJNJejpGKzVqsXHfIGa9lmOmFP5ySnjc6GrffYpd0ufLm4ipQGsrITxFgUYj\n+lQOvAT9pae92Qw2VjatZP2B52FgV0YZyqHYySk7rK65CRB200pBwuMpSOyAvPH0isJnnC0WtvGR\ndsywF3Qm4pZmnATo9GTmBSpWs9lOQQrVLordsSFq0eEwOgoTO4MFnNPKo9gNDcBbj9Kpc6CJC4vc\nYFjd31Ihcw01DXlTMQuNOoh1d2P+4nXYokH23fIDzMcsUvX8+aB8P0ykFbPFInqV1VoWfREfOo2u\noNLjMKSIXaEgnRzwRryYtCaaa5rVFxdS38cznaLoUVbFLpRHsQPRN9q6Stgxx1D/1Y486AyIthGF\nEM6tFWuo8fbZ7fXuZSg2pCoRMxduXHEjC+sWcuuqW2myNA1/UPksVoldFVWUCUoyZtdrk3sekEXs\n5oh/J9GOaTHq+PelU3hsx+G0clUyFMWuLtX/o0K1Uyqyc1OKnWcksRvqBUtj6viz0MhDtN32DWpW\nruTwF7+E97HHSz5tbyjGNKmblfIb/DH+PuQKD01REOvqQt+SOzgFhBWzwWZEWycWeaHePsIxdcEA\nI7Fp3yDLpzkx6Arf2uOD7oKJmCAGlMPwgIxKR8LvR1MgEAaEYicHg8ixEj9PSy8QvXBbix/2mwur\n21ez33+AvZpkRhmyNY3qsUsERE+RoVUssiqpzy7h9aJ1ONDVqh9mr2xvmJmH2IVEv4vW4sIpBTjs\nySh2yiK41daKSWtSH56SDOPUGHAanWOrNI0LykPsXrsfElH6NUbMkrhXelQSO4XUtFpbVSt2sZ4e\nDlxyCXg9fPU9V9HZrG5OXSH0pvqFJyo8xRf1MdU6Nf2z2n3tBnvemZ5QumLniXiwG+04TU71duCU\nYqcUJ7LDgMYLhdiNCk9RsOISUVA6uKHgcVosLWgkTdGKm0IAFUI40zmzLIPKd/SJNp3xKHYATpOT\nP37oj5wz+5zRDyqF7wqfjVsMqsSuisqAs114myuhz26oD3RmMcMIJi0ZU8Gale2EY0ke2T7OEBXl\nxlWXmlGkIkClxxfGZTHQYBUVWXcwhxXTmqqApYijJthJ229/Q82KFRy+5RZ8TzxR0mn7QjHWaNeT\nQMOf4qcQjI6P/BwpxLu60OUJTgHoD0SptxrR1YmqqjMcYF9/6X123lCMt7p9rJqef8wBgJxMCqXF\nNQaxc6aI3VGk2BVjxVQeVwiTatiaYN4HYPsfIK5+rpaC1W2rAVhfY84Mw7Y2CSt4VgqjMhJA3yru\nR5VF7DxoHQ60zvyKXd593W6kmhr0U6aI/x+ZjJlKqDPY6nES4HCWYqcsgutMdaUtquUYLl1NcYOp\nGxeIlF8VDodRkGVh321dRViK4jA0IMsafCrj+31RHxISLdaWPD12cezm0YmYsZ4eDlx8MYn+AdrX\nrmV/44xRs+zGg15fGJtJh9lQnBVZDZJykkA0wBSruE5KJXaFYNKZMGlNJYWnOIwOao21+KI+4sni\n01MVxW6afRoaSVN2K6bNYMOozaOgLvooGGxjFqf0Wj0tlpaiFTuFACo9dmadmXZbO+8MvlNotzGx\no38HDqODdlv7uI5TEMo6r6rYVVFFmSBJ0Ly4MpIxh/rB0gA1qYXvJCp2AEtaHSxosXP/pkPjC04I\neQBJWIsgk/5ZBMTwWSMGnQarUZfbimltED8riuDAbjQ1NbTdcTvm5cvovPkWfE89pfq0fUNBztX+\njT21J9GDKz2Et5KRDAZJeL3o84w6iCWSDA5FabAJKyZA7ThHHmw94EaWGTM4JenzQSKBbkzFLkWA\njhJip1gWtWOFp6SsmuMaHbDiUlEYefuxkg/RbGlmgcHF+pqajO3b2gTIGdcAmVEH+lahWFTSyIOE\nJ9NjF1er2Lnd6JxOdHXies1pxTQ50VrqqNOMIHYpxa7OXEetsVZ1f5MHGafemrZiFryvNiwQPUkD\ne1Q9xzAcfAUGdpFcfgmyFBQz1ZJmAiqJnT/qx6q34jA48lsxRyh2sZ4eDl58iSB1d99FzbKlo2bZ\njRe9/siE2TCHYkPIyBnFrgQr5ljEDkRqplrl1xvx4jQ606NN1BBD5ZqtM9XhNDrLSuz6Q/25bZgK\nDBZYfC68+dCY65tWW6sqxc6mt6UVUBB2zHIodovrFxdUXceNqhWziiomAC3Hih67Ms4MKglDfSJ1\nUUlHmmRiJ0kSn1rVxj+7fLzeOY5FthLla0kRMBWKXZ8/nE48c9boR8/WG+rLWDHtU0XyZmqWnaam\nhvY77sC8dCmdN96E7yl1oxBqDz1Dg+Sjc9YaIDOrqZIR604lYuZR7JRFVbYV0znOkQcb9w2i10os\nay9sJVFCK8ZKxdSYTEgmEwnv5CrWxUIhQJqxwlMUxa7UABWAmaeBoz1viEqxWI2ZHUYD/cmU8qeo\n3ll2TEWhMyiKnbcyiJ0sy2krpra2lqTXOzrZsgDiHmEH1tjtoNeTGBip2KXuV+ZabAxx2J0pegyE\nBtBpdNgNdhGAoqIPOhnx49FI1JqcOI1OYskYoXgo/w7pZMxx9H9vWQdGB4G5Z4IkYzfY0SRrCMbV\nK3Z2ox2bwUYgFhiVNugNDe+xi/X0cvDiS4j39dF211rMS5cCUGc1MjBUuto8Er3+yIQlYioKXVNN\nEzqNriTFzmYs3HcLFGfLHQFvxIvDIBQ7UBfi44l4sOqt6LV66sx1Zbdijhp1MBIrLoV4GHb8qeBm\nrdbWosNTDgUO0WprHUbA5tbOpSPQwVCstKJlIBpgj2fPuG2YY6JK7KqoYgLQvETcaPrLM/ekZAz1\nCfJjTikakxieouCcZVMx6TXjC1EJeYR/vCZ1w1dlxYzQlEo8c1kMw62YsZBIlLKmiJ1GIwJasirc\nGouFtjvuwHzssXTeeKMqcjf74J/pkOuRZokY+aNBscvMsMut2PUHxKKqwWoUISU6HW1ykL3jsGJu\n2jfAklYnJn1hO5RimdM6Cyt2kBlSfjRAUbLGDE9RFLtSRx5AKkTlYtj393EpOaf5vMiSxN8O/U38\nwpYqBGQFqCTTil1lWTHlYBBiMbROR0m23YTbg7a2FkmS0LlcxAdzKHZmJ9S40JLE58k4DAbCA7hM\nLiRJUq12+Dz7SEoStaa6TGhGoQV9/Vwx07TUZMzgILz5f7DkPHoiok/QbnCgk2oIJdTPZLMbBLFL\nyslhi+VkUiYQiad77GI9vRy8RCF1d1GzbFl6W5fFwGAZrZg9vvCEKXbZ4wrsBntOpXKs/YtR7Iqy\n5Y6ANyqsmIpip8YS7A6704PRXSZXea2Y4YHCih3AlKUwZRm8+ruCISpttjYGw4NFEbNOf2c6OEXB\nPJewme9ylxY29cbAG8jIHFs/vuCUMVEldlVUMQFoSVVkJrvPTrFimhyANOmKHYDdpOeDi6fwyPZO\nhiIlKlYpaxM1KaWmyPCURFKmLxDJUuwMw8NTlEWoQuxA9PGlFDsFWquFtjvvVEfuBvYwzbuZh6TT\nqbWKVDPfeENkjgDiKcVOl4fYKcPJ621GJI0GnctFK+GSFbtQNMGODu+YNkzIInZj9NiBIHbJo4TY\npRW7scJTyqHYASy7ACQtbL23tP2TCeb27WWqtkaMPYCMYpc18kBR6PQtLSBJJCokFVMJPxFWzBSx\nU9Fnl3BnAny0dS4S/bnDUzCLazrkHUhbJgdCA2lFwmVyqVJK3J6DADgtTemFdcH99WaonVF6gMqO\nP4kh5ysu5bBf3HNdZgd6yUIkqa6Q44/6sRlsaaKSTXL84TiyLIaTx3pTpK63l7a71lKzfNmw45TT\niinLsrBiTvAMO+V1T0SPHYhkTDXETpZlPBFPuscO1Ct2tSaxX7mJ3ZhWTAUrLoO+t+DQxrybpEce\njGHHTCQT6eHk2RhvMqYSnHJMwzEl7V80wl4RipU9sPwoRZXYVVE5qJsjLHyT2WcnyxkrpkYLJntF\nEDuA81e1MRRN8Ohrh0s7QDil2Gn1YsFUpGI3MBQhkZTTFdnaGv1wxU7pB7JkE7vZMLhvlK1WNbnb\neg8JtDxrPCvdO3JUKHaHu0CS0Dc25nxcIXZKGI22vo76eIC9fUMl9VFuO+gmnpSLInbxVEjFWD12\nkFLscgyerkQoBEg7BrFTFLvEeBQ7APsUmPt+2H5fabMu3fuR4mFWOxew4fAGgrFgpjgyTLFLvS6H\nA43dTnK8hLRMUNQ5kYopriX1xE4QK52rLn1dAuI+nApPUQpR5rgXT+q+MxAewJUifE6jk0AsQKzI\ncBN3aoHqsk7JpCGOFXPfuKA0xU4JTZmyHJoX0zMkXmOd2YlJYyUmqyN2Sr+YzSCu4WGDu1P3xbqw\nj4OXXEqst5e2tXdSs3z5qOPUWQ1ls2L6QnGi8eSEjjqAFLEz2lX12MmyrE6xUzHuIBQPEU/GhWKX\nKhCo6fV0h91pYldnKp8VMxQPMRQbyp+ImY1jPi5CVApYyosdedAb7CWejI9S7FosLVj11nERu5mO\nmUX9DccFpfB9lKRuF0KV2FVROdDqoGnR5Cp2ER8kopk+NHPtpKdiKlgxrZbZjVbu31yiHTPkyfQN\n1tRlBrGPgd708FlRka2tMQwPT8mp2M0WgQPeg6OOVzS5i0dh2328VnMCsZom7CaR9uYPHw09dl3o\n6uuRDIacj/cpVszUYkhXV48j5McfiacfU4NN+wfRSOIaGQsKURtr3AGA1nkUWTH9xRE7RbErC0Fa\ncakobOx8Uv2+fSIpbnX7aUSTUV4+/DLojOKeM6zHzg86HZLZjNZurxgrZjaxU66leJHETo5GSQYC\naQunrs5FIjs8JToEckLcrxQCJ/nTs+wGw4NpxU5ZHBe7qHYHhE3aaWtNE7sxlZaG+cJyqzYFtWOz\nUERWXApA35B4noYaF2atlYSkktileuyURW62euUNxagN+5j5g1uI9fTQvvZOalasyHkcl8VIOJYk\nGB3/vbTHn5phN1E9dikip7xuNYrdUGyIhJwYFuaRD0UF6WRBuWayw1PU9Hp6Ip40Iawz1xGMBwv3\nehaJgsPJR8JohSXnFQxRKZbYjRx1oECSpJIDVGRZZkffjonvr4NMT++7AFViV0VloXmyD9ZkAAAg\nAElEQVSJIHbjSX8cDxSyM4zYVYZiJ0kSa1a28dohD291lbC4UxQ7EMSuSMWuJzV8Njs8xR+OE0uk\nGvcDPeLfkcQO8vYfFUXu3n4Mgv08aTwbh1mPLRUKcFRYMbu689owQSh2NpMu3Q+nq6vDPCQWyqUk\nY27aN8jCKfaCw4kVJAYHkcxmNOb8A3sVaI6iHjtFsRszPMVSAxrN+BU7gNmni7EopYSopBSg5bM/\niN1gZ/2h9eL31qbhVky/D63NhiRJKWJXGX+P4VZMRbErbmGrJGjq0lbMeuKDg5lFtbJAToWnANSm\nRh7IsiysmOYRxK7I/iZPUBSiap3T0gtr71jz5BoXCKKpdij9lnVgsAplBOgPitfVZHVi0duQpZAq\nhd4f9WPT23Iqdv7OLn700m/RDfTRfucdeUkdCMUOKIsdM134m+AeO5tBvG41xC5b7RsLTqOTeDJe\nNLlSbJsOgwOj1kiNrkaVYueJeNIWTpdJFC/Uju3IhYLDyXNhxWUi2+C1B3I+bDOIlMuxrJj5iB3A\nnNo57HTvVO1G6fB34I64WVy/WNV+JUFxCLwLUCV2VVQWWpaID5jnwOQ8f9pWmLopmpwVQ+wAPr68\nFYNWw/2bRithBSHLoxW7oomd+OLODk8B0raozHvWkNkpa+RBPoxJ7rasA0c7LyYWYzfrMOg0mPVa\nfEeDYtfVhb45/wy7vkAkbcME0NXXofV6QJbZo7LPLhpPsvWgm5XTx7ZhQipmvgi1Do6u8JREWrEr\nvIiTJAmtzVYexU6jheUXwZ7nwb1f3b5974BtCrqaOk5pPYW/dfxNzMGyNg23Ynp9aRVS67CTrJBU\nTOW60DiywlOKVOxGqsa6OhdyOCwCWSATZGDO9ATXSoLY+WN+YslYWrErqk8uC+5UL5PTNlWdFRPU\n2THDXnjjLyJW3mhNPbd4nil2Fza9DaSksOAWgWgiSjgRTqdiQob0xHp6sXzxOurCPqTbfk7NcccV\nPFZd6h5ejll2vf7hhb9ywx/zIyFh1VtVK3bKtsVaMaH4kQXKNaPspyadNRQPEYqH0kqfci2Xw46p\nSrEDseaaukJ83+YhXm3WtjEVu45ABzpJR1NN06jH5rnmMRQb4vCQujaS1/pfA+DYhgkOToEqsaui\niglDc+oDPFl9diNJirm2IlIxFdRaDHxgcTMPbe1UZ6OJBYU1cphiV1yzdo8vjCRBfYqIOGsUYpda\nFAR6BWHUZVVsa+rETbIAsYMC5G5gD+z7G6y4GE9YTie92c26ilfsZFkm1t2dNxEThGJXn1Xh1tbV\nQyxGHRHVit3rnV7CsSTHF9FfBxB3DxZlwwTQOpzIkQjJcFjVOU0Gkj4/kl6PZBp7gamx29NhK+PG\nsgtFaqLaEJW+t9ODyVe3rcYb8bKtd5tIxsy2Yvr96UAYja2CrJielBXT6RSjMWpqVBC74cmsWpdY\n2KZn2WUPCzY5kJFwaYc47A1nhpObM+EpULza4Y54MMsy5v9n773DXLvra+/P3lu9l5nTm3svuBsw\nAdtgWkLK6xeDy7GxKYYYcom5F4dyA3kvJRdMh8S4F2y4IQkkl44DCS64ADbGNhjbp08f9b7L+8fW\nlkbSbtJo5miM1vP4meORNLOl2dr6rd9a37W8IXySj6An6EwK04frQTn9VB48/g2QK3DKzta3crUs\nmuphMqzPiwHMlNx9viwlKQaxy9fzzZ66yxAzC3zo7KuInXG6489KN6/lCwPYvrsxswqKXcQbQRTE\nVipmd82DFVo2TpfhKeB+g8C4n0HsEv6Ea8XOII/dit0wAlQMxc6x7mApTr1Cvx7tedD05i1R58qD\nvYW9bIpswiN6em5rBags9mfH/PXcrwl6ghyWOKyvxw2EMbEbY4wVwvpj9Q/QgzVnZ0bsRkixA7jk\nrO0UanJ/ISqthVL/it1soUo67Mcr6ZeLZEgnWa0AleJMpw0T9AHk9OGOxA5MyN13vgO/uE0/D06+\npKObKRbwjnx4iprLoVUqeCw67ECvO5iMdip2AMcHlb6TMR96Xl8MuFfsso4ddgakuP5BtxZUOyWf\nR4zFXJXY6ordkAhSfAsc8Sr45V3gMsADVdVrXSb1jrSXbH4JPtHH7b+5HTk8oW+WNHfP1bxuxQRG\na8Yum0UIhRCbc6SeRKJlz3TzWOhU7GAJsVsaPS5KCMEEm30V9mcrbWLXpdi5nrFrFEnSrgRx1V/m\n8etJv7MuFTtNg0dv00cLNrUTKfP1ApoSJBrwkGwuIqcK7hbzS22FEa+uANanpth92WXI8/P8+j0f\n5cn0Ia1NMDsMW7EL+yTC/t4F/TCQr+VbJDjuj/fUPNg+tt6ez3OCa/V2yXFB+/xLBBKuFTtjE8JQ\n7IwgoKEQu+o8AkLLouwKx/85+GPw6C2mN2+NbmWqOKU7Ciywr7CvJzjFwBGJI4D+kzEfn3uc4yeO\nNyWLQ8eY2I0xxgrBG9R7gw6aYtecsTO63oIJnRQdrJk/E5y2PcmR6yPc9fM+7JjGB85SxU6u6CEF\nDljaYQd6eArQDlApzbVj2pcifbjrjq8WuXvRyey/9n3k/uluOOo11EPrqTSUJYqdd+QLylvl5Bvs\nFbsOK2azpPxIX6PvLruHdy1y+LpIaxfeCcriYiuN0AktYpcdfWKnFvKOwSkGxFgMpTh4GXwPTr1c\nV9l+57KfMbdHV9Gbil3YG+bdp7ybn+z7Ce8v/oaGXG2Rm6WKnRSPDY+QLhNGObkBKZlEzrpU7Jr3\nM85DQ7FTjGTMFrFrnqfBFBu8ZQ5kKyxUOxU7Y0HuWrGTKySENvlxXUy97hg9CMUNDvwCZn4Np+7s\nSNkrNQoIWgiPJJIK6sc9U3R33EvVJ0mU2FoOcdJH/gllYZFtN93I/k1HIIkCYZ99jyW07fTD6LJb\nyXJyaFc8AKY1D06PXfo4O7gO0mnCuJ9BGpP+pPvNheb9uhU749xeDuYr8yQDyf7IkC8MJ/6/et+i\niZNna3QrsiYzVZqy/BF7C3tN5+sAQt4QW6Nb+yJ2VbnK04tPc+LEKgSnQLs38wWAMbEbY/Sw8cSD\np9i1bIXNNMNgUh+ar41GxDjoM0IXn7mdx/fleHyfS5uomWIHrlS72UK144M70VTsOqyYS+frDKQP\nh9xevcDcBaRImG3/+I+Ejt7Ggf+UyOWPb6lzRtVBLOAZecWucaBZTr7JnNhVGwqFqtyh2ElpfR7i\nELHK3sUyNVlx9bsUVePhXYuuag5aj8lk8CRdKnYJQ7EbHTuyFZRcHtFhvs7AUBU7gMNfCdGN7kNU\nmomYrdktYOdxO7n2tGv5fvE5/se6CRr5/YCuRBqEVYzF9UTJEbDGmhE7t+EphhXTY6RiTnRZMZeG\npwAEk6TFkk7suhQ7j+gh7o+7D0/RGiSl9vUs5o+5W8xPHqNXuLi5nj16q96HdcKFHd+uKAU8WhiA\niZD+3OfL7jZNWiTFH6MxNcV1t5fxFipsu+lGgief3HQ2eFwp1iGfRMArDsWKOZuvdlzLho18Pd9D\n7NzO2fUzY2cob27rFHK1HEFPEL/kbz3eNSlsnt+GYhf0BAl5QkOZsXPdYdeNU6/Q+xZNQlScuuxy\ntRz5ep4tEXPFDug7GfPpxaeRNXl1EjEbVT1AZqzYjTHGCmHDiVCYguLc6v/u0lwnSWkmso2aHfPP\nTtlM0Ctx14MuVTszxQ5cEbtuxa6922tYMWd7rZigW5cAFp9zd4yAGA6z9TUioY0iBz5zB5l//heA\nlmIXDXhHfsauMa0TO49FeEp3hx20F7abtAqqBnsW3AUqPD2dp1CVXc/XqbUaarncx4zdGrJiFgpI\nDomYBsRYdHgzdqBXtbzoUvj9jyDr4j1phHBMHNnx7Z3H7eS/H/oX/DAc4tqHP05DaehWzFjbignt\nBNCDCSWbbYWmgEHs3F0n5UwGMRJp1YEY1uBexa650AqliFNgtlBjrjyPKIithTjoyofr8BQUkk0r\nI/Sj2B0NaG1SboVKFn79T3oSZtdCsaoW8Qo6sVsf0d+DRlKmEwySElmssPuynYQrKv92zSkET9Ln\n0vPVRmsDzAmCIJAO+4dkxVxZxW5pwbihjvVDvkRBJOwNO97X+Nmuw1NquY4ahWQgSalRoq44v6bd\nih0Mr6R8sbI4GLHbcDxsOV23Y3Y5lJwqD4z5OyvFDnRitzu/23Xq6GNzenDK6lQddF1v1jjGxG6M\n0cPG5ht5+rHV/92l+U5iZyhcI0bsYgEvbzh5E99+7AA5N0Sn0rUD7pLYyYrKfLHGumj7gzvolfB5\nRF2xa1SgXrAgds7JmD1YeBZx/8/Yet2lhM8+i8bHP8qrdj9ELKjbSmJBz8inYspT0+D14pkw/3Cd\n7+qwAz2AAlFkojk78qzLAJX+5+uaFrhUf8ROXQPETs27t2JK0RWwNJ5ymW67c6Pazf1Wty+Hev9u\nlx79Jt6/sMi9C4/xvh++B61eb1U4GARPHYHKg17FLtFXKubSzQXR50OMRpHnl4Sn+GN66ihAMEVE\nLaBpsD8/R8KfQBLblsNkIOlOsWtUyIgCCV/7uN0Tu2P1r07JmI/do9tsT7+q99drRfySTirXh5uz\ngS7nsvL1PJNZDfnqv0HJZvk/7zyWZze1l3C5SsPVfJ2BdMS37LoDTdOYzddWLDgFzK2Y/Sh2UV/U\nlYrpl/zugnSayNVyrcAV6C+dNVvLIiB0KInpYHpoVsyBiB3olvL538Hu+zu+PRmcxCt6LQNUDMJn\nNWMHcFTyKDQ0ns26G894fO5xNoU3Df5c+kG39XuNY0zsxhg9bGh2lhyMObvSXLvqANqK3QglYxq4\n+MztVBoK//rL/c53rlpZMe13COeLdTStM8paEASSIa8+Y2fEsodNiF2qqdj1Q+wevRVED+JZV7Dl\ny1+mfvJp/LdffoPUT/QC6FhTseu3D2c10ZiawrtuHYJofnk1FLuJJYqdIElIqRSxir5gcVt58NDz\ni2xJBtmUcO6kg7Yi4lqxM2Ls1wCx08NT3FkxxVgUtVxGk4e4SZDYCkdcoKdjyg4L5iWJmD2IrOfi\nfJEPTL6UR5/9TwC0aKh53E0FdQTm7LqJnSeZRC0W0erOZEHJZHrOQU8qhbK4JDxl6e55KIW/oZ+D\nU6W51nydAbeJhLX8Acqi2JppAp0s5Oo556TF1KEgemHWZs5O0+CRm/X4+E0n99wsUyYo6efohpj+\n/HNVd3/Lxp69fOQuBYoltt1yC6XDN3YQnPySkCk3SIV9y56xK9RkKg2FdbHVIXZL00DdYKna5wZx\nf7yvuoMO1biPPsVMNUPcH+/YnBiGYqdpGvOV+Z73h2sc9+fgj/eEqEiixObIZksrpvF9O2LXSsZ0\nacd8fH6VislhrNiNMcaKI5iE+LaDM2e3RqyYACdsiXPiljh3/Xy3M9HpvnCF3Sl2Rjl5945sMuTT\nUzENYmem2Pkj+tyRywAV5Br86i446jUQ3YAYCLD3vR/l4fVH4//sJ8nc83ViQS+yqlFpuJtBOxho\nTE/ZVx2YKHagB6gI2Qzron5XlQeapvHQ8/3N18nGbJPLVEwhGETwekc+PEXTtL6smMb9hmrHBF2l\nKc3BU9+2vo/WtPM1EzF7EIiDJ8BFnjTvO/qdANyx55+pylWk+GhYMTVN67ViNv8tu0jG1Ild5+64\nlE4jLxhWzGzn7nkwhUcu4UVmvrLQE+XuVrHLZJ8HILHkGp/wJ1A1lWLDYTNF8sLEEfbEbtfPYP63\ncNqVPTc11AaaUCXk0RW7RNCPpgTIN5zPwdrzz3P8//w6/gZsv+1WgscfR9QX7QgR6VuxC/uXPWM3\n2+o4XRkrpqzKlOVyr2Ln0orZN7HzuSd22Vq2I22zX8VuKSmEJrGrLI/YFRoF6mq9v6qDpfCF4KQ3\nwpPf6tn03Rq17rLbV9hHKpCytbxujm4m6Am6Inaz5VmmS9NjYjcgxsRujNHExhNXX7FTZKgsdpKU\n4GhaMQ1cfOY2fjdT5OFdDsdXyeo7ccYOoT+u1wkYKaAWMIhd9wd3IuTVrZglG2IHrisPAHj633Wi\neerlrW9lFYG/O+NyvC85h+m//VsO/a/vAIx0MqY8NY3HhtjNF/Rd8nTE1/F9TzqNvLDAYZMRnpt3\nVux+O1NgoVTnDJc2TABl0UgjdKfYCYKAmBj9knKtWoVGo0V8nCBG9cW1Omxid9i5kNyhqzZWyO+H\netFasRME/f1UmOH81NkA/LL8O95977tpNOdb1cLBJXZqqQyy3BOeArgKUFEyGTyJLsUubaPYNa/D\nCQrkapkeRcJIJHTa4Mo2lYVkuP3+bMXcV93YMR2SMR+5SSekx/95z03dCY1eSQQ1SNFBfao9+yy7\nL7sMQVb4wlsmCRxzTOvnLCV2+arcsqy7QTriY6FUX5b7wSgnX6nwlO7XLOwNIwmSa8WuUCv0RewS\n/oTruoOeGbvmvJwb5ThbzfbUEaSDaTK1DIo6+Kal0WG3LPviqZeDUodffa3j21uiW9hX2Gd6vuwt\n7LVV6wBEQeSI5BGuiN2v534NrNJ8HfQ6mtY4xsRujNHEhhNh8dnVTaM01CszK2Zl9KyYAH980iai\nAQ93/Xy3/R2rWQguWSiJoj7f46TYFYwd2c4P7paNpzijf8PMigm6fcktsXvkFkhsg0PPbX0rX2nQ\nkDxs/vzniJx3Hlvv/DJ//sxPRjYZU1MUGjMzeC2CUwDmilWSIW+rF9CANJFGmZ/n0Mkwz82VHBdc\n9zy0F58kcv6xJlUTFmjN2LkkdqDP2Y06sTOsiaJbxc4IIckP+foiinDaW2D3fTBjUWZtdKFZKXYA\nkQ1QnGkRz4vPeBsPTj3Idb/6X8DBV+zUZkqqkZqq/9sgds4LWzmb7TkHOxW7rujx5izijlCNspI1\nVexkVXbsN1ss6N2fyejm1vf6UVqYPEYPx6mZbLwUZuCpf9ML67291uhM8zNk6VyWpIWoKNabONXf\n/Y7dl14GwLf/2+kUtnZaSIuNYosI5Cruw1NAv4bXZJVyfXAiMdsqJ18Zxa6b2AmCQNQX7c+K6aLD\nzkDMH3Ol2GmaRr6W71DdjIRLN112mVrGVLFTNdU1sTSDkaq5LGK3/jjYcoY+FrHkM2hrdCvFRtH0\nfbKvsM82OMXAkckj+e3ibx0/2x6bfwyv6OWY1DG29xsaulN41zjGxG6M0UQrQOWJ1fud3eXkoH9A\newIjq9iFfB7+4pQtfPfX0/a2mkq2dzfKRUn5bL6KKNDTkZYI+ciWG+3kUrO6A9AVu/KC8+s3/wzs\n+i84Zae+OG4iX2ng84gEw0G2fPYzVF/yCt76m3+ncsuN9j/vIEGeXwBZtqw6gGaHnckOtyc9gbyw\nwKETYXKVhu38S6km881H9/HaEzZ0zOo5Hl9mEUSxQ2lxghR3Xzx9sGAEobhV7IzC7xVRvk6+BCS/\ntWpnhG9M2ixaIuugONMicK849o/52Dkf4/78rwCoZOyV9pWGYbfsTsWEdkedFdRqFa1c7ngsgCeV\nRslk0BSleb1aqtjphGZbpIRCzXTGDpznm7JlfSMqmdje+l5fxdTrmmR83iQZ8xe3gyrrxN4E08XO\nUmoAjxCiqpiT0epTT7Hnsp0IHg/bb7udPWm1g6QY9sRio0i1oVCX1b5m7Fol5csIUDEUu+6Nv2HB\nIHbGcwWd5K3kjJ0bgl9qlJA1uYOkt/oUB1XsmpsVy7FjDkWxAzjtClh4RrcWN2FUGXTP2TWUBtPl\naVfE7qjkUeTreWaa70MrPD73OMekjsEn+WzvNzSMrZhjjLEK2GAQu1W0Y5oRO9AJ0QiGpxh485nb\nqCsq//So+WAz0FTszIid/YfITLOjSBI7U8WSIS/ZSgOtOKurmh6LC3ArGdOh8uDhG0Hy6cRuCfLV\n9tyI4PUifOij/HjLKfhuvYG5z39h5EJUZIeqA7AhdhNptFqNwyL6a21XVP4vv9xPoSZz6dk7+jo+\nJZNBSiQsg13MsLYUO7fhKSuk2IE+v3rcn+npiGbKztzTEJpoz7maIaordkqTeEqxKK8/9PV84uX/\nm7IPfvjEv7ieBVoJGCmp3amY4KzYGZsEvYpdCjRNf3w117kR1VTsJkL6Y80UO3BeVGeaG1nJJYvQ\nvoqpDTLePWenKrrCcejL2zUvXZgu6NfaiVD7NfMJYWpq7zlSeeI37L78CoRgkO133I7/0EN6SIpB\ndgr1QsvB0G8qJsBCafA5u9l8jaBXIuLvowy7DxhkexBip2la38Qu4U+Qr+UdP1eM41pqxfSKXqK+\nqKNip2maqWJnbFYsJxlzKIod6NevQLxjc8qq8mB/cT+qptp22BlwE6BSbpR5cuFJTpg8YZAjHwzV\nnL4Z51252o7VxJjYjTGaiG3SicdqztkZ82bdxC6YHFnFDuDI9VHOOCTF1x7ag6pafCANqNjpHXa9\nF7tkyIeiasj5aWsbJrirPKgVdT//sX8Kkc7X3ijdNRALB7j+1IvIvvzVzH/5y8xdf/1IkbvGVLOc\n3G7Grljv6LAzIKX1D/Ydgr7Qes4iGVPTNO58cDfHbYpxyrb+ZgKUxd40QiesJWLnvu5gBRU70ENU\n6gX49Td6b7MLTjEQ2QCVDGpT/TII6wU7LsCfSFHLLvLWH7zVdSn3sKGYEDujbFx2InYtO3CXYtc8\n/+W5Wf21M1Hsoj590bw01RLa801O5CxTyyBoGrElC3Jjge2KKKcO0ReA3cTud9+H/D7T0BQDc82+\nuslQ+/0XkCLIdHZWVh57jD1XXIEUibD9jtvxbdfVxaXpkNCZEGl0e/ZjxUyH9WvQchS7mUKNdTG/\nqzqBQdBtxQTdLllwMaJRkSvIqtzxmjkh7osja86WXuM8W0rsoD3raYeyXKahNjo67KB9Ti8nGXO+\nMo9H9PRFZk3hDerOg6e+DYVpQA8/AXoqD9x02Bk4InkEYE3sivUiV//oampKjfO2nTfw4feN7pne\nNY4xsRtjNCEIumq3ml12LcWua7crmBzZGTsDF5+5jd0LZX72ewuLlqVi5xyeYjY/kQjpu71KYcY6\nOAX0IAlBtCd2j38dank44609N+UrcscudCzoRRVEfn/pNSTedBELX72RmY9/fGTIXWNK/xC0Inaa\npjFXqJnaJz1p/bybaBTxeUTLZMyHd2V4errApWdt73tBpWQyeF6AxM6YRXNL7FZUsQPYcppe2/Lw\nTZ1lv61ETIvgFAPN95SyMIPg9yP62+dLKLWOsyLH81zuOd7y/be07FerCcXEiin4fIiRiKNt17i9\n+zxslZRPNxeOHcROv6/Ho5+HfrFrQd1U7JwWxdlGgThiR8y8sQh2RexECSaP7O2ye+QmPQH4qNda\nPnSh+RmyLtx+3iFPBEVoE7vSQw+x54q3ICWTOqnb0lZB8jVrxS7XDJNaugnmhFTTirmcyoPZfJX1\nKzRfB8uzYhr36WfGzq0t1zhXuoldIpBwVOyMzZhE10brsIjdRHBiOET79Ct1a/GjtwEQ9ASZDE72\nKHZuOuwMRH1RNoU3mRK7XC3H2374Nh6fe5y/f9nfc/qG05f/HNxiTOzGGGOVsPFEPWjAqRNqWCjN\ngejpVbaCiZEndq8+fgOpsM86RMVSsVsE1bq/aa5QM52fSIaaZKs0Z0/sPD5IbLcmdpqm2zA3nAhb\nei/k3YEA0ebCJV9X2fDhD5O87FIyt9/B9Ec/imbzPFYL8vQUQijUIg7dKNUVKg3F0ooJoC4usiMd\nsuyyu/2BXcQCHt5w8mbT222PL7PYv2KXiKOVy6gu+skOFoxZNKvXvRtiKASi2LI6Dh2CoKt2M0/A\n3ofa3y9MQy3nrNhFdSuvujjXQ1alWIx4w8MXz/si+4v7ueJ7VzBTsp9ZGTYMoi92zWpKyaRjKqZV\ngI9nQt/YkGeaxG7pRpQvDJIPVdAX+o1aZ6y6QeycFtWLcpmk0El+JFHSLXQui6mZPKZTsVt8Dn7/\nYz1NULImVgax2xhtP++wNwpCnYbSoPiz+9j7trfj2biR7XfcgXfTptb9FFWh0Ch0kBSD5BXqhZZi\nN5gVc/D39VyhxuQKd9gBPYS2L2LX54wdOJN8o26h206Z9CcdzyPj9m7FLu6PIwlSy045COar84NX\nHXQjfRgcfr5ux1T088us8mBfYR9+yc9k0GLOvgtHJo/kmcwzHd9brC5y1Q+u4unFp7n+5ddzwY4L\nhvMc3KJisvG9hjEmdmOMLjacCGrDPl56mDA67Lp3u0bcigng90hceNoWfvTULNO5aueNjQooNXPF\nTlP0haYJ6rLKQqlubsVs7vZ6ynP2VkywrzzYfT/MPglnvK33dadzxg705xnwiuQrDQRBYP1115F+\n61Vk776HqQ9+SA9eOIhoTE3j3bDBcsd0vmDeYQdtK6a8MK9XHpgodrP5Kt97YpoLT9tK0Cf13O4E\nJZNtKSNuYdjt1BFW7VqzaC5n7ARRRIxGUVdKsQM44ULwx/SNCwPGtcytYpdd7CGrUjyGmstz1saz\n+Mr5X2G2PMsV37+CqeLUMI/eFko2p29g+Dpna3ViZ3+tlK2InaHYzeqqd8cOuiBAMEUF/e9VKnde\nk0KeEF7Ry2LNQbFTaiRFEweCP+Ge2K07Rq+sMAIXHrlFdyWccpntw3K1HJriJxluJ2bGvPrfdvYH\n/5d9V1+Nb8cOtt9+G971nddUo2Mv6u21Yi6dsevHihnyeQh6pWV12emOjpUjdvl6Ho/gIehZ8pr5\nYq7m4AzyNQixc0vOehQ7f8J5ztNCsRMFkWQguSzFbqGysPz5uqU4/a1QnNariGhXHizF3sJetkS2\nuFYJj0gewfO556kp+nk3V57jLd97C8/nnucL536BV2x7xfCO3y3Git0YY6wSNp6kf51aJTtmab7X\nhglrgtgBXHzGdhRV4+sPd5WIGmqjmWIHlgEqRpG2uWLnI0ANj1yyV+ygSeye7bSkGXjohmbv01+Y\nPtSsdDcW8LYWMoIgMPne9zLxrneR++d/5sD73ofWOHhVCI0pd+XkplbMVAoEAQIkuEcAACAASURB\nVGV+gUMnw+xZLNNQOlXIex7ei6xqXHLW9p7HO0FTVb1UOtnfzqRB7EbZjqnm8oihEILHvRVNikZX\nTrEDXWU66U3w5L+253fnmmmK6xxivCNNxS6f6yGrYjTWmik8df2p3PCqG8hWs1z+vcvZk98z1Kdg\nBb2cvHchJCUTzuEpTUWvO5lVjMXA40Geb3Zj9lyvUpTUEpocYibf+R4XBIFkIOlsg0Mh4Qn1fN8I\nzXAF428391toVOGXd8LRr9Xnwm2Qr+fRlGCHXTIeiHH2Uyq5az+I/+ij2X7rLa1Zw+7HAqaKXb6e\nJzeAYgdLamsGQKkmU6orK1ZODu25wqWkIeaPIWsyFbli+9hBrJiGAud0LrSsmL5eS7DTOWil2IFu\nx1xOeIphxRwajnil7rh56KuATuxmy7MtUgY6sXMzX2fgqNRRKJrCc9nnmCpOcfn3LudA6QBfOf8r\nvGTzS4Z37P1gTOzGGGOVkDoMopvgiX9end9nKHbdCCSgUVo9S+iA2JYO8bIjJ7n7oT3ISwmB8UHT\nrdgZqXwWASpGObnZjF0y5GVCaC70HYndYfrr1xzCbiE/pe8EvugS8PUutjRNI19p9ER4x4LejoJy\nQRCYvOYvWfe+a8l/57vse/d7UGuD70IvB43pKTwb7RMxwVyxEzwepGSyWXkQQVY19iy2529kReVr\nP9/DOUdMcMhEuOfxTlDzeVCUljLiFuIaIHZKoeDahmlAjK2wYgd69L1Sh1/eof//3NP6RpFVPYiB\n8CQgoBSLiLFOYifF2sQO4KTJk7jxghspy2Uu/97l/D7jsjdyGVByOaR47waBJ+Gs2CmZDGI83kPC\nBVHE0zz/gd6FVjBFRqugKRH2Z7tcCbgIrpBrZARImiz0Y/5YH1bMpo129kl48ltQWbQNTTFQbBTQ\n1GBHguRJv3qW93xLpX704Wy75eaeCggDZpbEkDeEKIgdVsx+6g4AJiI+5gckdrMFo8NuZRW77vCT\npYTWDmavmRP6UexCnhBeqfP1TvgTVJWqLem0UuxAT3sdtO5AURUWq4s9VSDLgijplvLd98HMb9gS\n2YKGxv7ifkD/jN5f3O9qvs6AkYx57957ufx7l7NYXeSGV96wujN13RgTuzHGWCWIoj7A+9x/tEt9\nVxJWxM4gRCNceWDg4jO3MZ2v8uOnZ9vfbCl2XRcuQ7ErmYcvzBrEzkSxiwW8rBeaP9eNFRN67ZiP\n3qrHhJ9uvigq1mRUrXcXOhbwmBaUp6+8kg3/88MU/+M/2PuOd6CW7JPNhg21XkeZm8e7wb7DDsyJ\nHejJgPKCXlIOdNgxf/jkDNP5Kpf1WXFgQF7sv5wcaC3gR5nYqYW86+AUA1I0hlJYYWK37mjYcY5u\n11OVdiKmk21J8kB4AqVYRop1zbHFY2iVCtqSmcdj08dyywW3AHDF96/gNwu/GfpTWQqd2JkpdslW\nx53lYzOZVoJmz+PT6faMXg+xS7Co1vEJMQ5kexfOyUDSNiVUK86RlURTpaQvK2ZiO3hD+mfSIzfp\n17dD/sjxYWW5gES4pT5l7rmH02//Z57YLvDb91+JFIlYPtYgMUtJjiiIRLyRZnhKg6BXwufpb0mn\nK3aDbYLZbfwNC8shdgPN2PlcztjV8z02THA365mtZZEEqcNWayAVHFyxy9ayqJo6XMUO9I1XTwAe\n+mpLmTPsmAvVBSpypS9ity26Db/k5x8e+wdKcokbL7iRk9edPNxj7geaNiZ2Y4yxqjj1cj1e+qEb\nVv53leYtiF1zIbAG7JjnHb2OzYkgt963q/1N40OmqxC1bcW0UuwMK2bvB7coCmzzN0mHGysmdBI7\nuQ6P3qIPZ6cONX1YrhXh3bmzHw14WzvU3Ui+6U1s/MTHKf/8IfZc9dYOZWOlIc/oARZeG8VuvlhD\nEgWSIfPeP2ki3bRi6ou8pZUHtz+wm82JIOce7fB6W8AojpaSfc7YNS13SnZ0iZ2Sy/coW06QYtFW\nsfmK4rS3QHa3HrAx+5TzfJ2ByAbUch2p63m1Ej27SOnhycO59dW3EvKEuOr7V/GLmV8M5fDNoFsx\ne8mZlEzqQTvVXkWt/Vjryg1POo2cbf5NemaCUyxoMiEpYU7sHIIr8rndKIJAMtS78O3LiimK+t/w\n6X+HvT/X/74ueiFrahEv+obNwq23Mv23HyF/yov45IUis6qDrdBiXswIEslX5J7rpBukI/6B6w4M\nxW6lyslBV926n7NhrXT6exnELuK1Jszd8EpeQp6Qq1TM7uAUaFs57ZRjo8PObCYtFUgNPGM3tHLy\nboRScML/A49/na1e/bPACFAxCF4/VkxJlDh+4nhSgRQ3X3Azx6WPG+7x9otGRc9yMFFQ1yrGxG6M\n0UZ4Qr+oPHbPyiZT1ku6XdB0xq75hh/xZEwAjyRy6dnbeeC5BZ6ebn7wGUP+ZuEpYGvF9IgCKQsS\nstXXJB1OxC62Wd/xW0rsnv43KM7ooSkWMOyWPYpd0Eu+Kps9BIDEn/4pmz/zGSpPPMHuyy937NUa\nFtx02M0VaqTCvp7CdwOe9ATywgLxoJeJiK+l2P1+tsADzy3w5jO3WT7WCcqivmB4Ic7YKYVCj7Ll\nBHE1FDuAo18PkfXw00/omyxOiZhNaOFJlKqCGO1OxTT+Hr0L222xbdz2mtuYCE7w9h++nfsP3L/8\n4zeBpWLXJHt2lQdyJmtJ7KR0CiVX0tOJvV327GCKRRHivpQpsUsEEraL4mxz/jAZWt9zW9wXp9Ao\nIKvW15UOTB4Dub36de2kN7l6SF0t4hfCzH3hi8x+4pNEL7iA2oc/TMMjsFixf28ZtsJulSjmi7UU\nu37n6wDSYR8LpfpAdTGzq6DYdXf3QR+KXS1P1BvtqLZwg7g/7qjYZWtZ09k9V4pdNdu6XzfSgTQV\nuUK5UTa93Q5DKyc3w+lvhUaZ1FPfIegJtghdP1UHS/GZl3+Gf/uzf2vZMg8qqhYOgTWMMbEbY/Rx\nxtt00vWru1bud7Q67Na2Ygdw0elbCXjFtmpnFZ7iDekLExvFbl3Uj2hBJDZ5motip3khUdTnJRee\nbX/voRv1jrvDz7d8WM5ibiQW8Fgqdq37XPAqtn7pi9SffY7dl15KY2bW9v7DgDytzxB6HKyYZuXk\nBnQrpv73OHQi0qo8uOOB3fgkkYtOd78z2nN8TYLb94xdJAKShJIb3Y0NNdcbMuIEKRpt9d+tKDw+\nOGUn7H9U/3+Xip3mnwStt5tPiuv/r+bNF58bwhu45dW3sC22jb/88V9y7557Bz92s+PSNBsrZpPY\n2WymKBkbxS6VRs5X9WtVl6JRC8QoiCLrA1Gm89XOOWL0RXWhXqChml8bMoUDACSivTUhbmPuW1jX\nJOfH/4WuaDhA0zQUrcglP93D/Je+RPzP/ozNn/4UG5L6plim6mz9A3pITtQXbaVi9jtfB3rlQV1W\nKdX7TxOeLdTwecSBlEK3MCN2S4vZ7ZCv5/sKTjGQ8Cccz4NhKHZmWE6X3XxVV+yGVnewFJtOhi1n\nIDxyU0flwd7CXgQEtkT6I3bJQHL5JerDgvHeGxO7McZYRWw6Gbadrdsx1RWKszfmzF4AxC4R8vFn\nL9rCv/xyP5lS3XpHShDaXXYmmC1UWWeTeLZezJETYiC5WFCkD2srdjO/gT3364EDNhYmqwhvXbFr\nOO4yR172MrbecAPygSl2X3op9X37nY9zGWgcMBQ7eyum1Xwd6FZMrVxGLZc5dDLMc/MlijWZb/5i\nP687cSNpG1LoBGXAGTtBEEa+pHzg8JRSCU12qdIsB6fu1CPxwbVip4j64k+MdlrJxCaBtbMZTwQn\nuPmCmzk6dTTv/cl7+b/P/d8BDtocaqkEsmxqxTRKx62InaZpOrGznLFLoTUUVKn3b7no1a9FW/wh\nVA1mCp2zYcbsnNWiPFPSN15S8W09txkLbScLXgvbzgbRa+s4WIpKrcjbv1Pn3Ed3kbzsUjb+r/8P\nweNhIhJBUz3kXNgKJUEi1JXoaZR1D6rYpcL69WSQyoPZfJX1Mf9wyrAtkK/1krOWYufiNRuEPLgJ\n0snVcj2JmNA+B+0eb6vYNYNPBiJ2K2XFNHDG22DxWbYI/pZit6+wj/Xh9fgkc1fPmsCY2HVCEISU\nIAg/FAThmeZX07NVEARFEIRfNf/79nJ+5xh/oDjjbZDZBc/8cGV+fkuxM7koGkrXGghPMXD5i3dQ\nk1XueXivrtj5oubluaE0lM3DU2aaH9xWSJNjAZcXw/ThkHkeFFmPTvYE9KFsG1hFeMcCXhqKRrXh\nXEgePvMMtt1yM0o2y+6LL6b2+5VLDGxMTyElEojBoOV95go106oDA550s6R5YYHDJiMslurcdv8u\nijWZS8/uv+JgKZRMRu8eC/RvnZLi8ZHtsdNUFbVYHCg8BUAtmhfBDxXxLXDUa/X3W9Ra0V0KBf34\nJH/nwrltjbVf2Mb9cb76qq9yyvpTuO6/ruMbv/3GAAduclzNWUur8BTA0v6sVSpotZqlHdiTanY5\nqr1zUQuSvlzZHtTP3247ppEyaBWgki3r1/hErFf17lux23oGXLdP33R0gFqvc+C91/KKX2v85I9O\nZf111yE0N7SiAQ+aEqTQsFeOjVmzbhLVodgNaMWEwUrKZwu1FbVh1pQadbVuOlcoILiyYg5C7OI+\neyumqqnk6jnT8JSoL4ooiLYhPnaKnaG2DVJSPl+ZJ+gJEuq2MA8Lx74BwuvYmj3AvuI+VE1tddit\nabSI3XjGzsD7gR9rmnYE8OPm/5uhomnayc3//mSZv3OMP0Qc88d69cHP/2Flfr6dFTMQB4Q1o9gB\nHLUhyksOT3PHA7tQK5ne+ToDobSlFXO2ULPtKEpqGWYUlx+c6cNAlWH6cXj86/rcpIOFqRXh3aPY\n6QTVLBnTDMGTTmL7HbejqQq7L76EyuOPuzvmPiFPTeOxma/TNI05B8XOM9Fc2M63kzG//B+/57hN\nMV60dXkfPEpm0TKN0AlSPD6y4SlqoQCa1hMy4gQjbGVV5uwA/uQLcPl3nBMxm1DRF2iSp1NRNAis\nYmHFXIqwN8yXz/syL938Uv7uwb/jxl/fONA81VIYllzzHjtDsTPfBDOUPI+VFbN5/itKb53HQtMS\nfqhfJyPdxC7l168nVmrJYtMelwz0XneMhbZTB1kHvM6kRi2X2feOq2nc+5/ccr7IY68+t4OceSUR\nQQtSciB2+VpvOiS0iV2uPOCMXaRJ7AYIUFnpcnJjrrA7PVIURCK+SOt2u8cPasW0I42lRglVU02J\nnSRKxH1xy3NQ1VRLGycs04o57A67bnh8cOpOts4+Q02pMVeeY19xX1/BKSOJsWLXgzcAtzX/fRvw\np8v8eWOMYQ7J264+MEp+hwk7YidK+pt+DRE7gMtffAgHclXm5masd6MsiF21oZAtN2yJXUzOMKvF\nqbiZzzCSMe/9O2iU9WFsB+QrDQQBov5OpdGYJXGas1uKwFFHseOuuxCjUXZffgWlBx5w/Vi3aExP\n491gbcPMVRo0FM3eitksJ1YW2smYpbrCZWdvX7blSc5kkPqcr2sdVzxuG4hxMGEQM7HP8JQ2QVql\n5NRQqj2b5QKKqr/3RKkzYdI4brfzgQFPgM+d+zlee8hr+dwvPsenH/n0ssidcR6YpmIaaqLFuWJU\nIViGpxiKXaP3PbKAfp05xKcvW/b3q9jV8vg1CHp6FfWWYufWiukCSj7PniuvovTgg5TfdxXfPV0k\nYUYGtDAV2YHYWdgKo74oZblMoVbrKD53i1RTsRuk8sBp42+5sJorhLYF1enxAyl2zfAUq/eIQdrM\niB3o56HVOVioF1A0xdKKmQoOTuwWK4srS+wATr2CLbLulHkm+wzzlfm+g1NGDlbhcmsYyyV26zVN\nmwJofrWKxwsIgvCIIAgPCoJgSf4EQXhb836PzM3NLfPQxnjBYSWrD0rzul3Ra2GjCybWRCrmUpx7\n9Dq2poIszs/2rdjNuSifDTUWmNfiZMoudnsNYvfsvbDldFcWpnxVJur39IS3GAqeW8XOgG/bNrbf\ndRe+zZvZ+7a3k//hcG29jakp20TM+aJ9hx2AZ6JpxZxfYGsyiFcSiAU8/MlJvYEP/UJZtA6tcIKU\nGN0ZO+O4+lXsjLCVVQlQGQBKQ1+oS3Qm5Ak+H0Iw6GjFXAqv6OXj53yci466iNuevI0P3/9h9wmQ\nXTAsuWZWTMHjQYzHLWfsDCXPuu5AX9gq9V71aUHTrzObNIVEyNur2DXVDqtFdUYukRAk0w2Svq2Y\nDpAXFti983IqTzzB5s9+hr3nHA9AOtj7mnmFEFXVvnPTLEQElpAesTqgFVO/Fs33qdhV6gqFqmx7\nLVsuWhUPZoXyLomd2WvmhLg/jqIpFBvmFm3juKxUN7vaDeP7Vo/1S34i3shAXXYrrtgBxDezdds5\nADy472dAf1UHIwljXTeAujuqcCR2giD8SBCEJ0z+e0Mfv2ebpmmnAW8GPisIwmFmd9I07QZN007T\nNO20yUmHpL0x/vBgVB/86u7hk6zSnPl8nYFgcs0pdpIosPPsHYi1HDl6rU2ATuyqOVA6SVKrfNZq\nR7ZewqtUmHNL7ELpttXBhVoHusIVD/UuVoydaaMOoR94169j+x23Ezj2WPa/56/IfvObff8MM6il\nEmo+j8cmOMXofZqIWA+aG4mV8sI8HknktSds5F2vOJygr7/IbjMomQye1GDEThzh8BSDmIl9pmKK\nq63Y9Qm1rn88i/QenxSNurJiLoUoiPzNmX/D1Sddzb/+/l/565/8NTWlf6VGsSF2AJ5EwobYNQN8\nEhaKnTGjV+klXwtyhYiq4q/m2RQPciDbqWQa5MwqkTCjVEmJ5kQk4o3gETzuS8ptUN+3j11vfjP1\nXbvY+pWvEHvVq5gt6sc0Ge593j4xTF2zJ3ZWCY8tRUqsDETsgj6JkE9isc8Zu9mCUXWwClZMM8XO\nH7MNT6kpNWpKbWDFDqwtvY6KnT9hfQ5WDTuw9XU4FUixWBksFXNFEjG7sPGMqxE1jQd2/QDgBTBj\nl20mhK/hAJguOBI7TdPO1zTteJP/vgXMCIKwEaD51TRTXNO0A82vzwE/AV40tGcwxh8WVqr6oDRn\nH9u/BokdwIWnbSUhlHg6a/FWDzc/CLqeW7uc3OKDu6i/1eeJky27UM4EAdJHQGgCjnPn2M5VzCO8\nB1XsDEiJBNtuuZnw2Wcz9YEPsnDzLQP9nKVoNKsOvA5VB2C/GBK8Xt322Kw8+NxFL+Ltf2S6D9Y3\n5EzGckHtBCkeRy0W0RqDveYrCYOYWRENK0gR3eo6sopdRT9fJKV3gSnFYwOVqwuCwDtPfifvP+P9\n3Lv3Xt75o3dSrPcXHtOyYlq83lIyiZJ1IHYW4SmiB0SPimzS171Yy5JWNagssikR7FHsvKKXqDdq\nbcXUGiQkc0eGIAjE/LFlK3bV3/6WXW96E0o2x7abbiLy0pcAMF/WX7N1od73X1CKouCC2JmQFON7\nglQdqO4AdDtm/8TO+HxY2Q47GMyKaVXo7gZG2qUVcTTOEStilwwkLWc1DVJopGeaIR1M923FrCt1\ncrVcK1VzJeE99OVs1ER+V9VddWtesavmXlDzdbB8K+a3gZ3Nf+8EvtV9B0EQkoIg+Jv/ngBeAjy5\nzN87xh8qNp0MW88afvVBad6e2AUSayoV00A86CUplnliQWhZATtglJSXOpMxDcVuvVXqmUHstLj7\nRcFrPglvvAM87nZ58xYR3q0ZO5uScieIoRBbvvJloq9+NbN///fMXv+ZZc0dtaoONtlZMfXXaTJi\nvxiSJiaQ5/u34thBrVbRyuVlzNg1+8lGkAQZBKffHru2Yjd6zwlAzRcQvSCUe/dLxVi8LytmNy4+\n5mI+fs7HeXTmUa78wZV9LSSVbA4xFELwme9wS8kkslV4SjYDomidYFrJIgVUlHLvtX2hukAKCSoZ\nNicCPTN2oC+qTdUSuc6ioJG0sebF/dahF25QfuQRdl9yKYIosePOOwid0t6/Xqxm0TSRdZHeBWTI\nE0GliqqZp/xqmmZpKzS+J4iVgcJTANIRv/lngw1mmxt/62xSk5cLg7hZEVpbYle3tnE6wZjVtCL5\nxhymWd0BtM9Bs88TY9MhYZPAmAqk+rZiGu/fFbdiAghCa64u6glaEtw1gzGx68EngFcKgvAM8Mrm\n/yMIwmmCINzYvM8xwCOCIDwG/AfwCU3TxsRujMFx5tuHX33wArRiAiDX8Gk1FtUwd/98T+/tBrHr\nmrObKVTxSSIJEyskACV9sTmnJci6sWICbDkNtr/Y7ZFbKnbRlhVzeeqR6POx+dOfInHhhSzccANT\nH/rQwJ1mjekmsbMJT5kr1PBJzoW+S0vKhwUnpcQJ7VCM0bNjGsSs7x67cBgEAbUwmlZMJZ9HDEhQ\nnOm5TYrFlm0hff2hr+fz536eZ7PPsvO7O5kqTrk7rlwO0SQRs3VsyaSlFVPOZJDicQTJwlpczeEJ\nqMgmRGOhskBa8EJZV+wKVblHtU8EEuZqSXmBrCSRtJhtgmYaokM3mhUK997LniuvwjM5yY67v4b/\niCM6bs/W8mhKgESolwxHvFEQNMuZropcQVZly/AUaCp2AxaFpwdQ7FpW/RWsO3BU7Gz+Vnak0AkG\nYXOyYlqRxoQ/gazKlBq9KqwbxS4VSPWt2K14h10Xtqw/Rf+qsKI9hquCMbHrhKZpC5qmnadp2hHN\nr4vN7z+iadpVzX/fr2naCZqmndT8etMwDnyMP2AMu/pAVZ0Vu2BSn+tbZlT4qqM5i7hu3TrueHA3\ndblrV9iC2M3ma6yzK58tGsQuTsaNFXMA5Kvmil3AK+H3iANbMZdCkCQ2fPQjpK9+B7l/+ib7rnk3\nasXEB+YAeWoaBAHPOqv8KKPDzuf4QeiZSKPMm3cLDopWzPygil3C6E4bPdVayedAFHWi1gcEUUSM\nRkdWsVMKeaSQz5LYDWLF7MbLtryMf3zlP7JQWeCS717C7zK/cz6ubLal4JpBSuozdmaKhZLJ2gf4\nVHNIfgWlUO25aaG6QFoKtqyYAFNdc3Ypf8pUsWsUpymKIgkbq9qgil32m99k319eg//oo9h+1514\nN23quU++lgM1aG4tb5KPXNV808ROfWoTu2UodmFf33UHs4UaXkkgabXxNwQU6gX8kh+/1KsKxvwx\n6mrdckbUIIXLmbGzSkjN1/JEvBG8ovlzN+bnzM7DTC2DT/SZJrMaSAfTZKoZlD4cSatN7LYmDgFg\nS3EBFp9bld+5YqjmXlAddrB8xW6MMVYfkhdOf8vwqg+qWdAUB2KX0O9TG81FoCWai4XTjj6E2UKN\n7z7RtStvpdjlq/bzE8VZQKDuT7oLTxkAuUrDchc6FvQOFJ5iBkEQWPee97D+wx+i+JOfsOeKt1gW\nLFuhMTWFZ3ISwWu90HHqsDMgpSeGrtjJi4ZiN/iMHTCSASpqvoAUjQ60cyxFoyOr2Kn5AmI4CIVe\nYifGl6/YGTh1/anc+ppbQYPLv3s5D08/bHt/JZcz7bAz4Ekm0Wo1NJMNEiXjkMxazeqKXbZTvWqo\nDbK1LGlvtKXYgXlJudmMXSa7C4BUaL3lr7brHzODpmnM3/BVpj7wQcIvfjHbb77Zsp+v2CigKSHT\ngJNEQCcfs2Xz95aTcgUMHJ4CkIroil0/VvTZQpV10cCKqjV2qZbG83aagxvEimk8xk6xs7Mf2nUi\nZqtZEoGE7euWCqTQ0CwDWMxgFJqvmmLXtGJukVV48Cur8jtXDNXsWLEbY4yRwKlXDK/6oNVh52DF\nhLVnx2x+uByzYxuHToS55b5dnbe3iF2n9UMndjYkpDQLoRSRUNBdeEqfqMkK1YZquQsdC3iGotgt\nRerNb2bzZz9L9ckn2X3xJTQOHHD92Ma0fdUBwHzBHbHzpNOoxSJqrf/EQiu0rZiD99hBO+p+lKAU\nCoh9BqcYEGOxEVbsdMJKvQD1TluXFI3pYTbKcOaMj0weyZ2vvZPJ0CRv/+Hb+f6u71sfVy5nr9g1\n++3M7Jg6sbPZHa/mkPwqSr7zuRlkLe2LQ2WRzU1i1z1nl/QnyVR71cJMYT8AiYj1e9SpmHopNFVl\n9hOfZO7664m97nVs/fKXbBXjkpxHUIMEvL0W1FRzUTlTMLff2dkKg54gAiKiVCXiG8yKORH2U1dU\nCjX3G2WzeXfXsuXAroeuRews/l52HXhO8Ipewt6wLWm0I3aGzdJKsbOzYcJgJeWGYmc8dqWxLbpN\n/7rhRfDLO3vWD2sKYyvmGGOMCIZZfWBXTm5grRK75msjhpLsfPEOfrU3yy/3LHkOkhf8cSh3Wv9m\n8zX7+YniLITXkQz1P5/hBoYaZ7ULHQ14lz1jZ4bYBa9i2003Is/NseuiN1H9rbM1DXQrpseB2M0V\na0xEXBC7iWZJ+RDtmEpG/+Bd9ozdKBK7fK7v4BQDUjSKMqqKXS7XDhnpsmNK8eFXNWyMbOT219zO\ncenjeN9P38ddT5knD+tWTPsZO8A0QEXJZCxVLQAqumKHqnaca4YikQ6moJpjMuzBIwo9il0ykKSu\n1ql0xWpmmvODyfg2y18d98epyBXHCgi1XufAte9j8bbbSF52KZv+999bBskYqCpFPERMb0uH9Pfk\nXNn8c8xQ7MzCOgRBwCuE8PlqPX2fbtEqKe/DjjlbcNj4GwKsuvtgZYkd6CTfLjzFKjgF2sEoZoqf\nodjZwags6JfYxf1xfNLqRPYfnTqaD5/9YV7z0g9CowwPr9EJK00bE7sxxhgpnPkOvfrgkZuX93Pc\nEDvjYrzWkjGN4w0m+ItTtxDxe7jt/l2d9wmlOqyY5bpMoSY7WzEj60iEvO7DU/qAocZZKnZB77JS\nMe0QOv10tt95JwC7L7mE0kMP2d5f0zS9nNwmOEVRNRZcWzH1D/Zh2jHlTDONcFBlKxoFQRjJ8BQ1\nX0Dss5zcgBiLoo6wYicmmjvwXXZMIyhmGHN2SxH3x/nqq77Ky7e+nE88esz41gAAIABJREFU9Ak+\n++hnO9QvTdOaVky7GTuduHUrdpqmIWezto/Vw1N0pU5Zcv4bKYHpkD7DKtVybIgHeq2YTRtct1qS\nbSaLJqPWnVut/jKba7ySy7H3yqvIf+c7rLv2r1l/3XUIovMyqq4V8Ynmit66ZrfdfMl+xs6KpEiE\n8XkHV/dTzV7NhT426GacNv6GAFti57e3YuZreUKekOUcnBNivpilFdO1YmdiCc7Wss6KXVB/zxub\nGW6wUF1YlQ47A4IgcOGRFxLedAoc/kp46B+h0TsXO/KoF0FTx8RujDFGBhtPhMPO1T3ey7moGFH/\nL2DFjkCCiN/Dhadt4d8fn+pcEIXSHcRu1qnDDnQrZmQdqbBvRcJTck01zkqxiwU8FFZAsTMQOOpI\ndtxzN57JSfZe9Vby3/+B5X2VbBatVrOtOsiU66ga7qyYE7oleJiVB8piBimRcLUINYMgSbptcSQV\nuzxSbLAPZikaG8kKB01VUYtFpFTzmtSt2DWf70qUqwc8Aa5/+fVceOSF3PTETXzwvg/SUPX3mloq\ngaLYK3bNrsTuLju1VIJGw75LsZpFaipI8kJbsTDUi7RhpWx12XVe91vBFV2L6kzz8YmgtVXNIIVW\noRmNAwfYdfHFlH/1KzZ96lOkr7rK1YyZqqnIWpmgZE5S1kX037to4Txx6mQT1CCSZ/DPv4mwfk1a\ncFl5UG0o5CqNFVfs7GbsjO/bKXaDzNcZSPgTlueBE7ELe8N4RPOy+0wt0zrPrDCoYrda83U9ePE1\n+ub4418/OL9/OTACi8bEbowxRggv/W86yXjsa4P/jNIcIOjKlRXWKrFbotgBvOUlh6ABN/3s+fZ9\nuoidqyjr4lzLirkS4SktYmdRuqsrditblu3dtIntd91J4Nhj2f9Xf8XCrbeaBgzIU7rNy+NQdQAw\n6caK2VLshmnFdAitcAEpER9JYqfm80gDKnZSLDp01WsYUAsF0DSkdPOcWgUr5lJ4RA8fOutDvOvk\nd/HtZ7/NNT++hlKj5FhODm27r9JlxWw91ik8Ja5bFpee/4Z6kTIUt7I+Z9czY2dF7JqLbLtFdSsN\n0cSCV33qKXa98SLkmVm2ffWrxF//Ouvn0IVSowSCRshjbsVcH46jaQJZC/XJsGJGfOaPRw0iSIMT\nO0Oxc2upN65lq6HYLWfGbpBETANxf9z0PFA1lXw9b0vsBEFozXouhazK5Gv51jlqhZgvhkfw9E3s\nVqOc3BSHvAw2nAgPfFFPGF9LqHSuj14oGBO7MdY2dpwDm06B+z4/eGF5aU4nN6JFtxK03/jLnedb\nbVSy4A3rs3TA1lSIN5y0ibsf2kPG+CAPT3QMP88UHBS7WlG3wDatmIWqjKwM94JuzM9Zh6foqZjL\nKRV3A08yybZbbyF6/vnMfuKTzPyvj/UEVjSmpwFsw1OMxdBEH1ZMZYhWTGVx0X62yQWkeGIkiZ1S\nKPTdYWdAjMZQS6WB+wtXCoaKKKY3gNDbZSc2ZwpXkpQKgsA7TnoHH3nxR3hw6kF2fncns9PPAvaz\nmlIsBqLYo9i56lKs5pCSTdK6RLFbqCwQkAKEwk2iW1lkUyLAdL6KoravAYbNrVstyTSKxDQRj2gd\nMNJKM+x6bPG++9h9yaXg8bD9rjsJn3Wm9fGbwCAIEa85GYiHfKAEydmQFEMFMoMiB9DE/itaDKTD\n/VkxZ5tVFJMrqNhpmmZL7FqKnY0VcyWIXaFeQNVUR9UtEUj0nEf5eh4NzfGxgiDoJeV9WDEPqmIn\nCPDid8P87+AZa2fLSGKs2I0xxghCEHTVLvM8PPmtwX5GcdbehgngDYInsDYVu67dqHe8/DDKdYXb\nHtilfyOUattRgVlDsbOasWuWkxPRFTuA7JBtkfmWFdOq7sBDXVGpdffyrQDEQIDNn/ssqSuuIHPn\nnez7y2tQy+XW7Y0DzXJyF8TOjWIn+v2I0ehQrZhydgiKXXz0FDu1XkerVpGigy3iDKVPLZqXQx8s\nGIRNischsq5nxq4dZrPyauOfH/HnfOm8L7GvuI+P/+BvOn6/GQRJQorHeypDWl2KDuEpUiIBkoS8\n2Dljlw6mEcJNV0Ulw6ZEEEXVWkQD2opdt9qRUaokHeatzBS77L/8K3vf/g68W7aw4567CRx5pO3P\nMIOhKsX9FrbCgAdNDVKsm1uCndQnueFHFcqWtzsh4JUI+yTXXXYtq/4KKnYVuYKiKZZWTI/o0ZMr\nLchwoWFNCt0g7o+Tr+dRtc7PF4NI2il2gKliZ8xuOil2oM/ZuVXsyo0yFbly8IgdwHF/CrEtcP8X\nDt4xDIIxsRtjjBHF0a+D9OFw32cHKxAvzdtXHRgIJtcesatke8o3j1wf5fxj1nPr/bso1WRdrZQr\nUNcXBzP5KgGvSCxgsbtdNMJmdMUOaKt/Q4IRjGJpxWx+fyWSMc0giCLr/8d/Z/2HPkjxpz9l96WX\nIc/pr4M8PYXg9SLZlH/PN+dX3EaEe9Lp4VoxFzO2x+cGUjzestONCgwCNHB4SpMQjtqcnVHBIMZi\nEFkPxemO2420zJWyYnbjJZtfwm2vvo1wRb++/qr6e9v7S8lkrxWzpdjZF5QLwQRSKtmj2KUDaTBm\n5Cy67CLeCB6hd74pq9ZJStal0LAkPKWWRdM05r78Zaauu47wGafrxePrrTvw7GAUj1spNV5JRFCD\nlOXBiF294UPWBid2AOmIn8WSuxm7WcOKuYKKnZtUy5gvZm3FrFnP57lB3BdH1dSWDdaAcV7ZpWKC\n/rfuUY2bgT5Oih3oc3Zuid1qd9iZQvLC2e+E3T+D/Y8evOPoF2NiN8YYIwpR0q0AU4/ppeX9ojTn\nrNiBTpDWYiqmiX/86pcfRrbc4J6H9/aUlM/ka6yP2ZTPGrawZngKMPQAlVylgd8jmvY+QTtUZaXn\n7LqRuvhitnzxi9See45db7yI2jPP0JiaxrNhg20wyVyhRtArEfa765qSJtIoQ1LsNFXVI+oHrDpo\nHdMIKnYGsRk4PMVQ7EaO2Omvs9Qidp2KnRAIIHi9qPnV+3sclTqKdx26E4DrHvsY3/jtNyzvqxO7\nrhkjl8SOQAJPKo28uITYVRf0tMBAXLemdnTZtRU7QRB6S8qVBhlUEl6LGbUmgp4gfslPobjI1Puv\nY/7zXyD+hj9h6z/8A1LE/rF2mG/a91NBm7lEQlQUc9XYjqTUZAW5EUShTl0ZfHMtFfa5tmLO5Kt4\nRIFUaOWi9e26+wzYErvlhqc0N0O7rZ5GoIqjYhdI9m4u9KPY9WHFnK/qG4ATgYNI7ABOuUyvTrr/\niwf3OPpBi9iNZ+zGGGP0cNJFENkAP/ts/48tzet2JycEk2tzxs7konXq9iRnHpLixv96jobf2AU3\niF3V3mZjYsUcdoBKvtKwnK8DWmpirrL6s1HRc1/B9jvuQG3U2fXmiyn/4heO5eRzLqsODHjSE0Or\nO1ByOVBVPENQ7NR8fmil2MNAy7I4sGKnP27USsoNoilFoxBd32PFFAQBMR5fFSvmUoSrujXthEPP\n5u8e/Duuf+T6Hrsa6HN03cROyWRBklqvuSmqWQjE8aRTnXUHhmInCPpGVVOxEwT49b7Oa3Iy0GWD\nKy+SkURSLqx5m+QIp3zs38h961tMvPsaNn7iE44ddU6YKerHMhmyXtD7hDA11YLY2Sh2+YqMpurX\n6m51qR+kwz73VsyCfi0btDfPDYznYqvY+WOmM3YNtUFFrizPiulrq7dL0VLsHIidodgtfW/0o9il\nAroV080MuVFOftDCUwz4o3Da5fDkv0Jm18E9FrcwiN0yNgFGEWNiN8YLAx6/bgV4/qew/xfuHyfX\noJZ74VoxLRQ70FW7qVyV/9zfXKg3id1soWZvsykaKaITLSvmsLvscpWGZdUBHDzFzkDw+OM45J57\n8Kxfhzw1hXejdSIm6FbM/ohdenjELuMijdAFpEQcNG2k1C3DQikNGJ7SsjSOWEl5pxVzA5Tne8Kh\npNjqVzUo2SxiKMRnX/VF3njUG7nlN7dw7U+vpSp3pjJ6TBQ7I5nV0gmgqlDNQzCBlGqf/6qmkqll\n2gvXYAoqi0T8Hl57wka+9vM9HdefpL9TLdFKc2QkybbqAKD23PP8968uknp+kU2f/hST73ynqzoD\nJ8yX9dfB6Kszg1+M0LCwU9r1ueUqDTQl2LrfoEhHfCz0YcVc18e1bBA4VTwYt5kpdm4e64TWvGVX\n5YExf+lEzpKBZI+VM+simdVAOpimqlSpyM6hOCND7EDvFhZEvYJqLaCaBV8UJHdOmrWCMbEb44WD\nU6/QrQD39aHauemwMxBMrFHFznx38Y+OnOTYjTFue6y5U9xMxpzJVx3KyWd0+6bkWaLYDTk8peqk\n2Om3FVaopNwNvJs3s+NrXyP+hj8hesGrbe87V6i5Ck4xIE2kUXM5tPryCbOS0f+uUnL5ih0wUnZM\nQ7EaNBVTaqVLjg5ZBVALeRBFxHBYdxNoarOWpQ0pGl1VKyaAktXLyT2ihw+c+QGuPe1afrT7R1z5\n/StbC0zQu+zkbLZDcVAyGTx2duBaHtB6FDtD+WgVMIdSrQ22a849nFJd4eb7drV+TDKQ7JhPKub3\nIgsCyaD1Nb704IPsuugiAjWNr73rKOKvc19n4ISFShZN9ZAOmxeUAwQ9EWTKpgqNna0wX22gKYHW\n/QZFKuxnsVR3pRDN5qtMrnTVQUN/P9qRs6gvak7sDBvnMlQYq+oLgzQ6ze8Z5G2pcpypZgh6ggQ8\nzq9dKuC+pHy+Mo8oiI7F56uC2CY44UL4xR0dSdsji2ruBTdfB7CmaGqj0WDfvn1Uq2uw4X4ICAQC\nbNmyBa/XPt3rDxaBGJx+JfzsM7DwLKQPc36MsVhyRezWmGKnNPRaAgv/uCAIXP3yw/jg3QcgAJTn\nKdZkynXFoZx8rmVdDfkkfJI49PCUXKVh25NkpGWuVniKFaRYjE2f/KTj/eYKNc44xD2x8qSbJeWL\ni3ht+vHcwFXMvAuII0js1KbSJtnZ+2wgjqpil8sjRqP63Ga0+fcvTLf/DYjxWEfAyOocVw4xoZ8H\ngiCw87idbI5s5m9+9jdc9O8X8flzP8+x6WN1dbjRQC2VWvNpSibjUE7eDjKQUl7Uchm1UmGh2uyw\nMxS3YApy+wA4ekOMC45bzy33Pc9V5xxCLODtCa7I5vcCkIyY26Uz/+f/MP2Rj+I/ZAff3rmZpzzT\npvcbFNlaDk0J2m5UhT0RUGSqSpWgpx3y4mQrzFUaaOryFbuJiI+GopGvyrbHCbpid+r2lSURrqyY\nvpjpc3Yzn+eEpUE6S5GtZYl6o7a1GdCu3cjUMuxgh/7vasY1+WoRu+oCW2Nbbe+7UFkgFUgh2dU1\nrSbO/kt47G549BY4568P9tHYY0zsDj727dtHNBplx44dQ7FIrCVomsbCwgL79u3jkEMOOdiHM7o4\n62p44Etw/+fhjz/nfP9+FbtGCeQ6eFZucHxoMBZKNuWbrz1hI5/+/gRKWUQszbfKyR0VuyaxEwSB\nZNi7AjN2ModPWl+eWqmYB8mK2Q8aikqm3GAy4n6X2zPRLCmfX1g2sTNCKIYxYwejReyWq9iJ4TAI\nwsgpdkoh3yarkWYaY3G24z5SLE79+V2re1zZbE/Vwfnbz2dzZDPv/o93s/O7O/nYOR/j9KbtV8lk\nWsROzmbwH2qz2bYkyMAzoZMVZXGRBVEndh2K3fTjrYddc+4RfP83M9x23y6uOe8IkoEkuVoORVWQ\nRIlMUa8jSca2dPw6TVGY/fT1LN58M+GXvpTNn7ke8defJrv36cFeHAvkank0NWiZ8AsQ9cWgohOa\npcTOieDkKw1Qlj9jZ4RgLZbqtsSuLqssluorXk5ukDPLUnZ04laRKzSUBl6pfczG67AcYtcqQDcJ\nT3Gar4N2+EqHYlfLtL7vBMNW6SYZc6GycHATMbux4Xg47Dz4+T/CWe8C78qeK8vCC5TYrSkrZrVa\nJZ1O/8GROtAX0Ol0+g9WrXSNyDo4+c3wq6/pO9xOaCl2Li6MxkV5rSRjGrZRmw8TSRR42x8dQUaL\nMD19oEXsbD+4i7MQbofNJEO+FUnFtFtgBLwSPo9I/iCEp/QLI5Sg3xk7AGUIlQdDm7GL6+eRkh0h\nYlfII/j9iP7BZn4EUUSMRkeu7kDNF9oVDi1i11t5sFp1BwaUnG7F7MYx6WO4+3V3c2TqSN77k/fy\ng8z9+v2XzNkpmaxDIqZxvYq3qjnkxcWWHa09Y5fssHkdvznOeUev46b7nqdYk0n6k2horfmoTEkP\nnkkuUT6UYpF917ybxZtvJvnmN7H1H76CFI2S8CfI1XKuLIluUWzk0ZSQ/cxwk0hYWf+sw1Pait1y\nrJjppk3cqfJgrrjyVQegP++QJ2SrjBlWy+7nPYwZO4/oIeqNmip2boidocx1KMfV7ECKnRPmK/Oj\nMV+3FC/9K30D+NFbD/aR2KNqPaqylrGmiB3wB0nqDPwhP/e+8OJrQJXdDfD2a8WEtWPHNBZKNood\nwF+cupm8EGPPvr2t8lnLD25N67BiAiRC3qGGp6iqRr5qH54Cumq3FhQ7o5x8IuJe5ZUmmlbMIVQe\nKIuLCKEQYmB5O6dSYvQUOzVfGDg4xYAUibTSNUcFSqHQrnBoEbvOZEwxHkMtFNDU3lTKFTuuXM6y\nnHwiOMHNF9zMHx/6x9wz/R0Aygu6yqhpmq72mZDCFpY4DIyNDXl+vk3sAkuInVyBRjtY4przjiBb\nbnDHA7tbcfJGvHym+fhEc/Fb37WLXW+8iOJPf8r6D3yA9R/6EIJHJxAJfwJZkynLy+uFW4qyXAQl\nSNSqFxRIBvRzeLbUSSTa5ebmr3m+Kg8nPKWp2M07JGPOthwdK0vsCvWC44xcS1XrJnZDmLEzHt8d\nnpKv5V2FnyxXsTOI3WLFWbGbr8633xujgkNeBjvOgZ9d3/E+HTmMFbsxuvG3f/u3fOpTnwLgwx/+\nMD/60Y+W9fMUReFFL3oRr3/964dxeH+4SB8Gx74BHrm5vViwQmkOPAGwsXy0sNaInQvFDsDvkQjE\n16EWF/jhU/ri0dKKWS9Co9xB7P5/9s47zKkq/eOfm14mmUyjDx0BEUSqDUQFURGUFcW27rg21N/a\n1ga4FnZZ+66uvS6iK6hYsTd2RcQCgg1Fkd4GmJZMyaTd3x83N1PIpGeSDOfzPPPMJLn35mS4nDnv\n+b7v9021Ylfr8SHLRK31sJt1Ga+xi4W9tcpiKBHFzrcvBYpddRW6SAvqGAk5SNZkj2LtdzoTTsNU\n0WTAXTIaAWdNUyqm3qQsPlq1PNDa7BAIEKira5cxybIcDOzavpeMWiPzj57PjNEXAPDYp3dTXleu\nOKn6/ZHrPBuaK3ZBxbqykgp3BXqNvkmBsQRTipvNw8NLHYwbUMxTyzdi1iq/NzWNrSqomhQYC6hd\n/hmbzpyJf98+ej79FIW/P6/FhmlbtVXJ0OB3oZUt6LVtL7cKg5tvamsElVhSMY1aA3qNPmWpmJEI\nNSdPt3lKBCdQlaiBXRKKHRBSb5tT01gTU8Bo1pkxaU0tFbvG2BU7g9aAzWCLmoopyzL7GvZlVyqm\nyoTZymbUqmcyPZK2aaiJuvGdi4jALkXMmzePiRMnJnWNBx54gMGDB6doRAc4R12tuKxFm1Tq9ilq\nXSxqqDoB5IozZoyKHUBJ526UaF28/d0urAYteW010lbrfKzNFTtDSs1TaoJBYqSaFACbSY8zg66Y\nsbLPFX8qpsZsRmOx4EtBKqavsiqU2pYMkk6HJi8vuxS75rVoCaK4S2aZYtc8FROUlgetUzHz1UC7\nfcYeqK1VgrMomwSSJDFz7MUAuPft4ey3z+bH374AlDYIbdLMPEVXFEzFrKgMmUOEAjDVRKWV695V\nxw+gos7Dyl+U4ENdVFd5nOgDMu7nX2LbpZei79KF3q8swXr44fsNIR2BXWOgFoMm8sZhsUX5ne6t\nD6/YRTJPyTcb2nSIjBU1sKuojZyKuSeUqp9mxc7rwqaPEtgZw9fBORudmLQmDNrk6uDzjfn7BXbV\njdWhHnfRcJgcIcXO4/dQ562LSe1TKTIVRU3FdHqc+AK+7Azseh8FfY5RzOw87bP5FBeBgLJGFIqd\nYP78+QwcOJCJEyeyfv360PNlZWUsWbIEgN69ezNnzhyOOOIIRo0axTfffMPkyZPp168fjz32WNjr\nbt++nbfffpuLLrqoXT5Hh6fbcOh7rGKk0hi+8SugKHax1NdBDip2wXHGkP6htxXTVa9MvhGNU9TU\n1bym1NVCq57qBm/K6lLU9MroqZi5otipqZjxLYa0xcX4U5GKGewflgq0+fkEsiiw89c40eR3PMXO\n73IpipxKXqf9zFNUpbK9Wh6oAX1bqZjN0dhsoNVybrdpGLQG/vb+Dcq50QI7SQMGW2hjw19RQaW7\nsmUNUUixaxnYjepdyBF9i3jla2XeUxtCuxrqueot2Hv3PdgmTqT3ohcw9GhppKKiLrxbL+gTxRvw\n4seNSRM5SFF73FW0Duyi1dgFU9bbcoiMFZNe2cyriEGx00hNNXnpwtnYdosHFVXRC6fYJavWgdKk\nvPl94A/4cXlcMadTNu+nqH5X04RjQW1SHgm1xUhWBnYAx85R1gxfP53pkexPs/YqHY2ccsVszu1L\nf2TdztTuVB7czc6tU4e0+frq1atZvHgxa9aswefzMWLECEaOHBn22NLSUlauXMk111xDWVkZK1as\nwO12M2TIEGbNmrXf8VdffTV33303rixbYOQ0x86BpyfBl4/B+OvCH9OqXiwiuRbYxaHYYSnC4qvB\nqJMiK0tqnY9a94OSiukPxGaVHQs1DWpgF3l6spv17KjO4vz9IHtdjdhMOkz6+OyoU9Wk3F9ZibFf\n36SvA8qiPrvMU1wYknQJ1tpsuLOo3YHs9SLX14cUOUBpc7DtqxbHqTV47WWgEjLhcURfCEmShLag\nAFuDxIunvMijj1wI/Mgz217mUv9YjNowc4y7Gox20Cj7zdqiIsU8xV3RsoZInYfD9Mn60/H9Oeep\ncmzdlPom7+7dTHjRQ6dyKL7yTxTPmqW0kGiDtvqXJYoabFl0kRW7TnnK+1Y1tPy3VPu5RWpQnm/W\nYzTYkgrsINikPGqNXSPFeUa0mvTW+7s8LgYaBkY8JlIqZrL1dRBU7JrV2NV6a5GRY1fsjI7Q5oKq\n3MWl2JmL2Fi9MeIxav1p1gZ2PQ+HfsfBigdg1B/BGEPJS3vRLEOgoyEUuzhYvnw506dPx2KxYLfb\nmTZtWpvHqq8NHTqUsWPHYrPZKCkpwWQyUV3dclfurbfeolOnTm0GiYIEKR0DB50EK/7VdrNMNRUz\nFoz5gJRbrpg6M+hi2F21FCHJfv51Wj/+77j+bR/XRiomkDIDFdXpMmqNnUmfE66Ye12NcaVhquiK\ni1KTilldHbl/WBxoHY7sSsV0OtHak0vF1NhtWdXuQFUPNS0Uu87K/71mqnh7p2KGFLsY6zV1BQ78\nVVXkG/O5pOfZALy+bxkXvHcBu+vCOBa7W9a76AoL8VfsC6VihjDvX2OnckTfIkb3KoGAEXntT2w6\nfQb5lTKvn1VIyeWXRwzqIPWBnXqdvCgKUqHFjOw3UB3GFdOgMbTZ1NrZ4MNu0iWt2IGSjhmtxq7c\n5U67IybEVmOnBlitP7fL40qNYmfMx9noxB/wA02qWyyumKCkYqoGPokqdtFSMVXFLutcMZszYQ7U\n74Ovn8z0SFrSgQO7nFXsIilr6SRWZ0pj0H5bo9GEflYf+3wtF6MrVqzgzTff5J133sHtduN0Ojnv\nvPN4/vnnUzfwA5Xj/wKPHqXsGE26veVrqsNjrKmYGo0yCeSSYhdrYbBF+R1M7qODogiBbt1eJV2q\n2e+swKIEYFX1Xnql4O+Lml4ZrcbObtblhitmbSMlCaQuaYuL8X+9Kqn3DrjdivqTgho7UNQa786d\nKblWssiyjN/lSto8RWuzE6itRfb7kbSZb/Kr1vu1CFjzOitOkM1qQlQzm0A7qY2qaU4sqZgAWkdB\nqN2BHFR5bz7hLmZ/M4+Zb83k3mPuZXSX0U0nNLS0HtcWFeHdsSPmVExQ/j7/6dj+vPMPiaOXv4+m\nezcenAqFB3Xe79hwpLrGLlQjp4/i8GjWIwfM+wUp0dSnmgYv/Uqs6A02dtTuSGqsRVYDO6rbbqfk\n8QVYv9vFId3TuxD2B/xKjV2UwE6v1WPWmfevsfM46WJJrvcnKOqajEytt7ZFvV2sgV2BsaBJsWuM\nX7ErNBVS3ViNL+Brs+1D1qdiApSOhv6TlA320ReBMbmNuJTRrL1KR0ModnEwfvx4XnvtNRoaGnC5\nXCxdujQl173jjjvYvn07mzdvZvHixRx33HEiqEsVnYfA0DOUZpmt+9o1usDfGLtiB0oaUK4Edg3V\nMdXXAWAJLpzqo6T+1ZYrx2qaFsCqYpcqAxU1WMu3RFfsPL4Abq8/Je+bLva5GilORLErKsZfXY3s\nTTx4VRfWEd0I40CTn581il2grl4x87AlGdgFA6hAbYRa3HakSbFrtgCyBReqzersNPZ2Vuyq4wzs\nCgrwVVcFz61C0us5dtDJLJqyCLvBzsUfXMzCHxc21ea2sh7XFRXirdiHN+BtmYqpNyuZCGGyMPy1\ntfR56G/84X+1rOpro8cjf+enTtqYlRK9Ro9Vb025YpcfZfFoM+mQ/WZqvfsHdpECHLXGzpaKVEyr\nMaJ5yqKvtrKrxs05Y3sm9T7RqPUq/w9jUd3CmcY4GyP/zmKldZCvfo81OHOYHLg8LrwBb0i5i0ex\nU+/5SJsM+9z70Gv0UY1mMs6E2cpGzJePZ3okTYQUO+GKeUAzYsQIZs6cyfDhwzn99NMZN25cpock\niIVjZ0PAC5/e0/L5eHrYqZgdOeSKGYeVr7oLHjWw29siDROaK3apCexqGrxoJMgzRK+xA7Jetdvr\nSkyx0xUHWx5UJr6R4KtUFr+6VCl2wcCuPXuntYWqVGmTNU8JBoa2Ww6VAAAgAElEQVTZYqCi1sy1\nCKDUOuDqraGnNFYraLXtV2MXh3kKKIGdWpfnCxr4SJJEX0dfFk1ZxDE9juGeVfdw4/IbqffWB5sF\nN81X2qIiAlVVSLK8f6qZpXC/DTb3+l/YfPoMaj/5hPen9OKuKQ4+27AZl1ZDQRyKRjib+0SpcSv/\nNoVR5mG9VoNGtlDvC6PYtRHgBAIyzmCNnRrgJGNgVZinpGKGu4bL7eVfH//KEX2LmHBQHH8vEyBa\ni4fm2A32tNbYQVNwnohip56nKnaxngtQGEw5VuvowlHRUEGxuTj7exz3GAkHnQifPwjuLKlnFqmY\nApW5c+cyd+7c/Z5fsGBB6OfNmzeHfi4rK6OsrCzsa+GYMGECEyZMSG6QgpYU9oUR58PqBXDE/0Fh\n0GwhFNjFkcaQa4pdfnj3t/2IVbGr27Of2YxqlZ2qXnY1DV5sJj2aKAX69mDDX2eDj05ZumHp9vpx\nNfoSqrHTBnvZ+Sv2oe8co8FPK0KGFylzxXSEeqcl22YgWdSARpMqxS5LWh6EUjGb/367HaYEPV88\nAv2PB4IGJTYb/nZyxQzU1KCxWpH0sRkkaQsciuIcCOCvqm5xD+YZ8vjnsf/kqe+f4qE1D/FTxU/c\n563hoOaKXWER+ANYG7T7B3bmghaKXc0bb7Dr1tvQ2PLoteDf7G18HcOvn/HRd2uhCzissaVighIs\npCoVc0+98reiyBx98ajDgjvQyjzF42qz+XSdx0dAVjIXJIMNb8BLo7+xzXq8aBRZDfgCMs4G337Z\nEk8u30RFnYebThqU9iAimcDOH/BT661NWY0dNAV0oWbxcbQ7AKh2V1Ptrsamt6HXxG4uptaVRqqz\ny9oeduGYcBM8MUExszvmhkyPpkMHdkKxExwYjL8BNHr47x1NzyWk2OVQYNcqtSki8aRitgrs7CY9\nGimV5inemNw1c0Gx2xts6JuQeUqR8gc7GWdMf5Wy+NUWpE6xA7IiHTNsLVoChBS7LDFQUcfRonbQ\nlK8shjZ8BBs+Dj2tybcTaMdUzFjVOgj2rPP7CbhcYVtuaCQNlwy7hCdPeBKXx8U5Dh2vyjUhxUgb\n7GWXX8/+wU1wHg54POy67TZ23ngT5kMOoe+rr2IZPZoCYwFaXT0NbsXFt8DWPeZxp1Kx2xcM7Dpb\no2+sGDRWGgMt04EjpRU2dw9WA5lk0jGL8oK97OpapmPucbl5avlGpgzryqGl6U9bi6fBuN1ob1Fj\np37+VLU7gJapmBJSzGmeqmJX1VhFVWNVzG0SVNR7PlLLg30N+7LbOKU53Q6DgVNg5UPZkfXkrgEk\nxYm3gyECO8GBgb0rjL0EvnsJytcpz4UCuzjUEJMjd1wx4zFPMVhBa4wc2MlyMBWzZSCs0Ujkm/Up\nTcWM1uoAmsxVsrmX3baqeoDkUjGT6GWX6ho71eo+G1oehBS7ZM1TgoGhP0taHoRSTFt/rtEXgaMX\nfHgLBJ36tPb89kvFrK6J2RETmlRif1VVMLALf+7YrmNZcvILDHc3cmvNWuZ8Nod6bz26oGKdXxc+\nFdOzex9bzjmX6sUvUnjhH+m54N/oSpS5yWFy4Am46exQenMazV1jHrfD6Ghhc58MFfU1yH4jDkt0\nFc2kycMnt2zkHCkVs7l7sBpsJBXYWZU5qnUvuwc++hWPL8D1J0RuP5Aq4gnOWit2oaAwBYt1tZZO\nvWZNYw02gw2tJjaDJfX86kZFsVMDvViJlIrZ6G/kji/v4JeqX+iX3y+u62aUCTcpAdUXj2Z6JMo4\nmrVX6Uh0vE8kELTFUVcrjkyf/E15XBe0krfEseOlKnZZUGMUkYA/6KAX40JMkpSU1LoIQUSjS3Hm\ny9s/ranAYqCqLjUBVqz98PKDwZ/LnZ0tD2RZ5uFlG8g36xnRM/5USF2zVMxE8VVWgkYTl9ISiSbF\nLvObG6qytV8AFCeqYhdwZYl5itMFej2SqVUwoDPCxNug/Af4dhGgpGu2V0Dqr6mJqYedihoE+qur\n8VdXKwpeGxRLeh7fvYcrig/nnU3vMPOtmWzXKf++jnppP8OKmp8b2bS4Ds/WrXR/8F90vv56JF3T\nZpCaxuYoVvpcvv997P0u7cbUpWJWNVYj+81RHX4BzDobAakRX0CZzwJygFpvbXTFzqRvs6dbPKgp\n9c172W3cW8vir7dxztie9C62JnzteEgmFTMetS8a6vs3V+zicbVUjVKq3FXKuXEqdmrqZmvFblPN\nJs575zxe+PkFzht8HpcPvzyu62aUrsNg8FQlpTzTmU+tXHg7EiKwExw4WArhyCth/duw7WtFsTM5\nQGeI/RrmApADkKQDWdpR88djVexA+f1EUuzWBJ1auw7b7yWHJcWKXQwLoZBil6WpmB+uK2fFhgqu\nmTggqsNnODRWK5LZjG9v4oGdv6oarcMRtX9XrKiBXSAbUjHbUrbiJFRjlyWKnd9Zg9ZmC1/LNGQ6\ndB+lbE556to9FVMTxwaBqtj5KiqCQWGEuchdjRaYVXoCT056klpvLbNW3wRAF48FjaTcv4G6OnbO\nnsPOF77DmO+l76uvYJ80ab/LqQvwPbJyn766qpptlfUxjdthdLToX5YMzkYncsAc00ZVXrCJuRrY\n1HnrCMiBNg031HnPnirFLpiK2byX3T3vr8ek03Dl8QMSvm68qMFZrIFdnbcuFAynMrDTarTYDLam\nGrtGZ1zmJ80Vu6rGqriCQlBqaAtNhS0Cuzd/e5OZb81kd91uHjruIW4ccyMGbRzrl2zgmJuUTefP\nH8rsONw1EEPtay4iAjvBgcXhlyk92z6ZF+xhF6fDlxooZUOOeCTU3bB4dgktRW0HdnX74L93Qr/j\noc8x+71caDWkzDwl7hq7LGxS3ujzM/+dn+jfKY9zD++V8HWMAwZQ9eKLVC1alJDjnb+yEm1haoxT\nILtq7FSbf01eXlLX0eTlgSRlTY1dwOlq25hGkmDyfHDtgpUPt28qZrTgrBVqYOfZshUCAbSOCPdh\nMyODMV3H8PLUlxnQ6zACEnRuVFIE3evWsen0GdS8/jrFU0fR67h96IvC/9uraslGn6LCagIW7n5/\nfUzjbt6/LFlcHiey3xJTarnN2FJ1ixakqIpdqlIxmxQ7pcbum61VvPvDbi4e35fiBFLJE8XpcaKR\nNFj10RVCNeWy1lMbOhdiCwpjoXm9ZU1jTVwpngatAaveqih2CaRiQrBJeUMFdd46Zi+fzdzP5jKk\naAhLpi7hmNL9/w7nBF0OgUNOV2rtmrn8tjvumg7Z6gBEYCc40DDmwfjrYNOn8NuyBAK74OSc6TSC\naKh1gHEpdhECu4/ngbcOTrxTWVy2wmExpMw8Ramxix7YGXUaDFpNVip2z36+mS0V9dw8ZTB6beLT\nbOnDD2EZNYrdt89j+2WXx22k4q+qQhdpQR0nmmwK7FxONHl5STcVlzQaNHl5WVNj53e5IitjPQ+H\nwdPgs/vRmpR2B8nY3MeCHAgogV08il3wvvNs2qg8juTM2mq+KjYX8+gJj+O3Wxll6E/ls8+yeeZZ\nBOrr6blgASXnnIikoc15WF1E/0YjNjRcMn4gS7/dyeot0eftVDYpr/O5lFTMWFLL1XTKoBlItJRE\nZ8P+il0yqZhGnRabUUdFsOXBne/8THGekYvH9U34mong8rjI0+eFVNpItE5BVX93qVDsQDFQUQO7\neFMxQQkMd9ftxu13x52KCUqd3YbqDcx8aybvbHqHy4dfzlMnPEXnOFxes5KJtwMSfHBz5sYQj7lc\njiECO8GBx6g/Qn6pspiIp9UBNAV22W6goiqKqVDsdq6FbxbCmEuh5KCwpxakKBXT7fXT6AvEpNhJ\nkoTdrMs685R9tY08+PEGjh1YwoSBibUpUNGVlFD6xON0njOHus8/Z+Opp1H76acxn++rqkKboh52\nABqDAcliyQrzlECNM+k0TBWtzUYgaxQ7Z/RWEhNvA38j2r1fg8+HXB9bmmHCY6qtVVS3/NjnE43V\ngqTX07hxExAlsAvNV00LLa1GS16nbtg+Wk35HXdiPfpo+rzxOtaxY5r6bjaEdwxUFTunBA6NkUvH\n96WTzcjf3l4XNQhOZWDX4HdBwBK1JydAgVm5l/fUKe8bLUhxNniRJLAZdSlR7EBJx6yo8/DJz3v4\nanMlV00cgNXYvl2xXB5XzIrbfoFdCs1TQGksH1LsPDUxtzpQKTAWsKlmU+jneCkyFbGrbhdun5un\nT3iayw69LGbzlqzGUQrj/gzr3oCN/83MGERgJwjHbbfdxr333gvALbfcwkcffZTwtXr37s3QoUMZ\nPnw4o0aNStUQBeHQGRV3JohfsVMDpQ6p2BUr5/mbpTbKMrx7oxL0Reg947AYcHsDNHiSq0tpXjcS\nCzaTHmeWmafc98EvNHj93HzKwSm5nqTRUHj+7+n98svoCgrYdsml7P7bfAJud9Rzw9nMJ4vapDzT\n+F2upB0xVTR2e1Y1KNdEa+FQ1A9GX4xm76rQOWkdk9qcPI5UTEmS0BYU4NmoKnaRauzUVMyWx+i7\nd0cCOs+dS49HHm4yYAk6BlIffh62GWxoJWUBXKCzYDXquG7yQNZsreat73ZFHLeqyiTb8kCWZRoD\ndegla9SenABFwbm6vE75TNGCFKfbh82oQ6ORMGqNGLXGpAO7QquBvS43d733M32KrZw1ujSp6yVC\nJCfQ1qi/GzUIdnqc6DV6TNrEevm1Jt+QT3VjNb6AD5fHFb9iZ3KwxbUl9HO8TO03lbMHnc2SqUsY\n1aWDrQuP/BMU9FbWF/4MbM6KwE4QjXnz5jFx4sSkrrFs2TLWrl3LqlWrUjQqQZsMO0sxIhhwQnzn\n5UoqZkKKXZhd8B9egW1fwPG3RAwSCyxqk/LkVDu1Xk5tPh4Nuym7FLt1O528+PVWzj+iN/1Kkqv9\nao1p4EH0XvIyBef/nqrnn2fzGWfgXt923ZAcCCi9x1JYYwfZE9gFnKlW7LInFVMbS9P1Y25Aa1Fq\nn9JdH6gqtPG6q2oLCkItNyK5YoY2olottLr+dR793n+Pwt+f19JMJopip5E0odTGAr0SJJ8+ogcH\nd7Vz57s/4/a2vQHVujF1orj9bgJ4MWlimweKLcr8WlGv/C6ipWK2Tllv7RCZCEV5Rr7cVMkv5bVc\nP3lgUmnkieLyuGIP7MKkYtoN9pQ1Uc835lPjqWlqwRCnElhgLAgZuySi2B3e9XDmjJ2TUFCY9ehN\nMPkO2PszfPVk+76336cY4HXQwK59NfZU8u5NsPv71F6zy1A46c6Ih8yfP5+FCxdSWlpKSUkJI0eO\nBKCsrIxTTjmFGTNm0Lt3b8455xyWLVuG1+vliSeeYPbs2WzYsIHrr7+eWbNmpXbcgvjR6uCMBfGf\nlyvmKYnW2IGSjpnXCTx18MFfoOuhcNh5EU8ttCoLjKp6D90c5kRGDLQ0BIgFu1mfNTV2siwz760f\nyTfruSpNLnIao5Euc+aQN248O+fMZvOMMyi+8k8UXXBBC7t3CKosgUDkBXUCZEtg53c60fdMjaKg\nsdvx7tiRkmslS8DpRJsfwwLSUoh21Bnwv6UEfv4vDAyfJp0K/NXKfBJPuwNomX4ZucauRumjqW+p\ntKh96fZD3WCrb7t5c4HeSmUzN0KtRuLmKYM556kv+feKzVw2IXz/r+ZuhsmgqkgWXWxphWoT84r6\noAtjFPOU1iZTNoMt+VRMqwFZhkNLHZx0SJekrpUoLo+L3vbeMR3burbQ6XGmLA0TlHvB5XFR5VY2\nJ+JxxYSWKl2HDM6SZeBJiiHbf++AoTOUdUd7oDa176D/JkKxi4PVq1ezePFi1qxZw6uvvsrXX3/d\n5rGlpaWsXLmScePGUVZWxpIlS/jiiy+45ZZbwh4vSRInnHACI0eO5IknnkjXRxAki94MOlNuKHZa\nozLeWGke2AF89k9w7YST7oYoef2OoGJXnaQzZnNDgFiwm/RZo9i9/+NuvthYybWTDkqovUE85I07\nmr5vvEHehAnsve8fbD77HBp//bXFMU3NyVNXYwdKOl5W9LGLVdmKAW1eXlYodgG3G9njCfXWi4Zm\n9FkA+Jc/FWpang4SScWEpvRLyWRCY44wF7lr4tuEiiElvkCrvF9hs+bmR/YvZuLgzjy8bAP7gu6P\nrbEZbEhISSt2apPzvBgDuyKrFTmgpcrd5MIYyR3S6W7ZFiYVgV2JTVGAZ580KGWqV7w4G50J19jF\no/bFghrIbXNtA4g7FbO5SpeIYtfhkSQ46S7wNsDHt7ff+7aRIdBRyF3FLoqylg6WL1/O9OnTsVgs\nAEybNq3NY9XXhg4dSm1tLTabDZvNhslkorq6GkerP5ArVqygW7du7Nmzh0mTJjFo0CDGjx+fvg8j\nSBy1SXk2466Ob6EELQO7qs2w4l8w9AzFhS8KKUvFdMer2OmyosZObW9wUOc8zh7Ts13eU1dYSPd/\nPYDrvffYPe+vbPrd6RRfcQVFF12IpNM1C+zSoNhlhXlKTcpSMbOlxk6tldNGq7ELoi1SFC3/nq3w\n3Ysw/Jz0jCsYyMebiqmqxVHvwXibBWt1yvFtpGICFKBsRjmsLVWA2ScPYvI/P+WfH/7C/OlD9ztP\nI2lS0qRcVexsMRpu5JsNyAEzNc2ClEjukDUNXvoWN6V52gy2kLKUKOeM7clBnW0c3rco+sFpwuWN\nPTgz6UwYNIYWip3anD4VqOPY4lTq5OI1T1FVOgkppQFnh6J4gNKG6vN/wcg/Qo+R6X/PZu1VOiJC\nsYuTWHexjEZl50uj0YR+Vh/7fPsvRLt16wZAp06dmD59Ol999VUKRitIC+aC7HfFTKRHi+oQWl+h\n2BBrtEFb4ugUBBWqqrrkAjs1FTOWBuXqcdmg2D3z2Wa2VTbwl1MORteOdSmSJGE/6ST6vrWUvOOP\nZ+/997N55lm41/+Cr1JZ9OrSVGOXbov9SMg+H4H6+ugmIzGitdkI1NYiBwIpuV6iBILBpSaaK2YQ\nNbD1W3oqLUnc6Qm4Q6mYcQbSasuDiMYpkNh8ZS5sOxXTU0/BHqX+tKCwZVp0v5I8zju8F4u+2sov\n5eGD+eb9yxJFDTYcMaYG2s16ZL8ZV/O0wgjBgLPB16I/XioUu675ZqYe2i2paySD1++lwdcQVx86\nu9HeZJ7SGLvxSiyoCt1W19YWj2NFVenyjfkdw80yXRxzA+R1hneug/aYg0VgJ1AZP348r732Gg0N\nDbhcLpYuXZqS69bV1eEK/kGvq6vjgw8+4JBDDknJtQVpwOTI/hq7eHfAoclp7sfX4KelMO5ayO8e\n06mOkGKXqlTMGM1TzHoafYGIZgjpZo/LzUOf/MrEwZ0YNyBOl9UUoSsqosf9/6T7/ffj3bWLTTNm\nUPnss0AaFDtHPni9abfYj4SqrmntqfnDrLHbQJYVW/8M0qTYxfa51ObsgdKJUFsO789Nz7hqapSe\ngfr4UozVey9qL0V3AvOVpbBtxW7ZfBxBE5ICy/7/J686fgB5Rh3zloZvf5BvzE8+FTN4foE5ts9l\nM+nAb6Yu2Bjd5XFFrBeraVVjZzfYkw7sMo3LG9kwJhzNTWPicdSMBTUVU1Xs4q3fUwPBeAPCAw6j\nDSbNg53fwNr/pP/9RGDXNpIknSFJ0o+SJAUkSWrTi1WSpBMlSVovSdIGSZJuSuY9M8mIESOYOXMm\nw4cP5/TTT2fcuHEpuW55eTlHH300hx56KGPGjGHKlCmceOKJKbm2IA101FRMnQGMdqV5u6MXHPGn\nmE816DTkGXVJp2LWNHgx6TUYdbHtbqruma4MpmPe+/56PP4Ac6ekpr1BMthPnEzft9/CPmkSDatW\nA+lJxYTMNikPxJmyGA21Vi/d7pLRiPdzSVotGpsNv2yFo66CNc/Br4m33WlzXHE2J1fRxpqKmYj1\nuLkgvGK37StY+TAF3UcD4RfVBVYD1584iM827GPRV9v2e121uU+G6uDisTjGeViv1aDBTL1PuQed\nnrZrzTy+AA1ef4vMBjWwy6SSnixN6avxB3YBORA1GI4X9d7Z5tqGRtLENS5o6qeofhdEYNhMKB0L\nH92W/o3zMH0zOxLJ1tj9APwOeLytAyRJ0gIPA5OA7cDXkiS9KcvyuiTfOyPMnTuXuXP33xVdsGBB\n6OfNmzeHfi4rK6OsrCzsayp9+/bl22+/TeEoBWnFXAC7svzfq6EaigfGf56lUHGMmjx/P4e6aDgs\n+hSYp/hirq+DJpMVp9sbKvxvT5b/upeXVm3nkvF96VMc3uSgvdEVFND9H/dhn3Iynm3b0JhS09NJ\nRdMssNN3y0zalhqAxWoyEg01pTPgcgKxqdTpIJHPpbXb8TtrYMJfYf27sPRKuHxlShctvurqxAK7\nYC15VNOVeM1TQMkw2NfSMAivG964AvJ70Gf0LPTLb6SHrUfY088d05P3f9jN395ex9H9i+lZZAm9\n5jA6+K36t/jG04o99VXIsoYiS+y/Nx1WGgPbASWw62QJ7xIYrt+nzWDDJ/to8DVg0VvCnpftqIpj\nPO6TdqOdvfV7qfXWIiOnRbHbWbuTfGN+m/WObSEUuziQJMWo7YkJ8L+74MQ70vdeqmIX75yTIySl\n2Mmy/JMsy203UlIYA2yQZXmjLMseYDFwajLvKxBkFLOjYyp2ACWDYcBkGHRK3KcWWAwpUeziCuyC\nO9aZqLOrrvdw3cvf0r9THtdOSp/VfKLYjj+eomabSqkiGxQ7v1Ptq5aqPnbZodj5XfErkZp8O4Ea\nJ+iMcNoj4NoN789J6bgC1TVxO2JCU21dRMVOlhNLHbcU7j8P/+9O2PcLTL2fI3tN5L8z/0uxuTjs\n6RqNxN0zhqGVJK57+VsCgSalS+1flgyVDTXIflMoTT0WjBorHllJcY7k8OgM0xZGVZNyOR0zWu++\ncNgMNpweZ0jtS2Vgl6fPQ0JCRo671QE0BYZCsYuRbsNhZBl8+TiUp1H7cdeApAFDanvNZgvtUWPX\nHWie67CdTG6JCgTJYnaAtw58yQUxaSMQALczsR4tZ72gfCVgde2w6JOvsWtl4R0NtRavvVMxZVlm\n7ms/UFHr4f6ZwzHpD5zCeG2+cl9l0hkzXpORaGhbKHaZI6AqdnGYlGjt+aHaPLqPDKZkPg+/fJCy\ncflrauLuYQegKy4Jfg8fXAFKv0zZn5h5SqMT/ME5Z8c3ipPvYedB/4mKsVCURX43h5lbpw3hq82V\nPLNiU+j5fGM+dd46vP7E57PKhmrwW2KuFwYwafPwyfXIshzRCKQmTC1y655uuYjTG0zF1MeXiuny\nuBJuIh4JrUYbul4igZ1Oo2Nc93GM6txmpZKgNcf9RVljvXqJosCnAzX1O0MtPdJN1MBOkqSPJEn6\nIcxXrKpbuN9c2CRwSZIukSRplSRJq/bu3Rvj5QWCdkZtjputzpiNNYCcmGKn0ShW4glQYDGkxBUz\nIcWunZuUv7ZmB29/v4trJh3EId07Zp5+W6gL/Mwqdqqylbp2B8p1M6zYOZ1KzzdD7CqPkorZbDE/\n4SZFeV96ZcpqVfzV1aEU3HjQd+5Ej8ceJX9qhAyARHtKWYJmTw1VyibbG1coDY5PmB/XZU4f0Z2J\ngztz9/vr2bBH+fdXU+eSUe1qGp3IAXNcG1UWnQ2kAJXuSjwBT5tBitripaMpdonW2Lk8rtC/Varb\nCqgtDuJtdaDyyMRHmNpvaiqH1LGxFsFpj0L59/DRrel5j0RqenOIqIGdLMsTZVk+JMzXGzG+x3ag\ntNnjHsDONt7rCVmWR8myPKqkJDPucgJBVNTALlvTMUOFwe2bP15g0ackFTPW5uTQrMauof0Uu+1V\n9dz6xo+M7l3ArGP6tdv7ZgvZkIoZSHFgp7VliWLncobGEisau61lc3U1JbN2T0pSMuVAAL/TmVAq\nJoBtwgQ01gj1p4k61KnzcH0lLL8X9qyDU+6Pe0NLkiTu+N1QrAYt1770LV5/oCmwS8IZ0+WtQfab\n49qoUpWqHbU7WjxuTbi2MGpAk8uBXSKqm91gR0ZmV+2u0ONUIurkMsBBk2HsLPjyMVj/Xuqvn4gL\nbw7RHqmYXwMDJEnqI0mSATgLeLMd3lcgSA9qwJStgZ26A97OhcEFVgMutw+fP/E+NM4sV+z8AZlr\nX/oWGfjHmcPRajpmKkckNCYTktEYalqdCfxOF+h0SGZzSq6ntg3IvGLnQhNn3WCLVEyV7iPg6KsV\n6/Bf3k9qTIHaWggEEjJPiYlEjQzUwG7zclh+n+KqNzAxN+kSm5H504fy3fYaHv3vb6HAIhlnzDqv\nC9lvjmujSlWq1MCuTcUuQo1dLqdiujwudBodJm3shk/q72ibS6n4SXVgl0wqpiAJJt4OnYfCG5eD\nc1dqr51I38wcItl2B9MlSdoOHAG8LUnS+8Hnu0mS9A6ALMs+4P+A94GfgJdkWf4xuWFnB7fddhv3\n3nsvALfccgsffZS4zXR1dTUzZsxg0KBBDB48mJUrV6ZqmIJUE1LssjQVM0OKXbd8ZZH97g+7Ezo/\nEJBxNfpCLQxiwaTXoNdK7Wae8uTyjXy1qZJbpx5MaWFuOs+lArVJeabwO2vQ2u1IKaqRkLRaNHl5\nBGoz3O7A5QwZucSK1m5Hbmwk0NjY8oVjboROB8PSq5LahAo1J89P03ySqPW4mor5wV+UersT70xq\nGCcP7cq0Q7vxr49/paJGmYOSUezq/bXIfktcqZiOYPAQLUhpqrHrWIqd2ocunv/X6ufeXqu4iaay\nxg6aArpUX1cQBb0JZjwD3gZ47RIIpLBX7YGeihkJWZZfk2W5hyzLRlmWO8uyPDn4/E5Zlk9udtw7\nsiwfJMtyP1mW40uAzxHmzZvHxIkTEz7/qquu4sQTT+Tnn3/m22+/ZfDgwSkcnSClZHsqZoYUu9MO\n687IXgXcsOQ7ft4d/66xq9GHLBPXDrckSdhN+nZR7NbtdHLfB+s5cUgXZowMb6F+oKDNzyeQ0VRM\nV9wpi9HQ2G2ZV+xqnKHWC7GiOoPuF2g3T8l8L/GUTPW6iQYznPUAACAASURBVJinxEQoFTMB8xQA\nXwNMua8p0EuCeacOodBq4J8fKEFCooFdQA7gCdSikS2Y9LEvswrMyr/llhrl/duqNXO6vRh0mham\nTXlBh79cDuwiOYG2hXr8DtcOtJIWiy61G24iFTODlBwEJ92l9NZd8UDqrisCO0Fz5s+fz8CBA5k4\ncSLr1zd1eigrK2PJkiUA9O7dmzlz5nDEEUcwatQovvnmGyZPnky/fv147LHH9rum0+nk008/5cIL\nLwTAYDDgSLCeQdAOmLM8FTNDip1Bp+HRc0dgN+u4ZOFqquOst3OG2YWOBZtJl/YaO7fXz9UvrsFh\nMfD33w1NmVKUq2jz8zPqiul3ueJyjowFrc0eajeQKfwuV9yKnfp7CLROxwTodhgcfQ18+4LS4y6R\nMVWrrSXSNJ8kap5iLQaNDoZMh4OnpWQoDouBu04fxsZy5XGFuyKh66g91Ywaa1xzhdrMfKszqD5F\naHfQWgnUa/SYdeacT8WMtwm4qqRtr90et9oXC8mapwiS5LDfw8GnwSd/g+2rUnPNDh7YJdugPGPc\n9dVd/Fz5c0qvOahwEDeOubHN11evXs3ixYtZs2YNPp+PESNGMHLkyLDHlpaWsnLlSq655hrKyspY\nsWIFbrebIUOGMGvWrBbHbty4kZKSEi644AK+/fZbRo4cyQMPPIA1UsG5IHMY8wEpe10xM6TYAXSy\nm3j0vJGc9fgX/GnRGhZcMCbmOrSaMHUjsWA3p1+xu+f99fxSXsuCC0ZTaI3dsbCjonHk4926LfqB\naUJNxUwlWpst1G4gUwSczrg/l9YeNLMJF9gBHHODUmf36qVw4QfQaVBc1w+lYqZdsYvz+gYrXPQx\nlAxM6XCOHdSJs0b2Y2mVgwe/eYitzq1cPOxiSm2l0U8Ooro7WrTxBSklViUbZGddtBo7H/lh2ijY\nDLacV+ziDuyCwW+lu5Je9l4pH5OaiikUuwwhSTD1AaWdyZI/wqzlyQVlPg9460WNnUBh+fLlTJ8+\nHYvFgt1uZ9q0tncJ1deGDh3K2LFjsdlslJSUYDKZqK5uGRD4fD6++eYbLrvsMtasWYPVauXOO5Or\nFxCkEY0mu5uUu2tAowd9ZmrARvQsYN6pQ1j+6z7ufj/2zRdnGKe3WLCb9Gmtsfvs1308/dkmzj+i\nFxMGdkrb++QSimKXuY2NgNMVd8piNDR2O35X5hbFsiwHlcg4UzGDx7cZ2OmMcPYLSs3Kf84AV3lc\n1/fuUNSjRF0xo9JQDUY7aBLoBdltOOhTY6DTnJtPGUJhzZ/BeSRvbXybaa9N49bPb2W7a3tM56uq\nmTWOfmwAJdZ8ZFliX4Pyb9RWkNOWe7Bq/Z+rOD3OhAM7iK//XayoAZ0wT8kgZgec/hTUbIe3rgU5\nbMe02Eh0IymHyFnFLpKylk5ilfmNRiMAGo0m9LP62OdrmTbWo0cPevTowdixYwGYMWOGCOyyHVMW\nB3YN1RlvvnnWmJ58v6OGx/+3kUO65TP10G5Rz1FVt/gVOx27nelpZPrTLieX/2c1/TvlMfskUfeq\nonU4Mt7HTlWqUoXWZqOxWXp9exOoqwe/P7WpmCqOnnD2YlgwBRbNhLK3FcWrDWRZpn7lSvY98ST1\nX3yBoVevlCukIbIwLSrPqGPhHyZx+qNWzI2TmHj4Ot767VXe3PAm0/pP4+KhF9PD1nadrVqbZ4sz\nfc9hMUDASEDrxqwzo9eEnwudbm/YzIFcV+xU85R4MOvM6CQdPtmXFoOT8T3Gc9WIqxhUGJ/SLUgx\nPcfChNmw7G/Q/3gYfk5i10nUhTeHEIpdHIwfP57XXnuNhoYGXC4XS5cuTcl1u3TpQmlpaahm7+OP\nP+bggw9OybUFacJckL2umO7qrJi0bp06hFFBM5V1O6PXfYRSMS3Zodhtqajj909/hcWgY8EFozEb\nElAUOihahwO5sZF9Tz7ZtlKUJmRZDqYsdizFTu2hF795itpXMMq/Q/cRisvcrm/hlYvDuszJgQDO\nDz9k8xlnsvWPF+L57Tc63XADvV95BUmXpn3gLLUe71Ns5Zmy0VTWmFm9ZjxLpi5l5qCZvPXbW0x9\nbSq3fn4rG2s2hj1XVezy4ww07CY9sl/JtIgU4NSEqbFTz8nVGjtZlhNKxZQkKRTQpbrVASimNBcN\nvQhtIoqyILWMuxZ6HQ1vX5d4vd0BoNiJwC4ORowYwcyZMxk+fDinn34648aNS9m1H3zwQc4991yG\nDRvG2rVrmTMn+caygjRiLshyxS7zCyWDTsMj5wXNVJ5bRVVdZDOVpqa78S0g01FjV+50c97TX+IL\nBHjuwjH0KDhwWxuEw3HaaVgOP5y99/2DDROOpfyOO/Bs39Eu7y03NiJ7vWjiVLaiobXZCLhcyIHE\n+zAmg+rIGa8SqbqD+p0xKKgDT4IT74L1b8P7c0NPy14v1a+9zsap09jxpyvxO510uf12+n38EUV/\nvABtXhrrvbO4WfDwUgcPn3sYP+1yccsr2/jzyBt453fvcObAM3nrt7c49fVTueLjK/hy15fIzdLD\nVMWuMM552G7WIweUHm6RApy2+n3msmLn9rvxBrxxB3bQFNClI7ATZBEarZKSmVcCz/0Odq6J/xqJ\nmjXlEDmbipkp5s6dy9y5c/d7fsGCBaGfN2/eHPq5rKyMsrKysK81Z/jw4axalSLHH0H6MTugalOm\nRxEedzVYijI9CgA62Uw8dt5IZobMVEaj04bfT3I2+NBIShpUPNhNOtzeAI0+P0Zd8ruq1fUezn/6\nKypqPbxw8eEM6Jz6uo1cR1dSQq8F/8a9bh0V/15A5X9eoPK557GfOJnCCy7APHRo2t5bVaZSnRqo\nsdtAlgnU1aW8lUIsqIpdvEqkpNejsVgip2I2Z+wlULUZvngYn7aE6s12qhYvwrdzF8aBA+l2373Y\nJ09On0LXGncNFPRun/dKgOMGdeaO6UO54ZXvuPGV77jvjEOZPXY2lwy7hJd+eYnFPy/mog8u4qCC\ngzj/4PM5qc9JIfOUQkt8i0ebSYfsV2oG2wpSZFnG6fZhb8s8xZubgZ0akCYSnIUCO9FrruNj7wp/\nWAr/ngILT4Oyt6BLHH9vhGInEAjCUjwQKjfC/+5JrpA3HWSJYqdyWM8C/nbaIXy2YR/z3lpHIBD+\n96UaAsRrV62aCLjcybc8qPf4+OOCr9m0r44nzx/F8NLs+T1mI6aDD6b7PXfT/6MPKbygjNpPl7P5\njDPZfN55OD/4ANmb+hTZRAOgaKjBXMwBUopRU1oTUSI1dnv0VMwgsizT0HkGO9Ydwoarn2TvP/6B\noUcpPR57lD6vv0b+lCntF9RBU01wFnPm6FKunXQQr36zg3veV0omisxFXHboZXww4wPmHTmPgBzg\n5hU3M/mVyby76T3kgI5Cc15c76PXatDKwVTMNoKUOo8ff0AOm4qpKnYBOTOqczIkE9jZjLaEzxXk\nII6eULZUqRNeeCqUr4v93AMgsBOKnUCQCOOuVQK7ZX+D+n0w+Q7FLTMbyJIau+acObqUX8pdPPXZ\nJmoavNw9Y9h+6prTHT69KBrqAsfZ4KU4zxjl6Lbx+AJc+txq1m6r5pFzR3BU/+KEr3Wgoe/Shc7X\nX0/xZZdRvWQJlQsXsuPKq9AWFeGYfhr5p5+OsU+flLxXKABKsXmKRk1pdLmI/y5MHvVzJRKwamOo\nDww0NOB8+22qXliEe906NFYrjmFWCnrswnj1ldAjfOuetJOF5inh+NNx/dlV4+aR//5GZ7uJPxzZ\nGwCj1sj0AdM5rf9prNy1koXrFrJixwpkX0FC85lesuIjcg87CG8yZTfYCcgB6r31oYbluYIa2CWU\niqkXqZgHHAW9g8rdybBwGpS9ozQ0j8YBkIqZJStRgSDH0OrhtEfh8Cvgy8fg1YuV/iiZJhDIWjOC\nuVMGc8OJA3lj7U7Knvk6VFOn0pYhQDTUlCRnEoqdPyBzzUtrWf7rPu743VBOPKRrwtc6kNHm5VFU\nVkb/Dz6gx2OPYh4+nIp/L2DjSSez5ffnU/PmmwTcyTmYJhMARUJN7WxvMxiVQKjGLv7FqdZuJxDG\npVSWZRq+/4Hdf/87v044ll03/wXZ66HLrbfQ/3//o8tT72LsUaw4Ze5JbV/YmPD7wOPKyvmqNZIk\n8ddThzBxcGduW/oj7/2wa7/Xj+x2JI9NfIx/Hf0CDdv/EDZdMhpGjVLP2FaQEqpFbqPGDsjJOjvV\n9CWhwC6obiZyriCHKeqnBHdI8OxUqPgt+jkZbgfVHojATiBIFI0GJs+HibfBD0tg0VngqcvsmDwu\nkANZp9iBsvC5fEJ//jnzUFZtqeTMx1ays7oh9HpbhgDRUINBV4IGKrIs85c3fuDt73Yx+6RBzBzd\nM6HrCJqQdDpsEyZQ+vBD9F/2CSXXXou3vJydN9zIr+PGs3veX2lYu7aF4USsBILKlCbFdXDq9QIZ\ncsb0q66YefErLZr8/BYBqWfbNvY+8ggbT57C5jPOoHrRYqxHHEHPhc/S5803KTj7bMUQJa8TnLtE\nOemp4+HH11LyWWImWIuWK7vnOq2GB88+jOGlDq5cvJZXVofva2fTdifQ2CWhjSqzVvn3T1SxA3LS\nGVMds6ixE8RFyUHwhzch4FOCu8oo3gdqhkAG20GlGxHYCQTJIElw9DUw7UHYuAyenQb1lZkbj3On\n8j2Ld8CnH9aDBReMYWd1A7975HN+2qX8QVdq7OLf4VZ3rp0N8St2FbWNXPLcal74ciuzjunHpcf0\ni/sagsjoO3Wi+JKL6ffeu/RcsIC88eOpfvllNp91NhuOO57yO+6kfs2amN0oQ+Yp+SnuYxdS7DIT\n2AWcTjRWa0L1bVq7HV9lJZUvvMDms87mt0knsO9fD6IrKqLLvNsZ8Nlyetz/T6xjxuxfw1pyEFz6\nKXQ6GF4uU9wy/cnXq8aEmhaVhRtRbWE2aHnmD6M5rNTBn1/+lute/pZ6T8vfV6I9OaGpqXmk5uRA\nmzV2kJuKXVKpmMIV88Cm02A4/w3w1ivBXfXWto/NkdTvZBCBnUCQCkacD2c+B7u/h2dOhJr2sX4P\nIcvw/RIl31xrVHpWZTFH9S/mpVlHAHDmYytZsWEfTrcvuRq7OBW7Zev3MPn+5fxv/V5unjKYG08c\nGPd7C2JH0miwHj6W7vfdy4AVn9H1zjswDRxI1QsvsOXsc4JB3h1Rg7yQeUqKFbuQeYorU+YprlCz\n8XjR5ufj37eP8nl/JVBXS8m119L/44/o9fxzFJx5ZvQg2N5NaVo+5hJY+ZBiSOAqT2gscdGQm/Uu\nBVYD/7loLFce159XvtnOtIdWsH53UzClbjKFS5eMRl4wsGtLfVJTzttqdwAHXmDXydIJCYlis6iL\nPmDpcgj8/nUlC+CJY5X1ULiMkAMgsBPmKQJBqhh8Cpz3Ciw6G54+Ac5eBF2Hpf99a/fC29fAT0uh\n+0il9q8k+4OUwV3tvHbFkZQ98zVl//5KcXpLJLBTa+xibFLe4PFzx7s/sXDlFgZ2tvHchWMY3FXs\n9LYnWrsdx2mn4TjtNPwuF7WffILzvfepemERlc8uRNe5M9ajjsJ65JFYjzwCXWFh6Fx/jRPJYkHS\np9biRE2BzJRi53c5E27h4DjzDDR2G7bjjsM4cGDczrIA6Axw8j3QfRQsvQoeHw9nPgs9D09oTDGR\nww51Oq2Ga08YyJg+RVz94lpOffgzbp82hDNHlSbckxOCAZ0PbPooil0b7Q4gR1MxG52YtCYMWkPc\n557Q+wT65Pehk6VTGkYmyBm6DYc/vg+vXw6vXAjfvwxT/gH53ZuOOQACO6HYJcFtt93GvffeC8At\nt9zCRx99lNB11q9fz/Dhw0Nfdrud+++/P5VDFbQXfcbBBW+D36MsjF69VOkZlS5+eBUeGQu/vK/U\n+v3xg5wI6lS65pt5adYRjOpVSEAOn14UDbNei04jxaTY/bCjhqkPfcbClVu48Og+vPF/R4mgLsNo\nbTbyTz2V0kcfYcDnK+h2912YDz0U10cfsfO66/j1yKPY+Lvfsefee6lbuRJfRUVa+sxJOh0aqzVj\nil3A6Ur4cxn79qXk8ssxDRqUWFDXnENnwkUfgd4MC6bAl4+nr6VLKLDLnVTM1hw9oJh3rjqaET0L\nuPGV77nmxbXsqlEMghLZqOppPQhf7QAOKT4k7OvV9YpJly3MXKmmIuakYud1JZxKqdPoGFw0OMUj\nEuQknQYr89fkv8OmT+HhsfDVk4qxHOREe5VkEYpdipg3b17C5w4cOJC1a9cC4Pf76d69O9OnT0/V\n0ATtTddD4YovYcX9yqLoh1dg1AUw/nrFrCAV1O2Dt6+FdW9At8MUla5Tbv5hyzfrWfDH0Tz7+WZO\nHhq/G6UkSdhMuog1dv6AzBOfbuQfH66n0Grg+QvHcvQAkbaTbWhtNvKnTSN/2jRkvx/3jz9St2IF\ndSs+p2LBs1Q89TQAxgH90/L+Grs9c4qd04m+W7eMvPd+dDkELvkvvDYL3r0BtqxQaom7Dk+N6YAs\nw7YvYfUC5XGOL7Q62Uw8d+FYHvpkAw98/AsBGSwGLXpt/HvnnaxFNGy7ELO2oMXz32yt4qnlG3nv\nh910zTeh1ez/72DVK46aORnYeVzC1VKQGjRaOOIKGDQFll4N71ynpGZOe1DZTMqhmt5EyNnAbvff\n/07jT6m1ZzYOHkSXOXMiHjN//nwWLlxIaWkpJSUljByp9P4pKyvjlFNOYcaMGfTu3ZtzzjmHZcuW\n4fV6eeKJJ5g9ezYbNmzg+uuvZ9asWW1e/+OPP6Zfv3706tUrpZ9N0M5YCmHSPBg7C/53F3z9NKz5\nDxx+GRx1ZeILGVc5/PIufPxXJZf8+FvgyKtAm7P/lQEw6rRcMj5x4xK7WR9WsdteVc9H68p5bc0O\nvt1ew8lDu/D36UNxWOJP9xG0L5JWi3nYMMzDhlF82WX4a+uo//or6lauxDT44LS8p9ZmC7lTphtf\nZSWNv/xK46/Kl2fLFkwDs0htNzvgrBdgxT/hf3crm0hdhsJh58OwM8BcEP0arWmsVdKjvn4ayr8H\nox2OvFKp8ctxtBqJqyYOYEyfQq5avCYhtQ5a9uU067V8uK6cJ5dvZPWWKuwmHZeM78cFR/UOe65O\no8Oqt2Z9Kmajv5GN1Rv5peqX0Ne3e79lUOGgTA9N0JEo6A2/fw2+XQTvzYbHjlLcM3N8Iykaub0a\nbGdWr17N4sWLWbNmDT6fjxEjRoQCu9aUlpaycuVKrrnmGsrKylixYgVut5shQ4ZEDOwWL17M2Wef\nna6PIGhv7N1g6gPK4mXZfFh+L6x6Wnnc+2hw9FJUvLZ2wb0NsHUl/PYJ/LYMyn9Qnu92GJz6CHRO\nzwI317Cb9DgbvMiyzI87nXy4rpwP15WzLui42a/Eyn1nHMrvRnRPPlVNkBG0eVZsxx6L7dhj0/Ye\nGrst1E8uWWS/H19FBb7ycry7d+PbXY5n21YlkPvlV/wVFaFjtfn5mIcMIf+0U1Py3ilDo4Fxf4ZR\nFyotXb5ZCO9eDx/cDAdPg8N+D73HKcdFYu8vyry39gVlQ6rzIXDK/TDsTDBY2+eztBNH9Cvi4z8f\nQ4PHn9D5akD47xWb+GBdOVsq6ulRYObWqQdz5qhSrMbIyzaH0cHinxfz2Y7P6GHrQU9bT3rae1Jq\nK6XUVkqPvB7otamtTw2Hy+NiV90udtftZnfdbnbV7WKbaxu/Vv3KFucW/LLy+zFqjfR39Gdy78lM\n6zct7eMSHGBIEgw/B/pPhHdvhB9fBXv36OflMDkb2EVT1tLB8uXLmT59OhaL0thw2rS2JyH1taFD\nh1JbW4vNZsNms2Eymaiursbh2F8K9ng8vPnmm9xxxx3p+QCCzFHUD2Y8A0ddBR/Pg49vb3pNZ4aC\nXkqQp36X/bDxv7Dlc/C5QWtQTAwm3gb9joPOQ6Mvpg4g7GYda7ZVc/Rdy9hR3YAkwcieBcw+aRCT\nDu5M35L4e4MJDjy0Njvun3+m8rnnkfQ6pfWAToek1YUeyx4Pgfp6AvUNwe/1BBoaCNTXEXDV4tuz\nB295Ob69e8HXMj1Yslgw9u9P3oRjMA4YEPrSlZRk94aD2QGjL1K+dn0Ha56D715U1LeC3tBjNAT8\nyrwVUL98yuOGatj5jTKHHXyaco3SMR26j5TNpA9bAxcLqmL35PJNDC91cMPkQUwe0hldjGmdfz3q\nr6zYsYKtrq1sc23jm/JvqPfVh16XkLAb7TiMDvKN+RQYC0LfHSYHefo8tBotWkmLRtI0fQ8+5/V7\nqfXWUu+tp9ZbS523jnpfPbUe5efy+nJ21+2m1lvbYlw6SUcXaxcGFAxgUq9JDCgYwEEFB9HT1hOt\nRpvQ70ogiJm8TnDGv2HCTcoaqwOTs4Fdpoj1j6/RaARAo9GEflYf+3zha4HeffddRowYQefOnZMf\nqCA76Xqo4pxZ8ZvyVbUZqrco36u2KOqc2rS3ZLCyU97vWOh1ZIfb2U4l/UvyWL2lilG9Crnq+AEc\nN7gTxXnG6CcKBM0wDhhA7bJllM+fH/tJWi0aqxWN2YzGakXXqRPWMWPQdemCvktndJ2D37t0QVtQ\nkN0BXCx0HQZd71FSzX96C9Y+D9tXKXUtGh1IWmXTSf1ZZ1JSxg87H/JKMj36rGd0nwKuOn4A4wYU\nM7JX/PfL6C6jGd1ldOixLMtUuivZ5trGNtc2tru2U+mupLqxmurGasrry1lftZ6axhoafA1xj9eq\nt2LVWbHoLeTp8yi1lTKmyxi6WrvSJa+L8t3ShWJzsQjgBJknh8zlEkUEdnEwfvx4ysrKuOmmm/D5\nfCxdupRLL700ZddftGiRSMM8UCjqp3y1RpahoUrZ7U6V0coBwG3ThnDzKQcnZFYgEKiUXHM1RRdf\nhOzzgc+HrH55fcg+L/h8SAYDGosFjcUSaruQ88FaIujNSq3dsDMyPZIOhVGn5ZpJB6XsepIkUWQu\noshcxPBOwyMe6/a5qfXW4g/4CcgB/HLL776AD71WT54+D6veillnRiOJOVcgyCZEYBcHI0aMYObM\nmQwfPpxevXoxbty4lF27vr6eDz/8kMcffzxl1xTkIJKkGK8I4kKSJPTaA3BxLUgpkiSlpZWCQJAL\nmHQmTDpTpochEAiSQJLT1Z8mSUaNGiWvWrWqxXM//fQTgwfnpqV7qhC/A4FAIBAIBAKB4MBAkqTV\nsiyPiuVYoaELBAKBQCAQCAQCQY4jAjuBQCAQCAQCgUAgyHFyLrDL1tTR9uBA/uwCgUAgEAgEAoGg\nbXIqsDOZTFRUVByQAY4sy1RUVGAyicJmgUAgEAgEAoFA0JKccsXs0aMH27dvZ+/evZkeSkYwmUz0\n6NEj08MQCAQCgUAgEAgEWUZOBXZ6vZ4+ffpkehgCgUAgEAgEAoFAkFXkVCqmQCAQCAQCgUAgEAj2\nRwR2AoFAIBAIBAKBQJDjiMBOIBAIBAKBQCAQCHIcKVsdJiVJ2gtsyfQ4wlAM7Mv0IAQdHnGfCdoD\ncZ8J2gNxnwnSjbjHBO1Bpu6zXrIsl8RyYNYGdtmKJEmrZFkelelxCDo24j4TtAfiPhO0B+I+E6Qb\ncY8J2oNcuM9EKqZAIBAIBAKBQCAQ5DgisBMIBAKBQCAQCASCHEcEdvHzRKYHIDggEPeZoD0Q95mg\nPRD3mSDdiHtM0B5k/X0mauwEAoFAIBAIBAKBIMcRip1AIBAIBAKBQCAQ5DgisBMIBAKBQCAQCASC\nHEcEdnEgSdKJkiStlyRpgyRJN2V6PIKOgSRJpZIkLZMk6SdJkn6UJOmq4POFkiR9KEnSr8HvBZke\nqyC3kSRJK0nSGkmS3go+7iNJ0pfBe+xFSZIMmR6jILeRJMkhSdISSZJ+Ds5pR4i5TJBqJEm6Jvj3\n8gdJkhZJkmQS85kgWSRJekaSpD2SJP3Q7Lmw85ek8K9gTPCdJEkjMjfyJkRgFyOSJGmBh4GTgIOB\nsyVJOjizoxJ0EHzAn2VZHgwcDlwRvLduAj6WZXkA8HHwsUCQDFcBPzV7fBfwz+A9VgVcmJFRCToS\nDwDvybI8CDgU5X4Tc5kgZUiS1B24Ehgly/IhgBY4CzGfCZJnAXBiq+famr9OAgYEvy4BHm2nMUZE\nBHaxMwbYIMvyRlmWPcBi4NQMj0nQAZBleZcsy98Ef3ahLIS6o9xfzwYPexY4LTMjFHQEJEnqAUwB\nngo+loDjgCXBQ8Q9JkgKSZLswHjgaQBZlj2yLFcj5jJB6tEBZkmSdIAF2IWYzwRJIsvyp0Blq6fb\nmr9OBRbKCl8ADkmSurbPSNtGBHax0x3Y1uzx9uBzAkHKkCSpN3AY8CXQWZblXaAEf0CnzI1M0AG4\nH7gBCAQfFwHVsiz7go/FnCZIlr7AXuDfwZTfpyRJsiLmMkEKkWV5B3AvsBUloKsBViPmM0F6aGv+\nysq4QAR2sSOFeU70ihCkDEmS8oBXgKtlWXZmejyCjoMkSacAe2RZXt386TCHijlNkAw6YATwqCzL\nhwF1iLRLQYoJ1jidCvQBugFWlLS41oj5TJBOsvJvqAjsYmc7UNrscQ9gZ4bGIuhgSJKkRwnq/iPL\n8qvBp8tVWT/4fU+mxifIeY4CpkmStBkljfw4FAXPEUxlAjGnCZJnO7BdluUvg4+XoAR6Yi4TpJKJ\nwCZZlvfKsuwFXgWORMxngvTQ1vyVlXGBCOxi52tgQNB1yYBSqPtmhsck6AAEa52eBn6SZfkfzV56\nE/hD8Oc/AG+099gEHQNZlmfLstxDluXeKHPXJ7IsnwssA2YEDxP3mCApZFneDWyTJGlg8KnjgXWI\nuUyQWrYCh0uSZAn+/VTvMzGfCdJBW/PXm8D5QXfMw4EaNWUzk0iynHHVMGeQJOlklF1uLfCMLMvz\nMzwkQQdAkqSjgeXA9zTVP81BqbN7CeiJ8ofsDFmWWxf1CgRxIUnSBOA6WZZPkSSpL4qCVwisAc6T\nZbkxk+MT5DaSJA1HMegxABuBC1A2kcVcJkgZkiTdt1QMfwAAAIZJREFUDsxEcZVeA1yEUt8k5jNB\nwkiStAiYABQD5cCtwOuEmb+CmwoPobho1gMXyLK8KhPjbo4I7AQCgUAgEAgEAoEgxxGpmAKBQCAQ\nCAQCgUCQ4/x/+3VAAgAAACDo/+t2BPpCsQMAAJgTOwAAgDmxAwAAmBM7AACAObEDAACYEzsAAIC5\nAPc8DrLZGf1LAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.figure(figsize=(15, 5))\n",
"pe = PositionalEncoding(20,0.2)\n",
"y = pe(torch.zeros(1,100,20))\n",
"plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())\n",
"plt.legend([\"dim %d\"%p for p in [4,5,6,7]])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"---\n",
"\n",
"### Step 10: Words to learnable embeddings\n",
"\n",
"Similarly to other sequence transduction models, we use learned embeddings to convert the input tokens and output tokens to vectors of dimension `dim_model` or `dim_embedding`."
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"class Embedding(nn.Module):\n",
" def __init__(self, vocab_size, dim_embedding):\n",
" super(Embedding, self).__init__()\n",
" self.embed = nn.Embedding(vocab_size, dim_embedding)\n",
" self.scale = math.sqrt(dim_embedding)\n",
" \n",
" def forward(self, x):\n",
" # embedding is multiplied by scale to make the positional encoding relatively smaller\n",
" # See: https://towardsdatascience.com/how-to-code-the-transformer-in-pytorch-24db27c8f9ec\n",
" return self.embed(x) * self.scale"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"That's it. We have implemented all the components that constitute the transformer model. Now let's put them all together and create a model.\n",
"\n",
"---\n",
"\n",
"## Part 2: Full transformer model"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": [
"def make_model(src_vocab, tgt_vocab, num_enc_dec=6, dim_model=512, dim_feedfwd=2048, attn_heads=8, dropout=0.1):\n",
" # prepare the embeddings for encoder and decoder stacks\n",
" position_embeddings = PositionalEncoding(dim_model, dropout)\n",
" src_embed = nn.Sequential(Embedding(src_vocab, dim_model), copy.deepcopy(position_embeddings))\n",
" tgt_embed = nn.Sequential(Embedding(tgt_vocab, dim_model), copy.deepcopy(position_embeddings))\n",
" \n",
" # prepare reusable layers. we will copy.deepcopy them whenever needed\n",
" attn_layer = MultiHeadedAttention(attn_heads, dim_model)\n",
" feed_fwd_layer = PositionWiseFeedForward(dim_model, dim_feedfwd, dropout)\n",
" c = copy.deepcopy\n",
" \n",
" # prepare the encoder stack\n",
" encoder_layer = EncoderLayer(dim_model, c(attn_layer), c(feed_fwd_layer), dropout)\n",
" encoder = Encoder(encoder_layer, num_enc_dec)\n",
" \n",
" # prepare the decoder stack\n",
" decoder_layer = DecoderLayer(dim_model, c(attn_layer), c(attn_layer), c(feed_fwd_layer), dropout)\n",
" decoder = Decoder(decoder_layer, num_enc_dec)\n",
" \n",
" # prepare the generator\n",
" generator = Generator(dim_model, tgt_vocab)\n",
" \n",
" # creat the model\n",
" model = EncoderDecoder(encoder, decoder, src_embed, tgt_embed, generator)\n",
" \n",
" # Initialize parameters using Xavier initialization\n",
" for p in model.parameters():\n",
" if p.dim() > 1:\n",
" nn.init.xavier_uniform_(p)\n",
" \n",
" return model"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Let's create a small model which source and target vocabulary sizes of 10 and only two encoders/decoders in an encoder/decoder stack. Even for this small a model, the number of parameters is a staggering ~14 million."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"14730250"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"small_transformer = make_model(src_vocab=10, tgt_vocab=10, num_enc_dec=2)\n",
"sum( [param.numel() for param in small_transformer.parameters()] )"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Also note how a multi-headed attention in a model looks like. It's little more than a bunch of linear transformations and concatenation."
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"scrolled": false
},
"outputs": [
{
"data": {
"text/plain": [
"MultiHeadedAttention(\n",
" (dropout): Dropout(p=0.1)\n",
" (linears): ModuleList(\n",
" (0): Linear(in_features=512, out_features=512, bias=True)\n",
" (1): Linear(in_features=512, out_features=512, bias=True)\n",
" (2): Linear(in_features=512, out_features=512, bias=True)\n",
" (3): Linear(in_features=512, out_features=512, bias=True)\n",
" )\n",
")"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"small_transformer.encoder.layers[0].self_attn"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}