This website is a semi-functional mirror of the original Project Euler. More information is available on GitHub.

Triominoes
Problem 161
Published on 21 September 2007 at 06:00 pm [Server Time]
A triomino is a shape consisting of three squares joined via the edges. There are two basic forms:
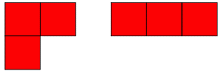
If all possible orientations are taken into account there are six:
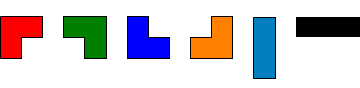
Any n by m grid for which nxm is divisible by 3 can be tiled with triominoes.
If we consider tilings that can be obtained by reflection or rotation from another tiling as different there are 41 ways a 2 by 9 grid can be tiled with triominoes:
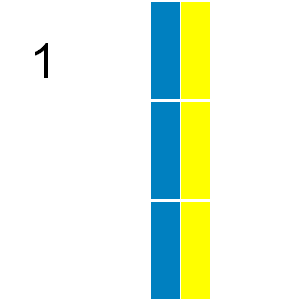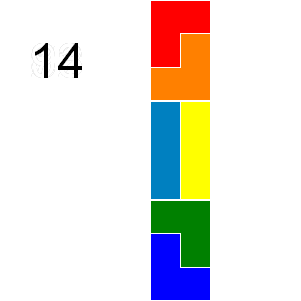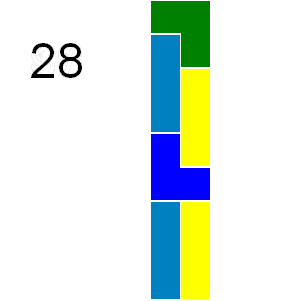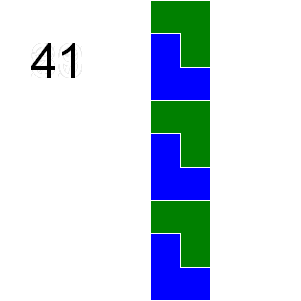
In how many ways can a 9 by 12 grid be tiled in this way by triominoes?
Go to back to Problems