This website is a semi-functional mirror of the original Project Euler. More information is available on GitHub.

Binary Circles
Problem 265
Published on 21 November 2009 at 09:00 am [Server Time]
2N binary digits can be placed in a circle so that all the N-digit clockwise subsequences are distinct.
For N=3, two such circular arrangements are possible, ignoring rotations:
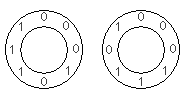
For the first arrangement, the 3-digit subsequences, in clockwise order, are:
000, 001, 010, 101, 011, 111, 110 and 100.
Each circular arrangement can be encoded as a number by concatenating the binary digits starting with the subsequence of all zeros as the most significant bits and proceeding clockwise. The two arrangements for N=3 are thus represented as 23 and 29:
00010111 2 = 23
00011101 2 = 29
Calling S(N) the sum of the unique numeric representations, we can see that S(3) = 23 + 29 = 52.
Find S(5).
Go to back to Problems