This website is a semi-functional mirror of the original Project Euler. More information is available on GitHub.

Eulerian Cycles
Problem 289
Published on 23 April 2010 at 01:00 pm [Server Time]
Let C(x,y) be a circle passing through the points (x, y), (x, y+1), (x+1, y) and (x+1, y+1).
For positive integers m and n, let E(m,n) be a configuration which consists of the m·n circles:
{ C(x,y): 0 ≤ x < m, 0 ≤ y < n, x and y are integers }
An Eulerian cycle on E(m,n) is a closed path that passes through each arc exactly once.
Many such paths are possible on E(m,n), but we are only interested in those which are not self-crossing:
A non-crossing path just touches itself at lattice points, but it never crosses itself.
The image below shows E(3,3) and an example of an Eulerian non-crossing path.
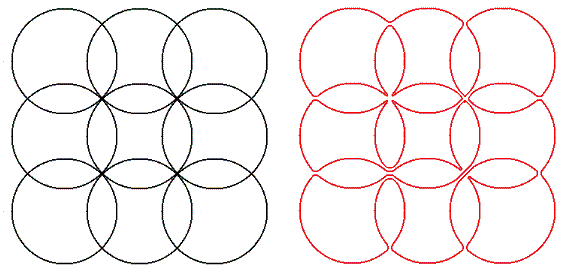
Let L(m,n) be the number of Eulerian non-crossing paths on E(m,n).
For example, L(1,2) = 2, L(2,2) = 37 and L(3,3) = 104290.
Find L(6,10) mod 1010.
Go to back to Problems