We call the convex area enclosed by two circles a lenticular hole if:

• The centres of both circles are on lattice points.
• The two circles intersect at two distinct lattice points.
• The interior of the convex area enclosed by both circles does not contain any lattice points.

Consider the circles:
C₀: x²+y²=25
C₁: (x+4)²+(y-4)²=1
C₂: (x-12)²+(y-4)²=65

The circles C₀, C₁ and C₂ are drawn in the picture below.

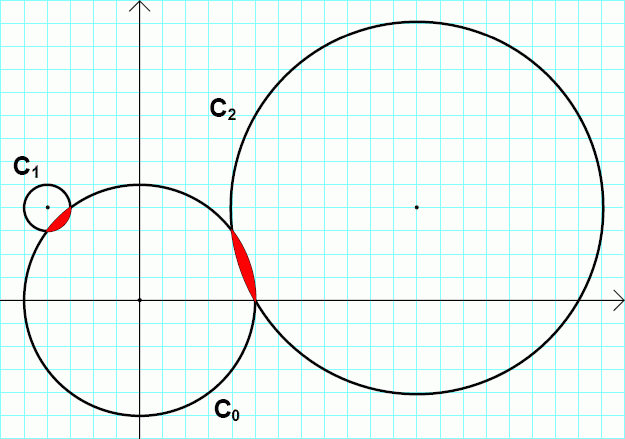
C₀ and C₁ form a lenticular hole, as well as C₀ and C₂.

We call an ordered pair of positive real numbers (r₁, r₂) a lenticular pair if there exist two circles with radii r₁ and r₂ that form a lenticular hole. We can verify that (1, 5) and (5, √65) are the lenticular pairs of the example above.

Let L(N) be the number of distinct lenticular pairs (r₁, r₂) for which 0 < r₁ ≤ r₂ ≤ N.
We can verify that L(10) = 30 and L(100) = 3442.

Find L(100 000).