This website is a semi-functional mirror of the original Project Euler. More information is available on GitHub.

Biclinic Integral Quadrilaterals
Problem 311
Published on 20 November 2010 at 10:00 pm [Server Time]
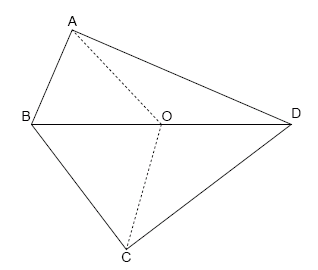
ABCD is a convex, integer sided quadrilateral with 1 ≤ AB < BC < CD < AD.
BD has integer length. O is the midpoint of BD. AO has integer length.
We'll call ABCD a biclinic integral quadrilateral if AO = CO ≤ BO = DO.
For example, the following quadrilateral is a biclinic integral quadrilateral:
AB = 19, BC = 29, CD = 37, AD = 43, BD = 48 and AO = CO = 23.
Let B(N) be the number of distinct biclinic integral quadrilaterals ABCD that satisfy AB2+BC2+CD2+AD2 ≤ N.
We can verify that B(10 000) = 49 and B(1 000 000) = 38239.
Find B(10 000 000 000).
Go to back to Problems