- A Sierpiński graph of order-1 (S₁) is an equilateral triangle.
- S_n+1 is obtained from S_n by positioning three copies of S_n so that every pair of copies has one common corner.

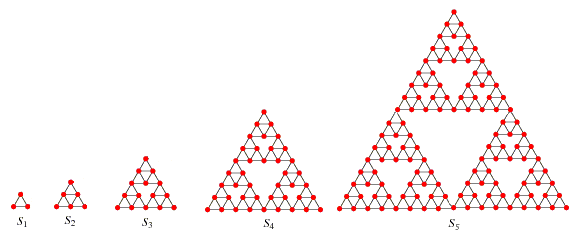
Let C(n) be the number of cycles that pass exactly once through all the vertices of S_n.
For example, C(3) = 8 because eight such cycles can be drawn on S₃, as shown below:

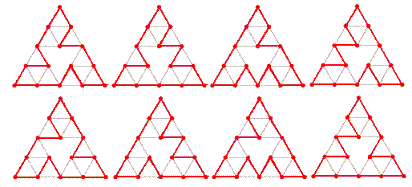
It can also be verified that :
C(1) = C(2) = 1
C(5) = 71328803586048
C(10 000) mod 10⁸ = 37652224
C(10 000) mod 13⁸ = 617720485

Find C(C(C(10 000))) mod 13⁸.