
Bézier Curves
Problem 363
A cubic Bézier curve is defined by four points: P0, P1, P2 and P3.
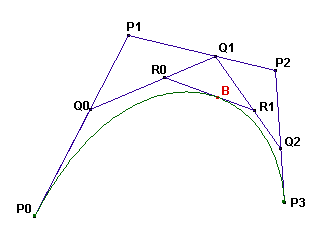
The curve is constructed as follows:
On the segments P0P1, P1P2 and P2P3 the points Q0,Q1 and Q2 are drawn such that
P0Q0 / P0P1 = P1Q1 / P1P2 = P2Q2 / P2P3 = t (t in [0,1]).
On the segments Q0Q1 and Q1Q2 the points R0 and R1 are drawn such that
Q0R0 / Q0Q1 = Q1R1 / Q1Q2 = t for the same value of t.
On the segment R0R1 the point B is drawn such that R0B / R0R1 = t for the same value of t.
The Bézier curve defined by the points P0, P1, P2, P3 is the locus of B as Q0 takes all possible positions on the segment P0P1.
(Please note that for all points the value of t is the same.)
At this (external) web address you will find an applet that allows you to drag the points P0, P1, P2 and P3 to see what the Bézier curve (green curve) defined by those points looks like. You can also drag the point Q0 along the segment P0P1.
From the construction it is clear that the Bézier curve will be tangent to the segments P0P1 in P0 and P2P3 in P3.
A cubic Bézier curve with P0=(1,0), P1=(1,v), P2=(v,1) and P3=(0,1) is used to approximate a quarter circle.
The value v > 0 is chosen such that the area enclosed by the lines OP0, OP3 and the curve is equal to π/4 (the area of the quarter circle).
| That is, if L is the length of the curve, calculate 100 × | L − π/2 π/2 |