This website is a semi-functional mirror of the original Project Euler. More information is available on GitHub.

Crisscross Ellipses
Problem 404
Published on 02 December 2012 at 01:00 am [Server Time]
Ea is an ellipse with an equation of the form x2 + 4y2 = 4a2.
Ea' is the rotated image of Ea by θ degrees counterclockwise around the origin O(0, 0) for 0° < θ < 90°.
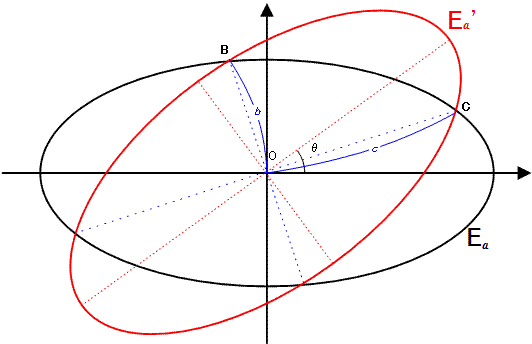
b is the distance to the origin of the two intersection points closest to the origin and c is the distance of the two other intersection points.
We call an ordered triplet (a, b, c) a canonical ellipsoidal triplet if a, b and c are positive integers.
For example, (209, 247, 286) is a canonical ellipsoidal triplet.
Let C(N) be the number of distinct canonical ellipsoidal triplets (a, b, c) for a ≤ N.
It can be verified that C(103) = 7, C(104) = 106 and C(106) = 11845.
Find C(1017).
Go to back to Problems