Let a, b and c be positive numbers.
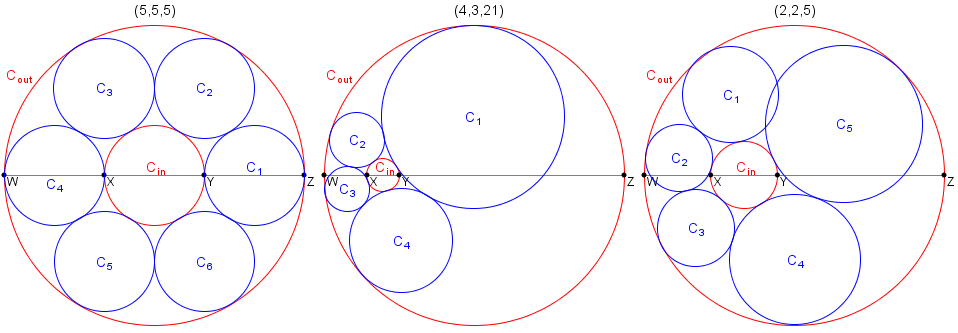
Let W, X, Y, Z be four collinear points where |WX| = a, |XY| = b, |YZ| = c and |WZ| = a + b + c.
Let C_in be the circle having the diameter XY.
Let C_out be the circle having the diameter WZ.

The triplet (a, b, c) is called a necklace triplet if you can place k ≥ 3 distinct circles C₁, C₂, ..., C_k such that:

• C_i has no common interior points with any C_j for 1 ≤ i, j ≤ k and i ≠ j,
• C_i is tangent to both C_in and C_out for 1 ≤ i ≤ k,
• C_i is tangent to C_i+1 for 1 ≤ i < k, and
• C_k is tangent to C₁.

For example, (5, 5, 5) and (4, 3, 21) are necklace triplets, while it can be shown that (2, 2, 5) is not.

Let T(n) be the number of necklace triplets (a, b, c) such that a, b and c are positive integers, and b ≤ n. For example, T(1) = 9, T(20) = 732 and T(3000) = 438106.

Find T(1 000 000 000).