This website is a semi-functional mirror of the original Project Euler. More information is available on GitHub.

GCD and Tiling
Problem 440
Published on 13 October 2013 at 07:00 am [Server Time]
We want to tile a board of length n and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:

For example, here are some of the ways to tile a board of length n = 8:
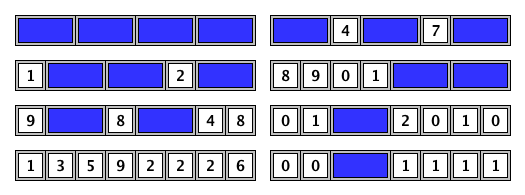
Let T(n) be the number of ways to tile a board of length n as described above.
For example, T(1) = 10 and T(2) = 101.
Let S(L) be the triple sum ∑a,b,c gcd(T(ca), T(cb)) for 1 ≤ a, b, c ≤ L.
For example:
S(2) = 10444
S(3) = 1292115238446807016106539989
S(4) mod 987 898 789 = 670616280.
Find S(2000) mod 987 898 789.
Go to back to Problems