The triangle ΔABC is inscribed in an ellipse with equation $\frac {x^2} {a^2} + \frac {y^2} {b^2} = 1$, 0 < 2b < a, a and b integers.

Let r(a,b) be the radius of the incircle of ΔABC when the incircle has center (2b, 0) and A has coordinates $\left( \frac a 2, \frac {\sqrt 3} 2 b\right)$.

For example, r(3,1) = ½, r(6,2) = 1, r(12,3) = 2.

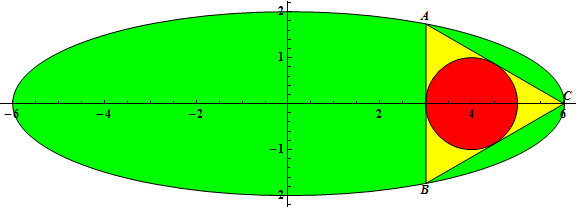
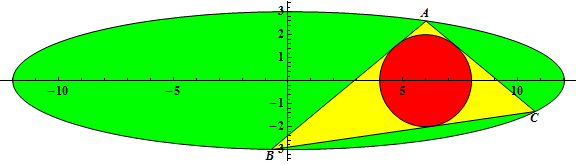
Let $G(n) = \sum_{a=3}^n \sum_{b=1}^{\lfloor \frac {a - 1} 2 \rfloor} r(a, b)$

You are given G(10) = 20.59722222, G(100) = 19223.60980 (rounded to 10 significant digits).

Find G(10¹¹).

Give your answer in scientific notation rounded to 10 significant digits. Use a lowercase e to separate mantissa and exponent.

For G(10) the answer would have been 2.059722222e1.