Circles A and B are tangent to each other and to line L at three distinct points.
Circle C is inside the space between A, B and L, and tangent to all three.
Let r_A, r_B and r_C be the radii of A, B and C respectively.

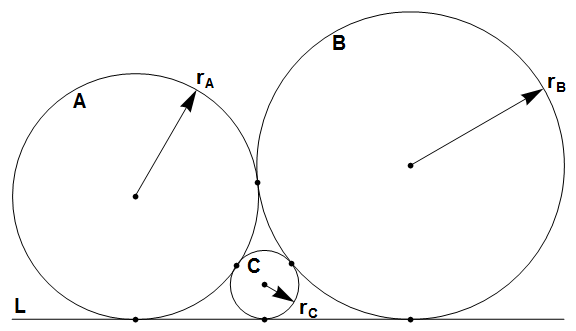
Let S(n) = Σ r_A + r_B + r_C, for 0 < r_A ≤ r_B ≤ n where r_A, r_B and r_C are integers. The only solution for 0 < r_A ≤ r_B ≤ 5 is r_A = 4, r_B = 4 and r_C = 1, so S(5) = 4 + 4 + 1 = 9. You are also given S(100) = 3072.

Find S(10⁹).