An arrangement of coins in one or more rows with the bottom row being a block without gaps and every coin in a higher row touching exactly two coins in the row below is called a fountain of coins. Let f(n) be the number of possible fountains with n coins. For 4 coins there are three possible arrangements:

Therefore f(4) = 3 while f(10) = 78.

Let T(n) be the number of all possible colorings with three colors for all f(n) different fountains with n coins, given the condition that no two touching coins have the same color. Below you see the possible colorings for one of the three valid fountains for 4 coins:

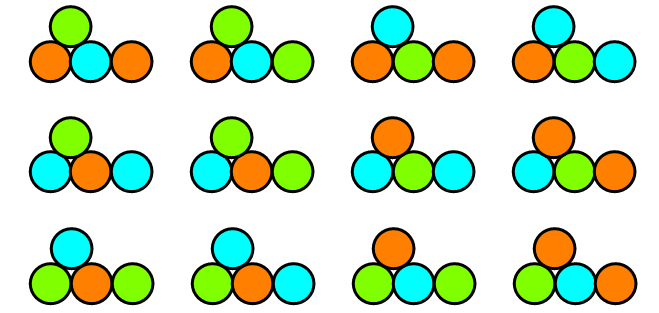
You are given that T(4) = 48 and T(10) = 17760.

Find the last 9 digits of T(20000).