---
template: overrides/main.html
title: Modelos NARX Gerais
---
# Modelos NARX Gerais
Exemplo criado por Wilson Rocha Lacerda Junior
> **Procurando mais detalhes sobre modelos NARMAX?**
> Para informações completas sobre modelos, métodos e uma ampla variedade de exemplos e benchmarks implementados no SysIdentPy, confira nosso livro:
> [*Nonlinear System Identification and Forecasting: Theory and Practice With SysIdentPy*](https://sysidentpy.org/book/0%20-%20Preface/)
>
> Este livro oferece orientação aprofundada para apoiar seu trabalho com o SysIdentPy.
Neste exemplo, criaremos modelos NARX usando diferentes estimadores como GradientBoostingRegressor, Bayesian Regression, Automatic Relevance Determination (ARD) Regression e Catboost.
```python
pip install sysidentpy
```
```python
import matplotlib.pyplot as plt
from sysidentpy.metrics import mean_squared_error
from sysidentpy.utils.generate_data import get_siso_data
from sysidentpy.general_estimators import NARX
from sklearn.linear_model import BayesianRidge, ARDRegression
from sklearn.ensemble import GradientBoostingRegressor
from catboost import CatBoostRegressor
from sysidentpy.basis_function import Polynomial, Fourier
from sysidentpy.utils.plotting import plot_residues_correlation, plot_results
from sysidentpy.residues.residues_correlation import (
compute_residues_autocorrelation,
compute_cross_correlation,
)
```
```python
# dataset simulado
x_train, x_valid, y_train, y_valid = get_siso_data(
n=10000, colored_noise=False, sigma=0.01, train_percentage=80
)
```
## Importância da arquitetura NARX
Para ter uma ideia da importância da arquitetura NARX, vamos observar o desempenho dos modelos sem a configuração NARX.
```python
catboost = CatBoostRegressor(iterations=300, learning_rate=0.1, depth=6)
```
```python
gb = GradientBoostingRegressor(
loss="quantile",
alpha=0.90,
n_estimators=250,
max_depth=10,
learning_rate=0.1,
min_samples_leaf=9,
min_samples_split=9,
)
```
```python
def plot_results_tmp(y_valid, yhat):
_, ax = plt.subplots(figsize=(14, 8))
ax.plot(y_valid[:200], label="Data", marker="o")
ax.plot(yhat[:200], label="Prediction", marker="*")
ax.set_xlabel("$n$", fontsize=18)
ax.set_ylabel("$y[n]$", fontsize=18)
ax.grid()
ax.legend(fontsize=18)
plt.show()
```
```python
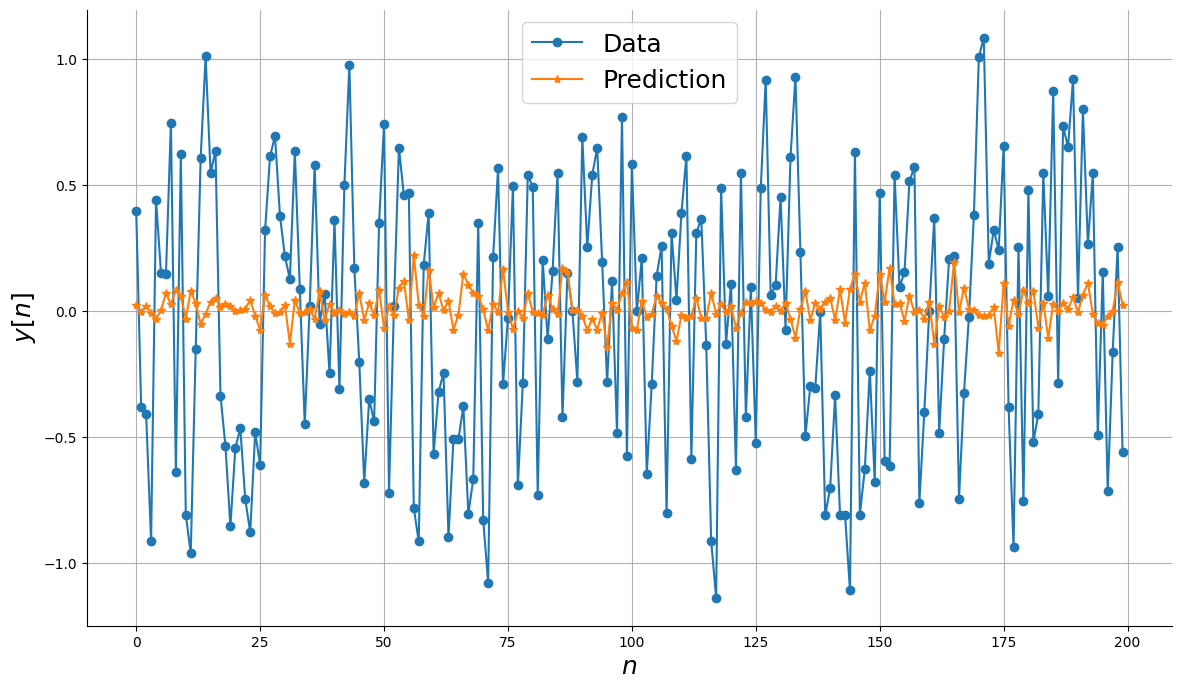
catboost.fit(x_train, y_train, verbose=False)
plot_results_tmp(y_valid, catboost.predict(x_valid))
```
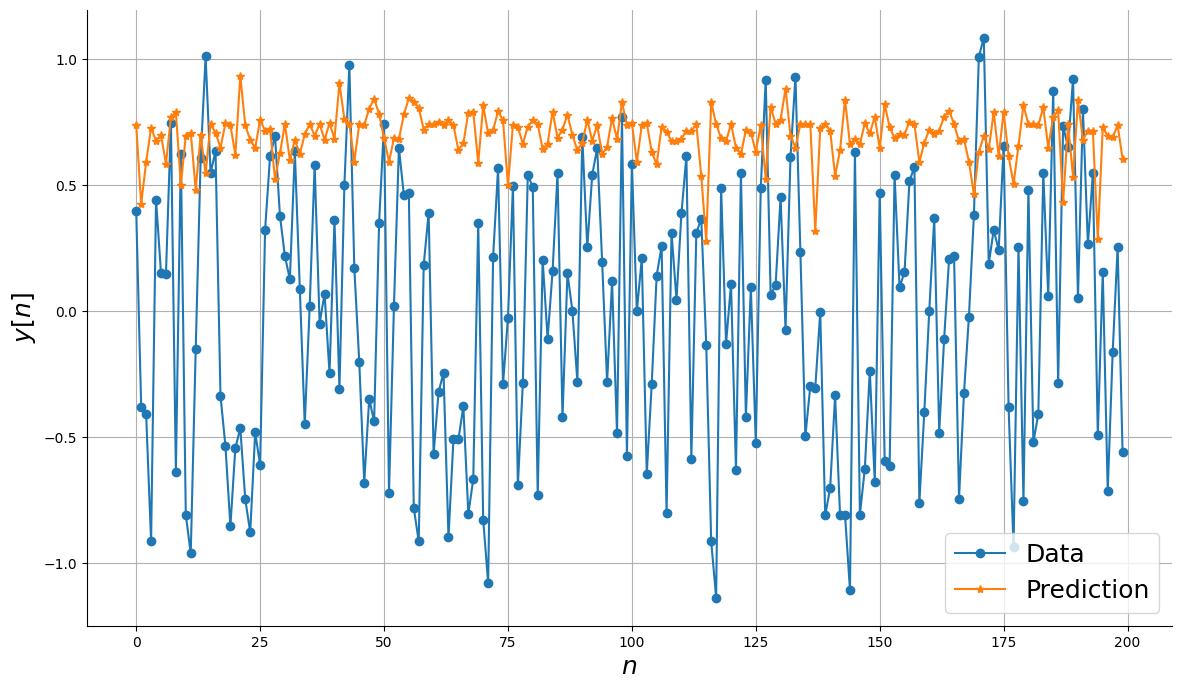
```python
gb.fit(x_train, y_train.ravel())
plot_results_tmp(y_valid, gb.predict(x_valid))
```
## Introduzindo a configuração NARX usando SysIdentPy
Como você pode ver, basta passar o estimador base desejado para a classe NARX do SysIdentPy para construir o modelo NARX! Você pode escolher os lags das variáveis de entrada e saída para construir a matriz de regressores.
Mantemos o método fit/predict para tornar o processo direto.
### NARX com Catboost
```python
basis_function = Fourier(degree=1)
catboost_narx = NARX(
base_estimator=CatBoostRegressor(iterations=300, learning_rate=0.1, depth=8),
xlag=10,
ylag=10,
basis_function=basis_function,
model_type="NARMAX",
fit_params={"verbose": False},
)
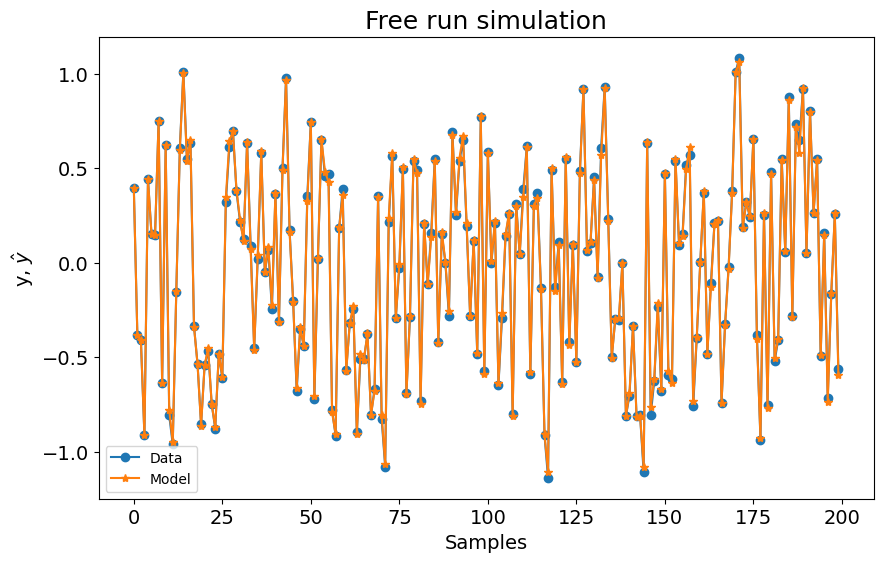
catboost_narx.fit(X=x_train, y=y_train)
yhat = catboost_narx.predict(X=x_valid, y=y_valid, steps_ahead=1)
print("MSE: ", mean_squared_error(y_valid, yhat))
plot_results(y=y_valid, yhat=yhat, n=200)
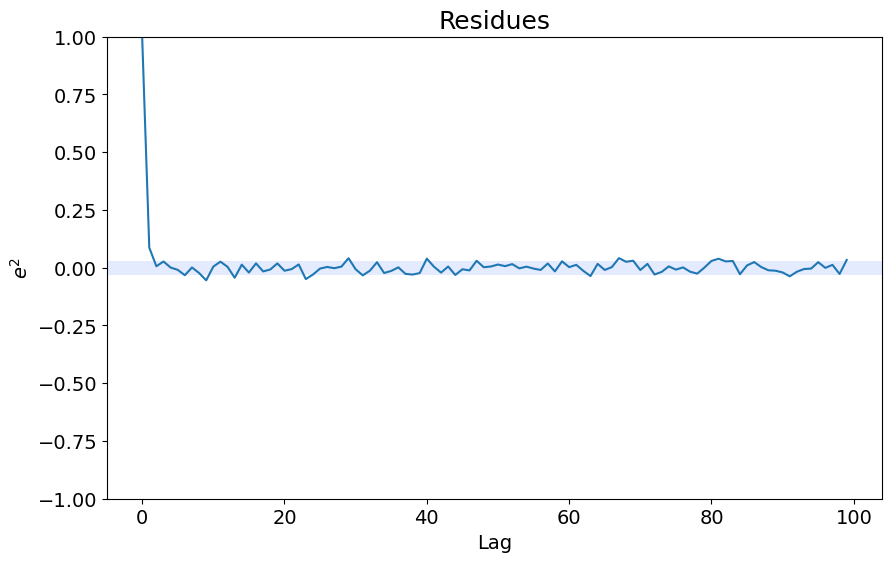
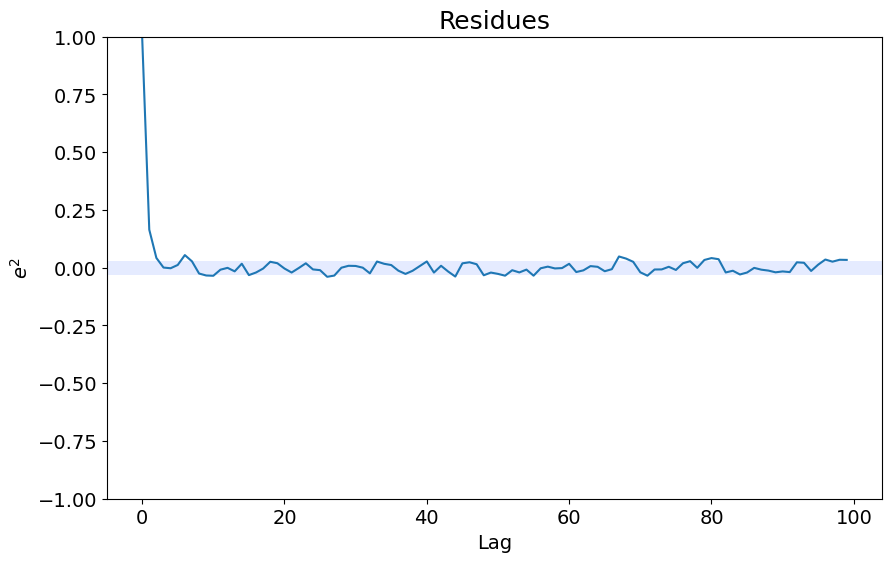
ee = compute_residues_autocorrelation(y_valid, yhat)
plot_residues_correlation(data=ee, title="Residues", ylabel="$e^2$")
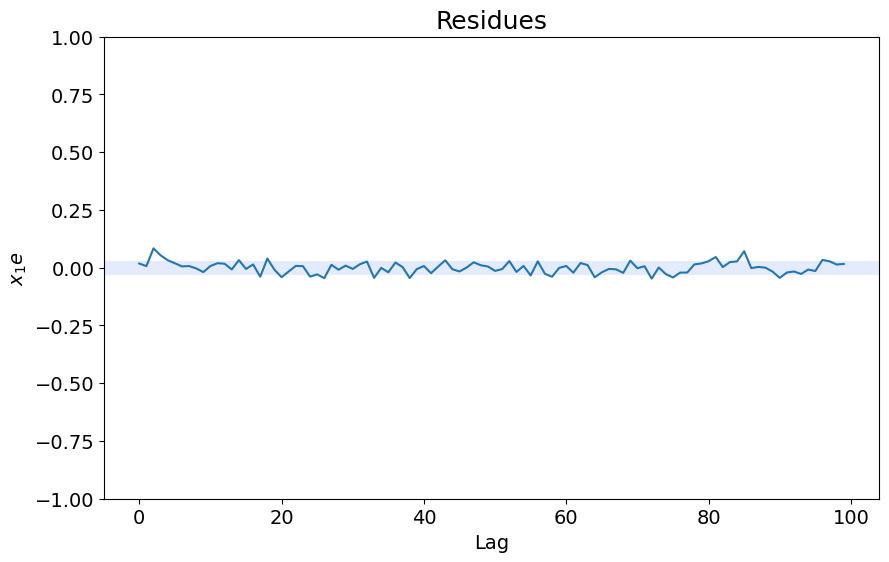
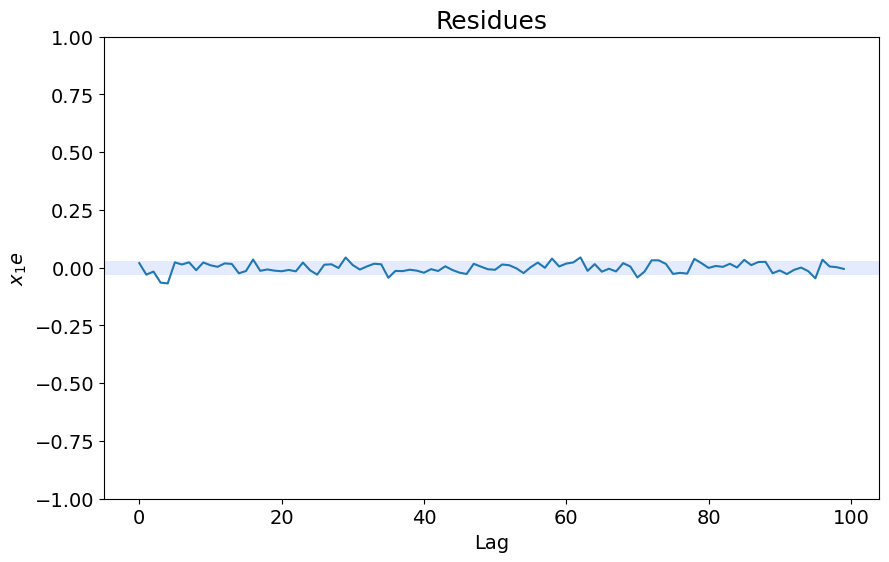
x1e = compute_cross_correlation(y_valid, yhat, x_valid)
plot_residues_correlation(data=x1e, title="Residues", ylabel="$x_1e$")
```
MSE: 0.00024145290395678653
### NARX com Gradient Boosting
```python
basis_function = Fourier(degree=1)
gb_narx = NARX(
base_estimator=GradientBoostingRegressor(
loss="quantile",
alpha=0.90,
n_estimators=250,
max_depth=10,
learning_rate=0.1,
min_samples_leaf=9,
min_samples_split=9,
),
xlag=2,
ylag=2,
basis_function=basis_function,
model_type="NARMAX",
)
gb_narx.fit(X=x_train, y=y_train)
yhat = gb_narx.predict(X=x_valid, y=y_valid)
print(mean_squared_error(y_valid, yhat))
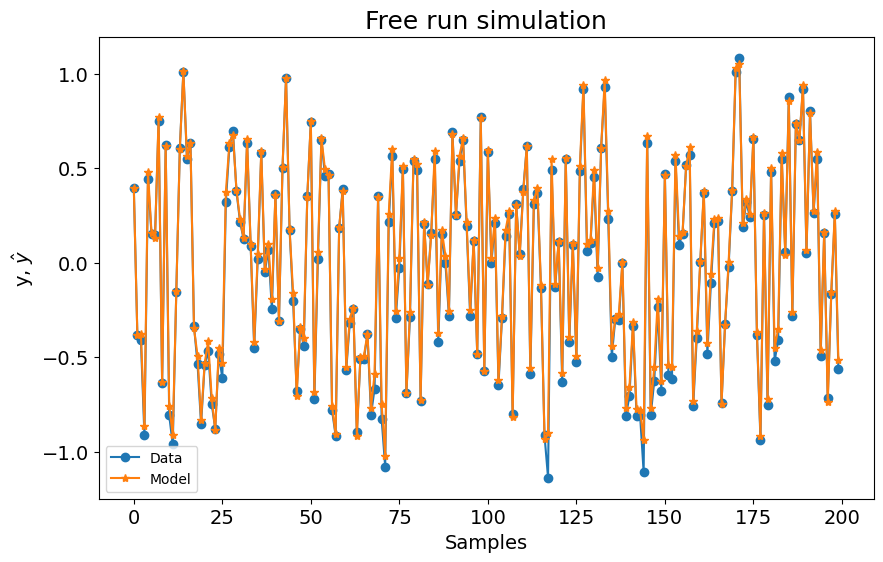
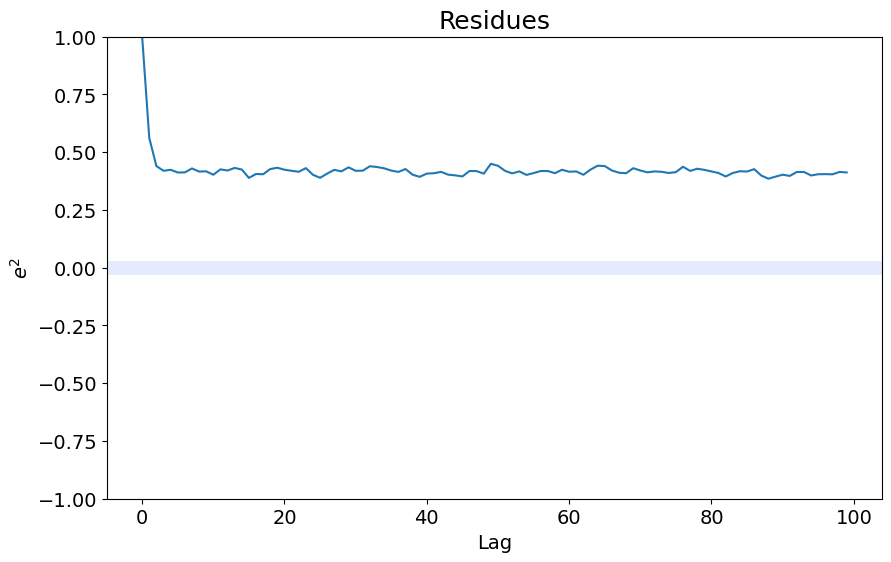
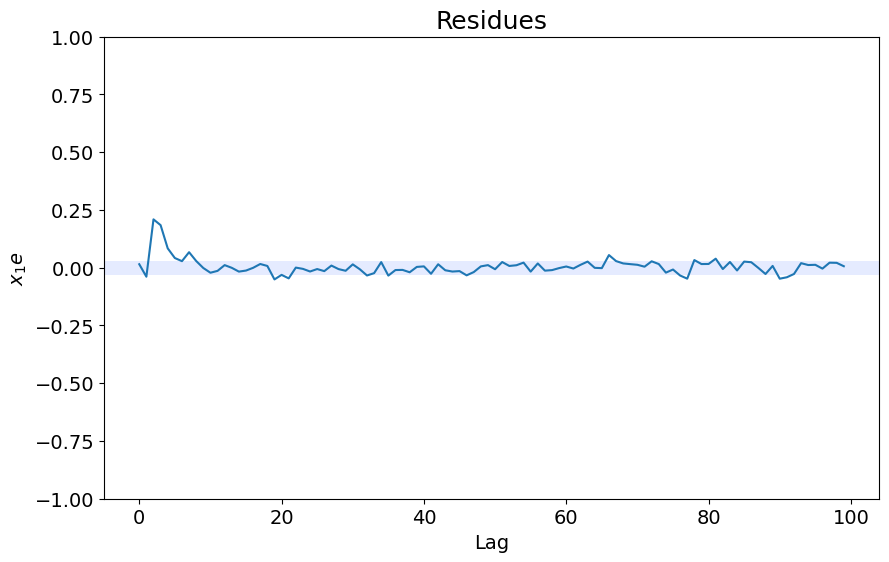
plot_results(y=y_valid, yhat=yhat, n=200)
ee = compute_residues_autocorrelation(y_valid, yhat)
plot_residues_correlation(data=ee, title="Residues", ylabel="$e^2$")
x1e = compute_cross_correlation(y_valid, yhat, x_valid)
plot_residues_correlation(data=x1e, title="Residues", ylabel="$x_1e$")
```
0.0011824693986863938
### NARX com ARD
```python
from sysidentpy.general_estimators import NARX
ARD_narx = NARX(
base_estimator=ARDRegression(),
xlag=2,
ylag=2,
basis_function=basis_function,
model_type="NARMAX",
)
ARD_narx.fit(X=x_train, y=y_train)
yhat = ARD_narx.predict(X=x_valid, y=y_valid)
print(mean_squared_error(y_valid, yhat))
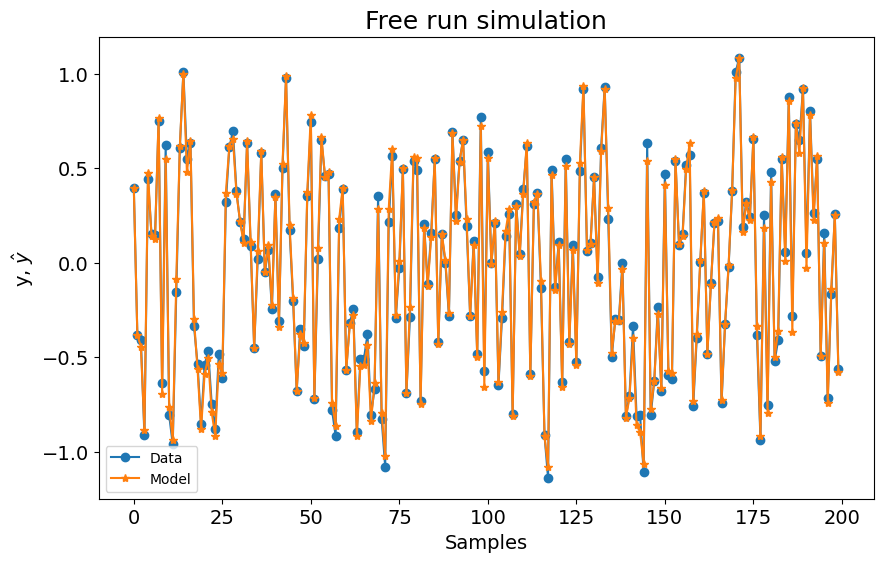
plot_results(y=y_valid, yhat=yhat, n=200)
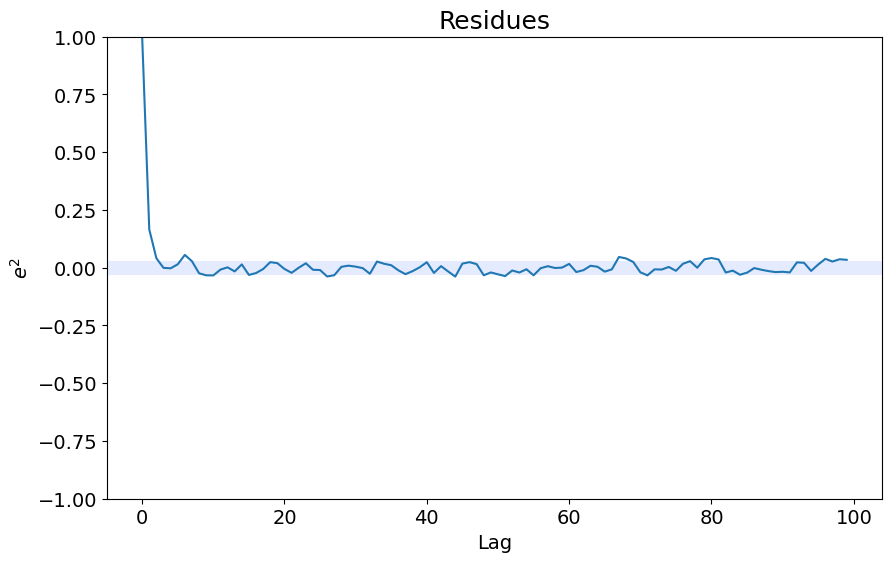
ee = compute_residues_autocorrelation(y_valid, yhat)
plot_residues_correlation(data=ee, title="Residues", ylabel="$e^2$")
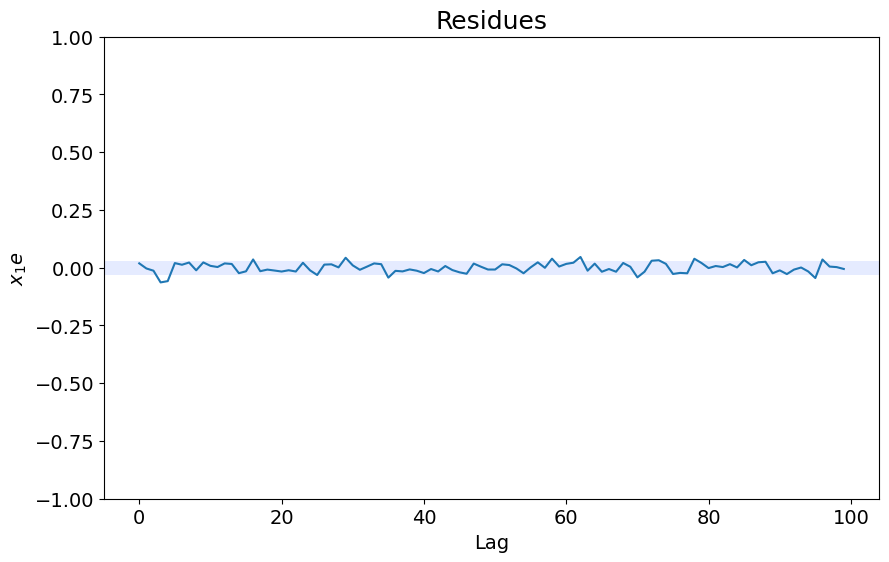
x1e = compute_cross_correlation(y_valid, yhat, x_valid)
plot_residues_correlation(data=x1e, title="Residues", ylabel="$x_1e$")
```
0.0011058934497373794
### NARX com Bayesian Ridge
```python
from sysidentpy.general_estimators import NARX
BayesianRidge_narx = NARX(
base_estimator=BayesianRidge(),
xlag=2,
ylag=2,
basis_function=basis_function,
model_type="NARMAX",
)
BayesianRidge_narx.fit(X=x_train, y=y_train)
yhat = BayesianRidge_narx.predict(X=x_valid, y=y_valid)
print(mean_squared_error(y_valid, yhat))
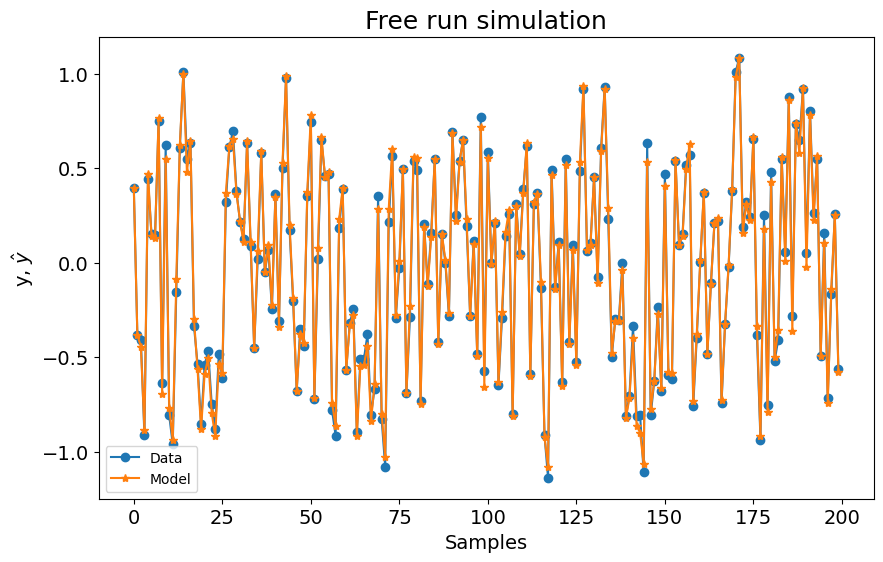
plot_results(y=y_valid, yhat=yhat, n=200)
ee = compute_residues_autocorrelation(y_valid, yhat)
plot_residues_correlation(data=ee, title="Residues", ylabel="$e^2$")
x1e = compute_cross_correlation(y_valid, yhat, x_valid)
plot_residues_correlation(data=x1e, title="Residues", ylabel="$x_1e$")
```
0.0011077874945734536
# Nota
Lembre-se que você pode usar predição n-steps-ahead e modelos NAR e NFIR agora. Confira como usá-los em seus respectivos exemplos.