---
template: overrides/main.html
title: Importância do Extended Least Squares
---
# Importância do Extended Least Squares
Exemplo criado por Wilson Rocha Lacerda Junior
> **Procurando mais detalhes sobre modelos NARMAX?**
> Para informações completas sobre modelos, métodos e uma ampla variedade de exemplos e benchmarks implementados no SysIdentPy, confira nosso livro:
> [*Nonlinear System Identification and Forecasting: Theory and Practice With SysIdentPy*](https://sysidentpy.org/book/0%20-%20Preface/)
>
> Este livro oferece orientação aprofundada para apoiar seu trabalho com o SysIdentPy.
Aqui importamos o modelo NARMAX, a métrica para avaliação do modelo e os métodos para gerar dados de amostra para testes. Também importamos pandas para uso específico.
```python
pip install sysidentpy
```
```python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sysidentpy.model_structure_selection import FROLS
from sysidentpy.basis_function import Polynomial
from sysidentpy.parameter_estimation import LeastSquares
from sysidentpy.metrics import root_relative_squared_error
from sysidentpy.utils.generate_data import get_siso_data
from sysidentpy.utils.display_results import results
```
## Gerando dados de amostra com 1 entrada e 1 saída
Os dados são gerados simulando o seguinte modelo:
$y_k = 0.2y_{k-1} + 0.1y_{k-1}x_{k-1} + 0.9x_{k-2} + e_{k}$
Se *colored_noise* for definido como True:
$e_{k} = 0.8\nu_{k-1} + \nu_{k}$
onde $x$ é uma variável aleatória uniformemente distribuída e $\nu$ é uma variável com distribuição gaussiana com $\mu=0$ e $\sigma$ definido pelo usuário.
No próximo exemplo, geraremos dados com 3000 amostras com ruído colorido e selecionando 90% dos dados para treinar o modelo.
```python
x_train, x_valid, y_train, y_valid = get_siso_data(
n=1000, colored_noise=True, sigma=0.2, train_percentage=90
)
```
## Construindo o modelo
Primeiro, treinaremos um modelo sem o Algoritmo Extended Least Squares para fins de comparação.
```python
basis_function = Polynomial(degree=2)
estimator = LeastSquares(unbiased=False)
model = FROLS(
order_selection=False,
n_terms=3,
ylag=2,
xlag=2,
info_criteria="aic",
estimator=estimator,
basis_function=basis_function,
err_tol=None,
)
```
```python
model.fit(X=x_train, y=y_train)
yhat = model.predict(X=x_valid, y=y_valid)
rrse = root_relative_squared_error(y_valid, yhat)
print(rrse)
```
0.5499799245432233
Claramente, há algo errado com o modelo obtido. Veja o notebook *basic_steps* para comparar os resultados obtidos usando os mesmos dados mas sem ruído colorido. Mas vamos ver o que está errado.
```python
r = pd.DataFrame(
results(
model.final_model,
model.theta,
model.err,
model.n_terms,
err_precision=8,
dtype="sci",
),
columns=["Regressors", "Parameters", "ERR"],
)
print(r)
```
Regressors Parameters ERR
0 x1(k-2) 8.9976E-01 7.41682256E-01
1 y(k-1) 2.8734E-01 8.33321202E-02
2 x1(k-1)y(k-1) 1.2348E-01 5.10334067E-03
## Estimação de parâmetros com bias
Como podemos observar acima, a estrutura do modelo é exatamente a mesma que gerou os dados. Você pode ver que o ERR ordenou os termos da forma correta. E esta é uma nota importante sobre o algoritmo Error Reduction Ratio usado aqui: __ele é muito robusto ao ruído colorido!!__
Esta é uma grande característica! No entanto, embora a estrutura esteja correta, os *parâmetros* do modelo não estão ok! Aqui temos uma estimação com bias! O parâmetro real para $y_{k-1}$ é $0.2$, não $0.3$.
Neste caso, estamos na verdade modelando usando um modelo NARX, não NARMAX. A parte MA existe para permitir uma estimação não-enviesada dos parâmetros. Para alcançar uma estimação não-enviesada dos parâmetros, temos o algoritmo Extended Least Squares. Lembre-se, se os dados têm apenas ruído branco, NARX é suficiente.
Antes de aplicar o Algoritmo Extended Least Squares, executaremos vários modelos NARX para verificar quão diferentes os parâmetros estimados são dos reais.
```python
parameters = np.zeros([3, 50])
for i in range(50):
x_train, x_valid, y_train, y_valid = get_siso_data(
n=3000, colored_noise=True, train_percentage=90
)
model.fit(X=x_train, y=y_train)
parameters[:, i] = model.theta.flatten()
# Definir o tema para seaborn (opcional)
sns.set_theme()
plt.figure(figsize=(14, 4))
# Plotar KDE para cada parâmetro
sns.kdeplot(parameters.T[:, 0], label="Parameter 1")
sns.kdeplot(parameters.T[:, 1], label="Parameter 2")
sns.kdeplot(parameters.T[:, 2], label="Parameter 3")
# Plotar linhas verticais onde os valores reais devem estar
plt.axvline(x=0.1, color="k", linestyle="--", label="Real Value 0.1")
plt.axvline(x=0.2, color="k", linestyle="--", label="Real Value 0.2")
plt.axvline(x=0.9, color="k", linestyle="--", label="Real Value 0.9")
plt.xlabel("Parameter Value")
plt.ylabel("Density")
plt.title("Kernel Density Estimate of Parameters")
plt.legend()
plt.show()
```
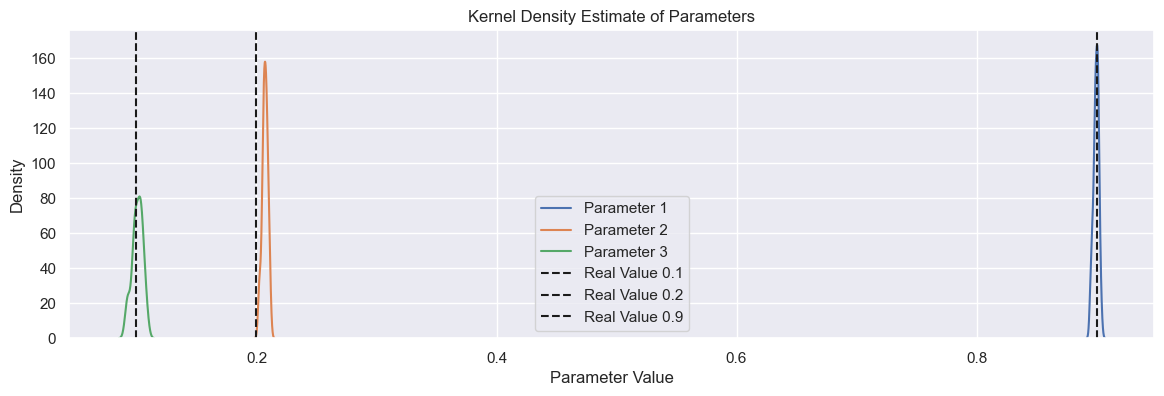
## Usando o algoritmo Extended Least Squares
Como mostrado na figura acima, temos um problema para estimar o parâmetro para $y_{k-1}$. Agora usaremos o Algoritmo Extended Least Squares.
No SysIdentPy, basta definir *extended_least_squares* como *True* e o algoritmo será aplicado.
```python
basis_function = Polynomial(degree=2)
estimator = LeastSquares(unbiased=True)
parameters = np.zeros([3, 50])
for i in range(50):
x_train, x_valid, y_train, y_valid = get_siso_data(
n=3000, colored_noise=True, train_percentage=90
)
model = FROLS(
order_selection=False,
n_terms=3,
ylag=2,
xlag=2,
elag=2,
info_criteria="aic",
estimator=estimator,
basis_function=basis_function,
)
model.fit(X=x_train, y=y_train)
parameters[:, i] = model.theta.flatten()
plt.figure(figsize=(14, 4))
# Plotar KDE para cada parâmetro
sns.kdeplot(parameters.T[:, 0], label="Parameter 1")
sns.kdeplot(parameters.T[:, 1], label="Parameter 2")
sns.kdeplot(parameters.T[:, 2], label="Parameter 3")
# Plotar linhas verticais onde os valores reais devem estar
plt.axvline(x=0.1, color="k", linestyle="--", label="Real Value 0.1")
plt.axvline(x=0.2, color="k", linestyle="--", label="Real Value 0.2")
plt.axvline(x=0.9, color="k", linestyle="--", label="Real Value 0.9")
plt.xlabel("Parameter Value")
plt.ylabel("Density")
plt.title("Kernel Density Estimate of Parameters")
plt.legend()
plt.show()
```
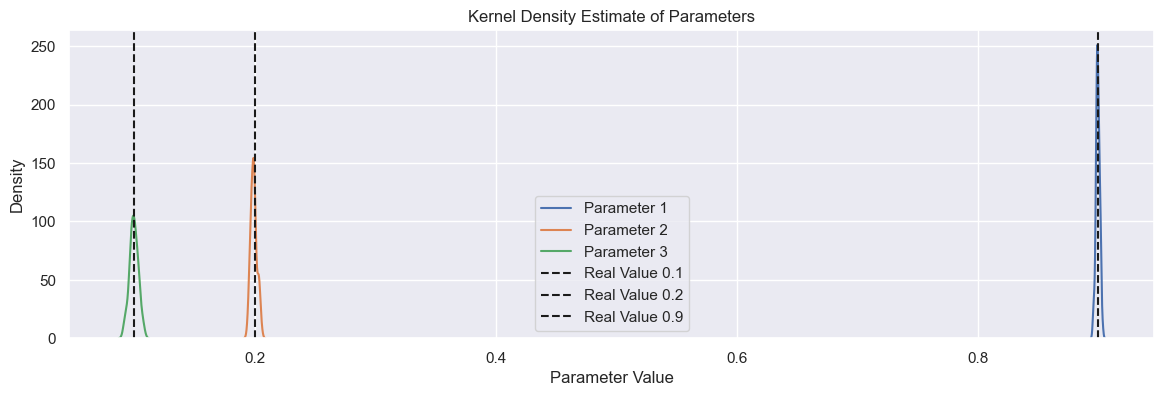
Ótimo! Agora temos uma estimação não-enviesada dos parâmetros!
## Nota
Nota: O Extended Least Squares é um algoritmo iterativo. No SysIdentPy, o padrão é 30 iterações (`uiter=30`) porque é conhecido da literatura que o algoritmo converge rapidamente (cerca de 10 ou 20 iterações).