{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"toc": "true"
},
"source": [
"# Table of Contents\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Optimization in Julia\n",
"\n",
"This lecture gives an overview of some optimization tools in Julia."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Julia Version 1.1.0\n",
"Commit 80516ca202 (2019-01-21 21:24 UTC)\n",
"Platform Info:\n",
" OS: macOS (x86_64-apple-darwin14.5.0)\n",
" CPU: Intel(R) Core(TM) i7-6920HQ CPU @ 2.90GHz\n",
" WORD_SIZE: 64\n",
" LIBM: libopenlibm\n",
" LLVM: libLLVM-6.0.1 (ORCJIT, skylake)\n",
"Environment:\n",
" JULIA_EDITOR = code\n"
]
}
],
"source": [
"versioninfo()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Flowchart\n",
"\n",
"* Statisticians do optimizations in daily life: maximum likelihood estimation, machine learning, ...\n",
"\n",
"* Category of optimization problems:\n",
"\n",
" 1. Problems with analytical solutions: least squares, principle component analysis, canonical correlation analysis, ...\n",
" \n",
" 2. Problems subject to Disciplined Convex Programming (DCP): linear programming (LP), quadratic programming (QP), second-order cone programming (SOCP), semidefinite programming (SDP), and geometric programming (GP).\n",
" \n",
" 3. Nonlinear programming (NLP): Newton type algorithms, Fisher scoring algorithm, EM algorithm, MM algorithms. \n",
" \n",
" 4. Large scale optimization: ADMM, SGD, ...\n",
" \n",
"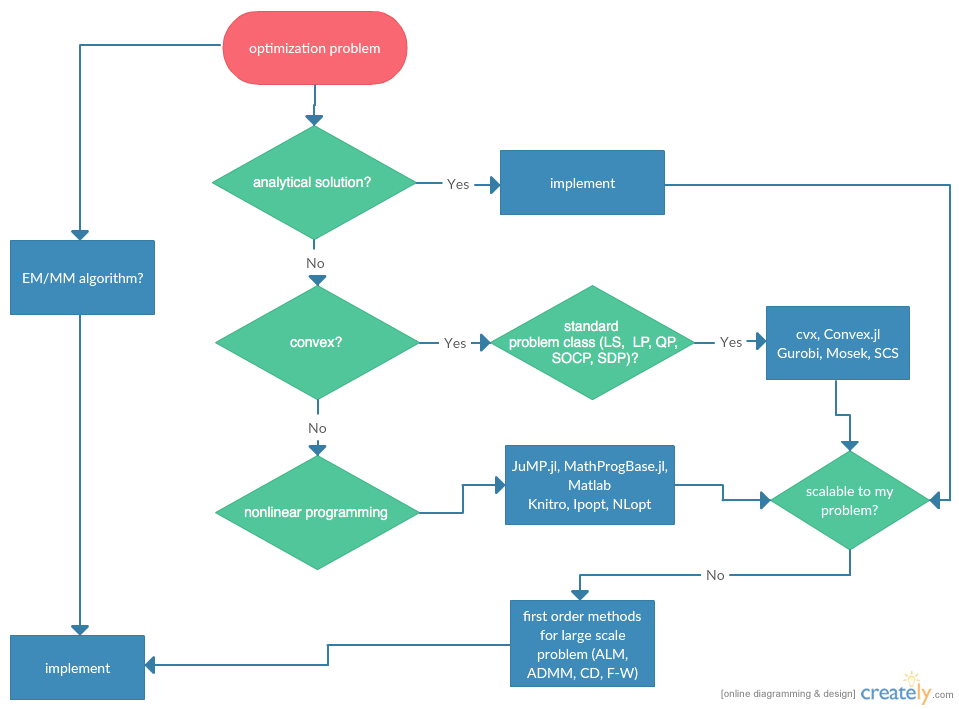 "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Modeling tools and solvers\n",
"\n",
"Getting familiar with **good** optimization softwares broadens the scope and scale of problems we are able to solve in statistics. Following table lists some of the best optimization softwares. \n",
"\n",
"\n",
"| | | LP | MILP | SOCP | MISOCP | SDP | GP | NLP | MINLP | | R | Matlab | Julia | Python | | Cost | \n",
"|:---------:|:-:|:--:|:----:|:----:|:--------------:|:---:|:--:|:---:|:-----:|:-:|:-:|:------:|:-----:|:------:|:-:|:----:| \n",
"| **modeling tools** | | | | | | | | | | | | | | | | | \n",
"| cvx | | x | x | x | x | x | x | | | | | x | | x | | A | \n",
"| Convex.jl | | x | x | x | x | x | | | | | | | x | | | O | \n",
"| JuMP.jl | | x | x | x | x | | | x | x | | | | x | | | O | \n",
"| MathProgBase.jl | | x | x | x | x | | | x | x | | | | x | | | O | \n",
"| MathOptInterface.jl | | x | x | x | x | | | x | x | | | | x | | | O | \n",
"| **convex solvers** | | | | | | | | | | | | | | | | | \n",
"| Mosek | | x | x | x | x | x | x | x | | | x | x | x | x | | A | \n",
"| Gurobi | | x | x | x | x | | | | | | x | x | x | x | | A | \n",
"| CPLEX | | x | x | x | x | | | | | | x | x | x | x | | A | \n",
"| SCS | | x | | x | | x | | | | | | x | x | x | | O | \n",
"| **NLP solvers** | | | | | | | | | | | | | | | | | \n",
"| NLopt | | x | | | | | | x | | | | x | x | x | | O | \n",
"| Ipopt | | x | | | | | | x | | | | x | x | x | | O | \n",
"| KNITRO | | x | x | | | | | x | x | | x | x | x | x | | $ | \n",
"\n",
"* O: open source \n",
"* A: free academic license \n",
"* $: commercial"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"* Difference between **modeling tool** and **solvers**\n",
"\n",
" - **Modeling tools** such as cvx (for Matlab) and Convex.jl (Julia analog of cvx) implement the disciplined convex programming (DCP) paradigm proposed by Grant and Boyd (2008) . DCP prescribes a set of simple rules from which users can construct convex optimization problems easily.\n",
" \n",
" - **Solvers** (Mosek, Gurobi, Cplex, SCS, ...) are concrete software implementation of optimization algorithms. My favorite ones are: Mosek/Gurobi/SCS for DCP and Ipopt/NLopt for nonlinear programming. Mosek and Gurobi are commercial software but free for academic use. SCS/Ipopt/NLopt are open source. \n",
" \n",
" - Modeling tools usually have the capability to use a variety of solvers. But modeling tools are solver agnostic so users do not have to worry about specific solver interface.\n",
" \n",
"* For this course, **install** following tools:\n",
" - Gurobi: 1. Download Gurobi at [link](http://www.gurobi.com/downloads/gurobi-optimizer). 2. Request free academic license at [link](https://user.gurobi.com/download/licenses/free-academic). 3. Run `grbgetkey XXXXXXXXX` command on terminal as suggested. It'll retrieve a license file and put it under the home folder.\n",
" - Mosek: 1. Request free academic license at [link](https://www.mosek.com/products/academic-licenses/). The license file will be sent to your edu email within minutes. Check Spam folder if necessary. 2. Put the license file at the default location `/home/YOURNAME/mosek/`.\n",
" - Convex.jl, SCS.jl, Gurobi.jl, Mosek.jl, MathProgBase.jl, NLopt.jl, Ipopt.jl."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## DCP Using Convex.jl"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Standard convex problem classes like LP (linear programming), QP (quadratic programming), SOCP (second-order cone programming), SDP (semidefinite programming), and GP (geometric programming), are becoming a **technology**.\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"### Example: microbiome regression analysis\n",
"\n",
"We illustrate optimization tools in Julia using microbiome analysis as an example.\n",
"\n",
"16S microbiome sequencing techonology generates sequence counts of various organisms (OTUs, operational taxonomic units) in samples. \n",
"\n",
"\n",
"\n",
"For statistical analysis, counts are normalized into **proportions** for each sample, resulting in a covariate matrix $\\mathbf{X}$ with all rows summing to 1. For identifiability, we need to add a sum-to-zero constraint to the regression cofficients. In other words, we need to solve a **constrained least squares problem** \n",
"$$\n",
" \\text{minimize} \\frac{1}{2} \\|\\mathbf{y} - \\mathbf{X} \\beta\\|_2^2\n",
"$$\n",
"subject to the constraint $\\sum_{j=1}^p \\beta_j = 0$. For simplicity we ignore intercept and non-OTU covariates in this presentation.\n",
"\n",
"Let's first generate an artifical data set."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"using Random, LinearAlgebra, SparseArrays\n",
"\n",
"Random.seed!(123) # seed\n",
"\n",
"n, p = 100, 50\n",
"X = rand(n, p)\n",
"lmul!(Diagonal(1 ./ vec(sum(X, dims=2))), X)\n",
"β = sprandn(p, 0.1) # sparse vector with about 10% non-zero entries\n",
"y = X * β + randn(n);"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Sum-to-zero regression\n",
"\n",
"The sum-to-zero contrained least squares is a standard quadratic programming (QP) problem so should be solved easily by any QP solver."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Modeling using Convex.jl\n",
"\n",
"We use the Convex.jl package to model this QP problem. For a complete list of operations supported by Convex.jl, see ."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"using Convex\n",
"\n",
"β̂cls = Variable(size(X, 2))\n",
"problem = minimize(0.5sumsquares(y - X * β̂cls)) # objective\n",
"problem.constraints += sum(β̂cls) == 0; # constraint"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Mosek\n",
"\n",
"We first use the Mosek solver to solve this QP."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Problem\n",
" Name : \n",
" Objective sense : min \n",
" Type : CONIC (conic optimization problem)\n",
" Constraints : 107 \n",
" Cones : 2 \n",
" Scalar variables : 157 \n",
" Matrix variables : 0 \n",
" Integer variables : 0 \n",
"\n",
"Optimizer started.\n",
"Presolve started.\n",
"Linear dependency checker started.\n",
"Linear dependency checker terminated.\n",
"Eliminator started.\n",
"Freed constraints in eliminator : 0\n",
"Eliminator terminated.\n",
"Eliminator - tries : 1 time : 0.00 \n",
"Lin. dep. - tries : 1 time : 0.00 \n",
"Lin. dep. - number : 0 \n",
"Presolve terminated. Time: 0.00 \n",
"Problem\n",
" Name : \n",
" Objective sense : min \n",
" Type : CONIC (conic optimization problem)\n",
" Constraints : 107 \n",
" Cones : 2 \n",
" Scalar variables : 157 \n",
" Matrix variables : 0 \n",
" Integer variables : 0 \n",
"\n",
"Optimizer - threads : 8 \n",
"Optimizer - solved problem : the dual \n",
"Optimizer - Constraints : 52\n",
"Optimizer - Cones : 3\n",
"Optimizer - Scalar variables : 106 conic : 106 \n",
"Optimizer - Semi-definite variables: 0 scalarized : 0 \n",
"Factor - setup time : 0.00 dense det. time : 0.00 \n",
"Factor - ML order time : 0.00 GP order time : 0.00 \n",
"Factor - nonzeros before factor : 1328 after factor : 1328 \n",
"Factor - dense dim. : 0 flops : 3.08e+05 \n",
"ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME \n",
"0 1.5e+00 7.5e-01 1.5e+00 0.00e+00 0.000000000e+00 -2.000000000e+00 1.0e+00 0.00 \n",
"1 1.7e-01 8.4e-02 7.0e-02 -7.80e-01 4.353550341e+00 2.260083736e+01 1.1e-01 0.00 \n",
"2 2.8e-02 1.3e-02 1.1e-02 -4.28e-01 2.091400155e+01 4.281754629e+01 1.8e-02 0.00 \n",
"3 2.0e-03 9.7e-04 4.9e-03 9.83e-01 2.693910885e+01 2.746907590e+01 1.3e-03 0.00 \n",
"4 1.9e-06 9.3e-07 1.2e-04 1.05e+00 2.645057050e+01 2.645136710e+01 1.2e-06 0.00 \n",
"5 8.0e-10 3.9e-10 2.5e-06 1.00e+00 2.645074168e+01 2.645074202e+01 5.2e-10 0.00 \n",
"Optimizer terminated. Time: 0.00 \n",
"\n",
"\n",
"Interior-point solution summary\n",
" Problem status : PRIMAL_AND_DUAL_FEASIBLE\n",
" Solution status : OPTIMAL\n",
" Primal. obj: 2.6450741681e+01 nrm: 5e+01 Viol. con: 8e-10 var: 0e+00 cones: 3e-08 \n",
" Dual. obj: 2.6450742020e+01 nrm: 1e+01 Viol. con: 0e+00 var: 1e-08 cones: 0e+00 \n",
" 0.006196 seconds (3.52 k allocations: 1.643 MiB)\n"
]
}
],
"source": [
"using Mosek\n",
"solver = MosekSolver(LOG=1)\n",
"@time solve!(problem, solver)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(:Optimal, 26.450741680579814, [20.1736; 2.11868; … ; 24.1402; -4.51783])"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check the status, optimal value, and minimizer of the problem\n",
"problem.status, problem.optval, β̂cls.value"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Gurobi\n",
"\n",
"Switch to Gurobi solver:"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Academic license - for non-commercial use only\n",
"Optimize a model with 107 rows, 157 columns and 5160 nonzeros\n",
"Model has 2 quadratic constraints\n",
"Coefficient statistics:\n",
" Matrix range [1e-05, 2e+00]\n",
" QMatrix range [1e+00, 1e+00]\n",
" Objective range [1e+00, 1e+00]\n",
" Bounds range [0e+00, 0e+00]\n",
" RHS range [4e-03, 3e+00]\n",
"Presolve removed 2 rows and 1 columns\n",
"Presolve time: 0.00s\n",
"Presolved: 105 rows, 156 columns, 5158 nonzeros\n",
"Presolved model has 2 second-order cone constraints\n",
"Ordering time: 0.00s\n",
"\n",
"Barrier statistics:\n",
" Free vars : 50\n",
" AA' NZ : 5.154e+03\n",
" Factor NZ : 5.262e+03\n",
" Factor Ops : 3.590e+05 (less than 1 second per iteration)\n",
" Threads : 1\n",
"\n",
" Objective Residual\n",
"Iter Primal Dual Primal Dual Compl Time\n",
" 0 1.18451802e+01 -5.01000000e-01 2.40e+01 1.00e-01 2.10e-01 0s\n",
" 1 3.33648461e+00 -3.24029170e-02 4.58e+00 4.72e-05 4.06e-02 0s\n",
" 2 3.12915622e+00 4.52501039e+00 3.61e+00 4.47e-05 1.99e-02 0s\n",
" 3 1.51263772e+01 7.51185121e+00 1.79e+00 4.02e-05 1.02e-01 0s\n",
" 4 1.38248014e+01 2.01142309e+01 1.08e+00 9.67e-05 1.68e-02 0s\n",
" 5 3.30715906e+01 2.40146272e+01 3.35e-03 1.01e-05 8.59e-02 0s\n",
" 6 2.71094293e+01 2.63988011e+01 3.68e-09 2.91e-06 6.71e-03 0s\n",
" 7 2.64515175e+01 2.64506426e+01 1.43e-10 4.75e-08 8.22e-06 0s\n",
" 8 2.64507432e+01 2.64507419e+01 5.58e-09 1.54e-09 1.39e-08 0s\n",
"\n",
"Barrier solved model in 8 iterations and 0.01 seconds\n",
"Optimal objective 2.64507432e+01\n",
"\n",
" 0.009493 seconds (2.00 k allocations: 1.699 MiB)\n"
]
}
],
"source": [
"using Gurobi\n",
"solver = GurobiSolver(OutputFlag=1)\n",
"@time solve!(problem, solver)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(:Optimal, 26.45074321661315, [20.1748; 2.11866; … ; 24.1422; -4.51908])"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check the status, optimal value, and minimizer of the problem\n",
"problem.status, problem.optval, β̂cls.value"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Cplex\n",
"\n",
"Switch to IBM Cplex solver:"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Tried aggregator 1 time.\n",
"QCP Presolve eliminated 2 rows and 1 columns.\n",
"Aggregator did 2 substitutions.\n",
"Reduced QCP has 103 rows, 204 columns, and 5154 nonzeros.\n",
"Reduced QCP has 52 quadratic constraints.\n",
"Presolve time = 0.00 sec. (0.42 ticks)\n",
"Parallel mode: using up to 8 threads for barrier.\n",
"Number of nonzeros in lower triangle of A*A' = 5151\n",
"Using Approximate Minimum Degree ordering\n",
"Total time for automatic ordering = 0.00 sec. (1.13 ticks)\n",
"Summary statistics for Cholesky factor:\n",
" Threads = 8\n",
" Rows in Factor = 103\n",
" Integer space required = 104\n",
" Total non-zeros in factor = 5255\n",
" Total FP ops to factor = 358959\n",
" Itn Primal Obj Dual Obj Prim Inf Upper Inf Dual Inf Inf Ratio\n",
" 0 2.0710678e-01 -5.0000000e-01 8.08e+01 0.00e+00 7.30e+01 1.00e+00\n",
" 1 3.8378132e+00 1.1892083e+01 8.08e+01 0.00e+00 7.30e+01 1.04e-01\n",
" 2 1.4760051e+01 2.6113460e+01 7.19e+01 0.00e+00 6.50e+01 7.99e-02\n",
" 3 3.2279497e+01 4.4035225e+01 5.51e+01 0.00e+00 4.98e+01 8.38e-02\n",
" 4 2.7177376e+01 3.1140706e+01 8.25e+00 0.00e+00 7.46e+00 2.50e-01\n",
" 5 2.6492206e+01 2.8891271e+01 1.58e+00 0.00e+00 1.43e+00 4.13e-01\n",
" 6 2.6546001e+01 2.6870962e+01 9.88e-01 0.00e+00 8.93e-01 3.05e+00\n",
" 7 2.6485052e+01 2.6785273e+01 1.38e-01 0.00e+00 1.24e-01 3.30e+00\n",
" 8 2.6477246e+01 2.6565213e+01 1.27e-01 0.00e+00 1.15e-01 1.13e+01\n",
" 9 2.6467787e+01 2.6525581e+01 3.83e-02 0.00e+00 3.46e-02 1.71e+01\n",
" 10 2.6453149e+01 2.6474596e+01 2.66e-02 0.00e+00 2.41e-02 4.61e+01\n",
" 11 2.6450770e+01 2.6450903e+01 1.11e-02 0.00e+00 1.00e-02 7.44e+03\n",
" 12 2.6450744e+01 2.6450748e+01 6.54e-05 0.00e+00 5.91e-05 2.05e+05\n",
" 13 2.6450742e+01 2.6450743e+01 2.36e-06 0.00e+00 2.14e-06 1.95e+06\n",
" 0.026841 seconds (1.99 k allocations: 1.698 MiB)\n"
]
}
],
"source": [
"# Use Cplex solver\n",
"using CPLEX\n",
"solver = CplexSolver(CPXPARAM_ScreenOutput=1)\n",
"@time solve!(problem, solver)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(:Optimal, 26.45074204102406, [20.1739; 2.11874; … ; 24.1406; -4.51808])"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check the status, optimal value, and minimizer of the problem\n",
"problem.status, problem.optval, β̂cls.value"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### SCS\n",
"\n",
"Switch to the open source SCS solver:"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" 0.027974 seconds (2.25 k allocations: 2.028 MiB)\n",
"----------------------------------------------------------------------------\n",
"\tSCS v2.0.2 - Splitting Conic Solver\n",
"\t(c) Brendan O'Donoghue, Stanford University, 2012-2017\n",
"----------------------------------------------------------------------------\n",
"Lin-sys: sparse-indirect, nnz in A = 5056, CG tol ~ 1/iter^(2.00)\n",
"eps = 1.00e-05, alpha = 1.50, max_iters = 5000, normalize = 1, scale = 1.00\n",
"acceleration_lookback = 20, rho_x = 1.00e-03\n",
"Variables n = 53, constraints m = 107\n",
"Cones:\tprimal zero / dual free vars: 2\n",
"\tlinear vars: 1\n",
"\tsoc vars: 104, soc blks: 2\n",
"Setup time: 2.20e-04s\n",
"----------------------------------------------------------------------------\n",
" Iter | pri res | dua res | rel gap | pri obj | dua obj | kap/tau | time (s)\n",
"----------------------------------------------------------------------------\n",
" 0| 4.23e+20 2.27e+20 1.00e+00 -5.02e+21 3.29e+21 8.65e+20 7.80e-04 \n",
" 100| 1.57e-05 1.89e-05 8.31e-07 2.64e+01 2.64e+01 1.62e-14 1.88e-02 \n",
" 120| 9.72e-07 4.25e-06 1.73e-09 2.65e+01 2.65e+01 5.98e-15 2.05e-02 \n",
"----------------------------------------------------------------------------\n",
"Status: Solved\n",
"Timing: Solve time: 2.05e-02s\n",
"\tLin-sys: avg # CG iterations: 7.60, avg solve time: 1.39e-04s\n",
"\tCones: avg projection time: 2.97e-07s\n",
"\tAcceleration: avg step time: 2.51e-05s\n",
"----------------------------------------------------------------------------\n",
"Error metrics:\n",
"dist(s, K) = 1.6815e-11, dist(y, K*) = 1.6816e-11, s'y/|s||y| = -1.7609e-13\n",
"primal res: |Ax + s - b|_2 / (1 + |b|_2) = 9.7212e-07\n",
"dual res: |A'y + c|_2 / (1 + |c|_2) = 4.2535e-06\n",
"rel gap: |c'x + b'y| / (1 + |c'x| + |b'y|) = 1.7334e-09\n",
"----------------------------------------------------------------------------\n",
"c'x = 26.4506, -b'y = 26.4506\n",
"============================================================================\n"
]
}
],
"source": [
"# Use SCS solver\n",
"using SCS\n",
"solver = SCSSolver(verbose=1)\n",
"@time solve!(problem, solver)"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(:Optimal, 26.45062094817076, [20.1736; 2.11862; … ; 24.1401; -4.51784])"
]
},
"execution_count": 16,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Check the status, optimal value, and minimizer of the problem\n",
"problem.status, problem.optval, β̂cls.value"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Sum-to-zero lasso\n",
"\n",
"Suppose we want to know which organisms (OTU) are associated with the response. We can answer this question using a sum-to-zero contrained lasso\n",
"$$\n",
" \\text{minimize} \\frac 12 \\|\\mathbf{y} - \\mathbf{X} \\beta\\|_2^2 + \\lambda \\|\\beta\\|_1\n",
"$$\n",
"subject to the constraint $\\sum_{j=1}^p \\beta_j = 0$. Varying $\\lambda$ from small to large values will generate a solution path."
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" 1.364175 seconds (1.25 M allocations: 838.979 MiB, 26.14% gc time)\n"
]
}
],
"source": [
"# Use Mosek solver\n",
"using Mosek\n",
"solver = MosekSolver(LOG=0)\n",
"\n",
"# # Use Gurobi solver\n",
"# using Gurobi\n",
"# solver = GurobiSolver(OutputFlag=0)\n",
"\n",
"# Use Cplex solver\n",
"# using CPLEX\n",
"# solver = CplexSolver(CPXPARAM_ScreenOutput=0)\n",
"\n",
"# # Use SCS solver\n",
"# using SCS\n",
"# solver = SCSSolver(verbose=0)\n",
"\n",
"# solve at a grid of λ\n",
"λgrid = 0:0.01:0.35\n",
"β̂path = zeros(length(λgrid), size(X, 2)) # each row is β̂ at a λ\n",
"β̂classo = Variable(size(X, 2))\n",
"@time for i in 1:length(λgrid)\n",
" λ = λgrid[i]\n",
" # objective\n",
" problem = minimize(0.5sumsquares(y - X * β̂classo) + λ * sum(abs, β̂classo))\n",
" # constraint\n",
" problem.constraints += sum(β̂classo) == 0 # constraint\n",
" solve!(problem, solver)\n",
" β̂path[i, :] = β̂classo.value\n",
"end"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"\n",
"\n"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"using Plots; gr()\n",
"using LaTeXStrings\n",
"\n",
"p = plot(collect(λgrid), β̂path, legend=:none)\n",
"xlabel!(p, L\"\\lambda\")\n",
"ylabel!(p, L\"\\hat \\beta\")\n",
"title!(p, \"Sum-to-Zero Lasso\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Sum-to-zero group lasso\n",
"\n",
"Suppose we want to do variable selection not at the OTU level, but at the Phylum level. OTUs are clustered into various Phyla. We can answer this question using a sum-to-zero contrained group lasso\n",
"$$\n",
" \\text{minimize} \\frac 12 \\|\\mathbf{y} - \\mathbf{X} \\beta\\|_2^2 + \\lambda \\sum_j \\|\\mathbf{\\beta}_j\\|_2\n",
"$$\n",
"subject to the constraint $\\sum_{j=1}^p \\beta_j = 0$, where $\\mathbf{\\beta}_j$ are regression coefficients corresponding to the $j$-th phylum. This is a second-order cone programming (SOCP) problem readily modeled by Convex.jl.\n",
"\n",
"Let's assume each 10 contiguous OTUs belong to one Phylum."
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" 0.801165 seconds (400.55 k allocations: 235.576 MiB, 10.67% gc time)\n"
]
}
],
"source": [
"# Use Mosek solver\n",
"using Mosek\n",
"solver = MosekSolver(LOG=0)\n",
"\n",
"# # Use Gurobi solver\n",
"# using Gurobi\n",
"# solver = GurobiSolver(OutputFlag=0)\n",
"\n",
"# # Use Cplex solver\n",
"# using CPLEX\n",
"# solver = CplexSolver(CPXPARAM_ScreenOutput=0)\n",
"\n",
"# # Use SCS solver\n",
"# using SCS\n",
"# solver = SCSSolver(verbose=0)\n",
"\n",
"# solve at a grid of λ\n",
"λgrid = 0.1:0.005:0.5\n",
"β̂pathgrp = zeros(length(λgrid), size(X, 2)) # each row is β̂ at a λ\n",
"β̂classo = Variable(size(X, 2))\n",
"@time for i in 1:length(λgrid)\n",
" λ = λgrid[i]\n",
" # loss\n",
" obj = 0.5sumsquares(y - X * β̂classo)\n",
" # group lasso penalty term\n",
" for j in 1:(size(X, 2)/10)\n",
" βj = β̂classo[(10(j-1)+1):10j]\n",
" obj = obj + λ * norm(βj)\n",
" end\n",
" problem = minimize(obj)\n",
" # constraint\n",
" problem.constraints += sum(β̂classo) == 0 # constraint\n",
" solve!(problem, solver)\n",
" β̂pathgrp[i, :] = β̂classo.value\n",
"end"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We it took Mosek <1 second to solve this seemingly hard optimization problem at **80** different $\\lambda$ values."
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {},
"outputs": [
{
"data": {
"image/svg+xml": [
"\n",
"\n"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"p2 = plot(collect(λgrid), β̂pathgrp, legend=:none)\n",
"xlabel!(p2, L\"\\lambda\")\n",
"ylabel!(p2, L\"\\hat \\beta\")\n",
"title!(p2, \"Sum-to-Zero Group Lasso\")"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Example: matrix completion\n",
"\n",
"Load the $128 \\times 128$ Lena picture with missing pixels."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAIAAAACACAAAAADmVT4XAAAESmlDQ1BrQ0dDb2xvclNwYWNlR2VuZXJpY0dyYXkAADiNjVVbaBxVGP535+wGJA4+aBtaaAcvbSlpmESricXa7Wa7SRM362ZTmyrKZHY2O93ZmXFmdpuEPpWCb1oQpK+C+hgLIlgv2LzYl4rFkko1DwoRWowgKH1S8DtnJpvZDV5mOOd857+d//wXDlHPH5rrWkmFqGEHXr6UmT09e0bpuUlJkqmX8Gm672aKxUmObcc2aNt3/zYl+HrrELe1nf+vX6pi+DrWaxhOxdcbRAmVKF3VXS8g6rkM+vC5wOX4JvDD9XIpC7wOLEe6/Hskb9iGZ+pK3tMWlaLnVE0r7ut/8f/X17Cam+ftxej169MTWA/C54uGPTMNfAB4WddyHPcD326ZpwohTibd4HgplE8ONOszmYh+uuqdmInoF2vNMY4HgJeXauWXgB8CXrPnClOR/EbdmeB2+oikPt3PngF+HFitGeM8Twpw2XNKUxE9qBijOeBngS+bwXg5tC9967emcyFmtFTLFsKz2MBZ7WQReAfwUcPKl0I7rOwGRW5zGHjBtgqToc/siuHnoruz74NaeSyUTyUDr8x1HwXeVzVPjIf+p8Zq3lgp9CcVuJaoraeBl71mid99H/C65uXyoc30AxVtlMf5KeAhOpXQyCCH5jDrZNNfuK9PJrUEcskDr4q9RXlI2Bgedjp4eSCNFoGKMSkDOy4T7hSqYKfQvNDyBeJW7kZWsnvepyaoNdoAtQb0Av0oKAv0EzWwZkFtgjffZTeL1aYleKBEnt2LbDpsJ1PZkxhH2CR7jg2zEVLY8+wYO8pGQR1hR2Lex33n3t1rW3od58Z9X4FEAB0LntnQ8UWkluhP8OtCMhatS7uaB1z3nTcveK+Z+jdv/dYRPR/yod2fYdER9Jju9fOf98Xju8o+eeVW7/XzNBXPkshbpTtLqfXU3dQq5juptbiN1A+pNfx3tt2X+7OZlc3cZsCzBK2BYQqO37bWBA4wV4XOoQ6Lcey07c9jONtOcf4xJhxropZiN6val3a57qsf8GgabxTuF+hCv3pF3VDfU79Tf1VX1XeBfpHelj6WvpCuSp9KN0iRrkkr0pfSV9KH0mfYfQTqinS1q5LmO6unXbN6VGGcG4h8Z2JR4dTN+50Fb8tTQ8Sh84TO6m+fJR+Xd8uPyaPyXvkJeVI+KB+Wj8k75SGMQXlM3g/O7naUrCgDZlfHmTQrYhXmyRbdpIHfwKzF/AplYzFPPIg4m11dvtn9pujGsDod7DWaATLpnND1RX5s0f3d2kvidCfxMo8g28MG2XjUgxl2GF040dGPw7xL07n0aDpDSvpgeiQ9mD7J8VbtpveDO4I5F/PeaEd2q4fmRJ3WRYxaQsLHTIGxEPBHJuu4i545XwuUIVV9RsngeTWUcVsf6Fc0y1IEy1c8wze8llEZIP52h8/T7y+KNzmx44be9FrRm5VIfE30N7ePkzQTJdzgAAAxPElEQVR4AT17B0AVV9r2M3Mvxbppm02y2bRNTIyCdOwae+8dEKSKdBBQ6qUK0nsvKlgRu8ZojD32buqXL5svm2zJpmksCHfmf94h+x9lypkzc855y/OWc64CbF4JKVvMtgtRGb5yc4hJqQIiKliXbMrM0tOytHQgW02Sg56MDViPzLRsRU9BrqYkIzslg88zdR3dOVhTbXwMtaoSBNSF1IU0mnrs3u4/5JMLF2z7FGC9yaogNzULSENmfAFa0dqCRtTLWzt279qCtStXBiEUWLNmjfGltMxMZAIZyMlFbk42snN4gewM1oFfyURuZgYyjP/SPgawyLkWdUA9//i/CTiFLz7fizVIXMdnSUhNSUEKR8ASoPZYEYjgunq0LV242FpQqFm1kJrV0KzVUXHSPI3tstidVYeezPd0TUNWSrqWhQyZB5IUJSM9HayVUhIR+lse0GqqNzU1BZuMiQXU4XtY1ddKq6HlrV+/XkeWzpnI6EOGN5kD0RjYpGnBm7x3wPooHm0IIB1DNQ69KBEpCiyWtKy0jCxNh8Kpp+ipkAsLeQNTbhK/kpbBnjNgUXQLYosRtq7MXjfzoS8CG6HUy8h+Qc/g/3FI+K2A/APWb8jhxDIzs3HrgbPKNqSR0uKLpT0rrAVrfQBys6YuZLWC/KTsDIsFWanZaqqJk80FyUAOcCBIU0galR9KBSWAA1LTLayIi7Aiyqqt8lfVLZuaTY3BymroNdbWR5+9+dJGg0pJMn6DeV/g49vX1UAEKAFBwaxs99qkxpvhrderqxFSJ810+Z+pQ0vNTNGzYIWepSRlZaVkWMkTjsgYDRmRnmZJ09h/srkISnSOrm/a4qf5+PpbAxFUu5rj+tXjnS8GUzIQnyiz4Hjz8pI2swdXtQEt/s1o9tsGa6sv8KSnTQ+pogwFK1rMug2caDqlQKispSKVpErNsqamWjmXdP7rtiIrW3QkM82ikQPIi6lQTMlhgb76Fl+0tAYCDQqZKQKt4cvOMBSYkpLJBs2s34EjHJyvqlQWKK22WA6rH0xFxdtIoTVrQlGvlyt6EnQL+5YpIp36IJLLUVitViG9LodUPT3DolAK+V6anlgCtYiy37xSQ8sqv2Z+WzWTmVElu7q+ML1VFYoeXU9KAvtvc7iF29c90cxGvxcSojDWyxvBWLMawdRFsGkaLMJk6Z3FwlN6SvJ6pHIoKRQ9PiEKcHyslwaxUVjL2obmVn63uQlNTVJbW12KE/jqa8QLLZJTRYPhCjdXuPNis/DCKJsagaXLVgWHAPIHGHoICz9PWYQovxAkNcV4tl6OWaKiSCdZpCQhAeEcMUfQ23cjz42oq65CEW4CX3BURlnuSAaM8HB1dlJ+x8FW+LX6bfItiMfSHat1A8LqYm2UvGQlm2+Ixqer0EXTjMGs1/IT89cWijJZFUu6alW1TKRbte6C2J5yNqm04QQaghp0PYRqzgqWD1+2eeOiZ7B9OTK/vHXT0eYq3Hust8y6PCO7BJF9ocaUYJW1ITSkLlgF8oEc6Vx00GLJkmmmm8iT3KSnnsFbeA1Jj9BlIgxmZqZnpot0A8VkzQDb8CpKn46gOn4lEBVaFEqsE68NxLPbT+nxdmlOVodbntSw61QQ39bNO9ufoKxXO6Es26E1EAagKPK59WRXelqWkgHFQom3ICOtBBjYmvj0gT/hr4c939mQ84g2Ik3giMzRVESHcyAxpdYqqy7yHVSP6kpRmhgFLm/izWWvKwXZeILbuAhcGYphCjbZqkulL7R5o9mf55U2NrUhdQirijepBuoggyiYnqoS7TAgriYUVO2d9nPQseh9W+XeV7EJG0kZdg8kkmZk2IAEOdUpuiZmpVzXe7C2KK6wr/MIqV+5mQdX80XXq3KnwmzursF6vskpG7NGU3egFoQqFGi5SSkpySDG6OkwZxTDaokrfkQ1rG9ZMqdzjxnTejDXA7YxSdQHMijRGoOINchSyoCKKqumh/awi8io6LV6YVyRsuYb6bHiJobC3XTR/SrcnAAzbBezdkNBU4DShm5ezu9eicaAJoSaKR+562haMkUB1BQ8Qk9aZiyKVDUYW3wW7Jt7RNXfg3bREzHRpYKM+XHkQnVkuR5VYdUi+K3aLuJCFC/IUDUG/wC++3PEG1CdL7vjMjwuOTrZYAe2AMvYZtu2Nh6j5wE+vn7UQ4TJJ1hSRPjoIVD7RShZSsXG7parY8dxGjhL/Y5by9s4RALhKaiUZ2VsRotWUl6CEhQVyU3LXY7hHTh5eAwnGQAnvEs3AGQhBX4bjw2IwuzlPtSbQEpQJGLWJqwj3rAkRxIUiDzZGWy6EdWtO/fsO3AYx/ERzp3jbCz+kPHyL4SdVtcYfkkBKkuLS1FaUlxUIqOmj7MJ7zg4usDDBe5ujoDjq+ggARbMDUcztrdLTyAoSwkMCpMZcQBJxggIckhNtXCohmDS0u/BkWP46NRZUuAsiUAlNuYvL9eioZrawpGKX8UBFJeWlleAoxo+GHDzcB0GT2LguBGvL4XR6wI23bYDBK2IOXOXraKjIjOJjGWn64T0+YgMJ8YmpaVkWpCflyffZXOWj04RYT46d1Wuycjg1Qhck1wq6IdMukdkhMExzr8c1Y3Au0OF9BjqDmeMlStpsZCkK2jCdrJgYzjmwJfdkwsy57UCxusNqAdhNilJbABJUMjqI0dx7Bg+IBOkfP494EW+ATS/9PHqq3IMK1iB8rISQxpIl2WcvzPg4gAMGwaMmSwCmL5iEd+gHOxAm7hQ87CSR2MEsTyvX5/M4xqIjMloMvPzN/BU3YyDhz/Afhy7zLsb14nzVKDlqwLgFyzN6OOxA+MNzr2UIlBGBgxh/54eoobAKEzhZ6rVvH886ViG8AS0L92K4DzM07HZj7RsRHiELr1KdzBBX4eEvIQUqImJJlZY/dt6tCnbNLxgy86dqIOD/vdve7Y96vZtRV4hcVirLkC3x7+FBZGIVog4thhtD9jqCkwjLjt6nJs+QHxf8zos97YuIVYaSI7wSvjYNPsrnIC1JlZBIpJISqq5KS/2CexMGTYFJpUDiKgz67M2UV5JzUserLjt8AZuV3/9vnge9EGCURMffvnSS4iqpH1ENKJrNPxgDzcNl3DTDbcI6DsYBUD1xrY2ReTTW/SQyDh3ix7YrFOcaogfa/PpdYkwxSGOCpVlUREfG438QoRYv2t//fKla7h4jv1bL3fh1t2+NROAJT3iVNbXqUX6Rfzgi3D2TwuF0M/xudXjimId6uZxBZ6jp75WRpsA85MVW7GVhH4mRF+Bhh+xoBN6I9SAeokx9ELkIf4BCaDRR1aIinYJBYoe36OgxAs43QXreY3khdmVjLD+FYv7r9kJrK0Lqg/BRoLXOXvkDESEjgq7XxIGfXFnuOdFJ5srfEE7G/ZCFPrzagn/vEilus1o39y4MWIBFdqPahAQJKiSYPguEnDEiESSG1JyWNuI0x9TBU/g7BVcuXIVN67dFLpKiRdkq6/l+xQ6yndpYT5PYvHcAPdhw52c3F3ciBoEzDZS31vR2xD66jPB7Tqe/CcBc/tsZ7wC3WQ2lYuf31tiixPNORl9lC5GaDlPHhSy9pg6kQMg0a+6AtfEJ1TsjB7ljQZdu5cgFy5/fe31NWVRtKFwvOWhi85g+AUeqh4kiAsEHy+vFVJZx+iwrZmoSDxZuYpquAYR0bEkwf8vaRm55AEKkBLH01F8CGKxGAIiMctFgwBf/TMfURur6VBQ+ieIiM4EruPKTgx2IgJ7jvDgA1cDg0paeNkC9k5ZZtnSzsNGGhOjEIxCaY0CKxAeLEYhNiHx9yckccXeQ8ew9zAHcVKAuPfBFfZzA/iWd3nVBgyEY8jbxEp8fBPf0QYNo/Kzb2AkjRAlvLmNcakUb/In2Lhqo/LPms6KAH9/iu2aKATv76QkUAcEEZC8LltOTfzr2L9nz6Hjxz86iTMURly8cpHqSG7wUdYKfl6wmFR/C1dOA1/h6x/xpiM8yREiofswlFcVU9HRIp8S4FsRQpzcvk1oMIck86cQGn65KGAgQiMjqUqZtElZlrSo9di/u30HZf3QfhCI+f/8OYa/4mJdu3qNROA4qhs4glwysoIf+JJ/+BfH4uru4iTXzgTzErloIctpw2S2LO07tqOlyLj0pzEOQhivkwz2ygWTAkm51AJxDjjQ/YdxGEQdDoLKdubMGXzMCwrXNeDwhjI01PMVen1scucqx/bPxr9iuBhgZzcicQPQyqdNTQ0wb4JJMDAnWV+6HWpc5Ld74CsDIyZFmR49447gerqHeJKwAbb8pBGSe7Xb6vr706AfnNVzxK5niq6PxUXPXc+PUy8qTy7YuvDloOr8RKqH2827Qx5bPW85ar+ozj1X+MTmEu6UWcui/Fp04hW7DgwU4xueC7GGLPPmwlcIwGoW8iiCPOgVkXWISTd8I+zC3t27gH38O4KjR4/hvDCD5eML4hyQBxXG53h5GZcuUzYJxm7Ors4UP0exUJTB3lJvnALIhPo2dHRsZTt4+xqV5MEa373v54kshfSCEj+MikphUye27sKe1n3Yc0i4cFw4cdRQiJP0D8j7LcY35CBMvAssNmCIQPT7g1ae6R8wCA+C1oSoMmy1VRZu+/fX/9cpLQKa/FWTqdp/1Rgk3FOrqQfm/LSHTz0dVhSHyr42mi/dckYy2DuvEzaz5Y0PJ344kQe5PKLYP366a+wlj2s9ovUsd4bSB7kDccRHPu/+bFfUJl2niDYE1TP+sTY0+QfQaK5YtLBzOYMvLPelVfcXi4I+Y46gX201kdqqIrPwmbDiOJSb/H18seQhHWoyrFPp6cYhXk2EfpwH4ACmm8ebH4+9bgsXj/OGVDIAwdu6k5uVOHD+9eTuKHHfWNRGhceAgFX+fmGU707s3sqBzINvr1qErEY0ZdqwBmE8ZxaXGcqDojJKcd2O/dhGaonk7APeP8izjGQf3eUTFH9OFhc+xuWr2E6V/QJvynMqwTQemuibbmrpjcvNImerJC8HrWMhymO+0bwVQwsC61jvgk2+dqk/39fjC1LT8piwKLULrYioeVSDZxZvJYRuZ6Zg2/IH6JxGCdhjnbl74SM8gwnk96lT42jOoSp7f+J8/j3uRw/9iXbb6Xr83NBa0yatRVjQrKyi/Sc1WlrC84FF+q72SAV6myI4xLcCn9hc2KsjwU7fhAeWZ3LXZaxHdGhxBEJNoaG/GSx4onrRqK/osOIhzfETLOx8+rB24SpOn4TyMZThV1zv/zSQX/vyuzuX9Js2w26gILRitZ/vKkZtLU3+eiOnD/hhlQTCHbuwtZKOHbki2BSIwKV82FZLoxwWIu2IRUSw3EKUCMDRjtRvJiS1ybU4M1vRaFzTRH5EA3EBly5dwY2tbS1kGIsLXNyckdGrd7zvBZsmM/x13b85hsxUFollortP70ODPw87eNtHA/r+9HT+Y9v12FC49gm0ftAH8AG6CoOJi1t7eLmli7Har/ij7YF+E6gKE3BmNExX3C673fnXCmSk42L4vc9VFwqUT3pVZV//Zgp4oH+THtgYGGAmo1oCViuJjcrC3XrPT18VYZm9QpqzsOvbP/9nZYP+S2NKYvZ6BsEafsthjqmfX9yAh7+tRn1wVuaKKtQ89skP/aTG5oBVo0aeHI/TZgWXFDfq/FBkfJWem3Th3984P7lFNXy9Tmip6JKdDEAD5UwJaGIgunrg82t3LunUu5et/bKn305CI9Wxya/Vsmgotv0zpuRb80bEPmdrTUy2S8NG+55fMpNzGGU3UVhW3x9Ys/SXo2O6w/o9fnr6uVE4MwZnR19QFA/ccPrw9qf/sX2dKPv251SA68Nu0gvqr1pXEYICBQTqCbH8hsgcsBO7O1EdT9vsSwE1LOLSaHx8ToJjKRm9DnoWHe343niRlYGk6gyat0GjsJnadvb0qTO0zufEMElZhcV+opuD6Ac4iXfCZBVVkOIjsUtvilraBdHPaUYHdm/H2nmkIocUFCDjoqtwwegsliEvLBRCKYmZiEs0rqL86H+PNy5J+zNncdK4PnvuoqSkli9YHBBLiJg9SOJgDMfssvKqzYYhZP6MBpNjqFPW6D1W1bbfn54K7KAmiuvGFIa/3uKvoMn3fue1J8NzbddmpFMALF0bcpItlvwfCrP/XruoY8THMw/5f/HnPq1Gn8yzgvaRhV7iGRvT9589zKAH82L4B+aq3YSFK3wyfFRRb1tSQPdvULWgBmagw7A6GKvp8GynaRNYmwUfw0WgV2Lw5rihOOIOplOes3Jo5xdDsEbKBPqQDvNoow6eJqkJRoxUDfuzUjS29fcIFmISPDGD6Zotbe1UXUMHGwVPYSYG1gfVxqJJWdyBHkhGRGGyKdBKiGxa/odaTOLAwp8zkeYZqVbqXULujF0Ycw+D39qP8YPeqsPt22WPD884AvXIVBywU+ijfbSw6wVYYtBn5xJ2ZtgguFrxl6qwyK2619bN0GkVKMHM4tUq9P16mJd44fkB0rh29dx98CaerGpZpdooPQ2bPb6buOccE4L3S9KfoI8p2at91sH5P59cQpFjmUUT4N1W5DiZ9D+ErgX7+k4+MaFyb59nn6K0GeVN+zsYIULp8tSoLC7L0A3R4dPqJw8bNWpBONaEBKwKF9tMLcC6uVhM0RM9CFq9RsT84gdIY4Z2fZYkSCQFgaXD356CQWPkE+QBffQTZ+mPHBCbdOgofTApgek8nKDgsbiNcHUcRnObY6naLnmgLVsoiYYq1NfVcgC9pZGwt8eY1iKpWOVP0iByNclyjqsD4pNSQ5NjMI0i4iHsJLZOode/kv7NUfa/Z+9eeU8sITYKMXOxde2QwY688uQwXF0lxGzZTuRua8NmigclsamBMkD0D2rwtm+0Lt29kNxn6Vixld4AL2qiysJtM9LtOfXIvo+0AsR1lUz9zfM+Lnk+5GOruGHPbk5Ax5PDU2A1z6OL+gfzqHMKvto5vk/fpLIVS6yfOXpeFH95qKIteAYbTNrWFaLbKzf5bqYCQBFcpOL5U97rtnd0EoyS5ht++n/RKUK86sLIdevjOX4EvYdppCXdmtEzokgBDCUQSXl/G3YdbN8m3vk50EGMoedHFZru4ODkwTyFqwOxyiD1FqM5ObCJNGgRKOLigGZt8LF75U8hu6EsqA9e8PgwG3G1J6gh1NZcFDKg8PyObjvxROKtxQ4vH4GTzXP0RBH+j3+dRUzfP0WWRvPZZuUPc9q8j9mPYdLwhhMsl7/6jLDXdl+9iRG2p+Bwm36N2fwHwV4mZOWFlVRFspn+QDU1QdHTSAxmE4NTTYcX+bA6hEzo/3RRrN290yP1/uw/FV/fRf8j78L+8k8Pxi6cUPnzd1T1nFdg2nHk8E47n59hD5Mq3+bBcsgWE3LXnL990xOq9O8Gn37agODanupa7yYRACn+sl6o0ufWAzYTGSUuRZ2+y0jc1deRBrYWqOW2N1HeTSkwh3X86vjxDFtobhdPP7Y/sfDPXcwd7DchQukzQ1va0A31+IRR/N4NxzuUNDs8/BmzXXFxlOk93CYI/Dk2uS9sTGs0OjB+aCRQ+VPFNKiraySXDEutJMt2hWTTJ/QT40AadCHBjEqKgQrb7PTPPC9oOHxjjALPsdb2Cd8o3+eq0PqgdMl4BtTmwI4F1tMyDafbQzGAzvijAth1e4w8d/ojV6jd+GN+5cq2gJCmNfwayh5WEQTr6thcpdFvNGGVZTU69ygkySKNFKI2KAjride6Y5CM+CJov07sfog7fGHgxR5bXPU8cYV49ufWeZOORu/vpDiJczdVw3nOhV8cyGncXIIO06XzY8bjqpvVHInEPu18Yscgg7in9JQ+RIhWL4uRwZrW7G1uJQ6p81H/Tc6sfjsClYYQ1DEgS4S+kZ0SnwO+HPCV2139hQG7htyF+x8fnhx6J87N1EVxkbLFbKZ9wDG7sWdH83z7wcnTf/sECLtGASQSezy+lWFnisdm3Vdao6HHGl6qx6AkRpJThlH3s9Rtw969uxqSpULyvUEha2IIPRC0YRnPP/93XEcNF8M6ciYzzgQgllNn6mmRqQj7RHk+IhMuiOEDBr+NihQi0MQxzq5USimt1DuSdwtj0zpUVVUUF/Ne5esKsZnWew+UxcihJAj9JdVWQpLV4oNBSSWYenIRFjZrNiZ7xt9Tnj805JWsl/aI9Rs35gf6XaXA3P/s6dhrHfshY2DDg/iU4plNdn94RrnqeSscOU1t4onT3nH5s0GpDwszm5UiyTqFMPT0+m+42EhTu9yP85ckFSIyJZFEt2vSKPaA+R5jIaLqMHU4Esv2HDiL3cf5dD2zNmFYQYrsBCnQSSQLDl3CB2nACIyTpbn3UmXqzcTeei6Uih2mNaSZL+EA2A8lyCudp337OuTJkpWBwYEBAf6rUFoqjeTRslXTJMU1UWj5Lt55k4BN2Hv/QMiMqeNGMOdCZyGVlJUw2ShjjDrMFr/BxZ3WQcwJswGNaGAoQOmvQ0Mt0xeFrPZjioTTqtnBAezi6qPYGY7JjwBrXEmeZQHdFKojZXuQK/PMfyVv9xw4f5bS4Ew87m2WIeJ67WKcB09O7iOYoovB3HHyzN0hoNhwQUTx6huYu2AOj4WM+70smysX+/YJNi+cRTvg7x/gK2ItUjKS85jkPm61v9OwIdKMJpZdsi2LMVjO/yBDmPW5RtUIt/fEbLAMD6vD1PEuHOKo1GJqarP03/tfOFtOg0kJkLJy+Rysr2Gcf2hPQ+qyeeR5CMICJkhUSi15G9MxafwiCU+HcfoOTu8wAUfWsMRg4ajwZUyW0zRE8n7rVV6R91vop8kFpX4UXD0wU4jT2FhHkZZtFXU1qCwvQ4F0zyZitubMWVfDefAmHYtWGoZr1Erq2O55nJ4vq+cjJHG8i8NQVwxjnBtD28c9BAnpRuo0dz+NE8WVLuUnFxJTCdD5k8gjtwnedFRZhCcFZD67r2vmEBjuV6C4gLVV/ONWAZWZ8v1QdlD5DrRmoGNzaGU0Z7uZOrZw7xvAD5gyvwtP5b9utio9w8zvdqPvzsWzzqakbOxLmATuz8H/4emUdOR2W+3znyFAnDl+genjE4+92me702qPR545sEGv41YGfyZnVmvl3QXdPfnAq1xzIgzQGzd4yYlwXl6cMeWtCHnkq0FIeIwUPaXxoA44O8GVOnX0QrIvtQ9clS7cWMKZVCE3Q+jZyaWaBNIUDpx4ByZzdYgszEGzBAFsVo0ati6iXvDuI/4RclZ0aXvecxZ5w4Ef/bCw/yZebej6+88233xMdeBXPV7cl7CRsYKRZ3l7fN22Z6fkXH9lYL/4xsAtzJ2s3KFTELjTIp1oPLn+twcPN8jHxp5GfIFLj81V5OvPqMZCLsOOKj28VLPGF7y65Kw2Fh+yf5nc+AnRHNdB7G/N8gJX7dZlUkjjp42g+xQUMIINpJHfLE8nisCENOpnDQITOZ+mduzZvZvPekuFrNsQXSzG7WjsSqMnBJcYalOjgKqUCkr/xlyZ/7lTQgGWBfPJJaqOrAMia/k8r7C0DflZmCpY4sNstZM08p1P+o914MEowyczPsmvIFn3yv/dHBExhVT8aCvKRR/HuAOjNxdgqLMjBZSzo/Qbi4lcQNooDc4ynfcRkVPBXE0n66MGPbvsgGL9adWKR3sQaScyOufXU1jT9/MDvHS2uzDyPFdzBpl6vkRp9JnKW5/G9s1Gqa19f9t5B5/o3Q8fWSNhGeAw5fTY1gcPEojBT66Oe3SpIkJS8xvVZ/z5EZZKMDMSlbcOH/QdfXrsaaY3VZUTPzhZFu+0ztlWApK+xy+ouyA8MRh/eAOe1VbrCCr/9Z5R3ehan9X/0y+xPvrG+RufQs/O3KBr3UvmESQXLut5EsngkZZzLPwUE7t6oo3VLiFixjsXnIITbP2JwlLCw61RWkH3RkzRT3Gn0SVJX2PW7BlG/NDe2bGPrFo6k55SESYJ1zHbF74jxmLwYA+alcwo1ngkGxlqomOSNJC8cYcRUhLVUvJ2fHKV+k7yzYHnJFquWn7FPRk14vLRAleUl5bylczWk7K7iwB24/IlGrnZ/KxneEV75+7eBWnOhHYsng2IRdKNy1s8TPhvenUnFv/FhdOGJTu/jA82G/3zIoVtr7Ojio1ZcQLY7IkgJ5rc2GJIYDUJXWoA4NnTMoAbuHEFynyrZn14Xx/xTiTTnmxMx+AlpdDv34d9f93rf6/DqBmmvWz7pvZPtf2tZ0ZR0PDWl3Otf37K3sZsaxdWF7JJ9WkIsvT06bagcegLp3/TwjP+cbHnNtvFFXGbic+Wkpgma3CNBCA0QNFyxCmF9OF4na9jkVy48KlkHfe18iZRgGgOL6YK+HjDVfSQi1vTSaky4hfewCgySkqxLIc2tbZSw9IKkZNOOytGLo3+9UhIbjILb5MaLQ111TVV1dWGc5EtbYwQXpa6eDWff550qrYaJi4n0AhMMTeG9t97pN9aIeb4QQZF2fAwNZUJF74Vuo6hqljU2sZm3iM72o/HI6itECPFKU3mENpzhhuJ1nppQSXgswKaOPFbwMUN3LxBQ2Cdg0l9ZpQyEOmkEiQ/nvk4kOvPNvdxBfcHtj7JCrkw7OQrr1+InOrk5p7+6wzO/wu+bmfSabigVFatJsBzailoJeHu7aWbnf29I9ctFMUBXsn2jGiI95w9G2kRXIBM3U5AuXDtOhXwloLr6rz9+szjJ/8gYLdgH1u1qds01I7q+rtHwExCXnnXi7NuYvLX+Pa3d64s/M+3GGbLRjRilUqqhfARbmUM1wybCjyX/0rxgWe79Cg8+PYWPKbbmczEvL5s29SINUwGVzG214s09D2L88PpJjjdcnTUVcwTbk5eJfq0G/u38AZ+CTnU6NXAtAVBEciMxfwwkpP6R81YAvcRvDFKenYBuJ77e9JTpPPcyW0EPTg5OY2ZPfM90YCliRUyeRp7YQBhGGXvnz17ieucuHmTd7eVGfqR6Ud4ha1mxU6ZDZ+fDvFmwglMP+Ix0GT7/P3X+6Zj0g830fjSjKUO/6hyhq39KazuGliWrpIHLNVrmLFEVRgvz8vYmElyUq5jWtf9K7zL7W/LTZNsw66jUKxRqM6pI0RfnVl124EJB6NkN3AdZp8sR01fxqTHJH84T5GElTjIacsGITSxnVfJxCMDvWiz11kysvNpAQpRXl7JORJrcPEMDyFDxQ2bQx1ioVwwH1dLurBNGZcUeX+ef9c5/VscwB31fd6Nh5eiQhEhpCC/EFWE4/cW2XWPx1MLsPhvyPz1i9Sa/OfRU5SDj12Yb3Cne++nWaAlQslfi/tc1SsOfViB3XfHIDu/7o6J89tvMxl/RUk/lNVDJzurwivLonr5ZcatG87Mmqp37zhAHTFy3ISTU1RVwSIT8zx0ykt/yI5w//nHC6aTs198Dg+PwfsIsk5RKYbeeJsDdBzByHNpe+tGKNYsyVjGfEEljsWtiMSF54B+iQ5Ol4W66jF8tSxmYIUazLQvbUwFokqjizWL/zkPSskNUmDoEEX825F4b9wcSdcbCx4GTBDMWWii4BUsdsyHFQdXZcPRVepHjR2PuQvkSjTM2FJinCmFxlfkZsy4WRg9DbOo+Ny6UtvrChg8wI5LBvG5m+zu3bt3jDfpukrZx7XQrSWYPz8zbvmMZYQSCgEXRaSU86/340y5GEowB0FxNBSW3GJ5SNtR3rarY7e0fZe+syvGz6fTLoQQ4ajnkbpQxrtsohej7Nt3cPcT3L5luGQ03h8j64UgHFAl3T7hRFrmlD9ab73QXxvcz8Lm0eRcwcvL97R8a75M43Z55PmJH04/MvkYom1scrNszabo7G5dM9vbdCnrK384ds9GFUM723zP9j9sXwszvbE6LbRKt0bxazj4uumd28rQTwffHXJd4zqaGx1oLPNhBLD/wMEDWyQNGyqibwQd8ZI2EexkIMR29E7dMGIMxknNXLaLR2bORgEAWJBMMlQUzGNE5C6e+PyFrJ1E4yylvp4JOXDNK5+NPv+cs//8M2M9DbdUkusKtvdJ74amz5rts3HX5MSahRMbRg7he4Xk/cv+30cR3F++OMRVk8yae/eZkRqfjX24sIaBrqbosQUoKHwWOS9zG9Tf/ul818U8WneasUcnB7uZBqwHOw8OogOtKEXcdwlF/VR919pzCy63qInmnhuylFJv4WrVnP349Tvgx7BvP8T5oYe5FwQRz3Y9rEH8d7iT7aRq6sfOin6F3bJYu3+c8zQnnyR7fAaGNBPwWzm7C8Nk+Zq2fon+Aa0ut1WqRroBukARcpNzTqr64LvQuI4JxxuO15RhN52UF160eSm93WuvgvvemPKB7zfmP351adp/+rsV8p2Un4ki8GrnYYTNvRu92xA9TaoJ964v285alKvh27UVW1e03wulfcdw24fmC1yrfaQdHutDXhq7JImFFd2xXCMH/re7m8pnrKZew2MxnE5jeV9JD3v//vb8JWNpF8QGT3ShDzd6MWQfMgsZ60K3CG6egqEERGLosNEUFpKgFPTPaXSo33xz+HtsTe2ZJ69R9KthbK6rLCuif5DAA9l/99M7ROOPSRwmutDziA3DKTdzdK/EnadbKICTzeMfaUNiKl/chd++T6xG4TrKiDrBFmO4VYKzNBE/NNw8iwbv3LjUaDzx4icCCmB1oxmmpJjgs2SvwHxdFH7MW/PYyoAkSiGAWp/5BNbbt7XBVvyGQ1PpKbrC4R36P4liDTv5lXT+OY/HuHE806maPDEAUTn8bYFUTzLqeKCTNJp4sISvGTEWndnmTe0CpCwe/ObwJXI1VYjAPXmyIbCoBIX52cnx+/HJTdZeZzJjgdHT+DG0mvxy6RauGe0WizKTS1DzBJvIA+A9FHgh1RuNyXCdOpnL09wQze0wo0fSIATQKbLIWlYlLU1FC04wMCldygcGAvFLSzlwdo6oyGiiVYYxO0P9bsinKQlzeFo2yXP4GHht2LxrJ++aOayJbzmQv5OF44n+KAheGsAHOfTWMZ4Xzs4cmetoEYOQ9bz/L0bKzrxzuHKDjMWbAgQEcy8OII84GWsgC/EFYUduiTt+Ay2L5HOLligbHmdg2oMH1J2dymLsWOrzVhoGK8+9tnnUsOqxP96Nuj+wFKE1SDef+WD6b2cohPpVDsJ8eeKHmPzawKIUsyXXnIAC1cZ+YP++E05Tnu/eH06Yst014/DED+vvmaO55SCjKxdB3d32TVjk9UaPjaa5YMnOKTaHFjM9TQJGr6S0ZGEnVw5lQswB9pbZo42NDzME61O8e+umk8We8HAdRQmbQqBII2ElJiwxHh+XDZbX8Gkd7yZPlSqjfiMvkuIieKRWigHgdI3UtK+cS+XgxAF0yrpxM/wYATuMoQyMkQfhE+idB4glCkP0bFYMJ3WpZhOmwnM8ElLXGRwoKCijS7Ub7x87YeymkcXJURSmSPoB5WWlxcjbkJGWFIOsMFykDeQHhjDupRAt81KjH/Ii2DQrdYtKvrWY6wZSMfvan4M76e3pUnmCjrMWyWdV+OFlSpf5Eq0HLp8wr7n4KMT0SGXoSWcxPooWv2fPtO4JJzVcu/XJ6CrKwyH0Ly9TIqP02CLTerPZ3CcltT88hwyRJZS72OKN6CbFTi1NKmf64urBHEXdt3+/2vPzp7g9VH0ER2ozLj7DBfUjM6z6LxasXfJCDbVHR4+MYIxt9dyerq7C3OwEhcFgCRXaunQ+UdqqXdAcNes0JrdGom9k1BqUxhTHxecnq5k2duiz71PO3hPTl/usbIspXWlno74N6w7bnFFIFvyYoz4wHeN2k34PXVX74FGesBu7dT4O3/vtF0tdnzv3Wtwx7hwDukmeLmf6wLa7x4ycFAqCSmsVIpHk7tmYqOlu0AaZzz+H8y42dIXJHCpBYn6K/EjEMnfwJ7i1G322bekT9XjF5tY6c/foGOywO0e03z8HB357HD9v7x3P4463MLGeEdH3r/AnOmGPf2wpDWHOapX4Dx5Pbjy56DqqT0SFi2rKIFCblbji2MrwehvVdyEO2dBk3lDw6rcT//0lM8sEWJRa45BnzXqSRes00H4wHn+9dIdEy1geqNar/9uTBtWKkdltTJKpy+2Y73CmZXTBh3z3i+v/gnXeE11fSSBxFGk5CVqh09DPNVXgmrJB5a7b+B5KjRXBVt+t6NSnaCO5AefOZ3+ZOODVy5QMOkx63MZcLYm/qDpyqY+N+untf3+zwzsgIg4r7MxWzmjozPyORW5XMt9cQW/l/vKMdBebiw63B9tP/77VpU8P5WXys3+6carIxCFwkXTKk8fcKsoSV0QhfilrQy8WoUw1hzKqslv4vs1EPr1tNtu89rzrEWNHKwq1Hq3HIm/hjq31/kUqZAgJ4NWvXqoGMywtJcBuJZIfJHS7j3RkreNy0dEJTtKCaBlKQMuTq5FygMfkMOOcQqoWII8BktzSHHTsO3KccecN6vq3FYy8qyrKuKdYioUbtD+XRf07SAlcSaUONqqXiTVcsds05WoqExW7u9sqyvud59uet/7nB6acT2hGK2yv2bAO3KqPuXaEOiYhj9nzODHMpOQUcAdpD2JJjzp/XVvUo006Bd1Jv4u/DIVdaZgSpcXQs9qQrefYH32bneFRQ7bdZn8lmrNfHYBu86saNtN9c+VcJGkuv+ci1PZ4Xpw06+BwukzuZoK73ysPMGv/QMx86kXzc53ul8/7FPEnFX3szGoSCtfyhY0KcaBBY5bxAOXDem3Y7U/efY8LeeWKzF+PR44Os82ng6lpP/0Tir+iE/+I8MTeN9hAXMekLYxmDqAmgdxwoMtHU0FIH/GO23CMmYuI2IgM8bil8Rh4zJNQdRp9EYMt2JBHRpRXoWlT+47OI1y1uUqk+YSMLmNA2ssCwx3nXscvbm6Xb3Bvhxf1yhd+xAuWxuXM9ezdx4R5rdyyH3cHWnz2TRmcSC+YiGsUNwyX9YdlkcmWmPf8pUq4ny/ncv5AjHjccfC4oPHNO3e/3NUrGuWE4vycbOSXMn/BycbwYBTfFVhFE/NXYxvS2ARagn1SP9uDk3fmxeiR44bDhfHN8im027PeY3xhyKQj506ye01mHMhmJYUMOfPpP1eirpFLlixEFcrap6TDGiN6KiOPCsrLkdvx2RdnCqPh7edt5F5Jgjl4642JstFivLHYs59pAHr2rpQC8UgkZDD8v1Hv0k2jJfu9LIiMT10/kTYSBUXcuk8i5DOzV2k85bcMHnAAkk0QfEzNyuv9pUMBV8KRQvFfNWsBLZwUsvp1carWIqqhYw99An7F6HrUiNGYMMaJTssYWcQbg0nezFLxVn4VgoR4yoBsvC8oRlFxkfGbhxJUVkullPNEAuBrzJC1nkVLGaWnVzSV04Z9RdGbL0Y+IJB0COYnzYO6XXTsXjiBP+whDnSFr/7tf4bdfPcT07nR4mE5ul79jT/YxLtvbJo25AjuOPbANPZ0JMy/urzolIO8+EImE4oIpfLjJi0cDWZbLy7VES20O8TXfrvQf+GjR/TX5rzCqW13/5xR4th5XMllDqotUBO33pNuHg4VTI2ox949dAh6CwVNygg5SMp/A1bRfgsB4DYzME7OyOZPPTaS972FZCytRH3Tpm3yDYrhbZr9GNmis0z4O2gSg/qDuFmP0VP4PMxvySKfUP/Z1PLXXzNnOczEAqYXlHlHphMMPrO75n5ZNv6MPqvSKLk8dR9Lrdnf9HG7or/7CRye6t+fv3D6fuhWdR0xVilUVc6euo4Ca3Ql+ctMy9GpIy6bZdd9yeLacPRZ/pBW5QtGFgMwzMvzLDvrrOIqyZaoBwdgyxcM8fOmAu6jDKYaSugED3cnJ0MaPPl8vIgzldORK3gs68RdJQU2bCzcSAAooxwUiSAV8udVXEc2HLuL127euUNmB/CXV0aZCZz5aCcHKAT4vazA2AnKrFf6FWD/v4JQ+9wiaiIlhERXL3PNpe+ffjorW1FHnh/X74XmqUe5O54MuMI1FFfbN5/vazablET+PLA4lqZE494cXedibEST2WbF73uquJU1oKtN8G5JTyf9XX55jHXAUelh+pGlf6zkLwtlKiuDJTVFl2sXebTXcNVE/cZRAMZPEyQiNPBvDoY4DB06lGlzDyO9yx/YSSkoKC5hlsq4pjRWMC9LKDhITeytWmhsEfcN4Oa946UM+UmIgEhxcAON/BXRzkiC7G2Wn3qTA3vlNUlykeLD50q2WIo3U4fh4xzgMAQuVNLVrEq3MDWQazwVt5Zp+CIYq+FiYfcc+uAjytwdUXtyLyIU0TERxtY4I2D0m433KNKs4cKKYvzYALsWo/wlO9X06OrZx13XSanz0/9pfuVzchFz9739Vp97b//03b/srpMQTw2wKUVKtsXCWFuFbmZ2jZFgFOh9okSN4l6sTeQBjk/iq/js71W2gkx0HmKLgxq4+bAdAY9J8Ll/6Z8nDeCqYLj51cXz5LpjEY7epxywjNRIQY9LDi9+EP33vw272+PQMt9Q0OHPHYywK0ywZa/Mq6XkJuVDSWDgwSR8uRJRHslXa8y2vthrItcum0zDrlf89FRruL2NZi2MKuOOCJ8t/t0/k0FBz21g1PdI+OTiTuxniaX6cNUqybgxDlOIoksRO3TFrN4WU950n0nyr8W65PTUdDbJEi+lsJDp2rIyYg2z8RQBWtb2rbv3HeW2VpZP5WCUtXFITSYI0+wxu5OEGJ/JBJvJy+jpu8w9JCPh6v/BIzv9xzg48wHtDcntzgDPjxdDJ/433PRBTEJSMrsnC7INM5gny5BlKOVPyaiD1cxMt7a37+zEh6f54k1hvHfvHiZsIJph3ixj5yztCNXRbZIX/h/C4cKxpJ3IkAAAAABJRU5ErkJggg==",
"text/plain": [
"128×128 Array{Gray{N0f8},2} with eltype Gray{Normed{UInt8,8}}:\n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.0) … Gray{N0f8}(0.627)\n",
" Gray{N0f8}(0.627) Gray{N0f8}(0.624) Gray{N0f8}(0.388)\n",
" Gray{N0f8}(0.612) Gray{N0f8}(0.612) Gray{N0f8}(0.0) \n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.0) Gray{N0f8}(0.192)\n",
" Gray{N0f8}(0.612) Gray{N0f8}(0.0) Gray{N0f8}(0.0) \n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.0) … Gray{N0f8}(0.2) \n",
" Gray{N0f8}(0.608) Gray{N0f8}(0.0) Gray{N0f8}(0.0) \n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.0) Gray{N0f8}(0.216)\n",
" Gray{N0f8}(0.62) Gray{N0f8}(0.62) Gray{N0f8}(0.208)\n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.0) Gray{N0f8}(0.188)\n",
" Gray{N0f8}(0.635) Gray{N0f8}(0.0) … Gray{N0f8}(0.0) \n",
" Gray{N0f8}(0.631) Gray{N0f8}(0.0) Gray{N0f8}(0.0) \n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.627) Gray{N0f8}(0.184)\n",
" ⋮ ⋱ \n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.129) Gray{N0f8}(0.0) \n",
" Gray{N0f8}(0.149) Gray{N0f8}(0.129) Gray{N0f8}(0.0) \n",
" Gray{N0f8}(0.216) Gray{N0f8}(0.0) Gray{N0f8}(0.208)\n",
" Gray{N0f8}(0.345) Gray{N0f8}(0.341) Gray{N0f8}(0.231)\n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.0) … Gray{N0f8}(0.259)\n",
" Gray{N0f8}(0.298) Gray{N0f8}(0.416) Gray{N0f8}(0.259)\n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.369) Gray{N0f8}(0.235)\n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.0) Gray{N0f8}(0.208)\n",
" Gray{N0f8}(0.22) Gray{N0f8}(0.0) Gray{N0f8}(0.2) \n",
" Gray{N0f8}(0.0) Gray{N0f8}(0.22) … Gray{N0f8}(0.0) \n",
" Gray{N0f8}(0.196) Gray{N0f8}(0.208) Gray{N0f8}(0.345)\n",
" Gray{N0f8}(0.192) Gray{N0f8}(0.0) Gray{N0f8}(0.0) "
]
},
"execution_count": 12,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"using Images\n",
"\n",
"lena = load(\"lena128missing.png\")"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"128×128 Array{Float64,2}:\n",
" 0.0 0.0 0.635294 0.0 … 0.0 0.0 0.627451\n",
" 0.627451 0.623529 0.0 0.611765 0.0 0.0 0.388235\n",
" 0.611765 0.611765 0.0 0.0 0.403922 0.219608 0.0 \n",
" 0.0 0.0 0.611765 0.0 0.223529 0.176471 0.192157\n",
" 0.611765 0.0 0.615686 0.615686 0.0 0.0 0.0 \n",
" 0.0 0.0 0.0 0.619608 … 0.0 0.0 0.2 \n",
" 0.607843 0.0 0.623529 0.0 0.176471 0.192157 0.0 \n",
" 0.0 0.0 0.623529 0.0 0.0 0.0 0.215686\n",
" 0.619608 0.619608 0.0 0.0 0.2 0.0 0.207843\n",
" 0.0 0.0 0.635294 0.635294 0.2 0.192157 0.188235\n",
" 0.635294 0.0 0.0 0.0 … 0.192157 0.180392 0.0 \n",
" 0.631373 0.0 0.0 0.0 0.0 0.0 0.0 \n",
" 0.0 0.627451 0.635294 0.666667 0.172549 0.0 0.184314\n",
" ⋮ ⋱ ⋮ \n",
" 0.0 0.129412 0.0 0.541176 0.0 0.286275 0.0 \n",
" 0.14902 0.129412 0.196078 0.537255 0.345098 0.0 0.0 \n",
" 0.215686 0.0 0.262745 0.0 0.301961 0.0 0.207843\n",
" 0.345098 0.341176 0.356863 0.513725 0.0 0.0 0.231373\n",
" 0.0 0.0 0.0 0.0 … 0.0 0.243137 0.258824\n",
" 0.298039 0.415686 0.458824 0.0 0.0 0.0 0.258824\n",
" 0.0 0.368627 0.4 0.0 0.0 0.0 0.235294\n",
" 0.0 0.0 0.34902 0.0 0.0 0.239216 0.207843\n",
" 0.219608 0.0 0.0 0.0 0.0 0.0 0.2 \n",
" 0.0 0.219608 0.235294 0.356863 … 0.0 0.0 0.0 \n",
" 0.196078 0.207843 0.211765 0.0 0.0 0.270588 0.345098\n",
" 0.192157 0.0 0.196078 0.309804 0.266667 0.356863 0.0 "
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# convert to real matrices\n",
"Y = Float64.(lena)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We fill out the missin pixels uisng a **matrix completion** technique developed by Candes and Tao\n",
"$$\n",
" \\text{minimize } \\|\\mathbf{X}\\|_*\n",
"$$\n",
"$$\n",
" \\text{subject to } x_{ij} = y_{ij} \\text{ for all observed entries } (i, j).\n",
"$$\n",
"Here $\\|\\mathbf{M}\\|_* = \\sum_i \\sigma_i(\\mathbf{M})$ is the nuclear norm. In words we seek the matrix with minimal nuclear norm that agrees with the observed entries. This is a semidefinite programming (SDP) problem readily modeled by Convex.jl.\n",
"\n",
"This example takes long because of high dimensionality."
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Problem\n",
" Name : \n",
" Objective sense : min \n",
" Type : CONIC (conic optimization problem)\n",
" Constraints : 73665 \n",
" Cones : 0 \n",
" Scalar variables : 49153 \n",
" Matrix variables : 1 \n",
" Integer variables : 0 \n",
"\n",
"Optimizer started.\n",
"Presolve started.\n",
"Linear dependency checker started.\n",
"Linear dependency checker terminated.\n",
"Eliminator started.\n",
"Freed constraints in eliminator : 0\n",
"Eliminator terminated.\n",
"Eliminator - tries : 1 time : 0.00 \n",
"Lin. dep. - tries : 1 time : 0.01 \n",
"Lin. dep. - number : 0 \n",
"Presolve terminated. Time: 0.05 \n",
"Problem\n",
" Name : \n",
" Objective sense : min \n",
" Type : CONIC (conic optimization problem)\n",
" Constraints : 73665 \n",
" Cones : 0 \n",
" Scalar variables : 49153 \n",
" Matrix variables : 1 \n",
" Integer variables : 0 \n",
"\n",
"Optimizer - threads : 8 \n",
"Optimizer - solved problem : the primal \n",
"Optimizer - Constraints : 32896\n",
"Optimizer - Cones : 1\n",
"Optimizer - Scalar variables : 24769 conic : 24769 \n",
"Optimizer - Semi-definite variables: 1 scalarized : 32896 \n",
"Factor - setup time : 231.01 dense det. time : 0.00 \n",
"Factor - ML order time : 206.00 GP order time : 0.00 \n",
"Factor - nonzeros before factor : 5.41e+08 after factor : 5.41e+08 \n",
"Factor - dense dim. : 2 flops : 1.19e+13 \n",
"ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME \n",
"0 1.0e+00 1.0e+00 1.0e+00 0.00e+00 0.000000000e+00 0.000000000e+00 1.0e+00 231.11\n",
"1 3.7e-01 3.7e-01 2.3e-01 -9.40e-01 2.723707186e+02 2.783663417e+02 3.7e-01 358.60\n",
"2 3.1e-01 3.1e-01 5.4e-01 2.89e-01 1.669310739e+02 1.662436137e+02 3.1e-01 499.40\n",
"3 5.4e-02 5.4e-02 5.3e-01 8.69e-01 1.629170332e+02 1.627092805e+02 5.4e-02 646.21\n",
"4 4.3e-03 4.3e-03 7.1e-02 1.20e+00 1.486177530e+02 1.486148653e+02 4.3e-03 796.20\n",
"5 1.6e-03 1.6e-03 4.2e-02 1.01e+00 1.483660057e+02 1.483651653e+02 1.6e-03 944.00\n",
"6 4.5e-05 4.5e-05 2.9e-02 1.00e+00 1.479825741e+02 1.479824023e+02 4.5e-05 1105.40\n",
"7 1.4e-05 1.4e-05 5.5e-03 1.00e+00 1.479752237e+02 1.479751933e+02 1.4e-05 1254.12\n",
"8 3.5e-07 3.5e-07 2.4e-03 1.00e+00 1.479711707e+02 1.479711694e+02 3.5e-07 1416.05\n",
"9 9.0e-08 8.3e-08 3.6e-04 1.00e+00 1.479711088e+02 1.479711087e+02 8.4e-08 1559.26\n",
"10 1.6e-09 1.5e-09 9.1e-05 1.00e+00 1.479710826e+02 1.479710826e+02 1.3e-09 1728.32\n",
"Optimizer terminated. Time: 1728.63 \n",
"\n",
"\n",
"Interior-point solution summary\n",
" Problem status : PRIMAL_AND_DUAL_FEASIBLE\n",
" Solution status : OPTIMAL\n",
" Primal. obj: 1.4797108260e+02 nrm: 1e+02 Viol. con: 3e-09 var: 0e+00 barvar: 0e+00 \n",
" Dual. obj: 1.4797108259e+02 nrm: 1e+00 Viol. con: 0e+00 var: 6e-10 barvar: 3e-09 \n",
"1735.908026 seconds (18.59 M allocations: 977.941 MiB, 0.04% gc time)\n"
]
}
],
"source": [
"# Use Mosek solver\n",
"using Mosek\n",
"solver = MosekSolver(LOG=1)\n",
"\n",
"# Linear indices of obs. entries\n",
"obsidx = findall(Y[:] .≠ 0.0)\n",
"# Create optimization variables\n",
"X = Convex.Variable(size(Y))\n",
"# Set up optmization problem\n",
"problem = minimize(nuclearnorm(X))\n",
"problem.constraints += X[obsidx] == Y[obsidx]\n",
"# Solve the problem by calling solve\n",
"@time solve!(problem, solver)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAIAAAACACAAAAADmVT4XAAAESmlDQ1BrQ0dDb2xvclNwYWNlR2VuZXJpY0dyYXkAADiNjVVbaBxVGP535+wGJA4+aBtaaAcvbSlpmESricXa7Wa7SRM362ZTmyrKZHY2O93ZmXFmdpuEPpWCb1oQpK+C+hgLIlgv2LzYl4rFkko1DwoRWowgKH1S8DtnJpvZDV5mOOd857+d//wXDlHPH5rrWkmFqGEHXr6UmT09e0bpuUlJkqmX8Gm672aKxUmObcc2aNt3/zYl+HrrELe1nf+vX6pi+DrWaxhOxdcbRAmVKF3VXS8g6rkM+vC5wOX4JvDD9XIpC7wOLEe6/Hskb9iGZ+pK3tMWlaLnVE0r7ut/8f/X17Cam+ftxej169MTWA/C54uGPTMNfAB4WddyHPcD326ZpwohTibd4HgplE8ONOszmYh+uuqdmInoF2vNMY4HgJeXauWXgB8CXrPnClOR/EbdmeB2+oikPt3PngF+HFitGeM8Twpw2XNKUxE9qBijOeBngS+bwXg5tC9967emcyFmtFTLFsKz2MBZ7WQReAfwUcPKl0I7rOwGRW5zGHjBtgqToc/siuHnoruz74NaeSyUTyUDr8x1HwXeVzVPjIf+p8Zq3lgp9CcVuJaoraeBl71mid99H/C65uXyoc30AxVtlMf5KeAhOpXQyCCH5jDrZNNfuK9PJrUEcskDr4q9RXlI2Bgedjp4eSCNFoGKMSkDOy4T7hSqYKfQvNDyBeJW7kZWsnvepyaoNdoAtQb0Av0oKAv0EzWwZkFtgjffZTeL1aYleKBEnt2LbDpsJ1PZkxhH2CR7jg2zEVLY8+wYO8pGQR1hR2Lex33n3t1rW3od58Z9X4FEAB0LntnQ8UWkluhP8OtCMhatS7uaB1z3nTcveK+Z+jdv/dYRPR/yod2fYdER9Jju9fOf98Xju8o+eeVW7/XzNBXPkshbpTtLqfXU3dQq5juptbiN1A+pNfx3tt2X+7OZlc3cZsCzBK2BYQqO37bWBA4wV4XOoQ6Lcey07c9jONtOcf4xJhxropZiN6val3a57qsf8GgabxTuF+hCv3pF3VDfU79Tf1VX1XeBfpHelj6WvpCuSp9KN0iRrkkr0pfSV9KH0mfYfQTqinS1q5LmO6unXbN6VGGcG4h8Z2JR4dTN+50Fb8tTQ8Sh84TO6m+fJR+Xd8uPyaPyXvkJeVI+KB+Wj8k75SGMQXlM3g/O7naUrCgDZlfHmTQrYhXmyRbdpIHfwKzF/AplYzFPPIg4m11dvtn9pujGsDod7DWaATLpnND1RX5s0f3d2kvidCfxMo8g28MG2XjUgxl2GF040dGPw7xL07n0aDpDSvpgeiQ9mD7J8VbtpveDO4I5F/PeaEd2q4fmRJ3WRYxaQsLHTIGxEPBHJuu4i545XwuUIVV9RsngeTWUcVsf6Fc0y1IEy1c8wze8llEZIP52h8/T7y+KNzmx44be9FrRm5VIfE30N7ePkzQTJdzgAAAxm0lEQVR4AR27R68ta5om9NnwEWvFstsff71NS3VWQtKtglY33QJRTBASP4B/wZw5EkMQPQCJniS01NVUFVVdVZnZmde74822y8cKH/EZnp2De3XuuXuvFfGZ933cS/9H7+DNdW/vHjHhtEX3ctEnnPbW+tZwkvBqYOvAnJNpwC6mVjLbEY/kxDu5pJYIY2g+0IPN3LS5taRPy5vOhAPrsTGjj9l4sJgRzpX7dpQN/+EfHJ/3DteUEN51niTBmhc/4f99YMLwjj/wGWeMtruSc80sk9Za5TUqZKSTzEvLgOYpJ/hSTqiQJmeMaxs2nlTG6FLuCY3iCbucOeMRTwc+IV48dklspdCSRN+9RUt/wTgPradCY3ntK17vmuUNUxoflA25NYxoXePTDBeMGd05kTP1CG9jQhxyoG1rm2dtbY3prZHG8JbamoQupW1ISqyFKq2NF7uCcOJyxns54rQhxFZNfomXuqucxNiqr2ylrXaFSzxBznPWNr0aDAnVxCijKe3xO7olFiu1sTWjmdx3xCWttS6VxO0tPp8KZm1LKbesL0lLtnXTdrppWl1s/Tr3PSsEEyxTLKCqkcTfUVVEHzpLG3ukb4zQbWkWjC2+LJ8wl1CP4CNdQZSrLXWwzjZyOecUq73pA0ld27OKE02EayPLO0ZKZSmVmjCv8cM4OUgGns8GB6Zi817bXpt2z5gQDrc57YntdFf75mhurDhwnYLmQvRcOI+D8dGM/6ogbrZyXCqUqGxf55z7RLWEUtEpNxSkCYiim6RnCTVZQqljcCosoWbQO0anpFEmV21fOM1qsKFUYak87obUNkQRPIyjGKHVNp8/qweNuNKOh8/2hm58LkJnseN/LqM69n0ije6Dtt/se4fkMamxAl4ge5xM1wrt08JZtkS6DIcmcywxniNzbayurOldHSnPELkUG66J46q6xy9IJtyQM2wZ6WjsjYO32+9jHB7m9dvQId80v98+6wmjMf7xHN9oTTqcRyooSXrbKZtRq3HedopnsZZpMx3qm4Y0nEy01rbOKxvJYBRYh3W0JIZQEtihIIxbOUxq4zN319aUMlFTXq76NuCP3rqwWKEGu2u/Jl+mJiESb9Q21Xq96Cw3xmJrOU47joEgQuHOG9LqKqhJr3FrdgPH4BhW1LgUv2qarsNjdPi1P/5rZ4WrOcGyrDSucbNJ7EZRva0yOaSr9QsbmWiRcZeiFuyxpD2+2fB/2YbBut85iaeDXhfutfU4z4VH+145orranihpPXxHQtyk7R27TAwJlaeaRo+YaXHh+6S1vYmpE1Udczvtn+I2kYNaPtGppcRvUmNXPDhdX/+sfrcNl2mZ3fyduQgswebyP1fMxUE5tFRxnN6blVA+cVpZeE7s0vwoDZjTd8qRFSXWd3IZ52675Q3XXhturK+06hSzLvf2orFatPZs2LmakXPC9dTa/NXkm/VVYWImD6f//r3dZxWrk/XX06XUg0ZrR6DgyUSvXx4woXCvaah9zZhnUQKJg+vtVZ1PuNC6iWo6qiNUgdXRvB/5DS81rTssl/IoSlDhWkJQMbpdFjtxKwfUJruEecnqLDGoU6tJmbTjFxz79PIrvYhQzGyXVPw/CyS3dTX0BVWUlfm+9ghrgmHDiBRq6JiA2sCQGo+a2uY66lLlTAZmFkb+ZHQY6CBz3WyKOuljmzSNdgblQnQo2qhTkhWe8FFe4mlYiK/WX+6pk99sr7eUj1nattrr+X/hOHSzxWN5aCYm2+fEwftS1nPuEBEIuixQu4njN9S0LIzdQKnhygmFbDufT06j/nAx7A1xPGsGZdqqMDLueBb0DL9FbOA6tSG62ZZdHXzwtM6fEFPXLRedXM66UTPi/zyQXb/qndjBSeb7Kteuppx0sVcQ0RJtnIEhN6GjaD+4dgUXytklkY/6hnKPO7N7l9zsqalHu76pNEpSxYivDLoDvh8VeFWtGOomG3d0z78ef1Dc/3/YjRRstj2q8zxWzHP2Rdm36D7U9YnFFveU1Mat9q6we6UW23rTovYSp6qFUlVd6UPWYHcII/iJWprDeFqXu61mA2aJb7aVsE61NrIPG2JEHAjmUHQsdie8unP8c/Mk5+i2dltWO+/2h8OLcXT1ZriJA0Ja1ZneOEZJVTiEKZbmHUpy2jv9+NoERaMPbFH7zZ224pX/bUrNQ1Q6PXv05QunopWbbEymUU483VfHvF6vN9GMkJnmrJWlI89M+TNWVI5Es+ces75byJL/i/Ry16lZ4viis6QrlpQzNBH0AO32zA1DNI4sXLI9bgVOLuWp51CfuKmYDYYiqIJdMF69sxE3d3YKmzg01D3GpfVjU1F5nBDCIlQqxpiNr8ovX69/85ncc2l7SZrSsU3O/7t2d/Mkd6YRKnJj9nkmJA4vXkJ6LkoQozj/Eq1vF6Kv4PtLX5u+086LEbMi7EMWNXWqT+4n3mN/kkvTadxzxydl3til/GHO1HmEw8AIKxr38+d/e8E8wVVvqOUDazY/Z22vyAR/oyUaGdo4RzdjlLUdQ5NxSUkk1WbEKtwCpqnSXsMddxiUMbrBcoNGU6FQUW/bJuObbV7kkcEnrZXgfX/llHRtbUoCPyUZYTjJ/Z6zQS+MdqUC/vHPKP+EXr0ehWIYWK5d1WWVZoJWHC2ER6YEjMt7x+vkehotg70D4GcH7W7v+uogjKYOBSYyF7mIuo8ftve+cKeKV0y0MToi7/oLJRIf79/p6MpdRHK9fXoidSBq1Je9TVzlfPgr/ol5bbDlCaqHZj29WssYoMcoboAFW+VQz3MWa21kSbukbOrEV6SmNow6j5jMEhmq4fIRWXT+tfnKNKoyLGyd0qGZKr9N0n1TC96K6mKeyOsXfzikO6elVaj8w37SjdNPOv5fvimctg0OJcAdzsSuAeSRSoU9GQDwtB67SuLAQ7V1mVcEIfWr1i+r0NsngjadGE2Ysxrsg3Ys79w7XW2oXcfqbBQR41j1bBEODmPeM0F0yL3Pn5HJcG+p3zosq30STYLlTqw8YG1tjLxFgWiyIW5IFdAspBqbGVJyJDNZFxxnrpspHksAzn4biImwVS37Ig/0bAXY5y7C/Kza/SluskPR1d1G7W28cZKEjOqwEtnM7Jbe6oKSMKz7O604WrvjoyeW39/ZvWcc1+UCZagoln3jezU2RBTc5UTYTY3nm+Jb9+Ja1TFvMuMfx2HnL5w780EC4JE3+H7dozss7ubj19yMHbzTLRBgu2SGZikz/P6b1RfjkgPF4ce1t2qLd97ehDj/78jAEWYSBTj/pK3zQnLHAw4JO3QpaqWvvJrusDZT6oTmGEUkEIDwig29Y3qL4XHTCYn3AVrixvzni9Hg3Tg1e7flTd9MySryIiZbpwn45ns3tEZ0PNaH0eZn6dlcJ+FY4Iz6lW27W+hmKIppHdkKkKVgypVM4xn0pLXcrxelq46fRYCdqSTt2OEHsmsISxqvHxMiqKEkbv+K1rkFuYoNMExTfXPvTC6ks9errLicH7L8gX1hvYxca5ZFGQ1EQPiPUfydxh8HHvCYqboC1a5HsyBcMpWL0yBo5PnNOl0NIzt2J04492i3J3a0Gai1Lf0cdWcnrK+tNfZsnB55x/K2hQGMm9HdJvtCOpPI4Mgvnm8V34ogDh376OHb947IEQ96wT+6BXRk5Y9lz6gus23ndh5tWkeWLnfLpqxInbPE6oHwJXmpjHzDqyEbn5AIyBkcbQDutBkQY5rArp3Z9C/JV4GHw7Nb1V/Y7+5/cPWL8OPFL9qnf684Yawtw1FZqmvWq0igHiqhO+N6t7TI4vBiIYVofH8ROFYChpT2tDzvonHn06Gp3csJ5xcL6t09lU7mt5wBeRtAVtNtHVAZbdLi+49k1hmUdWdMXk+/Vu/97J+/fsiGh+R31vJJJXZkPaic9T+9s2QDCSClRdz1ZSfSIdOs8jptKh1xOrKkidDxi/iOujBhK6vwZjSOLLphe3r9Dl13U0djkfAGxAeZwi3XTSEqla5fqTa7GqCW60anH/yBJlUqorC7d6icLeM5jpzouwdHJop8ExZaCmzYAMQhpC4Nje/csj7TUR00NZf1gWNuahfXnItBCsgZKkM37rRvIpM7AQpFL716SK3fVACr5cDSUfTu/IyUVHMpmg/Mn8of2l9enfMrQKtQotenOarap2/tYuxu2NlmwnIimOEx4DzOdwcM0wUOoY4OKVP1nh/7gy3gXM6COqoTNoyTIz9rTOOlGW3sZpmXvCpJxCLHZOpNvyvMsJte9gBkbaHn4z+5S6M29AB9A4MmrNKJrlgfTQ1IHwMqBbRL+d4Kr65DK3q3BW/2eof5psP1ZtN6VKkcNadLAfiNsw/P/Yi1tgb/tSeNtVAHfAriaZVwMwfLhxYhnQWKZ8vyiXz3an14+rTRYK5mx0oeGt7I9PSXj3TKQXPBtHHjP2hRTR2a4ObhRPWL3BiXa8AqWqm6eZefl4B/ytY66luxj8eVT5hOcr9vd4y3kSAFJAgd1A1tnLYB11Z9RURp5onqnPG68EDdGNk/+XJNQPTanb/+kHb5kBlC+s7JgCw9FpGq545wGQqBw1AcAKkbADs8+NjRSlYN7dzQND2bzcOhlevqZpi3ZBBsnT0gL0QLutrLKmlZVFzWTZ9M9npY1WnjfN+2y+RVsRTt64sg5X7kx+18ZdBhW6duY48HWHcTmgHvrAXccHpQi4qOaxyZDqW552M73uxDZ58SwLDKSTInUG6K2+97XQVw4lIQ+VJXfm+gMXWtGYBWdPRBk7bZvDycLiO7cGppd5frZRLvZ8ZfhONxm7MY24c9xHuHJeQQmlJcY+BhC6QkG96D7AJ7dNHGkeFoXwUdd/RYjqQb1Fwsj8EgUBbKNmwjCBDVsExy5qD/0H07KsT6YJk25oTaCzKmQXI9cCvv/EJUnd42/OhecqsZoCgBVyvKRUXReXSNP95eQNSiWzjvdMavoYHJ04tyNwJIxjLpDKegFKI2Yh10thv6GopJSyHRqFCHZc8AEQLaqw5HrhnShetP7Q/vq+u8GJBHQsdk1mva9FnPB2uB7oYXNNsD0Qa0s1QzTm/rF4VWxCEUCaBxcFdadtHI7bZ5qKc5Bd5sYlS8YlxLMloNtjYKDfHbprS0HW2nUS+aygmjnnXuMvCaktCHjPaVU4wWLwDDL0xcP7p7v3P5HGoC9QCbopiRFoQLipKm4PWG48EaAJMOWhXVnQRvDKpb1llWI88orBlAChS6fV60gjtFx1DXdO3qokJdgqoRpdwk8WzkEwo5J/fqfJOo/frJRYVyJctDvX/OSmg91ugGcmS34T8ifu83fuw5YKOqzrue9y5aK9Q72vhHGTQ3DXBxt1s4443tokx1BY6olwOfo34B83cF4LStRS1ysw62rAen69yYiDkNuvA5qxUXb8TRkoCzH334Vm9UViu596tro66H/E+MIr1wowRktPOa6jUhE0VMrKGYVPRHYD4LJbZDXBX/cnncypoNbuLhDamyYdk3b4AuCuH7fR7STAzjeEDH0ia1X5QhfZFuJ8uX+nLw5if/00vcs2hyLL3YH869IGBAYAnDbeMfESqtcHDAwQm78mbZh4A4WmhsAR390tbKjfQuGbfXrSeCvfVu5Di4znmNyzVo+g6AzamL/EnuypFhdd+FDZRVfnPENs36pn29/nJSPVd/ASloZlfze3dWPmQZi0XSEixOQJLaDT2IG7pOeuiFHUg9UBYFGcZNbFK6NrzIBmF32cuhE15EOH2clR3r28LUU9U3l3ky/2538Lz/H8I8pUeFg2OE0nePvBq+9ezhV9+tnHrbvfCOhP+GmEn95iBiGjuJq1aJffINOOCkKyG53gX9vS2EdD2livUGYp4a1rvfv2We5vmyiGw42Ixfo9PPXn36QqyPrkTk8Ha3TAr2qnz8k7+evmcVrWfaY7mBRrh4whcTu7p5tInpL/737393d528dqt5fNAVNqmGtKLZGKq3nVyJq+YsLuWuHANcKEbtRDWKDpahcYmTyfz1nUU3rTO3c9k2Gq6bbXHpDcJVPWnL7XqOdhF01Z3ZA3c6ORKchlmtXVpF5kA/+P3TFy1/dppucWU+IYskowfeWGGfXMvWI7uVg4b0oxn/szFtKGCb27qQGot91vsh6C9EKHI9Ksc/16qS6MKaPrvXyrFz6L6vdml1s6kfj95E+RPJoKHz9t0ozjJn0758JoYrFQpe/sNqbv5j8ujg/Xf+5/fn9347hepRf/q8v5Zjr49RhvoxI717C8I2ABRQMwQkGq0UyVyQ5ohGIJZH1Zx9KQ7K79sZ2td0O2Sd5MlF9MOut/n9tHm36Zy6d7588N5B9ih5OucxG54JOk3sv91fuocKXXr6xW+jB9/Xnx0Bpx833dkkpUq57mB3w/OEFGBN/LQaZK52eQSNET1yszfUWcQosHS/p3WzpnP6LW0SxzSbBhr/YpnkqOxdGX3vlavV21F4MD087N/xa4iau8bHPkj1N7+7useCTB4dfXZxqfJns0xuofPffz/XY8D/rmytZ5PkegTSzj/moVw18QDC/22Haa4MSvZJQTT1E08kn/zj4ubjm+XVcNscO8YX191q3XFlz96Sp9NIbf1ALu6Rj15RIAFL7uTOJnj55tdsIt3zbr/4NyT/fnNXrY7t5MGl/27nnt0Kqbf6WWjRbLgdcf6r1ZC4rqApSJ/s7WLFegF2HvQthOmB/Hb30P2cTQ723ugqKvy9KJOIny8n5v8zOc/P5+eRKB586A2gYIIzr3zqZvz+J7RqRwcP3/3R6++jcaSu+Wa7vZpPj9QtaT0P2K1QtovNJrB1JwjfgmODGOL2QYrHo8ATqb2Km/0IYvAet6p1dwUftvF5GatnenWwN4HITjfl3Tdl5QOCsf5ytgyAUP1+OUzWprn5tmjlKTH/9z+YaozuBh1Vk8Oh6AJyMxkJAGMfejR2mdprsQ4dWdsy1r1vwEyUbibGuQVFxmljgAxSjPIN/qaGLHzWlqrscUNp1QTRflz6qZ6a8RR6X+eKRnP/AFAYhejkD6Cu4fa1Pr2pkqBrSu2Z7D5UaDOr2m4E6aEdK4KXHuZsNkis00OeEyj+QIk06oTbQWb3e65aGrG7353wQaiburX735c05+Xa42r6juZX3TM+Lsi+AeCES6NZOyhrb9eTl3Z0MSre7HJ5zey+6wGU9OkRANBWL/1uAHBTeueEHpJ9lvH/CJwIqkwagSFQka+2tZcPwU0CogPp7pmVZ38H52PStZF3cSHPQe6nzE3UkHQ/Hp6mJ/44lmqLU7W30UAmztrOXu7565VSxye/6xgbKsiu7fyn47EnRhpacrKmDXR4A1oMEAz0i7aLV2cM308VELGjBufRlGYOicKrodrPvrPRarp3tzd5HgE0eHLjkrC93l5cuPXHw21xL7GFVdsZDD92MzOMjZZGOn4RkOOnkhbC6r26ccOjOq5dBRsnHhQaN6F3FhMIigzNHP+13lfowTCHbKDh38EdhDjklC2zzhcvd/1eboXTZEVBQMfqgWq8I3vcJkfpiAuX+hDDgathxXSnrD6J587pxLXVdtUwCeeLWxXo0TGPAy65Z+quZT3JVldXzbI2E+FUEHO6MADswWrQruEeinYNiAawN2NtmpWcnTrHr58VJz8oADiKYtlesP17f5KykYnaNa9tT0S9Z9rf0LBY8/MgTNKmvrjjwhurXQcXunWmTVgMV1K4Deu6FiB3UgXwJTyogbAZqVMp3D+YqkwbBYxYA2yiJRuAw7qeQHnOnvWVGWoTJDBSCK/JfJbY4wOQW28ao6C3BcMhhhIIea1XSRQMjuG1cceGrpkKLQQZ+AMTuG6nCnhaVIWVbGCBapZGwBwQRiyEWiARYFPaeFaGpCO3RoVkWXUlTbHp4z4sQze1LdzkiW9esdF9yS+fXS6fXrUiHA+b9ap3Yx0LGX7qB90P29h9F/7dYJhppu6O+zxbEffmcbfzmjCkFSHKb/Jcin3TRaBGgYNDCIIKuRtkPIYGhJ4kXt7L28dReLlTL+dh6dRhvjuRUF/o4IdHzO46f3TCev9vPv79e+ZQJmUttpEV1ZsX5pzZjRz1dpzVndmkjX8tPm0CvXNwU2JaczaDkg5YBM0IYJaCId9y0dtqLkphIyBapVfzKgomdzv7b/58+ldXU/tqXBnJJT0iarZZn/1scNqm69UmWsoPlveXTjOKudG7fpWbbR0k9ujqdUXZzvXz8t0n74+dsU36VTNbQ3JuGDCvoHCQ1fiSf0xgdWiPD4foTH23X3VwzUIIg4EZtseD3x6/EE15Ux1YduP17qGWm3rtV58+mJyJecZPS3Xeh1y+MN924irxYntzlOmnRauGbvgokDdtmw2uZP228gcNC2ISEGAkshZgcqi1Ojf8U/RAnMH5kEKrtO3mOfRqAZwN0efwwHVzc2dyMzeJXMrtUctfRW70xlsWQfTh5VnL6b/+zbevn0X/7ng1h2zk62Q1ev6Nn8v8h3app4fXy1WCE8d20QeOvMkHJndrGRMOSMAVMyXLnF7IvpIlvD3FXVg8+B99P1JmMbYvj37yaz+4iH8jv+D9Krkn6tfVCX0Rh1b106Mpvyv5b8uv6jt0Tf80yDIWrKvBycN+8Xc/L5tvpSp1MOrYcEXp2YV8IPqpUxLUg9tqr3PYaJXbS+kxn9/N4FrD2w1YAMetv2xN6mgbMPSi3ptkvxk8HSR9WdhJ87TpVnI0cs1Bmf7og7++fv7qzVcpm9Puw9E7X/ullFdq/fXvfqMznJvK3uX5/MfXHaR82oQf+ReHJ9zrSWjJIiBlW8s34asbqdeE/0z3ken4dCwQbnDRp8GZIlbF5pLcydYPt93L4xJi2jSG5g4K5l4Wxb3Z3bvLjUPjapLtzprk5M+et1hKz3/v5+93R0cfsJ8+j5fH+v549tTdBb06dN+6ca8C217EGw1piblzbQYqDAcmOhRD1GqOfALxGWvsjikIFGI9679/wNf/1ep/XbzzUz5XF+lEzV/uTQtLNC7sgZcerYy7SJof7dNw8N56/izJYq9n/v65k4+by30hrvdN+z7bnjTBKpg0sxSQzN5Ro+4aLYmt1omuILp2o5x/0gnaA++m+F5YFe0b04wTrwvHwWLyh98PkhN60WVJG6c36RqtoUHhiM8+eV3+6bPwNu2CK4tMxrZOW+uaaM79XrHsy3qUR33Eiq19029Zl8ycHk7xHoUOm1vCDYCqIx+MJurRjv+oaDvwzZPQ8WGqm2xjk1vr+bSfLf3ld1O52+UbmDo5pGSZUViUd/V/0qiP7v363AaETlyHgV/UbZj7NQuJm/cwUFmsrisxnv1qe1XVw25w4hUg5NhvC2UIjufOdTw16PrZFUSqR4T3qElTmGGMmnx/Cadh1kM5elk1r9M4xP4MdiPvrO9BnMqaHTz7R/JH93778uvD2PGHNPL8mKdotPmgM/L+vMBbUkfKfhpviNMP3hj14eyYzgk5L5bdKDPCbD0XQZi7zbtprw9nbAQzNMRnQ63CNSSQLs1tbCcYefd3QLCI7Nw0JwPTQs3bl/zIxsfzKH05iYcyBoQLRRSHPtvYnCMpYPbtOW3p2PWSppSmesvH7Tn8Ag13Qczd+35colqabgfTLO4g1Iq8WokWgYyeJICiLcQKQ0yLgM2A7Ysnk/1BQ8Pwsn5Ybjqxf/aj4b66PhCH2/Crrx7H73E/N4Aap5ejqJkHNeCE7W/k3SvH7vJ2wwuu8zq2/XY1SqkLiNebh3ZxqyeNOzWVkyGxRZAOjNjz3kKYMIjmoDZCHKFdwWuIujSXhYjND/Bw8pU7uXkU7abX/MWk+On07D8geMSKzlXemCSDTqKaRn1Q2hmgsasEqp8yd5/UL0bj2LrHKDfdJcQlG0yICzfeBNE4gA8bm6F7BG+F+AUrE2L6XucETTnEkS0iSEn3kw1a1Sux3Rr1CgmX00+iwyh47+r9v/v8vXetAynR9Js83xG2U12p4bbnkSp3FICy6sxjM3PJ91udhbnTJweDqSKPm0yvTNt3g8Lm9oYH6MpMQ/9hHQcyAyS71Qy61vqJ/X052e3IbMmmwH/QA+ZCnlY/QFWY1/Vid9A+hehat83esrFnWuc2sEOrXsWDW1uGEn6MVECF6Ms0lVMlkezC1k4+ckKyzkI7C9waElnjHESWmRzN4VYFvTXbgdTbxj8hWQvQl0NDBGc6CRYqHDV+MO3r2c/+pfpHq//lf8uhi5etQ2VbXvfXat11IXClQeKCeYjCjJAZoPpgoDNPXr33wkXJ1WVbUKjoJA633rmIIRJGYwhhe/4eBMa20ScTDlGi6ne5r11WV4VmFL1i/ma/NyguA+d99k23eLGYvnp16a6P4O9GAhkj5GKqxEIL3rUI8LhyPH3ZwoTfPNkK/wJsClvuTueIR5QRb51Ltg9dcpr4McJJXX7Dou2Y8RroD03C+AHnCeTz8mzb9qUIt2qn9CaJ0m2ZvsUevHm+a8bpfzuHL/FZUHm2UtzJiYJsrjTTHj7y1pza/WXdKqkX05ko9cvzbrB8PEMLApgnZu5E44FtEIhp3Po8JKN3Z9tJJ3Tk7bUMkUVolWt65CcWMYuuaMAvR+ZmEPFMMvJVuJ6eAHH99BH5IeCCjsddJAury7iG7G6YQRDnfBfOXZssRYmMU5u7ERU/PXxZHA9fQD5UOYTUaWq5q5odhOW4t1PI62MLRieB/n1Qk1tZHdW1YQ2HISLz4BHLk6g7UOPzR+LZPw5/uBH0n2V/f/XDg/bIgUVkRQodwaWw+ZA54ZLMqzTZu8wIeXkJLof7vHqODEDWnq/HcXK5hRtpeWnogUmb5BgXfn8EQZp/gH+ISEehK3thu/qqj/D2z53dxcmK+X1KBldvN7/c/ei77YPjX17Txy8RiThaLGLXE61HM+1shbC9oxo/Gtppkjd1XX3pD/ap06md8/BiMjx+NFbrOFo/Ile4DYodHwz8HXyCYtqugz/ayusm8A6GgjogqW0FRTkeXFTHd5es5TAN2Vu5fl0Wj97jF+usJMOKd/mJJQnOD/IFyGOiCQkT8Qa23ggyaLHYVIjDCcOdGzqNj475TdAccHMPto3YWToArRDHgEQgxfCF+H1wg0pfHQb+bRXsyx2ii8HuwrPLZo0K6VyH8aq93D1Kj999efX+4lVmkLyKbmOFQ1aaupUwCS1TDSCe9ifSCQu5G62o74Hop/4DL3VEHEq7/SHbD0wdSu8MKg3fIx25qJzeBzx1vdY/agIJmfBWrILpOWc1m13eTGf3Xlgeba7uPv7mwc6cPmkhPTcyQlio0Q66N4lln3pN3N72eZaooOTd8+W5/tyhIiY2irf23L0O5BkcCfSOVx5RWvc6G2yRB2QQDrb9YMK2grvWeBRSPZIbxKbsgPSB3kduXyyGTpO/jN9kH/9kTmYv1Effxg+UA8qw7dXS1KhujJZIX9EdGG3licNvtp65k3zKz2I3lI2GLBTKw1O0Hax6f6fJ+IKscyXS2XQHGw7KzwvCz4oSrSOeRZRJJdr8aQJUWT63FZOXyT2+6qLJ3n3vh/+meF08+vxzpyoyrO5IdvviGNZ2k/fk+tzkWbV51W/kb5xO/Ls/LOcXnQsmnorYSeZwQkzh9Xg9+PBDtJjTPfVrJGW3BXe+u4FrFika+XPheQBpZvG88Uejq0EQWxOhWYyCFKmLk2x2+Lcn333ug0mHpOfzguKmwmYi8ZD6gziIEv8wPBDBrNjmB3EioNsmC6j8n+YoUA3zs9Bvo8yBChZMxsCOebMZNkcOOY35I9tmwgtPBiEYqm66jWnurzc7d7WY6sNBUxcTZQ9G2j2foA7H6ob1DPIikMrQL9zeEwLgSRYJQ5448Iu9WP79Jr9sWi8stXMDGeQIVULkLqJ6gbqRrW3FwTCsUCfCeO2Zy4z10+PQyG3ewjKBQm9MNlbZOiUXQ+OkMVVyxav6s0k6fOvm4s1+zcHhkSzQ4U6CWiAbAijQlnSz2py/fvw4D7a/Acd0eJWo2zTUeHgPNhQMTySf7I548ES848jJA7qYlnar+u6E7a7zFpoP4r63iIzkSkfLcBB0px5pbCm5IuNYud96R7/3OW1nVN4GCM1E8gskRvsWncBwFDHB8gxKU/0FWhNDTLURyOMhjy2VfWXwm0KluDXMKUuJgsPYMSyjU70LUOeruu0KX8Gpg+8G1Oy49nxTXp+jhR9IOz0Rl9HQd09+8389RaPtSd/fKHO9M1XV7UGs8YIMKMEfM3My0fXL65uRBbV0YYKDCPVYoz+GaJqWIAaCe+7BB2AB01qR4tIhUyRXzY5gp28DwQgAID9A1vBOGkm7VlwX/ritukTd8K+RKgIIXQmLZBXpXx/qfp3A6kLsVHtdqj1YIM744od3PjvYCREtUZ38og6O8XwuefVwIQ7WlYIRWh7DoO2EohBoLgfj9QCwyoiDQ0BUCRaHp0N6AnkZFwmyVUTU4xm7v9UFb//i+MObJVKVtdtHsB096HfkDcy6HHpn5PiOkWOk1Z31Jw/r3KlgpR0rjXgneULlnaW/9oQZD/vvDmHG3pz1CNc7LepyZxB1vnOersvs5I9x3FuJArWu4eE1tALT1Eg0+PbkZRCq2b9+uKOT8nSheWVwvnxnHzcv42pejPOYZYG3XUyjcGXX8oIgmq2PI9LTYvTFaGwbO6ZhXyLyGSCVXQTreIVUUmpiFSDazDjEubrb7hAdzkpbaAh5TdkLEdbIKHSHwb64HD6qT/O+NKx0egeqeI9RAH0FWePkTtKVqPPfvehebliW3VD9FdLdNi05abKuDMJ7x9KsyXUDdQtQESE3PfrxVo+H5oX+q+Lm1//n65aHIlOnsERGfiQFYr5+XbEVxFQEdOCeHjytgwcbPvjiNJV5E167a6eX7pawEUJ990V7L4UA7k28xB2PJ/zuK/tfh2328Fmsk3GlP7q2XXe1Qy6k2cKH3QP2dOad5X11cT6Onpx+9vXk7r9tRKwhSvEbAXlOya6zS9GYMhjmzdS0t/KZmZGVTpn85MW65PNqDmu48obQr1VaTfwgS5iPVWnYnkcstMN3u+e2v/tcIu9Mr4U7d41IcoNsUWdm5XZQh8toEzTGfg8p+fHJ6anD/ySmyCc07iiGH+o24g/uXmU6gBvFpdPcl+Lhk5rVyJSsXDg6HM/YbXzSy4OyiZNhU9V6H+QEYwo+iu0HZ5P7Pzl5KP7gD3ZdsGvjh302ylmJqH+5v+W4z+2P79t2NgXI+3+j7ryDVPRR45BFWYi28KjEA4aPNkuhq3vn1cf5q/V0TC7WKLNbah4jwNTbBq7CiciEu5tUJYIeY4GtcjBzEEl57OZDtea/yB9E5O8RxrfG9fu7VboxozZDqdt714jHIyxnzF//oQu/kPOKwSPPR4QsqhZH1yoXvfKlKKDQXrLhLjfz+jI3tbOdVvpZ6EWXl2NZtMjCSN1A9UFyHVITVNUDJKivop07mevW7dv8JLVHhQQ+Oeh5Zlt9nPODOukmCSsGCB+tyYDOuconuPGCv32fqVhepPMw7ANauxR527YK+pztzPAmPrqe7FK/fIuCR0Uovm5t98jDAO7PnrEDD/ll5C2h7Yswmo2guJM8LYoOTnbydNKeTx0z9PwITiJeVRbIuxx86LJw9fibv4gqv6z9jkCsRthgx5EkvtWnKT/cQGz3PLCYt68b502S1si2hGxTeZvmZAMtaB+fBBms4PjOKwzLOMiczgzCD4A1yoHTk5h0KA7dIng+yr0IxL+0PkTtGmMLfj+I+m2r5uNX7kfk4CpI9tTloXOXT9bn4+Ohh+RCq9e/RWQTOn7OB3kH+ROaa++7Noh0cUyWY9bGVVHXRRdHu93Y8QLwo60LiOcOu6ZgtEKUEBSPvbX4V+Fr+0g3ZSS37nmDo557jmWfPLDF7sXFFx4v4/CawnA63+tjZ+agzqMXdgj7DERBwqpm3qDvpPtqU0ejfbGTR/7X+0+rqnazXjqqgxjk9EgPUQyF4Cg3bXFpOs/0fo2eVputOJvk4VqKIZqgKrp0RV3Az9GxWYTiZND5w4kPoDJBQe5fnoiZ2yAFjA1wewz9wDFolBzyfD++7M7Uzh+g/IQ338zE34C6oKpbCAO972d/zAB7HmL5mAlACCBAEAG5bHt1l6qL03/yr1zfK2WrJjM9VmPEMY4ifpx4ZdC8eO7xLoRYv48L5iknRFOrIJa7oJfQ84He4C91D8cROSE3kXaQPUA6yN9UzThKgORlUNj7tBmMAfew6OisiMFAIECTY7Y0BX5+MNr+E0xCrKHIRp2VETeu0s7koS8R0F+8YsDdtKoQ5PVZV7Q5rYFrWA9fDPJvnsGqCet6XJT71kmdSZnHO/De4SPvakSRTBGD+eQwHpR7hA9upxigL4J2C88lBi3SJ0W/e4NZtTsf1rEXIvMydpELM/mi3C9fI9dC6hfUB15oR9QR00CgUE3J8OxVDXUCOZrduvJwWWn1zsUuuRiWEPuPsvWhaPjqp6ug7Is5L1y9G1DJunhgM+j84CYEN6Xb+wA0mtvZJkltwac/iW56iF/9NeY0mPJG5vTD89G2OP3qBsxalOxZvJGINFnTYEqgiAHvLOLYSYDRoE7Vg6fLvpi0Bn9e6w7K/8WoPU4a4a5bpJTEgVdB1cV6GaHc21PWKI3DgWAzAoklanswOP/g0B1skVd3vCgNI0x5xd+1RmN0YOqOKY3EkE0C24uFQ/ooHjyHYQYU6cDpI7ehJHKWeXFPJ31WDKB7T0ry5reJj2ikuORfhBEp570DrMucPDb7sEEccYWGCz/KqZIzjZre7r6uPKhvDnnjBy30XSXk2StbX7JrcFoK+SySKwxG8HFyXw/Lx+3dMRgcCsHmam/63PerqOg63i8chsjrKjbm0c3Rd2VWX+7lKBulk8t2FcwdvnM55gDghGPzoZFgjivKO8ixRTRciO2M270bblpVoR2T+vLu1aPZG6I2mBgoBFxRrxsJKZCjxv2rgG+RsEN+nuMs9Zifk1EBmKdjTXZBaIsXLj/OVNV3/GGEC3OavT7iQ+YQPcW8E4ZVGFFdchs/SmrrIKNL/tPP/wOi/sjEHcGcxQSP01br7Pc5fZrCZ7fDDDMYBiNs8WbXtiX3kKQzQLEVj0k7ucPJKCUVPEmY/MmJ631bX746+wXpgtD1W5lxh90sBJQfApRdothRuc+sdFWBEczzS9NnX2II7v7d/Xf75s3VFYC8dAc+b8uf/PjdzPYg8VE1liijZi8yuxC4/qwD20GXcx3ulTsLVwWeo87UlHfXD/Riezi/0r8px8Na4J4FY0qGj+8dWFUGMBeDHBcNZK+h3obICohqPkZSLXj5hH64W6Y63YesSYF4MNDx7ze7and1hsmubosYf7+DXYmpLZG6sB1vJzqRs8RNMn1iMiBJr7ke93HI+Lg9P3ghm33ZccwcwCs3l2FvRI+pP3hvUQm5aNAhm7Zt1zQ3anpdWwjx/8f+M2/fmGXC5YjEZaLfY+HNennkFXFAkbxzS4ichFxZN4VuhGuA2aLlHoEZjM8BHriuRYCAFfxSRe/ZwerK5qxqSp54d4jIvtIn4tZJ5pBaodPdyt1GZmE88O6cfeBD1j+N9F3EWSNdL99cbz/74aVTDZ6o68tyfeH2RNawdY1Grj1lQeM6CZK7EAYBrXalHmmnZ7LSyKEfoNktVJrefZ4El1tXz3HR43awM/2PXR9gBgo/anffNdAnXNXmY6M8L0GoVmIG5Kk9CVeef9M14vp19asfn8tN415dBmO7GGGyyIfMiYZyzwpGOyRZlIF53VDlVBpjTEWBjJuS11NMeGEcSd955TtJgdbM5lEksuzyA8pynoJKIShIylRbHHgn9rLRXrw4rYI7wtDq6s73YSR82NTxiUmeVI+e/+XvXk0tMN4OrK53SrNy2NK4gDgIuiNiyZGHZRsB+xnZRiTJ/MmjZqeGNNc3ly/g/3FaOmN85XfL4ceTBOFoJFDtDuxrCH3F8+0aPV8HNq3lGmIPeWuUwItG+DFgt6Y6e9scfOsfdEOJidIZCa9fYtFc4U/DPhtHGHrhLa+iuoJAi5lSmJ4oD4hpj7wrZasyA9S5Qgyg9uf09YUjZ0jiAWNEIRmWDtgNdE6LbA7MSKH6zNvmYj15xP2kpTKXrKonYlL+bfDiOyQ7WaTDDRfxMEE+DxINAkx3svPreBhiypldAlOiImM6DG2eI6WVtCGH/IGtvqadahzwHzY7I5jPVlDDBx1mpIcIpEKOcDQgLs4xCJ7P+rOL6uXnosknXYBPCYk6Odmuvj4zxzSIVI0sZDdZOethxs96Gr4Vuk/9UeIjGPnqvIMCXCbIbogJDDdHenR1avtZ8LSZVjZUwcOjdBroI+RWMJ1Cc6A42yvEYKG5gmFDvhzZSHiDdDZ7a/gvwPotUqAJlNXi+ych5klTKqotK1INqFrZbSsaIrfbfoRGgJE4jInnUHRKWHt+hulJEH+1RWHyr5Id0wiTHZXDWG4CRB788lZUazAXCdMZLw5LWirZInCfyyvmnTxF+l/ru792JmGH7j6ieo8JqRw5dYxKT80gWo0IwhqVYI2KRqt1A9BQBhiJTjpcBcx+DhDkoYCz5xcfp9cfqjeETTBAncORIAcOm9gGE7O9fztGRgpgkd6jEDnkboCnGXrg1sEwRHpknG5KwDiZYtUlZh0j9PoMxW8W79tnmzrOKJ8SM4qbIotGoXVIud43PkL7CGpEiENQNYl/GPPKUm/E1XNvGqao0B6yYLTbDTqNVoANvh1B00gJAqT0dBtjDOC2pCD0c70+vjDHEHSHmOBmMfSag6pxQozhjDSt1vt0bE74AdX+n721eYFEKmi3+vzVttUBPOKo2Ys1sGa5xVCg57wIdA5lZbyciABA0CCIjaQVAefGNEiOWX5EL8irma+niKRAjEG7Msx56w9/a+tVSfemyweJxHDPutk7er8T6fLq1L8y8/L/BztKslstvIegAAAAAElFTkSuQmCC",
"text/plain": [
"128×128 reinterpret(Gray{Float64}, ::Array{Float64,2}):\n",
" Gray{Float64}(0.510136) Gray{Float64}(0.541837) … Gray{Float64}(0.627451)\n",
" Gray{Float64}(0.627451) Gray{Float64}(0.623529) Gray{Float64}(0.388235)\n",
" Gray{Float64}(0.611765) Gray{Float64}(0.611765) Gray{Float64}(0.337453)\n",
" Gray{Float64}(0.58598) Gray{Float64}(0.58162) Gray{Float64}(0.192157)\n",
" Gray{Float64}(0.611765) Gray{Float64}(0.581892) Gray{Float64}(0.277462)\n",
" Gray{Float64}(0.557051) Gray{Float64}(0.520124) … Gray{Float64}(0.2) \n",
" Gray{Float64}(0.607843) Gray{Float64}(0.582899) Gray{Float64}(0.197011)\n",
" Gray{Float64}(0.61125) Gray{Float64}(0.637072) Gray{Float64}(0.215686)\n",
" Gray{Float64}(0.619608) Gray{Float64}(0.619608) Gray{Float64}(0.207843)\n",
" Gray{Float64}(0.617212) Gray{Float64}(0.588928) Gray{Float64}(0.188235)\n",
" Gray{Float64}(0.635294) Gray{Float64}(0.594274) … Gray{Float64}(0.206484)\n",
" Gray{Float64}(0.631373) Gray{Float64}(0.592405) Gray{Float64}(0.184312)\n",
" Gray{Float64}(0.588056) Gray{Float64}(0.627451) Gray{Float64}(0.184314)\n",
" ⋮ ⋱ \n",
" Gray{Float64}(0.149179) Gray{Float64}(0.129412) Gray{Float64}(0.241798)\n",
" Gray{Float64}(0.14902) Gray{Float64}(0.129412) Gray{Float64}(0.265207)\n",
" Gray{Float64}(0.215686) Gray{Float64}(0.222663) Gray{Float64}(0.207843)\n",
" Gray{Float64}(0.345098) Gray{Float64}(0.341176) Gray{Float64}(0.231373)\n",
" Gray{Float64}(0.263512) Gray{Float64}(0.334629) … Gray{Float64}(0.258824)\n",
" Gray{Float64}(0.298039) Gray{Float64}(0.415686) Gray{Float64}(0.258824)\n",
" Gray{Float64}(0.268499) Gray{Float64}(0.368627) Gray{Float64}(0.235294)\n",
" Gray{Float64}(0.249184) Gray{Float64}(0.289783) Gray{Float64}(0.207843)\n",
" Gray{Float64}(0.219608) Gray{Float64}(0.251988) Gray{Float64}(0.2) \n",
" Gray{Float64}(0.229011) Gray{Float64}(0.219608) … Gray{Float64}(0.203565)\n",
" Gray{Float64}(0.196078) Gray{Float64}(0.207843) Gray{Float64}(0.345098)\n",
" Gray{Float64}(0.192157) Gray{Float64}(0.202593) Gray{Float64}(0.304792)"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"colorview(Gray, X.value)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Nonlinear programming (NLP)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"We use MLE of Gamma distribution to illustrate some rudiments of nonlinear programming (NLP) in Julia. \n",
"\n",
"Let $x_1,\\ldots,x_m$ be a random sample from the gamma density\n",
"$$\n",
"f(x) = \\Gamma(\\alpha)^{-1} \\beta^{\\alpha} x^{\\alpha-1} e^{-\\beta x}\n",
"$$\n",
"on $(0,\\infty)$. The loglikelihood function is\n",
"$$\n",
" L(\\alpha, \\beta) = m [- \\ln \\Gamma(\\alpha) + \\alpha \\ln \\beta + (\\alpha - 1)\\overline{\\ln x} - \\beta \\bar x],\n",
"$$\n",
"where $\\overline{x} = \\frac{1}{m} \\sum_{i=1}^m x_i$ and \n",
"$\\overline{\\ln x} = \\frac{1}{m} \\sum_{i=1}^m \\ln x_i$."
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"-2.7886541275400365"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"using Random, Statistics, SpecialFunctions\n",
"Random.seed!(280)\n",
"\n",
"function gamma_logpdf(x::Vector, α::Real, β::Real)\n",
" m = length(x)\n",
" avg = mean(x)\n",
" logavg = sum(log, x) / m\n",
" m * (- lgamma(α) + α * log(β) + (α - 1) * logavg - β * avg)\n",
"end\n",
"\n",
"x = rand(5)\n",
"gamma_logpdf(x, 1.0, 1.0)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Many optimization algorithms involve taking derivatives of the objective function. The `ForwardDiff.jl` package implements automatic differentiation. For example, to compute the derivative and Hessian of the log-likelihood with data `x` at `α=1.0` and `β=1.0`."
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"2-element Array{Float64,1}:\n",
" -1.058800554530917 \n",
" 2.2113458724599635"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"using ForwardDiff\n",
"ForwardDiff.gradient(θ -> gamma_logpdf(x, θ...), [1.0; 1.0])"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"2×2 Array{Float64,2}:\n",
" -8.22467 5.0\n",
" 5.0 -5.0"
]
},
"execution_count": 28,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"ForwardDiff.hessian(θ -> gamma_logpdf(x, θ...), [1.0; 1.0])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Generate data:"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"True parameter values:\n",
"α = 0.5535947086407722, β = 4.637963827225865\n"
]
}
],
"source": [
"using Distributions, Random\n",
"\n",
"Random.seed!(280)\n",
"(n, p) = (1000, 2)\n",
"(α, β) = 5.0 * rand(p)\n",
"x = rand(Gamma(α, β), n)\n",
"println(\"True parameter values:\")\n",
"println(\"α = \", α, \", β = \", β)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"We use JuMP.jl to define and solve our NLP problem."
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Max myf(α, β)\n",
"Subject to\n",
" α ≥ 1.0e-8\n",
" β ≥ 1.0e-8\n",
"Total number of variables............................: 2\n",
" variables with only lower bounds: 2\n",
" variables with lower and upper bounds: 0\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 0\n",
" inequality constraints with only lower bounds: 0\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 0\n",
"\n",
"\n",
"Number of Iterations....: 14\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: 1.8533848152383021e+03 1.8533848152383021e+03\n",
"Dual infeasibility......: 5.2040090087569420e-09 5.2040090087569420e-09\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 9.9999999999999994e-12 9.9999999999999994e-12\n",
"Overall NLP error.......: 5.2040090087569420e-09 5.2040090087569420e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 25\n",
"Number of objective gradient evaluations = 15\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 0\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 0\n",
"Number of Lagrangian Hessian evaluations = 0\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.019\n",
"Total CPU secs in NLP function evaluations = 0.001\n",
"\n",
"EXIT: Optimal Solution Found.\n",
"MLE (JuMP):\n",
"α = α, β = β\n",
"Objective value: -1853.384815238302\n",
"α = 0.5489317142212758, β = 4.9909639237115\n",
"MLE (Distribution package):\n",
"Gamma{Float64}(α=0.5489317142213413, θ=4.990963923701522)\n"
]
}
],
"source": [
"using JuMP, Ipopt, NLopt\n",
"\n",
"m = Model(with_optimizer(Ipopt.Optimizer, print_level=3))\n",
"# m = Model(with_optimizer(NLopt.Optimizer, algorithm=:LD_MMA))\n",
"\n",
"myf(a, b) = gamma_logpdf(x, a, b)\n",
"JuMP.register(m, :myf, 2, myf, autodiff=true)\n",
"@variable(m, α >= 1e-8)\n",
"@variable(m, β >= 1e-8)\n",
"@NLobjective(m, Max, myf(α, β))\n",
"\n",
"print(m)\n",
"status = JuMP.optimize!(m)\n",
"\n",
"println(\"MLE (JuMP):\")\n",
"println(\"α = \", α, \", β = \", β)\n",
"println(\"Objective value: \", JuMP.objective_value(m))\n",
"println(\"α = \", JuMP.value(α), \", β = \", 1 / JuMP.value(β))\n",
"println(\"MLE (Distribution package):\")\n",
"println(fit_mle(Gamma, x))"
]
}
],
"metadata": {
"@webio": {
"lastCommId": null,
"lastKernelId": null
},
"kernelspec": {
"display_name": "Julia 1.1.0",
"language": "julia",
"name": "julia-1.1"
},
"language_info": {
"file_extension": ".jl",
"mimetype": "application/julia",
"name": "julia",
"version": "1.1.0"
},
"toc": {
"colors": {
"hover_highlight": "#DAA520",
"running_highlight": "#FF0000",
"selected_highlight": "#FFD700"
},
"moveMenuLeft": true,
"nav_menu": {
"height": "153px",
"width": "252px"
},
"navigate_menu": true,
"number_sections": true,
"sideBar": true,
"skip_h1_title": true,
"threshold": 4,
"toc_cell": true,
"toc_position": {
"height": "510.6000061035156px",
"left": "0px",
"right": "812px",
"top": "109.4000015258789px",
"width": "179.39999389648438px"
},
"toc_section_display": "block",
"toc_window_display": true,
"widenNotebook": false
}
},
"nbformat": 4,
"nbformat_minor": 1
}