## Binary Expression Tree

???+note "問題"
	給一個運算式，如何轉乘 Binary expression tree
	
	<figure markdown>
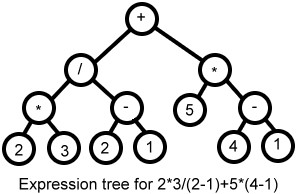	  ![Image title](./images/86.png){ width="300" }
	</figure>

有完整括號的版本，我們就用遞迴的方式來輸入，如下，複雜度 O(n)。

<figure markdown>
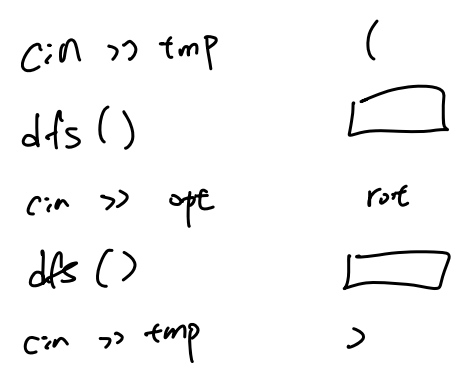  ![Image title](./images/87.png){ width="300" }
</figure>

若沒有完整的括號，作法如下。開兩個 stack，一個是 number，一個是 opt。先對運算式外圍加上一層括號，讓他最後會把 stack 中的東西運算完，接著我們從左到右掃描運算式

- 若遇到數字，就將他加入 number 中

- 若遇到左括號，則將其推入 opt 中

- 若遇到右括號，則 pop 掉 opt 中的運算符然後對 number 中的數字做運算，直到 pop 到左括號為止

- 若遇到運算符，則先將 opt 中優先級**大於等於**他的 pop 掉（若發現左括號則立刻停止 pop），對 number 中的數字做運算，再將自己推入 opt 中

至於怎麼對 number 做運算，我們每次挑 number 中的最後兩個依照運算符合併，再將運算結果推入 number 中。

<figure markdown>
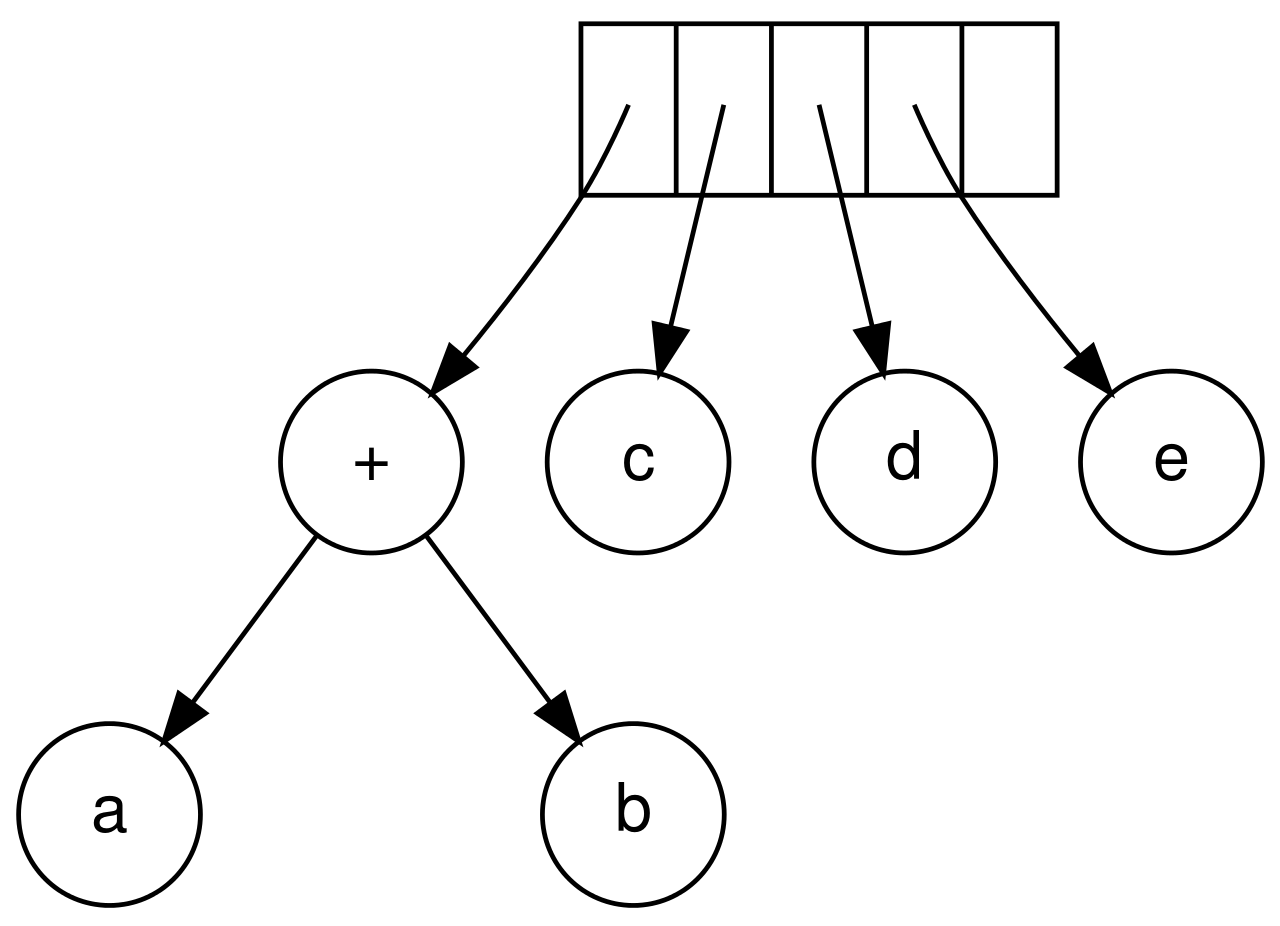  ![Image title](./images/88.png){ width="300" }
  <figcaption>number 的 stack 類似的樣子</figcaption>
</figure>

??? note "舉例"
	例如 `(5 + 2) * 3 * (4 + 6) - 2 * 3`，先加上一層括號 `((5 + 2) * 3 * (4 + 6) - 2 * 3)`

    - 目前遇到: `(`，`number = [], opt = [(]`
    
    - 目前遇到: `(`，`number = [], opt = [(, (]`
    
    - 目前遇到: `5`，`number = [5], opt = [(, (]`
    
    - 目前遇到: `+`，`number = [5], opt = [(, (, +]`
    
    - 目前遇到: `2`，`number = [5, 2], opt = [(, (, +]`
    
    - 目前遇到: `)`，`number = [7], opt = [(, ]`
    
    - 目前遇到: `*`，`number = [7], opt = [(, *]`
    
    - 目前遇到: `3`，`number = [7, 3], opt = [(, *]`
    
    - 目前遇到: `*`，`number = [21], opt = [(, *]`
    
    - 目前遇到: `(`，`number = [21], opt = [(, *, (]`
    
    - 目前遇到: `4`，`number = [21, 4], opt = [(, *, (]`
    
    - 目前遇到: `+`，`number = [21, 4], opt = [(, *, (, +]`
    
    - 目前遇到: `6`，`number = [21, 4, 6], opt = [(, *, (, +]`
    
    - 目前遇到: `)`，`number = [21, 10], opt = [(, *]`
    
    - 目前遇到: `-`，`number = [210], opt = [(, -]`
    
    - 目前遇到: `2`，`number = [210, 2], opt = [(, -]`
    
    - 目前遇到: `*`，`number = [210, 2], opt = [(, -, *]`
    
    - 目前遇到: `3`，`number = [210, 2, 3], opt = [(, -, *]`
    
    - 目前遇到: `)`，`number = [204], opt = []`

## 前序中序轉後序

<https://www.tinytsunami.info/preorder-inorder-postorder/>

???+note "[Zerojudge m300. 12347 - Binary Search Tree](https://zerojudge.tw/ShowProblem?problemid=m300)"
	給一個長度為 $n$ 的 Binary Tree 的前序 $a_1, \ldots ,a_n$，輸出後序
	
	$n\le 10^4, a_i\le 10^6$
	
	??? note "思路"
		中序其實就是將 $a$ sort。可以觀察到，前序的第一個字母一定是根節點，並由中序來判斷如何區分兩子樹的位置（也就是左子樹的長度），並遞迴下去建立樹
		
	??? note "code"
		```cpp linenums="1"
		void dfs(string A, string B) {  // string A : 前序字串, string B : 中序字串
	        int n = A.size();
	        if (n == 0) return;                                   // 如果 A 為空，表示已經達到葉子節點，遞迴終止條件。
	        char x = A[0];                                        // 取出前序字串的第一個字元，即當前子樹的根節點。
	        int pivot = find(B.begin(), B.end(), x) - B.begin();  // 找到 x 在 B 的哪個 index
	        // 處理左子樹
	        int lenL = pivot;
	        // 左子樹的長度
	        string A_left = A.substr(1, lenL);  // 從前序字串中截取左子樹部分
	        string B_left = B.substr(0, lenL);  // 從中序字串中截取左子樹部分
	        dfs(A_left, B_left);                // 遞迴輸出左子樹
	        // 處理右子樹
	
	        int lenR = n - lenL - 1;                    // 右子樹的長度
	        string A_right = A.substr(lenL + 1, lenR);  // 從前序字串中截取右子樹部分
	        string B_right = B.substr(lenL + 1, lenR);  // 從中序字串中截取右子樹部分
	        dfs(A_right, B_right);                      // 遞迴輸出右子樹
	        cout << x;
	        // 輸出根節點
	    }
	    ```

## Binary Tree 性質

- 每個 node 最多只能有 2 個 child node
- Level i 最大節點數： 2^(i-1), i>0，如level 3的Node數最多為 2^(3-1) = 4，如上圖之 DEFG
- Depth k 最大 node 數： 2^k -1, k>0，如上上面 depth 4的數最大可能的Node數量為 2^4 -1 ＝15