## Flow 問題介紹

???+note "s-t Flow Network"
	給一個有向圖，每條邊 (u, v) 都有一個邊權 c(u, v) 代表容量上限。有兩個特殊的點，源點和匯點，在所有種流量中最大的稱為最大流

- 網路(Network)：圖 G = (V, A) 為一有向圖，稱為網路。

- 源點與匯點(Source and Sink)：令一點 s 為源點、一點 t 為匯點，其餘點則為中間點。

- 容量(Capacity)：每條邊上定義一個非負數 c(u, v) 為該邊的容量

- 流量(Flow)：每條邊上定義一個非負數 f(u, v) 為流量

- 網路的流量(Flow of Network)：由源點發出，匯點匯集的總流量 ，匯點匯集的總流量，若其為該網路能產生的最大流量，則稱其為最大流(Maximum Flow)。

<figure markdown>
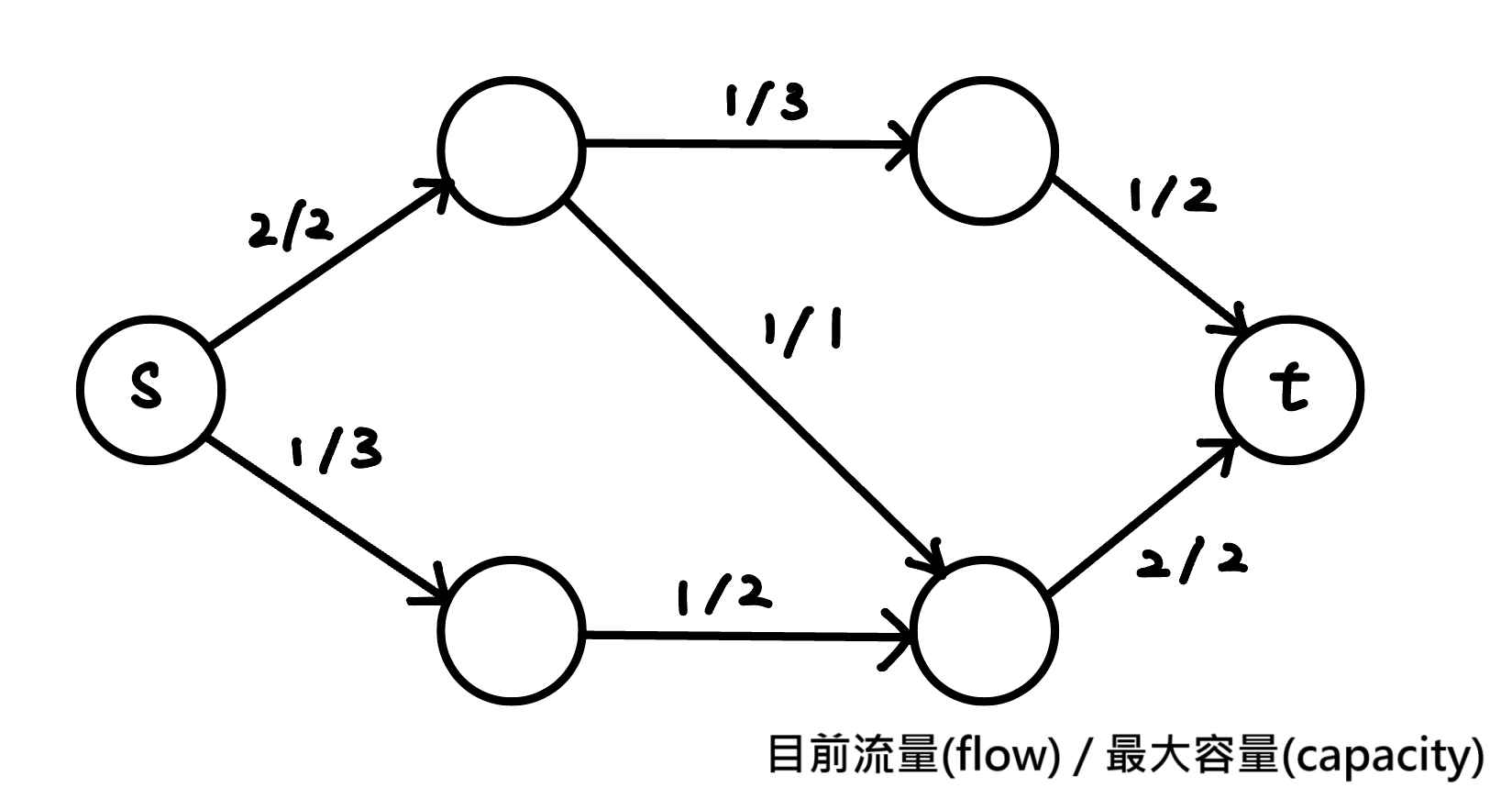  ![Image title](./images/94.png){ width="400" }
</figure>

## Flow 性質

- 容量限制(Capacity Constraints): 每條邊 (u, v) 所經過的流量 f(u, v) <= c(u, v)

- 流量守恆(Flow Conservation): 除了源點和匯點，每個點 u 所流入的流量 = 流出的流量

- 斜對稱(Skew Symmetry): 對於所有的 f(u, v) + f(v, u) = 0，由 u 到 v 淨流量加上由 v 到 u 的淨流量必須為零

- 可行流(Positive Flow)：若一個流符合上述三點限制，則稱其為可行流

## 一些定義

### 剩餘網路 (Residual Network)

將每條邊的最大容量扣掉已經流過的流量，即得到剩餘網路。也就是剩餘容量 $c_f(u, v)=c(u, v)-f(u, v)$ 

<figure markdown>
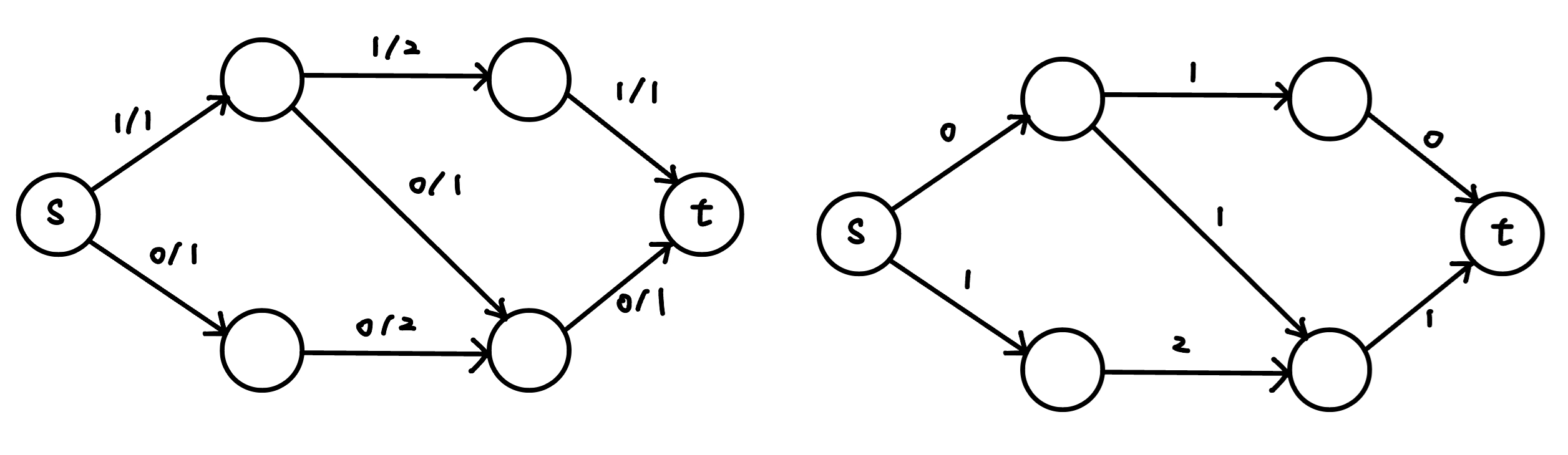  ![Image title](./images/95.png){ width="400" }
</figure>

### 增廣路徑(Augmenting Path)

一條從起點，到終點的路徑，其中每條邊的剩餘容量都 > 0

<figure markdown>
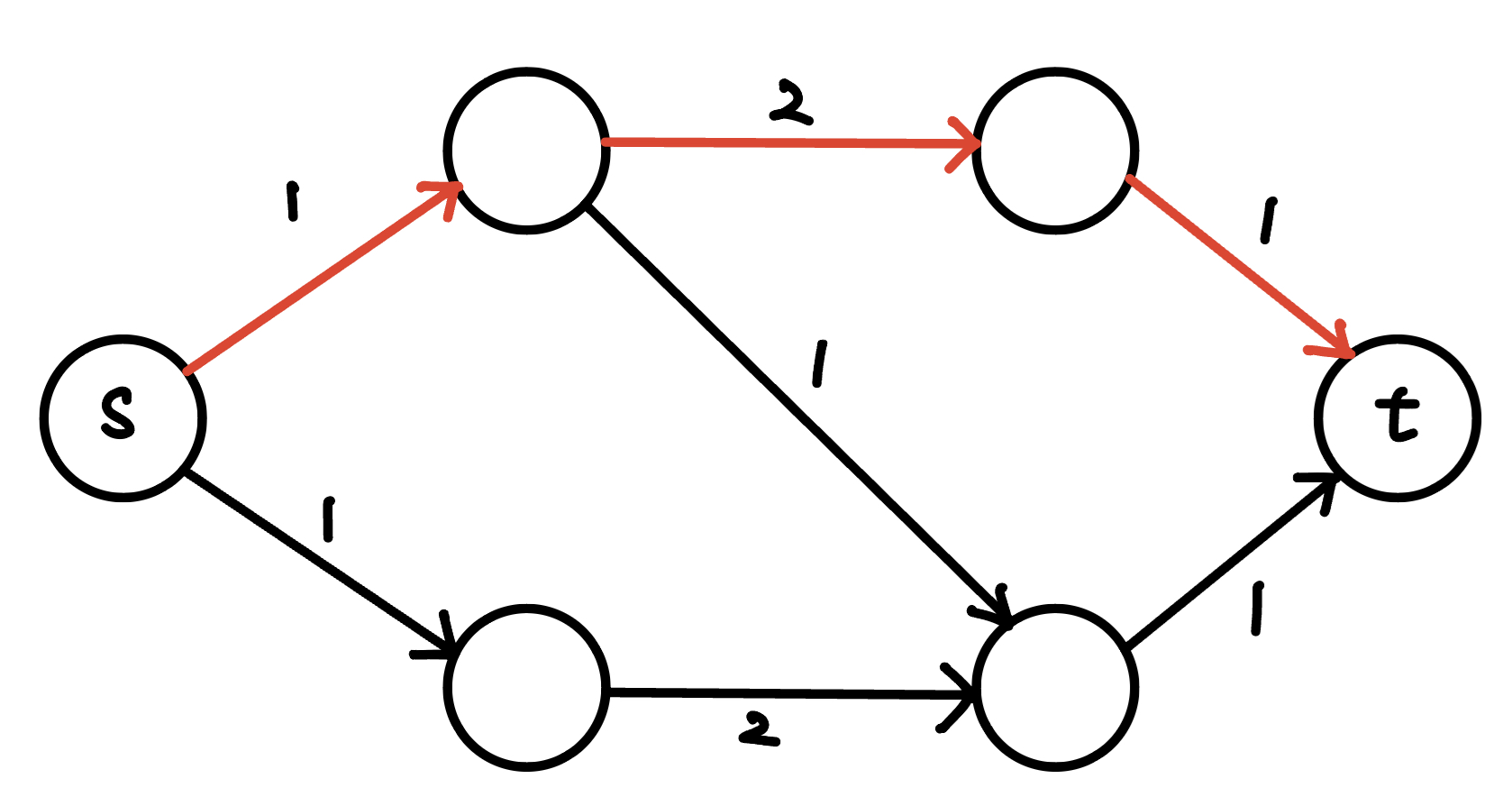  ![Image title](./images/96.png){ width="400" }
  <figcaption>紅色的路徑即為一條增廣路徑</figcaption>
</figure>

## Maximum s-t flow 演算法

???+note "模板測試 [Kattis - Max flow](https://open.kattis.com/problems/maxflow)"
	給一張 $n$ 點 $m$ 邊有向圖，每條邊給定容量 c(u, v)，問 $s$ 到 $t$ 的最大流，並輸出每條邊的流量
	
	$2\le n\le 500, 0\le m\le 10^4, 1\le c(u, v) \le 10^8$
	
	??? note "code"
		```cpp linenums="1"
		#include <bits/stdc++.h>
        #define int long long
        #define pii pair<int, int>
        #define ALL(x) x.begin(), x.end()
        #define pb push_back

        using namespace std;

        const int INF = 2e18;

        struct dinic {
            int n, m, s, t;
            struct Edge {
                int u, v, cap;  
            };
            vector<Edge> edges;
            vector<vector<int>> G;
            vector<int> lv;
            vector<int> cur;
            void init() {
                n = m = 0;
                edges = vector<Edge>();
                G = vector<vector<int>>();
            }
            void add_node() {
                n++;
                G.push_back({});
            }
            void add_edge(int u, int v, int cap) {
                edges.push_back({u, v, cap});
                G[u].push_back(m++);
                edges.push_back({v, u, 0LL});
                G[v].push_back(m++);
            }
            bool bfs() {
                lv = vector<int>(n, -1);
                queue<int> q;
                q.push(s);
                lv[s] = 0;
                while (q.size()) {
                    int u = q.front();
                    q.pop();
                    for (auto id : G[u]) {
                        Edge &e = edges[id];
                        if (e.cap > 0 && lv[e.v] < 0) {
                            lv[e.v] = lv[u] + 1;
                            q.push(e.v);
                        }
                    }
                }
                return lv[t] >= 0;
            }
            int dfs(int u, int f) {
                if (u == t || f == 0) {
                    return f;
                }
                int res = 0;
                for (int &i = cur[u]; i < G[u].size(); i++) {
                    Edge &e = edges[G[u][i]];
                    Edge &rev = edges[G[u][i] ^ 1];
                    if (e.cap > 0 && lv[e.v] == lv[u] + 1) {
                        int a = dfs(e.v, min(f, e.cap));
                        if (a > 0) {
                            e.cap -= a;
                            rev.cap += a;
                            res += a;
                            f -= a;
                            if (f == 0) {
                                break;
                            }
                        }
                    }
                }
                return res;
            }
            int max_flow(int _s, int _t) {
                s = _s, t = _t;
                int res = 0;
                while (bfs()) {
                    cur = vector<int>(n, 0);
                    while (true) {
                        int f = dfs(s, INF);
                        res += f;
                        if (f == 0) break;
                    }
                }
                return res;
            }
            void print(int flow) {
                vector<Edge> ans;
                for (int i = 1; i < edges.size(); i += 2) {
                    auto [u, v, cap] = edges[i];
                    if (cap == 0) continue;
                    ans.push_back({u, v, cap});
                    // cout << "u:" << v << ",v:" << u << ",cap:" << cap << "\n";
                }
                cout << n << " " << flow << " " << ans.size() << "\n";
                for (auto [u, v, cap] : ans) {
                    cout << v << " " << u << " " << cap << "\n";
                }
            }
        } flow;

        int n, m, s, t;

        void solve() {
            cin >> n >> m >> s >> t;
            flow.init();
            for (int i = 0; i < n; i++) flow.add_node();

            int u, v, cap;
            for (int i = 0; i < m; i++) {
                cin >> u >> v >> cap;
                flow.add_edge(u, v, cap);
            }
            int f = flow.max_flow(s, t);
            flow.print(f);
        }

        signed main() {
            // ios::sync_with_stdio (0);
            // cin.tie (0);
            int t = 1;
            while (t--) {
                solve();
            }
        }
        ```
	
### Ford–Fulkerson

???+note "算法概要"
	1. 每次從 s 開始 dfs 找到一條增廣路徑
	2. 找到路徑中流量最小的邊，並更新剩餘網路（亦對逆向邊做更新）
	3. 做 1. 2. 直到找不到增廣路徑為止

Ford–Fulkerson 雖然複雜度不佳，但他的精神在後續提到的演算法中都會用到。

每次從 s 開始 dfs 找到一條增廣路徑，找到路徑中流量最小的邊，並將整條路徑填滿，直到找不到 s 到 t 的增廣路徑即結束。

但這樣是否就找到了最大流 ? 我們觀察以下的剩餘網路：

<figure markdown>
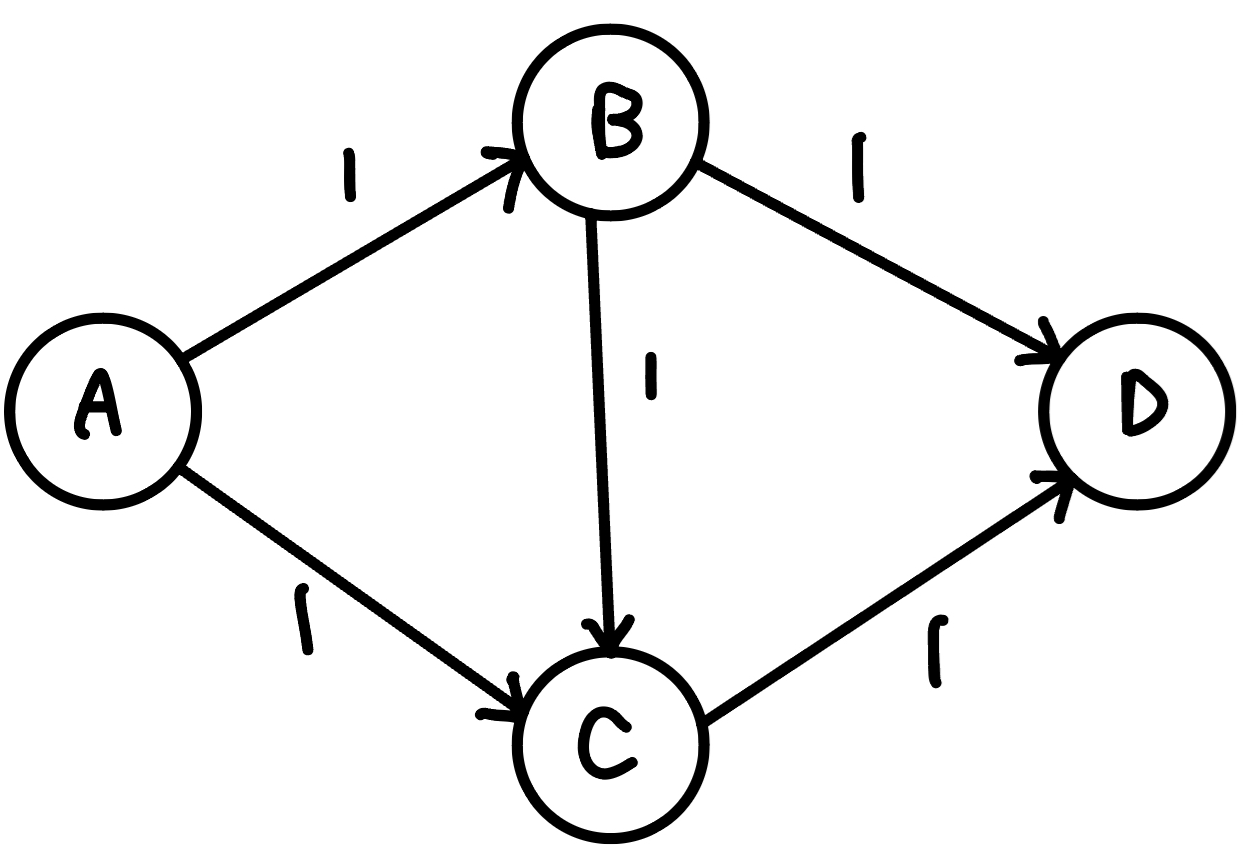  ![Image title](./images/105.png){ width="250" }
</figure>

若我們第一次選擇流 A → B → C → D 後，就會再也找不到任何增廣路徑

<figure markdown>
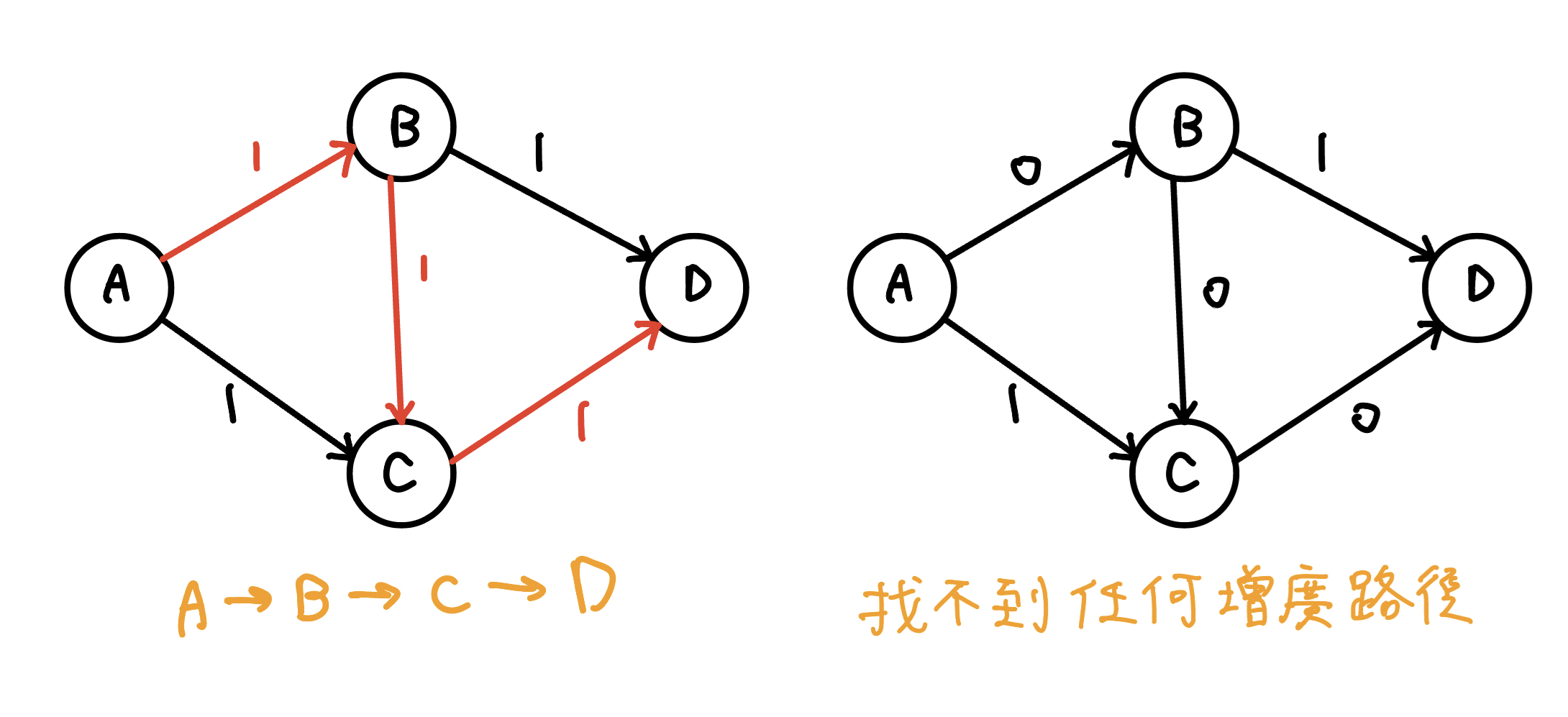  ![Image title](./images/104.png){ width="400" }
</figure>

但最大流明顯是 A → B → D,  A → C → D 這兩條。

因為我們沒有給予返回的機會，也就是相當於第一次找到的不是最優解，那怎麼辦 ?

所以，我們要有一個反向邊，來給程式反悔的機會，每條邊都創造一條反向邊，反向邊的初始容量是 0。

<figure markdown>
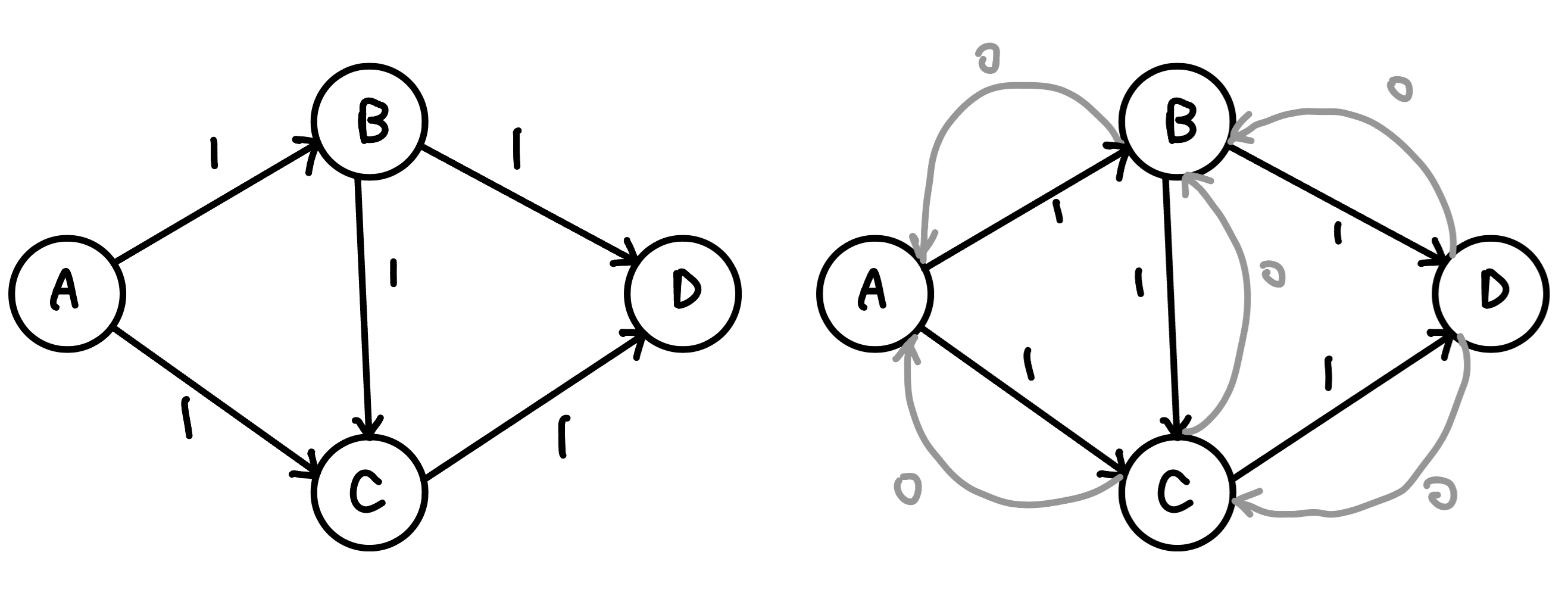  ![Image title](./images/103.png){ width="450" }
</figure>

當有 f 的流量從 (u, v) 流過時，反向邊 (v, u) 的剩餘流量就加 f

<figure markdown>
  ![Image title](./images/111.png){ width="500" }
</figure>

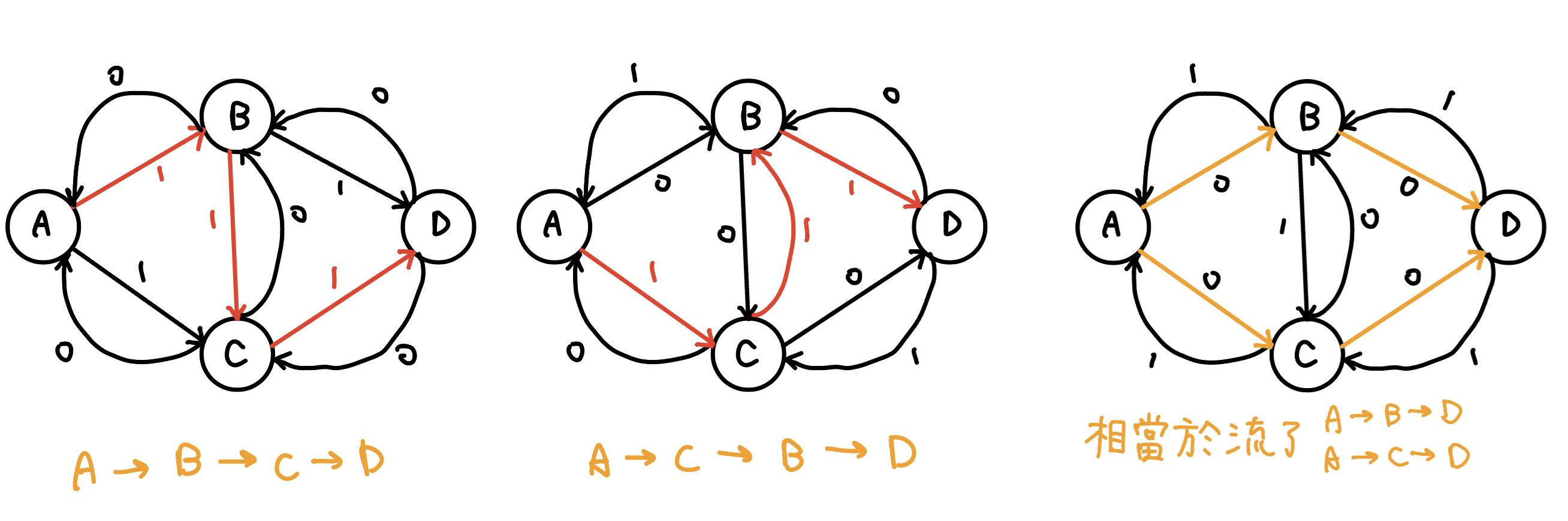
可以發現我們就會流過 A → B → C → D 後，還能再流 A → C → B → D，中間被流過去一次，又流回來一次，剛好抵銷掉。第一次我們流了 1 的流量，第二次我們也是流了 1 的流量，所以求出最大流就是 1 + 1 = 2

最差會需要跑 O(F) 回合，每回合做一次 DFS O(E)。

??? note "複雜度 worst case 說明"
	<figure markdown>
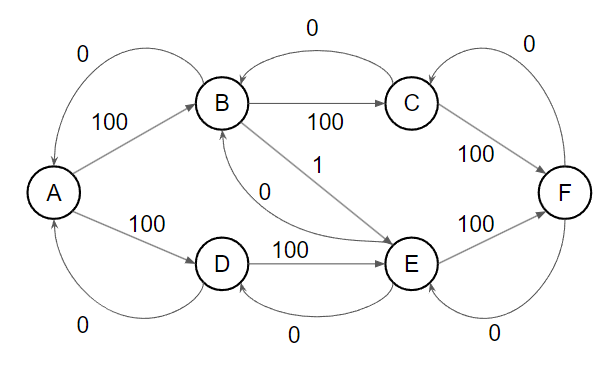      ![Image title](./images/112.png){ width="400" }
    </figure>
    
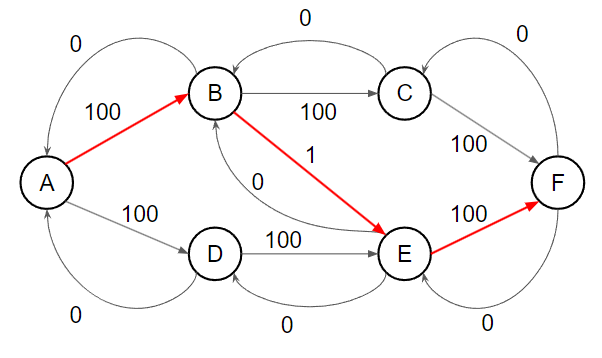
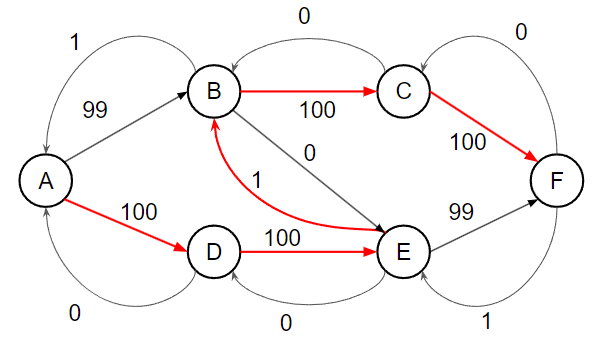
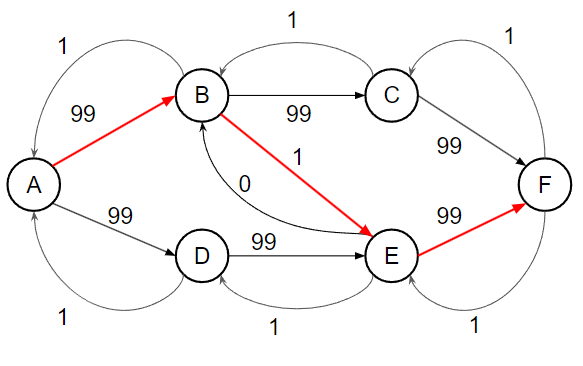
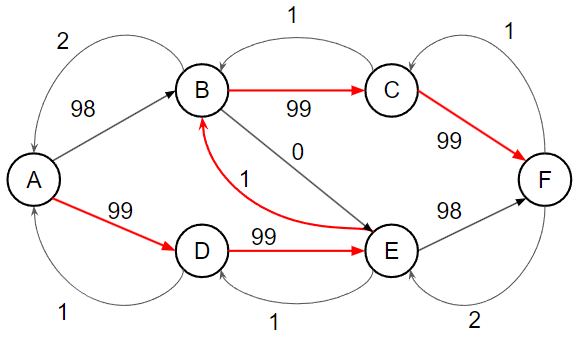
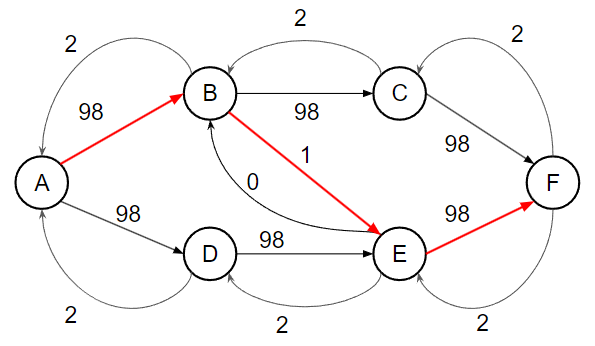
    考慮上面這張圖跑 Ford–Fulkerson，A 為源點，F 為匯點
    
    <figure markdown>
      ![Image title](./images/113.png){ width="400" }
    </figure>
    
    <figure markdown>
      ![Image title](./images/114.png){ width="400" }
    </figure>
    
    <figure markdown>
      ![Image title](./images/115.png){ width="400" }
    </figure>
    
    <figure markdown>
      ![Image title](./images/116.png){ width="400" }
    </figure>
    
    <figure markdown>
      ![Image title](./images/117.png){ width="400" }
    </figure>
    
    會發現如果我們這樣找增廣路徑 worst case 每次都只會將剩餘流量最大的邊流掉一單位的流量，所以最差會找 O(F) 次增廣路徑

??? note "code"
	```cpp linenums="1"
	struct FordFulkson {
        struct Edge {
            int u, v;
            long long cap;
        };

        int n, m, s, t;
        vector<vector<int>> G;
        vector<Edge> edges;
        vector<bool> vis;
        void init() {
            n = 0;
            m = 0;
            G.clear();
            edges.clear();
        }
        int add_node() {
            n++;
            G.push_back({});
            return n - 1;
        }
        void add_edge(int u, int v, long long cap) {
            edges.push_back({u, v, cap});
            G[u].push_back(m++);
            edges.push_back({v, u, 0ll});
            G[v].push_back(m++);
        }
        long long dfs(int u, long long f) {
            if (vis[u] || f == 0) return 0;
            vis[u] = true;
            if (u == t) return f;
            for (int ei : G[u]) {
                Edge& e = edges[ei];
                Edge& rev = edges[ei ^ 1];
                long long a = dfs(e.v, min(f, e.cap));
                if (a > 0) {
                    e.cap -= a;
                    rev.cap += a;
                    return a;
                }
            }
            return 0;
        }
        long long max_flow(int _s, int _t) {
            s = _s, t = _t;
            long long res = 0;
            while (true) {
                vis = vector<bool>(n, false);
                long long f = dfs(s, LLONG_MAX);
                if (f == 0) break;
                res += f;
            }
            return res;
        }
    } flow;
    ```

??? question "如果是無向圖怎麼處理 ?"
	跟 dijkstra 一樣，將無向邊看成兩條獨立的有向邊。因為最後只會使用來、回其中一側（若兩側都使用可以互相消掉），如圖
	
	<figure markdown>
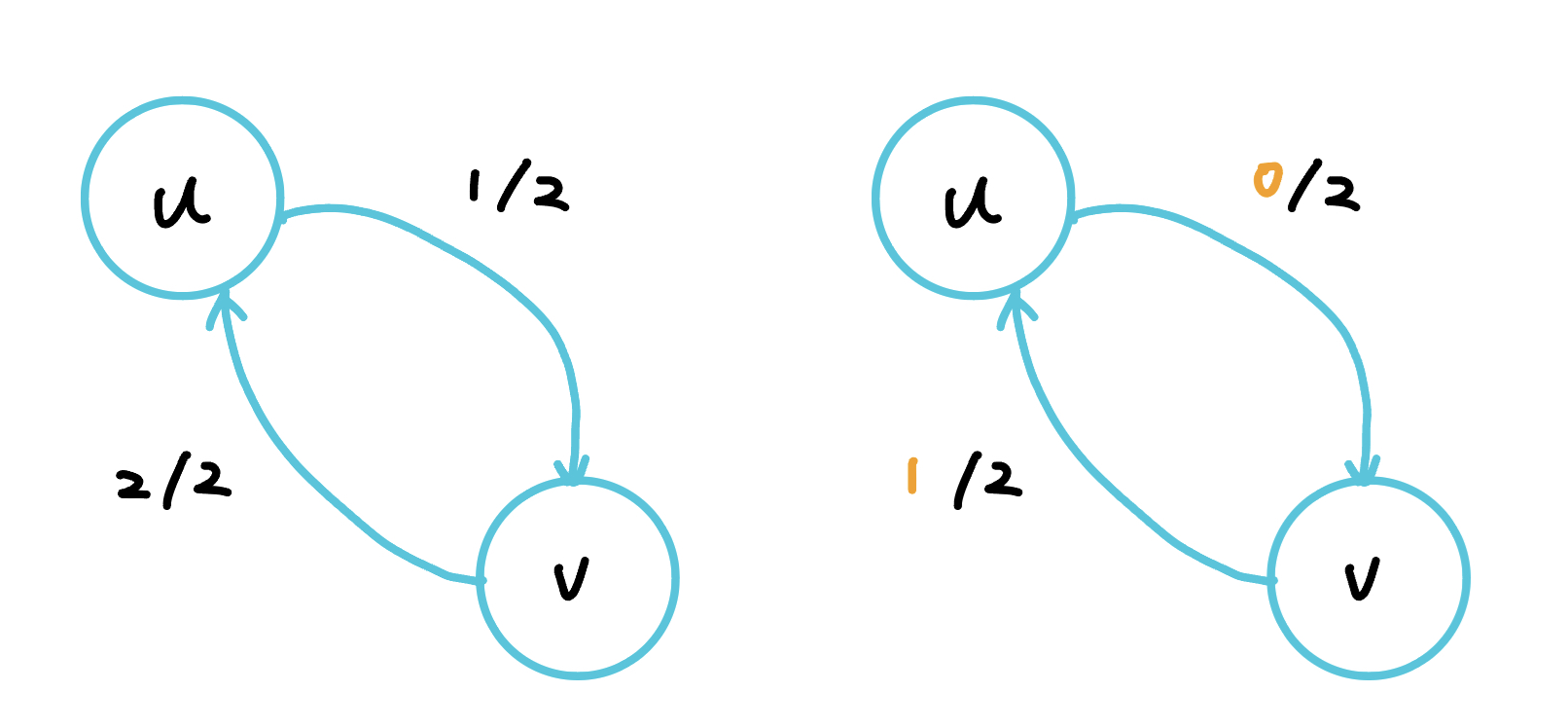	  ![Image title](./images/107.png){ width="400" }
	</figure>
	
	那要怎麼實作 ? 我們對於來、回這兩個有向邊，依照 Ford–Fulkerson，除了原本的方向外，都各自建立一條逆向邊，逆向邊的流量都會是 0，也就是 u 與 v 之間就會產生 4 條邊。輸出答案就看哪一側流過去的比較多，就輸出那個方向，也就是看來、回分別的「逆向邊」的剩餘流量。如下圖
	
	<figure markdown>
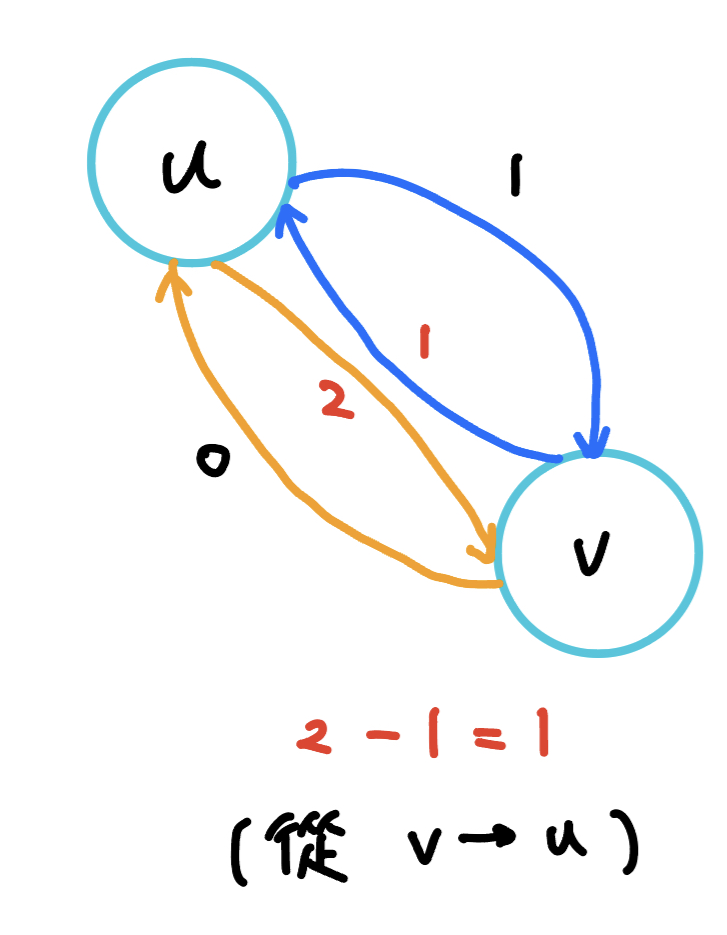	  ![Image title](./images/106.png){ width="200" }
	</figure>
	
	(v, u) 的逆向邊剩餘流量為 2，(u, v) 的逆向邊剩餘流量為 1，因為 2 - 1 = 1，所以最後就是輸出從 (v, u) 流過去 1 單位

### Edmond-Karp

???+note "算法概要"
	1. 每次從 s 開始 bfs 找到一條最短的增廣路徑
	2. 找到路徑中流量最小的邊，並更新剩餘網路（亦對逆向邊做更新）
	3. 做 1. 2. 直到找不到增廣路徑為止
	
Edmonds-Karp 跟 Ford–Fulkerson 只差在每次找的是**最短的一條**增廣路徑。

一個網路最多只有 O(VE) 條增廣路徑，而找一條增廣路徑需要 O(E) bfs，所以總複雜度為 O(min(VE<sup>2</sup>, FE))

??? info "證明: 最短增廣路的距離非遞減"
	先假設一些變數

    - 設 $\delta_f(s,x)$ 為增廣前的剩餘網路中，源點到 $x$ 的最短距離。
    
    - 令 $v$ 是在某次增廣後 $\delta_f(s,v)$ 變小的點中距離源點最近的點
    
    - 設 $\delta_{f'}(s,x)$ 為增廣後的剩餘網路中，源點到 $x$ 的最短距離。 則可以得到 $\delta_{f'}(s,v)<\delta_f(s,v)$
    
    - 令 $u$ 是在增廣後的剩餘網路中，從源點到 $v$ 之最短路徑的前一個節點，則 $\delta_{f'}(s,v)=\delta_{f'}(s,u)+1$
    
    又因為我們選擇 $v$ 的方式，因此
    
    $\delta_{f}(s,u) \le\delta_{f'}(s,u)$
    
    $\Rightarrow \delta_{f}(s,u) +1\le\delta_{f'}(s,u)+1$
    
    又 $\delta_{f'}(s,v)=\delta_{f'}(s,u)+1$，所以 $\delta_f(s,u)+1<\delta_{f'}(s,v)$
    
    而 $\delta_{f'}(s,v)<\delta_f(s,v)$，得 $\delta_f(s,u)+1<\delta_{f}(s,v)$
    
    也就是說 $(u,v)$ 邊沒有剩餘流量，因為如果 $(u,v)$ 邊還有剩餘流量的話代表 $\delta_f(s,v)\le \delta_{f}(s,u)+1$
    
    $(u,v)$ 邊在增廣前沒有剩餘流量，但增廣後有剩餘流量， 代表在這次增廣時有通過 $(v,u)$ 邊，所以 $\delta_f(s,v)+1=\delta_f(s,u)$ ，但是這與 $\delta_f(s,u)+1<\delta_{f}(s,v)$ 矛盾，因此不存在這樣的 $v$ 點 ⇒ 最短增廣路的距離非遞減

??? note "Edmonds-Karp 過程 - 範例"
	<figure markdown>
      ![Image title](./images/112.png){ width="400" }
    </figure>
    
    考慮上面這張圖跑 Edmonds-Karp，A 為源點，F 為匯點
    
    <figure markdown>
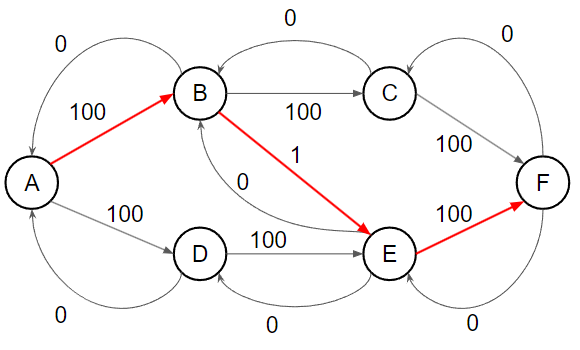      ![Image title](./images/118.png){ width="400" }
    </figure>
    
    找到 A → B → E → F，流量為 1
    
    <figure markdown>
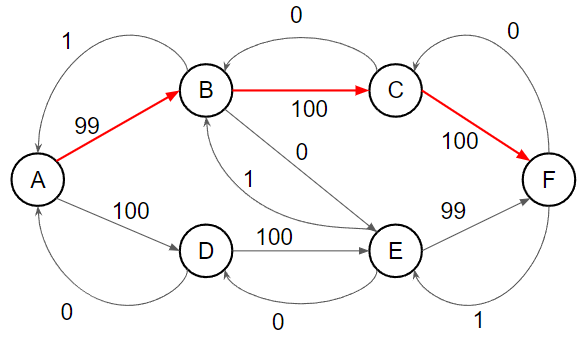      ![Image title](./images/119.png){ width="400" }
    </figure>
    
    找到 A → B → C → F，流量為 99
    
    <figure markdown>
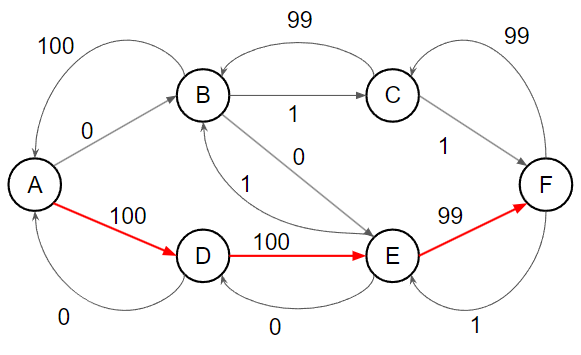      ![Image title](./images/120.png){ width="400" }
    </figure>
    
    找到 A → D → E → F，流量為 99
    
    <figure markdown>
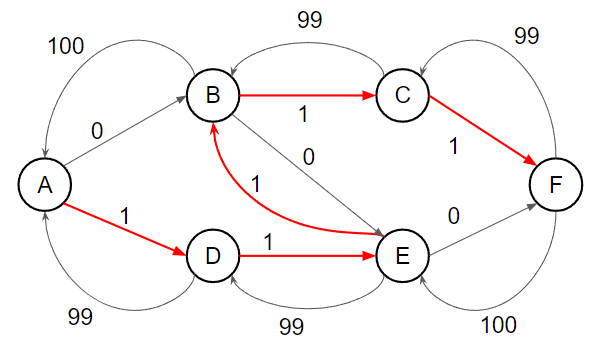      ![Image title](./images/121.png){ width="400" }
    </figure>
    
    找到 A → D → E → B → C → F，流量為 1
    
    <figure markdown>
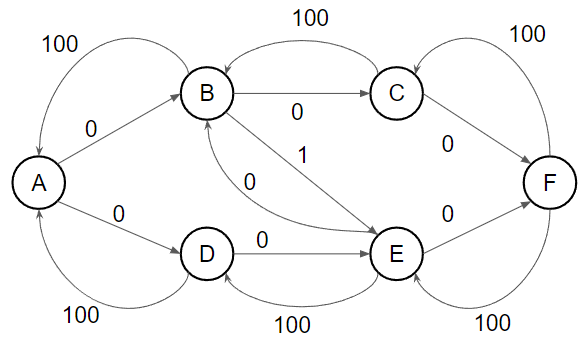      ![Image title](./images/122.png){ width="400" }
    </figure>
    
    A 無法走到 F，總流量為 200，可以發現因為我們每次都挑最短的走，比上面 Ford–Fulkerson 要少跑了好幾輪

??? note "code"
	```cpp linenums="1"
	struct EdmondsKarp {
        struct Edge {
            int u, v;
            long long cap;
        };

        int n, m, s, t;
        vector<vector<int>> G;
        vector<Edge> edges;
        void init() {
            n = 0;
            m = 0;
            G.clear();
            edges.clear();
        }
        int add_node() {
            n++;
            G.push_back({});
            return n - 1;
        }
        void add_edge(int u, int v, long long cap) {
            edges.push_back({u, v, cap});
            G[u].push_back(m++);
            edges.push_back({v, u, 0ll});
            G[v].push_back(m++);
        }
        long long bfs() {
            vector<pair<int, long long>> pre(n, {-1, 0});
            queue<int> que;
            que.push(s);
            pre[s] = {0, LLONG_MAX};
            while (que.size()) {
                int u = que.front();
                que.pop();
                for (int ei : G[u]) {
                    Edge& e = edges[ei];
                    if (e.cap > 0 && pre[e.v].first == -1) {
                        pre[e.v] = {ei, min(pre[u].second, e.cap)};
                        que.push(e.v);
                    }
                }
            }
            if (pre[t].first == -1) return 0;
            long long f = pre[t].second;
            int w = t;
            while (w != s) {
                int ei = pre[w].first;
                edges[ei].cap -= f;
                edges[ei ^ 1].cap += f;
                w = edges[ei].u;
            }
            return f;
        }
        long long max_flow(int _s, int _t) {
            s = _s, t = _t;
            long long res = 0;
            while (true) {
                long long f = bfs();
                if (f == 0) break;
                res += f;
            }
            return res;
        }
    } flow;
    ```

### Dinic

???+note "算法概要"
	1. 每次從 s 開始 bfs 建立最短路徑圖
	2. 在這個「最短路徑圖」上 dfs 找增廣路徑，直到找不到為止
	3. 重複 1. 2. 直到找不到增廣路徑

Dinic 演算法跟 Edmond-Karp 不同的是，每次把所有長度為 k 的增廣路找出來後，一直進行增廣。從 s 到 t 距離為 k 的點會形成最短路徑 DAG，網路上也有人稱這個叫層次圖(level graph)。Dinic 算法每次會先用 bfs 建立最短路徑 DAG，再用 dfs 在 DAG 上不斷的找增廣路，直到找不到，然後再用 bfs 再建立一張最短路徑 DAG，然後再用 dfs 在 DAG 上面不斷的找增廣路，一直做下去。

在最短路徑 DAG 上的增廣路長度最多 O(V)，每次做完一條邊就會從最短路徑 DAG 消失，最多消失 m 條邊，所以找到 blocking flow 會花費 O(VE)。每次 BFS s-t 距離至少增加 1，至多做 V 次 BFS，總時間為 O(min(V<sup>2</sup>E, FE))

dinic Matching 複雜度為 O(E * sqrt(V))

??? note "code"
	```cpp linenums="1"
	struct Dinic {
        struct Edge {
            int u, v;
            long long cap;
        };
        int n, m, s, t;
        vector<vector<int>> G;
        vector<Edge> edges;
        vector<int> lv;
        vector<int> cur;
        void init() {
            n = 0;
            m = 0;
            G.clear();
            edges.clear();
        }
        int add_node() {
            n++;
            G.push_back({});
            return n - 1;
        }
        void add_edge(int u, int v, long long cap) {
            edges.push_back({u, v, cap});
            G[u].push_back(m++);
            edges.push_back({v, u, 0});
            G[v].push_back(m++);
        }
        bool bfs() {
            lv = vector<int>(n, -1);
            queue<int> que;
            que.push(s);
            lv[s] = 0;
            while (!que.empty()) {
                int u = que.front();
                que.pop();
                for (int ei : G[u]) {
                    Edge &e = edges[ei];
                    if (lv[e.v] < 0 && e.cap > 0) {
                        lv[e.v] = lv[u] + 1;
                        que.push(e.v);
                    }
                }
            }
            return lv[t] >= 0;
        }
        long long dfs(int u, long long f) {
            if (u == t || f == 0) return f;
            long long res = 0;
            for (int &i = cur[u]; i < (int)G[u].size(); i++) {
                int ei = G[u][i];
                Edge &e = edges[ei];
                Edge &rev = edges[ei ^ 1];
                if (e.cap > 0 && lv[e.v] == lv[u] + 1) {
                    long long a = dfs(e.v, min(f, e.cap));
                    if (a > 0) {
                        e.cap -= a;
                        rev.cap += a;
                        res += a;
                        f -= a;
                        if (f == 0) break;
                    }
                }
            }
            return res;
        }
        long long max_flow(int _s, int _t) {
            s = _s, t = _t;
            long long res = 0;
            while (bfs()) {
                cur = vector<int>(n, 0);
                while (true) {
                    long long f = dfs(s, LLONG_MAX);
                    if (f == 0) break;
                    res += f;
                }
            }
            return res;
        }
    } flow;
	```

### 複雜度比較

|                   | Flow                       | Matching       |
| ----------------- | -------------------------- | -------------- |
| Ford-Fulkerson    |         O(EF)                   | O(VE)          |
| Edmond-Karp       | O(min(VE<sup>2</sup>, FE)) |                |
| Dinic（常數級小） | O(min(V<sup>2</sup>E, FE)) | O(E * sqrt(V)) |


## 最小割(Min Cut)

定義一個 s-t cut $C = (S \text{-component}, T\text{-component})$ 是將點分成與 s 同一塊或與 t 同一塊。定義 $C$ 的 cut-set 為 $\{(u, v) \in E \mid u \in S\text{-component}, v \in T\text{-component}\}$，使得在 cut-set 的邊都被刪掉後，s 到 t 的 Max Flow 是 0（i.e. s 和 t 不連通）。

s-t cut 的 cost 為 cut-set 內的邊的 capacity 總和，min cut 就是要最小化這個 cost。簡單來說就 Min Cut 是選一些邊，使得刪掉後 s, t 不連通，並且 capacity 最小

<figure markdown>
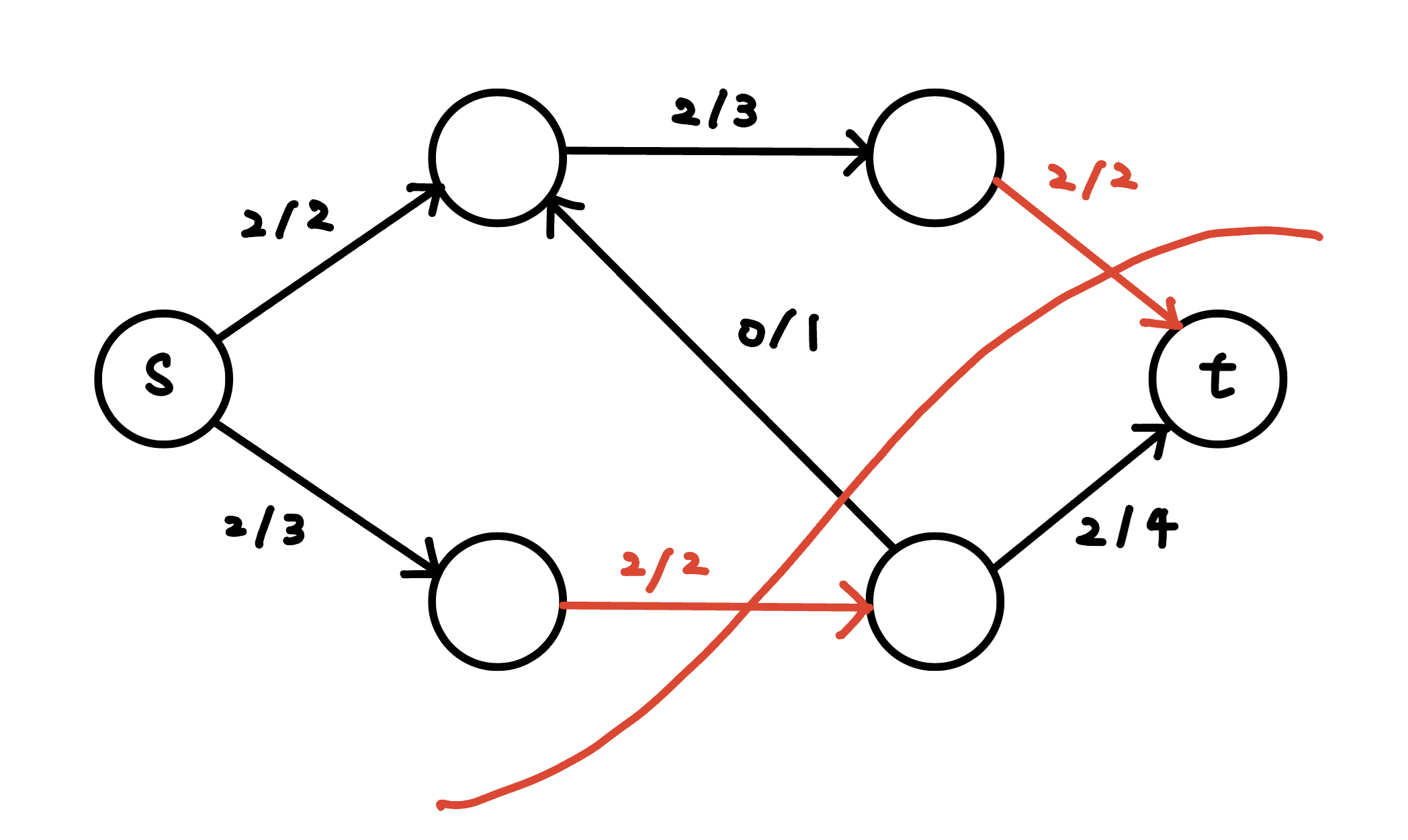  ![Image title](./images/97.png){ width="300" }
</figure>

以這個例子來說，min cut 就是 2 + 2 = 4（從 t 到 s 的邊雖有被切到，但不計算在 s-t 割，因為對 s 能不能走到 t 的連通性沒有影響）

min cut 為什麼很多圖片都會用一條線來切割，因為我們可以想成把 S-component 與 T-component 拔開，中間就會產生好幾條連通兩側的邊，這條線就代表著 min cut 會切割這些邊

??? info "【Max Flow Min Cut Theorm】: max flow = min cut"
	max flow <= cut

	Max Flow 可以想成很多個 disjoint path，任何的 cut 一定都會切到這些 path，所以任何 cut 不會比任何 flow 小。
	
	---
	
	感性的理解，s-t 若想要流出最大流量，必定會有瓶頸處形成 s-t 最小割
	
	---
	
	> 對偶性 Duality(from IOIC 2016)
	
	問題常常是一體兩面，某個求最大值的問題常常等價於另一個求最小值的問題，例如說:
	
	- 「你會的問題裡最難的一個」差不多就是 「你不會的問題裡最簡單的一個」
	
	- 「給你 1000 元你最多可以活多久」跟 「你要活一個月至少需要多少錢？」差不多
	
	那最大流的對偶是什麼呢 ? 一個網路的最大流，就是那些被「堵住」的水管的淨流量，這些堵住的水管會把點分成兩群。

### 如何輸出一個 mincut

min-cut 就是做 max-flow 後，從 s 半邊指到 t 半邊的那些邊。做完 max-flow 後做一次 bfs / dfs，並只走還沒流滿的邊，可以走到的點即為 s 半邊，不能走到的點即為 t 半邊的點，掃過所有的邊檢查兩端點的狀況，輸出符合條件的即為所求。

感性的理解，為什麼可以這樣做，其實可以把 s 開始走還沒流滿的邊視為無關緊要的邊，若碰到一個會流滿的地方就會是瓶頸處

???+note "code"
	```cpp linenums="1"
	bool side[MAXN];
    void cut(int u) {
        side[u] = 1;
        for (int i : G[u]) {
            if (!side[edges[i].v] && edges[i].cap) {
                cut(edges[i].v);
            }
        }
    }
    ```
    
??? question "求 S-component 點數最少/最多的 mincut"
	最少: 從 s 開始走沒有流滿的 edges，走到的點就是答案

	最多: 從 t 開始走沒有流滿的 edges，沒走到的點就是答案
	
???+note "模板測試 [Kattis - Min Cut](https://open.kattis.com/problems/mincut)"
	給一張 $n$ 點 $m$ 邊有向圖，每條邊給定容量 c(u, v)，問 $s$ 到 $t$ 的 min cut，並輸出 S-component 內的點
	
	$2\le n\le 500, 0\le m\le 10^4, 1\le c(u, v) \le 10^8$
	
	??? note "code"
		```cpp linenums="1"
		#include <bits/stdc++.h>
        #define int long long
        #define pii pair<int, int>
        #define ALL(x) x.begin(), x.end()
        #define pb push_back

        using namespace std;

        const int INF = 2e18;

        struct dinic {
            int n, m, s, t;
            struct Edge {
                int u, v, cap, w;
            };

            vector<vector<int>> G;
            vector<Edge> edge;
            vector<int> cur;
            vector<int> lv;
            vector<int> slide;
            vector<int> ans;

            void init() {
                n = m = 0;
                edge.clear();
                G.clear();
                cur.clear();
                lv.clear();
                slide.clear();
                ans.clear();
            }

            void add_node() {
                n++;
                G.pb({});
            }

            void add_edge(int u, int v, int cap) {
                G[u].pb(m++);
                edge.pb({u, v, cap});
                G[v].pb(m++);
                edge.pb({v, u, 0LL});
            }

            int bfs() {
                lv = vector<int>(n, -1);
                queue<int> q;
                q.push(s);
                lv[s] = 0;

                while (q.size()) {
                    int u = q.front();
                    q.pop();

                    for (auto id : G[u]) {
                        Edge &e = edge[id];

                        if (e.cap > 0 && lv[e.v] == -1) {
                            lv[e.v] = lv[e.u] + 1;
                            q.push(e.v);
                        }
                    }
                }
                return lv[t] >= 0;
            }

            int dfs(int u, int f) {
                if (u == t || f == 0) return f;
                int res = 0;

                for (int &i = cur[u]; i < G[u].size(); i++) {
                    Edge &e = edge[G[u][i]];
                    Edge &rev = edge[G[u][i] ^ 1];

                    if (e.cap > 0 && lv[e.v] == lv[e.u] + 1) {
                        int x = dfs(e.v, min(f, e.cap));

                        if (x > 0) {
                            res += x;
                            f -= x;
                            e.cap -= x;
                            rev.cap += x;
                            if (f == 0) break;
                        }
                    }
                }

                return res;
            }

            void cut(int u) {
                slide[u] = 1;
                ans.pb(u);
                for (auto id : G[u]) {
                    Edge &e = edge[id];

                    if (slide[e.v] == -1 && e.cap > 0) {
                        cut(e.v);
                    }
                }
            }

            void min_cut() {
                slide = vector<int>(n, -1);
                cut(s);

                cout << ans.size() << "\n";
                for (int it : ans) cout << it << "\n";
            }

            int max_flow(int _s, int _t) {
                s = _s, t = _t;

                int ans = 0;
                while (bfs()) {
                    cur = vector<int>(n, 0);
                    while (true) {
                        int f = dfs(s, INF);
                        if (f == 0) break;
                        ans += f;
                    }
                }
                return ans;
            }
        } flow;

        void solve() {
            int n, m, s, t;
            cin >> n >> m >> s >> t;
            flow.init();
            for (int i = 0; i < n; i++) flow.add_node();

            int u, v, cap;
            for (int i = 0; i < m; i++) {
                cin >> u >> v >> cap;
                flow.add_edge(u, v, cap);
            }
            int f = flow.max_flow(s, t);
            flow.min_cut();
        }

        signed main() {
            // ios::sync_with_stdio (0);
            // cin.tie (0);
            int t = 1;
            while (t--) {
                // init ();
                solve();
            }
        }
        ```

### min cut 應用

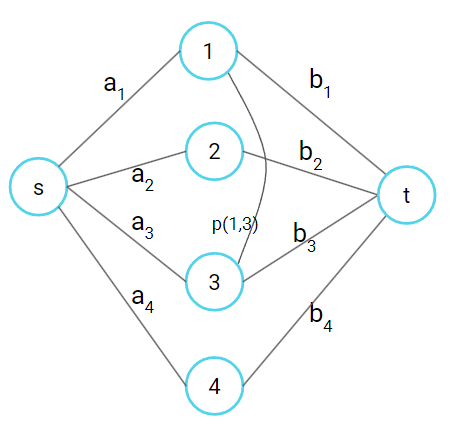
???+note "生產產品問題 [NCTUOJ 1138. 成本利潤問題 (Group 31)](https://oj.nctu.edu.tw/problems/1138/)"
	有 $n$ 種工具和 $m$ 種工作，每種工作需要若干種工具。第 $i$ 種工具需要花 $c_i$ 元買下來，第 $i$ 種工作的報酬為 $p_i$，求最大利潤
	
	<figure markdown>
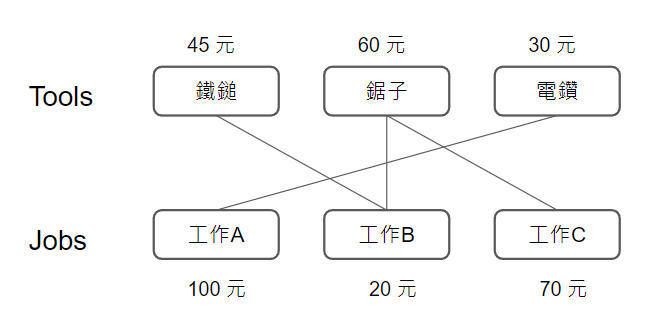	  ![Image title](./images/126.png){ width="300" }
	</figure>
	
	$1 \le n, m \le 500,$ 物品需求關係數量 $\le 2\times 10^4$
	
	??? note "思路"
		先建圖，左半排擺工具，右半排擺工作，成本和報酬為邊權，若方案 i 需要工具 j，則連邊 (j, i)
		
		<figure markdown>
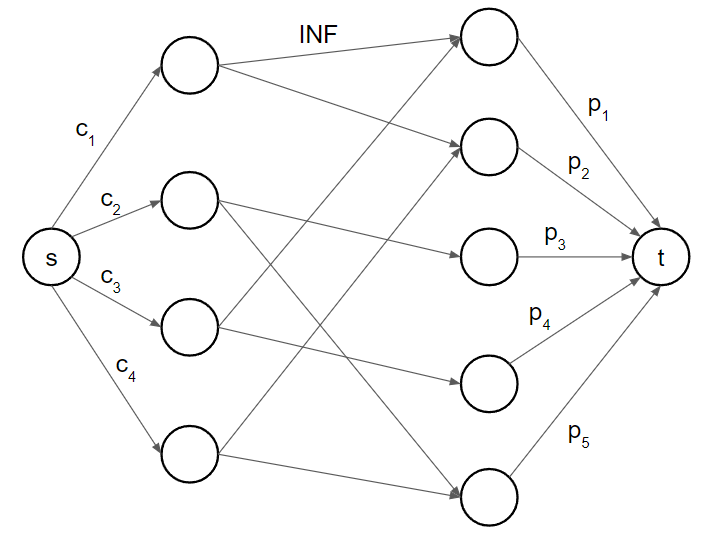	      ![Image title](./images/127.png){ width="400" }
	    </figure>
	    
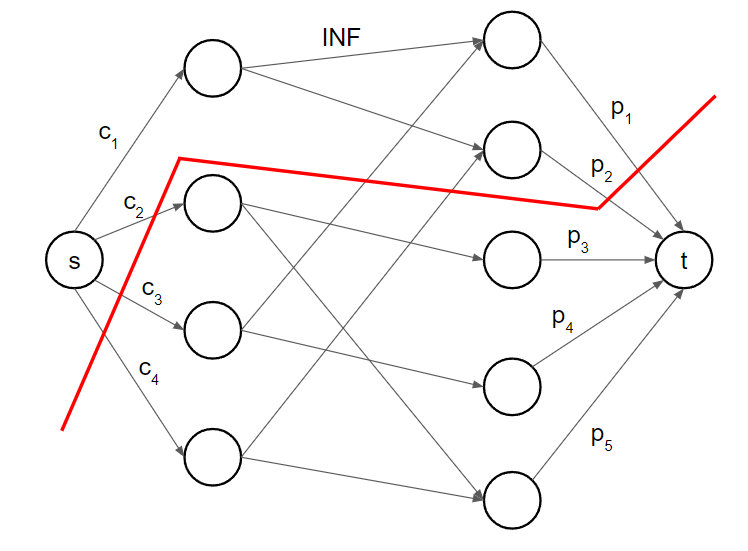
	    因為 min cut 要最小化，切到的就會是**要買的工具 C** 和**不賺的工作 P'**。若選完 maximum flow > 0
	    
	    <figure markdown>
	      ![Image title](./images/128.png){ width="400" }
	    </figure>
	    
	    最後答案就是 $\sum P$ - (C + P')
	    
	    我們來驗證為什麼這個問題可以轉換成 min cut，以上圖的工作 p1 來說:
	    
	    - 不做 p1 → c1, c3 選不選都無所謂
	    	- min cut 的角度: 切 p1 → c1, c3 切不切都無所謂
		
		- 做 p1 → c1, c3 一定要選
			- min cut 的角度: 不切 p1 → c1, c3 都一定要被切

???+note "最大權閉包問題 [NCTUOJ 731. 最大權閉包問題 (Group 19)](https://oj.nctu.edu.tw/problems/731/)"
	給 n 個人的受歡迎程度和每個人的好友列表 (好友並非雙向關係)，若第 i 個人要參加聚會的話則他的所有好友都要參加聚會，要邀請若干個人使得受歡迎程度總和最大
	
	1 ≤ n ≤ 100, 1 ≤ m ≤ 1000
	
	??? note "思路"
		將受歡迎程度為負的當成要付出成本的工具，將受歡迎程度為正的當成可以賺錢的方案，A 要來的話 B 就要來，就很像要用 A 方案賺錢，就要買 B 工具，因此若有關係 A 來的話 B 一定要來，則要連結邊 (B, A)
		
		<figure markdown>
	      ![Image title](./images/130.png){ width="400" }
	    </figure>
		
		得到的最小割為要來的負受歡程度的人和不來的正受歡迎程度的人，如同成本利潤問題，用正受歡迎程度的人的總和扣掉最小割即為答案
		
		---
		
		我們來驗證為什麼這個問題可以轉換成 min cut，假設如果 u 要選 v 就要選，我們有 edge(v, u):
		
		- 不選 u → v 選不選都無所謂
	    	- min cut 的角度: 切 u → v 切不切都無所謂
		
		- 選 u → v 一定要選
			- min cut 的角度: 不切 u → v 都一定要被切
		
		再來說明為何 edge 會從左到右。假設如果 u 要選 v 就要選，我們有 edge(v, u)，為左到右的 edge，且 weight = INF，使得 min cut 不可能會切這條邊，所以不會發生 u 有選 v 沒有選的情況

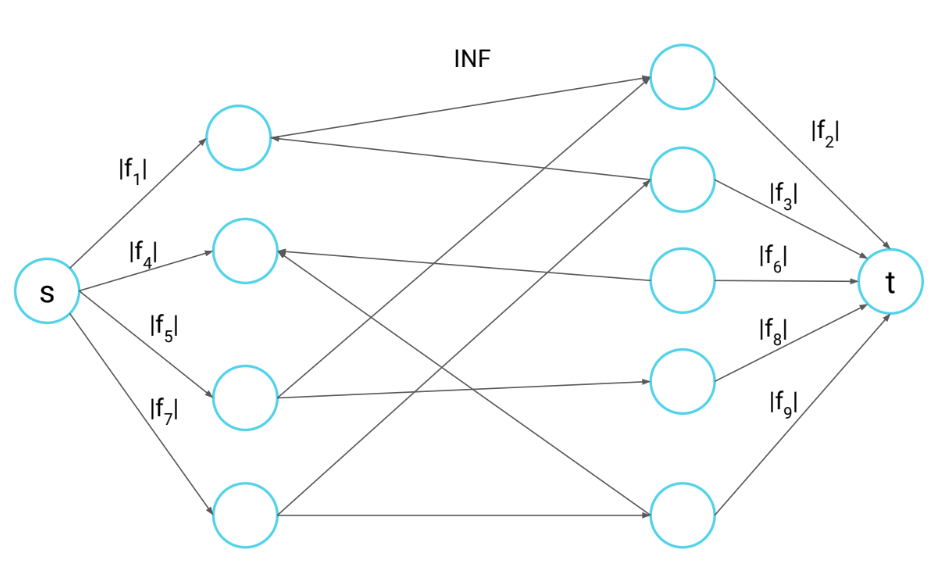
???+note "雙機工作分配"
	有兩台主機 A, B，有 n 個工作被執行，第 i 個工作在 A 主機執行需要耗電 a[i] 單位，在 B 主機執行需要耗電 b[i] 單位，有 m 組工作之間有相依關係，工作 i 與工作 j 若在不同主機執行，需要額外 p(i, j) 單位電力，決定每個工作依序要在哪個主機執行，最小化耗電
	
	1 ≤ n ≤ 500, 1 ≤ m ≤ 10000
	
	??? note "思路"
		mincut 會將點分成兩群，不同群的點之間的 cost 會被 cut 到
		
		<figure markdown>
	      ![Image title](./images/131.png){ width="400" }
	    </figure>
	
		S-component 給機器 B, T-component 給機器 A
		
	    ---
	    
	    我們來驗證轉換成 min cut 的正確性，假設每個工作都已經確定好是機器 A 還是機器 B 了:
	    
	    - 若為機器 A，必須產生 a[i] 的 cost
	    	-  i 在 T-component 內，所以在 edge(s, i) 上有 cost = a[i] 的 cut
	
		- 若為機器 B，必須產生 b[i] 的 cost
	    	-  i 在 S-component 內，所以在 edge(i, t) 上有 cost = b[i] 的 cut
	
		- i 在 B 執行 j 在 A 執行，必須產生 p(i, j) 的 cost
			- i 在 S-component 內，j 在 T-component 內，所以有 cost(i, j)

???+note "[TOI 2019 pE. 傳真修復 (fixing)](https://sorahisa-rank.github.io/oi-toi/2019/problems.pdf#page=6)"
	給一個 n * m 的 grid，每個格子上都有圖黑色或白色。問花費最少多少:
	
	- 若相鄰的格子不同顏色，會產生 1 單位的花費
	
	- 改變一個格子的顏色，會產生 2 單位的花費
	
	$n\le 30, m\le 30$
	
	??? note "思路"
		建圖，格子當點，格子與格子間建立無向邊，cost = 1，起點到白點建立有向邊，cost = 2，黑點到終點建立 cost = 1 的有向邊
		
		<figure markdown>
	      ![Image title](./images/129.png){ width="400" }
	    </figure>
			
		跟上一題一樣，要將點分兩群，變 S-component 與 T-component。，S-component 代表是白色，T-component 代表是黑色
	
	    ---
	    
	    我們來驗證為轉換成 min cut 的正確性，假設每個格子都已經確定好是白色或黑色:
	    
	    - 若 i 從白變黑，產生 2 的 cost
	    	-  i 在 T-component 內，所以在 edge(s, i) 上有 cost = 2 的 cut
	
		- 若 i 從黑變白，產生 2 的 cost
	    	-  i 在 S-component 內，所以在 edge(i, t) 上有 cost = 2 的 cut
	
		- i 是白，j 是黑，產生 1 的 cost
			- i 在 S-component 內，j 在 T-component 內，所以有 cost = 1

## 二分圖系列

### 二分圖最大匹配

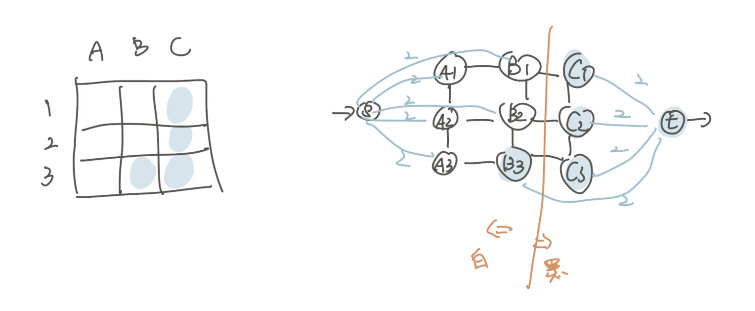
???+note "問題"
	給一個二分圖，選一些邊使任意兩條邊都沒有公共的頂點，且數量越大越好，也就是最大匹配，並輸出一組答案

創兩個超級源點和超級匯點，所有邊權都是 1，求 max flow 就是答案。輸出答案即看位於兩排中央流滿的邊，極為所求。

<figure markdown>
  ![Image title](./images/98.png){ width="300" }
</figure>

### DAG 最小路徑覆蓋

???+note "問題"
	給一張 n 點 m 邊的 DAG，最少選幾條路徑才可以蓋住所有的點，且任兩條路徑不能有共通的點，也就是問 disjoint path 數量
	
	<figure markdown>
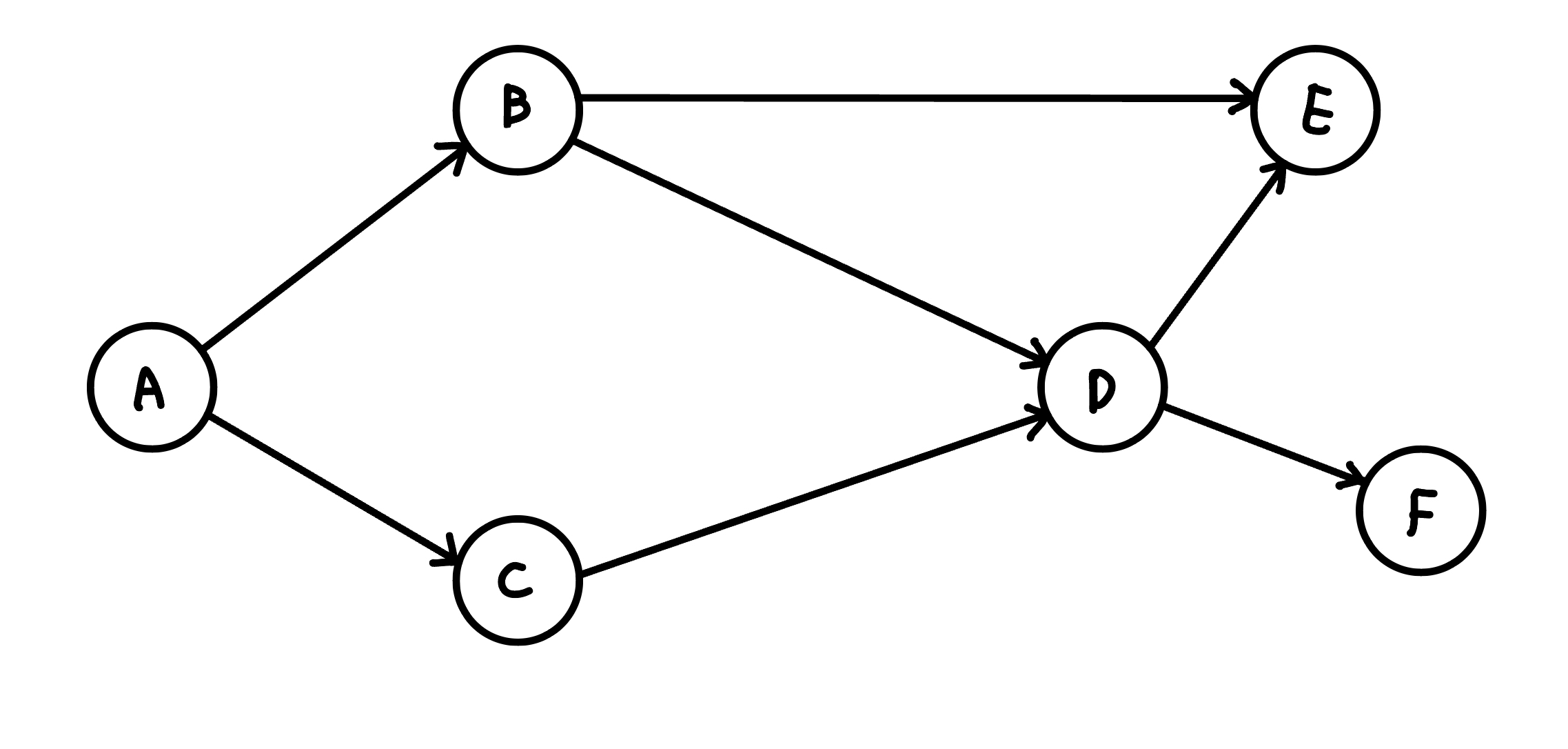	  ![Image title](./images/99.png){ width="300" }
	</figure>

??? info "不重疊路徑數  + 路徑長總和 = n"
	對於每個點，有被覆蓋到 iff 
	
	- 前面有一條邊連接
	
	- 為 disjoint path 的開頭
	
	因此每個點都貢獻都可以分成上述兩種 case，而點的數量為 n，不重疊路徑數 + 路徑長總和自然就是 n
	
	<figure markdown>
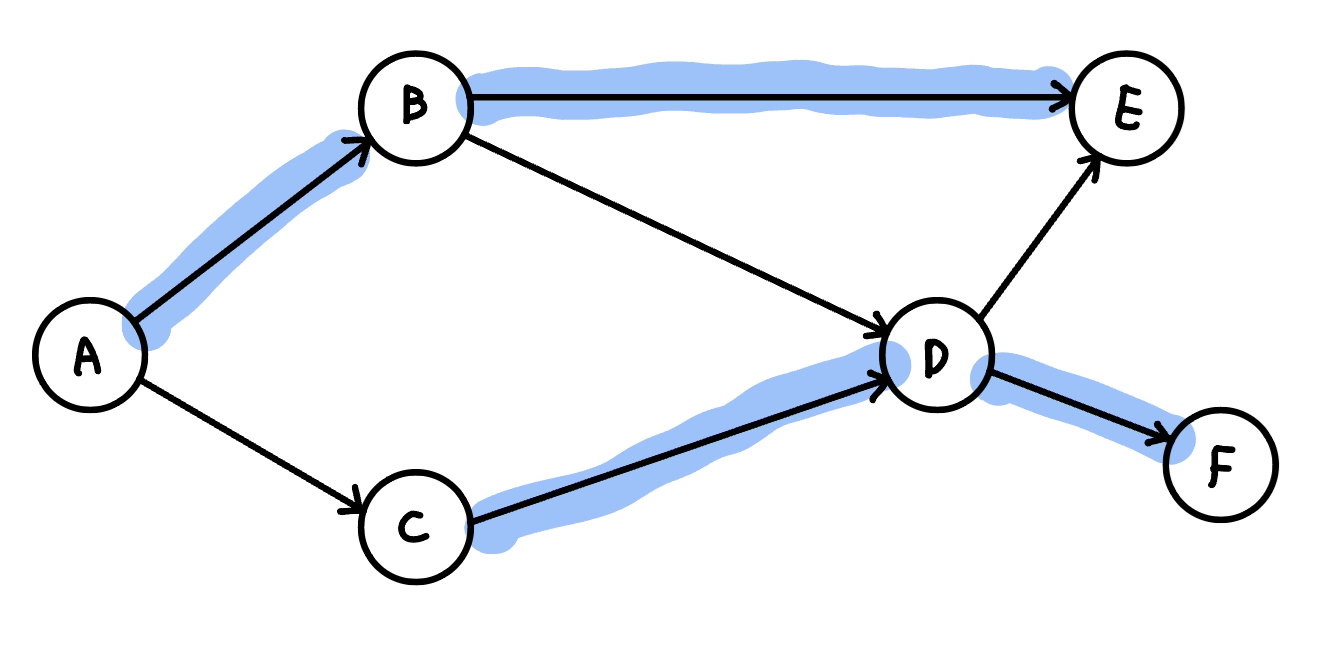	  ![Image title](./images/110.png){ width="300" }
	</figure>

路徑上會滿足每個點的 in-degree 和 out-degree 至多都是 1，所以我們可以將每個點拆成入點跟出點，進行二分圖最大匹配

<figure markdown>
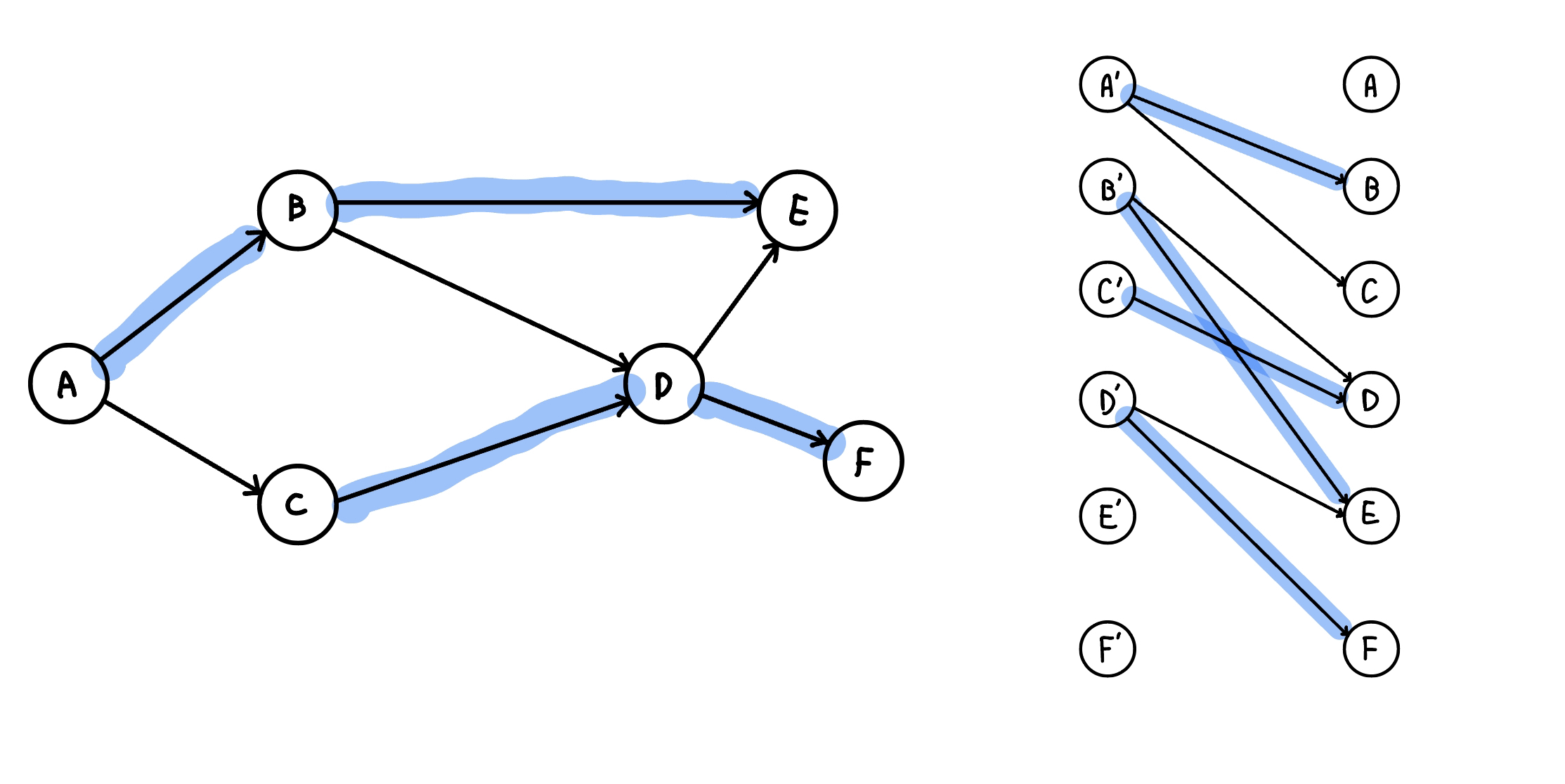  ![Image title](./images/109.png){ width="300" }
</figure>

### 二分圖最小點覆蓋

???+note "問題"
	給一個二分圖，選擇最少的點來覆蓋所有的邊，且數量越小越好，也就是最小點覆蓋，並輸出一組答案
	
??? info "【Kőnig's theorem】: 在二分圖中，|最小點覆蓋| = |最大匹配|"
    
    這邊給出 Kőnig's theorem 的構造法證明，也就是「為何一定找的到一組最小點覆蓋，其數量恰為 max flow」。
    
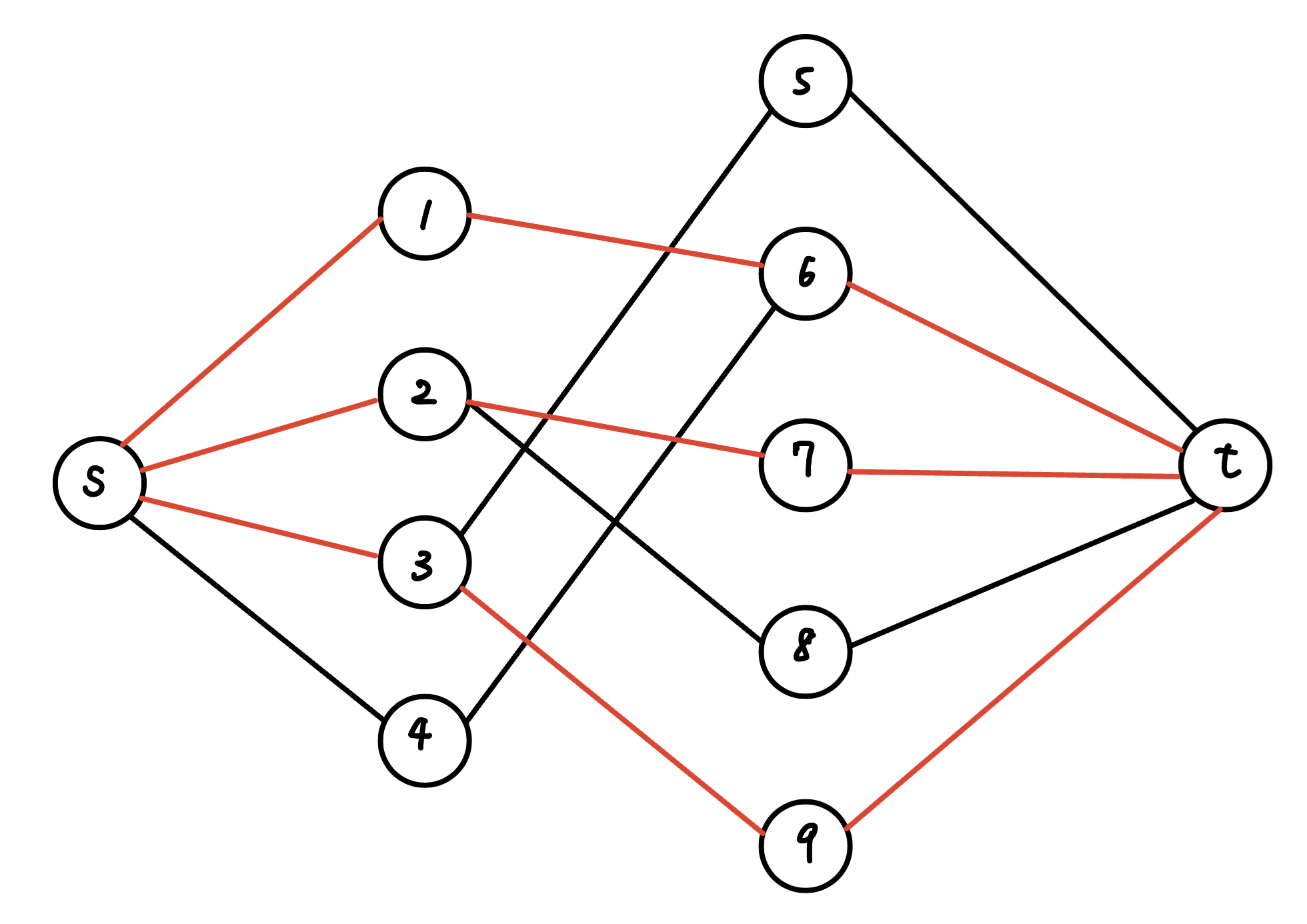
    最小點覆蓋顧名思義就是要找到一些重要的點，並且這些點要越少越好，考慮 min cut，min cut 可以找到重要的邊，使 s 跟 t 的 max flow = 0，而且數量最小化，我們使用找一組 min cut 的方法，從 s 開始走還沒流滿的邊，找出 S-component, T-component
    
    <figure markdown>
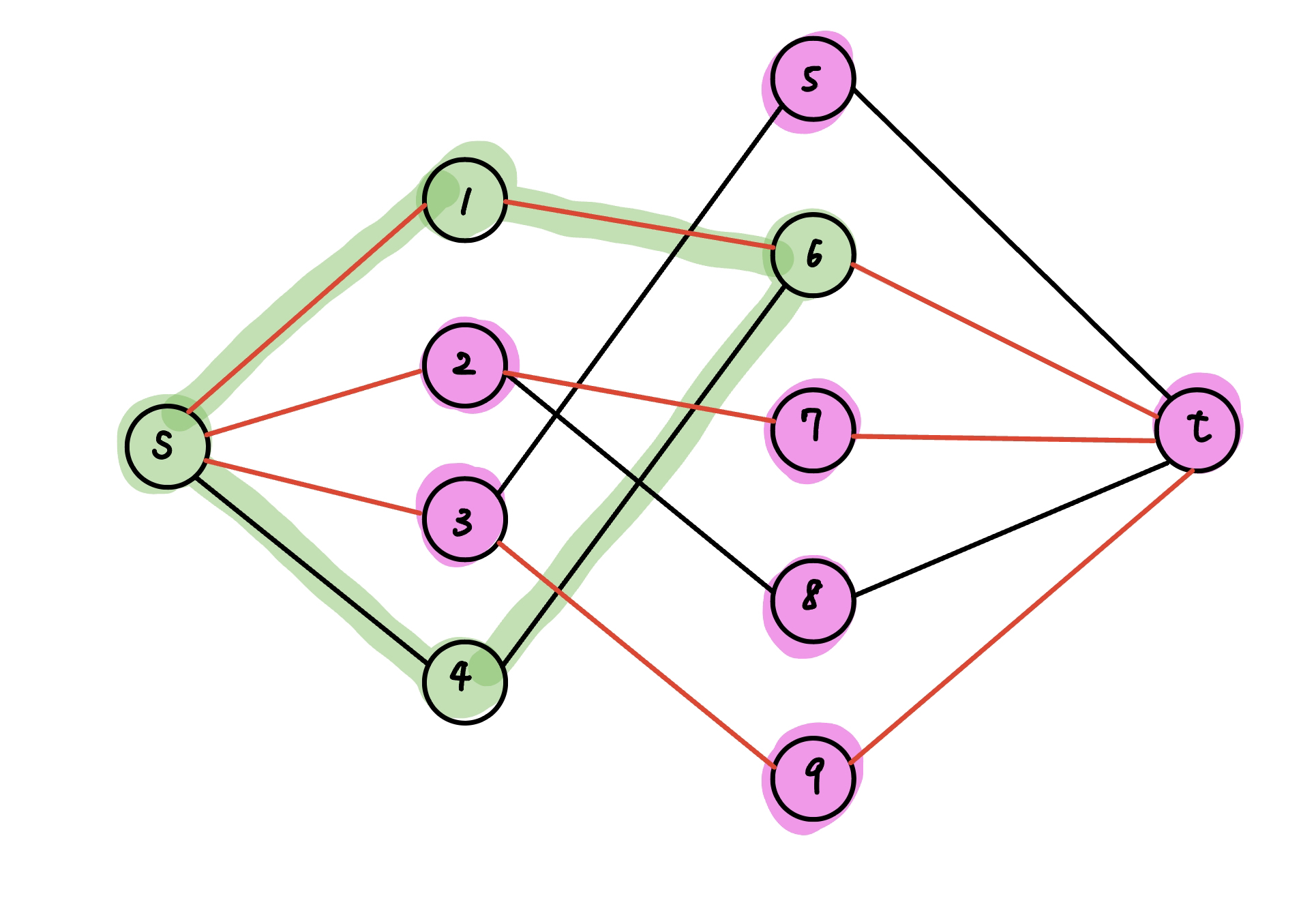      ![Image title](./images/100.png){ width="400" }
      <figcaption>綠色即為 S-component, 紫色即為 T-component</figcaption>
    </figure>
    
    以上圖來說，我們用 dfs 從 s → 4 → 6 → 1 找出 S-component，其餘的則是 T-component
    
    <figure markdown>
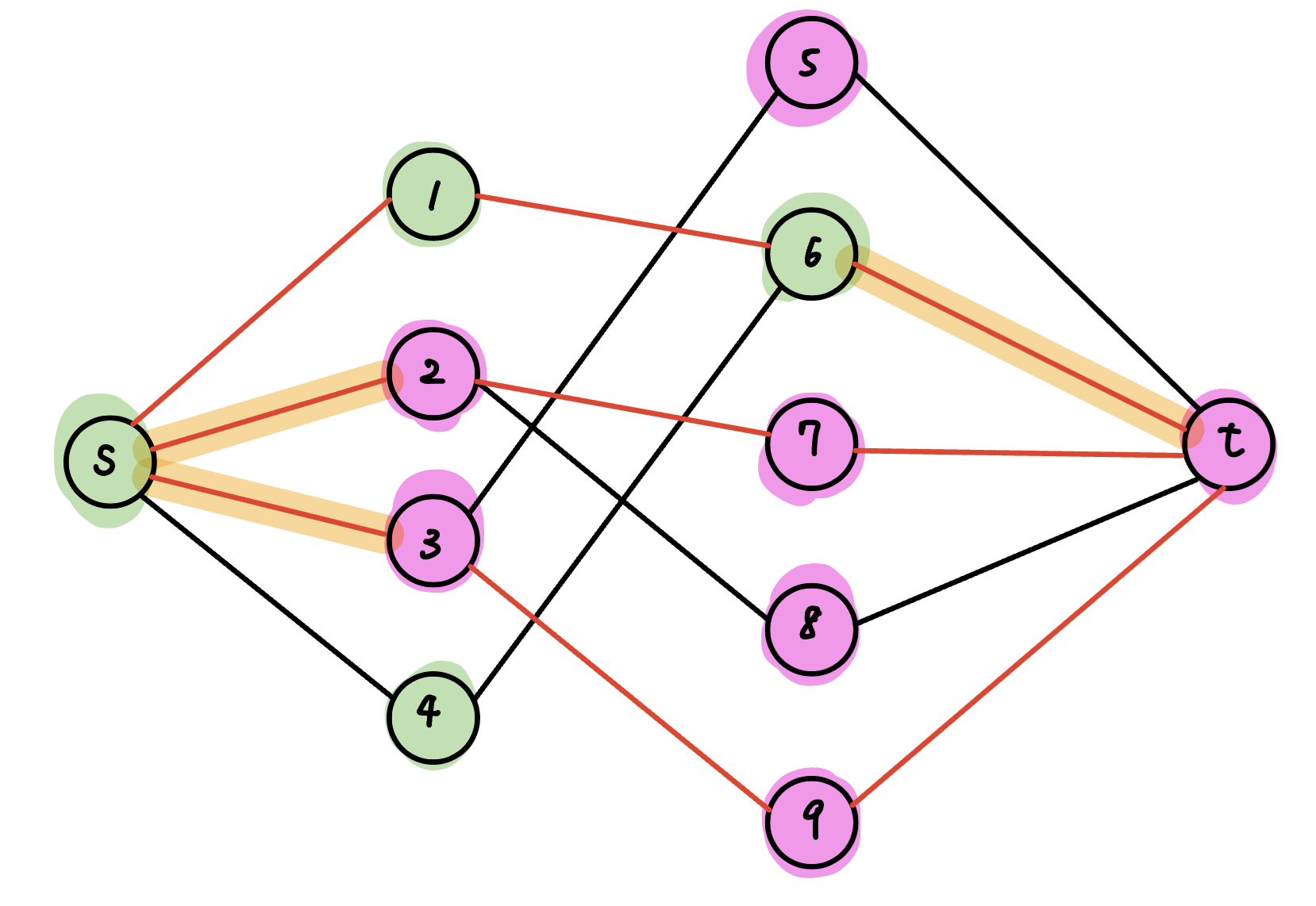      ![Image title](./images/108.png){ width="400" }
    </figure>
    
    將 (u ∈ S, v ∈ T) 的用橘色標記出來，即為 min cut
    
    因為依照 min cut 的定義，將橘色這些邊刪除後 s 到 t 的 max flow = 0，代表橘色這些邊相鄰且在中間的點足以支配中間的每一條邊，而又 min cut = max flow，所以最小點覆蓋數量 = min cut = max flow。具體要選哪些中間的點，如下:
    
    - 左邊且在 T-component 中
    
    - 右邊且在 S-component 中
    
    <figure markdown>
      ![Image title](./images/101.png){ width="400" }
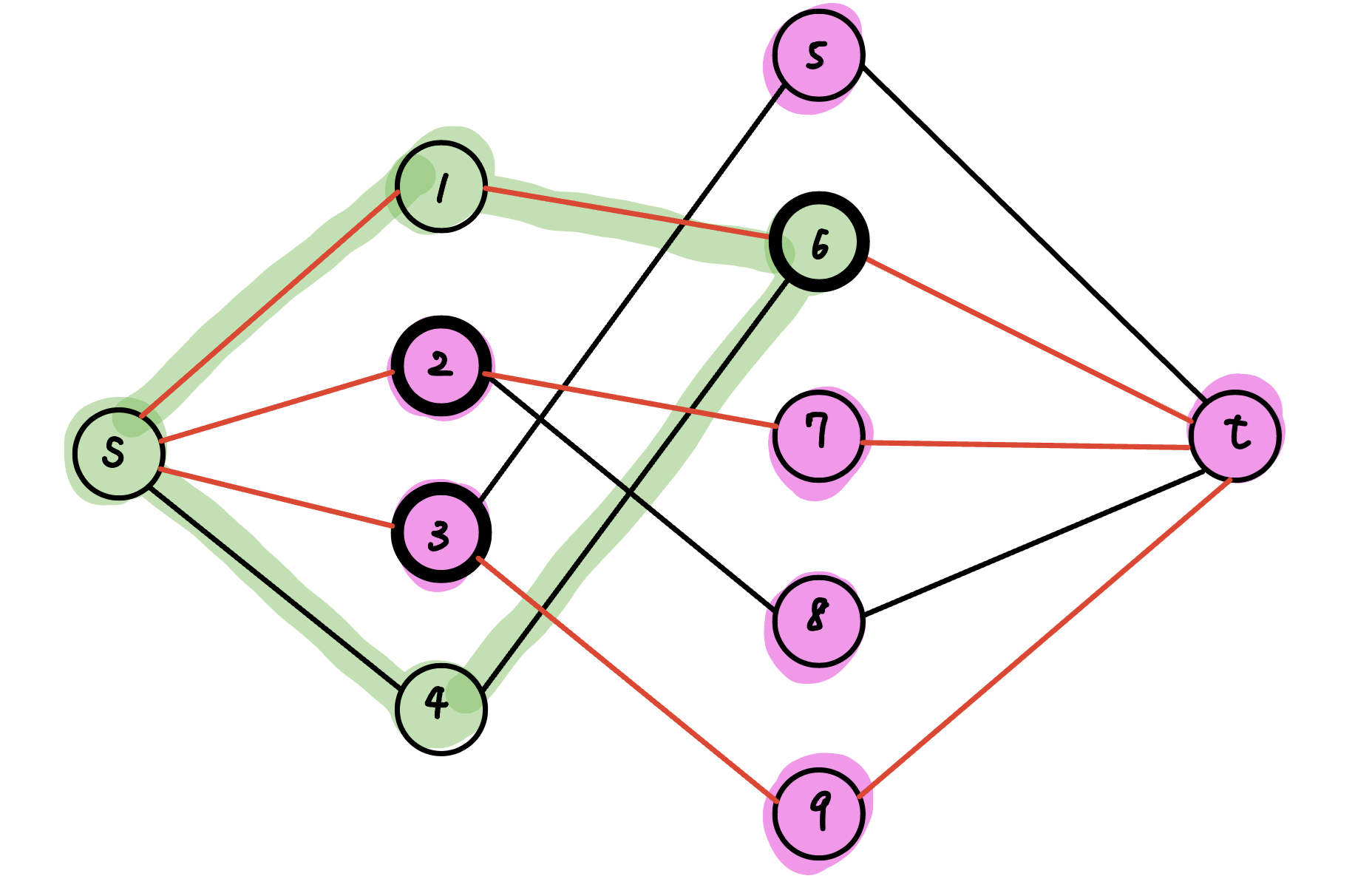
      <figcaption>粗框的點就是最小點覆蓋</figcaption>
    </figure>

根據 Kőnig's theorem，我們得知最小點覆蓋數量跟最大匹配的數量是一樣的，也就是 max flow。若要輸出答案，那我們就選以下這些點即可

- 左邊跟 mincut 同 t 側的的點

- 右邊跟 mincut 同 s 側的的點

具體為什麼可以這樣做在上面 Kőnig's theorem 的構造法證明中有提到

???+note "[CSES - Coin Grid](https://cses.fi/problemset/task/1709)"
    給一個 $n\times n$ 的 Grid，有些格子上有錢幣。每次可以移除一個 row 或一個 col 的所有錢幣，問最少要幾次操作
	

### 二分圖最大獨立集

???+note "問題"
	給一個二分圖，選一些點使選的點兩兩不相鄰，且數量越大越好，也就是最大獨立集，並輸出一組答案
	
??? info "定理: 在一般圖上，|最小點覆蓋| + |最大獨集| = n"
	【證明】: 最小點覆蓋以外都是最大獨立集

	每條邊都會被最小覆蓋支配（每條邊至少會有一個點被最小點覆蓋選到），所以剩餘的點跟點之間不可能會有一條邊（有的話代表沒被支配），符合最大獨立集定義

所以答案就是 n - max flow。輸出答案的話，就把最小點覆蓋沒選到的點都選起來

<figure markdown>
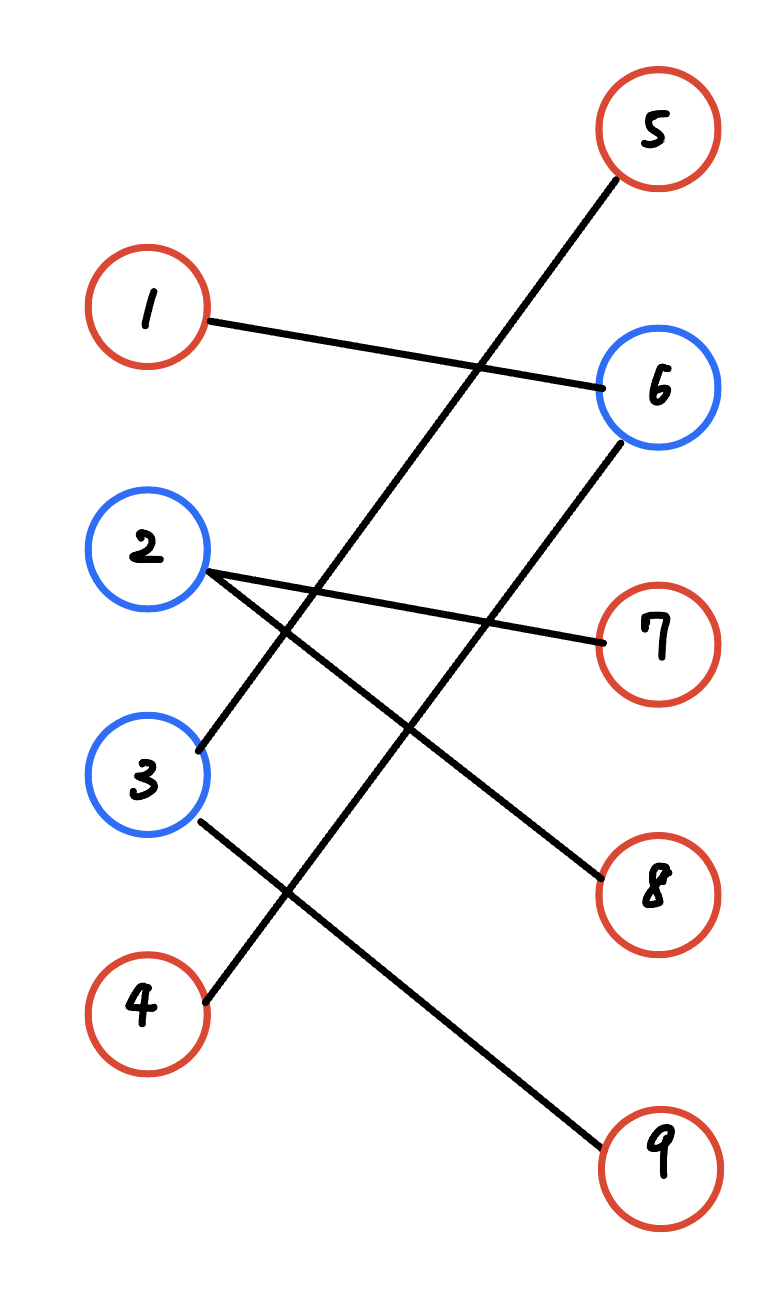  ![Image title](./images/102.png){ width="250" }
  <figcaption>藍色為最小點覆蓋, 紅色為最大獨集</figcaption>
</figure>

### 比較

- 在二分圖下
	- 最大匹配 (MM) = 最小點覆蓋 (MVC)
	- 最大獨立集 (MIS) + 最小點覆蓋 (MVC) = n
	- 都可以用 max flow 在多項式時間解出

- 在一般圖下
	- 最大獨立集 (MIS) + 最小點覆蓋 (MVC) = n
	- 最大獨立集,最小點覆蓋 : NP-hard 問題 (目前已知的演算法只能指數時間解出)
	- 最大匹配 : P 問題


## min cost max flow

???+note "題目"
	給一個有向圖，每條邊 (u, v) 都有一個邊權 c(u, v) 代表容量上限，有 cost(u, v)代表在這條邊流過一單位的流所需要的成本，找一個 flow 使 $\sum f(u,v)\times cost(u,v)$ 最小
	
概念和 Ford-Fulkson 一樣找增廣路徑，但是每次要找最便宜的。每條邊我們會多紀錄一個成本  cost(u, v)，對於反向邊的成本為負的正向邊成本，退流的時候等價於抵銷成本。因為圖上有負邊，所以必須用 Bellman-Ford 或是 SPFA 來找最短路徑

複雜度跟 Fulk-Fulkerson 就差在一個是 dfs，一個是 Bellman-Ford，而 Bellman-Ford 是 O(VE)，所以複雜度就是 O(F * VE)

??? note "code"
	```cpp linenums="1"
    const int INF = (1LL << 60);
    struct dinic {
        int n, m, s, t;
        struct Edge {
            int u, v, w, cap;
        };
        vector<vector<int>> G;
        vector<Edge> edges;
        void init() {
            n = m = 0;
            G = vector<vector<int>>();
            edges = vector<Edge>();
        }
        void add_node() {
            n++;
            G.push_back({});
        }
        void add_edge(int u, int v, int cap, int w) {
            edges.push_back({u, v, w, cap});
            G[u].push_back(m++);
            edges.push_back({v, u, -w, 0LL});
            G[v].push_back(m++);
        }
        pair<int, int> flow(int _s, int _t) {
            s = _s, t = _t;
            int cost = 0, fl = 0;
            while (true) {
                vector<bool> inq(n, 0);
                vector<int> dis(n, INF);
                vector<int> pre_node(n, -1);
                vector<int> pre_eid(n, -1);
                queue<int> q;
                q.push(s);
                dis[s] = 0;
                while (q.size()) {
                    int u = q.front();
                    q.pop();
                    if (inq[u]) {
                        inq[u] = false;
                    }
                    for (auto id : G[u]) {
                        Edge &e = edges[id];
                        if (e.cap > 0 && dis[u] + e.w < dis[e.v]) {
                            dis[e.v] = dis[u] + e.w;
                            pre_node[e.v] = u;
                            pre_eid[e.v] = id;
                            if (!inq[e.v]) {
                                inq[e.v] = true;
                                q.push(e.v);
                            }
                        }
                    }
                }
                if (dis[t] == INF) {
                    break;
                }
                int tf = INF;
                for (int u, v = t, eid; v != s; v = u) {
                    u = pre_node[v];
                    eid = pre_eid[v];
                    tf = min(tf, edges[eid].cap);
                }
                for (int u, v = t, eid; v != s; v = u) {
                    u = pre_node[v];
                    eid = pre_eid[v];
                    edges[eid].cap -= tf;
                    edges[eid ^ 1].cap += tf;
                }
                cost += tf * dis[t];
                fl += tf;
            }
            return {fl, cost};
        }
    } flow;
    ```

???+note "模板測試 [Kattis - Minimum Cost Maximum Flow](https://open.kattis.com/problems/mincostmaxflow)"
	給一張 $n$ 點 $m$ 邊有向圖，每條邊給定容量 c(u, v) 與 w(u, v)，問 $s$ 到 $t$ 的最大流，和 min cost
	
	$2\le n\le 250, 0\le m\le 10^5, 1\le c(u, v) \le 10^8$
	
	??? note "code"
        ```cpp linenums="1"
        #include <bits/stdc++.h>
        #define int long long

        using namespace std;

        const int INF = (1LL << 60);
        const int M = 1e9 + 7;

        struct dinic {
            int n, m, s, t;
            struct Edge {
                int u, v, w, cap;
            };
            vector<vector<int>> G;
            vector<Edge> edges;
            void init() {
                n = m = 0;
                G = vector<vector<int>>();
                edges = vector<Edge>();
            }
            void add_node() {
                n++;
                G.push_back({});
            }
            void add_edge(int u, int v, int cap, int w) {
                edges.push_back({u, v, w, cap});
                G[u].push_back(m++);
                edges.push_back({v, u, -w, 0LL});
                G[v].push_back(m++);
            }
            pair<int, int> flow(int _s, int _t) {
                s = _s, t = _t;
                int cost = 0, fl = 0;
                while (true) {
                    vector<bool> inq(n, 0);
                    vector<int> dis(n, INF);
                    vector<int> pre_node(n, -1);
                    vector<int> pre_eid(n, -1);
                    queue<int> q;
                    q.push(s);
                    dis[s] = 0;
                    while (q.size()) {
                        int u = q.front();
                        q.pop();
                        if (inq[u]) {
                            inq[u] = false;
                        }
                        for (auto id : G[u]) {
                            Edge &e = edges[id];
                            if (e.cap > 0 && dis[u] + e.w < dis[e.v]) {
                                dis[e.v] = dis[u] + e.w;
                                pre_node[e.v] = u;
                                pre_eid[e.v] = id;
                                if (!inq[e.v]) {
                                    inq[e.v] = true;
                                    q.push(e.v);
                                }
                            }
                        }
                    }
                    if (dis[t] == INF) {
                        break;
                    }
                    int tf = INF;
                    for (int u, v = t, eid; v != s; v = u) {
                        u = pre_node[v];
                        eid = pre_eid[v];
                        tf = min(tf, edges[eid].cap);
                    }
                    for (int u, v = t, eid; v != s; v = u) {
                        u = pre_node[v];
                        eid = pre_eid[v];
                        edges[eid].cap -= tf;
                        edges[eid ^ 1].cap += tf;
                    }
                    cost += tf * dis[t];
                    fl += tf;
                }
                return {fl, cost};
            }
        } flow;

        signed main() {
            ios::sync_with_stdio(0);
            cin.tie(0);

            int n, m, s, t;
            cin >> n >> m >> s >> t;
            flow.init();
            for (int i = 1; i <= n; i++) flow.add_node();
            for (int i = 0; i < m; i++) {
                int u, v, cap, w;
                cin >> u >> v >> cap >> w;
                flow.add_edge(u, v, cap, w);
            }
            auto [f, cost] = flow.flow(s, t);
            cout << f << " " << cost << "\n";
        }
        ```
	
???+note "[CSES - Distinct Routes II](https://cses.fi/problemset/task/2130)"
	給一張 n 點 m 邊有向圖，有源點 1 走到匯點 n，每條邊 (u, v) 最多只能走 c(u, v) 次，且經過的 cost 都是 1，最少需要花多少 cost 才能走出 k 條 disjoint path
	
	$n\le 10^5, m\le 10^5, 1\le k\le n - 1$
	
	??? note "思路"
		若邊的費用都是 0，只需要判斷 s-t maximum flow 是否大於等於 k
		
		邊有費用，權重都是 1 or -1，可以每次用 Bellman-Ford O(nm) 找到起點終點最便宜增廣路徑，共會跑 k 次，所以是 O(n * m * k)

???+note "[LOJ #6011. 「网络流 24 题」运输问题](https://loj.ac/p/6011)"
	有 $m$ 個倉庫和 $n$ 個零售店，第 $i$ 個倉庫有 $a_i$ 的貨物，第 $j$ 個零售店需要 $b_j$ 的貨物，供需平衡。從第 $i$ 個倉庫運送一單位貨物到第 $j$ 個零售店需要 $c_{i,j}$ 的費用，求滿足供需的最少費用。
	
	$n, m\le 100$
	
	??? note "思路"
		使用 MCMF
		
		- 將 s 向 m 個倉庫連邊，capacity = a[i], cost = 0
	
		- 將第 i 個倉庫與第 j 個零售店連邊，capacity = INF, cost = c[i][j]
	
		- n 個零售店向 t 連邊，capacity = c[i], cost = 0

???+note "二分圖帶權最大匹配 [CSES - Task Assignment](https://cses.fi/problemset/task/2129)"
	有 n 個人和 n 個工作，編號 i 的人做工作 j 要 cost(i, j) 的費用，每個工作分配給一個人做，每個人只能做一個工作，最小化總共的費用
	
	$n\le 200, 1\le c_{i, j}\le 1000$
	
	??? note "思路"
		用 MCMF，將人與工作個擺兩邊，中間用 capactity = 1, cost = cost(i, j) 的邊連接，s 連接所有人，capacity = 1, cost = 0，所有工作連接 t，capacity = 1, cost = 0
		
		複雜度為 O(n) 次 SPFA，SPFA 複雜度 O(V * E) = O(n * n^2)，所以是 O(n^4)

## 建模技巧(Flow Graph Modeling)

### 多源點多匯點

建立一個超級源點和超級匯點，和原本的源點與匯點連接，capacity 設為無限大

<figure markdown>
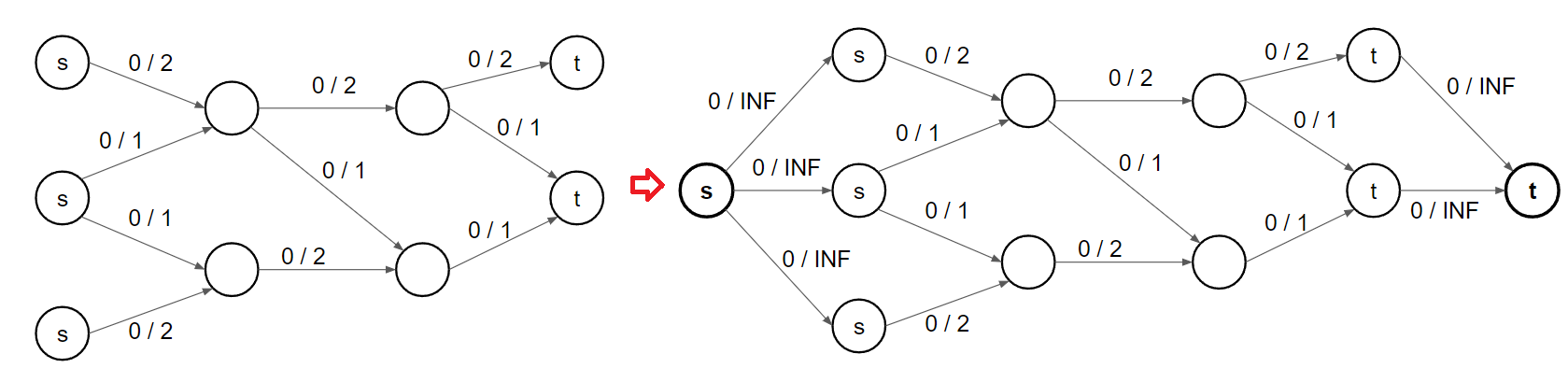  ![Image title](./images/124.png){ width="700" }
</figure>

### 點有流量限制

將每個點拆成兩個點，中間用對應的流量限制當邊的 capacity

<figure markdown>
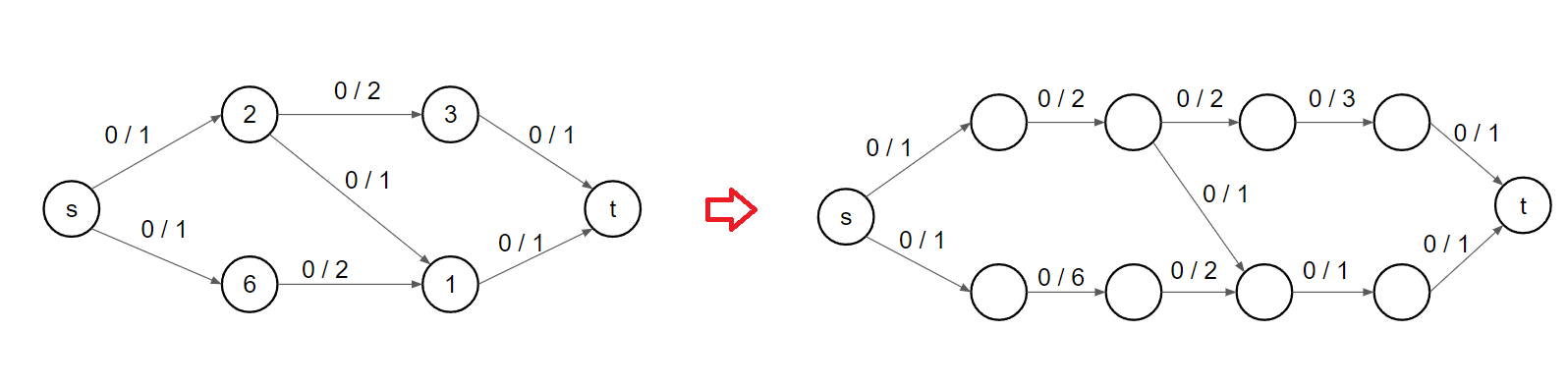  ![Image title](./images/125.png){ width="700" }
</figure>

## 題目

???+note "[CSES - Distinct Routes](https://cses.fi/problemset/task/1711)"
	給一張 n 點 m 邊的圖，最多找到幾條 disjoint path 

	$2\le n\le 500, 1\le m\le 1000$
	
	??? note "思路"
		edges capacity 設為 1，跑 max flow

- [LOJ 網路流 24 題](https://loj.ac/problems/tag/30)

## 參考資料

- <https://www.cnblogs.com/dijkstra2003/p/7598931.html>

- <https://www.mropengate.com/2015/01/algorithm-ch4-network-flow.html?m=1>

- <http://pisces.ck.tp.edu.tw/~peng/index.php?action=showfile&file=f3cec71910d4a0106624e839f2891b17198ef58be>

- <https://github.com/NCTU-PCCA/NCTU_Fox/tree/master/codebook/Graph/Flow>

- <https://web.ntnu.edu.tw/~algo/Matching.html>

- <https://nckuacm.github.io/2020/slides/week13_1.pdf>

- <https://chmnchiang.github.io/ioi-camp-2016-flow-slides/#/>