???+note "[2014 全國賽 p4](https://cs.cysh.cy.edu.tw/competition_problem_set/%E5%85%A8%E5%9C%8B103.pdf#page=9)"
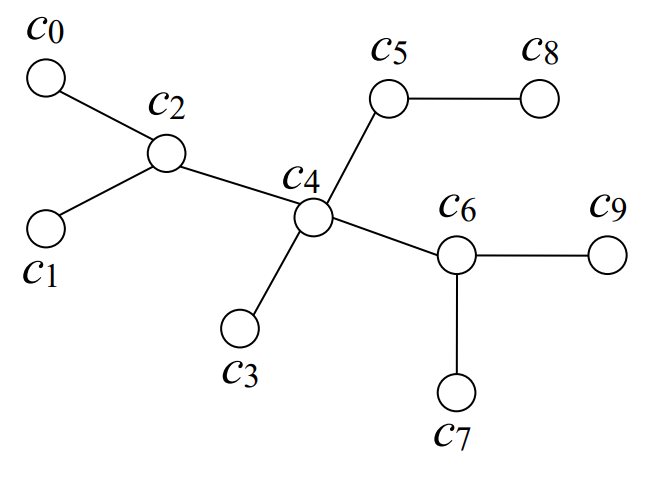
	給一顆 $n$ 個點，邊有權重的樹，選一個連通塊，連通塊內所有的邊權總和不能超過 $L$，問所有「沒被選到的點」到「有被選到的點」的最短距離最大的，最少可以是多少
	
	<figure markdown>
	  ![Image title](./images/14.png){ width="300" }
	</figure>
	
	$n\le 10^6,L\le 2\times 10^8$
	
	??? note "思路"
		顯然我們沒辦法去直接維護要選那些邊作為 optimal 的連通塊。那不如反著做 ?
		
		一開始我們把全部的邊都選起來，慢慢從 leaf 開始移除，每次移除時要選擇對答案影響最小的，直到當前未移除的連通塊的邊權總和 $\le L$。過程利用 priority queue 維護

???+note "[2015 全國賽 p5](https://tioj.ck.tp.edu.tw/problems/1915)"
	給一張 $n$ 點 $m$ 邊無向圖，你要將點由 $1\sim n$ 編號，問 $ans$ 最小可以是多少。計算方法如下 :
	
	$$cost_u = u \space 周圍的點 \space v \space 有幾個編號比他大 $$
	
	$$ans = \max \limits_{u=1\sim n}\{ cost_u \} $$
	
	也就是最小化最大值
	
	$n\le 5\times 10^5,m\le 8\times 10^5$
	
	??? note "思路"
		> 法 1 : 二分搜
	
		考慮二分搜答案，檢查答案是否合法
		
		??? note "check function 實作"
	        ```cpp linenums="1"
	        // 檢查只能用 degree <= x 的是否可以達成
	        bool topo(int x) {
	            queue<int> q;
	            vector<bool> vis(n + 1);
	
	            for (int i = 1; i <= n; i++) {
	                if (deg[i] <= x) q.push(i);
	            }
	            while (q.size()) {
	                int u = q.top();
	                q.pop();
	                vis[u] = true;
	
	                for (auto v : G[u]) {
	                    if (vis[v]) continue;
	
	                    deg[v]--;
	                    if (deg[v] <= x) q.push(v);
	                }
	            }
	
	            for (int i = 1; i <= n; i++) {
	                if (vis[i] == false) return false;
	            }
	            return true;
	        }
	        ```
		
		複雜度 : $O((n+m)\log n)$
		
		---
		
		> 法 2 : greedy 想法
		
		依序枚舉 1 ~ n，放在 `deg[i]` 最小的，用 pq 維護當前 deg 最小的
		
		將某個點 u 周圍的 `deg[v]--` 的話要怎麼做 ?
		
		想想看 dijkstra 是怎麼做到這件事的
		
		就像 dijkstra 那樣直接 push 一個新的進去 pq 即可
		
		pq 再拿某個點出來時記得檢查是否過期
		
		複雜度 : $O((n+m)\log n)$
		
		---
		
		> 法 3 : 優化法 2
		
		開 $n$ 個 vector，`v[i]` 放所有 degree = i 的點
		
		??? note "Data structure"
			```cpp linenums="1"
			struct DS {
	            vector<vector<int>> nodes;
	            int n, threshold = 0;
	
	            DS(int n) : n(n) {
	                nodes.resize(n + 1);
	            }
	
	            void push(int u) {
	                nodes[max(threshold, deg[u])].pb(u);
	            }
	
	            int get_min(int u) {
	                while (threshold <= n && nodes[threshold].empty()) {
	                    threshold++;
	                }
	
	                if (threshold <= n && nodes[threshold].size()) {
	                    int ret = nodes[threshold].back();
	                    nodes[threshold].pop_back();
	                    return ret;
	                } 
	                assert(0);
	            }
	        } pq;
	        ```
	    
		複雜度 : $O(n+m)$
		
	??? note "code"
		```cpp linenums="1"
		#include <bits/stdc++.h>
	    #define int long long
	    #define pii pair<int, int>
	    #define pb push_back
	    #define mk make_pair
	    #define F first
	    #define S second
	    #define ALL(x) x.begin(), x.end()
	
	    using namespace std;
	
	    const int INF = 2e18;
	    const int maxn = 5e5 + 5;
	    const int M = 1e9 + 7;
	
	    int n, m;
	    vector<int> G[maxn];
	    int deg[maxn], vis[maxn], ans[maxn];
	
	    struct DS {
	        vector<vector<int>> nodes;
	        int n, threshold = 0;
	
	        DS(int n) : n(n) {
	            nodes.resize(n + 1);
	        }
	
	        void push(int u) {
	            nodes[max(threshold, deg[u])].pb(u);
	        }
	
	        int get_min() {
	            while (threshold <= n && nodes[threshold].empty()) {
	                threshold++;
	            }
	
	            if (threshold <= n && nodes[threshold].size()) {
	                int ret = nodes[threshold].back();
	                nodes[threshold].pop_back();
	                return ret;
	            } 
	            assert(0);
	        }
	    };
	
	    void solve() {
	        DS ds(n);
	        for (int i = 0; i < n; i++) {
	            ds.push(i);
	        }
	        for (int i = 0; i < n; i++) {
	            int u = ds.get_min();
	            while (vis[u]) {
	                u = ds.get_min();
	            }
	            vis[u] = true;
	            for (auto v : G[u]) {
	                deg[v]--;
	                ds.push(v);
	            }
	        }
	        cout << ds.threshold << '\n';
	    }
	
	    void init() {
	        cin >> n >> m;
	        for (int i = 0; i < n; i++) {
	            G[i].clear();
	            deg[i] = 0;
	            vis[i] = 0;
	            ans[i] = 0;
	        }
	        for (int i = 0; i < m; i++) {
	            int u, v;
	            cin >> u >> v;
	            ans[min(u, v)]++;
	            G[u].pb(v);
	            G[v].pb(u);
	            deg[u]++;
	            deg[v]++;
	        }
	        cout << *max_element(ans, ans + n) << ' ';
	    }
	
	    signed main() {
	        ios::sync_with_stdio(0);
	        cin.tie(0);
	        int t = 1;
	        cin >> t;
	        while (t--) {
	            init();
	            solve();
	        }
	    } 
	    ```

???+note "[2017 全國賽 p5](https://tioj.ck.tp.edu.tw/problems/2038)"
	給你一張 $n$ 點 $m$ 邊無向圖，選一些點 ( 我們把這個點集合叫做 $S$ )，$S$ 內的點必須連通
	
	問 $F(S)$ 最大多少
	
	$$F(S) = \lvert S \rvert  \min\limits_{1\leq i \leq \lvert S \rvert} \{ D_i \}$$
	
	其中 $D_i$ 表示 $i$ 的鄰居裡面，有多少人在 $S$ 內
	
	$n\le 5000$
	
	??? note "思路"
		我們考慮從枚舉 $D_i$ 下手 
		
		- $D_i=1$ 這時其實就是整張圖
	    
	    - $D_i=2$ 因為 degree 是 $1$ 的點不能選，所以刪除 $\deg \le 1$ 的點，並將周圍的點的 degree -1
	    
	    - $D_i=3$ 刪除 $\deg \le 2$ 的點，並將周圍的點的 degree -1
	
		- $D_i=4$ 刪除 $\deg \le 3$ 的點，並將周圍的點的 degree -1
	
		- ...
	
		可以觀察到當 $D_i=k$ 的時候需要將 $\deg \le k-1$ 的點刪掉
		
		此時 $F(S)=$ 剩下的點的數量 $\times (k-1)$
		
		---
		
		實作方面沒辦法真的去刪邊，考慮時光倒流技巧，用加邊來看
		
		只是你並不能知道要依序加哪些點進去
		
		所以我們先預處理好 $D_i=k+1 \to D_i=k$ 的時候需要加入的點即可
		
		預處理就像 topo 排序那樣每輪找 $\deg = k$ 的點，將他們存在 vector `v[k]` 裡面
	
	??? note "code"
		```cpp linenums="1"
		#include <bits/stdc++.h>
	    #define int long long
	    #define pii pair<int, int>
	    #define pb push_back
	    #define mk make_pair
	    #define F first
	    #define S second
	    #define ALL(x) x.begin(), x.end()
	
	    using namespace std;
	
	    const int INF = 2e18;
	    const int maxn = 5e3 + 5;
	    const int M = 1e9 + 7;
	
	    int n, m;
	    vector<int> G[maxn];
	    vector<int> V[maxn];
	    int in[maxn], vis[maxn], par[maxn], sz[maxn];
	
	    void dsu_init() {
	        for (int i = 1; i <= n; i++) {
	            par[i] = i;
	            sz[i] = 1;
	        }
	    }
	
	    int find(int x) {
	        if (par[x] == x)
	            return x;
	        else
	            return par[x] = find(par[x]);
	    }
	
	    void merge(int a, int b) {
	        int x = find(a), y = find(b);
	        if (x == y) return;
	        par[x] = y;
	        sz[y] += sz[x];
	        sz[x] = 0;
	    }
	
	    void init() {
	        cin >> n >> m;
	        int u, v;
	        for (int i = 0; i < m; i++) {
	            cin >> u >> v;
	            G[u].pb(v);
	            G[v].pb(u);
	            in[u]++, in[v]++;
	        }
	    }
	
	    void topo() {
	        for (int i = 1; i <= n; i++) {
	            // 刪除 deg[u] <= i 的點
	            queue<int> q;
	            for (int j = 1; j <= n; j++) {
	                if (!vis[j] && in[j] == i) {
	                    q.push(j);
	                    vis[j] = 1;
	                }
	            }
	
	            while (q.size()) {
	                int u = q.front();
	                q.pop();
	                V[i].pb(u);
	
	                for (auto v : G[u]) {
	                    in[v]--;
	                    if (vis[v]) continue;
	
	                    if (in[v] <= i) {
	                        q.push(v);
	                        vis[v] = 1;
	                    }
	                }
	            }
	        }
	    }
	
	    void solve() {
	        topo();
	        dsu_init();
	        memset(vis, 0, sizeof vis);
	        int ans = 0;
	        for (int i = n; i >= 1; i--) {
	            for (auto u : V[i]) {
	                vis[u] = 1;
	                for (auto v : G[u]) {
	                    if (!vis[v]) continue;
	                    merge(u, v);
	                }
	            }
	            for (int u = 1; u <= n; u++) {
	                if (par[u] == u && vis[u]) {
	                    ans = max(ans, sz[u] * i);
	                }
	            }
	        }
	
	        cout << ans << "\n";
	    }
	
	    signed main() {
	        // ios::sync_with_stdio(0);
	        // cin.tie(0);
	        int t = 1;
	        // cin >> t;
	        while (t--) {
	            init();
	            solve();
	        }
	    }
	    ```