## 賽局 DP
簡單來說就是暴力跑
???+note "[CSES - Stick Game](https://cses.fi/problemset/task/1729)"
有 $n$ 個石頭,每次可以拿走 $P=\{p_1,p_2,\ldots,p_k\}$ 個,A, B 輪流取,不能拿就輸。問誰贏
$n\le 10^6,k\le 100,1\le p_i\le n$
??? note "思路"
???+note "[LeetCode 877. Stone Game](https://leetcode.com/problems/stone-game/description/)"
???+note "[Atcoder DP Contest L - Deque](https://atcoder.jp/contests/dp/tasks/dp_l)"
???+note "[Atcoder DP Contest K - Stones](https://atcoder.jp/contests/dp/tasks/dp_k)"
## Nim Game
### 證明
- 「先手會贏」的狀態,存在一個走法走到「先手會輸」的狀態
- 「先手會輸」的狀態,不管怎麼走都是走到「先手會贏」的狀態
### 例題
???+note "單堆 Nim Game"
有 $n$ 個石頭,每次要拿 $1\ldots 5$ 個,A, B 輪流拿,不能拿石頭的人就輸了。問誰贏
??? note "思路"
以不嚴謹的角度看,若先手取了 $x$ 個,那麼後手一定可以取 $y$ 使 $x+y=6$,這麼一來當 n % 6 == 0 時,先手就輸了。那當 n % 6 != 0 時,先手就可以先拿走 $x$ 個使得 n % 6 == 0,這樣又變回上面的 n % 6 == 0 先手必輸的 case 了。
先手可以贏 iff n % 6 != 0
- n % 6 != 0 的狀態存在一個走法走到 n % 6 = 0 的狀態
- n % 6 = 0 的狀態不管怎麼走都是走到 n % 6 != 0 的狀態
???+note "[CSES - Nim Game I](https://cses.fi/problemset/task/1730)"
有 $n$ 堆石頭,分別有 $a_1, \ldots , a_n$ 個,Alice, Bob 輪流玩一個 game,輪到自己時可以選其中一堆,拿至少一個石頭,不能拿就輸。問誰贏
$1\le n \le 2\times 10^5,1\le a_i \le 10^9$
??? note "思路"
n = 1,先手贏,iff $a_1 > 0$。
n = 2,先手贏 iff $a_1 \neq a_2$。
- $a_1 \neq a_2$ 的狀態 :
存在一個走法走到 $a_1 = a_2$ 的狀態
- $a_1 = a_2$ 的狀態 :
不管怎麼走都是走到 $a_1 \neq a_2$ 狀態
general $n$ : 先手會贏 iff $a_1 \oplus a_2 \oplus \ldots a_n \neq 0$
- $a_1 \oplus a_2 \oplus \ldots a_n \neq 0$ 的狀態 :
存在一個走法走到 $a_1 \oplus a_2 \oplus \ldots a_n = 0$ 的狀態
- $a_1 \oplus a_2 \oplus \ldots a_n = 0$ 的狀態 :
不管怎麼走都是走到 $a_1 \oplus a_2 \oplus \ldots a_n \neq 0$ 的狀態
- [11011, 01000, 00101] xor = 10110 → [01101, 01000, 00101] xor = 00000
- [01011, 11001, 10101] xor = 00111 → [01011, 11001, 10010] xor = 00000
## Grundy number
幫每個狀態定義一個 Grundy number(又稱 SG 函數) $G(x)$,輸的狀態的 $G(x) = 0$
其他的狀態 $G(x) = \text{mex} \{ G(y) \mid x \space 可以到 \space y\}$[^1]
???+note "單堆 Nim Game - 套用 Grundy number"
有 $n$ 個石頭,每次要拿 $1\ldots 5$ 個,A, B 輪流拿,不能拿石頭的人就輸了。問誰贏
??? note "思路"
我們可以列出轉移式,$G(n)=\text{mex}\{G(n-1),\ldots ,G(n-5) \}$,我們將表格列出來
$$
\begin{array}{c|ccccccccccccc}
n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12\\
\hline
G(n) & 0 & 1 & 2 & 3 & 4 & 5 & 0 & 1 & 2 & 3 & 4 & 5 & 0\\
\end{array}
$$
可以發現在這個題目 G(n) = n % 6
## Sprague–Grundy theorem
又稱 SG 定理,有 k 盤 Game(不管完任何 Game 都可以),每次可以選擇一個盤面做操作,直到沒有任何盤面能做操作為止,會有
$$
G(\{x_1,x_2,\ldots, x_k\})=G(x_1)\oplus G(x_2)\oplus \ldots \oplus G(x_k)
$$
??? info "證明"
【數學歸納法 - 證明】: G({X, Y}) = G(X) $\oplus$ G(Y)
Base case: G(0, 0) = 0 = G(0) $\oplus$ G(0)
Induction step: 已知 G({X, Y}) = mex{ G({x, y}) },又能走到的 G({x, y}) 已滿足 G({x, y}) = G(x) $\oplus$ G(y)
> 當 G(x) = t,一定會滿足 x 可以走到 grundy 值是 0 ... (t-1) 的狀態
令 G(X) $\oplus$ G(Y) = t,我們要證明 0 ... (t-1) 的 grundy number 都可以走到,且 t 走不到
- G({x, y}) 無法包含到 t :
令 u = G(X), v = G(Y),u $\oplus$ v = t。X, Y 只能動一個,分兩種 case :
- 動 X → x: (非 u) $\oplus$ v != t
- 動 Y → y: u $\oplus$ (非 v) != t
所以動了一步之後 G(x) $\oplus$ G(y) 一定不是 t
- G({x, y}) 可以完全包含到 0 ... (t-1) :
令 u = G(X), v = G(Y),如果想要變成 s,看 s 跟 t 從高位看過去哪一位開始 t[i] = 1, s[i] = 0,去看 u[i], v[i] 哪一個是 1 就是去改動他
有了這個證明後,k 盤 Game 就只是將 x[1], ..., x[k] 兩兩合併,也就是兩兩 xor 即可
???+note "[CSES - Nim Game II](https://cses.fi/problemset/task/1098)"
有 $n$ 堆石頭,分別有 $a_1, \ldots , a_n$ 個,Alice, Bob 輪流玩一個 game,輪到自己時可以選其中一堆,拿 1...3 個石頭,不能拿就輸。問誰贏
$1\le n \le 2\times 10^5,1\le a_i \le 10^9$
??? note "思路"
先把每一堆想成一個單獨的 game, 計算 G(x) = x % 4,利用 SG 定理將他們 xor 起來
???+note "例題"
有 $n$ 堆石頭,分別有 $a_1, \ldots , a_n$ 個,Alice, Bob 輪流玩一個 game,每次可以做其中一個操作
- 從某一堆拿走 $1$ 個石頭
- 或平分成相同數量的很多堆
不能拿就輸。問誰贏
??? note "思路"
[12] → [4, 4, 4] → [3, 4, 4] → [3, 2, 2, 4]
SG(6)
= mex{ SG(5), SG(3) $\oplus$ SG(3), SG(2) $\oplus$ SG(2) $\oplus$ SG(2), SG(1) $\oplus$ SG(1) $\oplus$ SG(1) $\oplus$ SG(1) $\oplus$ SG(1) $\oplus$ SG(1)}
= mex{SG(5), SG(2)}
n = 10^5 ,直接計算 SG(1) … SG(n)(枚舉因數,類似篩法),time: O(n log n)
n = 10^9 幫 SG(i) 找規律
???+note "[YTP 2022 高中程式挑戰營 p11](https://www.tw-ytp.org/wp-content/uploads/2022/12/YTP2022FinalContest_S2_TW.pdf#page=32)"
有 n 筆 query。每筆給出 x 堆石頭,兩種操作,無法操作就輸
- 選一堆,移除 1 個
- 選一堆,拆成 1, 2, 3, …, k 個,前提 n = 1+2+…+k
[2, 5, 10] → [1, 5, 10] → [1, 5, 1, 2, 3, 4]
x <= C = 10^9, n <= 2 * 10^5
??? note "思路"
- SG(x) =
- mex{ SG(x-1) } if x != k(k+1)/2
- mex{ SG(x-1), SG(1) $\oplus$ SG(2)$\oplus$ ... $\oplus$ SG(k) } if x = k(k+1)/2
- x = k(k+1)/2 的狀態不會太多,只有 O( sqrt(C) ) 個
- 假設 SG( k * (k+1)/2 ) = 2, 如何計算 SG( (k+1) * (k+2)/2 )?
- if x $\in$ [ k * (k+1)/2 + 1, (k+1) * (k+2)/2 - 1], SG(x) = 0 → SG(x+1) = 1
- 0, 1 交替,可以從上一個 k * (k + 1) / 2 很快的推出來
- 實作上把 x = k(k+1)/2 都建表算好,過程中可以用一個只會單調遞增的 pointer 紀錄 k 算到哪裡,每個 a[i] binary search 找到小於 a[i] 的第一個 k * (k+1)/2 的地方,即可推出是 0 還是 1
## Tree
### Min Max Tree
???+note "題目"
給一個 Tree,每個 leaf 上都有一個數字。從 root 開始,A, B 輪流,每次要往下走一層,A 希望停在小的,B 希望停在大的,問最後會停在哪裡
??? note "思路"
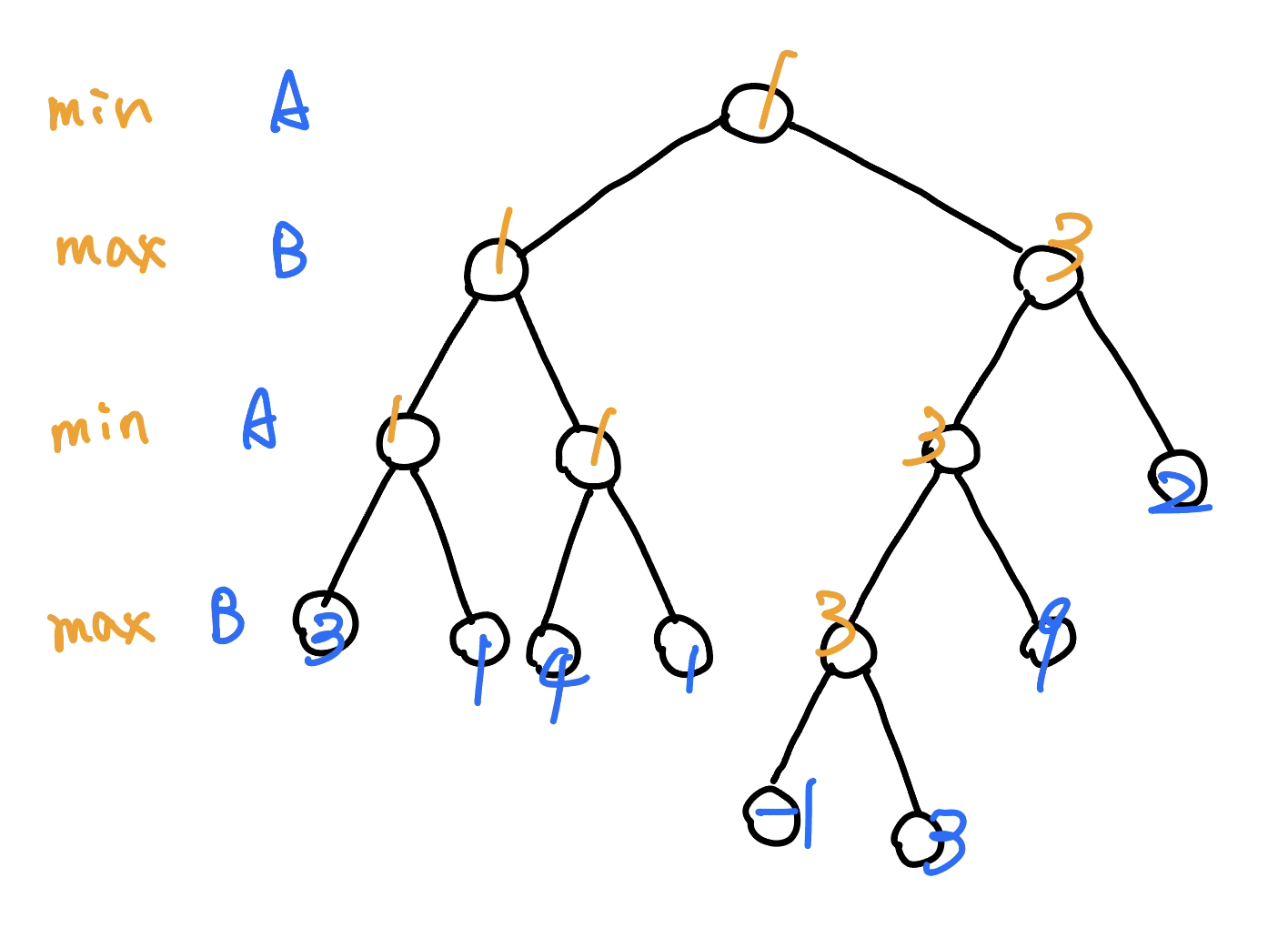{ width="300" }
從 leaf 往上做上去
???+note "[TIOJ 1092 . A.跳格子遊戲](https://tioj.ck.tp.edu.tw/problems/1092)"
給一張 $n$ 點 $m$ 邊的 DAG。A, B 從起點往終點輪流跳,跳到終點的人獲勝,問誰獲勝
$n\le 10^4,m\le 10^5$
??? note "思路"
我們先將 DAG 展開,變成 Tree 比較好套用 Min Max Tree 的概念。設先手是 $0$,後手是 $1$,那麼先手就要取 min,後手取 max。
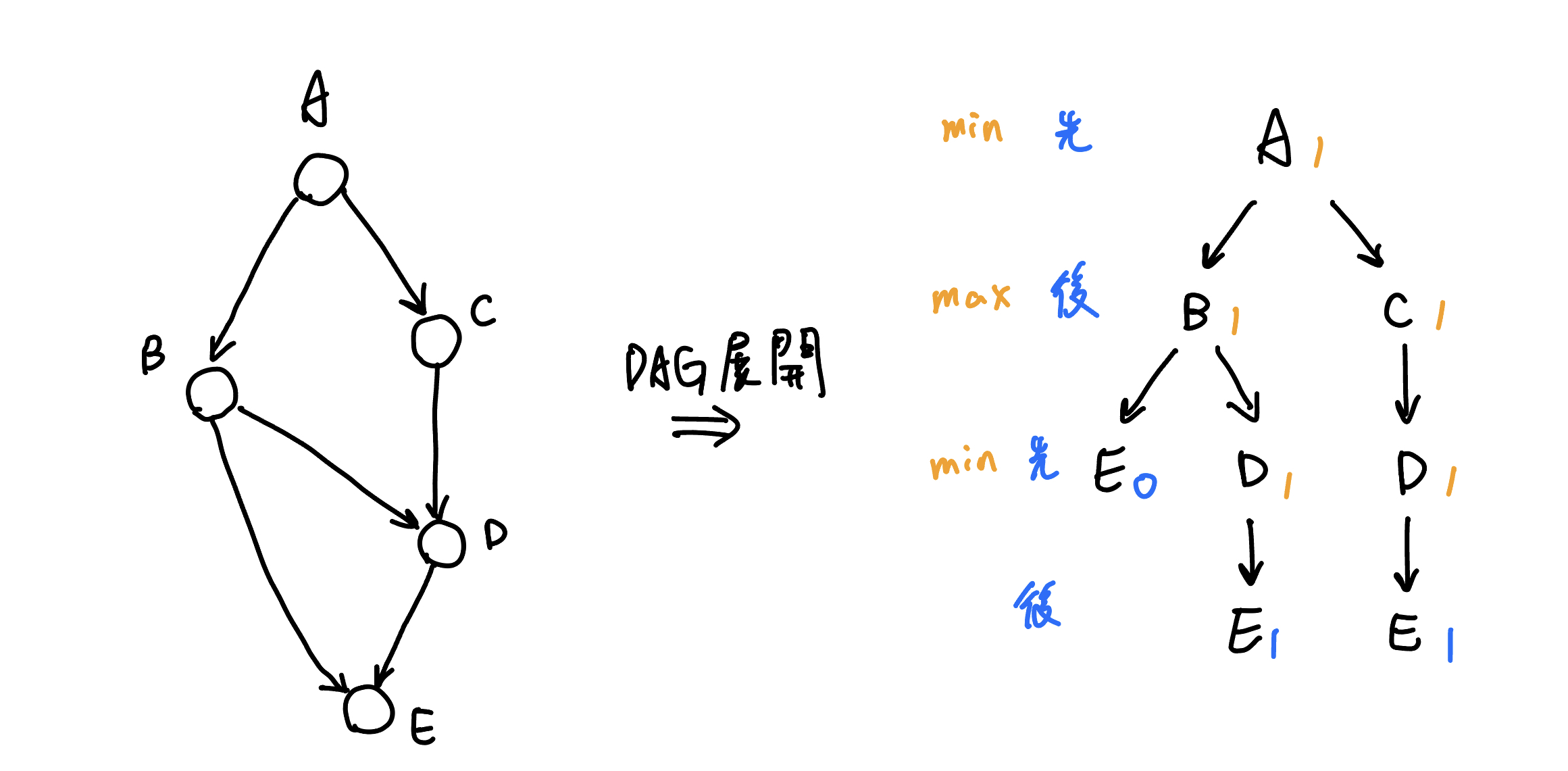{ width="500" }
我們重新回到 DAG 上考慮,DAG 上終點就是我們 Tree 上的 Leaf,所以我們可以從終點慢慢推回起點,每個點維護先手,與後手的值(這樣兩個點之間才能轉移,u 的先手從 v 的後手轉移,...),最後的答案就是起點的先手值
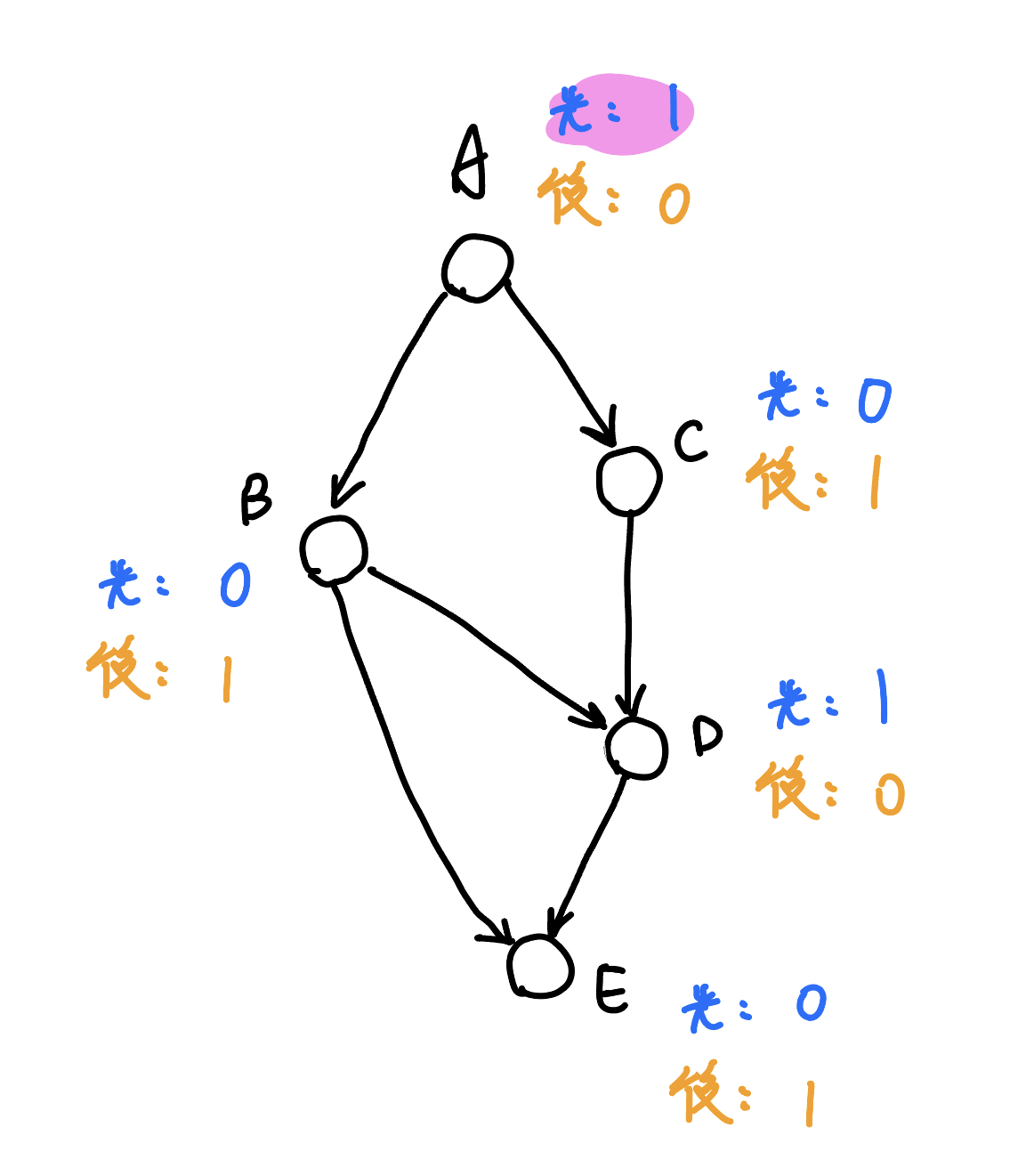{ width="300" }
---
這題也可以用下面的 Game Tree 做,一樣是將 Leaf(終點) 先定 Grundy Number = 0,然後慢慢做回起點去
### Game Tree
???+note "[LOJ #10243. 「一本通 6.7 例 3」移棋子游戏](https://loj.ac/p/10243)"
給一張 $n$ 點 $m$ 邊的 DAG。給定 $k$ 個棋子,A, B 輪流,每步可以將任意一顆棋子沿一條有向邊移動到另一個點,無法移動者輸掉遊戲,問誰先手贏還輸。
$n\le 2000,m\le 6000,1\le k\le n$
??? note "思路"
因為每個問題都是獨立的,可以利用 SG 定理將他們的 Grundy Number xor 起來。每個問題我們可以將 DAG 想成 Tree,這樣 Leaf 就會是那些 out degree 是 0 的點。先定這些點的 Grundy Number = 0,然後慢慢做回起點去
??? note "code"
```cpp linenums="1"
#include
#define int long long
#define pii pair
#define pb push_back
#define mk make_pair
#define F first
#define S second
#define ALL(x) x.begin(), x.end()
using namespace std;
const int INF = 2e18;
const int maxn = 3e5 + 5;
const int M = 1e9 + 7;
int n, m, k;
vector G[maxn];
int vis[maxn], sg[maxn];
int mex(vector& a) {
int n = a.size();
vector v(n + 1, false);
for (int x : a) {
if (x <= n) v[x] = true;
}
for (int i = 0; i <= n; i++) {
if (v[i] == false) return i;
}
return -1;
}
int dfs(int u) {
if (vis[u]) return sg[u];
if (G[u].size() == 0) {
sg[u] = 0;
return sg[u];
}
vis[u] = true;
vector used;
for (auto v : G[u]) {
used.pb(dfs(v));
}
sg[u] = mex(used);
return sg[u];
}
signed main() {
cin >> n >> m >> k;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
G[u].pb(v);
}
int res = 0;
while(k--) {
int x;
cin >> x;
res ^= dfs(x);
}
cout << (res == 0 ? "lose" : "win") << '\n';
}
```
## 題目
???+note "[CSES - Stair Game](https://cses.fi/problemset/task/1099)"
有 $n$ 個石堆編號 $1,2,\ldots ,n$,每堆一開始有 $a_i$ 個。A, B 輪流,每次可以將任意數量的石頭從 $k$ 移到 $k-1$,其中 $k\neq 1$,不能動就輸。問誰贏
$1\le n\le 2\times 10^5,0\le a_i \le 10^9$
??? note "思路"
相當於在 even 項玩 Nim Game
結論 : 先手會贏 iff $a_2\oplus a_4\oplus a_6\oplus \ldots \neq 0$
- 「先手會贏」的狀態,存在一個走法走到「先手會輸」的狀態
相當於玩 Nim Game,先手直接動 even 項的到 odd 項
- 「先手會輸」的狀態,不管怎麼走都是走到「先手會贏」的狀態
分兩種 case 討論 :
- 動 odd 到 even
下一輪,先手再把同個數的石頭從 even 動到 odd,又回到先手會輸的狀態
- 動 even 到 odd
相當於玩 Nim Game,不管怎麼走都是走到 $a_2\oplus a_4\oplus a_6\oplus \ldots \neq 0$ 的狀態
???+note "[CSES - Grundy's Game](https://cses.fi/problemset/task/2207)"
有一堆 $n$ 個石頭,A, B 輪流,每次可以將一堆 Split 成兩堆數量不同的,不能動就輸,問誰贏。共 $t$ 筆測資
$t\le 10^5,n\le 10^6$
??? note "思路"
觀察到若 $n > 2000$ 時先手必勝,$n\le 2000$ 暴力跑,$>2000$ 直接輸出 first
???+note "[CSES - Another Game](https://cses.fi/problemset/task/2208)"
有 $n$ 堆石頭,分別有 $a_1, \ldots , a_n$ 個,Alice, Bob 輪流玩一個 game,輪到自己時可以選其中好幾堆,每堆拿至少一個石頭,不能拿就輸,問誰贏
$1\le n\le 2\times 10^5,1\le a_i\le 10^9$
??? note "思路"
打表後可以觀察到,$a_i$ 都是偶數時,先手必輸
【證明】:
- 「$a_i$ 有一些奇數」的狀態,存在一個走法走到「$a_i$ 都是偶數」的狀態
- 「$a_i$ 都是偶數」的狀態,不管怎麼走都是走到「$a_i$ 有一些奇數」的狀態
???+note "[2016 全國賽 p3. 拈 (Nim)](https://tioj.ck.tp.edu.tw/problems/1940)"
有一堆 $n$ 個石頭,A, B 輪流,每次可從這堆石頭中取走 $1\ldots \lfloor n/k \rfloor$ 顆石頭,問 Grundy number $G(n)$
$n\le 10^9,k=1$ or $2$
??? note "思路"
$k=1$ 的 case 一定是 n % (n + 1) = n
$k=2$ 的 case 去觀察會發現 even 項都是 n / 2,odd 項恰好是自己能覆蓋的區間的前一個數,可以去遞迴,複雜度 $O(\log n)$
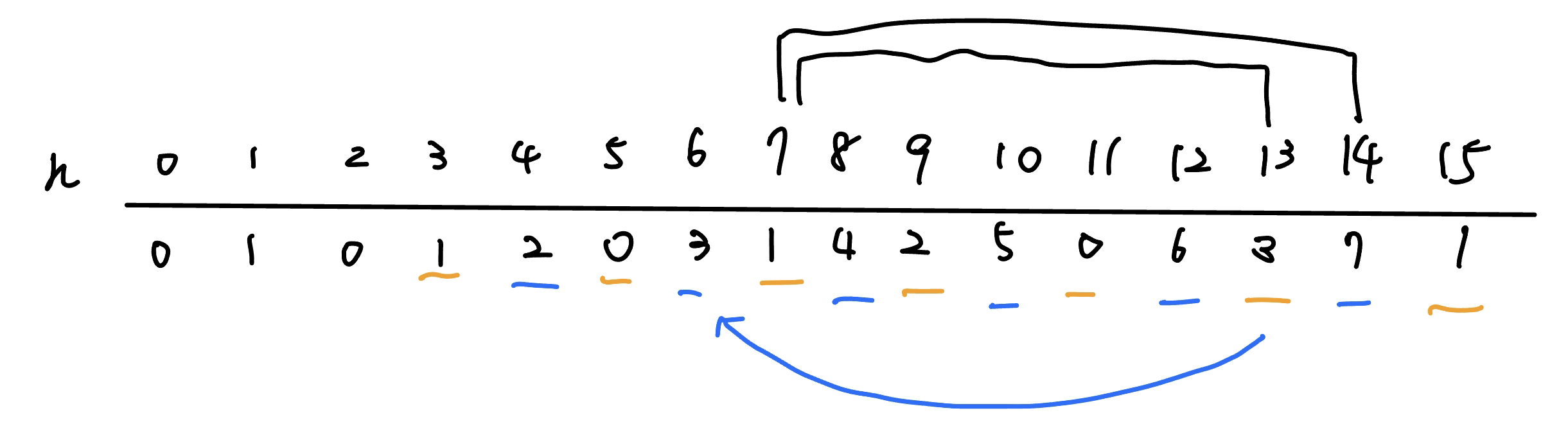{ width="500" }
??? note "code"
```cpp linenums="1"
#include
#define int long long
#define pii pair
#define pb push_back
#define mk make_pair
#define F first
#define S second
#define ALL(x) x.begin(), x.end()
using namespace std;
int f(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
if (n == 2) return 0;
if (n % 2 == 0) return n / 2;
else return f(n / 2);
}
signed main() {
int n, k;
cin >> k >> n;
if (k == 1) {
cout << n << '\n';
} else {
cout << f(n) << '\n';
}
}
```
???+note "Wythoff's game [洛谷 P2252 [SHOI2002] 取石子游戏|【模板】威佐夫博弈](https://www.luogu.com.cn/problem/P2252)"
一開始有兩堆個石頭,每個回合可以選一堆,A, B 輪流,每輪可以做其中一個操作
- 從其中一堆取走任意數量的石頭
- 或從兩堆取走相同數量的石頭
不能拿就輸。問誰贏
???+note "2022 IONC C. 取石子遊戲 (kgame)"
一開始有 $n$ 顆石頭與一個正整數 $k$,有兩個人會輪流取出一些石頭。
假設遊戲進行了 $m$ 輪,並且取出的石頭數量的序列為 $a_1, a_2, \ldots, a_m$,那麼必須要滿足以下兩個條件:
- 對於 $i = 1, 2, \ldots, m$,$1 \le a_i \le k-1$。
- 對於 $j = 1, 2, \ldots, m-1$,$a_j + a_{j+1} \le k$。
先將石頭取完的那個人獲勝,若是雙方都無法將石頭取完即視為平手。在已知 $n$、$k$ 的情況下,請問誰有必勝策略?在一筆測資中,你需要處理 $T$ 組輸入。
$1 \le T \le 10^5,1 \le k \le 10^{18},1 \le k \le n$
??? note "思路"
例如說先手取了 $x$ 之後,後手一定可以取 $y$ 使 $x+y=K$,也就代表當 n % k = 0 時先手必輸。那麼無解的 case 呢 ? 當 k = 1 時。
??? note "code"
```cpp linenums="1"
#include
#define int long long
using namespace std;
signed main() {
int q;
cin >> q;
while(q--) {
int n, k;
cin >> n >> k;
if (k == 1) {
cout << "RedLeaf\n";
} else if (n % k == 0) {
cout << "Leaf\n";
} else {
cout << "Red\n";
}
}
}
```
???+note "[TOI 2021 二模 p1. 石頭(Stone)](https://drive.google.com/file/d/1_mpY6D95d8Da7zR8YMabTMvCJIlNWBg6/view)"
有 $n$ 堆石頭,第 $i$ 堆 $a_i$ 個,Alice, Bob 進行 Nim,但每次拿的石頭數量單調遞減,且第一步不能拿超過 $r$ 個石頭,問第一步有幾種可能的拿取方式
$1 \le n \le 10^5, 1 \le r, a_i \le 10^9$
??? note "思路"
【subtask 1: 1 <= n <= 3, 1 <= r, a[i] <= 100】
令 dp(A, B, C, r) 為這一輪拿 r 個,是否會贏。可以令 S(A, B, C, r) = S(A, B, C, r-1) or dp(A, B, C, r),使用 prefix or 優化。
dp(A, B, C, r) = {dp(A-r, B, C, 1~r) or dp(A, B-r, C, 1~r) or dp(A, B, C-r, 1~r) }
【subtask 3: n = 1】
令 dp(A, B, C, r) 為目前最多拿 r 個,我們分別考慮 r = 1, 2, 3 的轉移:
r = 1 時我們只需要考慮 A 的奇偶性,所以列出:
dp(A, r = 1) = max{ 1-dp(A-1, r = 1) } = A % 2。
r = 2 我們可以拿一個或兩個,所以 dp(A, r = 2) = max{ 1-dp(A-2, r = 2), 1-dp(A-1, r = 1) },可以發現 1-dp(A-1, r = 1) 恰好是上面 dp(A, r = 1) 的狀態,所以我們又可以列出
dp(A, r = 2) = max{ 1-dp(A-2, r = 2), dp(A, r = 1) }
同理, r = 3 時列出
dp(A, r = 3) = max{ 1-dp(A-3, r = 3), 1-dp(A-2, r = 2), 1-dp(A-1, r = 1) }
= max{ 1-dp(A-3, r = 3), dp(A, r=2) }
如果打表的話會發現恰好是以 0111... 的循環節出現,例如若 r = 1,循環節為 01,長度為 2;若 r = 2 ~ 3,循環節為 0111,長度為 4;若 r = 4 ~ 7,循環節為 01111111,長度為 8。所以我們可以總結出 dp(A, r) 就是 [A % r 以下最大的二的冪次] % 4 != 0,例如說 r = 2 就是 [A % 4] != 0。
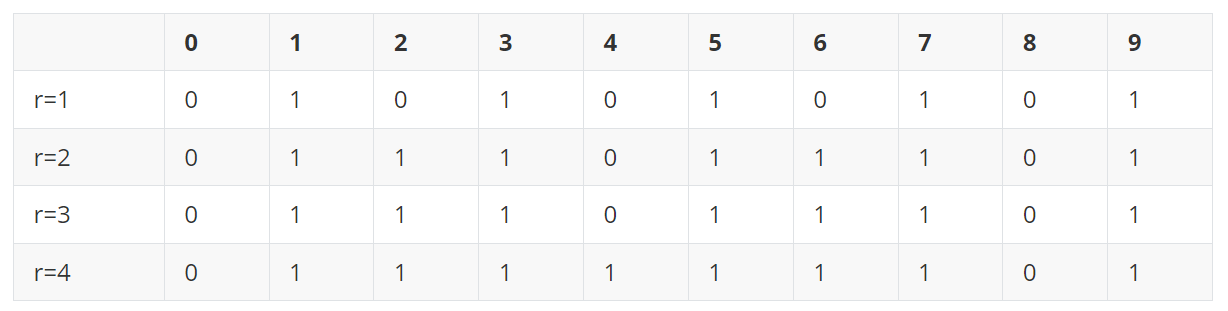{ width="500" }
用分析的角度想,就是我們可以發現每格都是上面那格與 1 - 前面那格取 max,所以在跑 r 的時候幾乎可以把 r - 1 那一個 row 給抄下來,看 0 的地方的前 r 格是不是 0,是的話這格就是 1。我們發現 r = 2 與 r = 3 是一模一樣的,因為 r = 3 在 r = 2 為 0 的地方往前 3 格並沒有碰到 0(手不夠長),但到 r = 4 時就剛好可以摸到了,然後要一直到 r = 8 才能使連續的 1 再變的更長。
{ width="400" }
【subtask 2: r = 1, r = 2】
我們用程式將 dp(A, B, C, r = 2) 都打表出來,會發現我們完全找不到規律,所以我們就先把是位置 (A, B, C) 給印出來,考慮賽局理論常常用 xor,我們試著將 A xor B xor C,結果發現他們都剛剛好是 2 的倍數,也就是 % 2 = 0,因為我們上面的子題有推理過會每 r 個循環一次,所以我們可以列出如果 dp(A, B, C, r) 是 0 iff (A ^ B ^ C) % 2 == 0 。
【subtask all】
我們一樣用程式去檢查 dp(A, B, C, r) 在 r = 1, 2, 4, 8 會不會像上面一樣具有讓循環節變長,且恰好是 2 的冪次的跡象,也就是例如 dp(A, B, C, 2) 需要去等於 dp(A, B, C, 3)。我們發現是確實的,所以我們可以得出最後的結論:ans = 0 iff xor{ a[i] } % d == 0,其中 d 為 r 以下最大的二的冪次。
???+note "[POI2016 Nim z utrudnieniem](https://www.luogu.com.cn/problem/P5970)"
有 $n$ 堆石頭,分別有 $a_1, \ldots , a_n$ 個,Alice, Bob 輪流玩一個 game,輪到自己時可以選其中一堆,拿至少一個石頭,不能拿就輸。在遊戲開始前問,B 可以丟掉若干堆石子,但是必須保證丟掉的堆數是 $d$ 的倍數,且不能丟掉所有石子。問 Bob 有幾種丟掉方案,可以讓 Bob 贏
$1\le n \le 2\times 10^5,1\le a_i \le 10^9$
??? note "思路"
首先我們要知道一個結論:Bob 必勝當且僅當最初的所有石子數異或和 = 0。這是 Nim 遊戲的結論。我們令 $dp(i, j, k)$ 表示現在看到 $i$,已丟掉的堆數$\mod d = j$,剩下的石堆 xor 起來是 $k$,轉移式為 $dp(i, j , k)=dp(i - 1,j,k) + dp(i-1,j-1,k\oplus a_i)$。這樣的複雜度是 $O(n\times d\times \max \{ a_i \})$,會 TLE。有一個很巧妙的性質是:對於一個任意的數字 $x$,他和比自己小的數字 xor 起來不會超過 $2x$。所以我們可以將 $a$ 數組由小到大排序,這樣掃到第 $i$ 堆的時候我們 $k$ 這維不用枚舉到 $m$,只需要枚舉到 $2a_i$ 就行了,這樣均攤下來會變 $O(d\times (2a_1+2a_2+\ldots +2a_n))$,差不多是 $O(d\times \sum a_i)=O(md)$。空間的部分可能有點大,我們使用滾動數組省略 $i$ 的那維即可。我們採用滾動數組是由 $j$ 大到小去更新,這樣才把新的狀態算過來,但當 $j=0$ 時應該要從 $j=d-1$ 這邊轉移過來,但此時 $j=d-1$ 已經是新的狀態,所以我們這個可能要開個 tmp 陣列另外存一下 $j=d-1$ 的 $dp(j,k)$。最後的答案 xor 出來應該要是 xor{a_i} ^ [刪掉的] 要 = 0,所以 [刪掉的] = xor{a_i}
??? note "code"
```cpp linenums="1"
#include
#define int long long
using namespace std;
const int N = 500000 + 5;
const int mod = 1e9 + 7;
int sum, n, d, a[N], dp[11][1 << 20], tmp[1 << 20];
signed main() {
cin >> n >> d;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
sum ^= a[i];
}
sort(a + 1, a + 1 + n);
dp[0][0] = 1;
for (int i = 1; i <= n; ++i) {
int max = 1;
while (max <= a[i]) {
max <<= 1;
}
for (int k = 0; k < max; ++k) {
tmp[k] = dp[d - 1][k];
}
for (int j = d - 1; j > 0; j--) {
for (int k = 0; k < max; k++) {
dp[j][k] = (dp[j][k] + dp[j - 1][k ^ a[i]]) % mod;
}
}
for (int k = 0; k < max; k++) {
dp[0][k] = (dp[0][k] + tmp[k ^ a[i]]) % mod;
}
}
if (n % d == 0) {
dp[0][sum] -= 1;
// 扣除所有都選的狀態
}
cout << (dp[0][sum] + mod) % mod;
return 0;
}
```
???+note "[USACO 2022 DEC Circular Barn S](https://www.luogu.com.cn/problem/P8901)"
有 n 堆石子,Alice 跟 Bob 輪流從每一堆依序取走 1 或任意質數枚,先無法操作者敗。給定初始狀態,求勝者。
$n\le 2\times 10^5, 1\le a_i\le 5\times 10^6$
??? note "思路"
先考慮 n = 1,打表可以觀察到,當 a[i] % 4 == 0 時,先手必敗。再考慮到 n > 1 的情況。考慮對於一個房間,那個贏的人必定想縮短操作次數(原因是對於這個房間可以盡快贏,以防止到後面的房間讓輸的人翻盤),輸的人想使操作次數越多越好(原因是這個房間操作次數多了,結束的時間會拖延,以給後面的房間製造機會),所以我們只要按照雙方的策略算出操作次數,取最早結束的那個房間即可。
接下來就要想如何快速地算一個房間會操作幾次(一人操作算一次)。我們繼續分類討論:
當 a[i] 為必敗點時,也就是 a[i] % 4 == 0,因為不管怎麼樣都是必敗,所以我們要盡量想辦法拖延後手的操作次數,我們發現當我們取奇數顆石頭(例如 1 顆)後,下一步後手可能就有機會一次取好幾顆(例如 7 顆,讓 (1 + 7) % 4 == 0),但如果我們取 2 顆,因為 2 作為唯一的偶質數,取完後後手就只能取 2 顆了,因為只有這樣才能到達 4 的倍數。所以我們可以得到操作次數就是 a[i] / 2 的結論。
當 a[i] 為必勝點時,也就是 a[i] % 4 != 0,我們要取越大越好讓遊戲盡快結束,而且又要到達先手必敗的狀態,所以令 p 為最大的質數,使 (a[i] - p % 4) == 0,接下來就是 a[i] 為必敗點的子問題。所以操作次數就是 (a[i] - p) / 2 + 1 次。
實作上,我們使用篩法先預處理出範圍內的全部質數,順便預處理每個數字的 p。最後就看每個 a[i] 的回合數的最小值是哪一個,然後再去看該 a[i] 是對應到誰贏即可。注意到回合數是操作次數的一半,因為一回合是有兩次操作的,所以例如三次操作與四次操作實際上都是第二回合。
??? note "code"
```cpp linenums="1"
#include
using namespace std;
const int N = 1e5 + 10, M = 5e6;
int T, n, x, cnt, ans, mx[4], v[M + 10], vis[M + 10], prime[M];
void get_prime(int n) {
vis[1] = 1;
mx[1] = 1;
v[1] = 1;
for (int i = 2; i <= n; i++) {
if (!vis[i]) {
prime[++cnt] = i;
mx[i % 4] = i;
}
for (int j = 1; j <= cnt && i * prime[j] <= n; j++) {
vis[i * prime[j]] = 1;
if (!(i % prime[j])) {
break;
}
}
v[i] = !(i % 4) ? i / 2 : (i - mx[i % 4]) / 2 + 1;
}
}
int main() {
scanf("%d", &T);
get_prime(M);
while (T--) {
scanf("%d", &n);
ans = 1e9;
for (int i = 1; i <= n; i++) {
scanf("%d", &x);
if (v[x] / 2 < ans / 2)
ans = v[x];
}
if (ans & 1) {
puts("Farmer John");
} else {
puts("Farmer Nhoj");
}
}
return 0;
}
```
???+note "[CF 1194 D. 1-2-K Game](https://codeforces.com/contest/1194/problem/D)"
有 $n$ 個石頭,每次拿 $1$ 個, $2$ 個, **或** $k$ 個,A, B 輪流拿,不能拿石頭的人就輸了。問誰贏
$0\le n\le 10^9,3\le k\le 10^9$
??? note "思路"
打表,觀察,詳細可見 [Yuihuang's 題解](https://yuihuang.com/cf-1194d/)
???+note "[codeforces 603C. Lieges of Legendre](https://codeforces.com/problemset/problem/603/C)"
???+note "[codeforces 305E. Playing with String](https://codeforces.com/problemset/problem/305/E)"
???+note "[2022 npsc 高中組初賽 pF.取蜜柑](https://tioj.ck.tp.edu.tw/problems/2303)"
??? note "思路"
如果數字>1,那可以都視為2,因為(x>1) x就可以決定要一次拿全部或者拿到剩1個,除了1,1,...1,x 和 1,1,1,1,1 都是1/2 ,1,11..x如果位數是偶數那是1/2,奇數是 (x/2+1)/x
---
## 參考資料
-
-
[^1]: mex : 最小不存在的非負整數。更詳細介紹見此處