## 介紹
### 算法精神
先想單一詢問的時候可以怎麼利用值域二分搜

一定會在「答案」所在的值域進行分治，我們將答案的值域列為 $[l,r]$

同時也需要維護在當前分治到的值域下的詢問編號，我們把它叫做 $[ql,qr]$

若詢問並沒有單調性，那就必須自己跑過 $ql\sim qr$，再開兩個陣列將他們分成左右兩類

若詢問有單調性，尋找切點，直接分治 (連結 : dp 優化 - 決策性單調)

我們假設 $[ql,qr]$ 的切點叫做 $t$， $\displaystyle\text{mid}=\frac{l+r}{2}$

$$
\texttt{solve (l, r, qL, qR)}=\begin{cases} \texttt{solve (l, mid, qL, t)} \\ \texttt{solve (mid + 1, r, t + 1, qR)}\end{cases}
$$

### 步驟

1. 將問題轉成單一詢問 (如果只有一個要怎麼做)
2. 如何計算 cost
3. 二分搜的範圍 (上界，下界)
4. 如何分治

### 複雜度分析

若每次切中位數，遞迴深度為 $O(\log n)$，若切值域範圍的 mid，深度則為 $O(\log C)$（其中 $C$ 為值域範圍）

## 範例

### 靜態區間 k 小

???+note "靜態區間第 k 小 [洛谷 P3834 - 【模板】可持久化线段树 2](https://www.luogu.com.cn/problem/P3834)"
	給長度為 $n$ 的序列，$q$ 筆詢問
	
	- $\text{query(}a_l\sim a_r,k):$ 回答 $a_l\sim a_r$ 中第 $k$ 小的數值是多少<br>
	
	$n,q\le 2\times 10^5,|a_i|\le 10^9$
	
	??? note "分析"
		BIT 複雜度 $O(n\log n \log C)$，若用前綴和則為 $O(n\log C)$
		
	??? note "code"
		```cpp linenums="1"
		#include <bits/stdc++.h>
        #define int long long
        #define pii pair<int, int>
        #define pb push_back
        #define mk make_pair
        #define F first
        #define S second
        #define ALL(x) x.begin(), x.end()
        #define lowbit(x) (x & (-x))

        using namespace std;

        const int MAXN = 3e5 + 5;

        struct BIT {
            int n;
            vector<int> bit;

            void init(int _n) {
                n = _n;
                bit.resize(n + 1);
            }

            void add(int x, int d) {
                while (x <= n) {
                    bit[x] += d;
                    x += lowbit(x);
                }
            }

            int query(int x) {
                int ret = 0;
                while (x > 0) {
                    ret += bit[x];
                    x -= lowbit(x);
                }
                return ret;
            }
        } bit;

        struct qry {
            int l, r, k, id;
        };

        int n, q;
        int arr[MAXN], a[MAXN], ans[MAXN];

        void solve(int l, int r, vector<int> &idx, vector<qry> &q) {
            if (l == r) {
                for (auto [ql, qr, k, id] : q) {
                    ans[id] = l;
                }
                return;
            }

            int mid = (l + r) / 2;

            vector<int> iLeft, iRight;
            for (auto id : idx) {
                if (a[id] <= mid) {
                    bit.add(id, 1);
                    iLeft.pb(id);
                } else {
                    iRight.pb(id);
                }
            }

            vector<qry> qLeft, qRight;
            for (auto [ql, qr, k, id] : q) {
                int t = bit.query(qr) - bit.query(ql - 1);
                if (k <= t) {
                    qLeft.pb({ql, qr, k, id});
                } else {
                    qRight.pb({ql, qr, k - t, id});
                }
            }

            for (auto id : idx) {
                if (a[id] <= mid) bit.add(id, -1);
            }
            vector<int>().swap(idx);
            vector<qry>().swap(q);

            solve(l, mid, iLeft, qLeft);
            solve(mid + 1, r, iRight, qRight);
        }

        signed main() {
            cin >> n >> q;
            vector<int> d;
            for (int i = 1; i <= n; i++) {
                cin >> arr[i];
                d.pb(arr[i]);
            }
            sort(ALL(d));
            d.resize(unique(ALL(d)) - d.begin());

            vector<int> idx;
            for (int i = 1; i <= n; i++) {
                a[i] = lower_bound(ALL(d), arr[i]) - d.begin() + 1;
            }
            for (int i = 1; i <= n; i++) {
                idx.pb(i);
            }
            vector<qry> qry;
            for (int i = 1; i <= q; i++) {
                int l, r, k;
                cin >> l >> r >> k;
                qry.pb({l, r, k, i});
            }
            bit.init(n);

            solve(1, d.size(), idx, qry);
            for (int i = 1; i <= q; i++) {
                cout << d[ans[i] - 1] << "\n";
            }
        }
	    ```


### 動態區間 k 小

???+note "[洛谷 P2617 - Dynamic Rankings](https://www.luogu.com.cn/problem/P2617)"
	給長度為 $n$ 的序列，$q$ 筆詢問
	
	- $\text{query(}a_l\sim a_r,k):$ 回答 $a_l\sim a_r$ 中第 $k$ 小的數值是多少<br>
	- $\text{modify(}a_i,x):$ 將 $a_i$ 的數值改成 $x$
	
	$n,q\le 2\times 10^5$
	
	??? note "思路"
		1. 把原先 $a_i$ 的貢獻給扣除<br>
		2. 將 $x$ 的貢獻加入
	
	??? note "code"
		```cpp linenums="1"
		#include <bits/stdc++.h>
        #define int long long
        #define pii pair<int, int>
        #define pb push_back
        #define mk make_pair
        #define lowbit(x) (x & (-x))
        #define F first
        #define S second
        #define ALL(x) x.begin(), x.end()

        using namespace std;
        using PQ = priority_queue<int, vector<int>, greater<int>>;

        const int INF = 2e18;
        const int maxn = 3e5 + 5;
        const int M = 1e9 + 7;

        int n, m, cnt = 0, tot = 0;
        int a[maxn], ans[maxn];

        struct query {
            int type, x, y, k, id;
            // 0, l, r, k, qry id
            // 1, index, number, 1/-1 add or del, qry id
        };

        query q1[2 * maxn], q2[2 * maxn], q[2 * maxn];
        query qry[maxn];

        struct BIT {
            vector<int> bit;

            void init() {
                bit.resize(n + 1);
            }

            void add(int x, int d) {
                while (x <= n) {
                    bit[x] += d;
                    x += lowbit(x);
                }
            }

            int query(int x) {
                int ret = 0;
                while (x > 0) {
                    ret += bit[x];
                    x -= lowbit(x);
                }
                return ret;
            }
        } bit;

        void divide(int l, int r, int qL, int qR) {
            if (l > r || qL > qR) return;
            if (l == r) {
                for (int i = qL; i <= qR; i++) {
                    if (q[i].type == 0) {
                        ans[q[i].id] = l;
                    }
                }
                return;
            }

            int mid = (l + r) / 2;

            int cnt1 = 0, cnt2 = 0;
            for (int i = qL; i <= qR; i++) {
                if (q[i].type == 0) {
                    int t = bit.query(q[i].y) - bit.query(q[i].x - 1);
                    if (q[i].k <= t) {
                        q1[++cnt1] = q[i];
                    } else {
                        q[i].k -= t, q2[++cnt2] = q[i];
                    }
                } else {
                    if (q[i].y <= mid) {
                        bit.add(q[i].x, q[i].k);  // q[i].x
                        q1[++cnt1] = q[i];
                    } else {
                        q2[++cnt2] = q[i];
                    }
                }
            }

            // undo
            for (int i = 1; i <= cnt1; i++)
                if (q1[i].type == 1) bit.add(q1[i].x, -q1[i].k);
            for (int i = 1; i <= cnt1; i++) q[qL + i - 1] = q1[i];
            for (int i = 1; i <= cnt2; i++) q[qL + cnt1 + i - 1] = q2[i];

            divide(l, mid, qL, qL + cnt1 - 1);
            divide(mid + 1, r, qL + cnt1, qR);
        }

        signed main() {
            cin >> n >> m;

            int x;
            for (int i = 1; i <= n; i++) {
                cin >> x;
                a[i] = x;
                q[++cnt] = {1, i, a[i], 1, -1};
            }

            for (int i = 1; i <= m; i++) {
                int x, y, k;
                char type;
                cin >> type;
                if (type == 'Q') {
                    cin >> x >> y >> k;
                    q[++cnt] = {0, x, y, k, ++tot};
                } else {
                    cin >> x >> y;
                    q[++cnt] = {1, x, a[x], -1, 0};
                    q[++cnt] = {1, x, a[x] = y, 1, 0};
                }
            }

            bit.init();

            divide(-2e9, 2e9, 1, cnt);

            for (int i = 1; i <= tot; i++) {
                cout << ans[i] << "\n";
            }
        }

	    ```

## 例題

### APCS 真假子圖
???+note "[zerojudge g598. 4. 真假子圖](https://zerojudge.tw/ShowProblem?problemid=g598)"
	有 $n$ 個點，$m$ 個 $\texttt{pair}(x,y)$ 代表 $x$ 跟 $y$ 在不同組
		
	再給你 $p$ 組資料，每組資料有 $k$ 個 $\texttt{pair}(x,y)$ 代表 $x$ 跟 $y$ 在不同組
	
	你要輸出哪幾筆資料跟原本的 $m$ 個 $\texttt{pair}$ 產生矛盾
	
	題目保證輸入的資料兩兩之間不矛盾
	
	??? note "思路"
	
	    > 法 1 : 
	
	    技巧 : <a href="/wiki/graph/MST/#3" target="_blank">最大邊最小化生成樹 法3</a>
	
	    考慮找第一個出錯的地方，$\displaystyle \text{mid}=\frac{l+r}{2}=t$
	
	    檢查只用 $\le t$ 的資料聯集是否矛盾
	
	    - 若矛盾，代表 $ans\le t$，刪掉後面的，少一半
	    - 若沒矛盾，代表 $ans> t$，將前面的二分圖縮點，少一半
	
	    複雜度 : $\displaystyle T(p)=T(\frac{p}{2})+O(p\times k)\Rightarrow O(p\times k)$
	
	    > 法 2 : rollback DSU
	
	    註 : 如果資料兩兩之間可以矛盾也是可以做的
	
	    將第 $i$ 個資料的 $k$ 個 $\texttt{pair}$ 加進 DSU，判斷，roll back
	
	    複雜度 : $O(p\times k \times \log C)$

### Atcoder Stamp Rally

???+note "[Atcoder AGC002 D - Stamp Rally](https://atcoder.jp/contests/agc002/tasks/agc002_d)"
	給 $n$ 點 $m$ 邊無向圖，邊的編號 $1 \sim m$
	
	$q$ 筆詢問 $x, y, z$
	
	回答從 $x$ 點出發和從 $y$ 點走的「點集聯集大小」至少是 $z$ 的最大「邊」編號最小值
	
	- $n,m,q \le 10^5$
	
	??? note "思路"
		> 暴力作法
	
		我們二分搜 $\displaystyle \text{mid}=\frac{l+r}{2}=t$ 
		
		檢查如果只走 $\le t$ 的邊 : 
		
		- $x$ 和 $y$ 是否在同一個連通塊
	
		- 連通塊大小是否 $\ge z$
		
		複雜度 : $O(q\times (n+m))$
		
		--- 
		
		這邊我們引入一個技巧，下面的方法會用到
		
		技巧詳見 : <a href="/wiki/graph/MST/#3" target="_blank">最大邊最小化生成樹 法3</a>
		
		> 方法一 : 把 graph 拆半，兩個子問題圖都只有本來的一半
		
		- $ans \le t$ 少一半的 edge
		
		- $ans > t$ 少一半的 edge，縮點
		
		時間複雜度 : $O(m \log m)$
		
		空間複雜度 : $O(m)$[^1]
		
		??? note "code"
			```cpp linenums="1"
			#include <iostream>
	        #include <utility>
	        #include <vector>
	
	        #define int long long
	        #define pii pair<int, int>
	        #define pb push_back
	        #define mk make_pair
	        #define F first
	        #define S second
	        #define ALL(x) x.begin(), x.end()
	
	        using namespace std;
	
	        struct Edge {
	            int u, v, w;
	        };
	
	        struct qry {
	            int x, y, z, id;
	        };
	
	        struct Graph {
	           public:
	            Graph(int n) : n(n) {
	                par = vector<int>(n);
	                sz = vector<int>(n, 1);
	                for (int i = 0; i < n; i++) {
	                    par[i] = i;
	                }
	            }
	            void add_edge(const Edge& e) {
	                int u = find(e.u), v = find(e.v);
	                if (u == v) return;
	                par[u] = v;
	                sz[v] += sz[u];
	                sz[u] = 0;
	            }
	            bool check(const qry& q) {
	                int u = find(q.x), v = find(q.y);
	                if (u != v) {
	                    return sz[u] + sz[v] >= q.z;
	                }
	                return sz[u] >= q.z;
	            }
	            int find(int x) {
	                if (par[x] == x) return x;
	                return par[x] = find(par[x]);
	            }
	            int size() {
	                return n;
	            }
	
	            vector<int> sz;
	
	           private:
	            int n;
	            vector<int> par;
	        };
	
	        const int maxn = 3e5 + 5;
	        int ans[maxn];
	        vector<Edge> edges;
	        vector<qry> queries;
	        vector<Graph> g;
	
	        void shrink(vector<Edge>& edge, vector<qry>& q, Graph& G) {
	            // query 有用到的 node 才要存
	            // 相同 CC 的點，要變成同樣編號
	            // 新圖的點邊號是 0 ~ (k-1)
	            int n = G.size();
	            vector<bool> need(n, false);
	
	            for (auto [x, y, z, id] : q) {
	                need[G.find(x)] = true;
	                need[G.find(y)] = true;
	            }
	            for (auto [u, v, w] : edge) {
	                need[G.find(u)] = true;
	                need[G.find(v)] = true;
	            }
	
	            vector<int> new_id(n, -1);
	            vector<int> sz;
	            int k = 0;
	            for (int i = 0; i < n; i++) {
	                if (need[i]) {
	                    new_id[i] = k++;
	                    sz.push_back(G.sz[i]);
	                }
	            }
	
	            for (auto& [x, y, z, id] : q) {
	                x = new_id[G.find(x)];
	                y = new_id[G.find(y)];
	            }
	            for (auto& [u, v, w] : edge) {
	                u = new_id[G.find(u)];
	                v = new_id[G.find(v)];
	            }
	            G = Graph(k);
	            for (int i = 0; i < k; i++) G.sz[i] = sz[i];
	        }
	
	        void solve(int el, int er, vector<Edge>& edge, vector<qry>& q, Graph& G) {
	            int emid = (el + er) / 2;
	
	            if (el == er) {
	                for (auto [x, y, z, id] : q) {
	                    ans[id] = el;
	                }
	                return;
	            }
	
	            shrink(edge, q, G);
	
	            Graph gLeft = G;
	            Graph& gRight = G;
	
	            vector<Edge> eLeft, eRight;
	            for (auto [u, v, w] : edge) {
	                if (w <= emid) {
	                    G.add_edge({u, v, w});
	                    eLeft.pb({u, v, w});
	                } else {
	                    eRight.pb({u, v, w});
	                }
	            }
	            vector<qry> qLeft, qRight;
	            for (auto query : q) {
	                if (G.check(query)) {
	                    qLeft.pb(query);
	                } else {
	                    qRight.pb(query);
	                }
	            }
	
	            solve(el, emid, eLeft, qLeft, gLeft);
	            solve(emid + 1, er, eRight, qRight, gRight);
	        }
	
	        int n, m, q;
	
	        void init() {
	            cin >> n >> m;
	
	            int u, v;
	            for (int i = 0; i < m; i++) {
	                cin >> u >> v;
	                u--, v--;
	                edges.pb({u, v, i});
	            }
	            cin >> q;
	            int x, y, z;
	            for (int i = 0; i < q; i++) {
	                cin >> x >> y >> z;
	                x--, y--;
	                queries.pb({x, y, z, i});
	            }
	        }
	
	        void work() {
	            // g.resize(21);
	            Graph G(n);
	            solve(0, m - 1, edges, queries, G);
	
	            for (int i = 0; i < q; i++) {
	                cout << ans[i] + 1 << '\n';
	            }
	        }
	
	        signed main() {
	            ios::sync_with_stdio(0);
	            cin.tie(0);
	            int t = 1;
	            // cin >> t;
	            while (t--) {
	                init();
	                work();
	            }
	        }
	        ```
		
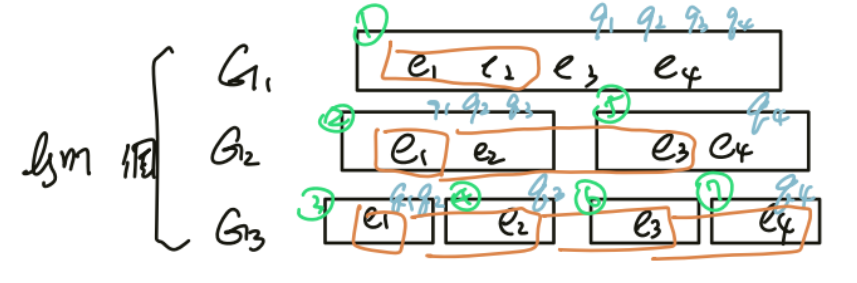
		> 方法二 : 存 $\log m$ 個 $n\text{-vertex graph}$
		
		為了避免每次都複製一次資料結構，可以開 $\log m$ 個資料結構慢慢長
		
		<figure markdown>
	      ![Image title](./images/4.png){ width="500" }
	    </figure>
	
		時間複雜度 : $O(m \log m + q)=O(m\log m)$
		
		空間複雜度 : $O(m \log m)$
		
	    ??? note "code"
	        ```cpp linenums="1"
	        #include <bits/stdc++.h>
            #define int long long
            #define pii pair<int, int>
            #define pb push_back
            #define mk make_pair
            #define F first
            #define S second
            #define ALL(x) x.begin(), x.end()

            using namespace std;

            const int INF = 2e18;
            const int maxn = 3e5 + 5;
            const int M = 1e9 + 7;

            struct Edge {
                int u, v, w;
            };

            struct qry {
                int x, y, z, id;
            };

            int n, m, q;

            struct Graph {
                Graph() {
                    par = vector<int>(n + 1);
                    sz = vector<int>(n + 1);
                    for (int i = 1; i <= n; i++) {
                        par[i] = i;
                        sz[i] = 1;
                    }
                }
                void add_edge(const Edge& e) {
                    int u = find(e.u), v = find(e.v);
                    if (u == v) return;
                    par[u] = v;
                    sz[v] += sz[u];
                    sz[u] = 0;
                }
                bool check(const qry& q) {
                    int u = find(q.x), v = find(q.y);
                    if (u != v) {
                        return sz[u] + sz[v] >= q.z;
                    }
                    return sz[u] >= q.z;
                }

               private:
                vector<int> par;
                vector<int> sz;

                int find(int x) {
                    if (par[x] == x) return x;
                    return par[x] = find(par[x]);
                }
            };

            int ans[maxn];
            vector<Edge> edges;
            vector<qry> queries;
            vector<Graph> g;

            void solve(int depth, int el, int er, vector<Edge>& edge, vector<qry>& q) {
                int emid = (el + er) / 2;
                Graph& G = g[depth];

                if (el == er) {
                    for (auto [x, y, z, id] : q) {
                        ans[id] = el;
                    }

                    for (auto [u, v, w] : edge) {
                        if (w <= emid) {
                            G.add_edge({u, v, w});
                        }
                    }

                    vector<qry>().swap(q);
                    vector<Edge>().swap(edge);
                    return;
                }

                vector<Edge> eLeft, eRight;
                for (auto [u, v, w] : edge) {
                    if (w <= emid) {
                        G.add_edge({u, v, w});
                        eLeft.pb({u, v, w});
                    } else {
                        eRight.pb({u, v, w});
                    }
                }
                vector<qry> qLeft, qRight;
                for (auto query : q) {
                    if (G.check(query)) {
                        qLeft.pb(query);
                    } else {
                        qRight.pb(query);
                    }
                }

                for (auto [u, v, w] : edge) {
                    if (w > emid) {
                        G.add_edge({u, v, w});
                    }
                }
                vector<qry>().swap(q);
                vector<Edge>().swap(edge);

                solve(depth + 1, el, emid, eLeft, qLeft);
                solve(depth + 1, emid + 1, er, eRight, qRight);
            }

            void init() {
                cin >> n >> m;

                int u, v;
                for (int i = 1; i <= m; i++) {
                    cin >> u >> v;
                    edges.pb({u, v, i});
                }
                cin >> q;

                int x, y, z;
                for (int i = 1; i <= q; i++) {
                    cin >> x >> y >> z;
                    queries.pb({x, y, z, i});
                }
            }

            void work() {
                g.resize(21);
                solve(0, 1, m, edges, queries);

                for (int i = 1; i <= q; i++) {
                    cout << ans[i] << "\n";
                }
            }

            signed main() {
                // ios::sync_with_stdio(0);
                // cin.tie(0);
                int t = 1;
                // cin >> t;
                while (t--) {
                    init();
                    work();
                }
            }
            ```

### 區間 gcd

???+note "原創 - 區間 gcd"
	給一個正整數陣列，查詢有幾個區間的 $\gcd = 1$ 
	
	- $O(n\log n)$ 
	
	??? note "思路"
		這題其實就直接 sparse table 預處理，two pointer 維護即可
		
		但是我們還是可以試試看以整體二分搜的觀點切入
		
		---
		對於每個 $l$，看最近的 $r$ 使得 $\gcd (a_l,\cdots a_r)=1$
		
		> 方法1 : 整體二分
		
		假設目前我們在處理左界 $=[ql,qr]$ 的這些 query，他們的右界在 $[l, r]$ 這個範圍
		
		$\displaystyle \text{mid}=\frac{l+r}{2}$，左界在 $[\text{mid}+1,r]$ 這些範圍的都可以往右遞迴
		
		再來考慮左界在 $[ql, \text{mid}]$ 的這些 query
		
		我們要尋找切點 $p$ 使得左界在 $p$ 這個位置他的右界剛好 $\ge \text{mid}$ 
		
		$\texttt{solve (ql, p - 1, l, mid)},\texttt{solve (p, qr, mid + 1, r)}$
		
		> 方法2 : 倍增法
	
		假設 $n=32$，我們考慮第 $i$ 個 query
		
		我們令當前合法區間為 $[i, r_i]$
		
		看能不能將 $r_i$ 往右移動 $32$ 步
		
		看能不能將 $r_i$ 往右移動 $16$ 步
		
		看能不能將 $r_i$ 往右移動 $8$ 步
		
		$\vdots$
		
		??? code "虛擬碼"
			```cpp linenums="1"
			init r[i] = i - 1, g[i] = 0;
			
			for (d = n, n / 2, n / 4, ...)
				build v[i] = gcd(a[i],..., a[i + d - 1])
				
				for i = 1 ~ Q :
					if gcd(g[i], v[r[i] + 1]) != 1 :
						g[i] = gcd(g[i], v[r[i] + 1])
						r_i = r_i + d
			```


### 成大賽 身分調查

???+note "[2023 成大賽初賽 pD.身分調查](https://codeforces.com/gym/437848/problem/D)"
	依序給你 $K$ 個 $\texttt{pair}(x_i,y_i)$ 代表 $x$ 跟 $y$ 在不同組
	
	已知編號 $1$ 的組別，求移除 $[l,r]$ 的 $\texttt{pair}$ 滿足
	
	1. 剩下的 $\texttt{pair}$ 還是能確定 $X$ 的組別
	2. $[l,r]$ 長度最大
	3. 若還是有多組解，輸出左界比最小的
	
	求 $l,r$
	
	??? note "思路"
		如果移除 [i, emid] 可以連通，那你的 ans[i] 有可能是 emid，也有可能在 emid 之後
		
		那不如我們把 ans[i] 的定義往後挪一格呢 ?
		
		---
		
		ans[i] 表示
		
	    - 移除 [i, ans[i] - 1] 會連通
	
	    - 移除 [i, ans[i]] 則不會連通，或者 ans[i] = m
	
		對於每個 i 要二分搜到 ans[i] 滿足：移除 [i, ans[i]] 是不連通的
	
	    一開始在 main 裡面要先找 qr 的目的就是為了保證 i = [ql, qr] 之間的 i 都可以找到上面定義的 ans[i]
	    如果 main 沒有先找 qr，有些 i 可能不管往後移除多少邊都不可能不連通
	
	    DC 的任何子問題都要滿足：
	    對於在 i = [ql, qr] 之間的, ans[i] 一定介於 [el, er]
	    
		二分搜尋的起始條件很重要，上面做很多事情都是在確保：搜尋的過程中答案會介於目前			的下界跟上界之間
		
		ans[i] : 移除 [i, ans[i]] 不能連通, 移除 [i, ans[i]-1] 可以連通
		
	    如果移除 [i, emid] 可以連通 ⇒ emid < ans[i]
	    
	    如果移除 [i, emid] 不能連通 ⇒ ans[i] <= emid
	
	??? note "code (44 points)"
		```cpp linenums="1"
		#include <iostream>
	    #include <utility>
	    #include <vector>
	
	    using namespace std;
	
	    struct Edge {
	        int u, v, w;
	    };
	
	    struct Graph {
	        Graph(int n, int s, int t) : s(s), t(t) {
	            par = vector<int>(n);
	            for (int i = 0; i < n; i++) {
	                par[i] = i;
	            }
	        }
	        void add_edge(const Edge& e) {
	            int u = find(e.u), v = find(e.v);
	            par[u] = v;
	        }
	        bool connected() {
	            return find(s) == find(t);
	        }
	
	       private:
	        int s, t;
	        vector<int> par;
	
	        int find(int x) {
	            if (par[x] == x) return x;
	            return par[x] = find(par[x]);
	        }
	    };
	
	    int n, m, x;
	    vector<Edge> edges;
	    vector<int> ans;
	
	    int s = 0, t;
	
	    void init() {
	        cin >> n >> m >> t;
	        t--;  // to 0-base
	
	        for (int i = 0; i < m; i++) {
	            int u, v, w;
	            cin >> u >> v >> w;
	            u--, v--;  // to 0-base
	            w--;
	            edges.push_back({u, v, w});
	        }
	    }
	
	    // ans[i] : 移除 [i, ans[i]] 不能連通, 移除 [i, ans[i]-1] 可以連通
	    // 如果移除 [i, emid] 可以連通 \imply emid < ans[i]
	    // 如果移除 [i, emid] 不能連通 \imply ans[i] <= emid
	    //
	    void DC(Graph g, int el, int er, int ql, int qr) {
	        // 假設 edges[0, ql-1] 和 edges[er+1, m-1] 都已經加入 g
	        // 如果移除 [qr, er] 一定不連通。 TODO: 寫一個迴圈檢查
	        if (el == er) {
	            for (int i = ql; i <= qr; i++) ans[i] = er;
	            return;
	        }
	        int emid = (el + er) / 2;
	
	        Graph h = g;
	        for (int i = emid + 1; i <= er; i++) {
	            h.add_edge(edges[i]);
	        }
	
	        int qmid = emid;
	        for (int i = ql; i <= emid; i++) {
	            if (i > ql) h.add_edge(edges[i - 1]);
	            if (h.connected()) {
	                // 移除 [i, emid] 會連通
	                // 移除 [i-1, emid] 不連通
	                qmid = i - 1;
	                break;
	            }
	        }
	
	        Graph gl = g;
	        Graph gr = g;
	        for (int i = emid + 1; i <= er; i++) gl.add_edge(edges[i]);
	        for (int i = ql; i <= qmid; i++) gr.add_edge(edges[i]);
	        DC(gl, el, emid, ql, qmid);
	        DC(gr, emid + 1, er, qmid + 1, qr);
	    }
	
	    vector<int> color;
	    vector<vector<pair<int, int>>> wg;
	    void dfs(int u) {
	        for (auto [v, c] : wg[u]) {
	            if (color[v] == -1) {
	                color[v] = color[u] ^ c;
	                dfs(v);
	            }
	        }
	    }
	
	    int main() {
	        cin.tie(0);
	        cin.sync_with_stdio(0);
	
	        init();
	
	        if (s == t) {
	            cout << n << ' ' << 1 << ' ' << n << ' ' << 1 << '\n';
	            return 0;
	        }
	
	        Graph tmp(n, s, t);
	        int ql = 0, qr = m;
	        for (int i = 0; i < m; i++) {
	            tmp.add_edge(edges[i]);
	            if (tmp.connected()) {
	                qr = i;
	                break;
	            }
	        }
	        if (qr == m) {
	            cout << -1 << '\n';
	            return 0;
	        }
	
	        ans = vector<int>(m, m);
	        DC(Graph(n, s, t), 0, m - 1, ql, qr);
	
	        int len = 0, best_l = -1, best_r = -1;
	        for (int i = 0; i < m; i++) {
	            if (ans[i] - i > len) {
	                len = ans[i] - i;
	                best_l = i;
	                best_r = ans[i] - 1;
	            }
	        }
	
	        color = vector<int>(n, -1);
	        wg.resize(n);
	        for (int i = 0; i < m; i++) {
	            if (best_l <= i && i <= best_r) continue;
	            Edge e = edges[i];
	            wg[e.u].push_back({e.v, e.w});
	            wg[e.v].push_back({e.u, e.w});
	        }
	        color[s] = 0;
	        dfs(s);
	
	        cout << len << ' ';
	        cout << best_l + 1 << ' ' << best_r + 1 << ' ';
	        cout << color[t] + 1 << '\n';
	
	        return 0;
	    }
	    ```
	??? note "code(by algoseacow)"
		```cpp linenums="1"
		#include <iostream>
	    #include <utility>
	    #include <vector>
	
	    using namespace std;
	
	    struct Edge {
	        int u, v, w;
	    };
	
	    struct Graph {
	        Graph(int n, int s, int t) : s(s), t(t) {
	            par = vector<int>(n);
	            for (int i = 0; i < n; i++) {
	                par[i] = i;
	            }
	        }
	        void add_edge(const Edge& e) {
	            int u = find(e.u), v = find(e.v);
	            par[u] = v;
	        }
	        bool connected() {
	            return find(s) == find(t);
	        }
	        void shrink(vector<Edge>& edges) {
	            int n = par.size();
	
	            vector<bool> used(n);
	            used[find(s)] = true;
	            used[find(t)] = true;
	            for (Edge e : edges) {
	                used[find(e.u)] = true;
	                used[find(e.v)] = true;
	            }
	
	            vector<int> cc(n, -1);
	            int cnt = 0;
	            for (int i = 0; i < n; i++) {
	                if (i == find(i) && used[i] == true) {
	                    cc[i] = cnt++;
	                }
	            }
	
	            for (Edge& e : edges) {
	                e.u = cc[find(e.u)];
	                e.v = cc[find(e.v)];
	            }
	            s = cc[find(s)];
	            t = cc[find(t)];
	
	            par = vector<int>(cnt);
	            for (int i = 0; i < cnt; i++) par[i] = i;
	        }
	
	       private:
	        int s, t;
	        vector<int> par;
	
	        int find(int x) {
	            if (par[x] == x) return x;
	            return par[x] = find(par[x]);
	        }
	    };
	
	    int n, m, x;
	    vector<Edge> edges;
	    vector<int> ans;
	
	    int s = 0, t;
	
	    void init() {
	        cin >> n >> m >> t;
	        t--;  // to 0-base
	
	        for (int i = 0; i < m; i++) {
	            int u, v, w;
	            cin >> u >> v >> w;
	            u--, v--;  // to 0-base
	            w--;
	            edges.push_back({u, v, w});
	        }
	    }
	
	    // ans[i] : 移除 [i, ans[i]] 不能連通, 移除 [i, ans[i]-1] 可以連通
	    // 如果移除 [i, emid] 可以連通 \imply emid < ans[i]
	    // 如果移除 [i, emid] 不能連通 \imply ans[i] <= emid
	    //
	    void DC(Graph g, int el, int er, int ql, int qr) {
	        // 假設 edges[0, ql-1] 和 edges[er+1, m-1] 都已經加入 g
	        // 如果移除 [qr, er] 一定不連通
	        if (ql > qr) return;
	        if (el == er) {
	            for (int i = ql; i <= qr; i++) ans[i] = er;
	            return;
	        }
	
	        // 先把圖變小
	        vector<Edge> edges_old(edges.begin() + ql, edges.begin() + er + 1);
	        vector<Edge> edges_new = edges_old;
	        g.shrink(edges_new);
	
	        // 把 edge[ql, er] 換成縮點後的
	        for (int i = 0; i <= er - ql; i++) edges[ql + i] = edges_new[i];
	
	        int emid = (el + er) / 2;
	        Graph h = g;
	        for (int i = emid + 1; i <= er; i++) {
	            h.add_edge(edges[i]);
	        }
	
	        int qmid = emid;
	        for (int i = ql; i <= emid; i++) {
	            if (i > ql) h.add_edge(edges[i - 1]);
	            if (h.connected()) {
	                // 移除 [i, emid] 會連通
	                // 移除 [i-1, emid] 不連通
	                qmid = i - 1;
	                break;
	            }
	        }
	
	        Graph gl = g;
	        for (int i = emid + 1; i <= er; i++) gl.add_edge(edges[i]);
	        DC(gl, el, emid, ql, qmid);  // edge [0, ql-1], [emid+1, m-1]
	
	        Graph gr = std::move(g);
	        for (int i = ql; i <= qmid; i++) gr.add_edge(edges[i]);
	        DC(gr, emid + 1, er, qmid + 1, qr);  // edge[0, qmid], [er+1,m-1]
	
	        // 把 edge[ql, qr] 換回舊編號
	        for (int i = 0; i <= er - ql; i++) edges[ql + i] = edges_old[i];
	    }
	
	    vector<int> color;
	    vector<vector<pair<int, int>>> wg;
	    void dfs(int u) {
	        for (auto [v, c] : wg[u]) {
	            if (color[v] == -1) {
	                color[v] = color[u] ^ c;
	                dfs(v);
	            }
	        }
	    }
	
	    int main() {
	        cin.tie(0);
	        cin.sync_with_stdio(0);
	
	        init();
	
	        if (s == t) {
	            cout << n << ' ' << 1 << ' ' << n << ' ' << 1 << '\n';
	            return 0;
	        }
	
	        int ql = 0, qr = m;
	
	        Graph tmp(n, s, t);
	        for (int i = 0; i < m; i++) {
	            tmp.add_edge(edges[i]);
	            if (tmp.connected()) {
	                qr = i;
	                break;
	            }
	        }
	        if (qr == m) {
	            cout << -1 << '\n';
	            return 0;
	        }
	
	        //
	        ans = vector<int>(m, m);  // 移除 edge[i, ans[i]-1] 之後依然是聯通的
	        DC(Graph(n, s, t), 0, m - 1, ql, qr);
	
	        int len = 0, best_l = -1, best_r = -1;
	        for (int i = 0; i < m; i++) {
	            if (ans[i] - i > len) {
	                len = ans[i] - i;
	                best_l = i;
	                best_r = ans[i] - 1;
	            }
	        }
	
	        // 重建一張有權重的圖，dfs 判斷 s t 是不是相同顏色
	        color = vector<int>(n, -1);
	        wg.resize(n);
	        for (int i = 0; i < m; i++) {
	            if (best_l <= i && i <= best_r) continue;
	            Edge e = edges[i];
	            wg[e.u].push_back({e.v, e.w});
	            wg[e.v].push_back({e.u, e.w});
	        }
	        color[s] = 0;
	        dfs(s);
	
	        // output
	        cout << len << ' ';
	        cout << best_l + 1 << ' ' << best_r + 1 << ' ';
	        cout << color[t] + 1 << '\n';
	
	        return 0;
	    }
	    ```



### BOI 2020 Joker

???+note "[LOJ #3334. 「BalticOI 2020」小丑](https://loj.ac/p/3334)"
	給你 $n$ 點 $m$ 邊的無向圖，邊以 $1\sim m$ 編號，有 $q$ 筆詢問，第 $i$ 筆詢問問
	
	- 移除編號在 $[l_i,r_i]$ 內的邊是否可以讓圖沒有奇環
	
	$n,m,q\le 2\times 10^5$
	
	??? note "思路"
		
		ans[i] 表示 
		
		- 移除 [i, ans[i] - 1] 有 odd cycle
		
		- 移除 [i, ans[i]] 沒 odd cycle
	
		對於每個 i，二分搜 ans[i]，使 [i, ans[i]] 沒 odd cycle
		
		再來要定義上界下界
		
		下界的部分有可能只移除第 i 個邊就沒有 odd cycle 了
		
		上界的部分就要保證移除 [i, m - 1] 就沒有 odd cycle
		
		所以我們找到第一個 prefix[0, qr] 滿足 :
		
		- 只用 [0, qr - 1] 的邊沒有 odd cycle
	
		- 只用 [0, qr] 的邊有 odd cycle
	
		i > qr 的部分不管移除多少個邊都還是會有 odd cycle
	
	??? note "code"
		```cpp linenums="1"
		#include <bits/stdc++.h>
        #define int long long
        #define pii pair<int, int>
        #define pb push_back
        #define mk make_pair
        #define F first
        #define S second
        #define ALL(x) x.begin(), x.end()

        using namespace std;

        const int INF = 2e18;
        const int maxn = 3e5 + 5;
        const int M = 1e9 + 7;

        struct Edge {
            int u, v;
        };

        struct Graph {
            Graph(int n) : n(n) {
                sz = vector<int>(n, 1);
                par = vector<int>(n);
                dis = vector<int>(n);
                cnt = 0;
                for (int i = 0; i < n; i++) {
                    par[i] = i;
                }
            }
            void add_edge(const Edge &e) {
                auto [x, disx] = find(e.u);
                auto [y, disy] = find(e.v);
                if (x == y) {
                    // if (disx == disy) => odd cycle
                    cnt += (disx == disy);
                    stk.push({-1, (disx == disy)});
                    return;
                }

                if (sz[x] < sz[y]) swap(x, y);
                sz[x] += sz[y];
                par[y] = x;
                dis[y] = disx ^ disy ^ 1;
                stk.push({x, y});
            }
            void undo() {
                auto [x, y] = stk.top();
                stk.pop();
                if (x == -1) {
                    cnt -= y;
                    return;
                }
                sz[x] -= sz[y];
                par[y] = y;
                dis[y] = 0;
            }
            bool check() {
                // return : 有沒有 odd cycle
                return (cnt > 0);
            }

           private:
            int n, cnt;
            vector<int> sz;
            vector<int> par;
            vector<int> dis;
            stack<pii> stk;

            pii find(int x) {
                if (par[x] == x)
                    return {x, 0};
                else {
                    auto [fa, d] = find(par[x]);
                    return {fa, d ^ dis[x]};
                }
            }
        };

        int n, m, q;
        int ans[maxn];
        vector<Edge> edges;

        void solve(Graph &g, int el, int er, int ql, int qr) {
            // [0, ql - 1] and [er + 1, m - 1] 都已加入 g
            if (ql > qr) return;
            if (el == er) {
                for (int i = ql; i <= qr; i++) {
                    ans[i] = el;
                }
                return;
            }
            int emid = (el + er) / 2, qmid = min(emid, qr);

            for (int i = emid + 1; i <= er; i++) {
                g.add_edge(edges[i]);
            }
            int cnt = 0;
            for (int i = ql; i <= min(emid, qr); i++) {
                if (i > ql) g.add_edge(edges[i - 1]), cnt++;
                if (g.check()) {
                    // 移除 [i, emid] 有 odd cycle
                    // 移除 [i - 1, emid] 沒 odd cycle
                    qmid = i - 1;
                    break;
                }
            }

            while (cnt--) {
                g.undo();
            }

            solve(g, el, emid, ql, qmid);  // [0, ql - 1] [emid + 1, m - 1]

            for (int i = emid + 1; i <= er; i++) {
                g.undo();
            }

            for (int i = ql; i <= qmid; i++) {
                g.add_edge(edges[i]);
            }

            solve(g, emid + 1, er, qmid + 1, qr);  // [0, qmid] [er + 1, m - 1]
            for (int i = ql; i <= qmid; i++) {
                g.undo();
            }
        }

        void init() {
            cin >> n >> m >> q;
            int u, v;
            for (int i = 0; i < m; i++) {
                cin >> u >> v;
                u--, v--;
                edges.pb({u, v});
            }
        }

        // 找到最小的 ans[i], 使移除 [i, ans[i]] 沒 odd cycle
        // 移除 [i, ans[i] - 1] 有 odd cycle
        // 移除 [i, ans[i]] 沒 odd cycle

        void build() {
            // 使得 ans[i] 有上界
            // TODO : 找到第一個 i 使得 用 [0, i] 的 edge 有 odd cycle
            Graph tmp(n);
            int ql = 0, qr = m;
            for (int i = 0; i < m; i++) {
                tmp.add_edge(edges[i]);
                if (tmp.check()) {
                    qr = i;
                    break;
                }
            }
            if (qr == m) {
                for (int i = 0; i < m; i++) {
                    ans[i] = i;
                }
                return;
            }
            for (int i = qr + 1; i < m; i++) {
                ans[i] = m;
            }

            Graph g(n);
            solve(g, 0, m - 1, ql, qr);
        }

        void work() {
            build();

            while (q--) {
                int l, r;
                cin >> l >> r;
                l--, r--;
                if (ans[l] <= r)
                    cout << "NO\n";
                else
                    cout << "YES\n";
            }
        }

        signed main() {
            // ios::sync_with_stdio(0);
            // cin.tie(0);
            int t = 1;
            // cin >> t;
            while (t--) {
                init();
                work();
            }
        }
	    ```

### POI 2011 Meteors

???+note "[POI2011 R3 Day2 Meteors](https://loj.ac/p/2169)"
	給你 $N$ 個人的目標金額 $V_1,V_2,\ldots ,V_n$，和 $M$ 塊農地 $a_1,a_2\ldots ,a_M$，代表第 $i$ 塊農地的主人，第 $M$ 塊農地連接第 $1$ 塊
	
	$Q$ 次對區間 $[L,R]$ 的農地加上 $C$，問每個人分別在哪次操作後達到目標，或是沒有達到
	
	$1\le N,M,Q\le 3\times 10^5,1\le V_i,C_i\le 10^9$
	
	??? note "思路"
		對於每個人二分搜哪一次操作後達到目標
		
		那對於每個人要怎麼計算一堆 query 的貢獻呢 ?
		
		我們可以使用 BIT 的單點查詢，區間修改的技巧
		
		對於每個人枚舉他有支配的土地，單點查詢該土地目前的權值

### TIOJ 王老先生

???+note "[TIOJ 1919.王老先生](https://tioj.ck.tp.edu.tw/problems/1919)"
	給你 $N$ 個人的目標金額 $V_1,V_2,\ldots ,V_n$，和 $M$ 塊農地 $a_1,a_2\ldots ,a_M$，代表第 $i$ 塊農地的主人
	
	$Q$ 次對區間 $[L,R]$ 的農地加上 $C$，如果有人在這個區間內擁有多個土地，他還是只會被加到一次 $C$，問每個人分別在哪次操作後達到目標，或是沒有達到
	
	$1\le N,M,Q\le 10^5,1\le V_i,C_i\le 10^9$
	
	??? note "提示"
		如果只有 $1$ 個主人
		
	??? note "思路"
		對於每個人二分搜哪一次操作後達到目標
		
		那對於每個人要怎麼計算一堆 query 的貢獻呢 ?
		
		對於 $i$ 支配的每塊地，我們考慮他後面第一個出現的位置
		
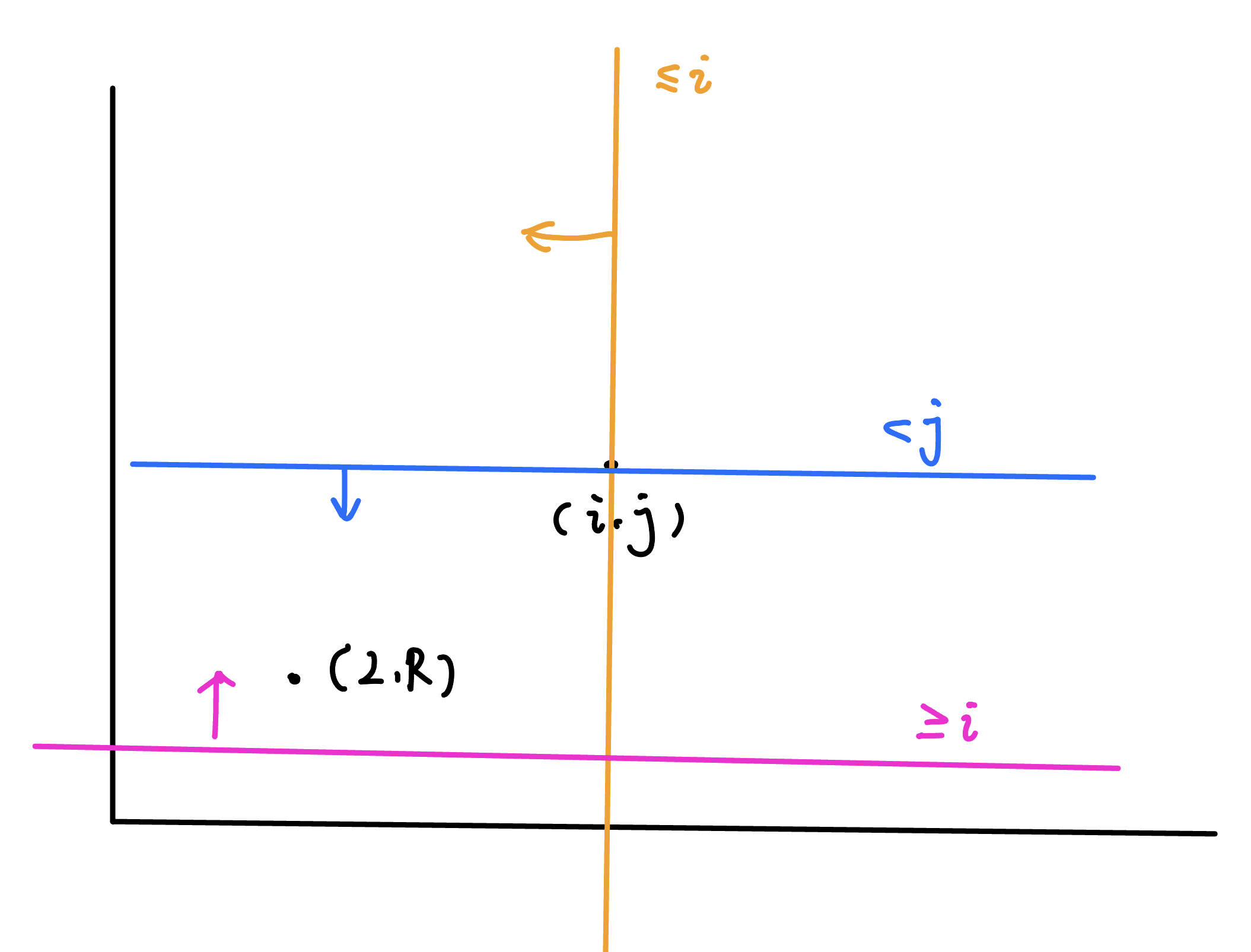
		我們把這塊地的 index 叫做 $i$，後面第一個出現的 index 叫做 $j$
		
		那就是要計算符合 $\begin{cases}L\le i \\ j > R \\ i \le R\end{cases}$ 的 $[L,R]$ 的貢獻總和
		
		就是一個二維平面問題，我們只要將第一維排序，第二維使用 BIT 即可
		
		<figure markdown>
	      ![Image title](./images/5.png){ width="300" }
	    </figure>
	    
	??? note "code"
		```cpp linenums="1"
		#include <bits/stdc++.h>
        #define int long long
        #define pii pair<int, int>
        #define pb push_back
        #define mk make_pair
        #define F first
        #define S second
        #define ALL(x) x.begin(), x.end()
        #define lowbit(x) (x & (-x))

        using namespace std;

        const int INF = 2e18;
        const int maxn = 3e5 + 5;
        const int M = 1e9 + 7;

        struct opr {
            int l, r, c;

            bool operator<(const opr &other) {
                return l < other.l;
            }
        };

        struct qry {
            // farmer id, need how much
            int id, goal;
        };

        struct BIT {
            BIT(int n) : n(n) {
                bit.resize(n + 1);
            }

            void add(int x, int d) {
                while (x <= n) {
                    bit[x] += d;
                    x += lowbit(x);
                }
            }

            int query(int x) {
                int ret = 0;
                while (x > 0) {
                    ret += bit[x];
                    x -= lowbit(x);
                }
                return ret;
            }

            bool clean() {
                for (int i = 1; i <= n; i++) {
                    if (bit[i]) return false;
                }
                return true;
            }

           private:
            int n;
            vector<int> bit;
        };

        int n, m, q;
        vector<int> G[maxn];
        vector<opr> operation;
        vector<qry> queries;
        int nxt[maxn], a[maxn], ans[maxn];

        void solve(BIT &bit, int el, int er, vector<qry> &q) {
            // 在 [el, er] 的這些操作中，我在哪個操作可以達到目標
            if (el == er) {
                for (auto [id, goal] : q) {
                    ans[id] = el;
                }
                return;
            }

            int emid = (el + er) / 2;
            vector<opr> op(operation.begin() + el - 1, operation.begin() + emid);

            sort(ALL(op));
            vector<pii> query;
            vector<int> cost;

            int cnt = 0;
            for (auto &[id, goal] : q) {
                for (auto i : G[id]) {
                    query.pb({i, cnt});
                }
                cnt++;
            }
            cost.resize(cnt);
            sort(ALL(query));
            int ptr = 0;

            for (auto [i, idx] : query) {
                int j = nxt[i];
                while (ptr < op.size() && op[ptr].l <= i) {
                    bit.add(op[ptr].r, op[ptr].c);
                    ptr++;
                }

                if (j == 0) {
                    int t = bit.query(m) - bit.query(i - 1);
                    cost[idx] += t;
                } else {
                    int t = bit.query(j - 1) - bit.query(i - 1);
                    cost[idx] += t;
                }
            }

            cnt = 0;
            vector<qry> qLeft, qRight;
            for (auto &[id, goal] : q) {
                if (goal <= cost[cnt]) {
                    qLeft.pb({id, goal});
                } else {
                    qRight.pb({id, goal - cost[cnt]});
                }
                cnt++;
            }

            for (int i = 0; i < ptr; i++) {
                bit.add(op[i].r, -op[i].c);
            }

            vector<pii>().swap(query);
            vector<int>().swap(cost);
            vector<opr>().swap(op);
            vector<qry>().swap(q);

            solve(bit, el, emid, qLeft);
            solve(bit, emid + 1, er, qRight);
        }

        void init() {
            cin >> n >> m >> q;

            for (int i = 1; i <= m; i++) {
                cin >> a[i];
                if (G[a[i]].size()) nxt[G[a[i]].back()] = i;
                G[a[i]].pb(i);
            }

            for (int i = 1; i <= n; i++) {
                int x;
                cin >> x;
                queries.pb({i, x});
            }

            for (int i = 1; i <= q; i++) {
                int l, r, c;
                cin >> l >> r >> c;
                operation.pb({l, r, c});
            }
        }

        void work() {
            q++;
            operation.pb({1, m, (int)2e9});
            BIT bit(m);
            solve(bit, 1, q, queries);

            for (int i = 1; i <= n; i++) {
                if (ans[i] == q)
                    cout << -1 << "\n";
                else
                    cout << ans[i] << "\n";
            }
        }

        signed main() {
            // ios::sync_with_stdio(0);
            // cin.tie(0);
            int t = 1;
            // cin >> t;
            while (t--) {
                init();
                work();
            }
        }
	    ```

### NPSC 上司的薪水

???+note "<a href="/wiki/offline/images/NPSC2015.pdf#page=7" target="_blank">NPSC 2015 高中組決賽 pB.上司的薪水</a>"
	給你一顆 $N$ 個點的有根樹還有一個正整數 $k$，每一個點一開始的值都是 $0$，有 $Q$ 次操作，每次選擇一個點 $u$ 跟一個正整數 $x$，代表把 $u$ 走到根每個點的值都加上 $x$，每次操作完問有整棵樹有幾個點的值 $\ge k$
	
	$N,Q\le 3\times 10^5$
	
	??? note "思路"
		製造 DFS 序列
	
		對每個 $i$ 二分搜第幾次操作後權重 $\ge k$
		
		對每個 $j$ 計算有幾個 $i$ 滿足 $\begin{cases}\texttt{in}_i \ge \texttt{in}_j \\ \texttt{out}_i \le \texttt{out}_j \end{cases}$，cost 就是這些的 $x$ 相加

### CSES New Roads Queries

???+note "[CSES - New Roads Queries](https://cses.fi/problemset/task/2101)"
	給一張 $n$ 個點的圖，依序加入 $m$ 條邊，回答 $q$ 筆詢問 :
	
    - $a,b$ 在加入第幾條邊時連通，或沒有連通
    
    $n,q\le 2\times 10^5$
    
    ??? note "思路"
    	用 Atcoder 那題的「存 $\log m$ 個 $n\text{-vertex graph}$」技巧
    	
    	另解 : 也有<a href="/wiki/graph/MST/?h=new+roads+queries#_4" target="_blank">並查集生成樹的解法</a>

### YTP When2meet

???+note "[2023 YTP 初賽 p5 When2meet](/wiki/offline/images/YTP2023PreliminaryContest_S1.pdf#page=21)"
	給一張 $n$ 個點的圖，有 $q$ 筆操作 :
	
    - $\text{union}(i,a_i,b_i):$ 在時間 $i$ 在 $a_i,b_i$ 間建邊
    
    - $\text{query}(k,\{x_1,x_2,\ldots, x_k \}):$ $x_1,x_2,\ldots, x_k$ 在何時連通，或沒有連通
    
    $n,q\le 2\times 10^5$
    
    ??? note "思路"
    	上一題的變化版，還是「存 $\log m$ 個 $n\text{-vertex graph}$」技巧
    	
    	並查集生成樹的話 $\text{LCA(a,b,c)}=\text{LCA}(\text{LCA}(a,b),c)$，一樣找路徑上最大值

### YTP 召喚到異世界

???+note "[2023 YTP 初賽 p7 召喚到異世界](http://127.0.0.1:8000/wiki/offline/images/YTP2023PreliminaryContest_S1.pdf#page=32)"
	給一張 $n$ 點 $m$ 邊的圖，圖不一定連通，有重邊，有 $q$ 筆以下查詢 :
    
    - 給兩點 $x,y$，找一條 $x$ 到 $y$ 的路徑，輸出路徑上第二大邊最小可以是多少
    
    $n,m,q\le 10^5$
    
    ??? note "思路"
    	一開始把所有 edge 標記成黑色，按照邊權由小到大的順序依序把邊變成白色
    
    	query(x, y) 就是在問：最早在哪個時間點開始，存在一條 x 到 y 的路徑，且這個路徑上只有一條黑色邊
    
    	可以用整體二分，先把一半的邊變成白色，然後白邊之間縮點，查詢每個 query(x, y) 是否 x 與 y 只相隔一條黑邊。遞迴兩個子問題，時間小的子問題，不會用到編號 [mid + 1, r] 之間的邊，所以邊數剩下一半，時間大的子問題，白色邊都縮點了，所以邊數也只剩下一半


[^1]: 每個邊只會往一邊走，上一層用完了就可以刪掉，所以同一時間只有 $m$ 條邊在跑，每個邊只出現在一個地方