???+note "[CF 1867 E2. Salyg1n and Array (hard version)](https://codeforces.com/contest/1867/problem/E2)"
有一個長度為 $n$ 的陣列 $a_1,\ldots ,a_n$,目標是輸出 $a_1\oplus \ldots \oplus a_n$。給 $k$,你可以做以下查詢至多 57 次 :
- $\text{query}(i):$ 問 $a_i \oplus a_{i + 1} \oplus \ldots \oplus a_{i + k - 1}$ 是多少,問了之後,這個區間內的元素就會被 reverse
$n,k\le 2500,n,k$ 皆為偶數
??? note "思路"
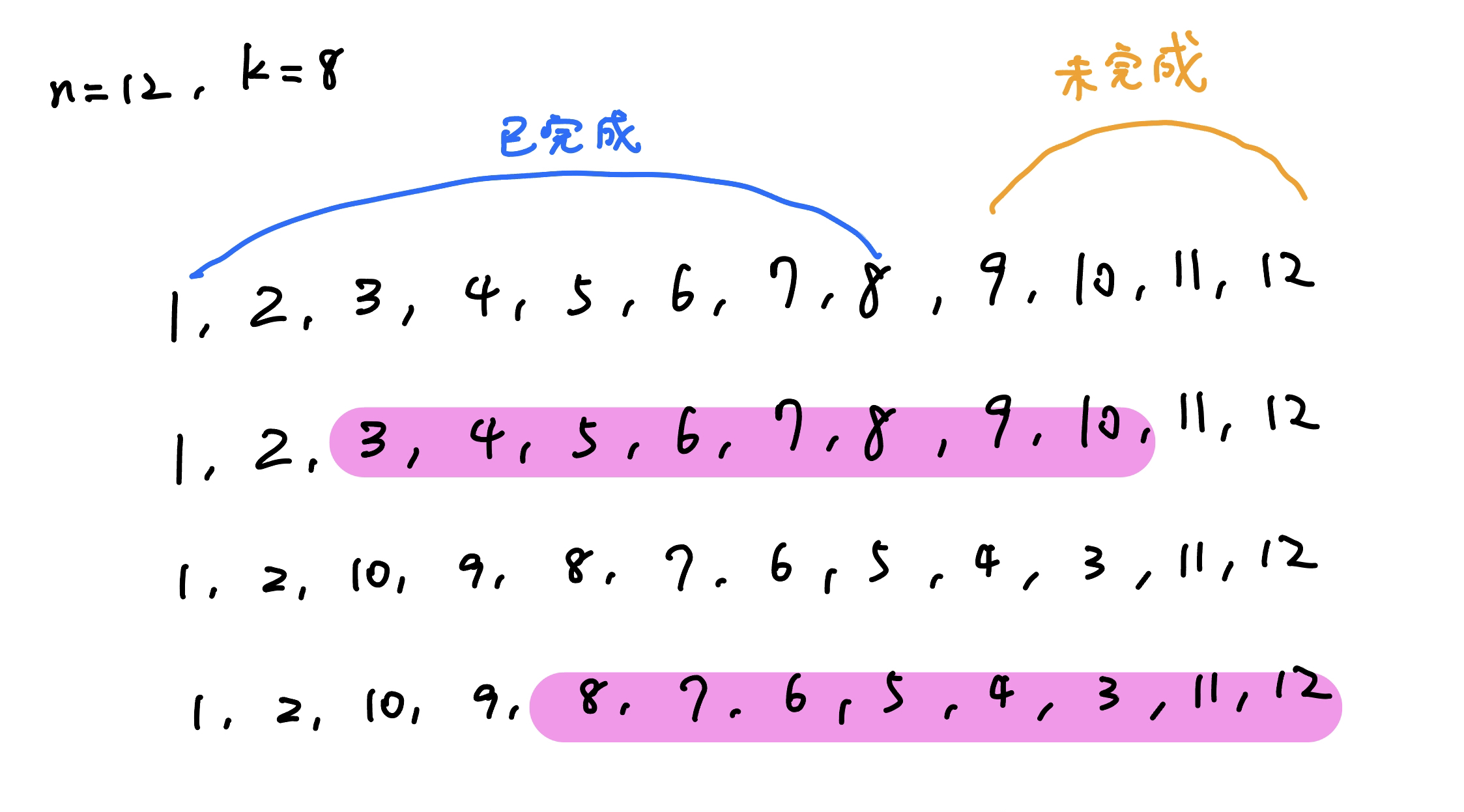
若 n % k == 0,那我們可以每次從左到右依序詢問長度為 k 的區間即可。若 n % k != 0,代表我們左到右依序詢問長度為 k 的區間後會剩下一段,我們的目標就是將這段的值算出來。可以發現若我們以剩下區間的一半做為 query 的結尾 query 一次,在以 n 作為結尾 query 一次,中間多餘的貢獻會剛好消除
{ width="400" }
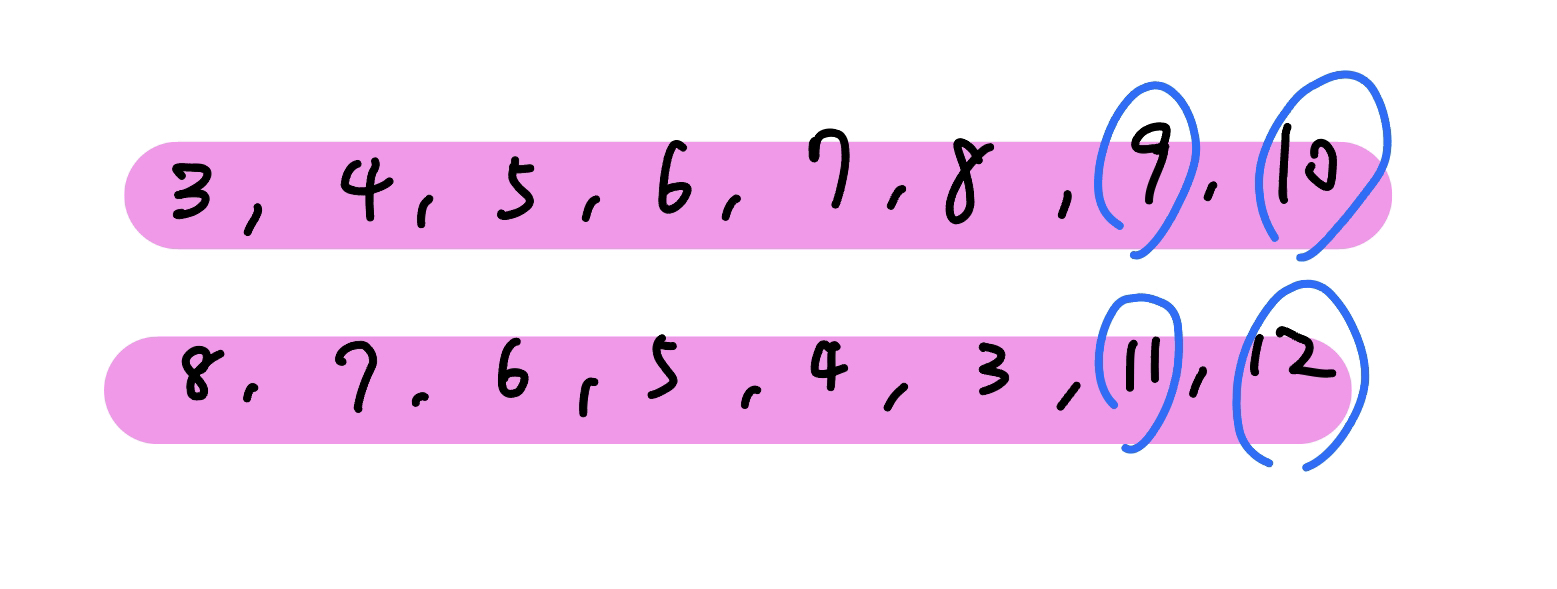{ width="400" }
??? note "code"
```cpp linenums="1"
#include
#define int long long
using namespace std;
int query(int i) {
cout << "? " << i << endl;
int res;
cin >> res;
return res;
}
void solve() {
int n, k;
cin >> n >> k;
int ans = 0, now = 1;
while (now + k - 1 <= n) {
int res = query(now);
ans ^= res;
now += k;
}
if (now < n) {
int tmp = (n - now + 1) / 2;
int res1 = query(now + tmp - k);
ans ^= res1;
int res2 = query(now + tmp + tmp - k);
ans ^= res2;
}
cout << "! " << ans << '\n';
}
signed main() {
int t = 1;
cin >> t;
while (t--) {
solve();
}
}
```
???+note "[CF 1918 E. ace5 and Task Order](https://www.luogu.com.cn/problem/CF1918E)"
有一個長度為 $n$ 的 $1\sim n$ 的 permutation 以及一個介於 $1$ 和 $n$ 之間的正整數$x$。目標是要去確定這個 permutation。可以通過 `? i` 進行詢問,返回值有三種:
- `<`:表示 $a_i`:表示 $a_i>x$,該次詢問後,$x\leftarrow x+1$
- `=`:表示 $a_i=x$
$n\leq 2000,$ 詢問次數 $\le 40n$
??? note "思路"
首先,對於一個有 $O(n^2)$ 次查詢的問題,解答很明顯:對於每個位置 i,持續查詢直到返回等於,然後通過大小關係直接對這 n 個數進行排序,從而獲得答案。
既然排序可以得到答案,我們考慮那些 $O(n \log n)$ 的排序算法,比如借鑒快速排序的思路。
但我們發現在無法確定 x 是多少個情況下,我們什麼都很難做。所以首先我們必須去能有權力控制 x,而最好的辦法就是知道 1 還有 n 在哪裡,一般題目在分析時也很常從最小和最大開始找。
具體來講,我們只要掃一遍 1 ~ n,對於每個位置,如果詢問返回 < 就繼續查直到不是 < 為止,否則直接不管。顯然這樣最多查詢 O(n) 次(因為 x 最多增大 n 次),並且在 x = 1 的地方一定可以取到 x = 1。我們只要看 x 在哪裡取到最小值即可。找 x = n 同理。
再來,我們借鑑快速排序的想法,我们需要對值域進行分治。在控制 x 的值不變的情況下,我們需要查詢若干個位置的答案,從而將這些位置分成兩組:「大於 x」 和 「小於 x 」的兩組(等於 x 的位置可以直接得到答案)。遞迴下去就可以得到答案。複雜度 O(n log n)。
> 參考:
??? note "code"
```cpp linenums="1"
#include
using namespace std;
int p1, pn;
int ans[2005];
int query(int x) {
cout << "? " << x << endl;
cout.flush();
string s;
cin >> s;
if (s[0] == '=') return 0;
if (s[0] == '<') return -1;
if (s[0] == '>') return 1;
return 0114507537;
}
int cur;
void solve(int l, int r, vector& v) {
// v 是值在 [l,r] 中的下标集合
if (l > r) return;
if (l == r) {
ans[v[0]] = l;
return;
}
int mid = (l + r) / 2;
while (cur > mid) {
query(p1);
cur--;
}
while (cur < mid) {
query(pn);
cur++;
}
vector vl, vr;
vl.clear();
vr.clear();
// 分成 [l,mid-1] 和 [mid+1,r]
for (int x : v) {
int tmp = query(x);
if (tmp == 0) ans[x] = mid;
if (tmp == -1) {
vl.push_back(x);
query(pn);
}
if (tmp == 1) {
vr.push_back(x);
query(p1);
}
}
solve(l, mid - 1, vl);
solve(mid + 1, r, vr);
}
int main() {
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
// find 1&n
p1 = pn = 1;
int md = 0x3f3f3f3f, d = 0;
for (int i = 1; i <= n; i++) {
int tmp = query(i);
d += tmp;
while (tmp == -1) {
tmp = query(i);
d += tmp;
}
if (d < md) p1 = i, md = d;
}
md = -0x3f3f3f3f, d = 0;
for (int i = 1; i <= n; i++) {
int tmp = query(i);
d += tmp;
while (tmp == 1) {
tmp = query(i);
d += tmp;
}
if (d > md) pn = i, md = d;
}
ans[p1] = 1, ans[pn] = n;
vector tmp;
tmp.clear();
for (int i = 1; i <= n; i++)
if (i != p1 && i != pn) tmp.push_back(i);
int val = query(pn);
while (val == 1) val = query(pn);
cur = n;
solve(2, n - 1, tmp);
cout << "! ";
for (int i = 1; i <= n; i++) cout << ans[i] << ' ';
cout << endl;
cout.flush();
}
return 0;
// quod erat demonstrandum
}
```