---
title : Stan demonstration
subtitle :
author : Ziyuan Lin
job :
framework : io2012 # {io2012, html5slides, shower, dzslides, ...}
highlighter : highlight.js # {highlight.js, prettify, highlight}
hitheme : tomorrow #
widgets : [mathjax, bootstrap] # {mathjax, quiz, bootstrap}
mode : selfcontained # {selfcontained, standalone, draft}
knit : slidify::knit2slides
output:
html_document:
fig_caption: true
---
## Why Stan?
> Optimization is bad, expectations are really important, Hamiltonian Monte Carlo is the right thing to do, and Stan is the right way to do the Hamiltonian Monte Carlo.
> -- Michael Betancourt, Reykjavik, 2014
## Workflow
1. Write the source code in the modeling language to specify the model ($P(\mathcal{D}\mid\theta)$);
2. Use the compiler or some wrapper to compile and do the inference ($P(\theta\mid\mathcal{D})$).
+ Shell, R, Python, MATLAB, Julia
We use RStan here.
--- &tabs
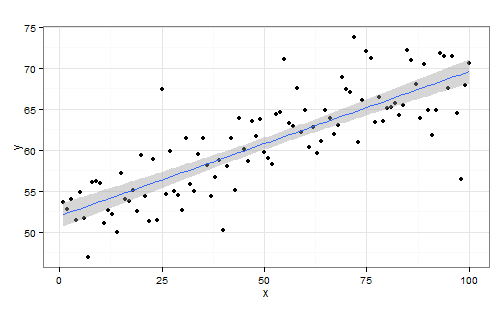
## Example 1: linear regression
$$
y_n=\alpha+\beta x_n+\epsilon_n\quad\mbox{where}\quad\epsilon_n\sim\mathcal{N}(0,\sigma^2)
$$
*** class:active id:figure
*** id:stan-code
```r
data {
int N;
vector[N] x;
vector[N] y;
}
parameters {
real alpha;
real beta;
real sigma_sqrt;
}
model {
y ~ normal(alpha + beta * x, sigma_sqrt); // no prior = improper prior
}
```
--- &twocol_with_width
## First things to learn
$$
y_n=\alpha+\beta x_n+\epsilon_n\quad\mbox{where}\quad\epsilon_n\sim\mathcal{N}(0,\sigma^2)
$$
*** =left width:50%
```r
data {
int N;
// multidimensional: matrix[N,K] x;
vector[N] x;
vector[N] y;
}
parameters {
real alpha;
// multidimensional: vector[K] beta;
real beta;
real sigma_sqrt;
}
model {
y ~ normal(alpha + beta * x, sigma_sqrt);
}
```
*** =right width:50%
Blocks:
1. required: `data`, `parameters`, `model`
2. optional:
+ `transformed data`,
`transformed parameters`:
"...allow new variables to be declared and then defined through a
sequence of statements."
+ `generated quantities`:
for direct generation (e.g., you need to predict some `y_new` given `x_new`)
--- &twocol_with_width
## First things to learn
$$
y_n=\alpha+\beta x_n+\epsilon_n\quad\mbox{where}\quad\epsilon_n\sim\mathcal{N}(0,\sigma^2)
$$
*** =left width:50%
```r
data {
int N;
// multidimensional: matrix[N,K] x;
vector[N] x;
vector[N] y;
}
parameters {
real alpha;
// multidimensional: vector[K] beta;
real beta;
real sigma_sqrt;
}
model {
y ~ normal(alpha + beta * x, sigma_sqrt);
}
```
*** =right width:50%
Data types:
1. primitive: `int`, `real`
2. vector/matrix: `vector`, `row_vector`, `matrix`
3. array: "any type can be made into an array type by declaring array arguments."
Examples:
`real x[10]; matrix[3,3] m[6,7];`
4. constraints
+ `upper` and `lower`
+ `unit_vector`, `cov_matrix`, ...
--- &tabs
## Compile and do inference
*** class:active id:R-code
```r
library(rstan)
N <- 100; x <- 1:N; alpha <- 50; beta <- 0.2
y <- alpha + beta * x + rnorm(n, mean=0, sd=4)
lr_stan_data <- list(N=N, x=x, y=y)
# stan source code stored in lr_stan_code
lr_fit <- stan(model_code=lr_stan_code, data=lr_stan_data, iter=1000, chains=4)
```
*** id:stan-result
```r
> lr_fit
Inference for Stan model: lr_code.
4 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=2000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha 52.16 0.03 0.79 50.56 51.62 52.18 52.72 53.65 679 1.00
beta 0.17 0.00 0.01 0.14 0.16 0.17 0.17 0.19 688 1.00
sigma_sqrt 3.97 0.01 0.29 3.45 3.77 3.96 4.15 4.59 609 1.00
lp__ -185.67 0.06 1.25 -188.86 -186.29 -185.35 -184.77 -184.26 497 1.01
Samples were drawn using NUTS(diag_e) at Sun Mar 22 22:21:52 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
```
--- &tabs
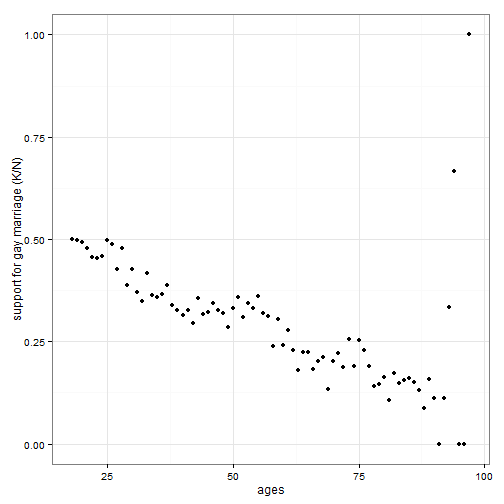
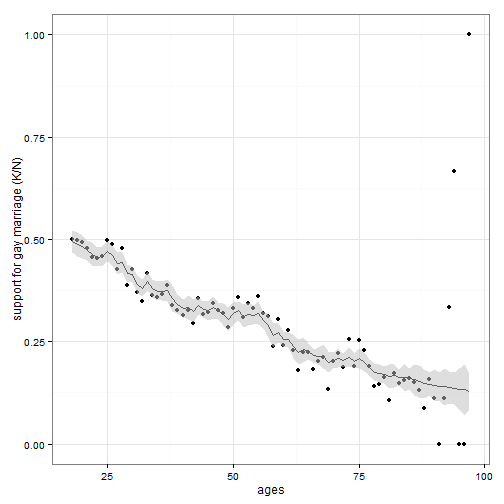
## Example 2: Gaussian process
### Younger Americans are more likely to support the statewide legalization of gay marriage
*** class:active id:data
*** id:gp-result
