Table of Contents
- Introduction to positive irreducible fraction.
- Implementation of irreducible fractions.
- Using irreducible fractions.
- Choosing your integers for fractions
- Instantiating fractions
- Obtaining quotients
- Obtaining all the convergents of a fraction
- Fractions are back insertable
- Computing reduced fractions
- Getting ancestors in the Stern-Brocot tree
- Inverse of a fraction
- Rational approximation of floating-point number
- Standard arithmetic operations '+', '-', '*', '/'
- Author(s) of this documentation:
- Jacques-Olivier Lachaud
Part of the Arithmetic package.
This part of the manual describes how to create and use irreducible fractions. More precisely, several representations of irreducible fractions are provided. They are based on the Stern-Brocot tree structure. With these fractions, amortized constant time operations are provided for computing reduced fractions.
Part of the code is a backport from ImaGene. [65]
Introduction to positive irreducible fraction.
A positive irreducible fraction is a fraction p / q, such that p and q are positive integers and gcd(p, q)=1. The fractions \(\frac{0}{1}\) (zero) and \(\frac{1}{0}\) (infinite) are added for convenience. Standard operations like '+', '-', '*', or '/' can be defined over these fractions: it is a matter of playing with numerators and denominators.
However, these fractions have other properties that are useful in the context of digital geometry, especially in digital straightness. These other properties are related to Euclid algorithm, the Stern-Brocot tree, and simple continued fractions.
Euclid algorithm
The well-known Euclid algorithm is useful to compute the greatest common divisor of two integers p and q. However, its intermediate computations are also useful. Let us play with 8/3 (see IntegerComputer::gcd).
| p | = | u | * | q | + | r |
|---|---|---|---|---|---|---|
| 8 | = | 2 | * | 3 | + | 2 |
| 3 | = | 1 | * | 2 | + | 1 |
| 2 | = | 2 | * | 1 | + | 0 |
| 1 | * | 0 |
At each iteration, p takes the former value of q, q takes the former value of r. The algorithm stops when q is null. Then p is the gcd (1 here).
The values of u are called the quotients of \(\frac{p}{q}\), and are numbered from 0. A unique way to describe \(\frac{p}{q}\) is the sequence \(u_0,u_1,\ldots,u_k\), which is in fact denoted as \([u_0;u_1,\ldots,u_k]\). This sequence characterizes the fraction.
Continued fraction
In fact, one can prove that \(\frac{p}{q}=u_0+\frac{1}{u_1+\frac{1}{\ldots+\frac{1}{u_k}}}\), which is the simple continued fraction of p / q.
The successive fractions \(\frac{p_i}{q_i}=[u_0;u_1,\ldots,u_i]\), for \(k < i\) are called the principal convergents of \(\frac{p}{q}\), and are the best approximations of this fraction for the size of their denominator.
A i-reduced of a continued fraction is its k - i-th convergent. The depth of the fraction is k.
A nice property of convergents with respect to their fraction is that even convergents are smaller than the fraction while odd convergents are greater.
Stern-Brocot tree
Another (but one-to-one) way of seeing irreducible fractions is the Stern-Brocot tree. Place the fractions 0/1 and 1/0 at the top, then for each pair of consecutive fractions \(\frac{p}{q}\) and \(\frac{p'}{q'}\) compute its mediant \(\frac{p+p'}{q+q'}\). The fraction 1/1 appears first, then 1/2 and 2/1, then 1/3, 2/3, 3/2, 3/1, etc.
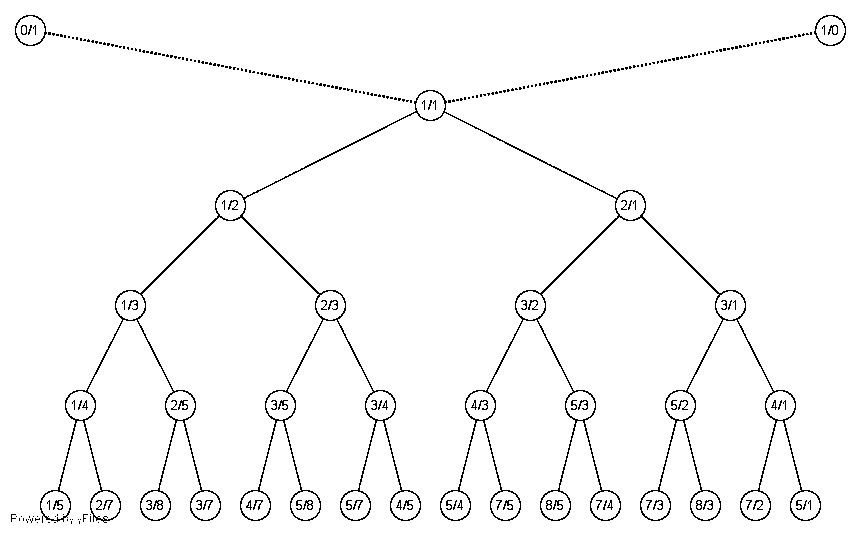
Now the sequence of quotients \(u_0, u_1,\ldots, u_k \) is exactly the sequence of right-then-left moves in the Stern-Brocot tree from node 1/1 when \( u_0 \ge 1 \), except for the last \( u_k \) where there is one less movement. Otherwise, when \( u_0 = 0 \), the sequence \( u_1,\ldots, u_k \) is exactly the sequence of left-then-right moves in the Stern-Brocot tree from node 1/1, except for the last \( u_k \) where there is one less movement.
Looking back at \( 8/3=[2;1,2] \) gives 2 right moves, 1 left move, then 2-1 right move.
Implementation of irreducible fractions.
When playing with irreducible fractions, computing reduced fractions or partial quotients is one of the main task. For instance, splitting formula and Berstel splitting formula is intensively used by algorithms related to digital straightness. Therefore, we must have representations of irreducible fractions which are efficient for that kind of requests.
Several representations have been implemented in the Arithmetic package. Their interface are common (see Irreducible fraction concept) so that a user can choose which representation suits him best.
Irreducible fraction concept
Irreducible fractions are first described abstractly with the concept CPositiveIrreducibleFraction. Note that the following operations are defined for each irreducible fraction.
| Name | Expression | Type requirements | Return type | Precondition | Semantics | Post condition | Complexity |
|---|---|---|---|---|---|---|---|
| Constructor | Fraction( p, q ) | X | creates the fraction p'/q', where p'=p/g, q'=q/g, g=gcd(p,q) | o(p+q) | |||
| numerator | x.p() | Integer | ! x.null() | returns the numerator | O(1) | ||
| denominator | x.q() | Integer | ! x.null() | returns the denominator | O(1) | ||
| quotient | x.u() | Size | ! x.null() | returns the quotient \(u_k\) | O(1) | ||
| depth | x.k() | Size | ! x.null() | returns the depth k | O(1) | ||
| null test | x.null() | bool | returns 'true' if the fraction is null 0/0 (default fraction) | O(1) | |||
| even parity | x.even() | bool | ! x.null() | returns 'true' iff the fraction is even, i.e. k is even | O(1) | ||
| odd parity | x.odd() | bool | ! x.null() | returns 'true' iff the fraction is odd, i.e. k is odd | O(1) | ||
| left descendant | x.left() | X | ! x.null() | returns the left descendant of p/q in the Stern-Brocot tree | O(1) | ||
| right descendant | x.right() | X | ! x.null() | returns the right descendant of p/q in the Stern-Brocot tree | O(1) | ||
| father | x.father() | X | ! x.null() | returns the father of this fraction, ie \([u_0,...,u_k - 1]\) | O(1) | ||
| m-father | x.father(m) | X | ! x.null(), m>=0 | returns the m-father of this fraction, ie \([u_0,...,u_{k-1}, m]\) | O( m) | ||
| previousPartial | x.previousPartial() | X | ! x.null() | returns the previous partial of this fraction, ie \([u_0,...,u_{k-1}]\) | O(1) | ||
| inverse | x.inverse() | X | ! x.null() | returns the inverse of this fraction, ie \([0,u_0,...,u_k]\) if \(u_0 \neq 0 \) or \([u_1,...,u_k]\) otherwise | O(1) | ||
| m-th partial | x.partial(m) | X | ! x.null() | returns the m-th partial of this fraction, ie \([u_0,...,u_m]\) | O(1) | ||
| m-th reduced | x.reduced(m) | X | ! x.null() | returns the m-th reduced of this fraction, equivalently the \(k-m\) partial, ie \([u_0,...,u_{k-m}]\) | O(1) | ||
| splitting formula | x.getSplit(x1, x2) | void | ! x.null() | modifies fractions x1 and x2 such that \( x1 \oplus x2 = x \) | O(1) | ||
| Berstel splitting formula | x.getSplitBerstel(x1, n1, x2, n2) | void | ! x.null() | modifies fractions x1 and x2 and integers n1 and n2 such that \( (x1)^{n1} \oplus (x2)^{n2} = x \) | O(1) | ||
| Continued fraction coefficients | x.getCFrac(quots) | void | modifies the vector quots such that it contains the quotients \(u_0,u_1,...,u_k \) | O(k) | |||
| equality | x.equals(p, q) | bool | returns 'true' iff the fraction is equal to \( p / q \). | O(1) | |||
| less than | x.lessThan(p, q) | bool | returns 'true' iff the fraction is inferior to \( p / q \). | O(1) | |||
| more than | x.moreThan(p, q) | bool | returns 'true' iff the fraction is superior to \( p / q \). | O(1) | |||
| equality == | x == y | bool | returns 'true' iff the fraction is equal to y. | O(1) | |||
| inequality != | x != y | bool | returns 'true' iff the fraction is different from y. | O(1) | |||
| less than < | x < y | bool | returns 'true' iff the fraction is inferior to y. | O(1) | |||
| more than > | x > y | bool | returns 'true' iff the fraction is superior to y. | O(1) | |||
| Next continued fraction | x.pushBack( pair ) | transforms this fraction \([0,u_0,...,u_k]\) into \([0,u_0,...,u_k,m]\), where pair is \((m,k+1)\) | O(m) | ||||
| Next continued fraction | x.push_back( pair ) | transforms this fraction \([0,u_0,...,u_k]\) into \([0,u_0,...,u_k,m]\), where pair is \((m,k+1)\) | O(m) | ||||
| Begin visiting quotients | x.begin() | ConstIterator | returns a forward iterator on the beginning of the sequence of quotients \([u_0,...,u_k]\) | ||||
| End visiting quotients | x.end() | ConstIterator | returns a forward iterator after the end of the sequence of quotients \([u_0,...,u_k]\) |
Inner types are:
- Integer: the type for representing a numerator or a denominator.
- Size: the type for representing partial quotients, i.e. the integers that appear in the continued fractions of p/q. Might be the same as Integer but may be also smaller, since quotients are generally much smaller than the convergent numerators and denominators.
- Value and value_type: the type
std::pair<Size,Size>, useful to create back insertion sequence. - ConstIterator and const_iterator: the type for visiting the quotients of the fraction in sequence. The value of the iterator has type Value.
Notations are:
- X : A type that is a model of CPositiveIrreducibleFraction
- x : object of type X, which is below some fraction written \([u_0, \ldots, u_k]\) as a continued fraction
- x1, x2, y : other objects of type X
- p, q : object of type Integer
- m, n1, n2 : objects of type Size
- quots : an object of type
std::vector<Size> - pair : a object of
std::pair<Size,Size>, here (m,k+1)
Naive approach
A naive approach is to represent an irreducible fraction with three arrays of integers: the numerators (p_i), the denominators (q_i), the quotients (u_i).
However, each time we duplicate the fraction, or each time we compute a reduced fraction, the complexity of the operation is proportional to the depth of the fraction, i.e. in O(k).
We wish to have amortized O(1) complexity for these operations. Therefore, we take another path.
First approach with Stern-Brocot tree
This approach is implemented in the class SternBrocot::Fraction (see also class SternBrocot). We construct on demand parts of the Stern-Brocot tree structure. For instance, if one wish to manipulate fraction 8/3, the following nodes of the tree are computed once and for all: 0/1, 1/0, 1/1, 2/1, 1/2, 3/1, 1/3, 5/2, 2/5, 8/3, 3/8.
Each node in the Stern-Brocot is created once. The node stores information on the irreducible fraction itself (p/q, the partial quotient u, the depth k), but also pointers to ascendants, descendants and inverse in the Stern-Brocot tree. Nodes are constructed on demand, when the user ask for descendant or for a specific fraction.
A fraction SternBrocot::Fraction is just a pointer to the corresponding node in the Stern-Brocot tree. Looking for a reduced partial is just moving from node to node.
You may have a look at testSternBrocot.cpp to see how to use these fractions.
Also inverses and reduced fractions are quickly computed, this representation has two disadvantages:
- it is memory costly: many nodes are created for a fraction. In fact \(2\sum_{i=1..k} u_i\) nodes may be created.
- it is not optimal in terms of complexity. Reduced takes O(1) but computing \([u_0,...,u_{k-1},m]\) takes O(u_k-m).
Second approach with Stern-Brocot tree
This approach is implemented in the class LighterSternBrocot::Fraction (see also class LighterSternBrocot).
There are two main differences with the class SternBrocot. The first one is that inverses are not stored. With this optimization, there are twice less nodes and each node is lighter. The second one lies in the access to the children of a node. Here, a map type M is provided so that a node \( [u_0; u_1, ..., u_n] \) can access its child node \( [u_0; u_1, ..., u_n, k] \) in the time of the operation M::operator[]. This representation is also different from LightSternBrocot in the sense that nodes have only one set of child nodes and that only fractions greater than 1/1 are stored.
In this representation, the fraction 1/1 has depth 0, like 2/1, 3/1, etc. Furthermore, each fraction \( [u_0,...,u_n] \) has an origin which is the fraction \( [u_0,...,u_{n-1},1] \). It is the top extremity of this branch. The origin has depth n-1 since \( [u_0,...,u_{n-1},1] \) = \( [u_0,...,u_{n-1}+1] \). Inversely a k-child of \( [u_0,...,u_n] \), for k >= 2, is the fraction \( [u_0,...,u_n - 1, k] \). A 1-child of a fraction f is itself, except for the fraction 1/0 where its 1-child is 1/1 by convention.
In practice, also this class has supposedly a better complexity than SternBrocot, it is 1% slower for integers smaller than 10^9 and 5% slower for integers smaller than 10^4. Note however that it takes like 7 times less memory (and asymptotically less when the number of computations tends toward infinity).
This class is not to be instantiated, since it is useless to duplicate it. Use static method LighterSternBrocot::fraction or constructor of LighterSternBrocot::Fraction to obtain your fractions.
You may have a look at testLighterSternBrocot.cpp to see how to use these fractions.
Using irreducible fractions.
Choosing your integers for fractions
Available fractions allows you to choose the ultimate precision you wish to have for your fractions.
You have two different integral types for irreducible fractions: TInteger and TSize. The type TInteger defines the integral type for the numerators and the denominators. The type TSize defines the integral type for the quotients and for the depth of the fraction.
- Note
- It is worthy to note that quotients are in general much much smaller than numerators and denominators (except for fractions p/1 or 1/q). You may choose thus a smaller type for TSize (like DGtal::int32_t) than for TInteger (for instance DGtal::int64_t).
You may for instance choose your fractions like:
- Note
- If you wish to instantiate fractions with integral types other than DGtal::int32_t, DGtal::int64_t, DGtal::BigInteger, then you must instantiate the singleton of the class. For instance, add somewhere in your code:
- Note
- In some sense, IntegralType2 should be promotable to IntegralType1. I.e., if t1 is of type IntegralType1 and t2 is of type IntegralType2 then
should be valid.
Instantiating fractions
You may instantiate a fraction directly by giving the numerator p and denominator q. Note that if \( g = gcd(p,q) \neq 1 \), the instantiated fraction is \( \frac{p'}{q'} \) where \( p'=p/g, q'=q/g \). We follow the example convergents.cpp.
First we give the correct includes:
Then the useful types:
The program is given p and q in arguments argv. The fraction is instantiated as follows:
Obtaining quotients
You may visit the quotients of a fraction by using the single-pass iterators provided by the class. A fraction is indeed a model of CSinglePassConstRange. The quotients are computed and stored with the call to begin(). We therefore advise you to store the begin() iterator in a variable. Then, all other operations with iterators (copy, displacement, comparison, dereferenciation) are O(1). We display the quotients of the fraction f as follows.
- Note
- The iterator value is the pair \( (u_i,i) \) where \( 0 \le i \le k \) and k is the depth of the fraction. The type is therefore a
std::pair<Size,Size>. This is done for consistency withpush_backmethod.
Obtaining all the convergents of a fraction
One way of obtaining all the convergents of a fraction is simply to create the fraction progressively by adding quotients one at a time. You may use the methods pushBack or push_back to do so. This can be done as follows:
You may now execute this program to get the quotients and the convergents of a given fraction. We give below several examples:
# A Fibonacci fraction $ ./examples/arithmetic/convergents 21 34 z = [0,1,1,1,1,1,1,2] z_0 = 0 / 1 z_1 = 1 / 1 z_2 = 1 / 2 z_3 = 2 / 3 z_4 = 3 / 5 z_5 = 5 / 8 z_6 = 8 / 13 z_7 = 21 / 34 # Approximations of pi $ ./examples/arithmetic/convergents 103993 33102 z = [3,7,15,1,292] z_0 = 3 / 1 z_1 = 22 / 7 z_2 = 333 / 106 z_3 = 355 / 113 z_4 = 103993 / 33102 # A huge fraction $ ./examples/arithmetic/convergents-biginteger 243224233245235253407096734543059 4324213412343432913758138673203834 z = [0,17,1,3,1,1,12,1,2,33,2,1,1,1,1,49,1,1,1,1,17,34,1,1,304,1,2,1,1,1,2,1,48,1,20,2,3,5,1,1,16,9,1,1,5,1,2,2,7,4,3,1,7,1,1,17,1,1,29,1,12,2,5] z_0 = 0 / 1 z_1 = 1 / 17 z_2 = 1 / 18 z_3 = 4 / 71 z_4 = 5 / 89 ... z_18 = 23610961 / 419772458 ... z_40 = 832739221613445323225 / 14805030169237188131024 ... z_62 = 243224233245235253407096734543059 / 4324213412343432913758138673203834
Fractions are back insertable
Since fractions have a push_back method, you can use std::back_inserter to create a std::back_insert_iterator on your fraction. The code for computing a fraction from its quotients looks like:
- See also
- fraction.cpp
which gives
# More precise approximation of pi $ ./examples/arithmetic/fraction 3 7 15 1 292 1 1 1 2 1 3 1 14 z = 80143857 / 25510582
Computing reduced fractions
If \( z_k \) is a fraction, its 1-reduced is \( z_{k-1} \), its 2-reduced is \( z_{k-2} \) and so on. Reduced are in particular used for computing Bézout vectors, or in splitting formulas. You may use the methods reduced (SternBrocot::Fraction::reduced, LighterSternBrocot::Fraction::reduced) or partial (SternBrocot::Fraction::partial, LighterSternBrocot::Fraction::partial) to obtain them.
Assume f is the fraction \( 103993 / 33102 = [3;7,15,1,292] \). Then
- Note
- The depth of a i-reduced fraction is necessarily \( k - i \). It may be \( k - i - 1 \).
You dispose also of the methods getSplit and getSplitBerstel to obtain directly the decomposition of a fraction into two fractions. Their "mediant sum" gives the fraction itself. Fractions are seen as vectors in this case.
- See also
- SternBrocot::Fraction::getSplit, LighterSternBrocot::Fraction::getSplit, SternBrocot::Fraction::getSplitBerstel, LighterSternBrocot::Fraction::getSplitBerstel.
Getting ancestors in the Stern-Brocot tree
Convergents or partials, and reduced fractions are ancestors of a given fractions. There exist in-between ancestors which are not given by these methods. We list them below with their exact definition, assuming f is \( [u_0,...,u_{k-1},u_k] \):
- i-convergent or i-partial: the fraction \( z_i=[u_0,...,u_i] \). Method
partial, SternBrocot::Fraction::partial, LighterSternBrocot::Fraction::partial. - i-reduced fraction: the fraction \( z_{k-i}=[u_0,...,u_{k-i}] \). Method
reduced, SternBrocot::Fraction::reduced, LighterSternBrocot::Fraction::reduced. - father fraction: the fraction \( z'=[u_0,...,u_{k-1},u_{k} - 1] \). Method
father, SternBrocot::Fraction::father, LighterSternBrocot::Fraction::father. - m-father fraction: the fraction \( z'=[u_0,...,u_{k-1},m] \). Method
father(Size m), SternBrocot::Fraction::father(Size m) const, LighterSternBrocot::Fraction::father(Size m) const. - origin fraction: the fraction \( z'=[u_0,...,u_{k-1},1] \). Method
origin, SternBrocot::Fraction::origin, LighterSternBrocot::Fraction::origin.
Inverse of a fraction
You can get the inverse of a fraction in O(1) with the method inverse (SternBrocot::Fraction::inverse, LighterSternBrocot::Fraction::inverse).
Rational approximation of floating-point number
A simple way to get rational approximation of a "real" number is to use the mapping: \( G(x)=\frac{1}{x- \lfloor x \rfloor} \). The successive \( \lfloor x \rfloor \) gives the successive quotients of the rational approximation. You may have a look at example approximation.cpp.
Standard arithmetic operations '+', '-', '*', '/'
There are not implemented yet and continued fractions are not the best representation for doing them. Here, you must use numerators and denominators to perform computations with these fractions.