 |
CMSIS-DSP
Verison 1.1.0
CMSIS DSP Software Library
|
 |
CMSIS-DSP
Verison 1.1.0
CMSIS DSP Software Library
|
Functions | |
| arm_status | arm_mat_mult_f32 (const arm_matrix_instance_f32 *pSrcA, const arm_matrix_instance_f32 *pSrcB, arm_matrix_instance_f32 *pDst) |
| Floating-point matrix multiplication. | |
| arm_status | arm_mat_mult_fast_q15 (const arm_matrix_instance_q15 *pSrcA, const arm_matrix_instance_q15 *pSrcB, arm_matrix_instance_q15 *pDst, q15_t *pState) |
| Q15 matrix multiplication (fast variant) for Cortex-M3 and Cortex-M4. | |
| arm_status | arm_mat_mult_fast_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_instance_q31 *pSrcB, arm_matrix_instance_q31 *pDst) |
| Q31 matrix multiplication (fast variant) for Cortex-M3 and Cortex-M4. | |
| arm_status | arm_mat_mult_q15 (const arm_matrix_instance_q15 *pSrcA, const arm_matrix_instance_q15 *pSrcB, arm_matrix_instance_q15 *pDst, q15_t *pState) |
| Q15 matrix multiplication. | |
| arm_status | arm_mat_mult_q31 (const arm_matrix_instance_q31 *pSrcA, const arm_matrix_instance_q31 *pSrcB, arm_matrix_instance_q31 *pDst) |
| Q31 matrix multiplication. | |
Multiplies two matrices.
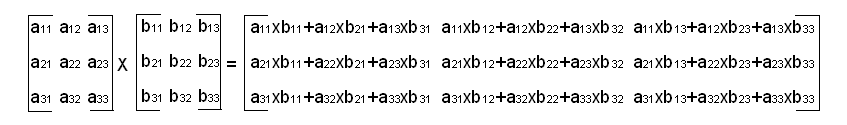
Matrix multiplication is only defined if the number of columns of the first matrix equals the number of rows of the second matrix. Multiplying an M x N matrix with an N x P matrix results in an M x P matrix. When matrix size checking is enabled, the functions check: (1) that the inner dimensions of pSrcA and pSrcB are equal; and (2) that the size of the output matrix equals the outer dimensions of pSrcA and pSrcB.
| arm_status arm_mat_mult_f32 | ( | const arm_matrix_instance_f32 * | pSrcA, |
| const arm_matrix_instance_f32 * | pSrcB, | ||
| arm_matrix_instance_f32 * | pDst | ||
| ) |
| [in] | *pSrcA | points to the first input matrix structure |
| [in] | *pSrcB | points to the second input matrix structure |
| [out] | *pDst | points to output matrix structure |
ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking. References ARM_MATH_SIZE_MISMATCH, ARM_MATH_SUCCESS, arm_matrix_instance_f32::numCols, arm_matrix_instance_f32::numRows, arm_matrix_instance_f32::pData, and status.
Referenced by main().
| arm_status arm_mat_mult_fast_q15 | ( | const arm_matrix_instance_q15 * | pSrcA, |
| const arm_matrix_instance_q15 * | pSrcB, | ||
| arm_matrix_instance_q15 * | pDst, | ||
| q15_t * | pState | ||
| ) |
| [in] | *pSrcA | points to the first input matrix structure |
| [in] | *pSrcB | points to the second input matrix structure |
| [out] | *pDst | points to output matrix structure |
| [in] | *pState | points to the array for storing intermediate results |
ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking.Scaling and Overflow Behavior:
arm_mat_mult_q15() for a slower implementation of this function which uses 64-bit accumulation to provide higher precision. References __SIMD32, ARM_MATH_SIZE_MISMATCH, ARM_MATH_SUCCESS, arm_matrix_instance_q15::numCols, arm_matrix_instance_q15::numRows, arm_matrix_instance_q15::pData, and status.
| arm_status arm_mat_mult_fast_q31 | ( | const arm_matrix_instance_q31 * | pSrcA, |
| const arm_matrix_instance_q31 * | pSrcB, | ||
| arm_matrix_instance_q31 * | pDst | ||
| ) |
| [in] | *pSrcA | points to the first input matrix structure |
| [in] | *pSrcB | points to the second input matrix structure |
| [out] | *pDst | points to output matrix structure |
ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking.Scaling and Overflow Behavior:
arm_mat_mult_q31() for a slower implementation of this function which uses 64-bit accumulation to provide higher precision. References ARM_MATH_SIZE_MISMATCH, ARM_MATH_SUCCESS, arm_matrix_instance_q31::numCols, arm_matrix_instance_q31::numRows, arm_matrix_instance_q31::pData, and status.
| arm_status arm_mat_mult_q15 | ( | const arm_matrix_instance_q15 * | pSrcA, |
| const arm_matrix_instance_q15 * | pSrcB, | ||
| arm_matrix_instance_q15 * | pDst, | ||
| q15_t * | pState | ||
| ) |
| [in] | *pSrcA | points to the first input matrix structure |
| [in] | *pSrcB | points to the second input matrix structure |
| [out] | *pDst | points to output matrix structure |
| [in] | *pState | points to the array for storing intermediate results |
ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking.Scaling and Overflow Behavior:
arm_mat_mult_fast_q15() for a faster but less precise version of this function for Cortex-M3 and Cortex-M4. References __SIMD32, ARM_MATH_SIZE_MISMATCH, ARM_MATH_SUCCESS, arm_matrix_instance_q15::numCols, arm_matrix_instance_q15::numRows, arm_matrix_instance_q15::pData, and status.
| arm_status arm_mat_mult_q31 | ( | const arm_matrix_instance_q31 * | pSrcA, |
| const arm_matrix_instance_q31 * | pSrcB, | ||
| arm_matrix_instance_q31 * | pDst | ||
| ) |
| [in] | *pSrcA | points to the first input matrix structure |
| [in] | *pSrcB | points to the second input matrix structure |
| [out] | *pDst | points to output matrix structure |
ARM_MATH_SIZE_MISMATCH or ARM_MATH_SUCCESS based on the outcome of size checking.Scaling and Overflow Behavior:
arm_mat_mult_fast_q31() for a faster but less precise implementation of this function for Cortex-M3 and Cortex-M4. References ARM_MATH_SIZE_MISMATCH, ARM_MATH_SUCCESS, arm_matrix_instance_q31::numCols, arm_matrix_instance_q31::numRows, arm_matrix_instance_q31::pData, and status.