Randomized Algorithms

The worst case: the employment agency sets us up, and sends us candidates in worst-to-best order, so we hire every single one.

We use probability theory to find an average-case running time.

Probability basics.

We best the employment agency by shuffling their list of candidates, and seeing them in random order: we get a much lower average cost, as we shall prove.

When we randomize the algorithm we speak of an expected running time.

If X is an indicator variable for A, then

Exp[X] = Prob[X=1] = Prob[A happens] .

This easily follows from the definition:

Exp[X] = 1 * Prob[X=1] + 0 * Prob[X=0] = Prob[X=1] = Prob[A happens]

Example:

We throw a fair die 100 times What is the expected number of times we get 1 or 6?

Let X_i be the indicator variable of the event "in i^th throw we got 1 or 6". Then notice that the number of times we get 1 or 6 is:



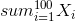
and we want the expectation of this. By linearity of expectations:



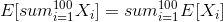
and by the indicator variable properties:



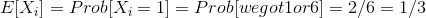
To summarize:



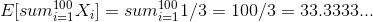
So we expect to get 1 or 6 about 33.33 times.

The first candidate we always hire. The second candidate will be better half the time, the third one will be better than the first two one third of the time, and so on, so we get the series:
1 + 1/2 + 1/3 + 1/4...
(Or y = 1/x.)

So:






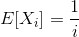
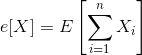
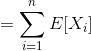
(By linearity of expectations.)





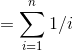
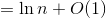
Why is the last step true? Video here.

Basically, the anti-derivative of 1/x is ln x:

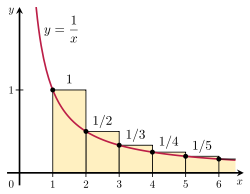
And what is that O(1) about?
It means that the sum - ln n is always bounded by a constant.

Probability that two people have the same birthday: 1/365

To generalize the problem, and see it doesn't just apply to birthdays, let's call the # of days in the year n.

Let's set up an indicator random variable so that X_ij is: 1 if persons i and j have the same birthday.
0 if the don't.

Let X count the number of pairs of people who have the same birthday.

k is the number of people in the room.



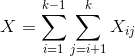
Take expectations and apply linearity of expectation:









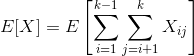
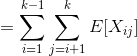
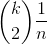
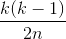
So we are looking at Θ(n^1/2), asymptotically speaking.