Exercises
Table 4: Dataset for building a linear regression model
| ID | \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|---|
| \(1\) | \(-0.15\) | \(-0.48\) | \(0.46\) |
| \(2\) | \(-0.72\) | \(-0.54\) | \(-0.37\) |
| \(3\) | \(1.36\) | \(-0.91\) | \(-0.27\) |
| \(4\) | \(0.61\) | \(1.59\) | \(1.35\) |
| \(5\) | \(-1.11\) | \(0.34\) | \(-0.11\) |
Here let’s consider the dataset in Table 4. Let’s build a linear regression model, i.e., \[ y = \beta_{0}+\beta_{1}x_1 +\beta_{2}x_2 + \epsilon, \] and \[ \epsilon \sim N\left(0, \sigma_{\varepsilon}^{2}\right). \] and calculate the regression parameters \(\beta_{0},\beta_{1},\beta_{2}\) manually.
Follow up the data on Q1. Use the R pipeline to build the linear regression model. Compare the result from R and the result by your manual calculation.
Read the following output in R.
## Call:
## lm(formula = y ~ ., data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.239169 -0.065621 0.005689 0.064270 0.310456
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.009124 0.010473 0.871 0.386
## x1 1.008084 0.008696 115.926 <2e-16 ***
## x2 0.494473 0.009130 54.159 <2e-16 ***
## x3 0.012988 0.010055 1.292 0.200
## x4 -0.002329 0.009422 -0.247 0.805
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1011 on 95 degrees of freedom
## Multiple R-squared: 0.9942, Adjusted R-squared: 0.994
## F-statistic: 4079 on 4 and 95 DF, p-value: < 2.2e-16(a) Write the fitted regression model. (b) Identify the significant variables. (c) What is the R-squared of this model? Does the model fit the data well? (d) What would you recommend as the next step in data analysis?
Consider the dataset in Table 5. Build a decision tree model by manual calculation. To simplify the process, let’s only try three alternatives for the splits: \(x_1\geq0.59\), \(x_1\geq0.37\), and \(x_2\geq0.35\).
Table 5: Dataset for building a decision tree
| ID | \(x_1\) | \(x_2\) | \(y\) |
|---|---|---|---|
| \(1\) | \(0.22\) | \(0.38\) | No |
| \(2\) | \(0.58\) | \(0.32\) | Yes |
| \(3\) | \(0.57\) | \(0.28\) | Yes |
| \(4\) | \(0.41\) | \(0.43\) | Yes |
| \(5\) | \(0.6\) | \(0.29\) | No |
| \(6\) | \(0.12\) | \(0.32\) | Yes |
| \(7\) | \(0.25\) | \(0.32\) | Yes |
| \(8\) | \(0.32\) | \(0.38\) | No |
Follow up on the dataset in Q5. Use the R pipeline for building a decision tree model. Compare the result from R and the result by your manual calculation.
Use the
mtcarsdataset in R, select the variablempgas the outcome variable and other variables as predictors, run the R pipeline for linear regression, and summarize your findings.Use the
mtcarsdataset in R, select the variablempgas the outcome variable and other variables as predictors, run the R pipeline for decision tree, and summarize your findings. Another dataset is to use theirisdataset, select the variableSpeciesas the outcome variable (i.e., to build a classification tree).Design a simulated experiment to evaluate the effectiveness of the
lm()in R. For instance, you can simulate \(100\) samples from a linear regression model with \(2\) variables, \[ y = \beta_{1}x_1 +\beta_{2}x_2 + \epsilon, \] where \(\beta_{1} = 1\), \(\beta_{2} = 1\), and \[ \epsilon \sim N\left(0, 1\right). \] You can simulate \(x_1\) and \(x_2\) using the standard normal distribution \(N\left(0, 1\right)\). Runlm()on the simulated data, and see how close the fitted model is with the true model.Follow up on the experiment in Q9. Let’s add two more variables \(x_3\) and \(x_4\) into the dataset but still generate \(100\) samples from a linear regression model from the same underlying model \[ y = \beta_{1}x_1 +\beta_{2}x_2 + \epsilon, \] where \(\beta_{1} = 1\), \(\beta_{2} = 1\), and \[ \epsilon \sim N\left(0, 1\right). \] In other words, \(x_3\) and \(x_4\) are insignificant variables. You can simulate \(x_1\) to \(x_4\) using the standard normal distribution \(N\left(0, 1\right)\). Run
lm()on the simulated data, and see how close the fitted model is with the true model.
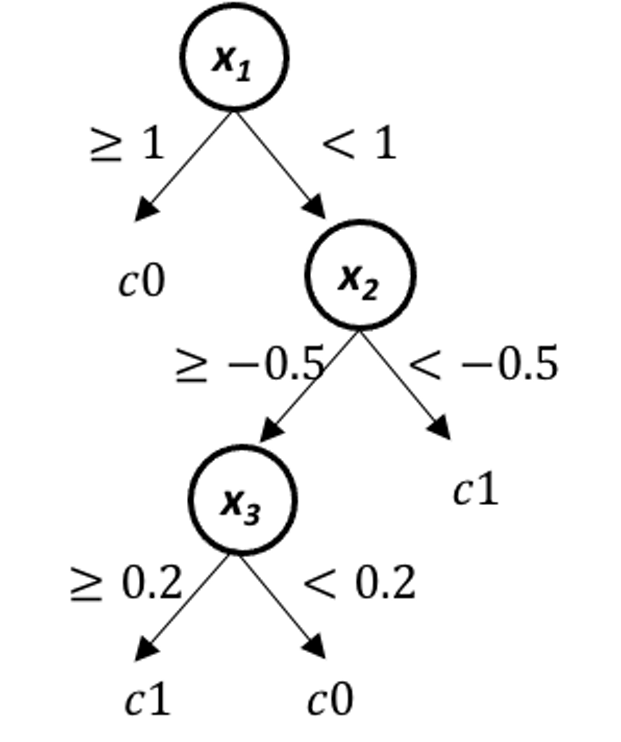 Figure 24: The true model for simulation experiment in Q12
Figure 24: The true model for simulation experiment in Q12
Follow up on the experiment in Q10. Run
rpart()on the simulated data, and see how close the fitted model is with the true model.Design a simulated experiment to evaluate the effectiveness of the
rpart()in R packagerpart. For instance, you can simulate \(100\) samples from a tree model as shown in Figure 24, runrpart()on the simulated data, and see how close the fitted model is with the true model.