Quantum Mechanical Puzzles of Supervenience¶
The story goes that quantum mechanics has two seemingly incompatible rules: on the one hand, unitary evolution governed by the Schrodinger equation for isolated systems; and on the other hand, the non-unitary collapse of the quantum state at random into an eigenspace of an observable upon measurement, with probabilities given by the amplitudes squared of the state vector expanded in the observerable's basis. Much of the interpretation of quantum mechanics centers around trying to reconcile these two rules. Part of the difficulty, however, is that we remain deeply ignorant about the exact relationship between our subjective experience and the world described by physics. It stands to reason that our “mental states” have some intimate relationship to our “brain states”: in the lingo of philosophers, in some way our mental life “supervenes” on the physics of our bodies. But if we take seriously the idea that quantum mechanics describes all of physical reality, from electrons to people, where does this leave us as regards supervenience? We’ll largely follow (plagiarize) the lively account of David Z Albert in his book “Quantum Mechanics and Experience,” and explore the (in every case, unsatisfying!) implications for the mind/body relation in several interpretations of QM: the Copenhagen interpretation, the “bare theory” (no collapse), Many Worlds, Many Minds, and Bohmian Mechanics. Get ready for some thought experiments!
Von Neumann¶
We should start with Von Neumann's account of the situation in his famous Mathematical Foundations of Quantum Mechanics. Adapting his discussion somewhat, we could say the following:
Suppose we have a qubit and we want to measure it, so we send it through a Stern-Gerlach apparatus. Initially, the qubit is in some state $\mid \psi \rangle = \begin{pmatrix}\alpha \\\beta \end{pmatrix}$, quantized along the $Z$ axis, and suppose the magnetic field in the apparatus is oriented along the $Z$ axis. So by the collapse rule, we predict that we'll get $\mid \uparrow \rangle$ with probability $\mid \alpha \mid^2$ and $\mid \downarrow \rangle$ with probability $\mid \beta \mid^2$, and that's indeed what we find.
But suppose we want to model this situation more carefully. In fact, by the dynamics of the apparatus, the qubit, which is the spin of some particle, becomes entangled with its position, leading to a state like: $$ \alpha\mid \uparrow \Uparrow \rangle + \beta \mid \downarrow \Downarrow \rangle$$, where the latter arrows represent two different position states. After all, if we send the qubit through the apparatus, it leaves by one of two paths, an upper path and a lower path, and if it takes the upper path, then the qubit is in the $\mid \uparrow \rangle$ state, and if it takes the lower path, then it's in the $\mid \downarrow \rangle$ state, which we can confirm by sending it through another Stern-Gerlach: if the spin came out the down port of the first, it always comes out the down port of the second, and so on. Moreover, we find that the qubit takes the upper or lower path with the same probabilities as before, $\mid \alpha \mid^2$ and $\mid \beta \mid^2$, and the spin is always correlated with the path by entanglement.
But we could go on. After all, we don't necessarily measure the position directly. In either case, the qubit causes a chemical reaction in the photographic plate, two different ones depending on whether it took the up or down path. If we include that in the unitary picture, we end up in a state like: $$ \alpha\mid \uparrow \Uparrow \upharpoonleft \rangle + \beta \mid \downarrow \Downarrow \downharpoonleft \rangle$$. The probabilities are the same as before, as are the correlations. But then again, we don't measure the photographic plate directly, but observe photons that bounce off it, two possible sets of photons corresponding to the two possibilities. Including them in the picture, we end up in a state like $$ \alpha\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \rangle + \beta \mid \downarrow \Downarrow \downharpoonleft \downharpoonright \rangle$$. But of course, the photons have to impinge on our eyes, which end up in two different possible states in each case, so we end up with: $$ \alpha\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \circlearrowleft \rangle + \beta \mid \downarrow \Downarrow \downharpoonleft \downharpoonright \circlearrowright \rangle$$. And then the two different states of our eyes lead to two possible sets of neurons firing in the optic nerve: $$ \alpha\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \circlearrowleft \curvearrowleft \rangle + \beta \mid \downarrow \Downarrow \downharpoonleft \downharpoonright \circlearrowright \curvearrowright \rangle$$. And those two possible sets of neurons firing lead to two possibilities for yet more neurons firing deeper in the brain: $$ \alpha\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \circlearrowleft \curvearrowleft \looparrowleft \rangle + \beta \mid \downarrow \Downarrow \downharpoonleft \downharpoonright \circlearrowright \curvearrowright \looparrowright \rangle$$, and then two more possibilities for yet more neurons: $$ \alpha\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \circlearrowleft \curvearrowleft \looparrowleft \Lsh \dots \rangle + \beta \mid \downarrow \Downarrow \downharpoonleft \downharpoonright \circlearrowright \curvearrowright \looparrowright \Rsh \dots \rangle$$, until... what?
Well, the buck stops somewhere, obviously, says Von Neumann, and it stops when we ourselves have a conscious perception of one outcome or another. And then when we go inspect the state of the spin, we find it agrees with our perception, supposing all our apparatuses are functioning as desired.
And yet, what's interesting about this, Von Neumann notes, is that having fixed the story from the beginning (we send a spin through the apparatus) to the end (we consciously apprehend the outcome of the experiment), it's actually a matter of complete indifference, physically speaking, "when" or "where" we regard the collapse as taking place. This is a natural consequence of the linear evolution.
We could say: Oh, the collapse took place when the qubit went through the magnetic field: it ended up in the $\mid \uparrow \rangle$ state, and so the unitary evolution after that led to: $\mid \uparrow \Uparrow \rangle$, and then $\mid \uparrow \Uparrow \upharpoonleft \rangle$, and then $\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \rangle$, and then $\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \circlearrowleft \rangle$, and then $\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \circlearrowleft \curvearrowleft \rangle$, and then $\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \circlearrowleft \curvearrowleft \looparrowleft \rangle$, and then $\mid \uparrow \Uparrow \upharpoonleft \upharpoonright \circlearrowleft \curvearrowleft \looparrowleft \Lsh \rangle$, and so on, until we had the perception of the one outcome. (And the reverse if the qubit had ended up $\mid \downarrow \rangle$.)
Or we could say: Oh, the collapse took place when the qubit hit the photographic plane--before that, it was in a superposition--and then it collapsed to one outcome or another, and then unitary evolution carried that outcome to us. Or we could say: Oh, the collapse took place when the photons bounced off the plate, or when they entered our eye, or when one neuron fired or another. In any case, we get exactly the same results with the same probability, because of the linear evolution and the fact that each step of the way, the unitary evolution is an entangling one, so that the collapse of one is the collapse of them all.
So Von Neumann says, it's completely arbitrary where we imagine the collapse taking place, and he takes this to be a feature of quantum mechanics. In other words, Von Neumann subscribes to a view of the mind/body relationship known as psychophysical parallelism, which says that insofar as the workings of the mind can be known, we situate the mind as a physical system in the physical world and that is what constitutes an explanation of what we perceive. Insofar as we care to analyze the workings of the mind, we justifiably appeal to explanations like: this neuron fired, as opposed to that one. But metaphysically, there is no actual dividing line between self and world, between mind and matter: where we make the "cut" between them is completely arbitrary. Originally, he'd say, we were treating the qubit quantum mechically, while treating the position of the qubit, the photographic plate, the photons, the eyeball, the neurons, as "observer." Then we moved the cut, and treated the qubit and the position quantum mechnically, while treating the rest as "observer." Then we moved the cut again, and treated the qubit, the position, and the photographic plate quantum mechnically, while treating the rest as "observer." That this cut can be pushed arbitrarily far back into the body of the actual observer, he says, is the content of the principle of psycho-physical parallelism.
In other words, a cut between observer and observed must always be made in any observation, but the physics is completely indifferent to where the cut is made. We can always trace the chain of entanglement deeper and deeper into our actual physiology, but: a) where the cut between observer and observed is placed precisely makes no difference as regards the physics c) the actual perception of an outcome is an irriducible, subjective, "extra-observational fact"--since what is directly perceived is not "some neurons firing in a brain," which is a description of an external state of affairs, but what is perceived is directly one outcome or another in experience. A perception in itself can't be "placed" somewhere in the physical world, but instead stands outside the physical world as such, as something directly given, which events in the world, like neurons firing, precisely serves to explain. And to the extent that we can explain more, we identify yet more quantum states in the chain of entanglement, yet more neurons firing upon neurons, governed by yet more physics. In other words, any further explanation reveals yet more physics. As far as you care to go, like a limit procedure converging on a real number, there's more physics: but the limiting point, is in fact, something that can't be placed in the physical world as such: a definite perception by you.
Of course, two caveats must be mentioned.
On the one hand, it matters that we fixed the story from beginning to end. For example, suppose our qubit started pointing up in the $X$ direction, e.g., $\mid \rightarrow \rangle = \frac{1}{\sqrt{2}} (\mid \uparrow \rangle + \mid \downarrow \rangle)$. We send it through a Stern-Gerlach oriented in the $Z$ direction, which means that if we put a photographic plate beyond it, we get a blip either above or below half the time, the former correlated with the spin being $\mid \uparrow \rangle$ and the latter with the spin being $\mid \downarrow \rangle$. And to dramatize this, if we were to place $X$ Stern-Gelachs along the upper path and the lower path, then whichever path is selected, we'd get $\mid \rightarrow \rangle$ or $\mid \leftarrow \rangle$ each half the time, since $\mid \uparrow \rangle = \frac{1}{\sqrt{2}}(\mid \rightarrow \rangle + \mid \leftarrow \rangle)$ and $\mid \downarrow \rangle = \frac{1}{\sqrt{2}}(\mid \rightarrow \rangle - \mid \leftarrow \rangle)$. But we could imagine a different set up: we could cleverly arrange things so that the upper and lower paths of the first SG are made to converge on each other, and then direct the combined "beam" into an $X$ Stern-Gerlach, after which the position is registered. What happens? The first SG separates out the two components of the spin in the $Z$ basis, entangling them with position, but then the positions are brought together, restoring the original state, so that 100% of the time, the qubit comes out of the $X$ Stern-Gerlach in its original state: $\mid \rightarrow \rangle$. In this case, we couldn't regard the collapse as having happened, for example, when the spin passes through the first SG, since even if the two components are "separated" there, they are later recombined. In other words, if we said the spin collapsed, say, to $\mid \uparrow \rangle$ in the first SG, then that's the state that would go through the $X$ apparatus, leading to $\mid \rightarrow \rangle$ or $\mid \leftarrow \rangle$, each half the time, which is not what happens. In other words, if in your story, "measurements" are "undone" before outcomes are finally registered in perception, you can't imagine the collapse taking place until after that point.
Which leads us to the next issue, which is this: Suppose these experiments with the qubit, including yourself as experimenter, take place in a closed box. For someone outside the box, they'd of course describe what's taking place within as completely unitary evolution, things getting entangled with other things, including you. Presumably, you, within the box, had your perception of a definite outcome, and yet: suppose an exceedingly clever person comes along and instigates precisely the inverse unitary evolution within the box which will reverse not only the experiment, but even your recording the outcome in memory, and so forth. Everything in the box would have to end up exactly where it started, with the spin in the $\mid \rightarrow \rangle$ state. But if we take seriously the idea that the state collapsed to $\mid \uparrow \rangle$, say, for you within the box, then when we reverse the time evolution, we would end up in the wrong state. Only if both possibilities remain in parallel, $\uparrow$ and $\downarrow$, can the unitary description from outside remain consistent. Of course, since your memory will have been wiped, there is perhaps no contradiction.
By the same token, however, we can explain the usual stability of outcomes by appealing to the very difficulty of "reversing time" after a quantum mechanical system interacts with any reasonably large macroscopic apparatus, open to interaction with the environment.
Many Worlds¶
I think we can agree that Von Neumann's view is admirably subtle, and unfortunately, it's often caricatured as the view that "consciousness causes collapse." That idea was more completely explored by Wigner as well as by London and Bauer. The difficulty, of course, comes when one regards the collapse as objectively taking place due to consciousness. After all, we've seen that insofar as unitary evolution can always be undone, this view is untenable. Moreover, it leads to deep and uncomfortable questions about what gets to be regarded as "conscious" and so able to trigger such collapses. The view that one's own consciousness causes collapses in one's personal world is perhaps workable in the sense that all one's later perceptions will be consistent with this (allowing that memories can be erased, and so forth), but strikes one as undesirably solipsistic.
Indeed: Suppose you measure a spin, and perceive a definite outcome at random. I'd, however, regard this as a unitary, entangling interaction between you and the spin. If I later ask you what you got, and you tell me, I'll find that the answer is always random, and the answer you give is always consistent with my own measurements of the spin. So from my point of view, everything's fine. You measured the spin, and when I asked you, and compared what you said to the spin, the two of you agreed. And yet, from my point of view, before I asked you, you and the spin were in an entangled superposition. Presumably, you had a definite experience of an outcome, but I can't regard a collapse as having taken place yet, since if I imagine that you and the spin have collapsed, then unitarily undoing the whole interaction, won't lead to the original starting place. Therefore, I have to imagine the collapse taking place when I make my measurement. Hence the solipsism: from my point of view, I get to have a definite perception, but everyone else remains in entangled superposition.
On the other hand, if I allow that you too experienced a definite outcome, I have no reason to believe you experienced the same outcome that I got, even though everything from my point of view is consistent: you measured the spin, and I always find that you and the spin agree on the answer.
So many people bite the bullet and say: Okay, so maybe the problem is the idea that only one outcome is realized. Maybe all of them are realized by somebody! And that leads us to "Many Worlds."
We're trying to interpret an entangled superposition like $\alpha \mid \uparrow \uparrow \rangle + \beta \mid \downarrow \downarrow \rangle$, where the first system represents a spin and the second system the experimenter's memory registering the outcome. Maybe we can have our cake and eat it too. Suppose there are in fact two "worlds": one world with a version of the experimenter that perceives $\uparrow$ and finds the spin in the corresponding $\uparrow$ state, and one world with the experimenter perceiving $\downarrow$ with the spin in the corresponding $\downarrow$ state. When a third person gets involved, as above, they too find themselves in one world or another, with a friend and a spin that agrees with them, but of course: there is another world corresponding to the opposite outcomes. This would explain the appearence of a definite outcome at all: the entangled superposition doesn't describe one world with two systems in "hazy" states, but instead two worlds, each definite in their own right.
Of course, these are not the parallel worlds of science fiction. Consider the interpretation of the double slit experiment in this context. We only ever measure a single electron to be one place or another. And yet, when we give the electron the opportunity to pass through a double slit, it takes both routes. Here are two "worlds," as it were, but they are most certainly not parallel (or orthogonal, as it were)-- the wavefunction passing through both slits, of course, interferes with itself, leading to a measurable interference pattern in the position of the electron detectable after many runs of the experiment. So here are two possible worlds whose existence is manifest precisely because they interfere with each other. On the other hand, adding into the mix a detector sensitive to which slit the electron goes through causes the interference pattern to dissapear. Before we had the state $\mid A \rangle + \mid B \rangle$, where $\mid A \rangle$ is the wavefunction of the electron having gone through the one slit, and $\mid B \rangle$ is the wave function of the electron having gone through the other slit. These vectors are not necessarily orthogonal to each other, so adding them up leads to interference. On the other hand, after the detector is added, we end up in the state $\mid A \rangle \mid \uparrow \rangle + \mid B \rangle \mid\downarrow \rangle$. Since $\mid \uparrow \rangle$ and $\mid \downarrow \rangle$ are orthogonal, therefore $\mid A \rangle \mid \uparrow \rangle$ and $ \mid B \rangle \mid\downarrow \rangle$ are orthogonal, and so can be added together without interference: this is "decoherence." The two wave functions $\mid A \rangle$ and $\mid B \rangle$ are kept on separate "branches" by the two orthogonal detector states $\mid \uparrow \rangle$ and $\mid \downarrow \rangle$. And now, they act somewhat like parallel worlds in the traditional sense, evolving side by side, without interfering with each other. Each world is consistent: in one world, the detector reads $\uparrow$ and the electron is detected along the upper path; in the other world, the detector reads $\downarrow$ and the electron is detected along the lower path. In each case, it's as if the electron took one path or the other as we'd normally expect from a single particle. On the other hand, if one should undo the entangling operation with the detector, before actually measuring the position of the electron, then the interference pattern will reappear: the branches will have rejoined, and the two worlds will interfere with each other again. So this is what makes "Many Worlds" different from "parallel universes."
What's appealing about Many Worlds is that it seems to remove the observer from the equation. We just have quantum mechanical systems, evolving unitarily, getting entangled, branching off and rejoining: and each branch constitutes a perfectly definite history of outcomes. Collapse is an illusion cause by the fact that quantum mechanics applies to us as well as electrons, and we only experience the one branch we happen to find ourselves in. This is of course at the cost of allowing that the other branches have other versions of us that experience the other possible outcomes.
There are two difficulties to this point of view. The first is that, if all branches are equally realized, then what to make of the specific probabilities attached to each branch? If it's literally true that all the possibilities really occur, then shouldn't we assign equal probability to finding ourselves in any of them?
This difficulty can be somewhat, but not entirely perhaps, vitiated by "fine graining." Suppose I have two pebbles red and blue, and I show them to you $\frac{1}{3}$ of the time and $\frac{2}{3}$ of the time respectively. I could imagine an "equivalent" situation where I have three pebbles, one red and two blue, and I show them to you each $\frac{1}{3}$ of the time. In both cases, the probability for seeing red or blue are the same. One can try to apply this kind of reasoning in the quantum case, imagining that a qubit in an equal superposition like $\sqrt{\frac{a}{n}}\mid \uparrow \rangle + \sqrt{\frac{b}{n}}\mid \uparrow \rangle$ gets entangled with an apparatus with many states, in just such a way that an even superposition of $a$ basis states of the apparatus are entangled with $\mid \uparrow \rangle$ and an even superposition of $b$ basis states are entangled with $\downarrow$ so that we end up with a state like:
$$ \sqrt{\frac{a}{n}}\mid \uparrow \rangle_{S} \frac{1}{\sqrt{a}}\sum_{i=0}^{a}\mid i \rangle_{A} + \sqrt{\frac{b}{n}}\mid \downarrow \rangle_{S} \frac{1}{\sqrt{b}}\sum_{i=a}^{b}\mid i \rangle_{A}$$Or:
$$ \frac{1}{\sqrt{n}}\Bigg{(}\sum_{i=0}^{a}\mid \uparrow \rangle_{S} \mid i \rangle_{A} + \sum_{i=a}^{b}\mid \downarrow \rangle_{S}\mid i \rangle_{A} \Bigg{)} $$In this way, we can convert unequal branches into equal branches. This is Zurek's trick in the context of his envariance argument for quantum probabilities. Thus we can imagine you'd find yourself in any of these branches with equal probability, but in $\frac{a}{n}$ of the branches the spin is $\uparrow$ and in $\frac{b}{n}$ of the branches the spin is $\downarrow$, and thus we have our probabilities. On the other hand, whether this kind of construction can adequately account for all measurement interactions that lead to probabilities in quantum mechanics is an open question. There is also the issue that if all branches are realized, then in some unlucky branches it will necessarily be the case that, say, all spin measurements happened to give $\uparrow$, which would make quantum mechanics impossible to discover in such a world!
Another riposte against Many Worlds is the preferred basis problem. After all, suppose I have the state $\frac{1}{\sqrt{2}} (\mid \uparrow \uparrow \rangle + \mid \downarrow \downarrow \rangle)$, where the first system represents the spin, and the second system represents the experimenter's memory. I want to say these are two worlds, one world where the spin is $\uparrow$ and the experimenter perceives $\uparrow$ and another world where the spin $\downarrow$ and the experimenter perceives $\downarrow$. But what's stopping me from rewriting the state in a different basis, for example in terms of $X$ eigenstates. I'd get: $\frac{1}{\sqrt{2}} (\mid \rightarrow \rightarrow \rangle + \mid \leftarrow \leftarrow \rangle)$. Which looks like a state where there are two possible worlds, one in which the spin is $\rightarrow$ and the experimenter perceives $\rightarrow$ and another world in which the spin is $\leftarrow$ and the experimenter perceives $\leftarrow$.
Worse, suppose I'm in a general superposition $\alpha \mid \uparrow \uparrow \rangle + \beta \mid \downarrow \downarrow \rangle$. Recalling that $\mid \uparrow \rangle = \frac{1}{\sqrt{2}}(\mid \rightarrow \rangle + \mid \leftarrow \rangle)$ and $\mid \mid \downarrow \rangle = \frac{1}{\sqrt{2}}(\mid \rightarrow \rangle - \mid \leftarrow \rangle)$:
$$ \alpha \mid \uparrow \uparrow \rangle + \beta \mid \downarrow \downarrow \rangle = \alpha\Bigg{(} \frac{1}{\sqrt{2}} \Big{\lbrack} \mid \rightarrow \rangle + \mid \leftarrow \rangle \Big{\rbrack} \frac{1}{\sqrt{2}} \Big{\lbrack} \mid \rightarrow \rangle + \mid \leftarrow \rangle \Big{\rbrack} \Bigg{)} + \beta\Bigg{(}\frac{1}{\sqrt{2}} \Big{\lbrack} \mid \rightarrow \rangle - \mid \leftarrow \rangle \Big{\rbrack} \frac{1}{\sqrt{2}} \Big{\lbrack} \mid \rightarrow \rangle - \mid \leftarrow \rangle \Big{\rbrack} \Bigg{)}$$$$ = \frac{\alpha}{2}\Big{\lbrack}\mid \rightarrow \rangle\mid \rightarrow \rangle + \mid \rightarrow \rangle\mid \leftarrow \rangle + \mid \leftarrow \rangle\mid \rightarrow \rangle + \mid \leftarrow \rangle\mid \leftarrow \rangle\Big{\rbrack} + \frac{\beta}{2}\Big{\lbrack} \mid \rightarrow \rangle\mid \rightarrow \rangle - \mid \rightarrow \rangle\mid \leftarrow \rangle - \mid \leftarrow \rangle\mid \rightarrow \rangle + \mid \leftarrow \rangle\mid \leftarrow \rangle\Big{\rbrack} $$= $$ \frac{\alpha + \beta}{2}\mid \rightarrow \rightarrow \rangle + \frac{\alpha-\beta}{2}\mid \rightarrow \leftarrow \rangle + \frac{\alpha-\beta}{2}\mid \leftarrow \rightarrow \rangle + \frac{\alpha + \beta}{2}\mid \rightarrow \rightarrow \rangle$$
In this basis, there are four different worlds!
Perhaps the "preferred basis" is picked out by the nature of the interaction. For example, one could imagine a continuous interaction between system and environment, and consider an observable of the system that commutes with the interaction between the two. In this basis, decoherence will generally set it as the evironment is large, leaving the density matrix of the spin in that particular basis diagonal. It could be the $Z$ basis. E.g., taking $\begin{pmatrix} |\alpha|^2 & \beta^{*}\alpha \\ \alpha^*\beta & \mid \beta \mid^2 \end{pmatrix} \rightarrow \begin{pmatrix} |\alpha|^2 & 0 \\ 0 & \mid \beta \mid^2 \end{pmatrix} $.
But such a basis is still not necessarily unique, and it's not entirely clear that one can derive a unique preferred basis from the dynamics alone. (See also work on "Consistency Histories.")
Moreover, consider the case where an observer, in addition to having a memory register entangled with a spin, also has another memory register which encodes the result of a joint meaurement (on the first memory register and the spin) of an observable for which the entangled superposition (between the first memory register and the spin) is in fact an eigenstate. If we interpret this in terms of Many Worlds, then in both "worlds" where the observer perceives $\uparrow$ or $\downarrow$ for the spin, they will also perceive that they are actually in a superposition of the two: which makes it inconsistent to suppose that the two worlds have "separated"! (More on this kind of objection later!)
Bare Theory¶
What if unitary quantum mechanics was all there was, no collapse, but also just one world? What would actually be the operational consequenes of this?
Suppose our experimenter measures a spin in the state $\alpha \mid \uparrow \rangle + \beta \mid \downarrow \rangle$, getting entangled with it, ending up in the $\alpha \mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E} + \beta \mid \downarrow \rangle_{S} \downarrow \rangle_{E}$ state, where $S$ refers to the spin and $E$ refers to the experimenter.
We're worried about whether the experimenter has had a definite experience at all, given the fact that they are in an entangled superposition. Well, why don't we ask them?
Now if we ask them which result they got, they can answer in two different possible ways, and then we ourselves would end up in a joint entangled state with the experimenter and the spin: $\alpha \mid \uparrow \uparrow \uparrow \rangle + \beta \mid \downarrow \downarrow \downarrow\rangle$, and that gets us nowhere.
So instead, let's just ask: Did you get some definite result? Following Barrett, let $\hat{D}$ be an observable of the experimenter such that eigenvalue $+1$ corresponds to a state where the experimenter has a disposition to report "Yes, I got a definite result" and eigenvalue $-1$ corresponds to any state orthogonal to that. We naturally suppose that:
$\hat{D}\mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E} = \mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E}$
and
$\hat{D}\mid \downarrow \rangle_{S} \mid \downarrow \rangle_{E} = \mid \downarrow \rangle_{S} \mid \downarrow \rangle_{E}$
If $S$ and $E$ are in two separable states and the two states are the same, then naturally these should be eigenstates of the "definite outcome" observable $\hat{D}$. There's no question here: there's no entanglement, no superposition, no funny business.
But: if $\mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E}$ and $\mid \downarrow \rangle_{S} \mid \downarrow \rangle_{E}$ are both eigenstates of $\hat{D}$, then any linear combination of them will also be an eigenstate of $\hat{D}$!
$\hat{D}(\alpha \mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E} + \beta \mid \downarrow \rangle_{S} \downarrow \rangle_{E}) = \alpha\hat{D}\mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E} + \beta \hat{D}\mid \downarrow \rangle_{S} \downarrow \rangle_{E} = \alpha \mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E} + \beta \mid \downarrow \rangle_{S} \downarrow \rangle_{E}$
So even if our experimenter is in an entangled superposition with the spin $\alpha \mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E} + \beta \mid \downarrow \rangle_{S} \downarrow \rangle_{E}$, when asked whether they got a determinate result to their experiment, they'll answer yes!
And so, from my point of view, the experimenter is apparently radically deceived about their own mental state!
Furthermore, suppose we get our experimenter to make a second measurement in the same direction. After this, the experimenter and the spin will be in the state:
$\alpha \mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E_{1}}\mid \uparrow \rangle_{E_{2}} + \beta \mid \downarrow \rangle_{S}\mid \downarrow \rangle_{E_{1}}\mid \downarrow \rangle_{E_{2}}$
Again, we don't ask them which answer they got, but instead consider an operator $\hat{C}$ such that:
$\hat{C}\mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E_{1}}\mid \uparrow \rangle_{E_{2}} = \mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E_{1}}\mid \uparrow \rangle_{E_{2}}$
and
$\hat{C}\mid \downarrow \rangle_{S} \mid \downarrow \rangle_{E_{1}}\mid \downarrow \rangle_{E_{2}} = \mid \downarrow \rangle_{S} \mid \downarrow \rangle_{E_{1}}\mid \downarrow \rangle_{E_{2}}$
So that the states where the experimenter's two measurements agree with each other have eigenvalue $+1$. We could think of this operator as asking the experimenter: "Did your two experiments agree with each other?"
Naturally, there's no question about whether this is true in the two states above. But by linearity, the same applies to any linear combination of these two states. And so when asked whether they got the same definite outcome in both cases, even though they are in the state $\alpha \mid \uparrow \rangle_{S} \mid \uparrow \rangle_{E_{1}}\mid \uparrow \rangle_{E_{2}} + \beta \mid \downarrow \rangle_{S}\mid \downarrow \rangle_{E_{1}}\mid \downarrow \rangle_{E_{2}}$, the experimenter will again answer yes!
The same would apply if there were two different experimenters, of course, and they were asked to compare results.
Finally, consider many copies of the qubit in the same initial state, and many "memory registers" of the experimenter, and imagine many measurements being done. After $N$ measurements, you ask the experimenter: "Don't tell me any of the results, but tell me did you get definite answers and what fraction of those $N$ spins turned out to be $\uparrow$?" Now in general, after responding to that question, the state of the world is going to be a superposition of states in which the experimenter responds in different ways--but here's the interesting thing. In the limit as $N\rightarrow\infty$ , it can be shown that the overall state will with certainty approach a state in which the experimenter will answer that question in a determinate way with exactly the correct proportions as predicted by standard quantum mechanics. In other words, one can define a "relative frequency operator" $\hat{F}$ such that in the infinite limit, the overall state approaches an eigenstate of this operator with an eigenvalue given by the correct frequency, ie. the amplitude squared. For details as to the precise argument, I refer you to the paper by Barrett. One can also formulate the question "Were the results you obtained randomly distributed?" in the same way. And in this same vein, one can show that if one does an infinite sequence of EPR experiments, then the experimenter will approach an eigenstate of answering "Were you results compatible with Bell's inequalities?" with "No!" with certainty in the infinite limit.
In other words, in the "bare theory," it can be shown that experimenters in entangled superpositions nevertheless answer questions in a way that is consistent with: determinate results, repeatability, agreement, relative frequency, randomness--despite the fact that physically speaking, they have no justification for this.
Indeed, in this picture, unitary evolution is all there is and all appearences to the contrary (definite outcomes, indeterminism) turn out to be "just the sort of delusions which those laws themselves can be shown to bring on" (Albert 123).
And yet, of course, we can't ever measure an infinite number of copies of systems, even if an infinite number of them existed, so one can rightly question the usefulness of this result. But it does suggest that there is more than meets the eye in the "bare theory" when one approaches the problem of what it means to be in an entangled superposition from an operational perspective.
Many Minds¶
Suppose there's just one world, and quantum states are full descriptions of physical systems, and the dynamical equations of motion, ie. Schrodinger's equation, are always exactly right. We also suppose that healthy people can correctly report whether they have a determinate belief about something. Now since we know that it follows from the bare theory that such people will report having a determinate belief even when they're in a superposition, we have to add something else into the mix to fix this.
So: We assume the evolution of the world is unitary and deterministic. We also assume that definite mental states of the experimenter will correspond to some "eigenstates of mentality", which will not be a matter of convention, but will depend on the physical structure of their brain (or whatever). The brain state corresponding to a belief that the spin was $\uparrow$ will be one that (in accordance with the Schrodinger equation) predisposes them to answer "Up!" to the question of what answer they got.
But also suppose that the evolution of our experimeter's mental state in the course of a measurement is probabilistic so that they end up in the mental state |believes $\uparrow$> or |believes $\mid \downarrow$> with probabilities given by the amplitude squared. By fiat. The physical state would still itself in a superposition, and so these beliefs would be false, but they would be "effectively valid" for the experimenter. If the experimenter makes another measurement, they'll have another belief state, entangled with the first and the system, but since we've imposed an internal "mental collapse" to a definite belief state, future beliefs will be consistent with past beliefs due to the entanglement.
The problem with this proposal is that most of the terms in any given superposition won't correspond to any experience, and moreover, which term which is randomly chosen to be experienced can't be deduced from the physics. So then suppose, that in fact, there is a continuous infinity of minds associated with the experimenter, such that the measure of a subset of these minds which happen to be in a given mental state at a given time is equal to the square of the amplitude. So that in an even superposition, half of the experimenter's minds would believe the spin was $\uparrow$ and half would believe the spin was $\downarrow$. Although the time evolution of any one mind would be probabilistic, since there is a continous infinity of minds, the minds of any observer as a whole would evolve deterministically. So the "global" mental state of any sentient being would be uniquely fixed by the physics.
In other words, we've cooked up a picture where a) there's no need for physical collapse b) mental states never superpose c) there's no preferred basis for the physics c) probabilities are completely objective, but refer not to physical events, but to sequences of mental states.
Interestingly, this would be a completely local picture. Consider an EPR type state like $\mid\uparrow\downarrow\rangle - \mid\downarrow\uparrow\rangle$. When one experimenter measures the first particle, half of their minds believe the outcome was $\uparrow$ and half their minds believe the outcome was $\downarrow$. And the same for the other experimenter. Later on, the two experimenters talk to each other, and one of each of their minds will develop a belief about whether the outcome of the other's measurement was correlated or anti-correlated, and the probability of these beliefs arising is going to be the usual quantum mechanical one. Nothing nonlocal at all!
On the other hand, there is a deep epistemological barrier for any observers in such a picture: given their beliefs, all they can really say about the actual quantum state of the world is that it at least isn't orthogonal to the state picked out by their beliefs.
Bohmian Mechanics¶
Here's a crash course in Bohmian mechanics, with a focus on the stories it tells about the world, and not the equations.
Every material particle in the world has a perfectly determinate position. Physics produces an account of their evolution. Force fields and anything else merely come up in order to account for the motion of these material particles. The motion of these particles is completely deterministic. We only have to introduce a wavefunction, conceived as literally a physical thing, whose job is to push the particles around.
Given a single particle and a wavefunction in a single spatial dimension, we can define a velocity for this particle, to be evaluated at the particle's position, and which depends on the wavefunction. We can then calculate the future position of the particle, as well as the future state of the wave function. Given a position of a particle and its wave function at any given time, its position and wavefunction at any other time can be calculated with certainty, given the forces the particle is subject to.
Now imagine a "swarm" of such particles, and imagine that it just so happens that their initial positions are distributed according to the usual quantum mechanical probabilities: in other words, the density in space of the possible positions of this initial swarm is equal to the absolute value squared of the initial wave function. Then it follows from the laws of Bohmian mechanics, that the density in space of this swarm at any later time will also be equal to the absolute value squared of the wavefunction at that later time.
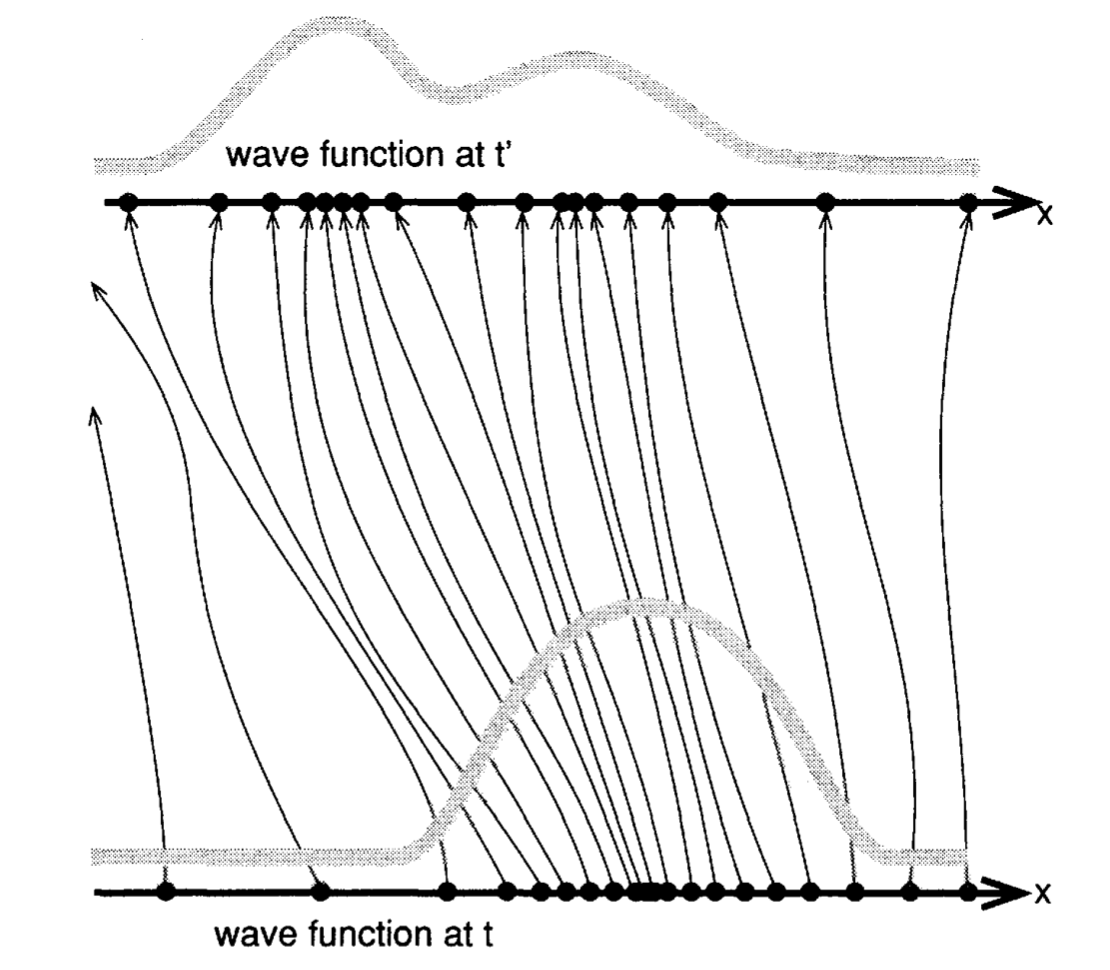
In other words, a particle gets carried along the flows of the amplitudes of the wave function like a "cork floating in a river".

Now suppose this was true, but you actually had no idea where any of the particles actually were, but you did have the wavefunction. Then it would stand to reason that the probability that a particle is at any given location will be given by the square of the absolute value of the wavefunction at that point. And so, Bohmian mechanics supposes that quantum indeterminism results from an ignorance of the initial conditions, just like in classical mechanics.
We can generalize this to three dimensions. We can also add in spin, which will be a property of the wavefunctions, but not the particles.
If you have a spin entangled state like:
$\alpha \mid \uparrow \rangle \mid \psi(x, y, z) \rangle + \beta \mid \downarrow \rangle \mid \phi(x, y, z) \rangle$
Then each part contributes to the velocity function:
$V(x, y, z) = \frac{|\alpha\psi(x, y, z)|^2 V(\psi(x, y, z)) + |\beta\phi(x, y, z)|^2V(\phi(x, y, z))}{|\alpha\psi(x, y, z)|^2 + |\beta\phi(x, y, z)|^2}$
If you have more than one particle, say, a pair of particles, then you have a wavefunction like $\psi(x, y, z, x', y', z')$, which you could look at as a function that takes values in a 6 dimensional space. The law treats the pair more or less as if it were a single particle being pushed around this 6 dimensional space. There will be 6 velocity functions to calculate, and each of those six will be functions of position in the 6 dimensional space, and the position of this two particle system in the 6 dimensional space will get carried along the quantum mechanical probability flows of the wavefunction. We make the same statistical assumption as before, supposing that the probability that the two particle system was located intially at any particular point in the 6 dimensional space is equal to the square of the absolute value of the wavefunction at that point, and this will guarantee that this will also be true at later times.
Now suppose we have a wavefunction with spin, and we go to measure the spin in, say, the $Z$ direction.
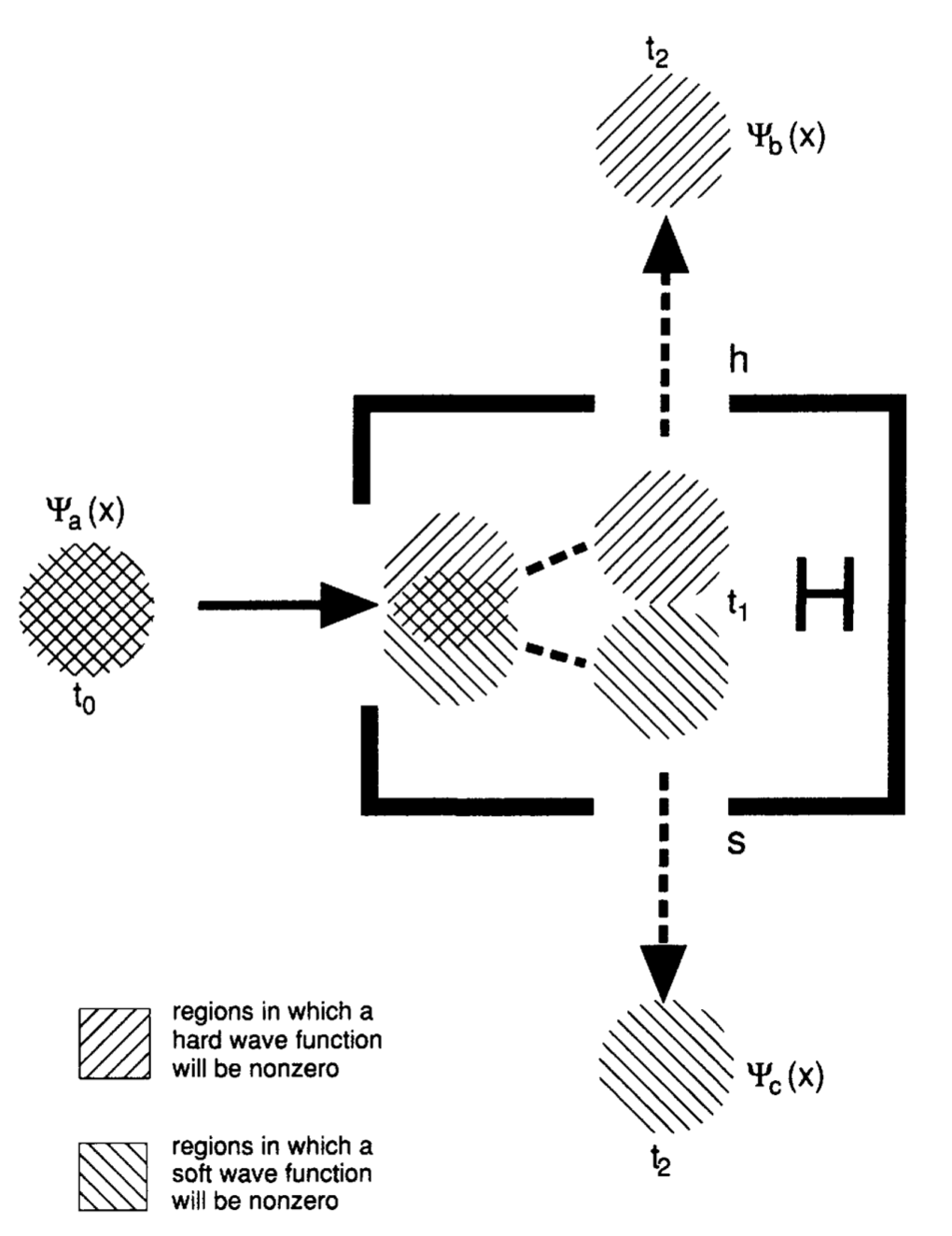
The wavefunction of the particle initially is a wavepacket to the left, in a superposition of $\uparrow$ and $\downarrow$. The dynamics within the apparatus cause the $\uparrow$ and the $\downarrow$ part of the wavefunction to evolve differently: they separate from each other, and the $\uparrow$ part of the wave function exits the top port and the $\downarrow$ part of the wave function exits the bottom port.
But the real question is: what does the particle do? The particle is carried along the local currents of the wavefunction. If the particle happened to be in the upper half of the initial region, then it will be carried upwards through the top port, and if the particle happened to be in the lower half of the initial region, then it will be carried downwards through the bottom part. In other words, the outcome entirely depends on where the particle happened to be located when things started out, and everything proceeds deterministically. (If the particle had been in a definite state, $\uparrow$ or $\downarrow$, then the particle exit out the top or bottom port respectively, regardless of where the little particle happened to be located in its region).
And if you send the particle through a second such box, then it'll come out the same port as the first box, since the particle is now floating around on either a $\uparrow$ or $\downarrow$ wavefunction, respectively. Similarly, if you measure in the $X$ or $Y$ directions, the $\uparrow$ or $\downarrow$ wavefunctions will separate out from each other, and the particle will be carried along whichever it happened to be closer to. And of course, one can imagine reuniting the particle with a "branch" of its wavefunction that wandered off.
Now if all we know about the particle is just its wavefunction, then this will reproduce all the familiar predictions of quantum mechanics.
On the other hand, and this is crucial, suppose the measurement apparatus had been flipped upside down: then since which port the particle exits depends on whether it happened to be a little bit above or below the midpoint of the box to begin with, then the outcome of the "spin" mesurement will be just the opposite! So the outcome of a spin measurement won't be pinned down even by specifying the position and wavefunction: one has to also specify the orientation of the apparatus. And thus one can't think of the spin as an intrinsic property of the particle or the wavefunction. The spin must be a "contextual property," and this is generally the case for all quantum mechanical observables other than position in any deterministic version of quantum mechanics. (Then again if the wavefunction is in an eigenstate of the apparatus, then the result won't be contextual, etc.)
The next thing to say is that the whole theory is deeply nonlocal. Each of the six velocity functions for two particles will depend on the location of the entire two particle system in its 6 dimensional space. The velocities of the particle will depend on each other no matter where they are located in space, instantaneously. If, however, the particle wavefunctions are in a separable state, then there won't be any nonlocality, and things will reduce to the case of a pair of one particle theories.
Suppose we have two particles whose wavefunctions are in the state: $\frac{1}{\sqrt{2}} \Big{(}\mid \uparrow \rangle_{1} \mid \psi(x, y, z) \rangle_{1} \mid \downarrow \rangle_{2} \mid\phi(x, y, z)\rangle_{2} - \mid \downarrow \rangle_{1} \mid \psi(x, y, z) \rangle_{1} \mid \uparrow \rangle_{2} \mid\phi(x, y, z)\rangle_{2} \Big{)}$
In other words, the two wavefunctions have spins in the antisymmetric state.
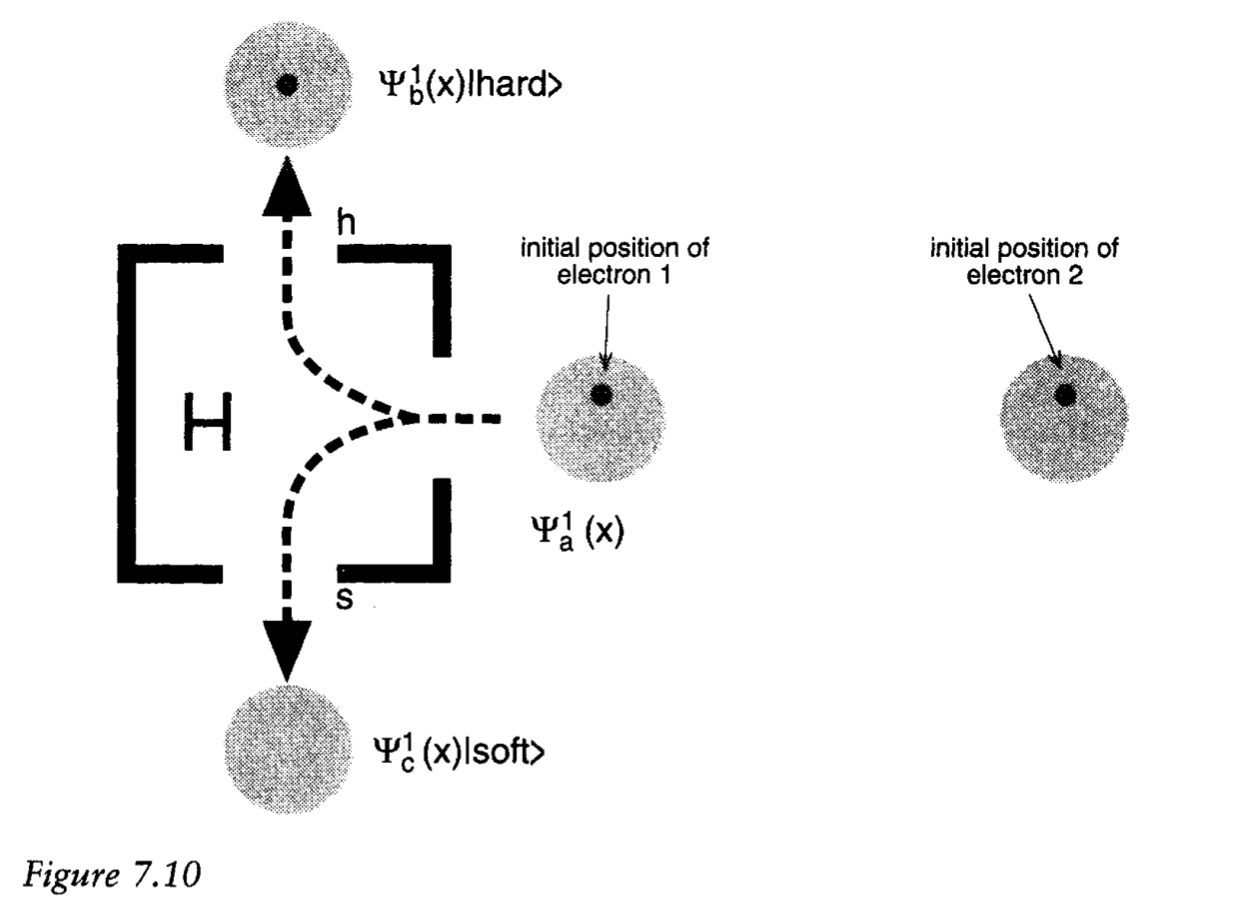
Now suppose we send the first particle through a spin apparatus, and its position happened to be in the upper half of its region, and it ends up leaving by the up port. And thereafter, unless the parts of the wavefunction are brought together again, the second term in the superposition will have no effect on the motion of either particle: and therefore particle 1 will behave like it's $\uparrow$ and particle 2 will behave like its $\downarrow$: there will be an effective collapse. And the same applies if we'd sent particle 2 through such a box first. And in general, as many systems interact with each other, outcomes become irreversible to the extent that we can't bring back together all the bits of the wavefunction that drift away from each other.
One consequence of all this is that if we knew the positions of these particles, then we'd have a means of transmitting information faster than the speed of light. If we knew the positions, we could decide to send the particle through an upsidedown or rightsideup spin apparatus, and so determine whether it would be $\uparrow$ or $\downarrow$ with certainty, and the other experimenter would be able to read off our message by sending their own particle through such a box. And so Bohmian mechanics violates special relativity. But of course, if we don't actually know the positions, then we could never tell which is the preferred Lorentz frame. So the statistical predictions of Bohmian theory (assuming the particles started out distributed according to the squared amplitude of their wavefunction) will be fully Lorentz covariant, even though the underlying theory isn't.
In other words, according to the Bohmian picture, quantum mechanics and special relativity are only "instrumentally" true about the world. (The problem comes in extending Bohmian mechanics to fields, althought work has been done in this direction.) Moreover, even though the outcomes of measurements do actually depend on the exact locations of particles and the orientations of the apparatus, and on the orientations of distant apparatuses that entangled particles are sent through, and all this depends on an absolute space and time, we'd never be able to discover any of this empirically and one could say that the fundamental laws of the world "are cooked up in such a way as to systematically mislead us about themselves" (Albert 169), appearing (falsely) to be relativistic and quantum mechanical.
Okay, but what about supervenience? Consider the following paradox.
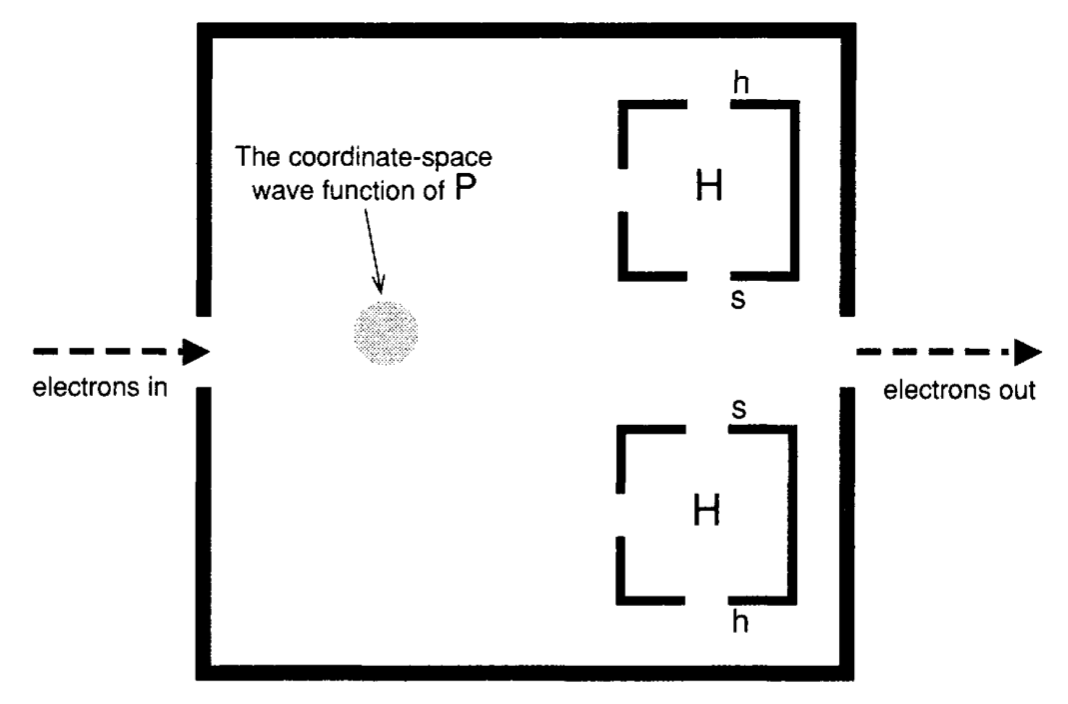
Suppose we have the device pictured above, which produces correlations between the spins of particles. If a $\uparrow$ particle is sent into the device, then its spin is unaffected, but $P$ ends up $\downarrow$. If a $\downarrow$ particle is sent in, $P$ ends up $\uparrow$. Then we can measure $P$'s spin in the $Z$ direction by sending it into either one of the two inner boxes. Now suppose that the device is implanted in the brain of our experimenter, and the way it's hooked up makes him function as if his beliefs about the spin of the particles that pass through the device are determined directly by the spin of $P$.
Now suppose the experimenter is given a $\uparrow$ particle, and it's sent through the device, which again is surgically implanted into his brain, through the right door, and then it's expelled out the other side. After this happens, the only place where the value of the spin of the particle is encoded is in the fact that $P$ is now $\downarrow$. The experimenter announces that he is presently consciously aware of the value of the spin in the $Z$ direction, and he's ready to tell us.
If we ask him, however, here's what happens. The experimenter is allowed to tell us either verbally or in writing. If we ask the experimenter to tell us verbally, they pass $P$ through the upper box, which has detectors at its output ports, which are connected to the experimenter's neurons, and ultimately their mouth in such a way that they'll say "up" if the original particle was $\uparrow$ and "down" if the original particle was $\downarrow$. On the other hand, if we ask the experimenter to report in writing, then they pass $P$ through the lower box (which note is upside down), which also has detectors at its output ports which are connected to the experimenter's neurons in such a way that he ends up writing "up" if the original particle was $\uparrow$, and so forth.
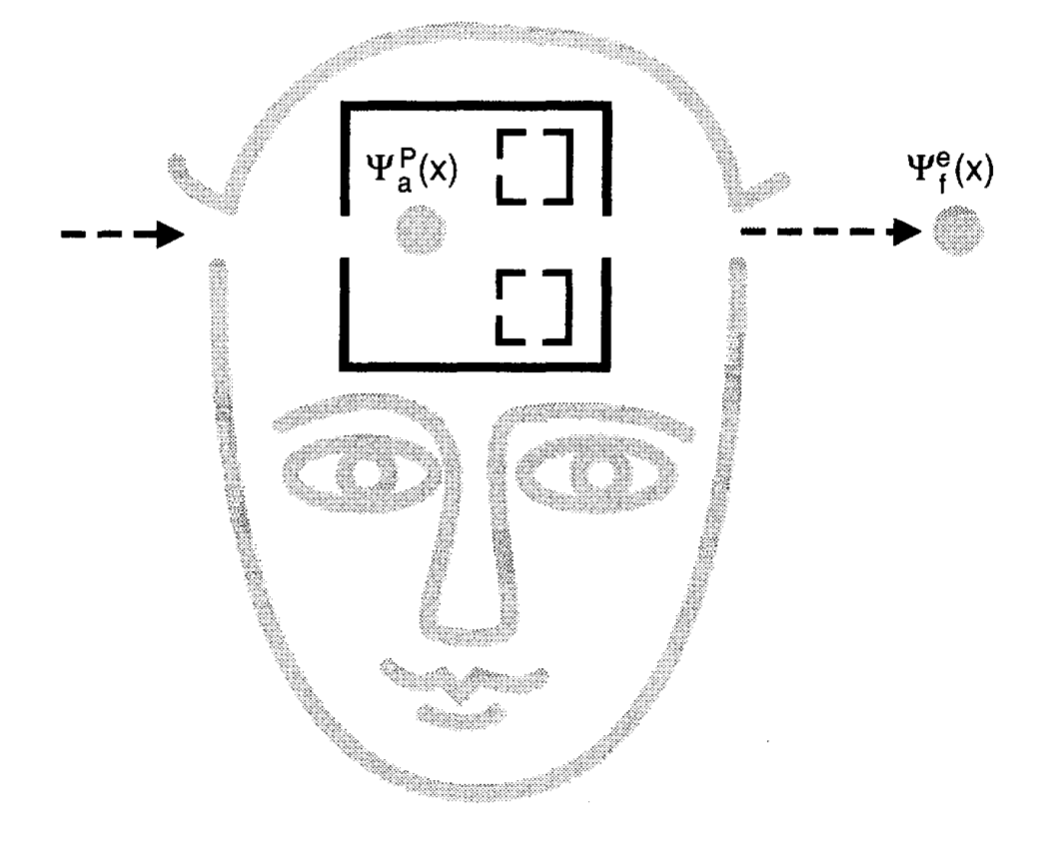
Okay, now what happens when the experimenter is presented with a $\mid \leftarrow \rangle$ particle? They pass the particle through their head, and they tell us they knows that value of the spin in the $Z$ direction; indeed, that they're consciously aware of the value, and can tell us if we want, either verbally or in writing. At that point the state is:
$\frac{1}{\sqrt{2}}\Big{(}\mid \downarrow \rangle_{P}\mid \psi_{a}(x)\rangle_{P}\mid \uparrow \rangle_{e}\mid \psi_{f}(x)\rangle_{e} - \mid \uparrow \rangle_{P}\mid \psi_{a}(x)\rangle_{P}\mid \downarrow \rangle_{e}\mid \psi_{f}(x)\rangle_{e} \Big{)}$
Where $P$ refers to the particle that's acting as the memory, and $e$ the particle which was measured. So if we ask the experimenter to report verbally, they'll say "up" or "down", all of which will lead to an effectively collapse of the wave function onto either its first or second term, and so whatever they say will be confirmed by subsequent measurements on the electron itself. Similarly, if we ask them to report in writing, they'll write "up" or "down" and there will be an effective collapse, and the electron will confirm his answer. If we ask for a verbal report and then a written report, then both will coincide, and vice versa, etc. So that whatever criteria one has for the experimenter really having a belief, indeed, a true, even justified belief about the value of the spin of the electron will be satisfied by someone wired up like this experimenter is.
But if Bohmian mechanics is right, that can't possibly be the case.
Suppose $P$ happens to be in the upper half of the region $a$, and suppose the experimenter is asked to first give a verbal report. They passes $P$ through the top box, and since the particle in the upper half of the region $a$, the particle will necessarily exit out the top $\uparrow$, implying the original particle was $\downarrow$. But if we'd asked the experimenter to give a written report instead, they'd pass $P$ through the lower box, and since it's in the upper half of the region $a$, the particle will necessarily exit out the top $\downarrow$ port (recall the boxes are flipped), implying the original particle was $\uparrow$. (And the reverse, if the particle had been in the lower half of $a$.) So the experimenter claims to be a knower of the spin in the $Z$ direction, and they are actually equipped to produce a report about it, which will indeed be confirmed by any subsequent measurements, and yet the content of their report (and indeed, the state of the particle!) will entirely depend on whether they're asked to give the report verbally or in writing which seems totally irrelevant.
Comparing Many Minds and Bohmian Mechanics¶
If either Many Minds or Bohmian Mechanics turned out to be true, then given no other constraints, the question of which one was true would be undeterminable by any conceivable empirical evidence. Each theory entails that unitary evolution governs everything, and each gives the right probabilities for all outcomes to experiments, and so there can't be any purely experimental means of deciding between them. Suppose collapse theories were ruled out, and these ended up being our only two options. We wouldn't be able to decide between them, which is very disconcerting insofar as the question of whether the world is deterministic or not and whether spacetime is relativistic or not would be questions without any scientific answers.
Moreover, consider a $Z$ measurement of a particle in the $\mid \rightarrow \rangle$ state. In Bohmian mechanics, there will be a completely deterministic matter of fact with regard to how the pointer of the measuring apparatus ends up, and where it ends up will count as "absolutely raw empirical data, the sort of thing (that is) that physics is fundamentally in the business of making predictions about" (Albert). In contrast, in Many Minds, there won't be any determinate matter of fact about where the pointer ends up (it remains in superposition), and the situation is just the opposite. Indeed, the conviction of a Bohmian that there is some matter of fact about the pointer will be "perfectly explicable in the context of a many-minds theory as a simple delusion,"--and so there can't be a means of resolving the dispute.
Suppose we give the experimenter from before a $\mid \rightarrow \rangle$ particle to measure with their brain implant. According to Many Minds, there will be a determinate matter of fact about what each of the experimenter's minds ends up thinking about the spin of the particle, and those thoughts will be the kind of things that count as raw empirical data, and what physics is in the business of predicting. But as we've seen, in Bohmian mechanics, there won't be any matter of fact about what the experimenter thinks about the spin of the electron, and consequently what they ends up thinking about can't be anything that counts as raw data or something that physics can predict. And just the same, the conviction of a Many Minds adherent that there is some matter of fact about what the experimenter is thinking will be perfectly explicable by a Bohmian as a delusion.
In other words, it's not merely that the two theories are empirically equivalent--it's that they are radically, empirically incommensurable with each other. "What a many-minds theory takes physics to be ultimately about is what observers think; and it entails that there will freqnently not even be matters of fact about where things go. And what Bohm's theory takes physics to be ultimately about...is where things go; and it entails that there will sometimes not even be matters of fact about what observers think."
Self-Measurement¶
Suppose an experimenter $E$ is in the state
$\mid A \rangle = \frac{1}{\sqrt{2}}$ (|believes $e$ $\uparrow\rangle_{E}\mid \uparrow \rangle_{m} \mid \uparrow \rangle_{e}$ + |believes $e$ $\downarrow\rangle_{E}\mid \downarrow \rangle_{m} \mid \downarrow \rangle_{e}$)
Where $E$ refers to the experimenter, $m$ their measuring apparatus, and $e$ the particle. Now $\mid A \rangle$ is an eigenstate of some complete set of observables. Call them $\{Q\}$ with associated eigenvalues $\{q\}$. Suppose now another experimenter $F$ measures $\{Q\}$, with a $\{Q\}$ measuring device and records the value in some set of pointers.
So we end up:
|believes $\{Q\}$=$\{q\}$$\rangle_{F}$|indicates$\{Q\}$=$\{q\}\rangle_{F_{m}}$$\mid A \rangle$
Suppose now that $F$ tells $E$ the result of their measurement. We could even imagine the $E$ actually did the measurement on themselves, and stored the result somewhere else in their memory. We end up with:
|believes $\{Q\}$=$\{q\}$$\rangle_{F}$|indicates$\{Q\}$=$\{q\}\rangle_{F_{m}}$ $\otimes$$\frac{1}{\sqrt{2}}$ (|believes $e$ $\uparrow$ and $\{Q\}$=$\{q\}$$\rangle_{E}\mid \uparrow \rangle_{m} \mid \uparrow \rangle_{e}$ + |believes $e$ $\downarrow$ and $\{Q\}$=$\{q\}$$\rangle_{E}\mid \downarrow \rangle_{m} \mid \downarrow \rangle_{e}$)
This seems like a state where the experimenter knows both the spin of the particle and $\{Q\}$, but how is this possible since they're incompatible with each other?!
If another experimenter wants to simultaneously know these things too, they can try to measure $\{Q\}$ and the spin, but doing this will entangle them with the spin, and that overall state can't be an eigenstate of $\{Q\}$.In other words, no one else but our original observer can ever simultaneously know both the spin and $\{Q\}$.
In Many Minds language: half of the experimenter's minds believe the spin is $\uparrow$ and half believe it is $\downarrow$, and by the rules of Many Minds, this is effectively true, since if they make another measurement, this will be confirmed. Moreover, all of their minds know genuinely that $\{Q\} = \{q\}$. And so all the minds are simultaneously aware of the existence of another branch of the wave function (which apparently invalidates their beliefs)!
In Bohmian language, let's suppose the experimenter's memories are encoded in positions. There are objective physical facts about how any subsequent spin or $\{Q\}$ measurements will turn out. And the experimenter could be said to have genuine access to what those facts are. And no other observer can ever be in a position to know those facts all at the same time. Suppose the experimenter allows a future decision to be determined by the results of an upcoming measurement on the spin and $\{Q\}$. Then they and they alone already know the answer, and so even though the theory is deterministic, it's as if the experimenter has an "inviolably private will."
To quote David Albert, "And so the mental lives of quantum-mechanical observers who could arrange to carry out these sorts of measurements on their own brains would perhaps be unimaginably (for us) rich."
Other views¶
If I had more time, I'd discuss the relationship between mind and matter in the context of yet more interpretations of QM. See Part 2!
Bibliography¶
Quantum Mechanics and Experience
The Preferred-Basis Problem and the Quantum Mechanics of Everything
The Suggestive Properties of Quantum Mechanics without the Collapse Postulate
The Single-Mind and Many-Minds Versions of Quantum Mechanics