k-Wave Toolbox

3D Time Reversal Reconstruction For A Spherical Sensor Example

Overview

This example demonstrates the use of k-Wave for the time-reversal reconstruction of a three-dimensional photoacoustic wave-field recorded over a spherical sensor. The sensor data is simulated and then time-reversed using kspaceFirstOrder3D. It builds on the 2D Time Reversal Reconstruction For A Circular Sensor and 3D Time Reversal Reconstruction For A Planar Sensor examples.

• open the file in the MATLAB Editor
• run the file in MATLAB

 Back to Top

Simulating the data

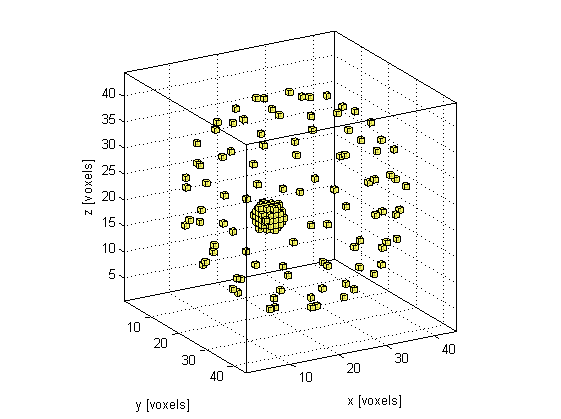
The sensor data is simulated using kspaceFirstOrder3D with an initial pressure distribution created using makeBall. A Cartesian sensor mask of 100 points evenly distributed around a sphere (using the Golden Section Spiral method) is created using makeCartSphere. A visualisation of the initial pressure and the sensor mask using cart2grid and voxelPlot is shown below.

 Back to Top

Running the reconstruction

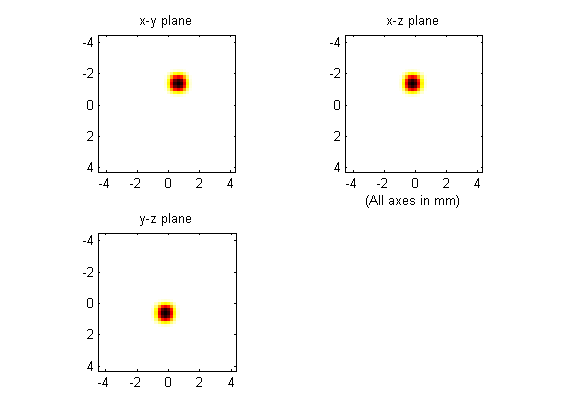
A plot of the initial pressure distribution and the reconstructed distribution using time-reversal are shown below (the three displayed image planes intersect at the centre of ball shown above). The plot scale for the reconstructed image has the plot limits reduced by a factor of 20.

 Back to Top

Interpolating incomplete sensor data

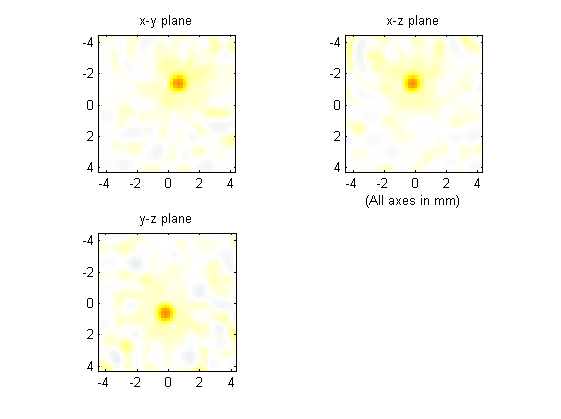
The reconstruction can again be improved by interpolating the sensor data onto a continuous sensor surface. This is achieved using interpCartData and a binary sensor mask of a continuous sphere (created here using makeSphere) that is spatially equivalent to the Cartesian measurement grid. This function calculates the equivalent time-series at the sensor positions on the binary sensor mask from those on the Cartesian sensor mask via interpolation (nearest neighbour is used by default).

% create a binary sensor mask of an equivalent continuous sphere 
pixel_radius = round(sensor_radius/kgrid_recon.dx);
binary_sensor_mask = makeSphere(kgrid_recon.Nx, kgrid_recon.Ny, kgrid_recon.Nz, pixel_radius);

% interpolate data to remove the gaps and assign to time reversal data
sensor.time_reversal_boundary_data = interpCartData(kgrid_recon, sensor_data, sensor_mask, binary_sensor_mask);

Details of the interpolation are printed to the command line.

Interpolating Cartesian sensor data...
  interpolation mode: nearest
  number of Cartesian sensor points: 100
  number of binary sensor points: 4234
  computation completed in 0.075839s

The reconstruction after interpolation is shown below. The plot limits are set to match those of the initial pressure plot shown above.

 Back to Top

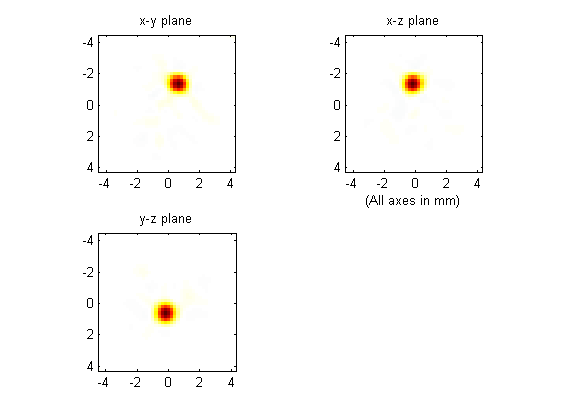
3D Time Reversal Reconstruction For A Planar Sensor

Image Reconstruction With Directional Sensors

© 2009-2014 Bradley Treeby and Ben Cox.