

| k-Wave Toolbox |
 
|
| On this page… |
|---|
This example illustrates the diffraction of a plane acoustic wave through a slit. It builds on the Monopole Point Source In A Homogeneous Propagation Medium and Simulating Transducer Field Patterns examples.
The current version of k-Wave cannot explicitly enforce impedance boundary conditions. However, rigid boundaries can still be modelled by assigning a boundary with a large sound speed and density compared to the rest of the propagation medium. As this impedance difference is increased, the behaviour of the interface will approach that of a rigid boundary. Note, increasing the sound speed of the boundary will similarly increase the computational requirements (the time step required for a stable simulation is dependent on the maximum sound speed within the medium).
Here, a diffraction slit is created by defining a thin layer with a significantly different sound speed and density to the background medium such that most of the incident wave is reflected. (Note, using barrier_scale = 20, some of the incident wave will still be transmitted through the barrier causing additional interference fringes. These can be reduced by increasing the barrier scale.)
% define the ratio between the barrier and background sound speed and density barrier_scale = 20; % create the time array using the barrier sound speed t_end = 40e-6; % [s] CFL = 0.5; % Courant–Friedrichs–Lewy number kgrid.t_array = makeTime(kgrid, c0*barrier_scale, CFL, t_end); % create a mask of a barrier with a slit slit_thickness = 2; % [grid points] slit_width = 10; % [grid points] slit_x_pos = Nx - Nx/4; % [grid points] slit_offset = Ny/2 - slit_width/2 - 1; % [grid points] slit_mask = zeros(Nx, Ny); slit_mask(slit_x_pos:slit_x_pos + slit_thickness, 1:1 + slit_offset) = 1; slit_mask(slit_x_pos:slit_x_pos + slit_thickness, end - slit_offset:end) = 1; % assign the slit to the properties of the propagation medium medium.sound_speed = c0*ones(Nx, Ny); medium.density = rho0*ones(Nx, Ny); medium.sound_speed(slit_mask == 1) = barrier_scale*c0; medium.density(slit_mask == 1) = barrier_scale*rho0;
In the first example (set example_number = 1 within the example m-file), a sinusoidal plane wave source is created with a wavelength equal to the slit width. A visualisation of the barrier is also produced by assigning the slit_mask created above to the optional input parameter 'DisplayMask'. The size and location of the perfectly matched layer are explicitly defined (see Controlling The Absorbing Boundary Layer Example), the simulation is run in single precision to reduce the computation time (see Optimising k-Wave Performance Example), and the final pressure and velocity fields are returned by sensor.record to {'p_final', 'u_final'} (see Recording The Particle Velocity Example).
% set the input options
input_args = {'PMLInside', false, 'PMLSize', PML_size, 'PlotPML', false, ...
'DisplayMask', slit_mask, 'DataCast', 'single'};
% run the simulation
sensor_data = kspaceFirstOrder2D(kgrid, medium, source, sensor, input_args{:});
A visualisation of the pressure field is given below. The wave field on the far side of the slit appears reasonably omni-directional.
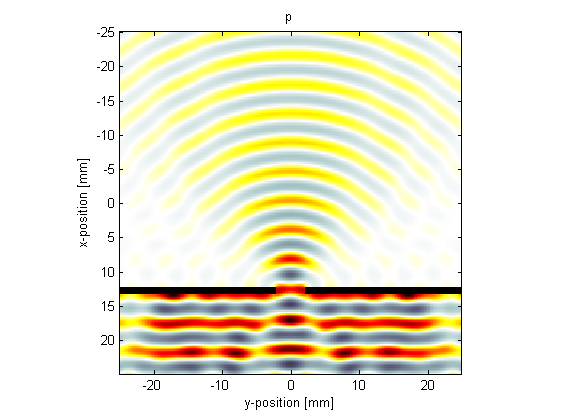
In the second example (set example_number = 2 within the example m-file), the slit size is increased and the wavelength is reduced to be a quarter of the slit width. A visualisation of the pressure field is given below. In this case, the directionality of the wavefield is increased, and interference fringes are visible.
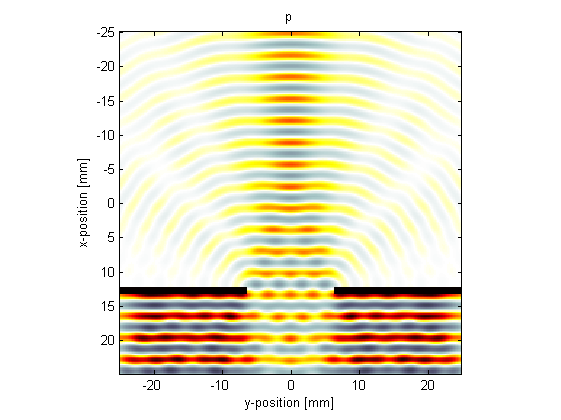
In the third example (set example_number = 3 within the example m-file), a double slit is used and the wavelength set equal to the slit width. The final velocity fields are also displayed.
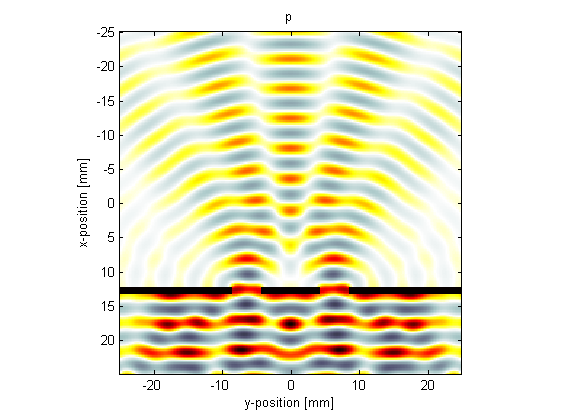
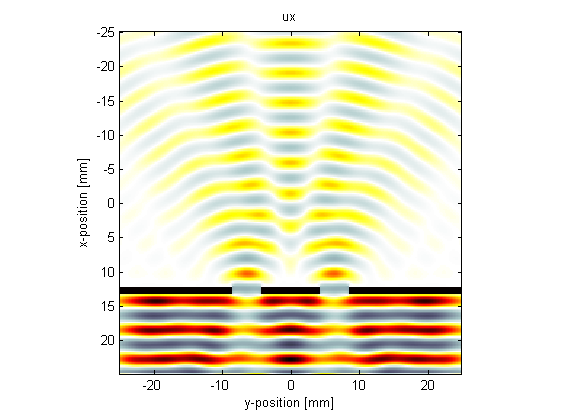
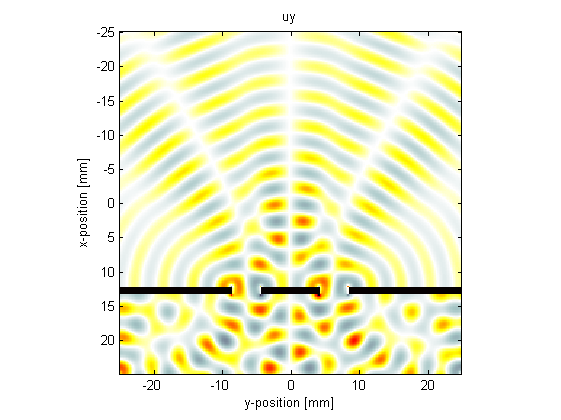
Note, the pictures shown here were computed using barrier_scale = 50 and scale = 2 within the example m-file.
 |
The Doppler Effect | Simulations In Three Dimensions |  |
© 2009-2014 Bradley Treeby and Ben Cox.