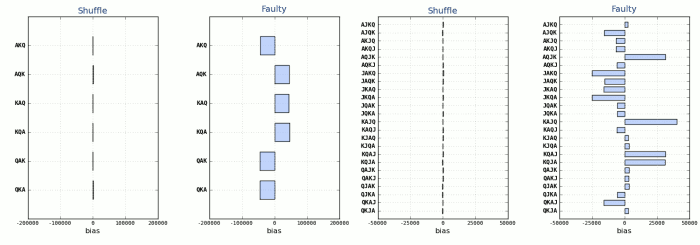
Los algoritmos shuffle se emplean para barajar o desordenar los elementos de una lista (como si fueran las cartas de una baraja) al azar. Se intenta reproducir lo que ocurre en la realidad cuando barajamos un mazo de cartas o extraemos bolas de un bombo para formar una combinación. El comportamiento ideal de estos algoritmos debe de ser imparcial, es decir que todas las posibles permutaciones de esta lista tengan las mismas oportunidades de aparecer como resultado. Este reparto uniforme es clave para el buen funcionamiento del mismo, pues de no ser así se crearían tendencias y el resultado seria predecible, lo que acabaría con la aleatoriedad que se pretende conseguir.

Imaginemos tres distintas cartas de una baraja inglesa: As, Rey y Reina (Ace, King & Queen) como una lista en Python, y ahora veamos todas las posibles permutaciones de la misma (n!, es decir, 3! = 6):

Representación gráfica de las distintas permutaciones.¹

>>> lista = ['A', 'K', 'Q']
>>> import itertools
>>> for i in itertools.permutations(lista):
...     print(i)
...
('A', 'K', 'Q')
('A', 'Q', 'K')
('K', 'A', 'Q')
('K', 'Q', 'A')
('Q', 'A', 'K')
('Q', 'K', 'A')
>>>

Vemos entonces que existen 6 permutaciones posibles que pueden darse como resultado de barajar las cartas. Ahora imaginemos que escogemos una estas permutaciones, y jugamos a barajar las cartas una y otra vez partiendo siempre desde esta permutación. Como ya adelantábamos, si el algoritmo shuffle fuese perfecto, el resultado de estas operaciones debería repartirse de forma imparcial (equiprobable) entre las distintas permutaciones posibles. Es decir, que al ejecutar un fragmento de código como el que sigue, donde empleamos el algoritmo shuffle que por defecto trae Python (en el modulo random de la librería estándar), ramdom.suffle()

>>> from random import shuffle
>>> for i in range(12):
...     lista = ['A', 'K', 'Q']
...     shuffle(lista)
...     print(lista)
...
['A', 'K', 'Q']
['K', 'Q', 'A']
['A', 'K', 'Q']
['Q', 'A', 'K']
['K', 'Q', 'A']
['Q', 'K', 'A']
['A', 'K', 'Q']
['Q', 'K', 'A']
['K', 'Q', 'A']
['K', 'A', 'Q']
['Q', 'K', 'A']
['Q', 'A', 'K']
>>>

los resultados en pantalla deberían irse repartiendo a partes iguales entre las distintas permutaciones. Del mismo modo, si ejecutáramos este algoritmo 600.000 veces sobre la misma permutación, los resultados deberían repartirse de esta forma:

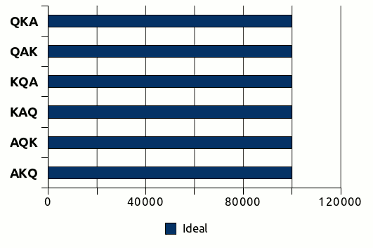
Donde las apariciones de cada permutación posible son idénticas, es decir, 600.000/6 = 100.000. Pero veremos que en la realidad ocurre algo distinto, como ya podíamos adivinar al ver los resultados del código anterior. Veamos con detalle que es lo que ocurre con el algoritmo shuffle para ese mismo número de ejecuciones.

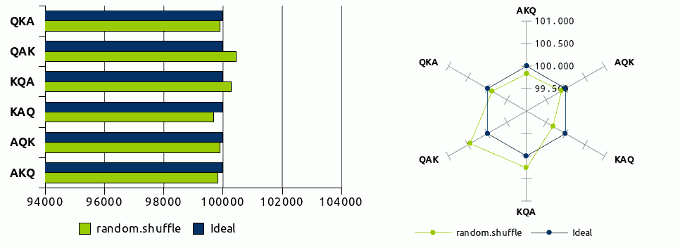
Como podemos ver, el comportamiento real de un algoritmo shuffle no se ajusta al comportamiento ideal. Unas combinaciones están sobre-representadas como QAK y KQA y el resto sub-representadas, siendo la combinación AQK la más cercana a los valores ideales. Pero estos valores no debemos verlos como una tendencia, puesto que si volvemos a ejecutar otras 100.000 operaciones de barajado, aunque seguirá sin ser un reparto equitativo, si es imparcial en cuanto que no se repiten las mismas desviaciones por permutación. Es decir, unas veces unas serán unas permutaciones las más sobre-representadas (y viceversa) y otras lo serán otras distintas, no hay una tendencia clara. Las variaciones en este caso oscilan entre 99.678 (-322) y 100.446 (+446) apariciones sobre un valor ideal de 100.000 con una desviación media de ±0.039%, unos valores no ideales pero si muy razonables y más que suficientes para la mayoría de necesidades.

Es importante volver a incidir en que un algoritmo de barajado bien diseñado siempre ha de ser imparcial, de hecho random.shuffle lo es, si no será erróneo y nos creara tendencias que pueden pasar inadvertidas a no ser que se comprueben correctamente (en este caso de forma estadística). Tendencias que pueden suponer un verdadero problema y echar al traste todos los cálculos y procesos que empleen este algoritmo como base. El emplear un algoritmo de barajado erróneo le ha causado más de un disgusto a algún casino online, ya que las tendencias permiten predecir el resultado de el barajado y usarlo para hacer trampas en el juego.

Pero si random.suffle es imparcial, ¿por qué no se reparten los resultados de manera uniforme? El problema es aquí entra en juego un segundo actor, que independientemente de lo bien diseñado que este nuestro algoritmo shuffle, nos condicionará que el reparto sea uniforme o no. Este segundo actor es la aleatoriedad, lo que precisamente intentamos conseguir. Para que nuestro algoritmo funcione necesitamos que se elijan las cartas al azar para ir desordenándolas también al azar. Y es aquí donde está el problema, el que impide que random.shuffle tenga un comportamiento ideal, que los ordenadores y la aleatoriedad, no son buenos "amigos". No existe algo así como un generador de números aleatorios perfecto basado en software (si los hay casi perfectos basados en hardware), debido a que son deterministas al estar basados en formulas matemáticas. Por lo que empleamos lo que se denomina generadores de números pseudoaleatorios. Estos generadores pueden ser más o menos "perfectos", pero al no generar verdadera aleatoriedad, nos impiden que nuestro algoritmo consiga efectuar un reparto uniforme. Matemáticamente se ha demostrado que algunos algoritmos, como el que emplea ramdon.shuffle (luego aclararemos cual es) tienen un funcionamiento ideal, y de hecho podemos acercarnos muchísimo al modelo ideal cuando empleamos un generador de aleatoriedad por hardware (que se acerca mucho a la verdadera aleatoriedad). Al final, aunque sean matemáticamente correctos, tu algoritmo de barajado será tan bueno como lo sea tu generador de números aleatorios.

Python, en su modulo random, emplea por defecto uno de los mejores generadores de números pseudoaleatorios existentes actualmente, el Mersenne twister (hasta la versión 2.4 se empleaba el Wichmann-Hill, que sigue disponible como clase) y está implementado en C. Los resultados entregados por él son muy fiables (excepto para su empleo en criptografía), generando números float con una precisión de 53 bits y con un elevado periodo de 2¹⁹⁹³⁷-1. Otra buena opción que nos ofrece el modulo random para entornos Unix/Linux es la clase random.SystemRandom() que nos ofrece la entropía generada por os.random() que a su vez la toma de la generada en /dev/random. Esta es una fuente bastante decente de aleatoriedad que en las pruebas me ha ofrecido resultados similares a el generador por defecto en Python.

Los algoritmos

Utilizar la función random.shuffle() es la forma más cómoda de barajar una lista en Python, y desde luego la más recomendable. Pero si quisiéramos desarrollar nuestro propio algoritmo, esta es una de esas ocasiones en las que o tienes unos solidos conocimientos matemáticos (o estadísticos) o mejor no intentes reinventar la rueda, recurre a lo conocido y solido, y como mínimo prueba siempre que los resultados que obtienes son lo que tu esperas. Esto no es una afirmación gratuita, esta es una de las ocasiones en la que la diferencia es tan sutil, que es facilísimo equivocarse sin siquiera darse cuenta. Veamos porqué.

La intuición a veces nos engaña, no seas ingenuo!

Aparentemente barajar una lista es de lo más sencillo, después de razonar un poco, podríamos acabar con un código parecido a este:

def faulty(lst):
    "An example of a intuitive but very bad algorithm."
    lst_length = len(lst)
    for i in range(lst_length):
        j = random.randrange(lst_length)
        lst[i], lst[j] = lst[j], lst[i]

Que aparentemente debería ser correcto, algo que han pensado muchos programadores ingenuamente hasta caer en la cuenta "a la fuerza" de que no es correcto. Es más, si por ejemplo nos limitáramos a ejecutarlo unas 360 veces para probarlo (las cuales aparentemente no son pocas), veríamos que tiene un comportamiento muy parecido al que nos da la función random.shuffle:

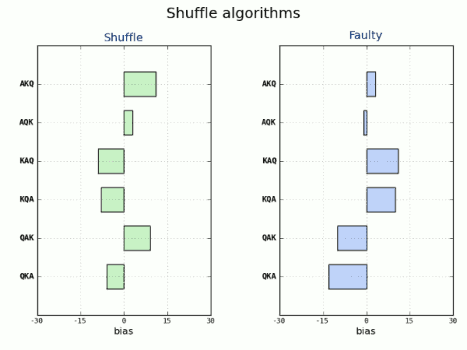
Como podemos ver las desviaciones del valor ideal son muy similares y con una desviación media muy parecida, ±2.130% para shuffle y ±2.222% para nuestro algoritmo, faulty. Y creeríamos erróneamente que nuestro algoritmo funcionaría correctamente. Pero es que para comprobar que no haya tendencia alguna es necesario ejecutarlo, muchas, pero muchas veces (por encima de los cientos de miles), ya que a mayor número de repeticiones, más se manifiestan esas tendencias. Al mismo tiempo, cuantos más elementos tenga la lista, mayores son las desviaciones y la tendencia. Además, con este número de ejecuciones aún no observamos las tendencias reales que se manifestarán luego en lo sucesivo. Veamos unos ejemplos para 2.400.000 ejecuciones para nuestra lista de tres cartas y para otra a la que hemos añadido la Sota (Jack).

En el gráfico de la izquierda ya se muestran claramente las diferencias, mientras la función shuffle varía entre -741 y +668 (sobre 400.000) con una desviación media de ±0.017%, nuestra función tiene una desviación media de ±1.869% (~110 veces superior) y varia entre -46.062 y +46.090. Como podemos ver es una autentica barbaridad. El gráfico de la derecha, nos confirma que a mayor número de elementos en la lista, mayores aún son las tendencias. Mientras que shuffle se sigue comportando correctamente con una desviación media de ±0.009% y varía entre -486 y +427 (sobre 100.000), nuestro pobre algoritmo se desmanda completamente, variando entre +31.326 y -25.254, una desviación media de ±0.541% (~61 veces más). Hay que tener en cuenta, que al ser mayor número de cartas, son 24 permutaciones, lo que nos da unas 4 veces menos repeticiones por permutación, es decir, que para tener el mismo número tendríamos que hacer 9.600.00 ejecuciones. Y como podemos ver, los resultados no son cuatro veces mejores, ni mucho menos, además sabemos que la tendencia se acentúa con el número de ejecuciones. Viendo estos resultados vemos claramente que determinadas permutaciones tienen muy pocas probabilidades de salir, cuando otras son altamente predecibles.

¿Entiendes ahora porqué no debes fiarte únicamente de tu instinto?

Vamos a conocer ahora los algoritmos que funcionan, están matemáticamente comprobados y son sobradamente conocidos (aunque a la vista está que no lo suficiente).

Fisher-Yates

Este algoritmo fue desarrollado por Ronald Fisher y Frank Yates en 1938² como un método a realizar con lápiz y papel. Para ello empleaban una tabla de números aleatorios calculada anteriormente para generar la aleatoriedad que necesitaban para el algoritmo. Este algoritmo esta comprobado matemáticamente y funciona correctamente siempre que la fuente de aleatoriedad sea completamente aleatoria. No deja de ser curioso, que un algoritmo que fue creado hace más de 70 años y que sigue actualmente vigente y presente en multitud de aplicaciones, sea al mismo tiempo desconocido por muchos desarrolladores, lo que les lleva a cometer los errores que comentaba anteriormente al implementar los suyos propios. Por eso como programadores deberíamos ser humildes y procurar no inventar siempre lo ya inventado y buscar siempre una solución previa para nuestros propósitos. Y probar, probar y volver a probar nuestro código...

La típica implementación del algoritmo en Python sería así:

def fisher_yates(lst):
    "Python implementation of the original Fisher-Yates algorithm."
    if len(lst) > 1:
        idx = len(lst) - 1
        while idx > 0:
            sel = random.randint(0, idx)
            lst[idx], lst[sel] = lst[sel], lst[idx]
            idx -= 1

Knuth-Durstenfeld

Este algoritmo es en realidad una variante del Fisher-Yates y fue publicado originalmente por Richard Durstenfeld en 1964³, pero fue popularizado por el genial Donald Knuth en el volumen 2 de su gran obra, The Art of Computer Programming, como el algoritmo P⁴. De ahí que sea generalmente conocido como Knuth-Durstenfeld o simplemente como Knuth Shuffle. Aunque curiosamente ninguno de los dos conocía anteriormente el trabajo previo de Fisher y Yates. Este algoritmo se ejecuta en tiempo polinómico lineal O(n), por lo que es muy eficiente.

Implementado en Python, sería algo así:

def knuth_durstenfeld(lst):
    "Python implementation of the Durstenfeld algorithm popularized by Knuth."
    for idx in reversed(range(1, len(lst))):
        # pick an element in lst[:idx+1] with which to exchange lst[idx]
        sel = random.randrange(idx + 1)
        lst[idx], lst[sel] = lst[sel], lst[idx]

Este algoritmo es el que está detrás de la función random.shuffle que hemos venido usando desde el principio del articulo. Lógicamente si está empleando el mejor algoritmo hasta la fecha, es absurdo implementar el nuestro propio cuando podemos usar esta función estándar de Python. De hecho el código de esta función es el siguiente:

def shuffle(self, x, random=None, int=int):
    """x, random=random.random -> shuffle list x in place; return None.

    Optional arg random is a 0-argument function returning a random
    float in [0.0, 1.0); by default, the standard random.random.
    """

    if random is None:
        random = self.random
    for i in reversed(xrange(1, len(x))):
        # pick an element in x[:i+1] with which to exchange x[i]
        j = int(random() * (i+1))
        x[i], x[j] = x[j], x[i]

Que como podemos ver, el algoritmo es el Knuth Shuffle.

A tener en cuenta

Conviene tener en cuenta una cosa, todos estos algoritmos modifican la propia lista in-place, es decir que no crean una nueva, y por lo tanto no devuelven ningún valor. Por lo tanto, no puedes asignar el resultado de una de estas operaciones a una variable, porque por defecto devuelven None. Es un error muy común, de hecho Mark Lutz lo define en su libro "Learning Python" como uno de los Common Coding Gotchas, es decir, uno de los errores más comunes en Python. Y dice claramente (pág. 388, cap. 15)

Don’t expect results from functions that change objects in-place

No esperes resultados desde funciones que cambien objetos en el sitio (sin crear nuevos objetos modificados). Y pone como ejemplos los métodos append, sort y reverse en listas.

Para verlo aún más claro, nada mejor que verlo con un ejemplo:

>>> from random import shuffle
>>> lista = [1,2,3]
>>> id(lista)  # Obtenemos el id del objeto (todo en Python es un objeto)
3077959916L
>>> shuffle(lista)
>>> lista      # La lista ya aparece barajada
[2, 3, 1]
>>> id(lista)  # Sin embargo vemos que el identificador es el mismo
3077959916L
>>> variable = shuffle(lista)  # Esto no tiene sentido, porque no se devuelve nada
>>> variable
>>> print(shuffle(lista))  # Aquí vemos que la función devuelve None
None
>>> id(lista)
3077959916L
>>> lista
[1, 3, 2]
>>>

En esta gráfica vemos los tres algoritmos comparados, los he ejecutado solamente 48.000 veces, para apreciar mejor las diferencias entre ellos.

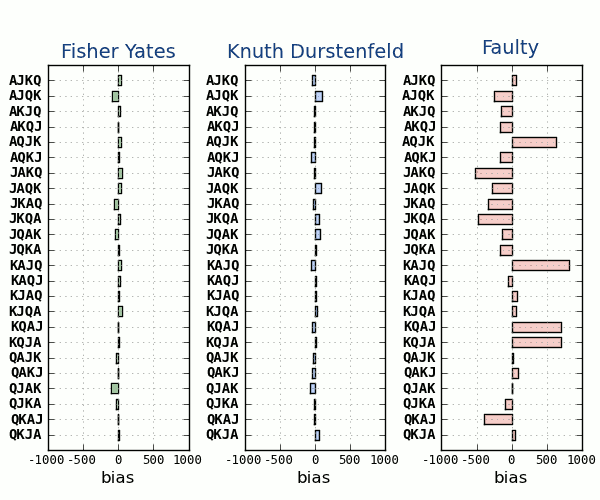
Las desviaciones medias son de ±0.068% para Fisher-Yates, ±0.069% para Knuth-Durstenfeld y de ±0.554% para Faulty.

Sattolo-Cycle

Este algoritmo es muy parecido a los anteriores, pero con una significativa diferencia, este algoritmo solo genera ciclos, de ahí su nombre. Es decir, reparte uniformemente los resultados solo entre algunas permutaciones que se van rotando (aunque comparte el mismo problema con los anteriores al depender de una aleatoriedad no perfecta). Para resumir su funcionamiento, lo que hace es que después de ejecutarlo, ningún elemento de la lista repite la posición anterior que tenía en la misma. Ese algoritmo fue publicado por Sandra Sattolo en 1986

El algoritmo en Python:

def sattolo_cycle(lst):
    "Python implementation of the original Sattolo Cycle algorithm."
    idx = len(lst)
    while idx > 1:
        idx = idx - 1
        sel = random.randrange(idx)  # 0 <= sel <= idx-1
        lst[sel], lst[idx] = lst[idx], lst[sel]
    return

Podemos ver aquí un ejemplo de su funcionamiento al ejecutarlo sucesivamente sobre la misma lista, sin partir siempre de la misma permutación, para comprobar como ningún elemento conserva su posición anterior.

lista = ['A', 'K', 'Q']
>>> for i in range(12):
...     sattolo_cycle(lista)
...     print(lista)
...
['K', 'Q', 'A']
['A', 'K', 'Q']
['K', 'Q', 'A']
['A', 'K', 'Q']
['Q', 'A', 'K']
['A', 'K', 'Q']
['K', 'Q', 'A']
['Q', 'A', 'K']
['K', 'Q', 'A']
['Q', 'A', 'K']
['K', 'Q', 'A']
['Q', 'A', 'K']
>>>

El código de estos algoritmos y los test de rendimiento se encuentran en el fichero shuffle.py de mi repositorio Python Recipes que se encuentra en github

Aunque estos algoritmos no tienen un funcionamiento perfecto, debido al generador de números pseudoaleatorios, son validos para la mayoría de las aplicaciones para las que son necesarios, digamos que son lo suficientemente buenos para las aplicaciones prácticas de los mismos.

Otras fuentes para saber más

The Danger of Naïveté, Jeff Atwood
Shuffling, Jeff Atwood
Computers are lousy random numbers generators, Jeff Atwood
The intuition behind Fisher-Yates shuffling, Eli Bendersky
Ramdom.org