DBSCAN Clustering

DBSCAN(Density-Based Spatial Clustering of Applications with Noise) is the most well-known density-based clustering algorithm, first introduced in 1996 by Ester et. al. Due to its importance in both theory and applications, this algorithm is one of three algorithms awarded the Test of Time Award at SIGKDD 2014.

Unlike K-Means, DBSCAN does not require the number of clusters as a parameter. Rather it infers the number of clusters based on the data, and it can discover clusters of arbitrary shape (for comparison, K-Means usually discovers spherical clusters). As I said earlier, the ɛ-neighborhood is fundamental to DBSCAN to approximate local density, so

The algorithm has two parameters:

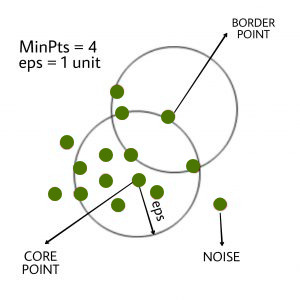
• eps : It defines the neighborhood around a data point i.e. if the distance between two points is lower or equal to ‘eps’ then they are considered as neighbors. If the eps value is chosen too small then large part of the data will be considered as outliers. If it is chosen very large then the clusters will merge and majority of the data points will be in the same clusters. One way to find the eps value is based on the k-distance graph.
• minPts : The minimum number of data points we want in a neighborhood to define a cluster.

Using these two parameters, DBSCAN categories the data points into three categories:

• Core Points: A point is a core point if it has more than MinPts points within eps.
• Border Points:A point which has fewer than MinPts within eps but it is in the neighborhood of a core point.
• Outlier: A data point o is an outlier if it is neither a core point nor a border point. Essentially, this is the “other” class.

DBSCAN algorithm can be abstracted in the following steps:

1. Find all the neighbor points within eps and identify the core points or visited with more than MinPts neighbors.
2. For each core point if it is not already assigned to a cluster, create a new cluster.
3. Find recursively all its density connected points and assign them to the same cluster as the core point.



A point a and b are said to be density connected if there exist a point c which has a sufficient number of points in its neighbors and both the points a and b are within the eps distance. This is a chaining process. So, if b is neighbor of c, c is neighbor of d, d is neighbor of e, which in turn is neighbor of a implies that b is neighbor of a.



4. Iterate through the remaining unvisited points in the dataset. Those points that do not belong to any cluster are noise.