Graph Coloring

Graph coloring is a fundamental concept in graph theory that involves assigning colors to the vertices of a graph in such a way that no two adjacent vertices share the same color. The goal is to use the minimum number of colors while satisfying this constraint. Graph coloring has applications in various fields, including scheduling problems, map coloring, register allocation in compilers, and task assignment.

Studying graph coloring has provided me with an understanding of how to assign colors to vertices of a graph while avoiding conflicts. I have learned about different coloring algorithms, such as greedy coloring and backtracking algorithms, which aim to find the minimum number of colors required to color a graph. Additionally, I have learned about the concept of chromatic number, which represents the minimum number of colors needed to color a graph. Understanding graph coloring has given me insights into solving practical problems that involve allocating resources, scheduling tasks, or assigning colors to regions on maps.

Rules in Graph Coloring:

1. No Adjacent Vertices Have the Same Color:
The primary rule in graph coloring is that no two adjacent vertices (connected by an edge) can be assigned the same color. This ensures that neighboring vertices are distinguishable and avoids conflicts in the coloring scheme.

2. Minimum Number of Colors:
The objective in graph coloring is to use the minimum number of colors necessary to color all the vertices in the graph. This means finding the smallest possible number of colors required to satisfy the first rule while ensuring that no adjacent vertices share the same color.

3. Choice of Colors:
The choice of colors used for vertex coloring is typically represented by integers or distinct labels. In practice, colors can be represented by numbers, names, or any other distinct symbols that can differentiate between vertices.

4. Coloring Constraints:
In some cases, additional constraints or rules may be imposed based on the specific problem being addressed. For example, in map coloring, regions with a shared boundary may have restrictions on the colors they can be assigned to, such as avoiding adjacent regions having the same color.

5. Chromatic Number:
The chromatic number of a graph represents the minimum number of colors required to properly color the graph. It is denoted by the symbol χ(G), where G is the graph. The chromatic number is a fundamental property of a graph and provides a measure of its colorability.

Examples of Chromatic Number

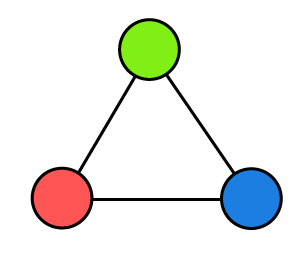
In the above cycle graph, there are 3 different colors for three vertices, and none of the adjacent vertices are colored with the same color. In this graph, the number of vertices is odd. Thus,
Chromatic number = 3

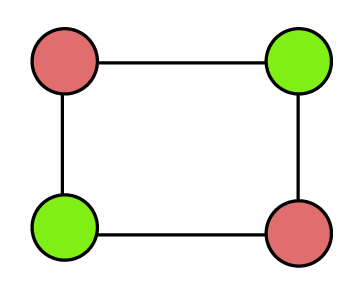
In the above cycle graph, there are 2 colors for four vertices, and none of the adjacent vertices are colored with the same color. In this graph, the number of vertices is even. Thus,
Chromatic number = 2

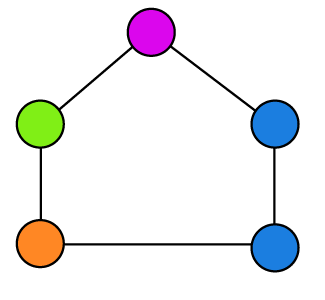
In the above graph, there are 4 different colors for five vertices, and two adjacent vertices are colored with the same color (blue). So this graph is not a cycle graph and does not contain a chromatic number.