Graphs and Graph Models

Graph theory is a branch of mathematics that deals with the study of graphs, which are mathematical structures composed of vertices (also called nodes) and edges (connections between vertices). Graphs provide a powerful framework for representing and analyzing relationships, connections, and dependencies between objects or entities. Graph models are used in various fields, including computer science, social networks, transportation systems, and data analysis, to solve problems related to connectivity, optimization, network analysis, and decision-making.

Studying graphs and graph models has provided me with a deep understanding of the properties and applications of these mathematical structures. I have learned about different types of graphs, such as directed graphs, undirected graphs, weighted graphs, and bipartite graphs, and their corresponding representations. Additionally, I have learned about various graph algorithms and techniques, such as breadth-first search (BFS), depth-first search (DFS), shortest path algorithms (e.g., Dijkstra's algorithm), and spanning tree algorithms (e.g., Prim's algorithm). Understanding graphs and graph models has enabled me to analyze complex systems, identify patterns, optimize routes, solve connectivity problems, and make informed decisions based on the underlying relationships and dependencies within a given problem domain.

5 Graphs Models

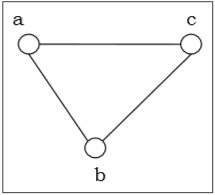
1. Undirected Graph

An undirected graph is a graph where edges have no specific direction. The relationships between vertices are symmetrical, meaning that if vertex A is connected to vertex B, then vertex B is also connected to vertex A. Undirected graphs are used to represent relationships that are mutual, such as friendships in a social network.

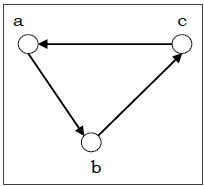
2. Directed Graph (Digraph)

A directed graph, or digraph, is a graph where edges have a specific direction. The relationships between vertices are asymmetric, meaning that if vertex A is connected to vertex B, it does not imply that vertex B is connected to vertex A. Directed graphs are used to represent relationships with a one-way flow, such as web page links or dependencies in a directed acyclic graph (DAG).

3. Weighted Graph

A weighted graph is a graph where edges have associated weights or costs. These weights can represent various attributes, such as distances, travel times, or costs between vertices. Weighted graphs are used in applications like route optimization, network flow analysis, and resource allocation.

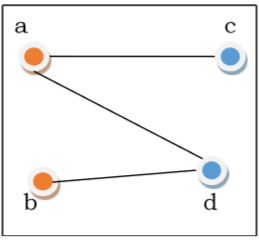
4. Bipartite Graph

A bipartite graph is a graph whose vertex set can be divided into two disjoint sets such that there are no edges connecting vertices within the same set. In other words, every edge connects a vertex from one set to a vertex in the other set. Bipartite graphs are used to model relationships between two distinct groups, such as matching students with internships or assigning tasks to workers.

5. Complete Graph

A complete graph is a graph where there is an edge between every pair of distinct vertices. In other words, every vertex is connected directly to every other vertex. Complete graphs are used in combinatorial problems, network analysis, and algorithms for their well-defined structure and properties.

These are just a few examples of the many types of graph models used in various fields. Each type has its own characteristics and applications, making graphs a versatile and powerful tool for modeling and analyzing relationships and dependencies in real-world scenarios.