14.2 Ex: One-way ANOVA
Let’s do an example by running both a one-way ANOVA on the poopdeck data. We’ll set cleaning time time as the dependent variable and the cleaner type cleaner as the independent variable. We can represent the data as a pirateplot:
yarrr::pirateplot(time ~ cleaner,
data = poopdeck,
theme = 2,
cap.beans = TRUE,
main = "formula = time ~ cleaner")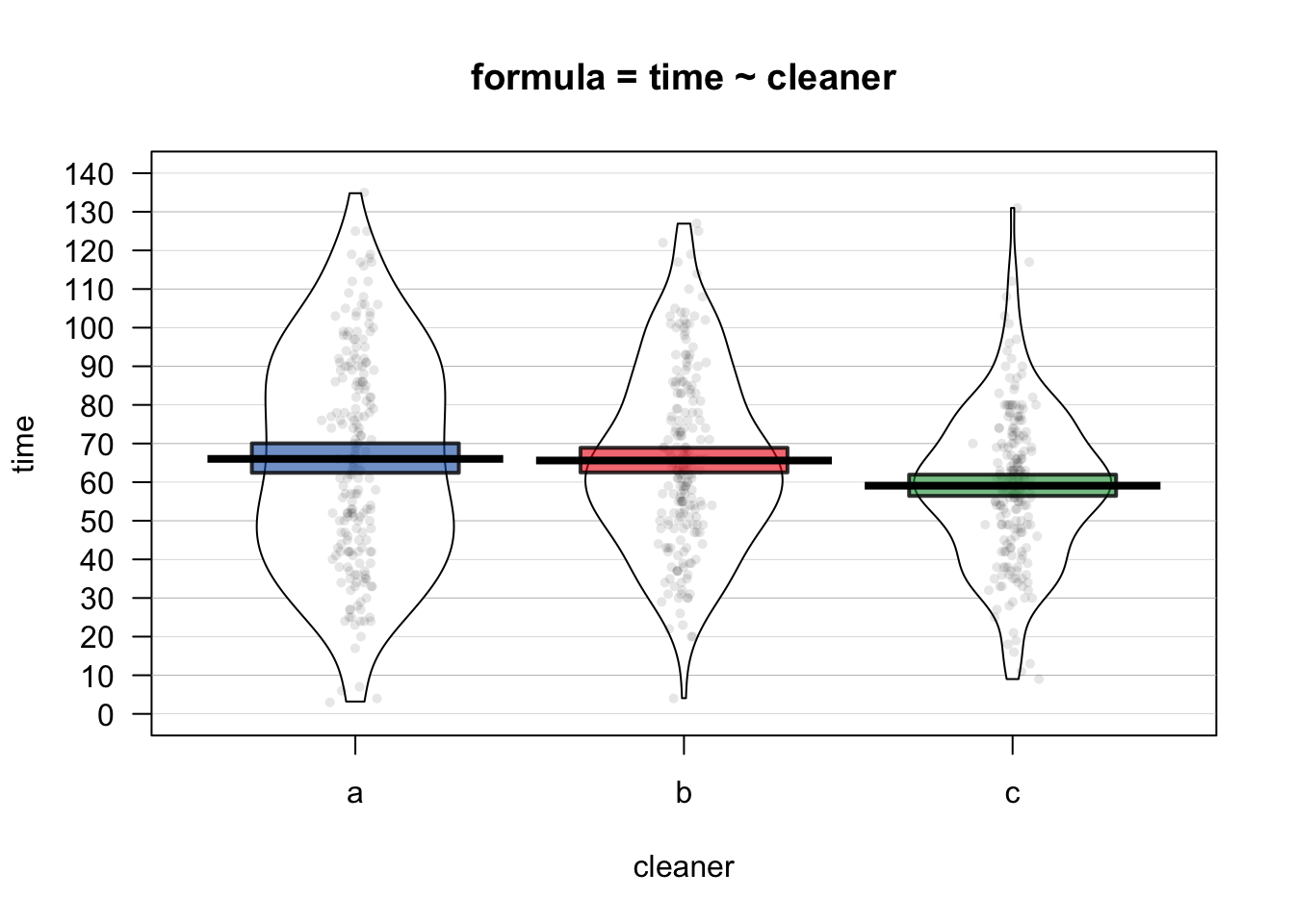
From the plot, it looks like cleaners a and b are the same, and cleaner c is a bit faster. To test this, we’ll create an ANOVA object with aov. Because time is the dependent variable and cleaner is the independent variable, we’ll set the formula to formula = time ~ cleaner
# Step 1: aov object with time as DV and cleaner as IV
cleaner.aov <- aov(formula = time ~ cleaner,
data = poopdeck)Now, to see a full ANOVA summary table of the ANOVA object, apply the summary() to the ANOVA object from Step 1.
# Step 2: Look at the summary of the anova object
summary(cleaner.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## cleaner 2 6057 3028 5.29 0.0053 **
## Residuals 597 341511 572
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The main result from our table is that we have a significant effect of cleaner on cleaning time (F(2, 597) = 5.29, p = 0.005. However, the ANOVA table does not tell us which levels of the independent variable differ. In other words, we don’t know which cleaner is better than which. To answer this, we need to conduct a post-hoc test.
If you’ve found a significant effect of a factor, you can then do post-hoc tests to test the difference between each all pairs of levels of the independent variable. There are many types of pairwise comparisons that make different assumptions. To learn more about the logic behind different post-hoc tests, check out the Wikipedia page here: https://en.wikipedia.org/wiki/Post_hoc_analysis. One of the most common post-hoc tests for standard ANOVAs is the Tukey Honestly Significant Difference (HSD) test. To see additional information about the Tukey HSD test, check out the Wikipedia page here: https://en.wikipedia.org/wiki/Tukey’s_range_test To do an HSD test, apply the TukeyHSD() function to your ANOVA object as follows:
# Step 3: Conduct post-hoc tests
TukeyHSD(cleaner.aov)
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = time ~ cleaner, data = poopdeck)
##
## $cleaner
## diff lwr upr p adj
## b-a -0.42 -6 5.2 0.98
## c-a -6.94 -13 -1.3 0.01
## c-b -6.52 -12 -0.9 0.02This table shows us pair-wise differences between each group pair. The diff column shows us the mean differences between groups (which thankfully are identical to what we found in the summary of the regression object before), a confidence interval for the difference, and a p-value testing the null hypothesis that the group differences are not different.
I almost always find it helpful to combine an ANOVA summary table with a regression summary table. Because ANOVA is just a special case of regression (where all the independent variables are factors), you’ll get the same results with a regression object as you will with an ANOVA object. However, the format of the results are different and frequently easier to interpret.
To create a regression object, use the lm() function. Your inputs to this function will be identical to your inputs to the aov() function
# Step 4: Create a regression object
cleaner.lm <- lm(formula = time ~ cleaner,
data = poopdeck)
# Show summary
summary(cleaner.lm)
##
## Call:
## lm(formula = time ~ cleaner, data = poopdeck)
##
## Residuals:
## Min 1Q Median 3Q Max
## -63.02 -16.60 -1.05 16.92 71.92
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 66.02 1.69 39.04 <2e-16 ***
## cleanerb -0.42 2.39 -0.18 0.8607
## cleanerc -6.94 2.39 -2.90 0.0038 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 24 on 597 degrees of freedom
## Multiple R-squared: 0.0174, Adjusted R-squared: 0.0141
## F-statistic: 5.29 on 2 and 597 DF, p-value: 0.00526As you can see, the regression table does not give us tests for each variable like the ANOVA table does. Instead, it tells us how different each level of an independent variable is from a default value. You can tell which value of an independent variable is the default variable just by seeing which value is missing from the table. In this case, I don’t see a coefficient for cleaner a, so that must be the default value.
The intercept in the table tells us the mean of the default value. In this case, the mean time of cleaner a was 66.02. The coefficients for the other levels tell us that cleaner b is, on average 0.42 minutes faster than cleaner a, and cleaner c is on average 6.94 minutes faster than cleaner a. Not surprisingly, these are the same differences we saw in the Tukey HSD test!
##Ex: Two-way ANOVA
To conduct a two-way ANOVA or a Menage a trois NOVA, just include additional independent variables in the regression model formula with the + sign. That’s it. All the steps are the same. Let’s conduct a two-way ANOVA with both cleaner and type as independent variables. To do this, we’ll set formula = time ~ cleaner + type.
# Step 1: Create ANOVA object with aov()
cleaner.type.aov <- aov(formula = time ~ cleaner + type,
data = poopdeck)# Step 2: Get ANOVA table with summary()
summary(cleaner.type.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## cleaner 2 6057 3028 6.94 0.001 **
## type 1 81620 81620 187.18 <2e-16 ***
## Residuals 596 259891 436
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1It looks like we found significant effects of both independent variables.
# Step 3: Conduct post-hoc tests
TukeyHSD(cleaner.type.aov)
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = time ~ cleaner + type, data = poopdeck)
##
## $cleaner
## diff lwr upr p adj
## b-a -0.42 -5.3 4.5 0.98
## c-a -6.94 -11.8 -2.0 0.00
## c-b -6.52 -11.4 -1.6 0.01
##
## $type
## diff lwr upr p adj
## shark-parrot 23 20 27 0The only non-significant group difference we found is between cleaner b and cleaner a. All other comparisons were significant.
# Step 4: Look at regression coefficients
cleaner.type.lm <- lm(formula = time ~ cleaner + type,
data = poopdeck)
summary(cleaner.type.lm)
##
## Call:
## lm(formula = time ~ cleaner + type, data = poopdeck)
##
## Residuals:
## Min 1Q Median 3Q Max
## -59.74 -13.79 -0.68 13.58 83.58
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 54.36 1.71 31.88 < 2e-16 ***
## cleanerb -0.42 2.09 -0.20 0.84067
## cleanerc -6.94 2.09 -3.32 0.00094 ***
## typeshark 23.33 1.71 13.68 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 21 on 596 degrees of freedom
## Multiple R-squared: 0.252, Adjusted R-squared: 0.248
## F-statistic: 67 on 3 and 596 DF, p-value: <2e-16Now we need to interpret the results in respect to two default values (here, cleaner = a and type = parrot). The intercept means that the average time for cleaner a on parrot poop was 54.36 minutes. Additionally, the average time to clean shark poop was 23.33 minutes slower than when cleaning parrot poop.
14.2.1 ANOVA with interactions
Interactions between variables test whether or not the effect of one variable depends on another variable. For example, we could use an interaction to answer the question: Does the effect of cleaners depend on the type of poop they are used to clean? To include interaction terms in an ANOVA, just use an asterix (*) instead of the plus (+) between the terms in your formula. Note that when you include an interaction term in a regression object, R will automatically include the main effects as well/
Let’s repeat our previous ANOVA with two independent variables, but now we’ll include the interaction between cleaner and type. To do this, we’ll set the formula to time ~ cleaner * type.
# Step 1: Create ANOVA object with interactions
cleaner.type.int.aov <- aov(formula = time ~ cleaner * type,
data = poopdeck)
# Step 2: Look at summary table
summary(cleaner.type.int.aov)
## Df Sum Sq Mean Sq F value Pr(>F)
## cleaner 2 6057 3028 7.82 0.00044 ***
## type 1 81620 81620 210.86 < 2e-16 ***
## cleaner:type 2 29968 14984 38.71 < 2e-16 ***
## Residuals 594 229923 387
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Looks like we did indeed find a significant interaction between cleaner and type. In other words, the effectiveness of a cleaner depends on the type of poop it’s being applied to. This makes sense given our plot of the data at the beginning of the chapter.
To understand the nature of the difference, we’ll look at the regression coefficients from a regression object:
# Step 4: Calculate regression coefficients
cleaner.type.int.lm <- lm(formula = time ~ cleaner * type,
data = poopdeck)
summary(cleaner.type.int.lm)
##
## Call:
## lm(formula = time ~ cleaner * type, data = poopdeck)
##
## Residuals:
## Min 1Q Median 3Q Max
## -54.28 -12.83 -0.08 12.29 74.87
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 45.76 1.97 23.26 < 2e-16 ***
## cleanerb 8.06 2.78 2.90 0.00391 **
## cleanerc 10.37 2.78 3.73 0.00021 ***
## typeshark 40.52 2.78 14.56 < 2e-16 ***
## cleanerb:typeshark -16.96 3.93 -4.31 1.9e-05 ***
## cleanerc:typeshark -34.62 3.93 -8.80 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 20 on 594 degrees of freedom
## Multiple R-squared: 0.338, Adjusted R-squared: 0.333
## F-statistic: 60.8 on 5 and 594 DF, p-value: <2e-16Again, to interpret this table, we first need to know what the default values are. We can tell this from the coefficients that are ‘missing’ from the table. Because I don’t see terms for cleanera or typeparrot, this means that cleaner = "a" and type = "parrot" are the defaults. Again, we can interpret the coefficients as differences between a level and the default. It looks like for parrot poop, cleaners b and c both take more time than cleaner a (the default). Additionally, shark poop tends to take much longer than parrot poop to clean (the estimate for typeshark is positive).
The interaction terms tell us how the effect of cleaners changes when one is cleaning shark poop. The negative estimate (-16.96) for cleanerb:typeshark means that cleaner b is, on average 16.96 minutes faster when cleaning shark poop compared to parrot poop. Because the previous estimate for cleaner b (for parrot poop) was just 8.06, this suggests that cleaner b is slower than cleaner a for parrot poop, but faster than cleaner a for shark poop. Same thing for cleaner c which simply has stronger effects in both directions.