Graph Data Stucture

A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges.
Formally, a graph is a pair of sets (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph −

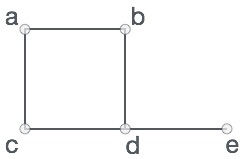
In the above graph,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}

Important Terminology

1. Vertex − Each node of the graph is represented as a vertex. In the following example, the labeled circle represents vertices. Thus, A to G are vertices. We can represent them using an array as shown in the following image. Here A can be identified by index 0. B can be identified using index 1 and so on.
2.Edge − Edge represents a path between two vertices or a line between two vertices. In the following example, the lines from A to B, B to C, and so on represents edges. We can use a two-dimensional array to represent an array as shown in the following image. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.
3.Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
4.Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.

Operations

Following are basic primary operations of a Graph −

• Add Vertex − Adds a vertex to the graph.
• Add Edge − Adds an edge between the two vertices of the graph.
• Display Vertex − Displays a vertex of the graph.

DFS(Depth First Search)

Because of the recursive nature, stack data structure can be used to implement the DFS algorithm

The step by step process to implement the DFS traversal is given as follows -
First, create a stack with the total number of vertices in the graph.
Now, choose any vertex as the starting point of traversal, and push that vertex into the stack.
After that, push a non-visited vertex (adjacent to the vertex on the top of the stack) to the top of the stack.
Now, repeat steps 3 and 4 until no vertices are left to visit from the vertex on the stack's top.
If no vertex is left, go back and pop a vertex from the stack.
Repeat steps 2, 3, and 4 until the stack is empty.

Pseudocode

DFS(G,v) ( v is the vertex where the search starts )
Stack S := {}; ( start with an empty stack )
for each vertex u, set visited[u] := false;
push S, v;
while (S is not empty) do
u := pop S;
if (not visited[u]) then
visited[u] := true;
for each unvisited neighbour w of uu
push S, w;
end if
end while
END DFS()

BFS(Breadth First Search)

There are many ways to traverse the graph, but among them, BFS is the most commonly used approach. It is a recursive algorithm to search all the vertices of a tree or graph data structure. BFS puts every vertex of the graph into two categories - visited and non-visited. It selects a single node in a graph and, after that, visits all the nodes adjacent to the selected node.

The steps involved in the BFS algorithm to explore a graph are given as follows -

Step 1: SET STATUS = 1 (ready state) for each node in G
Step 2: Enqueue the starting node A and set its STATUS = 2 (waiting state)
Step 3: Repeat Steps 4 and 5 until QUEUE is empty
Step 4: Dequeue a node N. Process it and set its STATUS = 3 (processed state).
Step 5: Enqueue all the neighbours of N that are in the ready state (whose STATUS = 1) and set
their STATUS = 2
(waiting state)
[END OF LOOP]
Step 6: EXIT