Heap

Heap data structure is a complete binary tree that satisfies the heap property.

Complete Binary Tree

A complete binary tree is a binary tree in which all the levels except the last level, i.e., leaf node should be completely filled, and all the nodes should be left-justified.

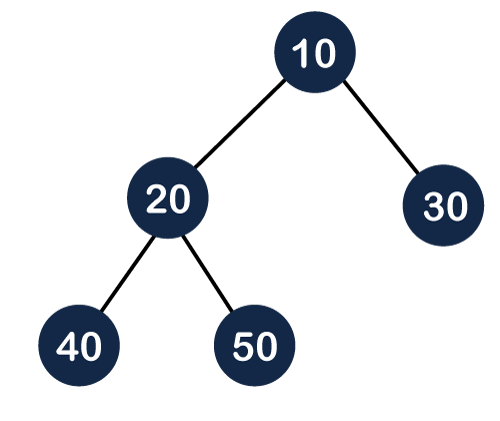
Types of Heap

1.Max Heap->The node is always greater than its child node/s and the key of the root node is the largest among all other nodes. This property is also called max heap property.

The above tree is a max heap tree as it satisfies the property of the max heap. Now, let's see the array representation of the max heap.

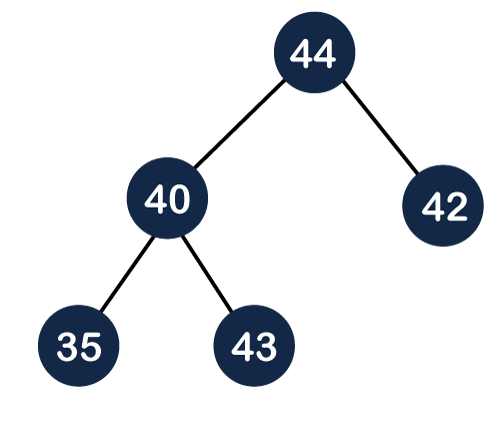2.Min Heap->The node is always smaller than the child node/s and the key of the root node is the smallest among all other nodes. This property is also called min heap property.

In the above figure, 11 is the root node, and the value of the root node is less than the value of all the other nodes (left child or a right child).

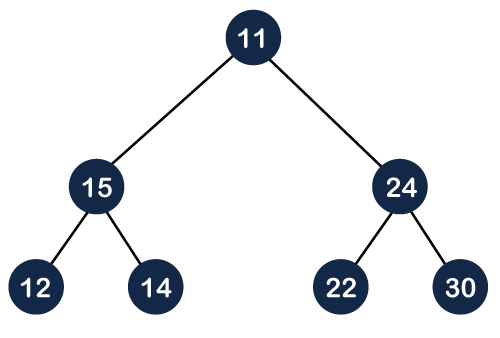
Insertion in Max Heap

// algorithm to insert an element in the max heap.
insertHeap(A, n, value)
{
n=n+1; // n is incremented to insert the new element
A[n]=value; // assign new value at the nth position
i = n; // assign the value of n to i
// loop will be executed until i becomes 1.
while(i>1)
{
parent= floor value of i/2; // Calculating the floor value of i/2
// Condition to check whether the value of parent is less than the given node or not
if(A[parent]<A[i])
{
swap(A[parent], A[i]);
i = parent;
}
else
{
return;
} } }

Heap Operations

Some of the important operations performed on a heap are described below along with their algorithms.

Heapify

Heapify is the process of creating a heap data structure from a binary tree. It is used to create a Min-Heap or a Max-Heap.

Algorithm to heapify the tree

MaxHeapify(A, n, i)
{
int largest =i;
int l= 2i;
int r= 2i+1;
while(l<=n && A[l]>A[largest])
{
largest=l;
}
while(r<=n && A[r]>A[largest])
{
largest=r;
}
if(largest!=i)
{
swap(A[largest], A[i]);
heapify(A, n, largest);
}}

Delete Element from Heap

Algorithm for deletion in Max Heap

If nodeToBeDeleted is the leafNode
remove the node
Else swap nodeToBeDeleted with the lastLeafNode
remove noteToBeDeleted
heapify the array

Peek (Find max/min)

Peek operation returns the maximum element from Max Heap or minimum element from Min Heap without deleting the node.

For both Max heap and Min Heap

return rootNode

Heap Data Structure Applications

1.Heap is used while implementing a priority queue.
2.Dijkstra's Algorithm
3.Heap Sort