Binary Tree

A tree is non-linear and a hierarchical data structure consisting of a collection of nodes such that each node of the tree stores a value, a list of references to nodes (the “children”).
Binary Tree is a special datastructure used for data storage purposes. A binary tree has a special condition that each node can have a maximum of two children. A binary tree has the benefits of both an ordered array and a linked list as search is as quick as in a sorted array and insertion or deletion operation are as fast as in linked list.

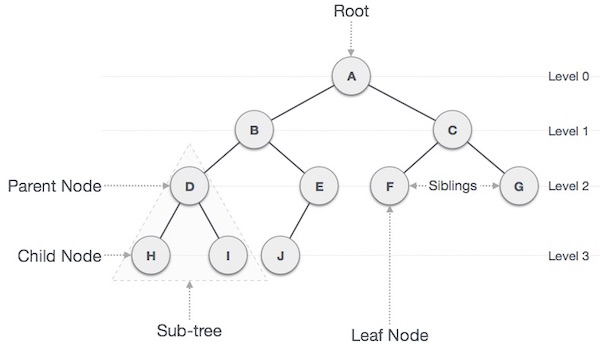
Important Terms

Following are the important terms with respect to tree.

• Path: Path refers to the sequence of nodes along the edges of a tree.
• Root: The node at the top of the tree is called root. There is only one root per tree and one path from the root node to any node.
• Parent: Any node except the root node has one edge upward to a node called parent.
• Child: The node below a given node connected by its edge downward is called its child node.
• Leaf: The node which does not have any child node is called the leaf node.
• Subtree: Subtree represents the descendants of a node.
• Visiting: Visiting refers to checking the value of a node when control is on the node.
• Traversing: Traversing means passing through nodes in a specific order.
• Levels: Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
• keys: Key represents a value of a node based on which a search operation is to be carried out for a node.

Binary Search Tree

Binary Search tree exhibits a special behavior. A node's left child must have a value less than its parent's value and the node's right child must have a value greater than its parent value.

Node Representation

struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};

Basic Operations On BST

The basic operations that can be performed on a binary search tree data structure, are the following:

• Insert: Inserts an element in a tree/create a tree.
• Search: Searches an element in a tree.
• Preorder Traversal: Traverses a tree in a pre-order manner.
• Inorder Traversal: Traverses a tree in an in-order manner.
• Postorder Traversal: Traverses a tree in a post-order manner.

Insert Operation

The very first insertion creates the tree. Afterwards, whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.

Implementation

void insert(int data) {
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty, create root node if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}
//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}

Search Operation

Whenever an element is to be searched, start searching from the root node, then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.

Implementation

struct node* search(int data) {
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data) {
if(current != NULL)
printf("%d ",current->data);
//go to left tree
if(current->data > data) {
current = current->leftChild;
}
//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
return current;
}
}

Traversal

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −

• In-order Traversal
• Pre-order Traversal
• Post-order Traversal

In-order Traversal

In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.
If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.

ALGORITHM

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.

Pre-order Traversal

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

ALGORITHM

Until all nodes are traversed −
Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.

Post-order Traversal

In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.

ALGORITHM

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.

Output of all traversals

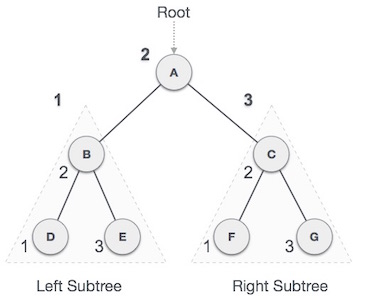
Inorder Traversal-> D → B → E → A → F → C → G

Pre-order Traversal-> A → B → D → E → C → F → G

Post-order Traversal-> D → E → B → F → G → C → A